Given a finite group G with a normal subgroup N, the simple graph 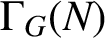$\Gamma _{\textit {G}}( \textit {N} )$ is a graph whose vertices are of the form 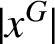$|x^G|$ , where 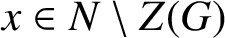$x\in {N\setminus {Z(G)}}$ and 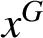$x^G$ is the G-conjugacy class of N containing the element x. Two vertices 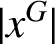$|x^G|$ and 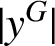$|y^G|$ are adjacent if they are not coprime. We prove that, if 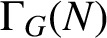$\Gamma _G(N)$ is a connected incomplete regular graph, then 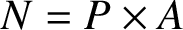$N= P \times {A}$ where P is a p-group, for some prime p, 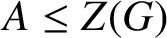$A\leq {Z(G)}$ and 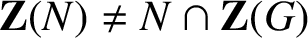$\textbf {Z}(N)\not = N\cap \textbf {Z}(G)$ .