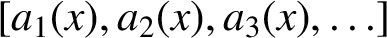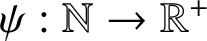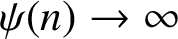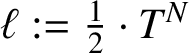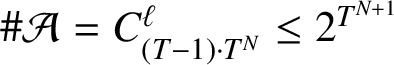1 Introduction
Continued fraction expansions can be defined in terms of the Gauss transformation
$T:[0,1)\rightarrow [0,1)$
given by
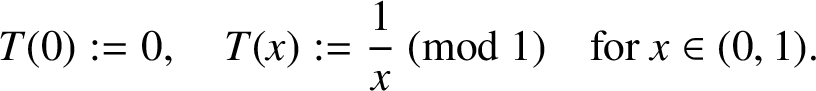$$ \begin{align*} T(0):=0, \quad T(x):=\frac{1}{x} \pmod 1 \quad\text{for } x\in(0,1). \end{align*} $$
Let
$a_{1}(x)=\lfloor x^{-1}\rfloor $
(where
$\lfloor \cdot \rfloor $
stands for the integer part) and
$a_{n}(x)=a_{1}(T^{n-1}(x))$
for
$n\geq 2$
. Every irrational number
$x\in [0,1)$
can be uniquely expanded into its infinite continued fraction expansion:
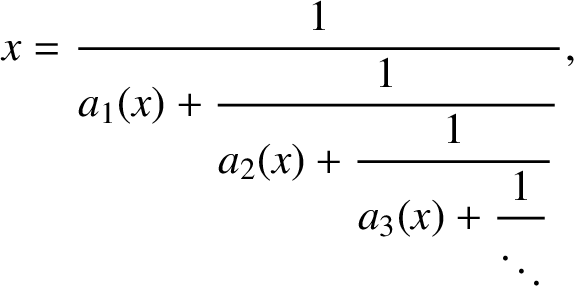$$ \begin{align*} x=\frac{\displaystyle1}{\displaystyle a_1(x)+\frac{\displaystyle1}{\displaystyle a_2(x)+ \frac{\displaystyle1}{\displaystyle a_3(x)+\frac{\displaystyle1}{\displaystyle\ddots}}}}, \end{align*} $$
which is simply written as
$x=[a_{1}(x),a_{2}(x),\ldots ].$
The integers
$\{a_n(x)\}_{n\ge 1}$
are called the partial quotients of x. The nth convergent is
$p_n(x)/q_n(x)=[a_{1}(x),\ldots ,a_{n}(x)]$
.
The convergents give the best rational approximations and the rate of approximation of the sequence of convergents can be characterised by
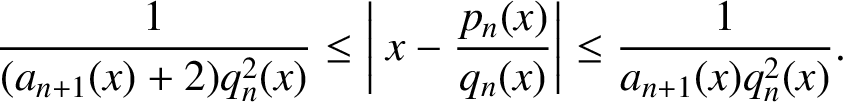$$ \begin{align*} \frac{1}{(a_{n+1}(x)+2)q_n^2(x)} \leq \bigg|\ {x}-\frac{p_n(x)}{q_n(x)}\bigg| \leq \frac{1}{a_{n+1}(x)q_n^2(x)}. \end{align*} $$
This implies that the Diophantine properties of a point
$x\in [0,1)$
are reflected in the growth rate of its partial quotients.
The metrical theory of Diophantine approximation concerns the quantitative study of the density of rationals in irrationals. In one dimension, this can be rephrased in terms of the growth of partial quotients of the continued fraction expansions of real numbers. For example, the set of badly approximable numbers comprises the points whose partial quotients are bounded. More generally, given an increasing function
$\psi \colon \mathbb {N}\to \mathbb {R}^+$
, the
$\psi \text {-approximable}$
set
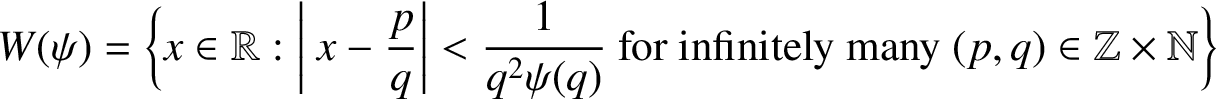$$ \begin{align*}W(\psi)=\bigg\{x\in\mathbb{R}:\bigg|\ {x}-\frac{p}{q}\bigg|<\frac{1}{q^2\psi(q)} \text{ for infinitely many } (p,q)\in \mathbb{Z}\times \mathbb{N}\bigg\} \end{align*} $$
can be estimated in terms of
$$ \begin{align*}K(\psi)=\{x\in\mathbb{R}\colon a_{n+1}(x)\geq \psi(q_{n}(x)) \text{ for infinitely many } n\in \mathbb{N}\}. \end{align*} $$
In fact, by using elementary properties of continued fractions,
$W(3\psi )\subset K(\psi )\subset W(\psi )$
.
As yet, there is no higher dimensional analogue of the Gauss map that captures all the features of continued fractions in one dimension. We attempt to extend the Diophantine approximation properties to two dimensions by characterising points in the plane in terms of the growth of the partial quotients of their coordinates.
For any positive integers s and t, define
$$ \begin{align*} E=\{(x,y)\in [0,1)^2: \max\{a_{sn}(x), a_{tn}(y)\}\to \infty \ {\text{as}}\ n\to \infty\}. \end{align*} $$
We investigate the size of the set E as measured by its Hausdorff dimension
${\dim _{\mathrm {H}}}\ E$
.
Theorem 1.1. We have
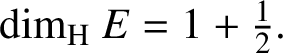$$ \begin{align*}{\dim_{\mathrm{H}}}\ E=1+\tfrac{1}{2}.\end{align*} $$
Let
$\psi :\mathbb {N}\to \mathbb {R}^+$
be such that
$\psi (n)\to \infty $
as
$n\to \infty $
. For any positive integers s and t, write
$$ \begin{align*} E(\psi)=\{(x,y)\in [0,1)^2: \max\{a_{sn}(x), a_{tn}(y)\}\ge \psi(n) \ {\text{for all sufficiently large}}\ n\in \mathbb{N}\}. \end{align*} $$
Theorem 1.2. If
$ \limsup _{n\to \infty } n^{-1}\log \log \psi (n)=\log b$
, then
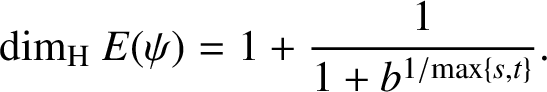$$ \begin{align*} {\dim_{\mathrm{H}}}\ E(\psi)=1+\frac{1}{1+b^{1/\!\max\{s,t\}}}. \end{align*} $$
The history of investigating the fractional dimensions of sets of real numbers whose continued fraction expansions satisfy various conditions on their partial quotients
$\{a_n(x)\colon n\ge 1\}$
can be traced back to the 1940s. Good [Reference Good3] considered such questions and more results were given by Feng et al. [Reference Feng, Wu, Liang and Tseng2], Hirst [Reference Hirst4], Łuczak [Reference Łuczak6] and Moorthy [Reference Moorthy7]. The set
$\{x\in [0,1)\colon a_n(x)\geq \phi (n)\; \text {for infinitely many} \; n\}$
, where
$\phi :{\mathbb N}\to {\mathbb R}^+$
is a positive function, was considered by Wang and Wu [Reference Wang and Wu8] and they completely determined its Hausdorff dimension. Wu and Xu [Reference Wu and Xu9] investigated the distribution of the largest digit in the continued fraction.
Throughout this paper, we use
$|A|$
to denote the diameter of a set
$A\subset \mathbb {R}$
,
$\# B$
to denote the cardinality of a set
$B\subset \mathbb {Z}$
and
$\mathcal {H}^{s}$
to denote the s-dimensional Hausdorff measure. We refer to [Reference Falconer1] for the definition and properties for Hausdorff measure and Hausdorff dimension.
2 Preliminaries
In this section, we first briefly recall some basic properties and known results of the continued fraction expansion that will be used later.
Let
$x\in [0,1)$
and
$[a_1(x),a_2(x),a_3(x),\ldots ]$
be its continued fraction expansion. For any
$n\ge 1$
and
$(a_1,a_2,\ldots ,a_n)\in \mathbb {N}^{n}$
, let
$q_n(a_1,a_2,\ldots ,a_n)$
be the denominator of the nth convergent
$[a_1,a_2,\ldots ,a_n]$
. If there is no confusion, we write
$q_n$
instead of
$q_n(a_1,a_2,\ldots ,a_n)$
for simplicity. With the conventional starting values
$p_{-1}=1$
,
${q_{-1}=0}$
,
$p_0=0$
,
$q_0=1$
,
$$ \begin{align*} p_{n+1}=a_{n+1}p_n+p_{n-1}, \quad q_{n+1}=a_{n+1}q_n+q_{n-1}, \quad n\ge0. \end{align*} $$
For any
$n\ge 1$
and
$(a_1,a_2,\ldots ,a_n)\in \mathbb {N}^{n}$
, define a basic cylinder of order n by
$$ \begin{align*} I_n(a_1,a_2,\ldots,a_n):=\{x\in[0,1)\colon a_1(x)=a_1,\ldots,a_n(x)=a_n\}. \end{align*} $$
The cylinder of order n consists of all real numbers in
$[0,1)$
whose continued fraction expansions begin with
$(a_1,a_2,\ldots ,a_n)$
. The length of the cylinder is given by the formula in the next lemma.
Lemma 2.1 [Reference Khintchine5].
For any
$n\ge 1$
and
$(a_1,a_2,\ldots ,a_n)\in \mathbb {N}^{n}$
,
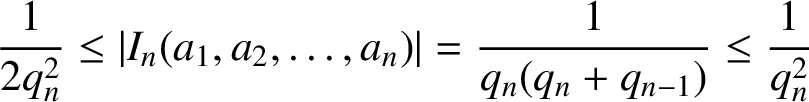$$ \begin{align} \frac{1}{2q_{n}^{2}}\leq|I_n(a_1,a_2,\ldots,a_n)|=\frac{1}{q_n(q_n+q_{n-1})}\leq\frac{1}{q_{n}^{2}} \end{align} $$
and
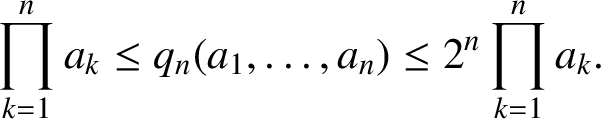$$ \begin{align} \prod_{k=1}^{n}a_{k}\leq q_{n}(a_{1},\ldots,a_{n})\leq 2^{n}\prod_{k=1}^{n}a_{k}. \end{align} $$
Lemma 2.2 [Reference Łuczak6].
For any
$a,b>1$
,
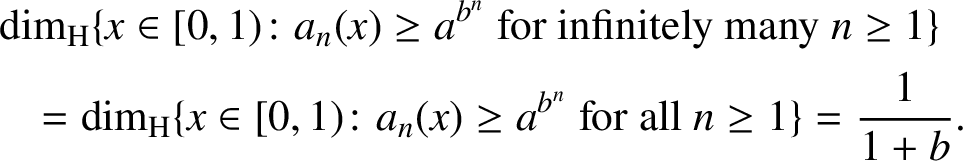$$ \begin{align*} \begin{split} {\dim_{\mathrm{H}}} & \{x\in[0,1) \colon a_n(x)\geq a^{b^n} \text{ for infinitely many } n\geq 1\}\\ &\hspace{-15pt}={\dim_{\mathrm{H}}} \{x\in[0,1)\colon a_n(x)\geq a^{b^n} \text{ for all } n\geq 1\}=\dfrac{1}{1+b}. \end{split} \end{align*} $$
Lemma 2.3 [Reference Good3].
If
$ F=\{x\in [0,1): a_n(x)\to \infty \ {\text {as}}\ n\to \infty \}, $
then
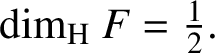${\dim _{\mathrm {H}}}\ F=\tfrac 12.$
Lemma 2.4 [Reference Falconer1].
If
$E\subset \mathbb {R}^{n}$
,
$F\subset \mathbb {R}^{m}$
are Borel sets, then
$$ \begin{align*}{\dim_{\mathrm{H}}}(E\times F)\geq{\dim_{\mathrm{H}}}\ E+{\dim_{\mathrm{H}}}\ F.\end{align*} $$
3 Proofs of Theorems 1.1 and 1.2
Proof of Theorem 1.1.
We divide the proof into two parts.
Lower bound. Recall that
$$ \begin{align*} E=\{(x,y)\in [0,1)^2: \max\{a_{sn}(x), a_{tn}(y)\}\to \infty \ {\text{as}}\ n\to \infty\}. \end{align*} $$
It follows immediately that the set E contains the set
$$ \begin{align*}\{x\in [0,1): a_n(x)\to \infty\ {\text{as}}\ n\to \infty\}\times [0,1), \end{align*} $$
which is of Hausdorff dimension
$1+1/2$
by Lemmas 2.3 and 2.4. This gives
$$ \begin{align*} {\dim_{\mathrm{H}}}\ E\geq 1+1/2. \end{align*} $$
Upper bound. By the definition of E, we can rewrite it as
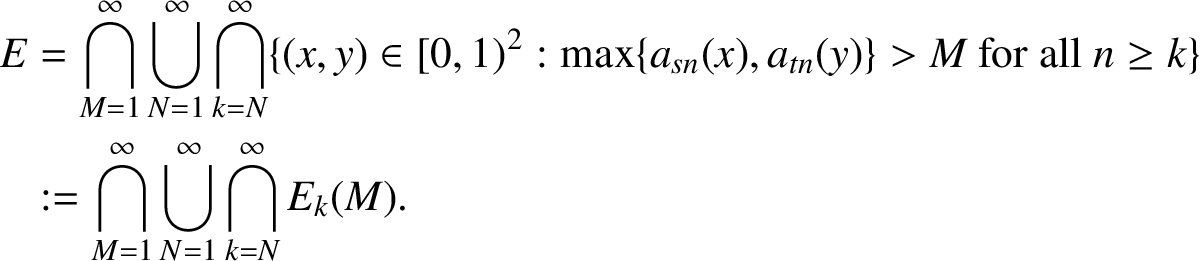$$ \begin{align}\begin{aligned} E &=\bigcap_{M=1}^{\infty}\bigcup_{N=1}^{\infty}\bigcap_{k=N}^{\infty}\{(x,y)\in [0,1)^2: \max\{a_{sn}(x),a_{tn}(y)\}> M \mbox{ for all } n\ge k\} \\ &:= \bigcap_{M=1}^{\infty}\bigcup_{N=1}^{\infty}\bigcap_{k=N}^{\infty}E_k(M). \end{aligned}\end{align} $$
It is clear that the set
$E_k(M)$
has the same Hausdorff dimension as
$$ \begin{align*} E(M)=\{(x,y)\in [0,1)^2: \max\{a_{sn}(x),a_{tn}(y)\}> M \mbox{ for all } n\ge 1\}. \end{align*} $$
Consequently, we only need to estimate the dimension of the latter set.
Set
$T=\max \{2s, 2t\}+1$
and fix
$\epsilon>0$
. There exists an integer
$M_{0}=M(\epsilon )$
such that
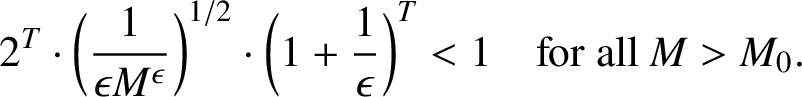$$ \begin{align*} 2^T\cdot \bigg(\frac{1}{\epsilon M^{\epsilon}}\bigg)^{{1}/{2}}\cdot \bigg(1+\frac{1}{\epsilon}\bigg)^T<1 \quad \mbox{for all }M>M_{0}. \end{align*} $$
Let
$M>M_{0}$
and
$(x,y)$
be an element in
$E(M)$
. Then, for any integers N and n with
$T^N< n\le 2\cdot T^{N}$
,
$$ \begin{align*} {\text{either}}\ a_{sn}(x)>M \quad{\text{or}}\quad a_{tn}(y)> M. \end{align*} $$
For this reason,
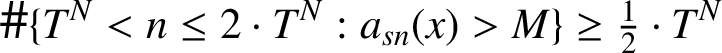$$ \begin{align*}\# \{T^N< n\le 2\cdot T^N: a_{sn}(x)> M\}\ge \tfrac{1}{2}\cdot T^N \end{align*} $$
or
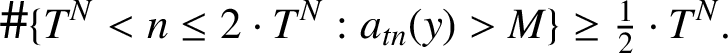$$ \begin{align*}\# \{T^N< n\le 2\cdot T^N: a_{tn}(y)> M\}\ge \tfrac{1}{2}\cdot T^N. \end{align*} $$
Note that
$T^N< \max \{sn,tn\}\le T^{N+1}$
when
$T^N< n\le 2\cdot T^N$
. From this, for any
$N\ge 1$
,
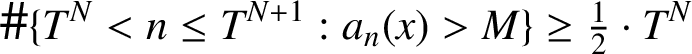$$ \begin{align*}\# \{T^N< n\le T^{N+1}: a_{n}(x)> M\}\ge \tfrac{1}{2}\cdot T^N \end{align*} $$
or
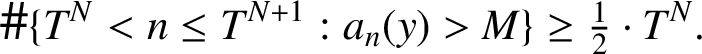$$ \begin{align*}\# \{T^N< n\le T^{N+1}: a_{n}(y)> M\}\ge \tfrac{1}{2}\cdot T^N. \end{align*} $$
Thus, if we write
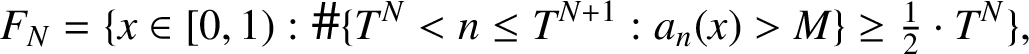$$ \begin{align*} F_N=\{x\in [0,1): \# \{T^N< n\le T^{N+1}: a_n(x)> M\}\ge \tfrac{1}{2}\cdot T^N\}, \end{align*} $$
it can be shown that
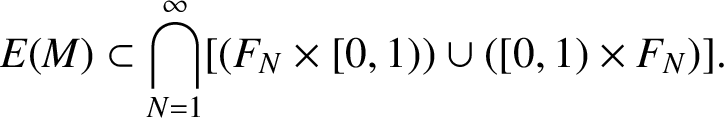$$ \begin{align*}E(M)\subset \bigcap_{N=1}^{\infty}[(F_N\times [0,1))\cup ([0,1)\times F_N)]. \end{align*} $$
Now we find a cover of
$F_N\times [0,1)$
and estimate its volume. The required cover of
$[0,1)\times F_N$
can clearly be constructed in the same way. We fix the following notation:
-
•
$\ell :=\tfrac 12\cdot T^N$
; -
•
$\mathcal {A}:= \{\mbox {all choices of } w=\{n_1, n_2,\ldots ,n_\ell \} \ \mbox { with }\ n_1<n_2<\cdots <n_{\ell }$
,
$T^N < n_i \le T^{N+1} \mbox { and } 1\le i\le \ell \}$
so that
$\# \mathcal {A}=C_{(T-1)\cdot T^N}^{\ell }\le 2^{T^{N+1}}$
; -
•
$w^c$
:= {the integers in
$[1, T^{n+1}]\setminus w$
}.
For any
$n\geq 1$
, set
$$ \begin{align*}D_n(w)=\{(\sigma_1,\sigma_2,\ldots, \sigma_n)\in{\mathbb N}^n, \ \sigma_n> M \ {\text{for}}\ n\in w, \ \ \sigma_n\ge 1 \ {\text{for}}\ n\in w^c\}. \end{align*} $$
From the definition of
$F_N$
,
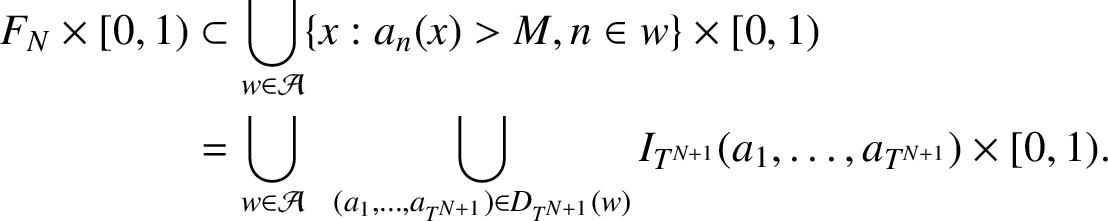$$ \begin{align*} F_N\times [0,1) &\subset \bigcup_{w\in\mathcal{A}}\{x: a_n(x)> M, n\in w\}\times [0,1)\\ &=\bigcup_{w\in \mathcal{A}}\ \ \bigcup_{(a_1,\ldots, a_{T^{N+1}})\in D_{T^{N+1}}(w)} I_{T^{N+1}}(a_1,\ldots, a_{T^{N+1}})\times [0,1). \end{align*} $$
For each
$(a_1,\ldots , a_{T^{N+1}})\in D_{T^{N+1}}(w)$
, the set
$ I_{T^{N+1}}(a_1,\ldots , a_{T^{N+1}})\times [0,1) $
can be covered by
$ |I_{T^{N+1}}(a_1,\ldots , a_{T^{N+1}})|^{-1} $
many squares, each of side length
$ |I_{T^{N+1}}(a_1,\ldots , a_{T^{N+1}})|, $
giving a cover of
$F_N\times [0,1)$
.
Let
$\alpha =(1+\epsilon )/2$
. A simple computation gives
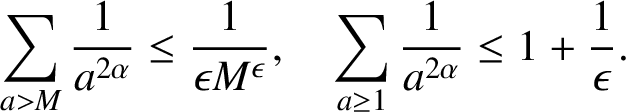$$ \begin{align*}\sum_{a>M}\frac{1}{a^{2\alpha}}\le \frac{1}{\epsilon M^{\epsilon}}, \quad \sum_{a\ge 1}\frac{1}{a^{2\alpha}}\le 1+\frac{1}{\epsilon}. \end{align*} $$
Using these inequalities, together with (2.1) and (2.2), the
$(1+\alpha )$
-dimensional volume of this cover can be estimated as
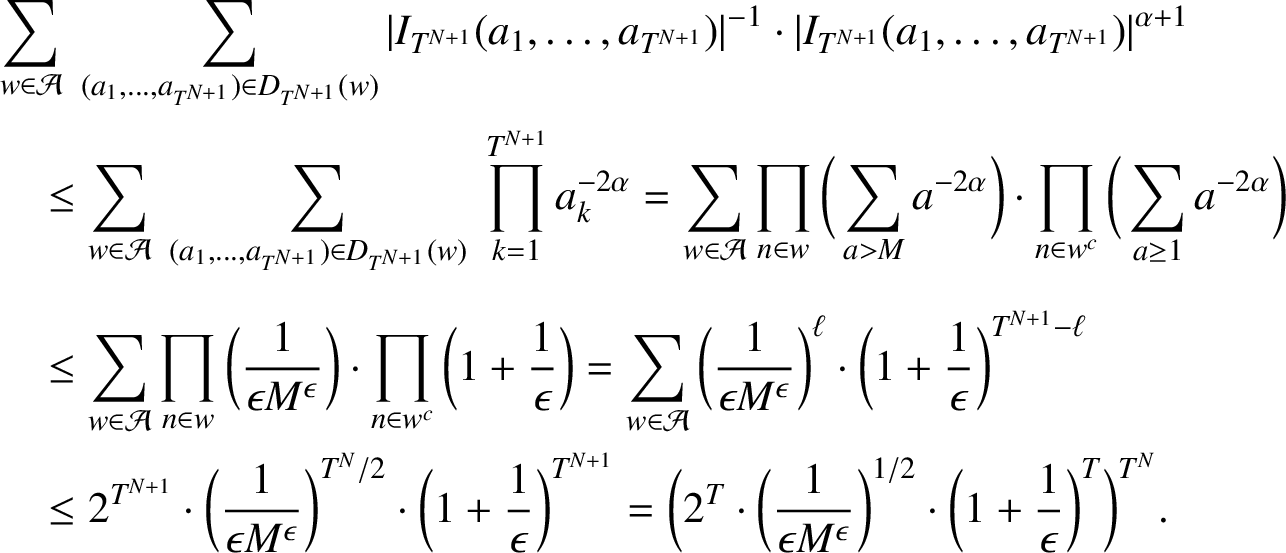$$ \begin{align*} &\sum_{w\in \mathcal{A}}\ \sum_{(a_1,\ldots, a_{T^{N+1}})\in D_{T^{N+1}}(w)} |I_{T^{N+1}}(a_1,\ldots, a_{T^{N+1}})|^{-1} \cdot |I_{T^{N+1}}(a_1,\ldots, a_{T^{N+1}})|^{\alpha+1}\\ & \quad\le \sum_{w\in \mathcal{A}}\ \sum_{(a_1,\ldots, a_{T^{N+1}})\in D_{T^{N+1}}(w)}\ \prod_{k=1}^{T^{N+1}}a_k^{-2\alpha} = \sum_{w\in \mathcal{A}}\prod_{n\in w}\bigg(\sum_{a> M}a^{-2\alpha}\bigg)\cdot \prod_{n\in w^c}\bigg(\sum_{a\ge 1}a^{-2\alpha}\bigg) \\[-12pt] \\ & \quad \le \sum_{w\in \mathcal{A}} \prod_{n\in w}\bigg(\frac{1}{\epsilon M^{\epsilon}}\bigg)\cdot \prod_{n\in w^c}\bigg(1+\frac{1}{\epsilon}\bigg) = \sum_{w\in \mathcal{A}}\bigg(\frac{1}{\epsilon M^{\epsilon}}\bigg)^{\ell}\cdot \bigg(1+\frac{1}{\epsilon}\bigg)^{T^{N+1}-\ell} \\ & \quad \le 2^{T^{N+1}}\cdot \bigg(\frac{1}{\epsilon M^{\epsilon}}\bigg)^{T^{N}/2}\cdot \bigg(1+\frac{1}{\epsilon}\bigg)^{T^{N+1}} = \bigg(2^T\cdot \bigg(\frac{1}{\epsilon M^{\epsilon}}\bigg)^{{1}/{2}}\cdot \bigg(1+\frac{1}{\epsilon}\bigg)^T\bigg)^{T^N}. \end{align*} $$
Therefore, by the choice of the integer M,
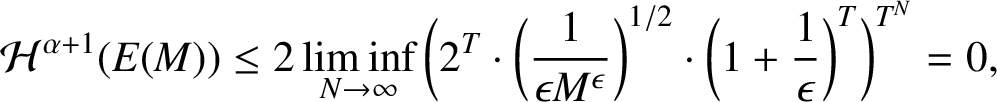$$ \begin{align*}\mathcal{H}^{\alpha+1}(E(M))\le 2\liminf_{N\to \infty}\bigg(2^T\cdot \bigg(\frac{1}{\epsilon M^{\epsilon}}\bigg)^{{1}/{2}}\cdot \bigg(1+\frac{1}{\epsilon}\bigg)^T\bigg)^{T^N}=0, \end{align*} $$
which shows that
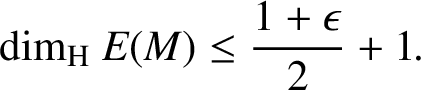$$ \begin{align*}{\dim_{\mathrm{H}}}\ E(M)\le \frac{1+\epsilon}{2}+1. \end{align*} $$
Since
$E_k(M)$
has the same Hausdorff dimension as
$E(M)$
, by equation (3.1), and
$\epsilon>0$
is arbitrary, we conclude that
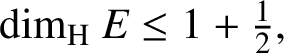$$ \begin{align*} {\dim_{\mathrm{H}}}\ E\le 1+\tfrac{1}{2}, \end{align*} $$
which completes the proof of Theorem 1.1.
Proof of Theorem 1.2.
Write
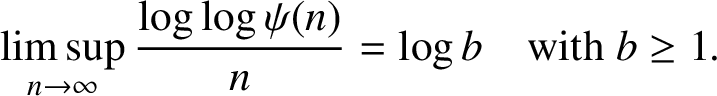$$ \begin{align*}\limsup_{n\to \infty}\frac{\log \log \psi(n)}{n}=\log b \quad {\text{with}} \ b\ge 1. \end{align*} $$
According as
$b=1$
or not, the proof will be divided into two cases.
Case 1:
$b=1$
. It is clear that
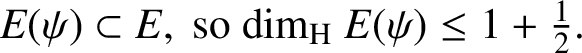$ E(\psi )\subset E, \ {\text {so}}\ {\dim _{\mathrm {H}}}\ E(\psi )\le 1+\tfrac 12. $
On the other hand,
$$ \begin{align*}\{x: a_n(x)\ge \psi(n) \ {\text{for all sufficiently large}}\ n\in \mathbb{N}\}\times [0,1)\subset E(\psi) \end{align*} $$
and
$ \psi (n)\leq e^{(1+{\varepsilon })^n} $
for any
${\varepsilon }>0$
and all sufficiently large n, so that
$$ \begin{align*}\{x: a_n(x)\ge e^{(1+{\varepsilon})^n} \ {\text{for all sufficiently large}}\ n\in \mathbb{N}\}\times [0,1)\subset E(\psi). \end{align*} $$
Since
${\varepsilon }$
is arbitrary, it follows from Lemma 2.2 that
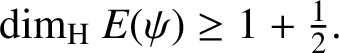$ {\dim _{\mathrm {H}}}\ E(\psi )\ge 1+\tfrac 12. $
Case 2:
$b>1$
. Take a point
$(x,y)\in E(\psi )$
. Let
$1<a<b$
. By the definition of b, there exists an infinite subset L of
$\mathbb {N}$
such that
$ \psi (n)\ge e^{a^n} \ {\text {for all}}\ n \in L. $
For each
$n\in L$
,
$ {\text {either}}\ a_{sn}(x)>e^{a^n} \ {\text {or}}\ a_{tn}(y)> e^{a^n}. $
Since L is infinite, at least one of the inequalities
$a_{sn}(x)>e^{a^n}$
and
$a_{tn}(y)>e^{a^n}$
holds for infinitely many n. This clearly forces
$$ \begin{align*}E(\psi)\subset E_1\times [0,1) \cup [0,1)\times E_2, \end{align*} $$
where
$$ \begin{align*} E_1&=\{x: a_{sn}(x)\ge e^{a^n} {\text{ for infinitely many}}\ n\in \mathbb{N}\},\\ E_2&=\{y: a_{tn}(y)\ge e^{a^n} {\text{ for infinitely many}}\ n\in \mathbb{N}\}. \end{align*} $$
Thus, by Lemma 2.2,
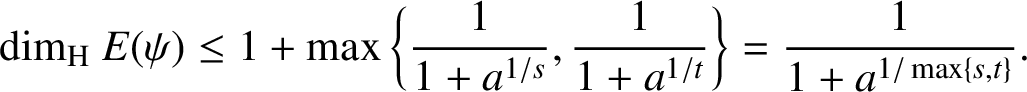$$ \begin{align*}{\dim_{\mathrm{H}}}\ E(\psi)\le 1+\max\bigg\{\frac{1}{1+a^{1/s}}, \frac{1}{1+a^{1/t}}\bigg\}=\frac{1}{1+a^{1/\max\{s,t\}}}. \end{align*} $$
On the other hand, for any
$c>b$
, we have
$\psi (n)\le e^{c^n}$
for all large n. Without loss of generality, we assume that
$s>t$
. So, it is clear that
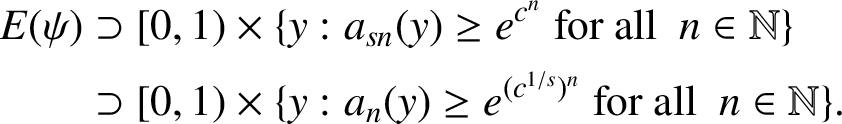$$ \begin{align*} E(\psi)&\supset [0,1)\times \{y: a_{sn}(y)\ge e^{c^n} {\text{ for all }}\ n\in \mathbb{N}\}\\ &\supset [0,1)\times \{y: a_{n}(y)\ge e^{(c^{1/s})^n} {\text{ for all }}\ n\in \mathbb{N}\}. \end{align*} $$
By Lemma 2.2,
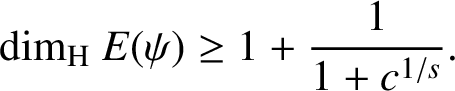$$ \begin{align*}{\dim_{\mathrm{H}}}\ E(\psi)\ge 1+\frac{1}{1+c^{1/s}}. \end{align*} $$
Since
$c>b$
is arbitrary, we conclude that
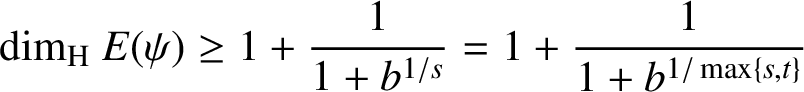$$ \begin{align*}{\dim_{\mathrm{H}}}\ E(\psi)\ge 1+\frac{1}{1+b^{1/s}}=1+\frac{1}{1+b^{1/\max\{s,t\}}} \end{align*} $$
and the proof of Theorem 1.2 is finished.
4 Final remark
With a slight change in the notation, Theorems 1.1 and 1.2 can be generalised to
$[0,1)^d$
in the same manner.
For
$1\leq i\leq d$
, let
$f_i(n)=b_in+c_i$
with
$b_i\ge 1$
and
$b_i, c_i$
positive real numbers. Define
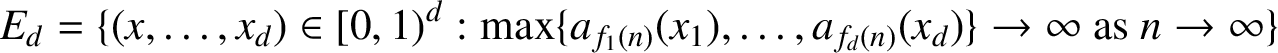$$ \begin{align*} E_d=\{(x,\ldots,x_d)\in [0,1)^d: \max\{a_{f_1(n)}(x_1),\ldots, a_{f_d(n)}(x_d)\}\to \infty\text{ as }n\rightarrow \infty\} \end{align*} $$
and
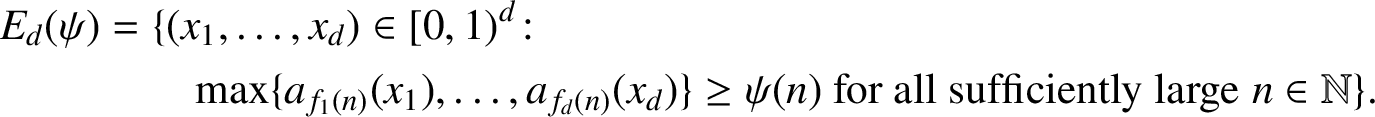$$ \begin{align*} \begin{split} E_d(\psi) &= \{(x_1,\ldots,x_d) \in[0,1)^d \colon \\ &\qquad \max\{a_{f_1(n)}(x_1),\ldots,a_{f_d(n)}(x_d)\}\geq \psi(n) \text{ for all sufficiently large}\;n\in \mathbb{N}\}. \end{split} \end{align*} $$
Take
$$ \begin{align*}T=\max\{2b_i, c_i: 1\le i\le d\}+1. \end{align*} $$
If
$T^k<n\le 2T^k$
, then
$$ \begin{align*}T^k<f_i(n)=b_in+c_i\le 2b_i T^k+c_i\le (2b_i+1)T^k\le T^{k+1}. \end{align*} $$
Following the proofs of Theorems 1.1 and 1.2 step by step, we can deduce analogous results in dimension d.
Theorem 4.1. We have
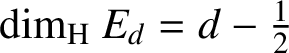${\dim _{\mathrm {H}}}\ E_d=d-\tfrac 12$
.
Theorem 4.2. We have
${\dim _{\mathrm {H}}}\ E_d(\psi )=(d-1)+{1}/{(1+b^{1/A})}$
, where
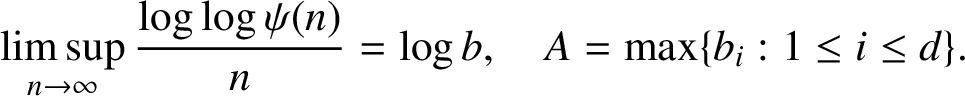$$ \begin{align*} \limsup_{n\to \infty}\frac{\log \log \psi(n)}{n}=\log b, \quad A=\max\{b_i: 1\le i\le d\}. \end{align*} $$
