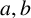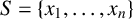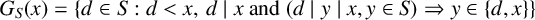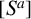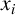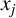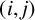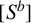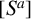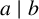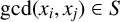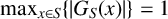1 Introduction
For arbitrary integers x and y, we denote by
![]() $(x,y)$
the greatest common divisor of x and y and by
$(x,y)$
the greatest common divisor of x and y and by
![]() $[x,y]$
their least common multiple. Let
$[x,y]$
their least common multiple. Let
![]() $a, b$
and n be positive integers. Let
$a, b$
and n be positive integers. Let
![]() $S = \{x_1, \ldots , x_n\}$
be a set of n distinct positive integers. Let
$S = \{x_1, \ldots , x_n\}$
be a set of n distinct positive integers. Let
![]() $\xi _a$
be the arithmetic function defined by
$\xi _a$
be the arithmetic function defined by
![]() $\xi _a=x^a$
for any positive integer x. Let
$\xi _a=x^a$
for any positive integer x. Let
![]() $(S^a)$
and
$(S^a)$
and
![]() $[S^a]$
stand for the
$[S^a]$
stand for the
![]() $n\times n$
matrices whose
$n\times n$
matrices whose
![]() $(i,j)$
-entry is
$(i,j)$
-entry is
![]() $\xi _a((x_i, x_j))$
and
$\xi _a((x_i, x_j))$
and
![]() $\xi _a([x_i, x_j])$
respectively. We call
$\xi _a([x_i, x_j])$
respectively. We call
![]() $(S^a)$
the
$(S^a)$
the
![]() $ath$
power GCD matrix and
$ath$
power GCD matrix and
![]() $[S^a]$
the
$[S^a]$
the
![]() $ath$
power LCM matrix. The set S is factor closed (FC) if
$ath$
power LCM matrix. The set S is factor closed (FC) if
![]() $(x\in S, d\mid x)\Rightarrow d\in S$
and gcd closed if
$(x\in S, d\mid x)\Rightarrow d\in S$
and gcd closed if
![]() $(x_i, x_j)\in S$
for all integers i and j with
$(x_i, x_j)\in S$
for all integers i and j with
![]() $1\le i,j\le n$
. Obviously, an FC set must be gcd closed but the converse is not true. Nearly 150 years ago, Smith [Reference Smith15] proved that
$1\le i,j\le n$
. Obviously, an FC set must be gcd closed but the converse is not true. Nearly 150 years ago, Smith [Reference Smith15] proved that
 $$ \begin{align} \det([x_i,x_j])=\prod_{k=1}^n\varphi(x_k)\pi(x_k) \end{align} $$
$$ \begin{align} \det([x_i,x_j])=\prod_{k=1}^n\varphi(x_k)\pi(x_k) \end{align} $$
if S is FC, where
![]() $\varphi $
is Euler’s totient function and
$\varphi $
is Euler’s totient function and
![]() $\pi $
is the multiplicative function defined for the prime power
$\pi $
is the multiplicative function defined for the prime power
![]() $p^r$
by
$p^r$
by
![]() $\pi (p^r)=-p$
. There are many generalisations of Smith’s determinant (1.1) and related results (see, for instance, [Reference Altinisik, Yildiz and Keskin1–Reference Korkee and Haukkanen14, Reference Tan and Li16–Reference Zhu, Cheng and Zhao21]). In particular, an elegant result was achieved by Hong et al. [Reference Hong, Hu and Lin8] stating that for any integer
$\pi (p^r)=-p$
. There are many generalisations of Smith’s determinant (1.1) and related results (see, for instance, [Reference Altinisik, Yildiz and Keskin1–Reference Korkee and Haukkanen14, Reference Tan and Li16–Reference Zhu, Cheng and Zhao21]). In particular, an elegant result was achieved by Hong et al. [Reference Hong, Hu and Lin8] stating that for any integer
![]() $n\ge 2$
,
$n\ge 2$
,
 $$ \begin{align*}\det([i,j])_{2\le i,j\le n}=\bigg(\prod_{k=1}^n \varphi (k)\pi(k)\bigg)\sum_{\substack{t=1\\ t \text{ is square free}}}^n\frac{t\mu(t)}{\varphi (t)}, \end{align*} $$
$$ \begin{align*}\det([i,j])_{2\le i,j\le n}=\bigg(\prod_{k=1}^n \varphi (k)\pi(k)\bigg)\sum_{\substack{t=1\\ t \text{ is square free}}}^n\frac{t\mu(t)}{\varphi (t)}, \end{align*} $$
where
![]() $\mu $
is the M
$\mu $
is the M
![]() $\ddot {\textrm {o}}$
bius function and an integer
$\ddot {\textrm {o}}$
bius function and an integer
![]() $x\ge 1$
is called square free if x is not divisible by the square of any prime number.
$x\ge 1$
is called square free if x is not divisible by the square of any prime number.
As usual,
![]() $\mathbb {Z}$
and
$\mathbb {Z}$
and
![]() $|S|$
denote the ring of integers and the cardinality of the set S. Hong [Reference Hong9] introduced the concept of greatest-type divisor when he solved the Bourque–Ligh conjecture. For any integer
$|S|$
denote the ring of integers and the cardinality of the set S. Hong [Reference Hong9] introduced the concept of greatest-type divisor when he solved the Bourque–Ligh conjecture. For any integer
![]() $x\in S$
, y is called a greatest-type divisor of x if
$x\in S$
, y is called a greatest-type divisor of x if
Let
![]() $ G_S(x):=\{y\in S: y \ \text {is a greatest-type divisor of} \ x \ \mathrm {in} \ S\} $
and let
$ G_S(x):=\{y\in S: y \ \text {is a greatest-type divisor of} \ x \ \mathrm {in} \ S\} $
and let
![]() $M_n(\mathbb {Z})$
stand for the ring of
$M_n(\mathbb {Z})$
stand for the ring of
![]() $n\times n$
matrices over the integers. Bourque and Ligh [Reference Bourque and Ligh4] proved that
$n\times n$
matrices over the integers. Bourque and Ligh [Reference Bourque and Ligh4] proved that
![]() $(S)$
divides
$(S)$
divides
![]() $[S]$
in the ring
$[S]$
in the ring
![]() $M_n(\mathbb {Z})$
(that is,
$M_n(\mathbb {Z})$
(that is,
![]() $[S]=B(S)$
or
$[S]=B(S)$
or
![]() $[S]=(S)B$
for some
$[S]=(S)B$
for some
![]() $B\in M_n(\mathbb {Z})$
) if S is FC. Hong [Reference Hong10] showed that such a factorisation is not true when S is gcd closed and
$B\in M_n(\mathbb {Z})$
) if S is FC. Hong [Reference Hong10] showed that such a factorisation is not true when S is gcd closed and
![]() $\max _{x \in S}\{|{G_S(x)}|\}=2$
. The results of Bourque–Ligh and Hong were generalised by Korkee and Haukkanen [Reference Korkee and Haukkanen14] and by Chen et al. [Reference Chen, Feng, Hong and Qiu6]. Feng et al. [Reference Feng, Hong and Zhao7], Zhao [Reference Zhao17], Altinisik et al. [Reference Altinisik, Yildiz and Keskin1] and Zhao et al. [Reference Zhao, Chen and Hong18] used the concept of greatest-type divisor to characterise the gcd-closed sets S with
$\max _{x \in S}\{|{G_S(x)}|\}=2$
. The results of Bourque–Ligh and Hong were generalised by Korkee and Haukkanen [Reference Korkee and Haukkanen14] and by Chen et al. [Reference Chen, Feng, Hong and Qiu6]. Feng et al. [Reference Feng, Hong and Zhao7], Zhao [Reference Zhao17], Altinisik et al. [Reference Altinisik, Yildiz and Keskin1] and Zhao et al. [Reference Zhao, Chen and Hong18] used the concept of greatest-type divisor to characterise the gcd-closed sets S with
![]() $\max _{x \in S}\{|{G_S(x)}|\}\le 3$
such that
$\max _{x \in S}\{|{G_S(x)}|\}\le 3$
such that
![]() $(S^a)\mid [S^a]$
which partially solved an open problem of Hong [Reference Hong10].
$(S^a)\mid [S^a]$
which partially solved an open problem of Hong [Reference Hong10].
Hong [Reference Hong12] investigated divisibility among power GCD matrices and among power LCM matrices. It was proved in [Reference Hong12] that
![]() $(S^a)\mid (S^b), (S^a) \mid [S^b]$
and
$(S^a)\mid (S^b), (S^a) \mid [S^b]$
and
![]() $[S^a] \mid [S^b]$
if
$[S^a] \mid [S^b]$
if
![]() $a \mid b$
and S is a divisor chain (that is,
$a \mid b$
and S is a divisor chain (that is,
![]() $x_{\sigma (1)}| \cdots |x_{\sigma (n)}$
for a permutation
$x_{\sigma (1)}| \cdots |x_{\sigma (n)}$
for a permutation
![]() $\sigma $
of
$\sigma $
of
![]() $\{1,\ldots , n\}$
), and such factorisations are no longer true if
$\{1,\ldots , n\}$
), and such factorisations are no longer true if
![]() $a\nmid b$
and
$a\nmid b$
and
![]() $|S|\ge 2$
. Evidently, a divisor chain is gcd closed but not conversely. Recently, Zhu [Reference Zhu19] confirmed two conjectures of Hong raised in [Reference Hong12] stating that if
$|S|\ge 2$
. Evidently, a divisor chain is gcd closed but not conversely. Recently, Zhu [Reference Zhu19] confirmed two conjectures of Hong raised in [Reference Hong12] stating that if
![]() $a\mid b$
and S is a gcd-closed set with
$a\mid b$
and S is a gcd-closed set with
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
, then both the bth power GCD matrix
$\max _{x\in S}\{|G_S(x)|\}=1$
, then both the bth power GCD matrix
![]() $(S^b)$
and the bth power LCM matrix
$(S^b)$
and the bth power LCM matrix
![]() $[S^b]$
are divisible by the ath power GCD matrix
$[S^b]$
are divisible by the ath power GCD matrix
![]() $(S^a)$
. At the end of [Reference Hong12], Hong also conjectured that if
$(S^a)$
. At the end of [Reference Hong12], Hong also conjectured that if
![]() $a \mid b$
and
$a \mid b$
and
![]() $S=\{x_1,\ldots , x_n \}$
is gcd closed and
$S=\{x_1,\ldots , x_n \}$
is gcd closed and
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
, then
$\max _{x\in S}\{|G_S(x)|\}=1$
, then
![]() $[S^a] \mid [S^b]$
in the ring
$[S^a] \mid [S^b]$
in the ring
![]() $M_n(\mathbb {Z})$
. Tan and Li [Reference Tan and Li16] partially confirmed this conjecture by proving that
$M_n(\mathbb {Z})$
. Tan and Li [Reference Tan and Li16] partially confirmed this conjecture by proving that
![]() $[S^a] \mid [S^b]$
in the ring
$[S^a] \mid [S^b]$
in the ring
![]() $M_{|S|}(\mathbb {Z})$
if
$M_{|S|}(\mathbb {Z})$
if
![]() $a \mid b$
and S consists of finitely many coprime divisor chains with
$a \mid b$
and S consists of finitely many coprime divisor chains with
![]() $1\in S$
and that such a divisibility relation is not true if
$1\in S$
and that such a divisibility relation is not true if
![]() $a\nmid b$
. However, the conjecture still remains open.
$a\nmid b$
. However, the conjecture still remains open.
Our goal is to present a proof of Hong’s conjecture. The main result of the paper is the following theorem.
Theorem 1.1. If a and b are positive integers such that
![]() $a \mid b$
and S is a gcd-closed set such that
$a \mid b$
and S is a gcd-closed set such that
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
, then the ath power LCM matrix
$\max _{x\in S}\{|G_S(x)|\}=1$
, then the ath power LCM matrix
![]() $[S^a]$
divides the bth power LCM matrix
$[S^a]$
divides the bth power LCM matrix
![]() $[S^b]$
in the ring
$[S^b]$
in the ring
![]() $M_{|S|}(\mathbb {Z})$
.
$M_{|S|}(\mathbb {Z})$
.
The proof of Theorem 1.1 is similar to that of Feng et al. [Reference Feng, Hong and Zhao7] in character, but it is more complicated. This paper is organised as follows. In Section 2, we supply several preliminary lemmas needed in the proof of Theorem 1.1. Section 3 is devoted to the proof of Theorem 1.1.
One can easily check that for any permutation
![]() $\sigma $
on the set
$\sigma $
on the set
![]() $\{1, \ldots , n \}$
,
$\{1, \ldots , n \}$
,
![]() $[S^a]\mid [S^b]\Leftrightarrow [S_{\sigma }^a]\mid [S_{\sigma } ^b]$
, where
$[S^a]\mid [S^b]\Leftrightarrow [S_{\sigma }^a]\mid [S_{\sigma } ^b]$
, where
![]() $S_\sigma :=\{x_{\sigma (1)},\ldots , x_{\sigma (n)}\}$
. Without loss of any generality, we can always assume that the set
$S_\sigma :=\{x_{\sigma (1)},\ldots , x_{\sigma (n)}\}$
. Without loss of any generality, we can always assume that the set
![]() $S=\{x_1,\ldots , x_n \}$
satisfies
$S=\{x_1,\ldots , x_n \}$
satisfies
![]() $x_1<\cdots <x_n$
.
$x_1<\cdots <x_n$
.
2 Auxiliary results
In this section, we provide several lemmas that will be needed in the proof of Theorem 1.1. We begin with a result due to Hong which gives the formula for the determinant of the power LCM matrix on a gcd-closed set.
Lemma 2.1 [Reference Hong11, Lemma 2.1].
If S is gcd closed, then
 $$ \begin{align} \det[S^a]=\prod\limits_{k=1}^n x_k^{2a}\alpha_{a,k}, \end{align} $$
$$ \begin{align} \det[S^a]=\prod\limits_{k=1}^n x_k^{2a}\alpha_{a,k}, \end{align} $$
where
 $$ \begin{align} \alpha_{a,k}:=\sum_{\substack{d|x_k\\ d\nmid x_t,\,x_t<x_k}} \bigg(\dfrac{1}{\xi_a}*\mu\bigg)(d) \end{align} $$
$$ \begin{align} \alpha_{a,k}:=\sum_{\substack{d|x_k\\ d\nmid x_t,\,x_t<x_k}} \bigg(\dfrac{1}{\xi_a}*\mu\bigg)(d) \end{align} $$
and
![]() ${1}/{\xi _a}$
is the arithmetic function defined for any positive integer x by
${1}/{\xi _a}$
is the arithmetic function defined for any positive integer x by
![]() ${({1}/{\xi _a})(x):= x^{-a}}$
.
${({1}/{\xi _a})(x):= x^{-a}}$
.
Lemma 2.2 [Reference Bourque and Ligh5, Theorem 3].
If S is a gcd-closed set and
![]() $(f((x_i,x_j)))$
is invertible, then
$(f((x_i,x_j)))$
is invertible, then
![]() $ (f((x_i,x_j)))^{-1}=(a_{ij}), $
where
$ (f((x_i,x_j)))^{-1}=(a_{ij}), $
where
 $$ \begin{align*}a_{ij}:=\sum_{\substack{x_i|x_k\\ x_j|x_k}} \dfrac{c_{ik}c_{jk}}{\delta_k}\end{align*} $$
$$ \begin{align*}a_{ij}:=\sum_{\substack{x_i|x_k\\ x_j|x_k}} \dfrac{c_{ik}c_{jk}}{\delta_k}\end{align*} $$
with
 $$ \begin{align} \delta_k:= \sum_{\substack{d|x_k\\ d\nmid x_t,\, x_t<x_k}} (f*\mu)(d) \quad\mbox{and}\quad c_{ij}:=\sum _{\substack{dx_i|x_j\\ dx_i\nmid x_t,\, x_t<x_j}} \mu(d). \end{align} $$
$$ \begin{align} \delta_k:= \sum_{\substack{d|x_k\\ d\nmid x_t,\, x_t<x_k}} (f*\mu)(d) \quad\mbox{and}\quad c_{ij}:=\sum _{\substack{dx_i|x_j\\ dx_i\nmid x_t,\, x_t<x_j}} \mu(d). \end{align} $$
Lemma 2.3 [Reference Hong11, Lemma 2.3].
Let m be a positive integer. Then
 $$ \begin{align*}{\underset{d|m}{\sum}}\bigg(\dfrac{1}{\xi_a}*\mu \bigg)(d)=m^{-a}. \end{align*} $$
$$ \begin{align*}{\underset{d|m}{\sum}}\bigg(\dfrac{1}{\xi_a}*\mu \bigg)(d)=m^{-a}. \end{align*} $$
Lemma 2.4 [Reference Feng, Hong and Zhao7, Lemma 2.2].
Let S be gcd closed and
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
. Let
$\max _{x\in S}\{|G_S(x)|\}=1$
. Let
![]() $\alpha _{a,k}$
be defined as in (2.2). If
$\alpha _{a,k}$
be defined as in (2.2). If
![]() $G_S(x_k)=\{x_{k_1}\}$
for
$G_S(x_k)=\{x_{k_1}\}$
for
![]() $2\le k\le |S|$
, then
$2\le k\le |S|$
, then
![]() $\alpha _{a,k}=x_k^{-a}-x_{k_1}^{-a}.$
$\alpha _{a,k}=x_k^{-a}-x_{k_1}^{-a}.$
Lemma 2.5. Let S be gcd closed and
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
. Let
$\max _{x\in S}\{|G_S(x)|\}=1$
. Let
![]() $\alpha _{a,k}$
and
$\alpha _{a,k}$
and
![]() $c_{ij}$
be defined as in (2.2) and (2.3), respectively. Then
$c_{ij}$
be defined as in (2.2) and (2.3), respectively. Then
![]() $[S^a]$
is nonsingular and
$[S^a]$
is nonsingular and
![]() $[S^a]^{-1}=(s_{ij})_{1\le i,j\le n}$
with
$[S^a]^{-1}=(s_{ij})_{1\le i,j\le n}$
with
 $$ \begin{align*} s_{ij}:=\dfrac{1}{x_i^a x_j^a} \sum_{\substack{x_i|x_k\\ x_j|x_k}} \dfrac{c_{ik}c_{jk}}{\alpha_{a,k}}. \end{align*} $$
$$ \begin{align*} s_{ij}:=\dfrac{1}{x_i^a x_j^a} \sum_{\substack{x_i|x_k\\ x_j|x_k}} \dfrac{c_{ik}c_{jk}}{\alpha_{a,k}}. \end{align*} $$
Proof. Since
![]() ${[x_i,x_j]}^a={x_i^ax_j^a}/{{(x_i,x_j)}^a}$
,
${[x_i,x_j]}^a={x_i^ax_j^a}/{{(x_i,x_j)}^a}$
,
 $$ \begin{align} [S^a]=D\bigg(\dfrac{1}{\xi_a}(x_i,x_j)\bigg)D, \end{align} $$
$$ \begin{align} [S^a]=D\bigg(\dfrac{1}{\xi_a}(x_i,x_j)\bigg)D, \end{align} $$
where
![]() $D:=\mathrm {diag}(x_1^a,\ldots ,x_n^a)$
. By (2.1) and (2.4),
$D:=\mathrm {diag}(x_1^a,\ldots ,x_n^a)$
. By (2.1) and (2.4),
 $$ \begin{align*} \det\bigg(\dfrac{1}{\xi_a}((x_i,x_j))\bigg) =\prod\limits_{k=1}^n\alpha_{a,k}. \end{align*} $$
$$ \begin{align*} \det\bigg(\dfrac{1}{\xi_a}((x_i,x_j))\bigg) =\prod\limits_{k=1}^n\alpha_{a,k}. \end{align*} $$
By Lemma 2.3,
![]() $\alpha _{a,1}=x_1^{-a}$
. For
$\alpha _{a,1}=x_1^{-a}$
. For
![]() $2\le k\le n$
, since
$2\le k\le n$
, since
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
, one may let
$\max _{x\in S}\{|G_S(x)|\}=1$
, one may let
![]() $G_S(x_k)=\{x_{k_1}\}$
. By Lemma 2.4,
$G_S(x_k)=\{x_{k_1}\}$
. By Lemma 2.4,
![]() $\alpha _{a,k}=x_k^{-a}-x_{k_1}^{-a}\neq 0$
. So the matrix
$\alpha _{a,k}=x_k^{-a}-x_{k_1}^{-a}\neq 0$
. So the matrix
![]() $(({1/\xi _a})((x_i,x_j)))$
is nonsingular. Now applying Lemma 2.2 gives
$(({1/\xi _a})((x_i,x_j)))$
is nonsingular. Now applying Lemma 2.2 gives
 $$ \begin{align} \bigg(\dfrac{1}{\xi_a}((x_i,x_j))\bigg)^{-1}=(h_{ij}), \end{align} $$
$$ \begin{align} \bigg(\dfrac{1}{\xi_a}((x_i,x_j))\bigg)^{-1}=(h_{ij}), \end{align} $$
where
 $$ \begin{align*}h_{ij}:=\sum_{\substack{x_i|x_k\\ x_j|x_k}} \dfrac{c_{ik}c_{jk}}{\alpha_{a,k}}.\end{align*} $$
$$ \begin{align*}h_{ij}:=\sum_{\substack{x_i|x_k\\ x_j|x_k}} \dfrac{c_{ik}c_{jk}}{\alpha_{a,k}}.\end{align*} $$
The desired result follows immediately from (2.4) and (2.5).
We next recall some basic results on gcd-closed sets.
Lemma 2.6 [Reference Feng, Hong and Zhao7, Lemma 2.3].
Let S be a gcd-closed set with
![]() $|S|\ge 2$
. Let
$|S|\ge 2$
. Let
![]() $c_{ij}$
be defined as in (2.3). Then
$c_{ij}$
be defined as in (2.3). Then
 $$ \begin{align*}c_{w1}=\left\{\begin{aligned} {1}& \quad \mbox{if } w=1,\\ {0}&\quad \mbox{otherwise}. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}c_{w1}=\left\{\begin{aligned} {1}& \quad \mbox{if } w=1,\\ {0}&\quad \mbox{otherwise}. \end{aligned} \right. \end{align*} $$
Further, if
![]() $G_S(x_m)=\{x_{m_1}\}$
for
$G_S(x_m)=\{x_{m_1}\}$
for
![]() $2\le m\le |S|$
, then
$2\le m\le |S|$
, then
 $$ \begin{align*}c_{wm}=\left\{ \begin{aligned} {-1}&\quad \mbox{if }w=m_1,\\ {1}&\quad \mbox{if } w=m,\\ {0}&\quad \mbox{otherwise}. \end{aligned} \right. \end{align*} $$
$$ \begin{align*}c_{wm}=\left\{ \begin{aligned} {-1}&\quad \mbox{if }w=m_1,\\ {1}&\quad \mbox{if } w=m,\\ {0}&\quad \mbox{otherwise}. \end{aligned} \right. \end{align*} $$
Lemma 2.7 [Reference Feng, Hong and Zhao7, Lemma 3.1].
Let S be gcd closed and
![]() $x,z\in S$
such that
$x,z\in S$
such that
![]() $x\nmid z$
. If
$x\nmid z$
. If
![]() ${G_S(x)=\{y\}}$
, then
${G_S(x)=\{y\}}$
, then
![]() $(x, z)=(y, z)$
.
$(x, z)=(y, z)$
.
Lemma 2.8. Let S be gcd closed and
![]() $x, y\in S$
with
$x, y\in S$
with
![]() $G_S(x)=\{y\}$
. If
$G_S(x)=\{y\}$
. If
![]() $a\mid b$
, then for any
$a\mid b$
, then for any
![]() $z, r\in S$
with
$z, r\in S$
with
![]() $r\mid x$
,
$r\mid x$
,
![]() $y^a[z,x]^b-x^a[z,y]^b$
is divisible by each of
$y^a[z,x]^b-x^a[z,y]^b$
is divisible by each of
![]() $x^a(y^a-x^a)$
and
$x^a(y^a-x^a)$
and
![]() $r^a(y^a-x^a)$
.
$r^a(y^a-x^a)$
.
Proof. We divide the proof into two cases.
Case 1:
![]() $x\nmid z$
. By Lemma 2.7,
$x\nmid z$
. By Lemma 2.7,
![]() $(x, z)=(y, z)$
, which implies
$(x, z)=(y, z)$
, which implies
 $$ \begin{align} y^a[z,x]^b-x^a[z,y]^b=y^a\dfrac{z^bx^b} {(z,x)^b}-x^a\dfrac{z^by^b}{(z,y)^b} =\dfrac{z^b}{(z,x)^b}x^ay^a(x^{b-a}-y^{b-a}). \end{align} $$
$$ \begin{align} y^a[z,x]^b-x^a[z,y]^b=y^a\dfrac{z^bx^b} {(z,x)^b}-x^a\dfrac{z^by^b}{(z,y)^b} =\dfrac{z^b}{(z,x)^b}x^ay^a(x^{b-a}-y^{b-a}). \end{align} $$
Since
![]() $a\mid b$
,
$a\mid b$
,
 $$ \begin{align*}x^{b-a}-y^{b-a}=(x^a-y^a)\sum _{i=0}^{{({b}/{a})}-2} (x^a)^{{({b}/{a})}-2-i}y^{ai} \quad\mbox{and}\quad \sum _{i=0}^{{({b}/{a})}-2} (x^a)^{{({b}/{a})}-2-i}y^{ai}\in \mathbb{Z}. \end{align*} $$
$$ \begin{align*}x^{b-a}-y^{b-a}=(x^a-y^a)\sum _{i=0}^{{({b}/{a})}-2} (x^a)^{{({b}/{a})}-2-i}y^{ai} \quad\mbox{and}\quad \sum _{i=0}^{{({b}/{a})}-2} (x^a)^{{({b}/{a})}-2-i}y^{ai}\in \mathbb{Z}. \end{align*} $$
Hence,
![]() $(x^a-y^a)\mid (x^{b-a}-y^{b-a})$
. Then by (2.6), we deduce that
$(x^a-y^a)\mid (x^{b-a}-y^{b-a})$
. Then by (2.6), we deduce that
![]() $y^a[z,x]^b-x^a[z,y]^b$
is divisible by each of
$y^a[z,x]^b-x^a[z,y]^b$
is divisible by each of
![]() $x^a(y^a-x^a)$
and
$x^a(y^a-x^a)$
and
![]() $r^a(y^a-x^a)$
.
$r^a(y^a-x^a)$
.
Case 2:
![]() $x\mid z$
. Then
$x\mid z$
. Then
![]() $[x, z]=[y, z]=z$
. It follows that
$[x, z]=[y, z]=z$
. It follows that
Since
![]() $a\mid b$
, the desired results follow immediately.
$a\mid b$
, the desired results follow immediately.
Lemma 2.9. Let S be gcd closed and
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
. If
$\max _{x\in S}\{|G_S(x)|\}=1$
. If
![]() $a\mid b$
, then all the elements of the nth column and the nth row of
$a\mid b$
, then all the elements of the nth column and the nth row of
![]() $[S^b][S^a]^{-1}$
are integers.
$[S^b][S^a]^{-1}$
are integers.
Proof. The proof of Lemma 2.9 is divided into two cases.
Case 1:
![]() $1\le i\le n$
and
$1\le i\le n$
and
![]() $j=n$
. By Lemmas 2.5 and 2.6,
$j=n$
. By Lemmas 2.5 and 2.6,
 $$ \begin{align*} {([S^b][S^a]^{-1})}_{in} =&\sum_{m=1}^n[x_i, x_m]^b\dfrac{1}{x_m^ax_n^a}\sum_{\substack{x_m|x_k\\ x_n|x_k}} \dfrac{c_{mk}c_{nk}}{\alpha _{a,k}}\\ =&\dfrac{1}{x_n^a}\sum_{m=1}^n\dfrac{[x_i,x_m]^bc_{mn}}{x_m^a\alpha_{a,n}} =\dfrac{1}{x_n^a\alpha_{a,n}}\sum_{m=1}^n\dfrac{[x_i,x_m]^bc_{mn}}{x_m^a}. \end{align*} $$
$$ \begin{align*} {([S^b][S^a]^{-1})}_{in} =&\sum_{m=1}^n[x_i, x_m]^b\dfrac{1}{x_m^ax_n^a}\sum_{\substack{x_m|x_k\\ x_n|x_k}} \dfrac{c_{mk}c_{nk}}{\alpha _{a,k}}\\ =&\dfrac{1}{x_n^a}\sum_{m=1}^n\dfrac{[x_i,x_m]^bc_{mn}}{x_m^a\alpha_{a,n}} =\dfrac{1}{x_n^a\alpha_{a,n}}\sum_{m=1}^n\dfrac{[x_i,x_m]^bc_{mn}}{x_m^a}. \end{align*} $$
Since
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
, we may let
$\max _{x\in S}\{|G_S(x)|\}=1$
, we may let
![]() $G_S(x_n)=\{x_{n_1}\}$
. Then by Lemmas 2.4, 2.6 and 2.8,
$G_S(x_n)=\{x_{n_1}\}$
. Then by Lemmas 2.4, 2.6 and 2.8,
 $$ \begin{align*}{([S^b])[S^a]^{-1})}_{in} =\dfrac{x_{n_1}^a[x_i,x_n]^b-x_n^a[x_i,x_{n_1}]^b}{x_n^a(x_{n_1}^a-x_n^a)}\in \mathbb{Z} \end{align*} $$
$$ \begin{align*}{([S^b])[S^a]^{-1})}_{in} =\dfrac{x_{n_1}^a[x_i,x_n]^b-x_n^a[x_i,x_{n_1}]^b}{x_n^a(x_{n_1}^a-x_n^a)}\in \mathbb{Z} \end{align*} $$
as required.
Case 2:
![]() $i=n,\ 1\le j\le n-1$
. Then
$i=n,\ 1\le j\le n-1$
. Then
 $$ \begin{align*} {( [S^b][S^a]^{-1})}_{nj} =\sum_{m=1}^n[x_n, x_m]^b\dfrac{1}{x_m^ax_j^a}\sum_{\substack{x_m|x_k\\ x_j|x_k}} \frac {c_{mk}c_{jk}}{\alpha _{a,k}} =\sum_{x_j|x_k}\frac{c_{jk}}{x_j^a\alpha _{a,k}}\sum_{x_m|x_k}\dfrac{1}{x_m^a}c_{mk}[x_m,x_n]^b. \end{align*} $$
$$ \begin{align*} {( [S^b][S^a]^{-1})}_{nj} =\sum_{m=1}^n[x_n, x_m]^b\dfrac{1}{x_m^ax_j^a}\sum_{\substack{x_m|x_k\\ x_j|x_k}} \frac {c_{mk}c_{jk}}{\alpha _{a,k}} =\sum_{x_j|x_k}\frac{c_{jk}}{x_j^a\alpha _{a,k}}\sum_{x_m|x_k}\dfrac{1}{x_m^a}c_{mk}[x_m,x_n]^b. \end{align*} $$
We claim that
 $$ \begin{align*}\gamma_k:={\frac{1}{x_j^a\alpha _{a,k}}\sum_{x_m|x_k}\dfrac{1}{x_m^a}c_{mk}[x_m,x_n]^b}\in \mathbb{Z}\end{align*} $$
$$ \begin{align*}\gamma_k:={\frac{1}{x_j^a\alpha _{a,k}}\sum_{x_m|x_k}\dfrac{1}{x_m^a}c_{mk}[x_m,x_n]^b}\in \mathbb{Z}\end{align*} $$
for any positive integer k with
![]() $x_j\mid x_k$
.
$x_j\mid x_k$
.
If
![]() $k=1$
, then
$k=1$
, then
![]() $m=j=1$
. In this case,
$m=j=1$
. In this case,
 $$ \begin{align*}\gamma_1=\dfrac{1}{\alpha _{a,1}}\cdot\dfrac{1} {x_1^{2a}}\cdot c_{11}\cdot[x_1,x_n]^b =\dfrac{[x_1,x_n]^b}{x_1^a} =\dfrac{x_1^{b-a}x_n^b}{{(x_1,x_n)}^b}\in \mathbb{Z}.\end{align*} $$
$$ \begin{align*}\gamma_1=\dfrac{1}{\alpha _{a,1}}\cdot\dfrac{1} {x_1^{2a}}\cdot c_{11}\cdot[x_1,x_n]^b =\dfrac{[x_1,x_n]^b}{x_1^a} =\dfrac{x_1^{b-a}x_n^b}{{(x_1,x_n)}^b}\in \mathbb{Z}.\end{align*} $$
Now let
![]() $k>1$
. We can set
$k>1$
. We can set
![]() $G_S(x_k)=\{x_{k_1}\}$
since
$G_S(x_k)=\{x_{k_1}\}$
since
![]() $|G_S(x_k)|=1$
. By Lemmas 2.4, 2.6 and 2.8,
$|G_S(x_k)|=1$
. By Lemmas 2.4, 2.6 and 2.8,
 $$ \begin{align*}\gamma_k={\frac{1}{x_j^a\alpha _{a,k}}\sum_{x_m|x_k} \dfrac{1}{x_m^a}c_{mk}[x_m,x_n]^b} ={\frac{x^a_{k_1}[x_k,x_n]^b-x_k^a[x_{k_1},x_n]^b} {x_j^a(x_{k_1}^a-x_k^a)}}\in \mathbb{Z} \end{align*} $$
$$ \begin{align*}\gamma_k={\frac{1}{x_j^a\alpha _{a,k}}\sum_{x_m|x_k} \dfrac{1}{x_m^a}c_{mk}[x_m,x_n]^b} ={\frac{x^a_{k_1}[x_k,x_n]^b-x_k^a[x_{k_1},x_n]^b} {x_j^a(x_{k_1}^a-x_k^a)}}\in \mathbb{Z} \end{align*} $$
as desired. This concludes the proof of the claim and of Lemma 2.9.
Finally, we can use Lemma 2.9 to establish the main result of this section.
Lemma 2.10. Let S be gcd closed and
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
. Let
$\max _{x\in S}\{|G_S(x)|\}=1$
. Let
![]() $S_1:=S\setminus \{x_n\}=\{x_1, \ldots , x_{n-1}\}$
. If
$S_1:=S\setminus \{x_n\}=\{x_1, \ldots , x_{n-1}\}$
. If
![]() $a\mid b$
, then
$a\mid b$
, then
![]() $[S^b][S^a]^{-1}\in M_n(\mathbb {Z})$
if and only if
$[S^b][S^a]^{-1}\in M_n(\mathbb {Z})$
if and only if
![]() $[S_1^b][S_1^a]^{-1}\in M_{n-1}(\mathbb {Z}).$
$[S_1^b][S_1^a]^{-1}\in M_{n-1}(\mathbb {Z}).$
Proof. First, it follows from the hypothesis and Lemma 2.9 that all the elements of the nth column and the nth row of
![]() $[S^b][S^a]^{-1}$
are integers. So it suffices to show that
$[S^b][S^a]^{-1}$
are integers. So it suffices to show that
for all integers i and j with
![]() $1\le i,j\le n-1$
.
$1\le i,j\le n-1$
.
To see this, define
 $$ \begin{align*} e_{uv}:=\left\{ \begin{aligned} 1&\quad \mbox{if} \ x_v\mid x_u,\\ 0&\quad \mbox{if} \ x_v\nmid x_u, \end{aligned} \right. \end{align*} $$
$$ \begin{align*} e_{uv}:=\left\{ \begin{aligned} 1&\quad \mbox{if} \ x_v\mid x_u,\\ 0&\quad \mbox{if} \ x_v\nmid x_u, \end{aligned} \right. \end{align*} $$
for all integers u and v between 1 and n. Then
![]() $e_{nj}=1$
if
$e_{nj}=1$
if
![]() $x_j\mid x_n$
and
$x_j\mid x_n$
and
![]() $e_{nj}=0$
otherwise. Furthermore, for any integer m with
$e_{nj}=0$
otherwise. Furthermore, for any integer m with
![]() $1\le m\le n-1$
, one has
$1\le m\le n-1$
, one has
![]() $e_{nm}=1$
if
$e_{nm}=1$
if
![]() $x_m\mid x_n$
and
$x_m\mid x_n$
and
![]() $e_{nm}=0$
otherwise. We then deduce that
$e_{nm}=0$
otherwise. We then deduce that
 $$ \begin{align} \mathcal{A}_{ij} & =\sum_{m=1}^n[x_i,x_m]^b\sum_{\substack{x_m|x_k\\ x_j|x_k}} \frac{c_{mk}c_{jk}}{x_m^ax_j^a\alpha _{a,k}} -\sum_{m=1}^{n-1}[x_i,x_m]^b\sum _{\substack{x_m|x_k\\ x_j|x_k,\, x_k\neq x_n}} \frac{c_{mk}c_{jk}}{x_m^ax_j^a\alpha _{a,k}}\notag\\ & =\frac{c_{nn}c_{jn}}{x_n^ax_j^a\alpha _{a,n}}[x_i,x_n]^b e_{nj}+ \sum_{m=1}^{n-1}\frac{c_{mn}c_{jn}}{x_m^ax_j^a\alpha _{a,n}} [x_i,x_m]^b e_{nj}e_{nm} \notag\\ & =e_{nj}\frac{c_{jn}}{x_j^a\alpha _{a,n}} \bigg(\dfrac{[x_i,x_n]^b}{x_n^a}+\sum_{m=1}^{n-1} \dfrac{[x_i,x_m]^bc_{mn}e_{nm}}{x_m^a} \bigg) :=e_{nj} A_{ij}. \end{align} $$
$$ \begin{align} \mathcal{A}_{ij} & =\sum_{m=1}^n[x_i,x_m]^b\sum_{\substack{x_m|x_k\\ x_j|x_k}} \frac{c_{mk}c_{jk}}{x_m^ax_j^a\alpha _{a,k}} -\sum_{m=1}^{n-1}[x_i,x_m]^b\sum _{\substack{x_m|x_k\\ x_j|x_k,\, x_k\neq x_n}} \frac{c_{mk}c_{jk}}{x_m^ax_j^a\alpha _{a,k}}\notag\\ & =\frac{c_{nn}c_{jn}}{x_n^ax_j^a\alpha _{a,n}}[x_i,x_n]^b e_{nj}+ \sum_{m=1}^{n-1}\frac{c_{mn}c_{jn}}{x_m^ax_j^a\alpha _{a,n}} [x_i,x_m]^b e_{nj}e_{nm} \notag\\ & =e_{nj}\frac{c_{jn}}{x_j^a\alpha _{a,n}} \bigg(\dfrac{[x_i,x_n]^b}{x_n^a}+\sum_{m=1}^{n-1} \dfrac{[x_i,x_m]^bc_{mn}e_{nm}}{x_m^a} \bigg) :=e_{nj} A_{ij}. \end{align} $$
Let us now show that
![]() $A_{ij}\in \mathbb {Z}$
. Since
$A_{ij}\in \mathbb {Z}$
. Since
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
, one may let
$\max _{x\in S}\{|G_S(x)|\}=1$
, one may let
![]() $G_S(x_n)=\{x_{n_1}\}$
. From Lemma 2.4,
$G_S(x_n)=\{x_{n_1}\}$
. From Lemma 2.4,
![]() $\alpha _{a,n}=x_n^{-a}-x_{n_1}^{-a}.$
However, by Lemma 2.6, for any integer m with
$\alpha _{a,n}=x_n^{-a}-x_{n_1}^{-a}.$
However, by Lemma 2.6, for any integer m with
![]() $1\le m\le n-1$
,
$1\le m\le n-1$
,
![]() $c_{mn}=-1$
if
$c_{mn}=-1$
if
![]() $m=n_1$
and
$m=n_1$
and
![]() $c_{mn}=0$
otherwise. It follows from (2.8) and Lemma 2.8 that
$c_{mn}=0$
otherwise. It follows from (2.8) and Lemma 2.8 that
 $$ \begin{align} {A_{ij}=\frac{x_{n_1}^a[x_i,x_n]^b-x_n^a[x_i,x_{n_1}]^b} {x_j^a(x_{n_1}^a-x_n^a)}\cdot c_{jn}}\in \mathbb{Z}. \end{align} $$
$$ \begin{align} {A_{ij}=\frac{x_{n_1}^a[x_i,x_n]^b-x_n^a[x_i,x_{n_1}]^b} {x_j^a(x_{n_1}^a-x_n^a)}\cdot c_{jn}}\in \mathbb{Z}. \end{align} $$
Since
![]() $e_{nj}\in \{0,1\}$
, (2.8) and (2.9) yield (2.7).
$e_{nj}\in \{0,1\}$
, (2.8) and (2.9) yield (2.7).
The proof of Lemma 2.10 is complete.
3 Proof of Theorem 1.1
We prove Theorem 1.1 by using induction on
![]() $n=|S|$
.
$n=|S|$
.
For
![]() $n=1$
, the statement is clearly true.
$n=1$
, the statement is clearly true.
Let
![]() $n=2$
. Since
$n=2$
. Since
![]() $S=\{x_1, x_2\}$
is gcd closed,
$S=\{x_1, x_2\}$
is gcd closed,
![]() $(x_1, x_2)=x_1$
and
$(x_1, x_2)=x_1$
and
![]() $x_1\mid x_2$
. It follows that
$x_1\mid x_2$
. It follows that
 $$ \begin{align*}\begin{aligned} {[S^b]}[S^a]^{-1}&= \begin{pmatrix} x_1^b&x_2^b\\[3pt] x_2^b&x_2^b \end{pmatrix} \cdot\frac {1}{x_2^a(x_1^a-x_2^a)} \begin{pmatrix} x_2^a&-x_2^a\\[3pt] -x_2^a&x_1^a \end{pmatrix} =\begin{pmatrix} \mathcal{B}&-x_1^a\mathcal{C}\\[3pt] 0&x_2^{b-a} \end{pmatrix}, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} {[S^b]}[S^a]^{-1}&= \begin{pmatrix} x_1^b&x_2^b\\[3pt] x_2^b&x_2^b \end{pmatrix} \cdot\frac {1}{x_2^a(x_1^a-x_2^a)} \begin{pmatrix} x_2^a&-x_2^a\\[3pt] -x_2^a&x_1^a \end{pmatrix} =\begin{pmatrix} \mathcal{B}&-x_1^a\mathcal{C}\\[3pt] 0&x_2^{b-a} \end{pmatrix}, \end{aligned} \end{align*} $$
where
 $$ \begin{align*}\mathcal{B}:=\dfrac {x_2^b-x_1^b}{x_2^a-x_1^a} \quad\mathrm{and}\quad \mathcal{C}:=\dfrac {x_2^{b-a}-x_1^{b-a}}{x_2^a-x_1^a}.\end{align*} $$
$$ \begin{align*}\mathcal{B}:=\dfrac {x_2^b-x_1^b}{x_2^a-x_1^a} \quad\mathrm{and}\quad \mathcal{C}:=\dfrac {x_2^{b-a}-x_1^{b-a}}{x_2^a-x_1^a}.\end{align*} $$
Since
![]() $a\mid b$
, implying that
$a\mid b$
, implying that
![]() $a\mid (b-a)$
, it follows that
$a\mid (b-a)$
, it follows that
![]() $\mathcal {B}\in \mathbb {Z}$
and
$\mathcal {B}\in \mathbb {Z}$
and
![]() $\mathcal {C}\in \mathbb {Z}$
, that is,
$\mathcal {C}\in \mathbb {Z}$
, that is,
![]() ${[S^b]}[S^a]^{-1}\in M_2(\mathbb {Z})$
. The statement is true for this case.
${[S^b]}[S^a]^{-1}\in M_2(\mathbb {Z})$
. The statement is true for this case.
Let
![]() $n=3$
. Since
$n=3$
. Since
![]() $S=\{x_1,x_2,x_3\}$
is gcd closed, we have
$S=\{x_1,x_2,x_3\}$
is gcd closed, we have
![]() $x_1\mid x_i\ (i=2, 3)$
and
$x_1\mid x_i\ (i=2, 3)$
and
![]() $(x_2,x_3)=x_1$
or
$(x_2,x_3)=x_1$
or
![]() $x_2$
. Consider the following two cases.
$x_2$
. Consider the following two cases.
Case 1:
![]() $(x_2,x_3)=x_1$
. Then one computes
$(x_2,x_3)=x_1$
. Then one computes
 $$ \begin{align*} \begin{split} {[S^b]}[S^a]^{-1} &=\begin{pmatrix} x_1^b&x_2^b&x_3^b\\[4pt] x_2^b&x_2^b&\dfrac{x_2^bx_3^b}{x_1^b}\\[4pt] x_3^b&\dfrac{x_2^bx_3^b}{x_1^b}&x_3^b \end{pmatrix} \cdot \frac {x_1^a}{x_2^ax_3^a(x_2^a-x_1^a)(x_3^a-x_1^a)}\\[4pt] &\quad \times \begin{pmatrix} \dfrac{x_1^{2a}x_2^ax_3^a-x_2^{2a}x_3^{2a}}{x_1^{2a}} &\dfrac{x_2^ax_3^{2a}-x_1^ax_2^ax_3^a}{x_1^a} &\dfrac{x_2^{2a}x_3^a-x_1^ax_2^ax_3^a}{x_1^a}\\[4pt] \dfrac{x_2^ax_3^{2a}-x_1^ax_2^ax_3^a}{x_1^a}&x_1^ax_3^a-x_3^{2a}&0\\[4pt] \dfrac{x_2^{2a}x_3^a-x_1^ax_2^ax_3^a}{x_1^a}&0&x_1^ax_2^a-x_2^{2a} \end{pmatrix}\\ &=\begin{pmatrix} \mathcal{B}+x_3^a\mathcal{F}&-x_1^a\mathcal{C}&-x_1^a\mathcal{F}\\[4pt] x_3^a\mathcal{D}\mathcal{F}&x_2^{b-a}&-x_1^a\mathcal{D}\mathcal{F}\\[4pt] x_2^a\mathcal{E}\mathcal{C}&-x_1^a\mathcal{E}\mathcal{C}&x_3^{b-a} \end{pmatrix}, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} {[S^b]}[S^a]^{-1} &=\begin{pmatrix} x_1^b&x_2^b&x_3^b\\[4pt] x_2^b&x_2^b&\dfrac{x_2^bx_3^b}{x_1^b}\\[4pt] x_3^b&\dfrac{x_2^bx_3^b}{x_1^b}&x_3^b \end{pmatrix} \cdot \frac {x_1^a}{x_2^ax_3^a(x_2^a-x_1^a)(x_3^a-x_1^a)}\\[4pt] &\quad \times \begin{pmatrix} \dfrac{x_1^{2a}x_2^ax_3^a-x_2^{2a}x_3^{2a}}{x_1^{2a}} &\dfrac{x_2^ax_3^{2a}-x_1^ax_2^ax_3^a}{x_1^a} &\dfrac{x_2^{2a}x_3^a-x_1^ax_2^ax_3^a}{x_1^a}\\[4pt] \dfrac{x_2^ax_3^{2a}-x_1^ax_2^ax_3^a}{x_1^a}&x_1^ax_3^a-x_3^{2a}&0\\[4pt] \dfrac{x_2^{2a}x_3^a-x_1^ax_2^ax_3^a}{x_1^a}&0&x_1^ax_2^a-x_2^{2a} \end{pmatrix}\\ &=\begin{pmatrix} \mathcal{B}+x_3^a\mathcal{F}&-x_1^a\mathcal{C}&-x_1^a\mathcal{F}\\[4pt] x_3^a\mathcal{D}\mathcal{F}&x_2^{b-a}&-x_1^a\mathcal{D}\mathcal{F}\\[4pt] x_2^a\mathcal{E}\mathcal{C}&-x_1^a\mathcal{E}\mathcal{C}&x_3^{b-a} \end{pmatrix}, \end{split} \end{align*} $$
where
![]() $\mathcal {B}$
and
$\mathcal {B}$
and
![]() $\mathcal {C}$
are as given earlier in this section,
$\mathcal {C}$
are as given earlier in this section,
![]() $\mathcal {D}:={x_2^b}/{x_1^b}$
,
$\mathcal {D}:={x_2^b}/{x_1^b}$
,
![]() $\mathcal {E}:={x_3^b}/{x_1^b}$
and
$\mathcal {E}:={x_3^b}/{x_1^b}$
and
![]() $\mathcal {F}:=({x_3^{b-a}-x_1^{b-a})}/({x_3^a-x_1^a}).$
Since
$\mathcal {F}:=({x_3^{b-a}-x_1^{b-a})}/({x_3^a-x_1^a}).$
Since
![]() $x_1\mid x_2$
,
$x_1\mid x_2$
,
![]() $x_1\mid x_3$
and
$x_1\mid x_3$
and
![]() $a\mid (b-a)$
, all of
$a\mid (b-a)$
, all of
![]() $\mathcal {B}, \mathcal {C}, \mathcal {D}, \mathcal {E}$
and
$\mathcal {B}, \mathcal {C}, \mathcal {D}, \mathcal {E}$
and
![]() $\mathcal {F}$
are integers. Hence,
$\mathcal {F}$
are integers. Hence,
![]() ${[S^b]}[S^a]^{-1}\in M_3(\mathbb {Z})$
. The statement holds in this case.
${[S^b]}[S^a]^{-1}\in M_3(\mathbb {Z})$
. The statement holds in this case.
Case 2:
![]() $(x_2,x_3)=x_2$
. Then
$(x_2,x_3)=x_2$
. Then
![]() $x_2\mid x_3$
. We compute
$x_2\mid x_3$
. We compute
 $$ \begin{align*}\begin{aligned} {[S^b]}[S^a]^{-1}&= \begin{pmatrix} x_1^b&x_2^b&x_3^b\\[4pt] x_2^b&x_2^b&x_3^b\\[4pt] x_3^b&x_3^b&x_3^b \end{pmatrix} \cdot \frac {1}{x_3^a(x_2^a-x_1^a)(x_3^a-x_2^a)}\\ &\quad \times \begin{pmatrix} x_3^a(x_2^a-x_3^a)&x_3^a(x_3^a-x_2^a)&0\\[4pt] x_3^a(x_3^a-x_2^a)&x_3^a(x_1^a-x_3^a)&x_3^a(x_2^a-x_1^a)\\[4pt] 0&x_3^a(x_2^a-x_1^a)&x_2^a(x_1^a-x_2^a) \end{pmatrix}\\ &=\begin{pmatrix} \mathcal{B}&-\mathcal{B}+\mathcal{G}&-x_2^a\mathcal{H}\\[4pt] 0&\mathcal{G}&-x_2^a\mathcal{H}\\[4pt] 0&0&x_3^{b-a} \end{pmatrix}, \end{aligned} \end{align*} $$
$$ \begin{align*}\begin{aligned} {[S^b]}[S^a]^{-1}&= \begin{pmatrix} x_1^b&x_2^b&x_3^b\\[4pt] x_2^b&x_2^b&x_3^b\\[4pt] x_3^b&x_3^b&x_3^b \end{pmatrix} \cdot \frac {1}{x_3^a(x_2^a-x_1^a)(x_3^a-x_2^a)}\\ &\quad \times \begin{pmatrix} x_3^a(x_2^a-x_3^a)&x_3^a(x_3^a-x_2^a)&0\\[4pt] x_3^a(x_3^a-x_2^a)&x_3^a(x_1^a-x_3^a)&x_3^a(x_2^a-x_1^a)\\[4pt] 0&x_3^a(x_2^a-x_1^a)&x_2^a(x_1^a-x_2^a) \end{pmatrix}\\ &=\begin{pmatrix} \mathcal{B}&-\mathcal{B}+\mathcal{G}&-x_2^a\mathcal{H}\\[4pt] 0&\mathcal{G}&-x_2^a\mathcal{H}\\[4pt] 0&0&x_3^{b-a} \end{pmatrix}, \end{aligned} \end{align*} $$
where
![]() $\mathcal {B}$
is as before,
$\mathcal {B}$
is as before,
![]() $\mathcal {G}:={({x_3^b-x_2^b)}/{(x_3^a-x_2^a})}$
and
$\mathcal {G}:={({x_3^b-x_2^b)}/{(x_3^a-x_2^a})}$
and
![]() $\mathcal {H}:={(x_3^{b-a}-x_2^{b-a})}/{(x_3^a-x_2^a)}$
. Since
$\mathcal {H}:={(x_3^{b-a}-x_2^{b-a})}/{(x_3^a-x_2^a)}$
. Since
![]() $a\mid b$
and
$a\mid b$
and
![]() $a\mid (b-a)$
imply that
$a\mid (b-a)$
imply that
![]() $\mathcal {G}\in \mathbb {Z}$
and
$\mathcal {G}\in \mathbb {Z}$
and
![]() $\mathcal {H}\in \mathbb {Z}$
, it follows immediately that
$\mathcal {H}\in \mathbb {Z}$
, it follows immediately that
![]() ${[S^b]}[S^a]^{-1}\in M_3(\mathbb {Z})$
. The statement is true for this case.
${[S^b]}[S^a]^{-1}\in M_3(\mathbb {Z})$
. The statement is true for this case.
Now let
![]() $n\ge 4$
. Assume that the statement is true for the
$n\ge 4$
. Assume that the statement is true for the
![]() $n-1$
case. In what follows, we show that the statement is true for the n case. Since S is gcd closed and
$n-1$
case. In what follows, we show that the statement is true for the n case. Since S is gcd closed and
![]() $\max _{x\in S}\{|G_S(x)|\}=1$
, it follows that
$\max _{x\in S}\{|G_S(x)|\}=1$
, it follows that
![]() $S_1:=\{x_1,\ldots , x_{n-1}\}$
is also gcd closed and
$S_1:=\{x_1,\ldots , x_{n-1}\}$
is also gcd closed and
![]() $\max _{x\in S_1}\{|G_{S_1}(x)|\}=1$
. Hence by the inductive hypothesis,
$\max _{x\in S_1}\{|G_{S_1}(x)|\}=1$
. Hence by the inductive hypothesis,
![]() $[S_1^b][S_1^a]^{-1}\in M_{n-1}( \mathbb {Z})$
. Finally, from Lemma 2.10,
$[S_1^b][S_1^a]^{-1}\in M_{n-1}( \mathbb {Z})$
. Finally, from Lemma 2.10,
![]() $[S^b][S^a]^{-1}\in M_n(\mathbb {Z})$
as desired.
$[S^b][S^a]^{-1}\in M_n(\mathbb {Z})$
as desired.
This finishes the proof of Theorem 1.1.
![]() $\Box $
$\Box $
Acknowledgement
The authors would like to thank the anonymous referee for careful reading of the paper and helpful suggestions that improved its presentation.