Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-06T07:56:23.181Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE CONNECTEDNESS OF THE CHABAUTY SPACE OF A LOCALLY COMPACT PRONILPOTENT GROUP

Part of: Locally compact groups and their algebras Fairly general properties Special aspects of infinite or finite groups Basic constructions

Published online by Cambridge University Press:  17 May 2021

BILEL KADRI Open the ORCID record for BILEL KADRI [Opens in a new window]
BILEL KADRI*
Affiliation:
Sfax Preparatory Engineering Institute, Department of Mathematics, Sfax University, 3018 Sfax, Tunisia
*
e-mail: bilel.kadri@yahoo.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

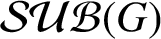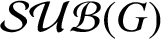Let G be a locally compact group and let ${\mathcal {SUB}(G)}$ be the hyperspace of closed subgroups of G endowed with the Chabauty topology. The main purpose of this paper is to characterise the connectedness of the Chabauty space ${\mathcal {SUB}(G)}$ . More precisely, we show that if G is a connected pronilpotent group, then ${\mathcal {SUB}(G)}$ is connected if and only if G contains a closed subgroup topologically isomorphic to 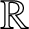${{\mathbb R}}$ .

Keywords

Chabauty topologylocally compact grouppronilpotent group

MSC classification

Primary: 54B20: Hyperspaces
Secondary: 20F19: Generalizations of solvable and nilpotent groups 22D05: General properties and structure of locally compact groups 54D05: Connected and locally connected spaces (general aspects)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 105 , Issue 1 , February 2022 , pp. 161 - 170
Check for updates
Copyright
© 2021 Australian Mathematical Publishing Association Inc.

References

Abert, M., Bergeron, N., Biringer, I., Gelander, T., Nikolov, N., Raimbault, J. and Samet, I., ‘On the growth of ${L}^2$ -invariants for sequences of lattices in Lie groups’, Ann. Math. 185 (2017), 711–790.CrossRefGoogle Scholar
Bekka, M. and Kaniuth, E., ‘Topological Frobenius properties for nilpotent groups’, Math. Scand. 63 (1988), 282–296.CrossRefGoogle Scholar
Benedetti, R. and Petronio, C., Lectures on Hyperbolic Geometry (Springer, Berlin, 1992).CrossRefGoogle Scholar
Bourbaki, N., Intégration, Éléments de Mathématique (Springer, Heidelberg, 2007), Chs. 7--8.Google Scholar
Bridson, M., de la Harpe, P. and Kleptsyn, V., ‘The Chabauty space of closed subgroups of the three-dimensional Heisenberg group’, Pacific J. Math. 240 (2009), 1–48.CrossRefGoogle Scholar
Cornulier, Y., ‘On the Chabauty space of locally compact abelian groups’, Algebr. Geom. Topol. 11 (2011), 2007–2035.CrossRefGoogle Scholar
Grosser, S. and Moskowitz, M., ‘On central topological groups’, Trans. Amer. Math. Soc. 127 (1967), 317–340.CrossRefGoogle Scholar
Haettel, T., ‘L’espace des sous-groupes fermés de $\mathbb{R}\times \mathbb{Z}$ ’, Algebr. Geom. Topol. 10 (2010), 1395–1415.CrossRefGoogle Scholar
Hamrouni, H. and Kadri, B., ‘On the compact space of closed subgroups of locally compact groups’, J. Lie Theory 23 (2014), 715–723.Google Scholar
Hamrouni, H. and Kadri, B., ‘On the connectedness of the Chabauty space of a locally compact prosolvable group’, Adv. Pure Appl. Math. 6 (2015), 97–111.Google Scholar
Hamrouni, H. and Kadri, B., ‘Locally compact groups with totally disconnected space of subgroups’, J. Group Theory 22 (2019), 119–132.CrossRefGoogle Scholar
Hazod, W., Hofmann, K. H., Scheffler, H. P., Wüstner, M. and Zeuner, H., ‘Normalizers of compact subgroups, the existence of commuting automorphisms, and application to operator semistable measures’, J. Lie Theory 8 (1998), 189–209.Google Scholar
Iwasawa, K., ‘On some types of topological groups’, Ann. of Math. (2) 50 (1949), 507–558.CrossRefGoogle Scholar
Khukhro, E. I. and Mazurov, V. D., Unsolved Problems in Group Theory, The Kourovka Notebook 18 (Russian Academy of Sciences Siberian Division, Institute of Mathematics, Novosibirsk, 2014).Google Scholar
Kloeckner, B., ‘The space of closed subgroups of ${\mathbb{R}}^n$ is stratified and simply connected’, J. Topol. 2 (2009), 570–588.CrossRefGoogle Scholar
Pourezza, I. and Hubbard, J., ‘The space of closed subgroups of ${\mathbb{R}}^2$ ’, Topology 18 (1979), 143–146.CrossRefGoogle Scholar
Protasov, I. V., ‘Local theorems for topological groups’, Math. USSR Izv. 15 (1980), 625–633.CrossRefGoogle Scholar
Protasov, I. V. and Tsybenko, Y. V., ‘Connectedness in the space of subgroups’, Ukraïn. Mat. Zh. 35 (1983), 382–385 (in Russian); English translation: Ukrainian Math. J. 35 (1983), 332–334.Google Scholar
Stroppel, M., Locally Compact Groups (European Mathematical Society, Berlin, 2006).CrossRefGoogle Scholar