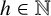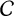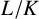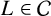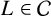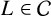1 Introduction
For a number field
$L/\Bbb {Q}$
, let
$n_L$
and
$d_L$
denote its degree and absolute discriminant, respectively. Let
$h_L$
denote the class number of L. Stark [Reference Stark13] conjectured that for any
$h\in \Bbb {N}$
, there are only finitely many CM-fields, that is, totally imaginary quadratic extensions of totally real fields, with class number h. Stark proved his conjecture for fields with fixed degree greater than or equal to 6.
A number field M is called almost normal if there exists a sequence of number fields
$ \Bbb {Q}= M_0 \subseteq M_1 \subseteq \cdots \subseteq M_{\ell } =M, $
for some
$\ell \in \Bbb {N}$
, such that each extension
$M_{i}/M_{i-1}$
is normal for
$1\le i\le \ell $
. In [Reference Odlyzko11], Odlyzko verified Stark’s conjecture for CM-fields L with
$n_L\ge 6$
whose maximal totally real subfields
$L^+$
are almost normal. In [Reference Hoffstein and Jochnowitz6], Hoffstein and Jochnowitz proved that there exists an effective absolute constant C such that the assumption of the almost normality of
$L^+$
in Odlyzko’s theorem can be replaced with the bound
$d_{L^+}>C^{[L^+:\Bbb {Q}]}$
. Murty [Reference Murty10] proved Stark’s conjecture for CM-fields L having solvable normal closures over
$\Bbb {Q}$
when
$n_L\ge 6$
.
For any CM-field L, class field theory tells us that the class number
$h_{L^+}$
divides
$h_L$
, where
$L^+$
is the maximal totally real subfield of L. Thus, the number
$h^-_L = h_L/h_{L^+}$
is a positive integer. This number is called the relative class number of L. One may also consider the following problem that generalises Stark’s conjecture.
Problem 1.1. Let H be a positive integer. Is the set of CM-fields L with
$h^{-}_L \le H$
finite?
If the answer to this problem is affirmative, then Stark’s conjecture is true. Since the class number of
$\Bbb {Q}$
is 1, Problem 1.1 for CM-fields L with
$n_L=2$
is, in fact, Gauss’s original class number conjecture proved by Deuring, Hecke, Heilbronn and Mordell. An effective version of Gauss’s conjecture has been established by Goldfeld [Reference Goldfeld4].
The first goal of this paper is to prove an instance of Problem 1.1. Let K be a subfield of a number field L. We say
$L/K$
has solvable Galois closure if
$\operatorname {\mathrm {Gal}}(\tilde {L}/K)$
is solvable, where
$\tilde {L}$
denotes the normal closure of L over K. Throughout this paper, we let
$\mathcal {C}$
be the class of number fields L for which L has an almost normal subfield K such that
$L/K$
has solvable Galois closure. Our first main result is the following theorem.
Theorem 1.2. Let H be a positive integer.
(i) The set of CM-fields
$L\in \mathcal {C}$
with
$n_L\neq 4$
and
$h^-_L\le H$
is finite and its cardinality can be bounded effectively (in terms of H). Moreover, if Artin’s conjecture is true, then the set of CM-fields L with
$n_L\neq 4$
and
$h^-_L\le H$
is finite and its cardinality can be bounded effectively.
(ii) Unconditionally, the set of CM-fields L with
$n_L= 4$
and
$h^-_L\le H$
is finite.
Remark 1.3. (i) The class
$\mathcal {C}$
contains every number field with solvable Galois closure over
$\Bbb {Q}$
. If the maximal totally real subfield of L is almost normal, then L is also almost normal and so
$L\in \mathcal {C}$
. Thus, the class
$\mathcal {C}$
includes the fields considered by Murty [Reference Murty10] and Odlyzko [Reference Odlyzko11] and Theorem 1.2 presents a common extension of their results. There is a further extension of Murty’s result because the Galois closure of
$L\in \mathcal {C}$
over
$\Bbb {Q}$
may not be solvable. For instance, if L contains a subfield K that is a nonsolvable Galois extension of
$\Bbb {Q}$
, then the Galois closure of L over
$\Bbb {Q}$
cannot be solvable even if the Galois closure of L over K is solvable.
(ii) The second part of Theorem 1.2 is ineffective since the proof requires Siegel’s ineffective bound on the exceptional zeros of Dedekind zeta functions of quadratic fields.
There are several questions and results concerning the behaviour of
$h_L$
as L varies. Most famously, in [Reference Brauer1], Brauer proved the following theorem.
Theorem 1.4 (Brauer–Siegel theorem).
Let
$\{L_i\}$
be a family of number fields (that is,
$L_i\neq L_j$
for any
$i\neq j$
) such that each
$L_i/\Bbb {Q}$
is Galois. If
$\lim _{i\rightarrow \infty } d_{L_i}^{1/n_{L_i}} = \infty ,$
then
$$ \begin{align*}\lim_{i\rightarrow \infty} \frac{\log(h_{L_i} R_{L_i} )}{\log \sqrt{d_{L_i}}}=1, \end{align*} $$
where
$R_{L_i} $
denotes the regulator of
$L_i$
. Moreover, the Galois condition on
$L_i/\Bbb {Q}$
can be removed if the generalised Riemann hypothesis is true.
Siegel [Reference Siegel12] proved this theorem for the case when
$\{L_i\}$
is a family of quadratic fields. If
$\{L_i\}$
is a family of imaginary quadratic fields, then
$R_{L_i}=1$
and hence the Brauer–Siegel theorem provides a rate at which
$h_{L_i}$
goes to infinity. Consequently, there are only finitely many imaginary quadratic fields with a bounded class number (see also [Reference Heilbronn5]).
In [Reference Stark13], Stark proved an effective and much stronger version of the Brauer–Siegel theorem for families of almost normal number fields that do not contain any quadratic fields. Stark was aware that the Brauer–Siegel theorem would hold over families of almost normal fields, but this was only made explicit in the work of Zykin [Reference Zykin15].
In [Reference Tsfasman and Vlăduţ14], Tsfasman and Vlăduţ formulated the generalised Brauer–Siegel conjecture (GBS) and proved some instances of it. Let
$\mathcal {L}=\{L_i\}$
be a family of number fields. By the definition of the Dedekind zeta function
$\zeta _{L_i}(s)$
of
$L_i$
, there are nonnegative integers
$N_q(L_i)$
such that
$$ \begin{align*}\zeta_{L_i}(s)=\prod_{q} (1 - q^{-s})^{-N_q(L_i)}, \end{align*} $$
for
${\mathrm {Re}}(s)>1$
, where the product is over prime powers q. We call
$\mathcal {L}=\{L_i\}$
asymptotically exact if the limits
$$ \begin{align*}\phi_q(\mathcal{L}) = \lim_{i\rightarrow \infty}\frac{N_q(L_i)}{g_{L_i}},\quad \phi_{\Bbb{R}}(\mathcal{L}) = \lim_{i\rightarrow \infty}\frac{r_1(L_i)}{g_{L_i}} \quad\text{and}\quad \phi_{\Bbb{C}}(\mathcal{L}) = \lim_{i\rightarrow \infty}\frac{r_2(L_i)}{g_{L_i}} \end{align*} $$
exist, for every prime power q, where
$g_{L_i}= \log \sqrt {d_{L_i}}$
, and
$r_1(L_i)$
and
$r_2(L_i)$
are the numbers of real and complex embeddings of
$L_i$
, respectively.
Conjecture 1.5 (Generalised Brauer–Siegel conjecture).
For any asymptotically exact family
$\mathcal {L}=\{L_i\}$
, the limit
$BS(\mathcal {L}) = \lim _{i\rightarrow \infty } {\log (h_{L_i}R_{L_i})}/{g_{L_i}}$
exists. Moreover,
$$ \begin{align*}BS(\mathcal{L})= 1 + \sum_{q} \phi_q(\mathcal{L}) \log \frac{q}{q-1} -\phi_{\Bbb{R}}(\mathcal{L})\log 2-\phi_{\Bbb{C}}(\mathcal{L})\log 2\pi. \end{align*} $$
Following [Reference Tsfasman and Vlăduţ14], an asymptotically exact family
$\mathcal {L}$
will be called asymptotically bad if
$\phi _q(\mathcal {L})=\phi _{\Bbb {R}}(\mathcal {L})=\phi _{\Bbb {C}}(\mathcal {L})=0$
for every prime power q. If an asymptotically exact family is not asymptotically bad, then it will be said to be asymptotically good.
Tsfasman and Vlăduţ [Reference Tsfasman and Vlăduţ14] proved their conjecture for any asymptotically exact family under the assumption of the generalised Riemann hypothesis. Also, unconditionally, they proved GBS for asymptotically good towers of almost normal fields. (Recall that a family
$\{L_i\}$
is called a tower if
$L_i\subsetneq L_{i+1}$
for each i.) Moreover, Zykin [Reference Zykin15] proved GBS for asymptotically bad families of almost normal fields. Recently, Dixit [Reference Dixit3] showed that GBS is true for asymptotically good towers and asymptotically bad families of number fields with solvable Galois closure over
$\Bbb {Q}$
. Our second goal is to prove the following extension of the work of Dixit, Tsfasman and Vlăduţ, and Zykin.
Theorem 1.6. If an exact family
$\mathcal {L} \subseteq \mathcal {C}$
is an asymptotically good tower or an asymptotically bad family, then GBS is true for
$\mathcal {L}$
. Furthermore, if Artin’s conjecture is true, then GBS is true for any asymptotically good tower and any asymptotically bad family.
Remark 1.7. (i) As noted by Dixit [Reference Dixit3], it follows from the class number formula that GBS for an exact family
$\mathcal {L}=\{L_i\}$
is equivalent to the statement that the limit
$$ \begin{align*}\rho(\mathcal{L})= \lim_{i\rightarrow \infty} \frac{\log \rho_{L_i}}{g_{L_i}} \end{align*} $$
exists and equals
$ \sum _{q} \phi _q(\mathcal {L}) \log ({q}/(q-1)), $
where
$\rho_{L_i}$
is the residue of the Dedekind zeta function
$\zeta _{L_i}(s)$
at
$s=1$
. We shall use this fact repeatedly in Section 4.
(ii) The family
$\mathcal {L}=\{L_i\}$
is asymptotically bad if and only if
$ \lim _{i\rightarrow \infty } d_{L_i}^{1/n_{L_i}} = \infty .$
From this, GBS for asymptotically bad families is equivalent to the classical Brauer–Siegel conjecture (that is, the Brauer–Siegel ‘theorem’ without the Galois condition on
$L_i$
).
2 Stark zeros in certain towers of number fields
Stark’s conjecture arose from his work on exceptional zeros of Dedekind zeta functions. These zeros are also crucial to the study of GBS. In this section, we will briefly review some results concerning ‘Stark zeros’ (see [Reference Murty10] for further discussion).
For any number field L, Stark showed that the Dedekind zeta function
$\zeta _L(s)$
has at most one zero in the region
$$ \begin{align} 1-\frac{1}{4 \log d_L}\le {\mathrm{Re}}(s) \le 1 \quad \text{and} \quad |{\mathrm{Re}}(s)|<\frac{1}{4 \log d_L}, \end{align} $$
and if the zero exists in this region, it must be real and simple. We call this possible zero the Stark zero of
$\zeta _L(s)$
and denote it by
$\beta _0$
. For any Galois extension
$L/K$
, if the Stark zero
$\beta _0$
of
$\zeta _L(s)$
exists, then there is a field M with
$K\subseteq M \subseteq L$
such that
$[M:K]\le 2$
and
$\zeta _{M}({\kern1pt}\beta _0)=0$
. In the case when L is almost normal, Stark [Reference Stark13, Lemma 10] showed that if the Stark zero
$\beta _0$
of
$\zeta _L(s)$
appears in the region
$$ \begin{align*} 1-\frac{1}{16 \log d_L}\le {\mathrm{Re}}(s) \le 1, \end{align*} $$
then there is a quadratic field
$F \subseteq L$
such that
$\zeta _F({\kern1pt}\beta _0)=0$
. These results play a key role in the argument of Odlyzko [Reference Odlyzko11].
Let m be a positive integer. We set
$$ \begin{align} e(m)=\max_{p^{\alpha} \parallel m} \alpha \quad\text{and}\quad \delta(m)= (e(m)+1)^2 3^{1/3} 12^{e(m)-1}. \end{align} $$
Theorem 2.1 (Murty, [Reference Murty10, Theorem 2.1]).
Let
$L/K$
be an extension with solvable Galois closure. Let m be the degree of
$L/K$
. There exists an absolute constant
$c_0> 0$
such that if
$\zeta _L(s)$
has a zero
$\beta _0$
in the region
$$ \begin{align*} 1-\frac{c_0}{m^{e(m)}\delta(m) \log d_L}\le {\mathrm{Re}}(s) \le 1 \quad\text{and}\quad |{\mathrm{Re}}(s)|<\frac{c_0}{m^{e(m)}\delta(m) \log d_L}, \end{align*} $$
then there is a field M with
$K\subseteq M \subseteq L$
such that
$[M:K]\le 2$
and
$\zeta _{M}({\kern1pt}\beta _0)=0$
.
As in the work of Odlyzko [Reference Odlyzko11], in order to ‘descend’ the Stark zero of
$\zeta _L(s)$
to a quadratic field, Murty considered the class of number fields with solvable Galois closure over
$\Bbb {Q}$
and applied his theorem with
$K=\Bbb {Q}$
.
We require the following refinement of Murty’s theorem for our main theorems.
Theorem 2.2. Let
$L/K$
be an extension with solvable Galois closure and let K be an almost normal field. Let m and n be the degrees of
$L/K$
and
$L/\Bbb {Q}$
, respectively. Let
$c_0$
be as in Theorem 2.1 and
$c_1=\min \{c_0,{1}/{16}\} $
. Suppose that
$\zeta _L(s)$
has a zero
$\beta _0$
in the region
$$ \begin{align} 1-\frac{c_1}{m^{e(m)}\delta(m) \log d_L}\le {\mathrm{Re}}(s) \le 1 \quad{and}\quad |{\mathrm{Re}}(s)|<\frac{1}{4 \log d_L}, \end{align} $$
where
$e(m)$
and
$\delta (m)$
are defined as in (2.2). Then
$\beta _0$
is real and simple and there is a quadratic field
$F \subseteq L$
such that
$\zeta _F({\kern1pt}\beta _0)=0$
. Consequently, if
$\zeta _L(s)$
has a zero
$\beta _0$
in the region
$$ \begin{align} 1-\frac{c_1}{n^{e(n)}\delta(n) \log d_L}\le {\mathrm{Re}}(s) \le 1 \quad{and}\quad |{\mathrm{Re}}(s)|<\frac{1}{4 \log d_L}, \end{align} $$
then
$\beta _0$
is real and simple and there is a quadratic field
$F \subseteq L$
such that
$\zeta _F({\kern1pt}\beta _0)=0$
.
Proof. As the region (2.3) is contained in the region (2.1),
$\beta _0$
must be real and simple. Since
$c_1\le c_0$
, by Theorem 2.1, there is a field M with
$K\subseteq M \subseteq L$
such that
$[M:K]\le 2$
and
$\zeta _{M}({\kern1pt}\beta _0)=0$
. As
$[M:K]\le 2$
, the extension
$M/K$
is normal. Since K is almost normal, M is also almost normal. Observing that
$$ \begin{align*}\frac{c_1}{m^{e(m)}\delta(m) \log d_L}\le \frac{1}{16 \log d_M}, \end{align*} $$
we have
$\beta _0\in [ 1-{1}/{16 \log d_M}, 1 ]$
. Finally, by the result on Stark zeros in almost normal extensions [Reference Stark13, Lemma 10], there is a quadratic field F with
$F\subseteq M\subseteq L$
such that
$\zeta _F({\kern1pt}\beta _0)=0$
.
To prove the second part of the theorem, it suffices to show that the region (2.4) is contained in the region (2.3). As
$m\mid n$
, we have
$e(m)\le e(n)$
and thus
$\delta (m)\le \delta (n)$
. This concludes the proof.
If Artin’s conjecture is true, one has the following improvement of these results.
Lemma 2.3 (Stark, [Reference Stark13, Lemma 13]).
Let L be a number field of degree
$n> 1$
and let
$\tilde {L}$
be the normal closure of L over
$\Bbb {Q}$
. Suppose that all the Artin L-functions
$L(s,\psi ,\tilde {L}/\Bbb {Q})$
are holomorphic at
$s\neq 1$
. If there is a zero
$\beta _0$
of
$\zeta _L(s)$
in the range
$$ \begin{align*}1 - \frac{1}{8(n-1)\log d_L} \le {\mathrm{Re}}(s)\le 1, \end{align*} $$
then there exists a quadratic field
$F\subseteq L$
such that
$\zeta _F({\kern1pt}\beta _0)=0$
.
Lastly, we recall the following bound for the exceptional zeros of Dedekind zeta functions of quadratic fields.
Lemma 2.4 [Reference Stark13, Lemma 11].
Let F be a quadratic field. Then there is an effective absolute constant
$c_2>0$
such that
$\zeta _F(\sigma )$
is nonvanishing for
$\sigma \ge 1- {c_2}/{d_F^{1/2}}$
.
3 Proof of Theorem 1.2
To prove Theorem 1.2, we shall prove the following lower bounds for
$h_L^-$
.
Theorem 3.1. Let L be a CM-field with maximal totally real subfield
$L^+$
. Assume either
$L\in \mathcal {C}$
or the truth of Artin’s conjecture. Write
$d_L=d_{L^+}^2 f$
and set
$n=[L^+:\Bbb {Q}].$
Then there are effective absolute constants
$c_3>0$
and
$c_4>1$
such that
$$ \begin{align} h^-_L\ge \frac{c_3}{ng(n)} c_4^{n} f^{({1}/{2})-({1}/{2n})}, \end{align} $$
where the function
$g(n)$
is defined by
$$ \begin{align*} g(n) =\begin{cases} (2n)^{e(2n)} \delta(2n) \quad&\text{if } L\in \mathcal{C}, \\ n-\frac{1}{2} \quad&\text{if } \text{Artin's conjecture is true}. \end{cases} \end{align*} $$
Moreover, for any
$\varepsilon \in [{1}/{(8\log d_L)},1]$
, there exists
$c(\varepsilon )>0$
, depending only on
$\varepsilon $
, such that
$$ \begin{align} h^-_L\ge \frac{c_3 c(\varepsilon)^n}{ng(n)} d_{L^+}^{({1}/{2}) -({1}/{n})-\varepsilon} f^{({1}/{2})-({1}/{2n})}. \end{align} $$
Proof. We shall follow the arguments used in [Reference Murty10, Reference Odlyzko11, Reference Stark13]. Note that there is a nontrivial Hecke character
$\chi $
of
${L^+}$
such that
$\zeta _{L}(s)=\zeta _{L^+}(s)L(s,\chi )$
, where
$L(s,\chi )$
is the Hecke L-function attached to
$\chi $
. Let
$\beta _0$
be the possible exceptional zero of
$L(s,\chi )$
satisfying
$$ \begin{align*}1-\frac{1}{4\log (d_{L^+}^2 f)} \le \beta_0 \le 1, \end{align*} $$
and set
$\beta _1 =\beta _0$
if it exists. Otherwise, set
$\beta _1= 1-{1}/{(4\log (d_{L^+}^2 f))}$
. By equation (31) in [Reference Stark13],
$$ \begin{align*}h^-_L= \frac{h_L}{h_{L^+}}\ge d_{L^+}^{{1}/{2}} f^{{1}/{2}}(2\pi)^{-n}L(1,\chi). \end{align*} $$
In addition, as in [Reference Stark13, Proof of Lemma 5] (see also [Reference Odlyzko11, Equation (4.2)]), for any
$\sigma _1$
such that
$$ \begin{align*}1+\frac{1}{4 \log d_L} \le \sigma_1 \le 2, \end{align*} $$
there is a
$c_5>0$
such that
$$ \begin{align*}L(1,\chi) \ge c_5 (1- \beta_1 ) d_{L^+}^{-({1}/{2})(\sigma_1-1) } \zeta_{L^+}(\sigma_1)^{-1}. \end{align*} $$
Thus,
$$ \begin{align} h_L^- \ge c_5 (1- \beta_1 ) d_{L^+}^{({1}/{2}) -({1}/{2})(\sigma_1-1) } f^{{1}/{2}}(2\pi)^{-n} \zeta_{L^+}(\sigma_1)^{-1}. \end{align} $$
Now, if
$L(s,\chi )$
has a zero
$\beta _0$
in the region
$$ \begin{align} 1-\frac{c_1}{g(n) \log d_L}\le {\mathrm{Re}}(s) \le 1, \end{align} $$
where
$c_1$
is defined as in Theorem 2.2, then
$\beta _0$
is also a zero of
$\zeta _L(s)$
. By Theorem 2.2 and Lemma 2.3, since
$\beta _0$
is in the region (3.4) and
$c_1\le {1}/{16}$
, there is a quadratic field
$F \subseteq L$
such that
$\zeta _F({\kern1pt}\beta _0)=0$
. By Lemma 2.4,
$ \beta _0 \le 1-{c_2}/{d_F^{1/2}}. $
Therefore,
$L(s,\chi )$
is nonzero on
$$ \begin{align*}\max\bigg\{ 1-\frac{c_1}{g(n) \log d_L}, 1-\frac{c_2}{d_L^{1/2n}} \bigg\}\le {\mathrm{Re}}(s) \le 1. \end{align*} $$
(Here, we used
$d_L\ge d_F^n$
.) Consequently, as
$d_L=d_{L^+}^2f$
,
$$ \begin{align*}1-\beta_1 \ge \frac{c_6}{g(n)} \min\{(\log d_L)^{-1}, d_{L}^{-1/2n} \} \ge \frac{c_6}{n g(n)} d_{L^+}^{-1/n}f^{-1/2n}, \end{align*} $$
where
$c_6= \min \{c_1,c_2\}>0$
. It follows from (3.3) that
$$ \begin{align} h_L^-\ge \frac{c_5c_6}{ng(n)} d_{L^+}^{({1}/{2}) -({1}/{2})(\sigma_1-1) -({1}/{n}) } f^{({1}/{2})-({1}/{2n})}(2\pi)^{-n} \zeta_{L^+}(\sigma_1)^{-1}. \end{align} $$
Now, as argued by Odlyzko [Reference Odlyzko11, pages 284–285], there are effective absolute positive constants
$c_7$
and
$c_8$
such that
$$ \begin{align*}h^-_L\ge \frac{c_5c_6c_7}{ng(n)} f^{({1}/{2})-({1}/{2n})} (1+c_8)^n. \end{align*} $$
This proves the first claimed bound.
To prove the second bound, we choose
$\sigma _1 =1 +2\varepsilon $
with
$\varepsilon \in [{1}/{(8\log d_L)},1]$
. Recall that for
$\sigma \in (1,3]$
,
$$ \begin{align*}0<\zeta_{L^+}(\sigma)\le \zeta(\sigma)^n \le \bigg( \frac{c_9}{\sigma-1}\bigg)^n \end{align*} $$
for some effective absolute
$c_9>0$
. Thus, by (3.5),
$$ \begin{align*} h^-_L&\ge \frac{c_5c_6}{ng(n)} d_{L^+}^{({1}/{2}) -({1}/{n}) -\varepsilon} f^{({1}/{2})-({1}/{2n})}(2\pi)^{-n} \zeta(1+2\varepsilon)^{-n}\\ &\ge \frac{c_5c_6}{ng(n)} d_{L^+}^{({1}/{2}) -({1}/{n}) -\varepsilon} f^{({1}/{2})-({1}/{2n})}\bigg( \frac{\varepsilon}{c_9\pi}\bigg)^n \end{align*} $$
as desired.
We are now in a position to prove Theorem 1.2. As mentioned before, for CM-fields of degree 2, the theorem follows from the works of Goldfeld, Gross and Zagier. So, we may restrict our attention to CM-fields of degree at least 6.
Proof of Theorem 1.2.
(i) Let L be a CM-field with
$h_L^- \le H$
,
$n_L+\ge 3$
and
$d_L=d_{L^+}^2f$
. Assume either
$L\in \mathcal {C}$
or the truth of Artin’s conjecture. Since
$e(n)\le {\log n}/{\log 2}$
,
$$ \begin{align*}n^{e(n)} \le \exp( (\log n)^2 ). \end{align*} $$
Thus, by (3.1), there exists an effective positive constant
$A_H>0$
, depending only on H, such that
$n_{L^+} \le A_H$
and
$f\le A_H$
.
Note that
$n_L\ge 6$
for
$[L^+ :\Bbb {Q}]>2$
. By Minkowski’s bound,
$ n_L \le {2\log d_L}/{\log 3}, $
and thus
$ {1}/{(8\log d_L)}\le {1}/{(4(\log 3)n_L)}\le {1}/{(24\log 3)}. $
To use (3.2), we may choose
$ \varepsilon = {1}/{(24\log 3)} $
so that
$$ \begin{align*}\frac{1}{2}-\frac{1}{n_{L^+}} -\varepsilon \ge \frac{1}{6} - \varepsilon>0. \end{align*} $$
Now, by (3.2) and the bounds
$n_{L^+} \le A_H$
and
$f\le A_H$
, there is an effective positive constant
$B_H>0$
, depending only on H, such that
$d_{L^{+}} \le B_H$
. Hence, we arrive at
$d_L = d_{L^+}^2 f \le B_H^2 A_H$
. This completes the proof because the number of number fields L with
$d_L \le B_H^2 A_H$
can be bounded effectively.
(ii) In the proof of Theorem 3.1, instead of using Lemma 2.4, we may use Siegel’s ineffective bound
$$ \begin{align*}\beta_0 \le 1-\frac{\tilde{c}_2}{d_F^{1/4}} \end{align*} $$
for some ineffective absolute
$\tilde {c}_2>0$
. This results in an ineffective improvement of the second bound of Theorem 3.1 to give
$$ \begin{align*} h^-_L\ge \frac{\tilde{c}_3c(\varepsilon)^n}{ng(n)} d_{L^+}^{({1}/{2}) -({1}/{2n})-\varepsilon} f^{({1}/{2})-({1}/{4n})} \end{align*} $$
for some ineffective
$\tilde {c}_3>0$
. This estimate, together with the first bound of Theorem 3.1, proves the finiteness of L with
$n_{L^+}=2$
and
$h_L^-\le H$
for any given
$H\in \Bbb {N}$
. Note that L must have Galois closure over
$\Bbb {Q}$
since
$n_L=4$
and so this finiteness result is unconditional.
4 Proof of Theorem 1.6
4.1 Auxiliary lemmas
Our proof of Theorem 1.6 builds on the works of Dixit [Reference Dixit3], Tsfasman and Vlăduţ [Reference Tsfasman and Vlăduţ14] and Zykin [Reference Zykin15].
Let L be a number field and let
$G_{L}(s)$
be the entire function such that
$$ \begin{align} \zeta_{L}(s)=\frac{\rho_L}{s-1} G_{L}(s). \end{align} $$
We shall set
$$ \begin{align*}Z_L(s) =\frac{d}{ds}\bigg(\frac{\log G_L(s)}{g_L} \bigg). \end{align*} $$
From Lagarias and Odlyzko [Reference Lagarias, Odlyzko and Fröhlich8, Theorem 9.2], based on an idea of Tsfasman and Vlăduţ [Reference Tsfasman and Vlăduţ14], Dixit proved the following lemma.
Lemma 4.1 (Dixit, [Reference Dixit3, Lemma 4.2]).
Let L belong to an asymptotically good family
$\mathcal {L}$
, and let
$n=[L:\Bbb {Q}]$
. Suppose that
$\zeta _L(s)$
has no zero in the region
$$ \begin{align} 1-\frac{c_1}{n^{e(n)}\delta(n) \log d_L}\le {\mathrm{Re}}(s) \le 1. \end{align} $$
Then there are positive constants
$C_1$
,
$C_2$
and
$C_3$
, dependent on
$c_1$
and
$\mathcal {L}$
, but independent of L, such that
$ |Z_L(1 + \theta )| \le C_1 g_L^{C_2 \log g_L} $
for any
$\theta \in (0, 1)$
and any
$g_L> C_3$
.
To control the possible exceptional zeros arising from an asymptotically good family, Tsfasman and Vlăduţ [Reference Tsfasman and Vlăduţ14] proved the following finiteness lemma.
Lemma 4.2 (Tsfasman and Vlăduţ, [Reference Tsfasman and Vlăduţ14, Lemma 7.3]; see also [Reference Dixit3, Lemma 4.3]).
Let
$\mathcal { L} = \{L_i\}$
be an asymptotically good family, and set
$$ \begin{align*}\mathcal{Q}(\mathcal{ L}) = \{F\mid [F : \Bbb{Q}] = 2 \text{ and } F\subseteq L_i \text{ for some } i\}. \end{align*} $$
Then
$\mathcal {Q}(\mathcal { L})$
is finite.
Lastly, we require the following bounds for the residues
$\rho _L$
.
Lemma 4.3 (Louboutin, [Reference Louboutin9, Theorem 1]).
For any number field
$L\neq \Bbb {Q}$
, if
$\zeta _L({\kern1pt}\beta ) = 0$
for some
$\beta \in [\tfrac 12,1)$
, then
$$ \begin{align*}\rho_L \le (1- \beta) \bigg( \frac{e \log d_L}{2n_L}\bigg)^{n_L}. \end{align*} $$
Lemma 4.4 (Stark, [Reference Stark13, Lemma 4]).
There exists an effective constant
$c'> 0$
such that for any number field
$L\neq \Bbb {Q}$
, one has
$ \rho _L> c'(1-\beta _0), $
where
$\beta _0$
is the possible exceptional zero of
$\zeta _L(s)$
in
$[1-{1}/{(4\log d_L)},1]$
. If the possible exceptional zero does not exist, then one can take
$\beta _0=1-{1}/{(4\log d_L)}$
.
4.2 Proof of Theorem 1.6 when
$\mathcal {L}$
is an asymptotically good tower
In light of the work of Dixit [Reference Dixit3] and Tsfasman and Vlăduţ [Reference Tsfasman and Vlăduţ14], to prove Theorem 1.6, we require the following general inequalities towards GBS for asymptotically good towers.
Lemma 4.5. Let
$\mathcal {L}= \{L_i\}$
be an asymptotically good tower. Let
$\{\theta _{L_i}\} \subset (0,1)$
be a sequence convergent to zero such that
$\log \theta _{L_i} =o(g_{L_i})$
. Then
$$ \begin{align*}\sum_q \phi_q(\mathcal{L})\log \frac{q}{q-1} \ge \limsup_{i \rightarrow \infty} \frac{\log\rho_{L_i}}{g_{L_i}} \end{align*} $$
and
$$ \begin{align*}\liminf_{i \rightarrow \infty} \frac{\log \rho_{L_i}}{g_{L_i}} \ge \sum_q \phi_q(\mathcal{L}) \log \frac{q}{q-1} - \limsup_{i \rightarrow \infty} \frac{\log G_{L_i}(1 +\theta_{L_i})}{g_{L_i}}. \end{align*} $$
Proof. The first inequality is established in [Reference Tsfasman and Vlăduţ14] for any asymptotically exact family, so it remains to prove the second inequality. By (4.1), for any
$\theta _L\in (0,1)$
,
$$ \begin{align} \frac{\log\zeta_L(1 +\theta_L)}{g_L} = \frac{\log \rho_L}{g_L} + \frac{\log G_L(1 +\theta_L)}{g_L} - \frac{\log \theta_L}{g_L}. \end{align} $$
Since
$\mathcal {L}=\{L_i\}$
is a tower, for
$\theta>0$
,
$$ \begin{align*} \frac{ \log \zeta_{L_i}(1+ \theta)}{g_{L_i}} &= \sum_{q} \frac{N_q(L_i)}{g_{L_i}} \log \frac{1}{1- q^{-1-\theta}}\\ &= \sum_{p} \frac{N_p(L_i)}{g_{L_i}} \log \frac{1}{1- p^{-1-\theta}} + \sum_{\substack{q= p^k\\ k\ge 2 }} \frac{N_q(L_i)}{g_{L_i}} \log \frac{1}{1- q^{-1-\theta}}\\ &\ge \sum_{p} \phi_p(\mathcal{L}) \log \frac{1}{1- p^{-1-\theta}} + \sum_{\substack{q= p^k\\ k\ge 2 }} \frac{N_q(L_i)}{g_{L_i}} \log \frac{1}{1- q^{-1-\theta}}. \end{align*} $$
In addition, there is a positive number
$\delta $
such that
$$ \begin{align*}\sum_{\substack{q= p^k\\ k\ge 2 }} \frac{N_q(L_i)}{g_{L_i}} \log \frac{1}{1- q^{-1-\theta}} \rightarrow \sum_{\substack{q= p^k\\ k\ge 2 }}\phi_q(\mathcal{L}) \log \frac{1}{1- q^{-1-\theta}} \end{align*} $$
uniformly in
$\theta>-\delta $
. Thus, as the sequence
$\{\theta _{L_i}\}$
converges to zero, we arrive at
$$ \begin{align} \liminf_{i \rightarrow \infty}\frac{ \log \zeta_{L_i}(1+ \theta_{L_i})}{g_{L_i}} \ge \sum_q \phi_q(\mathcal{L}) \log \frac{q}{q-1}. \end{align} $$
Gathering (4.3), (4.4) and the assumption
$\log \theta _{L_i} =o(g_{L_i})$
completes the proof.
We now prove Theorem 1.6 for asymptotically good towers.
Proof of Theorem 1.6 for asymptotically good towers.
Let
$\mathcal {L}=\{L_i\}$
be an asymptotically good tower. Assume either
$\mathcal {L}=\{L_i\} \subseteq \mathcal {C}$
or Artin’s conjecture. Following Dixit [Reference Dixit3, Section 5.1], we choose
$\theta _{L_i}= g_{L_i}^{-(C_2+1) \log g_{L_i}}$
, where
$C_2$
is the same as in Lemma 4.1. It is clear that the sequence
$\{\theta _{L_i}\}$
converges to zero and
$\log \theta _{L_i} =o(g_{L_i})$
. Therefore, by Lemma 4.5, it remains to show that
$$ \begin{align*}\limsup_{i \rightarrow \infty} \frac{\log G_{L_i}(1 +\theta_{L_i})}{g_{L_i}} \le 0. \end{align*} $$
By Theorem 2.2 and Lemma 2.3, if
$\zeta _{L_i}(s)$
has a zero
$\beta _0$
in the region (4.2) with
$L=L_i$
and
$n=n_{L_i}$
, then it must be a real zero of
$\zeta _F(s)$
for some
$F\in \mathcal {Q}(\mathcal {L})$
. By Lemmas 2.4 and 4.2,
$$ \begin{align*}\beta_0\le 1 - \frac{c_2}{\max_{F\in \mathcal{Q}(\mathcal{L})} d_{F}^{1/2}}<1. \end{align*} $$
Hence, for i sufficiently large,
$\zeta _{L_i}(s)$
has no zero in the region (4.2) with
$L=L_i$
and
$n=n_{L_i}$
. As
$G_{L_i}(1)=1$
, by Lemma 4.1, for i sufficiently large,
$$ \begin{align*}\frac{\log G_{L_i}(1 +\theta_{L_i})}{g_{L_i}}= \int^{\theta_{L_i}}_{0} Z_{L_i}(1+\theta) \,d\theta \ll g_{L_i}^{-\log g_{L_i}}. \end{align*} $$
Taking the
$\limsup $
on both sides completes the proof.
4.3 Proof of Theorem 1.6 when
$\mathcal {L}$
is an asymptotically bad family
For any asymptotically bad family
$\mathcal {L}=\{L_i\}$
, we have
$ 0\ge \limsup _{i \rightarrow \infty } {(\log \rho _{L_i})}/{g_{L_i}}. $
Thus, to prove GBS for an asymptotically bad family
$\mathcal {L}$
, it is sufficient to show that
$$ \begin{align} \liminf_{i \rightarrow \infty} \frac{\log\rho_{L_i}}{g_{L_i}} \ge 0 \end{align} $$
Let
$\mathcal {I}$
be the set of indices i for which
$\zeta _{L_i}(s)$
does not have any zero in the region (4.2) with
$L=L_i$
and
$n=n_{L_i}$
, and let
$\mathcal {J}$
be the set of indices i for which
$\zeta _{L_i}(s)$
has a zero in the region (4.2) with
$L=L_i$
and
$n=n_{L_i}$
. Without loss of generality, we may assume that both
$\mathcal {I}$
and
$\mathcal {J}$
are infinite.
If
$\zeta _{L_i}(s)$
is nonvanishing on the region (4.2), Lemma 4.4 gives
$$ \begin{align*}\rho_{L_{i}}> c' \min\bigg\{ \frac{c_1}{n_{L_i}^{e(n_{L_i})}\delta(n_{L_i}) \log d_{L_i}} , \frac{1}{4\log d_{L_i}}\bigg\}\ge \frac{c'c_1}{n_{L_i}^{e(n_{L_i})}\delta(n_{L_i}) \log d_{L_i}} \end{align*} $$
and thus we obtain
$$ \begin{align*}\frac{\log\rho_{L_i}}{g_{L_i}} \ge \frac{\log(c' c_1) - e(n_{L_i})\log n_{L_i} - \log \delta(n_{L_i}) -\log \log d_{L_i}}{g_{L_i}}. \end{align*} $$
Recall the estimates
$e(n)\le {\log n}/{\log 2}$
and
$\delta (n) \ll n^4$
. Since
$g_{L_i} \rightarrow \infty $
and
$n_{L_i}/g_{L_i} \rightarrow 0$
, by the above inequality, we obtain
$$ \begin{align*}\liminf_{\substack{ i \rightarrow \infty \\i\in \mathcal{I} }} \frac{\log\rho_{L_i}}{g_{L_i}} \ge 0 \end{align*} $$
Now suppose that
$\zeta _{L_i}(s)$
has a zero
$\beta _{0,i}$
in the region (4.2) with
$L=L_i$
and
$n=n_{L_i}$
. By Theorem 2.2 and Lemma 2.3, there is a quadratic field
$F_i\subseteq L_i$
such that
$\zeta _{F_i}({\kern1pt}\beta _{0,i})=0$
. By Lemmas 4.3 and 4.4,
$$ \begin{align*}\rho_{L_i} = \rho_{L_i} \frac{\rho_{F_i}}{\rho_{F_i}} \ge c'(1- \beta_{0,i}) \frac{1}{ (1- \beta_{0,i}) ({e \log d_{F_i}}/{2n_{F_i}})^{n_{F_i}}} \rho_{F_i}. \end{align*} $$
Hence,
$(\log \rho _{L_i})/g_{L_i}$
is bounded below by
$$ \begin{align*}\frac{ \log c' + 2\log ({4}/{e \log d_{F_i}} ) + \log \rho_{F_i}}{g_{L_i}} = \frac{ \log c' + 2\log ({4}/{e \log d_{F_i}} ) }{g_{L_i}} + \frac{g_{F_i}}{g_{L_i}} \frac{\log \rho_{F_i}}{g_{F_i}}. \end{align*} $$
By the classical Brauer–Siegel theorem, Theorem 1.4, for quadratic fields
$F_i$
,
$$ \begin{align*}\liminf_{\substack{ i \rightarrow \infty \\i\in \mathcal{J} }} \frac{\log \rho_{L_i}}{g_{L_i}} \ge 0. \end{align*} $$
Since
$\mathcal {I}\cup \mathcal {J}$
contains all the indices, this gives (4.5) and completes the proof.
5 Concluding remarks
In [Reference Odlyzko11], Odlyzko also showed that the generalised Riemann hypothesis implies Stark’s conjecture. We note that the generalised Riemann hypothesis can be replaced by a much weaker conjecture on the nonexistence of Stark zeros. More precisely, assume that none of the Dedekind zeta functions
$\zeta _L(s)$
of CM-fields L admits a zero in the region (2.1). Then arguing as in the proof of Theorem 3.1, for any CM-field L with
$n_{L^+}=n$
and applying Minkowski’s bound,
$$ \begin{align*}h^-_L\ge \frac{c_5c_7}{4} \frac{1}{\log d_{L}} d_{L^+}^{{1}/{n}} f^{{1}/{2}} c_4^{n} \ge \frac{c_5c_7 \sqrt{3}}{4} \frac{1}{\log (d_{L^+}^2 f)} f^{{1}/{2}}c_4^{n} \end{align*} $$
and
$$ \begin{align*}h^-_L \ge \frac{c_5 c(\varepsilon)^n}{4} \frac{1}{\log (d_{L^+}^2 f)} d_{L^+}^{({1}/{2}) -\varepsilon}f^{{1}/{2}}. \end{align*} $$
Consequently, the cardinality of the set of CM-fields L with
$h^-_L\le H$
is finite and can be bounded effectively (in terms of H).
In a slightly different vein, for GBS, suppose that a family
$\mathcal {L}=\{L_i\}$
is an asymptotically good tower or an asymptotically bad family such that each Dedekind zeta function
$\zeta _{L_i}(s)$
is nonzero in the region (2.1) with
$L=L_i$
and
$n=n_L$
. By the arguments used in Section 4 and observing that the region (4.2) is contained in the region (2.1), one can show that GBS is true for
$\mathcal {L}$
.
Last but not least, we note that Theorem 2.2 may have other applications. For instance, consider the Euler–Kronecker constant
$\gamma _L$
attached to a number field L in the expansion
$$ \begin{align*}\frac{\zeta^{\prime}_L}{\zeta_L}(s) = \frac{-1}{s-1} + \gamma_L +O(s-1). \end{align*} $$
Ihara [Reference Ihara and Ginzberg7] showed that under the generalised Riemann hypothesis,
$\gamma _L \le 2 \log \log \sqrt {d_L}$
, and unconditionally,
$\gamma _L \ge - \log \sqrt {d_L}$
. In [Reference Dixit2], Dixit proved that for every almost normal L not containing any quadratic fields,
$|\gamma _L| \le \kappa _0 (\log d_L)^4 n_L^3$
for some absolute
$\kappa _0>0$
. Moreover, he showed that if L has solvable Galois closure over
$\Bbb {Q}$
and does not contain any quadratic fields, then
$|\gamma _L| \le \kappa _1 (\log d_L)^{\kappa _2 \log \log d_L}$
for some absolute
$\kappa _1>0$
and
$\kappa _2>0$
. Now, if we consider a number field
$L\in \mathcal {C}$
of degree n such that L does not contain any quadratic fields, then by Theorem 2.2, any zero
$\beta _0$
of
$\zeta _L(s)$
in the region (2.1) must satisfy
$$ \begin{align*}1-\frac{1}{4\log d_L}\le \beta_0\le 1-\frac{c_1}{n^{e(n)}\delta(n) \log d_L}. \end{align*} $$
Hence, arguing as in [Reference Dixit2, Sections 2.3.1–2.3.2] yields the following theorem.
Theorem 5.1. Let
$L \in \mathcal {C}$
be a number field not containing any quadratic fields. Then
$$ \begin{align*}|\gamma_L| \le \kappa^{\prime}_1 (\log d_L)^{\kappa^{\prime}_2 \log\log d_L} \end{align*} $$
for some absolute
$\kappa ^{\prime }_1>0$
and
$\kappa ^{\prime }_2>0$
.
Acknowledgement
The author would like to thank the referee for helpful comments.
