Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-11T04:25:52.412Z Has data issue: false hasContentIssue false
  • English
  • Français

ON DISCRETENESS OF SUBGROUPS OF QUATERNIONIC HYPERBOLIC ISOMETRIES

Part of: Real and complex geometry Other groups of matrices

Published online by Cambridge University Press:  16 August 2019

KRISHNENDU GONGOPADHYAY Open the ORCID record for KRISHNENDU GONGOPADHYAY [Opens in a new window] ,
MUKUND MADHAV MISHRA Open the ORCID record for MUKUND MADHAV MISHRA [Opens in a new window]  and
DEVENDRA TIWARI Open the ORCID record for DEVENDRA TIWARI [Opens in a new window]
KRISHNENDU GONGOPADHYAY
Affiliation:
Indian Institute of Science Education and Research (IISER) Mohali, Knowledge City, Sector 81, SAS Nagar, Punjab 140306, India email krishnendu@iisermohali.ac.in, krishnendug@gmail.com
MUKUND MADHAV MISHRA
Affiliation:
Department of Mathematics, Hansraj College, University of Delhi, Delhi110007, India email mukund.math@gmail.com
DEVENDRA TIWARI*
Affiliation:
Department of Mathematics, University of Delhi, Delhi 110007, India email devendra9.dev@gmail.com
*
✉devendra9.dev@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\mathbf{H}_{\mathbb{H}}^{n}$ denote the $n$-dimensional quaternionic hyperbolic space. The linear group 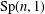$\text{Sp}(n,1)$ acts on $\mathbf{H}_{\mathbb{H}}^{n}$ by isometries. A subgroup $G$ of 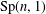$\text{Sp}(n,1)$ is called Zariski dense if it neither fixes a point on 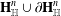$\mathbf{H}_{\mathbb{H}}^{n}\cup \unicode[STIX]{x2202}\mathbf{H}_{\mathbb{H}}^{n}$ nor preserves a totally geodesic subspace of $\mathbf{H}_{\mathbb{H}}^{n}$. We prove that a Zariski dense subgroup $G$ of $\text{Sp}(n,1)$ is discrete if for every loxodromic element 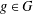$g\in G$ the two-generator subgroup 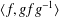$\langle f,gfg^{-1}\rangle$ is discrete, where the generator 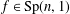$f\in \text{Sp}(n,1)$ is a certain fixed element not necessarily from 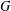$G$.

Keywords

hyperbolic spaceJørgensen inequalitydiscretenessquaternions

MSC classification

Primary: 20H10: Fuchsian groups and their generalizations
Secondary: 51M10: Hyperbolic and elliptic geometries (general) and generalizations
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 2 , April 2020 , pp. 283 - 293
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Footnotes

The first author acknowledges partial support from SERB MATRICS grant MTR/2017/000355; the third author is supported by NBHM-SRF.

References

Abikoff, W. and Haas, A., ‘Nondiscrete groups of hyperbolic motions’, Bull. Lond. Math. Soc. 22(3) (1980), 233–238.10.1112/blms/22.3.233Google Scholar
Cao, W. and Parker, J. R., ‘Jørgensen’s inequality and collars in n-dimensional quaternionic hyperbolic space’, Q. J. Math. 62(3) (2011), 523–543.10.1093/qmath/haq003Google Scholar
Cao, W. and Parker, J. R., ‘Shimizu’s lemma for quaternionic hyperbolic space’, Comput. Methods Funct. Theory 18(1) (2018), 159–191.10.1007/s40315-017-0212-4Google Scholar
Cao, W. and Tan, H., ‘Jørgensen’s inequality for quaternionic hyperbolic space with elliptic elements’, Bull. Aust. Math. Soc. 81(1) (2010), 121–131.10.1017/S0004972709000720Google Scholar
Chen, M., ‘Discreteness and convergence of Möbius groups’, Geom. Dedicata 104 (2004), 61–69.10.1023/B:GEOM.0000023036.55318.40Google Scholar
Chen, S. S. and Greenberg, L., ‘Hyperbolic spaces’, in: Contributions to Analysis (A Collection of Papers Dedicated to Lipman Bers) (Academic Press, New York, 1974), 49–87.Google Scholar
Friedland, S. and Hersonsky, S., ‘Jorgensen’s inequality for discrete groups in normed algebras’, Duke Math. J. 69(3) (1993), 593–614.10.1215/S0012-7094-93-06924-4Google Scholar
Gongopadhyay, K. and Mukherjee, A., ‘Discreteness criteria in Möbius groups by test maps’, Preprint, 2018.Google Scholar
Gongopadhyay, K., Mukherjee, A. and Sardar, S. K., ‘Test maps and discreteness in SL(2, ℍ)’, Glasg. Math. J. 61 (2019), 523–533.10.1017/S0017089518000332Google Scholar
Hersonsky, S. and Paulin, F., ‘On the volumes of complex hyperbolic manifolds’, Duke Math. J. 84(3) (1996), 719–737.10.1215/S0012-7094-96-08422-7Google Scholar
Jiang, Y., Kamiya, S. and Parker, J. R., ‘Jørgensen’s inequality for complex hyperbolic space’, Geom. Dedicata 97 (2003), 55–80.10.1023/A:1023627324013Google Scholar
Jørgensen, T., ‘On discrete groups of Möbius transformations’, Amer. J. Math. 98(3) (1976), 739–749.10.2307/2373814Google Scholar
Kim, I. and Parker, J. R., ‘Geometry of quaternionic hyperbolic manifolds’, Math. Proc. Cambridge Philos. Soc. 135(2) (2003), 291–320.10.1017/S030500410300687XGoogle Scholar
Markham, S. and Parker, J. R., ‘Collars in complex and quaternionic hyperbolic manifolds’, Geom. Dedicata 97 (2003), 199–213.10.1023/A:1023677417179Google Scholar
Markham, S. and Parker, J. R., ‘Jørgensen’s inequality for metric spaces with application to the octonions’, Adv. Geom. 7(1) (2007), 19–38.10.1515/ADVGEOM.2007.002Google Scholar
Martin, G. J., ‘On discrete Möbius groups in all dimensions: a generalization of Jørgensen’s inequality’, Acta Math. 163(3–4) (1989), 253–289.10.1007/BF02392737Google Scholar
Wang, X., Li, L. and Cao, W., ‘Discreteness criteria for Möbius groups acting on ℝn’, Israel J. Math. 150 (2005), 357–368.10.1007/BF02762387Google Scholar
Yang, S. and Zhao, T., ‘Test maps and discrete groups in SL(2, ℂ) II’, Glasg. Math. J. 56(1) (2014), 53–56.10.1017/S0017089513000062Google Scholar