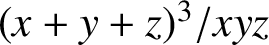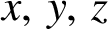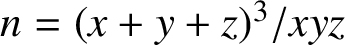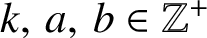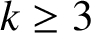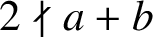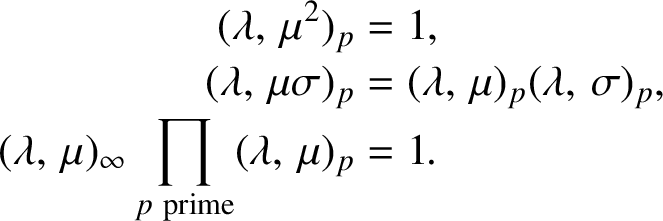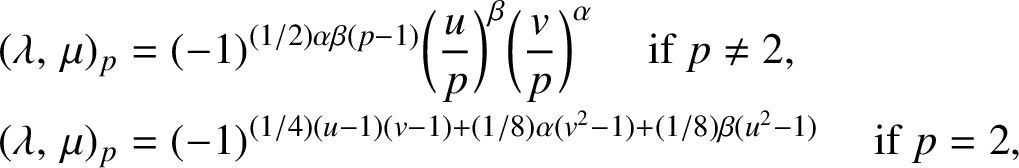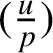1 Introduction
Let n be an integer. The equation
 $$ \begin{align} n=\dfrac{(x+y+z)^3}{xyz} \end{align} $$
$$ \begin{align} n=\dfrac{(x+y+z)^3}{xyz} \end{align} $$
has been studied by several authors. Guy [Reference Guy7] asked for integers n representable by (1.1), where
![]() $x,\,y,\,z\in \mathbb {Z}$
, preferably with
$x,\,y,\,z\in \mathbb {Z}$
, preferably with
![]() $x,\,y,\,z\in \mathbb {Z}^{+}$
. Guy’s question is still open and only partial results have been published. According to [Reference Guy7], Montgomery found 539 solutions to (1.1) with
$x,\,y,\,z\in \mathbb {Z}^{+}$
. Guy’s question is still open and only partial results have been published. According to [Reference Guy7], Montgomery found 539 solutions to (1.1) with
![]() $1\leq x\leq y\leq z\leq 46300$
. Bremner and Guy [Reference Bremner and Guy1] found several solutions to (1.1) when n is in the range
$1\leq x\leq y\leq z\leq 46300$
. Bremner and Guy [Reference Bremner and Guy1] found several solutions to (1.1) when n is in the range
![]() $|n|\leq 200$
. Brueggeman [Reference Brueggeman3] found four families of solutions to (1.1) involving only positive integers. In a short note [Reference Garaev6], Garaev sketched a proof that (1.1) does not have solutions in positive integers if n is of the form
$|n|\leq 200$
. Brueggeman [Reference Brueggeman3] found four families of solutions to (1.1) involving only positive integers. In a short note [Reference Garaev6], Garaev sketched a proof that (1.1) does not have solutions in positive integers if n is of the form
![]() $n=8k-1$
,
$n=8k-1$
,
![]() $16k-4$
,
$16k-4$
,
![]() $32k-16$
,
$32k-16$
,
![]() $64k$
or
$64k$
or
![]() $2^{2m+1}(2k-11)+27$
, where
$2^{2m+1}(2k-11)+27$
, where
![]() $k,\,m\in \mathbb {Z}^{+}$
. Garaev’s proof was based on his work [Reference Garaev5] on the cubic Diophantine equation
$k,\,m\in \mathbb {Z}^{+}$
. Garaev’s proof was based on his work [Reference Garaev5] on the cubic Diophantine equation
![]() $x^3+y^3+z^3=nxyz$
. In this paper, we find another family of integers n for which (1.1) has no solutions in positive integers.
$x^3+y^3+z^3=nxyz$
. In this paper, we find another family of integers n for which (1.1) has no solutions in positive integers.
Theorem 1.1. Let
![]() $k,a,b$
be positive with
$k,a,b$
be positive with
![]() $k\geq 3$
and
$k\geq 3$
and
![]() $2\nmid a+b$
. Then the equation
$2\nmid a+b$
. Then the equation
does not have positive integer solutions.
Garaev’s method is classical and uses the quadratic reciprocity law. Our method is based on an idea of Stoll [Reference Stoll9] and uses Hilbert symbols and elliptic curves. We briefly outline the main idea.
Assume that we want to show that a rational number X is positive. The key is to find a rational number
![]() $D<0$
such that
$D<0$
such that
![]() $(X,D)_p=1$
for all prime numbers p, where
$(X,D)_p=1$
for all prime numbers p, where
![]() $(X,D)_p$
denotes the Hilbert symbol. Then the product formula for the Hilbert symbol (see Serre [Reference Serre8, Theorem 3, page 23]) forces
$(X,D)_p$
denotes the Hilbert symbol. Then the product formula for the Hilbert symbol (see Serre [Reference Serre8, Theorem 3, page 23]) forces
![]() $(X,D)_{\infty }=1$
. Since
$(X,D)_{\infty }=1$
. Since
![]() $D<0$
, we must have
$D<0$
, we must have
![]() $X>0$
. Our experience shows that when X is the x-coordinate of a rational point on an elliptic curve of the form
$X>0$
. Our experience shows that when X is the x-coordinate of a rational point on an elliptic curve of the form
where f is a cubic polynomial with rational coefficients, D is usually a factor of the discriminant of
![]() $f(x)$
. This idea can be applied to several problems. For the representation of positive integers n in the form
$f(x)$
. This idea can be applied to several problems. For the representation of positive integers n in the form
![]() $n=(x+y+z)(1/x+1/y+1/z)$
or
$n=(x+y+z)(1/x+1/y+1/z)$
or
![]() $n=(x+y+z+w)(1/x+1/y+1/z+1/w)$
, where
$n=(x+y+z+w)(1/x+1/y+1/z+1/w)$
, where
![]() $x,y,z,w\in \mathbb {Z}^{+}$
, see [Reference Bremner and Tho2, Reference Tho11]. For the representation of positive integers n in the form
$x,y,z,w\in \mathbb {Z}^{+}$
, see [Reference Bremner and Tho2, Reference Tho11]. For the representation of positive integers n in the form
![]() $n=x/y+dy/z+z/w+dw/x$
, where
$n=x/y+dy/z+z/w+dw/x$
, where
![]() $x,y,z,w,d\in \mathbb {Z}^{+}$
, see [Reference Dofs and Tho4, Reference Tho10].
$x,y,z,w,d\in \mathbb {Z}^{+}$
, see [Reference Dofs and Tho4, Reference Tho10].
2 Preliminaries
Let p be a prime number. Let
![]() $\mathbb {Q}_p$
denote the p-adic completion of
$\mathbb {Q}_p$
denote the p-adic completion of
![]() $\mathbb {Q}$
with respect to p and
$\mathbb {Q}$
with respect to p and
![]() $\mathbb {Z}_p$
the ring of p-adic integers in
$\mathbb {Z}_p$
the ring of p-adic integers in
![]() $\mathbb {Q}_p$
. Let
$\mathbb {Q}_p$
. Let
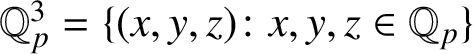 $\mathbb {Q}_p^3=\{(x,y,z)\colon x,y,z\in \mathbb {Q}_p\}$
and
$\mathbb {Q}_p^3=\{(x,y,z)\colon x,y,z\in \mathbb {Q}_p\}$
and
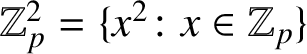 $\mathbb {Z}_p^2=\{x^2\colon x\in \mathbb {Z}_p\}$
. For
$\mathbb {Z}_p^2=\{x^2\colon x\in \mathbb {Z}_p\}$
. For
![]() $w\in \mathbb {Q}_p^{*}$
, denote by
$w\in \mathbb {Q}_p^{*}$
, denote by
![]() $v_p(w)$
the exponent of the highest power of p dividing w. For
$v_p(w)$
the exponent of the highest power of p dividing w. For
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
in
$\mu $
in
![]() $\mathbb {Q}_p^{*}$
, the Hilbert symbol
$\mathbb {Q}_p^{*}$
, the Hilbert symbol
![]() $(\lambda ,\,\mu )_p$
is defined by
$(\lambda ,\,\mu )_p$
is defined by
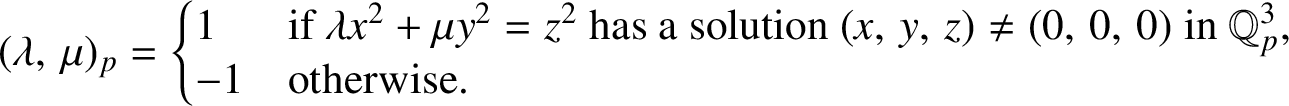 $$ \begin{align*}(\lambda,\,\mu)_p= \begin{cases}1& \text{if } \lambda x^2+\mu y^2=z^2 \text{ has a solution}\ (x,\,y,\,z)\neq (0,\,0,\,0)\ \text{in}\ \mathbb{Q}_p^3,\\[-2pt] -1& \text{otherwise.} \end{cases}\end{align*} $$
$$ \begin{align*}(\lambda,\,\mu)_p= \begin{cases}1& \text{if } \lambda x^2+\mu y^2=z^2 \text{ has a solution}\ (x,\,y,\,z)\neq (0,\,0,\,0)\ \text{in}\ \mathbb{Q}_p^3,\\[-2pt] -1& \text{otherwise.} \end{cases}\end{align*} $$
For
![]() $\lambda ,\mu \in \mathbb {R}$
, the symbol
$\lambda ,\mu \in \mathbb {R}$
, the symbol
![]() $(\lambda ,\,\mu )_{\infty }$
is
$(\lambda ,\,\mu )_{\infty }$
is
![]() $+1$
if
$+1$
if
![]() $\lambda>0$
or
$\lambda>0$
or
![]() $\mu>0$
and
$\mu>0$
and
![]() $-1$
otherwise. We implicitly understand that
$-1$
otherwise. We implicitly understand that
![]() $\mathbb {Q}$
is a subfield of both
$\mathbb {Q}$
is a subfield of both
![]() $\mathbb {Q}_p$
and
$\mathbb {Q}_p$
and
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
We need some properties of Hilbert symbols (see [Reference Serre8, pages 19–26] for proofs). Let
![]() $\lambda ,\,\mu ,\,\sigma \in \mathbb {Q}_p^{*}$
.
$\lambda ,\,\mu ,\,\sigma \in \mathbb {Q}_p^{*}$
.
-
(i) We have
 $$ \begin{align*}\begin{split} (\lambda,\,\mu^2)_p &=1,\\[-2pt] (\lambda,\,\mu\sigma)_p &=(\lambda,\,\mu)_p(\lambda,\,\sigma)_p,\\[-2pt] (\lambda,\,\mu)_\infty\prod\limits_{p\ \text{prime}}(\lambda,\,\mu)_p &=1. \end{split} \end{align*} $$
$$ \begin{align*}\begin{split} (\lambda,\,\mu^2)_p &=1,\\[-2pt] (\lambda,\,\mu\sigma)_p &=(\lambda,\,\mu)_p(\lambda,\,\sigma)_p,\\[-2pt] (\lambda,\,\mu)_\infty\prod\limits_{p\ \text{prime}}(\lambda,\,\mu)_p &=1. \end{split} \end{align*} $$
-
(ii) Let
 $\lambda =p^\alpha u$
and
$\lambda =p^\alpha u$
and
 $\mu =p^{\beta }v,$
where
$\mu =p^{\beta }v,$
where
 $\alpha =v_p(\lambda )$
and
$\alpha =v_p(\lambda )$
and
 $\beta =v_p(\mu )$
. Then where by
$\beta =v_p(\mu )$
. Then where by $$ \begin{align*} \begin{split}(\lambda,\,\mu)_p&=(-1)^{({1}/{2})\alpha\beta(p-1)}\bigg(\dfrac{u}{p}\bigg)^{\beta}\bigg(\dfrac{v}{p}\bigg)^{\alpha} \quad \text{ if } p\neq 2,\\[-2pt] (\lambda,\,\mu)_p&=(-1)^{({1}/{4})(u-1)(v-1)+({1}/{8})\alpha(v^2-1)+({1}/{8})\beta(u^2-1)} \quad \text{ if } p=2, \end{split} \end{align*} $$
$$ \begin{align*} \begin{split}(\lambda,\,\mu)_p&=(-1)^{({1}/{2})\alpha\beta(p-1)}\bigg(\dfrac{u}{p}\bigg)^{\beta}\bigg(\dfrac{v}{p}\bigg)^{\alpha} \quad \text{ if } p\neq 2,\\[-2pt] (\lambda,\,\mu)_p&=(-1)^{({1}/{4})(u-1)(v-1)+({1}/{8})\alpha(v^2-1)+({1}/{8})\beta(u^2-1)} \quad \text{ if } p=2, \end{split} \end{align*} $$
 $(\tfrac{u}{p})$
denotes the Legendre symbol.
$(\tfrac{u}{p})$
denotes the Legendre symbol.
3 Proof of Theorem 1.1
Assume that there exist positive integers
![]() $x,\,y,\,z$
such that
$x,\,y,\,z$
such that
Let
![]() $x+y+z=n\gamma z$
, where
$x+y+z=n\gamma z$
, where
![]() $\gamma \in \mathbb {Q}$
. Then
$\gamma \in \mathbb {Q}$
. Then
![]() $xy=n^2\gamma ^3z^2$
.
$xy=n^2\gamma ^3z^2$
.
Therefore,
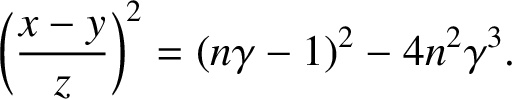 $$ \begin{align*}\bigg(\dfrac{x-y}{z}\bigg)^2=(n\gamma-1)^2-4n^2\gamma^3.\end{align*} $$
$$ \begin{align*}\bigg(\dfrac{x-y}{z}\bigg)^2=(n\gamma-1)^2-4n^2\gamma^3.\end{align*} $$
Let
![]() $X=-\gamma $
and
$X=-\gamma $
and
![]() $Y={(x-y)}/{z}$
. Then
$Y={(x-y)}/{z}$
. Then
Since
![]() $nX+1=-{(x+y)}/{z}<0$
,
$nX+1=-{(x+y)}/{z}<0$
,
We show that (3.2) is impossible via the following lemmas.
Lemma 3.1. In (3.2),
![]() $(-n,\,nX+1)_2=1.$
$(-n,\,nX+1)_2=1.$
Proof. Write
![]() $n=2^{2k}n_1$
, where
$n=2^{2k}n_1$
, where
![]() $2\not \mid n_1$
. We consider five cases according to the value of
$2\not \mid n_1$
. We consider five cases according to the value of
![]() $v_2(nX)$
.
$v_2(nX)$
.
Case 1:
![]() $v_2(nX)\geq 3$
. Then
$v_2(nX)\geq 3$
. Then
![]() $nX+1\equiv 1 \pmod 8$
, so that
$nX+1\equiv 1 \pmod 8$
, so that
 $nX+1\in \mathbb {Z}_2^{2}$
. Therefore,
$nX+1\in \mathbb {Z}_2^{2}$
. Therefore,
Case 2:
![]() $v_2(nX)=2$
. Then
$v_2(nX)=2$
. Then
![]() $nX+1\equiv 1 \pmod 4$
, so that
$nX+1\equiv 1 \pmod 4$
, so that
Case 3:
![]() $v_2(nX)=1$
. Then
$v_2(nX)=1$
. Then
![]() $v_2(X)=1-2k$
. Let
$v_2(X)=1-2k$
. Let
![]() $X=2^{1-2k}X_1$
, where
$X=2^{1-2k}X_1$
, where
![]() $2\nmid X_1$
. From (3.1),
$2\nmid X_1$
. From (3.1),
 $$ \begin{align*}Y^2=\dfrac{n_1^2X_1^3}{2^{2k-5}}+(2n_1X_1+1)^2.\end{align*} $$
$$ \begin{align*}Y^2=\dfrac{n_1^2X_1^3}{2^{2k-5}}+(2n_1X_1+1)^2.\end{align*} $$
Therefore,
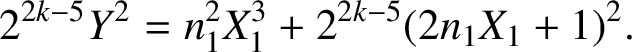 $$ \begin{align} 2^{2k-5}Y^2=n_1^2X_1^3+2^{2k-5}(2n_1X_1+1)^2. \end{align} $$
$$ \begin{align} 2^{2k-5}Y^2=n_1^2X_1^3+2^{2k-5}(2n_1X_1+1)^2. \end{align} $$
Since
![]() $2k-5>0$
and
$2k-5>0$
and
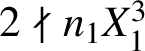 $2\nmid n_1X_1^3$
, it follows from (3.3) that
$2\nmid n_1X_1^3$
, it follows from (3.3) that
![]() $2k-5+2v_2(Y)=0$
. But this is impossible since
$2k-5+2v_2(Y)=0$
. But this is impossible since
![]() $2\nmid 2k-5$
.
$2\nmid 2k-5$
.
Case 4:
![]() $v_2(nX)=0$
. Then
$v_2(nX)=0$
. Then
![]() $v_2(X)=-2k$
. Let
$v_2(X)=-2k$
. Let
![]() $X=2^{-2k}X_1$
, where
$X=2^{-2k}X_1$
, where
![]() $2\nmid X_1$
. From (3.1),
$2\nmid X_1$
. From (3.1),
 $$ \begin{align*}Y^2=\dfrac{n_1^2X_1^3}{2^{2k-2}}+(n_1X_1+1)^2.\end{align*} $$
$$ \begin{align*}Y^2=\dfrac{n_1^2X_1^3}{2^{2k-2}}+(n_1X_1+1)^2.\end{align*} $$
Hence,
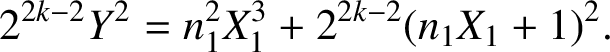 $$ \begin{align} 2^{2k-2}Y^2=n_1^2X_1^3+2^{2k-2}(n_1X_1+1)^2.\end{align} $$
$$ \begin{align} 2^{2k-2}Y^2=n_1^2X_1^3+2^{2k-2}(n_1X_1+1)^2.\end{align} $$
Since
![]() $2k-2>0$
and
$2k-2>0$
and
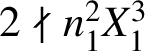 $2\nmid n_1^2X_1^3$
, it follows from (3.4) that
$2\nmid n_1^2X_1^3$
, it follows from (3.4) that
![]() $2k-2+2v_2(Y)=0$
. Taking (3.4) modulo
$2k-2+2v_2(Y)=0$
. Taking (3.4) modulo
![]() $8$
gives
$8$
gives
![]() $X_1 \equiv 1$
(mod
$X_1 \equiv 1$
(mod
![]() $8$
). Hence,
$8$
). Hence,
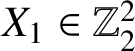 $X_1\in \mathbb {Z}_2^2$
. Let
$X_1\in \mathbb {Z}_2^2$
. Let
![]() $X_1=\delta ^2$
, where
$X_1=\delta ^2$
, where
![]() $\delta \in \mathbb {Z}_2$
. Since
$\delta \in \mathbb {Z}_2$
. Since
![]() $-n_1U^2+(n_1X_1+1) V^2=1$
has a solution
$-n_1U^2+(n_1X_1+1) V^2=1$
has a solution
![]() $(U,V)=(\delta ,1)$
,
$(U,V)=(\delta ,1)$
,
Therefore,
Case 5:
![]() $v_2(nX)<0$
. Then
$v_2(nX)<0$
. Then
![]() $v_2(X)<-2k$
. Let
$v_2(X)<-2k$
. Let
![]() $X=2^{-t}X_1$
, where
$X=2^{-t}X_1$
, where
![]() $2\nmid X_1$
,
$2\nmid X_1$
,
![]() $t\in \mathbb {Z}$
and
$t\in \mathbb {Z}$
and
![]() $t>2k$
. From (3.1),
$t>2k$
. From (3.1),
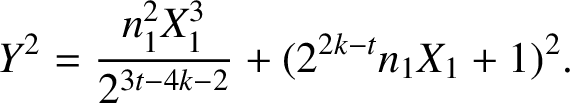 $$ \begin{align*}Y^2=\dfrac{n_1^2X_1^3}{2^{3t-4k-2}}+(2^{2k-t}n_1X_1+1)^2.\end{align*} $$
$$ \begin{align*}Y^2=\dfrac{n_1^2X_1^3}{2^{3t-4k-2}}+(2^{2k-t}n_1X_1+1)^2.\end{align*} $$
Hence,
 $$ \begin{align} 2^{3t-4k-2}Y^2=n_1^2X_1^3+2^{t-2}(n_1X_1+2^{t-2k})^2. \end{align} $$
$$ \begin{align} 2^{3t-4k-2}Y^2=n_1^2X_1^3+2^{t-2}(n_1X_1+2^{t-2k})^2. \end{align} $$
Since
![]() $t>2k>2$
and
$t>2k>2$
and
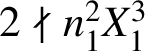 $2\nmid n_1^2X_1^3$
, it follows from (3.5) that
$2\nmid n_1^2X_1^3$
, it follows from (3.5) that
![]() $3t-4k-2+2v_2(Y)=0$
. Therefore,
$3t-4k-2+2v_2(Y)=0$
. Therefore,
![]() $2 \mid t$
. Since
$2 \mid t$
. Since
![]() $t>2k\geq 6$
, we also have
$t>2k\geq 6$
, we also have
![]() $t-2>4$
. Taking (3.5) modulo
$t-2>4$
. Taking (3.5) modulo
![]() $8$
gives
$8$
gives
![]() $X_1\equiv 1 \pmod 8$
. Since
$X_1\equiv 1 \pmod 8$
. Since
![]() $2 \mid 2k-t$
,
$2 \mid 2k-t$
,
 $$ \begin{align} (-n,\,nX+1)_2 &=(-2^{2k}n_1,\,2^{2k-t}(n_1X_1+2^{t-2k}))_2 \notag \\ &=(-n_1,\,n_1X_1+2^{t-2k})_2 =(-1)^{({1}/{4})(-n_1-1)(n_1X_1+2^{t-2k}-1)}. \end{align} $$
$$ \begin{align} (-n,\,nX+1)_2 &=(-2^{2k}n_1,\,2^{2k-t}(n_1X_1+2^{t-2k}))_2 \notag \\ &=(-n_1,\,n_1X_1+2^{t-2k})_2 =(-1)^{({1}/{4})(-n_1-1)(n_1X_1+2^{t-2k}-1)}. \end{align} $$
Here,
![]() $4 \mid 2^{t-2k}$
, because
$4 \mid 2^{t-2k}$
, because
![]() $2 \mid t$
, and
$2 \mid t$
, and
![]() $t>2k$
and
$t>2k$
and
![]() $X_1\equiv 1 \pmod 8$
.
$X_1\equiv 1 \pmod 8$
.
Therefore,
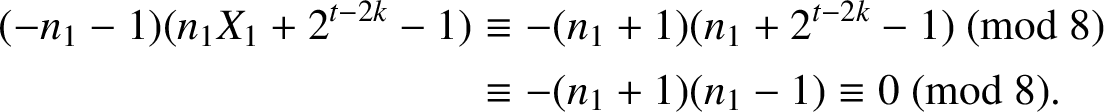 $$ \begin{align*} (-n_1-1)(n_1X_1+2^{t-2k}-1)&\equiv -(n_1+1)(n_1+2^{t-2k}-1) \pmod{8}\\ &\equiv -(n_1+1)(n_1-1) \equiv 0 \pmod{8}. \end{align*} $$
$$ \begin{align*} (-n_1-1)(n_1X_1+2^{t-2k}-1)&\equiv -(n_1+1)(n_1+2^{t-2k}-1) \pmod{8}\\ &\equiv -(n_1+1)(n_1-1) \equiv 0 \pmod{8}. \end{align*} $$
Therefore,
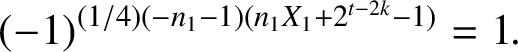 $$ \begin{align} (-1)^{({1}/{4})(-n_1-1)(n_1X_1+2^{t-2k}-1)}=1. \end{align} $$
$$ \begin{align} (-1)^{({1}/{4})(-n_1-1)(n_1X_1+2^{t-2k}-1)}=1. \end{align} $$
Lemma 3.2. Let p be an odd prime. In (3.1),
![]() $(-n,\,nX+1)_p=1.$
$(-n,\,nX+1)_p=1.$
Proof. We consider three cases according to the value of
![]() $v_p(nX)$
.
$v_p(nX)$
.
Case 1:
![]() $v_p(nX)\geq 1$
. Then
$v_p(nX)\geq 1$
. Then
![]() $nX+1\equiv 1 \pmod p$
, so that
$nX+1\equiv 1 \pmod p$
, so that
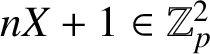 $nX+1\in \mathbb {Z}_p^2$
. Hence,
$nX+1\in \mathbb {Z}_p^2$
. Hence,
Case 2:
![]() $v_p(nX)=0$
. Then
$v_p(nX)=0$
. Then
![]() $v_p(X)=-v_p(n)$
. Let
$v_p(X)=-v_p(n)$
. Let
![]() $n=p^sn_1$
and
$n=p^sn_1$
and
![]() $X=p^{-s}X_1$
, where
$X=p^{-s}X_1$
, where
![]() $s\geq 0$
,
$s\geq 0$
,
![]() $p\nmid n_1$
and
$p\nmid n_1$
and
![]() $p\nmid X_1$
.
$p\nmid X_1$
.
Case 2.1:
![]() $s=0$
. First suppose that
$s=0$
. First suppose that
![]() $p\nmid (n_1X_1+1)$
. Since both
$p\nmid (n_1X_1+1)$
. Since both
![]() $-n_1$
and
$-n_1$
and
![]() $n_1X_1+1$
are units in
$n_1X_1+1$
are units in
![]() $\mathbb {Z}_p$
, we have
$\mathbb {Z}_p$
, we have
![]() $(-n_1,\,n_1X_1+1)_p=1$
. Therefore,
$(-n_1,\,n_1X_1+1)_p=1$
. Therefore,
On the other hand, if
![]() $p \mid (n_1X_1+1)$
, then, from (3.1),
$p \mid (n_1X_1+1)$
, then, from (3.1),
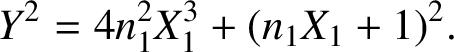 $$ \begin{align*}Y^2=4n_1^2X_1^3+(n_1X_1+1)^2.\end{align*} $$
$$ \begin{align*}Y^2=4n_1^2X_1^3+(n_1X_1+1)^2.\end{align*} $$
Therefore,
![]() $X_1$
is a square modulo p and so
$X_1$
is a square modulo p and so
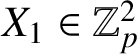 $X_1\in \mathbb {Z}_p^2$
. Let
$X_1\in \mathbb {Z}_p^2$
. Let
![]() $X_1=\omega ^2$
, where
$X_1=\omega ^2$
, where
![]() $\omega \in \mathbb {Z}_p$
and
$\omega \in \mathbb {Z}_p$
and
![]() $p\nmid \omega $
. Then
$p\nmid \omega $
. Then
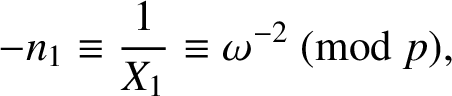 $$ \begin{align*}-n_1\equiv \dfrac{1}{X_1}\equiv \omega^{-2}\pmod{p},\end{align*} $$
$$ \begin{align*}-n_1\equiv \dfrac{1}{X_1}\equiv \omega^{-2}\pmod{p},\end{align*} $$
so that
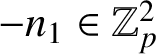 $-n_1\in \mathbb {Z}_p^2$
and
$-n_1\in \mathbb {Z}_p^2$
and
Case 2.2:
![]() $s>0$
. From (3.1),
$s>0$
. From (3.1),
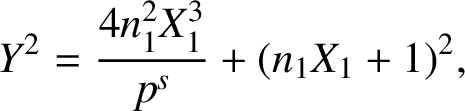 $$ \begin{align*}Y^2=\dfrac{4n_1^2X_1^3}{p^s}+(n_1X_1+1)^2,\end{align*} $$
$$ \begin{align*}Y^2=\dfrac{4n_1^2X_1^3}{p^s}+(n_1X_1+1)^2,\end{align*} $$
so that
 $$ \begin{align} p^sY^2=4n_1^2X_1^3+p^s(n_1X_1+1)^2. \end{align} $$
$$ \begin{align} p^sY^2=4n_1^2X_1^3+p^s(n_1X_1+1)^2. \end{align} $$
Since
 $p\nmid 4n_1^2X_1^3$
and
$p\nmid 4n_1^2X_1^3$
and
![]() $s>0$
, it follows from (3.8) that
$s>0$
, it follows from (3.8) that
![]() $s+2v_p(Y)=0$
. Therefore,
$s+2v_p(Y)=0$
. Therefore,
![]() $2 \mid s$
.
$2 \mid s$
.
First suppose that
![]() $p\nmid n_1X_1+1$
. Since both
$p\nmid n_1X_1+1$
. Since both
![]() $-n_1$
and
$-n_1$
and
![]() $n_1X_1+1$
are units in
$n_1X_1+1$
are units in
![]() $\mathbb {Z}_p$
, we have
$\mathbb {Z}_p$
, we have
![]() $(-n_1,\,n_1X_1+1)_p=1$
.
$(-n_1,\,n_1X_1+1)_p=1$
.
Therefore,
On the other hand, if
![]() $p \mid n_1X_1+1$
, then, from (3.8),
$p \mid n_1X_1+1$
, then, from (3.8),
![]() $X_1$
is a square modulo p.
$X_1$
is a square modulo p.
Therefore,
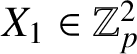 $X_1\in \mathbb {Z}_p^2$
. Let
$X_1\in \mathbb {Z}_p^2$
. Let
![]() $X_1=\zeta ^2$
, where
$X_1=\zeta ^2$
, where
![]() $\zeta \in \mathbb {Z}_p$
and
$\zeta \in \mathbb {Z}_p$
and
![]() $p\nmid \zeta $
. Then
$p\nmid \zeta $
. Then
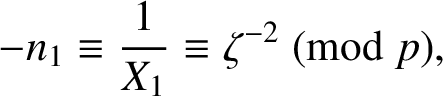 $$ \begin{align*}-n_1\equiv \dfrac{1}{X_1}\equiv \zeta^{-2}\pmod{p},\end{align*} $$
$$ \begin{align*}-n_1\equiv \dfrac{1}{X_1}\equiv \zeta^{-2}\pmod{p},\end{align*} $$
so that
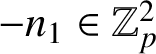 $-n_1\in \mathbb {Z}_p^2$
. Therefore,
$-n_1\in \mathbb {Z}_p^2$
. Therefore,
Case 3:
![]() $v_p(nX)<0$
. Let
$v_p(nX)<0$
. Let
![]() $n=p^sn_1$
and
$n=p^sn_1$
and
![]() $X=p^{-t}X_1$
, where
$X=p^{-t}X_1$
, where
![]() $t>s\geq 0$
,
$t>s\geq 0$
,
![]() $p\nmid n_1$
and
$p\nmid n_1$
and
![]() $p\nmid X_1$
. From (3.1),
$p\nmid X_1$
. From (3.1),
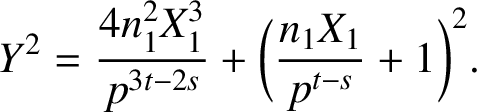 $$ \begin{align*}Y^2=\dfrac{4n_1^2X_1^3}{p^{3t-2s}}+\bigg(\dfrac{n_1X_1}{p^{t-s}}+1\bigg)^2.\end{align*} $$
$$ \begin{align*}Y^2=\dfrac{4n_1^2X_1^3}{p^{3t-2s}}+\bigg(\dfrac{n_1X_1}{p^{t-s}}+1\bigg)^2.\end{align*} $$
Therefore,
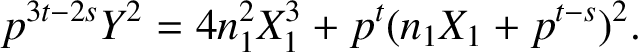 $$ \begin{align} p^{3t-2s}Y^2=4n_1^2X_1^3+p^t(n_1X_1+p^{t-s})^2.\end{align} $$
$$ \begin{align} p^{3t-2s}Y^2=4n_1^2X_1^3+p^t(n_1X_1+p^{t-s})^2.\end{align} $$
Since
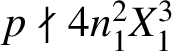 $p\nmid 4n_1^2X_1^3$
and
$p\nmid 4n_1^2X_1^3$
and
![]() $t>0$
, it follows from (3.9) that
$t>0$
, it follows from (3.9) that
![]() $3t-2s+2v_2(Y)=0$
. Thus,
$3t-2s+2v_2(Y)=0$
. Thus,
![]() $2 \mid t$
.
$2 \mid t$
.
Case 3.1:
![]() $2\mid s$
. Since
$2\mid s$
. Since
![]() $-n_1$
and
$-n_1$
and
![]() $n_1X_1+p^{t-s}$
are units in
$n_1X_1+p^{t-s}$
are units in
![]() $\mathbb {Z}_p$
,
$\mathbb {Z}_p$
,
Therefore,
Case 3.2:
![]() $2\nmid s$
. Then
$2\nmid s$
. Then
![]() $p^s \,||\, n=4^k(a^2+b^2)$
. We first show that
$p^s \,||\, n=4^k(a^2+b^2)$
. We first show that
![]() $p\equiv 1$
(mod
$p\equiv 1$
(mod
![]() $4$
). Indeed, if
$4$
). Indeed, if
![]() $p\equiv 3$
(mod
$p\equiv 3$
(mod
![]() $4$
), then
$4$
), then
![]() $a^2+b^2$
can only be divisible by an even power of p, contrary to the assumption that s is odd. Therefore,
$a^2+b^2$
can only be divisible by an even power of p, contrary to the assumption that s is odd. Therefore,
![]() $p\equiv 1$
(mod
$p\equiv 1$
(mod
![]() $4$
).
$4$
).
Taking (3.9) modulo p shows that
![]() $X_1$
is a square modulo p. Therefore,
$X_1$
is a square modulo p. Therefore,
 $X_1\in \mathbb {Z}_p^2$
. Since
$X_1\in \mathbb {Z}_p^2$
. Since
![]() $2\nmid s$
,
$2\nmid s$
,
![]() $2\nmid s-t$
,
$2\nmid s-t$
,
![]() $t-s>0$
and
$t-s>0$
and
![]() $(-n_1,\,n_1X_1+p^{t-s})_p=1$
,
$(-n_1,\,n_1X_1+p^{t-s})_p=1$
,
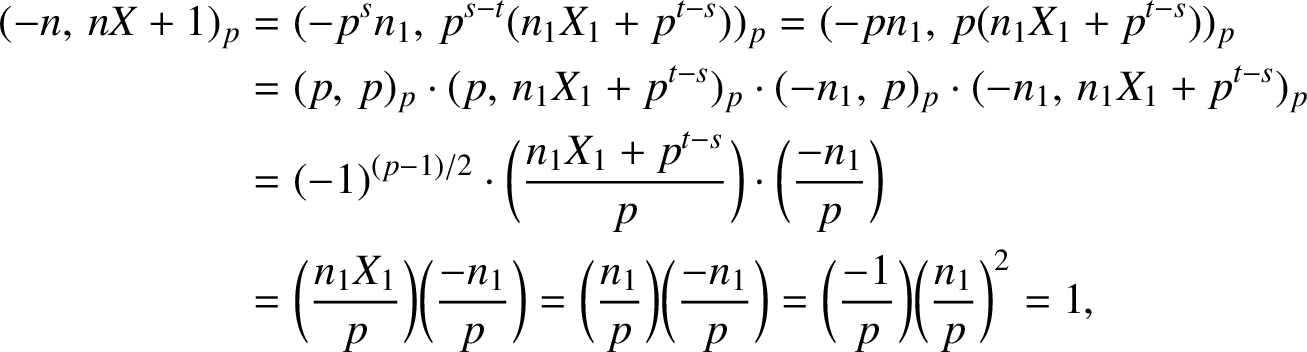 $$ \begin{align*} (-n,\,nX+1)_p&=(-p^{s}n_1,\,p^{s-t}(n_1X_1+p^{t-s}))_p =(-pn_1,\,p(n_1X_1+p^{t-s}))_p\\ &=(p,\,p)_p\cdot (p,\,n_1X_1+p^{t-s})_p\cdot (-n_1,\,p)_p\cdot (-n_1,\,n_1X_1+p^{t-s})_p\\ &=(-1)^{({p-1})/{2}}\cdot \bigg(\dfrac{n_1X_1+p^{t-s}}{p}\bigg)\cdot \bigg(\dfrac{-n_1}{p} \bigg) \\ &=\bigg(\dfrac{n_1X_1}{p} \bigg) \bigg(\dfrac{-n_1}{p} \bigg) =\bigg(\dfrac{n_1}{p} \bigg) \bigg(\dfrac{-n_1}{p} \bigg) =\bigg(\dfrac{-1}{p} \bigg)\bigg(\dfrac{n_1}{p}\bigg)^2 =1, \end{align*} $$
$$ \begin{align*} (-n,\,nX+1)_p&=(-p^{s}n_1,\,p^{s-t}(n_1X_1+p^{t-s}))_p =(-pn_1,\,p(n_1X_1+p^{t-s}))_p\\ &=(p,\,p)_p\cdot (p,\,n_1X_1+p^{t-s})_p\cdot (-n_1,\,p)_p\cdot (-n_1,\,n_1X_1+p^{t-s})_p\\ &=(-1)^{({p-1})/{2}}\cdot \bigg(\dfrac{n_1X_1+p^{t-s}}{p}\bigg)\cdot \bigg(\dfrac{-n_1}{p} \bigg) \\ &=\bigg(\dfrac{n_1X_1}{p} \bigg) \bigg(\dfrac{-n_1}{p} \bigg) =\bigg(\dfrac{n_1}{p} \bigg) \bigg(\dfrac{-n_1}{p} \bigg) =\bigg(\dfrac{-1}{p} \bigg)\bigg(\dfrac{n_1}{p}\bigg)^2 =1, \end{align*} $$
because
![]() $p\equiv 1\pmod 4$
and
$p\equiv 1\pmod 4$
and
![]() $X_1$
is a square modulo p.
$X_1$
is a square modulo p.
Lemma 3.3. We have
![]() $(-n,\,nX+1)_{\infty }=1.$
$(-n,\,nX+1)_{\infty }=1.$
Proof. By Lemmas 3.1 and 3.2,
![]() $(-n,\,nX+1)_p=1$
for all prime numbers p. Since
$(-n,\,nX+1)_p=1$
for all prime numbers p. Since
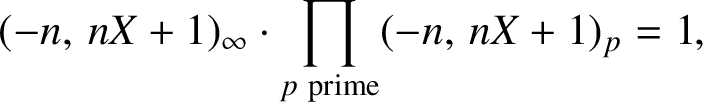 $$ \begin{align*}(-n,\,nX+1)_{\infty}\cdot \prod\limits_{p\ \text{prime}} (-n,\,nX+1)_p=1,\end{align*} $$
$$ \begin{align*}(-n,\,nX+1)_{\infty}\cdot \prod\limits_{p\ \text{prime}} (-n,\,nX+1)_p=1,\end{align*} $$
it follows that
![]() $(-n,\,nX+1)_{\infty }=1.$
$(-n,\,nX+1)_{\infty }=1.$
The consequence of Lemma 3.3 is that the equation
![]() $-n\alpha ^2+(nX+1)\beta ^2=1$
has real solutions. Hence,
$-n\alpha ^2+(nX+1)\beta ^2=1$
has real solutions. Hence,
![]() $nX+1>0$
, contradicting
$nX+1>0$
, contradicting
![]() $nX+1<0$
from (3.2).
$nX+1<0$
from (3.2).
Acknowledgements
The author is sincerely grateful to Professor Erik Dofs for pointing out the reference [Reference Garaev6] and many valuable conversations. The author would like to thank the referee for the careful reading and important comments. Part of this work was completed during the author’s stay at Vietnam Institute of Advanced Study in Mathematics (VIASM). The author would like to thank the Institute for its support and funding.