Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-12T02:13:49.607Z Has data issue: false hasContentIssue false
  • English
  • Français

ON A LATTICE CHARACTERISATION OF FINITE SOLUBLE PST-GROUPS

Part of: Structure and classification of infinite or finite groups Representation theory of groups

Published online by Cambridge University Press:  10 July 2019

ZHANG CHI Open the ORCID record for ZHANG CHI [Opens in a new window]  and
ALEXANDER N. SKIBA
ZHANG CHI*
Affiliation:
School of Mathematics, China University of Mining and Technology, Xuzhou 221116, PR China email zcqxj32@mail.ustc.edu.cn
ALEXANDER N. SKIBA
Affiliation:
Department of Mathematics and Technologies of Programming, Francisk Skorina Gomel State University, Gomel 246019, Belarus email alexander.skiba49@gmail.com
*
✉zcqxj32@mail.ustc.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

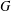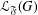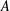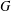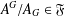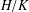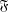Let $\mathfrak{F}$ be a class of finite groups and $G$ a finite group. Let ${\mathcal{L}}_{\mathfrak{F}}(G)$ be the set of all subgroups $A$ of $G$ with $A^{G}/A_{G}\in \mathfrak{F}$. A chief factor $H/K$ of $G$ is $\mathfrak{F}$-central in $G$ if 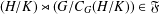$(H/K)\rtimes (G/C_{G}(H/K))\in \mathfrak{F}$. We study the structure of 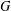$G$ under the hypothesis that every chief factor of 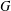$G$ between 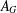$A_{G}$ and 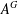$A^{G}$ is 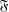$\mathfrak{F}$-central in 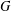$G$ for every subgroup 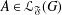$A\in {\mathcal{L}}_{\mathfrak{F}}(G)$. As an application, we prove that a finite soluble group 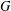$G$ is a PST-group if and only if 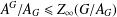$A^{G}/A_{G}\leq Z_{\infty }(G/A_{G})$ for every subgroup $A\in {\mathcal{L}}_{\mathfrak{N}}(G)$, where 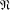$\mathfrak{N}$ is the class of all nilpotent groups.

Keywords

finite grouplattice of subgroups𝔉-central chief factorsaturated formationFitting formation

MSC classification

Primary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Secondary: 20D15: Nilpotent groups, $p$-groups 20D20: Sylow subgroups, Sylow properties, $pi$-groups, $pi$-structure 20E15: Chains and lattices of subgroups, subnormal subgroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 101 , Issue 2 , April 2020 , pp. 247 - 254
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Footnotes

Research of the first author is supported by the China Scholarship Council and NNSF of China (11771409).

References

Ballester-Bolinches, A., Doerk, K. and Pèrez-Ramos, M. D., ‘On the lattice of 𝔉-subnormal subgroups’, J. Algebra 148 (1992), 42–52.Google Scholar
Ballester-Bolinches, A. and Esteban-Romero, R., ‘Sylow permutable subnormal subgroups of finite groups II’, Bull. Aust. Math. Soc. 64 (2001), 479–486.Google Scholar
Ballester-Bolinches, A., Esteban-Romero, R. and Asaad, M., Products of Finite Groups (Walter de Gruyter, Berlin–New York, 2010).Google Scholar
Ballester-Bolinches, A. and Ezquerro, L. M., Classes of Finite Groups (Springer, Dordrecht, 2006).Google Scholar
Doerk, K. and Hawkes, T., Finite Soluble Groups (Walter de Gruyter, Berlin–New York, 1992).Google Scholar
Kegel, O., ‘Sylow-Gruppen and Subnormalteiler endlicher Gruppen’, Math. Z. 78 (1962), 205–221.Google Scholar
Kegel, O. H., ‘Untergruppenverbände endlicher Gruppen, die den Subnormalteilerverband echt enthalten’, Arch. Math. 30(3) (1978), 225–228.Google Scholar
Schmidt, R., Subgroup Lattices of Groups (Walter de Gruyter, Berlin, 1994).Google Scholar
Shemetkov, L. A. and Skiba, A. N., Formations of Algebraic Systems (Nauka, Moscow, 1989).Google Scholar
Skiba, A. N., ‘On 𝜎-subnormal and 𝜎-permutable subgroups of finite groups’, J. Algebra 436 (2015), 1–16.Google Scholar
Vasil’ev, A. F., Kamornikov, A. F. and Semenchuk, V. N., ‘On lattices of subgroups of finite groups’, in: Infinite Groups and Related Algebraic Structures (ed. Chernikov, N. S.) (Institut Matematiki AN Ukrainy, Kiev, 1993), 27–54 (in Russian).Google Scholar
Wielandt, H., ‘Eine Verallgemeinerung der invarianten Untergruppen’, Math. Z. 45 (1939), 200–244.Google Scholar