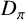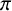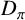1 Introduction
All groups considered here are finite. Let G be a group and let
$\pi $
be a set of primes. Recall that a subgroup H of a group G is called a
$\pi $
-subgroup of G if all primes dividing the order of H lie in
$\pi $
. Moreover, a subgroup H is called a Hall
$\pi $
-subgroup of G if it is a
$\pi $
-subgroup and its index is not divisible by the elements of
$\pi $
.
According to Hall [Reference Hall2], a group G is said to satisfy
$E_{\pi }$
(or
$G \in E_{\pi }$
for short) if there exists a Hall
$\pi $
-subgroup of G. If
$G \in E_{\pi }$
and all
$\pi $
-Hall subgroups are conjugate then we say that G satisfies
$C_{\pi }$
(
$G \in C_{\pi }$
). If
$G \in E_{\pi }$
and every
$\pi $
-subgroup of G is contained in a conjugate of a
$\pi $
-Hall subgroup of G then we say that G satisfies
$D_{\pi }$
.
In 1954, Wielandt [Reference Wielandt5] proved the classical result that a group G possessing a nilpotent
$\pi $
-Hall subgroup satisfies
$D_{\pi }$
. After several years, one of the earliest generalisations of Wielandt’s theorem was obtained by Wielandt himself in [Reference Wielandt6]. Suppose that a set of primes
$\pi $
is a union of disjoint subsets
$\sigma $
and
$\tau $
, and a group G possesses a Hall
$\pi $
-subgroup
$H = H_{\sigma } \times H_{\tau }$
, where
$H_{\sigma }$
is a nilpotent
$\sigma $
-subgroup of H and
$H_{\tau }$
is a
$\tau $
-subgroup of H. If G satisfies
$D_{\tau }$
, then G satisfies
$D_{\pi }$
. In the same paper, Wielandt conjectured that one can replace ‘the nilpotency of
$H_{\sigma }$
’ with the weaker condition that ‘G satisfies
$D_{\sigma }$
’ in the above theorem. This conjecture was completely confirmed by Guo et al. [Reference Guo, Revin and Vdovin1] by using the classification of finite simple groups. It is worth pointing out another inspiring result due to Rusakov [Reference Rusakov4] that if a group G possesses a Hall
$\pi $
-subgroup H whose Sylow subgroups are all cyclic, then G satisfies
$D_{\pi }$
.
In this paper, we try to weaken the ‘direct product relation’ between
$H_{\sigma }$
and
$H_{\tau }$
in Wielandt’s theorem, replacing it with a special semidirect product. Our main theorem is the following result.
Theorem 1.1. Let a set
$\pi $
of primes be a union of disjoint subsets
$\sigma $
and
$\tau $
. Let a group G possess a Hall
$\pi $
-subgroup
$H=H_{\sigma } H_{\tau }$
such that:
-
(1)
$H_{\sigma }$
is a normal
$\sigma $
-subgroup of H; -
(2)
$H_{\tau }$
is a
$\tau $
-subgroup of H with all Sylow subgroups cyclic; -
(3)
$H_{\tau }$
normalises every subgroup of
$H_{\sigma }$
.
If G satisfies
$D_{\sigma }$
, then G satisfies
$D_{\pi }$
.
It is worth mentioning that the proof of Theorem 1.1 does not depend on the classification of finite simple groups. In Theorem 1.1, neither of the hypotheses
$(2)$
or
$(3)$
can be removed. In fact, we can see this in the projective linear group
$G=\operatorname {\mathrm {PSL}}(2,11)$
. Let
$\pi =\{2,3\}$
and notice that Hall
$\pi $
-subgroups of G are isomorphic to the alternating group
$\operatorname {\mathrm {A}}_{4}$
or the dihedral group
$\operatorname {\mathrm {D}}_{12}$
. Hence
$G \notin D_{\pi }$
.
If
$H\cong D_{12}$
, then we can set
$\sigma =\{3\}$
and
$\tau =\{2\}$
. Hence
$H_{\sigma }\cong \operatorname {\mathrm {C}}_{3}$
and
$H_{\tau }\cong \operatorname {\mathrm {C}}_{2}\times \operatorname {\mathrm {C}}_{2}$
are the Sylow
$3$
-subgroup and the Sylow
$2$
-subgroup of H, respectively. Clearly
$G\in D_{\{3\}}$
,
$H_{\sigma }\unlhd H$
and
$H_{\tau }$
normalises every subgroup of
$H_{\sigma }$
, which means that all hypotheses in Theorem 1.1 hold except hypothesis
$(2)$
because
$H_{\tau }$
is not cyclic.
If
$H\cong A_{4}$
, we may assume that
$\sigma =\{2\}$
and
$\tau =\{3\}$
. Then
$H_{\sigma }\cong \operatorname {\mathrm {C}}_{2}\times \operatorname {\mathrm {C}}_{2}$
and
$H_{\tau }\cong \operatorname {\mathrm {C}}_{3}$
are the Sylow
$2$
-subgroup and the Sylow
$3$
-subgroup of H, respectively. We see that
$G\in D_{\{2\}}, H_{\sigma }\unlhd H$
and
$H_{\tau }$
is cyclic but
$H_{\tau }$
does not normalise all subgroups of
$H_{\sigma }$
.
The following two corollaries both follow directly from Theorem 1.1. The first unifies Wielandt’s and Rusakov’s results.
Corollary 1.2. Let a set
$\pi $
of primes be a union of disjoint subsets
$\sigma $
and
$\tau $
. Let a group G possess a Hall
$\pi $
-subgroup
$H=H_{\sigma } H_{\tau }$
such that:
-
(1)
$H_{\sigma }$
is a normal nilpotent
$\sigma $
-subgroup of H; -
(2)
$H_{\tau }$
is a
$\tau $
-subgroup with all Sylow subgroups cyclic; -
(3)
$H_{\tau }$
normalises every subgroup of
$H_{\sigma }$
.
Then G satisfies
$D_{\pi }$
.
The second corollary is a generalisation of Rusakov’s result following Wielandt’s idea; it is also a direct corollary of the result of Guo et al. [Reference Guo, Revin and Vdovin1].
Corollary 1.3. Let a set
$\pi $
of primes be a union of disjoint subsets
$\sigma $
and
$\tau $
. Let a group G possess a Hall
$\pi $
-subgroup
$H=H_{\sigma }\times H_{\tau }$
such that:
-
(1)
$H_{\sigma }$
is a
$\sigma $
-subgroup of H; -
(2)
$H_{\tau }$
is a
$\tau $
-subgroup with all Sylow subgroups cyclic.
If G satisfies
$D_{\sigma }$
, then G satisfies
$D_{\pi }$
.
2 Lemmas
In this section we list some lemmas, most of which are well known. The first is a direct consequence of Burnside’s p-nilpotency criterion.
Lemma 2.1 [Reference Huppert3, IV, Theorem 2.8].
Let G be a group and let p be the smallest prime dividing the order of G. If G possesses a cyclic Sylow p-subgroup, then G is p-nilpotent.
Lemma 2.2. Let G be a group with all Sylow subgroups cyclic. Then G has two cyclic subgroups
$N_{1},N_{2}$
such that
$G=N_{1}N_{2}, N_{1}\unlhd G$
and
$(|N_{1}|, |N_{2}|)=1$
.
Proof. This is a consequence of [Reference Huppert3, IV, Theorem 2.11].
The following lemma gives a property of groups with all Sylow subgroups cyclic and will be useful in the proof of our main theorem.
Lemma 2.3. Let G be a group with all Sylow subgroups cyclic and assume that p is the smallest prime dividing the order of G. If K is a
$p^{\prime }$
-subgroup of G, then there exists a Sylow p-subgroup P of G such that
$P\leq \operatorname {\mathrm {N}}_{G}(K)$
.
Proof. By Lemma 2.1, G is p-nilpotent. Denote by N the normal p-complement of G. Clearly
$K\leq N$
. Notice that all Sylow subgroups of N are also cyclic. By Lemma 2.2, we can assume that
$N=N_{1}N_{2}$
, where
$N_{1},N_{2}$
are cyclic,
$(|N_{1}|,|N_{2}|)=1$
and
$N_{1}\unlhd N$
.
Let
$K_{1}=K\cap N_{1}$
. As
$N_{1}$
is a normal Hall subgroup of N, it is easy to see that
$K_{1}$
is a normal Hall subgroup of K. By the Schur–Zassenhaus theorem, we may assume that
$K=K_{1}K_{2}$
, where
$K_{2}$
is a complement of
$K_{1}$
in K. Since
$N/N_{1}\cong N_{2}$
is cyclic, it follows that
$K_{2}N_{1}/N_{1}$
is a characteristic subgroup of
$N/N_{1}$
. Since
$N_{1}$
is a characteristic subgroup of N, it is not difficult to check, by definition, that
$K_{2}N_{1}$
is a characteristic subgroup of N. As
$N\unlhd G$
, it follows that
$K_{2}N_{1}\unlhd G$
. By a Frattini argument,
$G=\operatorname {\mathrm {N}}_{G}(K_{2})N_{1}$
. Since the index of
$\operatorname {\mathrm {N}}_{G}(K_{2})$
in G is a
$p^{\prime }$
-number, there exists a Sylow p-subgroup P of G such that
$P\leq \operatorname {\mathrm {N}}_{G}(K_{2})$
.
On the other hand, it is easy to see that
$K_{1}$
is a characteristic subgroup of
$N_{1}$
as
$N_{1}$
is cyclic. Since
$N_{1}$
is a characteristic subgroup of G, we deduce that
$K_{1}\unlhd G$
. It follows that P normalises
$K=K_{1}K_{2}$
. Hence
$P\leq \operatorname {\mathrm {N}}_{G}(K)$
, as desired.
Recall that a group G is called minimal non-p-nilpotent if G is not p-nilpotent but every proper subgroup of G is p-nilpotent. The structure of minimal non-p-nilpotent groups is well known, due to N. Itô.
Lemma 2.4. Let p be a prime and G be a minimal non-p-nilpotent group. Then G possesses a normal Sylow p-subgroup P and a cyclic Sylow q-subgroup
$Q\neq 1$
for some
$q\neq p$
such that
$G=PQ$
.
Proof. See [Reference Huppert3, IV, Theorem 5.4].
3 Proof of Theorem 1.1
Suppose that the theorem is false so that there exists a group G possessing a Hall
$\pi $
-subgroup
$H=H_{\sigma }H_{\tau }$
such that
$G, H_{\sigma },H_{\tau }$
satisfy the hypotheses of Theorem 1.1 but
$G \notin D_{\pi }$
, which means that there exists a
$\pi $
-subgroup K of G such that
$K^{g}\nleq H$
for each
$g\in G$
. Choose the counterexample triple
$(G, H, K)$
with
$|G|+|H|+|K|$
minimal and, without loss of generality, assume that
$\pi \subseteq \pi (G)$
.
By hypothesis, if
$\tau $
is empty, the result is trivial. Now let p be the smallest prime in
$\tau $
. Since all Sylow subgroups of
$H_{\tau }$
are cyclic,
$H_{\tau }$
is p-nilpotent. As
$H_{\sigma }\unlhd H$
, H is also p-nilpotent. Set
$\widetilde {\pi }=\pi -\{p\}$
and
$\widetilde {\tau }=\tau -\{p\}$
. Then we will derive a contradiction from the following three steps.
Step 1:
$p\in \pi (K)$
.
If
$p \notin \pi (K)$
, then K is a
$\widetilde {\pi }$
-subgroup of G. Let
$\widetilde {H}=H_{\sigma }H_{\widetilde {\tau }}$
, where
$H_{\widetilde {\tau }}$
is the normal p-complement of
$H_{\tau }$
. It is obvious that
$\widetilde {H}$
is a
$\widetilde {\pi }$
-Hall subgroup of G and
$\widetilde {H}\leq H$
. Considering the triple
$(G, \widetilde {H}, K)$
, by minimality, K is contained in a conjugate of
$\widetilde {H}$
and also in a conjugate of H, contrary to the choice of K.
Step 2: K is minimal non-p-nilpotent.
For any proper subgroup T of K, minimality implies that T is contained in a conjugate of H. As H is p-nilpotent, so is T. Now we will show that K is not p-nilpotent.
Assume that K is p-nilpotent and let
$K=K_{p}K_{\widetilde {\pi }}$
, where
$K_{p}$
and
$K_{\widetilde {\pi }}$
are the Sylow p-subgroup and the normal p-complement of K, respectively. Since
$p\in \pi (K)$
by Step 1,
$K_{p}\neq 1$
and
$K_{\widetilde {\pi }}<K$
. By minimality,
$K_{\widetilde {\pi }}$
is contained in a conjugate of H. Without loss of generality, we can assume that
$K_{\widetilde {\pi }} \leq H$
. Write
$K_{\sigma }=H_{\sigma }\cap K_{\widetilde {\pi }}$
. Since
$H_{\sigma }$
is a normal Hall
$\sigma $
-subgroup of H, it follows that
$K_{\sigma }$
is a normal Hall
$\sigma $
-subgroup of
$K_{\widetilde {\pi }}$
. By the Schur–Zassenhanus theorem, we may assume that
$K_{\widetilde {\tau }}$
is the complement of
$K_{\sigma }$
in
$K_{\widetilde {\pi }}$
, which is also a Hall
$\tau $
-subgroup of K.
Since H has a Hall
$\tau $
-subgroup
$H_{\tau }$
with all Sylow subgroups cyclic, by Rusakov’s theorem,
$H\in D_{\tau }$
. As
$K_{\widetilde {\tau }}$
is a
$\tau $
-subgroup of H,
$K_{\widetilde {\tau }}\leq H_{\tau }^{h}$
for some
$h\in H$
.
Moreover, as
$K_{\widetilde {\tau }}$
is a
$p^{\prime }$
-subgroup, it follows from Lemma 2.3 that there exists a Sylow p-subgroup P of
$H_{\tau }^{h}$
such that P normalises
$K_{\widetilde {\tau }}$
. On the other hand, by hypothesis,
$P^{h^{-1}}\leq H_{\tau }$
normalises every subgroup of
$H_{\sigma }$
. Since
$h\in H$
and
$H_{\sigma } \unlhd H$
,
$K_{\sigma }^{h^{-1}}\leq H_{\sigma }^{h^{-1}}=H_{\sigma }$
. Hence
$P^{h^{-1}}$
normalises
$K_{\sigma }^{h^{-1}}$
, and so P normalises
$K_{\sigma }$
. Thus P normalises
$K_{\widetilde {\pi }}=K_{\sigma }K_{\widetilde {\tau }}$
, that is,
$P \in \operatorname {\mathrm {N}}_{G}(K_{\widetilde {\pi }})$
.
Notice that P is also a Sylow p-subgroup of G and also of
$\operatorname {\mathrm {N}}_{G}(K_{\widetilde {\pi }})$
, and
$K_{p}\leq K\leq \operatorname {\mathrm {N}}_{G}(K_{\widetilde {\pi }})$
since
$K_{\widetilde {\pi }}\unlhd K$
. By Sylow’s theorem, there exists an element
$x\in \operatorname {\mathrm {N}}_{G}(K_{\widetilde {\pi }})$
such that
$K_{p}^{x}\leq P$
. Thus
$$ \begin{align*}K^{x}=K_{p}^{x}K_{\widetilde{\pi}}^{x}\leq K_{p}^{x}K_{\widetilde{\pi}}\leq PH\leq H^{h}_{\tau}H=H,\end{align*} $$
which is a contradiction. Hence K is minimal non-p-nilpotent.
Step 3: The final contradiction.
Since K is minimal non-p-nilpotent, it follows from Lemma 2.4 that
$K=K_{p}K_{q}$
, where
$K_{p}$
is the normal Sylow p-subgroup of K and
$K_{q}\neq 1$
is a cyclic Sylow q-subgroup of K for some prime
$q\neq p$
and
$q \in \pi $
. Notice that
$K_{q}\neq 1$
and so
$K_{p}< K$
. Minimality implies that
$K_{p}$
is contained in a conjugate of
$H_{\tau }$
. Since all Sylow subgroups of
$H_{\tau }$
are cyclic,
$K_{p}$
is cyclic. Hence, by the N/C theorem,
$$ \begin{align*}K/\operatorname{\mathrm{C}}_{K}(K_{p})\lesssim \operatorname{\mathrm{Aut}}(K_{p}).\end{align*} $$
Note that
$K\neq \operatorname {\mathrm {C}}_{K}(K_{p})$
otherwise
$K_{p}$
is in the centre of K and K is nilpotent, contrary to Step 2. Hence the order of
$K/\operatorname {\mathrm {C}}_{K}(K_{p})$
is a positive power of q, which implies that q divides
$|\!\operatorname {\mathrm {Aut}}(K_{p})|=p^{a}(p-1)$
for some nonnegative integer a. As
$p\neq q$
, q divides
$p-1$
. Since p is the smallest prime in
$\tau $
, it follows that
$q\notin \tau $
. As
$q\in \pi =\sigma \cup \tau $
, this forces
$q \in \sigma $
.
By Rusakov’s theorem, G satisfies
$D_{\tau }$
. Hence we can assume that
$K_{p} \leq H_{\tau }^{g}$
for some
$g \in G$
. Let Q be a Sylow q-subgroup of
$H_{\sigma }^{g}$
. By hypothesis,
$H_{\tau }^{g}$
normalises every subgroup of
$H_{\sigma }^{g}$
. This implies that
$K_{p}$
normalises every subgroup of Q. For each cyclic subgroup
$Q_{1}$
of Q,
$Q_{1}$
is also
$K_{p}$
-invariant and so
$ |K_{p}/\operatorname {\mathrm {C}}_{K_{p}}(Q_{1})|$
divides
$|\!\operatorname {\mathrm {Aut}}(Q_{1})|=q^{n-1}(q-1)$
, for some positive integer n. As
$q<p$
, it follows that
$K_{p}=\operatorname {\mathrm {C}}_{Q_{1}}(K_{p})$
and thus
$K_{p}$
acts trivially on each cyclic subgroup
$Q_{1}$
and also on Q. In particular,
$Q\leq \operatorname {\mathrm {N}}_{G}(K_{p})$
. Since Q is a Sylow q-subgroup of
$\operatorname {\mathrm {N}}_{G}(K_{p})$
and
$K_{q}\leq K\leq \operatorname {\mathrm {N}}_{G}(K_{p})$
, there exists an element
$y\in \operatorname {\mathrm {N}}_{G}(K_{p})$
such that
$K_{q}^{y}\leq Q$
. Now we see that
$$ \begin{align*}K^{y}=K_{p}^{y}K_{q}^{y}\leq K_{p}K_{q}^{y}\leq H^{g}_{\tau}Q\leq H^{g}_{\tau}H_{\sigma}^{g}=H^{g},\end{align*} $$
which is the final contradiction. The proof is complete.
