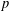Hostname: page-component-745bb68f8f-l4dxg Total loading time: 0 Render date: 2025-02-11T22:01:27.458Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON $p$-PARTS OF BRAUER CHARACTER DEGREES

Part of: Representation theory of groups

Published online by Cambridge University Press:  06 May 2020

JINBAO LI Open the ORCID record for JINBAO LI [Opens in a new window]  and
YONG YANG Open the ORCID record for YONG YANG [Opens in a new window]
JINBAO LI
Affiliation:
Key Laboratory of Group and Graph Theories and Applications,Chongqing University of Arts and Sciences, Chongqing402160, PR China email leejinbao25@163.com
YONG YANG*
Affiliation:
Department of Mathematics,Texas State University, 601 University Drive,San Marcos, TX78666, USA email yang@txstate.edu
*
✉yang@txstate.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 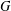$G$ be a finite group and 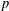$p$ be an odd prime. We show that if 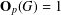$\mathbf{O}_{p}(G)=1$ and 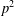$p^{2}$ does not divide every irreducible 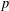$p$-Brauer character degree of 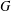$G$, then 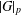$|G|_{p}$ is bounded by $p^{3}$ when 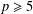$p\geqslant 5$ or 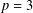$p=3$ and 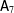$\mathsf{A}_{7}$ is not involved in 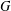$G$, and by 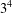$3^{4}$ if 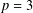$p=3$ and 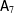$\mathsf{A}_{7}$ is involved in 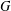$G$.

Keywords

finite groupsBrauer charactercharacter degreep-part

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20C20: Modular representations and characters 20D05: Finite simple groups and their classification
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 1 , February 2021 , pp. 83 - 87
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Footnotes

The project was supported by NSFC (11671063), the Natural Science Foundation of CSTC (cstc2018jcyjAX0060) and a grant from the Simons Foundation (No. 499532).

References

Lewis, M., Navarro, G., Tiep, P. H. and Tong-Viet, H. P., ‘p-parts of character degrees’, J. Lond. Math. Soc. 92(2) (2015), 483–497.CrossRefGoogle Scholar
Lewis, M., Navarro, G. and Wolf, T. R., ‘p-parts of character degrees and the index of the Fitting subgroup’, J. Algebra 411 (2014), 182–190.CrossRefGoogle Scholar
Manz, O., ‘On the modular version of Ito’s theorem on character degrees for groups of odd order’, Nagoya Math. J. 105 (1987), 121–128.CrossRefGoogle Scholar
Michler, G., ‘A finite simple group of Lie type has p-blocks with different defects, p≠2’, J. Algebra 104 (1986), 220–230.CrossRefGoogle Scholar
Qian, G., ‘A note on p-parts of character degrees’, Bull. Lond. Math. Soc. 50(4) (2018), 663–666.CrossRefGoogle Scholar