Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-02-06T13:51:09.812Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON DERIVED LENGTH AND CHARACTER DEGREES

Part of: Representation theory of groups

Published online by Cambridge University Press:  13 July 2020

BURCU ÇINARCI Open the ORCID record for BURCU ÇINARCI [Opens in a new window]  and
TEMHA ERKOÇ Open the ORCID record for TEMHA ERKOÇ [Opens in a new window]
BURCU ÇINARCI
Affiliation:
Maritime Faculty, Piri Reis University, 34940 Istanbul, Turkey email burcu-cinarci@hotmail.com
TEMHA ERKOÇ*
Affiliation:
Department of Mathematics, Faculty of Science,Istanbul University, 34134 Istanbul, Turkey email erkoctemha@gmail.com
*
✉erkoctemha@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Isaacs and Seitz conjectured that the derived length of a finite solvable group 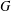$G$ is bounded by the cardinality of the set of all irreducible character degrees of $G$. We prove that the conjecture holds for 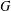$G$ if the degrees of nonlinear monolithic characters of 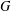$G$ having the same kernels are distinct. Also, we show that the conjecture is true when 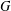$G$ has at most three nonlinear monolithic characters. We give some sufficient conditions for the inequality related to monolithic characters or real-valued irreducible characters of 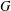$G$ when the commutator subgroup of 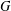$G$ is supersolvable.

Keywords

solvable groupsderived lengthreal and monolithic charactersTaketa inequalityIsaacs–Seitz conjecture

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 20C20: Modular representations and characters
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 271 - 277
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Footnotes

The work of the authors was supported by the Scientific Research Projects Coordination Unit of Istanbul University (project number 27148).

References

Berger, T. R., ‘Characters and derived length in groups of odd order’, J. Algebra 39 (1976), 199–207.Google Scholar
Berkovich, Y. G. and Zhmud, E. M., Characters of Finite Groups. Part 2, Translations of Mathematical Monographs, 181 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Çınarcı, B. and Erkoç, T., ‘Real characters, monolithic characters and the Taketa inequality’, J. Algebra Appl. 18(10) (2019), Article ID 19501834. doi:10.1142/S0219498819501834.Google Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, New York, 1976).Google Scholar
Isaacs, I. M. and Knutson, G., ‘Irreducible character degrees and normal subgroups’, J. Algebra 199 (1998), 302–326.Google Scholar
Navarro, G., Sanus, L. and Tiep, P. H., ‘Real characters and degrees’, Israel J. Math. 171 (2009), 157–173.Google Scholar
Yılmaztürk, U., Erkoç, T. and Güloğlu, İ. Ş., ‘Some sufficient conditions for the Taketa inequality’, Proc. Japan Acad. 89 (2013), 103–106.Google Scholar