Published online by Cambridge University Press: 25 January 2013
Let 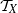 ${ \mathcal{T} }_{X} $ be the full transformation semigroup on a set
${ \mathcal{T} }_{X} $ be the full transformation semigroup on a set 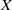 $X$ and
$X$ and 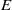 $E$ be a nontrivial equivalence relation on
$E$ be a nontrivial equivalence relation on 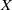 $X$. Denote so that
$X$. Denote so that  $$\begin{eqnarray*}{T}_{\exists } (X)= \{ f\in { \mathcal{T} }_{X} : \forall x, y\in X, (f(x), f(y))\in E\Rightarrow (x, y)\in E\} ,\end{eqnarray*}$$
$$\begin{eqnarray*}{T}_{\exists } (X)= \{ f\in { \mathcal{T} }_{X} : \forall x, y\in X, (f(x), f(y))\in E\Rightarrow (x, y)\in E\} ,\end{eqnarray*}$$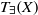 ${T}_{\exists } (X)$ is a subsemigroup of
${T}_{\exists } (X)$ is a subsemigroup of 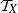 ${ \mathcal{T} }_{X} $. In this paper, we endow
${ \mathcal{T} }_{X} $. In this paper, we endow  ${T}_{\exists } (X)$ with the natural partial order and investigate when two elements are related, then find elements which are compatible. Also, we characterise the minimal and maximal elements.
${T}_{\exists } (X)$ with the natural partial order and investigate when two elements are related, then find elements which are compatible. Also, we characterise the minimal and maximal elements.