Hostname: page-component-745bb68f8f-hvd4g Total loading time: 0 Render date: 2025-02-05T23:15:22.190Z Has data issue: false hasContentIssue false
  • English
  • Français

LOOK, KNAVE

Part of: Sequences and sets

Published online by Cambridge University Press:  21 October 2020

THOMAS MORRILL Open the ORCID record for THOMAS MORRILL [Opens in a new window]
THOMAS MORRILL*
Affiliation:
School of Science, The University of New South Wales Canberra, Australia e-mail: morrillt@trine.edu
*
e-mail: t.morrill@adfa.edu.au
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We examine a recursive sequence in which $s_n$ is a literal description of what the binary expansion of the previous term 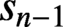$s_{n-1}$ is not. By adapting a technique of Conway, we determine the limiting behaviour of 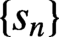$\{s_n\}$ and dynamics of a related self-map of $2^{\mathbb {N}}$ . Our main result is the existence and uniqueness of a pair of binary sequences, each the complement-description of the other. We also take every opportunity to make puns.

Keywords

recursionLook-Say sequenceKnights and Knaves

MSC classification

Primary: 11B37: Recurrences
Secondary: 11B05: Density, gaps, topology
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 103 , Issue 2 , April 2021 , pp. 210 - 217
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Footnotes

Dedicated to the life and works of John Horton Conway

Supported by Australian Research Council Discovery Project DP160100932.

References

Conway, J. H., ‘The weird and wonderful chemistry of audioactive decay’, Open Problems in Communication and Computation (eds. Cover, T. M. and Gopinath, B.) (Springer, New York, NY, 1987), 173–188.CrossRefGoogle Scholar
Johnston, N., ‘The binary ‘look-and-say’ sequence’, http://www.njohnston.ca/2010/11/the-binary-look-and-say-sequence/, 2010.Google Scholar
Smullyan, R. M., What is the Name of This Book? The Riddle of Dracula and Other Logical Puzzles (Prentice-Hall, Upper Saddle River, NJ, 1978).Google Scholar
The On-Line Encyclopedia of Integer Sequences (2020), https://oeis.org/A005150.Google Scholar
The On-Line Encyclopedia of Integer Sequences (2020), https://oeis.org/A014715.Google Scholar
The On-Line Encyclopedia of Integer Sequences (2020), https://oeis.org/A001387.Google Scholar