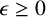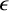1 Introduction
It was elementary, but not simple by any means. The problem turned out to be deep, the appearance of simplicity was deceptive. Khinchin [Reference Khinchin8]
Independent and pioneering results of Sharkovsky [Reference Sharkovsky17] and Li and Yorke [Reference Li and Yorke9] have led to a rich literature on continuous self-maps on the unit interval, and the phrase ‘Li–Yorke chaotic maps’ is now part of the vernacular of dynamical systems and affiliated applied fields, not only physics and engineering, but also evolutionary biology and economics. Sharkovsky defines an order relation on the possible periods of periodic points, establishing precise conditions under which such interval maps can have points of any period, while Li and Yorke furnish conditions under which nonperiodic chaotic behaviour is displayed by an uncountable subset of initial points of an interval map. Much effort has been expended to capture the apparently random behaviour of chaotic trajectories through precise mathematical definitions of chaos itself. The excellent monograph by Ruette [Reference Ruette16] contains a very precise taxonomy of the different notions of chaos that have been explored (see page VIII of the introduction for a clear schematic summary). For the distinctions between turning points, periodic points, periodic orbits, orbit portraits and their evolution under the general rubric of the concept of an orbit, see Milnor and Thurston’s monograph [Reference Milnor and Thurston10] and the extensive work that has followed it: the field of economic dynamics still has much to learn from this literature.
The result we present belongs more generally to the subject of the pervasiveness of Li–Yorke chaos, the existence of scrambled sets in the domain of a map that can be arbitrarily large or arbitrarily small as measured by the Lebesgue measure but are pervasive in being spread all over the domain. The result addresses the ‘observability’ of chaos exhibited by interval maps as tracked by the Lebesgue measure of sets of initial points with chaotic trajectories (see Misiurewicz [Reference Misiurewicz11] for the linkage between the Lebesgue measure of scrambled sets and observability of chaos). As background, let us note Jiménéz-López singling out in his review [Reference Jiménéz-López5] of Ruette [Reference Ruette16] ‘a very beautiful (and far from easy to prove) dichotomy result by Smítal: a continuous interval map is either Li–Yorke chaotic, or all points are (up to small errors) eventually periodic for it’.
In this connection, Nathanson [Reference Nathanson13] presents a continuous self-map on the interval that exhibits unobservable Li–Yorke chaos in a system exhibiting dynamics that can be made as regular (periodic) as one pleases. For any natural number
![]() $n\geq 3$
, he constructs a piecewise linear continuous map such that all trajectories except for a set of Lebesgue measure zero have eventually periodic trajectories of period
$n\geq 3$
, he constructs a piecewise linear continuous map such that all trajectories except for a set of Lebesgue measure zero have eventually periodic trajectories of period
![]() $n.$
On the other hand, there is a dual, apparently orthogonal, result due to Kan [Reference Kan6], which questions the prevailing sentiment of the negligibility of the set of initial conditions that give rise to Li–Yorke chaotic trajectories. His canonical example consists of a continuous self-map defined on the unit interval which has a scrambled set whose Lebesgue measure is 1/8. This result was soon generalised to show a scrambled set, first of full outer Lebesgue measure [Reference Smítal18] and then [Reference Misiurewicz12] and [Reference Rajan15] for extensions and [Reference Balibrea and Jiménéz-López1], [Reference Blanchard, Huang and Snoha2, footnote 66], [Reference Oono14, page 63] and [Reference Ruette16, page 111] for its framing more broadly in the current literature.
$n.$
On the other hand, there is a dual, apparently orthogonal, result due to Kan [Reference Kan6], which questions the prevailing sentiment of the negligibility of the set of initial conditions that give rise to Li–Yorke chaotic trajectories. His canonical example consists of a continuous self-map defined on the unit interval which has a scrambled set whose Lebesgue measure is 1/8. This result was soon generalised to show a scrambled set, first of full outer Lebesgue measure [Reference Smítal18] and then [Reference Misiurewicz12] and [Reference Rajan15] for extensions and [Reference Balibrea and Jiménéz-López1], [Reference Blanchard, Huang and Snoha2, footnote 66], [Reference Oono14, page 63] and [Reference Ruette16, page 111] for its framing more broadly in the current literature.
The point of this paper (the question posed and answered) is that we can extend Kan’s construction to find a chaotic interval map that has an arbitrarily large (but finite) number of mutually disjoint extremally scrambled sets which are homeomorphic to each other, and each of which has positive Lebesgue measure. Extremally scrambled sets of functions defined on the closed unit interval are scrambled sets in the Li–Yorke sense, which are comprised of initial points whose trajectories contain subsequences whose distance from an arbitrary periodic point can be bounded below by 1/2 (the largest possible positive constant in this context). A precise formal definition is given in Section 2. Our first theorem shows that extremally scrambled sets are dispersed all over the domain of a continuous self-map of the interval. Our second theorem, based on a similar construction, allows us to recover not only Kan’s result but also the theorems of Smítal and Rajan as particular cases. Equally to the point, our construction yields, with straightforward modifications, a continuous self-map whose scrambled set, though again dispersed all over the interval, can be of zero Lebesgue measure.
In terms of applications, and staying with economic dynamics, let us note that Nathanson’s map with parallel left and right arms was extended, by Khan and Rajan [Reference Khan and Rajan7], to yield a family of maps whose arms are not parallel, and thereby shown to constitute reduced forms of workhorse two-sector models in mathematical economics. In [Reference Deng, Fujio and Khan3], the application is shown to go beyond the technical into the substantive. The Khan–Rajan extension of Nathanson shows how in equilibrium growth ‘anything goes’ in the sense that, for any natural number n, there exists a prototypical two-sector model, associated with Shinkai, Uzawa and Srinivasan, that, while admitting Li–Yorke chaotic trajectories, exhibits eventually periodic trajectories of period n, starting from almost any initial condition. Equally importantly, while this is evident in (Keynesian) models of equilibrium growth, such trajectories are rendered impossible in (Ramseyan) models of optimal growth in which intertemporal arbitrage conditions play a determining role (see [Reference Deng, Fujio and Khan3]).
Before turning to the plan of the work and concluding this introduction, let us note some questions that are rendered open by our result: the open questions are arguably as important as the answers given here. The first is the observation that the map we construct, like that of [Reference Kan6], barring the two linear arms on left and right outside, has Cantor’s ‘devil’s staircase’ in the middle. We can then ask whether the parallelism of the left and right arms, reminiscent of Nathanson’s map, can be relaxed to nonparallel arms, à la Khan and Rajan [Reference Khan and Rajan7], to strengthen the results on the two-sector model available in [Reference Deng, Fujio and Khan3]. Technically, this would also strengthen the result of [Reference Rajan15]. However, as stated above, this is not merely of technical interest, but of substantive consequence for economic dynamics.
The second open question relates to an orthogonal direction of unobservable Li–Yorke chaos. Can Corollary 2.7 below be extended to show that for any natural numbers
![]() $n,m \in {\mathbb {N}},$
and for any piecewise linear map with the number of pieces less than or equal to n, the size of the m dispersed scrambled sets is zero?
$n,m \in {\mathbb {N}},$
and for any piecewise linear map with the number of pieces less than or equal to n, the size of the m dispersed scrambled sets is zero?
Finally, note that the our work has nothing to say about the closely related result of Misiurewicz [Reference Misiurewicz12] which uses topological conjugacy, and thereby different techniques, to obtain a continuous map for which there exists a scrambled set of Lebesgue measure 1. Progress in this direction would lead to a fuller exploration in economic dynamics of an idea that has not been sufficiently attended to on the topological conjugacy of economic models, and thereby an invariance of the qualitative properties of their dynamics.
After this introduction, Section 2 presents the results and Section 3 the proofs. Section 3 is divided into three subsections: the argument, the construction and the proofs of the ancillary results.
2 The result
Denote by
![]() $C([ 0,1])$
the space of continuous functions from the unit interval to itself.
$C([ 0,1])$
the space of continuous functions from the unit interval to itself.
Definition 2.1. An uncountable subset
![]() $K\subset [0,1] $
is called an extremally scrambled set for a function
$K\subset [0,1] $
is called an extremally scrambled set for a function
![]() $f\in C([0,1])$
, if, for any
$f\in C([0,1])$
, if, for any
![]() $ x,y\in K$
,
$ x,y\in K$
,
![]() $x\neq y$
:
$x\neq y$
:
-
(i)
 $\lim \sup _{k\rightarrow \infty }\vert f^{k}( x) -f^{k}( y) \vert =1$
;
$\lim \sup _{k\rightarrow \infty }\vert f^{k}( x) -f^{k}( y) \vert =1$
; -
(ii)
 $\lim \inf _{k\rightarrow \infty }\vert f^{k}( x) -f^{k}( y) \vert =0$
; and
$\lim \inf _{k\rightarrow \infty }\vert f^{k}( x) -f^{k}( y) \vert =0$
; and -
(iii)
 $\lim \sup _{k\rightarrow \infty }\vert f^{k}( x)-f^{k}( x_{0}) \vert \geq \tfrac 12$
for any periodic point
$\lim \sup _{k\rightarrow \infty }\vert f^{k}( x)-f^{k}( x_{0}) \vert \geq \tfrac 12$
for any periodic point
 $x_{0}$
of f.
$x_{0}$
of f.
Theorem 2.2. For any natural number k and any positive real number
![]() $\epsilon$
, there exists a continuous mapping
$\epsilon$
, there exists a continuous mapping
![]() $f_{k,\epsilon }\in C([0,1])$
such that for any
$f_{k,\epsilon }\in C([0,1])$
such that for any
![]() $x\in [ 0,1]$
, the interval
$x\in [ 0,1]$
, the interval
![]() $( x-\epsilon ,x+\epsilon ) \cap [0,1]$
contains k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other.
$( x-\epsilon ,x+\epsilon ) \cap [0,1]$
contains k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other.
If we set
![]() $k=1$
in Theorem 2.2, following a similar construction to Section 3.2 below, we can adjust the size of the extremally scrambled set to obtain the following result.
$k=1$
in Theorem 2.2, following a similar construction to Section 3.2 below, we can adjust the size of the extremally scrambled set to obtain the following result.
Theorem 2.3. For any
![]() $(\epsilon ,\delta )\in (0,1)\times (0,1]$
, there exists a continuous mapping
$(\epsilon ,\delta )\in (0,1)\times (0,1]$
, there exists a continuous mapping
![]() $g_{\epsilon ,\delta } \in C([0,1])$
that has an extremally scrambled set of Lebesgue measure
$g_{\epsilon ,\delta } \in C([0,1])$
that has an extremally scrambled set of Lebesgue measure
![]() $(1-\delta )$
, such that for any
$(1-\delta )$
, such that for any
![]() $x\in [ 0,1]$
, the interval
$x\in [ 0,1]$
, the interval
![]() $( x-\epsilon ,x+\epsilon ) \cap [0,1]$
contains an extremally scrambled set having positive Lebesgue measure.
$( x-\epsilon ,x+\epsilon ) \cap [0,1]$
contains an extremally scrambled set having positive Lebesgue measure.
On letting the Lebesgue measure of the union of the extremally scrambled sets be any real number in
![]() $[0,1)$
, Theorem 2.3 can be sharpened to yield the results in Kan [Reference Kan6], Smítal [Reference Smítal18] and Rajan [Reference Rajan15] as corollaries. It should be noted that in contrast to the proofs in [Reference Kan6, Reference Rajan15] which influence the methods used herein, Smítal obtains his result through a very different construction.
$[0,1)$
, Theorem 2.3 can be sharpened to yield the results in Kan [Reference Kan6], Smítal [Reference Smítal18] and Rajan [Reference Rajan15] as corollaries. It should be noted that in contrast to the proofs in [Reference Kan6, Reference Rajan15] which influence the methods used herein, Smítal obtains his result through a very different construction.
Corollary 2.4 (Kan)
There exists
![]() $f\in C([0,1])$
which possesses an extremally scrambled set of Lebesgue measure
$f\in C([0,1])$
which possesses an extremally scrambled set of Lebesgue measure
![]() $1/8$
.
$1/8$
.
Corollary 2.5 (Smítal)
For any
![]() $\epsilon \in (0,1)$
, there exists
$\epsilon \in (0,1)$
, there exists
![]() $f_\epsilon \in C([0,1])$
which possesses a scrambled set of Lebesgue measure greater than
$f_\epsilon \in C([0,1])$
which possesses a scrambled set of Lebesgue measure greater than
![]() $1-\epsilon $
.
$1-\epsilon $
.
Corollary 2.6 (Rajan)
For any
![]() $\epsilon \in (0,1)$
, there exists
$\epsilon \in (0,1)$
, there exists
![]() $f_\epsilon \in C([0,1])$
which possesses an extremally scrambled set of Lebesgue measure
$f_\epsilon \in C([0,1])$
which possesses an extremally scrambled set of Lebesgue measure
![]() $1-\epsilon $
.
$1-\epsilon $
.
Corollary 2.7. For any
![]() $\epsilon \in (0,1)$
, there exists a mapping
$\epsilon \in (0,1)$
, there exists a mapping
![]() $f_{\epsilon } \in C([0,1])$
that has an extremally scrambled set of Lebesgue measure
$f_{\epsilon } \in C([0,1])$
that has an extremally scrambled set of Lebesgue measure
![]() $0$
, such that for any
$0$
, such that for any
![]() $x\in [ 0,1]$
, the interval
$x\in [ 0,1]$
, the interval
![]() $( x-\epsilon ,x+\epsilon ) \cap [0,1]$
contains an extremally scrambled set having Lebesgue measure
$( x-\epsilon ,x+\epsilon ) \cap [0,1]$
contains an extremally scrambled set having Lebesgue measure
![]() $0$
.
$0$
.
3 The proofs
The proof of Theorem 2.2 rests on Proposition 3.1 stated and proved below. The proof of Theorem 2.3 follows similarly from a straightforward modification of Proposition 3.1 in the light of Remarks 3.2 and 3.3 in Section 3.2 below. The proofs of the four corollaries are straightforward and left to the reader.
3.1 The proof of Theorem 2.2
For any arbitrary positive integer m, define
 $$ \begin{align*} \mathcal{L}_{m} & =\bigg[ 0, \frac{1}{3^{m}}\bigg], \quad \mathcal{M}_{m}=\bigg[ \frac{1}{3^{m}},1-\frac{1}{3^{m}}\bigg], \quad \mathcal{R}_{m}=\bigg[ 1-\frac{1}{3^{m}},1\bigg], \quad \mathcal{M}_{m}^{\circ } =\bigg( \frac{1}{3^{m}},1-\frac{1}{3^{m}}\bigg), \\ & \quad\mathcal{G}_{m} =\bigg\{ g_{m}\in \mathrm{C}( [ 0,1] ) :g_{m}( x) =\bigg\{ \begin{array}{@{}ll} 3^{m}x & \text{if } x\in \mathcal{L}_{m} \\ 3^{m}x-( 3^{m}-1) & \text{if } x\in \mathcal{R}_{m} \end{array} \bigg\}. \end{align*} $$
$$ \begin{align*} \mathcal{L}_{m} & =\bigg[ 0, \frac{1}{3^{m}}\bigg], \quad \mathcal{M}_{m}=\bigg[ \frac{1}{3^{m}},1-\frac{1}{3^{m}}\bigg], \quad \mathcal{R}_{m}=\bigg[ 1-\frac{1}{3^{m}},1\bigg], \quad \mathcal{M}_{m}^{\circ } =\bigg( \frac{1}{3^{m}},1-\frac{1}{3^{m}}\bigg), \\ & \quad\mathcal{G}_{m} =\bigg\{ g_{m}\in \mathrm{C}( [ 0,1] ) :g_{m}( x) =\bigg\{ \begin{array}{@{}ll} 3^{m}x & \text{if } x\in \mathcal{L}_{m} \\ 3^{m}x-( 3^{m}-1) & \text{if } x\in \mathcal{R}_{m} \end{array} \bigg\}. \end{align*} $$
For any arbitrary positive integer n, partition
![]() $\mathcal {M}_{m}^{\circ }$
into
$\mathcal {M}_{m}^{\circ }$
into
![]() $2^{n}$
mutually disjoint intervals of length
$2^{n}$
mutually disjoint intervals of length
![]() $\delta _{m}^{n}={2^{-n}}\mu ( \mathcal {M}_{m}^{\circ }) $
with each interval defined as
$\delta _{m}^{n}={2^{-n}}\mu ( \mathcal {M}_{m}^{\circ }) $
with each interval defined as
Proposition 3.1. For any positive integers m, n and k, there exists a continuous mapping in
![]() $\mathcal {G}_{m}$
such that each interval
$\mathcal {G}_{m}$
such that each interval
![]() $M^n_{m,j}$
(for
$M^n_{m,j}$
(for
![]() $1\leq j\leq 2^{n}$
) contains k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other.
$1\leq j\leq 2^{n}$
) contains k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other.
Proof of Theorem 2.2
Choose positive integers m and n sufficiently large so that
![]() ${3^{-m}}+\delta _{m}^{n} <\epsilon $
. From Proposition 3.1, there exists a continuous mapping f in
${3^{-m}}+\delta _{m}^{n} <\epsilon $
. From Proposition 3.1, there exists a continuous mapping f in
![]() $\mathcal {G}_{m}$
such that each interval
$\mathcal {G}_{m}$
such that each interval
![]() $M^n_{m,j}$
(for
$M^n_{m,j}$
(for
![]() $1\leq j\leq 2^{n}$
) contains k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other. Define
$1\leq j\leq 2^{n}$
) contains k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other. Define
![]() $ f_{k,\epsilon }=f.$
Then,
$ f_{k,\epsilon }=f.$
Then,
![]() $[0,\epsilon )$
contains
$[0,\epsilon )$
contains
![]() $M^n_{m,1}$
and
$M^n_{m,1}$
and
![]() $(1-\epsilon ,1]$
contains
$(1-\epsilon ,1]$
contains
![]() $ M^n_{m,{2^{n}}}.$
For any
$ M^n_{m,{2^{n}}}.$
For any
![]() $x\in ( 0,1) ,$
the segment
$x\in ( 0,1) ,$
the segment
![]() $( x-\epsilon ,x+\epsilon ) \cap [0,1]$
contains some
$( x-\epsilon ,x+\epsilon ) \cap [0,1]$
contains some
![]() $M^n_{m,j}$
and hence contains k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other.
$M^n_{m,j}$
and hence contains k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other.
3.2 The construction
The construction is obtained through the following three steps. In step 1, divide the unit interval into three exhaustive segments
![]() $\mathcal {L}_{m}$
,
$\mathcal {L}_{m}$
,
![]() $\mathcal {M}_{m}$
and
$\mathcal {M}_{m}$
and
![]() $\mathcal {R}_{m}$
as defined above. We first construct
$\mathcal {R}_{m}$
as defined above. We first construct
![]() $2^n$
mutually disjoint sets in
$2^n$
mutually disjoint sets in
![]() $\mathcal {L}_{m}$
which are extremally scrambled sets for any function in
$\mathcal {L}_{m}$
which are extremally scrambled sets for any function in
![]() $\mathcal {G}_{m}$
. Then, in step 2, for the middle interval
$\mathcal {G}_{m}$
. Then, in step 2, for the middle interval
![]() $\mathcal {M}_{m}$
, we construct
$\mathcal {M}_{m}$
, we construct
![]() $2^n$
mutually disjoint Smith–Volterra–Cantor (SVC) sets each of which is contained in each of the
$2^n$
mutually disjoint Smith–Volterra–Cantor (SVC) sets each of which is contained in each of the
![]() $2^n$
intervals
$2^n$
intervals
![]() $M^n_{m,j}$
(
$M^n_{m,j}$
(
![]() $1\leq j\leq 2^n$
). Finally, in step 3, we construct a homeomorphism from the
$1\leq j\leq 2^n$
). Finally, in step 3, we construct a homeomorphism from the
![]() $2^n$
SVC sets to the
$2^n$
SVC sets to the
![]() $2^n$
extremally scrambled sets. Extending the homeomorphism to the unit interval gives the desired continuous map
$2^n$
extremally scrambled sets. Extending the homeomorphism to the unit interval gives the desired continuous map
![]() $f_{m,n}$
.
$f_{m,n}$
.
Step 1. Denote by
![]() $\Omega $
the space of infinite binary sequences, which is an ordered topological space when equipped with the lexicographic ordering and topologised with the topology of pointwise convergence. Consider the
$\Omega $
the space of infinite binary sequences, which is an ordered topological space when equipped with the lexicographic ordering and topologised with the topology of pointwise convergence. Consider the
![]() $2^{n+1}$
binary
$2^{n+1}$
binary
![]() $( n+1) $
-tuples
$( n+1) $
-tuples
Define a binary relation
![]() $0\prec 1$
and order the
$0\prec 1$
and order the
![]() $2^{n+1}$
binary
$2^{n+1}$
binary
![]() $( n+1) $
-tuples lexicographically so that
$( n+1) $
-tuples lexicographically so that
![]() $\varepsilon _{1} \prec \varepsilon _{2}\prec \cdots \prec \varepsilon _{2^{n+1}}. $
Define
$\varepsilon _{1} \prec \varepsilon _{2}\prec \cdots \prec \varepsilon _{2^{n+1}}. $
Define
Then
![]() $\Omega _{\varepsilon _{1}}\prec \cdots \prec \Omega _{\varepsilon _{2^{n+1}}}, \Omega _{\varepsilon _{i}}\cap \Omega _{\varepsilon _{j}}=\emptyset $
for
$\Omega _{\varepsilon _{1}}\prec \cdots \prec \Omega _{\varepsilon _{2^{n+1}}}, \Omega _{\varepsilon _{i}}\cap \Omega _{\varepsilon _{j}}=\emptyset $
for
![]() $i\neq j$
and
$i\neq j$
and
![]() $\Omega =\Omega _{\varepsilon _{1}}\cup \cdots \cup \Omega _{\varepsilon _{2^{n+1}}}.$
Hence the subsets
$\Omega =\Omega _{\varepsilon _{1}}\cup \cdots \cup \Omega _{\varepsilon _{2^{n+1}}}.$
Hence the subsets
![]() $ \{ \Omega _{\varepsilon _{1}},\ldots ,\Omega _{\varepsilon _{2^{n+1}}}\} $
form a partition of the space
$ \{ \Omega _{\varepsilon _{1}},\ldots ,\Omega _{\varepsilon _{2^{n+1}}}\} $
form a partition of the space
![]() $\Omega $
into
$\Omega $
into
![]() $2^{n+1}$
mutually disjoint subsets. Consider the shift mapping
$2^{n+1}$
mutually disjoint subsets. Consider the shift mapping
![]() $\sigma :\Omega \rightarrow \Omega $
given by
$\sigma :\Omega \rightarrow \Omega $
given by
Define
![]() $\phi _{m}:\Omega \rightarrow [ 0,1] $
by
$\phi _{m}:\Omega \rightarrow [ 0,1] $
by
 $$ \begin{align*} \phi _{m}( \omega ) =\sum_{k=1}^{\infty }\frac{( 3^{m}-1) \omega _{k}}{3^{mk}}, \end{align*} $$
$$ \begin{align*} \phi _{m}( \omega ) =\sum_{k=1}^{\infty }\frac{( 3^{m}-1) \omega _{k}}{3^{mk}}, \end{align*} $$
and observe the following routine facts:
-
(i)
 $\phi _{m}$
is an order-preserving homeomorphism;
$\phi _{m}$
is an order-preserving homeomorphism; -
(ii)
 $\phi _{m}( \Omega ) \cap \mathcal {M}_{m}^{\circ }=\emptyset $
; and
$\phi _{m}( \Omega ) \cap \mathcal {M}_{m}^{\circ }=\emptyset $
; and -
(iii)
 $\phi _{m}( \Omega ) $
is homeomorphic to the classical ‘middle-thirds’ Cantor set [Reference Dovgoshey, Martio, Ryazanov and Vuorinen4].
$\phi _{m}( \Omega ) $
is homeomorphic to the classical ‘middle-thirds’ Cantor set [Reference Dovgoshey, Martio, Ryazanov and Vuorinen4].
Consider
![]() $( \omega _{k}) _{k\geq 1}\in \Omega _{\varepsilon _{j}}$
for
$( \omega _{k}) _{k\geq 1}\in \Omega _{\varepsilon _{j}}$
for
![]() $1\leq j\leq 2^{n}$
. For any positive integer t, define
$1\leq j\leq 2^{n}$
. For any positive integer t, define
 $$ \begin{align*}\Lambda _{t} =\Big( \underbrace{\omega _{1}\cdots \omega _{1}}_{t\text{ times}}\underbrace{\omega _{2}\cdots \omega _{2}}_{t\text{ times}}\cdots \underbrace{\omega _{t}\cdots \omega _{t}}_{t\text{ times}}\Big) \quad\mbox{and}\quad B_{t} =\Big( \underbrace{0\cdots 0}_{t\text{ times}}\underbrace{1\cdots 1} _{t\text{ times}}\Big).\end{align*} $$
$$ \begin{align*}\Lambda _{t} =\Big( \underbrace{\omega _{1}\cdots \omega _{1}}_{t\text{ times}}\underbrace{\omega _{2}\cdots \omega _{2}}_{t\text{ times}}\cdots \underbrace{\omega _{t}\cdots \omega _{t}}_{t\text{ times}}\Big) \quad\mbox{and}\quad B_{t} =\Big( \underbrace{0\cdots 0}_{t\text{ times}}\underbrace{1\cdots 1} _{t\text{ times}}\Big).\end{align*} $$
The mapping
![]() $Z_{\varepsilon _{j}} :\Omega _{\varepsilon _{j}}\rightarrow Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) \subset \Omega _{\varepsilon _{j}}$
defined by
$Z_{\varepsilon _{j}} :\Omega _{\varepsilon _{j}}\rightarrow Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) \subset \Omega _{\varepsilon _{j}}$
defined by
is an order-preserving homeomorphism. We define
and observe that as
![]() $\Omega _{\varepsilon _{1}}\prec \cdots \prec \Omega _{\varepsilon _{2^{n}}}$
and
$\Omega _{\varepsilon _{1}}\prec \cdots \prec \Omega _{\varepsilon _{2^{n}}}$
and
![]() $Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) \subset \Omega _{\varepsilon _{j}}$
for
$Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) \subset \Omega _{\varepsilon _{j}}$
for
![]() $1\leq j\leq 2^{n},$
we have
$1\leq j\leq 2^{n},$
we have
![]() $Z_{\varepsilon _{1}}( \Omega _{\varepsilon _{1}}) \prec \cdots \prec Z_{\varepsilon _{2^{n}}}( \Omega _{\varepsilon _{2^{n}}}) .$
Since the function
$Z_{\varepsilon _{1}}( \Omega _{\varepsilon _{1}}) \prec \cdots \prec Z_{\varepsilon _{2^{n}}}( \Omega _{\varepsilon _{2^{n}}}) .$
Since the function
![]() $\phi _{m}$
is an order-preserving homeomorphism and since
$\phi _{m}$
is an order-preserving homeomorphism and since
![]() $\phi _{m}( \Omega _{\varepsilon _{j}}) \subset \mathcal {L}_{m}$
for
$\phi _{m}( \Omega _{\varepsilon _{j}}) \subset \mathcal {L}_{m}$
for
![]() $ 1\leq j\leq 2^{n},$
it follows that
$ 1\leq j\leq 2^{n},$
it follows that
![]() $\phi _{m}( Z_{\varepsilon _{1}}( \Omega _{\varepsilon _{1}}) ) =K_{\varepsilon _{1}}<\cdots <\phi _m ( Z_{\varepsilon _{2^{n}}}( \Omega _{\varepsilon _{2^{n}}}) ) =K_{\varepsilon _{2^{n}}}.$
Thus, the sets
$\phi _{m}( Z_{\varepsilon _{1}}( \Omega _{\varepsilon _{1}}) ) =K_{\varepsilon _{1}}<\cdots <\phi _m ( Z_{\varepsilon _{2^{n}}}( \Omega _{\varepsilon _{2^{n}}}) ) =K_{\varepsilon _{2^{n}}}.$
Thus, the sets
![]() $K_{\varepsilon _{1}},\ldots ,K_{\varepsilon _{2^{n}}}$
are a collection of
$K_{\varepsilon _{1}},\ldots ,K_{\varepsilon _{2^{n}}}$
are a collection of
![]() $2^{n}$
mutually disjoint subsets of the interval
$2^{n}$
mutually disjoint subsets of the interval
![]() $ \mathcal {L}_{m}.$
Later we will establish in Proposition 3.6 that each of the
$ \mathcal {L}_{m}.$
Later we will establish in Proposition 3.6 that each of the
![]() $2^{n}$
mutually disjoint subsets
$2^{n}$
mutually disjoint subsets
![]() $ K_{\varepsilon _{j}}$
is an extremally scrambled set for every function
$ K_{\varepsilon _{j}}$
is an extremally scrambled set for every function
![]() $g_{m}\in \mathcal {G}_{m}.$
$g_{m}\in \mathcal {G}_{m}.$
Step 2. For ease of exposition, let
![]() $M_{\varepsilon _{j}}=( \alpha _{j},\beta _{j}) \equiv M^n_{m,j-2^n}$
for
$M_{\varepsilon _{j}}=( \alpha _{j},\beta _{j}) \equiv M^n_{m,j-2^n}$
for
![]() $2^{n}+1\leq j\leq 2^{n+1}$
. We construct positive measure SVC sets
$2^{n}+1\leq j\leq 2^{n+1}$
. We construct positive measure SVC sets
![]() $\mathcal {C}_{\varepsilon _{j}}\subset M_{\varepsilon _{j}}$
such that
$\mathcal {C}_{\varepsilon _{j}}\subset M_{\varepsilon _{j}}$
such that
![]() $\mu ( \mathcal {C}_{\varepsilon _{j}}) =1/2^{n+2}$
. To this end, consider any one of the above intervals
$\mu ( \mathcal {C}_{\varepsilon _{j}}) =1/2^{n+2}$
. To this end, consider any one of the above intervals
![]() $M_{\varepsilon _{j}},$
and consider its midpoint
$M_{\varepsilon _{j}},$
and consider its midpoint
![]() $( \alpha _{j}+\beta _{j}) /2=m_{j}.$
Choose a positive real number
$( \alpha _{j}+\beta _{j}) /2=m_{j}.$
Choose a positive real number
![]() $ \epsilon $
such that
$ \epsilon $
such that
Define
![]() $E_{\varepsilon _{j}}^{0}=[ \ell _{\varepsilon _{j}},r_{\varepsilon _{j}} ] =[ m_{j}-\tfrac 12\epsilon ,m_{j}+\tfrac 12\epsilon ] $
and set
$E_{\varepsilon _{j}}^{0}=[ \ell _{\varepsilon _{j}},r_{\varepsilon _{j}} ] =[ m_{j}-\tfrac 12\epsilon ,m_{j}+\tfrac 12\epsilon ] $
and set
![]() $ \ell _{\varepsilon _{j}0} =\ell _{\varepsilon _{j}}+\tfrac 14\delta $
,
$ \ell _{\varepsilon _{j}0} =\ell _{\varepsilon _{j}}+\tfrac 14\delta $
,
![]() $r_{\varepsilon _{j}0}=m_{j}, \ell _{\varepsilon _{j}1} =m_{j}+\tfrac 14\delta , r_{\varepsilon _{j}1}=r_{\varepsilon _{j}}$
and
$r_{\varepsilon _{j}0}=m_{j}, \ell _{\varepsilon _{j}1} =m_{j}+\tfrac 14\delta , r_{\varepsilon _{j}1}=r_{\varepsilon _{j}}$
and
![]() $E_{\varepsilon _{j}}^{1}=[ \ell _{\varepsilon _{j}0},r_{\varepsilon _{j}0}] \cup [ \ell _{\varepsilon _{j}1},r_{\varepsilon _{j}1}].$
Observe that
$E_{\varepsilon _{j}}^{1}=[ \ell _{\varepsilon _{j}0},r_{\varepsilon _{j}0}] \cup [ \ell _{\varepsilon _{j}1},r_{\varepsilon _{j}1}].$
Observe that
![]() $\mu ( E_{\varepsilon _{j}}^{1}) =\mu ( E_{\varepsilon _{j}}^{0}) -\tfrac 12\delta .$
Next, set
$\mu ( E_{\varepsilon _{j}}^{1}) =\mu ( E_{\varepsilon _{j}}^{0}) -\tfrac 12\delta .$
Next, set
![]() $\ell _{\varepsilon _{j}00} =\ell _{\varepsilon _{j}0}+\tfrac {1}{16}\delta $
,
$\ell _{\varepsilon _{j}00} =\ell _{\varepsilon _{j}0}+\tfrac {1}{16}\delta $
,
![]() $r_{\varepsilon _{j}00}=\tfrac 12(\ell _{\varepsilon _{j}0}+r_{\varepsilon _{j}0})$
,
$r_{\varepsilon _{j}00}=\tfrac 12(\ell _{\varepsilon _{j}0}+r_{\varepsilon _{j}0})$
,
![]() $\ell _{\varepsilon _{j}01} =r_{\varepsilon _{j}00}+\tfrac {1}{16}\delta $
,
$\ell _{\varepsilon _{j}01} =r_{\varepsilon _{j}00}+\tfrac {1}{16}\delta $
,
![]() $r_{\varepsilon _{j}01}=r_{\varepsilon _{j}0},$
$r_{\varepsilon _{j}01}=r_{\varepsilon _{j}0},$
![]() $\ell _{\varepsilon _{j}10} =\ell _{\varepsilon _{j}1}+\tfrac {1}{16}\delta $
,
$\ell _{\varepsilon _{j}10} =\ell _{\varepsilon _{j}1}+\tfrac {1}{16}\delta $
,
![]() $r_{\varepsilon _{j}10}=\tfrac 12(\ell _{\varepsilon _{j}1}+r_{\varepsilon _{j}1}),$
$r_{\varepsilon _{j}10}=\tfrac 12(\ell _{\varepsilon _{j}1}+r_{\varepsilon _{j}1}),$
![]() $\ell _{\varepsilon _{j}11} =r_{\varepsilon _{j}10}+\tfrac {1}{16}\delta $
,
$\ell _{\varepsilon _{j}11} =r_{\varepsilon _{j}10}+\tfrac {1}{16}\delta $
,
![]() $r_{\varepsilon _{j}11}=r_{\varepsilon _{j}1}$
and define
$r_{\varepsilon _{j}11}=r_{\varepsilon _{j}1}$
and define
![]() $E_{\varepsilon _{j}}^{2}=[ \ell _{\varepsilon _{j}00},r_{\varepsilon _{j}00}] \cup [ \ell _{\varepsilon _{j}01},r_{\varepsilon _{j}01} ] \cup [ \ell _{\varepsilon _{j}10},r_{\varepsilon _{j}10}] \cup [ \ell _{\varepsilon _{j}11},r_{\varepsilon _{j}11}].$
Observe that
$E_{\varepsilon _{j}}^{2}=[ \ell _{\varepsilon _{j}00},r_{\varepsilon _{j}00}] \cup [ \ell _{\varepsilon _{j}01},r_{\varepsilon _{j}01} ] \cup [ \ell _{\varepsilon _{j}10},r_{\varepsilon _{j}10}] \cup [ \ell _{\varepsilon _{j}11},r_{\varepsilon _{j}11}].$
Observe that
![]() $\mu ( E_{\varepsilon _{j}}^{2}) =\mu ( E_{\varepsilon _{j}}^{1}) -\tfrac 12\delta =\mu ( E_{\varepsilon _{j}}^{0}) -( \tfrac 12\delta +\tfrac 14\delta ).$
Repeating this construction yields a decreasing sequence of sets
$\mu ( E_{\varepsilon _{j}}^{2}) =\mu ( E_{\varepsilon _{j}}^{1}) -\tfrac 12\delta =\mu ( E_{\varepsilon _{j}}^{0}) -( \tfrac 12\delta +\tfrac 14\delta ).$
Repeating this construction yields a decreasing sequence of sets
![]() $ E_{\varepsilon _{j}}^{k}$
for
$ E_{\varepsilon _{j}}^{k}$
for
![]() $k=0,1,2,\ldots $
in which every
$k=0,1,2,\ldots $
in which every
![]() $ E_{\varepsilon _{j}}^{k}$
is a finite union of disjoint closed and bounded intervals and is therefore compact. Observe that all the right end points of
$ E_{\varepsilon _{j}}^{k}$
is a finite union of disjoint closed and bounded intervals and is therefore compact. Observe that all the right end points of
![]() $E_{\varepsilon _{j}}^{k}$
are retained in
$E_{\varepsilon _{j}}^{k}$
are retained in
![]() $E_{\varepsilon _{j}}^{k+1},$
but that all the left end points of
$E_{\varepsilon _{j}}^{k+1},$
but that all the left end points of
![]() $E_{\varepsilon _{j}}^{k}$
have been replaced by new left end points which only survive one iteration of this construction of the SVC set. Thus, the decreasing sequence of nonempty compact sets
$E_{\varepsilon _{j}}^{k}$
have been replaced by new left end points which only survive one iteration of this construction of the SVC set. Thus, the decreasing sequence of nonempty compact sets
![]() $E_{\varepsilon _{j}}^{0}\supset E_{\varepsilon _{j}}^{1}\supset E_{\varepsilon _{j}}^{2}\supset \cdots $
must have a nonempty intersection
$E_{\varepsilon _{j}}^{0}\supset E_{\varepsilon _{j}}^{1}\supset E_{\varepsilon _{j}}^{2}\supset \cdots $
must have a nonempty intersection
![]() $ \mathcal {C}_{\varepsilon _{j}}=\bigcap _{k=0}^{\infty }E_{\varepsilon _{j}}^{k}\neq \emptyset $
where
$ \mathcal {C}_{\varepsilon _{j}}=\bigcap _{k=0}^{\infty }E_{\varepsilon _{j}}^{k}\neq \emptyset $
where
 $$ \begin{align*} \mu ( \mathcal{C}_{\varepsilon _{j}}) =\mu ( E_{\varepsilon _{j}}^{0}) -\sum_{k=1}^{\infty }\frac{\delta }{2^{k}} =\mu ( E_{\varepsilon _{j}}^{0}) -\delta=\epsilon -\delta =\epsilon -\bigg( \epsilon -\frac{1}{2^{n+2}}\bigg) = \frac{1}{2^{n+2}}. \end{align*} $$
$$ \begin{align*} \mu ( \mathcal{C}_{\varepsilon _{j}}) =\mu ( E_{\varepsilon _{j}}^{0}) -\sum_{k=1}^{\infty }\frac{\delta }{2^{k}} =\mu ( E_{\varepsilon _{j}}^{0}) -\delta=\epsilon -\delta =\epsilon -\bigg( \epsilon -\frac{1}{2^{n+2}}\bigg) = \frac{1}{2^{n+2}}. \end{align*} $$
Since
![]() $\mathcal {C}_{\varepsilon _{j}}\subset M_{\varepsilon _{j}},$
the
$\mathcal {C}_{\varepsilon _{j}}\subset M_{\varepsilon _{j}},$
the
![]() $2^{n}$
mutually disjoint SVC sets
$2^{n}$
mutually disjoint SVC sets
![]() $\mathcal {C}_{\varepsilon _{_{2^n+1}}}, \ldots ,\mathcal {C}_{\varepsilon _{2^{n+1}}}$
in
$\mathcal {C}_{\varepsilon _{_{2^n+1}}}, \ldots ,\mathcal {C}_{\varepsilon _{2^{n+1}}}$
in
![]() $\mathcal {M} _{m}^{\circ }$
all have positive Lebesgue measure
$\mathcal {M} _{m}^{\circ }$
all have positive Lebesgue measure
![]() $1/2^{n+2}.$
$1/2^{n+2}.$
Remark 3.2. For any
![]() $\delta \in (0,1),$
pick m such that the length of the middle interval is strictly greater than
$\delta \in (0,1),$
pick m such that the length of the middle interval is strictly greater than
![]() $1-\delta $
. We can adjust the measure of what we remove from each interval
$1-\delta $
. We can adjust the measure of what we remove from each interval
![]() $M_{\varepsilon _{j}}$
to make sure that the sum of the measures of the SVC sets adds up to
$M_{\varepsilon _{j}}$
to make sure that the sum of the measures of the SVC sets adds up to
![]() $1-\delta .$
$1-\delta .$
Remark 3.3. We can also make each Cantor set in our construction have measure 0 by the standard procedure of iteratively removing the open middle third from a set of intervals. This construction will yield pervasive scrambled sets of measure 0 as stated in Corollary 2.7.
Step 3. Fix any particular j with
![]() $2^{n}+1\leq j\leq 2^{n+1}$
. We shall construct an order-preserving homeomorphism
$2^{n}+1\leq j\leq 2^{n+1}$
. We shall construct an order-preserving homeomorphism
![]() $\xi _{\varepsilon _{j}}:\Omega _{\varepsilon _{j}}\rightarrow \mathcal {C} _{\varepsilon _{j}},$
where
$\xi _{\varepsilon _{j}}:\Omega _{\varepsilon _{j}}\rightarrow \mathcal {C} _{\varepsilon _{j}},$
where
![]() $\Omega _{\varepsilon _{j}}$
is constructed in step 1 and
$\Omega _{\varepsilon _{j}}$
is constructed in step 1 and
![]() $\mathcal {C} _{\varepsilon _{j}}$
is constructed in step 2. Towards this end, for every positive integer
$\mathcal {C} _{\varepsilon _{j}}$
is constructed in step 2. Towards this end, for every positive integer
![]() $k>1$
and for any
$k>1$
and for any
![]() $(k-1)$
-tuple
$(k-1)$
-tuple
![]() $( \omega _{1},\ldots ,\omega _{k-1})$
, replace in
$( \omega _{1},\ldots ,\omega _{k-1})$
, replace in
![]() $\Omega $
$\Omega $
where the first terminates in an infinite sequence of 0s and the second terminates in an infinite sequence of 1s.
Consider the set
![]() $\Omega _{\varepsilon _{j}}^{\mathbf {1}}$
of all binary sequences in
$\Omega _{\varepsilon _{j}}^{\mathbf {1}}$
of all binary sequences in
![]() $\Omega _{\varepsilon _{j}}$
that terminate in
$\Omega _{\varepsilon _{j}}$
that terminate in
![]() $1$
after a finite number of coordinates starting at
$1$
after a finite number of coordinates starting at
![]() $\omega _{n+2}$
(after the first
$\omega _{n+2}$
(after the first
![]() $n+1$
coordinates which are always equal to
$n+1$
coordinates which are always equal to
![]() $\varepsilon _{j}$
for every element of
$\varepsilon _{j}$
for every element of
![]() $\Omega _{\varepsilon _{j}}$
). It is clear that this is a countable dense subset of
$\Omega _{\varepsilon _{j}}$
). It is clear that this is a countable dense subset of
![]() $ \Omega _{\varepsilon _{j}}.$
Let
$ \Omega _{\varepsilon _{j}}.$
Let
![]() $\mathcal {C}_{\varepsilon _{j}}^{\mathbf {1}} $
consist of all the right end points that appear in the decreasing sequence of closed intervals
$\mathcal {C}_{\varepsilon _{j}}^{\mathbf {1}} $
consist of all the right end points that appear in the decreasing sequence of closed intervals
![]() $E_{\varepsilon _{j}}^{k}$
(
$E_{\varepsilon _{j}}^{k}$
(
![]() $k =0,1,2,\ldots $
) whose intersection is the SVC set
$k =0,1,2,\ldots $
) whose intersection is the SVC set
![]() $\mathcal {C}_{\varepsilon _{j}}.$
Observe that
$\mathcal {C}_{\varepsilon _{j}}.$
Observe that
![]() $\mathcal {C} _{\varepsilon _{j}}^{\mathbf {1}}$
is also a countably infinite dense subset of
$\mathcal {C} _{\varepsilon _{j}}^{\mathbf {1}}$
is also a countably infinite dense subset of
![]() $\mathcal {C}_{\varepsilon _{j}}.$
$\mathcal {C}_{\varepsilon _{j}}.$
We contend that all the right end points that comprise
![]() $\mathcal {C} _{\varepsilon _{j}}^{\mathbf {1}}$
are indexed by subscripts which are sequences in
$\mathcal {C} _{\varepsilon _{j}}^{\mathbf {1}}$
are indexed by subscripts which are sequences in
![]() $\Omega _{\varepsilon _{j}}^{\mathbf {1}}.$
To see that this is so, observe that the first time that the terminal binary digit
$\Omega _{\varepsilon _{j}}^{\mathbf {1}}.$
To see that this is so, observe that the first time that the terminal binary digit
![]() $1$
appears as a coordinate in the subscript that indexes a given right end point in
$1$
appears as a coordinate in the subscript that indexes a given right end point in
![]() $\mathcal {C}_{\varepsilon _{j}}$
, in the Nth coordinate say, counted after
$\mathcal {C}_{\varepsilon _{j}}$
, in the Nth coordinate say, counted after
![]() $\varepsilon _{j}$
(which always appears as the first
$\varepsilon _{j}$
(which always appears as the first
![]() $n+1$
coordinates of every element in
$n+1$
coordinates of every element in
![]() $\mathcal {C} _{\varepsilon _{j}}$
) so that
$\mathcal {C} _{\varepsilon _{j}}$
) so that
![]() $\omega _{N}=1$
and
$\omega _{N}=1$
and
![]() $\omega _{N-1}=0$
for
$\omega _{N-1}=0$
for
![]() $N>n+2$
, is in the set
$N>n+2$
, is in the set
![]() $E_{\varepsilon _{j}}^{N-n-1}$
at which the right end point
$E_{\varepsilon _{j}}^{N-n-1}$
at which the right end point
![]() $r_{\scriptsize {\underbrace {\varepsilon _{j},\ldots ,\omega _{N-1},1}_{N \text { subscripts}}\text { }}}$
appears. Now observe that after the infinite intersection
$r_{\scriptsize {\underbrace {\varepsilon _{j},\ldots ,\omega _{N-1},1}_{N \text { subscripts}}\text { }}}$
appears. Now observe that after the infinite intersection
![]() $\mathcal {C}_{\varepsilon _{j}}=\bigcap _{k=0}^{\infty }E_{\varepsilon _{j}}^{k}$
has been taken, this right end point
$\mathcal {C}_{\varepsilon _{j}}=\bigcap _{k=0}^{\infty }E_{\varepsilon _{j}}^{k}$
has been taken, this right end point
![]() $r_{\scriptsize {\underbrace {\varepsilon _{j},\ldots ,\omega _{N-1},1}_{N \text { subscripts}}\text { }}}$
in
$r_{\scriptsize {\underbrace {\varepsilon _{j},\ldots ,\omega _{N-1},1}_{N \text { subscripts}}\text { }}}$
in
![]() $\mathcal {C}_{\varepsilon _{j}}$
is indexed by the subscript
$\mathcal {C}_{\varepsilon _{j}}$
is indexed by the subscript
Thus, every right end point of each interval
![]() $E_{\varepsilon _{j}}^{n}$
is indexed by a subscript in
$E_{\varepsilon _{j}}^{n}$
is indexed by a subscript in
![]() $\Omega _{\varepsilon _{j}}^{\mathbf {1}}.$
$\Omega _{\varepsilon _{j}}^{\mathbf {1}}.$
We define an order-preserving bijection
![]() $\xi _{\varepsilon _{j}}^{\mathbf {1} }:\Omega _{\varepsilon _{j}}^{\mathbf {1}}\rightarrow \mathcal {C} _{\varepsilon _{j}}^{\mathbf {1}}$
by
$\xi _{\varepsilon _{j}}^{\mathbf {1} }:\Omega _{\varepsilon _{j}}^{\mathbf {1}}\rightarrow \mathcal {C} _{\varepsilon _{j}}^{\mathbf {1}}$
by
This map is plainly an order-preserving bijection, and extends to an order-preserving homeomorphism
![]() $\xi _{\varepsilon _{j}}:\Omega _{\varepsilon _{j}}\rightarrow \mathcal {C}_{\varepsilon _{j}}$
as the set
$\xi _{\varepsilon _{j}}:\Omega _{\varepsilon _{j}}\rightarrow \mathcal {C}_{\varepsilon _{j}}$
as the set
![]() $\Omega _{\varepsilon _{j}}^{\mathbf {1}}$
is dense in
$\Omega _{\varepsilon _{j}}^{\mathbf {1}}$
is dense in
![]() $\Omega _{\varepsilon _{j}}$
and
$\Omega _{\varepsilon _{j}}$
and
![]() $\mathcal {C}_{\varepsilon _{j}}^{\mathbf {1}}$
is dense in
$\mathcal {C}_{\varepsilon _{j}}^{\mathbf {1}}$
is dense in
![]() $\mathcal {C} _{\varepsilon _{j}}.$
$\mathcal {C} _{\varepsilon _{j}}.$
Now, consider the mapping
![]() $r:\Omega \rightarrow \Omega $
defined by
$r:\Omega \rightarrow \Omega $
defined by
![]() $r( ( \omega _{k}) _{k\geq 1}) =( r( \omega _{k}) _{k\geq 1})$
where, for every
$r( ( \omega _{k}) _{k\geq 1}) =( r( \omega _{k}) _{k\geq 1})$
where, for every
![]() $k\geq 1$
,
$k\geq 1$
,
 $$ \begin{align*} r( \omega _{k}) = \begin{cases} 0 \quad& \mbox{if } \omega _{k}=1, \\ 1 \quad& \mbox{if } \omega _{k}=0. \end{cases} \end{align*} $$
$$ \begin{align*} r( \omega _{k}) = \begin{cases} 0 \quad& \mbox{if } \omega _{k}=1, \\ 1 \quad& \mbox{if } \omega _{k}=0. \end{cases} \end{align*} $$
It is immediate that r is an order-reversing homeomorphism and that
To sum up, for all j with
![]() $2^{n}+1\leq j\leq 2^{n+1},$
$2^{n}+1\leq j\leq 2^{n+1},$
Since every mapping that appears in the sequence above is a homeomorphism, and all but one are order-preserving, the mapping
![]() $f_{\varepsilon _{j},m,n}:\mathcal {C}_{\varepsilon _{j}}\rightarrow K_{\varepsilon _{( 2^{n+1}+1) -j}}$
defined by
$f_{\varepsilon _{j},m,n}:\mathcal {C}_{\varepsilon _{j}}\rightarrow K_{\varepsilon _{( 2^{n+1}+1) -j}}$
defined by
must be an order-reversing homeomorphism.
To finish the construction of a continuous mapping in
![]() $\mathcal {G}_{m},$
define
$\mathcal {G}_{m},$
define
![]() $\mathcal {S} =\bigcup _{j=2^{n}+1}^{2^{n+1}}\mathcal {C}_{\varepsilon _{j}}$
,
$\mathcal {S} =\bigcup _{j=2^{n}+1}^{2^{n+1}}\mathcal {C}_{\varepsilon _{j}}$
,
![]() $\mathcal { K=}\bigcup _{j=1}^{2^{n}}K_{\varepsilon _{j}}$
and
$\mathcal { K=}\bigcup _{j=1}^{2^{n}}K_{\varepsilon _{j}}$
and
![]() $f_{m,n}:\mathcal {S} \rightarrow \mathcal {K}$
by setting
$f_{m,n}:\mathcal {S} \rightarrow \mathcal {K}$
by setting
![]() $f_{m,n}\mid _{\mathcal {C}_{\varepsilon _{j}}}=f_{\varepsilon _{j},m,n}.$
We define
$f_{m,n}\mid _{\mathcal {C}_{\varepsilon _{j}}}=f_{\varepsilon _{j},m,n}.$
We define
![]() $f_{m,n}$
on
$f_{m,n}$
on
![]() $\mathcal {L}_{m}\cup \mathcal {R}_{m}$
to ensure that
$\mathcal {L}_{m}\cup \mathcal {R}_{m}$
to ensure that
![]() $f_{m,n}\in \mathcal {G}_{m}$
by setting
$f_{m,n}\in \mathcal {G}_{m}$
by setting
We linearly interpolate to extend
![]() $f_{m,n}$
to
$f_{m,n}$
to
![]() $\mathcal {M}_m$
from S. So, for any
$\mathcal {M}_m$
from S. So, for any
![]() $s\in \mathcal {M}_{m}\backslash \mathcal {S},$
we define
$s\in \mathcal {M}_{m}\backslash \mathcal {S},$
we define
![]() $s_{\ell }=\sup ( \{ t\in \mathcal {S}:t<s\} \cup \{ 1/3^{m}\} ) , s_{r}=\inf ( \{ t\in S:t>s\} \cup \{ 1-{3^{-m}}\} )$
and
$s_{\ell }=\sup ( \{ t\in \mathcal {S}:t<s\} \cup \{ 1/3^{m}\} ) , s_{r}=\inf ( \{ t\in S:t>s\} \cup \{ 1-{3^{-m}}\} )$
and
3.3 The proofs of the ancillary results
In this subsection, we furnish the proof of Proposition 3.1. To this end, we first state and prove two lemmas. These lemmas will then be used to establish Proposition 3.6, which itself will be used in the proof of Proposition 3.1.
Lemma 3.4. For any positive integer m, let
![]() $\omega \in \Omega $
and
$\omega \in \Omega $
and
![]() $g_{m}\in \mathcal {G}_{m}.$
Then, for any positive integer
$g_{m}\in \mathcal {G}_{m}.$
Then, for any positive integer
![]() $k, g_{m}^{k}\circ \phi _{m}( \omega ) =\phi _{m}( \sigma ^{k}( \omega ) ).$
$k, g_{m}^{k}\circ \phi _{m}( \omega ) =\phi _{m}( \sigma ^{k}( \omega ) ).$
Proof of Lemma 3.4
We argue by mathematical induction on
![]() $k.$
If
$k.$
If
![]() $k=1,$
then
$k=1,$
then
 $$ \begin{align*} g_{m}\circ \phi _{m}( \omega ) &=g_{m}\bigg( \sum_{k=1}^{\infty }\frac{( 3^{m}-1) \omega _{k}}{3^{mk}}\bigg) =3^{m}\bigg( \sum_{k=1}^{\infty }\frac{( 3^{m}-1) \omega _{k}}{ 3^{mk}}\bigg) -( 3^{m}-1) \omega _{1} \\ &=\sum_{k=2}^{\infty }\frac{( 3^{m}-1) \omega _{k}}{3^{m( k-1) }} =\sum_{k=1}^{\infty }\frac{( 3^{m}-1) \omega _{k+1}}{3^{mk}} =\phi _{m}( \sigma ( \omega ) ). \end{align*} $$
$$ \begin{align*} g_{m}\circ \phi _{m}( \omega ) &=g_{m}\bigg( \sum_{k=1}^{\infty }\frac{( 3^{m}-1) \omega _{k}}{3^{mk}}\bigg) =3^{m}\bigg( \sum_{k=1}^{\infty }\frac{( 3^{m}-1) \omega _{k}}{ 3^{mk}}\bigg) -( 3^{m}-1) \omega _{1} \\ &=\sum_{k=2}^{\infty }\frac{( 3^{m}-1) \omega _{k}}{3^{m( k-1) }} =\sum_{k=1}^{\infty }\frac{( 3^{m}-1) \omega _{k+1}}{3^{mk}} =\phi _{m}( \sigma ( \omega ) ). \end{align*} $$
Assume now, as our induction hypothesis, that for any positive integer
![]() $ k\geq 1,$
$ k\geq 1,$
Then
 $$ \begin{align*} g_{m}^{k+1}\circ \phi _{m}( \omega ) &=( g_{m}\circ g_{m}^{k}) \circ \phi _{m}( \omega ) =g_{m}\circ ( g_{m}^{k}\circ \phi _{m}) ( \omega ) \\ &=g_{m}\circ \phi _{m}( \sigma ^{k}( \omega ) ) =\phi _{m}( \sigma ( \sigma ^{k}( \omega ) ) ) =\phi _{m}( \sigma ^{k+1}( \omega ) ). \end{align*} $$
$$ \begin{align*} g_{m}^{k+1}\circ \phi _{m}( \omega ) &=( g_{m}\circ g_{m}^{k}) \circ \phi _{m}( \omega ) =g_{m}\circ ( g_{m}^{k}\circ \phi _{m}) ( \omega ) \\ &=g_{m}\circ \phi _{m}( \sigma ^{k}( \omega ) ) =\phi _{m}( \sigma ( \sigma ^{k}( \omega ) ) ) =\phi _{m}( \sigma ^{k+1}( \omega ) ). \end{align*} $$
Hence, the lemma follows by mathematical induction.
Lemma 3.5. Let both
![]() $\omega =( \omega _{k}) _{k\geq 1}$
and
$\omega =( \omega _{k}) _{k\geq 1}$
and
![]() $\tau =( \tau _{k}) _{k\geq 1}$
be elements of
$\tau =( \tau _{k}) _{k\geq 1}$
be elements of
![]() $\Omega .$
Then, for any positive integers
$\Omega .$
Then, for any positive integers
![]() $m, k$
and N, the following three statements hold.
$m, k$
and N, the following three statements hold.
-
(i) If
 $\omega _{k+j}=\tau _{k+j}$
for
$\omega _{k+j}=\tau _{k+j}$
for
 $1\leq j\leq N,$
then
$1\leq j\leq N,$
then
 $ \vert g_{m}^{k}( \phi _{m}( \omega ) ) -g_{m}^{k}( \phi _{m}( \tau ) ) \vert \leq {3^{-mN}}.$
$ \vert g_{m}^{k}( \phi _{m}( \omega ) ) -g_{m}^{k}( \phi _{m}( \tau ) ) \vert \leq {3^{-mN}}.$
-
(ii) If
 $\omega _{k+j}=0$
for
$\omega _{k+j}=0$
for
 $1\leq j\leq N,$
then
$1\leq j\leq N,$
then
 $\vert g_{m}^{k}( \phi _{m}( \omega ) ) \vert =g_{m}^{k}( \phi _{m}( \omega ) ) \leq {3^{-mN}}. $
$\vert g_{m}^{k}( \phi _{m}( \omega ) ) \vert =g_{m}^{k}( \phi _{m}( \omega ) ) \leq {3^{-mN}}. $
-
(iii) If
 $\omega _{k+j}=1$
for
$\omega _{k+j}=1$
for
 $1\leq j\leq N,$
then
$1\leq j\leq N,$
then
 $\vert g_{m}^{k}( \phi _{m}( \omega ) ) \vert =g_{m}^{k}( \phi _{m}( \omega ) ) \geq 1- {3^{-mN}}. $
$\vert g_{m}^{k}( \phi _{m}( \omega ) ) \vert =g_{m}^{k}( \phi _{m}( \omega ) ) \geq 1- {3^{-mN}}. $
Proof of Lemma 3.5
From Lemma 3.4,
 $$ \begin{align*} g_{m}^{k}( \phi _{m}( \omega ) ) =\phi _{m}( \sigma ^{k}( \omega ) ) =\sum_{j=1}^{\infty }\frac{( 3^{m}-1) \omega _{k+j}}{3^{mj}} \end{align*} $$
$$ \begin{align*} g_{m}^{k}( \phi _{m}( \omega ) ) =\phi _{m}( \sigma ^{k}( \omega ) ) =\sum_{j=1}^{\infty }\frac{( 3^{m}-1) \omega _{k+j}}{3^{mj}} \end{align*} $$
and the three inequalities follow directly.
Proposition 3.6. For any positive integers m and n, each of the
![]() $2^{n}$
mutually disjoint subsets
$2^{n}$
mutually disjoint subsets
![]() $ K_{\varepsilon _{j}}$
(for
$ K_{\varepsilon _{j}}$
(for
![]() $1\leq j\leq 2^{n}$
) is an extremally scrambled set for every function
$1\leq j\leq 2^{n}$
) is an extremally scrambled set for every function
![]() $g_{m}\in \mathcal {G}_{m}. $
$g_{m}\in \mathcal {G}_{m}. $
Proof of Proposition 3.6
In order to prove the proposition, we must show that each of the three defining conditions of an extremally scrambled set are satisfied by any particular
![]() $ K_{\varepsilon _{j}}$
for
$ K_{\varepsilon _{j}}$
for
![]() $1\leq j\leq 2^{n}$
and for every
$1\leq j\leq 2^{n}$
and for every
![]() $g_{m}\in \mathcal {G}_{m}.$
To this end, choose any subset
$g_{m}\in \mathcal {G}_{m}.$
To this end, choose any subset
![]() $\{ x,y\} \subset K_{\varepsilon _{j}}$
such that
$\{ x,y\} \subset K_{\varepsilon _{j}}$
such that
![]() $x<y$
and any
$x<y$
and any
![]() $g_{m}\in \mathcal {G} _{m}.$
Assume also that
$g_{m}\in \mathcal {G} _{m}.$
Assume also that
![]() $x_{0}$
is a periodic point of
$x_{0}$
is a periodic point of
![]() $g_{m}$
having period
$g_{m}$
having period
![]() $p.$
Let
$p.$
Let
![]() $( \omega _{x},\omega _{y}) \in Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) \times Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) $
be such that
$( \omega _{x},\omega _{y}) \in Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) \times Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) $
be such that
Since
![]() $\phi _{m}$
is an order-preserving homeomorphism,
$\phi _{m}$
is an order-preserving homeomorphism,
![]() $\omega _{x}$
and
$\omega _{x}$
and
![]() $ \omega _{y}$
are unique elements of
$ \omega _{y}$
are unique elements of
![]() $\Omega ,$
with
$\Omega ,$
with
![]() $\omega _{x}\prec \omega _{y}.$
Now since
$\omega _{x}\prec \omega _{y}.$
Now since
![]() $\{ \omega _{x},\omega _{y}\} \subset Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) $
and
$\{ \omega _{x},\omega _{y}\} \subset Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) $
and
![]() $ \omega _{x}\prec \omega _{y},$
to every positive integer u there corresponds a strictly increasing sequence
$ \omega _{x}\prec \omega _{y},$
to every positive integer u there corresponds a strictly increasing sequence
![]() $\{ t_{u_{r}}\} _{r\geq 1}$
of positive integers such that
$\{ t_{u_{r}}\} _{r\geq 1}$
of positive integers such that
![]() $ ( \omega _{x}) _{t_{u_{r}}+j} =0$
and
$ ( \omega _{x}) _{t_{u_{r}}+j} =0$
and
![]() $( \omega _{y}) _{t_{u_{r}}+j} =1 $
for
$( \omega _{y}) _{t_{u_{r}}+j} =1 $
for
![]() $1\leq j\leq u$
. Thus, by Lemma 3.5,
$1\leq j\leq u$
. Thus, by Lemma 3.5,
 $$ \begin{align*} \vert g_{m}^{t_{u_{r}}}( \phi _{m}( \omega _{x}) ) -g_{m}^{t_{u_{r}}}( \phi _{m}( \omega _{y}) ) \vert &\geq \vert g_{m}^{t_{u_{r}}}( \phi _{m}( \omega _{y}) ) \vert -\vert g_{m}^{t_{u_{r}}}( \phi _{m}( \omega _{x}) ) \vert \\ &\geq \bigg( 1-\frac{1}{3^{mu}}\bigg) -\frac{1}{3^{mu}}=1-\frac{2}{3^{mu}}. \end{align*} $$
$$ \begin{align*} \vert g_{m}^{t_{u_{r}}}( \phi _{m}( \omega _{x}) ) -g_{m}^{t_{u_{r}}}( \phi _{m}( \omega _{y}) ) \vert &\geq \vert g_{m}^{t_{u_{r}}}( \phi _{m}( \omega _{y}) ) \vert -\vert g_{m}^{t_{u_{r}}}( \phi _{m}( \omega _{x}) ) \vert \\ &\geq \bigg( 1-\frac{1}{3^{mu}}\bigg) -\frac{1}{3^{mu}}=1-\frac{2}{3^{mu}}. \end{align*} $$
Since
we conclude that
For the same pair
![]() $\{ \omega _{x},\omega _{y}\} ,$
since
$\{ \omega _{x},\omega _{y}\} ,$
since
![]() $\{ \omega _{x},\omega _{y}\} \subset Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) ,$
there is an increasing sequence
$\{ \omega _{x},\omega _{y}\} \subset Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) ,$
there is an increasing sequence
![]() $\{ t_{u_{s}}\} _{s\geq 1}$
of positive integers such that
$\{ t_{u_{s}}\} _{s\geq 1}$
of positive integers such that
![]() $( \omega _{x}) _{t_{u_{s}}+j}=( \omega _{y}) _{t_{u_{s}}+j}=0$
for
$( \omega _{x}) _{t_{u_{s}}+j}=( \omega _{y}) _{t_{u_{s}}+j}=0$
for
![]() $1\leq j\leq u$
. This implies, by Lemma 3.5, that
$1\leq j\leq u$
. This implies, by Lemma 3.5, that
 $$ \begin{align*} \vert g_{m}^{t_{u_{s}}}( \phi _{m}( \omega _{x}) ) -g_{m}^{t_{u_{s}}}( \phi _{m}( \omega _{y}) ) \vert &\leq \vert g_{m}^{t_{u_{s}}}( \phi _{m}( \omega _{x}) ) \vert +\vert g_{m}^{t_{u_{s}}}( \phi _{m}( \omega _{y}) ) \vert \\ &\leq \frac{1}{3^{mu}}+\frac{1}{3^{mu}}=\frac{2}{3^{mu}}. \end{align*} $$
$$ \begin{align*} \vert g_{m}^{t_{u_{s}}}( \phi _{m}( \omega _{x}) ) -g_{m}^{t_{u_{s}}}( \phi _{m}( \omega _{y}) ) \vert &\leq \vert g_{m}^{t_{u_{s}}}( \phi _{m}( \omega _{x}) ) \vert +\vert g_{m}^{t_{u_{s}}}( \phi _{m}( \omega _{y}) ) \vert \\ &\leq \frac{1}{3^{mu}}+\frac{1}{3^{mu}}=\frac{2}{3^{mu}}. \end{align*} $$
As this estimate holds for every positive integer
![]() $u\geq 1,$
we conclude that
$u\geq 1,$
we conclude that
Finally, assume that
![]() $x_{0}$
is a periodic point of period p for the function
$x_{0}$
is a periodic point of period p for the function
![]() $g_{m}.$
We must prove that for any
$g_{m}.$
We must prove that for any
![]() $x\in K_{\varepsilon _{j}},$
$x\in K_{\varepsilon _{j}},$
Observe now that
![]() $\max _{k\geq 1}\vert g_{m}^{k}( x_{0}) \vert $
is a definite real number in
$\max _{k\geq 1}\vert g_{m}^{k}( x_{0}) \vert $
is a definite real number in
![]() $[ 0,1] $
since we are simply choosing the maximum value from a finite set consisting of p distinct real numbers in
$[ 0,1] $
since we are simply choosing the maximum value from a finite set consisting of p distinct real numbers in
![]() $[ 0,1] .$
Assume that
$[ 0,1] .$
Assume that
![]() $\omega _{x}=\phi _{m}^{-1}( x) \in Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) $
where
$\omega _{x}=\phi _{m}^{-1}( x) \in Z_{\varepsilon _{j}}( \Omega _{\varepsilon _{j}}) $
where
![]() $x\in K_{\varepsilon _{j}}.$
Then to every positive integer u there correspond strictly increasing sequences
$x\in K_{\varepsilon _{j}}.$
Then to every positive integer u there correspond strictly increasing sequences
![]() $( u_{r_{t}}) _{t\geq 1}$
and
$( u_{r_{t}}) _{t\geq 1}$
and
![]() $( u_{s_{t}}) _{t\geq 1}$
of positive integers such that
$( u_{s_{t}}) _{t\geq 1}$
of positive integers such that
![]() $ ( \omega _{x}) _{u_{r_{t}}+j} =0$
and
$ ( \omega _{x}) _{u_{r_{t}}+j} =0$
and
![]() $( \omega _{x}) _{u_{s_{t}}+j} =1$
, for
$( \omega _{x}) _{u_{s_{t}}+j} =1$
, for
![]() $1\leq j\leq (u+p)$
. Hence, by Lemma 3.5,
$1\leq j\leq (u+p)$
. Hence, by Lemma 3.5,
![]() $\vert g_{m}^{u_{r_{t}}}( x) \vert \leq {3^{-m( u+p) }}$
and
$\vert g_{m}^{u_{r_{t}}}( x) \vert \leq {3^{-m( u+p) }}$
and
for
![]() $0\leq j\leq p-1$
. Since the above inequalities hold for every positive integer
$0\leq j\leq p-1$
. Since the above inequalities hold for every positive integer
![]() $u,$
we conclude that
$u,$
we conclude that
Similarly, by Lemma 3.5,
 $$ \begin{align*} \vert g_{m}^{u_{s_{t}}}( x) -g_{m}^{u_{s_{t}}}( x_{0}) \vert &\geq \vert g_{m}^{u_{s_{t}}}( x) \vert -\vert g_{m}^{u_{s_{t}}}( x_{0}) \vert \\ &\geq \bigg( 1-\frac{1}{3^{mu}}\bigg) -\vert g_{m}^{u_{s_{t}}}( x_{0}) \vert \geq \bigg( 1-\frac{1}{3^{mu}}\bigg) -\max_{k\geq 1}\vert g_{m}^{k}( x_{0}) \vert. \end{align*} $$
$$ \begin{align*} \vert g_{m}^{u_{s_{t}}}( x) -g_{m}^{u_{s_{t}}}( x_{0}) \vert &\geq \vert g_{m}^{u_{s_{t}}}( x) \vert -\vert g_{m}^{u_{s_{t}}}( x_{0}) \vert \\ &\geq \bigg( 1-\frac{1}{3^{mu}}\bigg) -\vert g_{m}^{u_{s_{t}}}( x_{0}) \vert \geq \bigg( 1-\frac{1}{3^{mu}}\bigg) -\max_{k\geq 1}\vert g_{m}^{k}( x_{0}) \vert. \end{align*} $$
As this estimate holds for every positive integer
![]() $u,$
we conclude that
$u,$
we conclude that
Finally, since
 $$ \begin{align*} \lim \sup_{k\rightarrow \infty }\vert g_{m}^{k}( x) -g_{m}^{k}( x_{0}) \vert &\geq \max_{k\geq 1}\vert g_{m}^{k}( x_{0}) \vert \quad\text{and} \\ \lim \sup_{k\rightarrow \infty }\vert g_{m}^{k}( x) -g_{m}^{k}( x_{0}) \vert &\geq 1-\max_{k\geq 1}\vert g_{m}^{k}( x_{0}) \vert , \end{align*} $$
$$ \begin{align*} \lim \sup_{k\rightarrow \infty }\vert g_{m}^{k}( x) -g_{m}^{k}( x_{0}) \vert &\geq \max_{k\geq 1}\vert g_{m}^{k}( x_{0}) \vert \quad\text{and} \\ \lim \sup_{k\rightarrow \infty }\vert g_{m}^{k}( x) -g_{m}^{k}( x_{0}) \vert &\geq 1-\max_{k\geq 1}\vert g_{m}^{k}( x_{0}) \vert , \end{align*} $$
we have
proving that
![]() $K_{\varepsilon _{j}}$
must be an extremally scrambled set for any j with
$K_{\varepsilon _{j}}$
must be an extremally scrambled set for any j with
![]() $1\leq j\leq 2^{n}$
and for any particular
$1\leq j\leq 2^{n}$
and for any particular
![]() $g_{m}\in \mathcal {G} _{m}. $
$g_{m}\in \mathcal {G} _{m}. $
Proof of Proposition 3.1
For any positive integers n and k, define
![]() $n'=nk.$
From step 3 of the construction, we observe by definition that
$n'=nk.$
From step 3 of the construction, we observe by definition that
Moreover,
![]() $f_{m,n'}$
is decreasing and continuous on both
$f_{m,n'}$
is decreasing and continuous on both
![]() $\mathcal {S}$
and
$\mathcal {S}$
and
![]() $\mathcal {M}_{m}^{\circ }\backslash \mathcal {S}$
since it has been extended from
$\mathcal {M}_{m}^{\circ }\backslash \mathcal {S}$
since it has been extended from
![]() $\mathcal {S}$
to
$\mathcal {S}$
to
![]() $\mathcal {M}_{m}$
by linear interpolation in such a way that
$\mathcal {M}_{m}$
by linear interpolation in such a way that
![]() $f_{m,n'}( 1/3^{m}) =1$
and
$f_{m,n'}( 1/3^{m}) =1$
and
![]() $f_{m,n'}( 1-( 1/3^{m}) ) =0.$
Thus,
$f_{m,n'}( 1-( 1/3^{m}) ) =0.$
Thus,
![]() $f_{m,n'}$
is in
$f_{m,n'}$
is in
![]() $\mathcal {G}_{m}.$
Since
$\mathcal {G}_{m}.$
Since
![]() $f_{m,n'}\in \mathcal {G}_{m},$
by Proposition 3.6, for any j with
$f_{m,n'}\in \mathcal {G}_{m},$
by Proposition 3.6, for any j with
![]() $2^{n'}+1\leq j'\leq 2^{n'+1}, K_{\varepsilon _{( 2^{n'+1}+1) -j'}}$
must be an extremally scrambled set for
$2^{n'}+1\leq j'\leq 2^{n'+1}, K_{\varepsilon _{( 2^{n'+1}+1) -j'}}$
must be an extremally scrambled set for
![]() $f_{m,n'},$
and since
$f_{m,n'},$
and since
![]() $f_{m,n'}( \mathcal {C}_{\varepsilon _{j'}}) =K_{\varepsilon _{( 2^{n'+1}+1) -j'}}\!,$
for every
$f_{m,n'}( \mathcal {C}_{\varepsilon _{j'}}) =K_{\varepsilon _{( 2^{n'+1}+1) -j'}}\!,$
for every
![]() $ \mathcal {C}_{\varepsilon _{j'}}\!$
, it follows that every
$ \mathcal {C}_{\varepsilon _{j'}}\!$
, it follows that every
![]() $ \mathcal {C}_{\varepsilon _{j'}}$
must also be an extremally scrambled set for
$ \mathcal {C}_{\varepsilon _{j'}}$
must also be an extremally scrambled set for
![]() $f_{m,n'}\!.$
By construction it is clear that
$f_{m,n'}\!.$
By construction it is clear that
![]() $\mu ( \mathcal {C}_{\varepsilon _{j'}}) =1/2^{n'+2}$
and the
$\mu ( \mathcal {C}_{\varepsilon _{j'}}) =1/2^{n'+2}$
and the
![]() $\mathcal {C}_{\varepsilon _{j'}}$
are homomorphic to each other. Since
$\mathcal {C}_{\varepsilon _{j'}}$
are homomorphic to each other. Since
![]() $n'=nk,$
for
$n'=nk,$
for
![]() $1\leq j\leq 2^n$
,
$1\leq j\leq 2^n$
,
![]() $M_{m,j}^n$
contains k mutually disjoint sets
$M_{m,j}^n$
contains k mutually disjoint sets
![]() $M_{m,j'}^{n'}$
with
$M_{m,j'}^{n'}$
with
![]() $k({\kern1.5pt}j-1)+1\leq j'\leq kj,$
and thus k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other. Thus,
$k({\kern1.5pt}j-1)+1\leq j'\leq kj,$
and thus k mutually disjoint extremally scrambled sets of identical positive Lebesgue measure, homeomorphic to each other. Thus,
![]() $f_{m,n'}$
is the desired map.
$f_{m,n'}$
is the desired map.
Acknowledgement
The authors are grateful to Minako Fujio and Aniruddha Ghosh for conversation and collaboration.