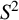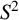1 Result and method
As pointed out by Birman and Hilden [Reference Birman and Hilden2] (see also [Reference Atalan, Medetogullari and Ozan1, Reference Ghaswala and Winarski4, Reference Margalit and Winarski5]), an interesting problem is to find branched covers of a surface with the property that each homeomorphism of the base surface preserving the branching set can be lifted.
Fix a set
![]() $\mathfrak {B}=\{\mathfrak {x}_{1},\ldots ,\mathfrak {x}_{n}\}\subset S^{2}$
, with
$\mathfrak {B}=\{\mathfrak {x}_{1},\ldots ,\mathfrak {x}_{n}\}\subset S^{2}$
, with
![]() $n\ge 2$
. Let
$n\ge 2$
. Let
![]() $\Sigma _{0,n}=S^{2}\setminus \mathfrak {B}$
. Let
$\Sigma _{0,n}=S^{2}\setminus \mathfrak {B}$
. Let
![]() $x_{i}\in H_{1}(\Sigma _{0,n};\mathbb {Z})$
denote the homology class of a small loop enclosing
$x_{i}\in H_{1}(\Sigma _{0,n};\mathbb {Z})$
denote the homology class of a small loop enclosing
![]() $\mathfrak {x}_{i}$
. Given an abelian group A, a regular A-cover
$\mathfrak {x}_{i}$
. Given an abelian group A, a regular A-cover
![]() $\pi :\Sigma \to S^{2}$
with branching set
$\pi :\Sigma \to S^{2}$
with branching set
![]() $\mathfrak {B}$
is determined by an epimorphism
$\mathfrak {B}$
is determined by an epimorphism
![]() $\phi _{\pi }: H_{1}(\Sigma _{0,n};\mathbb {Z})\twoheadrightarrow A$
, which satisfies
$\phi _{\pi }: H_{1}(\Sigma _{0,n};\mathbb {Z})\twoheadrightarrow A$
, which satisfies
![]() $\phi _{\pi }(x_{1})+\cdots +\phi _{\pi }(x_{n})=0$
. Call two such covers
$\phi _{\pi }(x_{1})+\cdots +\phi _{\pi }(x_{n})=0$
. Call two such covers
![]() $\phi :\Sigma \to S^{2}$
and
$\phi :\Sigma \to S^{2}$
and
![]() $\phi ^{\prime }:\Sigma ^{\prime }\to S^{2}$
equivalent if there exist homeomorphisms
$\phi ^{\prime }:\Sigma ^{\prime }\to S^{2}$
equivalent if there exist homeomorphisms
![]() $\tilde {g}:\Sigma \to \Sigma ^{\prime }$
,
$\tilde {g}:\Sigma \to \Sigma ^{\prime }$
,
![]() $g:S^{2}\to S^{2}$
such that
$g:S^{2}\to S^{2}$
such that
![]() $g(\mathfrak {B})=\mathfrak {B}$
and
$g(\mathfrak {B})=\mathfrak {B}$
and
![]() $g\circ \pi =\pi ^{\prime }\circ \tilde {g}$
.
$g\circ \pi =\pi ^{\prime }\circ \tilde {g}$
.
Denote by
![]() $\mathbf {e}_{i}$
the vector with
$\mathbf {e}_{i}$
the vector with
![]() $1$
at the ith position and
$1$
at the ith position and
![]() $0$
elsewhere.
$0$
elsewhere.
We extend the results of [Reference Atalan, Medetogullari and Ozan1, Reference Ghaswala and Winarski4] by proving the following result.
Theorem 1.1. Let A be a finite abelian p-group with exponent
![]() $p^{k}$
and
$p^{k}$
and
![]() $\pi :\Sigma \to S^{2}$
be a regular A-cover with branching set
$\pi :\Sigma \to S^{2}$
be a regular A-cover with branching set
![]() $\mathfrak {B}$
such that each homeomorphism of
$\mathfrak {B}$
such that each homeomorphism of
![]() $S^{2}$
preserving
$S^{2}$
preserving
![]() $\mathfrak {B}$
can be lifted. Then up to equivalence, one of the following occurs:
$\mathfrak {B}$
can be lifted. Then up to equivalence, one of the following occurs:
-
(1)
 $A=\mathbb {Z}_{p^{k}}^{n-1}$
and
$A=\mathbb {Z}_{p^{k}}^{n-1}$
and
 $\phi _{\pi }(x_{i})=\mathbf {e}_{i}$
,
$\phi _{\pi }(x_{i})=\mathbf {e}_{i}$
,
 $1\le i\le n-1$
;
$1\le i\le n-1$
; -
(2)
 $A=\mathbb {Z}_{p^{r}}^{n-2}\times \mathbb {Z}_{p^{k}}$
for some
$A=\mathbb {Z}_{p^{r}}^{n-2}\times \mathbb {Z}_{p^{k}}$
for some
 $k>r>0$
with
$k>r>0$
with
 $p^{k-r}\mid n$
and
$p^{k-r}\mid n$
and  $$ \begin{align*}\phi_{\pi}(x_{i})=(\mathbf{e}_{i},1), \ 1\le i\le n-2; \quad \phi_{\pi}(x_{n-1})=(\mathbf{0},1);\end{align*} $$
$$ \begin{align*}\phi_{\pi}(x_{i})=(\mathbf{e}_{i},1), \ 1\le i\le n-2; \quad \phi_{\pi}(x_{n-1})=(\mathbf{0},1);\end{align*} $$
-
(3)
 $A=\mathbb {Z}_{p^{k}}$
with
$A=\mathbb {Z}_{p^{k}}$
with
 $p^{k}\mid n$
and
$p^{k}\mid n$
and
 $\phi _{\pi }(x_{i})=1$
for all i.
$\phi _{\pi }(x_{i})=1$
for all i.
According to [Reference Atalan, Medetogullari and Ozan1, Section 3], this essentially solves the problem for abelian covers.
Let G denote the group of automorphisms of
![]() $H_{1}(\Sigma _{0,n};\mathbb {Z})$
induced by all homeomorphisms of
$H_{1}(\Sigma _{0,n};\mathbb {Z})$
induced by all homeomorphisms of
![]() $\Sigma _{0,n}$
. Clearly, G is isomorphic to the permutation group on
$\Sigma _{0,n}$
. Clearly, G is isomorphic to the permutation group on
![]() $\{x_{1},\ldots ,x_{n}\}$
. By [Reference Ghaswala and Winarski4, Lemma 2.1], a homeomorphism f of
$\{x_{1},\ldots ,x_{n}\}$
. By [Reference Ghaswala and Winarski4, Lemma 2.1], a homeomorphism f of
![]() $\Sigma _{0,n}$
can be lifted if and only if there exists
$\Sigma _{0,n}$
can be lifted if and only if there exists
![]() $\psi \in \text {Aut}(A)$
such that
$\psi \in \text {Aut}(A)$
such that
![]() $\psi \circ \phi _{\pi }=\phi _{\pi }\circ \alpha $
, where
$\psi \circ \phi _{\pi }=\phi _{\pi }\circ \alpha $
, where
![]() $\alpha \in G$
is induced by f. This is equivalent to
$\alpha \in G$
is induced by f. This is equivalent to
![]() $\alpha (\ker \phi _{\pi })=\ker \phi _{\pi }$
, which in turn is equivalent to
$\alpha (\ker \phi _{\pi })=\ker \phi _{\pi }$
, which in turn is equivalent to
where
![]() $\overline {\phi _{\pi }}: H_{1}(\Sigma _{0,n};\mathbb {Z}_{p^{k}}\kern-0.75pt)\twoheadrightarrow A$
is the map induced by
$\overline {\phi _{\pi }}: H_{1}(\Sigma _{0,n};\mathbb {Z}_{p^{k}}\kern-0.75pt)\twoheadrightarrow A$
is the map induced by
![]() $\phi _{\pi }$
. Instead of dealing with
$\phi _{\pi }$
. Instead of dealing with
![]() $\text {Aut}(A)$
, we work directly on
$\text {Aut}(A)$
, we work directly on
![]() $\ker \overline {\phi _{\pi }}$
, reducing the problem to finding all subgroups of
$\ker \overline {\phi _{\pi }}$
, reducing the problem to finding all subgroups of
![]() $H_{1}(\Sigma _{0,n};\mathbb {Z}_{p^{k}}\kern-0.75pt)$
that are invariant under all
$H_{1}(\Sigma _{0,n};\mathbb {Z}_{p^{k}}\kern-0.75pt)$
that are invariant under all
![]() $\alpha \in G$
. From this viewpoint,
$\alpha \in G$
. From this viewpoint,
![]() $\pi $
is equivalent to
$\pi $
is equivalent to
![]() $\pi ^{\prime }$
if and only if
$\pi ^{\prime }$
if and only if
![]() $\beta (\ker \overline {\phi _{\pi ^{\prime }}})=\ker \overline {\phi _{\pi }}$
for some
$\beta (\ker \overline {\phi _{\pi ^{\prime }}})=\ker \overline {\phi _{\pi }}$
for some
![]() $\beta \in G$
.
$\beta \in G$
.
For problems of this kind, a method was developed in [Reference Chen and Shen3].
Some notations and conventions. For a ring R, let
![]() $R^{\ell ,m}$
denote the set of
$R^{\ell ,m}$
denote the set of
![]() $\ell \times m$
matrices over R. For
$\ell \times m$
matrices over R. For
![]() $X\in R^{\ell ,m}$
, let
$X\in R^{\ell ,m}$
, let
![]() $X_{i,j}$
denote its
$X_{i,j}$
denote its
![]() $(i,j)$
-entry and let
$(i,j)$
-entry and let
![]() $\langle X\rangle $
denote the subgroup of
$\langle X\rangle $
denote the subgroup of
![]() $R^{m}$
generated by the row vectors of X. For
$R^{m}$
generated by the row vectors of X. For
![]() $Y\in \mathbb {Z}^{\ell ,m}$
, abusing the notation, we denote its image under the map
$Y\in \mathbb {Z}^{\ell ,m}$
, abusing the notation, we denote its image under the map
![]() $\mathbb {Z}^{\ell ,m}\rightarrow \mathbb {Z}_{p^{k}}^{\ell ,m}$
induced by the quotient map
$\mathbb {Z}^{\ell ,m}\rightarrow \mathbb {Z}_{p^{k}}^{\ell ,m}$
induced by the quotient map
![]() $\mathbb {Z}\twoheadrightarrow \mathbb {Z}_{p^{k}}$
also by Y. Let
$\mathbb {Z}\twoheadrightarrow \mathbb {Z}_{p^{k}}$
also by Y. Let
![]() $S_{m}$
denote the permutation group on m elements. Embed
$S_{m}$
denote the permutation group on m elements. Embed
![]() $S_{m}$
as a subgroup of
$S_{m}$
as a subgroup of
![]() $\textrm{GL}(m,\mathbb {Z})$
by identifying
$\textrm{GL}(m,\mathbb {Z})$
by identifying
![]() $\sigma \in S_{m}$
with the matrix (denoted by the same notation) whose
$\sigma \in S_{m}$
with the matrix (denoted by the same notation) whose
![]() $(i,j)$
-entry is
$(i,j)$
-entry is
![]() $\delta _{i,\sigma (j)}$
, where
$\delta _{i,\sigma (j)}$
, where
![]() $\delta $
is the Kronecker symbol.
$\delta $
is the Kronecker symbol.
Lemma 1.2 [Reference Chen and Shen3, Theorem 3.9].
Each subgroup
![]() $C\leqslant \mathbb {Z}_{p^{k}}^{m}$
is of the form
$C\leqslant \mathbb {Z}_{p^{k}}^{m}$
is of the form
![]() $\langle PQ\omega \rangle $
for some
$\langle PQ\omega \rangle $
for some
![]() $P\in \mathbb {Z}_{p^{k}}^{\ell ,m}$
,
$P\in \mathbb {Z}_{p^{k}}^{\ell ,m}$
,
![]() $Q\in \textrm{GL}(m,\mathbb {Z})$
,
$Q\in \textrm{GL}(m,\mathbb {Z})$
,
![]() $\omega \in S_{m}$
such that
$\omega \in S_{m}$
such that
-
•
 $0\le \ell \le m$
,
$0\le \ell \le m$
,
 $P_{i,j}=\delta _{i,j}p^{r_{i}}$
with
$P_{i,j}=\delta _{i,j}p^{r_{i}}$
with
 $0\le r_{1}\le \cdots \le r_{\ell }<k$
;
$0\le r_{1}\le \cdots \le r_{\ell }<k$
; -
•
 $Q_{i,i}=1$
for all i, and
$Q_{i,i}=1$
for all i, and
 $Q_{j,i}=0\le Q_{i,j}<p^{r_{j}-r_{i}}$
for all
$Q_{j,i}=0\le Q_{i,j}<p^{r_{j}-r_{i}}$
for all
 $i<j$
, where
$i<j$
, where
 $r_{i}=k$
for
$r_{i}=k$
for
 $\ell <i\le m$
.
$\ell <i\le m$
.
Clearly,
![]() $\mathbb {Z}_{p^{k}}^{m}/C\cong \mathbb {Z}_{p^{r_{\iota }}}\times \cdots \times \mathbb {Z}_{p^{r_{m}}}$
, with
$\mathbb {Z}_{p^{k}}^{m}/C\cong \mathbb {Z}_{p^{r_{\iota }}}\times \cdots \times \mathbb {Z}_{p^{r_{m}}}$
, with
![]() $\iota =\min \{i\colon r_{i}>0\}$
.
$\iota =\min \{i\colon r_{i}>0\}$
.
Let
![]() $b=n-1$
. Take
$b=n-1$
. Take
![]() $x_{1},\ldots ,x_{b}$
as generators for
$x_{1},\ldots ,x_{b}$
as generators for
![]() $H_{1}(\Sigma _{0,n};\mathbb {Z})\cong \mathbb {Z}^{b}$
. For each
$H_{1}(\Sigma _{0,n};\mathbb {Z})\cong \mathbb {Z}^{b}$
. For each
![]() $\alpha \in G\cong S_{b+1}$
, let
$\alpha \in G\cong S_{b+1}$
, let
![]() $T^{\alpha }\in \textrm {GL}(b,\mathbb {Z})$
denote the matrix determined by
$T^{\alpha }\in \textrm {GL}(b,\mathbb {Z})$
denote the matrix determined by
 $$ \begin{align*} \alpha(x_{i})=\sum_{j=1}^{b}(T^{\alpha})_{i,j}\cdot x_{j}, \quad i=1,\ldots,b. \end{align*} $$
$$ \begin{align*} \alpha(x_{i})=\sum_{j=1}^{b}(T^{\alpha})_{i,j}\cdot x_{j}, \quad i=1,\ldots,b. \end{align*} $$
Obviously, if
![]() $\alpha \in S_{b}$
, by which we mean
$\alpha \in S_{b}$
, by which we mean
![]() $\alpha (x_{b+1})=x_{b+1}$
, then
$\alpha (x_{b+1})=x_{b+1}$
, then
![]() $T^{\alpha }=\alpha $
.
$T^{\alpha }=\alpha $
.
If
![]() $\ker \overline {\phi _{\pi }}=\langle PQ\omega \rangle $
, then
$\ker \overline {\phi _{\pi }}=\langle PQ\omega \rangle $
, then
![]() $\alpha (\ker \overline {\phi _{\pi }})=\langle PQ\omega T^{\alpha }\rangle $
. Taking
$\alpha (\ker \overline {\phi _{\pi }})=\langle PQ\omega T^{\alpha }\rangle $
. Taking
![]() $\beta =\omega ^{-1}\in S_{b}$
, we have
$\beta =\omega ^{-1}\in S_{b}$
, we have
![]() $\beta (\ker \overline {\phi _{\pi }})=\langle PQ\rangle $
. Hence, up to equivalence, we can assume
$\beta (\ker \overline {\phi _{\pi }})=\langle PQ\rangle $
. Hence, up to equivalence, we can assume
![]() $\ker \overline {\phi _{\pi }}=\langle PQ\rangle $
. Then
$\ker \overline {\phi _{\pi }}=\langle PQ\rangle $
. Then
![]() $\alpha (\ker \overline {\phi _{\pi }})=\langle PQT^{\alpha }\rangle $
for each
$\alpha (\ker \overline {\phi _{\pi }})=\langle PQT^{\alpha }\rangle $
for each
![]() $\alpha \in G$
. By the criterion given by [Reference Chen and Shen3, Lemma 3.11],
$\alpha \in G$
. By the criterion given by [Reference Chen and Shen3, Lemma 3.11],
![]() $\alpha (\ker \overline {\phi _{\pi }})=\ker \overline {\phi _{\pi }}$
is equivalent to
$\alpha (\ker \overline {\phi _{\pi }})=\ker \overline {\phi _{\pi }}$
is equivalent to
Thus, it suffices to find tuples
![]() $(r_{1},\ldots ,r_{b};Q)$
consisting of integers
$(r_{1},\ldots ,r_{b};Q)$
consisting of integers
![]() $0\le r_{1}\le \cdots \le r_{b}>0$
and a matrix
$0\le r_{1}\le \cdots \le r_{b}>0$
and a matrix
![]() $Q\in \textrm{GL}(b,\mathbb {Z})$
, such that
$Q\in \textrm{GL}(b,\mathbb {Z})$
, such that
Such a tuple determines a regular branched A-cover
![]() $\pi $
, with
$\pi $
, with
![]() $A=\mathbb {Z}_{p^{r_{\iota }}}\times \cdots \times \mathbb {Z}_{p^{r_{b}}}$
,
$A=\mathbb {Z}_{p^{r_{\iota }}}\times \cdots \times \mathbb {Z}_{p^{r_{b}}}$
,
![]() $\iota =\min \{i\colon r_{i}>0\}$
, and
$\iota =\min \{i\colon r_{i}>0\}$
, and
with the understanding that
![]() $\phi _{\pi }(x_{b+1})=-\phi _{\pi }(x_{1})-\cdots -\phi _{\pi }(x_{b})$
.
$\phi _{\pi }(x_{b+1})=-\phi _{\pi }(x_{1})-\cdots -\phi _{\pi }(x_{b})$
.
2 Proof of Theorem 1.1
As a simple observation, (1.2) holds if and only if
for all X in the subgroup of
![]() $\mathbb {Z}^{b,b}$
generated by
$\mathbb {Z}^{b,b}$
generated by
![]() $T^{\alpha }$
,
$T^{\alpha }$
,
![]() $\alpha \in S_{b+1}$
.
$\alpha \in S_{b+1}$
.
Let I denote the identity matrix. Let
![]() $E_{u}^{v}$
denote the matrix whose
$E_{u}^{v}$
denote the matrix whose
![]() $(u,v)$
-entry is
$(u,v)$
-entry is
![]() $1$
and the other entries are all
$1$
and the other entries are all
![]() $0$
.
$0$
.
For the permutation
![]() $\eta _{i}\in S_{b+1}$
switching i and
$\eta _{i}\in S_{b+1}$
switching i and
![]() $b+1$
,
$b+1$
,
 $$ \begin{align*}T^{\eta_{i}}=\left(\begin{array}{ccccc} 1 & \ & \ & \ & \ \\ \ & \ddots & \ & \ & \ \\ -1 & \cdots & -1 & \cdots & -1 \\ \ & \ & \ & \ddots & \ \\ \ & \ & \ & \ & 1 \end{array}\right)=I-E_{i}^{i}-\sum\limits_{j=1}^{b}E_{i}^{j}.\end{align*} $$
$$ \begin{align*}T^{\eta_{i}}=\left(\begin{array}{ccccc} 1 & \ & \ & \ & \ \\ \ & \ddots & \ & \ & \ \\ -1 & \cdots & -1 & \cdots & -1 \\ \ & \ & \ & \ddots & \ \\ \ & \ & \ & \ & 1 \end{array}\right)=I-E_{i}^{i}-\sum\limits_{j=1}^{b}E_{i}^{j}.\end{align*} $$
Clearly, for each
![]() $\alpha \in S_{b+1}\setminus S_{b}$
, there uniquely exists
$\alpha \in S_{b+1}\setminus S_{b}$
, there uniquely exists
![]() $u\in \{1,\ldots ,b\}$
,
$u\in \{1,\ldots ,b\}$
,
![]() $\sigma \in S_{b}$
, such that
$\sigma \in S_{b}$
, such that
![]() $\alpha =\eta _{u}\sigma $
. Then
$\alpha =\eta _{u}\sigma $
. Then
 $$ \begin{align} T^{\sigma}-T^{\alpha}=(I-T^{\eta_{u}})T^{\sigma}=E_{u}^{\sigma^{-1}(u)}+\sum_{j=1}^{b}E_{u}^{j}. \end{align} $$
$$ \begin{align} T^{\sigma}-T^{\alpha}=(I-T^{\eta_{u}})T^{\sigma}=E_{u}^{\sigma^{-1}(u)}+\sum_{j=1}^{b}E_{u}^{j}. \end{align} $$
The difference of two such matrices can give rise to
![]() $E_{u}^{v}-E_{u}^{w}$
for any
$E_{u}^{v}-E_{u}^{w}$
for any
![]() $v\ne w$
.
$v\ne w$
.
Taking
![]() $i=1$
and
$i=1$
and
![]() $X=E_{1}^{v}-E_{1}^{w}$
in (2.1), we obtain
$X=E_{1}^{v}-E_{1}^{w}$
in (2.1), we obtain
In particular, setting
![]() $w=j=b-1$
and
$w=j=b-1$
and
![]() $v=b$
leads to
$v=b$
leads to
![]() $r_{b-1}=r_{1}$
(so that
$r_{b-1}=r_{1}$
(so that
![]() $r_{i}=r_{1}$
for all
$r_{i}=r_{1}$
for all
![]() $i<b$
). By (1.1),
$i<b$
). By (1.1),
![]() $Q_{i,j}=0$
for all
$Q_{i,j}=0$
for all
![]() $i,j$
with
$i,j$
with
![]() $1\le i<j<b$
.
$1\le i<j<b$
.
If
![]() $k=r_{b}=r_{1}$
, then
$k=r_{b}=r_{1}$
, then
![]() $Q_{i,b}=0$
for
$Q_{i,b}=0$
for
![]() $1\le i<b$
, so that
$1\le i<b$
, so that
![]() $Q=I$
. In this case,
$Q=I$
. In this case,
![]() $A=\mathbb {Z}_{p^{k}}^{b}$
, and by (1.3),
$A=\mathbb {Z}_{p^{k}}^{b}$
, and by (1.3),
![]() $\phi (x_{i})=\mathbf {e}_{i}$
.
$\phi (x_{i})=\mathbf {e}_{i}$
.
Now suppose
![]() $k>r_{1}$
. Setting
$k>r_{1}$
. Setting
![]() $w=j=b$
in (2.3) leads to
$w=j=b$
in (2.3) leads to
Hence
![]() $Q_{v,b}\equiv -1\pmod {p^{r_{b}-r_{1}}}$
for all
$Q_{v,b}\equiv -1\pmod {p^{r_{b}-r_{1}}}$
for all
![]() $v<b$
. From (2.2), we see that for
$v<b$
. From (2.2), we see that for
![]() $i<b$
,
$i<b$
,
so
![]() $p^{r_{b}-r_{1}}\mid (Q(T^{\sigma }-T^{\alpha })Q^{-1})_{i,b}$
is equivalent to
$p^{r_{b}-r_{1}}\mid (Q(T^{\sigma }-T^{\alpha })Q^{-1})_{i,b}$
is equivalent to
Once this holds, for each
![]() $\sigma \in S_{b}$
and all
$\sigma \in S_{b}$
and all
![]() $i<b$
,
$i<b$
,
 $$ \begin{align*}(QT^{\sigma} Q^{-1})_{i,b}\equiv\sum_{v=1}^{b}(Q\sigma)_{i,v}\equiv 0\pmod{p^{r_{b}-r_{1}}}.\end{align*} $$
$$ \begin{align*}(QT^{\sigma} Q^{-1})_{i,b}\equiv\sum_{v=1}^{b}(Q\sigma)_{i,v}\equiv 0\pmod{p^{r_{b}-r_{1}}}.\end{align*} $$
Therefore, (1.2) is fulfilled.
There are two possible cases.
-
• If
 $r_{1}>0$
, then
$r_{1}>0$
, then
 $A=\mathbb {Z}_{p^{r_{1}}}^{b-1}\times \mathbb {Z}_{p^{k}}$
and, by (1.3),
$A=\mathbb {Z}_{p^{r_{1}}}^{b-1}\times \mathbb {Z}_{p^{k}}$
and, by (1.3),  $$ \begin{align*}\phi(x_{i})=(\mathbf{e}_{i},1), 1\le i\le b-1; \quad \phi(x_{b})=(\mathbf{0},1).\end{align*} $$
$$ \begin{align*}\phi(x_{i})=(\mathbf{e}_{i},1), 1\le i\le b-1; \quad \phi(x_{b})=(\mathbf{0},1).\end{align*} $$
-
• If
 $r_{1}=0$
, then
$r_{1}=0$
, then
 $A=\mathbb {Z}_{p^{k}}$
and
$A=\mathbb {Z}_{p^{k}}$
and
 $\phi (x_{i})=1$
for each i.
$\phi (x_{i})=1$
for each i.