Hostname: page-component-6dbcb7884d-wnk8j Total loading time: 0 Render date: 2025-02-13T19:38:35.075Z Has data issue: false hasContentIssue false
  • English
  • Français

GENERAL STABILITY OF THE EXPONENTIAL AND LOBAČEVSKIǏ FUNCTIONAL EQUATIONS

Published online by Cambridge University Press:  08 March 2016

JAEYOUNG CHUNG
JAEYOUNG CHUNG*
Affiliation:
Department of Mathematics, Kunsan National University, Kunsan 573-701, Republic of Korea email jychung@kunsan.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $S$ be a semigroup possibly with no identity and 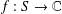$f:S\rightarrow \mathbb{C}$. We consider the general superstability of the exponential functional equation with a perturbation 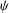$\unicode[STIX]{x1D713}$ of mixed variables

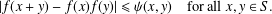$$\begin{eqnarray}\displaystyle |f(x+y)-f(x)f(y)|\leq \unicode[STIX]{x1D713}(x,y)\quad \text{for all }x,y\in S. & & \displaystyle \nonumber\end{eqnarray}$$
In particular, if $S$ is a uniquely 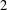$2$-divisible semigroup with an identity, we obtain the general superstability of Lobačevskiǐ’s functional equation with perturbation 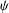$\unicode[STIX]{x1D713}$
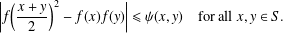$$\begin{eqnarray}\displaystyle \biggl|f\biggl(\frac{x+y}{2}\biggr)^{2}-f(x)f(y)\biggr|\leq \unicode[STIX]{x1D713}(x,y)\quad \text{for all }x,y\in S. & & \displaystyle \nonumber\end{eqnarray}$$

Keywords

exponential functional equationLobačevskiǐ functional equationstability

MSC classification

Primary: 39B82: Stability, separation, extension, and related topics
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 278 - 285
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Baker, J. A., ‘The stability of the cosine functional equation’, Proc. Amer. Math. Soc. 80 (1980), 411–416.Google Scholar
Baker, J. A., Lawrence, J. and Zorzitto, F., ‘The stability of the equation f (x + y) = f (x)f (y)’, Proc. Amer. Math. Soc. 74 (1979), 242–246.Google Scholar
Chung, J. and Chung, S.-Y., ‘Stability of exponential functional equations with involutions’, J. Funct. Spaces Appl. 2014 (2014), Article ID 619710, 9 pages.Google Scholar
Gǎvrutǎ, P., ‘An answer to a question of Th. M. Rassias and J. Tabor on mixed stability of mappings’, Bul. Ştiinţ. Univ. Politeh. Timiş. Ser. Mat. Fiz. 42(56) (1997), 1–6.Google Scholar
Hyers, D. H., ‘On the stability of the linear functional equation’, Proc. Natl. Acad. Sci. USA 27 (1941), 222–224.Google Scholar
Hyers, D. H., Isac, G. and Rassias, Th. M., Stability of Functional Equations in Several Variables (Birkhäuser, Boston, MA, 1998).Google Scholar
Jung, S.-M., Hyers–Ulam–Rassias Stability of Functional Equations in Nonlinear Analysis (Springer, New York, 2011).Google Scholar
Székelyhidi, L., ‘On a theorem of Baker, Lawrence and Zorzitto’, Proc. Amer. Math. Soc. 84 (1982), 95–96.Google Scholar
Ulam, S. M., A Collection of Mathematical Problems, Interscience Tracts in Pure and Applied Mathematics, 8 (Interscience, New York, 1960).Google Scholar