Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-02-06T06:34:25.105Z Has data issue: false hasContentIssue false
  • English
  • Français

FITTING SUBGROUP AND NILPOTENT RESIDUAL OF FIXED POINTS

Part of: Representation theory of groups

Published online by Cambridge University Press:  26 December 2018

EMERSON DE MELO Open the ORCID record for EMERSON DE MELO [Opens in a new window]  and
PAVEL SHUMYATSKY Open the ORCID record for PAVEL SHUMYATSKY [Opens in a new window]
EMERSON DE MELO*
Affiliation:
Department of Mathematics, University of Brasília, Brasília-DF 70910-900, Brazil email emerson@mat.unb.br
PAVEL SHUMYATSKY
Affiliation:
Department of Mathematics, University of Brasília, Brasília-DF, 70910-900, Brazil email pavel@unb.br
*
✉emerson@mat.unb.br
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 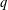$q$ be a prime and let 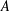$A$ be an elementary abelian group of order at least 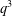$q^{3}$ acting by automorphisms on a finite 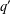$q^{\prime }$-group 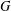$G$. We prove that if 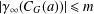$|\unicode[STIX]{x1D6FE}_{\infty }(C_{G}(a))|\leq m$ for any 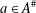$a\in A^{\#}$, then the order of 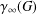$\unicode[STIX]{x1D6FE}_{\infty }(G)$ is 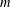$m$-bounded. If 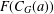$F(C_{G}(a))$ has index at most 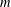$m$ in 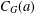$C_{G}(a)$ for any 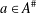$a\in A^{\#}$, then the index of 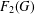$F_{2}(G)$ is 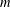$m$-bounded.

Keywords

centraliserautomorphismnilpotent residual

MSC classification

Primary: 20D45: Automorphisms
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 61 - 67
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported by FEMAT; the second author was supported by FAPDF and CNPq-Brazil.

References

Acciarri, C., Shumyatsky, P. and Thillaisundaram, A., ‘Conciseness of coprime commutators in finite groups’, Bull. Aust. Math. Soc. 89 (2014), 252–258.Google Scholar
de Melo, E., Lima, A. S. and Shumyatsky, P., ‘Nilpotent residual of fixed points’, Arc. Math. 111 (2018), 13–21.Google Scholar
de Melo, E. and Shumyatsky, P., ‘Finite groups and their coprime automorphisms’, Proc. Amer. Math. Soc. 145 (2017), 3755–3760.Google Scholar
Goldschmidt, D. M., ‘Weakly embedded 2-local subgroups of finite groups’, J. Algebra 21 (1972), 341–351.10.1016/0021-8693(72)90028-2Google Scholar
Gorenstein, D., Finite Groups (Harper and Row, New York–Evanston–London, 1968).Google Scholar
Guralnick, R. and Shumyatsky, P., ‘Derived subgroups of fixed points’, Israel J. Math. 126 (2001), 345–362.10.1007/BF02784161Google Scholar
Khukhro, E. I., Nilpotent Groups and their Automorphisms (de Gruyter, Berlin–New York, 1993).Google Scholar
Shumyatsky, P., ‘Finite groups and the fixed points of coprime automorphisms’, Proc. Amer. Math. Soc. 129 (2001), 3479–3484.Google Scholar
Shumyatsky, P., ‘Positive laws in fixed points’, Trans. Amer. Math. Soc. 356 (2003), 2081–2091.Google Scholar
Shumyatsky, P., ‘Linear groups with almost right Engel elements’, Proc. Edinb. Math. Soc., to appear.Google Scholar
Ward, J. N., ‘On finite groups admitting automorphisms with nilpotent fixed-point’, Bull. Aust. Math. Soc. 5 (1971), 281–282.Google Scholar