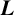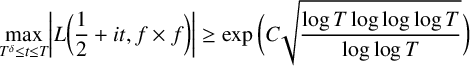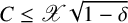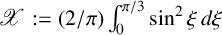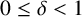1 Introduction
1.1 Background
The Lindelöf hypothesis (LH) asserts that for every
$\varepsilon>0$
,
$$ \begin{align*} \lvert\zeta(\tfrac12+it)\rvert=O(t^{\varepsilon})\quad \mathrm{as}\ t\rightarrow\infty. \end{align*} $$
In [Reference Littlewood9], Littlewood showed that a stronger form of LH follows from the Riemann hypothesis (RH): namely, for some positive constant
$C_1>0$
and for all large
$\lvert t\rvert $
,
$$ \begin{align*} \bigg\lvert \zeta\bigg(\frac12+it\bigg)\bigg\rvert =O\bigg(\exp\bigg(C_1\frac{\log \lvert t\rvert}{\log\log\lvert t\rvert}\bigg)\bigg), \end{align*} $$
where the sharpest size of the implicit constant
$C_1$
has been given by Chandee and Soundararajan [Reference Chandee and Soundararajan4].
In the opposite direction, Titchmarsh (see [Reference Titchmarsh12, Theorem 8.12]) proved that for any
$\alpha <1/2$
and large enough T,
$$ \begin{align*} \underset{t\in[0,T]}{\max}\lvert\zeta(\tfrac12+it)\rvert\geq\exp((\log T)^{\alpha}). \end{align*} $$
Using the resonance method, Soundararajan [Reference Soundararajan10] proved that there exists
$t\in [T,2T]$
such that
$$ \begin{align*} \bigg\lvert \zeta\bigg(\frac12+it\bigg)\bigg\rvert \geq\exp\bigg((1+o(1))\frac{\sqrt{\log T}}{\sqrt{\log\log T}}\bigg)\quad \mathrm{as}\ T\rightarrow\infty. \end{align*} $$
Recently, Bondarenko and Seip [Reference Bondarenko and Seip2] made a breakthrough by showing that for any constant
$C_2<1/\sqrt {2}$
,
$$ \begin{align*} \underset{t\in[\sqrt{T},T]}{\max}\bigg\lvert \zeta\bigg(\frac12+it\bigg)\bigg\rvert \geq \exp\bigg(C_2\frac{\sqrt{\log T\log\log\log T}}{\sqrt{\log\log T}}\bigg). \end{align*} $$
Later, Bondarenko and Seip [Reference Bondarenko and Seip3] improved their result by widening the allowable range of
$C_2$
, showing that the above bound holds for any
$C_2<1$
. Currently, the sharpest lower bound is due to De la Bretèche and Tenenbaum [Reference De la Bretèche and Tenenbaum5] who established
$$ \begin{align*} \underset{t\in [0,T]}{\max}\bigg\lvert \zeta\bigg(\frac12+it\bigg)\bigg\rvert \geq \exp\bigg((\sqrt{2}+o(1))\sqrt{\frac{\log T\log\log\log T}{\log\log T}}\bigg)\quad \mathrm{as}\ T\rightarrow\infty. \end{align*} $$
In this paper, we investigate the extreme values of the Rankin–Selberg L-functions associated with holomorphic cusp forms in the vertical direction. We begin with some definitions for these L-functions.
1.2 Rankin–Selberg L-functions
Let f be a primitive holomorphic cusp form of weight
$k\geq 1$
for
${\textrm {SL}}_2(\mathbb {Z})$
. Let
$$ \begin{align*} f(z)=\sum_{n\geq1}\lambda_f(n)n^{(k-1)/2}e(nz) \end{align*} $$
be its normalised Fourier expansion at the cusp
$\infty $
, where
$\lambda _f(n)\in \mathbb {R}\, (n=1, 2, \ldots )$
are eigenvalues of Hecke operators
$T(n)$
(that is,
$T(n)f=\lambda _f(n)f$
), normalised so that
$\lambda _f(1)=1$
. By the work of Deligne, there exist
$\alpha _f(p),\beta _f(p)\in \mathbb {C}$
, satisfying
$$ \begin{align*} \alpha_f(p)\beta_f(p)=1 \end{align*} $$
and
$$ \begin{align*} \lambda_f(p^{\nu})=\alpha_f(p)^{\nu}+\alpha_{f}(p)^{\nu-1}\beta_f(p) +\cdots+\beta_f(p)^{\nu}, \quad\mbox{for }\nu\geq1. \end{align*} $$
The Ramanujan conjecture states that
$$ \begin{align} \lvert {\alpha}_f(p)\rvert =\lvert {\beta}_f(p)\rvert =1 \end{align} $$
for all prime numbers p. For holomorphic f, this was proved by Deligne [Reference Deligne6] in 1974. Thus for each prime number p, there is a unique
$\xi _f(p)\in [0,\pi ]$
such that
$$ \begin{align*} \lambda_f(p)=2\cos\xi_f(p). \end{align*} $$
According to the Sato–Tate conjecture, the sequence
$\{\xi _f(p)\}_p$
is equi-distributed on
$[0,\pi ]$
with respect to the measure
$({2}/{\pi })\sin ^2\xi \,d\xi $
, that is, for a given subinterval
${[a,b]\subset [0,\pi ]}$
,
$$ \begin{align} \lvert\{p\leq x:\,\xi_f(p)\in[a,b]\}\rvert\sim\frac{x}{\log x}\frac{2}{\pi}\int_{a}^{b}\sin^2\xi\,d\xi\quad\mbox{as } x\rightarrow\infty. \end{align} $$
This has been proved by Barnet-Lamb et al. [Reference Barnet-Lamb, Geraghty, Harris and Taylor1]. (For Maass cusp forms, both (1.1) and (1.2) are still open.)
For
$\operatorname {Re} s>1$
, the Rankin–Selberg L-function attached to f is
$$ \begin{align*} L(s,f\times f):=\prod_{p}\bigg(1-\frac{\alpha_f(p)^2}{p^s}\bigg)^{-1}\bigg(1-\frac{\beta_f(p)^2}{p^s}\bigg)^{-1} \bigg(1-\frac{1}{p^s}\bigg)^{-2}. \end{align*} $$
It can be continued analytically to the whole complex plane with a simple pole at
$s=1$
and satisfies the functional equation
$$ \begin{align*} \Lambda(s,f\times f)=\Lambda(1-s,f\times f), \end{align*} $$
for the complete L-function
$$ \begin{align*} \begin{aligned} \Lambda(s,f\times f):=\gamma(s,f\times f)L(s,f\times f) \end{aligned} \end{align*} $$
and the gamma factor
$$ \begin{align*} \begin{aligned} \gamma(s,f\times f):=(2\pi)^{-2s}\Gamma(s)\Gamma(s+k-1). \end{aligned} \end{align*} $$
Following the argument of Bondarenko and Seip [Reference Bondarenko and Seip3], we establish the following theorem.
Theorem 1.1. Assume the GRH. Let
$0\leq \delta <1$
be given. If T is sufficiently large, then there exists t with
$T^{\delta }\leq t\leq T$
such that
$$ \begin{align} \bigg\lvert L\bigg(\frac12+it,f\times f\bigg)\bigg\rvert \geq\exp\bigg(C\sqrt{\frac{\log T\log\log\log T}{\log\log T}}\bigg), \end{align} $$
where C is a positive number depending on f, satisfying
$C < \mathscr {X}\sqrt {1-\delta }$
, and where
${\mathscr {X}:=({2}/{\pi })\int _{0}^{\pi /3}\sin ^2\xi \,d\xi} $
.
The assumption of the GRH is only needed in the proof of Theorem 1.1 to handle the moments
$\int _{1}^{T}\lvert L(\frac 12+it,f\times f)\rvert ^{2r}\,dt$
(see Lemma 2.2). In fact, the convexity bound is sufficient for the proof of Lemma 2.1 and subconvexity bounds will not lead to any improvement of the result.
The positivity of the coefficients of the Rankin–Selberg L-functions is necessary for the method in the proof. Hence, a principal difference between our version of the resonance method and that used earlier by Bondarenko and Seip [Reference Bondarenko and Seip3] is that we have to consider a suitable subcollection of the set of prime numbers in our resonator (see Section 2.3 for the details).
2 Preparation for the proof
2.1 Convolution formula for
$L(s,f\times f)$
We define the Fourier transform
$\widehat {F}$
of F on
$\mathbb {R}$
as
$$ \begin{align*} \widehat{F}(\xi)=\int_{-\infty}^{\infty}F(x)e^{-ix\xi}\,dx. \end{align*} $$
Lemma 2.1. Suppose that
$\tfrac 12 \leq \sigma <1$
and let
$F(x+iy)$
be an analytic function in the horizontal strip
$\sigma -2\leq y\leq 0$
satisfying the growth estimate
$$ \begin{align*} \begin{aligned} \underset{\sigma-2\leq y\leq0}{\max}\lvert F(x+iy)\rvert=O\bigg(\frac{1}{\lvert x\rvert ^2}\bigg) \end{aligned} \end{align*} $$
when
$\lvert x\rvert \rightarrow \infty $
. Then for every real t,
$$ \begin{align*} \int_{-\infty}^{\infty}L(\sigma+i(t+u),f\times f)F(u)\,du=\sum_{m=1}^{\infty}\frac{A(m)\widehat{F}(\log m)}{m^{\sigma+it}}- 2\pi i \rho_fF(-t+i(\sigma-1)), \end{align*} $$
where
$L(s,f\times f):=\sum _{m=1}^{\infty }A(m)m^{-s}$
and
$\rho _f$
is the residue of
$L(s,f\times f)$
at
$s=1$
.
Proof. Let T be a large positive number and let
$\mathscr {R}(T)$
denote the contour consisting of the line segments connecting
$\sigma -iT, 2-iT, 2+iT, \sigma +iT$
.
By the residue theorem applied to
$G(z):=L(z+it,f\times f)F(i\sigma -iz)$
in
$\mathscr {R}(T)$
,
$$ \begin{align*} &\frac{1}{2\pi i} \int_{\mathscr{R}(T)}G(z)\,dz \\[3pt] &\quad=\frac{1}{2\pi i}\bigg(\int_{\sigma+iT}^{\sigma-iT}+\int_{\sigma-iT}^{2-iT}+ \int_{2-iT}^{2+iT}+\int_{2+iT}^{\sigma+iT}\bigg)L(z+it,f\times f)F(i\sigma-iz)\,dz\\[3pt] &\quad=\underset{z=1-it}{\mathrm{Res}}G(z). \end{align*} $$
Since
$L(s,f\times f)$
is holomorphic in the s-plane except for a simple pole at
$s=1$
,
$$ \begin{align} &\int_{\sigma-iT}^{\sigma+iT} L(z+it,f\times f)F(i\sigma-iz)\,dz \nonumber \\[3pt] &\quad=\int_{2-iT}^{2+iT}L(z+it,f\times f)F(i\sigma-iz)\,dz-2\pi i \rho_fF(-t+i(\sigma-1)) \nonumber \\[3pt] &\quad\quad+\bigg(\int_{\sigma-iT}^{2-iT}+\int_{2+iT}^{\sigma+iT}\bigg)L(z+it,f\times f)F(i\sigma-iz)\,dz. \end{align} $$
Applying the upper bound for
$F(x+iy)$
in Lemma 2.1, (2.1) and the convexity bound [Reference Iwaniec and Kowalski8, (5.21)], we arrive at
$$ \begin{align*} \begin{aligned} \int_{-T}^{T}L(\sigma+i(t+u),f\times f)F(u)\,du &=\int_{-T}^{T}L(2+i(t+u),f\times f)F(u+i(\sigma-2))\,du\\[3pt] &\quad-2\pi i \rho_fF(-t+i(\sigma-1))+O(T^{-3/2+\varepsilon}). \end{aligned} \end{align*} $$
Also,
$$ \begin{align*} &\int_{-\infty}^{\infty} L(2+i(t+u),f\times f)F(u+i(\sigma-2))\,du\\[3pt] &\quad=\sum_{m=1}^{\infty}\frac{A(m)}{m^{2+it}}\int_{-\infty}^{\infty}F(u+i(\sigma-2))e^{-iu\log m} e^{(\sigma-2)\log m}e^{-(\sigma-2)\log m}\,du\\[3pt] &\quad=\sum_{m=1}^{\infty}\frac{A(m)}{m^{\sigma+it}}\widehat{F}(\log m). \end{align*} $$
Combining these two formulae completes the proof of Lemma 2.1.
2.2 Moments of L-functions
Define
$$ \begin{align} \begin{aligned} I_r(T,f\times f):=\int_{1}^{T}\bigg\lvert L\bigg(\frac12+it,f\times f\bigg)\bigg\rvert ^{2r}\,dt. \end{aligned} \end{align} $$
Lemma 2.2 [Reference Tang and Xiao11, Theorem 1.1].
Assume the GRH. Let f be a primitive holomorphic cusp form of weight
$k\geq 1$
for
${\textrm {SL}}_2(\mathbb {Z})$
. Let
$I_r(T,f\times f)$
be defined as in (2.2). Then for all real numbers
$r>0$
and sufficiently large T,
$$ \begin{align*} \begin{aligned} I_r(T,f\times f)\ll_{r,f}T(\log T)^{r^2}. \end{aligned} \end{align*} $$
2.3 Construction of the resonator
The resonance method can be traced back to a paper of Voronin [Reference Voronin13]. It was developed independently and significantly refined by Hilberdink [Reference Hilberdink7] and by Soundararajan [Reference Soundararajan10].
A resonator (in the spirit of [Reference Bondarenko and Seip3, Section 3]) is a function of the form
$R(t)$
, where
$$ \begin{align} R(t)=\sum_{m\in \mathscr{M}'}\frac{r(m)}{m^{it}}, \end{align} $$
and
$\mathscr {M}'$
is a suitable finite set of positive integers whose construction is given below.
Let
$0<\delta <1$
be a fixed real number, and let
$\kappa $
and
$\gamma $
with
$0<\kappa <1$
and
$0<\gamma <1$
be parameters still to be chosen. Define
$N=[T^{\kappa }]$
, where
$[x]$
denotes the integer part of x. Let P be the set of prime numbers p such that
$$ \begin{align} e\log N\log_2N<p<\exp((\log_2N)^{\gamma})\log N\log_2N\quad \mathrm{and}\quad 1\leq \lambda_f(p)\leq2. \end{align} $$
We define
$h(n)$
to be the multiplicative function supported on the set of square-free numbers such that
$$ \begin{align*} h(p):=\sqrt{\frac{\log N\log_2N}{\log_3N}}\frac{1}{\sqrt{p}(\log p-\log_2N-\log_3N)} \quad\mbox{for } p\in P, \end{align*} $$
and
$h(p)=0$
otherwise. Fix
$\Delta $
with
$1<\Delta <1/\gamma $
. For each
$\ell \in \{1,\ldots ,[(\log _2N)^{\gamma }]\}$
, we define the sets
$$ \begin{align*} P_\ell &:=\{p: e^\ell\log N\log_2N<p\leq e^{\ell+1}\log N\log_2N,\ 1\leq \lambda_f(p)\leq 2\}, \\ M_\ell &:=\bigg\{n\in\mathrm{supp}(h): n\,\,\mathrm{has\,\,at\,\,least}\,\,\frac{\Delta\log N}{\ell^2\log_3N}\,\,\mathrm{prime\,\,divisors\,\,in}\,\,P_\ell\bigg\}. \end{align*} $$
Next, we define the set
$$ \begin{align*} \mathscr{M}:=\mathrm{supp}(h) \,\backslash \bigcup_{\ell=1}^{[(\log_2N)^{\gamma}]}M_\ell. \end{align*} $$
Then
$\mathscr {M}$
is the set of square-free numbers n that have at most
$\Delta\log N/(\ell^2 \log_3N) $
divisors in
$P_{\ell }$
.
Now, let
$\mathscr {J}$
be the set of integers j such that
$$ \begin{align*} [(1+T^{-1})^{\,j},(1+T^{-1})^{\,j+1}]\bigcap\mathscr{M}\neq\emptyset, \end{align*} $$
and let
$m_j$
to be the minimum of
$[(1+T^{-1})^{\hspace{2pt}j},(1+T^{-1})^{\hspace{2pt}j+1}]\bigcap \mathscr {M}$
for j in
$\mathscr {J}$
. Consider the set
$$ \begin{align*} \mathscr{M}':=\{m_j: j\in\mathscr{J}\}, \end{align*} $$
and define
$$ \begin{align*} r(m_j):=\bigg(\sum_{n\in\mathscr{M},\,(1+T^{-1})^{\hspace{2pt}j-1}\leq n\leq(1+T^{-1})^{\hspace{2pt}j+2}}h(n)^2\bigg)^{1/2} \quad\mbox{for } m_j\in\mathscr{M}'. \end{align*} $$
Finally, we set
$\Phi (t)=e^{-t^2/2}$
.
Lemma 2.3. We have
-
(i)
$\lvert R(t)\rvert ^2\leq R(0)^2\ll N\sum _{l\in \mathscr {M}}h(l)^2$
; -
(ii)
$\int _{-\infty }^{\infty }\lvert R(t)\rvert ^2\Phi ({t}/{T})\,dt\ll T\sum _{l\in \mathscr {M}}h(l)^2$
.
Proof. The proof for
$(\mathrm {i})$
follows from the definition of
$R(t)$
in (2.3) and the Cauchy–Schwarz inequality. The proof for
$(\mathrm {ii})$
follows the same outline as in [Reference Bondarenko and Seip3, Lemma 5].
Define
$$ \begin{align} \mathcal{A}(N):=\frac{1}{\sum_{i\in\mathbb{N}}h(i)^2}\sum_{n\in \mathbb{N}}\frac{h(n)}{\sqrt{n}}\sum_{{d|n}}h(d)\sqrt{d} \quad \mathrm{and} \quad \mathscr{X}:=\frac{2}{\pi}\int_{0}^{\pi/3}\sin^2\xi\,d\xi. \end{align} $$
We make use of the following four lemmas.
Lemma 2.4. We have
$$ \begin{align*} \mathcal{A}(N) \geq\exp\bigg((\gamma\mathscr{X}+o(1))\sqrt{\frac{\log N\log_3N}{\log_2N}}\bigg) \quad\mbox{as } N\rightarrow\infty. \end{align*} $$
Proof. From the construction of h as a multiplicative function,
$$ \begin{align} \frac{1}{\sum_{i\in\mathbb{N}}h(i)^2}\sum_{n\in \mathbb{N}}\frac{h(n)}{\sqrt{n}}\sum_{d|n}h(d)\sqrt{d} &=\frac{\prod_{p\in P}(1+{h(p)}{p^{-1/2}}\prod_{d|p}h(d)\sqrt{d})}{\prod_{p\in P}(1+h(p)^2)} \nonumber\\[3pt] &=\prod_{p\in P}\frac{1+h(p)^2+h(p)p^{-1/2}}{1+h(p)^2} \nonumber\\[3pt] &=\exp\bigg((1+o(1))\sum_{p\in P}\frac{h(p)}{\sqrt{p}}\bigg). \end{align} $$
Following the proof of [Reference Bondarenko and Seip2, Lemma 1], (1.2) and the definitions of P in (2.4) and
$\mathscr {X}$
in (2.5) lead to
$$ \begin{align} \sum_{p\in P}\frac{h(p)}{\sqrt{p}}&=\sqrt{\frac{\log N\log_2 N}{\log_3N}}\sum_{p\in P}\frac{1}{p(\log p-\log_2N-\log_3N)} \nonumber\\[3pt] &=\sqrt{\frac{\log N\log_2 N}{\log_3N}}\int^{\hspace{1.5pt}\exp((\log_2N)^{\gamma})\log N\log_2N}_{e\log N\log_2N} \frac{d\,(\frac{(1+o(1))x}{\log x}\frac{2}{\pi}\int_{0}^{\pi/3}\sin^2\xi\,d\xi)}{x(\log x-\log_2N-\log_3N)} \nonumber\\[3pt] &=(\gamma\mathscr{X}+o(1))\sqrt{\frac{\log N\log_3N}{\log_2N}}. \end{align} $$
Inserting (2.7) into (2.6) completes the proof of the lemma.
Lemma 2.5 [Reference Bondarenko and Seip2, Lemma 3].
We have
$$ \begin{align*} \frac{1}{\sum_{i\in \mathbb{N}}h(i)^2}\sum_{n\in \mathscr{M}}\frac{h(n)}{\sqrt{n}}\sum_{\substack{d|n\\ d\leq n/N^{\varepsilon}}}h(d)\sqrt{d}=o(\mathcal{A}(N)) \quad\mbox{as } N\rightarrow\infty, \end{align*} $$
where the implicit constant depends only on
$\varepsilon $
.
Lemma 2.6 [Reference Bondarenko and Seip2, Lemma 2].
We have
$$ \begin{align*} \frac{1}{\sum_{i\in \mathbb{N}}h(i)^2}\sum_{\substack{n\in\mathbb{N}\\ n\notin \mathscr{M}}}\frac{h(n)}{\sqrt{n}}\sum_{d|n}h(d)\sqrt{d}=o(\mathcal{A}(N)) \quad\mbox{as } N\rightarrow\infty. \end{align*} $$
Lemma 2.7. Suppose that
$$ \begin{align*} L(t):=\sum_{m=1}^{\infty}\frac{A(m)a_m}{m^{1/2+it}} \end{align*} $$
is absolutely convergent and that
$a_n\geq 0$
for every n. Let
$\varepsilon $
be a positive number and
$\gamma $
be the parameter defining the set P. Then
$$ \begin{align*} \int_{-\infty}^{\infty}L(t)\lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,dt \geq T\underset{m\leq T^{\varepsilon}}{\min}\,a_m \cdot \exp\bigg((\gamma\mathscr{X}+o(1))\sqrt{\frac{\kappa \log T\log_3T}{\log_2T}}\bigg)\sum_{l\in \mathscr{M}}h(l)^2. \end{align*} $$
Proof. It follows from the explicit expression for
$R(t)$
that
$$ \begin{align} \int_{-\infty}^{\infty}L(t)\lvert R(t)\rvert^2\Phi\bigg(\frac tT\bigg)\,dt &=\sqrt{2\pi}T\sum_{m,n\in \mathscr{M}'}\sum_{k=1}^{\infty}\frac{A(k)a_kr(m)r(n)}{\sqrt{k}}\Phi\bigg(T\log\frac{km}{n}\bigg) \nonumber\\[3pt] &\geq\sqrt{2\pi}T \underset{j\leq T^{\varepsilon}}{\min}\,a_j \sum_{m,n\in\mathscr{M}'}\sum_{\substack{k\in \mathscr{M}\\k\leq T^{\varepsilon}}}\frac{r(m)r(n)}{\sqrt{k}}\Phi\bigg(T\log\frac{km}{n}\bigg). \end{align} $$
Here we used the fact that
$A(k)\geq 1$
for
$k\in \mathscr {M}$
by the construction of
$\mathscr {M}$
.
For a given k in
$\mathscr {M}$
, consider all pairs
$m'$
,
$n'$
in
$\mathscr {M}'$
such that
$\lvert km'/n'-1\rvert \leq 3/T$
. We use the notation
$$ \begin{align*} J(m'):=[(1+T^{-1})^{\hspace{2pt}j},(1+T^{-1})^{\hspace{2pt}j+1}), \end{align*} $$
where j is the unique integer such that
$(1+T^{-1})^{\hspace{2pt}j}\leq m'\leq (1+T^{-1})^{\hspace{2pt}j+1}$
. Using the Cauchy–Schwarz inequality and the definition of
$r(m')$
, we find
$$ \begin{align*} r(m')r(n')\geq\sum_{\substack{m,n\in\mathscr{M},\,mk=n\\ m\in J(m'),\,n\in J(n')}} h(m)h(n), \end{align*} $$
and hence, by the definition of
$\mathscr {M}'$
,
$$ \begin{align*} \sum_{\substack{m',n'\in\mathscr{M}'\\ \lvert km'/n'-1\rvert \leq3/T}} r(m')r(n')\geq\sum_{m,n\in\mathscr{M},\,mk=n}h(m)h(n). \end{align*} $$
Now dividing this inequality by
$\sqrt {k}$
and summing over all k in
$\mathscr {M}\cap [1,T^{\varepsilon }]$
and combining the result with (2.8), and Lemmas 2.5 and 2.6, we get
$$ \begin{align} \int_{-\infty}^{\infty}L(t)\lvert R(t)\rvert^2\Phi\bigg(\frac tT\bigg)\,dt &\gg T \underset{j\leq T^{\varepsilon}}{\min}\,a_j \sum_{n\in\mathscr{M}}\frac{h(n)}{\sqrt{n}}\sum_{d|n,d\geq n/T^{\varepsilon}}h(d)\sqrt{d} \nonumber\\[3pt] &\gg T \underset{j\leq T^{\varepsilon}}{\min}\,a_j \cdot \mathcal{A}(N)\sum_{n\in\mathscr{M}}h(n)^2. \end{align} $$
Combining Lemma 2.4 and (2.9) completes the proof of the lemma.
3 Proof of Theorem 1.1
We choose
$$ \begin{align} F(t):=\frac{\sin^2((\varepsilon\log T)t)}{(\varepsilon\log T)t^2} \end{align} $$
and note that
$$ \begin{align} \widehat{F}(\xi)=\frac{\pi}{2}\max\bigg(1-\frac{\lvert\xi\rvert}{2\varepsilon\log T},0\bigg). \end{align} $$
By the convexity bound [Reference Iwaniec and Kowalski8, (5.21)] and the growth estimate for
$F(x+iy)$
,
$$ \begin{align} & \int_{-T^{\delta}}^{T^{\delta}}\int_{-\infty}^{\infty} \bigg\lvert L\bigg(\frac12+i(t+u),f\times f\bigg)\bigg\rvert F(u)\,du\,dt \nonumber\\[3pt] &\quad\ll T^{\delta}+\int_{-T^{\delta}}^{T^{\delta}}\int_{\lvert u\rvert \leq T^{\delta}}\bigg\lvert L\bigg(\frac12+i(t+u),f\times f\bigg)\bigg\rvert F(u)\,du\,dt \nonumber\\[3pt] &\quad\ll T^{\delta}+\int_{-2T^{\delta}}^{2T^{\delta}}\bigg\lvert L\bigg(\frac12+it,f\times f\bigg)\bigg\rvert \,dt. \end{align} $$
By Lemma 2.2,
$$ \begin{align} \int_{-2T^{\delta}}^{2T^{\delta}}\bigg\lvert L\bigg(\frac12+it,f\times f\bigg)\bigg\rvert \,dt \ll_f T^{\delta+\varepsilon}. \end{align} $$
$$ \begin{align} \int_{-T^{\delta}}^{T^{\delta}}\int_{-\infty}^{\infty}\bigg\lvert L\bigg(\frac12+i(t+u),f\times f\bigg)\bigg\rvert F(u)\lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,du\,dt \ll_f T^{\delta+\kappa+\varepsilon}\sum_{l\in \mathscr{M}}h(l)^2 \end{align} $$
by a trival estimation of
$R(0)^2$
in Lemma 2.3. Because of the rapid decay of
$\Phi (t)$
,
$$ \begin{align} \int_{\lvert t\rvert>T\log T}\int_{-\infty}^{\infty}\bigg\lvert L\bigg(\frac12+i(t+u),f\times f\bigg)\bigg\rvert F(u)\lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,du\,dt=o\bigg(\sum_{l\in \mathscr{M}}h(l)^2\bigg). \end{align} $$
Combining (3.5) and (3.6), we deduce that
$$ \begin{align} &\int_{T^{\delta}\leq\lvert t\rvert\leq T\log T}\int_{-\infty}^{\infty}\bigg\lvert L\bigg(\frac12+i(t+u),f\times f\bigg)\bigg\rvert F(u)\lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,du\,dt \nonumber\\[3pt] &\quad=\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\bigg\lvert L\bigg(\frac12+i(t+u),f\times f\bigg)\bigg\rvert F(u)\lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,du\,dt +O_f\bigg(T^{\delta+\kappa+\varepsilon}\sum_{l\in \mathscr{M}}h(l)^2\bigg). \end{align} $$
We now require
$\delta +\kappa <1$
and apply Lemma 2.3(ii) to the left-hand side of (3.7). We obtain
$$ \begin{align} &\underset{T^{\delta}/2\leq t\leq 2T\log T}{\max}\bigg\lvert L\bigg(\frac12+it,f\times f\bigg)\bigg\rvert T\sum_{l\in\mathscr{M}}h(l)^2 \nonumber\\[3pt] &\quad \gg\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}\bigg\lvert L\bigg(\frac12+i(t+u),f\times f\bigg)\bigg\rvert F(u)\lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,du\,dt+O(T)\sum_{l\in \mathscr{M}}h(l)^2.\quad \end{align} $$
By Lemma 2.1,
$$ \begin{align} &\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}L\bigg(\frac12+i(t+u),f\times f\bigg)F(u)\lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,du\,dt \nonumber\\[3pt] &\quad=\int_{-\infty}^{\infty}\sum_{m=1}^{\infty}\frac{A(m)\widehat{F}(\log m)}{m^{1/2+it}}\lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,dt-2\pi i\rho_f\int_{-\infty}^{\infty}F(-t-i/2) \lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,dt. \end{align} $$
Setting
$a_m:=\widehat {F}(\log m)$
and applying Lemma 2.7,
$$ \begin{align} &\int_{-\infty}^{\infty}\sum_{m=1}^{\infty}\frac{A(m)\widehat{F}(\log m)}{m^{1/2+it}}\lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,dt \nonumber\\[3pt] &\quad\geq T \underset{m\leq T^{\varepsilon}}{\min}\,\widehat{F}(\log m) \cdot \exp\bigg((\gamma\mathscr{X}+o(1))\sqrt{\frac{\kappa\log T\log_3T}{\log_2T}}\bigg)\sum_{l\in \mathscr{M}}h(l)^2. \end{align} $$
Applying (3.1) and Lemma 2.3(i),
$$ \begin{align} \begin{aligned} \int_{-\infty}^{\infty}F(-t-i/2) \lvert R(t)\rvert^2\Phi\bigg(\frac{t}{T}\bigg)\,dt\ll T^{\kappa+\varepsilon}\sum_{l\in \mathscr{M}}h(l)^2. \end{aligned} \end{align} $$
In view of (3.2), we note that
$\min _{m\leq T^{\varepsilon }}\widehat {F}(\log m)\geq \pi /4$
. Hence, choosing
$\varepsilon $
small enough and combining (3.8)–(3.11), we find that the asserted bound (1.3) holds for some t satisfying
$T^{\delta }/2\leq t\leq 2T\log T$
. We obtain the desired restriction
$T^{\delta }\leq t\leq T$
after a trivial adjustment, changing T to
$T/(2\log T)$
and making
$\delta $
slightly smaller.
Acknowledgement
The authors are grateful to Xuanxuan Xiao for drawing their attention to the problem considered in this paper.
