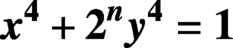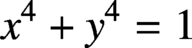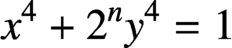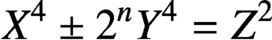Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Tho, Nguyen Xuan
2022.
Solutions to $$x^4+py^4=z^4$$ in cubic number fields.
Archiv der Mathematik,
Vol. 119,
Issue. 3,
p.
269.
Tho, N. X.
2022.
The equation $$x^4+2^ny^4=z^4$$ in algebraic number fields.
Acta Mathematica Hungarica,
Vol. 167,
Issue. 1,
p.
309.
THO, NGUYEN XUAN
2024.
POINTS ON
$x^4+y^4=z^4$
OVER QUADRATIC EXTENSIONS OF
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
.
Bulletin of the Australian Mathematical Society,
p.
1.