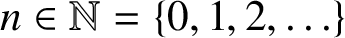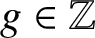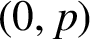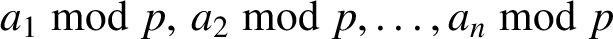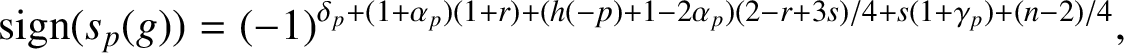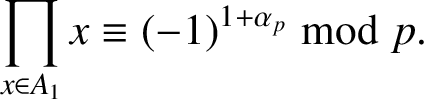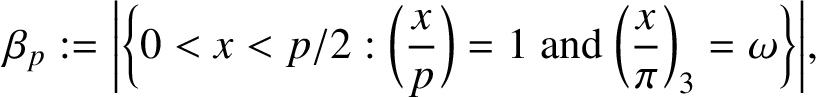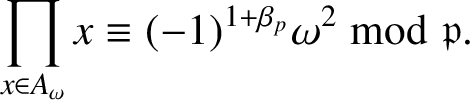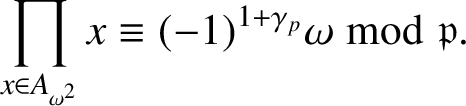1 Introduction
Investigating permutations over finite fields is an active topic in both number theory and finite fields. The Lagrange interpolation formula shows that each permutation over a finite field is in fact induced by a permutation polynomial. For example, let p be an odd prime and let a be an integer with
$p\nmid a$
. Then
$x \bmod p\mapsto ax \bmod p$
(for
$x=0,1,\ldots ,p-1$
) is a permutation over the finite field
$\Bbb F_p=\Bbb Z/p\Bbb Z$
. Zolotarev [Reference Zolotarev12] showed that the sign of this permutation is precisely the Legendre symbol
$({a}/{p})$
. Later, Lerch [Reference Lerch6] extended this result to the ring of residue classes modulo an arbitrary positive integer. In 2015, Brunyate and Clark [Reference Brunyate and Clark3] made a further extension to higher dimensional vector spaces over finite fields.
Recently, Sun [Reference Sun8, Reference Sun9] studied permutations involving squares in finite fields. In fact, let
$p=2m+1$
be an odd prime. Let
$0<b_1<\cdots <b_m<p$
be all the quadratic residues modulo p in the interval
$(0,p)$
. Then clearly the sequence
$$ \begin{align*}1^2 \bmod p,\, 2^2 \bmod p,\ldots,m^2 \bmod p\end{align*} $$
is a permutation
$\sigma _p$
of the sequence
$$ \begin{align*}b_1 \bmod p,\, b_2 \bmod p,\ldots, b_m \bmod p.\end{align*} $$
Let
$\text {sign}(\sigma _p)$
denote the sign of
$\sigma _p$
. Sun [Reference Sun8, Theorem 1.4] obtained
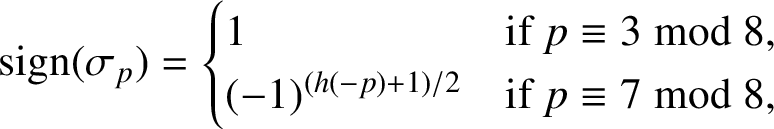$$ \begin{align*}\textrm{sign}(\sigma_p)= \begin{cases} 1 &\mbox{if}\ p \equiv 3\bmod 8,\\ (-1)^{{(h(-p)+1)}/{2}} &\mbox{if} \ p\equiv 7 \bmod 8, \end{cases} \end{align*} $$
where
$h(-p)$
denotes the class number of
$\Bbb Q(\sqrt {-p})$
. Later, Petrov and Sun [Reference Petrov and Sun7] determined the sign of
$\sigma _p$
in the case
$p\equiv 1\ ({\textrm{mod}}\ 4)$
.
With this motivation, we consider permutations involving cubes in
$\Bbb F_p=\Bbb Z/p\Bbb Z$
(where p is an odd prime). The case
$p\equiv 2\bmod 3$
is trivial. Clearly in this case
$$ \begin{align*}\{x^3 \bmod p : x=0,1,\ldots,p-1\}=\Bbb Z/p\Bbb Z\end{align*} $$
and hence
$x \bmod p\mapsto x^3 \bmod p\ (x=0,1,\ldots ,p-1)$
is a permutation
$\tau _p$
over
$\Bbb Z/p\Bbb Z$
. The sign of
$\tau _p$
is a direct consequence of Lerch’s result [Reference Lerch6] and we have
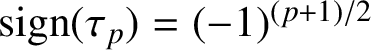$\text {sign}(\tau _p)=(-1)^{{(p+1)}/{2}}$
(see [Reference Wang and Wu10, Theorem 1.2] for details).
Now we consider the nontrivial case
$p\equiv 1\bmod 3$
. Let
$p=3n+1$
be a prime with
$n\in \Bbb N$
and let
$g\in \Bbb Z$
be a primitive root modulo p. Let
$0<a_1<\cdots <a_n<p$
be all the cubic residues modulo p in the interval
$(0,p)$
. Then clearly the sequence
$$ \begin{align*}a_1 \bmod p, \,a_2 \bmod p,\ldots, a_n \bmod p\end{align*} $$
is a permutation
$s_p(g)$
of the sequence
$$ \begin{align*}g^3 \bmod p,\, g^6 \bmod p,\ldots, g^{3n} \bmod p.\end{align*} $$
In order to state our result, we first introduce some notation. Let
$$ \begin{align*}\mathcal{P}:=\{0<x<p: x\ \text{is a primitive root modulo}\ p\}.\end{align*} $$
It is known (see [Reference Cox4]) that
$4p$
can be uniquely written as
$$ \begin{align} 4p=r^2+3s^2\quad (r,s\in\Bbb Z) \end{align} $$
with
$r\equiv 1\bmod 3$
,
$s\equiv 0\bmod 3$
and
$3s\equiv (2g^n+1)r\bmod p$
. Let
$\omega =e^{2\pi i/3}$
be a primitive cubic root of unity. As p splits in
$\Bbb Z[\omega ]$
and
$\Bbb Z[\omega ]$
is a principal ideal domain, we can write
$p=\pi \bar {\pi }$
for some primary prime
$\pi \in \Bbb Z[\omega ]$
with
$({g}/{\pi })_3=\omega $
, where
$\bar {\pi }$
denotes the conjugate of
$\pi $
and the symbol
$({\cdot }/{\pi })_3$
is the cubic residue symbol modulo
$\pi $
. For convenience, we briefly recall the definition of the cubic residue symbol (see [Reference Ireland and Rosen5, Ch. 9] for details). For any
$x\in \Bbb Z[\omega ]$
with
$\pi \nmid x$
, there is a unique
$i\in \{0,1,2\}$
such that
$x^n\equiv \omega ^i\bmod {\pi \Bbb Z[\omega ]}$
. Hence, for any
$x\in \Bbb Z[\omega ]$
with
$\pi \nmid x$
, we define the cubic residue symbol
$({x}/{\pi })_3$
by
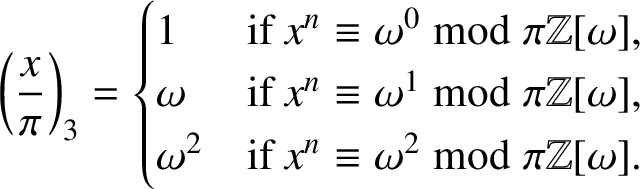$$ \begin{align*}\bigg(\frac{x}{\pi}\bigg)_3=\begin{cases} 1 &\mbox{if}\ x^n\equiv \omega^0\bmod {\pi\Bbb Z[\omega]},\\ \omega &\mbox{if} \ x^n\equiv \omega^1\bmod {\pi\Bbb Z[\omega]},\\ \omega^2 &\mbox{if}\ x^n\equiv \omega^2\bmod {\pi\Bbb Z[\omega]}. \end{cases}\end{align*} $$
We also define
$$ \begin{align} \delta_p &:=|\{0<x<p/4: x\ \text{is a cubic residue modulo}\ p\}|, \end{align} $$
$$ \begin{align} \alpha_p &:=|\{0<x<p/2: x\ \text{is a sixth power residue modulo } p\}|, \end{align} $$
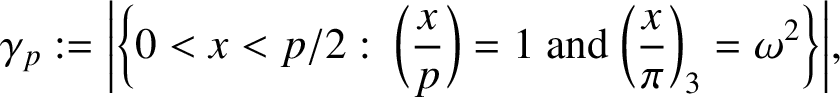$$ \begin{align} \gamma_p &:=\bigg|\bigg\{0<x<p/2:\ \bigg(\frac{x}{p}\bigg)=1\ \text{and}\ \bigg(\frac{x}{\pi}\bigg)_3=\omega^2\bigg\}\bigg|, \end{align} $$
where
$|S|$
denotes the cardinality of a set S.
With this notation, we now state our main result.
Theorem 1.1. Let
$p=3n+1$
be a prime with
$n\in \Bbb N$
.
-
(i) If
$p\equiv 1\bmod {12}$
, then
$$ \begin{align*}|\{g\in\mathcal{P}: \textrm{sign}(s_p(g))=1\}|=|\{g\in\mathcal{P}: \textrm{sign}(s_p(g))=-1\}|.\end{align*} $$
-
(ii) If
$p\equiv 7\ ({\textrm{mod}}\ 12)$
, then
$\textrm{sign}(s_p(g))$
is independent of the choice of g and where
$$ \begin{align*}\textrm{sign}(s_p(g))=(-1)^{\delta_p+(1+\alpha_p)(1+r)+(h(-p)+1-2\alpha_p)(2-r+3s)/4+s(1+\gamma_p)+(n-2)/4},\end{align*} $$
$h(-p)$
is the class number of
$\Bbb Q(\sqrt {-p})$
.
Remark 1.2. For any primitive roots
$g,g'$
modulo p, the product of
$\text {sign}(s_p(g))$
and
$\text {sign}(s_p(g'))$
is indeed equal to the sign of the permutation which sends the sequence
$$ \begin{align*}g^3\ \text{mod}\ p,\ g^6\ \text{mod}\ p,\ldots, g^{3n}\ \text{mod}\ p\end{align*} $$
to the sequence
$$ \begin{align*}g^{\prime3}\ \text{mod}\ p,\ g^{\prime6}\ \text{mod}\ p,\ldots, g^{\prime3n}\ \text{mod}\ p.\end{align*} $$
The signs of the permutations of this type are direct consequences of Lerch’s theorem [Reference Lerch6] and were investigated by Wang and the first author in [Reference Wang and Wu10, Theorem 3.2].
We will prove Theorem 1.1 in the next section.
2 Proof of Theorem 1.1
We first introduce some notation. Let
$p=3n+1$
be a prime with
$n\in \Bbb N$
and let
$g\in \Bbb Z$
be a primitive root modulo p. Let
$\omega =e^{2\pi i/3}$
be a primitive cubic root of unity.
As p splits in
$\Bbb Z[\omega ]$
and
$\Bbb Z[\omega ]$
is a principal ideal domain, we can write
$p=\pi \bar {\pi }$
for some primary prime element
$\pi \in \Bbb Z[\omega ]$
with
$({g}/{\pi })_3=\omega $
, where
$\bar {\pi }$
denotes the conjugate of
$\pi $
and the symbol
$({\cdot }/{\pi })_3$
is the cubic residue symbol modulo
$\pi $
. For convenience, we use the symbol
$\mathfrak {p}$
to denote the prime ideal
$\pi \Bbb Z[\omega ]$
. Recall that from (1.1),
$4p$
can be uniquely written as
$$ \begin{align*} 4p=r^2+3s^2\quad (r,s\in\Bbb Z) \end{align*} $$
with
$r\equiv 1\bmod 3$
,
$s\equiv 0\bmod 3$
and
$3s\equiv (2g^n+1)r\bmod p$
.
Lemma 2.1 [Reference Berndt, Evans and Williams1, Corollary 10.6.2(c)].
For any k with
$0<k<p$
, let
$$ \begin{align*}N(k):=|\{(x,y): 0<x,y<p, \,y^3-x^3\equiv k\bmod p\}|.\end{align*} $$
Then, with the above notation,
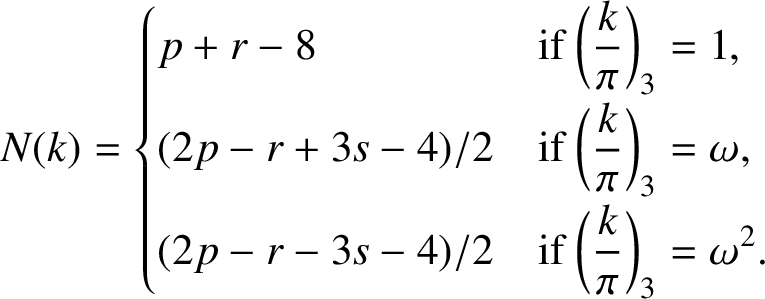$$ \begin{align*}N(k)=\begin{cases} p+r-8 &\mbox{if}\ \bigg(\displaystyle\frac{k}{\pi}\bigg)_3=1,\\[6pt] (2p-r+3s-4)/2 &\mbox{if} \ \bigg(\displaystyle\frac{k}{\pi}\bigg)_3=\omega,\\[6pt] (2p-r-3s-4)/2 &\mbox{if}\ \bigg(\displaystyle\frac{k}{\pi}\bigg)_3=\omega^2. \end{cases}\end{align*} $$
For any k with
$0<k<p$
, define
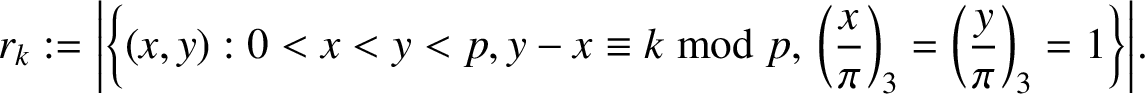$$ \begin{align} r_k:=\bigg|\bigg\{(x,y): 0<x<y<p,y-x\equiv k\bmod p, \,\bigg(\frac{x}{\pi}\bigg)_3=\bigg(\frac{y}{\pi}\bigg)_3=1\bigg\}\bigg|. \end{align} $$
We need the following result.
Lemma 2.2. We have
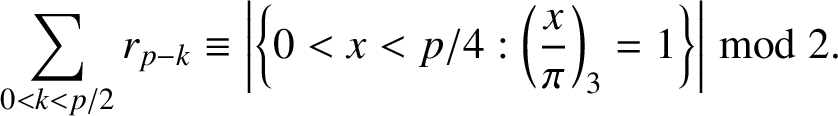$$ \begin{align*}\sum_{0<k<p/2}r_{p-k}\equiv\bigg|\bigg\{0<x<p/4: \bigg(\frac{x}{\pi}\bigg)_3=1\bigg\}\bigg| \bmod 2.\end{align*} $$
Proof. From the definition,
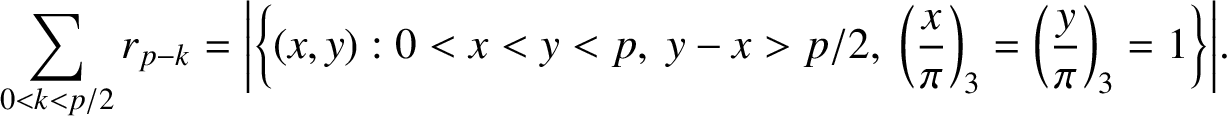$$ \begin{align} \sum_{0<k<p/2}r_{p-k} = \bigg|\bigg\{(x,y): 0<x<y<p,\ y-x>p/2,\ \bigg(\frac{x}{\pi}\bigg)_3=\bigg(\frac{y}{\pi}\bigg)_3=1\bigg\}\bigg|. \end{align} $$
Replacing y by
$p-y$
in the right-hand side of (2.2),
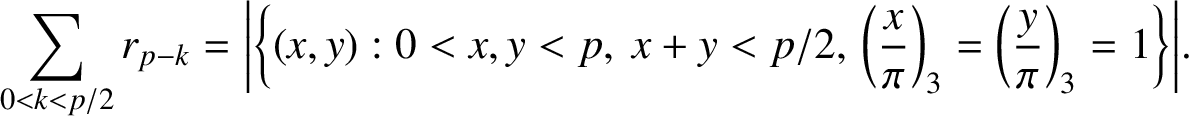$$ \begin{align*} \sum_{0<k<p/2}r_{p-k} = \bigg|\bigg\{(x,y): 0<x,y<p,\ x+y<p/2,\, \bigg(\frac{x}{\pi}\bigg)_3=\bigg(\frac{y}{\pi}\bigg)_3=1\bigg\}\bigg|. \end{align*} $$
By symmetry,
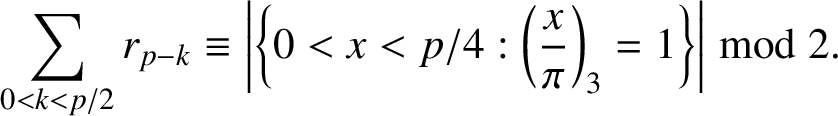$$ \begin{align*}\sum_{0<k<p/2}r_{p-k}\equiv\bigg|\bigg\{0<x<p/4: \bigg(\frac{x}{\pi}\bigg)_3=1\bigg\}\bigg| \bmod 2.\end{align*} $$
This completes the proof.
Now we define the following sets:
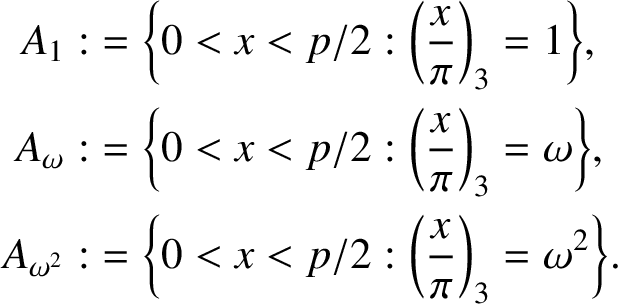$$ \begin{align*} A_1:&=\bigg\{0<x<p/2: \bigg(\frac{x}{\pi}\bigg)_3=1\bigg\},\\ A_{\omega}:&=\bigg\{0<x<p/2: \bigg(\frac{x}{\pi}\bigg)_3=\omega\bigg\},\\ A_{\omega^2}:&=\bigg\{0<x<p/2: \bigg(\frac{x}{\pi}\bigg)_3=\omega^2\bigg\}. \end{align*} $$
For the following result, recall that
$\mathfrak {p} = \pi \Bbb Z[\omega ]$
) and
$\alpha _p$
and
$\gamma _p$
were defined in (1.3) and (1.4).
Lemma 2.3. Let
$p\equiv 7\bmod {12}$
be a prime.
-
(i) We have
$$ \begin{align*}\prod_{x\in A_1}x\equiv(-1)^{1+\alpha_p}\bmod p.\end{align*} $$
-
(ii) If
then
$$ \begin{align*}\beta_p:=\bigg|\bigg\{0<x<p/2: \bigg(\frac{x}{p}\bigg)=1\ \text{and}\ \bigg(\frac{x}{\pi}\bigg)_3=\omega\bigg\}\bigg|,\end{align*} $$
$$ \begin{align*}\prod_{x\in A_{\omega}}x\equiv (-1)^{1+\beta_p}\omega^2\bmod {\mathfrak{p}}.\end{align*} $$
-
(iii) We have
$$ \begin{align*}\prod_{x\in A_{\omega^2}}x\equiv (-1)^{1+\gamma_p}\omega\bmod {\mathfrak{p}}.\end{align*} $$
Proof. (i) One can verify the following polynomial congruence:
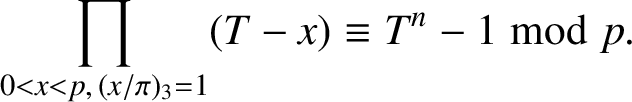$$ \begin{align*}\prod_{0<x<p,\,({x}/{\pi})_3=1}(T-x)\equiv T^{n}-1\bmod p.\end{align*} $$
Hence,
$$ \begin{align*}(-1)^{n/2}\bigg(\prod_{x\in A_1}x\bigg)^2\equiv -1\bmod p.\end{align*} $$
Since
$p\equiv 3\bmod 4$
,
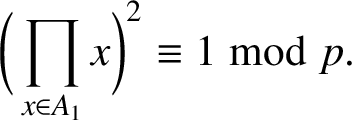$$ \begin{align*}\bigg(\prod_{x\in A_1}x\bigg)^2\equiv 1\bmod p.\end{align*} $$
Thus,
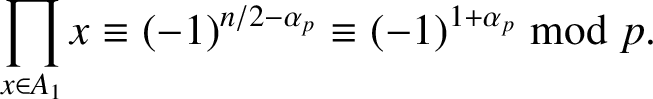$$ \begin{align*}\prod_{x\in A_1}x\equiv(-1)^{n/2-\alpha_p}\equiv(-1)^{1+\alpha_p}\bmod p.\end{align*} $$
(ii) As in (i),
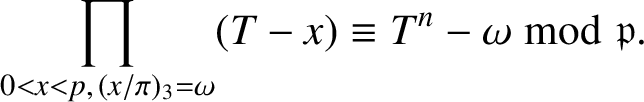$$ \begin{align*}\prod_{0<x<p,\,({x}/{\pi})_3=\omega}(T-x)\equiv T^n-\omega\bmod{\mathfrak{p}}.\end{align*} $$
Hence,
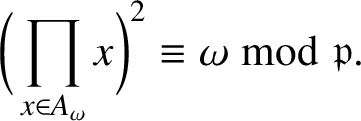$$ \begin{align*}\bigg(\prod_{x\in A_{\omega}}x\bigg)^2\equiv \omega\bmod{\mathfrak{p}}.\end{align*} $$
Noting that
$\omega =(\omega ^2)^2$
is a quadratic residue modulo
$\mathfrak {p}$
, by the definition of
$\beta _p$
,
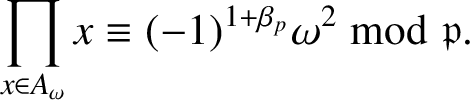$$ \begin{align*}\prod_{x\in A_{\omega}}x\equiv(-1)^{1+\beta_p}\omega^2\bmod{\mathfrak{p}}.\end{align*} $$
(iii) With essentially the same method as in (ii), one can verify (iii).
Let
$\Phi _{p-1}(T)$
be the
$(p-1)$
th cyclotomic polynomial and let
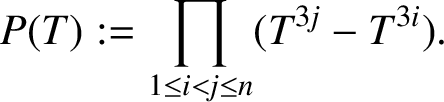$$ \begin{align*}P(T):=\prod_{1\le i<j\le n}(T^{3j}-T^{3i}).\end{align*} $$
Lemma 2.4 [Reference Wu and She11, Lemma 2.5].
Let
$G(T)$
be an integral polynomial defined by
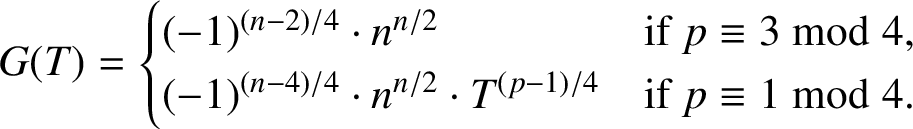$$ \begin{align*}G(T)=\begin{cases}(-1)^{(n-2)/4}\cdot n^{n/2}&\mbox{if}\ p\equiv3\bmod4, \\(-1)^{(n-4)/4}\cdot n^{n/2}\cdot T^{(p-1)/4}&\mbox{if}\ p\equiv1\bmod4.\end{cases}\end{align*} $$
Then
$\Phi _{p-1}(T)\mid (P(T)-G(T))$
.
Now we are in a position to prove our main result.
Proof of Theorem 1.1.
From the definition,
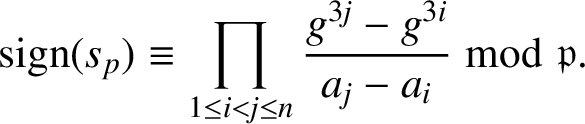$$ \begin{align*}\textrm{sign}(s_p)\equiv\prod_{1\le i<j\le n}\frac{g^{3j}-g^{3i}}{a_j-a_i}\bmod{\mathfrak{p}}.\end{align*} $$
We first consider the numerator. Since p splits completely in the cyclotomic field
$\Bbb Q(e^{2\pi i/(p-1)})$
, it follows that
$\Phi _{p-1}(T) \bmod p\Bbb Z[T]$
splits completely in
$\Bbb Z/p\Bbb Z[T]$
. Also, the set of all primitive
$(p-1)$
th roots of unity maps bijectively onto the set of all primitive
$(p-1)$
th roots of unity in the finite field
$\Bbb F_p=\Bbb Z/p\Bbb Z$
. Hence,
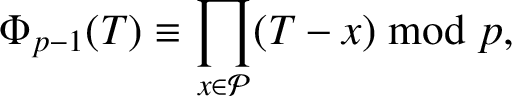$$ \begin{align} \Phi_{p-1}(T)\equiv \prod_{x\in\mathcal{P}}(T-x)\bmod{p}, \end{align} $$
where
$$ \begin{align*}\mathcal{P}:=\{0<x<p: x\ \text{is a primitive root modulo}\ p\}.\end{align*} $$
$$ \begin{align*}\prod_{1\le i<j\le n}(g^{3j}-g^{3i})=P(g)\equiv G(g)\bmod p,\end{align*} $$
that is,
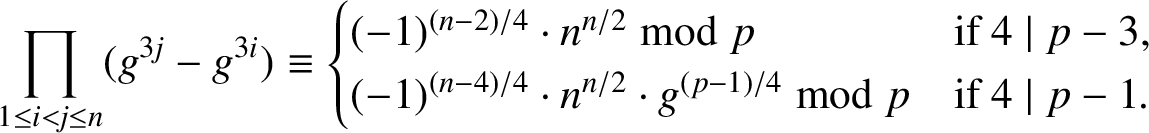$$ \begin{align} \prod_{1\le i<j\le n}(g^{3j}-g^{3i})\equiv \begin{cases}(-1)^{(n-2)/4}\cdot n^{n/2}\bmod p&\mbox{if}\ 4\mid p-3, \\(-1)^{(n-4)/4}\cdot n^{n/2}\cdot g^{(p-1)/4}\bmod p&\mbox{if}\ 4\mid p-1.\end{cases} \end{align} $$
By (2.4), for any
$g'\in \mathcal {P}$
,
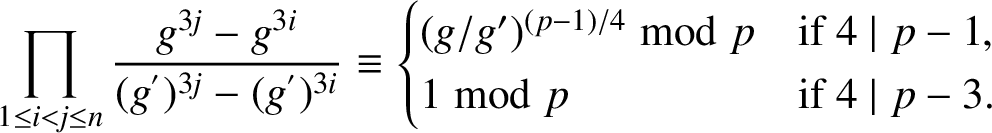$$ \begin{align*}\prod_{1\le i<j\le n}\frac{g^{3j}-g^{3i}}{(g^{'})^{3j}-(g^{'})^{3i}}\equiv \begin{cases} (g/g')^{{(p-1)}/{4}}\bmod p &\mbox{if}\ 4\mid p-1,\\ 1 \bmod p&\mbox{if} \ 4\mid p-3. \end{cases}\end{align*} $$
If
$p\equiv 1\bmod 4$
, this implies that
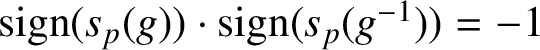$\text {sign}(s_p(g))\cdot \text {sign}(s_p(g^{-1}))=-1$
and so
$$ \begin{align*}|\{g\in\mathcal{P}: \textrm{sign}(s_p(g))=1\}|=|\{g\in\mathcal{P}: \textrm{sign}(s_p(g))=-1\}|.\end{align*} $$
If
$p\equiv 3\bmod 4$
, it is clear that
$\text {sign}(s_p(g))$
is independent of the choice of g.
We now consider the denominator and assume that
$p\equiv 3\bmod 4$
. From the definition of
$r_k$
in (2.1), it is clear that
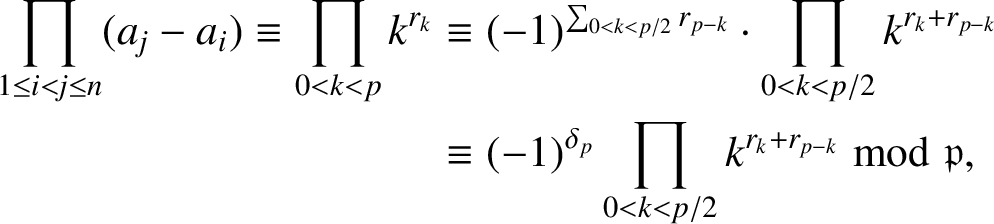$$ \begin{align*} \prod_{1\le i<j\le n}(a_j-a_i)\equiv \prod_{0<k<p}k^{r_k}&\equiv(-1)^{\sum_{0<k<p/2}r_{p-k}}\cdot\prod_{0<k<p/2}k^{r_k+r_{p-k}}\\ &\equiv(-1)^{\delta_p}\prod_{0<k<p/2}k^{r_k+r_{p-k}}\bmod {\mathfrak{p}}, \end{align*} $$
where
$\delta _p$
is defined in (1.2) and the last congruence follows from Lemma 2.2. From the definition of
$r_k$
, one can verify that for
$0<k<p$
,
$$ \begin{align*} r_k+r_{p-k}=N(k)/9, \end{align*} $$
where
$N(k)$
is defined in Lemma 2.1. Consequently,
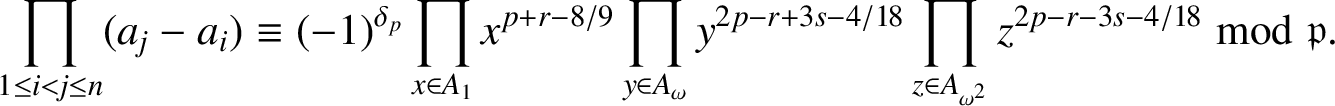$$ \begin{align*}\prod_{1\le i<j\le n}(a_j-a_i) \equiv (-1)^{\delta_p}\prod_{x\in A_1}x^{{p+r-8}/{9}}\prod_{y\in A_{\omega}}y^{{2p-r+3s-4}/{18}}\prod_{z\in A_{\omega^2}}z^{{2p-r-3s-4}/{18}} \bmod \mathfrak{p}.\end{align*} $$
By Lemma 2.3,
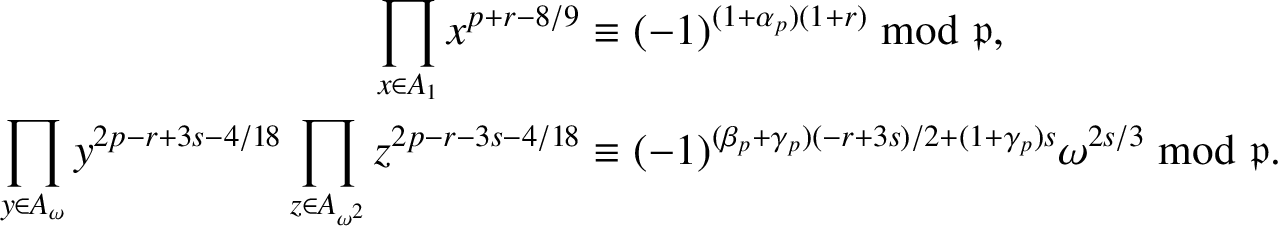$$ \begin{align*} \prod_{x\in A_1}x^{{p+r-8}/{9}} &\equiv(-1)^{(1+\alpha_p)(1+r)}\bmod {\mathfrak{p}}, \\ \prod_{y\in A_{\omega}}y^{{2p-r+3s-4}/{18}}\prod_{z\in A_{\omega^2}}z^{{2p-r-3s-4}/{18}} &\equiv (-1)^{(\beta_p+\gamma_p)(-r+3s)/2+(1+\gamma_p)s}\omega^{2s/3}\bmod{\mathfrak{p}}. \end{align*} $$
Note that
$$ \begin{align*}\alpha_p+\beta_p+\gamma_p=|\{0<x<p/2: x\ \text{is a quadratic residue modulo}\ p\}|.\end{align*} $$
By the class number formula of
$\Bbb Q(\sqrt {-p})$
(see [Reference Borevich and Shafarevich2, Theorem 4, page 346]),
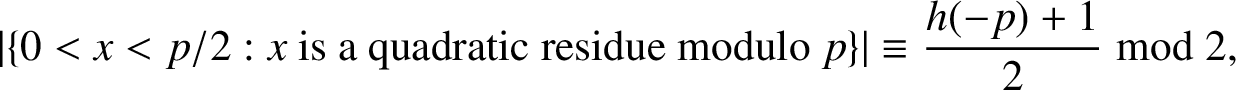$$ \begin{align*}|\{0<x<p/2: x\ \text{is a quadratic residue modulo}\ p\}|\equiv \frac{h(-p)+1}{2}\bmod 2,\end{align*} $$
where
$h(-p)$
is the class number of
$\Bbb Q(\sqrt {-p})$
. Thus,
$$ \begin{align} \prod_{1\le i<j\le n}(a_j-a_i) \equiv (-1)^{\delta_p+(1+\alpha_p)(1+r)+(h(-p)+1-2\alpha_p)(2-r+3s)/4+s(1+\gamma_p)}\omega^{2s/3}\ \text{mod}\ \mathfrak{p}. \end{align} $$
By (2.4),
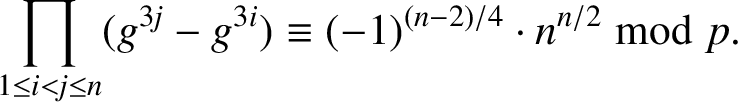$$ \begin{align} \prod_{1\le i<j\le n}(g^{3j}-g^{3i})\equiv (-1)^{(n-2)/4}\cdot n^{n/2}\bmod p. \end{align} $$
By the result in [Reference Cox4, Exercise 4.15]),
$3$
is a cubic residue modulo p if and only if the equation
$4p=X^2+243Y^2$
has integral solutions. With our notation in (1.1), this is equivalent to
$s\equiv 0\bmod 9$
. We now divide the remaining proof into two cases.
Case I:
$3$
is not a cubic residue modulo p. Since
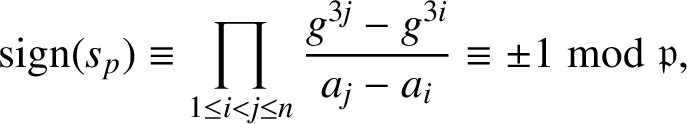$$ \begin{align*}\textrm{sign}(s_p)\equiv\prod_{1\le i<j\le n}\frac{g^{3j}-g^{3i}}{a_j-a_i}\equiv\pm1\bmod{\mathfrak{p}},\end{align*} $$
we must have
$n^{{n}/{2}}\equiv \varepsilon \omega ^{2s/3}$
for some
$\varepsilon \in \{\pm 1\}$
. Hence,
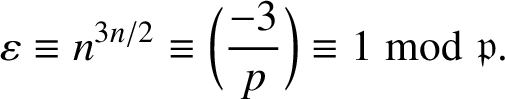$$ \begin{align*}\varepsilon\equiv n^{3n/2}\equiv\bigg(\frac{-3}{p}\bigg)\equiv1\bmod {\mathfrak{p}}.\end{align*} $$
Combining this with (2.5) and (2.6),
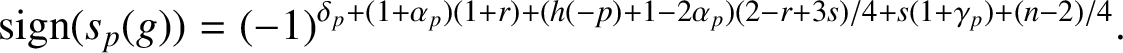$$ \begin{align*}\textrm{sign}(s_p(g))= (-1)^{\delta_p+(1+\alpha_p)(1+r)+(h(-p)+1-2\alpha_p)(2-r+3s)/4+s(1+\gamma_p)+(n-2)/4}.\end{align*} $$
Case II:
$3$
is a cubic residue modulo p. In this case,
$n^{n/2}=\pm 1$
and hence
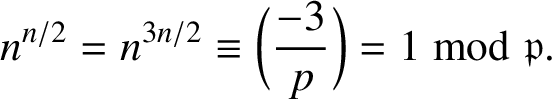$$ \begin{align*}n^{n/2}=n^{3n/2}\equiv \bigg(\frac{-3}{p}\bigg)=1\bmod{\mathfrak{p}}.\end{align*} $$
Combining this with (2.5) and (2.6),
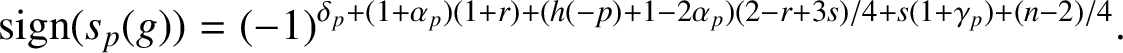$$ \begin{align*}\textrm{sign}(s_p(g))=(-1)^{\delta_p+(1+\alpha_p)(1+r)+(h(-p)+1-2\alpha_p)(2-r+3s)/4+s(1+\gamma_p)+(n-2)/4}.\end{align*} $$
This completes the proof.
Acknowledgements
We thank the referee for helpful comments. The first author would like to thank Professor Hao Pan for his encouragement.
