Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-02-06T17:16:17.658Z Has data issue: false hasContentIssue false
  • English
  • Français

CHARACTER GRAPHS WITH NONBIPARTITE HAMILTONIAN COMPLEMENT

Part of: Representation theory of groups Graph theory

Published online by Cambridge University Press:  25 November 2019

MAHDI EBRAHIMI Open the ORCID record for MAHDI EBRAHIMI [Opens in a new window]
MAHDI EBRAHIMI*
Affiliation:
School of Mathematics,Institute for Research in Fundamental Sciences (IPM), PO Box 19395-5746, Tehran, Iran email m.ebrahimi.math@ipm.ir
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a finite group 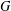$G$, let 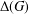$\unicode[STIX]{x1D6E5}(G)$ denote the character graph built on the set of degrees of the irreducible complex characters of 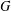$G$. In this paper, we obtain a necessary and sufficient condition which guarantees that the complement of the character graph 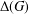$\unicode[STIX]{x1D6E5}(G)$ of a finite group 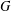$G$ is a nonbipartite Hamiltonian graph.

Keywords

character graphcharacter degreeHamiltonian graph

MSC classification

Primary: 20C15: Ordinary representations and characters
Secondary: 05C45: Eulerian and Hamiltonian graphs 05C25: Graphs and abstract algebra (groups, rings, fields, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 1 , August 2020 , pp. 91 - 95
Check for updates
Copyright
© 2019 Australian Mathematical Publishing Association Inc.

Footnotes

This research was supported in part by a grant from the School of Mathematics, Institute for Research in Fundamental Sciences (IPM).

References

Akhlaghi, Z., Casolo, C., Dolfi, S., Pacifici, E. and Sanus, L., ‘On the character degree graph of finite groups’, Ann. Mat. Pura Appl., to appear, 20 pages.Google Scholar
Ebrahimi, M., Iranmanesh, A. and Hosseinzadeh, M. A., ‘Hamiltonian character graphs’, J. Algebra 428 (2015), 54–66.CrossRefGoogle Scholar
Huppert, B., Endliche Gruppen I, Die Grundlehren der mathematischen Wissenschaften, 134 (Springer, Berlin–New York, 1967).10.1007/978-3-642-64981-3CrossRefGoogle Scholar
Huppert, B., ‘Some simple groups which are determined by the set of their character degrees I’, Illinois J. Math. 44 (2000), 828–842.CrossRefGoogle Scholar
Isaacs, I. M., Character Theory of Finite Groups (Academic Press, San Diego, CA, 1976).Google Scholar
Lewis, M. L., ‘An overview of graphs associated with character degrees and conjugacy class sizes in finite groups’, Rocky Mountain J. Math. 38(1) (2008), 175–211.CrossRefGoogle Scholar
Lewis, M. L. and White, D. L., ‘Connectedness of degree graphs of non-solvable groups’, J. Algebra 266(1) (2003), 51–76.10.1016/S0021-8693(03)00346-6CrossRefGoogle Scholar
Lewis, M. L. and White, D. L., ‘Non-solvable groups with no prime dividing three character degrees’, J. Algebra 336 (2011), 158–183.CrossRefGoogle Scholar
Manz, O., Staszewski, R. and Willems, W., ‘On the number of components of a graph related to character degrees’, Proc. Amer. Math. Soc. 103(1) (1988), 31–37.CrossRefGoogle Scholar
Sayanjali, Z., Akhlaghi, Z. and Khosravi, B., ‘On the regularity of character degree graphs’, Bull. Aust. Math. Soc. 100(3) (2019), 428–433.10.1017/S0004972719000315CrossRefGoogle Scholar
Tong-Viet, H. P., ‘Groups whose prime graphs have no triangles’, J. Algebra 378 (2013), 196–206.CrossRefGoogle Scholar
White, D. L., ‘Degree graphs of simple linear and unitary groups’, Comm. Algebra 34(8) (2006), 2907–2921.10.1080/00927870600639419CrossRefGoogle Scholar