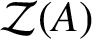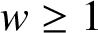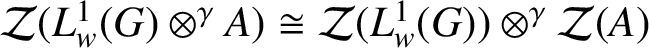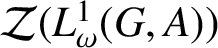1 Introduction
For two algebras A and B,
![]() $\mathcal {Z}(A) \otimes \mathcal {Z}(B) = \mathcal {Z}(A \otimes B)$
, where
$\mathcal {Z}(A) \otimes \mathcal {Z}(B) = \mathcal {Z}(A \otimes B)$
, where
![]() $\mathcal {Z}(C)$
denotes the centre of algebra C. If A and B are Banach algebras, then it is natural to ask whether
$\mathcal {Z}(C)$
denotes the centre of algebra C. If A and B are Banach algebras, then it is natural to ask whether
![]() $\mathcal {Z}(A \otimes ^{\gamma } B)$
is isometrically isomorphic to
$\mathcal {Z}(A \otimes ^{\gamma } B)$
is isometrically isomorphic to
![]() $\mathcal {Z}(A) \otimes ^{\gamma } \mathcal {Z}(B)$
,
$\mathcal {Z}(A) \otimes ^{\gamma } \mathcal {Z}(B)$
,
![]() $\otimes ^{\gamma }$
being the Banach space projective tensor product. This is known to be true if A and B are
$\otimes ^{\gamma }$
being the Banach space projective tensor product. This is known to be true if A and B are
![]() $C^ \ast $
-algebras (see [Reference Gupta and Jain7, Theorem 5.1]) and if
$C^ \ast $
-algebras (see [Reference Gupta and Jain7, Theorem 5.1]) and if
![]() $A = B = L^{1}(G)$
for any
$A = B = L^{1}(G)$
for any
![]() $\textbf {[FC]}^-$
group G (see [Reference Shepelska and Zhang18, Lemma 2.1]). Note that [Reference Shepelska and Zhang18] generalises the results of [Reference Alaghmandan, Choi and Samei1, Reference Azimifard, Samei and Spronk2] and in these three papers the major focus is on studying amenability and weak amenability properties. The idea behind the proofs given in [Reference Azimifard, Samei and Spronk2, Reference Shepelska and Zhang18] is to use a projection from
$\textbf {[FC]}^-$
group G (see [Reference Shepelska and Zhang18, Lemma 2.1]). Note that [Reference Shepelska and Zhang18] generalises the results of [Reference Alaghmandan, Choi and Samei1, Reference Azimifard, Samei and Spronk2] and in these three papers the major focus is on studying amenability and weak amenability properties. The idea behind the proofs given in [Reference Azimifard, Samei and Spronk2, Reference Shepelska and Zhang18] is to use a projection from
![]() $L^{1}(G)$
onto
$L^{1}(G)$
onto
![]() $\mathcal {Z}(L^{1}(G))$
. An ingenious construction of one such projection is given in [Reference Shepelska and Zhang18] which is somewhat different from the usual averaging technique used when working with
$\mathcal {Z}(L^{1}(G))$
. An ingenious construction of one such projection is given in [Reference Shepelska and Zhang18] which is somewhat different from the usual averaging technique used when working with
![]() $\textbf {[FIA]}^-$
groups. We used this technique in [Reference Gupta, Jain and Talwar8, Theorem 4.13] and gave an affirmative answer to the question about
$\textbf {[FIA]}^-$
groups. We used this technique in [Reference Gupta, Jain and Talwar8, Theorem 4.13] and gave an affirmative answer to the question about
![]() ${\mathcal {Z}(A \otimes ^{\gamma } B)}$
if A is a unital Banach algebra and
${\mathcal {Z}(A \otimes ^{\gamma } B)}$
if A is a unital Banach algebra and
![]() $B = L^{1}(G)$
, for specific classes of groups G. Analogues of results on
$B = L^{1}(G)$
, for specific classes of groups G. Analogues of results on
![]() $\mathcal {Z}(L^{1}(G))$
by Mosak [Reference Mosak12, Reference Mosak13] were also obtained in [Reference Gupta, Jain and Talwar8] for the centre
$\mathcal {Z}(L^{1}(G))$
by Mosak [Reference Mosak12, Reference Mosak13] were also obtained in [Reference Gupta, Jain and Talwar8] for the centre
![]() $\mathcal {Z}(L^{1}(G,A))$
of generalised group algebras.
$\mathcal {Z}(L^{1}(G,A))$
of generalised group algebras.
In this paper we generalise all the results discussed in the preceding paragraph, giving relatively simpler proofs, by working in the more general setting of A-valued Beurling algebras
![]() $L^{1}_{\omega }(G,A)$
. In particular, we drop some restrictions on G and A as imposed in [Reference Gupta, Jain and Talwar8, Lemma 4.4 and Theorems 4.7 and 4.13] and obtain a similar description for
$L^{1}_{\omega }(G,A)$
. In particular, we drop some restrictions on G and A as imposed in [Reference Gupta, Jain and Talwar8, Lemma 4.4 and Theorems 4.7 and 4.13] and obtain a similar description for
![]() $\mathcal {Z}(L^{1}_{\omega }(G,A))$
. After a series of technical and interesting results, we present Theorem 2.10 as the main result of this paper. It claims that
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
. After a series of technical and interesting results, we present Theorem 2.10 as the main result of this paper. It claims that
![]() $\mathcal {Z}(L^{1}_{w}(G) \otimes ^{\gamma } A) \cong \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A)$
when G is an
$\mathcal {Z}(L^{1}_{w}(G) \otimes ^{\gamma } A) \cong \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A)$
when G is an
![]() $\mathbf {[IN]}$
group (a group having a neighbourhood of the identity which is invariant under inner automorphisms of G), A has a bounded
$\mathbf {[IN]}$
group (a group having a neighbourhood of the identity which is invariant under inner automorphisms of G), A has a bounded
![]() $\mathcal {Z}(A)$
-approximate identity (see Definition 2.5) and the weight w is either constant on conjugacy classes or greater than or equal to 1 throughout G. As an application, we discuss some structure-theoretic questions for
$\mathcal {Z}(A)$
-approximate identity (see Definition 2.5) and the weight w is either constant on conjugacy classes or greater than or equal to 1 throughout G. As an application, we discuss some structure-theoretic questions for
![]() $\mathcal {Z}(L^{1}_{\omega }(G,A))$
.
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
.
2 Different identifications of centre
Let G be a locally compact group with identity e. Then
![]() $(G, \mathcal {B}, m)$
is a measure space, where
$(G, \mathcal {B}, m)$
is a measure space, where
![]() $\mathcal {B}$
is the Borel
$\mathcal {B}$
is the Borel
![]() $\sigma $
-algebra and
$\sigma $
-algebra and
![]() $m$
is the left Haar measure. A weight w on G is a measurable positive function such that
$m$
is the left Haar measure. A weight w on G is a measurable positive function such that
![]() $w(xy) \leq w(x)w(y)$
for every
$w(xy) \leq w(x)w(y)$
for every
![]() $x,y \in G$
. In view of [Reference Reiter and Stegeman14, Theorem 3.7.5], w can be assumed to be continuous. For any Banach algebra A, consider the set
$x,y \in G$
. In view of [Reference Reiter and Stegeman14, Theorem 3.7.5], w can be assumed to be continuous. For any Banach algebra A, consider the set
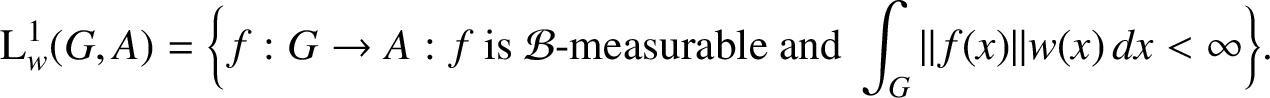 $$ \begin{align*}\text{L}^{1}_{w}(G,A)= \bigg\{ f: G \to A : f \text{ is }\mathcal{B}\text{-measurable and }\int_{G} \| f(x)\|w(x) \,dx < \infty \bigg\}.\end{align*} $$
$$ \begin{align*}\text{L}^{1}_{w}(G,A)= \bigg\{ f: G \to A : f \text{ is }\mathcal{B}\text{-measurable and }\int_{G} \| f(x)\|w(x) \,dx < \infty \bigg\}.\end{align*} $$
Let
![]() $f,g \in \text {L}^{1}_{w}(G,A)$
. Then
$f,g \in \text {L}^{1}_{w}(G,A)$
. Then
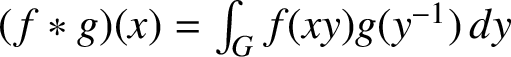 $(f \ast g)(x) = \int _{G} f(xy)g(y^{-1}) \,dy$
and
$(f \ast g)(x) = \int _{G} f(xy)g(y^{-1}) \,dy$
and
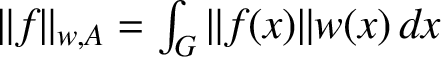 $\|f \|_{w,A} = \int _{G} \| f(x)\|w(x) \,dx$
define a multiplication and a seminorm on
$\|f \|_{w,A} = \int _{G} \| f(x)\|w(x) \,dx$
define a multiplication and a seminorm on
![]() $\text {L}^{1}_{w}(G,A)$
, respectively. When
$\text {L}^{1}_{w}(G,A)$
, respectively. When
![]() $A = \mathbb {C}$
, we write
$A = \mathbb {C}$
, we write
![]() $\|f\|_{1,w}$
for
$\|f\|_{1,w}$
for
![]() $\|f \|_{w,A}$
. The set
$\|f \|_{w,A}$
. The set
![]() $L^{1}_{\omega }(G,A)$
of all equivalence classes determined by this seminorm becomes a Banach algebra known as the A-valued Beurling algebra. As is customary, we will treat the elements of
$L^{1}_{\omega }(G,A)$
of all equivalence classes determined by this seminorm becomes a Banach algebra known as the A-valued Beurling algebra. As is customary, we will treat the elements of
![]() $L^{1}_{\omega }(G,A)$
as functions. For any
$L^{1}_{\omega }(G,A)$
as functions. For any
![]() $a \in A$
,
$a \in A$
,
![]() $x,y \in G$
and
$x,y \in G$
and
![]() $f \in L^{1}_{\omega }(G,A)$
, define
$f \in L^{1}_{\omega }(G,A)$
, define
![]() $(x \cdot f)(y) = f(x^{-1}y)$
,
$(x \cdot f)(y) = f(x^{-1}y)$
,
![]() $(f \cdot x)(y)= f(yx)$
,
$(f \cdot x)(y)= f(yx)$
,
![]() $(fa)(x) = f(x)a$
and
$(fa)(x) = f(x)a$
and
![]() $(af)(x) = a f(x)$
. It is easy to check that all these elements belong to
$(af)(x) = a f(x)$
. It is easy to check that all these elements belong to
![]() $L^{1}_{\omega }(G,A)$
.
$L^{1}_{\omega }(G,A)$
.
A part of the following result is proved in [Reference Dedania and Kansagara4, Lemma 2.7] and an analogous statement for
![]() $L^{1}(G,A)$
is proved in [Reference Gupta, Jain and Talwar8, Lemmas 3.2 and 3.3]. The fact that w is locally bounded [Reference Kaniuth9, Lemma 1.3.3] along with some necessary changes in that proof can be used to obtain the following result.
$L^{1}(G,A)$
is proved in [Reference Gupta, Jain and Talwar8, Lemmas 3.2 and 3.3]. The fact that w is locally bounded [Reference Kaniuth9, Lemma 1.3.3] along with some necessary changes in that proof can be used to obtain the following result.
Lemma 2.1. Let
![]() $f \in L^{1}_{\omega }(G,A)$
and
$f \in L^{1}_{\omega }(G,A)$
and
![]() $y \in G$
.
$y \in G$
.
-
(1) The maps
 $G \ni x \to x \cdot f, f \cdot x \in L^{1}_{\omega }(G,A)$
are continuous.
$G \ni x \to x \cdot f, f \cdot x \in L^{1}_{\omega }(G,A)$
are continuous. -
(2)
 $\| y \cdot f\|_{w,A} \leq w(y) \|f\|_{w,A}$
and
$\| y \cdot f\|_{w,A} \leq w(y) \|f\|_{w,A}$
and
 $\| f \cdot y \|_{w,A} \leq w(y^{-1})\Delta (y^{-1}) \|f\|_{w,A}$
.
$\| f \cdot y \|_{w,A} \leq w(y^{-1})\Delta (y^{-1}) \|f\|_{w,A}$
.
We next provide an analogue of the characterisation of the centre of a convolution algebra as given in [Reference Mosak13, Proposition 1.2]. If f is a function from G to A, we define
![]() $|f|(x):= \|f(x)\|$
for every
$|f|(x):= \|f(x)\|$
for every
![]() $x \in G$
.
$x \in G$
.
Lemma 2.2. Let G be a locally compact group and A be a Banach algebra. Then
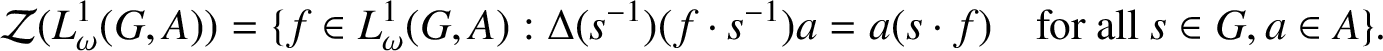 $$ \begin{align*}\mathcal{Z}(L^{1}_{\omega}(G,A)) = \{ f \in L^{1}_{\omega}(G,A) : \Delta(s^{-1})(f\cdot s^{-1})a = a(s\cdot f )\quad \mbox{for all } s \in G, a \in A\}.\end{align*} $$
$$ \begin{align*}\mathcal{Z}(L^{1}_{\omega}(G,A)) = \{ f \in L^{1}_{\omega}(G,A) : \Delta(s^{-1})(f\cdot s^{-1})a = a(s\cdot f )\quad \mbox{for all } s \in G, a \in A\}.\end{align*} $$
Proof. Let
![]() $f \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
. For any
$f \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
. For any
![]() $a \in A$
,
$a \in A$
,
![]() $s \in G$
and any compact symmetric set
$s \in G$
and any compact symmetric set
![]() $U \in \mathcal {B}$
, write
$U \in \mathcal {B}$
, write
![]() $a_{sU} = a \chi _{sU}$
. It follows from local boundedness of w that
$a_{sU} = a \chi _{sU}$
. It follows from local boundedness of w that
![]() $a_{sU} \in L^{1}_{\omega }(G,A)$
. Let
$a_{sU} \in L^{1}_{\omega }(G,A)$
. Let
![]() $\epsilon>0$
. It suffices to show that
$\epsilon>0$
. It suffices to show that
![]() $\|\Delta (s^{-1})(f\cdot s^{-1})a - a(s\cdot f )\|_{w,A} < \epsilon $
. Following the calculations in the proof of [Reference Gupta, Jain and Talwar8, Theorem 3.4],
$\|\Delta (s^{-1})(f\cdot s^{-1})a - a(s\cdot f )\|_{w,A} < \epsilon $
. Following the calculations in the proof of [Reference Gupta, Jain and Talwar8, Theorem 3.4],
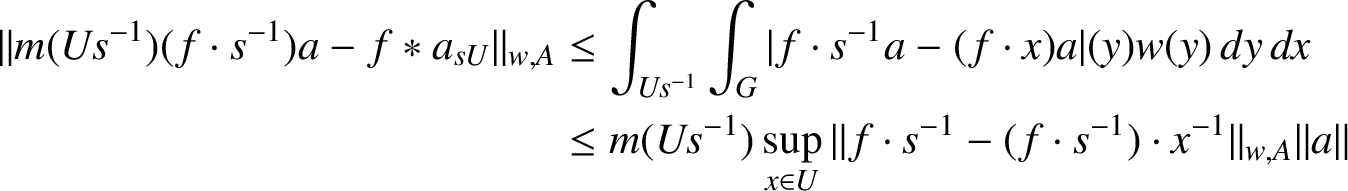 $$ \begin{align*} \| m(Us^{-1}) (f \cdot s^{-1}) a - f \ast a_{sU} \|_{w,A} & \leq \int_{U s^{-1}} \int_{G} | f \cdot s^{-1} a - (f \cdot x) a |(y)w(y) \,dy\, dx \\ & \leq m(Us^{-1}) \sup_{x \in U} \| f \cdot s^{-1} - (f \cdot s^{-1}) \cdot x^{-1}\|_{w,A} \|a\| \end{align*} $$
$$ \begin{align*} \| m(Us^{-1}) (f \cdot s^{-1}) a - f \ast a_{sU} \|_{w,A} & \leq \int_{U s^{-1}} \int_{G} | f \cdot s^{-1} a - (f \cdot x) a |(y)w(y) \,dy\, dx \\ & \leq m(Us^{-1}) \sup_{x \in U} \| f \cdot s^{-1} - (f \cdot s^{-1}) \cdot x^{-1}\|_{w,A} \|a\| \end{align*} $$
and
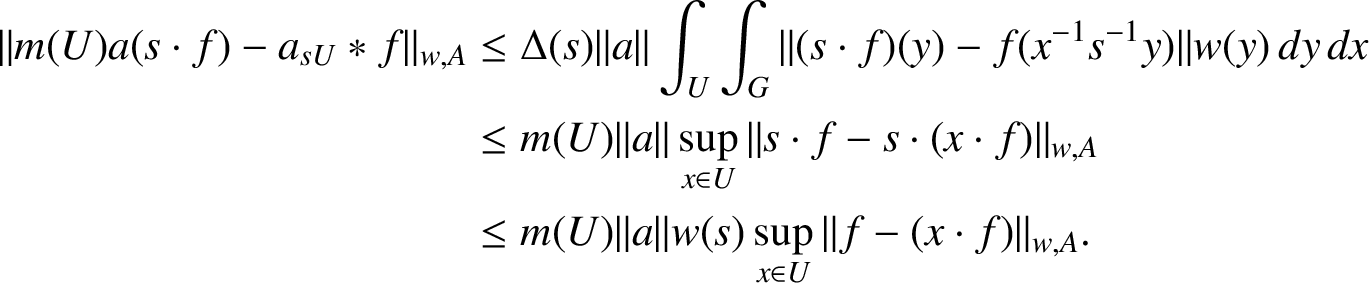 $$ \begin{align*} \|m(U) a(s \cdot f) - a_{sU} \ast f \|_{w,A} & \leq \Delta(s) \| a\| \int_{U} \int_{G} \| (s \cdot f)(y) - f(x^{-1}s^{-1} y) \|w(y) \,dy\, dx \\ &\leq m(U) \|a\| \sup_{x \in U} \| s \cdot f - s \cdot (x \cdot f)\|_{w,A}\\ & \leq m(U) \|a\| w(s) \sup_{x \in U} \|f - (x \cdot f)\|_{w,A}. \end{align*} $$
$$ \begin{align*} \|m(U) a(s \cdot f) - a_{sU} \ast f \|_{w,A} & \leq \Delta(s) \| a\| \int_{U} \int_{G} \| (s \cdot f)(y) - f(x^{-1}s^{-1} y) \|w(y) \,dy\, dx \\ &\leq m(U) \|a\| \sup_{x \in U} \| s \cdot f - s \cdot (x \cdot f)\|_{w,A}\\ & \leq m(U) \|a\| w(s) \sup_{x \in U} \|f - (x \cdot f)\|_{w,A}. \end{align*} $$
So
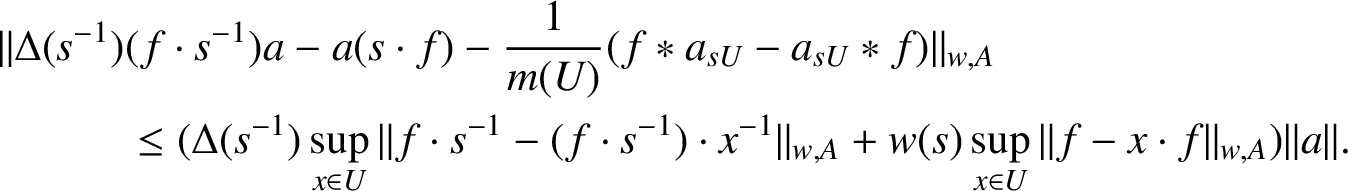 $$ \begin{align*} \| \Delta(s^{-1}) & (f\cdot s^{-1})a - a(s\cdot f ) - \frac{1}{m(U)} (f \ast a_{sU} - a_{sU} \ast f)\|_{w,A} \\& \leq (\Delta(s^{-1})\sup_{x \in U} \| f \cdot s^{-1} - (f \cdot s^{-1}) \cdot x^{-1}\|_{w,A} + w(s) \sup_{x \in U} \| f - x \cdot f\|_{w,A}) \|a\|. \end{align*} $$
$$ \begin{align*} \| \Delta(s^{-1}) & (f\cdot s^{-1})a - a(s\cdot f ) - \frac{1}{m(U)} (f \ast a_{sU} - a_{sU} \ast f)\|_{w,A} \\& \leq (\Delta(s^{-1})\sup_{x \in U} \| f \cdot s^{-1} - (f \cdot s^{-1}) \cdot x^{-1}\|_{w,A} + w(s) \sup_{x \in U} \| f - x \cdot f\|_{w,A}) \|a\|. \end{align*} $$
The desired result now follows from Lemma 2.1.
For the converse, it is sufficient to prove that
![]() $f \ast g = g \ast f$
for every continuous function g with compact support. This can be proved exactly as in [Reference Gupta, Jain and Talwar8, Theorem 3.4], by showing that in every neighbourhood of
$f \ast g = g \ast f$
for every continuous function g with compact support. This can be proved exactly as in [Reference Gupta, Jain and Talwar8, Theorem 3.4], by showing that in every neighbourhood of
![]() $f \ast g - g \ast f$
there is an element which belongs to the set
$f \ast g - g \ast f$
there is an element which belongs to the set
![]() $\text {span}\{ \Delta (s)^{-1} (f \cdot s^{-1}) a - a(s \cdot f): a \in A, s \in G\}$
.
$\text {span}\{ \Delta (s)^{-1} (f \cdot s^{-1}) a - a(s \cdot f): a \in A, s \in G\}$
.
With this in hand, the following analogue of [Reference Gupta, Jain and Talwar8, Lemma 4.3] can be given with a few adjustments in its proof.
Lemma 2.3. Let G be a locally compact group and A be a Banach algebra. Then
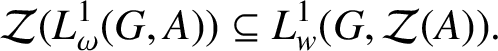 $$ \begin{align*} \mathcal{Z}(L^{1}_{\omega}(G,A)) \subseteq L^{1}_{w}(G, \mathcal{Z}(A)). \end{align*} $$
$$ \begin{align*} \mathcal{Z}(L^{1}_{\omega}(G,A)) \subseteq L^{1}_{w}(G, \mathcal{Z}(A)). \end{align*} $$
Proof. Consider a nonzero element f in
![]() $\mathcal {Z}(L^{1}_{\omega }(G,A))$
. Suppose there exists a Borel set E of positive and finite measure such that
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
. Suppose there exists a Borel set E of positive and finite measure such that
![]() $f(x) \notin \mathcal {Z}(A)$
for every
$f(x) \notin \mathcal {Z}(A)$
for every
![]() $x \in E$
.
$x \in E$
.
By Lemma 2.2,
![]() $f a = a f$
for every
$f a = a f$
for every
![]() $a \in A$
. Let
$a \in A$
. Let
![]() $\mathcal {B}_{E}$
denote the
$\mathcal {B}_{E}$
denote the
![]() $\sigma $
-algebra consisting of all Borel sets contained in E. Then, for any
$\sigma $
-algebra consisting of all Borel sets contained in E. Then, for any
![]() $F \in \mathcal {B}_{E}$
,
$F \in \mathcal {B}_{E}$
,
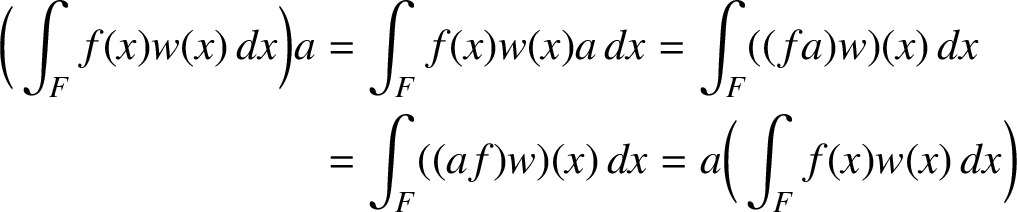 $$ \begin{align*} \bigg( \int_{F} f(x)w(x)\, dx\bigg)a &= \int_{F} f(x)w(x)a\, dx = \int_{F} ((fa)w)(x)\, dx\\ & = \int_{F} ((af)w)(x)\, dx = a \bigg(\int_{F} f(x)w(x)\, dx\bigg) \end{align*} $$
$$ \begin{align*} \bigg( \int_{F} f(x)w(x)\, dx\bigg)a &= \int_{F} f(x)w(x)a\, dx = \int_{F} ((fa)w)(x)\, dx\\ & = \int_{F} ((af)w)(x)\, dx = a \bigg(\int_{F} f(x)w(x)\, dx\bigg) \end{align*} $$
for all
![]() $a\in A$
, that is,
$a\in A$
, that is,
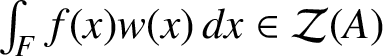 $\int _{F} f(x)w(x) \,dx \in \mathcal {Z}(A)$
for all
$\int _{F} f(x)w(x) \,dx \in \mathcal {Z}(A)$
for all
![]() $F \in \mathcal {B}_{E}$
. Define
$F \in \mathcal {B}_{E}$
. Define
![]() $H: \mathcal {B}_{E} \rightarrow \mathcal {Z}(A)$
by
$H: \mathcal {B}_{E} \rightarrow \mathcal {Z}(A)$
by
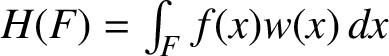 $H(F) = \int _{F} f(x)w(x) \,dx$
. Then H is a
$H(F) = \int _{F} f(x)w(x) \,dx$
. Then H is a
![]() $ m$
-continuous (that is,
$ m$
-continuous (that is,
![]() $\lim _{m(F) \to 0}H(F) = 0$
) vector measure of bounded variation [Reference Diestel and Uhl5, Theorem II.2.4]. Thus, by [Reference Diestel and Uhl5, Corollary III.2.5], there exists a
$\lim _{m(F) \to 0}H(F) = 0$
) vector measure of bounded variation [Reference Diestel and Uhl5, Theorem II.2.4]. Thus, by [Reference Diestel and Uhl5, Corollary III.2.5], there exists a
![]() $g \in L^{1}(E,\mathcal {Z}(A))$
such that
$g \in L^{1}(E,\mathcal {Z}(A))$
such that
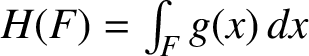 $H(F) = \int _{F} g(x) \,dx$
for all
$H(F) = \int _{F} g(x) \,dx$
for all
![]() $F \in \mathcal {B}_{E}$
. This shows that
$F \in \mathcal {B}_{E}$
. This shows that
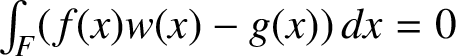 $\int _{F} (f(x)w(x) - g(x)) \,dx = 0$
for every
$\int _{F} (f(x)w(x) - g(x)) \,dx = 0$
for every
![]() $F \in \mathcal {B}_{E}$
, so that
$F \in \mathcal {B}_{E}$
, so that
![]() $fw = g$
almost everywhere on E by [Reference Diestel and Uhl5, Corollary II.2.5]. Since
$fw = g$
almost everywhere on E by [Reference Diestel and Uhl5, Corollary II.2.5]. Since
![]() $g(E) \subseteq \mathcal {Z}(A)$
and
$g(E) \subseteq \mathcal {Z}(A)$
and
![]() $w(E) \subseteq (0, \infty )$
, this contradicts the existence of E. Hence,
$w(E) \subseteq (0, \infty )$
, this contradicts the existence of E. Hence,
![]() $f(x) \in \mathcal {Z}(A)$
for almost every
$f(x) \in \mathcal {Z}(A)$
for almost every
![]() $x \in G$
.
$x \in G$
.
Remark 2.4. Unlike
![]() $L^{1}(G)$
[Reference Mosak12], it can be seen from Lemma 2.3 that for
$L^{1}(G)$
[Reference Mosak12], it can be seen from Lemma 2.3 that for
![]() $\mathcal {Z}(L^{1}_{\omega }(G,A))$
to be nontrivial it is not sufficient that G be an
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
to be nontrivial it is not sufficient that G be an
![]() $\mathbf {[IN]}$
group. This is because
$\mathbf {[IN]}$
group. This is because
![]() $\mathcal {Z}(A)$
might be trivial. However, if G is an
$\mathcal {Z}(A)$
might be trivial. However, if G is an
![]() $\mathbf {[IN]}$
group and A is a Banach algebra with nontrivial centre, then
$\mathbf {[IN]}$
group and A is a Banach algebra with nontrivial centre, then
![]() $\mathcal {Z}(L^{1}_{\omega }(G,A)) \neq \{0\}$
. To prove this, choose a compact neighbourhood E of e which is invariant under inner automorphisms. Then
$\mathcal {Z}(L^{1}_{\omega }(G,A)) \neq \{0\}$
. To prove this, choose a compact neighbourhood E of e which is invariant under inner automorphisms. Then
![]() $\chi _{E} \in \mathcal {Z}(L^{1}(G))$
[Reference Mosak12]. Since w is locally bounded, we have
$\chi _{E} \in \mathcal {Z}(L^{1}(G))$
[Reference Mosak12]. Since w is locally bounded, we have
![]() $\chi _{E} \in L^{1}_{w}(G)$
. Using the fact that G is unimodular, we obtain from Lemma 2.2 that
$\chi _{E} \in L^{1}_{w}(G)$
. Using the fact that G is unimodular, we obtain from Lemma 2.2 that
![]() $\chi _{E}a \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
for every
$\chi _{E}a \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
for every
![]() $a \in \mathcal {Z}(A)$
.
$a \in \mathcal {Z}(A)$
.
We will now present some necessary conditions for
![]() $\mathcal {Z}(L^{1}_{\omega }(G,A))$
to be nontrivial. Note that G being an
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
to be nontrivial. Note that G being an
![]() $\mathbf {[IN]}$
group is not a necessity as can be demonstrated by taking A to be a Banach algebra with trivial multiplication, in which case
$\mathbf {[IN]}$
group is not a necessity as can be demonstrated by taking A to be a Banach algebra with trivial multiplication, in which case
![]() $\mathcal {Z}(L^{1}_{\omega }(G,A)) \neq \{0\}$
no matter which group G one takes. To get rid of such pathological examples, it is usual to work with Banach algebras having a bounded approximate identity. However, we only need the following relaxed condition.
$\mathcal {Z}(L^{1}_{\omega }(G,A)) \neq \{0\}$
no matter which group G one takes. To get rid of such pathological examples, it is usual to work with Banach algebras having a bounded approximate identity. However, we only need the following relaxed condition.
Definition 2.5. A
![]() $\mathcal {Z}(A)$
-approximate identity of a Banach algebra A is a net
$\mathcal {Z}(A)$
-approximate identity of a Banach algebra A is a net
![]() $\{a_{\alpha }\}$
in A such that
$\{a_{\alpha }\}$
in A such that
![]() $a_{\alpha } a \to a$
for every
$a_{\alpha } a \to a$
for every
![]() $a \in \mathcal {Z}(A)$
. If, in addition, the net
$a \in \mathcal {Z}(A)$
. If, in addition, the net
![]() $\{a_{\alpha }\}$
is bounded, then we call it a bounded
$\{a_{\alpha }\}$
is bounded, then we call it a bounded
![]() $\mathcal {Z}(A)$
-approximate identity.
$\mathcal {Z}(A)$
-approximate identity.
Note that a Banach algebra A has a bounded
![]() $\mathcal {Z}(A)$
-approximate identity if either A or
$\mathcal {Z}(A)$
-approximate identity if either A or
![]() $\mathcal {Z}(A)$
has a left or right bounded approximate identity. From now on, the Banach algebra A will be assumed to have a bounded
$\mathcal {Z}(A)$
has a left or right bounded approximate identity. From now on, the Banach algebra A will be assumed to have a bounded
![]() $\mathcal {Z}(A)$
-approximate identity
$\mathcal {Z}(A)$
-approximate identity
![]() $\{a_{\alpha }\}$
.
$\{a_{\alpha }\}$
.
Lemma 2.6. Let G be a locally compact group and let A be a Banach algebra. If
![]() $0 \neq f \in L^{1}_{w}(G,\mathcal {Z}(A))$
, then the net
$0 \neq f \in L^{1}_{w}(G,\mathcal {Z}(A))$
, then the net
![]() $\{a_{\alpha } f\}$
in
$\{a_{\alpha } f\}$
in
![]() $L^{1}_{\omega }(G,A)$
converges to f.
$L^{1}_{\omega }(G,A)$
converges to f.
Proof. Let
![]() $\{a_{\alpha } \}$
be bounded by M. For any
$\{a_{\alpha } \}$
be bounded by M. For any
![]() $\epsilon>0$
, since
$\epsilon>0$
, since
![]() $L^{1}_{w}(G) \otimes \mathcal {Z}(A)$
is dense in
$L^{1}_{w}(G) \otimes \mathcal {Z}(A)$
is dense in
![]() $L^{1}_{w}(G,\mathcal {Z}(A))$
[Reference Samei17, Theorem 2.2], there exists
$L^{1}_{w}(G,\mathcal {Z}(A))$
[Reference Samei17, Theorem 2.2], there exists
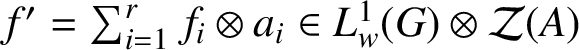 $f^{\prime } = \sum _{i=1}^{r} f_{i} \otimes a_{i} \in L^{1}_{w}(G) \otimes \mathcal {Z}(A)$
such that
$f^{\prime } = \sum _{i=1}^{r} f_{i} \otimes a_{i} \in L^{1}_{w}(G) \otimes \mathcal {Z}(A)$
such that
![]() $\| f- f^{\prime } \|_{w,A} < \epsilon $
. As
$\| f- f^{\prime } \|_{w,A} < \epsilon $
. As
![]() $a_{\alpha } a_{i} \to a_{i}$
for every
$a_{\alpha } a_{i} \to a_{i}$
for every
![]() $1 \leq i \leq r$
, we can choose
$1 \leq i \leq r$
, we can choose
![]() $\alpha $
such that
$\alpha $
such that
![]() $\| a_{\beta } a_{i} - a_{i} \| \leq \epsilon /( \sum _{i=1}^{r} \| f_{i}\|_{1,w})$
for every
$\| a_{\beta } a_{i} - a_{i} \| \leq \epsilon /( \sum _{i=1}^{r} \| f_{i}\|_{1,w})$
for every
![]() $1 \leq i \leq r$
and
$1 \leq i \leq r$
and
![]() $\beta \geq \alpha $
. For every
$\beta \geq \alpha $
. For every
![]() $\beta \geq \alpha $
,
$\beta \geq \alpha $
,
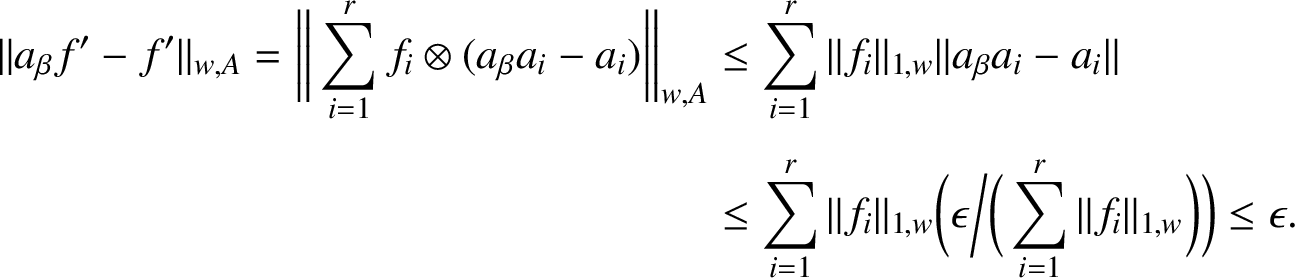 $$ \begin{align*} \| a_{\beta} f^{\prime} - f^{\prime} \|_{w,A} = \bigg\| \sum_{i=1}^{r} f_{i} \otimes (a_{\beta} a_{i} - a_{i}) \bigg\|_{w,A} & \leq \sum_{i=1}^{r} \| f_{i} \|_{1,w} \| a_{\beta} a_{i} - a_{i} \| \\[4pt] & \leq \sum_{i=1}^{r} \| f_{i} \|_{1,w} \bigg(\epsilon\bigg/\bigg( \sum_{i=1}^{r} \| f_{i}\|_{1,w}\bigg)\bigg) \leq \epsilon. \end{align*} $$
$$ \begin{align*} \| a_{\beta} f^{\prime} - f^{\prime} \|_{w,A} = \bigg\| \sum_{i=1}^{r} f_{i} \otimes (a_{\beta} a_{i} - a_{i}) \bigg\|_{w,A} & \leq \sum_{i=1}^{r} \| f_{i} \|_{1,w} \| a_{\beta} a_{i} - a_{i} \| \\[4pt] & \leq \sum_{i=1}^{r} \| f_{i} \|_{1,w} \bigg(\epsilon\bigg/\bigg( \sum_{i=1}^{r} \| f_{i}\|_{1,w}\bigg)\bigg) \leq \epsilon. \end{align*} $$
Hence,
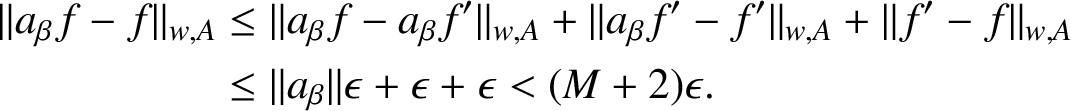 $$ \begin{align*} \| a_{\beta} f - f \|_{w,A} &\leq \| a_{\beta} f - a_{\beta} f^{\prime} \|_{w,A} + \|a_{\beta} f^{\prime} - f^{\prime} \|_{w,A} + \| f^{\prime} - f \|_{w,A} \\ & \leq \| a_{\beta} \| \epsilon + \epsilon + \epsilon < (M+2)\epsilon. \end{align*} $$
$$ \begin{align*} \| a_{\beta} f - f \|_{w,A} &\leq \| a_{\beta} f - a_{\beta} f^{\prime} \|_{w,A} + \|a_{\beta} f^{\prime} - f^{\prime} \|_{w,A} + \| f^{\prime} - f \|_{w,A} \\ & \leq \| a_{\beta} \| \epsilon + \epsilon + \epsilon < (M+2)\epsilon. \end{align*} $$
This proves the result.
Techniques from [Reference Mosak12] are used to prove the latter half of the following result.
Lemma 2.7. Let G be a locally compact group with a weight w which is either constant on conjugacy classes or satisfies
![]() $w \geq 1$
, and let A be a Banach algebra. Then G is an
$w \geq 1$
, and let A be a Banach algebra. Then G is an
![]() $\mathbf {[IN]}$
group whenever
$\mathbf {[IN]}$
group whenever
![]() $\mathcal {Z}(L^{1}_{\omega }(G,A)) \neq \{0\}$
.
$\mathcal {Z}(L^{1}_{\omega }(G,A)) \neq \{0\}$
.
Proof. Let
![]() $0 \neq f \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
. From Lemma 2.3,
$0 \neq f \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
. From Lemma 2.3,
![]() $x \cdot f, f \cdot x^{-1} \in L^{1}_{w}(G, \mathcal {Z}(A))$
for any
$x \cdot f, f \cdot x^{-1} \in L^{1}_{w}(G, \mathcal {Z}(A))$
for any
![]() $x \in G$
. Thus, by Lemma 2.6, Δ(x
−1)(f ⋅ x
−1)a
α
→Δ(x
−1)f ⋅ x
−1 and a
α
(x ⋅ f) → (x ⋅ f). Hence, in
$x \in G$
. Thus, by Lemma 2.6, Δ(x
−1)(f ⋅ x
−1)a
α
→Δ(x
−1)f ⋅ x
−1 and a
α
(x ⋅ f) → (x ⋅ f). Hence, in
![]() $L^{1}_{w}(G)$
,
$L^{1}_{w}(G)$
,
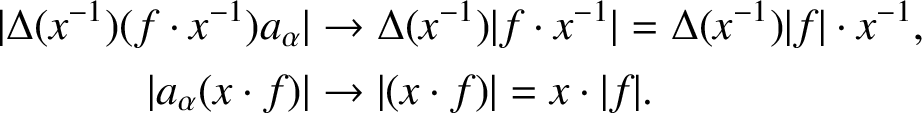 $$ \begin{align*} |\Delta(x^{-1}) (f \cdot x^{-1})a_{\alpha} | & \to \Delta(x^{-1})| f \cdot x^{-1} | = \Delta(x^{-1})| f | \cdot x^{-1}, \\ | a_{\alpha} (x \cdot f)| & \to | (x \cdot f)| = x \cdot | f|. \end{align*} $$
$$ \begin{align*} |\Delta(x^{-1}) (f \cdot x^{-1})a_{\alpha} | & \to \Delta(x^{-1})| f \cdot x^{-1} | = \Delta(x^{-1})| f | \cdot x^{-1}, \\ | a_{\alpha} (x \cdot f)| & \to | (x \cdot f)| = x \cdot | f|. \end{align*} $$
Case (i):
![]() $w \geq 1$
. It follows from Lemma 2.2 that
$w \geq 1$
. It follows from Lemma 2.2 that
![]() $0 \neq | f| \in \mathcal {Z}(L^{1}_{w}(G))$
, which in turn implies that G is an
$0 \neq | f| \in \mathcal {Z}(L^{1}_{w}(G))$
, which in turn implies that G is an
![]() $\mathbf {[IN]}$
group, as
$\mathbf {[IN]}$
group, as
![]() $w\geq 1$
(see [Reference Liukkonen and Mosak11]).
$w\geq 1$
(see [Reference Liukkonen and Mosak11]).
Case (ii): w is constant on conjugacy classes. The proof of [Reference Gupta, Jain and Talwar8, Lemma 4.4] works here except for the trivial modifications we now describe. Put
![]() $h(x) = \| f(x) w(x) \|^{1/2}$
. Then using Lemmas 2.2 and 2.6, we obtain
$h(x) = \| f(x) w(x) \|^{1/2}$
. Then using Lemmas 2.2 and 2.6, we obtain
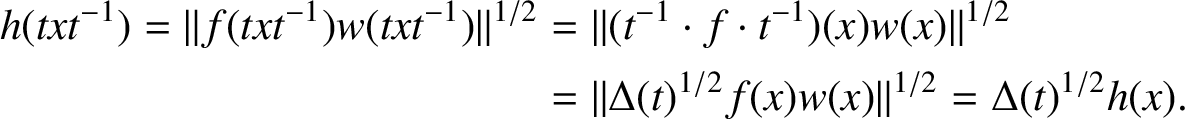 $$ \begin{align*}h(txt^{-1}) = \| f(txt^{-1}) w(txt^{-1}) \|^{1/2} & = \| (t^{-1} \cdot f \cdot t^{-1})(x) w(x) \|^{1/2} \\& = \| \Delta(t)^{1/2}f(x) w(x) \|^{1/2} = \Delta(t)^{1/2} h(x).\end{align*}$$
$$ \begin{align*}h(txt^{-1}) = \| f(txt^{-1}) w(txt^{-1}) \|^{1/2} & = \| (t^{-1} \cdot f \cdot t^{-1})(x) w(x) \|^{1/2} \\& = \| \Delta(t)^{1/2}f(x) w(x) \|^{1/2} = \Delta(t)^{1/2} h(x).\end{align*}$$
Now the continuous function
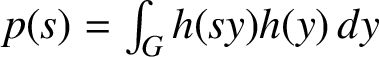 $p(s) = \int _{G} h(sy)h(y)\,dy$
will give a compact neighbourhood of e which is invariant under inner automorphisms.
$p(s) = \int _{G} h(sy)h(y)\,dy$
will give a compact neighbourhood of e which is invariant under inner automorphisms.
Restrictions on the weight in the previous result are not artificial. In fact, if G is an abelian group with a weight w, then there is an equivalent weight
![]() $\tilde {w} \geq 1$
on G such that
$\tilde {w} \geq 1$
on G such that
![]() $L^{1}_{w}(G)$
and
$L^{1}_{w}(G)$
and
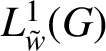 $L^{1}_{\tilde {w}}(G)$
are isomorphic as Banach algebras [Reference Dedania and Kansagara4, Lemma 3.2]. Also, every weight on an abelian group is trivially constant on conjugacy classes. Moreover, if G is a compact group, then
$L^{1}_{\tilde {w}}(G)$
are isomorphic as Banach algebras [Reference Dedania and Kansagara4, Lemma 3.2]. Also, every weight on an abelian group is trivially constant on conjugacy classes. Moreover, if G is a compact group, then
![]() $w \geq 1$
[Reference Kaniuth9, Corollary 1.3.4].
$w \geq 1$
[Reference Kaniuth9, Corollary 1.3.4].
Before presenting our main results, let us derive some consequences of what we have obtained so far. In the rest of the paper,
![]() $\text {Inn}(G)$
denotes the group of all inner automorphisms (
$\text {Inn}(G)$
denotes the group of all inner automorphisms (
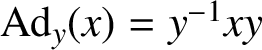 $\text {Ad}_{y}(x) = y^{-1}xy$
) of G. For any function f on G, define
$\text {Ad}_{y}(x) = y^{-1}xy$
) of G. For any function f on G, define
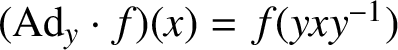 $(\text {Ad}_{y} \cdot f)(x) = f(yxy^{-1})$
for every
$(\text {Ad}_{y} \cdot f)(x) = f(yxy^{-1})$
for every
![]() $x,y \in G$
.
$x,y \in G$
.
Lemma 2.8. Let G be an
![]() $\mathbf {[IN]}$
group and A a Banach algebra. Then
$\mathbf {[IN]}$
group and A a Banach algebra. Then
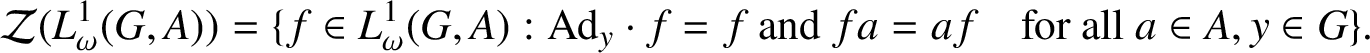 $$ \begin{align*}\mathcal{Z}(L^{1}_{\omega}(G,A)) = \{ f \in L^{1}_{\omega}(G,A) : \mathrm{Ad}_{y} \cdot f = f \text{ and } fa = af \quad \mbox{for all } a \in A, y \in G \}.\end{align*} $$
$$ \begin{align*}\mathcal{Z}(L^{1}_{\omega}(G,A)) = \{ f \in L^{1}_{\omega}(G,A) : \mathrm{Ad}_{y} \cdot f = f \text{ and } fa = af \quad \mbox{for all } a \in A, y \in G \}.\end{align*} $$
Proof. Note that for every
![]() $f \in L^{1}_{\omega }(G,A)$
we have
$f \in L^{1}_{\omega }(G,A)$
we have
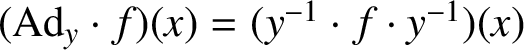 $(\text {Ad}_{y} \cdot f )(x) = (y^{-1} \cdot f \cdot y^{-1})(x)$
. Using Lemma 2.2 and the fact that every
$(\text {Ad}_{y} \cdot f )(x) = (y^{-1} \cdot f \cdot y^{-1})(x)$
. Using Lemma 2.2 and the fact that every
![]() $\mathbf {[IN]}$
group is unimodular, we obtain
$\mathbf {[IN]}$
group is unimodular, we obtain
 $$ \begin{align} \mathcal{Z}(L^{1}_{\omega}(G,A)) = \{ f \in L^{1}_{\omega}(G,A) : a (\mathrm{Ad}_{y} \cdot f) = f a\quad \mbox{for all } a \in A, y \in G \}. \end{align} $$
$$ \begin{align} \mathcal{Z}(L^{1}_{\omega}(G,A)) = \{ f \in L^{1}_{\omega}(G,A) : a (\mathrm{Ad}_{y} \cdot f) = f a\quad \mbox{for all } a \in A, y \in G \}. \end{align} $$
If
![]() $f \in L^{1}_{\omega }(G,A)$
is such that
$f \in L^{1}_{\omega }(G,A)$
is such that
![]() $fa = af$
and
$fa = af$
and
![]() $\text {Ad}_{y} \cdot f = f$
for every
$\text {Ad}_{y} \cdot f = f$
for every
![]() $y \in G$
and
$y \in G$
and
![]() $a \in A$
, then it readily follows that
$a \in A$
, then it readily follows that
![]() $a (\text {Ad}_{y} \cdot f) = a f = f a$
for every
$a (\text {Ad}_{y} \cdot f) = a f = f a$
for every
![]() $y \in G$
and
$y \in G$
and
![]() $a \in A$
.
$a \in A$
.
To prove the opposite inclusion, let
![]() $0 \neq f \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
. Taking
$0 \neq f \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
. Taking
![]() $y=e$
in (2.1), we obtain
$y=e$
in (2.1), we obtain
![]() $fa = af$
for every
$fa = af$
for every
![]() $a \in A$
. From Lemma 2.3,
$a \in A$
. From Lemma 2.3,
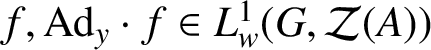 ${f, \text {Ad}_{y} \cdot f \in L^{1}_{w}(G,\mathcal {Z}(A))}$
for every
${f, \text {Ad}_{y} \cdot f \in L^{1}_{w}(G,\mathcal {Z}(A))}$
for every
![]() $y \in G$
. So, by Lemma 2.6, 0 = (a
α
(Ad
y
⋅ f) − fa
α
) → (Ad
y
⋅ f) − f for every
$y \in G$
. So, by Lemma 2.6, 0 = (a
α
(Ad
y
⋅ f) − fa
α
) → (Ad
y
⋅ f) − f for every
![]() $y \in G$
. Hence,
$y \in G$
. Hence,
![]() $\text {Ad}_{y} \cdot f = f$
for every
$\text {Ad}_{y} \cdot f = f$
for every
![]() $y \in G$
.
$y \in G$
.
Corollary 2.9. Let G be an
![]() $\mathbf {[IN]}$
group and A a Banach algebra. Then
$\mathbf {[IN]}$
group and A a Banach algebra. Then
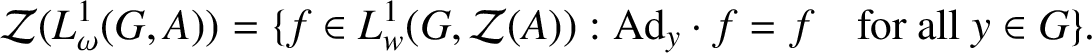 $$ \begin{align*} \mathcal{Z}(L^{1}_{\omega}(G,A)) = \{ f \in L^{1}_{w}(G, \mathcal{Z}(A)) : \text{Ad}_{y} \cdot f = f \quad\mbox{for all } y \in G\}. \end{align*} $$
$$ \begin{align*} \mathcal{Z}(L^{1}_{\omega}(G,A)) = \{ f \in L^{1}_{w}(G, \mathcal{Z}(A)) : \text{Ad}_{y} \cdot f = f \quad\mbox{for all } y \in G\}. \end{align*} $$
In particular, if
![]() $\mathcal {Z}(A)$
has a bounded approximate identity, then
$\mathcal {Z}(A)$
has a bounded approximate identity, then
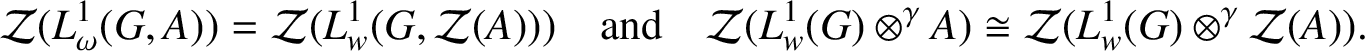 $$ \begin{align*} \mathcal{Z}(L^{1}_{\omega}(G,A)) = \mathcal{Z}(L^{1}_{w}(G, \mathcal{Z}(A))) \quad\text{and}\quad \mathcal{Z}(L^{1}_{w}(G) \otimes^{\gamma} A) \cong \mathcal{Z}(L^{1}_{w}(G) \otimes^{\gamma} \mathcal{Z}(A)). \end{align*} $$
$$ \begin{align*} \mathcal{Z}(L^{1}_{\omega}(G,A)) = \mathcal{Z}(L^{1}_{w}(G, \mathcal{Z}(A))) \quad\text{and}\quad \mathcal{Z}(L^{1}_{w}(G) \otimes^{\gamma} A) \cong \mathcal{Z}(L^{1}_{w}(G) \otimes^{\gamma} \mathcal{Z}(A)). \end{align*} $$
Proof. The first statement is a direct consequence of Lemmas 2.3 and 2.8. The second statement follows from Lemma 2.3 and the fact that
![]() $\mathcal {Z}(A)$
has a bounded
$\mathcal {Z}(A)$
has a bounded
![]() $\mathcal {Z}(\mathcal {Z}(A))$
-approximate identity. The third statement is a consequence of the well-known fact that
$\mathcal {Z}(\mathcal {Z}(A))$
-approximate identity. The third statement is a consequence of the well-known fact that
![]() $L^{1}_{w}(G) \otimes ^{\gamma } A \cong L^{1}_{\omega }(G,A)$
[Reference Samei17, Theorem 2.2].
$L^{1}_{w}(G) \otimes ^{\gamma } A \cong L^{1}_{\omega }(G,A)$
[Reference Samei17, Theorem 2.2].
Let G be an
![]() $\mathbf {[IN]}$
group and w a weight which is constant on conjugacy classes. Just as in [Reference Gupta, Jain and Talwar8], we consider the
$\mathbf {[IN]}$
group and w a weight which is constant on conjugacy classes. Just as in [Reference Gupta, Jain and Talwar8], we consider the
![]() $\sigma $
-subalgebra
$\sigma $
-subalgebra
![]() $\mathcal {B}_{\text {inv}}=\{B \in \mathcal {B}: \text {Ad}_{y}(B) = B \text { for all } y \in G\}$
and define the corresponding Banach algebra
$\mathcal {B}_{\text {inv}}=\{B \in \mathcal {B}: \text {Ad}_{y}(B) = B \text { for all } y \in G\}$
and define the corresponding Banach algebra
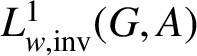 $L^{1}_{w,{\text {inv}}}(G,A)$
arising from the triple
$L^{1}_{w,{\text {inv}}}(G,A)$
arising from the triple
![]() $(G, \mathcal {B}_{\text {inv}}, m_{\text {inv}} = m_{|_{\mathcal {B}_{\text {inv}}}})$
. If
$(G, \mathcal {B}_{\text {inv}}, m_{\text {inv}} = m_{|_{\mathcal {B}_{\text {inv}}}})$
. If
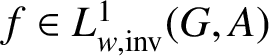 $f \in L^{1}_{w,\text {inv}}(G,A)$
, then f is
$f \in L^{1}_{w,\text {inv}}(G,A)$
, then f is
![]() $\mathcal {B}_{\text {inv}}$
-measurable and hence
$\mathcal {B}_{\text {inv}}$
-measurable and hence
![]() $\mathcal {B}$
-measurable [Reference Gupta, Jain and Talwar8, Lemma 4.6]. Clearly,
$\mathcal {B}$
-measurable [Reference Gupta, Jain and Talwar8, Lemma 4.6]. Clearly,
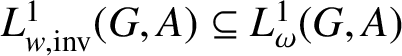 $L^{1}_{w,\text {inv}}(G,A) \subseteq L^{1}_{\omega }(G,A)$
. If w is a weight such that
$L^{1}_{w,\text {inv}}(G,A) \subseteq L^{1}_{\omega }(G,A)$
. If w is a weight such that
![]() $w \geq 1$
, then we may define
$w \geq 1$
, then we may define
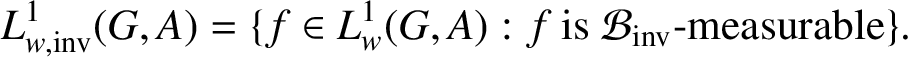 $$ \begin{align*}L^{1}_{w,\mathrm{inv}}(G,A) = \{ f \in L^{1}_{w}(G, A) : f \text{ is } \mathcal{B}_{\mathrm{inv}}\text{-measurable} \}.\end{align*} $$
$$ \begin{align*}L^{1}_{w,\mathrm{inv}}(G,A) = \{ f \in L^{1}_{w}(G, A) : f \text{ is } \mathcal{B}_{\mathrm{inv}}\text{-measurable} \}.\end{align*} $$
In both these cases, from [Reference Gupta, Jain and Talwar8, Lemma 4.6],
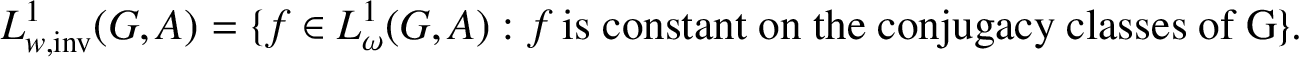 $$ \begin{align*}L^{1}_{w,\mathrm{inv}}(G,A) =\{f \in L^{1}_{\omega}(G,A): f \text{ is constant on the conjugacy classes of G}\}.\end{align*} $$
$$ \begin{align*}L^{1}_{w,\mathrm{inv}}(G,A) =\{f \in L^{1}_{\omega}(G,A): f \text{ is constant on the conjugacy classes of G}\}.\end{align*} $$
As in [Reference Samei17, Theorem 2.2],
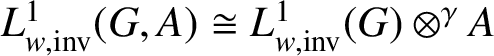 $L^{1}_{w,\text {inv}}(G,A) \cong L^{1}_{w,\text {inv}}(G) \otimes ^{\gamma } A$
for such weights.
$L^{1}_{w,\text {inv}}(G,A) \cong L^{1}_{w,\text {inv}}(G) \otimes ^{\gamma } A$
for such weights.
Theorem 2.10. Let G be an
![]() $\mathbf {[IN]}$
group with a weight w which is either constant on conjugacy classes or satisfies
$\mathbf {[IN]}$
group with a weight w which is either constant on conjugacy classes or satisfies
![]() $w \geq 1$
, and let A be a Banach algebra. Then
$w \geq 1$
, and let A be a Banach algebra. Then
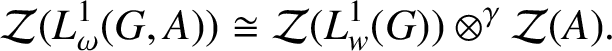 $$ \begin{align*}\mathcal{Z}(L^{1}_{\omega}(G,A)) \cong \mathcal{Z}(L^{1}_{w}(G)) \otimes^{\gamma} \mathcal{Z}(A).\end{align*} $$
$$ \begin{align*}\mathcal{Z}(L^{1}_{\omega}(G,A)) \cong \mathcal{Z}(L^{1}_{w}(G)) \otimes^{\gamma} \mathcal{Z}(A).\end{align*} $$
Proof. We claim that
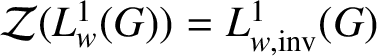 $\mathcal {Z}(L^{1}_{w}(G)) = L^{1}_{w,\text {inv}}(G)$
.
$\mathcal {Z}(L^{1}_{w}(G)) = L^{1}_{w,\text {inv}}(G)$
.
Let us first assume that w is constant on conjugacy classes. We know that
![]() $\mathcal {Z}(L^{1}(G))$
has a uniformly bounded approximate identity (see the proof of [Reference Liukkonen and Mosak10, Corollary 1.6]). Since convolution of an
$\mathcal {Z}(L^{1}(G))$
has a uniformly bounded approximate identity (see the proof of [Reference Liukkonen and Mosak10, Corollary 1.6]). Since convolution of an
![]() $L^{1}$
function with an
$L^{1}$
function with an
![]() $L^{\infty }$
function gives a continuous function,
$L^{\infty }$
function gives a continuous function,
![]() $\mathcal {Z}(L^{1}(G)) \cap C(G)$
is dense in
$\mathcal {Z}(L^{1}(G)) \cap C(G)$
is dense in
![]() $\mathcal {Z}(L^{1}(G))$
. From [Reference Mosak13],
$\mathcal {Z}(L^{1}(G))$
. From [Reference Mosak13],
![]() $fw \in \mathcal {Z}(L^{1}(G))$
for a fixed
$fw \in \mathcal {Z}(L^{1}(G))$
for a fixed
![]() $f \in \mathcal {Z}(L^{1}_{w}(G))$
, so
$f \in \mathcal {Z}(L^{1}_{w}(G))$
, so
![]() $fw$
is approximated in
$fw$
is approximated in
![]() $L^{1}(G)$
by a sequence
$L^{1}(G)$
by a sequence
![]() $\{g_{n}\} \in \mathcal {Z}(L^{1}(G)) \cap C(G)$
. Since both
$\{g_{n}\} \in \mathcal {Z}(L^{1}(G)) \cap C(G)$
. Since both
![]() $g_{n}$
and w are constant on conjugacy classes, f is constant on conjugacy classes. So,
$g_{n}$
and w are constant on conjugacy classes, f is constant on conjugacy classes. So,
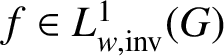 $f \in L^{1}_{w,\text {inv}}(G)$
, proving that
$f \in L^{1}_{w,\text {inv}}(G)$
, proving that
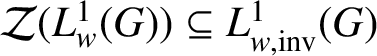 $\mathcal {Z}(L^{1}_{w}(G)) \subseteq L^{1}_{w,\text {inv}}(G)$
. It now follows from Corollary 2.9 that
$\mathcal {Z}(L^{1}_{w}(G)) \subseteq L^{1}_{w,\text {inv}}(G)$
. It now follows from Corollary 2.9 that
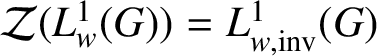 $\mathcal {Z}(L^{1}_{w}(G)) = L^{1}_{w,\text {inv}}(G)$
.
$\mathcal {Z}(L^{1}_{w}(G)) = L^{1}_{w,\text {inv}}(G)$
.
If
![]() $w\geq 1$
, then
$w\geq 1$
, then
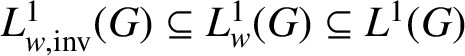 $L^{1}_{w, \text {inv}}(G) \subseteq L^{1}_{w}(G) \subseteq L^{1}(G)$
. Thus, being constant on conjugacy classes, every element of
$L^{1}_{w, \text {inv}}(G) \subseteq L^{1}_{w}(G) \subseteq L^{1}(G)$
. Thus, being constant on conjugacy classes, every element of
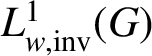 $L^{1}_{w, \text {inv}}(G)$
is contained in
$L^{1}_{w, \text {inv}}(G)$
is contained in
![]() $\mathcal {Z}(L^{1}(G))$
. This further implies that
$\mathcal {Z}(L^{1}(G))$
. This further implies that
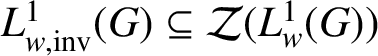 $L^{1}_{w, \text {inv}}(G)\subseteq \mathcal {Z}(L^{1}_{w}(G))$
. Conversely, if
$L^{1}_{w, \text {inv}}(G)\subseteq \mathcal {Z}(L^{1}_{w}(G))$
. Conversely, if
![]() $f \in \mathcal {Z}(L^{1}_{w}(G))$
, then
$f \in \mathcal {Z}(L^{1}_{w}(G))$
, then
![]() $f \in L^{1}_{w}(G)$
and
$f \in L^{1}_{w}(G)$
and
![]() $f \cdot x = x^{-1} \cdot f$
for every
$f \cdot x = x^{-1} \cdot f$
for every
![]() $x \in G$
since G is unimodular. This proves that
$x \in G$
since G is unimodular. This proves that
![]() $f \in \mathcal {Z}(L^{1}(G))$
and hence f is constant on conjugacy classes, proving the claim.
$f \in \mathcal {Z}(L^{1}(G))$
and hence f is constant on conjugacy classes, proving the claim.
Thus, in both cases,
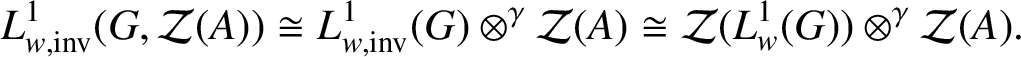 $$ \begin{align*}L^{1}_{w,\mathrm{inv}}(G,\mathcal{Z}(A)) \cong L^{1}_{w,\mathrm{inv}}(G) \otimes^{\gamma} \mathcal{Z}(A) \cong \mathcal{Z}(L^{1}_{w}(G)) \otimes^{\gamma} \mathcal{Z}(A).\end{align*} $$
$$ \begin{align*}L^{1}_{w,\mathrm{inv}}(G,\mathcal{Z}(A)) \cong L^{1}_{w,\mathrm{inv}}(G) \otimes^{\gamma} \mathcal{Z}(A) \cong \mathcal{Z}(L^{1}_{w}(G)) \otimes^{\gamma} \mathcal{Z}(A).\end{align*} $$
From Corollary 2.9,
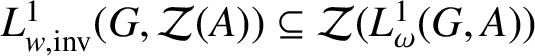 $L^{1}_{w, \text {inv}}(G,\mathcal {Z}(A)) \subseteq \mathcal {Z}(L^{1}_{\omega }(G,A))$
, so we only need to check the reverse inclusion. Further, since an arbitrary
$L^{1}_{w, \text {inv}}(G,\mathcal {Z}(A)) \subseteq \mathcal {Z}(L^{1}_{\omega }(G,A))$
, so we only need to check the reverse inclusion. Further, since an arbitrary
![]() $f \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
is a member of
$f \in \mathcal {Z}(L^{1}_{\omega }(G,A))$
is a member of
![]() $L^{1}_{w}(G,\mathcal {Z}(A))$
, it is sufficient to show that f is
$L^{1}_{w}(G,\mathcal {Z}(A))$
, it is sufficient to show that f is
![]() $\mathcal {B}_{\text {inv}}$
-measurable.
$\mathcal {B}_{\text {inv}}$
-measurable.
As f is
![]() $\mathcal {B}$
-essentially separably valued [Reference Ryan16, Proposition 2.15], there exists
$\mathcal {B}$
-essentially separably valued [Reference Ryan16, Proposition 2.15], there exists
![]() $E \in \mathcal {B}$
with zero measure such that
$E \in \mathcal {B}$
with zero measure such that
![]() $f(E^{c})$
is contained in a separable space. We can redefine f to be zero on E and hence f is
$f(E^{c})$
is contained in a separable space. We can redefine f to be zero on E and hence f is
![]() $\mathcal {B}_{\text {inv}}$
-essentially separably valued. In view of Corollary 2.9, for every
$\mathcal {B}_{\text {inv}}$
-essentially separably valued. In view of Corollary 2.9, for every
![]() $\phi \in A^{\ast }$
and
$\phi \in A^{\ast }$
and
![]() $y \in G$
we have
$y \in G$
we have
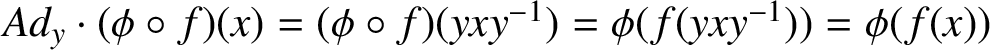 $Ad_{y} \cdot (\phi \circ f)(x) = (\phi \circ f)(yxy^{-1}) = \phi (f(yxy^{-1})) = \phi (f(x))$
for almost every
$Ad_{y} \cdot (\phi \circ f)(x) = (\phi \circ f)(yxy^{-1}) = \phi (f(yxy^{-1})) = \phi (f(x))$
for almost every
![]() $x \in G$
. Thus,
$x \in G$
. Thus,
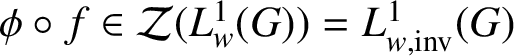 $\phi \circ f \in \mathcal {Z}(L^{1}_{w}(G)) = L^{1}_{w,\text {inv}}(G)$
and hence f is weakly
$\phi \circ f \in \mathcal {Z}(L^{1}_{w}(G)) = L^{1}_{w,\text {inv}}(G)$
and hence f is weakly
![]() $\mathcal {B}_{\text {inv}}$
-measurable. It now follows from [Reference Ryan16, Proposition 2.15] that f is
$\mathcal {B}_{\text {inv}}$
-measurable. It now follows from [Reference Ryan16, Proposition 2.15] that f is
![]() $\mathcal {B}_{\text {inv}}$
-measurable.
$\mathcal {B}_{\text {inv}}$
-measurable.
The following result generalises [Reference Gupta, Jain and Talwar8, Theorem 4.13] (by taking
![]() $w \equiv 1$
). It also generalises [Reference Shepelska and Zhang18, Lemma 2.1] fully and [Reference Shepelska and Zhang18, Proposition 2.2] to some extent.
$w \equiv 1$
). It also generalises [Reference Shepelska and Zhang18, Lemma 2.1] fully and [Reference Shepelska and Zhang18, Proposition 2.2] to some extent.
Corollary 2.11. Let G be an
![]() $\mathbf {[IN]}$
group and A a Banach algebra. Then
$\mathbf {[IN]}$
group and A a Banach algebra. Then
We note the following interesting consequences of Theorem 2.10 without giving the definitions of the concepts discussed as they are not being used rigorously. We would also like to point out that (2) and (3) below generalise [Reference Shepelska and Zhang18, Proposition 2.3].
Corollary 2.12. Let G be an
![]() $\mathbf {[IN]}$
group with a weight
$\mathbf {[IN]}$
group with a weight
![]() $w \geq 1$
and A a Banach algebra.
$w \geq 1$
and A a Banach algebra.
-
(1)
 $\mathcal {Z}(L^{1}_{\omega }(G,A))$
is semisimple if and only if
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
is semisimple if and only if
 $\mathcal {Z}(A)$
is semisimple.
$\mathcal {Z}(A)$
is semisimple. -
(2) If
 $\mathcal {Z}(L^{1}_{w}(G))$
and
$\mathcal {Z}(L^{1}_{w}(G))$
and
 $\mathcal {Z}(A)$
are weakly amenable, then so is
$\mathcal {Z}(A)$
are weakly amenable, then so is
 $\mathcal {Z}(L^{1}_{\omega }(G,A))$
.
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
. -
(3) If
 $\mathcal {Z}(L^{1}_{\omega }(G,A))$
is weakly amenable and semisimple, then both
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
is weakly amenable and semisimple, then both
 $\mathcal {Z}(L^{1}_{w}(G))$
and
$\mathcal {Z}(L^{1}_{w}(G))$
and
 $\mathcal {Z}(A)$
are weakly amenable.
$\mathcal {Z}(A)$
are weakly amenable. -
(4) If
 $\mathcal {Z}(L^{1}_{\omega }(G,A))$
is Tauberian and semisimple, then both
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
is Tauberian and semisimple, then both
 $\mathcal {Z}(L^{1}_{w}(G))$
and
$\mathcal {Z}(L^{1}_{w}(G))$
and
 $\mathcal {Z}(A)$
are Tauberian.
$\mathcal {Z}(A)$
are Tauberian. -
(5) If both
 $\mathcal {Z}(L^{1}_{w}(G))$
and
$\mathcal {Z}(L^{1}_{w}(G))$
and
 $\mathcal {Z}(A)$
are Tauberian, then so is
$\mathcal {Z}(A)$
are Tauberian, then so is
 $\mathcal {Z}(L^{1}_{\omega }(G,A))$
.
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
. -
(6)
 $\mathcal {Z}(L^{1}_{\omega }(G,A))$
is regular if and only if both
$\mathcal {Z}(L^{1}_{\omega }(G,A))$
is regular if and only if both
 $\mathcal {Z}(L^{1}_{w}(G))$
and
$\mathcal {Z}(L^{1}_{w}(G))$
and
 $\mathcal {Z}(A)$
are regular.
$\mathcal {Z}(A)$
are regular. -
(7)
 $\mathcal {Z}(L^{1}_{\omega }(G,A)) = \{ f \in L^{1}_{w}(G,\mathcal {Z}(A)): f \text { is constant on conjugacy classes}\}.$
$\mathcal {Z}(L^{1}_{\omega }(G,A)) = \{ f \in L^{1}_{w}(G,\mathcal {Z}(A)): f \text { is constant on conjugacy classes}\}.$
Proof. (1) We know that
![]() $L^{1}(G)$
has the approximation property [Reference Kaniuth9, page 325]. So,
$L^{1}(G)$
has the approximation property [Reference Kaniuth9, page 325]. So,
![]() $L^{1}_{w}(G)$
has the approximation property because the map
$L^{1}_{w}(G)$
has the approximation property because the map
![]() $f \in L^{1}_{w}(G) \to fw \in L^{1}(G)$
is a Banach space isomorphism. Hence, the natural map from
$f \in L^{1}_{w}(G) \to fw \in L^{1}(G)$
is a Banach space isomorphism. Hence, the natural map from
![]() $L^{1}_{w}(G) \otimes ^{\gamma } A$
to
$L^{1}_{w}(G) \otimes ^{\gamma } A$
to
![]() $L^{1}_{w}(G) \otimes ^{\lambda } A$
, the Banach space injective tensor product, is injective [Reference Kaniuth9, Theorem A.2.12]. The restriction of the natural map from
$L^{1}_{w}(G) \otimes ^{\lambda } A$
, the Banach space injective tensor product, is injective [Reference Kaniuth9, Theorem A.2.12]. The restriction of the natural map from
![]() $\mathcal {Z}(L^{1}_{w}(G) \otimes ^{\gamma } A) = \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A)$
to
$\mathcal {Z}(L^{1}_{w}(G) \otimes ^{\gamma } A) = \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A)$
to
![]() ${\mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\lambda } \mathcal {Z}(A) \subseteq L^{1}_{w}(G) \otimes ^{\lambda } A}$
is also injective from the injectivity of
${\mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\lambda } \mathcal {Z}(A) \subseteq L^{1}_{w}(G) \otimes ^{\lambda } A}$
is also injective from the injectivity of
![]() $\otimes ^{\lambda }$
. Since
$\otimes ^{\lambda }$
. Since
![]() $\mathcal {Z}(L^{1}_{w}(G))$
is a semisimple and commutative Banach algebra [Reference Rickart15, Corollary 2.3.7], the result now follows from [Reference Kaniuth9, Theorem 2.11.6].
$\mathcal {Z}(L^{1}_{w}(G))$
is a semisimple and commutative Banach algebra [Reference Rickart15, Corollary 2.3.7], the result now follows from [Reference Kaniuth9, Theorem 2.11.6].
(2) This follows from the fact that the projective tensor product of weakly amenable commutative Banach algebras is weakly amenable (see [Reference Dales3, Proposition 2.8.71]).
(3) Since
![]() $\mathcal {Z}(L^{1}_{w}(G))$
and
$\mathcal {Z}(L^{1}_{w}(G))$
and
![]() $\mathcal {Z}(A)$
are semisimple, there exist multiplicative linear functionals
$\mathcal {Z}(A)$
are semisimple, there exist multiplicative linear functionals
![]() $\phi _{1}$
and
$\phi _{1}$
and
![]() $\phi _{2}$
on
$\phi _{2}$
on
![]() $\mathcal {Z}(L^{1}_{w}(G))$
and
$\mathcal {Z}(L^{1}_{w}(G))$
and
![]() $\mathcal {Z}(A)$
, respectively, see [Reference Kaniuth9, Definition 2.1.9]. Then
$\mathcal {Z}(A)$
, respectively, see [Reference Kaniuth9, Definition 2.1.9]. Then
![]() $\phi _{1} \otimes ^{\gamma } 1_{\mathcal {Z}(A)} : \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A) \to \mathcal {Z}(A)$
and
$\phi _{1} \otimes ^{\gamma } 1_{\mathcal {Z}(A)} : \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A) \to \mathcal {Z}(A)$
and
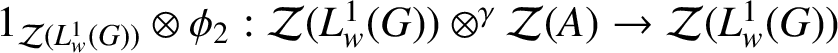 $1_{\mathcal {Z}(L^{1}_{w}(G))} \otimes \phi _{2} : \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A) \to \mathcal {Z}(L^{1}_{w}(G))$
are surjective homomorphisms and [Reference Dales3, Proposition 2.8.64] gives the result.
$1_{\mathcal {Z}(L^{1}_{w}(G))} \otimes \phi _{2} : \mathcal {Z}(L^{1}_{w}(G)) \otimes ^{\gamma } \mathcal {Z}(A) \to \mathcal {Z}(L^{1}_{w}(G))$
are surjective homomorphisms and [Reference Dales3, Proposition 2.8.64] gives the result.
(4) This follows from (1) and [Reference Tewari, Dutta and Madan19, Lemma 2.1].
(5) Since both
![]() $\mathcal {Z}(L^{1}_{w}(G))$
and
$\mathcal {Z}(L^{1}_{w}(G))$
and
![]() $\mathcal {Z}(A)$
are commutative, the result follows from [Reference Gelbaum6, Theorem 1.
$\mathcal {Z}(A)$
are commutative, the result follows from [Reference Gelbaum6, Theorem 1.
![]() ${\mathrm{P}}_2$
].
${\mathrm{P}}_2$
].
(6) This follows from Theorem 2.10 and [Reference Tomiyama20, Theorem 3].
(7) This is the same as saying that
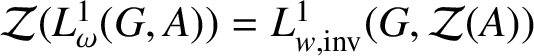 $\mathcal {Z}(L^{1}_{\omega }(G,A)) = L^{1}_{w,\text {inv}}(G,\mathcal {Z}(A))$
, which is proved in Theorem 2.10.
$\mathcal {Z}(L^{1}_{\omega }(G,A)) = L^{1}_{w,\text {inv}}(G,\mathcal {Z}(A))$
, which is proved in Theorem 2.10.
Remark 2.13. Note that the hypothesis
![]() $w \geq 1$
is merely used to obtain semisimplicity of
$w \geq 1$
is merely used to obtain semisimplicity of
![]() $\mathcal {Z}(L^{1}_{w}(G))$
. Results (2), (5), (6) and (7) are true if w is constant on conjugacy classes.
$\mathcal {Z}(L^{1}_{w}(G))$
. Results (2), (5), (6) and (7) are true if w is constant on conjugacy classes.