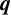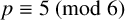1 Introduction
For any complex variable x, define the shifted-factorial by
$$ \begin{align*}(x)_{0}=1\quad \text{and}\quad (x)_{n} =x(x+1)\cdots(x+n-1)\quad \text{for } n\in\mathbb{Z}^{+},\end{align*} $$
and let
$\Gamma _{p}(x)$
denote the p-adic Gamma function. Throughout the paper, p denotes an odd prime. In 1997, Van Hamme [Reference Van Hamme, Schikhof, Perez-Garcia and Kakol9, (H.2)] proved that
$$ \begin{align} \sum_{k=0}^{(p-1)/2}\frac{(\frac{1}{2})_k^3}{(1)_k^3}\equiv \begin{cases} \displaystyle -\Gamma_p\biggl(\frac{1}{4}\biggr)^4 \pmod{p^2} &\text{if } p\equiv 1\pmod 4,\\[3pt] 0\pmod{p^2} &\text{if } p\equiv 3\pmod 4. \end{cases} \end{align} $$
In 2016, Long and Ramakrishna [Reference Long and Ramakrishna6] gave an extension of (1.1):
$$ \begin{align} \sum_{k=0}^{(p-1)/2}\frac{(\frac{1}{2})_k^3}{(1)_k^3}\equiv \begin{cases} \displaystyle -\Gamma_p\biggl(\frac{1}{4}\biggr)^4 \pmod{p^3} &\text{if } p\equiv 1\pmod 4,\\[8pt] \displaystyle -\frac{p^2}{16}\Gamma_p\biggl(\frac{1}{4}\biggr)^4\pmod{p^3} &\text{if } p\equiv 3\pmod 4. \end{cases} \end{align} $$
In the same year, Deines et al. [Reference Deines, Fuselier, Long, Swisher, Tu and Lauter1] discovered the nice supercongruence: for
$p\equiv {1}\pmod {6}$
,
$$ \begin{align*}\sum_{k=0}^{p-1}\frac{(\frac{2}{3})_k^3}{(1)_k^3}\equiv-\Gamma_{p}\biggl(\frac{1}{3}\biggr)^3\pmod{p^3}.\end{align*} $$
Several years later, Mao and Pan [Reference Mao and Pan7] (see also Sun [Reference Sun8, Theorem 1.3]) found a result similar to (1.1): for
$p\equiv 1\pmod {4}$
,
$$ \begin{align} \sum_{k=0}^{(p+1)/2}\frac{(-\frac{1}{2})_k^3}{(1)_k^3}\equiv0\pmod{p^2}. \end{align} $$
For any complex numbers x and q, define the q-shifted factorial by
$$ \begin{align*} (x;q)_{0}=1\quad\text{and}\quad (x;q)_n=(1-x)(1-xq)\cdots(1-xq^{n-1})\quad \text{for } n\in\mathbb{Z}^{+}. \end{align*} $$
For simplicity, we also adopt the compact notation
$$ \begin{align*} (x_1,x_2,\ldots,x_m;q)_{n}=(x_1;q)_{n}(x_2;q)_{n}\cdots(x_m;q)_{n}, \end{align*} $$
where
$m\in \mathbb {Z}^{+}$
and
$n\in \mathbb {Z}^{+}\cup \{0,\infty \}.$
Let
$[n]=(1-q^n)/(1-q)$
be the q-integer and let
$\Phi _n(q)$
stand for the nth cyclotomic polynomial in q:
$$ \begin{align*} \Phi_n(q)=\prod_{\substack{1\leqslant k\leqslant n\\[3pt] \gcd(k,n)=1}}(q-\zeta^k), \end{align*} $$
where
$\zeta $
is a primitive nth root of unity. Recently, Wei [Reference Wei11] and Wang [Reference Wang10] established q-analogues of (1.2) for the first case: if
$n\equiv 1\pmod 4$
, then modulo
$\Phi _n(q)^3$
,
$$ \begin{align*} \sum_{k=0}^{(n-1)/2}\frac{(q;q^2)_k^2(q^2;q^4)_k}{(q^2;q^2)_k^2(q^4;q^4)_k}q^{2k} & \equiv q^{(n-1)/2}\frac{(q^2;q^4)_{(n-1)/4}^2}{(q^4;q^4)_{(n-1)/4}^2}\bigg\{1+2[n]^2\sum_{i=1}^{(n-1)/4}\frac{q^{4i-2}}{[4i-2]^2}\bigg\},\\[3pt] \sum_{k=0}^{(n-1)/2}\frac{(q;q^2)_k^2(q^{2};q^4)_k}{(q^2;q^2)_k^2(q^4;q^4)_k}q^{2k} & \equiv[n]\frac{(q^3;q^4)_{(n-1)/2}}{(q^5;q^4)_{(n-1)/2}} \\[3pt] &\quad+ [n]^3\sum_{k=0}^{(n-3)/2}\frac{(1+q^{2k+1})(q^3;q^4)_k}{[2k+1]^2(q^5;q^4)_k}q^{2k+1}. \end{align*} $$
Guo and Zudilin [Reference Guo and Zudilin5] and Guo [Reference Guo3] gave q-analogues of (1.2) for the second case: if
$n\equiv 3\pmod 4$
, then
$$ \begin{align} \sum_{k=0}^{(n-1)/2}\frac{1+q^{1+4k}}{1+q}\frac{(q^{2};q^4)_k^3}{(q^4;q^4)_k^3}q^{k} & \equiv [n]_{q^2}\frac{(q^3;q^4)_{(n-1)/2}}{(q^5;q^4)_{(n-1)/2}}q^{(1-n)/2}\pmod{\Phi_n(q)^3}, \notag\\[2mm] \sum_{k=0}^{(n-1)/2}\frac{(q;q^2)_k^2(q^{2};q^4)_k}{(q^2;q^2)_k^2(q^4;q^4)_k}q^{2k} & \equiv [n]\frac{(q^3;q^4)_{(n-1)/2}}{(q^5;q^4)_{(n-1)/2}}\pmod{\Phi_n(q)^3}. \end{align} $$
Guo and Zudilin [Reference Guo and Zudilin5] also found the q-supercongruence: for any positive integer
$n>1$
with
$n\equiv 1\pmod 4$
,
$$ \begin{align} \sum_{k=0}^{(n+1)/2}\frac{1+q^{4k-1}}{1+q}\frac{(q^{-2};q^4)_k^3}{(q^4;q^4)_k^3}q^{7k} \equiv [n]_{q^2}\frac{(q;q^4)_{(n-1)/2}}{(q^5;q^4)_{(n-1)/2}}q^{(n-3)/2}\pmod{\Phi_n(q)^3}. \end{align} $$
Setting
$n=p$
and then letting
$q\to 1$
in (1.5), they obtain the extension of (1.3): for
$p\equiv 1\pmod 4$
,
$$ \begin{align*} \sum_{k=0}^{(p+1)/2}\frac{(-\frac{1}{2})_k^3}{k!^3}\equiv p\frac{(\frac{1}{4})_{(p-1)/2}}{(\frac{7}{4})_{(p-1)/2}}\pmod{p^3}. \end{align*} $$
Motivated by the results just mentioned, we shall establish the following theorem.
Theorem 1.1. Let
$n, d$
be positive integers such that
$n-dn+2d\leq r\leq n+d$
,
$\gcd (n, d) = 1$
and
$n\equiv r\pmod {2d}$
. Then
$$ \begin{align*} &\sum_{k=0}^{(n-r+d)/d}\frac{1+q^{r-d+2dk}}{1+q^{r-d}}\frac{(q^{2r-2d};q^{2d})_k^3}{(q^{2d};q^{2d})_k^3}q^{(5d-3r)k} \\[3pt] &\quad\equiv \frac{1-q^{2n}}{1-q^{2r-2d}}\frac{(q^{3r-3d};q^{2d})_{(n-r+d)/d}}{(q^{r+d};q^{2d})_{(n-r+d)/d}}q^{(d-r)(n-r+d)/d}\pmod{\Phi_n(q)^3}. \end{align*} $$
Obviously, the
$d=2, r=3$
case of Theorem 1.1 is exactly (1.4). When
$d=2, r=1$
, Theorem 1.1 reduces to (1.5). Taking
$n=p$
and then letting
$q\to 1$
in Theorem 1.1 gives the following supercongruence.
Proposition 1.2. Let p be an odd prime and let d be a positive integer such that
$p-dp+2d\leq r\leq p+d$
and
$p\equiv r\pmod {2d}$
. Then
$$ \begin{align*} \sum_{k=0}^{(p-r+d)/d}\frac{(\frac{r-d}{d})_k^3}{(1)_k^3}\equiv \frac{p}{r-d}\frac{(\frac{3r-3d}{2d})_{(p-r+d)/d}}{(\frac{r+d}{2d})_{(p-r+d)/d}}\pmod{p^3}. \end{align*} $$
Specialising the parameters d and r, Proposition 1.2 can produce many concrete supercongruences. Six of these are given in the following corollaries.
Corollary 1.3. Let p be a prime with
$p\equiv 1\pmod {6}$
. Then
$$ \begin{align*} \sum_{k=0}^{(p+2)/3}\frac{(-\frac{2}{3})_k^3}{(1)_k^3}\equiv 0\pmod{p^3}. \end{align*} $$
Proof. Take
$d=3, r=1$
in Proposition 1.2.
Corollary 1.4. Let p be a prime with
$p\equiv 5\pmod {6}$
. Then
$$ \begin{align*} \sum_{k=0}^{(p-2)/3}\frac{(\frac{2}{3})_k^3}{(1)_k^3}\equiv \frac{p}{2}\frac{(1)_{(p-2)/3}}{(\frac{4}{3})_{(p-2)/3}}\pmod{p^3}. \end{align*} $$
Proof. Take
$d=3, r=5$
in Proposition 1.2.
Corollary 1.5. Let p be a prime with
$p\equiv 1\pmod {8}$
. Then
$$ \begin{align*} \sum_{k=0}^{(p+3)/4}\frac{(-\frac{3}{4})_k^3}{(1)_k^3}\equiv -\frac{p}{3}\frac{(-\frac{9}{8})_{(p+3)/4}}{(\frac{5}{8})_{(p+3)/4}}\pmod{p^3}. \end{align*} $$
Proof. Take
$d=4, r=1$
in Proposition 1.2.
Corollary 1.6. Let p be a prime with
$p\equiv 3\pmod {8}$
. Then
$$ \begin{align*} \sum_{k=0}^{(p+1)/4}\frac{(-\frac{1}{4})_k^3}{(1)_k^3}\equiv -p\frac{(-\frac{3}{8})_{(p+1)/4}}{(\frac{7}{8})_{(p+1)/4}}\pmod{p^3}. \end{align*} $$
Proof. Take
$d=4, r=3$
in Proposition 1.2.
Corollary 1.7. Let p be a prime with
$p\equiv 5\pmod {8}$
. Then
$$ \begin{align*} \sum_{k=0}^{(p-1)/4}\frac{(\frac{1}{4})_k^3}{(1)_k^3}\equiv p\frac{(\frac{3}{8})_{(p-1)/4}}{(\frac{9}{8})_{(p-1)/4}}\pmod{p^3}. \end{align*} $$
Proof. Take
$d=4, r=5$
in Proposition 1.2.
Corollary 1.8. Let p be a prime with
$p\equiv 7\pmod {8}$
. Then
$$ \begin{align*} \sum_{k=0}^{(p-3)/4}\frac{(\frac{3}{4})_k^3}{(1)_k^3}\equiv \frac{p}{3}\frac{(\frac{9}{8})_{(p-3)/4}}{(\frac{11}{8})_{(p-3)/4}}\pmod{p^3}. \end{align*} $$
Proof. Take
$d=4, r=7$
in Proposition 1.2.
We shall prove Theorem 1.1 in the next section by means of the creative microscoping method recently introduced by Guo and Zudilin [Reference Guo and Zudilin4].
2 Proof of Theorem 1.1
Following Gasper and Rahman [Reference Gasper and Rahman2], define the basic hypergeometric series by
$$ \begin{align*} _{r+1}\phi_{r}\left[\begin{array}{c} a_1,a_2,\ldots,a_{r+1}\\[3pt] b_1,b_2,\ldots,b_{r} \end{array};q,\, z \right] =\sum_{k=0}^{\infty}\frac{(a_1,a_2,\ldots, a_{r+1};q)_k} {(q,b_1,b_2,\ldots,b_{r};q)_k}z^k. \end{align*} $$
To prove Theorem 1.1, we require the q-Dixon formula:
$$ \begin{align} _{4}\phi_{3}\!\left[\begin{array}{c} a, \, -qa^{{1}/{2}}, \, b, \, c \\[3pt] -a^{{1}/{2}}, \, aq/b, \, aq/c \end{array};q,\,\frac{qa^{{1}/{2}}}{bc} \right] =\frac{(aq,aq/bc,qa^{{1}/{2}}/b,qa^{{1}/{2}}/c;q)_{\infty}}{(aq/b,aq/c,qa^{{1}/{2}},qa^{{1}/{2}}/bc;q)_{\infty}}, \end{align} $$
where
$|qa^{{1}/{2}}/bc|<1$
.
Proof of Theorem 1.1.
Setting
$a=q^{-1-2n}$
in (2.1), we obtain
$$ \begin{align*} _{4}\phi_{3}\!\left[\begin{array}{c} q^{-1-2n},\, -q^{{1}/{2}-n},\, b,\, c \\[3pt] -q^{-{1}/{2}-n},\, q^{-2n}/b,\, q^{-2n}/c \end{array};q,\,\frac{q^{{1}/{2}-n}}{bc} \right] =0. \end{align*} $$
Performing the simultaneous replacements
$n\mapsto (n-r)/2d$
,
$q\mapsto q^{2d}$
,
$b\mapsto bq^{2r-2d}$
,
$c\mapsto q^{2r-2d}/b$
in the above identity, we get
$$ \begin{align*} _{4}\phi_{3}\!\left[\begin{array}{c} q^{2r-2d-2n},\, -q^{r+d-n},\, bq^{2r-2d},\, q^{2r-2d}/b \\[6pt] -q^{r-d-n},\, q^{2d-2n}/b,\, bq^{2d-2n} \end{array};q^{2d},\,q^{5d-3r-n} \right] =0. \end{align*} $$
This gives the following congruence: modulo
$(a^2-q^{2n})$
,
$$ \begin{align} \sum_{k=0}^{(n-r+d)/d}\frac{1+q^{r-d+2dk}/a}{1+q^{r-d}/a}\frac{(q^{2r-2d}/a^2,bq^{2r-2d},q^{2r-2d}/b;q^{2d})_k} {(q^{2d},q^{2d}/a^2b,q^{2d}b/a^2;q^{2d})_k}\bigg(\frac{q^{5d-3r}}{a}\bigg)^k \equiv 0. \end{align} $$
However, taking
$c=q^{-1-2n}$
in (2.1), we obtain
$$ \begin{align*} _{4}\phi_{3}\!\left[\begin{array}{c} a,\, -qa^{{1}/{2}},\, b,\, q^{-1-2n} \\[6pt] -a^{{1}/{2}},\, aq/b,\, aq^{2+2n} \end{array};q,\,\frac{q^{2+2n}a^{{1}/{2}}}{b} \right] =\frac{(aq,qa^{{1}/{2}}/b;q)_{1+2n}}{(aq/b,qa^{{1}/{2}};q)_{1+2n}}. \end{align*} $$
Employing the substitutions
$n\mapsto (n-r)/2d$
,
$q\mapsto q^{2d}$
,
$a\mapsto q^{2r-2d}/a^2$
,
$b\mapsto q^{2r-2d+2n}$
, we arrive at
$$ \begin{align*} &_{4}\phi_{3}\!\left[\begin{array}{c} q^{2r-2d}/a^2,\, -q^{r+d}/a,\, q^{2r-2d+2n},\, q^{2r-2d-2n} \\[6pt] -q^{r-d}/a,\, q^{2d-2n}/a^2,\, q^{2d+2n}/a^2 \end{array};q^{2d},\,\frac{q^{5d-3r}}{a} \right]\\[2mm] &\quad=(aq^{d-r})^{(n-r+d)/d}\frac{(q^{2r}/a^2,aq^{3r-3d};q^{2d})_{(n-r+d)/d}}{(q^{r+d}/a,a^2q^{2r-2d};q)_{(n-r+d)/d}}. \end{align*} $$
This gives the following congruence: modulo
$(b-q^{2n})(1-bq^{2n})$
,
$$ \begin{align} &\sum_{k=0}^{(n-r+d)/d}\frac{1+q^{r-d+2dk}/a}{1+q^{r-d}/a}\frac{(q^{2r-2d}/a^2,bq^{2r-2d},q^{2r-2d}/b;q^{2d})_k} {(q^{2d},q^{2d}/a^2b,q^{2d}b/a^2;q^{2d})_k}\bigg(\frac{q^{5d-3r}}{a}\bigg)^k\notag\\[2pt] &\quad\equiv (aq^{d-r})^{(n-r+d)/d}\frac{(q^{2r}/a^2,aq^{3r-3d};q^{2d})_{(n-r+d)/d}}{(q^{r+d}/a,a^2q^{2r-2d};q)_{(n-r+d)/d}}. \end{align} $$
Note that the right-hand side of (2.2) can also be written as that of (2.3), since
$(q^{2r}/a^2,aq^{3r-3d};q^{2d})_{(n-r+d)/d}$
contains the factor
$a^2-q^{2n}$
. It is clear that the polynomials
$(a^2-q^{2n})$
and
$(b-q^{2n})(1-bq^{2n})$
are relatively prime. Therefore, from (2.2) and (2.3) we deduce that, modulo
$(a^2-q^{2n})(b-q^{2n})(1-bq^{2n})$
,
$$ \begin{align} &\sum_{k=0}^{(n-r+d)/d}\frac{1+q^{r-d+2dk}/a}{1+q^{r-d}/a}\frac{(q^{2r-2d}/a^2,bq^{2r-2d},q^{2r-2d}/b;q^{2d})_k} {(q^{2d},q^{2d}/a^2b,q^{2d}b/a^2;q^{2d})_k}\bigg(\frac{q^{5d-3r}}{a}\bigg)^k\notag\\[2pt] &\quad\equiv (aq^{d-r})^{(n-r+d)/d}\frac{(q^{2r}/a^2,aq^{3r-3d};q^{2d})_{(n-r+d)/d}}{(q^{r+d}/a,a^2q^{2r-2d};q)_{(n-r+d)/d}}. \end{align} $$
Letting
$a {\kern2pt\to\kern2pt} 1$
,
$b{\kern2pt\to\kern2pt} 1$
in (2.4), we are led to the q-supercongruence in Theorem 1.1.
3 Two open problems
Numerical calculations indicate the following two open problems related to Corollaries 1.3 and 1.5.
Conjecture 3.1. Let p be a prime with
$p\equiv 1\pmod {6}$
and let s be a positive integer. Then
$$ \begin{align*} \sum_{k=0}^{(p^s+2)/3}\frac{(-\frac{2}{3})_k^3}{(1)_k^3}\equiv 0\pmod{p^{3s}}. \end{align*} $$
Conjecture 3.2. Let p be a prime with
$p\equiv 1\pmod {8}$
and let s be a positive integer. Then
$$ \begin{align*} \sum_{k=0}^{(p^s+3)/4}\frac{(-\frac{3}{4})_k^3}{(1)_k^3}\equiv -\frac{p^s}{3}\frac{(-\frac{9}{8})_{(p^s+3)/4}}{(\frac{5}{8})_{(p^s+3)/4}}\pmod{p^{s+2}}. \end{align*} $$
Acknowledgement
The author is grateful to the reviewer for a careful reading and valuable comments.
