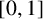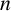1 Introduction and preliminaries
When the line joining
$0$
to
$1$
(or a rectangular piece of paper with
$[0,1] $
at its edge) is folded in half, right over left, the point
$1/2$
is at the fold. When the line is then folded in half again, right over left, the points
$1/4,3/4$
are at this second fold, in that order, from the outside of the fold to its interior as shown in Figure 1, where the second fold sequence is shown by the horizontal arrow and the third fold sequence is shown by the vertical arrow.
Figure 1 Points in a fold after two folds.
The line when unfolded forms the paperfolding sequence, a sequence of
$\vee $
and
$\wedge $
creases. It has a rich history commencing with Davis and Knuth [Reference Davis and Knuth4]. Other important contributions include Dekking et al. [Reference Dekking, France and van der Poorten5], Allouche and Shallit [Reference Allouche and Shallit1], Mendès France and van der Poorten [Reference France and van der Poorten8] and Mendès France and Shallit [Reference France and Shallit7]. Our interest, in this paper, is to explore paperfolding when it remains in its folded form.
After n folds, the paper strip is partitioned by the folds into
$2^{n}$
segments which we call intervals. In Bunder et al. [Reference Bunder, Tognetti and Bates3], we identified the location of points in a paperfold. The present paper provides some new results by utilising two different and relatively unknown techniques that can be readily converted into algorithms. The first technique (Section 2) identifies the point at each location within a fold (Theorem 3.1). The second technique (Section 4) does the reverse: for each point of the form
${(2k+1)}/{2^{n}}<1,$
it identifies its location within a fold (Theorem 5.1).
The first technique involves normalised additive factorisation, which has been used in the Stern–Brocot tree (Bates et al. [Reference Bates, Bunder and Tognetti2]). Normalised additive factorisation is a binary signed-digit representation of an integer (see Monroe [Reference Monroe9], Ebeid and Hasan [Reference Ebeid and Hasan6], Tůma and Vábek [Reference Tůma and Vábek13] and Shallit [Reference Shallit11]). The second technique is a different binary signed-digit representation of an integer. It makes use of what we have called odd unit factorisation, which is possibly novel, although it may exist in the literature under other guises.
We recall from Bunder et al. [Reference Bunder, Tognetti and Bates3], the following definitions and results, with minor changes. In particular, Theorems 1.5–1.7 below are [Reference Bunder, Tognetti and Bates3, Lemma 2.5 and Theorems 2.6 and 2.7] and Theorem 1.8 is a corollary of [Reference Bunder, Tognetti and Bates3, Theorem 3.1].
Definition 1.1 (nth fold sequence)
After we have folded the line n times, the sequence of points from the outside of the nth fold to the inside is the nth fold sequence,
$S_{n}=\langle S_{n,j}\rangle $
. We define the zeroth fold sequence,
$S_{0}=\langle S_{0,1}\rangle =1.$
We call
$S_{n,j}$
the address of the point found at
$S_{n,j}$
as well as the point itself.
Example 1.2. The zeroth, first, second and third fold sequences are
$$ \begin{align*} S_{0} &=\langle S_{0,1}\rangle =1, \\ S_{1} &=\langle S_{1,1}\rangle =\tfrac{1}{2}, \\ S_{2} & =\langle S_{2,1},S_{2,2}\rangle =\big\langle \tfrac{1}{4}, \tfrac{3}{4}\big\rangle \quad \text{(horizontal arrow in Figure 1)}, \\ S_{3} &=\langle S_{3,1},S_{3,2},S_{3,3},S_{3,4}\rangle =\big\langle \tfrac{1}{8},\tfrac{7}{8},\tfrac{5}{8},\tfrac{3}{8}\big\rangle \quad \text{(vertical arrow in Figure 1). } \end{align*} $$
Definition 1.3 (
${n}$
th prefold sequence)
Fold the line from
$0$
to
$1\ n$
times, where
$n\geq 0$
. Let j be an integer with
$0<j\leq 2^{n}$
and a a real number with
$0<a<1/2^{n}.$
We make the following definitions:
-
(1)
$F_{n}(a,j)$
, the jth term from the bottom lying at or directly above a, is the jth term of the nth prefold sequence at a (in particular,
$F(a,1)=a$
); -
(2)
$F_{n}(a)=\langle F_{n}(a,1),F_{n}(a,2),F_{n}(a,3),\ldots , F_{n}(a,2^{n})\rangle $
is the sequence of all terms in the nth prefold sequence at a; -
(3)
$\widetilde {F_{n}}(a)=\langle F_{n}(a,2^{n}),\ldots ,F_{n}(a,3),F_{n}(a,2),F_{n}(a,1)\rangle $
is the reverse nth prefold sequence at
$a.$
Lemma 1.4. For
$n>0$
,
$S_{n}=F_{n-1}({1}/{2^{n}})$
and
$S_n$
has
$2^{n-1}$
terms.
Proof. At the
$(n-1)$
th fold, there are
$2^{n-1}$
intervals each of size
${1}/{ 2^{n-1}}$
units. By Definition 1.3,
$F_{n-1}({1}/{2^{n}})$
represents the sequence of consecutive midpoints of consecutive intervals in this
$(n-1)$
th fold. By Definition 1.1, at the nth fold, this sequence of consecutive midpoints becomes the nth fold sequence, giving the result.
Theorem 1.5 (Form of
$F_{n}(a)$
)
For
$0<a<1/2^{n}$
,
$$\begin{align*}F_{n}(a)= \langle F_{n-1}(a),\widetilde{F_{n-1}}(({1}/ {2^{n-1}})-a)\rangle. \end{align*}$$
Theorem 1.6 (Recursive expression of prefolds)
We have
$$ \begin{align*} F_{n}(a,j)=\left\{ \begin{array}{ll} F_{n-1}(a,j)\text{ } & \text{if }\,0<j\leq 2^{n-1}, \\ F_{n-1}(({1}/{2^{n-1}})-a,2^{n}-j+1) & \text{if }\,2^{n-1}<j\leq 2^{n}. \end{array} \right. \notag \end{align*} $$
Theorem 1.7 (Prefold expression of folds)
For
$n>1,$
$$ \begin{align*} S_{n} &=\bigg\langle F_{n-2}\bigg(\frac{1}{2^{n}},1\bigg),F_{n-2}\bigg(\frac{1}{2^{n}} ,2\bigg),\ldots ,F_{n-2}\bigg(\frac{1}{2^{n}},2^{n-2}\bigg), \\ &\quad\ \ F_{n-2}\bigg(\frac{3}{2^{n}},2^{n-2}\bigg),F_{n-2}\bigg(\frac{3}{ 2^{n}},2^{n-2}-1\bigg),\ldots ,F_{n-2}\bigg(\frac{3}{2^{n}},1\bigg)\bigg\rangle. \end{align*} $$
Theorem 1.8 (Alternating differences within prefolds)
For
$n\geq 0$
and
$ 0<j\leq 2^{n}$
,
$$ \begin{align*} F_{n}\bigg(\frac{1}{2^{n+2}},j\bigg)=F_{n}\bigg(\frac{3}{2^{n+2}},j\bigg)+\frac{( -1)^{\,j}}{2^{n+1}}. \end{align*} $$
Theorem 1.9 (Alternating differences within folds)
For
$n\geq 2, 0<j\leq 2^{n-2}$
,
$$ \begin{align*} S_{n,j}=S_{n,2^{n-1}-j+1}+\frac{( -1) ^{\,j}}{2^{n-1}}. \end{align*} $$
Theorem 1.10 (Couplet addition within prefolds)
For
$n\geq 1$
and
$k=1,2,3,\ldots,2^{n-1}$
,
$$ \begin{align*} F_{n}(a,2k-1)+F_{n}(a,2k)=1. \end{align*} $$
Proof. We prove the result by induction on n. The result holds for
$n=1$
because
$$ \begin{align*} F_{1}(a,1)+F_{1}(a,2)=a+(1-a) =1. \end{align*} $$
Suppose the result is true for some n, that is, it is true for both
$ F_{n}(a)$
and
${F_{n}({1}/{2^{n}}-a).}$
By Theorem 1.5,
$$ \begin{align*} F_{n+1}(a)=\bigg\langle F_{n}(a),\widetilde{F_{n}}\bigg(\frac{1}{2^{n}} -a\bigg)\bigg\rangle. \end{align*} $$
Here,
$\widetilde {F_{n}}(1/2^n-a)$
is the reverse of
$F_{n}({1}/{2^{n}}-a)$
, and so even terms of
$F_{n}({1}/{ 2^{n}}-a)$
become odd terms in
$\widetilde {F_{n}}({1}/{2^{n}}-a)$
. This means that the result is true for both
$F_n(a)$
and
$\widetilde {F_{n}}({1}/{2^{n} }-a).$
It follows that the result is true for
$F_{n+1}(a)$
and therefore by induction for all
$n\geq 1.$
Theorem 1.11 (Couplet addition within folds)
For
$n\geq 2$
and
$k=1,2,3,\ldots ,2^{n-1},$
$$ \begin{align*} S_{n,2k-1}+S_{n,2k}=1. \end{align*} $$
Lemma 1.12 (Order of points in a fold)
For
$n\geq 0$
and
$0<a<{1}/{2^{n}} , $
let the jth interval of the nth fold be the interval containing
$ F_{n}(a,j).$
Then
-
• for j odd,
$F_{n}(a,j)$
increases as a increases, and -
• for j even,
$F_{n}(a,j)$
decreases as a increases.
Proof. We prove the result by induction on
$n.$
For
$n=0$
and
$0<a<b<1, F_{0}(a,1)\,{=}\,a$
and
$F_{0}(b,1)=b$
and so the result holds for
$n=0.$
Suppose the result is true for some
$n.$
For
$0<j\leq 2^{n},$
at the
$(n+1)$
th fold, the rightmost half of the jth interval in the nth fold is rotated
$180^{\circ }$
anticlockwise around
${1}/{2^{n+1}}$
to become the
$ ( 2^{n+1}-j+1) $
th interval in the
$(n+1)$
th fold. This rotation reverses the order of the points in this interval. That is, if we have
$0<j\leq 2^{n} $
and
$0<a<{1}/{2^{n+1}},$
-
• for j odd,
$F_{n+1}(a,2^{n+1}-j+1)$
decreases as a increases, -
• for j even,
$F_{n+1}(a,2^{n+1}-j+1)$
increases as a increases.
Since
$2^{n+1}-j+1$
has opposite parity to j, it follows that the result holds for
$n+1$
and so for all
$n.$
Theorem 1.13. For
$0<j\leq 2^{n-1},\label {pg}$
$$ \begin{align*} F_{n-1}\bigg(\frac{1}{2^{n+1}},j\bigg)=F_{n-1}\bigg(\frac{1}{2^{n}},j\bigg)+\frac{( -1) ^{\,j}}{2^{n+1}}. \end{align*} $$
Proof. By Lemma 1.12, since
${1}/{2^{n+1}}<{1}/{2^{n}},$
for j odd,
$F_{n-1}({1}/{2^{n+1}},j)$
must be less than
$F_{n-1}({1}/{2^{n}},j)$
by
${1}/{2^{n}}-{1}/{2^{n+1}}= {1}/{2^{n+1}}$
units. Similarly, for j even,
$F_{n-1}({1}/{2^{n+1}},j)$
must be greater than
$F_{n-1}({1}/{2^{n}},j)$
by
${1}/{2^{n+1}}$
units.
The next theorem shows the relationship between terms found in different folds.
Theorem 1.14 (Alternating differences between folds)
For
$n>0$
and
$0<j\leq 2^{n-1}$
,
$$ \begin{align*} S_{n+1,j}=S_{n,j}+\frac{(-1)^{\,j}}{2^{n+1}} \quad\mbox{and}\quad S_{n+1,2^{n}-j+1}=S_{n,j}+\frac{(-1)^{\,j+1}}{2^{n+1}}. \end{align*} $$
Proof. Suppose
$0<j\leq 2^{n-1}$
. By Lemma 1.4, Theorems 1.5 and 1.13 and Lemma 1.4 again,
$$ \begin{align*}S_{n+1,j} =F_{n}\bigg(\frac{1}{2^{n+1}},j\bigg) =F_{n-1}\bigg(\frac{1}{2^{n+1}},j\bigg) =F_{n-1}\bigg(\frac{1}{2^{n}},j\bigg)+\frac{( -1)^{\,j}}{2^{n+1}} =S_{n,j}+\frac{( -1)^{\,j}}{2^{n+1}} \end{align*} $$
and, by Theorem 1.9 and the result just established,
$$ \begin{align*} S_{n+1,2^{n}-j+1} =S_{n+1,j}+\frac{( -1) ^{\,j+1}}{2^{n}} =S_{n,j}+\frac{( -1) ^{\,j}}{2^{n+1}}+\frac{( -1)^{\,j+1}}{2^{n}} =S_{n,j}+\frac{( -1) ^{\,j+1}}{2^{n+1}}.\\[-38pt] \end{align*} $$
2 Normalised additive factorisation
From [Reference Bates, Bunder and Tognetti2], each positive integer can be represented by its unique set of normalised additive factors. This representation is part of a wider family of binary signed-digit representations of an integer defined as follows.
Definition 2.1 (After Tůma and Vábek [Reference Tůma and Vábek13])
A binary signed-digit representation of an integer z is a string
$\beta =b_{0},b_{1},\ldots ,b_{k}$
with
$b_{i}\in \{ -1,0,1\} $
such that
$z=\sum _{i=0}^{k}b_{i}2^{i}.$
We will use such representations in which k is even and the nonzero
$b_{i} $
values are alternately positive and negative. It is easy to see that such a representation is unique.
Normalised additive factorisation is used to represent a positive integer
$ j$
as an alternating series that contains an odd number of terms such that consecutive terms involve the value
$2$
raised to consecutive normalised additive factors of j. We designate the ordered set of normalised additive factors of j as
, where, for
$k $
even,
The algorithm for obtaining the normalised additive factors of j is as follows.
-
• Let
$b_{j,0}$
be the smallest nonnegative integer for which
$ j\leq 2^{b_{j,0}}.$
-
• If
$j=2^{b_{j,0}},$
then
$b_{j,0}$
is the only normalised additive factor of j. -
• If
$j<2^{b_{j,0}},$
then
$b_{j,0}$
is a positive integer. Let
$b_{j,1}$
be the smallest positive integer less than
$b_{j,0},$
for which
$ j>2^{b_{j,0}}-2^{b_{j,1}}.$
-
• Let
$b_{j,2}$
be the smallest nonnegative integer for which
$ j\leq 2^{b_{j,0}}-2^{b_{j,1}}+2^{b_{j,2}}.$
-
• If
$j=2^{b_{j,0}}-2^{b_{j,1}}+2^{b_{j,2}},$
then
$\{ b_{j,0},b_{j,1},b_{j,2}\} $
is the set of normalised additive factors of j. -
• If
$j<2^{b_{j,0}}-2^{b_{j,1}}+2^{b_{j,2}},$
let
$b_{j,3}$
be the smallest positive integer less than
$b_{j,2},$
for which
$ j>2^{b_{j,0}}-2^{b_{j,1}}+2^{b_{j,2}}-2^{b_{j,3}}.$
-
• Let
$b_{j,4}$
be the smallest positive integer for which
$ j\leq 2^{b_{j,0}}-2^{b_{j,1}}+2^{b_{j,2}}-2^{b_{j,3}}+2^{b_{j,4}}.$
-
• Continuing in this way, the process must eventually terminate at
$ b_{j,k},$
where k is even, such that
$j=\sum _{i=0}^{k}( -1) ^{i}2^{b_{j,i}}.$
The ordered set of normalised additive factors of j is then
and has odd cardinality. Note that for j odd,
$b_{j,k}=0 $
and for j even,
$b_{j,k}>0.$
The Maple code for this algorithm appears at the end of this section.
Example 2.2. The set of normalised additive factors of
$12=2^{4}-2^{3}+2^{2}$
is
$\{ 4,3,2\} ,$
not
$\{ 4,2\} ,$
since the set must have odd cardinality. Similarly, the set of normalised additive factors of
$15$
is
$ \{ 4,1,0\} ,$
not
$\{ 4,0\} .$
Theorem 2.3 (Normalised additive factors)
If
then
Proof. Since
$j=2^{b_{j,0}}-2^{b_{j,1}}+2^{b_{j,2}}-\cdots +2^{b_{j,k}}$
, for j even, we must have
$b_{j,k}>0,$
so
$$ \begin{align*} 2^{b_{j,0}}-j+1=2^{b_{j,1}}-2^{b_{j,2}}+2^{b_{j,3}}-\cdots -2^{b_{j,k}}+2^{0}. \end{align*} $$
That is,
Similarly, for j odd, we must have
$b_{j,k}=0,$
so
$$ \begin{align*} 2^{b_{j,0}}-j+1 &=2^{b_{j,1}}-2^{b_{j,2}}+2^{b_{j,3}}-\cdots +2^{b_{j,k-1}}-2^{b_{j,k}}+2^{0} \\ &=2^{b_{j,1}}-2^{b_{j,2}}+2^{b_{j,3}}-\cdots +2^{b_{j,k-1}}. \end{align*} $$
That is,
.
2.1 Maple code for the normalised additive factors of j
The method for obtaining the normalised additive factors of j is translated into Maple code, graciously provided by the referee. Let b be the least integer such that
$2^{b}\geq x.$
That is, b is the ceiling of the base
$2$
logarithm of x and, for integers b and
$x,b<x$
which is the same as
$ b\leq x+1.$
for j to
$5$
do
$m:=0$
;
$i:=0$
;
finished
$:=$
false;
while finished
$=$
false do
$\;\qquad b[2\ast i]:=$
ceil
$(\log [2](j-m))$
;
;
$\;\qquad $
if
$m=j$
then finished
$:=$
true end if;
$\;\qquad $
if finished
$=$
false then
$b[2\ast i+1]:=$
ceil
$(\log [2](m-j+1))$
;
;
$\;\qquad i:=i+1$
$\;\qquad $
end if
$\;\qquad $
end do;
$\;\qquad $
printf(‘
$j=\%2d \#\#$
’, j);
$\;\qquad $
for k from
$0$
to
$2\ast i$
do printf(‘
$\%2d$
’,
$b[k]$
)
$\;\qquad $
end do;
$\;\qquad $
printf(‘
$\backslash n$
’, x)
$\;\qquad $
end do;
$\;\qquad j=1\ \#\#\ 0$
$\;\qquad j=2\ \#\#\ 1$
$\;\qquad j=3\ \#\#\ 2 1 0$
$\;\qquad j=4\ \#\#\ 2$
$\;\qquad j=5\ \#\#\ 3 2 0$
3 Finding points from folds
We now show that
$S_{n,j}$
can be represented using an alternating series of unit fractions based on n and the set of normalised additive factors of
$ j. $
Thus we can find every point in every fold using only n and j.
Theorem 3.1 (Points from addresses)
Let
and
$n\geq 1$
. Then
$$ \begin{align*} S_{n,j} & =\sum_{i=0}^{k}\frac{( -1)^{i}}{2^{b_{j,i}-1}}-\frac{1}{ 2^{n}} \quad \text{if}\ j\ \text{is even}, \\ S_{n,j} & =\sum_{i=0}^{k-1}\frac{( -1)^{i+1}}{2^{b_{j,i}-1}}+\frac{1 }{2^{n}} \quad \text{if}\ j\ \text{is odd}. \end{align*} $$
Proof. We prove the result by induction on n. We have
and the result holds for
$n=1$
because
$$ \begin{align*} S_{1,1}=\frac{1}{2}=\sum_{i=0}^{0-1}\frac{(-1) ^{i+1}}{ 2^{b_{j,i}-1}}+\frac{1}{2^{1}}=0+\frac{1}{2}. \end{align*} $$
Suppose the result holds for n. We consider two cases.
Case 1:
$0<j\leq 2^{n-1}.$
We use Theorem 1.14 and the induction hypothesis. For j even,
$$ \begin{align*} S_{n+1,j} =S_{n,j}+\frac{1}{2^{n+1}} =\sum_{i=0}^{k}\frac{( -1) ^{i}}{2^{b_{j,i}-1}}-\frac{1}{2^{n}}+ \frac{1}{2^{n+1}} =\sum_{i=0}^{k}\frac{( -1) ^{i}}{2^{b_{j,i}-1}}-\frac{1}{2^{n+1} }. \end{align*} $$
For j odd,
$$ \begin{align*} S_{n+1,j} =S_{n,j}-\frac{1}{2^{n+1}} =\sum_{i=0}^{k-1}\frac{( -1) ^{i+1}}{2^{b_{j,i}-1}}+\frac{1}{ 2^{n}}-\frac{1}{2^{n+1}} =\sum_{i=0}^{k-1}\frac{( -1) ^{i+1}}{2^{b_{j,i}-1}}+\frac{1}{ 2^{n+1}}. \end{align*} $$
Thus, for
$0<j\leq 2^{n-1},$
our result is true for
$n+1.$
Case 2:
$2^{n-1}<j\leq 2^{n}.$
For this case, we have
$b_{j,0}=n.$
There are two subcases. For j even,
$2^{n}-j+1\leq 2^{n-1}$
is odd. By Theorem 2.3,
and so by Case 1 and Theorem 1.14,
$$ \begin{align*} S_{n+1,j} =S_{n,2^{n}-j+1}+\frac{1}{2^{n+1}} =\sum_{i=1}^{k}\frac{( -1) ^{i}}{2^{b_{j,i}-1}}+\frac{1}{2^{n}}+ \frac{1}{2^{n+1}} =\sum_{i=0}^{k}\frac{( -1) ^{i}}{2^{b_{j,i}-1}}-\frac{1}{2^{n+1}}, \end{align*} $$
since
${1}/{2^{b_{j,0}-1}}={1}/{2^{n-1}}$
. For j odd,
$2^{n}-j+1\leq 2^{n-1}$
is even. By Theorem 2.3,
and so by Case 1 and Theorem 1.14,
$$ \begin{align*} S_{n+1,j} =S_{n,2^{n}-j+1}-\frac{1}{2^{n+1}} =\sum_{i=1}^{k-1}\frac{( -1) ^{i+1}}{2^{b_{j,i}-1}}-\frac{1}{ 2^{n}}-\frac{1}{2^{n+1}} =\sum_{i=0}^{k-1}\frac{( -1) ^{i+1}}{2^{b_{j,i}-1}}+\frac{1}{ 2^{n+1}}, \end{align*} $$
where again
${1}/{2^{b_{j,0}-1}}={1}/{2^{n-1}}$
. Thus, for
$2^{n-1}<j\leq 2^{n},$
the result is true for
$n+1.$
By induction the result is true for all
$n.$
Example 3.2. We have
. From Theorem 3.1,
$$ \begin{align*} S_{6,11} =\sum_{i=0}^{3}\frac{( -1) ^{i+1}}{2^{b_{11,i}-1}}+ \frac{1}{2^{6}} =\frac{41}{64}. \end{align*} $$
Remark 3.3. Appendix A identifies all points from addresses for
$n=6$
and illustrates many of the results obtained so far. The numerators of the sequence of addresses
$(1,63,33,31,\ldots )$
are a subset of sequence A119608 in the on-line Encyclopedia of Integer Sequences [Reference Quet10]. In fact, A119608 concatenates the sequence of numerators for each n.
4 Odd unit factorisation
We now examine the reverse situation and identify the address (fold n and location j) of the point
${(2k+1)}/{2^{n}}<1.$
Definition 4.1 (Initial odd factorisation)
If p is an odd integer, then there is an odd integer q such that either
$p=2q+1$
or
$p=2q-1.$
This q is called the initial odd factor of
$p.$
Theorem 4.2 (Odd factorisation)
Let p be an odd integer.
-
(i) If
$p\equiv 1 \pmod 4,$
then p has initial odd factorisation
$p=2\lceil {p}/{2}\rceil -1$
. -
(ii) If
$p\equiv 3 \pmod 4,$
then p has initial odd factorisation
$p=2\lfloor {p}/{2}\rfloor +1.$
Proof. For
$p\equiv 1 \pmod 4, \lfloor {p}/{2} \rfloor $
is even and
$\lceil {p}/{2}\rceil $
is odd. It follows that the initial odd factorisation of p is given by
$ p=2\lceil {p}/{2}\rceil -1.$
For
$p\equiv 3 \pmod 4, \lceil {p}/{2} \rceil $
is even and
$\lfloor {p}/{2}\rfloor $
is odd. It follows that the initial odd factorisation of p is given by
$ p=2\lfloor {p}/{2}\rfloor +1.$
For p odd, we obtain the odd factorisation of p as follows. (Note that, for each iteration,
$\pm $
denotes
$+$
or
$-$
but not both, and is determined via Theorem 4.2.)
-
• Let
$q_{0}$
be the initial odd factor of
$p.$
Then
$p=2q_{0}\pm 1.$
-
• Let
$q_{1}$
be the initial odd factor of
$q_{0}.$
Then
$ q_{0}=2q_{1}\pm 1$
and
$p=2( 2q_{1}\pm 1) \pm 1.$
-
• Continuing in this way, the process terminates at
$q_{t}=1$
and (4.1)If at this stage, t of these factorisation steps have occurred, we call this expression the tth odd unit factorisation of
$$ \begin{align} p=2( \cdots ( 2( 2( 2.\mathbf{1}+1) \pm 1) \pm 1) \cdots ) \pm 1. \end{align} $$
$p.$
The
$\mathbf {1}$
in the middle of (4.1) can be replaced with
$$ \begin{align} \mathbf{1} =2.\mathbf{1}-1 =2( 2.\mathbf{1}-1) -1) = \cdots =( 2(\cdots (2(2( 2.\mathbf{1}-1) -1)-1)\cdots )-1). \end{align} $$
Thus we can extend (4.1) indefinitely by replacing the
$\mathbf {1}$
in the middle of (4.1) with (4.2). With these replacements we obtain the
$( t+1) $
th,
$( t+2) $
th,
$\ldots $
odd unit factorisations of
$p.$
Definition 4.3 (Odd unit factorisations of p)
For p an odd integer, let
$p_{(n)}=$
$$ \begin{align*}\underset{n\text{ pairs of brackets}}{\underbrace{(2\cdots (2\cdots (2(2\cdots (2(2\cdots ( 2( 2.\boldsymbol{1}-1) -1) \cdots -1)+1)\cdots +1)-1)\cdots -1)\cdots \pm 1)}}\end{align*} $$
be the nth odd unit factorisation of p. The nth odd unit set of
$p,$
styled
$p_{\mathrm {ou}n},$
is a set
$p_{\mathrm {ou}n}=\{ p_{0},p_{1},\ldots ,p_{k}\} $
where
$p_{i}>0$
for
$i>0$
and
$n=\sum _{i=0}^{k}p_{i},$
such that:
-
•
$p_{0}$
is the number of consecutive innermost brackets ending in
$-1)$
; -
•
$p_{1}$
is the number of consecutive innermost brackets ending in
$+1)$
enclosing the innermost
$p_{0}$
brackets; -
•
$p_{2}$
is the number of consecutive brackets ending in
$-1)$
enclosing the innermost
$( p_{0}+p_{1}) $
brackets, and so on until -
•
$p_{k}$
is the number of consecutive brackets ending in
$+1)$
for k odd, or
$-1)$
for k even, enclosing the innermost
$\sum _{i=0}^{k-1}p_{i}$
brackets
Example 4.4. What are the odd unit sets of
$17?$
We progressively odd-factorise
$17$
until we obtain its odd unit factorisation:
$$ \begin{align*} 17 =2.\mathbf{9}-1 =2(2.\mathbf{5}-1)-1 =2(2(2.\mathbf{3}-1)-1)-1 =2(2(2(2.\mathbf{1}+1)-1)-1)-1. \end{align*} $$
So the odd unit factorisations of
$17$
are
$$ \begin{align*} 17_{( 4) } &=( 2( 2( 2( 2.\boldsymbol{1} +1) -1) -1) -1), \\ 17_{( 5) } &=( 2( 2( 2( 2( 2. \boldsymbol{1}-1) +1) -1) -1) -1), \\ 17_{( 6) } &=( 2( 2( 2( 2( 2( 2. \boldsymbol{1}-1) -1) +1) -1) -1) -1), \\ &\vdots \end{align*} $$
Accordingly, the odd unit sets of
$17$
are
$$ \begin{align*} 17_{\mathrm{ou}4} =\{ 0,1,3\}, \quad 17_{\mathrm{ou}5} =\{ 1,1,3\} , \quad 17_{\mathrm{ou}6} =\{ 2,1,3\} , \quad\ldots,\quad17_{\mathrm{ou}n} =\{ n-4,1,3\}. \end{align*} $$
5 Finding folds from points
We now find the address of the point
${p}/{2^{n}}<1$
, where p is an odd positive integer, by examining the odd unit sets of
$p.$
Theorem 5.1 contains two binary signed-digit expansions: in (i),
$j-1$
is written as an alternating series where each term is
$2$
raised to a power that is the sum of the members of a subset of an odd unit set; while in (ii), similar comments apply for
$j.$
Theorem 5.1 (Addresses from points)
Let
$p<2^{n}$
be an odd positive integer where
$p_{\mathrm {ou}n}=\{ p_{0},p_{1},\ldots ,p_{k}\} $
and
$ n=\sum _{i=0}^{k}p_{i}.$
The point
${p}/{2^{n}}$
is the point
$S_{n,j}$
where:
-
(i) if k is even, then j is odd and
$j=\sum _{i=0}^{k-1}( -1) ^{i+1}2^{p_{0}+p_{1}+\cdots +p_{i}}+1$
; -
(ii) if k is odd, then j is even and
$j=\sum _{i=0}^{k-1}( -1) ^{i}2^{p_{0}+p_{1}+\cdots +p_{i}}$
.
Proof. We prove the result by induction on n. For
$n=1$
, the point
$\tfrac 12$
has
$1_{\mathrm {ou}1}=\{ 1\} $
and so
$k=0,$
which is even. So (i) holds with
$j=1$
, that is,
$\tfrac 12=S_{1,1}.$
Suppose the result is true for
$S_{n},$
where
$0<j\leq 2^{n-1}.$
We consider two cases.
Case (i): j odd. Then k is even. Let
$S_{n+1,j}={p^{\prime }}/{ 2^{n+1}}.$
For
$0<j\leq 2^{n-1}$
, by Theorem 1.14,
$p^{\prime }=2p-1$
, so
$ p_{i}^{\prime }=p_{i}$
for
$0\leq i\leq k-1$
and by the induction hypothesis,
$$ \begin{align*} j=\sum_{i=0}^{k-1}( -1) ^{i+1}2^{p_{0}^{\prime }+p_{1}^{\prime }+\cdots +p_{i}^{\prime }}+1. \end{align*} $$
For
$2^{n-1}<j\leq 2^{n}$
, by Theorem 1.14,
$ S_{n+1,j}=S_{n,2^{n}-j+1}+{1}/{2^{n+1}}.$
If
$S_{n,2^{n}-j+1}={ p^{\prime \prime }}/{2^{n}},$
then
$p^{\prime }=2p^{\prime \prime }+1$
,
$ p_{i}^{\prime }=p_{i}^{\prime \prime }$
for
$0\leq i\leq k$
and
$ p_{k+1}^{\prime }=1.$
By the induction hypothesis, as j is odd,
$2^{n}-j+1$
is even and
$$ \begin{align*} 2^{n}-j+1=\sum_{i=0}^{k}( -1) ^{i}2^{p_{0}^{\prime }+p_{1}^{\prime }+\cdots +p_{i}^{\prime }}. \end{align*} $$
Since
$n=p_{0}^{\prime }+p_{1}^{\prime }+\cdots +p_{k}^{\prime },$
this again gives the required result for
$ j $
.
Thus for
$0<j\leq 2^{n}$
, the result is true for all odd values of j in
$ S_{n+1}.$
Case (ii): j even. Then k is odd. This case proceeds identically as for (i).
It follows that if our result is true for each
$S_{n,j}$
where
$0<j\leq 2^{n-1},$
it is also true for each
$S_{n+1,j}$
where
$0<j\leq 2^{n}.$
Example 5.2. What is the address of the point
${25}/{64}?$
Since
${25}/{64}={25}/{2^{6}},$
it is found in the
$6$
th fold. We have
$$ \begin{align*} 25_{(6)}=2( 2( 2( 2( 2( 2.1-1) -1) +1) +1) -1) -1. \end{align*} $$
Thus
$25_{\mathrm {ou}6}=\{ 2,2,2\} .$
By Theorem 5.1(i), for k even,
${25}/{64}$
must be at the position
$$ \begin{align*} 2^{2+2}-2^{2}+1=16-4+1=13. \end{align*} $$
Thus
${25}/{64}$
is the point
$S_{6,13}.$
Remark 5.3. Appendix B, for
$n=6,$
identifies each address that is generated from each point
$.$
The numerators of the sequence of addresses
$(1,32,17,16,\ldots )$
are a subset of the paperfolding sequence A281589 in the on-line Encyclopedia of Integer Sequences [Reference Sigrist12]. The comments in [Reference Sigrist12] link the sequence to a 2-regular sequence.
Acknowledgements
We thank the anonymous referee for providing helpful and thorough comments and especially for providing the Maple code for normalised additive factorisation in Section 2 and drawing our attention to the sequences A119608 and A281589 in the on-line Encyclopedia of Integer Sequences [Reference Quet10, Reference Sigrist12].
My (BB) introduction to paperfolding occurred as an undergraduate student of Alf van der Poorten. He casually mentioned it at a residential school. It never occurred to me that I would become fascinated by it.
Appendix A Identifying points from addresses for
$n=6$
.
Appendix B Identifying addresses from points for
$n=6$
.
