1 Introduction
The germinal idea of this investigation was the definition of nuclear dimension in [Reference Winter and Zacharias15, Definition 2.1], which quantifies the completely positive approximation property (CPAP) of nuclear maps (although this notion goes back even further to the decomposition rank in [Reference Kirchberg and Winter14]).
Definition 1.1 [Reference Brown and Ozawa4, Ch. 2].
A contractive completely positive map
![]() $\pi :A\rightarrow B$
between C*-algebras (or to a von Neumann algebra B) is called nuclear (respectively weakly nuclear) if there exist a net
$\pi :A\rightarrow B$
between C*-algebras (or to a von Neumann algebra B) is called nuclear (respectively weakly nuclear) if there exist a net
![]() $(F_n)$
of finite-dimensional C*-algebras and contractive completely positive maps
$(F_n)$
of finite-dimensional C*-algebras and contractive completely positive maps
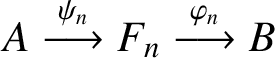 $A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }B$
such that
$A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }B$
such that
![]() $(\varphi _n\circ \psi _n)$
converges to
$(\varphi _n\circ \psi _n)$
converges to
![]() $\pi $
in the point-norm (respectively point-
$\pi $
in the point-norm (respectively point-
![]() $\sigma $
-weak) topology. If
$\sigma $
-weak) topology. If
![]() $\pi $
is the identity, then we say that A itself is nuclear; if
$\pi $
is the identity, then we say that A itself is nuclear; if
![]() $\pi $
is an inclusion, we say that A is exact.
$\pi $
is an inclusion, we say that A is exact.
Methods for strengthening the completely positive approximation property were first explored in [Reference Hirshberg, Kirchberg and White13]. This was synthesised with results of [Reference Blackadar and Kirchberg2] on quasidiagonal nuclear C*-algebras into [Reference Brown, Carrión and White3], which was built upon in [Reference Carrión and Schafhauser6]. This paper builds further by providing a partial answer to the final question in [Reference Carrión and Schafhauser6].
The case of nuclear A was examined in [Reference Hirshberg, Kirchberg and White13, Theorem 1.4], showing that we may then find
![]() $\varphi _n:F_n\rightarrow A$
(as in Definition 1.1) that are convex combinations of finitely many contractive completely positive order zero maps. From [Reference Brown, Carrión and White3, Theorem 3.1], the net
$\varphi _n:F_n\rightarrow A$
(as in Definition 1.1) that are convex combinations of finitely many contractive completely positive order zero maps. From [Reference Brown, Carrión and White3, Theorem 3.1], the net
![]() $(\psi _n:A\rightarrow F_n)$
may be chosen to be approximately order zero. Furthermore, drawing from [Reference Blackadar and Kirchberg2], if both A and all of its traces are quasidiagonal, then
$(\psi _n:A\rightarrow F_n)$
may be chosen to be approximately order zero. Furthermore, drawing from [Reference Blackadar and Kirchberg2], if both A and all of its traces are quasidiagonal, then
![]() $(\psi _n)$
may be chosen to be approximately multiplicative. In fact, [Reference Brown, Carrión and White3, Theorem 2.2] shows that the converse is true as well.
$(\psi _n)$
may be chosen to be approximately multiplicative. In fact, [Reference Brown, Carrión and White3, Theorem 2.2] shows that the converse is true as well.
Using the result from [Reference Hirshberg, Kirchberg and White13] as a starting point, Carrión and Schafhauser [Reference Carrión and Schafhauser6] began the process of generalising to nonnuclear A: provided that the nuclear map
![]() $\pi $
is order zero, we may find
$\pi $
is order zero, we may find
![]() $(\psi _n)$
that is approximately order zero and
$(\psi _n)$
that is approximately order zero and
![]() $\varphi _n$
that are convex combinations of contractive completely positive order zero maps [Reference Carrión and Schafhauser6, Theorem 1]. Additionally, approximate multiplicativity of
$\varphi _n$
that are convex combinations of contractive completely positive order zero maps [Reference Carrión and Schafhauser6, Theorem 1]. Additionally, approximate multiplicativity of
![]() $(\psi _n)$
is attainable for weakly nuclear
$(\psi _n)$
is attainable for weakly nuclear
![]() $\pi $
with quasidiagonal A [Reference Carrión and Schafhauser6, Proposition 3].
$\pi $
with quasidiagonal A [Reference Carrión and Schafhauser6, Proposition 3].
The question is, then, ‘What is necessary or sufficient to get approximate multiplicativity for nuclear
![]() $\pi $
?’ We give two necessary conditions.
$\pi $
?’ We give two necessary conditions.
Lemma 1.2. Let
![]() $\pi :A\rightarrow B$
be a *-homomorphism between C*-algebras
$\pi :A\rightarrow B$
be a *-homomorphism between C*-algebras
![]() $A,B$
that admits an approximately multiplicative norm-decomposition (see Definition 2.5) and let
$A,B$
that admits an approximately multiplicative norm-decomposition (see Definition 2.5) and let
![]() $\tau $
be a trace on
$\tau $
be a trace on
![]() $\pi (A)$
. Then
$\pi (A)$
. Then
![]() $\tau \circ \pi $
is a quasidiagonal trace on A.
$\tau \circ \pi $
is a quasidiagonal trace on A.
Theorem 1.3. Let
![]() $\pi :A\rightarrow B\subseteq B^{**}$
be a *-homomorphism that admits an approximately multiplicative
$\pi :A\rightarrow B\subseteq B^{**}$
be a *-homomorphism that admits an approximately multiplicative
![]() $\sigma $
-strong*-decomposition (see Definition 2.2). Then the inclusion
$\sigma $
-strong*-decomposition (see Definition 2.2). Then the inclusion
![]() $\pi (A)\subseteq B$
is nuclear.
$\pi (A)\subseteq B$
is nuclear.
We also reach a full characterisation in the exact case, which stems from a more general sufficient condition given in Proposition 2.9.
Theorem 1.4. Let A be an exact C*-algebra and
![]() $\pi :A\rightarrow B$
be a *-homomorphism to another C*-algebra B. Then
$\pi :A\rightarrow B$
be a *-homomorphism to another C*-algebra B. Then
![]() $\pi $
admits an approximately multiplicative norm- decomposition if and only if it is nuclear and quasidiagonal and
$\pi $
admits an approximately multiplicative norm- decomposition if and only if it is nuclear and quasidiagonal and
![]() $\tau \circ \pi $
is a quasidiagonal trace on A for every trace
$\tau \circ \pi $
is a quasidiagonal trace on A for every trace
![]() $\tau $
on
$\tau $
on
![]() $\pi (A)$
.
$\pi (A)$
.
We shall use the fact that the
![]() $\sigma $
-strong* topology on a von Neumann algebra N agrees on bounded subsets with the topology generated by seminorms
$\sigma $
-strong* topology on a von Neumann algebra N agrees on bounded subsets with the topology generated by seminorms
 $$ \begin{align*}\|x\|_{\rho}:= \sqrt{\rho\bigg(\frac{x^*x+xx^*}{2}\bigg)}\end{align*} $$
$$ \begin{align*}\|x\|_{\rho}:= \sqrt{\rho\bigg(\frac{x^*x+xx^*}{2}\bigg)}\end{align*} $$
for a separating family of normal states
![]() $\rho $
on N (see, for example, [Reference Blackadar1, Proposition III.2.2.19]).
$\rho $
on N (see, for example, [Reference Blackadar1, Proposition III.2.2.19]).
For simplicity, we shall assume that our C*-algebras are separable and unital.
2 Results
Our results are only possible through use of the following as yet unpublished result, which is something of a folklore theorem (see [Reference Castillejos, Evington, Tikuisis and White7]). We thank the authors of [Reference Carrión, Castillejos, Evington, Schafhauser, Tikuisis and White5] for allowing us to reproduce the proof here.
Theorem 2.1 [Reference Carrión, Castillejos, Evington, Schafhauser, Tikuisis and White5].
Let
![]() $\theta ,\pi :A\rightarrow N$
be weakly nuclear *-homomorphisms from a C*-algebra A to a finite von Neumann algebra N that agree on traces (that is,
$\theta ,\pi :A\rightarrow N$
be weakly nuclear *-homomorphisms from a C*-algebra A to a finite von Neumann algebra N that agree on traces (that is,
![]() $\tau \circ \theta = \tau \circ \pi $
for every trace
$\tau \circ \theta = \tau \circ \pi $
for every trace
![]() $\tau $
on N). Then
$\tau $
on N). Then
![]() $\theta $
and
$\theta $
and
![]() $\pi $
are strong* approximately unitarily equivalent.
$\pi $
are strong* approximately unitarily equivalent.
Proof. Let
![]() $\tau _0$
be a normal trace on N. Replacing N with
$\tau _0$
be a normal trace on N. Replacing N with
![]() $\pi _{\tau _0}(N)$
(where
$\pi _{\tau _0}(N)$
(where
![]() $\pi _\tau $
is the Gelfand–Naimark–Segal representation corresponding to
$\pi _\tau $
is the Gelfand–Naimark–Segal representation corresponding to
![]() $\tau _0$
) if necessary, we may assume that
$\tau _0$
) if necessary, we may assume that
![]() $\tau _0$
is faithful. We need to show that
$\tau _0$
is faithful. We need to show that
![]() $\theta $
and
$\theta $
and
![]() $\pi $
are unitarily equivalent as maps into the tracial ultrapower
$\pi $
are unitarily equivalent as maps into the tracial ultrapower
![]() $N^\omega _\tau $
of N with respect to
$N^\omega _\tau $
of N with respect to
![]() $\tau _0$
.
$\tau _0$
.
Define
![]() $\mu :A\rightarrow \mathbb {M}_2(N^\omega _\tau )$
by
$\mu :A\rightarrow \mathbb {M}_2(N^\omega _\tau )$
by
 $$ \begin{align*}\mu(a)= \begin{bmatrix}\theta(a)&0\\0&\pi(a)\end{bmatrix}.\end{align*} $$
$$ \begin{align*}\mu(a)= \begin{bmatrix}\theta(a)&0\\0&\pi(a)\end{bmatrix}.\end{align*} $$
Then
![]() $\mu $
is a weakly nuclear *-homomorphism. We claim that
$\mu $
is a weakly nuclear *-homomorphism. We claim that
![]() $M:=\pi (A)''$
is hyperfinite.
$M:=\pi (A)''$
is hyperfinite.
Indeed, let
![]() $\psi _n:A\rightarrow F_n$
and
$\psi _n:A\rightarrow F_n$
and
![]() $\varphi _n:F_n\rightarrow M$
be contractive completely positive maps for finite-dimensional C*-algebras
$\varphi _n:F_n\rightarrow M$
be contractive completely positive maps for finite-dimensional C*-algebras
![]() $F_n$
such that
$F_n$
such that
![]() $(\varphi _n\circ \psi _n)$
converges in the point-weak* topology to
$(\varphi _n\circ \psi _n)$
converges in the point-weak* topology to
![]() $\mu $
. Fix a unital normal representation
$\mu $
. Fix a unital normal representation
![]() $M\subseteq \mathbb {B}(\mathcal {H})$
and define maps
$M\subseteq \mathbb {B}(\mathcal {H})$
and define maps
![]() $\eta ,\eta _n:A\otimes _{\mathrm {alg}} M'\rightarrow \mathbb {B}(\mathcal {H})$
by
$\eta ,\eta _n:A\otimes _{\mathrm {alg}} M'\rightarrow \mathbb {B}(\mathcal {H})$
by
![]() $\eta (a\otimes b)= \mu (a)b$
and
$\eta (a\otimes b)= \mu (a)b$
and
![]() ${\eta _n(a\otimes b)}= {\varphi _n\circ \psi _n(a)b}$
, so that
${\eta _n(a\otimes b)}= {\varphi _n\circ \psi _n(a)b}$
, so that
![]() $(\eta _n)$
converges to
$(\eta _n)$
converges to
![]() $\eta $
in the point-weak* topology. The
$\eta $
in the point-weak* topology. The
![]() $\eta _n$
are continuous with respect to the minimal tensor product since they factor through
$\eta _n$
are continuous with respect to the minimal tensor product since they factor through
![]() $F_k\otimes M'$
and hence so is
$F_k\otimes M'$
and hence so is
![]() $\eta $
. A conditional expectation of
$\eta $
. A conditional expectation of
![]() $\mathbb {B}(\mathcal {H})$
onto
$\mathbb {B}(\mathcal {H})$
onto
![]() $M'$
is then provided by [Reference Brown and Ozawa4, Proposition 3.6.5], confirming that M is injective and hence hyperfinite by Connes’ theorem [Reference Connes9, Theorem 6].
$M'$
is then provided by [Reference Brown and Ozawa4, Proposition 3.6.5], confirming that M is injective and hence hyperfinite by Connes’ theorem [Reference Connes9, Theorem 6].
Define projections
 $$ \begin{align*}p_1= \begin{bmatrix}1&0\\0&0\end{bmatrix},\quad p_2= \begin{bmatrix}0&0\\0&1\end{bmatrix}\end{align*} $$
$$ \begin{align*}p_1= \begin{bmatrix}1&0\\0&0\end{bmatrix},\quad p_2= \begin{bmatrix}0&0\\0&1\end{bmatrix}\end{align*} $$
in
![]() $\mathbb {M}_2(N^\omega _\tau )\cap \pi (A)'$
. Then
$\mathbb {M}_2(N^\omega _\tau )\cap \pi (A)'$
. Then
![]() $\tau (p_1x)= \tau (p_2x)$
for every normal trace
$\tau (p_1x)= \tau (p_2x)$
for every normal trace
![]() $\tau $
and every
$\tau $
and every
![]() $x\in \pi (A)$
and hence also for every
$x\in \pi (A)$
and hence also for every
![]() $x\in \pi (A)''$
. By [Reference Castillejos, Evington, Tikuisis, White and Winter8, Lemma 4.5],
$x\in \pi (A)''$
. By [Reference Castillejos, Evington, Tikuisis, White and Winter8, Lemma 4.5],
![]() $\tau (p_1)= \tau (p_2)$
for every trace
$\tau (p_1)= \tau (p_2)$
for every trace
![]() $\tau $
on
$\tau $
on
![]() $\mathbb {M}_2(N^\omega _\tau )\cap \pi (A)'$
. Thus, there is a unitary
$\mathbb {M}_2(N^\omega _\tau )\cap \pi (A)'$
. Thus, there is a unitary
![]() $u=[u_{i,j}]\in \mathbb {M}_2(N^\omega _\tau )\cap \pi (A)'$
such that
$u=[u_{i,j}]\in \mathbb {M}_2(N^\omega _\tau )\cap \pi (A)'$
such that
![]() $u^*p_1u=p_2$
and hence
$u^*p_1u=p_2$
and hence
![]() $u_{1,1}= 0$
and
$u_{1,1}= 0$
and
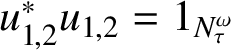 $u_{1,2}^*u_{1,2}= 1_{N^\omega _\tau }$
. Therefore,
$u_{1,2}^*u_{1,2}= 1_{N^\omega _\tau }$
. Therefore,
![]() $u_{1,2}$
is unitary since
$u_{1,2}$
is unitary since
![]() $N^\omega _\tau $
is finite, and
$N^\omega _\tau $
is finite, and
![]() $\theta (a)u_{1,2}=u_{1,2}\pi (a)$
since
$\theta (a)u_{1,2}=u_{1,2}\pi (a)$
since
![]() $u\in \pi (A)'$
.
$u\in \pi (A)'$
.
Most of the proof of the following lemma is borrowed from [Reference Brown, Carrión and White3]; improvements are due to mixing in material from [Reference Carrión and Schafhauser6] and Theorem 2.1. To properly state our results, we need (the W* half of) the paper’s central definition.
Definition 2.2. Let
![]() $\pi :A\rightarrow N$
be a *-homomorphism from a C*-algebra A to a von Neumann algebra N. An approximately multiplicative
$\pi :A\rightarrow N$
be a *-homomorphism from a C*-algebra A to a von Neumann algebra N. An approximately multiplicative
![]() $\sigma $
-strong*-decomposition of
$\sigma $
-strong*-decomposition of
![]() $\pi $
is a net of unitary completely positive maps
$\pi $
is a net of unitary completely positive maps
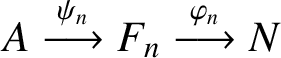 $A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }N$
for finite-dimensional C*-algebras
$A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }N$
for finite-dimensional C*-algebras
![]() $F_n$
such that:
$F_n$
such that:
-
(i)
 $\varphi _n\circ \psi _n(x)\rightarrow \pi (x)$
in the
$\varphi _n\circ \psi _n(x)\rightarrow \pi (x)$
in the
 $\sigma $
-strong* topology for all
$\sigma $
-strong* topology for all
 $x\in A$
;
$x\in A$
; -
(ii)
 $\|\psi _n(x)\psi _n(y)-\psi _n(xy)\|\rightarrow 0$
for all
$\|\psi _n(x)\psi _n(y)-\psi _n(xy)\|\rightarrow 0$
for all
 $x,y\in A$
;
$x,y\in A$
; -
(iii) every
 $\varphi _n$
is a *-homomorphism.
$\varphi _n$
is a *-homomorphism.
Lemma 2.3. Let A be a quasidiagonal C*-algebra and
![]() $\pi :A\rightarrow N$
be a weakly nuclear *-homomorphism such that, for every trace
$\pi :A\rightarrow N$
be a weakly nuclear *-homomorphism such that, for every trace
![]() $\tau $
on
$\tau $
on
![]() $\pi (A)$
, the trace
$\pi (A)$
, the trace
![]() $\tau \circ \pi $
is quasidiagonal. Then
$\tau \circ \pi $
is quasidiagonal. Then
![]() $\pi $
admits an approximately multiplicative
$\pi $
admits an approximately multiplicative
![]() $\sigma $
-strong*-decomposition.
$\sigma $
-strong*-decomposition.
Remark 2.4. Note that the ‘quasidiagonal
![]() $\tau \circ \pi $
’ condition is satisfied if either every trace on A or every trace on
$\tau \circ \pi $
’ condition is satisfied if either every trace on A or every trace on
![]() $\pi (A)$
is quasidiagonal. As foreshadowed in Lemma 1.2, this property is essential.
$\pi (A)$
is quasidiagonal. As foreshadowed in Lemma 1.2, this property is essential.
Proof of Lemma 2.3.
Let
![]() $\mathcal {F}\subset A$
be a finite set of contractions,
$\mathcal {F}\subset A$
be a finite set of contractions,
![]() $\mathcal {S}$
a finite set of normal states on N and
$\mathcal {S}$
a finite set of normal states on N and
![]() $\epsilon>0$
. Define a normal state
$\epsilon>0$
. Define a normal state
![]() $\rho = \sum _{\rho '\in \mathcal {S}}\rho '/|\mathcal {S}|$
, so that
$\rho = \sum _{\rho '\in \mathcal {S}}\rho '/|\mathcal {S}|$
, so that
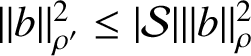 $\|b\|_{\rho '}^2\leq |\mathcal {S}|\|b\|_\rho ^2$
for every
$\|b\|_{\rho '}^2\leq |\mathcal {S}|\|b\|_\rho ^2$
for every
![]() $\rho '\in \mathcal {S}$
and
$\rho '\in \mathcal {S}$
and
![]() $b\in N$
. Thus, we need only make reference to
$b\in N$
. Thus, we need only make reference to
![]() $\rho $
in the proof, rather than the entire set
$\rho $
in the proof, rather than the entire set
![]() $\mathcal {S}$
.
$\mathcal {S}$
.
Note that N may be decomposed into
![]() $N_{1}\oplus N_\infty $
for von Neumann algebras
$N_{1}\oplus N_\infty $
for von Neumann algebras
![]() $N_{1},N_\infty $
that are respectively finite and properly infinite. Similarly,
$N_{1},N_\infty $
that are respectively finite and properly infinite. Similarly,
![]() $\pi = \pi _{1}\oplus \pi _\infty $
for weakly nuclear *-homomorphisms
$\pi = \pi _{1}\oplus \pi _\infty $
for weakly nuclear *-homomorphisms
![]() $\pi _{1}:A\rightarrow N_{1}$
and
$\pi _{1}:A\rightarrow N_{1}$
and
![]() $\pi _{\infty }:A\rightarrow N_{\infty }$
. We shall deal with each summand separately by assuming that it composes all of N.
$\pi _{\infty }:A\rightarrow N_{\infty }$
. We shall deal with each summand separately by assuming that it composes all of N.
Case 1. N is properly infinite. We begin by following the proof of [Reference Carrión and Schafhauser6, Proposition 3]. By the assumption of weak nuclearity, there are
![]() $k\in \mathbb {Z}^+$
and unitary completely positive maps
$k\in \mathbb {Z}^+$
and unitary completely positive maps
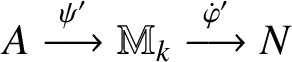 $A\stackrel {\psi '}{\longrightarrow }\mathbb {M}_{k}\stackrel {\dot {\varphi }'}{\longrightarrow }N$
such that
$A\stackrel {\psi '}{\longrightarrow }\mathbb {M}_{k}\stackrel {\dot {\varphi }'}{\longrightarrow }N$
such that
![]() $\|\dot {\varphi }'\circ \psi '(x)-\pi (x)\|_{\rho }\leq \epsilon $
for every
$\|\dot {\varphi }'\circ \psi '(x)-\pi (x)\|_{\rho }\leq \epsilon $
for every
![]() $x\in \mathcal {F}$
. Since A is separable, we may fix a faithful unital representation
$x\in \mathcal {F}$
. Since A is separable, we may fix a faithful unital representation
![]() $A\subseteq \mathbb {B}(\mathcal {H})$
such that
$A\subseteq \mathbb {B}(\mathcal {H})$
such that
![]() $\mathcal {H}$
is separable and A contains no nonzero compact operators. Voiculescu’s theorem [Reference Davidson11, Theorem II.5.3] provides an isometry
$\mathcal {H}$
is separable and A contains no nonzero compact operators. Voiculescu’s theorem [Reference Davidson11, Theorem II.5.3] provides an isometry
![]() $v:\mathbb {C}^{k}\rightarrow \mathcal {H}$
such that
$v:\mathbb {C}^{k}\rightarrow \mathcal {H}$
such that
![]() $\|v^*xv-\psi '(x)\|\leq \epsilon $
for every
$\|v^*xv-\psi '(x)\|\leq \epsilon $
for every
![]() $x\in \mathcal {F}$
. Likewise, quasidiagonality provides a finite-rank projection
$x\in \mathcal {F}$
. Likewise, quasidiagonality provides a finite-rank projection
![]() $p\in \mathbb {B}(\mathcal {H})$
such that
$p\in \mathbb {B}(\mathcal {H})$
such that
![]() $\|pv-p\|\leq \epsilon $
and
$\|pv-p\|\leq \epsilon $
and
![]() $\|px-xp\|\leq \epsilon $
for every
$\|px-xp\|\leq \epsilon $
for every
![]() $x\in \mathcal {F}$
. Define unitary completely positive maps
$x\in \mathcal {F}$
. Define unitary completely positive maps
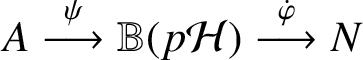 $A\stackrel {\psi }{\longrightarrow }\mathbb {B}(p\mathcal {H})\stackrel {\dot {\varphi }}{\longrightarrow }N$
by
$A\stackrel {\psi }{\longrightarrow }\mathbb {B}(p\mathcal {H})\stackrel {\dot {\varphi }}{\longrightarrow }N$
by
![]() $\psi (a)= pap$
and
$\psi (a)= pap$
and
![]() $\dot {\varphi }(T)= \dot {\varphi }'(v^*Tv)$
. Thus, for all
$\dot {\varphi }(T)= \dot {\varphi }'(v^*Tv)$
. Thus, for all
![]() $x,y\in \mathcal {F}$
,
$x,y\in \mathcal {F}$
,
 $$ \begin{align*} \|\psi(x)\psi(y)-\psi(xy)\|&\leq \|p\|\,\|xp-px\|\,\|yp\|\leq\epsilon,\\ \|\dot{\varphi}\circ\psi(x)-\pi(x)\|_{\rho}& \leq \|\dot{\varphi}'\|\,\|v^*\psi(x)v-\psi'(x)\|+\epsilon \\&\leq \|v^*p-v^*\|\,\|xpv\|+\|v^*x\|\,\|pv-v\|+2\epsilon\leq 4\epsilon. \end{align*} $$
$$ \begin{align*} \|\psi(x)\psi(y)-\psi(xy)\|&\leq \|p\|\,\|xp-px\|\,\|yp\|\leq\epsilon,\\ \|\dot{\varphi}\circ\psi(x)-\pi(x)\|_{\rho}& \leq \|\dot{\varphi}'\|\,\|v^*\psi(x)v-\psi'(x)\|+\epsilon \\&\leq \|v^*p-v^*\|\,\|xpv\|+\|v^*x\|\,\|pv-v\|+2\epsilon\leq 4\epsilon. \end{align*} $$
We now follow the proof of [Reference Brown, Carrión and White3, Lemma 2.4], beginning on page 50 with the explanation that the reference itself is following the proof of [Reference Haagerup12, Proposition 2.2]. Our properly infinite assumption finally kicks in, allowing us to find a unital embedding
![]() $\iota :\mathbb {B}(p\mathcal {H})\rightarrow N$
. By [Reference Haagerup12, Proposition 2.1], there is an isometry
$\iota :\mathbb {B}(p\mathcal {H})\rightarrow N$
. By [Reference Haagerup12, Proposition 2.1], there is an isometry
![]() $w\in N$
such that
$w\in N$
such that
![]() $\dot {\varphi }(T)= w^*\iota (T)w$
for all
$\dot {\varphi }(T)= w^*\iota (T)w$
for all
![]() $T\in \mathbb {B}(p\mathcal {H})$
. Then [Reference Haagerup12, page 167] shows how w may be approximated by a unitary u so that
$T\in \mathbb {B}(p\mathcal {H})$
. Then [Reference Haagerup12, page 167] shows how w may be approximated by a unitary u so that
for every
![]() $T\in \psi (\mathcal {F})\subset \mathbb {B}(p\mathcal {H})$
. Therefore, this case is proven by defining the *-homomorphism
$T\in \psi (\mathcal {F})\subset \mathbb {B}(p\mathcal {H})$
. Therefore, this case is proven by defining the *-homomorphism
![]() $\varphi = \operatorname {\mathrm {Ad}}(u^*)\circ \iota $
.
$\varphi = \operatorname {\mathrm {Ad}}(u^*)\circ \iota $
.
Case 2. N is finite. This proof follows exactly in the footsteps of that of [Reference Brown, Carrión and White3, Lemma 2.5], until its last two paragraphs. At that point we note that
![]() $\theta $
is nuclear by definition: we have finite-dimensional unitary completely positive maps
$\theta $
is nuclear by definition: we have finite-dimensional unitary completely positive maps
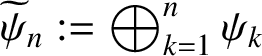 $\widetilde {\psi }_n:=\bigoplus _{k=1}^n\psi _k$
mapping
$\widetilde {\psi }_n:=\bigoplus _{k=1}^n\psi _k$
mapping
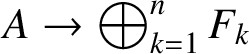 $A\rightarrow \bigoplus _{k=1}^nF_k$
and *-homomorphisms
$A\rightarrow \bigoplus _{k=1}^nF_k$
and *-homomorphisms
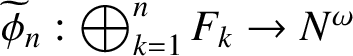 $\widetilde {\phi }_n:\bigoplus _{k=1}^nF_k\rightarrow N^\omega $
given by
$\widetilde {\phi }_n:\bigoplus _{k=1}^nF_k\rightarrow N^\omega $
given by
Thus,
![]() $\theta = \lim _\omega \phi _n\circ \psi _n= \lim _n\widetilde {\phi }_n\circ \widetilde {\psi }_n$
. This allows us to use Theorem 2.1 to deduce that
$\theta = \lim _\omega \phi _n\circ \psi _n= \lim _n\widetilde {\phi }_n\circ \widetilde {\psi }_n$
. This allows us to use Theorem 2.1 to deduce that
![]() $\theta $
is strong* approximately unitarily equivalent to
$\theta $
is strong* approximately unitarily equivalent to
![]() $\pi ^\omega $
, and the proof is finished using Kirchberg’s
$\pi ^\omega $
, and the proof is finished using Kirchberg’s
![]() $\epsilon $
-test as in the original.
$\epsilon $
-test as in the original.
Just as in [Reference Carrión and Schafhauser6] and the other preceding papers, our interest in this form of W*-decomposition is due solely to its relationship with the following C*-counterpart.
Definition 2.5. Let
![]() $\pi :A\rightarrow B$
be a *-homomorphism between C*-algebras
$\pi :A\rightarrow B$
be a *-homomorphism between C*-algebras
![]() $A,B$
. An approximately multiplicative norm-decomposition of
$A,B$
. An approximately multiplicative norm-decomposition of
![]() $\pi $
is a sequence of unitary completely positive maps
$\pi $
is a sequence of unitary completely positive maps
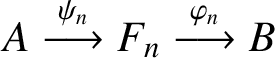 $A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }B$
for finite-dimensional C*-algebras
$A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }B$
for finite-dimensional C*-algebras
![]() $F_n$
such that:
$F_n$
such that:
-
(i)
 $\|\varphi _n\circ \psi _n(x)-\pi (x)\|\rightarrow 0$
for all
$\|\varphi _n\circ \psi _n(x)-\pi (x)\|\rightarrow 0$
for all
 $x\in A$
;
$x\in A$
; -
(ii)
 $\|\psi _n(x)\psi _n(y)-\psi _n(xy)\|\rightarrow 0$
for all
$\|\psi _n(x)\psi _n(y)-\psi _n(xy)\|\rightarrow 0$
for all
 $x,y\in A$
;
$x,y\in A$
; -
(iii) every
 $\varphi _n$
is a convex combination of unitary completely positive order zero maps.
$\varphi _n$
is a convex combination of unitary completely positive order zero maps.
Proof of Lemma 1.2.
The composition of a trace with an order-zero map is again (rescalable into) a trace [Reference Winter and Zacharias15, Corollary 3.4], so each
![]() $\tau \circ \varphi _n$
is a trace on the finite-dimensional C*-algebra
$\tau \circ \varphi _n$
is a trace on the finite-dimensional C*-algebra
![]() $F_n$
. By assumption, the
$F_n$
. By assumption, the
![]() $\psi _n$
are approximately multiplicative and
$\psi _n$
are approximately multiplicative and
![]() $\tau \circ \varphi _n\circ \psi _n\rightarrow \tau \circ \pi $
in the weak* topology. Therefore,
$\tau \circ \varphi _n\circ \psi _n\rightarrow \tau \circ \pi $
in the weak* topology. Therefore,
![]() $\tau \circ \pi $
is quasidiagonal.
$\tau \circ \pi $
is quasidiagonal.
Proof of Theorem 1.3.
Let
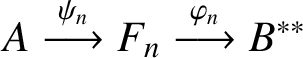 $A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }B^{**}$
be an approximately multiplicative
$A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }B^{**}$
be an approximately multiplicative
![]() $\sigma $
-strong*-decomposition. By Arveson’s extension theorem, we have conditional expectations
$\sigma $
-strong*-decomposition. By Arveson’s extension theorem, we have conditional expectations
![]() $E_n:B^{**}\rightarrow \varphi _n(F_n)$
. Moreover, by Alaoglu’s theorem, we may pass
$E_n:B^{**}\rightarrow \varphi _n(F_n)$
. Moreover, by Alaoglu’s theorem, we may pass
![]() $(E_n)$
to a subsequence that converges to a linear map
$(E_n)$
to a subsequence that converges to a linear map
![]() $E:B^{**}\rightarrow B^{**}$
in the point-
$E:B^{**}\rightarrow B^{**}$
in the point-
![]() $\sigma $
-weak topology (see [Reference Brown and Ozawa4, Theorem 1.3.7]).
$\sigma $
-weak topology (see [Reference Brown and Ozawa4, Theorem 1.3.7]).
Fix
![]() $\epsilon>0$
,
$\epsilon>0$
,
![]() $a\in A$
and a normal functional
$a\in A$
and a normal functional
![]() $\eta \in B^*$
. Then
$\eta \in B^*$
. Then
![]() $\eta \circ E$
is also a normal functional, so by the previous paragraph there exists
$\eta \circ E$
is also a normal functional, so by the previous paragraph there exists
![]() $m\in \mathbb {N}$
such that
$m\in \mathbb {N}$
such that
![]() $n>m$
implies that each of the following hold:
$n>m$
implies that each of the following hold:
 $$ \begin{align*} |\eta(E_n(\pi(a))-E(\pi(a)))|&\leq\epsilon/4,\\ |\eta\circ E(\pi(a)-\varphi_n\circ\psi_n(a))|&\leq\epsilon/4,\\ |\eta(E(\varphi_n\circ\psi_n(a))-E_n(\varphi_n\circ\psi_n(a)))|&\leq\epsilon/4,\\ |\eta(\varphi_n\circ\psi_n(a)-\pi(a))|&\leq\epsilon/4. \end{align*} $$
$$ \begin{align*} |\eta(E_n(\pi(a))-E(\pi(a)))|&\leq\epsilon/4,\\ |\eta\circ E(\pi(a)-\varphi_n\circ\psi_n(a))|&\leq\epsilon/4,\\ |\eta(E(\varphi_n\circ\psi_n(a))-E_n(\varphi_n\circ\psi_n(a)))|&\leq\epsilon/4,\\ |\eta(\varphi_n\circ\psi_n(a)-\pi(a))|&\leq\epsilon/4. \end{align*} $$
Combined,
and therefore the inclusion
![]() $\pi (A)\subseteq B^{**}$
is weakly nuclear.
$\pi (A)\subseteq B^{**}$
is weakly nuclear.
We now use a Hahn–Banach argument akin to the proof (as in [Reference Brown and Ozawa4, Proposition 2.3.6]) that if
![]() $A^{**}$
is semidiscrete, then A is nuclear. Let X be the set of all maps from
$A^{**}$
is semidiscrete, then A is nuclear. Let X be the set of all maps from
![]() $\pi (A)$
to
$\pi (A)$
to
![]() $B^{**}$
of the form
$B^{**}$
of the form
![]() $\varphi \circ \psi $
for two unitary completely positive maps
$\varphi \circ \psi $
for two unitary completely positive maps
![]() $\psi :\pi (A)\rightarrow F$
and
$\psi :\pi (A)\rightarrow F$
and
![]() $\varphi :F\rightarrow B^{**}$
and finite-dimensional F. Then X is convex.
$\varphi :F\rightarrow B^{**}$
and finite-dimensional F. Then X is convex.
Indeed, let
![]() $w\in (0,1)$
and
$w\in (0,1)$
and
![]() $\varphi _0\circ \psi _0,\varphi _1\circ \psi _{1}\in X$
. Then it follows that
$\varphi _0\circ \psi _0,\varphi _1\circ \psi _{1}\in X$
. Then it follows that
![]() ${\psi :=\psi _0\oplus \psi _1:\pi (A)\rightarrow F_0\oplus F_1}$
is unitary completely positive, as is the map
${\psi :=\psi _0\oplus \psi _1:\pi (A)\rightarrow F_0\oplus F_1}$
is unitary completely positive, as is the map
![]() $\varphi :F_0\oplus F_1\rightarrow B^{**}$
given by
$\varphi :F_0\oplus F_1\rightarrow B^{**}$
given by
![]() $\varphi ((M_0,M_1))= w\varphi _0(M_0)+(1-w)\varphi _1(M_1)$
. Thus,
$\varphi ((M_0,M_1))= w\varphi _0(M_0)+(1-w)\varphi _1(M_1)$
. Thus,
![]() $w\varphi _0\circ \psi _0+(1-w)\varphi _1\circ \psi _1= \varphi \circ \psi \in ~X$
.
$w\varphi _0\circ \psi _0+(1-w)\varphi _1\circ \psi _1= \varphi \circ \psi \in ~X$
.
Fix
![]() $\mathcal {F}=\{b_i~|~i\in [1,k]\}\subset \pi (A)$
. By weak nuclearity, the k-tuple
$\mathcal {F}=\{b_i~|~i\in [1,k]\}\subset \pi (A)$
. By weak nuclearity, the k-tuple
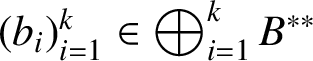 $(b_i)_{i=1}^k\in \bigoplus _{i=1}^kB^{**}$
is in the weak-closure of the set
$(b_i)_{i=1}^k\in \bigoplus _{i=1}^kB^{**}$
is in the weak-closure of the set
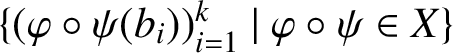 $\{(\varphi \circ \psi (b_i))_{i=1}^k~|~\varphi \circ \psi \in X\}$
and hence also in its norm-closure by the Hahn–Banach theorem. Therefore, there is a map
$\{(\varphi \circ \psi (b_i))_{i=1}^k~|~\varphi \circ \psi \in X\}$
and hence also in its norm-closure by the Hahn–Banach theorem. Therefore, there is a map
![]() $\varphi \circ \psi \in X$
such that
$\varphi \circ \psi \in X$
such that
 $$ \begin{align*} \max_i\|b_i-\varphi\circ\psi(b_i)\|= \|(b_i)_{i=1}^k-(\varphi\circ\psi(b_i))_{i=1}^k\|<\epsilon.\\ \end{align*} $$
$$ \begin{align*} \max_i\|b_i-\varphi\circ\psi(b_i)\|= \|(b_i)_{i=1}^k-(\varphi\circ\psi(b_i))_{i=1}^k\|<\epsilon.\\ \end{align*} $$
Proposition 2.6. Let
![]() $\pi :A\rightarrow B$
be a *-homomorphism between C*-algebras
$\pi :A\rightarrow B$
be a *-homomorphism between C*-algebras
![]() $A,B$
. Then
$A,B$
. Then
![]() $\pi $
admits an approximately multiplicative norm-decomposition if and only if
$\pi $
admits an approximately multiplicative norm-decomposition if and only if
![]() $\pi :A\rightarrow B^{**}$
admits an approximately multiplicative
$\pi :A\rightarrow B^{**}$
admits an approximately multiplicative
![]() $\sigma $
-strong*-decomposition.
$\sigma $
-strong*-decomposition.
Proof.
![]() $\boldsymbol {\Rightarrow }$
: We retread the proof of Lemma 2.3, beginning by fixing normal state
$\boldsymbol {\Rightarrow }$
: We retread the proof of Lemma 2.3, beginning by fixing normal state
![]() $\rho $
, finite
$\rho $
, finite
![]() $\mathcal {F}\subset A$
and
$\mathcal {F}\subset A$
and
![]() $\epsilon>0$
.
$\epsilon>0$
.
We may skip the first paragraph of the properly infinite case, instead using the assumed approximately multiplicative norm-decomposition to provide
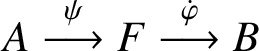 $A\stackrel {\psi }{\longrightarrow }F\stackrel {\dot {\varphi }}{\longrightarrow }B$
that satisfy the necessary inequalities. We now need only use [Reference Haagerup12] to find a unitary
$A\stackrel {\psi }{\longrightarrow }F\stackrel {\dot {\varphi }}{\longrightarrow }B$
that satisfy the necessary inequalities. We now need only use [Reference Haagerup12] to find a unitary
![]() $u\in N$
so that
$u\in N$
so that
![]() $\varphi = \operatorname {\mathrm {Ad}}(u^*)\circ \iota $
approximates
$\varphi = \operatorname {\mathrm {Ad}}(u^*)\circ \iota $
approximates
![]() $\dot {\varphi }$
for a unital embedding
$\dot {\varphi }$
for a unital embedding
![]() $\iota :F\rightarrow B^{**}$
.
$\iota :F\rightarrow B^{**}$
.
The finite case does not require that A be quasidiagonal. Of course, property (i) of our norm-decomposition witnesses the nuclearity of
![]() $\pi $
and hence
$\pi $
and hence
![]() $\pi :A\rightarrow B^{**}$
is weakly nuclear. Therefore, Lemma 1.2 allows us finish this case, and this direction.
$\pi :A\rightarrow B^{**}$
is weakly nuclear. Therefore, Lemma 1.2 allows us finish this case, and this direction.
![]() $\boldsymbol {\Leftarrow }$
: This is a perturbation of [Reference Hirshberg, Kirchberg and White13, Theorem 1.4]. Let
$\boldsymbol {\Leftarrow }$
: This is a perturbation of [Reference Hirshberg, Kirchberg and White13, Theorem 1.4]. Let
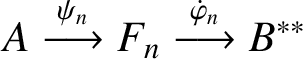 $A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\dot {\varphi }_n}{\longrightarrow }B^{**}$
be an approximately multiplicative
$A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\dot {\varphi }_n}{\longrightarrow }B^{**}$
be an approximately multiplicative
![]() $\sigma $
-strong*-decomposition. Using [Reference Hirshberg, Kirchberg and White13, Lemma 1.1], we can find order-zero unitary completely positive maps
$\sigma $
-strong*-decomposition. Using [Reference Hirshberg, Kirchberg and White13, Lemma 1.1], we can find order-zero unitary completely positive maps
![]() $\varphi _{n}:F_n\rightarrow B$
(note the range) such that
$\varphi _{n}:F_n\rightarrow B$
(note the range) such that
![]() $\varphi _n\circ \psi _n(x)\rightarrow \pi (x)$
in the
$\varphi _n\circ \psi _n(x)\rightarrow \pi (x)$
in the
![]() $\sigma $
-weak topology for every
$\sigma $
-weak topology for every
![]() $x\in A$
. We once again conclude with a Hahn–Banach argument.
$x\in A$
. We once again conclude with a Hahn–Banach argument.
With the equivalence of these decompositions, we hope to find a way to characterise their existence. An important component seems to be that
![]() $\pi $
is a quasidiagonal *-homomorphism.
$\pi $
is a quasidiagonal *-homomorphism.
Definition 2.7. A *-homomorphism
![]() $\pi :A\rightarrow B$
is quasidiagonal if it factors through a quasidiagonal C*-algebra D. That is, there exist *-homomorphisms
$\pi :A\rightarrow B$
is quasidiagonal if it factors through a quasidiagonal C*-algebra D. That is, there exist *-homomorphisms
![]() $\pi _1:A\rightarrow D$
and
$\pi _1:A\rightarrow D$
and
![]() $\pi _2:D\rightarrow B$
such that
$\pi _2:D\rightarrow B$
such that
![]() $\pi _1$
is surjective and
$\pi _1$
is surjective and
![]() $\pi = \pi _2\circ \pi _1$
.
$\pi = \pi _2\circ \pi _1$
.
Definition 2.8. An extension
is called locally split if every finite subset
![]() $\mathcal {G}\subset B$
of contractions admits a unitary completely positive local lifting
$\mathcal {G}\subset B$
of contractions admits a unitary completely positive local lifting
![]() $\lambda :\mathrm {span}(\mathcal {G})\rightarrow A$
such that
$\lambda :\mathrm {span}(\mathcal {G})\rightarrow A$
such that
![]() $\pi \circ \lambda (b)= b$
for every
$\pi \circ \lambda (b)= b$
for every
![]() $b\in \mathrm {span}\,\mathcal {G}$
.
$b\in \mathrm {span}\,\mathcal {G}$
.
For exact A, every extension
![]() $0\rightarrow \ker \pi \rightarrow A\rightarrow B\rightarrow 0$
is locally split (see, for example, [Reference Brown and Ozawa4, Proposition 9.1.4]). However, it is of note that the full power of exactness is not required for the following result.
$0\rightarrow \ker \pi \rightarrow A\rightarrow B\rightarrow 0$
is locally split (see, for example, [Reference Brown and Ozawa4, Proposition 9.1.4]). However, it is of note that the full power of exactness is not required for the following result.
Proposition 2.9. Let A be a C*-algebra,
![]() $\pi :A\rightarrow B$
be a nuclear, quasidiagonal *-homomorphism to another C*-algebra B and
$\pi :A\rightarrow B$
be a nuclear, quasidiagonal *-homomorphism to another C*-algebra B and
![]() $D,\pi _1,\pi _2$
be as in Definition 2.8. Further, suppose that the trace
$D,\pi _1,\pi _2$
be as in Definition 2.8. Further, suppose that the trace
![]() $\tau \circ \pi $
is quasidiagonal for every trace
$\tau \circ \pi $
is quasidiagonal for every trace
![]() $\tau $
on
$\tau $
on
![]() $\pi (A)$
and that the extension
$\pi (A)$
and that the extension
is locally split. Then
![]() $\pi $
admits an approximately multiplicative decomposition.
$\pi $
admits an approximately multiplicative decomposition.
Proof. Fix
![]() $\epsilon>0$
and a finite subset of contractions
$\epsilon>0$
and a finite subset of contractions
![]() $\mathcal {G}\subset D$
. Let
$\mathcal {G}\subset D$
. Let
![]() $\lambda :\mathrm {span}(\mathcal {G})\rightarrow A$
be a local lifting. By nuclearity, there are
$\lambda :\mathrm {span}(\mathcal {G})\rightarrow A$
be a local lifting. By nuclearity, there are
![]() $i\in \mathbb {N}$
and unitary completely positive maps
$i\in \mathbb {N}$
and unitary completely positive maps
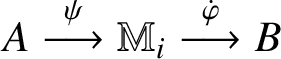 $A\stackrel {\psi }{\longrightarrow }\mathbb {M}_i\stackrel {\dot {\varphi }}{\longrightarrow }B$
such that
$A\stackrel {\psi }{\longrightarrow }\mathbb {M}_i\stackrel {\dot {\varphi }}{\longrightarrow }B$
such that
![]() $\|\dot {\varphi }\circ \psi (a)-\pi (a)\|<\epsilon $
for every
$\|\dot {\varphi }\circ \psi (a)-\pi (a)\|<\epsilon $
for every
![]() $a\in \lambda (\mathcal {G})$
. Arveson’s extension theorem then provides a unitary completely positive
$a\in \lambda (\mathcal {G})$
. Arveson’s extension theorem then provides a unitary completely positive
![]() $\psi ':D\rightarrow \mathbb {M}_i$
that agrees with
$\psi ':D\rightarrow \mathbb {M}_i$
that agrees with
![]() $\psi \circ \lambda $
on
$\psi \circ \lambda $
on
![]() $\mathrm {span}(\mathcal {G})$
. Thus, for any
$\mathrm {span}(\mathcal {G})$
. Thus, for any
![]() $d\in \mathcal {G}$
,
$d\in \mathcal {G}$
,
From this, we conclude that
![]() $\pi _2$
is nuclear. This allows us to apply the properly infinite case of Lemma 2.3 to get approximately multiplicative decompositions of
$\pi _2$
is nuclear. This allows us to apply the properly infinite case of Lemma 2.3 to get approximately multiplicative decompositions of
![]() $\pi _2:D\rightarrow B^{**}$
. This case may then be extended to work for A itself by replacing the resultant
$\pi _2:D\rightarrow B^{**}$
. This case may then be extended to work for A itself by replacing the resultant
![]() $\psi _n$
with
$\psi _n$
with
![]() $\psi _n\circ \pi _1$
. The finite case goes through for A unmodified, resulting in approximately multiplicative decompositions of
$\psi _n\circ \pi _1$
. The finite case goes through for A unmodified, resulting in approximately multiplicative decompositions of
![]() $\pi :A\rightarrow B^{**}$
.
$\pi :A\rightarrow B^{**}$
.
However, exactness does provide us with the converse as stated in Theorem 1.4.
Proof of Theorem 1.4.
As mentioned, Proposition 2.9 already provides the backward direction, so we need now only address the forward one. Let
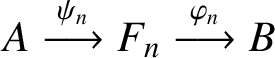 $A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }B$
be the approximately multiplicative norm-decomposition. The decomposition itself witnesses the nuclearity of
$A\stackrel {\psi _n}{\longrightarrow }F_n\stackrel {\varphi _n}{\longrightarrow }B$
be the approximately multiplicative norm-decomposition. The decomposition itself witnesses the nuclearity of
![]() $\pi $
. The quasidiagonality of every
$\pi $
. The quasidiagonality of every
![]() $\tau \circ \pi $
was shown in Lemma 1.2. The quasidiagonality of
$\tau \circ \pi $
was shown in Lemma 1.2. The quasidiagonality of
![]() $\pi $
itself is a consequence of [Reference Dadarlat10, Theorem 4.8]; for the convenience of the reader, we present a distillation of the proof.
$\pi $
itself is a consequence of [Reference Dadarlat10, Theorem 4.8]; for the convenience of the reader, we present a distillation of the proof.
Since A is exact, we may treat it as a C*-subalgebra of some C*-algebra C such that the inclusion is nuclear. Using Arveson’s extension theorem, we may treat the domains of the
![]() $\psi _n$
as C. They induce a unitary completely positive map
$\psi _n$
as C. They induce a unitary completely positive map
![]() $\Psi $
from C to an ultraproduct
$\Psi $
from C to an ultraproduct
![]() $\prod _\omega F_n$
, where
$\prod _\omega F_n$
, where
![]() $(\psi _n(a))_n$
is a representative sequence of
$(\psi _n(a))_n$
is a representative sequence of
![]() $\Psi (a)$
. Note that the approximate multiplicativity of
$\Psi (a)$
. Note that the approximate multiplicativity of
![]() $(\psi _n)$
makes
$(\psi _n)$
makes
![]() $\Psi |_A$
a *-homomorphism. Likewise, we have a contractive completely positive map
$\Psi |_A$
a *-homomorphism. Likewise, we have a contractive completely positive map
![]() $\Phi $
from
$\Phi $
from
![]() $\prod _\omega F_n$
to the ultrapower
$\prod _\omega F_n$
to the ultrapower
![]() $B^\omega $
given by
$B^\omega $
given by
![]() $\Phi ((T_n)_n)= (\varphi _n(T_n))_n$
. Thus,
$\Phi ((T_n)_n)= (\varphi _n(T_n))_n$
. Thus,
![]() $\Phi \circ \Psi (a)= (\varphi _n\circ \psi _n(a))_n= (\pi (a))_n$
, which we may identify with
$\Phi \circ \Psi (a)= (\varphi _n\circ \psi _n(a))_n= (\pi (a))_n$
, which we may identify with
![]() $\pi (a)$
itself by treating B as a C*-subalgebra of
$\pi (a)$
itself by treating B as a C*-subalgebra of
![]() $B^\omega $
through constant sequences. Thus,
$B^\omega $
through constant sequences. Thus,
![]() $\Phi |_{\Psi (A)}$
must also be a *-homomorphism.
$\Phi |_{\Psi (A)}$
must also be a *-homomorphism.
Fix
![]() $\epsilon>0$
and a finite subset of contractions
$\epsilon>0$
and a finite subset of contractions
![]() $\mathcal {G}\subset \Psi (A)$
. Also, let
$\mathcal {G}\subset \Psi (A)$
. Also, let
![]() $\lambda :\mathrm {span}(\mathcal {G})\rightarrow A$
be a local lifting of
$\lambda :\mathrm {span}(\mathcal {G})\rightarrow A$
be a local lifting of
![]() $\Psi $
. By nuclearity of
$\Psi $
. By nuclearity of
![]() $A\subseteq C$
, there exist a finite-dimensional C*-algebra G and contractive completely positive maps
$A\subseteq C$
, there exist a finite-dimensional C*-algebra G and contractive completely positive maps
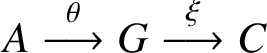 $A\stackrel {\theta }{\longrightarrow }G\stackrel {\xi }{\longrightarrow }C$
such that, for every
$A\stackrel {\theta }{\longrightarrow }G\stackrel {\xi }{\longrightarrow }C$
such that, for every
![]() $d\in \mathcal {G}$
,
$d\in \mathcal {G}$
,
Another use of Arveson’s extension theorem yields
![]() $\theta ':\Psi (A)\rightarrow G$
with restriction
$\theta ':\Psi (A)\rightarrow G$
with restriction
![]() $\theta '|_{\mathcal {G}}= \theta \circ \lambda $
.
$\theta '|_{\mathcal {G}}= \theta \circ \lambda $
.
Thus, the inclusion
![]() $\Psi (A)\subseteq \prod _\omega F_n$
is nuclear. By the Choi–Effros lifting theorem [Reference Brown and Ozawa4, Theorem C.3], this inclusion lifts to a contractive completely positive map to
$\Psi (A)\subseteq \prod _\omega F_n$
is nuclear. By the Choi–Effros lifting theorem [Reference Brown and Ozawa4, Theorem C.3], this inclusion lifts to a contractive completely positive map to
![]() $\prod _n F_n$
. Therefore,
$\prod _n F_n$
. Therefore,
![]() $\Psi (A)$
is quasidiagonal (see, for example, [Reference Brown and Ozawa4, Exercise 7.1.3]).
$\Psi (A)$
is quasidiagonal (see, for example, [Reference Brown and Ozawa4, Exercise 7.1.3]).
Remark 2.10. It seems probable to the author that this theorem may be strengthened to show that
![]() $\pi $
admits an approximately multiplicative decomposition if and only if it factors through a quasidiagonal C*-algebra D via
$\pi $
admits an approximately multiplicative decomposition if and only if it factors through a quasidiagonal C*-algebra D via
![]() $A\stackrel {\pi _1}{\rightarrow }D\stackrel {\pi _2}{\rightarrow }B$
such that
$A\stackrel {\pi _1}{\rightarrow }D\stackrel {\pi _2}{\rightarrow }B$
such that
![]() $\pi _2$
admits an approximately multiplicative decomposition. All that is needed for this is to show that the trace
$\pi _2$
admits an approximately multiplicative decomposition. All that is needed for this is to show that the trace
![]() $\tau \circ \pi _2$
is quasidiagonal for every trace
$\tau \circ \pi _2$
is quasidiagonal for every trace
![]() $\tau $
on
$\tau $
on
![]() $\pi _2(D)= \pi (A)$
. This is of course satisfied if every trace on B is quasidiagonal, but the common theme of these results has been moving requirements away from the C*-algebras and onto the *-homomorphism itself.
$\pi _2(D)= \pi (A)$
. This is of course satisfied if every trace on B is quasidiagonal, but the common theme of these results has been moving requirements away from the C*-algebras and onto the *-homomorphism itself.
Acknowledgments
The author would like to thank his advisor, José Carrión, for much guidance and – alongside Christopher Schafhauser – for asking the question that led to this paper.



