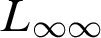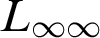1 Introduction
To say that the syllogism
All
![]() $A^{\prime }s$
are
$A^{\prime }s$
are
![]() $B^{\prime }s$
.
$B^{\prime }s$
.
Some
![]() $C^{\prime }s$
are
$C^{\prime }s$
are
![]() $A^{\prime }s$
.
$A^{\prime }s$
.
Some
![]() $C^{\prime }s$
are
$C^{\prime }s$
are
![]() $B^{\prime }s$
.
$B^{\prime }s$
.
is a valid argument form is to say that the conclusion follows from the premises no matter which predicates are substituted for the nonlogical terms A, B, C, whether ‘men’, ‘mortal’, ‘Greek’ or ‘tulips’, ‘bridges’ and ‘pious’, or whatnot, as long as the substitution is done uniformly. That the conclusion follows from the premises is a matter of logic—“is obviously true in a purely logical way,” to quote Carnap.Footnote 1
But what is it that makes a concept distinctively logical, as opposed to, say, mathematical? How to circumscribe the logical? The question is an urgent one for the logician, as the model-theoretic notion of consequence is parasitic on the distinction between logical and nonlogical expressions. For on this account of logical consequence, a sentence
![]() $\phi $
is held to be a semantic consequence of a sentence
$\phi $
is held to be a semantic consequence of a sentence
![]() $\psi $
, if for every uniform substitution of the nonlogical expressions in
$\psi $
, if for every uniform substitution of the nonlogical expressions in
![]() $\phi $
and
$\phi $
and
![]() $\psi $
, if
$\psi $
, if
![]() $\psi $
is true, then so is
$\psi $
is true, then so is
![]() $\phi $
.
$\phi $
.
In 1968 in a (posthumously published) lecture called “What are logical notions?” Reference Tarski[52] Tarski proposed a definition of “logical notion,” or alternatively of “logical constant,” modelled on the Erlanger program due to Felix Klein. The core observation is the following: for a given subject area, the number of concepts classified as invariant are inversely related to the number of transformations—the more transformations there are, the fewer invariant notions there are. If one thinks of logic as the most general of all the mathematical sciences, why not then declare “logical” notions to be the limiting cases? Thus a notion is to be thought of as logical if it is invariant under all permutations of the relevant domain.
As expected, the standard logical constants, namely conjunction, disjunction, negation and quantification, together with the equality relation, are all judged to be logical operations under this criterion, being all isomorphism invariant. This has the consequence that first order definability is classified as logical, tout court, being generated by these constants.Footnote 2
As was clear to Tarski, the criterion overgenerates, in the sense that concepts one does not immediately assimilate to logic turn out to be included, such as the cardinality of the underlying domain, which is clearly isomorphism invariant. A second problem has to do with domain relativity: Tarski’s criterion identifies the logical operations on a fixed domain, but that a domain consists of this or that type of object should not have anything to do with logicality—shouldn’t a logical concept be domain independent? Sher Reference Sher[48] repaired this problem by extending Tarski’s criterion to cover notions invariant across isomorphic structures, and accordingly the criterion is now known as the Tarski-Sher invariance criterion.
The Tarski–Sher criterion has generated a substantial literature, both for and against. Feferman’s Reference Feferman[22], based on his earlier Reference Feferman[21], proposes a notion of homomorphism invariance. His critique of the Tarski–Sher thesis is the following:
I critiqued the Tarski–Sher thesis in Reference Feferman[21] on three grounds, the first of which is that it assimilates logic to mathematics, the second that the notions involved are not set-theoretically robust, i.e., not absolute, and the third that no natural explanation is given by the thesis of what constitutes the same logical operation over arbitrary basic domains.Footnote 3
Feferman’s suggestion that Tarski assimilates logic to mathematics, in particular to set theory, sets aside Tarski’s lifelong program to carry out exactly what Feferman criticizes Tarski of here, namely expressing metamathematical concepts in mathematical and set-theoretical terms.Footnote 4 Feferman’s second objection has to do with overgeneration, in particular he resists the idea that a canonically mathematical but non-absolute notion such as cardinality is rendered logical under the criterion.Footnote 5
One way of thinking about topic neutrality is in terms of absoluteness, by which we mean general independence from the background set theory. As is well-known, a set may have one cardinality in one model of set theory but another cardinality in another model.Footnote 6 This shows that cardinality is not an absolute notion. On the other hand, whether a given set is empty or not, whether it is included in another given set, and whether it is the cartesian product of two given sets are all independent of the (transitive) model in which such questions are evaluated. Thus those notions are considered absolute. A possible reason to consider absoluteness a necessary quality of logical notions is that whatever depends on set theory could be considered a mathematical rather than logical notion.
Quine has extensively argued against taking set-theoretic notions as logical,Footnote
7
and in his seminal paper Reference Tarski[52] Tarski raises the question whether mathematical notions are logical. According to Tarski, if we construe mathematical notions in the framework of higher order logic, they are logical, while if we use the set-theoretical framework, based on a single binary relation
![]() $x\in y$
, mathematical notions are not logical. Tarski concludes that the question of logicality of mathematical notions is unresolved and depends on how we construe mathematics. In this paper we take the set-theoretical approach to mathematics. However, we operate with model classes, namely classes of structures of the same similarity type, but possibly of different cardinality, that are closed under isomorphism,Footnote
8
which are part of the higher order logic framework. For example, according to Tarski the notion of a binary relation R being a well-order is non-logical, as it is defined by reference to the
$x\in y$
, mathematical notions are not logical. Tarski concludes that the question of logicality of mathematical notions is unresolved and depends on how we construe mathematics. In this paper we take the set-theoretical approach to mathematics. However, we operate with model classes, namely classes of structures of the same similarity type, but possibly of different cardinality, that are closed under isomorphism,Footnote
8
which are part of the higher order logic framework. For example, according to Tarski the notion of a binary relation R being a well-order is non-logical, as it is defined by reference to the
![]() $\in $
-relation of set theory, but the notion of a structure
$\in $
-relation of set theory, but the notion of a structure
![]() $(M,<)$
being a well-order is logical, as it is second order definable. This example shows how delicate the question of logicality of mathematical notions is.
$(M,<)$
being a well-order is logical, as it is second order definable. This example shows how delicate the question of logicality of mathematical notions is.
Feferman proposes restricting the Tarski–Sher invariance criterion to operations that are absolute with respect to set theories making no assumptions about the size of the given domain. Feferman cites Reference Akkanen[2],Footnote 9 in which it is shown that operations on relational structures that are definable in an absolute way relative to KPU-Inf, i.e., Kripke–Platek set theory with urelements and without the Axiom of Infinity, are exactly those expressible in ordinary first-order predicate calculus with equality—another endorsement of the idea that first order logic captures the notion of “logical concept.”
Feferman’s solution solves the overgeneration problem, while giving a nice characterisation of first order logic along the way. But this comes at the expense of a strong absoluteness assumption, and for restricted classes of structures.
Setting overgeneration aside for the moment, and considering Feferman’s third objection, namely the problem of domain relativity, it would seem that following Feferman’s line we should consider model classes in general. How then to formulate the concept of logicality for a model class? Originally the question of logicality arises in connection with operations such as connectives, quantifiers and their generalisations. As McGee explains in Reference McGee[41], the question can be restated as a question about model classes, as the question whether the property of a given model being in a given model class is a logical property of the model.Footnote
10
In other words, any relevant operation O can be (re)formulated as a property P of models (see §2.1) and then the logicality of O translates into the question whether the property P is a logical property of models. Typical examples of logical properties of a unary model
![]() $(M,A)$
, where
$(M,A)$
, where
![]() $A\subseteq M$
, would be the non-emptiness of A, and the property of A of being equal to M. On the side of operators these example would correspond to the existential and the universal quantifiers.
$A\subseteq M$
, would be the non-emptiness of A, and the property of A of being equal to M. On the side of operators these example would correspond to the existential and the universal quantifiers.
Let’s back up and ask when would we call a property of an individual structure
![]() ${\mathcal M}$
logical. With Sher, certainly we should consider the elements of
${\mathcal M}$
logical. With Sher, certainly we should consider the elements of
![]() ${\mathcal M}$
irrelevant as long as the arrangement of the elements remains the same, as was mentioned. It would then be natural to call a property of
${\mathcal M}$
irrelevant as long as the arrangement of the elements remains the same, as was mentioned. It would then be natural to call a property of
![]() ${\mathcal M}$
logical only if the property is closed under permutations of the elements of
${\mathcal M}$
logical only if the property is closed under permutations of the elements of
![]() ${\mathcal M}$
in the sense that if f is a permutation of M then the image of
${\mathcal M}$
in the sense that if f is a permutation of M then the image of
![]() ${\mathcal M}$
as a structure under f has the property. But then it is a short step to require closure under isomorphisms.
${\mathcal M}$
as a structure under f has the property. But then it is a short step to require closure under isomorphisms.
A theorem due to McGee Reference McGee[41] characterises logicality for an arbitrary model class, provided the cardinality of the models in the class is fixed in advance. It is a weakness of this characterisation that it depends on the cardinality of the models in the class. One might then ask, whether there is a sentence in a logic
![]() $L^*$
, perhaps other than
$L^*$
, perhaps other than
![]() $L_{\infty \infty }$
, which characterises the logical property, not just in one cardinality, but in many cardinalities. This leads to an analysis of spectra, as we call them,Footnote
11
and Löwenheim–Skolem style properties of logics as expressed in their Löwenheim and Hanf numbers, which we now define:
$L_{\infty \infty }$
, which characterises the logical property, not just in one cardinality, but in many cardinalities. This leads to an analysis of spectra, as we call them,Footnote
11
and Löwenheim–Skolem style properties of logics as expressed in their Löwenheim and Hanf numbers, which we now define:
Definition 1. Suppose C and D are classes of cardinal numbers. A logic
![]() $L^*$
satisfies the Löwenheim–Skolem property
$L^*$
satisfies the Löwenheim–Skolem property
![]() $\text {LS}(C,D)$
if every sentence in
$\text {LS}(C,D)$
if every sentence in
![]() $L^*$
which has a model of some cardinality in C has a model of some cardinality in D. The smallest
$L^*$
which has a model of some cardinality in C has a model of some cardinality in D. The smallest
![]() $\kappa $
such that
$\kappa $
such that
![]() $L^*$
satisfies
$L^*$
satisfies
![]() $\text {LS}([1,\infty ),[1,\kappa ])$
is called the Löwenheim number of
$\text {LS}([1,\infty ),[1,\kappa ])$
is called the Löwenheim number of
![]() $L^*$
and denoted
$L^*$
and denoted
![]() $\ell (L^*)$
. The smallest
$\ell (L^*)$
. The smallest
![]() $\kappa $
such that
$\kappa $
such that
![]() $L^*$
satisfies
$L^*$
satisfies
![]() $\text {LS}([\kappa ,\infty ),[\lambda ,\infty ))$
for all
$\text {LS}([\kappa ,\infty ),[\lambda ,\infty ))$
for all
![]() $\lambda $
is called the Hanf number of
$\lambda $
is called the Hanf number of
![]() $L^*$
and denoted
$L^*$
and denoted
![]() $h(L^*)$
.
$h(L^*)$
.
As Sagi notes in her Reference Sagi[46], the Löwenheim number of a logic encodes the degree to which the logic is indifferent to cardinality. This is due to the fact that if a sentence satisfied by a model is also satisfied by a model of size less than or equal to a given cardinality
![]() $\kappa $
, then all the validitiesFootnote
12
which are captured in the full range of models are captured already on an initial segment (of V). In the case of first order logic the Löwenheim–Skolem theorem tells us that
$\kappa $
, then all the validitiesFootnote
12
which are captured in the full range of models are captured already on an initial segment (of V). In the case of first order logic the Löwenheim–Skolem theorem tells us that
![]() $\kappa $
can be taken to be
$\kappa $
can be taken to be
![]() $\aleph _0$
, so in this sense first order logic is indifferent to cardinalities above
$\aleph _0$
, so in this sense first order logic is indifferent to cardinalities above
![]() $\aleph _0$
. First order logic is already classified as logical because its logical constants are permutation invariant; this is now witnessed by the Löwenheim–Skolem theorem.
$\aleph _0$
. First order logic is already classified as logical because its logical constants are permutation invariant; this is now witnessed by the Löwenheim–Skolem theorem.
The strength of the Löwenheim–Skolem property of a given logic—or if you like, the degree of its indifference to cardinality—is measured, then, by its Löwenheim number. As an example, the quantifier
![]() $Q_{\alpha }$
associated with the logic
$Q_{\alpha }$
associated with the logic
![]() $\mathcal {L}(Q_{\alpha })$
, having Löwenheim number
$\mathcal {L}(Q_{\alpha })$
, having Löwenheim number
![]() $\aleph _{\alpha }$
, is in a sense indifferent to cardinalities greater than
$\aleph _{\alpha }$
, is in a sense indifferent to cardinalities greater than
![]() $\aleph _{\alpha }$
.Footnote
13
First order logic and
$\aleph _{\alpha }$
.Footnote
13
First order logic and
![]() $\mathcal {L}(Q_0)$
are maximally logical under the criterion assigning logicality according to Löwenheim number, and the degree of logicality decreases as
$\mathcal {L}(Q_0)$
are maximally logical under the criterion assigning logicality according to Löwenheim number, and the degree of logicality decreases as
![]() $\alpha $
increases. Thus if
$\alpha $
increases. Thus if
![]() $\alpha \leq \beta $
, then
$\alpha \leq \beta $
, then
![]() $Q_{\alpha }$
is more logical than
$Q_{\alpha }$
is more logical than
![]() $Q_{\beta }$
.Footnote
14
$Q_{\beta }$
.Footnote
14
The criterion for logicality presented in Sagi’s paper is based on a particular philosophical position, to wit: a metaphysical view of the cumulative hierarchy of sets, as well as a view about how the meaning of the terms of a logic are fixed.
…the higher set-theoretic infinite is metaphysically loaded…The lower the cardinalities to which the meaning
Footnote
15
of a term may be sensitive, the more logical it is. …[We] view Löwenheim numbers as telling us how much structure a term [in this case the quantifiers
![]() $Q_\alpha $
JK/JV] requires in order to be fixed in the context of a logic.”Footnote
16
$Q_\alpha $
JK/JV] requires in order to be fixed in the context of a logic.”Footnote
16
In short, the smaller the Löwenheim number of the logic, the less metaphysically involved e.g. the quantifier
![]() $Q_{\alpha }$
is.
$Q_{\alpha }$
is.
Sagi’s criterion partitions logical space in ways that differ from ours. In this paper we will not take account of the possible metaphysical commitments of set theory; and while her analysis of meaning is one we potentially endorse, we will not take a stand on the meanings of the terms of a logic in this paper. Our basic thesis is simply this: if first order logic is taken to be the fundamental exemplar of logicality, then logics that resemble, to a degree, first order logic in their model theoretic properties should be graded as logical to that degree.
Why do we take first order logic to be the fundamental exemplar of logicality? Considerations of space do not allow us to argue for this contested point here.Footnote
17
Indeed those opposed to the thesis that first order logic is maximally logical can perhaps find this paper useful as a test of that very thesis, given the complexity of the landscape of higher order logics laid out here, with respect to their (graded) degrees of logicality. For example, we suggest in this paper that logics such as
![]() $\mathcal {L}(Q_1)$
have, arguably, a higher degree of logicality than
$\mathcal {L}(Q_1)$
have, arguably, a higher degree of logicality than
![]() $\mathcal {L}(Q_0)$
, on the basis of the completeness of the former with respect to the Keisler axioms (see (1) in §7).
$\mathcal {L}(Q_0)$
, on the basis of the completeness of the former with respect to the Keisler axioms (see (1) in §7).
As is well known, Quine was a forceful advocate for the thesis that logic is first order logic on various grounds, including: First, the fact that first order logic has a complete proof system. Second, first order logic is the basis of the distinction between logic and set theory, as we mentioned above. Finally, there is Quine’s view of semantics, in particular his view that first order quantification is the optimal instrument for reading off the ontological commitments of a given theory, being itself ontologically minimal.Footnote 18
Apart from completeness, we do not take a stand on these stalwarts of Quinean logical theory here,Footnote
19
rather referring to what seems to be a consensus among writers on the topic that the connectives (
![]() $\wedge ,\vee ,\neg ,\to $
, etc.) as well as the quantifiers (
$\wedge ,\vee ,\neg ,\to $
, etc.) as well as the quantifiers (
![]() $\exists ,\forall $
) are logical operations, being closed under bijections, and also on the basis of what seems to be a strong intuition that they have the same meaning across domains of even different sizes. In fact, in many cases these operations are where the discussion on logicality starts. First order logic consists of iterations of these operations. Why would logicality disappear in this iteration? When we go beyond first order logic, e.g., to infinitary connectives and generalized quantifiers, we recognise the emerging problem whether we remain in the realm of logicality.
$\exists ,\forall $
) are logical operations, being closed under bijections, and also on the basis of what seems to be a strong intuition that they have the same meaning across domains of even different sizes. In fact, in many cases these operations are where the discussion on logicality starts. First order logic consists of iterations of these operations. Why would logicality disappear in this iteration? When we go beyond first order logic, e.g., to infinitary connectives and generalized quantifiers, we recognise the emerging problem whether we remain in the realm of logicality.
Thus while taking up Sagi’s suggestion that logicality may be calibrated by Löwenheim numbers, we also give weight to the other model theoretic properties of a logic, such as whether they have a Completeness Theorem or not.Footnote
20
As we will point out below, logics that have, for example, a Completeness Theorem do not seem to be tied to the
![]() $\aleph $
-hierarchy in any obvious way.
$\aleph $
-hierarchy in any obvious way.
Another drawback of McGee’s theorem which we address in this paper has to do with the model-theoretic properties of the logic
![]() $L_{\infty \infty }$
, namely that it is highly non-absolute (see Definition 17), that it fails to have a strong Löwenheim–Skolem theorem, and also that it is unbounded
Footnote
21
in the sense that it can define the concept of well-ordering leading to very large Hanf numbers.Footnote
22
This leads us to ask whether
$L_{\infty \infty }$
, namely that it is highly non-absolute (see Definition 17), that it fails to have a strong Löwenheim–Skolem theorem, and also that it is unbounded
Footnote
21
in the sense that it can define the concept of well-ordering leading to very large Hanf numbers.Footnote
22
This leads us to ask whether
![]() $L_{\infty \infty }$
can be replaced by a “tamer” logic, one closer to being first order in its model-theoretic properties. If such were to exist, then even with the problem of dependence on the cardinality of the models in the class unsolved, the relevant logicality claim would be strengthened by virtue of its proximity to first order logic.
$L_{\infty \infty }$
can be replaced by a “tamer” logic, one closer to being first order in its model-theoretic properties. If such were to exist, then even with the problem of dependence on the cardinality of the models in the class unsolved, the relevant logicality claim would be strengthened by virtue of its proximity to first order logic.
In sum: in this paper we develop further this aspect of logicality identified by Sagi, namely that it is graded, albeit with a different philosophical agenda than is laid out in Reference Sagi[46]. We especially point out problems in the Löwenheim–Skolem properties of
![]() $L_{\infty \infty }$
, along with other ways in which it diverges from first order logic. As was mentioned above, we take first order definability as a particularly strong form of logicality. Accordingly, our suggestion here is that definability in a logic which resembles with its model theoretic properties first order logic should represent an intermediate form of logicality. We calibrate these intermediate forms according to the model theoretic properties of these logics, considering mainly absoluteness, having a Löwenheim–Skolem theorem, and having a completeness theorem.
$L_{\infty \infty }$
, along with other ways in which it diverges from first order logic. As was mentioned above, we take first order definability as a particularly strong form of logicality. Accordingly, our suggestion here is that definability in a logic which resembles with its model theoretic properties first order logic should represent an intermediate form of logicality. We calibrate these intermediate forms according to the model theoretic properties of these logics, considering mainly absoluteness, having a Löwenheim–Skolem theorem, and having a completeness theorem.
While
![]() $L_{\infty \infty }$
is sufficient for McGee’s theorem, there is a weaker logic, namely the so-called
$L_{\infty \infty }$
is sufficient for McGee’s theorem, there is a weaker logic, namely the so-called
![]() $\Delta $
-extension of
$\Delta $
-extension of
![]() $L_{\infty \omega }$
which does the job as well. We shall explain in which way this weaker logic is better than
$L_{\infty \omega }$
which does the job as well. We shall explain in which way this weaker logic is better than
![]() $L_{\infty \infty }$
as a test of logicality, and also point out in which respects it may be lacking. Looking ahead, our refinement of McGee’s theorem replaces
$L_{\infty \infty }$
as a test of logicality, and also point out in which respects it may be lacking. Looking ahead, our refinement of McGee’s theorem replaces
![]() $L_{\infty \infty }$
by a logic which is absolute and which has a good Löwenheim–Skolem theorem, along with a number of other desirable properties. The improvement here is partial in the sense that it is still the case that the definition is given relative to the size of the models in the class. In §6 below we give a theorem which does not rely on this assumption, namely we present a logic in which any model class is definable irrespective of the cardinality of the models in the class.
$L_{\infty \infty }$
by a logic which is absolute and which has a good Löwenheim–Skolem theorem, along with a number of other desirable properties. The improvement here is partial in the sense that it is still the case that the definition is given relative to the size of the models in the class. In §6 below we give a theorem which does not rely on this assumption, namely we present a logic in which any model class is definable irrespective of the cardinality of the models in the class.
In spite of the seemingly clear intuition behind the syllogistic example with which we opened this paper, logicality is an elusive concept. It is by no means obvious what it should mean, even informally. But then, without such a clear informal intuition of its meaning it is difficult to judge whether this or that improvement of Tarski’s original definition hits the mark or not, or even whether it is a step in the right direction. The only thing there seems to be a consensus on in the wake of Tarski’s suggestion to identify logicality with isomorphism invariance is that Tarski’s criterion, extended by Sher, is a necessary but not sufficient one.Footnote 23
In this paper we create a base map of the landscape relevant for logicality. Following Tarski’s, ours is a semantic approach. Beginning with McGee’s Theorem Reference McGee[41] to the effect that logical operations in the sense of Tarski–Sher can be described in each cardinality separately in
![]() $L_{\infty \infty }$
, the landscape that opens in front of us is the world of different logics and the question, do the model-theoretic properties of these logics shed any light on the logicality problem?
$L_{\infty \infty }$
, the landscape that opens in front of us is the world of different logics and the question, do the model-theoretic properties of these logics shed any light on the logicality problem?
2 McGee’s theorem
To describe McGee’s result and to put it into a more general framework we define what we mean by a “logic”: A logic (a.k.a. abstract logic) in the sense of Reference Lindström[33] is a pair
![]() $L^*=(\Sigma ,T)$
, where
$L^*=(\Sigma ,T)$
, where
![]() $\Sigma $
is an arbitrary set (sometimes also a class) and T is a binary relation between members of
$\Sigma $
is an arbitrary set (sometimes also a class) and T is a binary relation between members of
![]() $\Sigma $
on the one hand and structures on the other. Members of
$\Sigma $
on the one hand and structures on the other. Members of
![]() $\Sigma $
are called
$\Sigma $
are called
![]() $L^*$
-sentences. Classes of the form
$L^*$
-sentences. Classes of the form
where
![]() $\phi $
is an
$\phi $
is an
![]() $L^*$
-sentence, are called
$L^*$
-sentence, are called
![]() $L^*$
-characterizable, or
$L^*$
-characterizable, or
![]() $L^*$
-definable, classes. Abstract logics are assumed to satisfy five axioms expressed in terms of
$L^*$
-definable, classes. Abstract logics are assumed to satisfy five axioms expressed in terms of
![]() $L^*$
-characterizable classes, corresponding to being closed under isomorphism, conjunction, negation, permutation of symbols, and “free” expansions.Footnote
24
A class
$L^*$
-characterizable classes, corresponding to being closed under isomorphism, conjunction, negation, permutation of symbols, and “free” expansions.Footnote
24
A class
![]() $\mathcal {K}$
of models is said to be definable in a logic
$\mathcal {K}$
of models is said to be definable in a logic
![]() $L^*$
if there is a sentence
$L^*$
if there is a sentence
![]() $\phi $
in
$\phi $
in
![]() $L^*$
such that
$L^*$
such that
Every model class is definable in some logic because we can take the model class as a generalized quantifier in the sense of Reference Lindström[32]: Suppose
![]() $\mathcal {K}$
is a model class with vocabulary L. For simplicity we assume
$\mathcal {K}$
is a model class with vocabulary L. For simplicity we assume
![]() $L=\{R\}$
where R is a binary predicate symbol. We can associate with
$L=\{R\}$
where R is a binary predicate symbol. We can associate with
![]() $\mathcal {K}$
the generalized quantifier
$\mathcal {K}$
the generalized quantifier
![]() $Q_{\mathcal {K}}$
with the semantics
$Q_{\mathcal {K}}$
with the semantics
 $$ \begin{align*}{\mathcal M}\models Q_{\mathcal{K}} xy\phi(x,y,\vec{a})\iff (M,\{(b,c)\in M^2 : {\mathcal M}\models\phi(b,c,\vec{a})\})\in\mathcal{K}.\end{align*} $$
$$ \begin{align*}{\mathcal M}\models Q_{\mathcal{K}} xy\phi(x,y,\vec{a})\iff (M,\{(b,c)\in M^2 : {\mathcal M}\models\phi(b,c,\vec{a})\})\in\mathcal{K}.\end{align*} $$
Now
![]() $\mathcal {K}$
is trivially definable in the extension
$\mathcal {K}$
is trivially definable in the extension
![]() $\mathcal {L}_{\omega \omega }(Q_{\mathcal {K}})$
of first order logic by the quantifier
$\mathcal {L}_{\omega \omega }(Q_{\mathcal {K}})$
of first order logic by the quantifier
![]() $Q_{\mathcal {K}}$
by the sentence
$Q_{\mathcal {K}}$
by the sentence
Conversely, every class of models definable in
![]() $\mathcal {L}_{\omega \omega }(Q_{\mathcal {K}})$
, or indeed in any abstract logic, is a model class i.e. is closed under isomorphisms. We obtain the following simple and at the same time basic characterization:
$\mathcal {L}_{\omega \omega }(Q_{\mathcal {K}})$
, or indeed in any abstract logic, is a model class i.e. is closed under isomorphisms. We obtain the following simple and at the same time basic characterization:
Theorem 2 [Reference Lindström32]
If
![]() $\mathcal {K}$
is a class of models of the same vocabulary, then the following conditions are equivalent:
$\mathcal {K}$
is a class of models of the same vocabulary, then the following conditions are equivalent:
-
1.
 $\mathcal {K}$
is closed under isomorphisms i.e.
$\mathcal {K}$
is closed under isomorphisms i.e.
 $\mathcal {K}$
is a model class.
$\mathcal {K}$
is a model class. -
2.
 $\mathcal {K}$
is definable in some extension of first order logic by a generalized quantifier.
$\mathcal {K}$
is definable in some extension of first order logic by a generalized quantifier. -
3.
 $\mathcal {K}$
is definable in some logic.
$\mathcal {K}$
is definable in some logic.
2.1 Operations vs. model classes
In the literature, logical operations and model classes are considered to be carriers of logicality. Our paper focuses on model classes and on the extent to which they can be called logical, but here we take a moment to establish the connection between model classes and logical operations. McGee Reference McGee[41] defines an abstract concept of what he calls a logical operation. He goes on to define what it means for a logical operation to be described by a formula of a logic. We review these definitions and establish a close connection between model classes and connectives as well as between definability of a model class and describability of a logical operation.
Suppose M is a non-empty set. By the semantic value (on M) of a formula (of any logic) we mean the set of assignments into M that satisfy the formula. Abstractly, these are just subsets A of
![]() $M^{n}$
for some n. A (local) operation f on M maps sequences
$M^{n}$
for some n. A (local) operation f on M maps sequences
![]() $\langle A_\alpha : \alpha <\beta \rangle $
of sets
$\langle A_\alpha : \alpha <\beta \rangle $
of sets
![]() $A_\alpha \subseteq M^{n_\alpha }$
to sets
$A_\alpha \subseteq M^{n_\alpha }$
to sets
![]() $f(\langle A_\alpha : \alpha <\beta \rangle )\subseteq M^n$
. Such a local operation is a logical operation, if it is closed under permutations of M, i.e., if for all permutations
$f(\langle A_\alpha : \alpha <\beta \rangle )\subseteq M^n$
. Such a local operation is a logical operation, if it is closed under permutations of M, i.e., if for all permutations
![]() $\pi $
of M
$\pi $
of M
where for any
![]() $s=(a_1,\ldots ,a_n)\in A\subseteq M^n$
we define
$s=(a_1,\ldots ,a_n)\in A\subseteq M^n$
we define
![]() $\pi (s)=(\pi (a_1),\ldots ,\pi (a_n))$
.
$\pi (s)=(\pi (a_1),\ldots ,\pi (a_n))$
.
Example 3. Suppose
![]() $A_0,A_1 \subseteq M^n$
. Conjunction is the logical operation
$A_0,A_1 \subseteq M^n$
. Conjunction is the logical operation
![]() $f^n_\wedge (\langle A_0,A_1\rangle )=A_0\cap A_1$
. Disjunction is the logical operation
$f^n_\wedge (\langle A_0,A_1\rangle )=A_0\cap A_1$
. Disjunction is the logical operation
![]() $f^n_\vee (\langle A_0,A_1\rangle )=A_0\cup A_1$
. Suppose
$f^n_\vee (\langle A_0,A_1\rangle )=A_0\cup A_1$
. Suppose
![]() $A\subseteq M^{n+1}$
. The existential quantifier with respect to n is the logical operation
$A\subseteq M^{n+1}$
. The existential quantifier with respect to n is the logical operation
 $f^{n}_{\exists }(\langle A\rangle )=\{s\upharpoonright \{0,\ldots ,n-1\}:s\in A\}$
.
$f^{n}_{\exists }(\langle A\rangle )=\{s\upharpoonright \{0,\ldots ,n-1\}:s\in A\}$
.
For the existential second (and higher) order quantifiers to be logical operations would require an extension of the approach to include more general assignments, which we however disregard in this paper. Still, every formula of second (or higher) order logic gives rise (separately) to a logical operation in the above sense. The situation is the same with the so-called team semantics Reference Väänänen[56] where semantic values are sets of sets of assignments, rather than sets of assignments as above.
More generally we have an operation
![]() $f_M$
for every non-empty set M. Here we assume that
$f_M$
for every non-empty set M. Here we assume that
![]() $f_M$
is always an operation on M. We call the (class) mapping
$f_M$
is always an operation on M. We call the (class) mapping
![]() $M\mapsto f_M$
a global operation and denote it
$M\mapsto f_M$
a global operation and denote it
![]() $\bar {f}$
. We call the global operation
$\bar {f}$
. We call the global operation
![]() $\bar {f}$
a logical operation if it is closed under bijections, i.e., if for all bijections
$\bar {f}$
a logical operation if it is closed under bijections, i.e., if for all bijections
![]() $\pi :M\to N$
$\pi :M\to N$
A formula
![]() $\phi (\vec {x})$
with an
$\phi (\vec {x})$
with an
![]() $n_\alpha $
-ary predicate symbol
$n_\alpha $
-ary predicate symbol
![]() $P_\alpha $
for each
$P_\alpha $
for each
![]() $\alpha <\beta $
is said to describe a local operation f on M if in any model
$\alpha <\beta $
is said to describe a local operation f on M if in any model
![]() ${\mathcal M}$
with domain M and
${\mathcal M}$
with domain M and
 $P_\alpha ^{\mathcal M}=A_\alpha \subseteq M^{n_\alpha }$
the semantic value of
$P_\alpha ^{\mathcal M}=A_\alpha \subseteq M^{n_\alpha }$
the semantic value of
![]() $\phi (\vec {x})$
is
$\phi (\vec {x})$
is
![]() $f(\langle A_\alpha : \alpha <\beta \rangle )$
. The concept of a formula describing a global operation is defined similarly.
$f(\langle A_\alpha : \alpha <\beta \rangle )$
. The concept of a formula describing a global operation is defined similarly.
Example 4. The formula
![]() $P_0(\vec {x})\wedge P_1(\vec {x})$
describes the operation
$P_0(\vec {x})\wedge P_1(\vec {x})$
describes the operation
![]() $f^n_\wedge $
. The formula
$f^n_\wedge $
. The formula
![]() $P_0(\vec {x})\vee P_1(\vec {x})$
describes the operation
$P_0(\vec {x})\vee P_1(\vec {x})$
describes the operation
![]() $f^n_\vee $
. The formula
$f^n_\vee $
. The formula
![]() $\exists x_n P_0(\vec {x},x_n)$
describes the operation
$\exists x_n P_0(\vec {x},x_n)$
describes the operation
![]() $f^n_\exists $
.
$f^n_\exists $
.
If
![]() $\phi (\vec {x})$
is a formula of a logic
$\phi (\vec {x})$
is a formula of a logic
![]() $L^*$
in the above sense, then the operation described by
$L^*$
in the above sense, then the operation described by
![]() $\phi (\vec {x})$
is a logical operation, since we assume that truth in every logic
$\phi (\vec {x})$
is a logical operation, since we assume that truth in every logic
![]() $L^*$
that we consider is closed under isomorphisms (cf. Reference Lindström[33]).
$L^*$
that we consider is closed under isomorphisms (cf. Reference Lindström[33]).
An operation
![]() $\bar {f}$
can be represented alternatively as the model class in the vocabulary L which has in addition to the predicate symbols
$\bar {f}$
can be represented alternatively as the model class in the vocabulary L which has in addition to the predicate symbols
![]() $P_\alpha $
,
$P_\alpha $
,
![]() $\alpha <\beta $
, a new predicate symbol P:
$\alpha <\beta $
, a new predicate symbol P:
 $$ \begin{align*}\mathcal{K}_{\bar{f}}= \{{\mathcal M}: {\mathcal M} \text{ is an } L \text{-structure and }P^{\mathcal M}=f_M(\langle P^{\mathcal M}_\alpha:\alpha<\beta\rangle))\}.\end{align*} $$
$$ \begin{align*}\mathcal{K}_{\bar{f}}= \{{\mathcal M}: {\mathcal M} \text{ is an } L \text{-structure and }P^{\mathcal M}=f_M(\langle P^{\mathcal M}_\alpha:\alpha<\beta\rangle))\}.\end{align*} $$
It is easy to see that the class
 $\mathcal {K}_{\bar {f}}$
is closed under isomorphisms if and only if the operation
$\mathcal {K}_{\bar {f}}$
is closed under isomorphisms if and only if the operation
![]() $\bar {f}$
is preserved by bijections.
$\bar {f}$
is preserved by bijections.
On the other hand, any model class
![]() $\mathcal {K}$
can be turned into a logical operation
$\mathcal {K}$
can be turned into a logical operation
 $\bar {f^{\mathcal {K}}}$
as follows. Let for any non-empty set M and relations
$\bar {f^{\mathcal {K}}}$
as follows. Let for any non-empty set M and relations
![]() $\vec {R}$
on M of the right arity:
$\vec {R}$
on M of the right arity:
 $$ \begin{align*}f^{\mathcal{K}}_M(\vec{R})=\left\{\begin{array}{ll} M&\text{if } (M,\vec{R})\in\mathcal{K},\\ \emptyset&\text{otherwise.} \end{array}\right.\end{align*} $$
$$ \begin{align*}f^{\mathcal{K}}_M(\vec{R})=\left\{\begin{array}{ll} M&\text{if } (M,\vec{R})\in\mathcal{K},\\ \emptyset&\text{otherwise.} \end{array}\right.\end{align*} $$
It is easy to see that the class
![]() $\mathcal {K}$
is closed under isomorphisms if and only if the operation
$\mathcal {K}$
is closed under isomorphisms if and only if the operation
 $\bar {f^{\mathcal {K}}}$
is preserved by bijections.
$\bar {f^{\mathcal {K}}}$
is preserved by bijections.
2.2 Cardinal dependent definability
The theorem of McGee improves “some logic” of Theorem 2 to a very specific logic, namely
![]() $L_{\infty \infty }$
, but at a price: we obtain a different definition for each cardinality separately.Footnote
25
$L_{\infty \infty }$
, but at a price: we obtain a different definition for each cardinality separately.Footnote
25
Note that Theorem 2 has some uniformity in the sense that the defining sentence does not depend on the cardinality of the model in question, but it is also lacking in uniformity in the sense that we do not have one single logic but possibly a different logic for each model class.
We now isolate this property of cardinality dependence. For any cardinal
![]() $\lambda $
let
$\lambda $
let
![]() $\mathcal {K}_\lambda $
be the class of elements of
$\mathcal {K}_\lambda $
be the class of elements of
![]() $\mathcal {K}$
with a domain of size
$\mathcal {K}$
with a domain of size
![]() $\lambda $
.
$\lambda $
.
Definition 5. A model class
![]() $\mathcal {K}$
is cardinal dependently definable, or CD-definable, in a logic
$\mathcal {K}$
is cardinal dependently definable, or CD-definable, in a logic
![]() $L^*$
, or cardinal dependently
$L^*$
, or cardinal dependently
![]() $L^*$
-definable, if
$L^*$
-definable, if
![]() $\mathcal {K}_\lambda $
is
$\mathcal {K}_\lambda $
is
![]() $L^*$
-definable for every
$L^*$
-definable for every
![]() $\lambda $
.
$\lambda $
.
Note that a model class can be CD-definable even in first order logic without being definable even in
![]() $L_{\infty \infty }$
: Consider the class
$L_{\infty \infty }$
: Consider the class
![]() $\mathcal {K}_{\text {lim}}$
of models
$\mathcal {K}_{\text {lim}}$
of models
![]() $(M,P)$
, where either
$(M,P)$
, where either
![]() $|M|$
is a limit cardinal and
$|M|$
is a limit cardinal and
![]() $P=\emptyset $
or else
$P=\emptyset $
or else
![]() $|M|$
is a successor cardinal and
$|M|$
is a successor cardinal and
![]() $P\ne \emptyset $
. It is a consequence of the Löwenheim–Skolem Theorem of
$P\ne \emptyset $
. It is a consequence of the Löwenheim–Skolem Theorem of
![]() $L_{\infty \infty }$
(see Proposition 14 and the proof of Theorem 15) that this model class cannot be definable in it. The following theorem relates isomorphism closure to CD-definability in the case of classes of models:
$L_{\infty \infty }$
(see Proposition 14 and the proof of Theorem 15) that this model class cannot be definable in it. The following theorem relates isomorphism closure to CD-definability in the case of classes of models:
Theorem 6 [Reference McGee41]
If
![]() $\mathcal {K}$
is a class of models of the same vocabulary, then the following conditions are equivalent:
$\mathcal {K}$
is a class of models of the same vocabulary, then the following conditions are equivalent:
-
1.
 $\mathcal {K}$
is closed under isomorphisms.
$\mathcal {K}$
is closed under isomorphisms. -
2.
 $\mathcal {K}$
is CD-definable in
$\mathcal {K}$
is CD-definable in
 $L_{\infty \infty }$
.
$L_{\infty \infty }$
.
Proof Let us fix an infinite cardinal
![]() $\lambda $
. Let
$\lambda $
. Let
![]() ${\mathcal M}_\alpha $
,
${\mathcal M}_\alpha $
,
![]() $\alpha <2^\lambda $
, list all elements of
$\alpha <2^\lambda $
, list all elements of
![]() $\mathcal {K}$
with domain
$\mathcal {K}$
with domain
![]() $\lambda $
. Let
$\lambda $
. Let
![]() $\theta _\alpha \in L_{\lambda ^+\lambda ^+}$
characterize up to isomorphism the model
$\theta _\alpha \in L_{\lambda ^+\lambda ^+}$
characterize up to isomorphism the model
![]() ${\mathcal M}_\alpha $
. The sentence
${\mathcal M}_\alpha $
. The sentence
 $\bigvee _{\alpha <2^\lambda }\theta _\alpha $
defines the model class
$\bigvee _{\alpha <2^\lambda }\theta _\alpha $
defines the model class
![]() $\mathcal {K}_\lambda $
.
$\mathcal {K}_\lambda $
.
The fact that McGee’s theorem depends on the cardinality of the models in the class means that the sentence of
![]() $\phi _\lambda $
of
$\phi _\lambda $
of
![]() $L_{\infty \infty }$
defining the model class
$L_{\infty \infty }$
defining the model class
![]() $\mathcal {K}_\lambda $
may very well depend on
$\mathcal {K}_\lambda $
may very well depend on
![]() $\lambda $
, as in the above example
$\lambda $
, as in the above example
![]() $\mathcal {K}_{\text {lim}}$
. That is, the class size mapping
$\mathcal {K}_{\text {lim}}$
. That is, the class size mapping
![]() $\lambda \mapsto \phi _\lambda $
may encode information that has to be analysed as to its logicality. In the above example, when we ask whether the property of a model of belonging to the model class
$\lambda \mapsto \phi _\lambda $
may encode information that has to be analysed as to its logicality. In the above example, when we ask whether the property of a model of belonging to the model class
![]() $\mathcal {K}_{\text {lim}}$
is logical or not, we essentially ask whether the property of a model of having a limit cardinality is logical or not. According to the Tarski–Sher criterion it undoubtedly is logical. On the other hand, it is fair to say that it is a mathematical property rather than a logical one. As we will see below, the logicality of membership in
$\mathcal {K}_{\text {lim}}$
is logical or not, we essentially ask whether the property of a model of having a limit cardinality is logical or not. According to the Tarski–Sher criterion it undoubtedly is logical. On the other hand, it is fair to say that it is a mathematical property rather than a logical one. As we will see below, the logicality of membership in
![]() $\mathcal {K}_{\text {lim}}$
manifests in our below analysis a rather low degree of logicality.
$\mathcal {K}_{\text {lim}}$
manifests in our below analysis a rather low degree of logicality.
As we pointed out earlier, McGee Reference McGee[41] considers describability of logical operations rather than definability of model classes. Let us now draw a further connection, using the
![]() $\Delta $
-operation on logics, between describability of logical operations and definability of model classes.
$\Delta $
-operation on logics, between describability of logical operations and definability of model classes.
Suppose
![]() $\mathcal {K}$
is a class of models of vocabulary L and
$\mathcal {K}$
is a class of models of vocabulary L and
![]() $L^{\prime }\subseteq L$
. We use
$L^{\prime }\subseteq L$
. We use
![]() $\mathcal{K}\upharpoonright L^{\prime }$
to denote the class of reducts
$\mathcal{K}\upharpoonright L^{\prime }$
to denote the class of reducts
![]() ${\mathcal M}\upharpoonright L^{\prime }$
of models
${\mathcal M}\upharpoonright L^{\prime }$
of models
![]() ${\mathcal M}\in \mathcal{K}$
. We call
${\mathcal M}\in \mathcal{K}$
. We call
![]() $\mathcal{K}\upharpoonright L^{\prime }$
a projection of
$\mathcal{K}\upharpoonright L^{\prime }$
a projection of
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Definition 7. A model class
![]() $\mathcal {K}$
is
$\mathcal {K}$
is
![]() $\Sigma (L^*)$
-definable, or in
$\Sigma (L^*)$
-definable, or in
![]() $\Sigma (L^*)$
, if it is a projection of an
$\Sigma (L^*)$
, if it is a projection of an
![]() $L^*$
-definable model class. A model class is
$L^*$
-definable model class. A model class is
![]() $\Delta $
-definable in
$\Delta $
-definable in
![]() $L^*$
, or definable in
$L^*$
, or definable in
![]() $\Delta (L^*)$
, if both
$\Delta (L^*)$
, if both
![]() $\mathcal {K}$
and the complement of
$\mathcal {K}$
and the complement of
![]() $\mathcal {K}$
are
$\mathcal {K}$
are
![]() $\Sigma (L^*)$
.
$\Sigma (L^*)$
.
It should be noted that
![]() $\Delta (L_{\omega \omega })=L_{\omega \omega }$
Reference Craig[19],
$\Delta (L_{\omega \omega })=L_{\omega \omega }$
Reference Craig[19],
![]() $\Delta (L_{\omega _1\omega })=L_{\omega _1\omega }$
Reference Lopez-Escobar[34] and
$\Delta (L_{\omega _1\omega })=L_{\omega _1\omega }$
Reference Lopez-Escobar[34] and
![]() $\Delta (L_{\infty \omega })\subseteq L_{\infty \infty }$
Reference Malitz[40].
$\Delta (L_{\infty \omega })\subseteq L_{\infty \infty }$
Reference Malitz[40].
Lemma 8. Suppose f is a logical operation on M and
![]() $L^*$
is a logic. Then (1)
$L^*$
is a logic. Then (1)
![]() $\to $
(2)
$\to $
(2)
![]() $\to $
(3), where:
$\to $
(3), where:
-
(1) f is describable in
 $L^*$
.
$L^*$
. -
(2) The model class
 $\mathcal {K}_f$
is definable in
$\mathcal {K}_f$
is definable in
 $L^*$
.
$L^*$
. -
(3) f is describable in
 $\Delta (L^*)$
.
$\Delta (L^*)$
.
Proof Suppose f is described on M by the formula
![]() $\psi (\vec {x})\in L^*$
.
$\psi (\vec {x})\in L^*$
.
![]() $\mathcal {K}_f$
is defined by the sentence
$\mathcal {K}_f$
is defined by the sentence
 $\forall \vec {x}(P(\vec {x})\leftrightarrow \psi (\vec {x},\vec {R})).$
This proves the first implication. Suppose then
$\forall \vec {x}(P(\vec {x})\leftrightarrow \psi (\vec {x},\vec {R})).$
This proves the first implication. Suppose then
![]() $\mathcal {K}_f$
is defined by the sentence
$\mathcal {K}_f$
is defined by the sentence
![]() $\phi \in L^*$
with vocabulary
$\phi \in L^*$
with vocabulary
![]() $\{P_\alpha :\alpha <\beta \}\cup \{P\}$
. Consider the formula
$\{P_\alpha :\alpha <\beta \}\cup \{P\}$
. Consider the formula
![]() $\psi (\vec {x})\equiv \exists P(\phi \wedge P(\vec {x}))$
with the second order quantifier
$\psi (\vec {x})\equiv \exists P(\phi \wedge P(\vec {x}))$
with the second order quantifier
![]() $``\exists P."$
This clearly describes f but is not, a priori, in
$``\exists P."$
This clearly describes f but is not, a priori, in
![]() $L^*$
. However
$L^*$
. However
![]() $\psi (\vec {x})\equiv \forall P(\phi \to P(\vec {x}))$
and therefore
$\psi (\vec {x})\equiv \forall P(\phi \to P(\vec {x}))$
and therefore
![]() $\psi (\vec {x})$
is in
$\psi (\vec {x})$
is in
![]() $\Delta (L^*)$
.
$\Delta (L^*)$
.
Lemma 9. Suppose
![]() $\mathcal {K}$
is a model class. Then
$\mathcal {K}$
is a model class. Then
![]() $\mathcal {K}_\lambda $
is definable in
$\mathcal {K}_\lambda $
is definable in
![]() $L^*$
if and only if the logical operation
$L^*$
if and only if the logical operation
 $f^{\mathcal {K}}_\lambda $
is describable in
$f^{\mathcal {K}}_\lambda $
is describable in
![]() $L^*$
.
$L^*$
.
Proof Suppose
![]() $\mathcal {K}_\lambda $
is defined in cardinality
$\mathcal {K}_\lambda $
is defined in cardinality
![]() $\lambda $
by the sentence
$\lambda $
by the sentence
![]() $\phi \in L^*$
.
$\phi \in L^*$
.
 $f^{\mathcal {K}}_\lambda $
is defined by the formula
$f^{\mathcal {K}}_\lambda $
is defined by the formula
![]() $\phi $
(without free variables). Suppose then
$\phi $
(without free variables). Suppose then
 $f^{\mathcal {K}}_\lambda $
is defined by the formula
$f^{\mathcal {K}}_\lambda $
is defined by the formula
![]() $\psi ({x})\in L^*$
. Then
$\psi ({x})\in L^*$
. Then
![]() $\mathcal {K}_\lambda $
is defined by the sentence
$\mathcal {K}_\lambda $
is defined by the sentence
![]() $\exists {x}\psi ({x})$
.
$\exists {x}\psi ({x})$
.
The above two lemmas demonstrate the close relationship between logicality of operations on semantic values and logicality of properties of models. The next lemma, based on the method of [Reference Lindström33, Theorem 5], shows that the relationship is not perfect.
Lemma 10. There is a logical operation
![]() $\bar {f}$
such that
$\bar {f}$
such that
![]() $\mathcal {K}^{\bar {f}}$
is definable in
$\mathcal {K}^{\bar {f}}$
is definable in
![]() $L(Q_0)$
but
$L(Q_0)$
but
![]() $\bar {f}$
is not describable in
$\bar {f}$
is not describable in
![]() $L(Q_0)$
.
$L(Q_0)$
.
Bonnay [Reference Bonnay, Speitel, Sagi and Woods9] suggests that the concept of potential isomorphism is a better criterion for logicality than isomorphism itself. For potential isomorphism closure there is the following version of McGee’s theorem:
Theorem 11 [Reference Barwise and Morley5]
If
![]() $\mathcal {K}$
is a class of models of the same vocabulary, then the following conditions are equivalent:
$\mathcal {K}$
is a class of models of the same vocabulary, then the following conditions are equivalent:
-
1.
 $\mathcal {K}$
is closed under potential isomorphisms.
$\mathcal {K}$
is closed under potential isomorphisms. -
2.
 $\mathcal {K}$
is CD-definable in
$\mathcal {K}$
is CD-definable in
 $L_{\infty \omega }$
.
$L_{\infty \omega }$
.
A problem with closure under potential isomorphism is that well-ordered structures
![]() $(\alpha ,\in ,P_1,\ldots ,P_n)$
and
$(\alpha ,\in ,P_1,\ldots ,P_n)$
and
 $(\beta ,\in ,P^{\prime }_1,\ldots ,P^{\prime }_n)$
are never potentially isomorphic if
$(\beta ,\in ,P^{\prime }_1,\ldots ,P^{\prime }_n)$
are never potentially isomorphic if
![]() $\alpha \ne \beta $
. Just as an isomorphism closed model class can have models with domains of different cardinalities and the isomorphism closure gives no information across the domains, a potential isomorphism closed model class can have models
$\alpha \ne \beta $
. Just as an isomorphism closed model class can have models with domains of different cardinalities and the isomorphism closure gives no information across the domains, a potential isomorphism closed model class can have models
![]() $(\alpha ,\in ,P_1,\ldots ,P_n)$
with different
$(\alpha ,\in ,P_1,\ldots ,P_n)$
with different
![]() $\alpha $
and the potential isomorphism closure also gives no information across such domains.
$\alpha $
and the potential isomorphism closure also gives no information across such domains.
2.3 The model-theoretic properties of
 $L_{\infty \infty }$
$L_{\infty \infty }$
We now note the different respects in which
![]() $L_{\infty \infty }$
deviates from first order logic. First of all,
$L_{\infty \infty }$
deviates from first order logic. First of all,
![]() $L_{\infty \infty }$
is badly nonabsolute.Footnote
26
For example, the sentence
$L_{\infty \infty }$
is badly nonabsolute.Footnote
26
For example, the sentence
 $$ \begin{align} \begin{array}{l} \forall x\forall y(\forall z(E(z,x)\leftrightarrow E(z,y))\to x=y)\wedge\\ \forall x_0\forall x_1\ldots\exists y\forall z(E(z,y)\leftrightarrow\bigvee_{n<\omega}z=x_n) \end{array}\end{align} $$
$$ \begin{align} \begin{array}{l} \forall x\forall y(\forall z(E(z,x)\leftrightarrow E(z,y))\to x=y)\wedge\\ \forall x_0\forall x_1\ldots\exists y\forall z(E(z,y)\leftrightarrow\bigvee_{n<\omega}z=x_n) \end{array}\end{align} $$
of
![]() $L_{\infty \infty }$
which has models exactly in cardinalities
$L_{\infty \infty }$
which has models exactly in cardinalities
![]() $\mu $
such that
$\mu $
such that
![]() $\mu ^\omega =\mu $
, is highly non-absolute.Footnote
27
Other failures of absoluteness can be generated by replacing
$\mu ^\omega =\mu $
, is highly non-absolute.Footnote
27
Other failures of absoluteness can be generated by replacing
![]() $\omega $
here by any regular cardinal.
$\omega $
here by any regular cardinal.
A second important model-theoretic property of first order logic is its downward Löwenheim–Skolem theorem. Consider (1). Such a
![]() $\mu $
cannot have cofinality
$\mu $
cannot have cofinality
![]() $\omega $
and thus
$\omega $
and thus
![]() $L_{\infty \infty }$
does not have a Löwenheim–Skolem theorem in the same strong sense as first order logic, or even in the sense of, e.g.,
$L_{\infty \infty }$
does not have a Löwenheim–Skolem theorem in the same strong sense as first order logic, or even in the sense of, e.g.,
![]() $L_{\infty \omega }$
(see Theorem 13). That is,
$L_{\infty \omega }$
(see Theorem 13). That is,
![]() $L_{\infty \infty }$
can “omit” cardinals of cofinality
$L_{\infty \infty }$
can “omit” cardinals of cofinality
![]() $\omega $
in this special sense given by the Löwenheim–Skolem theorem. In contrast, a typical consequence of a Löwenheim–Skolem theorem of
$\omega $
in this special sense given by the Löwenheim–Skolem theorem. In contrast, a typical consequence of a Löwenheim–Skolem theorem of
![]() $L_{\kappa ^+\omega }$
is that if a definable model class has a model of cardinality
$L_{\kappa ^+\omega }$
is that if a definable model class has a model of cardinality
![]() $\lambda>\kappa $
then it has models of all cardinalities
$\lambda>\kappa $
then it has models of all cardinalities
![]() $\mu $
such that
$\mu $
such that
![]() $\kappa \le \mu \le \lambda $
(Theorem 13), whatever their cofinality.
$\kappa \le \mu \le \lambda $
(Theorem 13), whatever their cofinality.
The logic behind Theorem 7,
![]() $L_{\kappa ^+\kappa ^+}$
, fails in a strong sense to have a Completeness Theorem. By a result of Dana Scott (published in Reference Karp[29]) the set of valid sentences of
$L_{\kappa ^+\kappa ^+}$
, fails in a strong sense to have a Completeness Theorem. By a result of Dana Scott (published in Reference Karp[29]) the set of valid sentences of
![]() $L_{\kappa ^+\kappa ^+}$
is not
$L_{\kappa ^+\kappa ^+}$
is not
![]() $L_{\kappa ^+\kappa ^+}$
-definable over
$L_{\kappa ^+\kappa ^+}$
-definable over
![]() $H(\kappa ^+)$
, the set of sets of hereditary cardinality
$H(\kappa ^+)$
, the set of sets of hereditary cardinality
![]() $\le \kappa $
. In contrast, the set of valid sentences of
$\le \kappa $
. In contrast, the set of valid sentences of
![]() $L_{\kappa ^+\omega }$
is
$L_{\kappa ^+\omega }$
is
![]() $\Sigma _1$
-definable over
$\Sigma _1$
-definable over
![]() $H(\kappa ^+)$
Reference Karp[29], reminiscent of the Completeness Theorem of first order logic which implies that the set of (Gödel numbers of) valid sentences of first order logic is recursively enumerable i.e.,
$H(\kappa ^+)$
Reference Karp[29], reminiscent of the Completeness Theorem of first order logic which implies that the set of (Gödel numbers of) valid sentences of first order logic is recursively enumerable i.e.,
![]() $\Sigma _1$
over
$\Sigma _1$
over
![]() $HF$
, the set of hereditarily finite sets. In fact, Karp gives a complete axiomatization for
$HF$
, the set of hereditarily finite sets. In fact, Karp gives a complete axiomatization for
![]() $L_{\kappa ^+\omega }$
in Reference Karp[29].
$L_{\kappa ^+\omega }$
in Reference Karp[29].
In §5 we replace
![]() $L_{\infty \infty }$
by a logic which is almost absolute and which has a strong Löwenheim–Skolem theorem, together with other desirable properties, though it is still the case that the definition is given relative to the size of the models in the class.
$L_{\infty \infty }$
by a logic which is almost absolute and which has a strong Löwenheim–Skolem theorem, together with other desirable properties, though it is still the case that the definition is given relative to the size of the models in the class.
3 Löwenheim–Skolem theorems viewed through the spectra of model classes
The fact that the class of all models of cardinality
![]() $\kappa $
, for example, satisfies the Tarski–Sher criterion, irrespective of what
$\kappa $
, for example, satisfies the Tarski–Sher criterion, irrespective of what
![]() $\kappa $
is, raises the question, is cardinality a logical property? We saw that in the more subtle case of
$\kappa $
is, raises the question, is cardinality a logical property? We saw that in the more subtle case of
![]() $\mathcal {K}_{\text {lim}}$
the property of a model of being of a limit cardinality is, according to this criterion, logical; by modifying
$\mathcal {K}_{\text {lim}}$
the property of a model of being of a limit cardinality is, according to this criterion, logical; by modifying
![]() $\mathcal {K}_{\text {lim}}$
one can generate many other cases. For example, if A is a property of natural numbers, we can consider the class
$\mathcal {K}_{\text {lim}}$
one can generate many other cases. For example, if A is a property of natural numbers, we can consider the class
![]() $\mathcal {K}$
of models of cardinality
$\mathcal {K}$
of models of cardinality
![]() $\aleph _n$
, such that n has property A. The property of a model of belonging to
$\aleph _n$
, such that n has property A. The property of a model of belonging to
![]() $\mathcal {K}$
is a logical property of the model by the Tarski–Sher criterion, even though to judge whether a particular model is in
$\mathcal {K}$
is a logical property of the model by the Tarski–Sher criterion, even though to judge whether a particular model is in
![]() $\mathcal {K}$
one has to first determine whether the size of the universe is some
$\mathcal {K}$
one has to first determine whether the size of the universe is some
![]() $\aleph _n$
, and after that one has to determine whether n has property A. This stretches the concept of logicality and entangles it with the concept of what is mathematical. Earlier writers have observed this, so we are not saying essentially anything new here.
$\aleph _n$
, and after that one has to determine whether n has property A. This stretches the concept of logicality and entangles it with the concept of what is mathematical. Earlier writers have observed this, so we are not saying essentially anything new here.
Of Feferman’s three objections to the Tarski–Sher criterion of logicality, the third is that it leaves unexplained how logicality is to be understood across domains of different sizes. The existential quantifier, for example, is, in a sense, the same on any domain of any cardinality, but this is not true of many properties which satisfy the Tarski–Sher criterion, for example
![]() $\mathcal {K}_{\text {lim}}$
. We suggest that in order that a property of models manifests a greater degree of logicality than is provided by the Tarski–Sher criterion, it should have a definition by a sentence in
$\mathcal {K}_{\text {lim}}$
. We suggest that in order that a property of models manifests a greater degree of logicality than is provided by the Tarski–Sher criterion, it should have a definition by a sentence in
![]() $L_{\infty \infty }$
or in some other logic in such a way that the same sentence defines the model class in as many cardinalities as possible.Footnote
28
We explore this suggestion below via the concept of a spectrum. Our second suggestion is that a higher grade of logicality would be assigned to the degree to which the logic in question had “first-order-like” model-theoretic properties: absoluteness, a Löwenheim–Skolem theorem, and completeness.
$L_{\infty \infty }$
or in some other logic in such a way that the same sentence defines the model class in as many cardinalities as possible.Footnote
28
We explore this suggestion below via the concept of a spectrum. Our second suggestion is that a higher grade of logicality would be assigned to the degree to which the logic in question had “first-order-like” model-theoretic properties: absoluteness, a Löwenheim–Skolem theorem, and completeness.
![]() $L_{\infty \infty }$
would thus be given a low grade on the logicality scale, being non-absolute, having a limited Löwenheim–Skolem theorem and failing to have a Completeness Theorem. We explore this suggestion in §7
Footnote
29
.
$L_{\infty \infty }$
would thus be given a low grade on the logicality scale, being non-absolute, having a limited Löwenheim–Skolem theorem and failing to have a Completeness Theorem. We explore this suggestion in §7
Footnote
29
.
3.1 Spectra
In analysing the structure of a model class, in order to determine whether it is in some sense logical or not or to find out whether it is definable in some interesting logic, it is useful to investigate the cardinalities of models in the class. One might think that mere cardinalities are too rough a measure of any form of logicality but this is, in fact, surprisingly informative. This leads naturally to the concept of a spectrumFootnote 30 :
Definition 12. If
![]() $\mathcal {K}$
is a model class, the spectrum of
$\mathcal {K}$
is a model class, the spectrum of
![]() $\mathcal {K}$
is the class
$\mathcal {K}$
is the class
![]() $\text {sp}(\mathcal {K})$
of cardinalities of models in
$\text {sp}(\mathcal {K})$
of cardinalities of models in
![]() $\mathcal {K}$
i.e.,
$\mathcal {K}$
i.e.,
Depending on
![]() $\mathcal {K}$
, the spectrum can be a singleton, an interval of cardinals, an initial (or final) segment of the class of all cardinals, or something more complicated, such as the class of all limit cardinals, or all limit cardinals of cofinality
$\mathcal {K}$
, the spectrum can be a singleton, an interval of cardinals, an initial (or final) segment of the class of all cardinals, or something more complicated, such as the class of all limit cardinals, or all limit cardinals of cofinality
![]() $\omega $
(see Figure 1). Even the patterns of finite numbers in spectra of first order sentences is highly interesting [Reference Asser3, Reference Jones and Selman27]. However, we are here concerned with infinite cardinals in a spectrum.
$\omega $
(see Figure 1). Even the patterns of finite numbers in spectra of first order sentences is highly interesting [Reference Asser3, Reference Jones and Selman27]. However, we are here concerned with infinite cardinals in a spectrum.

Figure 1 Spectra of some model classes.
The property of a logic which reflects regularity patterns in its spectra is captured by the Löwenheim–Skolem theorem. The spectrum gives indirect information of the possibility that the model class is definable in some logic. Roughly speaking, if the logic has a strong Löwenheim–Skolem property, then the spectra of definable model classes reflect this. If every sentence in the logic which has an infinite model has also a countably infinite model, the most famous case of a Löwenheim–Skolem property, then every spectrum with an infinite cardinal in it has also
![]() $\aleph _0$
in it.
$\aleph _0$
in it.
Skolem proved that first order logic satisfies
![]() $\text {LS}([\aleph _0,\infty ),\{\aleph _0\})$
(see Definition 1) giving rise to the so-called Skolem Paradox: countable first order theories such as set theory have countable models if they have models at all. Now, 100 years after Skolem’s discovery, the indifference of first order logic to the infinite cardinality of its models is often considered a positive rather than negative aspect. Indifference to cardinality is of course closely related to set-theoretical absoluteness and thereby to a desirable quality of logicality. In consequence, the stronger form of
$\text {LS}([\aleph _0,\infty ),\{\aleph _0\})$
(see Definition 1) giving rise to the so-called Skolem Paradox: countable first order theories such as set theory have countable models if they have models at all. Now, 100 years after Skolem’s discovery, the indifference of first order logic to the infinite cardinality of its models is often considered a positive rather than negative aspect. Indifference to cardinality is of course closely related to set-theoretical absoluteness and thereby to a desirable quality of logicality. In consequence, the stronger form of
![]() $\text {LS}(C,D)$
a logic satisfies the more appropriate the logic is for expressing logical properties.
$\text {LS}(C,D)$
a logic satisfies the more appropriate the logic is for expressing logical properties.
If a logic satisfies
![]() $\text {LS}(C,D)$
, there are consequences for the spectra of definable model classes. Suppose
$\text {LS}(C,D)$
, there are consequences for the spectra of definable model classes. Suppose
![]() $\mathcal {K}$
is definable in a logic with
$\mathcal {K}$
is definable in a logic with
![]() $\text {LS}(C,D)$
. Then we can make the following conclusions: If there is
$\text {LS}(C,D)$
. Then we can make the following conclusions: If there is
![]() ${\mathcal M}\in \mathcal {K}$
with
${\mathcal M}\in \mathcal {K}$
with
![]() $|M|\in C$
, then there is
$|M|\in C$
, then there is
![]() ${\mathcal N}\in \mathcal {K}$
with
${\mathcal N}\in \mathcal {K}$
with
![]() $|N|\in D$
. On the other hand, if
$|N|\in D$
. On the other hand, if
![]() $\mathcal {K}$
contains a model of cardinality
$\mathcal {K}$
contains a model of cardinality
![]() $\kappa $
but no models of cardinality
$\kappa $
but no models of cardinality
![]() $\lambda $
, then
$\lambda $
, then
![]() $\mathcal {K}$
cannot be definable in a logic with
$\mathcal {K}$
cannot be definable in a logic with
![]() $\text {LS}(C,D)$
such that
$\text {LS}(C,D)$
such that
![]() $\kappa \in C$
and
$\kappa \in C$
and
![]() $\lambda \notin D$
. The point is that by looking at the spectrum of
$\lambda \notin D$
. The point is that by looking at the spectrum of
![]() $\mathcal {K}$
we can make inferences about its definability in different logics. Thus, if we are given a model class
$\mathcal {K}$
we can make inferences about its definability in different logics. Thus, if we are given a model class
![]() $\mathcal {K}$
but no logic in which it would be definable (apart from the trivial
$\mathcal {K}$
but no logic in which it would be definable (apart from the trivial
![]() $L(Q_{\mathcal {K}})$
), and we can discern regular patterns in
$L(Q_{\mathcal {K}})$
), and we can discern regular patterns in
![]() $\text {sp}(\mathcal {K})$
, we may take it as an indirect indication (albeit not a proof) that
$\text {sp}(\mathcal {K})$
, we may take it as an indirect indication (albeit not a proof) that
![]() $\mathcal {K}$
is definable in a logic with
$\mathcal {K}$
is definable in a logic with
![]() $\text {LS}(C,D)$
for some C and D explaining the found patterns. On the other hand, if
$\text {LS}(C,D)$
for some C and D explaining the found patterns. On the other hand, if
![]() $\text {sp}(\mathcal {K})$
does not seem to have regular patterns, we may take it as an indication that no such logic can be found. Thus
$\text {sp}(\mathcal {K})$
does not seem to have regular patterns, we may take it as an indication that no such logic can be found. Thus
![]() $\text {sp}(\mathcal {K})$
gives implicit information about the possibility of finding a syntax for
$\text {sp}(\mathcal {K})$
gives implicit information about the possibility of finding a syntax for
![]() $\mathcal {K}$
.
$\mathcal {K}$
.
Let us look at the Löwenheim–Skolem properties of the logics
![]() $L_{\infty \omega }$
and
$L_{\infty \omega }$
and
![]() $L_{\infty \infty }$
.Footnote
31
We first recall a basic construction in infinitary logic, based on a class of important formulas due to Scott Reference Scott, Addison, Henkin and Tarski[47]. For any ordinal
$L_{\infty \infty }$
.Footnote
31
We first recall a basic construction in infinitary logic, based on a class of important formulas due to Scott Reference Scott, Addison, Henkin and Tarski[47]. For any ordinal
![]() $\alpha $
let the formula
$\alpha $
let the formula
![]() $\eta _\alpha (x)$
with one free variable x and a binary relation symbol
$\eta _\alpha (x)$
with one free variable x and a binary relation symbol
![]() $<$
be defined, by transfinite recursion, as follows:
$<$
be defined, by transfinite recursion, as follows:
 $$ \begin{align} \eta_\alpha(x)\leftrightarrow\forall y(y<x\to\bigvee_{\beta<\alpha}\eta_\beta(y)) \wedge\bigwedge_{\beta<\alpha}\exists y(y<x\wedge\eta_\beta(y)). \end{align} $$
$$ \begin{align} \eta_\alpha(x)\leftrightarrow\forall y(y<x\to\bigvee_{\beta<\alpha}\eta_\beta(y)) \wedge\bigwedge_{\beta<\alpha}\exists y(y<x\wedge\eta_\beta(y)). \end{align} $$
Then for a linear order
![]() $(A,<)$
and
$(A,<)$
and
![]() $a\in A$
we have
$a\in A$
we have
Let
 $$ \begin{align} \eta^{\prime}_\alpha\leftrightarrow\forall y\bigvee_{\beta<\alpha}\eta_\beta(y) \wedge\bigwedge_{\beta<\alpha}\exists y\ \eta_\beta(y). \end{align} $$
$$ \begin{align} \eta^{\prime}_\alpha\leftrightarrow\forall y\bigvee_{\beta<\alpha}\eta_\beta(y) \wedge\bigwedge_{\beta<\alpha}\exists y\ \eta_\beta(y). \end{align} $$
For a linear order
![]() $(A,<)$
we have
$(A,<)$
we have
 $$ \begin{align} (A,<)\models\eta^{\prime}_\alpha\iff(A,<)\cong(\alpha,<). \end{align} $$
$$ \begin{align} (A,<)\models\eta^{\prime}_\alpha\iff(A,<)\cong(\alpha,<). \end{align} $$
Now
![]() $\eta ^{\prime }_\alpha $
is in
$\eta ^{\prime }_\alpha $
is in
![]() $L_{\kappa \omega }$
whenever
$L_{\kappa \omega }$
whenever
![]() $\alpha <\kappa $
. It follows that by combining the sentences
$\alpha <\kappa $
. It follows that by combining the sentences
![]() $\eta ^{\prime }_\alpha $
, the logic
$\eta ^{\prime }_\alpha $
, the logic
![]() $L_{\kappa \omega }$
can manifest totally arbitrary patterns of spectra in cardinalities below
$L_{\kappa \omega }$
can manifest totally arbitrary patterns of spectra in cardinalities below
![]() $\kappa $
, roughly for the same reason that any finite set of finite numbers can be the spectrum of a first order sentence. More exactly, if X is an arbitrary set of cardinal numbers below
$\kappa $
, roughly for the same reason that any finite set of finite numbers can be the spectrum of a first order sentence. More exactly, if X is an arbitrary set of cardinal numbers below
![]() $\kappa $
, then
$\kappa $
, then
 $$ \begin{align*}\bigvee_{\lambda\in X}\eta^{\prime}_\lambda\in L_{\kappa^+\omega}\text{ and }X=\text{sp}(\bigvee_{\lambda\in X}\eta^{\prime}_\lambda).\end{align*} $$
$$ \begin{align*}\bigvee_{\lambda\in X}\eta^{\prime}_\lambda\in L_{\kappa^+\omega}\text{ and }X=\text{sp}(\bigvee_{\lambda\in X}\eta^{\prime}_\lambda).\end{align*} $$
This shows that when dealing with extensions of
![]() $L_{\kappa \omega }$
it makes sense to focus on cardinals
$L_{\kappa \omega }$
it makes sense to focus on cardinals
![]() $\ge \kappa $
.
$\ge \kappa $
.
The basic facts about the
![]() $\text {LS}(C,D)$
type properties of infinitary languages are the following:
$\text {LS}(C,D)$
type properties of infinitary languages are the following:
Theorem 13 [Reference Dickmann20]
Suppose
![]() $\kappa \le \lambda $
are cardinals and
$\kappa \le \lambda $
are cardinals and
![]() $\kappa $
is regular.
$\kappa $
is regular.
-
1.
 $L_{\kappa ^+\omega }$
satisfies
$L_{\kappa ^+\omega }$
satisfies
 $\text {LS}([\lambda ,\infty )\},\{\mu \})$
for all
$\text {LS}([\lambda ,\infty )\},\{\mu \})$
for all
 $\mu $
such that
$\mu $
such that
 $\kappa \le \mu \le \lambda $
.
$\kappa \le \mu \le \lambda $
. -
2.
 $L_{\kappa ^+\kappa ^+}$
satisfies
$L_{\kappa ^+\kappa ^+}$
satisfies
 $\text {LS}([\lambda ,\infty ),\{\mu \})$
for all
$\text {LS}([\lambda ,\infty ),\{\mu \})$
for all
 $\mu $
such that
$\mu $
such that
 $\kappa \kern1.2pt{\le}\kern1.2pt \mu \kern1.2pt{\le}\kern1.2pt \lambda $
and
$\kappa \kern1.2pt{\le}\kern1.2pt \mu \kern1.2pt{\le}\kern1.2pt \lambda $
and
 $\mu ^\kappa \kern1.2pt{=}\kern1.2pt\mu $
.
$\mu ^\kappa \kern1.2pt{=}\kern1.2pt\mu $
. -
3.
 $L_{\kappa ^+\omega }$
satisfies
$L_{\kappa ^+\omega }$
satisfies
 $\text {LS}([\beth _{(2^\kappa )^+},\infty ),[\mu ,\infty ))$
for all
$\text {LS}([\beth _{(2^\kappa )^+},\infty ),[\mu ,\infty ))$
for all
 $\mu $
.
$\mu $
. -
4.
 $L_{\omega _1\omega _1}$
does not satisfy “For all
$L_{\omega _1\omega _1}$
does not satisfy “For all
 $\mu \text {LS}([\lambda ,\infty ),[\mu ,\infty ))$
” for any
$\mu \text {LS}([\lambda ,\infty ),[\mu ,\infty ))$
” for any
 $\lambda $
below the first inaccessible cardinal (assuming there are inaccessible cardinals).
$\lambda $
below the first inaccessible cardinal (assuming there are inaccessible cardinals).
For a class size logic such as
![]() $L_{\infty \omega }$
or
$L_{\infty \omega }$
or
![]() $L_{\infty \infty }$
the
$L_{\infty \infty }$
the
![]() $\text {LS}(C,D)$
properties hold via their connection to
$\text {LS}(C,D)$
properties hold via their connection to
![]() $L_{\kappa \omega }$
or
$L_{\kappa \omega }$
or
![]() $L_{\kappa \lambda }$
: If
$L_{\kappa \lambda }$
: If
![]() $\phi \in L_{\infty \infty }$
, then
$\phi \in L_{\infty \infty }$
, then
![]() $\phi \in L_{\kappa \lambda }$
for some (least)
$\phi \in L_{\kappa \lambda }$
for some (least)
![]() $\kappa $
and
$\kappa $
and
![]() $\lambda $
and then Theorem 13 applies.
$\lambda $
and then Theorem 13 applies.
The above theorem shows that the spectra of
![]() $L_{\infty \infty }$
are much more complicated than the spectra of
$L_{\infty \infty }$
are much more complicated than the spectra of
![]() $L_{\infty \omega }$
. For example, let
$L_{\infty \omega }$
. For example, let
![]() $\theta $
be the sentence (1) of
$\theta $
be the sentence (1) of
![]() $L_{\omega _1\omega _1}$
which has a model of cardinality
$L_{\omega _1\omega _1}$
which has a model of cardinality
![]() $\mu $
if and only if
$\mu $
if and only if
![]() $\mu ^\omega =\mu $
. Thus
$\mu ^\omega =\mu $
. Thus
![]() $\text {sp}(\theta )$
(i.e.,
$\text {sp}(\theta )$
(i.e.,
![]() $\text {sp}(\text {Mod}(\theta ))$
) is full of “holes” as it misses all cardinals, such as e.g., each
$\text {sp}(\text {Mod}(\theta ))$
) is full of “holes” as it misses all cardinals, such as e.g., each
![]() $\aleph _{\alpha +\omega }$
, that are
$\aleph _{\alpha +\omega }$
, that are
![]() $\omega $
-cofinal. Whereas the spectra of sentences of
$\omega $
-cofinal. Whereas the spectra of sentences of
![]() $L_{\kappa \omega }$
cannot have such holes above
$L_{\kappa \omega }$
cannot have such holes above
![]() $\kappa $
. (See Figure 2.)
$\kappa $
. (See Figure 2.)

Figure 2 A difference between
![]() $L_{\infty \omega }$
and
$L_{\infty \omega }$
and
![]() $L_{\infty \infty }$
.
$L_{\infty \infty }$
.
What does it reveal about logicality if the spectrum is full of ‘holes’? It suggests that we are very far from the situation in which we can claim we have the same logical operation independently of the domain. In the case of
![]() $L_{\kappa ^+\omega }$
the spectrum is (above
$L_{\kappa ^+\omega }$
the spectrum is (above
![]() $\kappa $
) a homogeneous segment of cardinals, either bounded by
$\kappa $
) a homogeneous segment of cardinals, either bounded by
 $\beth _{(2^\kappa )^+}$
or unbounded, and we are closer to having the same logical operation independently of the domain. Thus we judge a model class definable in
$\beth _{(2^\kappa )^+}$
or unbounded, and we are closer to having the same logical operation independently of the domain. Thus we judge a model class definable in
![]() $L_{\infty \omega }$
as having a greater degree of logicality than a model class definable in
$L_{\infty \omega }$
as having a greater degree of logicality than a model class definable in
![]() $L_{\infty \infty }$
.
$L_{\infty \infty }$
.
In Definition 1 we defined the Löwenheim the Hanf number of an arbitrary logic. These numbers always exist if the class of formulas of the logic is a set. Thus they exist for
![]() $L_{\kappa \lambda }$
for any
$L_{\kappa \lambda }$
for any
![]() $\kappa $
and
$\kappa $
and
![]() $\lambda $
but not for
$\lambda $
but not for
![]() $L_{\infty \omega }$
and
$L_{\infty \omega }$
and
![]() $L_{\infty \infty }$
.
$L_{\infty \infty }$
.
The Hanf-number and Löwenheim number of
![]() $L^*$
can be easily defined in terms of spectra. Below a spectrum is called bounded if it is a set (rather than a proper class).
$L^*$
can be easily defined in terms of spectra. Below a spectrum is called bounded if it is a set (rather than a proper class).
 $$ \begin{align}\ell(L^*)&=\textrm{sup} \{ \min(\text{sp}(\phi)):\phi\in L^*, \text{sp}(\phi)\ne\emptyset \}\notag\\h(L^*)& = \textrm{sup} \{ \textrm{sup}(\text{sp}(\phi)):\phi\in L^* \text{ and sp}(\phi)\ne\emptyset\ \text{is bounded}\}.\end{align} $$
$$ \begin{align}\ell(L^*)&=\textrm{sup} \{ \min(\text{sp}(\phi)):\phi\in L^*, \text{sp}(\phi)\ne\emptyset \}\notag\\h(L^*)& = \textrm{sup} \{ \textrm{sup}(\text{sp}(\phi)):\phi\in L^* \text{ and sp}(\phi)\ne\emptyset\ \text{is bounded}\}.\end{align} $$
We saw that Sagi employs Löwenheim numbers as a measure of logicality: the smaller the Löwenheim number the greater the degree of logicality. Thus model classes definable in
![]() $L(Q_\alpha )$
have a stronger degree of logicality than those definable in
$L(Q_\alpha )$
have a stronger degree of logicality than those definable in
 $L(Q_\beta )$
, for
$L(Q_\beta )$
, for
![]() $\beta>\alpha $
.
$\beta>\alpha $
.
The logic
![]() $L(Q_\alpha )$
satisfies for trivial reasons the Löwenheim–Skolem property
$L(Q_\alpha )$
satisfies for trivial reasons the Löwenheim–Skolem property
![]() $\text {LS}([\omega ,\aleph _\alpha ),\{\mu \})$
for all
$\text {LS}([\omega ,\aleph _\alpha ),\{\mu \})$
for all
![]() $\mu <\aleph _\alpha $
and the rather strong Löwenheim–Skolem property
$\mu <\aleph _\alpha $
and the rather strong Löwenheim–Skolem property
![]() $\text {LS}([\aleph _\alpha ,\infty )),\{\mu \})$
for all
$\text {LS}([\aleph _\alpha ,\infty )),\{\mu \})$
for all
![]() $\mu \ge \aleph _\alpha $
. Thus the spectra have no holes and
$\mu \ge \aleph _\alpha $
. Thus the spectra have no holes and
![]() $\ell (L(Q_\alpha ))=\aleph _\alpha $
. It should be noted that the class size logic
$\ell (L(Q_\alpha ))=\aleph _\alpha $
. It should be noted that the class size logic
![]() $L(Q_\alpha )_{\alpha \in \mathrm {On}}$
is a sublogic of
$L(Q_\alpha )_{\alpha \in \mathrm {On}}$
is a sublogic of
![]() $L_{\infty \infty }$
. Its spectra have a greater degree of regularity than those of
$L_{\infty \infty }$
. Its spectra have a greater degree of regularity than those of
![]() $L_{\infty \infty }$
, and thus in that respect it resembles more
$L_{\infty \infty }$
, and thus in that respect it resembles more
![]() $L_{\infty \omega }$
. In sum, these two logics, namely
$L_{\infty \omega }$
. In sum, these two logics, namely
![]() $L_{\infty \omega }$
and
$L_{\infty \omega }$
and
![]() $L(Q_\alpha )_{\alpha \in \mathrm {On}}$
, both manifest a greater degree of logicality than
$L(Q_\alpha )_{\alpha \in \mathrm {On}}$
, both manifest a greater degree of logicality than
![]() $L_{\infty \infty }$
, if regularity in spectrum patterns is used as a criterion.
$L_{\infty \infty }$
, if regularity in spectrum patterns is used as a criterion.
4 Is every model class definable in
 $L_{\infty \infty }$
irrespective of the cardinality?
$L_{\infty \infty }$
irrespective of the cardinality?
Why is it that we cannot replace condition (2) of Theorem 7 with the apparently better condition
This would solve the problems of cardinality and domain-relativity—the logical concept would have the same definition in terms of a formal language independently of the cardinality of the domain. However, there is a very simple reason why condition (2) of Theorem 7 cannot be improved to (1): Not every model class is definable in
![]() $L_{\infty \infty }$
.
$L_{\infty \infty }$
.
Recall the definition of
![]() $\mathcal {K}_{\text {lim}}$
above in §2. It is, strictly speaking, a generalized quantifier in the sense of Reference Mostowski[43] but a rather curious one. It is the existential quantifier in models of successor cardinality and the quantifier “for no x” in models of limit cardinality.
$\mathcal {K}_{\text {lim}}$
above in §2. It is, strictly speaking, a generalized quantifier in the sense of Reference Mostowski[43] but a rather curious one. It is the existential quantifier in models of successor cardinality and the quantifier “for no x” in models of limit cardinality.
Proposition 14. The model class
![]() $\mathcal {K}_{\text {lim}}$
is not definable in
$\mathcal {K}_{\text {lim}}$
is not definable in
![]() $L_{\infty \infty }$
.
$L_{\infty \infty }$
.
Proof Similar to the proof of Proposition 15.
A different kind of generalized quantifier is the class
This is potential isomorphism closed and not definable even in
![]() $L_{\infty \infty }$
Reference Malitz[40]. Note that this model class is clearly second order definable. The model class
$L_{\infty \infty }$
Reference Malitz[40]. Note that this model class is clearly second order definable. The model class
![]() $W_2$
has a particularly nice spectrum, its infinite part being simply the class of all infinite cardinals. This model class is also set-theoretically absolute (see below §5). In the light of the spectrum criterion, a model being an element of
$W_2$
has a particularly nice spectrum, its infinite part being simply the class of all infinite cardinals. This model class is also set-theoretically absolute (see below §5). In the light of the spectrum criterion, a model being an element of
![]() $W_2$
is a logical property of the model of a very high degree of logicality. Looking at a model, can we say that its being a well-order, let alone of a well-order of type
$W_2$
is a logical property of the model of a very high degree of logicality. Looking at a model, can we say that its being a well-order, let alone of a well-order of type
![]() $\alpha +\alpha $
for some
$\alpha +\alpha $
for some
![]() $\alpha $
, is a logical property? Undoubtedly some would say it is a mathematical rather than a logical property. But it is logical in the Tarski–Sher sense and it has a second order definition which is the same definition in each cardinality. However much it feels like a genuinely mathematical concept, it fulfils the Tarski–Sher criterion of logicality, escapes two of Feferman’s criticisms, and fulfils Sagi’s as well as Bonnay’s criteria. So we may conclude that it is logical of a very high degree.
$\alpha $
, is a logical property? Undoubtedly some would say it is a mathematical rather than a logical property. But it is logical in the Tarski–Sher sense and it has a second order definition which is the same definition in each cardinality. However much it feels like a genuinely mathematical concept, it fulfils the Tarski–Sher criterion of logicality, escapes two of Feferman’s criticisms, and fulfils Sagi’s as well as Bonnay’s criteria. So we may conclude that it is logical of a very high degree.
A third example of a model class undefinable in
![]() $L_{\infty \infty }$
is particularly interesting, namely the Härtig quantifier.
$L_{\infty \infty }$
is particularly interesting, namely the Härtig quantifier.
4.1 The Härtig quantifier
The Härtig quantifier is defined as follows:
 $$ \begin{align*}\begin{array}{lcl} Ixy\phi(x)\psi(y)&\iff&\text{ there are as many } x\ \text{satisfying } \phi(x)\\&&\text{ as there are } y \text{ satisfying } \psi(y). \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{lcl} Ixy\phi(x)\psi(y)&\iff&\text{ there are as many } x\ \text{satisfying } \phi(x)\\&&\text{ as there are } y \text{ satisfying } \psi(y). \end{array}\end{align*} $$
Proposition 15 [Reference Herre, Krynicki, Pinus and Väänänen25]
The class of models
![]() $(M,A,B)$
, where
$(M,A,B)$
, where
![]() $A,B\subseteq M$
and
$A,B\subseteq M$
and
![]() $|A|=|B|$
, is not definable in
$|A|=|B|$
, is not definable in
![]() $L_{\infty \infty }$
. Equivalently, the Härtig quantifier is not definable in
$L_{\infty \infty }$
. Equivalently, the Härtig quantifier is not definable in
![]() $L_{\infty \infty }$
.
$L_{\infty \infty }$
.
Proof Two sentences of the logic
![]() $L_{\omega \omega }(I)$
are useful here: the sentence
$L_{\omega \omega }(I)$
are useful here: the sentence
![]() $\phi _{\mathrm {lim}}$
which has the class of limit cardinals as its spectrum, and the sentence
$\phi _{\mathrm {lim}}$
which has the class of limit cardinals as its spectrum, and the sentence
![]() $\phi _{suc}$
which has the class of infinite successor cardinals as its spectrum. The sentence
$\phi _{suc}$
which has the class of infinite successor cardinals as its spectrum. The sentence
![]() $\phi _{\mathrm {lim}}$
says that the universe is totally ordered by a linear order in which every element determines an initial segment which has smaller cardinality than the initial segment determined by some bigger element. The sentence
$\phi _{\mathrm {lim}}$
says that the universe is totally ordered by a linear order in which every element determines an initial segment which has smaller cardinality than the initial segment determined by some bigger element. The sentence
![]() $\phi _{suc}$
says that the universe is totally ordered by a linear order in which some element determines an initial segment which has the same cardinality as the initial segment determined by any bigger element, but smaller cardinality than the entire universe. Suppose the Härtig quantifier was definable in
$\phi _{suc}$
says that the universe is totally ordered by a linear order in which some element determines an initial segment which has the same cardinality as the initial segment determined by any bigger element, but smaller cardinality than the entire universe. Suppose the Härtig quantifier was definable in
![]() $L_{\kappa ^+\kappa ^+}$
, where
$L_{\kappa ^+\kappa ^+}$
, where
![]() $\kappa $
is regular. Let
$\kappa $
is regular. Let
![]() $\lambda =2^\kappa $
. If
$\lambda =2^\kappa $
. If
![]() $\lambda $
is a limit cardinal, we can use
$\lambda $
is a limit cardinal, we can use
![]() $\phi _{\mathrm {lim}}$
to derive a contradiction as follows: Let
$\phi _{\mathrm {lim}}$
to derive a contradiction as follows: Let
![]() ${\mathcal M}$
be a model of
${\mathcal M}$
be a model of
![]() $\phi _{\mathrm {suc}}$
of cardinality
$\phi _{\mathrm {suc}}$
of cardinality
![]() $\lambda ^+$
. By Theorem 13 there is a model
$\lambda ^+$
. By Theorem 13 there is a model
![]() ${\mathcal N}$
of cardinality
${\mathcal N}$
of cardinality
![]() $\lambda $
such that
$\lambda $
such that
![]() ${\mathcal N}\models \phi _{\mathrm {suc}}$
, a contradiction. The case that
${\mathcal N}\models \phi _{\mathrm {suc}}$
, a contradiction. The case that
![]() $\lambda $
is a successor cardinal is similar, but using
$\lambda $
is a successor cardinal is similar, but using
![]() $\phi _{\mathrm {lim}}$
instead of
$\phi _{\mathrm {lim}}$
instead of
![]() $\phi _{\mathrm {suc}}$
.
$\phi _{\mathrm {suc}}$
.
While the logic
![]() $L(I)$
with the Härtig quantifier is not a sublogic of
$L(I)$
with the Härtig quantifier is not a sublogic of
![]() $L_{\infty \infty }$
it has some of the properties of the latter that we associate with being very far from first order logic (see §7). For example, it is highly non-absolute. It is also unbounded i.e., capable of defining well-ordering with additional predicates Reference Lindström[32].
$L_{\infty \infty }$
it has some of the properties of the latter that we associate with being very far from first order logic (see §7). For example, it is highly non-absolute. It is also unbounded i.e., capable of defining well-ordering with additional predicates Reference Lindström[32].
Note that the equicardinality concept, built around the existence of a bijection, lies at the very heart of the definition of logicality in the sense of Tarski! It is almost paradoxical then, that equicardinality itself, or more precisely the logic built on the equicardinality quantifier, represents a particularly weak degree of logicality.
4.2 Vopěnka’s principle
While it is not true that every model class is definable in
![]() $L_{\infty \infty }$
, there is a weaker result which depends on large cardinals. Tarski proved that a model class
$L_{\infty \infty }$
, there is a weaker result which depends on large cardinals. Tarski proved that a model class
![]() $\mathcal {K}$
is definable by a universal first order sentence if and only if
$\mathcal {K}$
is definable by a universal first order sentence if and only if
![]() $\mathcal {K}$
is closed under substructures and any model all of whose finite substructures are in
$\mathcal {K}$
is closed under substructures and any model all of whose finite substructures are in
![]() $\mathcal {K}$
, is itself in
$\mathcal {K}$
, is itself in
![]() $\mathcal {K}$
. The following result removes the assumption on finite substructures but lifts the result to an infinitary level. Recall that Vopěnka’s principle is the axiom schema stating that if
$\mathcal {K}$
. The following result removes the assumption on finite substructures but lifts the result to an infinitary level. Recall that Vopěnka’s principle is the axiom schema stating that if
![]() $\{A_\alpha : \alpha \in \mathrm {On}\}$
is a (definable) proper class of structures of the same vocabulary, there are
$\{A_\alpha : \alpha \in \mathrm {On}\}$
is a (definable) proper class of structures of the same vocabulary, there are
![]() $\alpha \ne \beta $
such that
$\alpha \ne \beta $
such that
![]() $A_\alpha $
can be embedded into
$A_\alpha $
can be embedded into
![]() $A_\beta $
. Despite its formulation, which suggests no connection to large cardinals, this principle is actually a large cardinal axiom schema. It implies the existence of extendible (and hence supercompact) cardinals Reference Magidor[36], and its consistency follows from the existence of an almost huge cardinal (see e.g., [Reference Kanamori28, p. 338]). Magidor has proved the following characterisation of Vopěnka’s principle:Footnote
32
$A_\beta $
. Despite its formulation, which suggests no connection to large cardinals, this principle is actually a large cardinal axiom schema. It implies the existence of extendible (and hence supercompact) cardinals Reference Magidor[36], and its consistency follows from the existence of an almost huge cardinal (see e.g., [Reference Kanamori28, p. 338]). Magidor has proved the following characterisation of Vopěnka’s principle:Footnote
32
Theorem 16 [Reference Magidor37]
The following are equivalent:
-
1. Every model class which is closed under substructures is
 $L_{\infty \infty }$
-definable by a universal sentence.
$L_{\infty \infty }$
-definable by a universal sentence. -
2. Vopěnka’s principle.
Proof (2) implies (1): Suppose
![]() $\mathcal {K}$
is a model class which is closed under substructures. By Vopěnka’s Principle there is a
$\mathcal {K}$
is a model class which is closed under substructures. By Vopěnka’s Principle there is a
![]() $\mathcal {K}$
-supercompact cardinal
$\mathcal {K}$
-supercompact cardinal
![]() $\kappa $
(see Reference Solovay, Reinhardt and Kanamori[51]). For any
$\kappa $
(see Reference Solovay, Reinhardt and Kanamori[51]). For any
![]() ${\mathcal M}$
of cardinality
${\mathcal M}$
of cardinality
![]() $\le \kappa $
, let
$\le \kappa $
, let
![]() $\theta _{\mathcal M}\in L_{\kappa ^+\kappa ^+}$
be an existential sentence such that
$\theta _{\mathcal M}\in L_{\kappa ^+\kappa ^+}$
be an existential sentence such that
![]() $\theta _{\mathcal M}$
is true exactly in models which have an isomorphic copy of
$\theta _{\mathcal M}$
is true exactly in models which have an isomorphic copy of
![]() ${\mathcal M}$
as a substructure. We show that for all
${\mathcal M}$
as a substructure. We show that for all
![]() ${\mathcal N}$
,
${\mathcal N}$
,
![]() ${\mathcal N}\notin \mathcal{K}$
if and only if
${\mathcal N}\notin \mathcal{K}$
if and only if
![]() ${\mathcal N}\models \psi $
, where
${\mathcal N}\models \psi $
, where
![]() $\psi $
is
$\psi $
is
![]() $\bigvee \{\theta _{\mathcal M}: M\subseteq \kappa , {\mathcal M}\notin \mathcal{K}\}$
. Suppose first
$\bigvee \{\theta _{\mathcal M}: M\subseteq \kappa , {\mathcal M}\notin \mathcal{K}\}$
. Suppose first
![]() ${\mathcal N}\notin \mathcal{K}$
. By the
${\mathcal N}\notin \mathcal{K}$
. By the
![]() $\mathcal {K}$
-supercompactness of
$\mathcal {K}$
-supercompactness of
![]() $\kappa $
there is an
$\kappa $
there is an
![]() $L_{\omega \omega }(Q_{\mathcal{K}})$
-elementary substructure
$L_{\omega \omega }(Q_{\mathcal{K}})$
-elementary substructure
![]() ${\mathcal M}$
of
${\mathcal M}$
of
![]() ${\mathcal N}$
of cardinality
${\mathcal N}$
of cardinality
![]() $\le \kappa $
. Now
$\le \kappa $
. Now
![]() ${\mathcal N}\notin \mathcal{K}$
implies
${\mathcal N}\notin \mathcal{K}$
implies
![]() ${\mathcal M}\notin \mathcal{K}$
. Trivially,
${\mathcal M}\notin \mathcal{K}$
. Trivially,
![]() ${\mathcal N}\models \theta _{\mathcal M}$
. Hence
${\mathcal N}\models \theta _{\mathcal M}$
. Hence
![]() ${\mathcal N}\models \psi $
. Conversely, suppose
${\mathcal N}\models \psi $
. Conversely, suppose
![]() ${\mathcal N}\models \theta _{\mathcal M}$
for some
${\mathcal N}\models \theta _{\mathcal M}$
for some
![]() ${\mathcal M}\notin \mathcal{K}$
such that
${\mathcal M}\notin \mathcal{K}$
such that
![]() $M \subseteq \kappa $
. W.l.o.g.
$M \subseteq \kappa $
. W.l.o.g.
![]() ${\mathcal M}\subseteq {\mathcal N}$
. By closure under substructures,
${\mathcal M}\subseteq {\mathcal N}$
. By closure under substructures,
![]() ${\mathcal N}\notin \mathcal{K}$
.
${\mathcal N}\notin \mathcal{K}$
.
(1) implies (2): Suppose Vopěnka’s principles fails as witnessed by the class
![]() $\mathcal {C}=\{{\mathcal M}_\alpha : \alpha \in \mathrm {On}\}$
. Let
$\mathcal {C}=\{{\mathcal M}_\alpha : \alpha \in \mathrm {On}\}$
. Let
![]() $\mathcal {K}$
be the class of structures
$\mathcal {K}$
be the class of structures
![]() ${\mathcal N}$
of the same vocabulary as each
${\mathcal N}$
of the same vocabulary as each
![]() ${\mathcal M}_\alpha $
such that
${\mathcal M}_\alpha $
such that
![]() ${\mathcal N}$
is isomorphic to an substructure of
${\mathcal N}$
is isomorphic to an substructure of
![]() ${\mathcal M}_\alpha $
for arbitrarily large
${\mathcal M}_\alpha $
for arbitrarily large
![]() $\alpha $
. By (1) we may choose
$\alpha $
. By (1) we may choose
![]() $\kappa $
such that
$\kappa $
such that
![]() $\mathcal {K}$
is definable in
$\mathcal {K}$
is definable in
![]() $L_{\kappa ^+\kappa ^+}$
. By our choice of
$L_{\kappa ^+\kappa ^+}$
. By our choice of
![]() $\mathcal {C}$
, every
$\mathcal {C}$
, every
![]() ${\mathcal M}_\alpha $
satisfies
${\mathcal M}_\alpha $
satisfies
![]() ${\mathcal M}_\alpha \notin \mathcal {K}$
. By Theorem 13 there is for each
${\mathcal M}_\alpha \notin \mathcal {K}$
. By Theorem 13 there is for each
![]() $\alpha $
an
$\alpha $
an
![]() $L_{\kappa ^+\kappa ^+}$
-elementary substructure
$L_{\kappa ^+\kappa ^+}$
-elementary substructure
![]() ${\mathcal N}_\alpha $
of
${\mathcal N}_\alpha $
of
![]() ${\mathcal M}_\alpha $
of cardinality
${\mathcal M}_\alpha $
of cardinality
![]() $\le 2^\kappa $
such that
$\le 2^\kappa $
such that
![]() ${\mathcal N}_\alpha \notin \mathcal {K}$
. There are only a set of non-isomorphic structures of cardinality
${\mathcal N}_\alpha \notin \mathcal {K}$
. There are only a set of non-isomorphic structures of cardinality
![]() $\le 2^\kappa $
. Hence
$\le 2^\kappa $
. Hence
![]() ${\mathcal N}_\alpha \cong {\mathcal N}_\beta $
for a proper class of
${\mathcal N}_\alpha \cong {\mathcal N}_\beta $
for a proper class of
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
. Let
$\beta $
. Let
![]() $\alpha $
be one of those. Then
$\alpha $
be one of those. Then
![]() ${\mathcal N}_\alpha \in \mathcal {K}$
, a contradiction.
${\mathcal N}_\alpha \in \mathcal {K}$
, a contradiction.
The moral of the story here is that we can obtain the McGee style characterization of logicality independently of the cardinality of the model if we restrict to model classes closed under substructures, but we have to make a strong set theoretical assumption, namely Vopěnka’s principle. This is not to suggest that we propose closure under substructures as a criterion for logicality.
5 Defining an arbitrary model class in an absolute logic, but still cardinal dependently
We shall now offer a refinement of McGee’s result (Theorem 7), by replacing
![]() $L_{\infty \infty }$
by a substantially weaker infinitary logicFootnote
33
. Let us first note that we cannot replace
$L_{\infty \infty }$
by a substantially weaker infinitary logicFootnote
33
. Let us first note that we cannot replace
![]() $L_{\infty \infty }$
by
$L_{\infty \infty }$
by
![]() $L_{\infty \omega }$
because the quantifier
$L_{\infty \omega }$
because the quantifier
![]() $Q_1$
is not CD-definable in the latter.Footnote
34
For another example, the well-ordering quantifier
$Q_1$
is not CD-definable in the latter.Footnote
34
For another example, the well-ordering quantifier
is definable in
![]() $L_{\omega _1\omega _1}$
(see (1)) but not in
$L_{\omega _1\omega _1}$
(see (1)) but not in
![]() $L_{\infty \omega }$
Reference Lopez-Escobar[35].
$L_{\infty \omega }$
Reference Lopez-Escobar[35].
An important quality of
![]() $L_{\infty \omega }$
is its absoluteness. Let us recall:
$L_{\infty \omega }$
is its absoluteness. Let us recall:
Definition 17 [Reference Barwise4]
A logic
![]() $(\Sigma ,T)$
is called an absolute logic if the predicate
$(\Sigma ,T)$
is called an absolute logic if the predicate
![]() $\Sigma (\phi )$
is
$\Sigma (\phi )$
is
![]() $\Sigma _1$
in
$\Sigma _1$
in
![]() $\phi $
, and the predicate
$\phi $
, and the predicate
![]() $T(\phi ,{\mathcal M})$
is
$T(\phi ,{\mathcal M})$
is
![]() $\Delta _1$
in
$\Delta _1$
in
![]() $\phi $
and
$\phi $
and
![]() ${\mathcal M}$
. A logic is absolute with respect to a set theory S if the predicates
${\mathcal M}$
. A logic is absolute with respect to a set theory S if the predicates
![]() $\Sigma $
and T are
$\Sigma $
and T are
![]() $\Sigma _1^S$
and
$\Sigma _1^S$
and
 $\Delta _1^S$
, respectively.
$\Delta _1^S$
, respectively.
For example,
![]() $L_{\infty \omega }$
and
$L_{\infty \omega }$
and
![]() $L(W)$
are absolute logics but
$L(W)$
are absolute logics but
![]() $L_{\infty \infty }$
is not.
$L_{\infty \infty }$
is not.
We defined the
![]() $\Delta $
-operation in Definition 8. As argued for in Reference Makowsky, Shelah and Stavi[39],
$\Delta $
-operation in Definition 8. As argued for in Reference Makowsky, Shelah and Stavi[39],
![]() $\Delta (L^*)$
can be considered a logic in itself. There is a many-sorted version and a single-sorted version of the
$\Delta (L^*)$
can be considered a logic in itself. There is a many-sorted version and a single-sorted version of the
![]() $\Delta $
-extension. In the many-sorted version the model class
$\Delta $
-extension. In the many-sorted version the model class
![]() $\mathcal {K}$
may have a many-sorted vocabulary. If
$\mathcal {K}$
may have a many-sorted vocabulary. If
![]() $L^*$
is the logic
$L^*$
is the logic
![]() $L_{\infty \omega }$
, or
$L_{\infty \omega }$
, or
![]() $L_{\kappa ^+\omega }$
, for regular
$L_{\kappa ^+\omega }$
, for regular
![]() $\kappa $
, there is no difference between the two versions i.e., they coincide Reference Oikkonen, Jensen, Mayoh and Møller[44]. Therefore we continue with the single-sorted version.
$\kappa $
, there is no difference between the two versions i.e., they coincide Reference Oikkonen, Jensen, Mayoh and Møller[44]. Therefore we continue with the single-sorted version.
Some of the nice properties of the
![]() $\Delta $
-operation are:
$\Delta $
-operation are:
-
• Exactly the same classes of cardinals are spectra of
 $\Delta (L^*)$
as are of
$\Delta (L^*)$
as are of
 $L^*$
.
$L^*$
. -
•
 $\Delta (L^*)$
satisfies
$\Delta (L^*)$
satisfies
 $LS(C,D)$
iff
$LS(C,D)$
iff
 $L^*$
does.
$L^*$
does. -
•
 $\Delta (L^*)$
satisfies the Compactness Theorem iff
$\Delta (L^*)$
satisfies the Compactness Theorem iff
 $L^*$
does.
$L^*$
does. -
•
 $\Delta (L^*)$
satisfies the (abstract) Completeness TheoremFootnote
35
iff
$\Delta (L^*)$
satisfies the (abstract) Completeness TheoremFootnote
35
iff
 $L^*$
does.
$L^*$
does. -
• If
 $L^*$
satisfies the Craig Interpolation Theorem, then
$L^*$
satisfies the Craig Interpolation Theorem, then
 $\Delta (L^*)$
and
$\Delta (L^*)$
and
 $L^*$
are equivalent logics.
$L^*$
are equivalent logics. -
•
 $\ell (\Delta (L^*))=\ell (L^*)$
.
$\ell (\Delta (L^*))=\ell (L^*)$
. -
•
 $h(\Delta (L^*))=h(L^*)$
.Footnote
36
$h(\Delta (L^*))=h(L^*)$
.Footnote
36
If
![]() $L^*$
is an absolute logic in the sense of Reference Barwise[4], then
$L^*$
is an absolute logic in the sense of Reference Barwise[4], then
![]() $\Delta (L^*)$
is still absolute in the weaker sense that every definable model class is
$\Delta (L^*)$
is still absolute in the weaker sense that every definable model class is
![]() $\Delta _1$
-definable in set theory (with the defining sentence as a parameter). This is a direct consequence of the definition of
$\Delta _1$
-definable in set theory (with the defining sentence as a parameter). This is a direct consequence of the definition of
![]() $\Delta (L^*)$
. However,
$\Delta (L^*)$
. However,
![]() $\Delta (L^*)$
has a complication which prevents us from concluding that the
$\Delta (L^*)$
has a complication which prevents us from concluding that the
![]() $\Delta $
-operation preserves absoluteness. Namely, there may be an absolute logic
$\Delta $
-operation preserves absoluteness. Namely, there may be an absolute logic
![]() $L^*$
and model classes
$L^*$
and model classes
![]() $\mathcal{K}_0$
and
$\mathcal{K}_0$
and
![]() $\mathcal{K}_1$
such that both
$\mathcal{K}_1$
such that both
![]() $\mathcal{K}_0$
and
$\mathcal{K}_0$
and
![]() $\mathcal{K}_1$
are in
$\mathcal{K}_1$
are in
![]() $\Sigma (L^*)$
,
$\Sigma (L^*)$
,
![]() $\mathcal{K}_0\cap \mathcal{K}_1= \emptyset $
but the proposition that every model (of the right type) is in
$\mathcal{K}_0\cap \mathcal{K}_1= \emptyset $
but the proposition that every model (of the right type) is in
![]() $\mathcal{K}_0$
or
$\mathcal{K}_0$
or
![]() $\mathcal{K}_1$
is not absolute.Footnote
37
Thus we may not have a
$\mathcal{K}_1$
is not absolute.Footnote
37
Thus we may not have a
![]() $\Sigma _1$
-definition for the set of sentences of
$\Sigma _1$
-definition for the set of sentences of
![]() $\Delta (L^*)$
even if we have for
$\Delta (L^*)$
even if we have for
![]() $L^*$
. Despite this shortcoming of the
$L^*$
. Despite this shortcoming of the
![]() $\Delta $
-operation, we do have a
$\Delta $
-operation, we do have a
![]() $\Sigma _1$
-definition for the set of sentences of
$\Sigma _1$
-definition for the set of sentences of
![]() $\Sigma (L^*)$
when
$\Sigma (L^*)$
when
![]() $L^*$
is absolute because with
$L^*$
is absolute because with
![]() $\Sigma (L^*)$
the above problem (
$\Sigma (L^*)$
the above problem (
![]() $\mathcal{K}_0$
and
$\mathcal{K}_0$
and
![]() $\mathcal{K}_1$
) does not arise.
$\mathcal{K}_1$
) does not arise.
Theorem 18 [Reference Kennedy31]
If
![]() $\mathcal {K}$
is a class of models of the same vocabulary, then the following conditions are equivalent:
$\mathcal {K}$
is a class of models of the same vocabulary, then the following conditions are equivalent:
-
1.
 $\mathcal {K}$
is closed under isomorphisms.
$\mathcal {K}$
is closed under isomorphisms. -
2.
 $\mathcal {K}$
is CD-definable in
$\mathcal {K}$
is CD-definable in
 $\Delta (L_{\infty \omega })$
.
$\Delta (L_{\infty \omega })$
.
Proof The proof is similar to the proof of Theorem 7 in Reference McGee[41]. Recall the formulas
![]() $\eta ^{\prime }_\alpha $
and
$\eta ^{\prime }_\alpha $
and
![]() $\eta ^{\prime }_\alpha $
defined in (1) and (3), with the properties (2) and (4). Suppose
$\eta ^{\prime }_\alpha $
defined in (1) and (3), with the properties (2) and (4). Suppose
![]() $\mathfrak {A}$
is a model of the vocabulary L and
$\mathfrak {A}$
is a model of the vocabulary L and
![]() $|A|=\lambda $
. Let
$|A|=\lambda $
. Let
![]() $f_A:\lambda \to A$
be a bijection and
$f_A:\lambda \to A$
be a bijection and
 $a<_Ab\iff f_A^{-1}(a)<f_A^{-1}(b)$
. For
$a<_Ab\iff f_A^{-1}(a)<f_A^{-1}(b)$
. For
![]() $\alpha ,\beta <\lambda $
let
$\alpha ,\beta <\lambda $
let
 $$ \begin{align*}\rho_{\alpha,\beta}(x,y)=\left\{\begin{array}{ll} R(x,y)&\text{ if } \mathfrak{A}\models R(f_A(\alpha),f_B(\beta)),\\ \neg R(x,y)&\text{ if }\mathfrak{A}\not\models R(f_A(\alpha),f_B(\beta)). \end{array}\right.\end{align*} $$
$$ \begin{align*}\rho_{\alpha,\beta}(x,y)=\left\{\begin{array}{ll} R(x,y)&\text{ if } \mathfrak{A}\models R(f_A(\alpha),f_B(\beta)),\\ \neg R(x,y)&\text{ if }\mathfrak{A}\not\models R(f_A(\alpha),f_B(\beta)). \end{array}\right.\end{align*} $$
Let
 $$ \begin{align*}\Phi_{\mathfrak{A}}\leftrightarrow\forall x\forall y\bigwedge_{\alpha,\beta<\lambda}((\eta_\alpha(x)\wedge\eta_\beta(y))\to\rho_{\alpha,\beta}(x,y)).\end{align*} $$
$$ \begin{align*}\Phi_{\mathfrak{A}}\leftrightarrow\forall x\forall y\bigwedge_{\alpha,\beta<\lambda}((\eta_\alpha(x)\wedge\eta_\beta(y))\to\rho_{\alpha,\beta}(x,y)).\end{align*} $$
Now
 $(\mathfrak {A},<_A)\models \eta ^{\prime }_\lambda $
and
$(\mathfrak {A},<_A)\models \eta ^{\prime }_\lambda $
and
![]() $(\mathfrak {A},<_A)\models \eta _\alpha (a)\iff a=f_A(\alpha )$
. Hence
$(\mathfrak {A},<_A)\models \eta _\alpha (a)\iff a=f_A(\alpha )$
. Hence
 $(\mathfrak {A},<) \models \eta ^{\prime }_\lambda \wedge \Phi _{\mathfrak {A}}.$
On the other hand,
$(\mathfrak {A},<) \models \eta ^{\prime }_\lambda \wedge \Phi _{\mathfrak {A}}.$
On the other hand,
 $(\mathfrak {A}^{\prime },<^{\prime })\models \eta ^{\prime }_\lambda \wedge \Phi _{\mathfrak {A}}$
implies
$(\mathfrak {A}^{\prime },<^{\prime })\models \eta ^{\prime }_\lambda \wedge \Phi _{\mathfrak {A}}$
implies
![]() $\mathfrak {A}'\cong \mathfrak {A},$
for if
$\mathfrak {A}'\cong \mathfrak {A},$
for if
 $(\mathfrak {A}^{\prime },<^{\prime })\models \eta ^{\prime }_\lambda \wedge \Phi _{\mathfrak {A}}$
and
$(\mathfrak {A}^{\prime },<^{\prime })\models \eta ^{\prime }_\lambda \wedge \Phi _{\mathfrak {A}}$
and
![]() $g:(A^{\prime },<')\cong (A,<_A)$
, then
$g:(A^{\prime },<')\cong (A,<_A)$
, then
![]() $g:\mathfrak {A}'\cong \mathfrak {A}$
. Let
$g:\mathfrak {A}'\cong \mathfrak {A}$
. Let
 $$ \begin{align*}\Theta_{\mathcal{K}}\leftrightarrow\bigvee\{\Phi_{\mathfrak{A}}\ : \ \mathfrak{A}\in\mathcal{K}, A=\lambda\}.\end{align*} $$
$$ \begin{align*}\Theta_{\mathcal{K}}\leftrightarrow\bigvee\{\Phi_{\mathfrak{A}}\ : \ \mathfrak{A}\in\mathcal{K}, A=\lambda\}.\end{align*} $$
Now by the above,
 $$ \begin{align*}\begin{array}{lcl} \mathfrak{A}\in\mathcal{K}_\lambda&\iff&(\mathfrak{A},<)\models\eta^{\prime}_\lambda\wedge\Theta_{\mathcal{K}}\text{ for some } < \\ &\iff&(\mathfrak{A},<)\models\eta^{\prime}_\lambda\to\Theta_{\mathcal{K}}\text{ for all } <. \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{lcl} \mathfrak{A}\in\mathcal{K}_\lambda&\iff&(\mathfrak{A},<)\models\eta^{\prime}_\lambda\wedge\Theta_{\mathcal{K}}\text{ for some } < \\ &\iff&(\mathfrak{A},<)\models\eta^{\prime}_\lambda\to\Theta_{\mathcal{K}}\text{ for all } <. \end{array}\end{align*} $$
Since
 $\eta ^{\prime }_\lambda ,\Theta _{\mathcal {K}}\in L_{(2^\lambda )^+\omega }$
, we are done.
$\eta ^{\prime }_\lambda ,\Theta _{\mathcal {K}}\in L_{(2^\lambda )^+\omega }$
, we are done.
Why is this an improvement?
![]() $\Delta (L_{\infty \omega })$
is a sublogic of
$\Delta (L_{\infty \omega })$
is a sublogic of
![]() $L_{\infty \infty }$
, a consequence of the result of Malitz Reference Malitz[40] to the effect that for regular
$L_{\infty \infty }$
, a consequence of the result of Malitz Reference Malitz[40] to the effect that for regular
![]() $\kappa $
a valid implication in
$\kappa $
a valid implication in
![]() $L_{\kappa \omega }$
can be interpolated in
$L_{\kappa \omega }$
can be interpolated in
![]() $L_{2^{(<\kappa )^+\kappa }}$
. It is a proper sublogic because well-ordering is definable in the latter but not in the former. Secondly, the logic
$L_{2^{(<\kappa )^+\kappa }}$
. It is a proper sublogic because well-ordering is definable in the latter but not in the former. Secondly, the logic
![]() $L_{\infty \omega }$
is an absolute logic Reference Barwise[4] and
$L_{\infty \omega }$
is an absolute logic Reference Barwise[4] and
![]() $\Delta (L_{\infty \omega })$
inherits much of the absoluteness of
$\Delta (L_{\infty \omega })$
inherits much of the absoluteness of
![]() $L_{\infty \omega }$
(see above) while
$L_{\infty \omega }$
(see above) while
![]() $L_{\infty \infty }$
is badly non-absolute.
$L_{\infty \infty }$
is badly non-absolute.
The improvement that Theorem 18 represents over Theorem 7 is also based on the fact that
![]() $L_{\infty \omega }$
, and thereby also
$L_{\infty \omega }$
, and thereby also
![]() $\Delta (L_{\infty \omega })$
, is a much “tamer” logic than
$\Delta (L_{\infty \omega })$
, is a much “tamer” logic than
![]() $L_{\infty \infty }$
. In particular:
$L_{\infty \infty }$
. In particular:
-
•
 $\Delta (L_{\infty \omega })$
, even
$\Delta (L_{\infty \omega })$
, even
 $\Sigma (L_{\infty \omega })$
, has a strong Löwenheim–Skolem theorem. This is in contrast to
$\Sigma (L_{\infty \omega })$
, has a strong Löwenheim–Skolem theorem. This is in contrast to
 $L_{\infty \infty }$
, which does not have a Löwenheim–Skolem theorem in the same strong form (see Theorem 13).
$L_{\infty \infty }$
, which does not have a Löwenheim–Skolem theorem in the same strong form (see Theorem 13). -
• The class of well-orderings is not definable in
 $\Delta (L_{\infty \omega })$
, while it is definable in
$\Delta (L_{\infty \omega })$
, while it is definable in
 $L_{\omega _1\omega _1}$
(see (1)). This is a kind of threshold difference. In general, logics in which the concept of well-order is not definable are much better behaved (in many different respects) than those in which it is. If well-order is definable, the logic can talk about well-founded models of set theory, and thereby about transitive models of set theory. In this way the logic can break through the object theory/metatheory barrier and have access to the background set theory. For a concrete example, consider a sentence
$L_{\omega _1\omega _1}$
(see (1)). This is a kind of threshold difference. In general, logics in which the concept of well-order is not definable are much better behaved (in many different respects) than those in which it is. If well-order is definable, the logic can talk about well-founded models of set theory, and thereby about transitive models of set theory. In this way the logic can break through the object theory/metatheory barrier and have access to the background set theory. For a concrete example, consider a sentence
 $\phi $
which is the conjunction of a sufficiently large finite part
$\phi $
which is the conjunction of a sufficiently large finite part
 $T_0$
of the ZFC axioms, the first order set-theoretical statement
$T_0$
of the ZFC axioms, the first order set-theoretical statement
 $\phi _0$
that there are no inaccessible cardinals, and the
$\phi _0$
that there are no inaccessible cardinals, and the
 $L_{\omega _1\omega _1}$
-sentence (8)Suppose
$L_{\omega _1\omega _1}$
-sentence (8)Suppose $$ \begin{align} \displaystyle{\forall x_0\forall x_1\ldots\bigvee_{n<\omega}}\neg x_{n+1}\in x_n. \end{align} $$
$$ \begin{align} \displaystyle{\forall x_0\forall x_1\ldots\bigvee_{n<\omega}}\neg x_{n+1}\in x_n. \end{align} $$
 $\kappa $
is the smallest inaccessible cardinal. Then
$\kappa $
is the smallest inaccessible cardinal. Then
 $\phi $
has a model of cardinality
$\phi $
has a model of cardinality
 $\kappa $
, namely
$\kappa $
, namely
 $V_\kappa $
, but none of bigger cardinality. For suppose M is a model of
$V_\kappa $
, but none of bigger cardinality. For suppose M is a model of
 $\phi $
of cardinality
$\phi $
of cardinality
 $>\kappa $
. By Mostowski’s Collapsing Lemma Reference Mostowski[42] we may assume M is a transitive model of
$>\kappa $
. By Mostowski’s Collapsing Lemma Reference Mostowski[42] we may assume M is a transitive model of
 $T_0$
. Since the cardinality of M is bigger than
$T_0$
. Since the cardinality of M is bigger than
 $\kappa $
, the ordinal
$\kappa $
, the ordinal
 $\kappa $
is in M and is therefore inaccessible in M by the downward persistency of inaccessibility. But this contradicts the fact that M is a model of
$\kappa $
is in M and is therefore inaccessible in M by the downward persistency of inaccessibility. But this contradicts the fact that M is a model of
 $\phi _0$
. This argument, due to Silver Reference Silver[50], demonstrates the power of (1) to penetrate the object theory/metatheory barrier, which sentences of
$\phi _0$
. This argument, due to Silver Reference Silver[50], demonstrates the power of (1) to penetrate the object theory/metatheory barrier, which sentences of
 $\Delta (L_{\infty \omega })$
are unable to do Reference Lopez-Escobar[35].
$\Delta (L_{\infty \omega })$
are unable to do Reference Lopez-Escobar[35].
-
• The Hanf number of
 $\Delta (L_{\kappa ^+\omega })$
is only moderately large, namely
$\Delta (L_{\kappa ^+\omega })$
is only moderately large, namely
 $<\beth _{(2^\kappa )^+}$
, while the Hanf number of
$<\beth _{(2^\kappa )^+}$
, while the Hanf number of
 $L_{\omega _1\omega _1}$
is bigger than the first weakly inaccessible cardinalFootnote
38
(and consistently bigger than the first measurable cardinal). The smallness of the Hanf number is another indication of regularity of patterns in spectra (see (5)).
$L_{\omega _1\omega _1}$
is bigger than the first weakly inaccessible cardinalFootnote
38
(and consistently bigger than the first measurable cardinal). The smallness of the Hanf number is another indication of regularity of patterns in spectra (see (5)).
A weakness of
![]() $\Delta (L_{\infty \omega })$
as compared to
$\Delta (L_{\infty \omega })$
as compared to
![]() $L_{\infty \infty }$
is that the former does not have as explicit a syntax as the latter, although we can overcome this by replacing
$L_{\infty \infty }$
is that the former does not have as explicit a syntax as the latter, although we can overcome this by replacing
![]() $\Delta (L_{\infty \omega })$
by
$\Delta (L_{\infty \omega })$
by
![]() $\Sigma (L_{\infty \omega })$
. A strength is that its spectra are as regular as those of
$\Sigma (L_{\infty \omega })$
. A strength is that its spectra are as regular as those of
![]() $L_{\infty \omega }$
, it is equally completely axiomatizable as
$L_{\infty \omega }$
, it is equally completely axiomatizable as
![]() $L_{\infty \omega }$
, and it is absolute in the sense that its definable model classes are absolute in set theory. Thus it avoids Feferman’s second and third criticisms.
$L_{\infty \omega }$
, and it is absolute in the sense that its definable model classes are absolute in set theory. Thus it avoids Feferman’s second and third criticisms.
6 Sort logic
We can ask, is there a logic in which every model class whatsoever is definable, irrespective of the cardinality of the domain? That is, not just cardinal dependently? We know already
![]() $L_{\infty \infty }$
is not that kind of a logic (§4). McGee points out that we could take a class size disjunction of
$L_{\infty \infty }$
is not that kind of a logic (§4). McGee points out that we could take a class size disjunction of
![]() $L_{\infty \infty }$
sentences and obtain a single ‘sentence’ which works in all cardinalities. As he points out, if we accept class size formulas we should also accept class size logical operations and then we are back in the starting point: to account for class size logical operations we need classes of classes and we start climbing up the type hierarchy beyond first order set theory. If we stick to set size logical operations we can operate within first order set theory.
$L_{\infty \infty }$
sentences and obtain a single ‘sentence’ which works in all cardinalities. As he points out, if we accept class size formulas we should also accept class size logical operations and then we are back in the starting point: to account for class size logical operations we need classes of classes and we start climbing up the type hierarchy beyond first order set theory. If we stick to set size logical operations we can operate within first order set theory.
We could, of course, take every model class as a generalized quantifierFootnote 39 but there is a more canonical logic for this task.
In Reference Väänänen, Chong, Feng, Slaman and Woodin[57] a logic
![]() $L^s$
called sort logic was introduced. It is a kind of many-sorted version of second order logic
$L^s$
called sort logic was introduced. It is a kind of many-sorted version of second order logic
![]() $L^2$
, which allows quantification not only over subsets and relations on the domain of the model but also over subsets and relations on new domains outside the current one. Such quantification happens, for example, when we ask of a given group, whether it is the multiplicative group of a field? We have to “guess” the addition of the field but also the neutral element
$L^2$
, which allows quantification not only over subsets and relations on the domain of the model but also over subsets and relations on new domains outside the current one. Such quantification happens, for example, when we ask of a given group, whether it is the multiplicative group of a field? We have to “guess” the addition of the field but also the neutral element
![]() $0$
and those are both outside the multiplicative group.
$0$
and those are both outside the multiplicative group.
More exactly, sort logic arises from
![]() $L^2$
by repeated applications of operation
$L^2$
by repeated applications of operation
![]() $L^*\mapsto \Sigma (L^*)$
(see Definition 8) and negation. Let us define
$L^*\mapsto \Sigma (L^*)$
(see Definition 8) and negation. Let us define
![]() $\Delta _0=L^2$
. If
$\Delta _0=L^2$
. If
![]() $\Delta _n$
has been defined, let
$\Delta _n$
has been defined, let
![]() $\Delta _{n+1}$
consist of model classes
$\Delta _{n+1}$
consist of model classes
![]() $\mathcal {K}$
such that both
$\mathcal {K}$
such that both
![]() $\mathcal {K}$
and the complement of
$\mathcal {K}$
and the complement of
![]() $\mathcal {K}$
are
$\mathcal {K}$
are
 $\Sigma (\Delta _n(L^2))$
-definable. We get an increasing hierarchy of logics
$\Sigma (\Delta _n(L^2))$
-definable. We get an increasing hierarchy of logics
the union of which is sort logic. A fine point is that every level
![]() $\Delta _n$
of sort logic is definable in set theory but there is no single formula that defines the entire sort logic.
$\Delta _n$
of sort logic is definable in set theory but there is no single formula that defines the entire sort logic.
Theorem 19 [Reference Väänänen, Chong, Feng, Slaman and Woodin57]
If
![]() $\mathcal {K}$
is a class of models of the same finite vocabulary, definable in set theory without parameters,Footnote
40
then the following conditions are equivalent:
$\mathcal {K}$
is a class of models of the same finite vocabulary, definable in set theory without parameters,Footnote
40
then the following conditions are equivalent:
-
1.
 $\mathcal {K}$
is closed under isomorphisms.
$\mathcal {K}$
is closed under isomorphisms. -
2.
 $\mathcal {K}$
is definable in sort logic.
$\mathcal {K}$
is definable in sort logic.
The above characterization of isomorphism closure is not as elegant as McGee’s theorem 7 simply because the definition of sort logic is more complicated than that of
![]() $L_{\infty \infty }$
. However, this theorem has the remarkable advantage over Theorem 7 that the definition of the model class in sort logic holds for models of all cardinalities. As McGee points out, if he wanted to obtain the same level of generality with his method, he would have to take a disjunction of a proper class of
$L_{\infty \infty }$
. However, this theorem has the remarkable advantage over Theorem 7 that the definition of the model class in sort logic holds for models of all cardinalities. As McGee points out, if he wanted to obtain the same level of generality with his method, he would have to take a disjunction of a proper class of
![]() $L_{\infty \infty }$
-formulas. Sort logic may be complicated but at least its formulas are sets and not proper classes. In McGee’s case we may need a formula which is not even a set. In the case of sort logic each formula is a set, but the whole logic is not definable, only each level
$L_{\infty \infty }$
-formulas. Sort logic may be complicated but at least its formulas are sets and not proper classes. In McGee’s case we may need a formula which is not even a set. In the case of sort logic each formula is a set, but the whole logic is not definable, only each level
![]() $\Delta _n$
separately is.
$\Delta _n$
separately is.
7 Is having a Completeness theorem a marker of logicality?
We saw that first order logic and
![]() $\mathcal {L}(Q_0)$
are maximally logical under Sagi’s criterion, grading the logicality of these logics by their Löwenheim numbers. We also saw that the degree of logicality of the logics
$\mathcal {L}(Q_0)$
are maximally logical under Sagi’s criterion, grading the logicality of these logics by their Löwenheim numbers. We also saw that the degree of logicality of the logics
![]() $\mathcal {L}(Q_{\alpha })$
decreases as
$\mathcal {L}(Q_{\alpha })$
decreases as
![]() $\alpha $
increases: if
$\alpha $
increases: if
![]() $\alpha \leq \beta $
, then
$\alpha \leq \beta $
, then
![]() $Q_{\beta }$
is less logical than
$Q_{\beta }$
is less logical than
![]() $Q_{\alpha }$
.
$Q_{\alpha }$
.
As for other kinds of quantifiers, the quantifiers “more” or Rescher quantifier
 $$ \begin{align*}\begin{array}{lcl} Jxy\phi(x)\psi(y)&\iff&\text{there are at least as many } x \text{ satisfying } \phi(x)\\ &&\text{as there are } y \text{ satisfying }\psi(y) \end{array}\end{align*} $$
$$ \begin{align*}\begin{array}{lcl} Jxy\phi(x)\psi(y)&\iff&\text{there are at least as many } x \text{ satisfying } \phi(x)\\ &&\text{as there are } y \text{ satisfying }\psi(y) \end{array}\end{align*} $$
and the equicardinality or Härtig quantifier (see §4.1) both have the same (very high) Löwenheim number, and are thus less logical than
![]() $Q_{\alpha }$
at least for
$Q_{\alpha }$
at least for
![]() $\alpha $
below the first
$\alpha $
below the first
![]() $\alpha $
such that
$\alpha $
such that
![]() $\alpha =\aleph _\alpha $
.Footnote
41
We suggested earlier that the Härtig quantifier is a singular case, in seeming to express the core concept of isomorphism invariance, which is defined in terms of the concept of equicardinality. Under our criteria, the Härtig quantifier is classified as (only) weakly logical even so, not only due to its high Löwenheim number but also because it lacks very seriously a complete axiomatization Reference Väänänen[54].
$\alpha =\aleph _\alpha $
.Footnote
41
We suggested earlier that the Härtig quantifier is a singular case, in seeming to express the core concept of isomorphism invariance, which is defined in terms of the concept of equicardinality. Under our criteria, the Härtig quantifier is classified as (only) weakly logical even so, not only due to its high Löwenheim number but also because it lacks very seriously a complete axiomatization Reference Väänänen[54].
We remarked earlier that Sagi’s demarcation of logicality for a fixed class of logical constants, which is based on Löwenheim numbers, partitions logical space differently than ours. As we observed, logics that have a completeness theorem do not seem to be tied to the
![]() $\aleph $
-hierarchy in any obvious way. For example, Keisler’s axioms
$\aleph $
-hierarchy in any obvious way. For example, Keisler’s axioms
 $$ \begin{align} \left\{\begin{array}{ll} \text{Axiom} 0 &\text{Axiom schemes for }\mathcal{L}_{\omega\omega}\\ \text{Axiom} 1 &\neg Qx(x=y\vee x=z)\\ \text{Axiom} 2 &\forall x(\phi\to\psi)\to(Qx\phi\to Qx\psi)\\ \text{Axiom} 3 &Qx\phi(x)\to Qy\phi(y)\\ \text{Axiom} 4 &Qy\exists x\phi\to(\exists xQy\phi\vee Qx\exists y\phi) \end{array}\right. \end{align} $$
$$ \begin{align} \left\{\begin{array}{ll} \text{Axiom} 0 &\text{Axiom schemes for }\mathcal{L}_{\omega\omega}\\ \text{Axiom} 1 &\neg Qx(x=y\vee x=z)\\ \text{Axiom} 2 &\forall x(\phi\to\psi)\to(Qx\phi\to Qx\psi)\\ \text{Axiom} 3 &Qx\phi(x)\to Qy\phi(y)\\ \text{Axiom} 4 &Qy\exists x\phi\to(\exists xQy\phi\vee Qx\exists y\phi) \end{array}\right. \end{align} $$
are complete for
![]() $\mathcal {L}(Q_1)$
, and if
$\mathcal {L}(Q_1)$
, and if
![]() $GCH$
is assumed, then they are complete for all
$GCH$
is assumed, then they are complete for all
![]() $\aleph _{\alpha +1}$
for which
$\aleph _{\alpha +1}$
for which
![]() $\aleph _{\alpha }$
is regular (hence for
$\aleph _{\alpha }$
is regular (hence for
![]() $\aleph _n$
for all
$\aleph _n$
for all
![]() $n>0$
). Whereas while
$n>0$
). Whereas while
![]() $\mathcal {L}(Q_0)$
satisfies the Keisler Axioms, these (or any other recursive set of axioms) are not a complete axiomatisation of
$\mathcal {L}(Q_0)$
satisfies the Keisler Axioms, these (or any other recursive set of axioms) are not a complete axiomatisation of
![]() $\mathcal {L}(Q_0)$
.Footnote
42
$\mathcal {L}(Q_0)$
.Footnote
42
The suggestion here is that having a complete axiomatisation should be a marker of logicality on the simple ground that logics of this kind resemble first order logic in one of its essential, if not most essential property, namely completeness. Except for
![]() $Q_0$
, one would then classify “there are very (i.e., uncountably) many” as logical, as dictated by Keisler’s axioms; in particular, the quantifier
$Q_0$
, one would then classify “there are very (i.e., uncountably) many” as logical, as dictated by Keisler’s axioms; in particular, the quantifier
![]() $Q_1$
would be graded as having a higher degree of logicality than
$Q_1$
would be graded as having a higher degree of logicality than
![]() $Q_0$
, as
$Q_0$
, as
![]() $\mathcal {L}(Q_1)$
is complete with respect to the Keisler Axioms whereas
$\mathcal {L}(Q_1)$
is complete with respect to the Keisler Axioms whereas
![]() $\mathcal {L}(Q_0)$
is not complete in this respect.Footnote
43
In short, our criterion of logicality, which turns on the degree to which a logic resembles first order logic in its model theoretic properties, comes apart from Sagi’s already at the level of the logics
$\mathcal {L}(Q_0)$
is not complete in this respect.Footnote
43
In short, our criterion of logicality, which turns on the degree to which a logic resembles first order logic in its model theoretic properties, comes apart from Sagi’s already at the level of the logics
![]() $\mathcal {L}(Q_0)$
and
$\mathcal {L}(Q_0)$
and
![]() $\mathcal {L}(Q_1)$
.
$\mathcal {L}(Q_1)$
.
A possible objection might come from the fact that Keisler’s axioms are satisfied by many different quantifiers, in fact by every
![]() $Q_\alpha $
, where
$Q_\alpha $
, where
![]() $\aleph _\alpha $
is regular. On the other hand, we may consider
$\aleph _\alpha $
is regular. On the other hand, we may consider
![]() $Q_1$
logical admitting that from the point of view of logicality it cannot be separated from some other similar quantifiers. What is logical, according to this view, is not so much the cardinality
$Q_1$
logical admitting that from the point of view of logicality it cannot be separated from some other similar quantifiers. What is logical, according to this view, is not so much the cardinality
![]() $\aleph _1$
, as, simply, uncountable cardinality—or “very many”—in general, while the failure of
$\aleph _1$
, as, simply, uncountable cardinality—or “very many”—in general, while the failure of
![]() $Q_0$
to permit a recursive axiomatization is an indication that there is something mathematical, as against logical, in
$Q_0$
to permit a recursive axiomatization is an indication that there is something mathematical, as against logical, in
![]() $Q_0$
. The permutation invariance characterization of logicality does not differentiate between
$Q_0$
. The permutation invariance characterization of logicality does not differentiate between
![]() $Q_1$
and
$Q_1$
and
![]() $Q_0$
, as the Completeness Theorem criterion does. By the invariance criterion every
$Q_0$
, as the Completeness Theorem criterion does. By the invariance criterion every
![]() $Q_\alpha $
is logical, which may seem unintuitive. By further applying the Completeness theorem criterion we can make finer distinctions and see a difference:
$Q_\alpha $
is logical, which may seem unintuitive. By further applying the Completeness theorem criterion we can make finer distinctions and see a difference:
![]() $Q_1$
is “more logical” than
$Q_1$
is “more logical” than
![]() $Q_0$
.
$Q_0$
.
For singular strong limit
![]() $\aleph _{\alpha }$
Keisler Reference Keisler, van Rootselaar and Staal[30] proved a Completeness theorem, but with different axioms (no simple set of axioms is currently known). Thus there are (at least) two different “logical” concepts of “very many,” one for
$\aleph _{\alpha }$
Keisler Reference Keisler, van Rootselaar and Staal[30] proved a Completeness theorem, but with different axioms (no simple set of axioms is currently known). Thus there are (at least) two different “logical” concepts of “very many,” one for
![]() $\aleph _{\alpha }$
the successor of regular and one for the singular case. (Successor of singular is open.) The two concepts have different logical content: Keisler’s Axioms for
$\aleph _{\alpha }$
the successor of regular and one for the singular case. (Successor of singular is open.) The two concepts have different logical content: Keisler’s Axioms for
![]() $Q_{\alpha }$
are valid for all regular
$Q_{\alpha }$
are valid for all regular
![]() $\aleph _\alpha $
, and in some cardinalities (successor of regular) they have a Completeness theorem, modulo the
$\aleph _\alpha $
, and in some cardinalities (successor of regular) they have a Completeness theorem, modulo the
![]() $GCH$
, as was noted above. In some other cardinalities (singular) different axioms have to be employed in order to get a completeness theorem. In the base case
$GCH$
, as was noted above. In some other cardinalities (singular) different axioms have to be employed in order to get a completeness theorem. In the base case
![]() $\alpha =0$
no effectively given additional axioms can be added to give a completeness theorem.
$\alpha =0$
no effectively given additional axioms can be added to give a completeness theorem.
According to Sagi, “We should distinguish between a logic
![]() $\mathcal {L}(Q)$
used to measure the logicality of Q and the logic we ultimately use for validity and logical consequence.”Footnote
44
But if metaphysical involvement is inversely related to logicality, then having a completeness theorem should possibly be considered as a marker of logicality also under the Sagi criterion. This is because what the completeness theorem precisely does is to enable the conversion of semantic content, which is metaphysically involved (from the Sagi point of view, presumably), into syntactic content which, presumably, is not. In this connection, the following caveat is important: As Carnap observed [Reference Carnap16] the rules do not fix the interpretation of the logical constants, they have non-standard interpretations. In their Reference Bonnay and Westerståhl[12] Bonnay and Westerståhl present a way to sidestep the problem:
$\mathcal {L}(Q)$
used to measure the logicality of Q and the logic we ultimately use for validity and logical consequence.”Footnote
44
But if metaphysical involvement is inversely related to logicality, then having a completeness theorem should possibly be considered as a marker of logicality also under the Sagi criterion. This is because what the completeness theorem precisely does is to enable the conversion of semantic content, which is metaphysically involved (from the Sagi point of view, presumably), into syntactic content which, presumably, is not. In this connection, the following caveat is important: As Carnap observed [Reference Carnap16] the rules do not fix the interpretation of the logical constants, they have non-standard interpretations. In their Reference Bonnay and Westerståhl[12] Bonnay and Westerståhl present a way to sidestep the problem:
Our take on Carnap’s Problem is that it is made artificially difficult by considering all possible interpretations, no matter how bizarre. As speakers, we know that our language is going to be compositional, that it will have some true and some false sentences, and that its logical constituents will be topic-neutral. Therefore attention may be restricted to interpretations which satisfy these principles. Following Church’s advice, this amounts to explicitly factoring out the role of semantic principles and the role of inference rules in fixing the interpretation of logical constants, rather than covertly using semantic notions to make sense of extended inference rules. This strategy proves successful both for propositional connectives and for quantifiers.
There is also the issue of expressive power, with respect to which the logics built on the quantifiers “most,” “more” and the Härtig quantifier differ. In certain models with an equivalence relation the Härtig quantifier can be seen to be eliminable while the Rescher quantifier is not Reference Hauschild[24]. Thus the Rescher quantifier is strictly stronger than the Härtig quantifier from the point of view of expressive power. The point here is that expressive power should be inversely related to logicality.
Bonnay also ties logicality to syntax via a Completeness theorem, as is spelled out in some detail in [Reference Bonnay10].Footnote
45
Here Bonnay proposes a modification of the program of Carnap’s Aufbau [Reference Carnap18], calling for logical expressions to be defined syntactically. It is a feature of his treatment that the absoluteness of a logic plays a crucial role in guaranteeing the robustness of the syntactic definition. Thus
![]() $L(Q_0)$
is an absolute logic because it has a recursive syntax, just like first order logic, and its semantics is absolute in transitive models of (even weak) set theory.Footnote
46
On the other hand,
$L(Q_0)$
is an absolute logic because it has a recursive syntax, just like first order logic, and its semantics is absolute in transitive models of (even weak) set theory.Footnote
46
On the other hand,
![]() $L(Q_1)$
is not absolute, even though it has a recursive syntax.Footnote
47
$L(Q_1)$
is not absolute, even though it has a recursive syntax.Footnote
47
Burgess’s Reference Burgess[14] forges a link between absoluteness and the idea of having a proof procedure. He exhibits a quasi-constructive complete proof procedure involving rules with
![]() $\aleph _1$
premisses for the hereditary countable part of any absolute logic.
$\aleph _1$
premisses for the hereditary countable part of any absolute logic.
In sum, if one classifies the first order existential quantifier “there is at least one,” as inherently logical, and if as such this quantifier is thought of as having minimal or no semantic content, then is there a principled way to determine when and how higher quantification acquires semantic content, e.g., at what level in the cumulative hierarchy? Sagi’s answer is that logicality diminishes the higher up we are in cumulative hierarchy; while we suggest that logicality kicks in arbitrarily high up, e.g., for all
![]() $\aleph _{\alpha +1}$
for which
$\aleph _{\alpha +1}$
for which
![]() $\aleph _{\alpha }$
is regular, with the
$\aleph _{\alpha }$
is regular, with the
![]() $\aleph _0$
case an anomaly, again because of completeness. The intuition here is that logics which have a completeness theorem are close to first order logic in this special sense. This is because completeness enables the conversion of semantic consequence into syntactic consequence via the two Keisler axiomatisations—albeit conditioned on the continuum hypothesis in certain important cases.Footnote
48
$\aleph _0$
case an anomaly, again because of completeness. The intuition here is that logics which have a completeness theorem are close to first order logic in this special sense. This is because completeness enables the conversion of semantic consequence into syntactic consequence via the two Keisler axiomatisations—albeit conditioned on the continuum hypothesis in certain important cases.Footnote
48
8 Conclusions
McGee’s theorem translates the Tarski–Sher criterion into definability in a logic, obtaining cardinal dependent definability in
![]() $L_{\infty \infty }$
. The cardinal dependency aspect of the theorem leads to criticism of logicality across domains (Feferman’s third critique), to criticism of entanglement with mathematics (Feferman’s first critique) and of non-absoluteness (Feferman’s second critique). Maintaining cardinal dependency we lowered
$L_{\infty \infty }$
. The cardinal dependency aspect of the theorem leads to criticism of logicality across domains (Feferman’s third critique), to criticism of entanglement with mathematics (Feferman’s first critique) and of non-absoluteness (Feferman’s second critique). Maintaining cardinal dependency we lowered
![]() $L_{\infty \infty }$
to
$L_{\infty \infty }$
to
![]() $\Delta (L_{\infty \omega })$
which is more palatable from the point of view of model theoretic properties. A stronger degree of logicality is obtained by abandoning cardinal dependency and investigating logics in which a candidate for logicality is definable. Since every class of models which is closed under isomorphisms is definable in some logic, this seems reasonable. Following and expanding on Sagi’s suggestion to delineate degrees of logicality according to their Löwenheim numbers, we delineate logicality according to their Löwenheim numbers but also according to a wider spectrum of model theoretic properties of logics, such as Completeness Theorems and absoluteness properties, together with Löwenheim-Skolem properties, all considered from a logicality point of view.
$\Delta (L_{\infty \omega })$
which is more palatable from the point of view of model theoretic properties. A stronger degree of logicality is obtained by abandoning cardinal dependency and investigating logics in which a candidate for logicality is definable. Since every class of models which is closed under isomorphisms is definable in some logic, this seems reasonable. Following and expanding on Sagi’s suggestion to delineate degrees of logicality according to their Löwenheim numbers, we delineate logicality according to their Löwenheim numbers but also according to a wider spectrum of model theoretic properties of logics, such as Completeness Theorems and absoluteness properties, together with Löwenheim-Skolem properties, all considered from a logicality point of view.
Acknowledgments
The first author would like to thank the Academy of Finland, grant no: 322488. The second author would like to thank the Academy of Finland, grant no: 322795. This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 101020762).The authors are grateful to Denis Bonnay, Dag Westerståhl and two anonymous referees for comments.