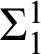1 Introduction
The original Goodstein sequence [Reference Goodstein14] was derived from the unique base-x representation of a natural number
$n> x \ge 2$
:
$$ \begin{align*} n=x^{b_{0}}+x^{b_{1}}+\cdots+x^{b_{m}}, \end{align*} $$
where for each i,
$x^{b_{i}}\geq x^{b_{i+1}}$
.
If each positive
$b_{i}$
is in turn base-x represented as
$b_{i}=x^{b_{i0}}+\cdots +x^{b_{ik_{i}}}$
, and then each positive
$b_{ij}$
is base-x represented, and so on until no further decomposition is possible, this produces the so-called hereditary base-x representation of n.
The non-hereditary or hereditary base-x representations then give rise to two “Goodstein sequences”
$\{B_{k}(x;n)\}_{k}$
,
$\{C_{k}(x; n)\}_{k}$
as follows, where again,
$n> x\geq 2$
are natural numbers. In all cases, however, and those that follow, the Goodstein sequence is generated by iterating a “Goodstein process”: increase the base by
$1$
and subtract
$1$
from the numerical value. The chosen method of representation is what gives rise to the variation in “strength” of the processes.
-
1.
$B_{0}(x;n)=C_{0}(x;n)=n$
. -
2. If
$B_{k}(x;n)=0$
, then
$B_{k+1}(x;n)=0$
. Similarly for
$C_{k}(x;n)$
. -
3. If
$B_{k}(x;n)>0$
then throughout the base-
$(x+k)$
representation of
$B_{k}(x,n)$
, replace the base parameter
$(x+k)$
by
$(x+k+1)$
, and then subtract by
$1$
to get the next term
$B_{k+1}(x;n)$
.This means if
$B_{k}(x;n)=(x+k)^{b_{0}}+\cdots +(x+k)^{b_{m}}$
, then
$B_{k+1}(x;n)=(x+k+1)^{b_{0}}+\cdots +(x+k+1)^{b_{m}}-1$
. -
4. If
$C_{k}(x;n)>0$
then throughout the hereditary base-
$(x+k)$
representation of
$C_{k}(x,n)$
, replace the base parameter
$(x+k)$
by
$(x+k+1)$
, and then subtract by
$1$
to get the next term
$C_{k+1}(x;n)$
.
Clearly both B and C are recursive sequences, so termination-in-
$0$
is expressible in the language of arithmetic.
$\{C_{k}(x; n)\}_{k}$
is (a special case of) the Goodstein sequence originating in Goodstein [Reference Goodstein14]. See Rathjen [Reference Rathjen, Kahle and Rathjen16] for a more recent discussion of this.
The known independence results, stemming from Goodstein’s work, are summarized as follows. Kirby and Paris [Reference Kirby and Paris15] were the first to prove independence from PA, and Cichon [Reference Cichon10] supplied the concise recursion-theoretic method which underpins this paper.
Proposition 1.1.
-
1. (Abrusci, Girard and Van de Wiele [Reference Abrusci, Girard, Van de Wiele and Simpson1] and Cichon [Reference Cichon10]) Every sequence
$\{B_{k}(x;n)\}_{k}$
terminates in
$0$
for any
$x\geq 2$
and
$n>x$
, and this fact is expressible in but independent from PRA, or the fragment
${{\textrm {I}}}{\kern2pt}\Sigma ^{0}_{1}$
of first-order arithmetic. -
2. (Kirby and Paris [Reference Kirby and Paris15] and Cichon [Reference Cichon10]) Every sequence
$\{C_{k}(x;n)\}_{k}$
terminates in
$0$
for any
$x\geq 2$
and n, and this fact is expressible in but independent from first-order arithmetic PA.
These representations, based on the exponential function, provide “compact” representation of natural numbers. In what follows, even more compact representations are considered, based on parameterized versions of the Ackermann-Péter function
$F_a(b)$
on natural numbers
$a, b$
, given by:
$$ \begin{align*} F_0(b) = b+1, \;\;\;\; F_{a+1}(b) = F_{a}^{(b)}(b) = \overbrace{F_{a}\circ \cdots \circ F_{a}}^{b \mbox{ times}}\, (b)\, .\end{align*} $$
There is a hierarchy of such representations, each with associated Goodstein sequences. Calibration of their proof-theoretic strengths is achieved here by assigning appropriate levels of the Hardy hierarchy as in Cichon’s original [Reference Cichon10]. For other related approaches, see [Reference Abrusci, Girard, Van de Wiele and Simpson1, Reference Arai3–Reference Arai, Fernández-Duque, Wainer and Weiermann6, Reference Buchholz, Wainer and Simpson8, Reference Weiermann19, Reference Wilken and Weiermann20].
2 Level-one and -two Goodstein sequences
At the first level (see [Reference Arai4, Reference Arai5]) one obtains a new unique representation of numbers n, relative to a given “starting base”
$x \ge 2$
, as follows (assuming obvious majorization properties of F):
If
$n<x$
then n is its own representation. Otherwise take the least a such that
$x \le n < F_{a+1}(x)$
and the least
$i<x$
such that
$n < F_{a}^{(i+1)}(x)$
. If
$F_{a}^{(i)}(x) = n$
then this is the representation of n. If
$F_{a}^{(i)}(x) < n$
then repeat the process with x replaced by
$x_1 = F_{a}^{(i)}(x)$
. One thus obtains an
$a_1 < a$
and an
$i_1 < x_1$
such that
$F_{a_1}^{(i_1)}(x_1) \le n < F_{a_1}^{(i_1 +1)}(x_1)$
. Continuing this process, and since
$F_0$
is the successor, one must reach a final stage
$\ell $
at which
$$ \begin{align*} n = F_{a_\ell}^{(i_\ell)} \cdots \, F_{a_2}^{(i_2)}\, F_{a_1}^{(i_1)}\, F_{a}^{(i)}(x) \end{align*} $$
where
$a_\ell < \cdots a_2 < a_1 < a$
and each
$i_j < F_{a_{j-1}}^{(i_{j-1})} \cdots \,F_{a_1}^{(i_1)}\, F_{a}^{(i)}(x)$
. This is our next base-x representation of n. Note that the form of representation is preserved under any increase in the base. It is clear from the construction that this representation is unique, modulo the base x (a more formal proof would follow the lines of Lemma 3.2).
Now
$F_a = H_{\omega ^a}$
where
$\{H_\alpha \}$
is the so-called “Hardy hierarchy” (see e.g., [Reference Fairtlough, Wainer and Buss12, Reference Schwichtenberg and Wainer17]) given by:
$$ \begin{align*} H_0(x) = x, \;\;\;H_{\beta +1}(x) = H_{\beta}(x+1), \;\;\; H_{\lambda}(x) = H_{\lambda_x}(x)\;\;\; \mbox{at limits } \lambda = \mathop{\mathrm{sup}}_i \lambda_i \end{align*} $$
where the subscripts are“tree ordinals,” that is: each “limit”
$\lambda $
is determined by a fixed choice of fundamental sequence
$\{\lambda _i\}$
. In particular,
$\omega $
is chosen to be the identity sequence
$\omega = \mathop {\mathrm {sup}}_i i$
and
$\omega ^{a+1} = \mathop {\mathrm {sup}}_i \omega ^a \cdot i$
. It is easy to check, by induction on
$\gamma $
, that H then satisfies
$$ \begin{align*}H_{\alpha + \gamma} = H_\alpha \circ H_\gamma \end{align*} $$
and hence, for all a and n,
$H_{\omega ^a}(n) = F_a(n)$
.
Therefore the above base-x representation of n may be rewritten:
$$ \begin{align*}n = H_\alpha(x) \;\;\; \mbox{where} \;\;\; \alpha = \omega^{a_\ell}\cdot i_\ell + \cdots + \omega^{a_1}\cdot i_1 + \omega^{a}\cdot i\, .\end{align*} $$
In other words, this representation of n has an ordinal notation as a code:
$n = H_\alpha (x)$
, but
$\alpha $
is written in reverse Cantor normal form. Conversely, any such normal form will, under H, be an x-representation.
If we begin with
$n = F_{a}(x) = H_{\omega ^a}(x)$
and subtract
$1$
then, by unravelling the recursion down to
$F_0$
, and removing the outermost occurrence of
$F_0$
, we obtain the base-x representation of the predecessor:
$$ \begin{align*} n-1 = F_0^{(x_a)}\, F_1^{(x_{a-1})} \cdots \, F_{a-2}^{(x_2)}\, F_{a-1}^{(x_1)}(x) = H_{\beta}(x), \end{align*} $$
where
$x_1 = x-1$
,
$x_{i+1} = F_{a-i}^{(x_i)}(x_i +1)-1$
and (in reverse Cantor normal form),
$\beta = x_a + \omega \cdot x_{a-1} + \cdots + \omega ^{a-2}\cdot x_2 + \omega ^{a-1}\cdot x_1 $
.
This
$\beta $
, when written in standard Cantor normal form, has rank
$\|\beta \| < \omega ^a \le \|\alpha \|$
. We denote
$\beta $
by
$\beta = Q_x(\omega ^a)$
with
$Q_x$
defined accordingly as follows:
Definition 2.1.
$Q_x(\omega ^0) = 0$
and if
$a>0$
,
$Q_x(\omega ^a) = Q_{x_1}(\omega ^{a-1}) + \omega ^{a-1}\cdot {(x-1)}$
where
$x_1 = H_{\omega ^{a-1}\cdot (x-1)}(x) = F_{a-1}^{(x-1)}(x)$
.
Then on (reversed) Cantor normal forms
$\alpha = \omega ^{a_\ell }\cdot i_\ell + \alpha '$
, define:
$$ \begin{align*} Q_x(\alpha ) = Q_{x'}(\omega ^{a_\ell }) + \omega ^{a_\ell }\cdot (i_\ell -1) + \alpha ' \textrm{ where } x' = H_{\omega ^{a_\ell }\cdot (i_\ell -1) + \alpha '}(x).\end{align*} $$
Thus
$\|Q_x(\alpha )\| < \|\alpha \| < \omega ^\omega $
. (
$Q_x$
is a more complex variant of Cichon’s [Reference Cichon10] original predecessor function
$P_x$
, which will play a crucial role in later sections. In contrast to
$Q_x$
,
$P_x$
operates on standard Cantor normal forms thus:
$P_x(\omega ^a) = \omega ^{a-1}\cdot (x-1) + P_x(\omega ^{a-1})$
.)
Lemma 2.2.
$H_{Q_x(\alpha )}(x) = H_{\alpha }(x) -1$
.
Proof Proceed by induction on
$|\alpha |$
where
$\alpha = \omega ^{a_\ell }\cdot i_\ell + \alpha '$
in reversed Cantor normal form (
$i_\ell>0$
). If
$\alpha '$
is non-zero or
$i_\ell> 1$
then
$\omega ^{a_\ell } < |\alpha |$
so with
$Q_x(\alpha )$
and
$x'$
defined as above, we have, inductively:
$H_{Q_x(\alpha )}(x) = H_{Q_{x'}(\omega ^{a_\ell })}(x') = H_{\omega ^{a_\ell }}(x')-1 = H_{\alpha }(x)-1$
. If, on the other hand,
$\alpha $
is
$\omega ^{a_\ell }$
with
$a_\ell>0$
, then again by induction,
$H_{Q_x(\alpha )}(x) = H_{Q_{x'}(\omega ^{a_\ell -1})}(x') = H_{\omega ^{a_\ell -1}}(x')-1 = H_{\alpha }(x)-1$
. Finally, if
$\alpha = 1$
then
$Q_x(\alpha ) = 0$
and so
$H_{Q_x(\alpha )}(x) = x = H_\alpha (x)-1$
.⊣
Our “first level” Goodstein sequence
$\{D_k(x;n)\}$
now runs as follows, beginning with n represented in base-x form as
$n = H_\alpha (x)$
(
$\alpha $
in reverse Cantor normal form):
Update base x to
$x+1$
; subtract
$1$
;
$D_1(x;n) = H_{\alpha _1}(x+1)$
with
$\alpha _1 = Q_{x+1}(\alpha )$
.
Update base
$x+1$
; subtract
$1$
;
$D_2(x;n) = H_{\alpha _2}(x+2)$
with
$\alpha _2 = Q_{x+2}(\alpha _1)$
.
Repeat
$\cdots D_k(x;n) = H_{\alpha _k}(x+k)$
where
$\alpha _k = Q_{x+k}\, Q_{x+ k-1} \, \ldots \, Q_{x+1} \,(\alpha )$
.
Theorem 2.3 cf. Prop.1.1.1
$\forall n \forall x\ge 2 \exists k (D_k(x;n) =0)$
is a consequence of transfinite induction up to
$\omega ^\omega $
, and this fact is independent of Primitive Recursive Arithmetic (PRA), or the fragment
${{\textrm {I}}}{\kern1.5pt}\Sigma ^{0}_{1}$
of first-order arithmetic.
Proof Beginning with
$n = H_{\alpha }(x)$
, the sequence
$\{\alpha _k\}$
is a decreasing sequence of ordinals below
$\omega ^\omega $
. Therefore, by induction up to
$\omega ^\omega $
, there is a stage k at which
$\alpha _k =0$
and hence
$D_k(x;n) = x+k$
. From this point on, since the number is less than the base, it takes
$x+k$
more predecessors to reach
$D_{x+2k}(x;n) = 0$
.
Assuming termination of the Goodstein sequence starting with
$n = F_a(x)$
, the stage s at which
$D_s(x;n) =0$
is
$s = x+2k$
where
$\alpha _k =0$
. Hence
$n = H_{\omega ^a}(x) \le H_{\alpha _1}(x+1) \le H_{\alpha _2}(x+2) \le \cdots \le H_{\alpha _k}(x+k) = x+k$
. This k bounds the number of steps needed to compute
$F_a(x)$
. Hence termination of all Goodstein sequences implies the computability of
$F_a(x)$
which, as a function of both variables, is not primitive recursive. Thus, termination of all level-one Goodstein sequences is not provable in PRA.⊣
Note. It is a general feature of Goodstein sequences that they increase up to a maximum where
$\alpha _k =0$
, and from there descend, in as many steps, to
$0$
.
2.1 Level-two Goodstein sequences
These are based on a stronger form of representation than that used above. As before, one first uniquely represents n relative to base x as
$$ \begin{align*}n = F_{a_\ell}^{(i_\ell)}\, \cdots \, F_{a_2}^{(i_2)}\, F_{a_1}^{(i_1)}\, F_{a}^{(i)}(x) = H_{\alpha}(x)\end{align*} $$
with
$\alpha = \omega ^{a_\ell }\cdot i_\ell + \cdots + \omega ^{a_1}\cdot i_1 + \omega ^{a}\cdot i\,$
in reverse Cantor normal form. But now, each F-subscript
$a_j$
is again uniquely represented relative to base x, and each of their subscripts
$a_{j,k}$
etcetera, hereditarily until no further decomposition is possible. A more formal proof that this hereditary representation is unique would again follow similar lines to that of Lemma 3.2.
Whereas, at level one,
$\alpha $
ranged over ordinals less than
$\omega ^\omega $
, the hereditary nesting means that
$\alpha $
must now vary below
$\varepsilon _0$
.
Definition 2.4. With each hereditary base-x representation
$$ \begin{align*}n = F_{a_\ell}^{(i_\ell)}\, \cdots \, F_{a_2}^{(i_2)}\, F_{a_1}^{(i_1)}\, F_{a}^{(i)}(x)\end{align*} $$
associate its “representing ordinal”
$\alpha = \omega ^{\alpha _\ell }\cdot i_\ell + \cdots + \omega ^{\alpha _1}\cdot i_1 + \omega ^{\alpha }\cdot i\,$
where, inductively, each
$\alpha _j$
is the representing ordinal of
$a_j$
.
The definition of
$Q_x$
is extended appropriately at limit ordinals
$\lambda = \mathop {\mathrm {sup}}_i \lambda _i$
, to preserve reverse Cantor normal forms.
Definition 2.5.
$$ \begin{align*} Q_x(\omega^0) = 0, \;\;\; Q_x(\omega^{\beta +1}) = Q_{x_1}(\omega^\beta) + \omega^\beta \cdot (x-1), \;\;\; Q_x(\omega^\lambda) = Q_x(\omega^{\lambda_x}),\end{align*} $$
where
$x_1 = H_{\omega ^\beta \cdot (x-1)}(x)$
.
If
$\alpha = \omega ^{\alpha _\ell } + \alpha '$
in reverse Cantor normal form, then define
$$ \begin{align*} Q_x(\alpha) = Q_{x'}(\omega^{\alpha_\ell}) + \alpha' \;\; \mbox{where } x' = H_{\alpha'}(x).\end{align*} $$
Lemma 2.6. If
$\alpha $
is the representing ordinal of n relative to starting-base x then
$$ \begin{align*} H_\alpha(x)\, = \, n \;\;\; \mbox{and} \;\;\; H_{Q_x(\alpha)}(x)\, = \, n -1 \, ,\end{align*} $$
that is,
$Q_x(\alpha )$
is the representing ordinal of
$n -1$
.
Proof Note first that if
$\beta $
is the representing ordinal of m relative to the starting base x, then by Definition 2.4,
$\omega ^\beta $
is the representing ordinal of
$F_m(x)$
. That
$H_\alpha (x) = n$
now follows by induction, assuming
$\alpha = \omega ^{\alpha _\ell }\cdot i_\ell + \cdots + \omega ^{\alpha }\cdot i$
where each
$\alpha _j$
is the representing ordinal of
$a_j$
relative to the appropriate
$x_j$
,
$$ \begin{align*} H_\alpha(x)\, = \, H_{\omega^{\alpha_\ell}}^{(i_\ell)}\,\cdots \, H_{\omega^{\alpha}}^{(i)}(x) \, = \, F_{a_\ell}^{(i_\ell)}\, \cdots \, F_{a}^{(i)}(x)\, = \, n\, .\end{align*} $$
For
$H_{Q_x(\alpha )}(x) = n -1$
unravel the recursive definition of
$Q_x(\alpha )$
. One has, letting
$\alpha = \omega ^{\alpha _\ell } + \alpha '$
as above,
$Q_x(\alpha ) = Q_x(\omega ^{\alpha _{\ell }}) + \alpha ' = Q_{x_1}(\omega ^{\beta }) + \alpha ''$
where
$\|\beta \| < \|\alpha _\ell \|$
and
$H_{Q_x(\alpha )}(x) = H_{Q_{x_1}(\omega ^\beta )}(x_1)$
with
$x_1 = H_{\alpha ''}(x)$
. The next stage yields
$Q_x(\alpha ) = Q_{x_2}(\omega ^{\beta '}) + \alpha '''$
where
$\|\beta '\| < \|\beta \|$
,
$H_{Q_x(\alpha )}(x) = H_{Q_{x_2}(\omega ^{\beta '})}(x_2)$
and
$x_2 = H_{\alpha '''}(x_1)$
. Continuing this, one has at some terminal stage k,
$Q_x(\alpha ) = Q_{x_k}(\omega ^0 + \alpha ^{''\cdots '}) = \alpha ^{''\cdots '}$
and hence
$H_{Q_x(\alpha )}(x) = H_{\alpha ^{''\cdots '}}(x)$
. At each stage of this process, the numerical value of
$H_\alpha (x)$
is preserved - only at the final stage is one successor
$H_{\omega ^0}$
removed. Thus,
$$ \begin{align*}H_{Q_x(\alpha)}(x) = H_{\alpha}(x)-1\, .\end{align*} $$
Note that the reduction
$\alpha \mapsto Q_x(\alpha )$
preserves reverse Cantor normal form. As a consequence note also that representing ordinals are always in reverse Cantor normal form. For suppose n has x-representation
$F_{a_\ell }^{(i_\ell )}\, \cdots \, F_{a_1}^{(i_1)}\, F_{a}^{(i)}(x)$
with representing ordinal
$\alpha = \omega ^{\alpha _\ell }\cdot i_\ell + \cdots + \omega ^{\alpha _1}\cdot i_1 + \omega ^{\alpha }\cdot i$
. Assume inductively that each
$\alpha _j$
(representing
$a_j$
) is in reverse Cantor form. If
$a_{j_1} < a_{j_2}$
we have, for an appropriately large
$x_1$
and appropriate sequence of applications of
$Q_x$
,
$H_{\omega ^{\alpha _{j_1}}}(x_1) = H_{Q_x Q_x \ldots Q_x (\omega ^{\alpha _{j_2}})}(x)$
. This means
$\|\omega ^{\alpha _{j_1}}\| < \|\omega ^{\alpha _{j_2}}\|$
, so
$\alpha $
is in reverse Cantor form.⊣
Lemma 2.7. If n has hereditary base-x representation
$F_{a_\ell }^{(i_\ell )}\, \cdots \, F_{a_1}^{(i_1)}\, F_{a}^{(i)}(x)$
, let
$n'$
denote the result of increasing the base from x to
$x+1$
throughout. Then the resulting term
$F_{a_\ell ^{\prime }}^{(i_\ell )}\, \cdots \, F_{a_1^{\prime }}^{(i_1)}\, F_{a^{\prime }}^{(i)}(x+1)$
is the base-
$x+1$
representation of
$n^{\prime }$
. Furthermore
$(n-1)^{\prime } < n^{\prime }$
; hence if
$m<n$
then
$m^{\prime }<n^{\prime }$
.
Proof Proceeding by induction on (the numerical value of) n, one has
$a_j < a_{j+1} <n$
, hence
$a_j^{\prime } < a_{j+1}^{\prime }$
. The bounding conditions on the iterates
$(i_j)$
continue to hold under the “dash” operation because it increases the upper bounds. Therefore
$F_{a_\ell ^{\prime }}^{(i_\ell )} \cdots F_{a_1^{\prime }}^{(i_1)} F_{a^{\prime }}^{(i)}(x+1)$
is a hereditary base-
$x+1$
representation. For shorthand, write it as
$n^{\prime } = F_{a_\ell ^{\prime }}^{(i_\ell )}(z^{\prime })$
with
$z = F_{a_{\ell -1}}^{(i_{\ell -1})} \cdots F_{a_1}^{(i_1)} F_{a}^{(i)}(x+1)$
. Now the predecessor is represented as:
$n-1 = F_0^{(x_a)} F_1^{(x_{a-1})} \cdots F_{a-2}^{(x_2)} F_{a-1}^{(x_1)} F_{a_\ell }^{(i_\ell -1)}(z)$
where
$a=a_\ell $
and each
$x_{j+1}=F_{a-j}^{(x_j)}(x_j+1)-1$
. Therefore
$(n-1)^{\prime } = F_0^{(x_a)}\, F_1^{(x_{a-1})} \cdots F_{(a-2)^{\prime }}^{(x_2)} F_{(a-1)^{\prime }}^{(x_1)} F_{a_\ell ^{\prime }}^{(i_\ell -1)}(z^{\prime })$
. Applying the successor
$F_0$
to this, and repeatedly using the recursion equation
$F_c (F_c^{(y-1)}(y)) = F_{c+1}(y)$
, one obtains
$(n-1)^{\prime } < \cdots < F_{(a-1)^{\prime }}(F_{(a-1)^{\prime }}^{(x_1)} F_{a_\ell ^{\prime }}^{(i_\ell -1)}(z^{\prime })) < F_{a^{\prime }}F_{a_\ell ^{\prime }}^{(i_\ell -1)}(z^{\prime })$
, using the induction hypothesis
$(a-1)^{\prime } \le a^{\prime }-1$
. Since
$a=a_\ell $
this last term gives
$(n-1)^{\prime } < F_{a_\ell ^{\prime }}^{(i_\ell )}(z^{\prime }) = n^{\prime }$
.⊣
Definition 2.8. Let
$\{E_k(x;n)\}_k$
denote the “level-two” Goodstein sequence starting with
$E_0(x;n)$
as the hereditary base-x representation of n, then successively updating the base and subtracting one.
Theorem 2.9 cf. Prop.1.1.2
$\forall n \forall x\ge 2 \exists k (E_k(x;n) =0)$
is (over PRA) a consequence of transfinite induction up to
$\varepsilon _0$
, and this fact is independent of Peano Arithmetic.
Proof The first step of the Goodstein sequence is to increase the base from x to
$x+1$
, and subtract one. By the lemmas we therefore have
$E_1(x;n) = H_{Q_{x+1}(\alpha )}(x+1)$
where
$\alpha $
is the representing ordinal of n relative to base x, which is the same as the representing ordinal of the updated
$n^{\prime }$
relative to base
$x+1$
. Repeating this, with
$\alpha $
replaced by
$Q_{x+1}(\alpha )$
,
$E_2(x;n) = H_{Q_{x+2}Q_{x+1}(\alpha )}(x+2)$
and at stage s,
$E_s(x;n) = H_{Q_{x+s}\cdots Q_{x+2}Q_{x+1}(\alpha )}(x+s)$
. Transfinite induction up to
$\varepsilon _0$
now yields a stage k where
$E_k(x;n) = H_0(x+k) = x+k$
after which the sequence terminates at
$0$
in a further
$x+k$
steps.
Conversely, termination of the sequence implies the “computability” (“defined-ness”) of
$H_\alpha (x)$
. Termination of all level-two Goodstein sequences is therefore a re-statement of the computability of all
$H_\alpha $
functions, for
$\alpha \prec \varepsilon _0$
. This cannot be proven in PA.⊣
3 Level-three and -four Goodstein sequences
Again we represent natural numbers, with respect to a “base” x, by terms
$F_a^{(i)}(\ldots )$
built up from the Ackermann–Péter function, but whereas the iteration number i previously remained fixed throughout the Goodstein process, it too will now be subject to representation, and representing ordinals will now be more complex. In order to distinguish from the previous section, base-x representations will now be called “base-x normal forms.” There will again be two kinds, according as whether or not the subscript a is hereditarily decomposed. We concentrate on the case where it is (so decomposed) and call this the level-four Goodstein process. This yields an independence result for ATR
$_0$
, the subsystem of second order arithmetic commonly regarded as codifying predicative methods. The other (level-three) case, in which the a’s remain as fixed numerals, gives an independence from
$\Sigma ^1_1$
-DC
$_0$
, but this will follow easily. A later section then deals with a further generalization to ID
$_1$
, the theory of uniterated inductive definability.
Definition 3.1. For any fixed
$x \ge 2$
, a base-x normal form is a term
$F_a^{(r)}(b)$
where
$a, b, r$
are themselves base-x normal forms, r is numerically less than b, and b is either x or a term
$F_c^{(s)}(d)$
where
$a<c$
.
If
$F_a^{(r)}(b)$
is a base-x normal form with numerical value m, we say that m has base-x normal form
$F_a^{(r)}(b)$
and write
$m =_{xNF} F_a^{(r)}(b)$
.
A weak base-x normal form is one in which the subscripts
$a, c$
are numerals (independent of x).
Lemma 3.2. Base-x normal forms are unique.
Proof Whereas level-one and level-two representations were, from their construction, easily seen to be unique, it is not quite the case for normal forms, and so a more detailed proof is given.
Suppose m has two different normal forms
$F_a^{(r)}(b)$
and
$F_c^{(s)}(d)$
. We derive a contradiction, assuming inductively that the result already holds for numbers less than m. (Identity between F-terms is denoted
$t_1 \equiv t_2$
and numerical equality/inequality are denoted
$t_1 = t_2$
/
$t_1 < t_2$
.)
If, numerically,
$a<c$
(and similarly with roles reversed if
$c<a$
) we may unravel the recursive definition of
$F_c^{(s)}(d)$
to
$F_a^{(s_i)}( \cdots F_{c-1}^{(s_1-1)}(F_c^{(s-1)}(d))\cdots )$
where
$s_i = d_i = \cdots F_{c-1}^{(s_1-1)}(F_c^{(s-1)}(d))\cdots $
. Then, by cancelling the outermost occurrence of
$F_a$
, we obtain, using the induction hypothesis, two identical base-x normal forms:
$F_a^{(r-1)}(b)\,\equiv \, F_a^{(s_i -1)}(d_i)$
. Hence
$r = s_i = d_i = b$
and this contradicts the demand of the normal form
$F_a^{(r)}(b)$
that
$r < b$
.
Therefore a and c are identical and m has the two normal forms
$F_a^{(r)}(b)$
and
$F_a^{(s)}(d)$
. If, say,
$r<s$
, then we can cancel r occurrences of
$F_a$
to obtain
$b \equiv F_a^{(s-r)}(d)$
, but this contradicts the demand that the term b does not begin with any occurrences of
$F_a$
. Similarly we cannot have
$s<r$
. Hence
$r \equiv s$
and m has the two normal forms
$F_a^{(r)}(b)$
and
$F_a^{(r)}(d)$
. Cancelling
$F_a^{(r)}$
from both leaves
$b=d$
. Thus by the induction hypothesis,
$b \equiv d$
, so the normal forms are identical.⊣
Lemma 3.3. If
$m =_{xNF} F_a^{(r)}(b)$
then its predecessor in base x is
$$ \begin{align*} m - 1 =_{xNF} F_0^{(r_a -1)}(\cdots F_{a-2}^{(r_2 -1)}(F_{a-1}^{(r_1-1)}(F_a^{(r_0-1)}(b_0))\cdots)\end{align*} $$
where
$r_0 \equiv r$
,
$b_0 \equiv b$
,
$r_{i+1} \equiv b_{i+1}$
and
$b_{i+1} \equiv F_{a-i}^{(r_i -1)}(b_i)$
.
Proof This follows by unravelling the recursive definition of
$F_a^{(r)}(b)$
as
$F_a^{(r)}(b) = F_a(F_a^{(r-1)}(b)) = F_{a-1}^{(r_1)}(F_a^{(r-1)}(b))= F_{a-1}^{(r_1)}(b_1) \cdots $
etc., finally cancelling one
$F_0$
.⊣
Lemma 3.4. For any base-x normal form t, let
$t^{\prime }$
be the result of updating the base x to
$x+1$
throughout. Then
$t^{\prime }$
is a base-
$x+1$
normal form. Furthermore
$(t-1)^{\prime } < t^{\prime }$
hence
$t_1 < t_2$
implies
$t_1^{\prime } < t_2^{\prime }$
.
Proof Proceed by induction on the numerical value of t. If
$t \equiv F_a^{(r)}(b)$
then
$t^{\prime } \equiv F_{a^{\prime }}^{(r^{\prime })}(b^{\prime })$
. The induction hypothesis gives: (i) assuming
$F_c$
to be the leading term in b,
$a<c$
implies
$a^{\prime } < c^{\prime }$
; and (ii) if
$r < b$
then
$r^{\prime }< b^{\prime }$
. Thus
$t^{\prime }$
is in base-
$x+1$
normal form.
The base-x predecessor of t is, as above,
$$ \begin{align*} t-1 \; \equiv \; F_0^{(r_a -1)}(\cdots F_{a-2}^{(r_2 -1)}(F_{a-1}^{(r_1-1)}(F_a^{(r-1)}(b)))\cdots) \, .\end{align*} $$
Updating the base from x to
$x+1$
then yields:
$$ \begin{align*}(t-1)^{\prime} \,\equiv \,F_0^{(r_a -1)^{\prime}}(\cdots F_{(a-2)^{\prime}}^{(r_2 -1)^{\prime}}(F_{(a-1)^{\prime}}^{(r_1-1)^{\prime}}(F_{a^{\prime}}^{(r-1)^{\prime}}(b^{\prime})))\cdots),\end{align*} $$
whereas, by unravelling a steps in the recursive definition of
$t^{\prime }$
, one obtains
$$ \begin{align*} t^{\prime} \, = \, F_{a^{\prime}-a}^{(r^{\prime}_{a})}(\cdots F_{(a^{\prime}-2)}^{(r^{\prime}_2 -1)}(F_{(a^{\prime}-1)}^{(r^{\prime}_1-1)}(F_{a^{\prime}}^{(r^{\prime}-1)}(b^{\prime})))\cdots)\, .\end{align*} $$
Now comparing these two numerically, starting from the right-hand end, we have by induction,
$(r-1)^{\prime } \le (r^{\prime }-1)$
. Then
$(a-1)^{\prime } \le (a^{\prime }-1)$
and
$(r_1 -1)^{\prime } \le (r^{\prime }_1-1)$
. Therefore as
$F_a^{(r)}(b)$
is increasing in each variable,
$$ \begin{align*}F_{(a-1)^{\prime}}^{(r_1-1)^{\prime}}(F_{a'}^{(r-1)'}(b')) \,\le \,F_{(a'-1)}^{(r^{\prime}_1-1)}(F_{a'}^{(r'-1)}(b')).\end{align*} $$
Similarly
$F_{(a-2)'}^{(r_2 -1)'}(F_{(a-1)'}^{(r_1-1)'}(F_{a'}^{(r-1)'}(b')))$
is numerically less than or equal to
$F_{(a'-2)}^{(r^{\prime }_2 -1)}(F_{(a'-1)}^{(r^{\prime }_1-1)}(F_{a'}^{(r'-1)}(b')))$
. Continuing in this way one finally obtains
$$ \begin{align*}(t-1)' \,\equiv \,F_0^{(r_a -1)'}(\cdots) \, \le \, F_{a'-a}^{(r^{\prime}_{a}-1)}(\cdots) \, < \, t' \, .\end{align*} $$
This completes the proof.⊣
3.1 Ordinal assignment, tree ordinals
The level-four Goodstein process is, given m represented in base-x normal form:
Update the base to
$x+1$
, and subtract
$1$
(in base
$x+1$
).
Then continue updating the base and subtracting
$1$
.
The sequence obtained is here denoted
$\{A_k(x; m)\}_k$
. Termination:
$$ \begin{align*}\forall m \forall x \ge 2 \exists k (A_k(x;m) =0)\end{align*} $$
will be shown independent of ATR
$_0$
by a new ordinal assignment
$\textit{ord}_x(m)$
.
By ordinals we mean (countable) tree ordinals generated inductively by the rules: (i)
$0$
is a tree ordinal; (ii) if
$\beta $
is a tree ordinal then so is
$\beta +1$
(coded, for instance, as
$\beta \cup \{ \beta \}$
); (iii) if, for each natural number i,
$\lambda _i$
is a tree ordinal, then the sequence
$\lambda = \langle \lambda _i \rangle _{i\in N}$
is also a tree ordinal, in which case we write
$\lambda = \mathop {\mathrm {sup}}_i \lambda _i$
and call
$\lambda $
a “limit.” Thus tree ordinals are partially ordered by the well-founded “subtree” relation
$\prec $
and each limit comes equipped with a specified approximating sequence. Every tree ordinal clearly represents a countable ordinal as its set-theoretic rank, and different limits with the same rank simply correspond to different choices of approximating sequence. Such approximating sequences may not always be increasing “fundamental sequences” in the strict sense, however the “structured” ones singled out below will be.
Definition 3.5 Structuredness
-
1.
$P_x$
is Cichon’s [Reference Cichon10] predecessor:
$P_x(0) = 0, \; P_x(\beta +1) = \beta , \; P_x(\lambda ) = P_x (\lambda _x)$
. Thus if
$\alpha \not = 0$
then
$P_x(\alpha )$
is the immediate predecessor of the first successor encountered in the descending sequence
$\alpha \succ \alpha _{x} \succ \alpha _{x,x} \succ \cdots \;$
. -
2.
$\alpha [x] = \{\,P_x^{(i)}(\alpha )\,\}_{i>0}$
. -
3.
$\alpha $
is said to be structured if for every limit
$\lambda \preceq \alpha $
and every x,
$\lambda _x \in \lambda [x+1]$
.
Note. In the sense of Buchholz et al. [Reference Buchholz, Cichon and Weiermann7],
$\alpha [x]$
consists of those predecessors of
$\alpha $
with “norm”
$< x$
.
Lemma 3.6. For every structured tree ordinal
$\alpha $
,
$\alpha [0]\subseteq \alpha [1]\subseteq \alpha [2]\subseteq \cdots $
and furthermore,
$\beta \prec \alpha $
if and only if
$\beta \in \alpha [n]$
for some n. Thus the well-ordering
$\{\beta :\beta \prec \alpha \}$
is the direct union of the finite embeddings
$\alpha [x] \hookrightarrow \alpha [x+1]$
.
Proof See [Reference Fairtlough, Wainer and Buss12, Reference Schwichtenberg and Wainer17] and Aguilera et al. [Reference Aguilera, Freund, Rathjen and Weiermann2].⊣
Definition 3.7. Extend
$F_a(b)$
to a tree-ordinal function
$\chi _\alpha (\beta )$
by defining:
$$ \begin{align*} \chi_0(\beta) \, = \, \beta +1, \;\;\;\; \chi_{\alpha +1}(\beta) \, = \, \chi_{\alpha}^{(\beta)}(\beta), \; \;\;\; \chi_{\lambda}(\beta) \, = \, \mathop{\mathrm{sup}}_i \chi_{\lambda_i}(\beta)\, .\end{align*} $$
We choose
$\omega $
to be the identity sequence
$\mathop {\mathrm {sup}}_i i$
, and the iterate
$\chi _{\alpha }^{(\gamma )}(\beta )$
is defined to be
$\beta $
if
$\gamma =0$
,
$\chi _\alpha (\chi _{\alpha }^{(\gamma -1)}(\beta ))$
if
$\gamma $
is a successor, and
$\mathop {\mathrm {sup}}_i \chi _\alpha ^{(\gamma _i)}(\beta )$
if
$\gamma $
is a limit.
Note.
$\chi $
preserves structuredness (as in e.g., [Reference Fairtlough, Wainer and Buss12, Reference Schwichtenberg and Wainer17] for different functions).
Definition 3.8. The Slow Growing hierarchy
$\{G_x(\alpha )\}$
is defined pointwise at each
$x\in N$
, over tree ordinals
$\alpha $
, by
$$ \begin{align*}G_x(0) = 0, \;\;\; G_x(\beta +1) = G_x(\beta) +1, \;\;\; G_x(\lambda) = G_x(\lambda_x)\; .\end{align*} $$
It is easy to see, by induction on
$\beta $
, that it preserves addition:
$G_x(\alpha + \beta ) = G_x(\alpha ) + G_x(\beta )$
and exponentiation:
$G_x(2^\beta ) = 2^{G_x(\beta )}$
where addition is defined continuously on tree ordinals by:
$\alpha + 0 = \alpha ,\, \alpha + (\beta +1) = (\alpha + \beta ) +1, \alpha + \lambda = \mathop {\mathrm {sup}}_i (\alpha + \lambda _i)$
, and exponentiation by:
$2^0 = 1, 2^{\beta +1} = 2^\beta + 2^\beta ,\, 2^\lambda = \mathop {\mathrm {sup}}_i 2^{\lambda _i}$
. In fact
$G_x$
homomorphically collapses “all” natural operations on tree ordinals onto their corresponding operations on numbers. See e.g., [Reference Fairtlough, Wainer and Buss12, Reference Schwichtenberg and Wainer17]. In particular, for countable tree ordinals
$\alpha $
it is immediate that
$$ \begin{align*}G_x P_x(\alpha) = G_x(\alpha) \mathbin{...} 1,\end{align*} $$
hence
$G_x(\alpha ) = |\, \alpha [x]\,|$
, the cardinality of the finite set
$\alpha [x]$
.
Lemma 3.9. For all countable tree ordinals
$\alpha $
,
$\beta $
,
$$ \begin{align*}G_x(\chi_\alpha(\beta)) = F_{G_x(\alpha)}(G_x(\beta)) \end{align*} $$
and for all
$\gamma $
,
$$ \begin{align*}G_x(\chi_\alpha^{(\gamma)}(\beta) = F_{G_x(\alpha)}^{(G_x(\gamma))}(G_x(\beta))\, .\end{align*} $$
Proof By induction on
$\alpha $
, we first show
$G_x(\chi _\alpha (\beta )) = F_{G_x(\alpha )}(G_x(\beta ))$
:
-
1.
$G_x(\chi _0(\beta )) = G_x(\beta +1) = G_x(\beta ) +1 = F_0(G_x(\beta )) $
. -
2.
$G_x(\chi _{\alpha +1}(\beta )) = G_x(\chi _{\alpha }^{(\beta )}(\beta )) = F_{G_x(\alpha )}^{(G_x(\beta ))}(G_x(\beta )) = F_{G_x(\alpha )+1}(G_x(\beta )) = F_{G_x(\alpha +1)}(G_x(\beta ))$
. -
3.
$G_x(\chi _\lambda (\beta )) = G_x(\chi _{\lambda _x}(\beta )) = F_{G_x(\lambda _x)}(G_x(\beta )) = F_{G_x(\lambda )}(G_x(\beta ))$
.
It is now easy to check, by induction on
$\gamma $
, that
$G_x(\chi _\alpha (\beta )) = F_{G_x(\alpha )}(G_x(\beta ))$
implies
$G_x(\chi _\alpha ^{(\gamma )}(\beta ) = F_{G_x(\alpha )}^{(G_x(\gamma ))}(G_x(\beta ))$
. The successor case is:
$G_x(\chi _\alpha ^{(\gamma +1)}(\beta )) =$
$G_x(\chi _\alpha (\chi _\alpha ^{(\gamma )}(\beta ))) = F_{G_x(\alpha )}(G_x(\chi _\alpha ^{(\gamma )}(\beta ))) = F_{G_x(\alpha )}(F_{G_x(\alpha )}^{(G_x(\gamma ))}(G_x(\beta ))) =$
$F_{G_x(\alpha )}^{(G_x(\gamma )+1)}(G_x(\beta )) = F_{G_x(\alpha )}^{(G_x(\gamma +1))}(G_x(\beta ))$
. The other cases are immediate.⊣
The next lemma shows that the numerical level-four Goodstein process can be exactly mimicked by a parallel process on tree ordinals—namely repeated application of
$P_{x+1}$
,
$P_{x+2}$
,
$P_{x+3}$
…This is exactly analogous to the previous situation at level-two, which relies upon repeated applications of
$Q_{x+1}$
,
$Q_{x+2}$
,
$Q_{x+3}$
…The difference between the two processes lies in the different forms of recursion defining the Hardy function. One “unravels” applications of successor, whereas the other “accumulates” them:
$$ \begin{align*} (i) \;\; H_\alpha(x) = H_{Q_x(\alpha)}(x) +1\,. \;\;\; (ii) \;\; H_\alpha(x) = H_{P_x(\alpha)}(x+1) \,.\end{align*} $$
Definition 3.10. Given
$m =_{xNF} F_a^{(r)}(b)$
, let
$\textit{ord}_x(m)$
denote the structured tree ordinal
$\chi _\alpha (\beta )$
obtained by lifting x to
$\omega $
as in Definition 3.7. Note that by Lemma 3.9,
$G_x(\textit{ord}_x(m)) = m$
.
Lemma 3.11. For all base-x normal forms
$t \equiv F_a^{(r)}(b)$
:
$$ \begin{align*}\textit{ord}_x(t-1) = P_x(\textit{ord}_x(t)) \; .\end{align*} $$
Proof Proceeding by induction on the numerical value of t, with a sub-induction on the value of a, we have (as in Lemma 3.3):
$$ \begin{align*} t-1 \; \equiv \; F_0^{(r_a -1)}(\cdots F_{a-2}^{(r_2 -1)} (F_{a-1}^{(r_1-1)}(F_a^{(r-1)}(b)))\cdots) \, .\end{align*} $$
Therefore, suppressing the “x” from
$P_x$
and
$ord_x$
,
$$ \begin{align*}\textit{ord}(t-1) = \chi_0^{(P \textit{ord}(r_a))}(\cdots \chi_{PP\textit{ord}(a)}^{(P \textit{ord}(r_2))} (\chi_{P\textit{ord}(a)}^{(P \textit{ord}(r_1))} (\chi_{\textit{ord}(a)}^{(P\textit{ord}(r))}(\textit{ord}(b)))) \cdots)\, .\end{align*} $$
We claim this is
$P(\textit{ord}(t))$
as required. For, writing
$\beta = \textit{ord}(b)$
,
$\alpha = \textit{ord}(a)$
,
$\rho = \textit{ord}(r)$
,
$\rho _i = \textit{ord}(r_i)$
and using the induction hypothesis and the recursion equations,
$$ \begin{align*}\begin{array}{ll} P( ord_x t)\, &= \, P(\chi_\alpha^{(\rho)}(\beta))\\ &= \, P(\chi_{P\alpha}^{(\rho_1)} (\chi_\alpha^{(P \rho))}(\beta)))\\ &= \, P(\chi_{PP\alpha}^{(\rho_2)} (\chi_{P\alpha}^{(P(\rho_1))} (\chi_\alpha^{(P \rho))}(\beta)))\\ &= \, \cdots \\ &= \, P(\chi_{0}^{(\rho_a)}( \cdots (\chi_{PP\alpha}^{(P\rho_2)} (\chi_{P\alpha}^{(P(\rho_1))} (\chi_\alpha^{(P \rho))}(\beta)))) \cdots )\\ &= \, \chi_{0}^{(P(\rho_a))}( \cdots (\chi_{PP\alpha}^{(P\rho_2)} (\chi_{P\alpha}^{(P(\rho_1))} (\chi_\alpha^{(P \rho))}(\beta)))) \cdots ) \end{array} \end{align*} $$
and this last expression is just
$\textit{ord}_x(t-1)$
.⊣
Theorem 3.12.
-
1. The
$\Pi ^0_2$
sentence
$\forall n\forall x\geq 2\exists k(A_{k}(x;n)=0)$
follows from transfinite induction up to the first strongly critical ordinal
$\Gamma _0$
and is independent of
${{\textrm {ATR}}}_{0}$
. -
2. Similarly, termination of all Goodstein sequences based on weak base-x normal forms follows from transfinite induction up to the first primitive recursively closed ordinal
$\phi _\omega (0)$
and is independent of
$\Sigma ^{1}_{1}{{\textrm {-DC}}}_{0}$
.
Proof For
$A_k (x;m)$
the Goodstein process is, starting with the base-x normal form representation of m, and using
$'$
to denote update of base:
$$ \begin{align*} A_k (x;m)\; = \; ( \cdots (((m'-1)'-1)'-1) \cdots )'-1 \,. \end{align*} $$
Beginning with
$m =_{xNF} t$
, let
$\alpha = \textit{ord}_x(m)$
. The first step of the process is to update the base x to
$x+1$
. Another way to think of this is to do
$x:= \omega $
, then
$\omega := x+1$
. Therefore
$\textit{ord}_{x+1}(m') = \textit{ord}_{x}(m) = \alpha $
and
$m' = G_{x+1}(\alpha )$
by Lemma 3.9. The first step is then completed by subtracting
$1$
, using Lemma 3.11 thus:
$m'-1 = G_{x+1}(\textit{ord}_{x+1}(m'-1)) = G_{x+1}(\, P_{x+1} (\alpha )\, )$
. In the same way, with
$\alpha _1 =P_{x+1}(\alpha )$
, the second step yields
$\textit{ord}_{x+2}((m'-1)') = \textit{ord}_{x+1}(m'-1)$
and
$(m'-1)'-1 = G_{x+2}(\textit{ord}_{x+2}((m'-1)'-1)) = G_{x+2}(\, P_{x+2}(\textit{ord}_{x+2}((m'-1)'))\,) = G_{x+2}(\, P_{x+2}(\alpha _1)\,) = G_{x+2}(\, P_{x+2}P_{x+1} (\alpha )\, )$
. Repeating gives
$$ \begin{align*} A_{k}(x;m)\, = \, G_{x+k}(\, P_{x+k}\cdots P_{x+2} P_{x+1}(\alpha)\,)\, .\end{align*} $$
That the process terminates in
$A_{k}(x;m) = 0$
is now easily seen to be provable by induction up to
$\alpha = \textit{ord}_x(t)$
.
On the other hand, assuming that the process terminates in
$0$
, it follows that, with
$\alpha = \textit{ord}_x(t)$
,
$$ \begin{align*} H_{\alpha}(x+1) \, = \, \mbox{least}\; x+k \;\mbox{such that}\; P_{x+k}\cdots P_{x+2} P_{x+1}(\alpha)=0 \end{align*} $$
is defined. But this is the Hardy function which, as
$\alpha $
ranges over the provable ordinals of a theory, dominates all the provably recursive functions of it. See, for example, [Reference Fairtlough, Wainer and Buss12, Reference Schwichtenberg and Wainer17, Reference Weiermann18].
Now the set-theoretic ordinal ranks of the (structured) tree ordinals named by
$\chi $
can be compared with those in the Veblen hierarchy
$\phi $
of normal functions, equipped with fundamental sequences as in Feferman [Reference Feferman13]. Lemma 4.11, giving the comparison, is postponed to the end of the paper because it deals also with a more general case needed in the final section. But for
$\omega \preceq \beta $
one has
$$ \begin{align*}\|\, \phi_\alpha(\beta) \,\| \;\le \;\| \,\chi_{\alpha +2}(\omega \cdot\beta)\,\|\, .\end{align*} $$
It follows that the ordinals, named by the above
$\chi $
-terms
$\textit{ord}_x(t)$
, range over the ordinals less than the first strongly critical ordinal
$\Gamma _0$
. So induction up to
$\Gamma _0$
proves that every level-four Goodstein sequence terminates in zero. Conversely, termination of every Goodstein sequence implies that
$H_\gamma $
is totally defined for every
$\gamma \le \Gamma _0$
, and therefore it cannot be proven in
${\textrm {ATR}}_{0}$
. In particular, Lemma 4.11 gives
$\|\phi _\alpha (\omega )\| \le \| \chi _{\alpha +2} (\omega ^2)\| \le \| \chi _{\alpha +2} (\chi _{\alpha +2}(\omega )) \|$
so by iterating the operation
$\alpha \mapsto \chi _{\alpha +2}^{(2)}(\omega )$
, starting with
$\alpha = 1$
, the sequence
$\{\gamma _x \}_x$
so obtained is essentially the “standard” fundamental sequence to
$\Gamma _0$
. But
$\gamma _x = \textit{ord}_x (m_x)$
where
$m_x$
is the result of iterating x times the numerical operation
$a \mapsto F_{a+2}^{(2)}(x)$
. Thus
$H_{\textit{ord}_x (m_x)}(x+1) \ge H_{\Gamma _0}(x)$
.
If one works instead with weak normal forms then only
$\chi _n$
-terms are used where
$n \in N$
. Thus the ordinals named are just those below the first primitive recursively closed ordinal. Termination of Goodstein sequences is therefore independent of
$\Sigma ^{1}_{1}{{\textrm {-DC}}}_{0}$
by Cantini [Reference Cantini9].⊣
4 Extension to ID
$_1$
The final base-x representation we consider is constructed with respect to the Fast-Growing, Extended Grzegorczyk hierarchy
$\{F_{a}\}_{a \prec \varepsilon _0}$
, rather than the Ackermann–Péter F. Here, the components a of base-x representations are not integers, but Cantor normal forms to the base
$\omega $
. Clearly this requires the definition of
$F_a(b)$
to be extended to limits a with standard fundamental sequences
$i \mapsto a_i$
. The simplest way to do this is by diagonalization:
$$ \begin{align*} F_a(b) \, = \, F_{a_b}(b) \, .\end{align*} $$
Unravelling this, one sees that
$$ \begin{align*}F_a(b) \, = \, F_{P_b(a)}^{(b)}(b)\end{align*} $$
where
$P_b$
is Cichon’s predecessor (as in Definition 3.5). It easily follows that
$$ \begin{align*} a \in c[b] \Rightarrow F_a(b) < F_c(b). \end{align*} $$
The base-x normal form of m, defined below, is constructed as follows, where
$\omega _k$
is the
$k+1$
-th member of the fundamental sequence to
$\varepsilon _0$
given by
$\omega _0 = 0$
and
$\omega _{k+1} = \omega ^{\omega _k}$
. First choose k so that
$F_{\omega _k}(x) \le m < F_{\omega _{k+1}}(x)$
. If
$m = F_{\omega _k}(x)$
then this term is the base-x normal form of m. If not choose a to be the least element of
$\omega _{k+1}[x]$
such that for some
$i < x$
,
$F_a^{(i)}(x) \le m < F_a^{(i+1)}(x)$
. If
$m = F_a^{(i)}(x)$
then this term is the base-x normal form of m. If not set
$x_1 = F_a^{(i)}(x)$
and choose
$a_1$
to be the least element of
$a[x_1]$
such that for some
$i_1 < x_1$
,
$F_{a_1}^{(i_1)}(x_1) \le m < F_{a_1}^{(i_1+1)}(x_1)$
. If
$m = F_{a_1}^{(i_1)}(x_1)$
then this term is the base-x normal form of m. Otherwise continue this process until, at some stage n,
$m = F_{a_n}^{(i_n)}(x_n)$
.
Definition 4.1. For fixed
$x \ge 2$
, a base-x normal form relative to the Fast Growing hierarchy is either a numeral less than x or a term
$F_a^{(r)}(b)$
where: a is a Cantor normal form to base
$\omega $
;
$\,b, r$
and all numerical coefficients in a are themselves expressed as base-x normal forms (rel. to the FG hierarchy);
$\,r$
is numerically less than b; and either (i) b is x and for some k,
$\omega _k \preceq a \in \omega _{k+1}[x]$
or (ii) b is a term
$F_c^{(s)}(d)$
where
$a \in c[b]$
(that is
$a = P_n^i(c)$
for some
$i>0$
where n is the numerical value of the normal form b).
Note. The base-x normal form of a number
$m \ge x$
(rel. to the FG hierarchy) is therefore expressed as
$$ \begin{align*} m =_{xNF} F_{a_n}^{(r_n)}(\cdots F_{a_2}^{(r_2)}(F_{a_1}^{(r_1)}(F_{a_0}^{(r_0)}(x)))\cdots), \end{align*} $$
where
$a_{i+1} \in a_i [b_i]$
and
$b_i \equiv F_{a_i}^{(r_i)}(\cdots F_{a_0}^{(r_0)}(x)\cdots )$
. The requirements on
$r_i$
imply that
$F_{a_0}^{(r_0)}(x) \le m < F_{a_0}^{(r_0 +1)}(x) \le F_{a_0}^{(x)}(x) \le F_{\omega _{k+1}}(x)$
.
Lemma 4.2. Base-x normal forms (rel. to the FG hierarchy) are unique.
Proof The proof runs much as before, by induction on numerical value. Suppose m has two base-x normal forms
$$ \begin{align*} m =_{xNF} F_{a_n}^{(r_n)}(\cdots F_{a_2}^{(r_2)}(F_{a_1}^{(r_1)}(F_{a_0}^{(r_0)}(x))\cdots) \, ,\end{align*} $$
$$ \begin{align*} m =_{xNF} F_{c_\ell}^{(s_\ell)}(\cdots F_{c_2}^{(s_2)}(F_{c_1}^{(s_1)}(F_{c_0}^{(s_0)}(x))\cdots) \, .\end{align*} $$
We show, by induction on
$i \le \min (n, \ell )$
that
$b_i$
and
$d_i$
are identical, where
$$ \begin{align*} b_i \equiv F_{a_i}^{(r_i)}(\cdots F_{a_2}^{(r_2)}(F_{a_1}^{(r_1)}(F_{a_0}^{(r_0)}(x)))\cdots) \, ,\end{align*} $$
$$ \begin{align*} d_i \equiv F_{c_i}^{(s_i)}(\cdots F_{c_2}^{(s_2)}(F_{c_1}^{(s_1)}(F_{c_0}^{(s_0)}(x)))\cdots) \, .\end{align*} $$
If
$a_0 \in \omega _{k+1}[x]$
and
$c_0 \in \omega _{k' +1}[x]$
and
$k<k'$
is assumed, then by the previous note,
$m < F_{\omega _{k+1}}(x) \le F_{\omega _{k'}}(x) \le m$
, a contradiction. Similarly if
$k' < k$
. Hence
$k = k'$
and then both
$a_0$
and
$c_0$
lie in the linearly ordered set
$\omega _{k+1}[x]$
. If
$a_0 \prec c_0$
then, as above,
$m < F_{a_0}^{(x)}(x) \le F_{c_0}(x) \le m$
, again a contradiction, and similarly if
$c_0 \prec a_0$
. They are therefore identical, and hence
$b_0 \equiv F_{a_0}^{(r_0)}(x)$
and
$d_0 \equiv F_{c_0}^{(s_0)}(x)$
are identical, for if
$r_0 \not \equiv s_0$
then the values of m would be different (again by the same argument).
For the induction step, assume
$b_i$
and
$d_i$
are identical, where
$i < \min (n, \ell )$
. Then
$b_{i+1} \equiv F_{a_{i+1}}^{(r_{i+1})}(b_i)$
where
$a_{i+1} \in a_i[b_i]$
and
$d_{i+1} \equiv F_{c_{i+1}}^{(s_{i+1})}(b_i)$
where, also,
$c_{i+1} \in a_i[b_i]$
. Since
$a_{i+1}$
and
$c_{i+1}$
are both
$P_{b_i}$
-predecessors of
$a_i$
they may be compared. If
$a_{i+1} \prec c_{i+1}$
then we obtain a contradiction:
$$ \begin{align*} m < F_{a_{i+1}}^{(b_i)}(b_i) \le F_{c_{i+1}}(b_i) \le m \end{align*} $$
and similarly if
$c_{i+1} \prec a_{i+1}$
. Hence
$a_{i+1} = c_{i+1}$
and consequently
$r_{i+1} \equiv s_{i+1}$
. Thus
$b_{i+1}$
and
$d_{i+1}$
are identical and this completes the induction.
It now only remains to note that since the two normal forms of m are identical up to length
$\min (n, \ell )$
, neither can be longer than the other (otherwise their values would be different). Hence they are identical.⊣
Lemma 4.3. If
$m =_{xNF} F_a^{(r)}(b)$
then for some n,
$$ \begin{align*} m - 1 =_{xNF} F_0^{(r_n -1)}(\cdots F_{a_2}^{(r_2 -1)}(F_{a_1}^{(r_1-1)}(F_a^{(r-1)}(b)))\cdots),\end{align*} $$
where
$r_{i+1} \equiv b_{i+1}$
,
$b_{i+1} \equiv F_{a_i}^{(r_i -1)}(b_i)$
and
$a_{i+1} = P_{b_{i+1}}(a_{i})$
.
Proof As before, this follows by unravelling the outermost
$F_a$
in the recursive definition of
$F_a^{(r)}(b)$
and finally subtracting
$1$
by canceling one
$F_0$
.⊣
Lemma 4.4. For any base-x normal form t (rel. to the FG hierarchy) let
$t'$
be the result of updating the base x to
$x+1$
throughout. Then
$t'$
is a base-
$x+1$
normal form. Furthermore,
$(t-1)' < t'$
hence
$t_1 < t_2$
implies
$t_1' < t_2'$
.
Proof Proceed by induction on the numerical value of t. If
$t \equiv F_a^{(r)}(b)$
then
$t' \equiv F_{a'}^{(r')}(b')$
where
$a'$
is the result of updating the base throughout all the coefficients in the Cantor normal form a.
Claim, to be proven at the end:
$a \in c[b]$
implies
$a' \in c'[b']$
.
Now if
$b\equiv x$
then
$\omega _k \preceq a \in \omega _{k+1}[x]$
for some k, so by the claim,
$\omega _k \preceq a' \in \omega _{k+1}[x+1]$
because
$\omega _k$
is an exponential stack with no coefficients other than
$1$
, which is
$< x$
. If
$b \not \equiv x$
and
$F_c$
is the leading term in b then
$a \in c[b]$
and so
$a' \in c'[b']$
. Also, if
$r < b$
then
$r' < b'$
by the induction hypothesis. Since the normal form requirements are met after update,
$t'$
is in base-
$x+1$
normal form.
The base-x predecessor of t is as in the lemma above:
$$ \begin{align*} t-1 \, \equiv \, F_0^{(r_n -1)}(\cdots F_{a_2}^{(r_2 -1)}(F_{a_1}^{(r_1-1)}(F_a^{(r-1)}(b)))\cdots) \, .\end{align*} $$
Updating the base from x to
$x+1$
then yields:
$$ \begin{align*}(t-1)' \,\equiv \,F_0^{(r_n -1)'}(\cdots F_{(a_2)'}^{(r_2 -1)'}(F_{(a_1)'}^{(r_1-1)'}(F_{a'}^{(r-1)'}(b')))\cdots)\, .\end{align*} $$
However, applying the last lemma to
$t'$
gives, for an appropriate
$\ell $
,
$$ \begin{align*} t'-1 \, \equiv \, F_{0}^{((r')_{\ell}-1)}(\cdots F_{c_2}^{((r')_2 -1)}(F_{c_1}^{((r')_1-1)}(F_{a'}^{(r'-1)}(b')))\cdots)\end{align*} $$
where, by the induction hypothesis,
$r'-1 \ge (r-1)'$
. Therefore
$(b')_1 = F_{a'}^{(r'-1)}(b') \ge F_{a'}^{(r-1)'}(b') = (b_1)'$
. Hence
$(r')_1 \ge (r_1)'$
and
$a'[b^{\prime }_1] \supset a'[(b_1)']$
, so by the claim,
$c_1 = P_{(b')_1}(a')$
lies above
$(a_1)' = (P_{b_1}(a))'$
inside
$a'[(b')_1]$
. Consequently,
$(b')_2 = F_{c_1}^{((r')_1-1)}((b')_1) \ge F_{(a_1)'}^{(r_1-1)'}(b_1)') = (b_2)'$
, hence
$(r')_2 \ge (r_2)'$
and
$c_1[(b')_2] \supset (a_1)'[(b_2)']$
, so
$c_2 = P_{(b')_2}((a')_1)$
lies above
$(a_2)' = (P_{b_2}(a_1))'$
inside
$(a')_1[(b')_2]$
. Continuing in this way, one sees that
$c_{i+1} = P_{(b')_{i+1}}(c_{i})$
lies above
$(a_{i+1})' = (P_{b_{i+1}}(a_{i}))'$
inside
$c_{i}[(b')_{i+1}]$
. Thus
$\ell \ge n$
and the subterms of
$t'-1$
are correspondingly greater than or equal to the subterms of
$(t-1)'$
. Hence
$(t-1)' \le t'-1$
. It follows immediately that
$t_1 < t_2$
implies
$t_1' < t_2'$
.
Proof of the Claim
It is sufficient to show that
$(P_b(c))' = P_{b'}^{(i)}(c')$
for some
$i>0$
, where
$c = d + \omega ^e$
is a Cantor normal form to the base
$\omega $
, with numerical coefficients written in base-x normal form. Then
$$ \begin{align*} P_b(c) = d + \omega^{P_b(e)}\cdot (b-1) + \omega^{P_bP_b(e)} \cdot (b-1) + \cdots + (b-1)\end{align*} $$
and so
$$ \begin{align*} (P_b(c))' = d' + \omega^{(P_b(e))'}\cdot (b-1)' + \omega^{(P_bP_b(e))'} \cdot (b-1)' + \cdots + (b-1)'\, .\end{align*} $$
Inductively on c we may assume that each exponent
$(P_b(e))'$
,
$(P_bP_b(e))'$
etc. can be expressed as an iterate of
$P_{b'}$
applied to
$e'$
. Also
$(b-1)' \le b'-1$
by induction. Therefore, starting with
$c' = d' + \omega ^{e'}$
, one may reconstruct
$(P_b(c))'$
by iterating
$P_{b'}$
an appropriate number of times. This completes the proof.⊣
4.1 Goodstein sequences up to Bachmann–Howard
Definition 4.5. Definition 3.7 of the tree ordinal function
$\chi _\alpha (\beta )$
is now extended to elements
$\alpha $
of the third number-class, by addition of the following diagonalization clause in the case where
$\alpha $
is a “large” limit,
$\alpha = \mathop {\mathrm {sup}}\limits _{\xi }\alpha _\xi $
obtained by sequencing over all countable tree ordinals
$\xi $
:
$$ \begin{align*} \chi_\alpha(\beta)\, = \,\chi_{\alpha_\beta}(\beta)\, .\end{align*} $$
In [Reference Cichon and Wainer11, Reference Fairtlough, Wainer and Buss12, Reference Schwichtenberg and Wainer17] it is shown how
$G_x$
extends also to the third number class by means of the definition
$G_x(\mathop {\mathrm {sup}}\limits _\xi \alpha _\xi ) = \mathop {\mathrm {sup}}\limits _{i\in N} G_x(\alpha _i)$
. Thus for sequences
$<\alpha _\xi>$
which satisfy the “
$G_x$
-condition”:
$G_x(\alpha _\xi ) = G_x(\alpha _{G_x(\xi )})$
one has the so-called “separation property”:
$$ \begin{align*}G_x(\alpha_\xi) = G_x(\alpha)_{G_x(\xi)}\,.\end{align*} $$
Now choose
$\Omega = \mathop {\mathrm {sup}}\limits _\xi \xi $
in the third number class, and note that
$G_x(\Omega ) = \mathop {\mathrm {sup}}_i G_x(i) = \mathop {\mathrm {sup}}_i i = \omega $
. Then Cantor normal forms to base
$\Omega $
satisfy the
$G_x$
-condition, and so they are collapsed under
$G_x$
onto their corresponding Cantor normal forms to base
$\omega $
. Lemma 3.9 extends accordingly.
Lemma 4.6. For
$\alpha $
a countable tree ordinal, or an element of the third number class
$\prec \varepsilon _{\Omega +1}$
given by a Cantor normal form to the base
$\Omega $
,
$$ \begin{align*}G_x(\chi_\alpha(\beta)) = F_{G_x(\alpha)}( G_x(\beta)). \end{align*} $$
Proof The proof goes just as before in Lemma 3.9, by induction over
$\alpha $
in the second and third number class below
$\varepsilon _{\Omega +1}$
. The additional case, where
$\alpha $
is a large limit, is handled immediately because of the aforementioned separation property:
$$ \begin{align*} \begin{array}{ll} G_x (\chi_\alpha (\beta)) \, = \, G_x (\chi_{\alpha_\beta}(\beta)) \, &= \, F_{G_x(\alpha_\beta)}( G_x(\beta)) \\ &= \, F_{G_x(\alpha)_{G_x(\beta)}}( G_x(\beta)) \\ &= \, F_{G_x(\alpha)}( G_x(\beta)) \, .\end{array} \\[-36pt] \end{align*} $$
⊣
Definition 4.7. If t is a base-x normal form relative to the Fast Growing hierarchy, let
$\textit{ord}_x (t)$
be the tree ordinal obtained recursively by (i) changing F to
$\chi $
throughout, (ii) updating the base x to
$\omega $
throughout, and (iii) lifting each Cantor normal form
$a \prec \varepsilon _0$
to
$\alpha \prec \varepsilon _{\Omega +1}$
by replacing
$\omega $
with
$\Omega $
throughout, and each coefficient c with
$\textit{ord}_x(c)$
.
Note that by lemma 4.6,
$G_x$
reverses the “lifting” procedure from t to
$\textit{ord}_x(t)$
, that is
$G_x (\textit{ord}_x(t)) = t$
.
Lemma 4.8. If t is a base-x normal form relative to the Fast Growing hierarchy then
$$ \begin{align*} \textit{ord}_x(t-1) \, = \,P_x(\textit{ord}_x(t)) \, .\end{align*} $$
Proof (A more complex version of Lemma 3.11.) If
$t \equiv F_a^{(r)}(b)$
then
$\textit{ord}_x (t) = \chi _\alpha ^{(\rho )}(\beta )$
where
$\rho = \textit{ord}_x (r)$
,
$\beta = \textit{ord}_x (b)$
and
$\alpha \prec \varepsilon _{\Omega +1}$
is the lifted version of
$a \prec \varepsilon _0$
. (Since the base x is fixed we suppress it). We have (as in Lemma 4.3):
$$ \begin{align*} t - 1 \equiv F_0^{(r_n -1)}(\cdots F_{a_2}^{(r_2 -1)}(F_{a_1}^{(r_1-1)}(F_a^{(r_0-1)}(b_0)))\cdots)\end{align*} $$
where
$r_0 \equiv r$
,
$b_0 \equiv b$
,
$r_{i+1} \equiv b_{i+1}$
,
$b_{i+1} \equiv F_{a_i}^{(r_i -1)}(b_i)$
and
$a_0 = a$
,
$a_{i+1} = P_{b_{i+1}}(a_{i})$
. Proceeding by induction over the numerical value of t,
$$ \begin{align*}\textit{ord}(t-1) = \chi_0^{(P \textit{ord}(r_n))}(\cdots \chi_{\alpha_2}^{(P \textit{ord}(r_2))} (\chi_{\alpha_1}^{(P \textit{ord}(r_1))} (\chi_{\alpha}^{(P\textit{ord}(r))}(\textit{ord}(b)))) \cdots)\, .\end{align*} $$
Here,
$\alpha _{i+1}$
is the “lifted” version of
$a_{i+1} = P_{b_{i+1}}(a_{i})$
. It may be written as
$\alpha _{i+1} = P_{x, { ord}(b_{i+1})}(\alpha _{i})$
where
$P_{x,\xi }(\gamma )$
is the generalized Cichon predecessor, defined to be
$0$
if
$\gamma =0$
,
$\gamma -1$
if
$\gamma $
is a successor,
$P_{x, \xi }(\gamma _x)$
if
$\gamma $
is a small limit, and
$P_{x, \xi }(\gamma _\xi )$
if
$\gamma $
is a large limit. To see this, one easily notes (using the separation property) that
$G_x P_{x, \xi }(\gamma ) = P_{G_x(\xi )}(G_x(\gamma ))$
. Hence with
$\xi = \textit{ord}(b_{i+1})$
and
$\alpha _{i+1} = P_{x, { ord}(b_{i+1})}(\alpha _{i})$
we have
$G_x(\alpha _{i+1}) = P_{b_{i+1}}(a_{i}) = a_{i+1}$
as required. We informally denote
$\alpha _{i+1}$
as
$P \alpha _i$
. Then, writing
$\beta = \textit{ord}(b)$
,
$\rho = \textit{ord}(r)$
and using the induction hypothesis and the recursion equations,
$$ \begin{align*}\begin{array}{ll} P( ord_x t)\, &= \, P(\chi_\alpha^{(\rho)}(\beta))\\ &= \, P(\chi_{P\alpha}^{(\rho_1)} (\chi_\alpha^{(P \rho))}(\beta)))\\ &= \, P(\chi_{PP\alpha}^{(\rho_2)} (\chi_{P\alpha}^{(P(\rho_1))} (\chi_\alpha^{(P \rho))}(\beta))))\\ &= \, \cdots \\ &= \, P(\chi_{0}^{(\rho_n)}( \cdots (\chi_{PP\alpha}^{(P\rho_2)} (\chi_{P\alpha}^{(P(\rho_1))} (\chi_\alpha^{(P \rho))}(\beta))))\cdots ))\\ &= \, \chi_{0}^{(P(\rho_n))}( \cdots (\chi_{PP\alpha}^{(P\rho_2)} (\chi_{P\alpha}^{(P(\rho_1))} (\chi_\alpha^{(P \rho))}(\beta))))\cdots ) \end{array} \end{align*} $$
and this last expression is just
$\textit{ord}_x(t-1)$
.⊣
Definition 4.9. The Goodstein sequence relative to the Fast Growing hierarchy is denoted
$\{I_k(x;m)\}_{k \in N}$
where
$I_{0}(x;m)=m$
and if
$I_{k}(x;m)>0$
, then
$I_{k+1}(x;m)$
is the result of increasing the base by
$1$
and subtracting
$1$
.
Theorem 4.10. The
$\Pi ^0_2$
sentence
$\forall m\, \forall x\ge 2 \, \exists k \, (\,I_k(x; m) =0 \,)$
is (over PRA) a consequence of induction up to the Bachmann–Howard ordinal, and is independent of ID
$_1$
or parameter-free
$\Pi ^1_1$
-CA
$_0$
.
Proof This goes much as before. Take a number m with base-x normal form
$t \equiv F_a^{(r)}(b)$
. Then
$\textit{ord}_x(t)$
is the structured tree ordinal
$\chi _\alpha ^{(\rho )}(\beta )$
where, by Lemma 4.6,
$G_x(\alpha ) = a$
,
$G_x(\rho ) = r$
, and
$G_x(\beta ) = b$
. Thus
$I_0(x;m) = m = G_x(\textit{ord}_x(t))$
. Now the first step of the Goodstein process yields
$I_1(x;m) = m_1-1$
where
$m_1 =_{(x+1)NF} t'$
, the result of the first base-update. Thus
$t'$
has exactly the same structure as t, but with the base x increased to
$x+1$
throughout. So replacing either base by
$\omega $
yields the same tree ordinal; that is,
$\textit{ord}_x(t) = \textit{ord}_x(F_a^{(r)}(b)) = \chi _{\textit{ord}(a)}^{\textit{ord}(r)}(\textit{ord}(b)) = \chi _{\textit{ord}(a')}^{\textit{ord}(r')}(\textit{ord}(b')) = \textit{ord}_{x+1}(t')$
. Therefore
$$ \begin{align*} I_1(x; m) &= G_{x+1}(\textit{ord}_{x+1}(t'))-1 = G_{x+1}(\textit{ord}_{x}(t))-1\\ &= G_{x+1}( P_{x+1}(\textit{ord}_x(t))).\end{align*} $$
Updating the base again yields
$m_2 =_{(x+2)NF} (t'-1)' = G_{x+2}(\textit{ord}_{x+2}((t'-1)'))$
. But, as before,
$\textit{ord}_{x+2}((t'-1)') = \textit{ord}_{x+1}(t'-1)$
and this
$= P_{x+1}(\textit{ord}_{x+1}(t')))$
by Lemma 4.8. Therefore, since
$\textit{ord}_{x+1}(t') = \textit{ord}_{x}(t)$
, we have
$$ \begin{align*} I_2(x; m) = m_2 -1 = G_{x+2}(P_{x+1}(\textit{ord}_x(t)))- 1 = G_{x+2}(P_{x+2} P_{x+1}(\textit{ord}_x(t)))\, .\end{align*} $$
Repeating the process,
$$ \begin{align*} I_k(x;m) \, = \, G_{x+k} (\, P_{x+k} P_{x+k-1} \cdots P_{x+2} P_{x+1} (\textit{ord}_x(t)) \, )\, .\end{align*} $$
Transfinite induction up to
$\textit{ord}_x(t)$
now proves that the Goodstein process terminates in zero. Conversely, assuming that the Goodstein process does terminate, it follows that the Hardy function
$$ \begin{align*} H_{\textit{ord}_x(t)}(x+1) \, = \, \mbox{least } x+k \, \mbox{ s.t. } \, P_{x+k} P_{x+k-1} \cdots P_{x+2} P_{x+1} (\textit{ord}_x(t)) = 0 \end{align*} $$
is defined/computed.
As t ranges over all base-x normal forms relative to the fast growing hierarchy,
$\textit{ord}_x(t)$
ranges over the (set-theoretic) ordinals
$ < \mathop {\mathrm {sup}}_i \|\chi _{\Omega _i}(\omega ) \|$
where
$\Omega _0 = 0$
and
$\Omega _{i+1} = \Omega ^{\Omega _i}$
. But by the Ordinal Comparison Lemma 4.11 below,
$\|\phi _\alpha (0)\| \le \| \chi _{\alpha +2}^{(2)}(\omega ) \| $
, so with
$\alpha = \varepsilon _{\Omega +1}$
it follows that the Bachmann–Howard ordinal is
$\le \mathop {\mathrm {sup}}_i \|\chi _{\Omega _i +2}^{(2)}(\omega )\| = \mathop {\mathrm {sup}}_i \|\chi _{\Omega _{i+1}}(\omega ) \|$
. Hence the first order formula expressing termination of every Goodstein sequence (relative to the Fast Growing hierarchy) implies (modulo PRA) that
$\forall \gamma \preceq \mbox {the Bachmann--Howard ordinal } (\,H_\gamma \mbox {is totally defined })$
. It therefore cannot be proven in ID
$_1$
. In particular, choosing
$t \equiv F_{\omega _{x-1}}(x)$
we have
$\omega _{x-1} \in \omega _{x}[x]$
and so
$\textit{ord}_x(t) = \chi _{(\varepsilon _{\Omega +1})_{x-1}}(\omega )$
. Therefore as x varies,
$H_{\textit{ord}_x(t)}$
computes the Hardy function at the Bachmann–Howard ordinal itself.⊣
Lemma 4.11. Comparing the set-theoretic ranks of the tree ordinals
$\chi _\alpha (\beta )$
and
$\phi _\alpha (\beta )$
, we have, for infinite
$\beta $
:
$$ \begin{align*} \| \phi_\alpha(\beta) \| \le \| \chi_{\alpha +2}(\omega \cdot \beta) \| \, .\end{align*} $$
Proof In what follows we shall abbreviate
$\| \phi _\alpha (\beta ) \| \le \| \chi _{\alpha +2}(\omega \cdot \beta ) \|$
as
$\phi _\alpha (\beta ) \ll \chi _{\alpha +2}(\omega \cdot \beta )$
. Proceed by induction on
$\alpha \prec \varepsilon _{\Omega +1}$
, noting that for structured limits,
$ \lambda _i +1 \preceq \lambda _{i +1}$
.
If
$\alpha = 0$
then
$\phi _\alpha (\beta ) = \omega ^\beta \ll 2^{\omega \cdot \beta } = \chi _1^{(\omega \cdot \beta )}(1) \ll \chi _2(\omega \cdot \beta )$
.
If
$\alpha $
is a successor we may assume inductively that
$\phi _{\alpha -1}(\beta ) \ll \chi _{\alpha +1}(\omega \cdot \beta )$
. Since
$\chi _\alpha $
is positive and increasing, this is
$\ll \chi _{\alpha +1}(\omega \cdot 2^\beta ) = \chi _{\alpha +1}(\chi _1^\beta (\omega ))\ll \chi _{\alpha +1}(\chi _2(\beta ))$
if
$\omega \preceq \beta $
. Therefore
$\phi _{\alpha -1}(\beta )\ll \chi _{\alpha +1}^{(2)}(\beta )$
on infinite
$\beta $
and hence, with S the ordinal successor,
$$ \begin{align*}\phi_\alpha(\beta) = (\phi_{\alpha -1}^{(\omega)} \circ S)^{(\beta)}(0) \ll (\chi_{\alpha +1}^{(\omega)})^{(\beta)}(\beta) \ll \chi_{\alpha +1}^{(\omega\cdot\beta)}(\beta) \ll \chi_{\alpha +2}(\omega \cdot\beta) \, .\end{align*} $$
Similarly, if
$\alpha $
is a small limit, the induction hypothesis again gives
$$ \begin{align*}\phi_{\alpha}(\beta) &= (\mathop{\mathrm{sup}}_i \phi_{\alpha_i}^{(i)}\circ S)^{(\beta)}(0) \ll (\mathop{\mathrm{sup}}_i \chi_{\alpha_{i+2}}^{(i)}\circ S)^{(\beta)}(\beta) \ll (\chi_\alpha^{(\omega)})^{(\beta)}(\beta)\\ &\ll \chi_{\alpha +2}(\omega \cdot \beta).\end{align*} $$
If
$\alpha $
is a large limit then by structuredness
$\alpha _\gamma +1 \preceq \alpha _{\gamma +1}$
and so on infinite
$\gamma $
,
$\phi _{\alpha _\gamma }(0) \ll \chi _{\alpha _{\gamma } +2}(\gamma ) \ll \chi _{\alpha _{\gamma +2}}(\gamma )\ll \chi _{\alpha _{\gamma +2}}(\gamma +2) = \chi _\alpha (\gamma +2)\ll \chi _\alpha ^{(2)}(\gamma )$
. Therefore with
$\xi _\alpha (\gamma ) =_{\mbox {def}} \phi _{\alpha _\gamma }(0)$
,
$$ \begin{align*} \phi_\alpha(\beta) = (\xi_\alpha^{(\omega)} \circ S)^{(1+\beta)}(0) \ll (\chi_\alpha^{(\omega)})^{(\beta)}(\beta) \ll (\chi_\alpha^{(\omega\cdot\beta)}(\beta) \ll \chi_{\alpha +2}(\omega \cdot\beta)\, .\end{align*} $$
For an alternative ordinal comparison involving
$\chi $
see Aguilera et al. [Reference Aguilera, Freund, Rathjen and Weiermann2].⊣
