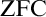1 Introduction
In this paper, we introduce an axiomatic framework for class forcing over models of second order set theory, that avoids the usual technicalities connected with any usual standard setup for (class) forcing, in particular the concepts of genericity, forcing names and their evaluations, and the recursively defined forcing predicates. Instead, we provide a natural collection of axioms, and show that they induce the common standard concepts: that is, they allow us to derive the usual concept of genericity, the usual recursive definitions of forcing predicates, an analogue of the structure of names for elements of generic extensions and their evaluations, thus exactly the same forcing extensions, and also the preservation of the axioms of set theory to our extensions. The aim of this paper is essentially twofold. First, it is to provide an interesting new viewpoint on what is probably the most important technical tool in modern set theory. Second, it is supposed to provide a self-contained way of introducing (class) forcing axiomatically. The only point in the paper where it is strictly necessary to refer to some sort of standard (class) forcing setup is when we briefly argue for our axioms to actually be consistent (modulo the axioms of set theory) in Section 7, after we introduce our final axiom (8). We will consider various base theories (Gödel–Bernays set theory
![]() $\mathrm {GB}$
, Kelley–Morse set theory
$\mathrm {GB}$
, Kelley–Morse set theory
![]() $\mathrm {KM}$
, and some of their variants), and also deduce the somewhat simpler axioms for the special case of set forcing over
$\mathrm {KM}$
, and some of their variants), and also deduce the somewhat simpler axioms for the special case of set forcing over
![]() $\mathrm {ZFC}$
and some of its weakenings in Section 8. In this introductory section, we want to provide a rough description of our axiomatic framework, which will be followed with formal definitions in Sections 2–7.
$\mathrm {ZFC}$
and some of its weakenings in Section 8. In this introductory section, we want to provide a rough description of our axiomatic framework, which will be followed with formal definitions in Sections 2–7.
We require forcing extensions to be based on preordersFootnote
1
in a ground model—let us fix such a transitive ground model
![]() $\mathcal {M}\in V$
for this discussion, and a class preorder
$\mathcal {M}\in V$
for this discussion, and a class preorder
![]() $\mathbb {P}$
from
$\mathbb {P}$
from
![]() $\mathcal {M}$
. We require
$\mathcal {M}$
. We require
![]() $\mathcal {M}$
to satisfy the axioms of some axiom system T for set theory that is suitable for class forcing (either Gödel–Bernays set theory
$\mathcal {M}$
to satisfy the axioms of some axiom system T for set theory that is suitable for class forcing (either Gödel–Bernays set theory
![]() $\mathrm {GB}$
, Kelley–Morse set theory
$\mathrm {GB}$
, Kelley–Morse set theory
![]() $\mathrm {KM}$
, or some variants of those). We think of conditions (elements) of
$\mathrm {KM}$
, or some variants of those). We think of conditions (elements) of
![]() $\mathbb {P}$
as having partial information on properties of our extensions. We require that stronger conditions have more such information, and that any particular forcing extension is based on a choice of filter on
$\mathbb {P}$
as having partial information on properties of our extensions. We require that stronger conditions have more such information, and that any particular forcing extension is based on a choice of filter on
![]() $\mathbb {P}$
. We think of such a filter as a selection of conditions which have correct information about our extension, and we will refer to such conditions as being correct. The motivation for using a filter of conditions could be explained as follows.
$\mathbb {P}$
. We think of such a filter as a selection of conditions which have correct information about our extension, and we will refer to such conditions as being correct. The motivation for using a filter of conditions could be explained as follows.
-
• If we consider the information that a condition q has to be correct, then any weaker condition p has less information than q, and this information should therefore also be correct. This corresponds to the upwards closure property of filters.
-
• If p and q are correct conditions, we consider the information that is jointly collected by p and q to be correct. We require that there is a condition that collects this joint information and that we consider to be correct. This corresponds to the property of a filter that any two of its elements are compatible, as witnessed by yet another element of the filter.
We require that for any condition
![]() $p\in \mathbb {P}$
, there exists a filter G of correct conditions of which p is an element, so that no condition is a priori incorrect. Given any particular such filter G, we require the generic extension
$p\in \mathbb {P}$
, there exists a filter G of correct conditions of which p is an element, so that no condition is a priori incorrect. Given any particular such filter G, we require the generic extension
![]() $\mathcal {M}[G]$
to contain
$\mathcal {M}[G]$
to contain
![]() $\mathcal {M}$
as a subset and G as an element. There are a number of natural axioms which make sure that we have ground model control over our generic extensions, in a sufficiently simple way. One necessary requirement for this is that elements of
$\mathcal {M}$
as a subset and G as an element. There are a number of natural axioms which make sure that we have ground model control over our generic extensions, in a sufficiently simple way. One necessary requirement for this is that elements of
![]() $\mathcal {M}[G]$
are connected to elements of the ground model so that the latter serve as a sort of name for the former. We require the existence of a definable relation on our ground model, which, following [Reference Freire3], we call the
$\mathcal {M}[G]$
are connected to elements of the ground model so that the latter serve as a sort of name for the former. We require the existence of a definable relation on our ground model, which, following [Reference Freire3], we call the
![]() $\mathbb {P}$
-membership relation. It is supposed to relate to partial knowledge about the membership relation in forcing extensions. If a and b are elements of
$\mathbb {P}$
-membership relation. It is supposed to relate to partial knowledge about the membership relation in forcing extensions. If a and b are elements of
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $p\in \mathbb {P}$
, we say that a is an element of b according to p, and write
$p\in \mathbb {P}$
, we say that a is an element of b according to p, and write
![]() $a\in _p b$
in case the triple
$a\in _p b$
in case the triple
![]() $\langle p,a,b\rangle $
stands in this relation.Footnote
2
We want to define a membership relation for
$\langle p,a,b\rangle $
stands in this relation.Footnote
2
We want to define a membership relation for
![]() $\mathcal {M}[G]$
, letting the object denoted by a be an element of the object denoted by b in case a is an element of b according to some correct condition (that is,
$\mathcal {M}[G]$
, letting the object denoted by a be an element of the object denoted by b in case a is an element of b according to some correct condition (that is,
![]() $\exists p\in G\ a\in _p b$
). In order to be able to obtain a transitive model as our forcing extension, we thus require the relation
$\exists p\in G\ a\in _p b$
). In order to be able to obtain a transitive model as our forcing extension, we thus require the relation
![]() $\exists p\in \mathbb {P}\ a\in _p b$
to be well-founded. The relation
$\exists p\in \mathbb {P}\ a\in _p b$
to be well-founded. The relation
![]() $\exists p\in G\ a\in _p b$
will usually not be extensional, but we nevertheless obtain a transitive
$\exists p\in G\ a\in _p b$
will usually not be extensional, but we nevertheless obtain a transitive
![]() $\in $
-structure (which will serve as our generic extension
$\in $
-structure (which will serve as our generic extension
![]() $\mathcal {M}[G]$
) as the image of the homomorphism that is our evaluation map
$\mathcal {M}[G]$
) as the image of the homomorphism that is our evaluation map
![]() $F_G$
, recursively defined by setting
$F_G$
, recursively defined by setting
![]() $F_G(b)=\{F_G(a)\mid a\in _G b\}$
for every
$F_G(b)=\{F_G(a)\mid a\in _G b\}$
for every
![]() $b\in \mathcal {M}$
.
$b\in \mathcal {M}$
.
In order to be able to show that
![]() $\mathcal {M}[G]$
is well-defined and satisfies the axioms of T, we will need to require the following:
$\mathcal {M}[G]$
is well-defined and satisfies the axioms of T, we will need to require the following:
-
• A strong form of set-likeness: for any
 $b\in \mathcal {M}$
,
$b\in \mathcal {M}$
,
 $\{\langle a,p\rangle \mid a\in _p b\}$
is a set in
$\{\langle a,p\rangle \mid a\in _p b\}$
is a set in
 $\mathcal {M}$
.
$\mathcal {M}$
. -
• High degrees of freedom for the
 $\mathbb {P}$
-membership relation: for any relation S on
$\mathbb {P}$
-membership relation: for any relation S on
 $\mathcal {M}\times P$
in
$\mathcal {M}\times P$
in
 $\mathcal {M}$
, we find
$\mathcal {M}$
, we find
 $b\in \mathcal {M}$
for which
$b\in \mathcal {M}$
for which
 $\{\langle a,p\rangle \mid a\in _p b\}=S$
.
$\{\langle a,p\rangle \mid a\in _p b\}=S$
.
Furthermore, we also require the existence of forcing predicates in
![]() $\mathcal {M}$
, individually for each first order formula, and also for each second order formula in the case of
$\mathcal {M}$
, individually for each first order formula, and also for each second order formula in the case of
![]() $\mathrm {KM}$
. We do not require any particular defining instances for these predicates, we only require them to be connected to truth in generic extensions by the following two axioms (these requirements correspond to what is usually known as the forcing theorem in a standard class forcing setup):
$\mathrm {KM}$
. We do not require any particular defining instances for these predicates, we only require them to be connected to truth in generic extensions by the following two axioms (these requirements correspond to what is usually known as the forcing theorem in a standard class forcing setup):
-
• Whatever holds in
 $\mathcal {M}[G]$
is forced by some condition in G.
$\mathcal {M}[G]$
is forced by some condition in G. -
• Whatever is forced by some condition
 $p\in G$
holds true in
$p\in G$
holds true in
 $\mathcal {M}[G]$
.
$\mathcal {M}[G]$
.
Finally, we will have to assume that our class forcing notion
![]() $\mathbb {P}$
is pretame or tame, which are technical conditions on
$\mathbb {P}$
is pretame or tame, which are technical conditions on
![]() $\mathbb {P}$
that are equivalent to the preservation of the axioms from T in a standard class forcing setup.
$\mathbb {P}$
that are equivalent to the preservation of the axioms from T in a standard class forcing setup.
2 The basic setup
We want to verify our results for models of the base theory that is Gödel–Bernays set theory
![]() $\mathrm {GB}$
, and also for some of its variants. In Section 9, we will also consider the stronger theory
$\mathrm {GB}$
, and also for some of its variants. In Section 9, we will also consider the stronger theory
![]() $\mathrm {KM}$
, and we will consider yet another strengthening of it in Section 10. These theories are usually presented as theories in a two-sorted language, with variables for sets and for classes, and their models will be of the form
$\mathrm {KM}$
, and we will consider yet another strengthening of it in Section 10. These theories are usually presented as theories in a two-sorted language, with variables for sets and for classes, and their models will be of the form
![]() $\mathcal {M}=\langle M,\mathcal {C}\rangle $
, where M denotes the domain of sets, and
$\mathcal {M}=\langle M,\mathcal {C}\rangle $
, where M denotes the domain of sets, and
![]() $\mathcal {C}$
denotes the domain of classes of
$\mathcal {C}$
denotes the domain of classes of
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Let
![]() $\mathcal L(\in )$
denote the collection of first order formulas in the language with the
$\mathcal L(\in )$
denote the collection of first order formulas in the language with the
![]() $\in $
-predicate in which we additionally allow for second order variables, and atomic formulas of the form
$\in $
-predicate in which we additionally allow for second order variables, and atomic formulas of the form
![]() $x\in X$
, where x is a first order variable and X is a second order variable. We consider equality between first or second order elements to abbreviate the statement that they have the same elements. The axioms of
$x\in X$
, where x is a first order variable and X is a second order variable. We consider equality between first or second order elements to abbreviate the statement that they have the same elements. The axioms of
![]() $\mathrm {GB}$
are given by the axioms of
$\mathrm {GB}$
are given by the axioms of
![]() $\mathrm {ZF}$
for sets, allowing class parameters in the axiom schemes of separation and replacement (that is, allowing for formulas from
$\mathrm {ZF}$
for sets, allowing class parameters in the axiom schemes of separation and replacement (that is, allowing for formulas from
![]() $\mathcal L(\in )$
in which second order variables are replaced by second order parameters from
$\mathcal L(\in )$
in which second order variables are replaced by second order parameters from
![]() $\mathcal {C}$
), together with the class axiom of first order class comprehension, that is comprehension for classes using
$\mathcal {C}$
), together with the class axiom of first order class comprehension, that is comprehension for classes using
![]() $\mathcal L(\in )$
-formulas with second order parameters from
$\mathcal L(\in )$
-formulas with second order parameters from
![]() $\mathcal {C}$
. If
$\mathcal {C}$
. If
![]() $\mathcal {M}\models \mathrm {GB}$
(or any of its variants), we usually use lowercase letters to denote first order elements of
$\mathcal {M}\models \mathrm {GB}$
(or any of its variants), we usually use lowercase letters to denote first order elements of
![]() $\mathcal {M}$
, that is elements of M, and uppercase letters to denote second order elements of
$\mathcal {M}$
, that is elements of M, and uppercase letters to denote second order elements of
![]() $\mathcal {M}$
, that is elements of
$\mathcal {M}$
, that is elements of
![]() $\mathcal {C}$
. Note that by the separation axiom, we have
$\mathcal {C}$
. Note that by the separation axiom, we have
![]() $M\subseteq \mathcal {C}$
.
$M\subseteq \mathcal {C}$
.
We will also consider the strengthenings of
![]() $\mathrm {GB}$
that are obtained by adding the axiom of choice (
$\mathrm {GB}$
that are obtained by adding the axiom of choice (
![]() $\mathrm {GBc}$
) in the form of the statement that every set can be well-ordered, or (
$\mathrm {GBc}$
) in the form of the statement that every set can be well-ordered, or (
![]() $\mathrm {GBC}$
) the axiom that there is a well-order of all sets in order-type
$\mathrm {GBC}$
) the axiom that there is a well-order of all sets in order-type
![]() $\operatorname {\mathrm {Ord}}$
(or equivalently, a set-like global well-order), as well as the axiom systems
$\operatorname {\mathrm {Ord}}$
(or equivalently, a set-like global well-order), as well as the axiom systems
![]() $\mathrm {GB}^-$
,
$\mathrm {GB}^-$
,
![]() $\mathrm {GBc}^-$
, and
$\mathrm {GBc}^-$
, and
![]() $\mathrm {GBC}^-$
, which are obtained from
$\mathrm {GBC}^-$
, which are obtained from
![]() $\mathrm {GB}$
,
$\mathrm {GB}$
,
![]() $\mathrm {GBc}$
, or
$\mathrm {GBc}$
, or
![]() $\mathrm {GBC}$
respectively by removing the powerset axiom and using the axiom scheme of collection rather than replacement. We fix a base theory T to be one of the above theories.
$\mathrm {GBC}$
respectively by removing the powerset axiom and using the axiom scheme of collection rather than replacement. We fix a base theory T to be one of the above theories.
We next provide the definition of a class forcing generic framework, which will be the basic formal concept in our approach. As in [Reference Holy, Krapf, Lücke, Njegomir and Schlicht7], we will use the more general notion of preorders rather than (the perhaps more common restriction to) partial orders, dropping the requirement of antisymmetry. If
![]() $\vec A$
is a finite sequence, we will use the statement
$\vec A$
is a finite sequence, we will use the statement
![]() $\vec A\in \mathcal {C}$
to abbreviate the property that all sequents of
$\vec A\in \mathcal {C}$
to abbreviate the property that all sequents of
![]() $\vec A$
are elements of
$\vec A$
are elements of
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Definition 2.1. A class forcing generic framework is a tuple of the form
 $$ \begin{align*}\left\langle\mathcal{M},\mathbb{P},R,\left(\operatorname{\mathrm{\Vdash}}_\varphi^{\vec A}\right)_{\varphi\in\mathcal L(\in),\vec A\in\mathcal{C}},\mathfrak G\right\rangle\textrm{ with the following properties}.\end{align*} $$
$$ \begin{align*}\left\langle\mathcal{M},\mathbb{P},R,\left(\operatorname{\mathrm{\Vdash}}_\varphi^{\vec A}\right)_{\varphi\in\mathcal L(\in),\vec A\in\mathcal{C}},\mathfrak G\right\rangle\textrm{ with the following properties}.\end{align*} $$
-
•
 $\mathcal {M}$
is a transitive set-size model of
$\mathcal {M}$
is a transitive set-size model of
 $T: M$
is transitive,
$T: M$
is transitive,
 $\bigcup \mathcal {C}\subseteq M$
, and
$\bigcup \mathcal {C}\subseteq M$
, and
 $\mathcal {M}$
is a set such that
$\mathcal {M}$
is a set such that
 $\mathcal {M}\models T$
.
$\mathcal {M}\models T$
. -
•
 $\mathbb {P}=\langle P,\le \rangle $
is a preorder with weakest element
$\mathbb {P}=\langle P,\le \rangle $
is a preorder with weakest element
 $\operatorname {\mathrm {\mathsf {1}}}_P$
(that is
$\operatorname {\mathrm {\mathsf {1}}}_P$
(that is
 $p\le \operatorname {\mathrm {\mathsf {1}}}_P$
for every
$p\le \operatorname {\mathrm {\mathsf {1}}}_P$
for every
 $p\in P$
) such that both P and
$p\in P$
) such that both P and
 $\le $
are in
$\le $
are in
 $\mathcal {C}$
.
$\mathcal {C}$
. -
• The
 $\mathbb {P}$
-membership relation R is a relation on
$\mathbb {P}$
-membership relation R is a relation on
 $P\times M\times \mathcal {C}$
that is definable over
$P\times M\times \mathcal {C}$
that is definable over
 $\mathcal {M}$
by an
$\mathcal {M}$
by an
 $\mathcal L(\in )$
-formula
$\mathcal L(\in )$
-formula
 $\varphi (p,a,B)$
with first order variables p and a, and a second order variable B, so that for
$\varphi (p,a,B)$
with first order variables p and a, and a second order variable B, so that for
 $p\in P$
,
$p\in P$
,
 $a\in M$
, and
$a\in M$
, and
 $B\in \mathcal {C}$
we have
$B\in \mathcal {C}$
we have
 $R(p,a,B)$
if and only if
$R(p,a,B)$
if and only if
 $\varphi (p,a,B)$
.Footnote
3
We denote the property
$\varphi (p,a,B)$
.Footnote
3
We denote the property
 $R(p,a,B)$
as
$R(p,a,B)$
as
 $a\in _p B$
.Footnote
4
$a\in _p B$
.Footnote
4
-
•
 $\mathfrak G$
is a second order unary predicate on P, i.e., a unary predicate on
$\mathfrak G$
is a second order unary predicate on P, i.e., a unary predicate on
 $\mathcal P(P)$
, and we require that
$\mathcal P(P)$
, and we require that
 $\mathfrak G(G)$
implies that
$\mathfrak G(G)$
implies that
 $G\subseteq P$
is a filter. If
$G\subseteq P$
is a filter. If
 $\mathfrak G(G)$
holds, we say that G is a generic filter, or a
$\mathfrak G(G)$
holds, we say that G is a generic filter, or a
 $\mathbb {P}$
-generic filter on M. Whenever we quantify over G in the following, we assume that we quantify over G’s such that
$\mathbb {P}$
-generic filter on M. Whenever we quantify over G in the following, we assume that we quantify over G’s such that
 $\mathfrak G(G)$
holds.
$\mathfrak G(G)$
holds. -
• For every
 $\vec A\in \mathcal {C}$
and
$\vec A\in \mathcal {C}$
and
 $\varphi \in \mathcal L(\in )$
for which the number of second order variables corresponds to the length of
$\varphi \in \mathcal L(\in )$
for which the number of second order variables corresponds to the length of
 $\vec A$
,
$\vec A$
,
 $\operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}\in \mathcal {C}$
is a predicate (which we also call a forcing relation for
$\operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}\in \mathcal {C}$
is a predicate (which we also call a forcing relation for
 $\varphi $
) on
$\varphi $
) on
 $P\times M^m$
, where m denotes the number of free first order variables of
$P\times M^m$
, where m denotes the number of free first order variables of
 $\varphi $
. If
$\varphi $
. If
 $\langle q,a_0,\ldots ,a_{m-1}\rangle \in \operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}$
, we also write
$\langle q,a_0,\ldots ,a_{m-1}\rangle \in \operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}$
, we also write
 $q\operatorname {\mathrm {\Vdash }}\varphi (a_0,\ldots ,a_{m-1},\vec A)$
.
$q\operatorname {\mathrm {\Vdash }}\varphi (a_0,\ldots ,a_{m-1},\vec A)$
.
3 The basic axioms
In this section, we present our basic axioms for class forcing generic frameworks.
-
(1) Existence of generic filters:
 $\forall p\in P\,\exists G\ p\in G$
.Footnote
5
$\forall p\in P\,\exists G\ p\in G$
.Footnote
5
-
(2) Well-Foundedness: The binary relation
 $\exists p\in P\ a\in _p b$
on M is well-founded.
$\exists p\in P\ a\in _p b$
on M is well-founded. -
(3) Growth of Information: For all
 $\vec A\in \mathcal {C}$
and
$\vec A\in \mathcal {C}$
and
 $\varphi \in \mathcal L(\in )$
, for all
$\varphi \in \mathcal L(\in )$
, for all
 $\vec a\in M$
, and
$\vec a\in M$
, and
 $p,q\in P$
, if
$p,q\in P$
, if
 $p\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
and
$p\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
and
 $q\le p$
, then
$q\le p$
, then
 $q\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
.
$q\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
.
Assume that G is such that
![]() $\mathfrak G(G)$
holds. Define a relation
$\mathfrak G(G)$
holds. Define a relation
![]() $\in _G$
on
$\in _G$
on
![]() $\mathcal {C}$
by letting
$\mathcal {C}$
by letting
![]() $a\in _G B$
if
$a\in _G B$
if
![]() $\exists p\in G\ a\in _p B$
. Using axiom (2), this relation on
$\exists p\in G\ a\in _p B$
. Using axiom (2), this relation on
![]() $\mathcal {C}$
is well-founded, and since
$\mathcal {C}$
is well-founded, and since
![]() $\mathcal {M}\in V$
, it is clearly set-like in V. We may thus recursively define our evaluation function
$\mathcal {M}\in V$
, it is clearly set-like in V. We may thus recursively define our evaluation function
![]() $F_G$
along the relation
$F_G$
along the relation
![]() $\in _G$
, letting
$\in _G$
, letting
![]() $F_G(B)=\{F_G(a)\mid a\in _G B\}$
for each
$F_G(B)=\{F_G(a)\mid a\in _G B\}$
for each
![]() $B\in \mathcal {C}$
.Footnote
6
Let
$B\in \mathcal {C}$
.Footnote
6
Let
![]() $\mathcal {M}[G]$
denote the
$\mathcal {M}[G]$
denote the
![]() $\in $
-structure on the transitive set
$\in $
-structure on the transitive set
![]() $F_G[\mathcal {C}]$
:Footnote
7
That is, let
$F_G[\mathcal {C}]$
:Footnote
7
That is, let
![]() $\mathcal {M}[G]=\langle M[G],\mathcal {C}[G]\rangle $
, where
$\mathcal {M}[G]=\langle M[G],\mathcal {C}[G]\rangle $
, where
![]() $M[G]=F_G[M]$
, and
$M[G]=F_G[M]$
, and
![]() $\mathcal {C}[G]=F_G[\mathcal {C}]$
.
$\mathcal {C}[G]=F_G[\mathcal {C}]$
.
The next two axioms state that a natural form of the forcing theorem holds, that is based on our forcing relations. Given a finite tuple
![]() $\vec A=\langle A_i\mid i<n\rangle \in \mathcal {C}$
, let
$\vec A=\langle A_i\mid i<n\rangle \in \mathcal {C}$
, let
![]() $F_G(\vec A)=\langle F_G(A_i)\mid i<n\rangle $
.
$F_G(\vec A)=\langle F_G(A_i)\mid i<n\rangle $
.
-
(4) Truth Lemma: For all
 $\vec A\in \mathcal {C}$
and
$\vec A\in \mathcal {C}$
and
 $\varphi \in \mathcal L(\in )$
for which the number of second order variables corresponds to the length of
$\varphi \in \mathcal L(\in )$
for which the number of second order variables corresponds to the length of
 $\vec A$
, all
$\vec A$
, all
 $\vec a\in M$
, and all G,
$\vec a\in M$
, and all G,  $$ \begin{align*}\mathcal{M}[G]\models\varphi(F_G(\vec a),F_G(\vec A))\textrm{ iff }\exists p\in G\ p\operatorname{\mathrm{\Vdash}}\varphi(\vec a,\vec A).\end{align*} $$
$$ \begin{align*}\mathcal{M}[G]\models\varphi(F_G(\vec a),F_G(\vec A))\textrm{ iff }\exists p\in G\ p\operatorname{\mathrm{\Vdash}}\varphi(\vec a,\vec A).\end{align*} $$
-
(5) Definability Lemma: For all
 $\vec A\in \mathcal {C}$
and
$\vec A\in \mathcal {C}$
and
 $\varphi \in \mathcal L(\in )$
for which the number of second order variables corresponds to the length of
$\varphi \in \mathcal L(\in )$
for which the number of second order variables corresponds to the length of
 $\vec A$
, all
$\vec A$
, all
 $\vec a\in M$
, and
$\vec a\in M$
, and
 $p\in P$
, Footnote 8
$p\in P$
, Footnote 8 $$ \begin{align*}p\operatorname{\mathrm{\Vdash}}\varphi(\vec a,\vec A)\textrm{ iff }\forall G\ni p\ \mathcal{M}[G]\models\varphi(F_G(\vec a),F_G(\vec A)).\end{align*} $$
$$ \begin{align*}p\operatorname{\mathrm{\Vdash}}\varphi(\vec a,\vec A)\textrm{ iff }\forall G\ni p\ \mathcal{M}[G]\models\varphi(F_G(\vec a),F_G(\vec A)).\end{align*} $$
Our next axiom (
![]() $\bar 6$
) states that within M, a weak form of set-likeness holds for the
$\bar 6$
) states that within M, a weak form of set-likeness holds for the
![]() $\mathbb {P}$
-membership relation. We will later replace it by the stronger axiom (6).Footnote 9
$\mathbb {P}$
-membership relation. We will later replace it by the stronger axiom (6).Footnote 9
-
(
 $\bar 6$
) Weak Set-Likeness: If
$\bar 6$
) Weak Set-Likeness: If
 $b\in M$
, then
$b\in M$
, then
 $\{a\mid \exists p\in P\ a\in _p b\}\in M$
.
$\{a\mid \exists p\in P\ a\in _p b\}\in M$
.
We will also introduce two additional axioms, axioms (7) and (8), later on in our paper. For the moment, we introduce two other additional axioms, stating that all elements of M have a name in M, and that there is a (class) name for our generic filters. They will later be replaced by the stronger axiom (7) which will imply both these axioms. Since those are only temporary axioms, we will not provide them with a number.
-
(*) Names for ground model objects:
-
•
 $\forall a\in M\,\exists \check a\in M\,\forall G\ F_G(\check a)=a$
, and
$\forall a\in M\,\exists \check a\in M\,\forall G\ F_G(\check a)=a$
, and -
•
 $\forall A\in \mathcal {C}\,\exists \check A\in \mathcal {C}\,\forall G\ F_G(\check A)=A$
.
$\forall A\in \mathcal {C}\,\exists \check A\in \mathcal {C}\,\forall G\ F_G(\check A)=A$
.
-
-
(**) Name for generic filters:
 $\exists \dot G\in \mathcal {C}\ \forall G\ F_G(\dot G)=G$
.
$\exists \dot G\in \mathcal {C}\ \forall G\ F_G(\dot G)=G$
.
Given
![]() $a\in M$
and
$a\in M$
and
![]() $A\in \mathcal {C}$
, we will use
$A\in \mathcal {C}$
, we will use
![]() $\check a$
and
$\check a$
and
![]() $\check A$
to denote names for a and A as provided by axiom (*) above, and we will use
$\check A$
to denote names for a and A as provided by axiom (*) above, and we will use
![]() $\dot G$
to denote a (class) name for G as provided by axiom (**) above.
$\dot G$
to denote a (class) name for G as provided by axiom (**) above.
4 Forcing predicates and density
Our axioms (1)–(5) together with the axioms (*) and (**) suffice to verify some of the basic properties of forcing, and in particular to verify that the forcing predicates satisfy their usual defining clauses, by arguments that are similar to the arguments of [Reference Freire3, Section 4]. For the sake of completeness, and for the benefit of our readers, we would nevertheless like to present some of these arguments here. The first step will be to verify an auxiliary result on the forcing of negated statements.
Lemma 4.1. For all
![]() $\varphi \in \mathcal L(\in )$
,
$\varphi \in \mathcal L(\in )$
,
![]() $p\in P$
,
$p\in P$
,
![]() $\vec a\in M$
, and
$\vec a\in M$
, and
![]() $\vec A\in \mathcal {C}$
, we have that
$\vec A\in \mathcal {C}$
, we have that
Proof Let us assume that
-
(i)
 $p\operatorname {\mathrm {\Vdash }}\lnot \varphi (\vec a,\vec A)$
.
$p\operatorname {\mathrm {\Vdash }}\lnot \varphi (\vec a,\vec A)$
.
By axiom (5), equivalently
-
(ii)
 $\forall G\ni p\ \mathcal {M}[G]\models \lnot \varphi (F_G(\vec a),F_G(\vec A))$
.
$\forall G\ni p\ \mathcal {M}[G]\models \lnot \varphi (F_G(\vec a),F_G(\vec A))$
.
By axiom (4), this is equivalent to
-
(iii)
 $\forall G\ni p\,\forall q\in G\ q\not \operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
.
$\forall G\ni p\,\forall q\in G\ q\not \operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
.
We want to argue that this in turn is equivalent to our desired statement that
-
(iv)
 $\forall q\le p\ q\not \operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
.
$\forall q\le p\ q\not \operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
.
Thus, assume first that (iii) holds, and let
![]() $q\le p$
. By axiom (1), we may pick a generic filter
$q\le p$
. By axiom (1), we may pick a generic filter
![]() $G\ni q$
, which will thus also contain p as an element. By (iii), we thus have that
$G\ni q$
, which will thus also contain p as an element. By (iii), we thus have that
![]() $q\not \operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
, as desired.
$q\not \operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
, as desired.
Conversely, assume that (iv) holds. Let G be a generic filter that contains p as an element, and assume for a contradiction that there is
![]() $r\in G$
such that
$r\in G$
such that
![]() $r\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
. Since G is a filter, we may pick q below both p and r. By axiom (3), it follows that
$r\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
. Since G is a filter, we may pick q below both p and r. By axiom (3), it follows that
![]() $q\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
, contradicting (iv).
$q\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
, contradicting (iv).
We are now ready to show that our axioms imply generic filters to intersect all dense classes in
![]() $\mathcal {C}$
.
$\mathcal {C}$
.
Lemma 4.2. Let
![]() $D\in \mathcal {C}$
be such that D is dense in
$D\in \mathcal {C}$
be such that D is dense in
![]() $\mathbb {P}$
. If G is a generic filter, then G intersects D.
$\mathbb {P}$
. If G is a generic filter, then G intersects D.
Proof Let G be a generic filter and assume for a contradiction that
![]() $G\cap D=\emptyset $
. Making use of axioms (*) and (**), it follows that
$G\cap D=\emptyset $
. Making use of axioms (*) and (**), it follows that
By axiom (4), we may thus find
![]() $p\in G$
such that
$p\in G$
such that
By Lemma 4.1, equivalently
Since D is dense, we may fix
![]() $q\le p$
in D. But then,
$q\le p$
in D. But then,
contradicting the above.
We next need another auxiliary result on open dense sets (which could easily be extended to arbitrary dense sets, but the current version is sufficient for our purposes). We say that a subset A of a preorder P is open if it is downward closed, that is if
![]() $p\in A$
and
$p\in A$
and
![]() $q\le p$
, then also
$q\le p$
, then also
![]() $q\in A$
.
$q\in A$
.
Lemma 4.3. If
![]() $D\subseteq P$
is open,
$D\subseteq P$
is open,
![]() $D\in \mathcal {C}$
, then D is dense below p if and only if
$D\in \mathcal {C}$
, then D is dense below p if and only if
Proof Assume first that
![]() $(\dagger )$
holds. Let
$(\dagger )$
holds. Let
![]() $r\le p$
, and using axiom (1), let G be a generic filter with
$r\le p$
, and using axiom (1), let G be a generic filter with
![]() $r\in G$
. It follows that also
$r\in G$
. It follows that also
![]() $p\in G$
, and thus using
$p\in G$
, and thus using
![]() $(\dagger )$
, we obtain
$(\dagger )$
, we obtain
![]() $s\in D\cap G$
. Since D is open and G is a filter, we obtain q below both r and s that is an element of
$s\in D\cap G$
. Since D is open and G is a filter, we obtain q below both r and s that is an element of
![]() $D\cap G$
, showing that D is dense below p.
$D\cap G$
, showing that D is dense below p.
On the other hand, assume that D is dense below p, and let G be a generic filter containing p as an element. Let E be the dense set of conditions which are either below p and in D, or incompatible to p. By Lemma 4.2, it follows that
![]() $G\cap E\ne \emptyset $
. Since
$G\cap E\ne \emptyset $
. Since
![]() $p\in G$
and G is a filter, it thus follows that
$p\in G$
and G is a filter, it thus follows that
![]() $G\cap D\ne \emptyset $
, as desired.
$G\cap D\ne \emptyset $
, as desired.
It is now possible to show, as in [Reference Freire3], that the usual defining clauses for the forcing relation can be recovered from our basic axioms. The only additional clause that we need is the one for the elementhood relation with respect to classes. Its proof is very similar to the one for the elementhood relation with respect to sets; however we would like to provide one sample argument here in this paper for the benefit of our readers, and we will refer them to [Reference Freire3] for the other clauses below (note that since
![]() $M\subseteq \mathcal {C}$
, the below lemma also covers the case of the elementhood relation with respect to sets). Let
$M\subseteq \mathcal {C}$
, the below lemma also covers the case of the elementhood relation with respect to sets). Let
![]() $a\operatorname {\mathrm {\overline {\in }}}_p B$
if and only if
$a\operatorname {\mathrm {\overline {\in }}}_p B$
if and only if
![]() $\exists q\ge p\ a\in _q B$
.Footnote
10
$\exists q\ge p\ a\in _q B$
.Footnote
10
Lemma 4.4.
![]() $p\operatorname {\mathrm {\Vdash }} a\in A\textrm { iff }\,\forall r\le p\,\exists s\le r\,\exists x\ [x\operatorname {\mathrm {\overline {\in }}}_s A\,\land \,s\operatorname {\mathrm {\Vdash }} a=x]$
.
$p\operatorname {\mathrm {\Vdash }} a\in A\textrm { iff }\,\forall r\le p\,\exists s\le r\,\exists x\ [x\operatorname {\mathrm {\overline {\in }}}_s A\,\land \,s\operatorname {\mathrm {\Vdash }} a=x]$
.
Proof Let us assume that
-
(i)
 $p\operatorname {\mathrm {\Vdash }} a\in A$
.
$p\operatorname {\mathrm {\Vdash }} a\in A$
.
By axiom (5), this is equivalent to
-
(ii)
 $\forall G\ni p\ F_G(a)\in F_G(A)$
.
$\forall G\ni p\ F_G(a)\in F_G(A)$
.
By the definition of
![]() $F_G$
and of
$F_G$
and of
![]() $\in _G$
, this in turn is equivalent to
$\in _G$
, this in turn is equivalent to
-
(iii)
 $\forall G\ni p\,\exists x\in M\ [F_G(a)=F_G(x)\,\land \,\exists q\in G\ x\in _q A]$
.
$\forall G\ni p\,\exists x\in M\ [F_G(a)=F_G(x)\,\land \,\exists q\in G\ x\in _q A]$
.
Using axiom (4), we obtain the following equivalence:
-
(iv)
 $\forall G\ni p\,\exists x\in M\ [\exists r\in G\ r\operatorname {\mathrm {\Vdash }} a=x\,\land \,\exists q\in G\ x\in _q A]$
.
$\forall G\ni p\,\exists x\in M\ [\exists r\in G\ r\operatorname {\mathrm {\Vdash }} a=x\,\land \,\exists q\in G\ x\in _q A]$
.
Now we make use of axiom (3), equivalently obtaining that
-
(v)
 $\forall G\ni p\,\exists s\in G\,\exists x\in M\ [s\operatorname {\mathrm {\Vdash }} a=x\,\land \,x\operatorname {\mathrm {\overline {\in }}}_s A]$
.
$\forall G\ni p\,\exists s\in G\,\exists x\in M\ [s\operatorname {\mathrm {\Vdash }} a=x\,\land \,x\operatorname {\mathrm {\overline {\in }}}_s A]$
.
Using Lemma 4.3 yields our final desired equivalence:
-
(vi)
 $\forall r\le p\,\exists s\le r\,\exists x\in M\ [x\operatorname {\mathrm {\overline {\in }}}_s A\,\land \,s\operatorname {\mathrm {\Vdash }} a=x].\\[-34pt]$
$\forall r\le p\,\exists s\le r\,\exists x\in M\ [x\operatorname {\mathrm {\overline {\in }}}_s A\,\land \,s\operatorname {\mathrm {\Vdash }} a=x].\\[-34pt]$
In the next lemma, we list the remaining results with respect to the forcing predicates obeying their usual defining clauses, which are shown exactly as in [Reference Freire3, Section 5], simply carrying along additional second order predicates (in case there are any). For the detailed arguments to verify these properties, we refer the interested reader to [Reference Freire3]. We consider the relations
![]() $\in $
and
$\in $
and
![]() $\ne $
as our atomic relations in the below; however
$\ne $
as our atomic relations in the below; however
![]() $a\ne b$
could be seen as abbreviating
$a\ne b$
could be seen as abbreviating
![]() $\lnot (a=b)$
, and
$\lnot (a=b)$
, and
![]() $a\not \in b$
should be seen as abbreviating
$a\not \in b$
should be seen as abbreviating
![]() $\lnot (a\in b)$
.
$\lnot (a\in b)$
.
Lemma 4.5. Let
![]() $\varphi \in \mathcal L(\in )$
,
$\varphi \in \mathcal L(\in )$
,
![]() $p\in P$
, and let
$p\in P$
, and let
![]() $\vec a$
and
$\vec a$
and
![]() $\vec A$
be finite tuples from M and from
$\vec A$
be finite tuples from M and from
![]() $\mathcal {C}$
respectively. Then the following hold true.
$\mathcal {C}$
respectively. Then the following hold true.
-
•
 $p\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)\textrm { iff }\,\forall q\le p\,\exists r\le q\ r\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
.
$p\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)\textrm { iff }\,\forall q\le p\,\exists r\le q\ r\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
. -
•
 $p\operatorname {\mathrm {\Vdash }}[\varphi \lor \psi ](\vec a,\vec A)\textrm { iff }\,\forall r\le p\,\exists q\le r\ [q\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)\,\lor \,q\operatorname {\mathrm {\Vdash }}\psi (\vec a,\vec A)]$
.
$p\operatorname {\mathrm {\Vdash }}[\varphi \lor \psi ](\vec a,\vec A)\textrm { iff }\,\forall r\le p\,\exists q\le r\ [q\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)\,\lor \,q\operatorname {\mathrm {\Vdash }}\psi (\vec a,\vec A)]$
. -
•
 $p\operatorname {\mathrm {\Vdash }}\exists x\varphi (\vec a,\vec A)\textrm { iff }\,\forall r\le p\,\exists q\le r\,\exists x\in M\ q\operatorname {\mathrm {\Vdash }}\varphi (x,\vec a,\vec A)$
.
$p\operatorname {\mathrm {\Vdash }}\exists x\varphi (\vec a,\vec A)\textrm { iff }\,\forall r\le p\,\exists q\le r\,\exists x\in M\ q\operatorname {\mathrm {\Vdash }}\varphi (x,\vec a,\vec A)$
. -
•
 $p\operatorname {\mathrm {\Vdash }}[\varphi \,\land \,\psi ](\vec a,\vec A)\textrm { iff }p\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)\,\land \,p\operatorname {\mathrm {\Vdash }}\psi (\vec a,\vec A)$
.
$p\operatorname {\mathrm {\Vdash }}[\varphi \,\land \,\psi ](\vec a,\vec A)\textrm { iff }p\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)\,\land \,p\operatorname {\mathrm {\Vdash }}\psi (\vec a,\vec A)$
. -
•
 $p\operatorname {\mathrm {\Vdash }} a\ne b$
iff
$p\operatorname {\mathrm {\Vdash }} a\ne b$
iff
 $\,\forall r\le p\,\exists q\le r\,\exists c$
$\,\forall r\le p\,\exists q\le r\,\exists c$
 $$ \begin{align*}(c\operatorname{\mathrm{\overline{\in}}}_q a\,\land\,q\operatorname{\mathrm{\Vdash}} c\not\in b)\,\lor\,(c\operatorname{\mathrm{\overline{\in}}}_q b\,\land\,q\operatorname{\mathrm{\Vdash}} c\not\in a).\end{align*} $$
$$ \begin{align*}(c\operatorname{\mathrm{\overline{\in}}}_q a\,\land\,q\operatorname{\mathrm{\Vdash}} c\not\in b)\,\lor\,(c\operatorname{\mathrm{\overline{\in}}}_q b\,\land\,q\operatorname{\mathrm{\Vdash}} c\not\in a).\end{align*} $$
The existence of forcing relations for atomic formulas is usually a problematic aspect in the case of class forcing (for a detailed account of this see [Reference Holy, Krapf, Lücke, Njegomir and Schlicht7]). The fundamental difference in our setup is that the definability of forcing predicates is already an integral assumption. In the above, we only show that any single step, reducing forcing statements about atomic formulas to ones for names of lower rank, proceeds as usual. We thus avoid the usual problem of having to obtain the definability of the forcing predicates for atomic formulas by recursion (which a priori is a recursion on classes, and is thus not guaranteed by the axioms of
![]() $\mathrm {GBC}$
, see [Reference Holy, Krapf, Lücke, Njegomir and Schlicht7], or also [Reference Gitman, Hamkins, Holy, Schlicht and Williams6]). The existence of such recursions is an axiom of
$\mathrm {GBC}$
, see [Reference Holy, Krapf, Lücke, Njegomir and Schlicht7], or also [Reference Gitman, Hamkins, Holy, Schlicht and Williams6]). The existence of such recursions is an axiom of
![]() $\mathrm {KM}$
on the other hand, and this is the reason why every notion of class forcing satisfies the forcing theorem in
$\mathrm {KM}$
on the other hand, and this is the reason why every notion of class forcing satisfies the forcing theorem in
![]() $\mathrm {KM}$
(see [Reference Holy, Krapf, Lücke, Njegomir and Schlicht7], [Reference Gitman, Hamkins, Holy, Schlicht and Williams6], or [Reference Antos-Kuby1]).
$\mathrm {KM}$
(see [Reference Holy, Krapf, Lücke, Njegomir and Schlicht7], [Reference Gitman, Hamkins, Holy, Schlicht and Williams6], or [Reference Antos-Kuby1]).
5 An axiomatization that assumes the preservation of the axioms of set theory
In this section, we introduce two further temporary axioms.
-
(***) Preservation of axioms:
 $\forall G\ \mathcal {M}[G]\models T$
Footnote
11
and
$\forall G\ \mathcal {M}[G]\models T$
Footnote
11
and -
(****) Absoluteness of
 $\mathbb {P}$
-membership: The formula
$\mathbb {P}$
-membership: The formula
 $\varphi $
defining the
$\varphi $
defining the
 $\mathbb {P}$
-membership relation R is absolute for transitive models of T containing
$\mathbb {P}$
-membership relation R is absolute for transitive models of T containing
 $\mathcal {C}$
.
$\mathcal {C}$
.
Building on the terminology from [Reference Freire3, Section 3], let us say that a class forcing generic extension is a class forcing generic framework together with a particular choice of generic filter G. Our next theorem shows that under a suitable set of axioms, this notion corresponds to the usual notion of a class forcing extension, and in particular it shows that
![]() $\mathcal {M}[G]$
is well-defined, in the sense that it only depends on
$\mathcal {M}[G]$
is well-defined, in the sense that it only depends on
![]() $\mathcal {M}$
and on G.
$\mathcal {M}$
and on G.
Theorem 5.1. Given a particular class forcing generic extension, assuming axioms
![]() $(2)$
, (
$(2)$
, (
![]() $\bar 6$
), (*), (**), (***), and (****) to hold,
$\bar 6$
), (*), (**), (***), and (****) to hold,
![]() $\mathcal {M}[G]$
is the
$\mathcal {M}[G]$
is the
![]() $\subseteq $
-smallest model of T that contains
$\subseteq $
-smallest model of T that contains
![]() $\mathcal {C}\cup \{G\}$
as a subset of its collection of classes.
$\mathcal {C}\cup \{G\}$
as a subset of its collection of classes.
Proof If
![]() $\mathcal {N}=\langle N,\mathcal D\rangle \models T$
is transitive such that
$\mathcal {N}=\langle N,\mathcal D\rangle \models T$
is transitive such that
![]() $\mathcal {C}\cup \{G\}\subseteq \mathcal D$
, then we can construct
$\mathcal {C}\cup \{G\}\subseteq \mathcal D$
, then we can construct
![]() $M[G]$
within
$M[G]$
within
![]() $\mathcal {N}$
: Working in
$\mathcal {N}$
: Working in
![]() $\mathcal {N}$
, define the relation
$\mathcal {N}$
, define the relation
![]() $\in _G$
on M by letting
$\in _G$
on M by letting
![]() $a\in _G b$
if
$a\in _G b$
if
![]() $\exists p\in G\ a\in _p b$
. By axiom (****), this definition of
$\exists p\in G\ a\in _p b$
. By axiom (****), this definition of
![]() $\in _G$
is absolute between
$\in _G$
is absolute between
![]() $\mathcal {N}$
and V. This relation on M is well-founded by axiom (2), and set-like by axiom (
$\mathcal {N}$
and V. This relation on M is well-founded by axiom (2), and set-like by axiom (
![]() $\bar 6$
). We thus may define the restriction of
$\bar 6$
). We thus may define the restriction of
![]() $F_G$
to M in
$F_G$
to M in
![]() $\mathcal {N}$
: Let
$\mathcal {N}$
: Let
![]() $Q(f,b)$
be the formula asserting that f is a function whose domain d includes b as an element and is closed under
$Q(f,b)$
be the formula asserting that f is a function whose domain d includes b as an element and is closed under
![]() $\in _G$
-predecessors, and for every
$\in _G$
-predecessors, and for every
![]() $a\in d$
we have
$a\in d$
we have
![]() $f(a)=\{f(c)\mid c\in _G a\}$
. Now
$f(a)=\{f(c)\mid c\in _G a\}$
. Now
![]() $F_G$
is defined by letting
$F_G$
is defined by letting
![]() $F_G(b)=f(b)$
if there is an
$F_G(b)=f(b)$
if there is an
![]() $f\in N$
such that
$f\in N$
such that
![]() $Q(f,b)$
holds, and is
$Q(f,b)$
holds, and is
![]() $\emptyset $
otherwise. By axioms (2) and (
$\emptyset $
otherwise. By axioms (2) and (
![]() $\bar 6$
), for any
$\bar 6$
), for any
![]() $b\in M$
, such function
$b\in M$
, such function
![]() $f\in N$
actually exists. We thus have
$f\in N$
actually exists. We thus have
![]() $M[G]\subseteq N$
.
$M[G]\subseteq N$
.
If
![]() $A\in \mathcal {C}$
, we obtain
$A\in \mathcal {C}$
, we obtain
![]() $F_G(A)=\{F_G(a)\mid a\in _G A\}\in \mathcal D$
by using first order class comprehension in
$F_G(A)=\{F_G(a)\mid a\in _G A\}\in \mathcal D$
by using first order class comprehension in
![]() $\mathcal {N}$
, and thus we also have
$\mathcal {N}$
, and thus we also have
![]() $\mathcal {C}[G]=F_G[\mathcal C]\subseteq \mathcal D$
. It thus follows that
$\mathcal {C}[G]=F_G[\mathcal C]\subseteq \mathcal D$
. It thus follows that
![]() $\mathcal {M}[G]\subseteq \mathcal {N}$
, and by axioms (*), (**), and (***),
$\mathcal {M}[G]\subseteq \mathcal {N}$
, and by axioms (*), (**), and (***),
![]() $\mathcal {M}[G]$
therefore is the
$\mathcal {M}[G]$
therefore is the
![]() $\subseteq $
-smallest model of T that contains all classes from
$\subseteq $
-smallest model of T that contains all classes from
![]() $\mathcal {C}$
and the generic filter G as one of its classes, if any such model exists, as desired.
$\mathcal {C}$
and the generic filter G as one of its classes, if any such model exists, as desired.
6 On the notion of tameness
One of the classical results about set forcing is that it preserves the axioms of
![]() $\mathrm {ZF}^-$
,
$\mathrm {ZF}^-$
,
![]() $\mathrm {ZF}$
, and
$\mathrm {ZF}$
, and
![]() $\mathrm {ZFC}$
, and this easily extends to any of the second order theories that we consider in this paper. However the situation is completely different for class forcing, for any of the second order theories that we consider in this paper may easily be destroyed by class forcing. For example, simply consider the notion of forcing which adds a function from
$\mathrm {ZFC}$
, and this easily extends to any of the second order theories that we consider in this paper. However the situation is completely different for class forcing, for any of the second order theories that we consider in this paper may easily be destroyed by class forcing. For example, simply consider the notion of forcing which adds a function from
![]() $\omega $
to
$\omega $
to
![]() $\operatorname {\mathrm {Ord}}$
using finite conditions. This notion of class forcing will provide us with a class function mapping
$\operatorname {\mathrm {Ord}}$
using finite conditions. This notion of class forcing will provide us with a class function mapping
![]() $\omega $
surjectively onto
$\omega $
surjectively onto
![]() $\operatorname {\mathrm {Ord}}$
in any of its generic extensions, clearly yielding
$\operatorname {\mathrm {Ord}}$
in any of its generic extensions, clearly yielding
![]() $\mathrm {GB}^-$
to fail. A key notion in this context is that of pretameness, which was implicit in earlier work of A. Zarach and of M. Stanley, and which was isolated by Friedman in [Reference Friedman5]. In the following, when we talk about sequences of classes, we will assume some suitable coding so that these sequences can themselves be viewed as classes.
$\mathrm {GB}^-$
to fail. A key notion in this context is that of pretameness, which was implicit in earlier work of A. Zarach and of M. Stanley, and which was isolated by Friedman in [Reference Friedman5]. In the following, when we talk about sequences of classes, we will assume some suitable coding so that these sequences can themselves be viewed as classes.
Definition 6.1.
![]() $\mathbb {P}$
is pretame (for
$\mathbb {P}$
is pretame (for
![]() $\mathcal {M}=\langle M,\mathcal {C}\rangle $
) if for every
$\mathcal {M}=\langle M,\mathcal {C}\rangle $
) if for every
![]() $p\in P$
and every sequence
$p\in P$
and every sequence
![]() $\langle D_i\mid i\in I\rangle \in \mathcal {C}$
of dense subclasses of
$\langle D_i\mid i\in I\rangle \in \mathcal {C}$
of dense subclasses of
![]() $\mathbb {P}$
with
$\mathbb {P}$
with
![]() $I\in M$
, there is
$I\in M$
, there is
![]() $q\le p$
and
$q\le p$
and
![]() $\langle d_i\mid i\in I\rangle \in M$
such that for every
$\langle d_i\mid i\in I\rangle \in M$
such that for every
![]() $i\in I$
,
$i\in I$
,
![]() $d_i\subseteq D_i$
is predense below q in
$d_i\subseteq D_i$
is predense below q in
![]() $\mathbb {P}$
.
$\mathbb {P}$
.
M. Stanley showed that pretameness is actually equivalent to the property that forcing with
![]() $\mathbb {P}$
preserves the axioms of
$\mathbb {P}$
preserves the axioms of
![]() $\mathrm {GB}^-$
in a standard class forcing setup (see [Reference Holy, Krapf and Schlicht8, Theorem 3.1]), and it is shown in [Reference Holy, Krapf and Schlicht8, Theorem 1.12] that pretameness is equivalent to a large number of desirable niceness features of forcing notions. It therefore seems very natural to restrict ones attention to pretame notions of forcing in the context of class forcing. Pretame notions of forcing also preserve the axiom of choice, and the existence of a global well-order in order type
$\mathrm {GB}^-$
in a standard class forcing setup (see [Reference Holy, Krapf and Schlicht8, Theorem 3.1]), and it is shown in [Reference Holy, Krapf and Schlicht8, Theorem 1.12] that pretameness is equivalent to a large number of desirable niceness features of forcing notions. It therefore seems very natural to restrict ones attention to pretame notions of forcing in the context of class forcing. Pretame notions of forcing also preserve the axiom of choice, and the existence of a global well-order in order type
![]() $\operatorname {\mathrm {Ord}}$
: regarding the axiom of choice, if x is a set in a generic extension
$\operatorname {\mathrm {Ord}}$
: regarding the axiom of choice, if x is a set in a generic extension
![]() $\mathcal {M}[G]$
by a pretame forcing notion
$\mathcal {M}[G]$
by a pretame forcing notion
![]() $\mathbb {P}$
, we pick a
$\mathbb {P}$
, we pick a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot x$
for x, and a well-order
$\dot x$
for x, and a well-order
![]() $\prec $
of
$\prec $
of
![]() $X=\{\sigma \mid \exists p\in P\ \langle \sigma ,p\rangle \in \dot x\}$
. We then construct a well-order of x as follows: given two of its elements y and z, we let
$X=\{\sigma \mid \exists p\in P\ \langle \sigma ,p\rangle \in \dot x\}$
. We then construct a well-order of x as follows: given two of its elements y and z, we let
![]() $y\triangleleft z$
if the
$y\triangleleft z$
if the
![]() $\prec $
-least
$\prec $
-least
![]() $\mathbb {P}$
-name for y in X (that is, the
$\mathbb {P}$
-name for y in X (that is, the
![]() $\prec $
-least
$\prec $
-least
![]() $\sigma \in X$
so that
$\sigma \in X$
so that
![]() $\sigma ^G=y$
) is
$\sigma ^G=y$
) is
![]() $\prec $
-below any
$\prec $
-below any
![]() $\mathbb {P}$
-name for z in X. The argument for the preservation of the existence of a global well-order in order type
$\mathbb {P}$
-name for z in X. The argument for the preservation of the existence of a global well-order in order type
![]() $\operatorname {\mathrm {Ord}}$
is essentially the same, and presented within [Reference Holy, Krapf and Schlicht8, Theorem 3.1].
$\operatorname {\mathrm {Ord}}$
is essentially the same, and presented within [Reference Holy, Krapf and Schlicht8, Theorem 3.1].
However, pretame notions of forcing need not preserve the powerset axiom. This can easily be observed by considering the pretame notion of forcing that adds a proper class of Cohen subsets of
![]() $\omega $
. Since in any of its extensions, the powerset of
$\omega $
. Since in any of its extensions, the powerset of
![]() $\omega $
would have to be a proper class, it cannot exist as a set. For the preservation of the powerset axiom, we need the notion of tameness. In his [Reference Friedman4], Friedman introduces tameness of a class forcing notion
$\omega $
would have to be a proper class, it cannot exist as a set. For the preservation of the powerset axiom, we need the notion of tameness. In his [Reference Friedman4], Friedman introduces tameness of a class forcing notion
![]() $\mathbb {P}$
as the axiom requiring that
$\mathbb {P}$
as the axiom requiring that
![]() $\mathbb {P}$
is pretame and that the weakest condition of
$\mathbb {P}$
is pretame and that the weakest condition of
![]() $\mathbb {P}$
forces the powerset axiom to hold (in the generic extension). Since pretameness of
$\mathbb {P}$
forces the powerset axiom to hold (in the generic extension). Since pretameness of
![]() $\mathbb {P}$
implies the
$\mathbb {P}$
implies the
![]() $\mathbb {P}$
-forcing relation to be definable, forcing the powerset axiom to hold is a first order property of
$\mathbb {P}$
-forcing relation to be definable, forcing the powerset axiom to hold is a first order property of
![]() $\mathbb {P}$
. Previously, in his [Reference Friedman5], a more combinatorial definition of tameness was provided, which however seems potentially problematic to us (we do not see how a crucial step in the argument of [Reference Friedman5, Theorem 2.21] proceeds, which is supposed to show that this combinatorial version of tameness implies the preservation of the powerset axiom), but this issue can easily be fixed by slightly strengthening the original property of tameness from [Reference Friedman5] (we will let tameness denote this strengthened property in the below)—we will show that (our version of) tameness is equivalent to the preservation of the powerset axiom under certain additional axioms (which all hold in any standard setup for class forcing) in Section 7.Footnote
12
$\mathbb {P}$
. Previously, in his [Reference Friedman5], a more combinatorial definition of tameness was provided, which however seems potentially problematic to us (we do not see how a crucial step in the argument of [Reference Friedman5, Theorem 2.21] proceeds, which is supposed to show that this combinatorial version of tameness implies the preservation of the powerset axiom), but this issue can easily be fixed by slightly strengthening the original property of tameness from [Reference Friedman5] (we will let tameness denote this strengthened property in the below)—we will show that (our version of) tameness is equivalent to the preservation of the powerset axiom under certain additional axioms (which all hold in any standard setup for class forcing) in Section 7.Footnote
12
Definition 6.2. Let
![]() $\mathcal {M}=\langle M,\mathcal {C}\rangle \models \mathrm {GB}$
and let
$\mathcal {M}=\langle M,\mathcal {C}\rangle \models \mathrm {GB}$
and let
![]() $\mathbb {P}\in \mathcal {C}$
be a notion of forcing.
$\mathbb {P}\in \mathcal {C}$
be a notion of forcing.
-
• If
 $p\in P$
, a predense
$p\in P$
, a predense
 $\le p$
partition (of
$\le p$
partition (of
 $\mathbb {P}$
) is a pair
$\mathbb {P}$
) is a pair
 $\langle D_0,D_1\rangle $
of classes such that
$\langle D_0,D_1\rangle $
of classes such that
 $D_0\cup D_1$
is predense below p and such that
$D_0\cup D_1$
is predense below p and such that
 $p_0\in D_0\,\land \,p_1\in D_1$
implies that
$p_0\in D_0\,\land \,p_1\in D_1$
implies that
 $p_0\perp p_1$
.
$p_0\perp p_1$
. -
• Suppose that
 $\langle \langle D_0^i,D_1^i\rangle \mid i\in a\rangle $
and
$\langle \langle D_0^i,D_1^i\rangle \mid i\in a\rangle $
and
 $\langle \langle E_0^i,E_1^i\rangle \mid i\in a\rangle $
are sequences of predense
$\langle \langle E_0^i,E_1^i\rangle \mid i\in a\rangle $
are sequences of predense
 $\le p$
partitions of
$\le p$
partitions of
 $\mathbb {P}$
. We say that they are equivalent
$\mathbb {P}$
. We say that they are equivalent
 $\le p$
if for each
$\le p$
if for each
 $i\in a$
, is dense below p in
$i\in a$
, is dense below p in $$ \begin{align*}\{q\in P\mid D_0^i\textrm{ is predense below }q\ \iff\ E_0^i\textrm{ is predense below }q\}\end{align*} $$
$$ \begin{align*}\{q\in P\mid D_0^i\textrm{ is predense below }q\ \iff\ E_0^i\textrm{ is predense below }q\}\end{align*} $$
 $\mathbb {P}$
.
$\mathbb {P}$
.
-
•
 $\mathbb {P}$
is tame (for
$\mathbb {P}$
is tame (for
 $\mathcal {M}$
) if
$\mathcal {M}$
) if
 $\mathbb {P}$
is pretame (for
$\mathbb {P}$
is pretame (for
 $\mathcal {M}$
) and for each
$\mathcal {M}$
) and for each
 $a\in M$
and
$a\in M$
and
 $p\in P$
, there is
$p\in P$
, there is
 $q\le p$
and
$q\le p$
and
 $\alpha \in \operatorname {\mathrm {Ord}}(M)$
s.t. whenever
$\alpha \in \operatorname {\mathrm {Ord}}(M)$
s.t. whenever
 $r\le q$
and is a sequence of predense
$r\le q$
and is a sequence of predense $$ \begin{align*}\vec d=\langle\langle d_0^i,d_1^i\rangle\mid i\in a\rangle\in M\end{align*} $$
$$ \begin{align*}\vec d=\langle\langle d_0^i,d_1^i\rangle\mid i\in a\rangle\in M\end{align*} $$
 $\le r$
partitions of
$\le r$
partitions of
 $\mathbb {P}$
, then there is
$\mathbb {P}$
, then there is
 $s\le r$
such that
$s\le r$
such that
 $\vec d$
is equivalent
$\vec d$
is equivalent
 ${\le }s$
to some Footnote 13
${\le }s$
to some Footnote 13 $$ \begin{align*}\vec e=\langle\langle e_0^i,e_1^i\rangle\mid i\in a\rangle\in V_\alpha^M.\end{align*} $$
$$ \begin{align*}\vec e=\langle\langle e_0^i,e_1^i\rangle\mid i\in a\rangle\in V_\alpha^M.\end{align*} $$
Note that if
![]() $\langle D_0,D_1\rangle $
is a predense
$\langle D_0,D_1\rangle $
is a predense
![]() $\le p$
partition of
$\le p$
partition of
![]() $\mathbb {P}$
for some
$\mathbb {P}$
for some
![]() $p\in P$
, and
$p\in P$
, and
![]() $q\le p$
, then
$q\le p$
, then
![]() $\langle D_0,D_1\rangle $
is also a predense
$\langle D_0,D_1\rangle $
is also a predense
![]() $\le q$
partition of
$\le q$
partition of
![]() $\mathbb {P}$
. We will tacitly make use of this in the below.
$\mathbb {P}$
. We will tacitly make use of this in the below.
7 An axiomatization that does not assume the preservation of the axioms of set theory
Alternatively, we can replace (
![]() $\bar 6$
), (*), (**), (***), and (****) by the following axioms, and in particular we can derive the preservation of the axioms of set theory from natural axioms rather than requiring it. Axiom (6) below is a strengthening of axiom (
$\bar 6$
), (*), (**), (***), and (****) by the following axioms, and in particular we can derive the preservation of the axioms of set theory from natural axioms rather than requiring it. Axiom (6) below is a strengthening of axiom (
![]() $\bar 6$
), which seems to be a natural requirement in the context of class forcing, and could be seen to essentially say that the objects that are our version of names for sets correspond to set-sized objects in a standard class forcing setup. Axiom (7) essentially says that we can freely (from the perspective of
$\bar 6$
), which seems to be a natural requirement in the context of class forcing, and could be seen to essentially say that the objects that are our version of names for sets correspond to set-sized objects in a standard class forcing setup. Axiom (7) essentially says that we can freely (from the perspective of
![]() $\mathcal {M}$
) construct our version of names in
$\mathcal {M}$
) construct our version of names in
![]() $\mathcal {M}$
. Axiom (8) is (pre)tameness, and is only required in the case of class forcing (for it is trivial in the case of set forcing).
$\mathcal {M}$
. Axiom (8) is (pre)tameness, and is only required in the case of class forcing (for it is trivial in the case of set forcing).
-
(6) Strong Set-Likeness: If
 $b\in M$
, then
$b\in M$
, then
 $\{\langle a,p\rangle \mid a\in _p b\}\in M$
.
$\{\langle a,p\rangle \mid a\in _p b\}\in M$
. -
(7) Universality: If
 $S\in \mathcal {C}$
is a relation on
$S\in \mathcal {C}$
is a relation on
 $M\times P$
, then there exists
$M\times P$
, then there exists
 $B\in \mathcal {C}$
such that Moreover, if
$B\in \mathcal {C}$
such that Moreover, if $$ \begin{align*}S(a,p)\textrm{ if and only if }a\in_p B.\end{align*} $$
$$ \begin{align*}S(a,p)\textrm{ if and only if }a\in_p B.\end{align*} $$
 $S\in M$
, then we obtain the above B to be in M, and there is a map
$S\in M$
, then we obtain the above B to be in M, and there is a map
 $\Gamma $
that is first order definable over M which on input
$\Gamma $
that is first order definable over M which on input
 $S\in M$
yields one such witnessing
$S\in M$
yields one such witnessing
 $B\in M$
.Footnote
14
$B\in M$
.Footnote
14
-
(8)
-
• Pretameness:
 $\mathbb {P}$
is pretame (for
$\mathbb {P}$
is pretame (for
 $\mathcal {M}$
).
$\mathcal {M}$
). -
• Tameness: If T contains the power set axiom, then we make the stronger requirement that
 $\mathbb {P}$
is tame (for
$\mathbb {P}$
is tame (for
 $\mathcal {M}$
).
$\mathcal {M}$
).
-
Let us make the important remark that our axioms (1)–(8), as well as the axioms (*), (**), (***), and (****), hold in the standard setup for class forcing, as described for example in [Reference Holy, Krapf, Lücke, Njegomir and Schlicht7]. Given a transitive model
![]() $\mathcal {M}=\langle M,\mathcal {C}\rangle $
of T, and a pretame, or tame (in case T contains the powerset axiom) notion of class forcing
$\mathcal {M}=\langle M,\mathcal {C}\rangle $
of T, and a pretame, or tame (in case T contains the powerset axiom) notion of class forcing
![]() $\mathbb {P}\in \mathcal {C}$
such that for every condition p from
$\mathbb {P}\in \mathcal {C}$
such that for every condition p from
![]() $\mathbb {P}$
, there is a
$\mathbb {P}$
, there is a
![]() $\mathbb {P}$
-generic filter over
$\mathbb {P}$
-generic filter over
![]() $\mathcal {M}$
that contains p as an element (this is the case in particular if
$\mathcal {M}$
that contains p as an element (this is the case in particular if
![]() $\mathcal {M}$
is countableFootnote
15
), interpreting
$\mathcal {M}$
is countableFootnote
15
), interpreting
![]() $a\in _p B$
as
$a\in _p B$
as
![]() $\langle a,p\rangle \in B$
, we arrive at such a standard setup, and it is well-known how to verify axioms (1)–(8), (*), (**), (***), and (****) with respect to
$\langle a,p\rangle \in B$
, we arrive at such a standard setup, and it is well-known how to verify axioms (1)–(8), (*), (**), (***), and (****) with respect to
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathbb {P}$
in this context—for the forcing theorem, as described in our axioms (4) and (5), see [Reference Holy, Krapf, Lücke, Njegomir and Schlicht7, Reference Holy, Krapf and Schlicht8].
$\mathbb {P}$
in this context—for the forcing theorem, as described in our axioms (4) and (5), see [Reference Holy, Krapf, Lücke, Njegomir and Schlicht7, Reference Holy, Krapf and Schlicht8].
Lemma 7.1. The axioms (*) and (**) can be derived from axiom (7).
Proof Essentially, axiom (7) allows us to construct analogues of the usual canonical names for ground model objects and for the generic filter. That is, using axiom (7), by recursion on rank, for
![]() $b\in M$
, we define
$b\in M$
, we define
![]() $\check b$
to be such that
$\check b$
to be such that
![]() $x\in _p\check b$
if and only if
$x\in _p\check b$
if and only if
![]() $p=1$
and x is of the form
$p=1$
and x is of the form
![]() $\check a$
for some
$\check a$
for some
![]() $a\in b$
, and we do this in a definable way, making use of the map
$a\in b$
, and we do this in a definable way, making use of the map
![]() $\Gamma $
. Note that using
$\Gamma $
. Note that using
![]() $\Gamma $
, we in fact obtain a strong form of axiom (*): we have the extra property that the map from b to
$\Gamma $
, we in fact obtain a strong form of axiom (*): we have the extra property that the map from b to
![]() $\check b$
described above is definable over M. We then use this to define
$\check b$
described above is definable over M. We then use this to define
![]() $\dot G$
to be such that
$\dot G$
to be such that
![]() $x\in _p\dot G$
if and only if
$x\in _p\dot G$
if and only if
![]() $p\in P$
and
$p\in P$
and
![]() $x=\check p$
.
$x=\check p$
.
Making heavy use of axioms (6) and (7), our next lemma shows that standard forcing names and their evaluations essentially coincide with elements of our ground model
![]() $\mathcal {M}$
and their images under our evaluation function
$\mathcal {M}$
and their images under our evaluation function
![]() $F_G$
.
$F_G$
.
Lemma 7.2.
-
(i) If
 $\sigma $
is a (class)
$\sigma $
is a (class)
 $\mathbb {P}$
-name in M (or in
$\mathbb {P}$
-name in M (or in
 $\mathcal {C}$
) in the standard sense, then there is
$\mathcal {C}$
) in the standard sense, then there is
 $a\in M$
(or
$a\in M$
(or
 $a\in C$
) such that
$a\in C$
) such that
 $F_G(a)=\sigma ^G$
, where
$F_G(a)=\sigma ^G$
, where
 $\sigma ^G$
denotes the standard evaluation of the name
$\sigma ^G$
denotes the standard evaluation of the name
 $\sigma $
by the generic filter G.
$\sigma $
by the generic filter G. -
(ii) If
 $a\in M$
(or
$a\in M$
(or
 $a\in \mathcal {C}$
), then there is a (class)
$a\in \mathcal {C}$
), then there is a (class)
 $\mathbb {P}$
-name
$\mathbb {P}$
-name
 $\sigma $
in M (or in
$\sigma $
in M (or in
 $\mathcal {C}$
) such that
$\mathcal {C}$
) such that
 $\sigma ^G=F_G(a)$
.
$\sigma ^G=F_G(a)$
.
Thus, in particular,
![]() $\mathcal {M}[G]$
is the standard generic extension of the model
$\mathcal {M}[G]$
is the standard generic extension of the model
![]() $\mathcal {M}$
by the generic filter G.
$\mathcal {M}$
by the generic filter G.
Proof Let us first verify (i). Let
![]() $\sigma $
be a
$\sigma $
be a
![]() $\mathbb {P}$
-name in M. Making use of the map
$\mathbb {P}$
-name in M. Making use of the map
![]() $\Gamma $
that was introduced in axiom (7), we recursively define a translation function h, letting
$\Gamma $
that was introduced in axiom (7), we recursively define a translation function h, letting
It follows that
![]() $F_G(h(\sigma ))=\{F_G(a)\mid \exists p\in G\ a\in _p h(\sigma )\}$
$F_G(h(\sigma ))=\{F_G(a)\mid \exists p\in G\ a\in _p h(\sigma )\}$
Now if
![]() $\sigma \in \mathcal {C}$
, using axiom (7), we can define
$\sigma \in \mathcal {C}$
, using axiom (7), we can define
![]() $h(\sigma )$
to be such that for all
$h(\sigma )$
to be such that for all
![]() $\mathbb {P}$
-names
$\mathbb {P}$
-names
![]() $\tau \in M$
and
$\tau \in M$
and
![]() $p\in P$
,
$p\in P$
,
We thus obtain
![]() $h(\sigma )\in \mathcal {C}$
, and then the same argument as above shows that
$h(\sigma )\in \mathcal {C}$
, and then the same argument as above shows that
![]() $F_G(h(\sigma ))=\sigma ^G$
.
$F_G(h(\sigma ))=\sigma ^G$
.
Now let us verify (ii), in a similar way. Let
![]() $b\in M$
, and making use of axiom (6), we obtain a map
$b\in M$
, and making use of axiom (6), we obtain a map
![]() $E\in \mathcal {C}$
with domain M such that for every
$E\in \mathcal {C}$
with domain M such that for every
![]() $a\in M$
,
$a\in M$
,
![]() $E(a)=\{\langle x,p\rangle \mid x\in _p a\}\in M$
. Making use of this map, we recursively define another translation function g, letting
$E(a)=\{\langle x,p\rangle \mid x\in _p a\}\in M$
. Making use of this map, we recursively define another translation function g, letting
![]() $g(b)=\{\langle g(a),p\rangle \mid a\in E(b),a\in _p b\}$
for
$g(b)=\{\langle g(a),p\rangle \mid a\in E(b),a\in _p b\}$
for
![]() $b\in M$
. Similar to before, it now follows that
$b\in M$
. Similar to before, it now follows that
If
![]() $B\in \mathcal {C}$
, we can define
$B\in \mathcal {C}$
, we can define
![]() $g(B)=\{\langle g(a),p\rangle \mid a\in _p B\}$
, and then the same argument as above shows that
$g(B)=\{\langle g(a),p\rangle \mid a\in _p B\}$
, and then the same argument as above shows that
![]() $g(b)^G=F_G(b)$
.
$g(b)^G=F_G(b)$
.
Our next goal is to show that we can derive axiom (***) as well as the consequences of Theorem 5.1 from axioms (1)–(8). There are two somewhat different ways to do this. The first possibility is to make use of Lemma 7.2, and then invoke the relevant standard results about the preservation of the axioms of set theory in standard generic extensions,Footnote
16
and also about their minimality. The second possibility is to directly verify the individual axioms of set theory in our generic extension
![]() $\mathcal {M}[G]$
from our axioms. The advantage of this second option is that we do not make use of any standard results in this case (but of course, the arguments to verify the individual axioms in our generic extension are essentially analogous to the corresponding classical arguments). We can then infer minimality of
$\mathcal {M}[G]$
from our axioms. The advantage of this second option is that we do not make use of any standard results in this case (but of course, the arguments to verify the individual axioms in our generic extension are essentially analogous to the corresponding classical arguments). We can then infer minimality of
![]() $\mathcal {M}[G]$
by invoking Theorem 5.1 with respect to the standard setup for class forcing.Footnote
17
We would like to present both approaches in the below.
$\mathcal {M}[G]$
by invoking Theorem 5.1 with respect to the standard setup for class forcing.Footnote
17
We would like to present both approaches in the below.
Theorem 7.3. Axioms (1)–(8) imply that
![]() $\mathcal {M}[G]$
is the
$\mathcal {M}[G]$
is the
![]() $\subseteq $
-smallest model of T that contains
$\subseteq $
-smallest model of T that contains
![]() $\mathcal {C}\cup \{G\}$
as a subset of its collection of classes. In particular thus, axiom (***) holds.
$\mathcal {C}\cup \{G\}$
as a subset of its collection of classes. In particular thus, axiom (***) holds.
First Proof Lemma 7.2 shows that our extension
![]() $\mathcal {M}[G]$
is exactly the standard class forcing extension of
$\mathcal {M}[G]$
is exactly the standard class forcing extension of
![]() $\mathcal {M}$
by G, and thus one can apply the standard arguments to show that
$\mathcal {M}$
by G, and thus one can apply the standard arguments to show that
![]() $\mathcal {M}[G]$
is the
$\mathcal {M}[G]$
is the
![]() $\subseteq $
-smallest model
$\subseteq $
-smallest model
![]() $\mathcal {N}$
of T that contains
$\mathcal {N}$
of T that contains
![]() $\mathcal {C}\cup \{G\}$
as a subset of its collection of classes.
$\mathcal {C}\cup \{G\}$
as a subset of its collection of classes.
Second Proof We directly verify the individual axioms in our generic extension. This argument mostly proceeds similar to the proof of [Reference Holy, Krapf and Schlicht8, Theorem 3.1(1)]. The verification of the powerset axiom in
![]() $\mathcal {M}[G]$
proceeds somewhat similar to the proof of [Reference Friedman5, Theorem 2.21], however making use of our modified definition of tameness.
$\mathcal {M}[G]$
proceeds somewhat similar to the proof of [Reference Friedman5, Theorem 2.21], however making use of our modified definition of tameness.
Since
![]() $\mathcal {M}[G]$
is a transitive
$\mathcal {M}[G]$
is a transitive
![]() $\in $
-structure, it clearly satisfies Regularity and Extensionality. Using axiom (7), it is easy to see that
$\in $
-structure, it clearly satisfies Regularity and Extensionality. Using axiom (7), it is easy to see that
![]() $M[G]$
satisfies Pairing, and by axiom (*), it satisfies Infinity.
$M[G]$
satisfies Pairing, and by axiom (*), it satisfies Infinity.
Let us treat the union axiom: Let
![]() $a\in M[G]$
be given; we need to show that for some
$a\in M[G]$
be given; we need to show that for some
![]() $b\in M[G]$
,
$b\in M[G]$
,
![]() $\bigcup a\subseteq b$
. Let
$\bigcup a\subseteq b$
. Let
![]() $X=\{c\mid \exists p\ c\in _p a\}\in M$
by axiom (
$X=\{c\mid \exists p\ c\in _p a\}\in M$
by axiom (
![]() $\bar 6$
). Let
$\bar 6$
). Let
![]() $Y=\{d\mid \exists c\in X\,\exists q\ d\in _q c\}\in M$
by axiom (
$Y=\{d\mid \exists c\in X\,\exists q\ d\in _q c\}\in M$
by axiom (
![]() $\bar 6$
). Using axiom (7), let
$\bar 6$
). Using axiom (7), let
![]() $\dot b\in M$
be such that
$\dot b\in M$
be such that
![]() $d\in _r\dot b$
if and only if
$d\in _r\dot b$
if and only if
![]() $d\in Y$
and
$d\in Y$
and
![]() $r=1$
. Using the definition of
$r=1$
. Using the definition of
![]() $F_G$
, it is straightforward to check that
$F_G$
, it is straightforward to check that
![]() $b=F_G(\dot b)$
is as desired.
$b=F_G(\dot b)$
is as desired.
Let us verify first order class comprehension in
![]() $\mathcal {M}[G]$
. If
$\mathcal {M}[G]$
. If
![]() $\varphi \in \mathcal L(\in )$
and
$\varphi \in \mathcal L(\in )$
and
![]() $B\in \mathcal {C}$
, using axiom (7), let
$B\in \mathcal {C}$
, using axiom (7), let
![]() $A\in \mathcal {C}$
be such that
$A\in \mathcal {C}$
be such that
![]() $a\in _p A$
if and only if
$a\in _p A$
if and only if
![]() $p\operatorname {\mathrm {\Vdash }}\varphi (a,B)$
. It then follows that
$p\operatorname {\mathrm {\Vdash }}\varphi (a,B)$
. It then follows that
![]() $F_G(A)=\{x\in M[G]\mid \mathcal {M}[G]\models \varphi (x,F_G(B))\}$
.
$F_G(A)=\{x\in M[G]\mid \mathcal {M}[G]\models \varphi (x,F_G(B))\}$
.
We now show that
![]() $\mathcal {M}[G]$
satisfies collection. Let
$\mathcal {M}[G]$
satisfies collection. Let
![]() $a\in M$
,
$a\in M$
,
![]() $A\in \mathcal {C}$
, and assume that
$A\in \mathcal {C}$
, and assume that
![]() $\mathcal {M}[G]\models \forall x\in F_G(a)\,\exists y\ \langle x,y\rangle \in F_G(A)$
. We need to find
$\mathcal {M}[G]\models \forall x\in F_G(a)\,\exists y\ \langle x,y\rangle \in F_G(A)$
. We need to find
![]() $b\in M$
such that
$b\in M$
such that
![]() $\mathcal {M}[G]\models \forall x\in F_G(a)\,\exists y\in F_G(b)\ \langle x,y\rangle \in F_G(A)$
.
$\mathcal {M}[G]\models \forall x\in F_G(a)\,\exists y\in F_G(b)\ \langle x,y\rangle \in F_G(A)$
.
By axiom (4), we may pick some
![]() $p\in G$
such that
$p\in G$
such that
![]() $p\operatorname {\mathrm {\Vdash }}\forall x\in a\,\exists y\ \langle x,y\rangle \in A$
. By axiom (6),
$p\operatorname {\mathrm {\Vdash }}\forall x\in a\,\exists y\ \langle x,y\rangle \in A$
. By axiom (6),
![]() $X=\{\langle c,r\rangle \mid c\in _r a\}\in M$
. For each
$X=\{\langle c,r\rangle \mid c\in _r a\}\in M$
. For each
![]() $\langle c,r\rangle \in X$
, let
$\langle c,r\rangle \in X$
, let
By Lemma 4.5, it follows that each
![]() $D_{\langle c,r\rangle }$
is dense below p in
$D_{\langle c,r\rangle }$
is dense below p in
![]() $\mathbb {P}$
. Using that
$\mathbb {P}$
. Using that
![]() $\mathbb {P}$
is pretame by axiom (8), there is
$\mathbb {P}$
is pretame by axiom (8), there is
![]() $q\in G$
below p and there is a sequence
$q\in G$
below p and there is a sequence
![]() $\langle d_{\langle c,r\rangle }\mid \langle c,r\rangle \in X\rangle \in M$
such that
$\langle d_{\langle c,r\rangle }\mid \langle c,r\rangle \in X\rangle \in M$
such that
![]() $d_{\langle c,r\rangle }\subseteq D_{\langle c,r\rangle }$
and
$d_{\langle c,r\rangle }\subseteq D_{\langle c,r\rangle }$
and
![]() $d_{\langle c,r\rangle }$
is predense below q in
$d_{\langle c,r\rangle }$
is predense below q in
![]() $\mathbb {P}$
for each
$\mathbb {P}$
for each
![]() $\langle c,r\rangle \in X$
.
$\langle c,r\rangle \in X$
.
Using collection in M, there is a set
![]() $Y\in M$
such that for each
$Y\in M$
such that for each
![]() $\langle c,r\rangle \in X$
and for each
$\langle c,r\rangle \in X$
and for each
![]() $s\in d_{\langle c,r\rangle }$
that is compatible with r, there is
$s\in d_{\langle c,r\rangle }$
that is compatible with r, there is
![]() $d\in Y$
such that
$d\in Y$
such that
![]() $s\operatorname {\mathrm {\Vdash }}\varphi (c,d,A)$
. Using axiom (7), let
$s\operatorname {\mathrm {\Vdash }}\varphi (c,d,A)$
. Using axiom (7), let
![]() $b\in M$
be such that
$b\in M$
be such that
![]() $d\in _s b$
if and only if
$d\in _s b$
if and only if
![]() $d\in Y$
and there is
$d\in Y$
and there is
![]() $\langle c,r\rangle \in X$
such that
$\langle c,r\rangle \in X$
such that
![]() $s\in d_{\langle c,r\rangle }$
and
$s\in d_{\langle c,r\rangle }$
and
![]() $s\operatorname {\mathrm {\Vdash }}\varphi (c,d,A)$
. Then, by construction,
$s\operatorname {\mathrm {\Vdash }}\varphi (c,d,A)$
. Then, by construction,
![]() $\mathcal {M}[G]\models \forall x\in F_G(a)\,\exists y\in F_G(b)\ \langle x,y\rangle \in F_G(A)$
, as desired.
$\mathcal {M}[G]\models \forall x\in F_G(a)\,\exists y\in F_G(b)\ \langle x,y\rangle \in F_G(A)$
, as desired.
Let us next show that
![]() $\mathcal {M}[G]$
satisfies separation. Let
$\mathcal {M}[G]$
satisfies separation. Let
![]() $a\in M$
and
$a\in M$
and
![]() $A\in \mathcal {C}$
. We need to find
$A\in \mathcal {C}$
. We need to find
![]() $b\in M$
such that
$b\in M$
such that
![]() $\mathcal {M}[G]\models F_G(b)=F_G(a)\cap F_G(A)$
. By axiom (6),
$\mathcal {M}[G]\models F_G(b)=F_G(a)\cap F_G(A)$
. By axiom (6),
![]() $X=\{\langle c,r\rangle \mid c\in _r a\}\in M$
. For each
$X=\{\langle c,r\rangle \mid c\in _r a\}\in M$
. For each
![]() $\langle c,r\rangle \in X$
, let
$\langle c,r\rangle \in X$
, let
![]() $D_{\langle c,r\rangle }=\{q\in P\mid q\le r\textrm { decides }c\in A\,\lor \,q\perp r\}\in \mathcal {C}$
. By an easy application of Lemma 4.1, it follows that each
$D_{\langle c,r\rangle }=\{q\in P\mid q\le r\textrm { decides }c\in A\,\lor \,q\perp r\}\in \mathcal {C}$
. By an easy application of Lemma 4.1, it follows that each
![]() $D_{\langle c,r\rangle }$
is dense in
$D_{\langle c,r\rangle }$
is dense in
![]() $\mathbb {P}$
. Using that
$\mathbb {P}$
. Using that
![]() $\mathbb {P}$
is pretame by axiom (8), we may pick
$\mathbb {P}$
is pretame by axiom (8), we may pick
![]() $p\in G$
and a sequence
$p\in G$
and a sequence
![]() $\langle d_{\langle c,r\rangle }\mid \langle c,r\rangle \in X\rangle \in M$
such that
$\langle d_{\langle c,r\rangle }\mid \langle c,r\rangle \in X\rangle \in M$
such that
![]() $d_{\langle c,r\rangle }\subseteq D_{\langle c,r\rangle }$
and
$d_{\langle c,r\rangle }\subseteq D_{\langle c,r\rangle }$
and
![]() $d_{\langle c,r\rangle }$
is predense below p in
$d_{\langle c,r\rangle }$
is predense below p in
![]() $\mathbb {P}$
for each
$\mathbb {P}$
for each
![]() $\langle c,r\rangle \in X$
. Using axiom (7), let
$\langle c,r\rangle \in X$
. Using axiom (7), let
![]() $b\in M$
be such that
$b\in M$
be such that
![]() $c\in _q b$
if and only if there is
$c\in _q b$
if and only if there is
![]() $r\in P$
such that
$r\in P$
such that
![]() $q\le r$
,
$q\le r$
,
![]() $\langle c,r\rangle \in X$
,
$\langle c,r\rangle \in X$
,
![]() $q\in d_{\langle c,r\rangle }$
, and
$q\in d_{\langle c,r\rangle }$
, and
![]() $q\operatorname {\mathrm {\Vdash }} c\in A$
. It clearly follows that b is as desired.
$q\operatorname {\mathrm {\Vdash }} c\in A$
. It clearly follows that b is as desired.
Let us observe at this point that we have by now verified the axioms of
![]() $\mathrm {GB}^-$
in
$\mathrm {GB}^-$
in
![]() $\mathcal {M}[G]$
. By our absoluteness assumptions on the
$\mathcal {M}[G]$
. By our absoluteness assumptions on the
![]() $\mathbb {P}$
-membership relation, this allows us to perform the relevant recursion to obtain
$\mathbb {P}$
-membership relation, this allows us to perform the relevant recursion to obtain
![]() $F_G\in \mathcal {C}[G]$
.
$F_G\in \mathcal {C}[G]$
.
Let us argue that the axiom of choice is preserved. Let
![]() $a\in M$
. We have to find a well-order
$a\in M$
. We have to find a well-order
![]() $\triangleleft $
of
$\triangleleft $
of
![]() $F_G(a)$
in
$F_G(a)$
in
![]() $M[G]$
. Using axiom (
$M[G]$
. Using axiom (
![]() $\bar 6$
), let
$\bar 6$
), let
![]() $X=\{c\mid \exists r\in P\ c\in _r a\}\in M$
, and let
$X=\{c\mid \exists r\in P\ c\in _r a\}\in M$
, and let
![]() $\prec $
be a well-order of X, using the axiom of choice in M. Now given x and y in
$\prec $
be a well-order of X, using the axiom of choice in M. Now given x and y in
![]() $F_G(a)$
, making use of our above observation, we simply let
$F_G(a)$
, making use of our above observation, we simply let
![]() $x\triangleleft y$
if and only if there is
$x\triangleleft y$
if and only if there is
![]() $\dot x\in X$
such that
$\dot x\in X$
such that
![]() $x=F_G(\dot x)$
and for all
$x=F_G(\dot x)$
and for all
![]() $\dot y\in X$
such that
$\dot y\in X$
such that
![]() $y=F_G(\dot y)$
, we have
$y=F_G(\dot y)$
, we have
![]() $\dot x\prec \dot y$
. Using that separation holds in
$\dot x\prec \dot y$
. Using that separation holds in
![]() $\mathcal {M}[G]$
, we thus obtain
$\mathcal {M}[G]$
, we thus obtain
![]() $\triangleleft \in M[G]$
.
$\triangleleft \in M[G]$
.
Let’s argue that if
![]() $\mathcal {M}$
has a set-like global well-order
$\mathcal {M}$
has a set-like global well-order
![]() $\prec \,\in \mathcal {C}$
, then we can find a set-like global well-order
$\prec \,\in \mathcal {C}$
, then we can find a set-like global well-order
![]() $\triangleleft $
of
$\triangleleft $
of
![]() $M[G]$
in
$M[G]$
in
![]() $\mathcal {C}[G]$
. Using our above observation, we simply let
$\mathcal {C}[G]$
. Using our above observation, we simply let
![]() $x\triangleleft y$
if and only if there is
$x\triangleleft y$
if and only if there is
![]() $\dot x\in M$
such that
$\dot x\in M$
such that
![]() $x=F_G(\dot x)$
and for all
$x=F_G(\dot x)$
and for all
![]() $\dot y\in M$
such that
$\dot y\in M$
such that
![]() $y=F_G(\dot y)$
, we have
$y=F_G(\dot y)$
, we have
![]() $\dot x\prec \dot y$
. Using that first order class comprehension holds in
$\dot x\prec \dot y$
. Using that first order class comprehension holds in
![]() $\mathcal {M}[G]$
, we thus obtain
$\mathcal {M}[G]$
, we thus obtain
![]() $\triangleleft \in \mathcal {C}[G]$
.
$\triangleleft \in \mathcal {C}[G]$
.
Finally, we argue that assuming
![]() $\mathbb {P}$
to be tame, the powerset axiom is preserved. Working in
$\mathbb {P}$
to be tame, the powerset axiom is preserved. Working in
![]() $\mathcal {M}[G]$
, it suffices to show that
$\mathcal {M}[G]$
, it suffices to show that
![]() $\mathcal P(a)$
exists in
$\mathcal P(a)$
exists in
![]() $M[G]$
for every
$M[G]$
for every
![]() $a\in M$
: If
$a\in M$
: If
![]() $b\in M[G]$
,
$b\in M[G]$
,
![]() $b=F_G(\sigma )$
, using axiom (
$b=F_G(\sigma )$
, using axiom (
![]() $\bar 6$
), let
$\bar 6$
), let
![]() $X=\{c\mid \exists r\in P\ c\in _r\sigma \}\in M$
. Using that
$X=\{c\mid \exists r\in P\ c\in _r\sigma \}\in M$
. Using that
![]() $F_G\in \mathcal {C}[G]$
, and using that replacement holds in
$F_G\in \mathcal {C}[G]$
, and using that replacement holds in
![]() $\mathcal {M}[G]$
, there is a surjection from X onto b in
$\mathcal {M}[G]$
, there is a surjection from X onto b in
![]() $M[G]$
, and this surjection naturally induces a surjection from
$M[G]$
, and this surjection naturally induces a surjection from
![]() $\mathcal P(X)$
onto
$\mathcal P(X)$
onto
![]() $\mathcal P(b)$
in
$\mathcal P(b)$
in
![]() $\mathcal {C}[G]$
. Using replacement in
$\mathcal {C}[G]$
. Using replacement in
![]() $\mathcal {M}[G]$
once again, if
$\mathcal {M}[G]$
once again, if
![]() $\mathcal P(X)\in M[G]$
, it follows that
$\mathcal P(X)\in M[G]$
, it follows that
![]() $\mathcal P(b)\in M[G]$
.
$\mathcal P(b)\in M[G]$
.
Therefore, let
![]() $a\in M$
. By Lemma 4.2, we may pick
$a\in M$
. By Lemma 4.2, we may pick
![]() $q\in G$
and
$q\in G$
and
![]() $\alpha \in \operatorname {\mathrm {Ord}}(M)$
witnessing the tameness of
$\alpha \in \operatorname {\mathrm {Ord}}(M)$
witnessing the tameness of
![]() $\mathbb {P}$
with respect to a. Now for any
$\mathbb {P}$
with respect to a. Now for any
![]() $\sigma \in M$
such that
$\sigma \in M$
such that
![]() $q\operatorname {\mathrm {\Vdash }}\sigma \subseteq \check a$
, consider the sequence of classes
$q\operatorname {\mathrm {\Vdash }}\sigma \subseteq \check a$
, consider the sequence of classes
![]() $\vec D=\langle \langle D_0^i,D_1^i\rangle \mid i\in a\rangle $
defined by letting
$\vec D=\langle \langle D_0^i,D_1^i\rangle \mid i\in a\rangle $
defined by letting
![]() $D_0^i=\{r\le q\mid r\operatorname {\mathrm {\Vdash }}\check i\not \in \sigma \}$
and
$D_0^i=\{r\le q\mid r\operatorname {\mathrm {\Vdash }}\check i\not \in \sigma \}$
and
![]() $D_1^i=\{r\le q\mid r\operatorname {\mathrm {\Vdash }}\check i\in \sigma \}$
. For every
$D_1^i=\{r\le q\mid r\operatorname {\mathrm {\Vdash }}\check i\in \sigma \}$
. For every
![]() $i\in a$
and
$i\in a$
and
![]() $j\in \{0,1\}$
, let
$j\in \{0,1\}$
, let
![]() $E_j^i$
be the dense set obtained as the downward closure of
$E_j^i$
be the dense set obtained as the downward closure of
![]() $D_j^i$
. By pretameness, for every
$D_j^i$
. By pretameness, for every
![]() $r\le q$
, we obtain
$r\le q$
, we obtain
![]() $s\le r$
and a predense
$s\le r$
and a predense
![]() $\le s$
partition
$\le s$
partition
![]() $\vec d=\langle \langle d_0^i,d_1^i\rangle \mid i\in a\rangle $
such that
$\vec d=\langle \langle d_0^i,d_1^i\rangle \mid i\in a\rangle $
such that
![]() $d_0^i\subseteq E_0^i$
and
$d_0^i\subseteq E_0^i$
and
![]() $d_1^i\subseteq E_1^i$
for every
$d_1^i\subseteq E_1^i$
for every
![]() $i\in a$
. By our choice of q and
$i\in a$
. By our choice of q and
![]() $\alpha $
, we find
$\alpha $
, we find
![]() $\vec e\in V_\alpha ^M$
and
$\vec e\in V_\alpha ^M$
and
![]() $t\le s$
such that
$t\le s$
such that
![]() $\vec d$
and
$\vec d$
and
![]() $\vec e$
are equivalent
$\vec e$
are equivalent
![]() $\le s$
.Footnote
18
Since this yields a dense set of conditions t, we may pick such
$\le s$
.Footnote
18
Since this yields a dense set of conditions t, we may pick such
![]() $t\in G$
. Thus,
$t\in G$
. Thus,
and therefore using axiom (7), letting
![]() $\sigma _0\in M$
be such that
$\sigma _0\in M$
be such that
![]() $c\in _s\sigma _0$
if and only if
$c\in _s\sigma _0$
if and only if
![]() $c=\check i$
for some
$c=\check i$
for some
![]() $i\in a$
and
$i\in a$
and
![]() $s\in e_1^i$
, it follows that
$s\in e_1^i$
, it follows that
![]() $F_G(\sigma )=F_G(\sigma _0)$
. Making use of the map
$F_G(\sigma )=F_G(\sigma _0)$
. Making use of the map
![]() $\Gamma $
described in axiom (7), we have a definable choice of such
$\Gamma $
described in axiom (7), we have a definable choice of such
![]() $\sigma _0$
’s in M given a predense
$\sigma _0$
’s in M given a predense
![]() $\le r$
partition
$\le r$
partition
![]() $\vec e\in V_\alpha ^M$
, and using replacement in M, we thus obtain a set
$\vec e\in V_\alpha ^M$
, and using replacement in M, we thus obtain a set
![]() $\Sigma \in M$
containing a suitable
$\Sigma \in M$
containing a suitable
![]() $\sigma _0$
for every predense
$\sigma _0$
for every predense
![]() $\le r$
partition
$\le r$
partition
![]() $\vec e\in V_\alpha ^M$
. Using axiom (7) once again, let
$\vec e\in V_\alpha ^M$
. Using axiom (7) once again, let
![]() $\pi \in M$
be such that
$\pi \in M$
be such that
![]() $c\in _s\pi $
if and only if
$c\in _s\pi $
if and only if
![]() $c\in \Sigma $
and
$c\in \Sigma $
and
![]() $s=1$
. Using separation in
$s=1$
. Using separation in
![]() $\mathcal {M}[G]$
, this clearly yields
$\mathcal {M}[G]$
, this clearly yields
![]() $\{x\in F_G(\pi )\mid x\subseteq a\}\in M[G]$
to be the powerset of a in
$\{x\in F_G(\pi )\mid x\subseteq a\}\in M[G]$
to be the powerset of a in
![]() $\mathcal {M}[G]$
, as desired.
$\mathcal {M}[G]$
, as desired.
Having verified all axioms of T in
![]() $\mathcal {M}[G]$
, there are two ways to end the proof: In case axiom (****) holds, the statement of our theorem is a direct consequence of Theorem 5.1, and we have not made any use of the standard setup for class forcing in this case. Without axiom (****), we use that all of our axioms hold in the standard setup for class forcing with
$\mathcal {M}[G]$
, there are two ways to end the proof: In case axiom (****) holds, the statement of our theorem is a direct consequence of Theorem 5.1, and we have not made any use of the standard setup for class forcing in this case. Without axiom (****), we use that all of our axioms hold in the standard setup for class forcing with
![]() $\mathbb {P}$
over
$\mathbb {P}$
over
![]() $\mathcal {M}$
, and that
$\mathcal {M}$
, and that
![]() $\mathcal {M}[G]$
is just the standard class forcing extension of
$\mathcal {M}[G]$
is just the standard class forcing extension of
![]() $\mathcal {M}$
by G by Lemma 7.2, and therefore
$\mathcal {M}$
by G by Lemma 7.2, and therefore
![]() $\mathcal {M}[G]$
is the
$\mathcal {M}[G]$
is the
![]() $\subseteq $
-smallest model of T that contains
$\subseteq $
-smallest model of T that contains
![]() $\mathcal {C}\cup \{G\}$
as a subset of its collection of classes by Theorem 5.1 used within the standard setup.
$\mathcal {C}\cup \{G\}$
as a subset of its collection of classes by Theorem 5.1 used within the standard setup.
Our next proposition shows in particular that notions of forcing that preserve
![]() $\mathrm {GB}$
need to be tame (in the sense of Definition 6.2), thus strengthening [Reference Friedman5, Proposition 2.20]. Its proof is similar to the proof that is provided for [Reference Friedman5, Proposition 2.20].
$\mathrm {GB}$
need to be tame (in the sense of Definition 6.2), thus strengthening [Reference Friedman5, Proposition 2.20]. Its proof is similar to the proof that is provided for [Reference Friedman5, Proposition 2.20].
Proposition 7.4. Axioms (1)–(7) together with axiom (***) imply axiom (8).
Proof If
![]() $\mathbb {P}$
is not pretame, then there is a sequence
$\mathbb {P}$
is not pretame, then there is a sequence
![]() $\vec D=\langle D_i\mid i\in I\rangle \in \mathcal {C}$
of dense subclasses of
$\vec D=\langle D_i\mid i\in I\rangle \in \mathcal {C}$
of dense subclasses of
![]() $\mathbb {P}$
with
$\mathbb {P}$
with
![]() $I\in M$
and a condition
$I\in M$
and a condition
![]() $p\in P$
witnessing that pretameness fails with respect to
$p\in P$
witnessing that pretameness fails with respect to
![]() $\vec D$
. Using axiom (1), let G be a
$\vec D$
. Using axiom (1), let G be a
![]() $\mathbb {P}$
-generic filter over
$\mathbb {P}$
-generic filter over
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $p\in G$
. In the extension
$p\in G$
. In the extension
![]() $\mathcal {M}[G]$
, consider the (class) function
$\mathcal {M}[G]$
, consider the (class) function
![]() $F\colon I\to \operatorname {\mathrm {Ord}}^M$
defined by letting
$F\colon I\to \operatorname {\mathrm {Ord}}^M$
defined by letting
which is an element of
![]() $\mathcal {C}[G]$
by first order class comprehension in
$\mathcal {C}[G]$
by first order class comprehension in
![]() $\mathcal {M}[G]$
. Since replacement holds in
$\mathcal {M}[G]$
. Since replacement holds in
![]() $\mathcal {M}[G]$
, there is some
$\mathcal {M}[G]$
, there is some
![]() $x\in M[G]$
with
$x\in M[G]$
with
![]() $\operatorname {\mathrm {ran}} F\subseteq x$
. Let
$\operatorname {\mathrm {ran}} F\subseteq x$
. Let
![]() $\gamma =\sup x$
. Using axiom (4), let
$\gamma =\sup x$
. Using axiom (4), let
![]() $q\le p$
be a condition in G that forces this property of
$q\le p$
be a condition in G that forces this property of
![]() $\check \gamma $
. Using our assumption on p and on
$\check \gamma $
. Using our assumption on p and on
![]() $\vec D$
however,
$\vec D$
however,
yielding
![]() $G\cap D_i\cap V_\gamma ^M=\emptyset $
, a contradiction.
$G\cap D_i\cap V_\gamma ^M=\emptyset $
, a contradiction.
If T contains the powerset axiom however
![]() $\mathbb {P}$
is not tame, we may thus choose
$\mathbb {P}$
is not tame, we may thus choose
![]() $a\in M$
and
$a\in M$
and
![]() $p\in P$
such that for every
$p\in P$
such that for every
![]() $\alpha \in \operatorname {\mathrm {Ord}}(M)$
and
$\alpha \in \operatorname {\mathrm {Ord}}(M)$
and
![]() $q\le p$
, there is
$q\le p$
, there is
![]() $r\le q$
and a sequence
$r\le q$
and a sequence
![]() $\vec d\in M$
of predense
$\vec d\in M$
of predense
![]() $\le r$
partitions of
$\le r$
partitions of
![]() $\mathbb {P}$
with domain a such that whenever
$\mathbb {P}$
with domain a such that whenever
![]() $s\le r$
, then
$s\le r$
, then
![]() $\vec d$
is not equivalent
$\vec d$
is not equivalent
![]() $\le s$
to any
$\le s$
to any
![]() $\vec e$
in
$\vec e$
in
![]() $V_\alpha ^M$
. Using axiom (1), let G be a
$V_\alpha ^M$
. Using axiom (1), let G be a
![]() $\mathbb {P}$
-generic filter over
$\mathbb {P}$
-generic filter over
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $p\in G$
. Since the above yields a dense set of such conditions r for every
$p\in G$
. Since the above yields a dense set of such conditions r for every
![]() $\alpha \in \operatorname {\mathrm {Ord}}(M)$
, by Lemma 4.2, there are
$\alpha \in \operatorname {\mathrm {Ord}}(M)$
, by Lemma 4.2, there are
![]() $r_\alpha \in G$
and a sequence of predense
$r_\alpha \in G$
and a sequence of predense
![]() $\le r_\alpha $
partitions
$\le r_\alpha $
partitions
![]() $\vec d_\alpha =\langle \langle d_{\alpha ,0}^i,d_{\alpha ,1}^i\rangle \mid i\in a\rangle \in M$
for every
$\vec d_\alpha =\langle \langle d_{\alpha ,0}^i,d_{\alpha ,1}^i\rangle \mid i\in a\rangle \in M$
for every
![]() $\alpha \in \operatorname {\mathrm {Ord}}(M)$
, witnessing that
$\alpha \in \operatorname {\mathrm {Ord}}(M)$
, witnessing that
![]() $\mathbb {P}$
is not tame.Footnote
19
Whenever
$\mathbb {P}$
is not tame.Footnote
19
Whenever
![]() $\vec d=\langle \langle d_0^i,d_1^i\rangle \mid i\in a\rangle \in M$
is a sequence of predense
$\vec d=\langle \langle d_0^i,d_1^i\rangle \mid i\in a\rangle \in M$
is a sequence of predense
![]() $\le t$
partitions for some
$\le t$
partitions for some
![]() $t\in G$
, we use axiom (7) to define
$t\in G$
, we use axiom (7) to define
![]() $\dot f_{\vec d}\in M$
, letting
$\dot f_{\vec d}\in M$
, letting
![]() $x\in _u\dot f_{\vec d}$
if and only if
$x\in _u\dot f_{\vec d}$
if and only if
That is,
![]() $\dot f_{\vec d}$
can be seen as a canonical name for the function
$\dot f_{\vec d}$
can be seen as a canonical name for the function
![]() $f_{\vec d}\in M[G]$
,
$f_{\vec d}\in M[G]$
,
![]() $f_{\vec d}\colon a\to 2$
that is defined by letting
$f_{\vec d}\colon a\to 2$
that is defined by letting
![]() $f_{\vec d}(i)=0\,\iff \,G\cap d_0^i\ne \emptyset $
for every
$f_{\vec d}(i)=0\,\iff \,G\cap d_0^i\ne \emptyset $
for every
![]() $i\in a$
. Note that, using axioms (4) and (5), two sequences
$i\in a$
. Note that, using axioms (4) and (5), two sequences
![]() $\vec d$
and
$\vec d$
and
![]() $\vec d'$
of predense
$\vec d'$
of predense
![]() $\le t$
partitions with domain a of
$\le t$
partitions with domain a of
![]() $\mathbb {P}$
in
$\mathbb {P}$
in
![]() $\mathcal {C}$
are equivalent
$\mathcal {C}$
are equivalent
![]() $\le t$
if and only if
$\le t$
if and only if
![]() $t\operatorname {\mathrm {\Vdash }}\dot f_{\vec d}=\dot f_{\vec d'}$
. Thus, for any
$t\operatorname {\mathrm {\Vdash }}\dot f_{\vec d}=\dot f_{\vec d'}$
. Thus, for any
![]() $\alpha \in \operatorname {\mathrm {Ord}}^M$
,
$\alpha \in \operatorname {\mathrm {Ord}}^M$
,
![]() $r_\alpha $
forces that
$r_\alpha $
forces that
![]() $\dot f_{\vec d_\alpha }\ne \dot f_{\vec e}$
for any predense
$\dot f_{\vec d_\alpha }\ne \dot f_{\vec e}$
for any predense
![]() $\le r_\alpha $
partition
$\le r_\alpha $
partition
![]() $\vec e\in V_\alpha ^M$
with domain a. This implies that in
$\vec e\in V_\alpha ^M$
with domain a. This implies that in
![]() $\mathcal {M}[G]$
, we obtain a cofinal partial function F from
$\mathcal {M}[G]$
, we obtain a cofinal partial function F from
![]() $\{f\in M[G]\mid f\colon a\to 2\}$
to
$\{f\in M[G]\mid f\colon a\to 2\}$
to
![]() $\operatorname {\mathrm {Ord}}$
, by letting
$\operatorname {\mathrm {Ord}}$
, by letting
![]() $F(f)$
be the least
$F(f)$
be the least
![]() $\alpha $
such that there is a condition
$\alpha $
such that there is a condition
![]() $r\in G$
and a predense
$r\in G$
and a predense
![]() $\le r$
partition
$\le r$
partition
![]() $\vec e\in V_\alpha ^M$
with domain a such that
$\vec e\in V_\alpha ^M$
with domain a such that
![]() $f=f_{\vec e}$
. By replacement in
$f=f_{\vec e}$
. By replacement in
![]() $\mathcal {M}[G]$
thus, the powerset of a cannot exist as a set in
$\mathcal {M}[G]$
thus, the powerset of a cannot exist as a set in
![]() $M[G]$
, and hence
$M[G]$
, and hence
![]() $\mathcal {M}[G]$
does not satisfy the powerset axiom.
$\mathcal {M}[G]$
does not satisfy the powerset axiom.
8 Set forcing
The axioms for set forcing, which are essentially as in [Reference Freire3], can easily be derived from the case of class forcing over models of
![]() $\mathrm {GBc}$
that was treated in this paper. In addition, we will also consider the base theories
$\mathrm {GBc}$
that was treated in this paper. In addition, we will also consider the base theories
![]() $\mathrm {ZF}^-$
,
$\mathrm {ZF}^-$
,
![]() $\mathrm {ZFC}^-$
, and
$\mathrm {ZFC}^-$
, and
![]() $\mathrm {ZF}$
, which correspond to the second order theories
$\mathrm {ZF}$
, which correspond to the second order theories
![]() $\mathrm {GB}^-$
,
$\mathrm {GB}^-$
,
![]() $\mathrm {GBc}^-$
, and
$\mathrm {GBc}^-$
, and
![]() $\mathrm {GB}$
. Let T thus denote our base theory, which will either be
$\mathrm {GB}$
. Let T thus denote our base theory, which will either be
![]() $\mathrm {ZF}^-$
,
$\mathrm {ZF}^-$
,
![]() $\mathrm {ZFC}^-$
,
$\mathrm {ZFC}^-$
,
![]() $\mathrm {ZF}$
, or
$\mathrm {ZF}$
, or
![]() $\mathrm {ZFC}$
. Our terminology will be slightly different from that of [Reference Freire3]. In this section, let
$\mathrm {ZFC}$
. Our terminology will be slightly different from that of [Reference Freire3]. In this section, let
![]() $\mathcal L(\in )$
denote the collection of first order formulas.
$\mathcal L(\in )$
denote the collection of first order formulas.
Definition 8.1. A set forcing generic framework is a tuple of the form
-
• M is a transitive set-size model of T.
-
•
 $\mathbb {P}=\langle P,\le \rangle \in M$
is a preorder.
$\mathbb {P}=\langle P,\le \rangle \in M$
is a preorder. -
• The
 $\mathbb {P}$
-membership relation R is a relation on
$\mathbb {P}$
-membership relation R is a relation on
 $P\times M^2$
that is definable over M by an
$P\times M^2$
that is definable over M by an
 $\mathcal L(\in )$
-formula. We denote the property
$\mathcal L(\in )$
-formula. We denote the property
 $R(p,a,b)$
as
$R(p,a,b)$
as
 $a\in _p b$
.Footnote
20
$a\in _p b$
.Footnote
20
-
•
 $\mathfrak G$
is a second order unary predicate on P, i.e., a unary predicate on
$\mathfrak G$
is a second order unary predicate on P, i.e., a unary predicate on
 $\mathcal P(P)$
, and we require that
$\mathcal P(P)$
, and we require that
 $\mathfrak G(G)$
implies that
$\mathfrak G(G)$
implies that
 $G\subseteq \mathbb {P}$
is a filter. If
$G\subseteq \mathbb {P}$
is a filter. If
 $\mathfrak G(G)$
holds, we say that G is a generic filter, or a
$\mathfrak G(G)$
holds, we say that G is a generic filter, or a
 $\mathbb {P}$
-generic filter on M. Whenever we quantify over G in the following, we assume that we quantify over G’s such that
$\mathbb {P}$
-generic filter on M. Whenever we quantify over G in the following, we assume that we quantify over G’s such that
 $\mathfrak G(G)$
holds.
$\mathfrak G(G)$
holds. -
• For every
 $\varphi \in \mathcal L(\in )$
,
$\varphi \in \mathcal L(\in )$
,
 $\operatorname {\mathrm {\Vdash }}_\varphi \in \mathcal {C}$
is a predicate (which we also call a forcing relation for
$\operatorname {\mathrm {\Vdash }}_\varphi \in \mathcal {C}$
is a predicate (which we also call a forcing relation for
 $\varphi $
) on
$\varphi $
) on
 $P\times M^m$
, where m denotes the number of free variables of
$P\times M^m$
, where m denotes the number of free variables of
 $\varphi $
. If
$\varphi $
. If
 $\langle q,a_0,\ldots ,a_{m-1}\rangle \in \operatorname {\mathrm {\Vdash }}_\varphi $
, we also write
$\langle q,a_0,\ldots ,a_{m-1}\rangle \in \operatorname {\mathrm {\Vdash }}_\varphi $
, we also write
 $q\operatorname {\mathrm {\Vdash }}\varphi (a_0,\ldots ,a_{m-1})$
.
$q\operatorname {\mathrm {\Vdash }}\varphi (a_0,\ldots ,a_{m-1})$
.
Let us briefly provide the list of corresponding axioms for set forcing.
-
(S1) Existence of generic filters:
 $\forall p\in P\,\exists G\ p\in G$
.
$\forall p\in P\,\exists G\ p\in G$
. -
(S2) Well-Foundedness: The binary relation
 $\exists p\in \mathbb {P}\ a\in _p b$
on M is well-founded.
$\exists p\in \mathbb {P}\ a\in _p b$
on M is well-founded. -
(S3) Growth of Information: For all
 $\varphi \in \mathcal L(\in )$
, for all
$\varphi \in \mathcal L(\in )$
, for all
 $\vec a\in M$
, and
$\vec a\in M$
, and
 $p,q\in P$
, if
$p,q\in P$
, if
 $p\operatorname {\mathrm {\Vdash }}\varphi (\vec a)$
and
$p\operatorname {\mathrm {\Vdash }}\varphi (\vec a)$
and
 $q\le p$
, then
$q\le p$
, then
 $q\operatorname {\mathrm {\Vdash }}\varphi (\vec a)$
.
$q\operatorname {\mathrm {\Vdash }}\varphi (\vec a)$
.
Define the relation
![]() $\in _G$
on M by letting
$\in _G$
on M by letting
![]() $a\in _G b$
if
$a\in _G b$
if
![]() $\exists p\in G\ a\in _p b$
. Recursively define our evaluation function
$\exists p\in G\ a\in _p b$
. Recursively define our evaluation function
![]() $F_G$
along the relation
$F_G$
along the relation
![]() $\in _G$
, letting
$\in _G$
, letting
![]() $F_G(a)=\{F_G(b)\mid b\in _G a\}$
for each
$F_G(a)=\{F_G(b)\mid b\in _G a\}$
for each
![]() $a\in M$
. Let
$a\in M$
. Let
![]() $M[G]$
denote the
$M[G]$
denote the
![]() $\in $
-structure on the transitive set
$\in $
-structure on the transitive set
![]() $F_G[M]$
.
$F_G[M]$
.
-
(S4) Truth Lemma: For all
 $\varphi \in \mathcal L(\in )$
, all
$\varphi \in \mathcal L(\in )$
, all
 $\vec a\in M$
, and all G,
$\vec a\in M$
, and all G,  $$ \begin{align*}M[G]\models\varphi(F_G(\vec a))\textrm{ iff }\exists p\in G\ p\operatorname{\mathrm{\Vdash}}\varphi(\vec a).\end{align*} $$
$$ \begin{align*}M[G]\models\varphi(F_G(\vec a))\textrm{ iff }\exists p\in G\ p\operatorname{\mathrm{\Vdash}}\varphi(\vec a).\end{align*} $$
-
(S5) Definability Lemma: For all
 $\varphi \in \mathcal L(\in )$
, all
$\varphi \in \mathcal L(\in )$
, all
 $\vec a\in M$
, and
$\vec a\in M$
, and
 $p\in P$
,
$p\in P$
,  $$ \begin{align*}p\operatorname{\mathrm{\Vdash}}\varphi(\vec a)\textrm{ iff }\forall G\ni p\ M[G]\models\varphi(F_G(\vec a)).\end{align*} $$
$$ \begin{align*}p\operatorname{\mathrm{\Vdash}}\varphi(\vec a)\textrm{ iff }\forall G\ni p\ M[G]\models\varphi(F_G(\vec a)).\end{align*} $$
-
(S6) Set-Likeness: If
 $b\in M$
, then
$b\in M$
, then
 $\{a\mid \exists p\in P\ a\in _p b\}\in M$
.
$\{a\mid \exists p\in P\ a\in _p b\}\in M$
. -
(S*) Names for ground model objects:
 $\forall a\in M\,\exists \check a\in M\,\forall G\ F_G(\check a)\,{=}\,a$
.
$\forall a\in M\,\exists \check a\in M\,\forall G\ F_G(\check a)\,{=}\,a$
. -
(S**) Name for generic filters:
 $\exists \dot G\in M\ \forall G\ F_G(\dot G)=G$
.
$\exists \dot G\in M\ \forall G\ F_G(\dot G)=G$
. -
(S***) Preservation of axioms:
 $\forall G\ M[G]\models T$
.
$\forall G\ M[G]\models T$
. -
(S****) Absoluteness of
 $\mathbb {P}$
-membership: The formula
$\mathbb {P}$
-membership: The formula
 $\varphi $
defining the
$\varphi $
defining the
 $\mathbb {P}$
-membership relation R is absolute for transitive models of T containing M.
$\mathbb {P}$
-membership relation R is absolute for transitive models of T containing M.
We can use these axioms to deduce the following version of Theorem 5.1 (by essentially using the same argument). A set forcing generic extension is a set forcing generic framework together with a particular choice of generic filter G.
Theorem 8.2. Given a particular set forcing generic extension, assuming axioms (S1)–(S6), and also axioms (S*), (S**), (S***), and (S****), to hold,
![]() $M[G]$
is actually well-defined in the sense that it depends only on M and on G, and is in fact the
$M[G]$
is actually well-defined in the sense that it depends only on M and on G, and is in fact the
![]() $\subseteq $
-smallest model N of T that contains
$\subseteq $
-smallest model N of T that contains
![]() $M\cup \{G\}$
as a subset.
$M\cup \{G\}$
as a subset.
Proceeding toward a set forcing analogue of the results of Section 7, we introduce one further axiom.
-
(S7) Universality: If
 $s\in M$
is a relation on
$s\in M$
is a relation on
 $M\times P$
, then there exists
$M\times P$
, then there exists
 $b\in \mathcal {M}$
such that We additionally assume that there is a map
$b\in \mathcal {M}$
such that We additionally assume that there is a map $$ \begin{align*}s(a,p)\textrm{ if and only if }a\in_p b.\end{align*} $$
$$ \begin{align*}s(a,p)\textrm{ if and only if }a\in_p b.\end{align*} $$
 $\Gamma $
that is first order definable over M which on input s yields one such witnessing
$\Gamma $
that is first order definable over M which on input s yields one such witnessing
 $b\,{\in}\, M$
.Footnote
21
$b\,{\in}\, M$
.Footnote
21
The arguments from Section 7 then also yield the following.
Theorem 8.3. Axioms (S1)–(S7) imply axioms (S*), (S**), and (S***), and also that
![]() $M[G]$
is the
$M[G]$
is the
![]() $\subseteq $
-smallest model of T that contains
$\subseteq $
-smallest model of T that contains
![]() $M\cup \{G\}$
as a subset.
$M\cup \{G\}$
as a subset.
Another way of verifying Theorem 8.3 is to observe that a set forcing generic framework satisfying axioms (S1)–(S7) corresponds exactly to a class forcing generic framework over a model
![]() $\mathcal {M}=\langle M,\mathcal {C}\rangle $
satisfying axioms (1)–(8) for which
$\mathcal {M}=\langle M,\mathcal {C}\rangle $
satisfying axioms (1)–(8) for which
![]() $\mathcal {C}$
is just the collection of subsets of M that are first order definable over M, and to then apply Theorem 7.3:Footnote
22
$\mathcal {C}$
is just the collection of subsets of M that are first order definable over M, and to then apply Theorem 7.3:Footnote
22
In one direction, it should be pretty clear that starting from a class forcing generic framework in this setting, when
![]() $\mathbb {P}\in M$
however is a set-sized partial order, we can easily isolate a corresponding set forcing generic framework with respect to
$\mathbb {P}\in M$
however is a set-sized partial order, we can easily isolate a corresponding set forcing generic framework with respect to
![]() $\mathbb {P}$
and verify our set forcing axioms for that framework from their class forcing counterparts.
$\mathbb {P}$
and verify our set forcing axioms for that framework from their class forcing counterparts.
Let us provide a few more details on the other direction, which is relevant for verifying Theorem 8.3. We start with a set forcing generic framework
We first have to extend our
![]() $\mathbb {P}$
-membership relation R. Using the same letter R also for its extension, we simply do so by letting
$\mathbb {P}$
-membership relation R. Using the same letter R also for its extension, we simply do so by letting
![]() $R(p,a,B)$
if and only if
$R(p,a,B)$
if and only if
![]() $\langle a,p\rangle \in B$
in case
$\langle a,p\rangle \in B$
in case
![]() $B\in \mathcal {C}\setminus M$
. That is, at the top level, when B is a proper class, we define our
$B\in \mathcal {C}\setminus M$
. That is, at the top level, when B is a proper class, we define our
![]() $\mathbb {P}$
-membership relation to behave analogous to the relation
$\mathbb {P}$
-membership relation to behave analogous to the relation
![]() $\langle a,p\rangle \in B$
from the classical setting. For every nonzero length
$\langle a,p\rangle \in B$
from the classical setting. For every nonzero length
![]() $\vec A\in \mathcal {C}$
and
$\vec A\in \mathcal {C}$
and
![]() $\varphi \in \mathcal L(\in )$
, we have to define relations
$\varphi \in \mathcal L(\in )$
, we have to define relations
![]() $\operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}$
; however we simply define them to equal the corresponding first order forcing relations from our set forcing generic framework for the formulas obtained by replacing the elements of
$\operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}$
; however we simply define them to equal the corresponding first order forcing relations from our set forcing generic framework for the formulas obtained by replacing the elements of
![]() $\vec A$
by their defining formulas. Using our extended
$\vec A$
by their defining formulas. Using our extended
![]() $\mathbb {P}$
-membership relation, we can now define
$\mathbb {P}$
-membership relation, we can now define
![]() $a\in _G B$
if
$a\in _G B$
if
![]() $\exists p\in G\ a\in _p B$
in case B is a proper class, and we can thus also define
$\exists p\in G\ a\in _p B$
in case B is a proper class, and we can thus also define
![]() $F_G(B)$
for
$F_G(B)$
for
![]() $B\in \mathcal {C}\setminus M$
, letting
$B\in \mathcal {C}\setminus M$
, letting
![]() $F_G(B)=\{F_G(a)\mid \exists p\in G\langle a,p\rangle \in B\}$
. We then let
$F_G(B)=\{F_G(a)\mid \exists p\in G\langle a,p\rangle \in B\}$
. We then let
![]() $\mathcal {M}[G]=\langle F_G[M],F_G[\mathcal {C}]\rangle $
, as we did in Section 3. It is then easy to see that each of axioms (S1)–(S6) implies its corresponding axiom from (1)–(6). In order to verify axiom (7), assume that
$\mathcal {M}[G]=\langle F_G[M],F_G[\mathcal {C}]\rangle $
, as we did in Section 3. It is then easy to see that each of axioms (S1)–(S6) implies its corresponding axiom from (1)–(6). In order to verify axiom (7), assume that
![]() $S\in \mathcal C\setminus M$
is a relation on
$S\in \mathcal C\setminus M$
is a relation on
![]() $M\times P$
. Let
$M\times P$
. Let
![]() $B\in \mathcal {C}$
be such that
$B\in \mathcal {C}$
be such that
![]() $S(a,p)$
holds if and only if
$S(a,p)$
holds if and only if
![]() $\langle a,p\rangle \in B$
. Then B witnesses the relevant instance of axiom (7). Finally, it is well-known and easy to check that any notion of set forcing is pretame for models of
$\langle a,p\rangle \in B$
. Then B witnesses the relevant instance of axiom (7). Finally, it is well-known and easy to check that any notion of set forcing is pretame for models of
![]() $\mathrm {GB}^-$
, and tame for models of
$\mathrm {GB}^-$
, and tame for models of
![]() $\mathrm {GB}$
, thus yielding axiom (8).
$\mathrm {GB}$
, thus yielding axiom (8).
9 Kelley–Morse set theory
Kelley–Morse set theory
![]() $\mathrm {KM}$
extends the axioms of
$\mathrm {KM}$
extends the axioms of
![]() $\mathrm {GBC}$
by the scheme of second order class comprehension. Let
$\mathrm {GBC}$
by the scheme of second order class comprehension. Let
![]() $\mathcal L^2(\in )$
denote the collection of all second order formulas in the language with the
$\mathcal L^2(\in )$
denote the collection of all second order formulas in the language with the
![]() $\in $
-predicate.
$\in $
-predicate.
Definition 9.1. A class forcing generic framework for
![]() $\mathrm {KM}$
is a tuple of the form
$\mathrm {KM}$
is a tuple of the form
 $$ \begin{align*}\left\langle\mathcal{M},\mathbb{P},R,\left(\operatorname{\mathrm{\Vdash}}_\varphi^{\vec A}\right)_{\varphi\in\mathcal L^2(\in),\vec A\in\mathcal{C}}\!,\mathfrak G\right\rangle\end{align*} $$
$$ \begin{align*}\left\langle\mathcal{M},\mathbb{P},R,\left(\operatorname{\mathrm{\Vdash}}_\varphi^{\vec A}\right)_{\varphi\in\mathcal L^2(\in),\vec A\in\mathcal{C}}\!,\mathfrak G\right\rangle\end{align*} $$
with the same properties as those of a class forcing generic framework in Definition 2.1, except that the last item from that definition has to be changed to the following.
-
• For every
 $\vec A\in \mathcal {C}$
and
$\vec A\in \mathcal {C}$
and
 $\varphi \in \mathcal L^2(\in )$
for which the number of free second order variables corresponds to the length of
$\varphi \in \mathcal L^2(\in )$
for which the number of free second order variables corresponds to the length of
 $\vec A$
,
$\vec A$
,
 $\operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}\in \mathcal {C}$
is a predicate (which we also call a forcing relation for
$\operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}\in \mathcal {C}$
is a predicate (which we also call a forcing relation for
 $\varphi $
) on
$\varphi $
) on
 $P\times M^m$
, where m denotes the number of free first order variables of
$P\times M^m$
, where m denotes the number of free first order variables of
 $\varphi $
.
$\varphi $
.If
 $\langle q,a_0,\ldots ,a_{m-1}\rangle \in \operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}$
, we also write
$\langle q,a_0,\ldots ,a_{m-1}\rangle \in \operatorname {\mathrm {\Vdash }}_\varphi ^{\vec A}$
, we also write
 $q\operatorname {\mathrm {\Vdash }}\varphi (a_0,\ldots ,a_{m-1},\vec A)$
.
$q\operatorname {\mathrm {\Vdash }}\varphi (a_0,\ldots ,a_{m-1},\vec A)$
.
Axioms (1)–(5) are the same as in Section 3, except that
![]() $\mathcal L(\in )$
has to be replaced by
$\mathcal L(\in )$
has to be replaced by
![]() $\mathcal L^2(\in )$
throughout, and that in axioms (4) and (5), we have to refer to the number of free second order variables, rather than just the number of second order variables. Axioms (
$\mathcal L^2(\in )$
throughout, and that in axioms (4) and (5), we have to refer to the number of free second order variables, rather than just the number of second order variables. Axioms (
![]() $\bar 6$
), (*), and (**) are exactly as in Section 3.
$\bar 6$
), (*), and (**) are exactly as in Section 3.
We can then use the above axioms to show that the forcing predicates obey their usual defining clauses as in Section 4, except that we have to consider additional types of formulas. As in the case of
![]() $\mathrm {GBC}$
we can avoid atomic formulas expressing (in)equality for classes, for we may consider those to be defined in terms of the
$\mathrm {GBC}$
we can avoid atomic formulas expressing (in)equality for classes, for we may consider those to be defined in terms of the
![]() $\in $
-relation. But we need to treat second order quantification, extending Lemma 4.5 by the following clause. It is verified essentially by the same argument as for first order quantification in [Reference Freire3]; however we would like to provide the argument for the benefit of our readers.
$\in $
-relation. But we need to treat second order quantification, extending Lemma 4.5 by the following clause. It is verified essentially by the same argument as for first order quantification in [Reference Freire3]; however we would like to provide the argument for the benefit of our readers.
Lemma 9.2.
![]() $p\operatorname {\mathrm {\Vdash }}\exists X\varphi (\vec a,\vec A)\textrm { iff }\,\forall r\le p\,\exists q\le r\,\exists X\in \mathcal {C}\ q\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
.
$p\operatorname {\mathrm {\Vdash }}\exists X\varphi (\vec a,\vec A)\textrm { iff }\,\forall r\le p\,\exists q\le r\,\exists X\in \mathcal {C}\ q\operatorname {\mathrm {\Vdash }}\varphi (\vec a,\vec A)$
.
Proof Let us assume that
-
(i)
 $p\operatorname {\mathrm {\Vdash }}\exists X\varphi (X,\vec a,\vec A)$
.
$p\operatorname {\mathrm {\Vdash }}\exists X\varphi (X,\vec a,\vec A)$
.
By axiom (5), this is equivalent to
-
(ii)
 $\forall G\ni p\ \mathcal {M}[G]\models \exists X\varphi (X,F_G(\vec a),F_G(\vec A))$
.
$\forall G\ni p\ \mathcal {M}[G]\models \exists X\varphi (X,F_G(\vec a),F_G(\vec A))$
.
By the definition of
![]() $\mathcal {M}[G]$
, this is in turn equivalent to
$\mathcal {M}[G]$
, this is in turn equivalent to
-
(iii)
 $\forall G\ni p\ \exists \dot X\in \mathcal {C}\ \mathcal {M}[G]\models \varphi (F_G(\dot X),F_G(\vec a),F_G(\vec A))$
.
$\forall G\ni p\ \exists \dot X\in \mathcal {C}\ \mathcal {M}[G]\models \varphi (F_G(\dot X),F_G(\vec a),F_G(\vec A))$
.
Making use of axiom (4), we equivalently obtain
-
(iv)
 $\forall G\ni p\ \exists \dot X\in \mathcal {C}\ \exists q\in G\ q\operatorname {\mathrm {\Vdash }}\varphi (\dot X,\vec a,\vec A)$
.
$\forall G\ni p\ \exists \dot X\in \mathcal {C}\ \exists q\in G\ q\operatorname {\mathrm {\Vdash }}\varphi (\dot X,\vec a,\vec A)$
.
Applying Lemma 4.3 yields equivalence to
-
(v)
 $\forall r\le p\ \exists q\le r\ \exists \dot X\in \mathcal {C}\ q\operatorname {\mathrm {\Vdash }}\varphi (\dot X,\vec a,\vec A)$
,
$\forall r\le p\ \exists q\le r\ \exists \dot X\in \mathcal {C}\ q\operatorname {\mathrm {\Vdash }}\varphi (\dot X,\vec a,\vec A)$
,
as desired.
We can now let axioms (***) and (****) be as in Section 5, and verify the analogue of Theorem 5.1 when
![]() $T=\mathrm {KM}$
exactly as in that section, showing that
$T=\mathrm {KM}$
exactly as in that section, showing that
![]() $\mathcal {M}[G]$
is the least model of
$\mathcal {M}[G]$
is the least model of
![]() $\mathrm {KM}$
that contains
$\mathrm {KM}$
that contains
![]() $\mathcal {C}\cup \{G\}$
as a subset of its collection of classes.
$\mathcal {C}\cup \{G\}$
as a subset of its collection of classes.
Let axiom (6) be exactly as in Section 7. Let axiom (7) be exactly as in Section 7, except that we can ignore its additional definability assumption, for the axioms of
![]() $\mathrm {KM}$
include the existence of a global well-order. Let axiom (8) be the assumption that
$\mathrm {KM}$
include the existence of a global well-order. Let axiom (8) be the assumption that
![]() $\mathbb {P}$
is tame (for
$\mathbb {P}$
is tame (for
![]() $\mathcal {M}$
), as in Section 7, noting that the axioms of
$\mathcal {M}$
), as in Section 7, noting that the axioms of
![]() $\mathrm {KM}$
include the power set axiom.
$\mathrm {KM}$
include the power set axiom.
As in Section 7, we would like to show that our axioms (1)–(8) imply axioms (*), (**), and (***), and that
![]() $\mathcal {M}[G]$
is the
$\mathcal {M}[G]$
is the
![]() $\subseteq $
-smallest model of T that contains
$\subseteq $
-smallest model of T that contains
![]() $\mathcal {C}\cup \{G\}$
as a subset of its collection of classes. For (*) and (**), this is shown exactly as in Lemma 7.1. The verification of (***) and the minimality of
$\mathcal {C}\cup \{G\}$
as a subset of its collection of classes. For (*) and (**), this is shown exactly as in Lemma 7.1. The verification of (***) and the minimality of
![]() $\mathcal {M}[G]$
proceeds exactly as in the proofs of Theorem 7.3; however we have to additionally verify second order class comprehension in
$\mathcal {M}[G]$
proceeds exactly as in the proofs of Theorem 7.3; however we have to additionally verify second order class comprehension in
![]() $\mathcal {M}[G]$
in the second proof. This is done by essentially the same argument as for first order class comprehension from the second proof of Theorem 7.3.
$\mathcal {M}[G]$
in the second proof. This is done by essentially the same argument as for first order class comprehension from the second proof of Theorem 7.3.
Proposition 9.3.
![]() $\mathcal {M}[G]$
satisfies second order class comprehension.
$\mathcal {M}[G]$
satisfies second order class comprehension.
Proof If
![]() $\varphi \in \mathcal L^2(\in )$
and
$\varphi \in \mathcal L^2(\in )$
and
![]() $B\in \mathcal {C}$
, using axiom (7), let
$B\in \mathcal {C}$
, using axiom (7), let
![]() $A\in \mathcal {C}$
be such that
$A\in \mathcal {C}$
be such that
![]() $a\in _p A$
if and only if
$a\in _p A$
if and only if
![]() $p\operatorname {\mathrm {\Vdash }}\varphi (a,B)$
. It then follows that
$p\operatorname {\mathrm {\Vdash }}\varphi (a,B)$
. It then follows that
![]() $F_G(A)=\{x\in M[G]\mid \mathcal {M}[G]\models \varphi (x,F_G(B))\}$
.
$F_G(A)=\{x\in M[G]\mid \mathcal {M}[G]\models \varphi (x,F_G(B))\}$
.
10 Extensions of
 $\mathrm {KM}$
$\mathrm {KM}$
The results of the previous section can also be extended to base theories beyond
![]() $\mathrm {KM}$
. As a sample result, let us finally investigate the case of the base theory T that is
$\mathrm {KM}$
. As a sample result, let us finally investigate the case of the base theory T that is
![]() $\mathrm {KM}$
together with the axiom of class choice (
$\mathrm {KM}$
together with the axiom of class choice (
![]() $\operatorname {\mathrm {CC}}$
), which was first studied by Mostowski and Marek in [Reference Marek and Mostowski9].
$\operatorname {\mathrm {CC}}$
), which was first studied by Mostowski and Marek in [Reference Marek and Mostowski9].
Definition 10.1.
-
• Given
 $Y\in \mathcal {C}$
and
$Y\in \mathcal {C}$
and
 $\alpha \in \operatorname {\mathrm {Ord}}$
, we let
$\alpha \in \operatorname {\mathrm {Ord}}$
, we let
 $Y_\alpha =\{x\mid \langle \alpha ,x\rangle \in Y\}$
.
$Y_\alpha =\{x\mid \langle \alpha ,x\rangle \in Y\}$
. -
•
 $\operatorname {\mathrm {CC}}$
is the statement that whenever
$\operatorname {\mathrm {CC}}$
is the statement that whenever
 $\varphi \in \mathcal L^2(\in )$
,
$\varphi \in \mathcal L^2(\in )$
,
 $A\in \mathcal {C}$
, and for every ordinal
$A\in \mathcal {C}$
, and for every ordinal
 $\alpha $
there is some
$\alpha $
there is some
 $X\in \mathcal {C}$
such that
$X\in \mathcal {C}$
such that
 $\varphi (\alpha ,X,A)$
holds, then there is
$\varphi (\alpha ,X,A)$
holds, then there is
 $Y\in \mathcal {C}$
such that for every ordinal
$Y\in \mathcal {C}$
such that for every ordinal
 $\alpha $
, we have
$\alpha $
, we have
 $\varphi (\alpha ,Y_\alpha ,A)$
.
$\varphi (\alpha ,Y_\alpha ,A)$
.
Note that in the above, we could equivalently use arbitrary sets rather than just ordinals as indices, for our base theory
![]() $\mathrm {KM}$
provides us with a global well-order in order-type
$\mathrm {KM}$
provides us with a global well-order in order-type
![]() $\operatorname {\mathrm {Ord}}$
. We will tacitly make use of this in the below.
$\operatorname {\mathrm {Ord}}$
. We will tacitly make use of this in the below.
It is shown in [Reference Antos-Kuby2] that tame forcing preserves
![]() $\mathrm {KM}+\operatorname {\mathrm {CC}}$
. All results from the previous section thus apply to the stronger base theory
$\mathrm {KM}+\operatorname {\mathrm {CC}}$
. All results from the previous section thus apply to the stronger base theory
![]() $T=\mathrm {KM}+\operatorname {\mathrm {CC}}$
as well—we only need to verify that axioms (1)–(8) from Section 9 imply the preservation of
$T=\mathrm {KM}+\operatorname {\mathrm {CC}}$
as well—we only need to verify that axioms (1)–(8) from Section 9 imply the preservation of
![]() $\operatorname {\mathrm {CC}}$
. Our proof of this is based on the argument from [Reference Antos-Kuby2]. Given
$\operatorname {\mathrm {CC}}$
. Our proof of this is based on the argument from [Reference Antos-Kuby2]. Given
![]() $x,y\in M$
, let
$x,y\in M$
, let
![]() $\check {\{x,y\}}$
be defined by letting
$\check {\{x,y\}}$
be defined by letting
![]() $a\in _p\check {\{x,y\}}$
if and only if
$a\in _p\check {\{x,y\}}$
if and only if
![]() $a\in \{x,y\}$
and
$a\in \{x,y\}$
and
![]() $p=1$
. Let
$p=1$
. Let
![]() $\check {\langle x,y\rangle }$
be defined by letting
$\check {\langle x,y\rangle }$
be defined by letting
![]() $a\in _p\check {\langle x,y\rangle }$
if and only if
$a\in _p\check {\langle x,y\rangle }$
if and only if
![]() $a\in \{\check {\{x,x\}},\check {\{x,y\}}\}$
and
$a\in \{\check {\{x,x\}},\check {\{x,y\}}\}$
and
![]() $p=1$
. Thus,
$p=1$
. Thus,
![]() $\check {\langle x,y\rangle }$
is a canonical name for the ordered pair
$\check {\langle x,y\rangle }$
is a canonical name for the ordered pair
![]() $\langle F_G(x),F_G(y)\rangle $
in our setup.
$\langle F_G(x),F_G(y)\rangle $
in our setup.
Proposition 10.2.
![]() $\mathcal {M}[G]\models \operatorname {\mathrm {CC}}$
.
$\mathcal {M}[G]\models \operatorname {\mathrm {CC}}$
.
Proof Let
![]() $A\in \mathcal {C}$
. As a first step, we will argue that a strong form of Lemma 9.2 holds, namely whenever
$A\in \mathcal {C}$
. As a first step, we will argue that a strong form of Lemma 9.2 holds, namely whenever
![]() $p\operatorname {\mathrm {\Vdash }}\exists X\varphi (X,A)$
, then there is
$p\operatorname {\mathrm {\Vdash }}\exists X\varphi (X,A)$
, then there is
![]() $X\in \mathcal {C}$
such that
$X\in \mathcal {C}$
such that
![]() $p\operatorname {\mathrm {\Vdash }}\varphi (X,A)$
. Using (second order) class comprehension in
$p\operatorname {\mathrm {\Vdash }}\varphi (X,A)$
. Using (second order) class comprehension in
![]() $\mathcal {M}$
, let
$\mathcal {M}$
, let
![]() $D\in \mathcal {C}$
be the dense class of all
$D\in \mathcal {C}$
be the dense class of all
![]() $q\le p$
for which there is some
$q\le p$
for which there is some
![]() $X_q\in \mathcal {C}$
such that
$X_q\in \mathcal {C}$
such that
![]() $q\operatorname {\mathrm {\Vdash }}\varphi (X_q,A)$
. Let A be a maximal antichain in D. Using
$q\operatorname {\mathrm {\Vdash }}\varphi (X_q,A)$
. Let A be a maximal antichain in D. Using
![]() $\operatorname {\mathrm {CC}}$
in
$\operatorname {\mathrm {CC}}$
in
![]() $\mathcal {M}$
, for every
$\mathcal {M}$
, for every
![]() $q\in A$
, we may pick some
$q\in A$
, we may pick some
![]() $X_q\in \mathcal {C}$
such that
$X_q\in \mathcal {C}$
such that
![]() $q\operatorname {\mathrm {\Vdash }}\varphi (X_q,A)$
. Now we obtain our desired
$q\operatorname {\mathrm {\Vdash }}\varphi (X_q,A)$
. Now we obtain our desired
![]() $X\in \mathcal {C}$
making use of axiom (7), letting
$X\in \mathcal {C}$
making use of axiom (7), letting
![]() $a\in _r X$
if and only if
$a\in _r X$
if and only if
Now suppose that
![]() $\mathcal {M}[G]\models \forall \alpha \,\exists X\ \varphi (\alpha ,X,F_G(A))$
. By axiom (4), there is
$\mathcal {M}[G]\models \forall \alpha \,\exists X\ \varphi (\alpha ,X,F_G(A))$
. By axiom (4), there is
![]() $p\in G$
such that
$p\in G$
such that
![]() $p\operatorname {\mathrm {\Vdash }}\forall \alpha \,\exists X\ \varphi (\alpha ,X,A)$
. For any
$p\operatorname {\mathrm {\Vdash }}\forall \alpha \,\exists X\ \varphi (\alpha ,X,A)$
. For any
![]() $\alpha \in \operatorname {\mathrm {Ord}}^{\mathcal {M}}$
, by the above, we find some
$\alpha \in \operatorname {\mathrm {Ord}}^{\mathcal {M}}$
, by the above, we find some
![]() $X^\alpha \in \mathcal {C}$
such that
$X^\alpha \in \mathcal {C}$
such that
![]() $p\operatorname {\mathrm {\Vdash }}\varphi (\alpha ,X^\alpha ,A)$
. Using that our forcing relations are in
$p\operatorname {\mathrm {\Vdash }}\varphi (\alpha ,X^\alpha ,A)$
. Using that our forcing relations are in
![]() $\mathcal {C}$
, and using
$\mathcal {C}$
, and using
![]() $\operatorname {\mathrm {CC}}$
in
$\operatorname {\mathrm {CC}}$
in
![]() $\mathcal {M}$
, we may obtain
$\mathcal {M}$
, we may obtain
![]() $X\in \mathcal {C}$
such that
$X\in \mathcal {C}$
such that
![]() $\forall \alpha \ p\operatorname {\mathrm {\Vdash }}\varphi (\alpha ,X_\alpha ,A)$
. Making use of axiom (7), define
$\forall \alpha \ p\operatorname {\mathrm {\Vdash }}\varphi (\alpha ,X_\alpha ,A)$
. Making use of axiom (7), define
![]() $Y\in \mathcal {C}$
by letting
$Y\in \mathcal {C}$
by letting
![]() $a\in _r Y$
if and only if for some
$a\in _r Y$
if and only if for some
![]() $\alpha \in \operatorname {\mathrm {Ord}}^{\mathcal {M}}$
,
$\alpha \in \operatorname {\mathrm {Ord}}^{\mathcal {M}}$
,
![]() $a=\check {\langle \alpha ,x\rangle }$
and r is such that
$a=\check {\langle \alpha ,x\rangle }$
and r is such that
![]() $x\in _r X_\alpha $
. It follows that for all
$x\in _r X_\alpha $
. It follows that for all
![]() $\alpha \in \operatorname {\mathrm {Ord}}$
,
$\alpha \in \operatorname {\mathrm {Ord}}$
,
![]() $\mathcal {M}[G]\models \varphi (\alpha ,F_G(X)_\alpha ,F_G(A))$
, as desired.
$\mathcal {M}[G]\models \varphi (\alpha ,F_G(X)_\alpha ,F_G(A))$
, as desired.
11 Open questions and possible future directions
One obvious question is whether our axiom system can be simplified, or whether some of its axioms could be weakened or even omitted. We have already remarked that the definability of the map
![]() $\Gamma $
provided by axiom (7) is not necessary in many cases, and it is not hard to see that for any of the axiom systems we consider, it would instead suffice, in the terminology of axiom (7), to have a map
$\Gamma $
provided by axiom (7) is not necessary in many cases, and it is not hard to see that for any of the axiom systems we consider, it would instead suffice, in the terminology of axiom (7), to have a map
![]() $\Gamma $
which provides a set of witnesses for each
$\Gamma $
which provides a set of witnesses for each
![]() $S\in M$
. Moreover, axiom (7) could in fact be replaced by the weaker Item (i) from Lemma 7.2, or some equivalent form of that item, which however seems less desirable as an axiom due to its reference to generic filters. All other requirements made by our axioms seem to be necessary as far as we know. Let us remark that Proposition 7.4 shows that axiom (8) cannot be omitted.
$S\in M$
. Moreover, axiom (7) could in fact be replaced by the weaker Item (i) from Lemma 7.2, or some equivalent form of that item, which however seems less desirable as an axiom due to its reference to generic filters. All other requirements made by our axioms seem to be necessary as far as we know. Let us remark that Proposition 7.4 shows that axiom (8) cannot be omitted.
Question 11.1. Are there possible improvements to our axiomatization of forcing, either by using a proper subset of our axioms, or perhaps by replacing some of our axioms by weaker or, in some other sense, better axioms?
In the present paper, we considered base theories containing at least the axioms of
![]() $\mathrm {GB}^-$
, or the corresponding first order theory
$\mathrm {GB}^-$
, or the corresponding first order theory
![]() $\mathrm {ZF}^-$
. The following question was posed to us by Ali Enayat.
$\mathrm {ZF}^-$
. The following question was posed to us by Ali Enayat.
Question 11.2. Is there a similar axiom system for forcing over suitable base theories that are strictly weaker than
![]() $\mathrm {ZF}^-$
(and perhaps also their corresponding second order theories, when such exist), over which it is possible to develop a suitable machinery of forcing?
$\mathrm {ZF}^-$
(and perhaps also their corresponding second order theories, when such exist), over which it is possible to develop a suitable machinery of forcing?
One such weaker base theory would be Kripke–Platek set theory; however in his [Reference Mathias10], Mathias developed a weaker axiom system of provident set theory, and shows that models of this theory support a smooth theory of set forcing. It seems plausible that a careful adaption of our axioms could make them work in the context of such weaker models of set theory as well.
A topic that is somewhat implicit in our paper is touched by the following.
Question 11.3. To what extent does our axiomatization shed light on the uniqueness of the forcing method as a means to extending models of set theory without giving up (ground model) control over the extension?
Another future direction of research would be the following.
Question 11.4. Is it possible to provide natural and interesting axiomatizations for other technical concepts in set theory? For example, for symmetric submodels of forcing extensions, for (generic) ultrapowers or for (certain) canonical inner models of set theory?
Acknowledgments
The research of the first author was supported by CNPq and Fapesp. The research of the second author was supported by the Italian PRIN 2017 Grant Mathematical Logic: models, sets, computability. Both authors would very much like to thank the anonymous referees, whose comments were a great help in improving both the presentation of and the technicalities in this article.