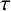1 Introduction
The notion of a fractional derivative, one of the most interesting topics in the mathematical world, is more than 300 years old. The basis of the idea of the fractional derivative dates back to 1695. Many mathematicians have been involved in this subject since the idea of fractional derivation emerged. For a long time, only theoretical mathematicians were involved in this topic, but recently, we have come across the work of quite a few applied mathematicians and scientists from various branches of science. Scientists working on fractional derivative calculations used the classical definition of the derivative and developed it. Riemann, Grünwald, Letnikov, Liouville, Caputo, Euler, Abel, Fourier, Kobel, Erdelyi, Hadamard, Riesz and Laplace are major contributors of fractional derivatives [Reference Podlubny28]. In recent years, fractional calculus has attracted much attention. It is well known that the differential equations with fractional order are generalizations of ordinary differential equations to non-integer order, and they occur more frequently in different research areas, such as physics, dynamical control system, biology and so forth. Since fractional calculus is a powerful tool for more complex phenomena, we do not have more applications. Until recently, experiments and reality tell us that there are many complex systems in nature with anomalous dynamics, which can not be characterized by classical integer-order derivative models.
In contrast, fractional models can present a more vivid and accurate description over things than integral ones. As most of us know, a lot of biological, physical and engineering systems have long-range temporal memory and long-range spatial interactions. Describing such systems with fractional-order differential equations has more advantages than classical integer-order, since the fractional-order derivative is an excellent instrument for the description of memory and hereditary properties of various materials and processes. Fractional differential equations have gained considerable importance due to their valuable applications [Reference Angstmann, Henry and McGann1, Reference Hilfer16, Reference Kilbas, Srivastava and Trujillo20, Reference Miller and Ross25, Reference Oldham and Spanier26, Reference Podlubny28, Reference Samko, Kilbas and Marichev30] in viscoelasticity, electroanalytical chemistry as well as in various engineering and physical problems. The combination of time-delay with fractional calculus was used successfully in many areas of science and engineering, especially when models were used to describe complex systems with a memory effect [Reference Bhalekar, Daftardar-Gejji, Baleanu and Magin3, Reference Chen, Vinagre and Podlubny11, Reference Deng, Li and Lu12, Reference Jarad, Abdeljawad (Maraaba) and Baleanu19]. In fact, by using such a combination, we are able to recover the fractional calculus model by making the delay zero and by making the order of derivatives one. This specific behaviour leads us to the conclusion that the combined models can reveal new aspects of a given complex model. A bifurcation of a dynamical system is a qualitative change in its dynamics, produced by varying parameters [Reference Chen and Moore10, Reference Guckenheimer, Holmes, Marsden and Sirovich15, Reference Izhikevich18, Reference Kuznetsov, Antman, Marsden and Sirovich21]. Bifurcation theory provides a strategy for investigating the bifurcations that occur within a family. It does so by identifying ubiquitous patterns of bifurcations. Each bifurcation type or singularity has a name, for example, Andronov–Hopf bifurcation [Reference Marsden and McCracken24]. No distinction has been made in the literature between “bifurcation” and “bifurcation type” both being called “bifurcations.” The Hopf–Hopf bifurcation [Reference Marsden and McCracken24] is a bifurcation of an equilibrium point in a two parameter family of autonomous ordinary differential equations (ODEs) at which the critical equilibrium has two pairs of purely imaginary eigenvalues. This phenemenon is also called the double Hopf bifurcation [Reference Chen and Moore10, Reference Guckenheimer, Holmes, Marsden and Sirovich15, Reference Izhikevich18].
In recent years, the dynamical properties of the predator-prey models which have significant biological background have received much attention from many applied mathematicians and ecologists. To incorporate various realistic physical effects that may cause at least one of the physical variables to depend on the past history of the system, it is often necessary to introduce time delays into these models. Many theoreticians and experimentalists have concentrated on the stability of predator-prey systems and, more specifically, they investigated the stability of such systems when time delays are incorporated into the models. A time delay may have a very complicated impact on the dynamical behaviour of the system such as the periodic structure, bifurcation and so forth. For references, see [Reference Çelik4–Reference Chen9, Reference Fowler and Ruxton13, Reference Gopalsamy14, Reference Huang, Song, Fang, Xiao and Cao17, Reference Li, Zhang, Hu, Jiang and Teng22, Reference Liu and Fang23, Reference Pan, Cui, Xue and Liu27, Reference Wang and Wang31–Reference Zhou, Wu, Li and Yau33]. There have been many works which are devoted to the studies of dynamical behaviours for predator-prey systems with various functional responses. However, recently, many researchers found that when predators have to search for food and, therefore, have to share or compete for food, a more suitable general predator-prey theory should be based on the so-called ratio-dependent theory, which is important, because of their suitability for modelling the real ecological interactions between predator and prey species.
In this study, we examine the fractional-order form of this model [Reference Çelik7] by considering the model that Çelik has previously studied in integer order [Reference Çelik7]. So our aim in this paper is to investigate the fractional form of the following delayed predator-prey system with Holling–Tanner-type [Reference Sáez and González-Olivares29] functional response
$$ \begin{align} \begin{aligned} \frac {dN(t)}{dt}&=N(t)(1-N(t))-\frac{N(t)P(t-\tau)}{N(t)+\alpha P(t-\tau)}, \\[3pt] \frac{dP(t)}{dt}&=\beta P(t-\tau)\bigg(\delta-\frac {P(t-\tau)}{N(t)}\bigg), \end{aligned} \end{align} $$
where
$\alpha $
,
$\beta $
and
$\delta $
are positive constants;
$N(t)$
and
$P(t)$
can be interpreted as the densities of prey and predator populations at time t, respectively; and
$\tau \ge 0$
denotes the time delay for the predator density. In this model, prey density is logistic with time delay and the carrying capacity proportional to predator density. In many of the studies related to stability of predator prey models, the authors have considered a constant carrying capacity; however, in this study, we focus on the carrying capacity proportional to prey density (ratio dependent), which shows very interesting behaviour in terms of dynamical structure. We will consider the following fractional-order predator-prey model:
$$ \begin{align} \begin{aligned} {}_{t_{0}}^{c}D_{t}^{q} N(t)&=N(t)(1-N(t))-\frac{N(t)P(t-\tau)}{N(t)+\alpha P(t-\tau)}, \\[3pt] {}_{t_{0}}^{c}D_{t}^{q} P(t)&=\beta P(t-\tau)\bigg(\delta-\frac{P(t-\tau)}{N(t)}\bigg). \end{aligned} \end{align} $$
2 Preliminaries
In this section, we give the basic definitions related to the fractional order derivative.
Definition 2.1 [Reference Podlubny28].
The Caputo fractional derivative with order q of a function
$f(t)$
is defined as
$$ \begin{align*} {}_{0}^{c}D_{t}^{q}f(t)=\frac{1}{\Gamma(n-q)}\int_{0}^{t}\frac{f^{(n)}(\tau)}{(t-\tau)^{q-n+1}}\,d\tau , \end{align*} $$
where n is a positive integer such that
$n-1<q\leq n$
.
Definition 2.2. The Laplace transform L of a function
$f(t)$
for
$t> 0$
is defined by
$$ \begin{align*} L\{ f(t)\}=\int_{0}^{\infty} {e^{-st}f(t)\,dt}. \end{align*} $$
The resulting expression is a function of s, which we write as
$F(s)$
. We say “The Laplace transform of
$f(t)$
equals function F of s” and write
$$ \begin{align*} L\{\,f(t)\}=F(s). \end{align*} $$
Similarly, the Laplace transform of a function
$g(t)$
would be written as
$$ \begin{align*} L\{ g(t)\}=G(s). \end{align*} $$
Definition 2.3 [Reference Podlubny28].
The Laplace transform of the Caputo fractional derivative is
$$ \begin{align*} L\{_{0}^{c}D_{t}^{q}f(t);s\}=s^{q}F(s)-\sum_{k=0}^{n-1}s^{q-k-1}f^{k}(0), \quad n-1<q \le n, \end{align*} $$
where
$F(s)$
is the Laplace transform of
$f(t)$
and
$f^{k}(0)$
,
$k=0,1,2,\ldots , n-1$
are the initial conditions. If
$f^{k}(0)=0$
,
$k=0,1,2,\ldots , n-1$
, then
$$ \begin{align*}L\{_{0}^{c}D_{t}^{q}f(t);s\}=s^{q}F(s).\end{align*} $$
3 Stability and Hopf bifurcation analysis of a fractional model
System (1.1) has a unique positive equilibrium point
$E_{0}^{*}=(N_{0}^{*},P_{0}^{*})$
, where
$$ \begin{align*}N_{0}^{*}=\frac{1+\alpha\delta-\delta}{1+\alpha\delta}\quad \text{and}\quad P_{0}^{*}=\delta\bigg(\frac{1+\alpha\delta-\delta}{1+\alpha\delta}\bigg).\end{align*} $$
To analyse the local stability of the positive equilibrium,
$E_{0}^{*}=(N_{0}^{*},P_{0}^{*})$
, we first use the linear transformations
$n(t)=N(t)-N_{0}^{*}$
and
$p(t)=P(t)-P_{0}^{*}$
, where
$n<<1$
and
$p<<1$
for which the system (1.1) turns out as
$$ \begin{align*} \begin{aligned} \frac{dn}{dt}&=(n(t)+N_{0}^{*})(1-n(t)-N_{0}^{*})-\frac{(n(t)+N_{0}^{*})(p(t-\tau)+P_{0}^{*})}{n(t)+N_{0}^{*}+\alpha(p(t-\tau)+P_{0}^{*})}, \nonumber\\[3pt] \frac{dp}{dt}&=\beta(p(t-\tau)+P_{0}^{*})\bigg(\delta-\frac{p(t-\tau)+P_{0}^{*}}{n(t)+N_{0}^{*}}\bigg). \end{aligned} \end{align*} $$
Then using relations
$$ \begin{align*}N_{0}^{*}(1-N_{0}^{*})-\frac{N_{0}^{*}P_{0}^{*}}{N_{0}^{*}+\alpha P_{0}^{*}}=0\quad \text{and} \quad \beta P_{0}^{*}\bigg(\delta-\frac{P_{0}^{*}}{N_{0}^{*}}\bigg)=0,\end{align*} $$
and ignoring the higher order terms yield the following linear system:
$$ \begin{align*} \begin{aligned} \frac{dn}{dt}&=\bigg(1-2N_{0}^{*}-\frac{P_{0}^{*}}{N_{0}^{*}+\alpha P_{0}^{*}}+\frac{P_{0}^{*}N_{0}^{*}}{(N_{0}^{*}+\alpha P_{0}^{*})^{2}}\bigg) n(t)\nonumber \\[3pt] &\quad +\bigg(-\frac{N_{0}^{*}}{N_{0}^{*}+\alpha P_{0}^{*}}+\frac{\alpha P_{0}^{*}N_{0}^{*}}{(N_{0}^{*}+\alpha P_{0}^{*})^{2}}\bigg)p(t-\tau), \nonumber \\[3pt] \frac{dp}{dt}&=\bigg(\beta\delta-\frac{2\beta P_{0}^{*}}{N_{0}^{*}}\bigg)p(t-\tau)+\frac{\beta (P_{0}^{*})^{2}}{(N_{0}^{*})^{2}}n(t). \end{aligned} \end{align*} $$
Now, by replacing integer-order derivatives of the above system with fractional derivatives of order
$ q \in (0,1]$
in the sense of Caputo [Reference Podlubny28], we consider the fractional-order model as follows:
$$ \begin{align} {}_{t_{0}}^{c}D_{t}^{q}n(t)&=\bigg(1-2N_{0}^{*}-\frac{P_{0}^{*}}{N_{0}^{*}+\alpha P_{0}^{*}}+\frac{P_{0}^{*}N_{0}^{*}}{(N_{0}^{*}+\alpha P_{0}^{*})^{2}}\bigg)\,n(t)\nonumber\\[3pt] &\quad +\bigg(-\frac{N_{0}^{*}}{N_{0}^{*}+\alpha P_{0}^{*}}+\frac{\alpha P_{0}^{*}N_{0}^{*}}{+(N_{0}^{*}+\alpha P_{0}^{*})^{2}}\bigg)\,p(t-\tau), \\[3pt] {}_{t_{0}}^{c}D_{t}^{q}p(t)&=\bigg(\beta\delta-\frac{2\beta P_{0}^{*}}{N_{0}^{*}}\bigg)p(t-\tau)+\frac{\beta (P_{0}^{*})^{2}}{(N_{0}^{*})^{2}}n(t),\nonumber \end{align} $$
where
$a_{i}\, (i=1,2,3,4,5)$
are determined by
$$ \begin{align*} a_{1}&=1-2N_{0}^{*}, \quad a_{2}=-\frac{1}{N_{0}^{*}+\alpha P_{0}^{*}}, \quad a_{3}=\frac{P_{0}^{*}N_{0}^{*}}{(N_{0}^{*}+\alpha P_{0}^{*})^{2}}, \\[3pt] a_{4}&=\beta\delta-\frac{2\beta P_{0}^{*}}{N_{0}^{*}}, \quad a_{5}=\frac{\beta (P_{0}^{*})^{2}}{(N_{0}^{*})^{2}}. \end{align*} $$
By taking the Laplace transform on both sides of system (3.1), we get
$$ \begin{align*} L\{_{t_{0}}^{c}D_{t}^{q}n(t)\}&=L\{(a_{1}+a_{2}P_{0}^{*}+a_{3})n(t)+(a_{2}N_{0}^{*}+\alpha a_{3})P(t-\tau)\}\\[3pt] &=a_{1}N(s)+a_{2}P_{0}^{*}N(s)+a_{3}N(s)+(a_{2}N_{0}^{*}+\alpha a_{3})L\{P(t-\tau )\}, \end{align*} $$
and
$$ \begin{align*} s^{q}N(s)-s^{q-1}N(0)&=(a_{1}+a_{2}P_{0}^{*}+a_{3})N(s) \\ &\quad +(a_{2}N_{0}^{*}+\alpha a_{3})e^{-s\tau}\bigg(\int_{-\tau}^{0}\theta(t)e^{-st}\,dt+P(s)\bigg). \end{align*} $$
Similarly,
$$ \begin{align} \begin{aligned} L\{_{t_{0}}^{c}D_{t}^{q}p(t)\}&=L\{a_{4}P(t-\tau)+a_{5}n(t)\}, \\[3pt] L\{_{t_{0}}^{c}D_{t}^{q}p(t)\}&=a_{4}e^{-s\tau}\bigg(\int_{-\tau}^{0}\theta(t)e^{-st}\,dt+P(s)\bigg)+a_{5}N(s), \\[3pt] s^{q}P(s)-s^{q-1}P(0)&=a_{4}e^{-s\tau}\bigg(\int_{-\tau}^{0}\theta(t)e^{-st}\,dt+P(s)\bigg)+a_{5}N(s). \end{aligned} \end{align} $$
System (3.2) can be written as
$$ \begin{align*} \Delta(s) \left( \begin{array}{ccc} N(s)\\ P(s)\\ \end{array} \right)=\left(\begin{array}{ccc}b_{1}(s)\\b_{2}(s)\\ \end{array}\right), \end{align*} $$
where
$$ \begin{align*} \Delta (s)=\left(\begin{array}{ccc} s^{q}-a_{1}-a_{2}P_{0}^{*}-a_{3}&(-a_{2}N_{0}^{*}-\alpha a_{3})e^{-s\tau}\\ -a_{5}&s^{q}-a_{4}e^{-s\tau}\\ \end{array}\right), \end{align*} $$
$$ \begin{align*} \left(\begin{array}{ccc}b_{1}(s)\\b_{2}(s)\\ \end{array}\right) =\left (\begin{array}{ccc} s^{q-1}N(0)+(a_{2}N_{0}^{*}+\alpha a_{3})e^{-s\tau}.\int_{-\tau}^{0}\theta(t)e^{-st}\,dt\\ s^{q-1}P(0)+a_{4}e^{-s\tau}.\int_{-\tau}^{0}\theta(t)e^{-st}\,dt\\ \end{array} \right), \end{align*} $$
and
$$ \begin{align} \text{det}(\Delta(s))&=(s^{q}-a_{1}-a_{2}P_{0}^{*}-a_{3})(s^{q}-a_{4}e^{-s\tau})+a_{5}(-a_{2}N_{0}^{*}-\alpha a_{3})e^{-s\tau} \nonumber\\[3pt] &=s^{2q}+(-a_{1}-a_{2}P_{0}^{*}-a_{3})s^{q}-s^{q}a_{4}e^{-s\tau}\nonumber\\[3pt] &\quad +(a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*}-a_{5}\alpha a_{3})e^{-s\tau}. \end{align} $$
Here,
$\Delta (s)$
is considered as the characteristic matrix of system (3.1) for simplicity. Next, we look for the conditions that guarantee that the characteristic equation (3.3) has a pair of pure imaginary roots
$s=^{+}_{-}\omega i$
,
$ (\omega>0).$
Assume that equation (3.3) has a pure imaginary root
$s=\omega i (\omega>0)$
. Substituting
$s=\omega i$
into equation (3.3) yields
$$ \begin{align*} \text{ det}(\Delta(s))&=(\omega i)^{2q}+(-a_{1}-a_{2}P_{0}^{*}-a_{3})(\omega i)^{q}-a_{4}e^{-(\omega i)\tau}(\omega i)^{q}\nonumber\\[3pt] &\quad+ (a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*}-a_{5}\alpha a_{3})e^{-(\omega i)\tau}\nonumber\\[3pt] &=0. \end{align*} $$
Since
$$ \begin{align*} i^{2q}&=\cos(q\pi)+i\sin(q\pi),\\[3pt] i^{q}&=\cos\bigg(\frac{q\pi}{2}\bigg) + i\sin\bigg(\frac{q\pi}{2}\bigg),\\[3pt] e^{-i\omega \tau}&=\cos(\omega \tau)-i\sin(\omega \tau), \end{align*} $$
we have
$$ \begin{align} \text{det}(\Delta(s))&=\omega {}^{2q}(\cos(q\pi)+i\sin(q\pi)) +\omega {}^{q}(-a_{1}-a_{2}P_{0}^{*}-a_{3})\bigg(\cos\bigg(\frac{q\pi}{2}\bigg) +i\sin\bigg(\frac{q\pi}{2}\bigg)\bigg)\nonumber\\ &\quad -a_{4}\omega^{q}\bigg(\cos\bigg(\frac{q\pi}{2}\bigg)+i\sin\bigg(\frac{q\pi}{2}\bigg)\bigg)(\cos(\omega \tau)-i\sin(\omega \tau))\nonumber\\ &\quad + (a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*}-a_{5}\alpha a_{3})(\cos(\omega \tau)-i\sin(\omega \tau))\nonumber\\ &=0. \end{align} $$
Separating real and imaginary parts of equation (3.4) gives
$$ \begin{align} \omega^{2q}&\cos(q\pi)-\omega^{q}(a_{1}+a_{2}P_{0}^{*}+a_{3})\cos\bigg(\frac{q\pi}{2}\bigg)\nonumber \\ &=a_{4}\omega^{q}\cos\bigg(\omega \tau-\frac{q\pi}{2}\bigg) - ( a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*} -a_{5}\alpha a_{3}) \nonumber \\[-14pt] &\quad \times \cos(\omega \tau) \omega^{2q}\sin(q\pi)-\omega^{q}(a_{1}+a_{2}P_{0}^{*}+a_{3})\sin\bigg(\frac{q\pi}{2}\bigg)\nonumber \\ &=a_{4}\omega^{q}\sin\bigg(\frac{q\pi}{2}-\omega \tau\bigg)+ (a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*}-a_{5}\alpha a_{3})\sin(\omega \tau). \end{align} $$
By squaring and adding both sides of equation (3.5),
$$ \begin{align*} \omega^{4q}&-2\omega^{3q}(a_{1}+a_{2}P_{0}^{*}+a_{3})\cos\bigg(\frac{q\pi}{2}\bigg)+\omega^{2q}(a_{1}+a_{2}P_{0}^{*}+a_{3})^{2}\nonumber-a_{4}^{2}\omega^{2q}\nonumber\\ &+2a_{4}\omega^{q} (a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*}-a_{5}\alpha a_{3})\cos\bigg(\frac{q\pi}{2}\bigg)\nonumber\\[3pt] &- (a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*}-a_{5}\alpha a_{3})^{2}=0. \end{align*} $$
Since
$\cos (q\pi /2)>0$
,
$\omega ^{q}>0$
and
$0<q<1$
. Put
$v=\omega ^{q}$
, then this yields
$h(v)=v^{4}+av^{3}+bv^{2}+cv+d=0$
. Since
$h(0)=d<0$
and
$\lim _{v\rightarrow \infty } h(v)=\infty $
, there exists a
$v_{0}>0$
such that
$h(v_{0})=0$
. Finally, we calculate the delay
$\tau _{0}$
, which guarantees the existence of pure imaginary roots in this equation. Since
$$ \begin{align*} \text{det}(\Delta(s))&=s^{2q}+(-a_{1}-a_{2}P_{0}^{*}-a_{3})s^{q}-s^{q}a_{4}e^{-s\tau} \\[3pt] &\quad + (a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*}-a_{5}\alpha a_{3})e^{-s\tau}, \end{align*} $$
we have
$$ \begin{align*} C_{1}&=-a_{1}-a_{2}P_{0}^{*}-a_{3},\\[3pt] C_{2}&=-a_{4}, \\[3pt] D&=a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*}-a_{5}\alpha a_{3}, \end{align*} $$
and also
$$ \begin{align*} \text{det}(\Delta(s))&=s^{2q}+C_{1}s^{q}+(C_{2}s^{q}+D)e^{-s\tau}=0, \\[3pt] A&=s^{2q}+C_{1}s^{q},\\[3pt] E&=C_{2}s^{q}+D, \\[3pt] A+Ee^{-s\tau}&=0. \end{align*} $$
Let
$s=\omega i$
,
$(\omega>0)$
and
$A_{j}, E_{j}\, (j=1,2)$
be the real and imaginary parts of
$A,E$
, respectively. Thus,
$$ \begin{align*} (A_{1}+iA_{2})+(E_{1}+iE_{2})(\cos(\omega \tau)-i\sin(\omega \tau))=0 , \end{align*} $$
where
$$ \begin{align*} A_{1}&=\omega^{2q}\cos(q\pi)+C_{1}\omega^{q}\cos\bigg(\frac{q\pi}{2}\bigg),\\ A_{2}&=\omega^{2q}\sin(q\pi)+C_{1}\omega^{q}\sin\bigg(\frac{q\pi}{2}\bigg),\\ E_{1}&=C_{2}\omega^{q}\cos\bigg(\frac{q\pi}{2}\bigg)+D,\\ E_{2}&=C_{2}\omega^{q}\sin\bigg(\frac{q\pi}{2}\bigg).\\[-1pc] \end{align*} $$
Separating the real and imaginary parts of this equation yields
$$ \begin{align*} A_{1}+E_{1}\cos(\omega \tau)+E_{2}\sin(\omega \tau)&=0, \\[3pt] A_{2}+E_{2}\cos(\omega \tau)-E_{1}\sin(\omega \tau)&= 0. \end{align*} $$
Simplifying,
$$ \begin{align*} H_{1}(\omega)&=\sin(\omega\tau)=\frac{E_{1}A_{2}-E_{2}A_{1}}{E_{1}^{2}+E_{2}^{2}}, \\[3pt] H_{2}(\omega)&=\cos(\omega\tau)=-\frac{E_{1}A_{1}+E_{2}A_{2}}{E_{1}^{2}+E_{2}^{2}}, \\[3pt] \tan(\omega\tau)&=\frac{\sin(\omega\tau)}{\cos(\omega\tau)}=\frac{E_{1}A_{2}-E_{2}A_{1}}{-(E_{1}A_{1}+E_{2}A_{2})}, \\[3pt] \omega\tau&=\arctan\bigg(\frac{E_{1}A_{2}-E_{2}A_{1}}{-(E_{1}A_{1}+E_{2}A_{2})}\bigg), \\[3pt] \omega\tau&=\arctan\bigg(\frac{H_{1}(\omega)}{H_{2}(\omega)}\bigg), \end{align*} $$
which lead to
$$ \begin{align*} \tau_{k} = \frac{\arctan(H_{1}(\omega)/H_{2}(\omega))}{\omega}+2k\pi \quad \text{for } k=0,1,2,\ldots. \end{align*} $$
Let
$s(\tau )=\alpha (\tau )+i\omega (\tau )$
denote the root of equation (3.3) near
$\tau =\tau _{k}$
, satisfying
$a(\tau _{k})=0$
and
$\omega (\tau _{k})=\omega _{1}$
,
$k=0,1,2,\ldots .$
Then we have the following result.
Lemma 3.1. Suppose
$g^{\prime }(z_{1})\neq 0$
, then the following transversality condition is satisfied:
$$ \begin{align*}\frac{d(\mathrm{Re}(s(\tau_{k})))}{d\tau}\neq 0, \quad k=0,1,2,3, \ldots ,\end{align*} $$
and
$g^{\prime }(z_{1})$
,
${d(\mathrm{Re}(s(\tau _{k})))}/{d\tau }$
have the same sign.
Proof. Suppose that for
$\tau =\tau _{k}$
, let
$s=i\omega $
be a root of equation (3.3) with
$\omega $
real, and without loss of generality
$\omega>0$
. Differentiating the characteristic equation (3.3) with respect to
$\tau $
,
$$ \begin{align*} 2qs^{2q-1}\frac{ds}{d\tau}+C_{1}qs^{q-1}\frac{ds}{d\tau}+\bigg(C_{2}qs^{q-1} \frac{ds}{d\tau}\bigg)e^{-s\tau}-e^{-s\tau}\bigg(\tau\frac{ds}{d\tau}+s\bigg)(C_{2}s^{q}+D)=0 , \end{align*} $$
that is,
$$ \begin{align*} \frac{d\tau}{ds}=\frac{2qs^{2q-1}+C_{1}qs^{q-1}}{s(C_{2}s^{q}+D)}e^{s\tau}+\frac{C_{2}qs^{q-1}}{s(C_{2}s^{q}+D)}-\frac{\tau}{s}. \end{align*} $$
Then for
$s=i\omega ,$
$$ \begin{align*} \text{ Re}\bigg(\frac{d\tau}{ds}\bigg)\bigg|_{s=i\omega}&=\text{Re} \bigg[\frac{2q(i\omega)^{2q-1}+C_{1}q(i\omega)^{q-1}}{(i\omega) (C_{2}(i\omega)^{q}+D)}e^{i\omega\tau}+\frac{C_{2}q(i\omega)^{q-1}}{(i\omega)(C_{2}(i\omega)^{q}+D)}-\frac{\tau}{i\omega}\bigg], \\[3pt] \text{Re}\bigg(\frac{d\tau}{ds}\bigg)\bigg|_{s=i\omega}&=\text{Re}\bigg[\frac{(2q(i\omega)^{2q-1}+C_{1}q(i\omega)^{q-1})(\cos(\omega\tau) + i\sin(\omega\tau))+C_{2}q(i\omega)^{q-1}}{(i\omega)(C_{2}(i\omega)^{q}+D)}\bigg], \end{align*} $$
and using the expressions for
$\cos (\omega \tau )$
and
$\sin (\omega \tau )$
above,
$$ \begin{align*} &\text{Re}\bigg(\frac{d\tau}{ds}\bigg)\bigg|_{s=i\omega}\\[3pt] &\quad=\frac{-(\omega^{3q}2q+DC_{1}\omega^{q} q)(\cos(q\pi/2)+\omega\tau)-(C_{1}C_{2}\omega^{2q}q+D\omega^{2q}2q)(\cos(q\pi)+\omega\tau)}{(C_{2}\cos(q\pi/2) \omega^{q+1}+D\omega)^{2}+(C_{2}\sin(q\pi/2)\omega^{q+1})^{2}} \\[3pt] &\qquad +\frac{-C_{2}^{2}q\omega^{2q-2}-DC_{2}q\omega^{q-2}\cos(q\pi/2)}{(C_{2}\cos(q\pi/2)\omega^{q}+D)^{2}+(C_{2}\sin(q\pi/2)\omega^{q})^{2}}. \end{align*} $$
Here, since the denominators are positive, it can be continued with the numerators. Note that
$$ \begin{align*} \text{sgn}\bigg(\text{Re}\bigg(\frac{d\tau}{ds}\bigg)\bigg|_{s=i\omega}\bigg)&=-(\omega^{3q}2q+DC_{1}\omega^{q} q)\bigg(\cos\frac{q\pi}{2}+\omega\tau\bigg)\\[3pt] &\quad -(C_{1}C_{2}\omega^{2q}q+D\omega^{2q}2q)(\cos(q\pi)+\omega\tau) \\[3pt] &\quad -C_{2}^{2} q \omega^{2q-2}-DC_{2}q\omega^{q-2}\cos\frac{q\pi}{2}, \end{align*} $$
where
$0<q<1$
,
$\omega ^{q}>0$
,
$\cos (q\pi /2)>0, \sin (q\pi /2)>0$
and
$-1<\cos (q\pi )<1$
, so,
$$ \begin{align*} \text{Re}\bigg(\frac{d\tau}{ds}\bigg)\bigg|_{s=i\omega}\neq 0. \end{align*} $$
This completes the proof of the lemma.
Summarizing the above results, we have the following theorem on stability and Hopf bifurcation of system (3.1).
Theorem 3.2. For system (3.1), the following results hold.
4 A numerical example
In this section, some numerical simulations are presented to verify the theoretical results that we obtained in the previous sections for the existence of Hopf bifurcation. To perform the simulations, we modified the Adama–Bashforth–Moulton predictor-corrector scheme using Matlab programming as in [Reference Bhalekar and Daftardar-Gejji2].
We simulate the fractional predator-prey system (1.2) by choosing the parameters,
$\alpha = 0.7$
,
$\beta = 0.9$
,
$\delta = 0.6$
and
$q=0.98$
. We consider the following system:
$$ \begin{align*} \begin{aligned} {}_{t_{0}}^{c}D_{t}^{0.98} N(t)&=N(t)(1-N(t))-\frac{N(t)P(t-\tau)}{N(t)+0.7 P(t-\tau)},\nonumber\\[8pt] {}_{t_{0}}^{c}D_{t}^{0.98}P(t)&=0.9P(t-\tau)\bigg(0.6-\frac{P(t-\tau)}{N(t)}\bigg) , \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} N^{*}_{0}&=\frac{1+\alpha\gamma-\gamma}{1+\alpha\gamma}=\frac{1+(0.7).(0.6)-0.6}{1+(0.7).(0.6)}=0.5775,\\[8pt] P^{*}_{0}&=\gamma\bigg(\frac{1+\alpha\gamma-\gamma}{1+\alpha\gamma}\bigg)=0.6\bigg(\frac{1+(0.7).(0.6)-0.6}{1+(0.7).(0.6)}\bigg)=0.3465. \end{aligned} \end{align*} $$
It has only one positive equilibrium
$E^{*}_{0} = (N^{*}_{0},P^{*}_{0} ) = (0.5775,0.3465)$
,
$$ \begin{align*} a_{1}&=1-2N_{0}^{*}=-0.155, \quad a_{2}=-\frac{1}{N_{0}^{*}+\alpha, P_{0}^{*}}=-1.2194, \\[3pt] a_{3}&=\frac{P_{0}^{*}N_{0}^{*}}{(N_{0}^{*}+\alpha, P_{0}^{*})^{2}}=0.2975, \quad a_{4}=\beta\delta-\frac{2\beta P_{0}^{*}}{N_{0}^{*}}=-0.54, \\[3pt] a_{5}&=\frac{\beta (P_{0}^{*})^{2}}{(N_{0}^{*})^{2}}=0.3240. \end{align*} $$
Taking
$\alpha = 0.7$
,
$N^{*}_{0}=0.5775$
,
$P^{*}_{0}=0.3465$
,
$q=0.98$
,
$a_{1}=-0.155$
,
$a_{2}=-1.2194$
,
$a_{3}=0.2975$
,
$a_{4}=-0.54$
and
$a_{5}=0.3240$
in equation (3.5), for
$v=\omega ^{0.98}$
, the following equation is obtained:
$$ \begin{align*} v^{4}+0.0175v^{3}-0.2132v^{2}-0.0105v-0.0972=0. \end{align*} $$
Solving this equation, we obtain
$v=0.6625$
and
$\omega =0.6570$
, and then
$$ \begin{align*} C_{1}&=(-a_{1}-a_{2}P_{0}^{*}-a_{3})=0.28, \nonumber\\[3pt]C_{2}&=-a_{4}=0.54, \nonumber\\[3pt]D&=a_{1}a_{4}+a_{2}P_{0}^{*}a_{4}+a_{3}a_{4}-a_{2}a_{5}N_{0}^{*}-a_{5}\alpha a_{3}=0.3119, \nonumber\\[-14pt]E_{1}&=C_{2}\omega^{q} \cos\bigg(\frac{q\pi}{2}\bigg)+D=0.3231,\nonumber\\[3pt]E_{2}&=C_{2}\omega^{q} \sin\bigg(\frac{q\pi}{2}\bigg)=0.3576, \nonumber\\[3pt]A_{1}&=\omega^{2q}\cos(q\pi)+C_{1}\omega^{q}\cos\bigg(\frac{q\pi}{2}\bigg)=-0.4322, \nonumber\\[3pt]A_{2}&=\omega^{2q}\sin(q\pi)+C_{1}\omega^{q}\sin\bigg(\frac{q\pi}{2}\bigg)=0.2130, \nonumber\\[3pt]\tau_{0}&=\frac{1}{\omega}\arctan\bigg(\frac{E_{1}A_{2}-E_{2}A_{1}}{-(E_{1}A_{1}+E_{2}A_{2})}\bigg),\nonumber\\[3pt]\tau_{0}&=\frac{1}{0.6570}\arctan\bigg(\frac{(0.3231).(0.2130)+(0.3576).(0.4322)}{-((-0.3231).(0.4322)+(0.3576).(0.2130))}\bigg)\nonumber\\[3pt]&=1.9693. \end{align*} $$
Here, we will calculate using the result we got in Lemma 3.1. From Lemma 3.1, we know the following:
$$ \begin{align*} &\text{Re}\bigg(\frac{d\tau}{ds}\bigg)\bigg|_{s=i\omega} \\[5pt] &\quad=\frac{-(\omega^{3q}2q+DC_{1}\omega^{q} q)(\cos(q\pi/2)+\omega\tau)-(C_{1}C_{2}\omega^{2q}q+D\omega^{2q}2q)(\cos(q\pi) +\omega\tau)}{[(C_{2}\cos(q\pi/2)\omega^{q+1}+D\omega)^{2}+(C_{2}\sin(q\pi/2)\omega^{q+1})^{2}]} \\[5pt] &\qquad +\frac{-C_{2}^{2}q\omega^{2q-2}-DC_{2}q\omega^{q-2}\cos(q\pi/2)}{[(C_{2}\cos(q\pi/2)\omega^{q}+D)^{2}+(C_{2}\sin(q\pi/2)\omega^{q})^{2}]}. \end{align*} $$
Using all these values, we obtain the following:
$$ \begin{align*} \text{Re}\bigg(\frac{d\tau}{ds}\bigg)\bigg|_{s=i\omega}=-6.4459. \end{align*} $$
With this result, it has been shown that
$\text {Re}(d\tau /ds)|_{s=i\omega }$
is non-zero.
As we stated at the beginning of this section, by modification of Adama–Bashforth– Moulton predictor-corrector method [Reference Bhalekar and Daftardar-Gejji2] for our fractional model in equation (1.2) with the parameters
$\tau _{0}$
and
$\omega $
, we also perform the graphs of our predator and prey functions to show the dynamical behaviour. In these simulations, we take the initial conditions
$(N_{0}, P_{0}) = (0.8, 0.5)$
and we first take
$\tau = 1.4 < \tau _{0}$
and plot the prey and predator functions
$N(t)$
and
$P(t)$
in Figures 1, 2 and 3, respectively, which shows that the positive equilibrium is asymptotically stable for
$\tau < \tau _{0}$
. However, in Figures 4, 5 and 6, we take
$\tau = 1.97$
sufficiently close to
$\tau _{0}$
, which illustrates the existence of bifurcating periodic solutions from the equilibrium point
$E^{*}_{0}$
.
Figure 1 Trajectory of prey density versus time with the initial conditions
$N_{0} = 0.8, P_{0} = 0.5$
, when
$q=0.98$
and
$ \tau = 1.4 < \tau _{0}=1.9693$
where the equilibrium point
$E^{*}_{0}$
is asymptotically stable.
Figure 2 Trajectory of predator density versus time with the initial conditions
$N_{0} = 0.8, P_{0} = 0.5$
, when
$q=0.98$
and
$ \tau = 1.4 < \tau _{0}=1.9693$
where the equilibrium point
$E^{*}_{0}$
is asymptotically stable.
Figure 3 Phase portrait of predator density versus prey density for the same parameters as in Figure 1, when
$\tau =1.4 <\tau _{0}$
.
Figure 4 Trajectory of prey density versus time with the initial conditions
$ N_{0}=0.8, P_{0} = 0.5$
, when
$\tau = 1.97$
is the system periodic structure.
Figure 5 Trajectory of predator density versus time with the initial conditions,
$ N_{0}=0.8, P_{0} = 0.5$
, when
$\tau = 1.97$
is the system periodic structure.
Figure 6 Phase portrait of predator density versus prey density for the same parameters as in Figure 1. When
$\tau = 1.97$
, the system shows the bifurcating periodic solutions from
$E^{*}_{0}$
.
5 Conclusion
In this paper, a fractional-order delayed predator-prey model with Holling–Tanner-type functional response is studied. By taking the time delay
$\tau $
as the bifurcation parameter, we show that Hopf bifurcation can occur as the time delay
$\tau $
passes some critical values which is determined by analysing the characteristic equation. Finally, we perform a numerical example to illustrate the theoretical results. For our numerical example, we determine
$E^{*}_{0} = (N^{*}_{0},P^{*}_{0} ) = (0.5775,0.3465)$
,
$\omega =0.6570$
and
$\tau _{0}=1.9693$
. To show the existence of Hopf bifurcation, we also determine the suitable fractional order q. We first take
$q=0.98$
and
$\tau = 1.4 < \tau _{0}$
and plot the prey and predator functions
$N(t)$
and
$P(t)$
in Figures 1 and 2, respectively, which shows that the positive equilibrium is asymptotically stable for
$\tau < \tau _{0}$
. However, in Figures 4 and 5, we take
$q=0.98$
and
$\tau = 1.97$
sufficiently close to
$\tau _{0}$
, which illustrates the existence of bifurcating periodic solutions from the equilibrium point
$E^{*}_{0}$
. For the validity of our theoretical and numerical results, we also check the case
$q=1$
, where there is no fractional derivative which was studied by Çelik [Reference Çelik7]. Moreover, we observed that figures for
$\tau =1.8$
and
$\tau =2.3$
as in [Reference Çelik7] are obtained similarly by using our Matlab program for
$q=1$
.
