2. The QIS5 probability model for the MTPL man-made catastrophe gross risk capital

The QIS5 man-made catastrophe motor vehicle liability risk sub-module requires input data:

• V_c : the number of vehicles insured (in Mio.) per country indexed by c

• L_c : the highest sums insured (or limit of exposure) (in Mio.) per country indexed by c

Any MTPL catastrophe model of the total loss is based on three assumptions about

1. (i) the frequency of catastrophe claims for single motor vehicles

2. (ii) the size of loss if a catastrophe claim occurs

3. (iii) the total loss that can occur

First, the frequency of the Europe-wide scenario per vehicle per annum in terms of the variable parameters

• RP : return period of Europe-wide scenario

• VY : total vehicle years (in Mio.) assumed in Europe-wide scenario

is described by the following function (usual actuarial letter lambda for claim frequencies)

$${{\lambda }_{MTPL}}(RP,VY)\, = \,{\rm{ - }}\frac{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}}{{VY}}.$$

The total expected claim frequency of the Europe-wide scenario is then defined by

$${{\lambda }_{TOTAL}}(RP,VY)\, = \,{{\lambda }_{MTPL}}(RP,VY) \cdot \left( {{\mathop{\sum }\limits_{c}} {{V}_c}} \right).$$

Second, the size S of loss given a catastrophe claim occurs, is described by a Pareto claim size distribution with survival function

$${{\bar{F}}_{PAR}}(S;GL,\gamma )\, = \,{{\left( {\frac{S}{{GL}}} \right)}^{{\rm{ - }}\gamma }}, \;S\, \gt \,GL\, \gt \,0,\;\gamma \,\geq \,1,$$

with the variable parameters

• GL : (minimum) gross loss of Europe-wide scenario

• γ : Pareto shape parameter of the extreme claim size distribution of Europe-wide scenario

Third, an assumption about the total loss across all countries or about the joint modelling of claim frequency and claim size is made.

To punctuate the above, let us summarize the three basic assumptions:

1. (A1) The total expected claim frequency of a catastrophe event (2.2) is the product of the frequency per vehicle per annum (2.1) by the total number of vehicles.

2. (A2) The size of a loss (given it occurs) is the Pareto distribution (2.3) with the minimum gross loss as threshold.

3. (A3) The total loss is described by a probability joint model of claim frequency and claim size.

While we shall continue in the next Subsection with the QIS5 modelling choice for the main assumption (A3), we will present in Section 3 some alternative classical and more recent risk theoretical economic capital models of great importance in insurance business.

2.1. The QIS5 probability model excluding limits of coverage

Concerning the total loss that can occur, let us first make the following simple model assumption (note that this is a bit more precise than QIS5 (2010), SCR 9.119, p. 129):

(M1) In a MTPL man-made catastrophe event, each motor vehicle is equally likely involved, and all vehicles subject to a catastrophe event build a set of mutually exclusive events.

Since the probability of a single catastrophe loss of size S > GL is described by (2.3), and through application of the additive rule of probability, which holds under (M1), one sees that a man-made catastrophe event of size S > GL occurs with the total probability (use (2.2) for the total claim frequency)

$${{\bar{F}}_{TOTAL}}(S;RP,VY,GL,\gamma )\, = \,{{\lambda }_{TOTAL}}(RP,VY) \cdot {{\left( {\frac{S}{{GL}}} \right)}^{{\rm{ - }}\gamma }} \, = \,{{\lambda }_{MTPL}}(RP,VY) \cdot \left( {{\mathop{\sum }\limits_{c}} {{V}_c}} \right) \cdot {{\left( {\frac{S}{{GL}}} \right)}^{{\rm{ - }}\gamma }} .$$

Now, if a man-made catastrophe event is allowed to occur with a return period of 1 in 200 years, then the corresponding risk capital, denoted by $$$ CAT_{m}^{{ec}} \, = \,CAT_{m}^{{ec}} (RP,VY,GL,\alpha ) $$$, is the unique solution of the equation $$${{\bar{F}}_{TOTAL}}(S;RP,VY,GL,\gamma )\, = \,{\rm{ - }}\ln (1{\rm{ - }}{{200}^{{\rm{ - }}1}} )\, \approx \,0.005$$$, i.e.

$$CAT_{m}^{{ec}} \, (RP,VY,GL,\gamma )\, = \,{{\left( {\frac{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}}{{\ln (1{\rm{ - }}{{{200}}^{{\rm{ - }}1}} )}} \cdot \frac{{\mathop{\sum}\limits_c {{{V}_c}} }}{{VY}}} \right)}^{{{\gamma }^{{\rm{ - }}1}} }} \, \cdot GL.$$

As will be seen later in formula (2.10), this capital requirement corresponds to the full QIS5 model (including limits of coverage) in case the insured limits are ignored. This is the reason why we denote (2.5) with a superscript “ec” and call (by abuse of language) this simple model the “QIS5 model that excludes limits of coverage”.

2.2. The QIS5 probability model including limits of coverage

According to QIS5 (2010), SCR 9.122 and 9.123, limits of coverage provided by undertakings in different countries must be taken into account, and allowance must also be made for losses caused outside the “home” country of insurance. This is done by including a “limit failure factor” for each country, which represents a proportion of the extreme losses that are considered to occur in such a way that the cover under the original policy is unlimited. The used value of this factor is 6% for each country except Iceland, Cyprus and Malta, where it is 0%. Note that this parameter has no effect for countries with unlimited risk exposures.

Then, under the model assumption (M1) and similarly to (2.4), the probability of a total loss of size S > GL ignoring limits, which depends on the variable parameters and the fixed proportions of “limit failure losses” amongst extreme losses per country defined by

$$\openup 5pt{{U}_c}\, = \,\left\{ {\matrix{ {6\%, \;\;c\, \ne \,Iceland,\;Cyprus,\;Malta,} \hfill\cr {0\%, \;\;c\, = \,Iceland,\;Cyprus,\;Malta,}} \right$$

is described by the following function

$$\bar{F}_{{TOTAL}}^{{un\lim }} (S;RP,VY,GL,\gamma )\, = \,{{\lambda }_{MTPL}}(RP,VY) \cdot \left( {{\mathop{\sum }\limits_{c}} {{U}_c} \cdot {{V}_c}} \right) \cdot {{\left( {\frac{S}{{GL}}} \right)}^{{\rm{ - }}\gamma }} .$$

On the other hand, the probability of a total loss allowing for insured limits is described by

$$\bar{F}_{{TOTAL}}^{{\lim }} (S;RP,VY,GL,\gamma )\, = \,{{\lambda }_{MTPL}}(RP,VY) \cdot \left( {{\mathop{\sum }\limits_{{c\vert S\, \lt \,{{L}_c}}}} (1{\rm{ - }}{{U}_c}) \cdot {{V}_c}} \right) \cdot {{\left( {\frac{S}{{GL}}} \right)}^{{\rm{ - }}\gamma }} .$$

Given parameter values for RP, VY, GL, γ, the gross motor catastrophe capital requirement, denoted by CAT_m = CAT_m (RP, VY, GL, γ), is defined to be the (unique) solution S = CAT_m (if it exists) of the equation (cf. QIS5 errata (2010), SCR 9.116, 9.126)

$$\bar{F}_{{TOTAL}}^{{un\lim }} (S;RP,VY,GL,\gamma )\, + \,\bar{F}_{{TOTAL}}^{{\lim }} (S;RP,VY,GL,\gamma )\, + \,\ln (1{\rm{ - }}{{200}^{{\rm{ - }}1}} )\, = \,0.$$

It is not difficult to see that the unique solution to (2.9), in case insured limits are ignored, coincides with the capital requirement (2.5) excluding limits of coverage, i.e.

$$CAT_{m}^{{un\lim }} \, (RP,VY,GL,\gamma )\, = \,CAT_{m}^{{ec}} \, (RP,VY,GL,\gamma ).$$

In general, for a fixed pattern of insured limits (L_c), such that $$$CAT_{m}^{{un\lim }} \, \gt \,{{L}_c}$$$ for at least one country, and a fixed choice of RP, VY, GL, γ, the solution to (2.9) is denoted by $$$CAT_{m}^{{ic}} \:(RP,VY,GL,\gamma )$$$ (model including limits of coverage). In this situation, the strict inequality

$$CAT_{m}^{{ic}} \, (RP,VY,GL,\gamma )\, \lt \,CAT_{m}^{{ec}} \, (RP,VY,GL,\gamma )$$

holds because limits restrict the total expected claim frequency and capital requirement is decreased accordingly. It remains to discuss the existence question and the computational evaluation of the solvency risk equation (2.9). Solving this equation is equivalent to finding the zero of the function

$$f(S;RP,VY,GL,\gamma )\, = \,\left( {{\mathop{\sum }\limits_{c}} {{U}_c} \cdot {{V}_c}\, + \,{\mathop{\sum }\limits_{{c|S \lt {{L}_c}}}} (1{\rm{ - }}{{U}_c}) \cdot {{V}_c}} \right) \cdot {{S}^{ - \gamma }} {\rm{ - }}\frac{{\ln (1{\rm{ - }}{{{200}}^{{\rm{ - }}1}} )}}{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}} \cdot VY \cdot G{{L}^{{\rm{ - }}\gamma }} .$$

For ease of notation we write f (S) instead of f (S, RP, VY, GL, γ) in the following. The graph of this function shows that it is a decreasing piecewise continuous function with discontinuities at the insured limits (L_c). Since at a discontinuity the function is not defined, and it can happen that $$$f(L_{c}^{ - } )\, \gt \,0$$$ while $$$f(L_{c}^{ + } )\, \lt \,0$$$ for some particular choice of insured limit and parameter values (the entries in italic print in Tables 2 and 4 are of this kind), the catastrophe risk capital must in general be defined by

$$CAT_{m}^{{ic}} \, (RP,VY,GL,\gamma )\, = \,\inf \left\{ {S\left| {f(S,RP,VY,GL,\gamma )\,\leq \,0} \right.} \right\}.$$

The QIS5 parameters are RP = 20, VY = 300, GL = 275, γ = 2. In this situation (2.13) tells us that $$$CAT_{m}^{{ic}} $$$ is the smallest value of S satisfying the inequality (note that the right-hand side figure in (2.11) is not correct in EC-Draft L2 IM (2010), pp. 91–92)

$$\left( {{\mathop{\sum }\limits_{c}} {{U}_c} \cdot {{V}_c}\, + \,{\mathop{\sum }\limits_{{c|S \lt {{L}_c}}}} (1{\rm{ - }}{{U}_c}) \cdot {{V}_c}} \right) \cdot \left( {\frac{1}{{{{S}^2} }}} \right)\,\leq \,3.877 \cdot {{10}^{{\rm{ - }}4}} $$

It has been felt that the implementation of a catastrophe risk capital formula like (2.14) is not simple enough, and the requirement of a closed-form solution has been expressed (e.g. CEA CAT Risk (2011), p. 5). However, the decreasing piecewise continuous property of the function (2.12) can be used to derive a closed-form formula for (2.13), and a fortiori for (2.14). First of all, rewrite the relevant sum in the bracket of (2.12) as

$${\mathop{\sum }\limits_{c}} {{U}_c} \cdot {{V}_c}\, + \,{\mathop{\sum }\limits_{{c|S \lt {{L}_c}}}} (1{\rm{ - }}{{U}_c}) \cdot V_c\, = \,{\mathop{\sum }\limits_{{c|S\:\geq \, {{L}_c}}}} {{U}_c} \cdot {{V}_c}\, + \,{\mathop{\sum }\limits_{{c|S \lt {{L}_c}}}} {{V}_c}.$$

Then, renumber the insured limits in increasing order such that L ₁ < L ₂ < … < L_N, where N is the number of involved countries, and consider the following quantities

$$CA{{T}_k}\, = \,CA{{T}_k}\:(RP,VY,GL,\gamma )\, = \,{{\left( {\frac{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}}{{\ln (1{\rm{ - }}{{{200}}^{{\rm{ - }}1}} )}} \cdot \frac{{\mathop{\sum}\limits_{i\, = \,1}^k {{{U}_i} \cdot {{V}_i}} \, + \,\mathop{\sum}\limits_{i\, = \,k\, + \,1}^N {{{V}_i}} }}{{VY}}} \right)}^{{{\gamma }^{{\rm{ - }}1}} }} \, \cdot GL,\;\,k\, = \,0, \ldots, N.$$

Note that $$$CA{{T}_0}\, = \,CAT_{m}^{{ec}} $$$ is (2.10) and $$$CA{{T}_j}\, \gt \,CA{{T}_{j\, + \,1}},\;\,j\, = \,0, \ldots, N{\rm{ - }}1$$$. We obtain the following result.

Theorem 2.1. (QIS5 MTPL man-made catastrophe risk capital) The QIS5 risk capital associated to the catastrophe risk model (M1) including limits of coverage, with individual motor claim frequency (2.1) and Pareto claim size distribution (2.3), is given by the closed-form formula

$$\openup 2pt CAT_{m}^{{ic}} \,(RP,VY,GL,\gamma )\, = \,\left\{ {\matrix{ {CA{{T}_0},} \hfill &amp; {f(L_{1}^{ - } )\, \lt \,0,} \hfill\hfill \cr {{{L}_j},} \hfill &amp; {f(L_{j}^{ - } )\,\geq \,0 \wedge f(L_{j}^{ + } )\, \lt \,0,\;\,j\, = \,1,\ldots,N,} \hfill \cr {CA{{T}_j},} \hfill &amp; {f(L_{j}^{ + } )\,\geq \,0 \wedge f(L_{{j + 1}}^{ + } )\, \lt \,0,\,\;j\, = \,1,\ldots,N - 1,} \hfill \cr {CA{{T}_N},} \hfill &amp; {f(L_{N}^{ + } )\,\geq \,0.} \hfill \right$$

Proof. The proof is simple and makes use of the decreasing piecewise continuous property of the function (2.12). ◊

3. The modified QIS5 economic capital model

The QIS5 CAT formula is not consistent with current economic capital modelling within risk management. We observe that (2.13)–(2.14) is the value-at-risk measure of the total loss to the confidence level $$$ \alpha \, = \,1\, + \,\ln (1{\rm{ - }}{{200}^{{\rm{ - }}1}} )\, \approx \,0.995 $$$, and not the value-at-risk measure of the increase of the total loss with respect to the mean, also called total insurance risk, which is the accepted standard (see Hürlimann (Reference Hürlimann2011), formula (2.9), for a recent general justification of the latter concept). In this respect, the current solution even contradicts the QIS5 principle used to measure the non-life risk capital, which is specified according to the accepted standard (e.g. Hürlimann, Reference Hürlimann2010). However, it is not difficult to modify the QIS5 formula to render it consistent with the accepted standard economic capital approach. For this, we must subtract the expected total loss (calculated according to model assumption (M1)) from the corresponding value-at-risk measure.

3.1. Economic capital for model (M1) excluding limits of coverage

Using (2.5) and the formula for the mean of a Pareto distribution with shape parameter γ > 1 (we assume here a finite mean), we obtain the modified VaR QIS5 economic capital formula

$$EC_{{(M1)}}^{{ec}} \, (RP,VY,GL,\gamma )\, = \,\left\{ {{{{\left( {\frac{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}}{{\ln (1{\rm{ - }}{{{200}}^{{\rm{ - }}1}} )}} \cdot \frac{{\mathop{\sum}\limits_c {{{V}_c}} }}{{VY}}} \right)}}^{{{\gamma }^{{\rm{ - }}1}} }} \, + \,\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} ) \cdot \frac{\gamma }{{\gamma {\rm{ - }}1}} \cdot \frac{{\mathop{\sum}\limits_c {{{V}_c}} }}{{VY}}} \right\} \cdot GL.$$

3.2. Economic capital for model (M1) including limits of coverage

Similarly, using (2.7)–(2.8), we see that the economic capital is defined to be the (unique) zero $$$ S = EC_{{(M1)}}^{{ic}} $$$ (if it exists) of the function (modified version of (2.12))

$$f(S)\, = \,\left\{ \matrix{ {\displaystyle{{\left( {\frac{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}}{{\ln (1{\rm{ - }}{{{200}}^{{\rm{ - }}1}} )}} \cdot \frac{{\mathop{\sum}\limits_c {{{U}_c} \cdot {{V}_c}} \, + \,\mathop{\sum}\limits_{c\left&#x007C; {S\, \lt \,{{L}_c}} \right.} {(1{\rm{ - }}{{U}_c}) \cdot {{V}_c}} }}{{VY}}} \right)}^{{{\gamma }^{{\rm{ - }}1}} }}}\hfill \cr \displaystyle+ \ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} ) \cdot \frac{\gamma }{{\gamma {\rm{ - }}1}} \cdot \frac{{\mathop{\sum}\limits_c {{{U}_c} \cdot {{V}_c}} \, + \,\mathop{\sum}\limits_{c\left&#x007C; {S\, \lt \,{{L}_c}} \right.} {(1{\rm{ - }}{{U}_c}) \cdot {{V}_c}} }}{{VY}}} \cr \end\right\} \cdot \frac{{GL}}{S}{\rm{ - }}1.$$

Again, we note that this function is a decreasing piecewise continuous function with discontinuities at the insured limits (L_c). To solve it in closed-form we proceed as in Subsection 2.2. Renumber the insured limits such that L ₁ < L ₂ < … < L_N, and consider the quantities

$$E{{C}_k}\, = \,E{{C}_k}(RP,VY,GL,\gamma )\, = \,\left\{ \matrix {\displaystyle{{\left( {\frac{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}}{{\ln (1{\rm{ - }}{{{200}}^{{\rm{ - }}1}} )}} \cdot \frac{{\mathop{\sum}\limits_{i\, = \,1}^k {{{U}_i} \cdot {{V}_i}} \, + \,\mathop{\sum}\limits_{i\, = \,k\, + \,1}^N {{{V}_i}} }}{{VY}}} \right)}^{{{\gamma }^{{\rm{ - }}1}} }} \hfill\cr \displaystyle + \ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} ) \cdot \frac{\gamma }{{\gamma {\rm{ - }}1}} \cdot \frac{{\mathop{\sum}\limits_{i\, = \,1}^k {{{U}_i} \cdot {{V}_i}} \, + \,\mathop{\sum}\limits_{i\, = \,k + 1}^N {{{V}_i}} }}{{VY}}} \right\} \cdot GL,\,\;k\, = \,0,\ldots,N.$$

Note that $$$E{{C}_0}\, = \,EC_{{(M1)}}^{{ec}} $$$ and $$$E{{C}_j}\, \gt \,E{{C}_{j\, + \,1}},\,\;j\, = \,0, \ldots, N{\rm{ - }}1$$$. We obtain the following modified QIS5 MTPL man-made catastrophe risk capital formula.

Theorem 3.1. The modified QIS5 economic capital associated to the catastrophe risk model (M1) including limits of coverage, with individual motor claim frequency (2.1) and Pareto claim size distribution (2.3) with shape parameter γ > 1, is given by the closed-form formula

$$EC_{{(M1)}}^{{ic}} (RP,VY,GL,\gamma )\, = \,\left\{ {\matrix {{E{{C}_0},} \hfill &amp; {f(L_{1}^{ - } )\, \lt \,0,} \hfill \cr {{{L}_j},} \hfill &amp; {f(L_{j}^{ - } )\,\geq \,0\, \wedge \,f(L_{j}^{ + } )\, \lt \,0, \ j\, = \,1,\ldots,N,} \hfill \cr {E{{C}_j},} \hfill &amp; {f(L_{j}^{ + } )\,\geq \,0\, \wedge \,f(L_{{j + 1}}^{ + } )\, \lt \,0, \ j\, = \,1,\ldots,N{\rm{ - }}1,} \hfill \cr {E{{C}_N},} \hfill &amp; {f(L_{N}^{ + } )\,\geq \,0.} \hfill \right.$$

Proof. This is similar to the proof of Theorem 2.1. ◊

4. Risk theoretical economic capital models for man-made catastrophe risks

The crucial total loss probability model assumed in QIS5 is a simple though not very satisfactory model from an actuarial viewpoint. The model assumption (M1) implicitly implies that the total loss is made of a single catastrophe claim in case it occurs over a one-year time period. However, since Cramér-Lundberg, the total loss should rather be dynamically modelled by a sequence of claims of varying size, where claims occur over time according to a Poisson process. For this reason, we alternatively model the total loss using a compound Poisson Pareto model of the aggregate extreme losses, i.e. a Poisson distributed frequency driven by the return period and the number of vehicle years as in (2.2) or (2.7)–(2.8), and a Pareto distribution for the extreme loss size driven by a Pareto shape γ > 1 as in (2.3) (in contrast to (2.3) we assume a finite mean).

In the Subsections 3.1 and 3.2, we propose two alternatives to the current and modified QIS5 man-made catastrophe risk approach. Recall the basic relevant facts taken from Hürlimann (Reference Hürlimann2011), Section 2. The one-year total loss is described by one of the two models:

(M2) The total loss follows a compound Poisson Pareto aggregate claims model defined by

$$TL\, = \,\mathop{\sum}\limits_{i\, = \,1}^N {{{S}_i}}, $$

where the number of claims N is Poisson (λ) distributed, the catastrophe claim sizes S ₁,…,S_N are independent and identically distributed and follow a Pareto distribution of the type (2.3) with γ > 1, and N is independent of the sequence S ₁,…,S_N.

(M3) The total loss follows a compound Poisson Pareto aggregate claims model with Black-Scholes-Merton returns, defined by

$$TL\, = \,\mathop{\sum}\limits_{k\, = \,1}^N {{{R}_{{{M}_k}}} \cdot {{S}_k}}, $$

where the number of claims N is Poisson (λ) distributed, M_k is the exponentially distributed moment of time at which the k-th claim occurs (arrival time associated to the number of claims), S ₁,…,S_N are independent and identically Pareto (2.3) distributed catastrophe claim sizes occurring at the times M ₁,…,M_N, $$${{R}_s}\, = \,\exp \left( {{{Y}_1}{\rm{ - }}{{Y}_s}} \right),0\, \lt \,s\, \lt \,1$$$, represents the random accumulation factor over the time period [s,1) for a geometric Brownian return process {Y_s, s ≥ 0} with drift and Lévy exponent $$$\psi (z)\, = \,\tfrac{1}{2}{{\sigma }^2} \cdot {{z}^2} \, + \,\delta \cdot z$$$, and the sources of randomness N, {S ₁,…,S_N} and {Y_s, s ≥ 0} are mutually independent.

The models (M2) and (M3) are two of the most important special instances of the more general Sparre Andersen model with geometric Lévy returns (see Hürlimann (Reference Hürlimann2011), Examples 3.1). The Poisson parameter of these models will be either the deterministic quantity

$$\lambda \, = \,{{\lambda }_{MTPL}}\,(RP,VY) \cdot \left( {\mathop{\sum}\limits_c {{{V}_c}} } \right),$$

defined in (2.2), for the models excluding limits of coverage, or the piecewise continuous random function of the (unknown) total loss TL

$$\lambda \, = \,\lambda (TL)\, = \,{{\lambda }_{MTPL}}(RP,VY) \cdot \left( {\mathop{\sum}\limits_c {{{U}_c} \cdot {{V}_c}} \, + \,\mathop{\sum}\limits_{c\left&#x007C; {TL\, \lt \,{{L}_c}} \right.} {(1{\rm{ - }}{{U}_c}) \cdot {{V}_c}} } \right),$$

defined similarly to the quantities in (2.7)–(2.8), for the models including limits of coverage. Finally, the end-of-year VaR economic capital to the confidence level α associated to the total insurance risk $$$ T{{L}^I} \, = \,TL\,{\rm{ - }}\,E\left[ {TL} \right] $$$ is defined by (see Hürlimann (Reference Hürlimann2011), formula (2.9), for a justification)

$$EC_{\alpha }^{I} \, = \,Va{{R}_\alpha }{\rm{[}}T{{L}^I} {\rm{]}}{\rm{.}}$$

Clearly, the evaluation of the economic capital (4.5) requires the knowledge of the distribution of the total loss random variables defined in (4.1) and (4.2). A direct computational evaluation of this distribution relies on advanced numerical methods (see Sundt & Vernic (Reference Sundt and Vernic2009) for a survey of this topic). In particular, the stochastic specification (4.4) should perhaps require new methods. Since in catastrophe risk modelling one is only interested in the right tail of the distribution, some asymptotic analytical approximations might suffice for practical purposes.

4.1. The risk theoretical economic capital models excluding limits of coverage

For a homogeneous Poisson claim number process with parameter (4.3) the survival distribution of the total loss satisfies the following asymptotic equivalence (see Hürlimann (Reference Hürlimann2011), Theorem 3.1 and Examples 3.1, special case of a unit time period):

$$P\left( {TL\, \gt \,S} \right)\,\sim \,\lambda \cdot {{\bar{F}}_{PAR}}(S) \cdot \left\{ {\matrix {{1,} \hfill &amp; {(M2),} \hfill \cr {({{e}^{\psi (\gamma )}}\, {\rm{ - }}\,1)/\psi (\gamma ),} \hfill &amp; {(M3),} \hfill \right$$

where in model (M3) the function $$$\psi (z)\, = \,\ln E\left[ {{{e}^{z{{Y}_1}}} } \right]\, = \,\delta z\, + \,\tfrac{1}{2}{{\sigma }^2} {{z}^2}, \,z\, \in \,\left( {{\rm{ - }}\infty, \infty } \right)$$$, is the Lévy exponent of the Black-Scholes-Merton return model (a geometric Brownian process). It is interesting to observe that the right-hand side of (4.6) for model (M2) coincides with the survival distribution (2.4) obtained for model (M1). Therefore, we conclude that asymptotically as the total loss increases without limits the model assumption (M2) is equivalent to the model assumption obtained from (M1) by replacing a single catastrophe claim by the total loss. In other words, the QIS5 simple model (M1) is justified as limiting asymptotic approximation to the classical compound Poisson Pareto model (M2). Conversely, we obtain the following asymptotic approximation to the (M2) VaR economic capital.

Corollary 4.1. The end-of-year VaR economic capital associated to the catastrophe risk model (M2) excluding limits of coverage, with Poisson parameter (4.3) and Pareto shape parameter γ > 1, is asymptotically determined by the formula (3.1), i.e.

$$EC_{{(M2)}}^{{ec}} (RP,VY,GL,\gamma )\sim EC_{{(M1)}}^{{ec}} (RP,VY,GL,\gamma ).$$

Proof. This is the special case n = 1 of (3.12) in the Examples 3.1 illustrating Theorem 3.2 in Hürlimann (Reference Hürlimann2011). ◊

A similar result holds for the model (M3).

Theorem 4.1. The end-of-year VaR economic capital associated to the compound Poisson Pareto Black-Scholes-Merton model (M3) excluding limits of coverage, with Poisson parameter (4.3), Pareto shape parameter γ > 1, and Lévy exponent $$$\psi (z)\, = \,\delta z\, + \,\tfrac{1}{2}{{\sigma }^2} {{z}^2} $$$, is asymptotically determined by the formula

$$EC_{{(M3)}}^{{ec}} (RP,VY,GL,\gamma )\sim \left\{ \matrix {\displaystyle{{\left( {\frac{{{{e}^{\psi (\gamma )}} {\rm{ - }}1}}{{\psi (\gamma )}} \cdot \frac{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}}{{\ln (1{\rm{ - }}{{{200}}^{{\rm{ - }}1}} )}} \cdot \frac{{\mathop{\sum}\limits_c {{{V}_c}} }}{{VY}}} \right)}^{{{\gamma }^{{\rm{ - }}1}} }} \hfill \cr\displaystyle + \frac{{{{e}^{\psi (1)}} {\rm{ - }}1}}{{\psi (1)}} \cdot \ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} ) \cdot \frac{\gamma }{{\gamma {\rm{ - }}1}} \cdot \frac{{\mathop{\sum}\limits_c {{{V}_c}} }}{{VY}} }\right\} \cdot GL.$$

Proof. Use the formulas (3.5)–(3.6) of Theorem 3.2 in Hürlimann (Reference Hürlimann2011) as explained in the Examples 3.1 there. ◊

4.2. The risk theoretical economic capital models including limits of coverage

Since the Poisson parameter (4.4) is a random function of the total loss, it cannot a priori be stated that the asymptotic equivalence (4.6) remains valid in this situation, a point left open for future research. Nevertheless, it is very intuitive to preserve the asymptotic similarity between model (M2) and (M1) stated in Subsection 4.1. Therefore, we will approximate the survival distribution of the total loss by (4.6) with Poisson parameter (4.4) for the models including limits of coverage. Then, the above results can be extended accordingly.

Corollary 4.2. The end-of-year VaR economic capital associated to the catastrophe risk model (M2) including limits of coverage, with random Poisson parameter (4.4) and Pareto shape parameter γ > 1, is asymptotically approximately determined by Theorem 3.1, i.e.

$$EC_{{(M2)}}^{{ic}} \, (RP,VY,GL,\gamma )\sim EC_{{(M1)}}^{{ic}} \, (RP,VY,GL,\gamma ).$$

The model (M3) can be handled in the manner of Subsection 3.2. The asymptotic approximation to the economic capital is defined to be the (unique) zero $$$ S\, = \,EC_{{(M3)}}^{{ic}} $$$ (if it exists) of the function (modify the function (3.2) using (4.8))

$$f(S)\, = \,\left\{ \matrix{\displaystyle {{\left( {\frac{{{{e}^{\psi (\gamma )}} {\rm{ - }}1}}{{\psi (\gamma )}} \cdot \frac{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}}{{\ln (1{\rm{ - }}{{{200}}^{{\rm{ - }}1}} )}} \cdot \frac{{\mathop{\sum}\limits_c {{{U}_c} \cdot {{V}_c}} \, + \,\mathop{\sum}\limits_{c\left&#x007C; {S\, \lt \,{{L}_c}} \right.} {(1{\rm{ - }}{{U}_c}) \cdot {{V}_c}} }}{{VY}}} \right)}^{{{\gamma }^{{\rm{ - }}1}} }} \cr \displaystyle+ \frac{{{{e}^{\psi (1)}} {\rm{ - }}1}}{{\psi (1)}} \cdot \ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} ) \cdot \frac{\gamma }{{\gamma {\rm{ - }}1}} \cdot \frac{{\mathop{\sum}\limits_c {{{U}_c} \cdot {{V}_c}} \, + \,\mathop{\sum}\limits_{c\left&#x007C; {S\, \lt \,{{L}_c}} \right.} {(1{\rm{ - }}{{U}_c}) \cdot {{V}_c}} }}{{VY}} }\right\} \cdot \frac{{GL}}{S}{\rm{ - }}1$$

This function is again a decreasing piecewise continuous function with discontinuities at the insured limits. To solve it, renumber the latter such that L ₁ < L ₂ < … < L_N, and consider the quantities

$$E{{C}_k}\, = \,E{{C}_k}\,(RP,VY,GL,\gamma )\, = \,\left\{ \matrix{\displaystyle {{\left( {\frac{{{{e}^{\psi (\gamma )}} {\rm{ - }}1}}{{\psi (\gamma )}} \cdot \frac{{\ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} )}}{{\ln (1{\rm{ - }}{{{200}}^{{\rm{ - }}1}} )}} \cdot \frac{{\mathop{\sum}\limits_{i\, = \,1}^k {{{U}_i} \cdot {{V}_i}} \, + \,\mathop{\sum}\limits_{i\, = \,k\, + \,1}^N {{{V}_i}} }}{{VY}}} \right)}^{{{\gamma }^{{\rm{ - }}1}} }} \cr \displaystyle+ \frac{{{{e}^{\psi (1)}} {\rm{ - }}1}}{{\psi (1)}} \cdot \ln (1{\rm{ - }}R{{P}^{{\rm{ - }}1}} ) \cdot \frac{\gamma }{{\gamma {\rm{ - }}1}} \cdot \frac{{\mathop{\sum}\limits_{i\, = \,1}^k {{{U}_i} \cdot {{V}_i}} \, + \,\mathop{\sum}\limits_{i\, = \,k\, + \,1}^N {{{V}_i}} }}{{VY}} }\\ \right\} \cdot GL,} \ k\, = \,0,\ldots,N. $$

Note that EC ₀ equals the right-hand side in (4.8) and $$$E{{C}_j}\, \gt \,E{{C}_{j\, + \,1}}, \ j\, = \,0, \ldots, N{\rm{ - }}1$$$. We obtain the following result.

Theorem 4.2. The end-of-year VaR economic capital associated to the catastrophe risk model (M3) including limits of coverage, with random Poisson parameter (4.4) and Pareto shape parameter γ > 1, is asymptotically approximately determined by the closed-form formula

$$EC_{{(M3)}}^{{ic}} (RP,VY,GL,\gamma )\sim \left\{ {\matrix{ {E{{C}_0},} \hfill &amp; {f(L_{1}^{ - } )\, \lt \,0,} \hfill \cr {{{L}_j},} \hfill &amp; {f(L_{j}^{ - } )\,\geq \,0\, \wedge \,f\:(L_{j}^{ + } )\, \lt \,0, \ j\, = \,1,\ldots,N,} \hfill \cr {E{{C}_j},} \hfill &amp; {f(L_{j}^{ + } )\,\geq \,0\, \wedge \,f\:(L_{{j + 1}}^{ + } )\, \lt \,0, \ j\, = \,1,\ldots,N{\rm{ - }}1,} \hfill \cr {E{{C}_N},} \hfill &amp; {f(L_{N}^{ + } )\,\geq \,0.} \hfill \right$$

Proof. This is similar to the proof of Theorems 2.1 and 3.1. ◊

5. Numerical illustration, simulation study and further comments

The calibration of the parameters VY, GL is related to the market size of the MTPL Europe-wide insurance business. QIS5 has specified their values (in Mio. EUR) as VY = 300, GL = 275. The level of CAT_m strongly depends upon the remaining model parameters RP, γ. QIS5 calibration assumes that RP = 20, γ = 2. Actuarial research, internal models and OSRA (own solvency risk assessment) are likely to provide very different figures varying in a wide range of possible values γ ∈ [1,3]. The choice γ = 1 (with no finite moment of the claim size) has been suggested by Zajdenweber (Reference Zajdenweber1996) for business interruption (e.g. the 9/11 terrorist attacks represented a business interruption claim of 11 billion USD) (see also Charpentier (Reference Charpentier2007b) and Berliner (Reference Berliner1985) on the limits of insurability). It is also possible to argue that the relatively safe QIS5 choice γ = 2 (without finite variance) might be too conservative for the MTPL insurance business. Typical statistical parameter estimation yields a value γ ≈ 2.5 (e.g. Hürlimann (Reference Hürlimann2010), Table 5.3, and Hürlimann (Reference Hürlimann2007), Table 4.1, for the Swiss MTPL market). Even γ = 2.9 has been suggested in the CEIOPS consultation paper CP71 (2010), Section 5, 5.26, p. 109. Further research is urgently needed to clarify which Pareto shape parameter should be appropriate for man-made catastrophe risk capital calculation. On the other hand, statistical estimation studies about the return period have only rarely been published in actuarial circles (e.g. Hürlimann, Reference Hürlimann2006) and should also been encouraged.

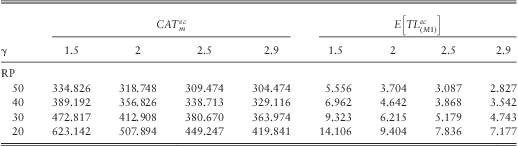
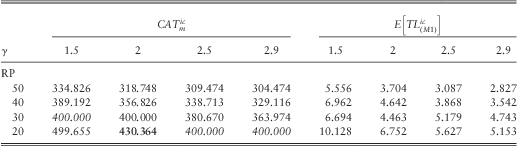
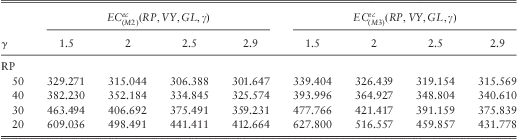
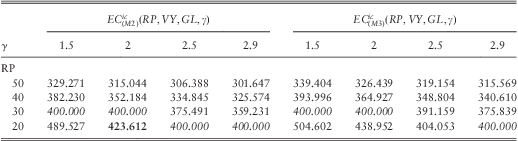
For the sake of illustration, we have computed the different capital requirements by fixed VY = 300, GL = 275 for the portfolio V_c = (30,50,20), L_c = (400,600,800). The CAT values under the QIS5 model (M1) are calculated according to the formulas (2.5)–(2.10) and (2.17) as listed in Tables 1 and 2 (the bold entry is the current QIS5 value). These two tables also contain the expected values of the total loss under this model. The (M1) asymptotic approximations to the economic capital models (M2) and (M3) are given in Tables 3 and 4 (the bold entry compares with the current QIS5 value in Table 2). Table entries are stated in Mio. EUR. The drift and volatility of the Black-Scholes-Merton return model are set equal to $$$ \delta \, = \,r{\rm{ - }}\tfrac{1}{2}{{\sigma }^2}, \,\,r\, = \,5\%, \,\,\sigma \, = \,20\% $$$. We note that the (M2) asymptotic economic capital approximations from the modified QIS5 approach differ from the QIS5 CAT values by the total loss means (except when these values coincide with insured limits due to the discontinuities). A comparison of (2.5)–(2.10) with (3.1), respectively (2.16)–(2.17) with (3.3)–(3.4), shows that this is always true.

Table 1 QIS5 CAT model ignoring insured limits

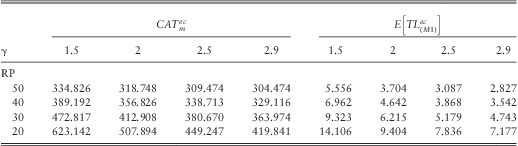
Table 2 QIS5 CAT model for a fixed pattern of insured limits

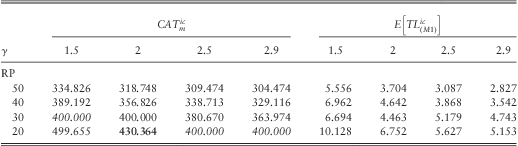
Table 3 (M1) approximations to EC models (M2) and (M3) ignoring insured limits

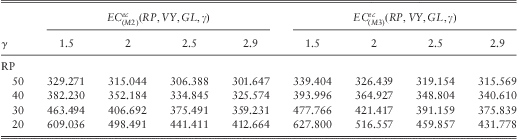
Table 4 (M1) approximations to EC models (M2) and (M3) for fixed insured limits

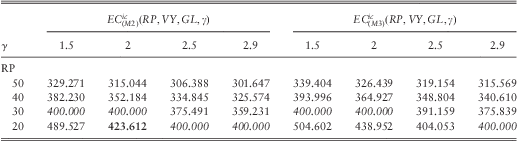
Since the results corresponding to models (M2) and (M3) are based on asymptotic approximations, it is necessary to investigate whether they lead to appropriate results. To support the made asymptotic approximations, a Monte Carlo simulation study will do. For simplicity we restrict ourselves to the models ignoring insured limits. For each set of parameter values, we have generated a sample of n = 1 Mio. total loss random variables in the usual way. To each simulated exponentially distributed inter claim time within a one year time horizon we associate a simulated Pareto claim size. For model (M2) we simply sum them over the possible inter claim times, and for model (M3) we multiply the claims with the corresponding simulated accumulation factors before summing. In this way we obtain two simulated samples of the random variables $$$TL_{{(M2)}}^{{ec}}, TL_{{(M3)}}^{{ec}} $$$ in (4.1) and (4.2), whose order statistics are denoted by

$$TL_{{(1)}}^{{M2}} \,\leq \,TL_{{(2)}}^{{M2}} \,\leq \, \ldots \,\leq \,TL_{{(n)}}^{{M2}}, TL_{{(1)}}^{{M3}} \,\leq \,TL_{{(2)}}^{{M3}} \,\leq \, \ldots \,\leq \,TL_{{(n)}}^{{M3}} .$$

Estimates of the value-at-risk measure of the total losses to the confidence level α = 0.995 are simply given by

$${{{\mathop{{VaR}}\limits^{ \wedge }} }_\alpha }\left[ {TL_{{(M2)}}^{{ec}} } \right]\, = \,TL_{{(\left[ {\alpha n} \right])}}^{{M2}}, {{{\mathop{{VaR}}\limits^{ \wedge }} }_\alpha }\left[ {TL_{{(M3)}}^{{ec}} } \right]\, = \,TL_{{(\left[ {\alpha n} \right])}}^{{M3}} .$$

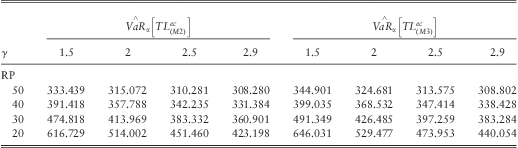
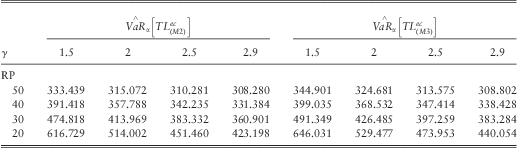
Table 5, which lists the results of our simulation study for this, should be compared with Tables 1 and 3 (the latter adjusted for the means). It confirms that the (M1) asymptotic approximations for our Poisson Pareto risk models can be used. The approximations are close to the simulated values and often on the safe side.

Table 5 Monte Carlo VaR estimates of models (M2) and (M3) ignoring insured limits

We observe that the conditional value-at-risk measure (CVaR), which is a coherent risk measure, can also be used instead of value-at-risk (see Hürlimann, Reference Hürlimann2011). In this situation we have used the estimates

$${{{\mathop{{CVaR}}\limits^{ \wedge }} }_\alpha }\left[ {TL_{{(M2)}}^{{ec}} } \right]\, = \,\frac{1}{{(1{\rm{ - }}\alpha )n}}\mathop{\sum}\limits_{i\, = \,\left[ {\alpha n} \right]}^n {TL_{{(i)}}^{{M2}} }, {{{\mathop{{CVaR}}\limits^{ \wedge }} }_\alpha }\left[ {TL_{{(M3)}}^{{ec}} } \right]\, = \,\frac{1}{{(1{\rm{ - }}\alpha )n}}\mathop{\sum}\limits_{i\, = \,\left[ {\alpha n} \right]}^n {TL_{{(i)}}^{{M3}} } .$$

To obtain them, consider the representation $$$CVa{{R}_\alpha }\left[ X \right]\, = \,{{(1{\rm{ - }}\alpha )}^{{\rm{ - }}1}} \cdot \left\{ {E\left[ X \right]{\rm{ - }}{{L}_\alpha }\left[ X \right]} \right\}$$$, where $$$ {{L}_\alpha }\left[ X \right]\, = \,\mathop{\int}\nolimits_0^\alpha {Q(u)du} $$$, Q(u) a quantile function, denotes the Lorenz transform of X (e.g. Hürlimann (Reference Hürlimann2003), Proposition 2.1, equation (2.8)). Then (5.3) follows by inserting the usual estimate for the mean and the following estimate for the Lorenz transform (given the order statistics X ₍₁₎ ≤ … ≤ X _{(n )} of a random sample X = (X ₁,…,X_n) of size n):

$$\hat{L}_{\alpha }^{{}} \left[ X \right]\, = \,{{n}^{{\rm{ - }}1}} \cdot \mathop{\sum}\limits_{i\, = \,1}^{\left[ {\alpha n} \right]\, + \,1} {{{X}_{(i)}}}. $$

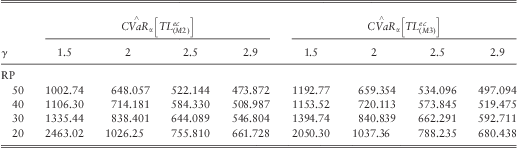
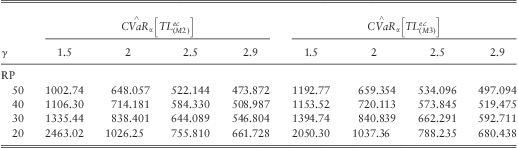
We note that the CVaR values in Table 6 exceed considerably the VaR values in Table 5, a fact which is related to the well-known dangerousness property of the Pareto distribution.

Table 6 Monte Carlo CVaR estimates of models (M2) and (M3) ignoring insured limits

Some further comments can be made. The required man-made catastrophe MTPL risk capital is sensitive to the assumed parameter values RP, γ, and illustrates clearly the need to understand better the role of these parameters. We note that the Pareto distribution is more dangerous by decreasing shape parameter and that this property is preserved for the capital requirements, at least in our numerical and simulation examples. The integration of returns in model (M3) has the effect to increase moderately the economic capital.