Integrated mixed-model ASP and ALB

An example of a mixed-model assembly line is found in vehicle production, where the assembly line runs one specific car type, but with different model variants, such as right- or left-hand drive and manual or automatic transmission. In addition, some of the cars require additional accessories to fulfill specific customer requirements. In this assembly line, there is only one product, that is, a specific car type, but the assembly process will vary due to differences between models. Assembly problems are commonly represented by assembly precedence graphs and assembly data table. The precedence graph consists of a set of nodes and arcs that represent assembly tasks and their precedence constraints. The outgoing arc from node i toward node j meaning the assembly task i must be completed before starting the assembly task j. Meanwhile the assembly data table represents the assembly information such as assembly direction, tool, and time for the particular assembly tasks.

The most common approach to express the mixed-model assembly problem is by transforming the precedence graphs into a joint graph as used in many existing mixed-model ALB works (Kara et al., Reference Kara, Özgüven, Seçme and Chang2011; Buyukozkan et al., Reference Buyukozkan, Kucukkoc, Satoglu and Zhang2016). The joint graph represents the precedence constraint for all models.

When the precedence diagram of model y is represented by a graph G _y = (V _y, C _y), where V _y is the set of tasks of model y and C _y is the set of precedence relations, the combined graph is G = (V, C), where V = U _y V_y and C = U _y C_y. An arc (i, j) is redundant if there exists another path from i to j in G. The mixed-model defines the number of units to be produced from each model during a shift of T time units. The processing time of y ∈V is equal to the total time required for the processing of this task in a given mixed-model.

For example, an assembly line runs two models of the product, Model A and Model B. The precedence graphs for both models are shown in Figure 1(a) and (b). To establish the joint graph, the followers for specific tasks in each model are bundled together in one graph. For example, in Figure 1, the followers for task 1 in Model A are tasks 2 and 3, while tasks 3 and 4 in Model B. The combination of task 1 followers from both models is tasks 2, 3, and 4 as shown in the joint graph. The joint graph is updated by removing the shortest repetitive routes from the graph. In the example below, the route connecting tasks 4 and 7 in Model B is removed from the Joint Model because task 7 cannot be started although task 4 has been performed, because there is dependence on completion of task 6 in Model A. Once the joint graph has been established, similar representation scheme as in simple assembly line problem can be used, except for assembly data representation.

Fig. 1. Precedence graph of (a) Model A, (b) Model B, and (c) Joint Model.

In the mixed-model assembly line, the assembly data set should represent the data for each model. In this case, the assembly data for similar tasks within different models might be different, depending on the actual processing task.

Objective functions and constraints

There are known objective functions to evaluate single-model assembly problems. To evaluate the fitness in the mixed-model assembly problem, the objective function is evaluated for every model, and the mean of these values is used as the fitness value. For the mixed-model assembly problem with M model:

Objective 1: Minimize the mean of the total direction changes

(1)$$\eqalign{{\bar{n}}_{{\rm dc}} &= \displaystyle{1 \over M}\sum\limits_{m = 1}^M {\sum\limits_{s = 1}^{n-1} {{\rm d}_s^m } } ;\;\;\;\;\;\;\;\;\;\;{\rm d}_s^m \cr & = \left\{ {\matrix{ {1\;{\rm if}\;\;{\rm direction}\;s\;\ne \;{\rm direction}\;s + 1\;{\rm for}\;m^{{\rm th}}\;{\rm model}} \cr {0\;{\rm if}\;\;{\rm direction}\;s = {\rm direction}\;s + 1\;{\rm for}\;m^{{\rm th}}\;{\rm model}} \cr } } \right..} $$

Objective 2: Minimize the mean of the total tool changes

(2)$$\eqalign{& {\bar{n}}_{{\rm tc}} = \displaystyle{1 \over M}\sum\limits_{m = 1}^M {\sum\limits_{s = 1}^{n-1} {t_s^m } } ; \cr & t_s^m = \left\{ {\matrix{ {1\;{\rm if}\;\;{\rm tool}\;s\;\ne \;{\rm tool}\;s + 1\;{\rm for}\;m^{{\rm th}}\;{\rm model}} \cr {0\;{\rm if}\;\;{\rm tool}\;s = {\rm tool}\;s + 1\;{\rm for}\;m^{{\rm th}}\;{\rm model}} \cr } } \right..} $$

Objective 3: Minimize the mean of cycle times

(3)$$\eqalign{& \overline {{\rm ct}} = \displaystyle{1 \over M}\sum\limits_{m = 1}^M {\rm c} {\rm t}_m; \cr & {\rm t}_m:\;{\rm Cycle}\;\;{\rm time}\;\;{\rm for}\;m^{{\rm th}}\;\;{\rm model}.} $$

Objective 4: Minimize the number of workstations

The number of workstation (nws) is determined once the assembly tasks assignment is completed. The number of workstation that generated for all models will be the same because similar tasks within different models are assigned into a similar workstation.

Objective 5: Minimize the mean of workload variations

(4)$$\eqalign{& \bar{v} = \displaystyle{1 \over M}\sum\limits_{m = 1}^M {\displaystyle{{\sum\nolimits_{i = 1}^{{\rm nws}} ( {\rm c}{\rm t}_m-{\rm pt}_i^m {\rm )}} \over {{\rm nws}}};} \cr & {\rm t}_i^m :\;{\rm processing}\;\;{\rm time}\;\;{\rm in}\;i^{{\rm th}}{\rm workstation}\;\;{\rm for}\;\;{\rm model}\;m \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm nws}\;:{\rm total}\;\;{\rm number}\;\;{\rm of}\;\;{\rm workstation}.} $$

Subjected to:

(5)$$\mathop \sum \limits_{k = 1}^{{\rm nws}} x_{ik} = 1\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; {\rm i} = 1\comma \, \ldots\comma \, n$$

(6)$$\mathop \sum \limits_{k = 1}^{{\rm nws}} x_{ak}-\mathop \sum \limits_{k = 1}^{{\rm nws}} x_{bk} \le 0\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; a\in n\comma \,\; b\in F_a$$

(7)$$\mathop \sum \limits_{{\rm i} = 1}^n t_i^m x_{ik} \le {\rm c}{\rm t}_{{\rm m}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \;} \forall m\comma \,\forall k.$$

The first constraint [Eq. (5)] ensures that an assembly task is assigned to one workstation. This constraint also means that the same assembly task from different models will be assembled in a similar workstation. Equation (6) represents the precedence constraint that needs to be followed. The F _a refers to the set of the successor for task i. In a different word, this constraint ensures that the successor/s for task i will be assigned in a similar or the following workstation. The constraint in Eq. (7) ensures that the maximum cycle time for a respective model (ct_m) is obeyed. In the case of any ct_m constraint is violated, the particular assembly task cannot be assigned into that workstation.

Multi-objective Discrete Particle Swarm Optimization

Various algorithms have been developed to optimize the combinatorial optimization problem. For instance, Hu et al. (Reference Hu, Wang, Wang, Wang and Zhang2014) implemented a new Discrete Particle Swarm Optimization for a combinatorial problem, involving a machining scheme selection. Besides that, the researcher also introduced a probability increment-based swarm algorithm to optimize the combinatorial optimization problem in a printed circuit board assembly (Zeng et al., Reference Zeng, Tan, Dong and Yang2014). Another popular algorithm to optimize the combinatorial optimization problem is GA, as implemented for scheduling and vehicle routing problems (Mirabi, Reference Mirabi2015; Rahman et al., Reference Rahman, Sarker and Essam2017).

In this work, we implement MODPSO to optimize the integrated mixed-model ASP and ALB (Ab. Rashid, Reference Ab. Rashid2013). The general procedure of MODPSO is presented in Figure 2.

Fig. 2. Flowchart of MODPSO algorithm.

Initialization

The initialization stage starts with defining the number of particles (n _par), the maximum iteration (iter_max), the inertia weight (c ₁), and learning coefficients (c ₂, c ₃). In this work, the default coefficient values for PSO are used (i.e. c ₁ = 0.4, c ₂ = c ₃ = 1.4). Next, the initial population is generated. The initial population consists of n _par particles. Each of the position/solution contains random integer permutation, X _i^t = x _i,1^t, x _i,2^t, … x _i,n^t. Since the solution is randomly generated, the solution most probably will violate the precedence constraint. Therefore, the sorting procedure based on the earliest position in position X is applied. The example of this procedure is presented in Figure 3.

Fig. 3. Example of decoding procedure.

Update position and velocity

In PSO, the particle reproduction process is performed using two formulas:

(8)$$V_i^{t + 1} = c_1V_i^t + c_2({\rm Pbest}_i^t -X_i^t ) + c_3({\rm Gbes}{\rm t}_t-X_i^t )$$

(9)$$X_i^{t + 1} = X_i^t + V_i^{t + 1} $$

Equation (8), calculate the velocity for (t + 1)^th iteration. This formula takes into account the current velocity and distance between Pbest and Gbest with the current position, X _i^t. Meanwhile, Eq. (9) updates the position for (t + 1)^th iteration, X _i^t+1. For the discrete representation, the following procedures are applied (Rameshkumar et al., Reference Rameshkumar, Suresh and Mohanasundaram2005).

Subtraction operator (position–position): (X ₁−X ₂).

If the j ^th element of X₁, x _1,j = x _2,j then v _1,j = 0, else v _1,j = x _1,j

Multiplication operator (coefficient × velocity): (V ₂ = c.V ₁).

If r and<c, v ₂ = v ₁, else, v ₂ = 0

c∊[0,1]

Addition operator (velocity + velocity): (V = V ₁ + V ₂)

The j ^th element of V can be derived as follows:

(10)$$v_j = \left\{ {\matrix{ {v_{1\comma \,j}\; if\; v_{1\comma \,j}\ne 0\comma \,\; v_{2\comma \,j} = 0} \cr {v_{1\comma \,j}\; if\; v_{1\comma \,j}\ne 0\comma \,\; v_{2\comma \,j}\ne 0\comma \,\; \,r \lt {\rm cp}} \cr {v_{2\comma \,j}\; {\rm otherwise}} \cr}} \right.\comma \,$$

r is a random number between 0 and 1, while cp∊[0, 1].

Addition operator (position + velocity): (X ₁^t + V ₁).

If the j ^th element of V ₁, v _1,j = 0 then x_1,j^t+1 = x _1,j^t, else x _1,j^t+1 = v _1,j

Experiment design

In the previous work, a tuneable test problem generator to provide sufficient test problem for integrated ASP and ALB has been developed (Ab Rashid et al., Reference Ab Rashid, Hutabarat and Tiwari2012). The results indicate that the ASP and ALB problem difficulties can be increased using a larger number of tasks (n), lower Order Strength (OS), lower Time Variability Ratio (TV), and higher Frequency Ratio (FR). For the testing of integrated mixed-model ASP and ALB, we proceed as follows:

1. (1) The tuneable test problem generator creates a precedence graph that is assumed as the joint model.

2. (2) The original tuneable test problem generator creates one assembly data set that corresponds to the precedence graph. This is modified, such that three sets of assembly data, representing different product models, are generated instead.

For the purpose of this experiment, every input variable is divided into five levels from low to high difficulty values as shown in Table 1. Then a reference variable setting (datum) is selected as a baseline, while the rest of the problem variable settings are generated by changing only one variable value at a time. In total, there are 17 test problems (including the reference setting) generated from one reference variable setting. In order to confirm algorithm performance, three different reference variable settings will be used (Levels 1, 3, and 5). Therefore, the complete number of test problem in this experiment is 51 problems as shown in Table 2. The bolded problem settings (Problems 1, 18, and 35) represent the reference variable settings for Levels 1, 3, and 5, respectively. The detail of the test problem is accessible at the following link: (https://drive.google.com/file/d/0B1FocUClXEMUSmFNdDN2ZFV4QTA/view?usp=sharing).

Table 1. Level of tuneable input setting

Table 2. Experimental design for mixed-model ASP and ALB

In general, the integrated ASP and ALB for a single model employed three types of algorithms; Evolutionary algorithms (including the hybridized version), ACO, and Discrete PSO algorithms. This work therefore will compare the MODPSO with the following algorithms for optimization purpose:

1. (i) Multi-objective GA (MOGA): This algorithm is one of the most frequently used algorithms to optimize the independent ASP and ALB problem, according to the survey (Rashid et al., Reference Rashid, Hutabarat and Tiwari2011).

2. (ii) ACO: The ACO algorithm has been implemented for a single-model integrated ASP and ALB optimization (Yang et al., Reference Yang, Lu and Zhao2013; Lu and Yang, Reference Lu and Yang2016).

3. (iii) Hybrid GA (HGA): The HGA that is proposed by Chen et al. is the most cited published work on integrated ASP and ALB optimization for a single model (Chen et al., Reference Chen, Lu and Yu2002). This algorithm combined the heuristic approach in line with balancing GA. The output solution from the heuristic approaches will be inserted into the initial population for GA.

4. (iv) Elitist Non-Dominated Sorting GA (NSGA-II): NSGA-II was introduced by Deb (Reference Deb2002). This algorithm is selected because of its popularity in solving multi-objective optimization.

5. (v) Multi-objective Particle Swarm Optimization (MOPSO): The MOPSO algorithm introduced to extend the PSO application for multi-objective optimization (Coello Coello and Lechuga, Reference Coello Coello and Lechuga2002).

6. (vi) Discrete Particle Swarm Optimization (DPSO): DPSO presents the discrete updating procedure to update the position and velocity (Rameshkumar et al., Reference Rameshkumar, Suresh and Mohanasundaram2005). The discrete representation is suitable to be used for ASP and ALB problem.

In addition to this experiment, another set of computational experiment was conducted to identify the best coefficient values for MODPSO. There are three coefficients that influence the MODPSO performance: inertia weight (c ₁), cognitive coefficient (c ₂), and social coefficient (c ₃). In MODPSO, c ₁ coefficient influences the particle velocity, while c ₂ and c ₃ influence the exploring and exploiting of the search space, respectively. The limit for these coefficients is suggested as follows: c ₁ [0, 1], c ₂ and c ₃ [0, 3]. In this study, a Taguchi approach with L9 orthogonal array is used. The three levels of coefficient values are as follows:

$$c_{\rm 1} = \lcub {0.{\rm 2}\comma \,{\rm} 0.{\rm 5}\comma \,{\rm} 0.{\rm 8}} \rcub \comma \,c_{\rm 2} = \lcub {0.{\rm 5}\comma \,{\rm 1}.{\rm 5}\comma \,{\rm 2}.{\rm 5}} \rcub {\rm\comma \, and}\,c_{\rm 3} = \lcub {0.{\rm 5}\comma \,{\rm 1}.{\rm 5}\comma \,{\rm 2}.{\rm 5}} \rcub $$

In this experiment, 15 test problems from Table 2 are selected, which consist of five problems in each reference setting. The selected problems are problems 1–5, 18–22, and 35–39.

In this work, the population or swarm size is set at 20 with 500 iterations. For each problem, 30 runs with different random seeds are performed and the output from each run is collected and filtered to find the non-dominated solution set.

Results of computational experiment

Due to the large size data from the optimization, the results simplified the data by using a standard competition rank approach. The best algorithm for a particular indicator and test problem was assigned rank 1 while the worst was assigned as rank 7. When the algorithm performance is a tie, an equal rank will be assigned and the next rank will be left empty. Table 3 presents the frequency of the rank obtained by each algorithm for different indicators and test problems. For the non-dominated solution in Pareto optimal (ῆ) indicator, the MODPSO comes out with better solution sets in 96% of test problems, while the remaining 4% belong to NSGA-II. The Error Ratio (ER) indicator also shows that the leading algorithms are MODPSO and NSGA-II. The MODPSO and NSGA-II show better performance with 41.5% and 58.5%, respectively. Both algorithms also dominate the best performance for Generational Distance (GD) indicator with 43% of the better performance for MODPSO and 53% for NSGA-II. Meanwhile, the Spacing indicator shows different patterns, where the largest percentages of better performance are MOPSO (22%), followed by HGA (20%), ACO (19%), DPSO (17%), MOGA (14%), MODPSO (6%), and NSGA-II (2%). On the other hand, the Spread_max indicator that measures the extent of solution distribution presents that the MODPSO algorithm produces a better solution in 70% of the problem. The MOPSO performs better with 18%, while the remaining balances are shared among DPSO (6%), MOGA (4%), and HGA (2%).

Table 3. Frequency of the rank obtained by each algorithm

Table 4 presents the mean of performance indicators for all test problems. Based on the mean values, the best performance of ῆ indicator is observed in the MODPSO followed by the NSGA-II algorithms. Meanwhile, the best mean performance for ER and GD indicators is achieved by NSGA-II, while the MODPSO in second place. In the meantime, two PSO-based algorithms, MOPSO and DPSO, are leading the mean of Spacing indicator. Furthermore, the PSO-based algorithms also show better performance compared with other algorithms in Spread_max indicator.

Table 4. Mean of performance indicators

^a Larger the better indicator.

^b Smaller the better indicator.

Table 5 shows the average CPU time for different problem sizes. In general, the ACO and MOPSO were among the fastest algorithm to complete the iteration. Meanwhile, the MODPSO was roughly in the second last position, in front of NSGA-II in term of CPU time. For comparison, the MODPSO was just 2–3% behind the DPSO. In DPSO and MODPSO, a longer time is taken to conduct discrete updating procedures compared with regular updating procedures in MOPSO. However, the NSGA-II required mostly double CPU time compared with MODPSO. This is because the NSGA-II combined the existing population and new offspring for the non-dominated sorting procedure. Therefore, the time taken to complete the iteration was increased compared with other algorithms.

Table 5. Average CPU time for different problem size

MODPSO coefficient tuning

Table 6 shows the results of the MODPSO coefficient experiment. The experimental table was designed using Taguchi L9 orthogonal array. Based on the general observation, experiment number 4 led in term of the best solution of cardinality, which was represented by ῆ and ER. The same experiment also came out with the best accuracy (i.e. GD indicator).

Table 6. MODPSO coefficient experiment results

Meanwhile, Figure 4 presents the main effect plots of c ₁, c ₂, and c ₃ for different performance indicators. Based on the main effect plots, medium c ₁, low c ₂, and medium c ₃ coefficients were preferable as observed in ῆ and ER plots to produce a solution with good cardinality. Similar coefficients' levels were also required to generate accurate solutions as represented by the GD indicator. On the other hand, the main effect plots by Spacing and Spread_max indicated that high c ₁, medium c ₂, and medium c ₃ coefficients' respective levels contributed to better solution distribution.

Fig. 4. Effect of w, c ₁, and c ₂ on performance indicators: (a) ῆ, (b) ER, (c) GD, (d) Spacing, and (e) Spread_max.

Discussion of results

In general, the result from the experiment shows that the performance of algorithms in optimizing the integrated mixed-model ASP and ALB appears to be dominated by NSGA-II and the proposed MODPSO algorithms, especially in four performance indicators (i.e. ῆ, ER, GD, and Spread_max). However, further analyses are required to quantify the results. Therefore, a statistical test is conducted to measure the significance of the improvements achieved by the MODPSO in optimizing the integrated mixed-model ASP and ALB.

The Analysis of Variance (ANOVA) test was then carried out to evaluate any significant improvement between the results obtained by different algorithms. The “null hypothesis” stated that there is no significant improvement among the means of all algorithm results. The alternative hypothesis states that there is a significant improvement among means in the result of at least one algorithm. The null hypothesis will be accepted when the calculated f-value is smaller than the critical f-value (f*) as suggested in the f-distribution table (Coolidge, Reference Coolidge2000). The result of the ANOVA test is presented in Table 7.

Table 7. Summary of ANOVA test

f*: critical f-value; f: calculated f-value.

The result shows that the calculated f-value for all performance indicators are consistently larger than f* at 0.05 confidence interval. Therefore, the null hypothesis is rejected and the alternative is accepted for all indicators, which bring the meaning that there are significant improvements achieved for all indicators in at least one algorithm. However, the ANOVA test cannot differentiate the exact improvement of one algorithm in comparison with another algorithm.

Therefore, a posteriori test known as Tukey's Honestly Significant Difference (HSD) is performed. This test is performed by calculating the absolute mean difference between the results of one algorithm over another algorithm, which is then compared with the critical HSD (HSD*) value. The HSD* value for algorithm i is calculated as follows.

(11)$${\rm HSD}_i^{^\ast} = q.\sqrt {\displaystyle{{{\rm MS}{\rm W}_i} \over n}}. $$

The q value is acquired from Tukey's table, MSW is the mean squares within groups from the ANOVA test, and n is the number of data in each group. When the absolute mean difference is larger than HSD*, a significant improvement has been identified in one algorithm over another algorithm. At this point, we are interested to know the performance of MODPSO over the other algorithms. Table 8 presents the HSD* and absolute mean difference between MODPSO and the other algorithms.

Table 8. Summary of Tukey's HSD test for MODPSO algorithm

^a Better absolute mean difference for MODPSO.

^b Better absolute mean difference for comparison algorithm.

In Table 8, the values that are labeled “a” show the MODPSO has a better mean difference over the comparison algorithm, while the values labeled “b” mean that the comparison algorithm has a better mean difference over MODPSO. On the other hand, the bold values in Table 8 indicate the significant improvements achieved by MODPSO over other algorithms, since the absolute mean difference is larger than HSD*. Based on Table 8, the MODPSO algorithm shows better performance and significant improvement when compared with the set of algorithms for ῆ indicator. The MODPSO also show significant improvements for ER and GD indicators compared with other algorithms, with the exception of NSGA-II. In both indicators, the NSGA-II algorithm shows better mean difference compared with MODPSO; however, the difference is not significant because the absolute mean difference is smaller than HSD*.

Meanwhile, the Spacing indicator did not show any significant improvement of MODPSO, although it has a better mean difference when compared with NSGA-II. Except for NSGA-II, all other algorithms show better performance over MODPSO, where significant improvements are presented by four algorithms (MOGA, HGA, MOPSO, and DPSO). For Spread_max indicator, the MODPSO algorithm shows significant improvement compared with other algorithms, except MOPSO. In comparison with MOPSO, although no significant improvement is achieved, the MODPSO algorithm still produces a better solution.

In this work, the solution quality toward Pareto optimal is measured using three performance indicators, that is, ῆ, ER, and GD. The Spacing indicator measures the uniformity of the found solutions and Spread_max measures the ability of the algorithm to explore the extreme solutions within the solution space. The results from the statistical test explain that, the MODPSO algorithm shows significant improvement in term of finding a better solution toward Pareto optimal over comparison algorithms, with the exception of NSGA-II at 0.05 confidence intervals.

Furthermore, the Spread_max result means that the MODPSO algorithm is significantly able to explore better extreme solutions when compared with MOGA, ACO, HGA, DPSO, and NSGA-II. Meanwhile, in term of uniformity of solution spread, the MODPSO algorithm did not perform significantly better than other algorithms. The Spacing indicator considers all non-dominated solutions that were found by a particular algorithm, regardless of Pareto or non-Pareto optimal solutions. In general, for similar search space, the algorithm that generated more non-dominated solutions has greater chances to produce better Spacing. From the experiment, the mean number of non-dominated solutions generated by the algorithms (regardless of Pareto or non-Pareto optimal), in ascending order, are: NSGA-II (33.84), ACO (46.9), MODPSO (55.37), MOGA (56.14), HGA (68.91), DPSO (80.47), and MOPSO (85.02). These numbers clearly present the algorithms that show significant improvement over MODSPO for Spacing indicator are the algorithms with a larger mean of generated solutions.

The results from the experiments and statistical tests summarize that the MODPSO has shown significant improvement over the majority of compared algorithms in ῆ, ER, GD, and Spread_max indicators. In comparison with all other algorithms, the performance of MODPSO is closely followed by NSGA-II, where MODPSO only shows significant improvement over NSGA-II in ῆ and Spread_max indicators. In order to compare the performance of NSGA-II, the mean difference between NSGA-II and other algorithms is calculated and presented in Table 9.

Table 9. Summary of Tukey's HSD test for NSGA-II

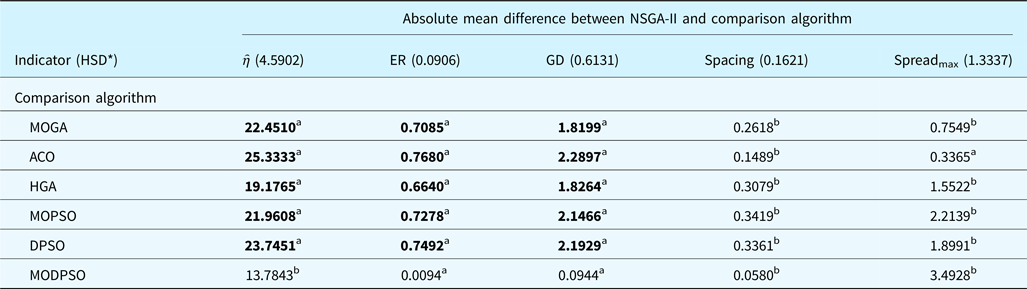
^a Better absolute mean difference for NSGA-II.

^b Better absolute mean difference for comparison algorithm.

Table 9 indicates that the NSGA-II has a significant improvement for solution quality leading to Pareto optimal compared with other algorithms except the MODPSO. Besides that, the NSGA-II did not show any significant improvement for solution uniformity (Spacing) and extreme solution exploration (Spread_max). Based on the significant improvement achieved by MODPSO (Table 8) and NSGA-II (Table 9) over other algorithms, the MODPSO is found to perform better than NSGA-II. This is because the MODPSO has shown a significant improvement over NSGA-II in two of the indicators (i.e. ῆ and Spread_max), while there is no significant improvement of NSGA-II over MODPSO algorithm. Furthermore, for Spread_max indicator, the NSGA-II did not show any significant improvement as MODPSO shows when compared with all other algorithms. In addition, the NSGA-II required double CPU time to complete the iteration compared with MODPSO as presented in Table 5. These facts give more advantages to MODPSO in terms of solution quality and also algorithm effort.

The result from Tukey's HSD test for integrated mixed-model ASP and ALB clearly shows that the MODPSO performed better than other algorithms for all test problems. Another question that arises is the problem category that the MODPSO algorithm performed best and worst. Therefore, the Tukey's HSD test based on different problem reference setting is conducted. The result of Tukey's HSD test for different problem setting is presented in Table 10. Based on Table 10, the MODPSO shows significant improvement in ῆ indicator over all algorithms for all reference setting. For ER indicator, the MODPSO consistently demonstrates significant improvement over other algorithms except NSGA-II. Meanwhile for GD indicator in low-level reference setting (Level 1), significant improvements for MODPSO are only found over ACO, MOPSO, and DPSO algorithms. However, when the reference setting is changed to medium (Level 3) and high (Level 5) levels, significant improvements are also observed in comparison with MOGA and NSGA-II.

Table 10. Summary of Tukey's HSD test for MODPSO by reference setting level

^a Better absolute mean difference for MODPSO.

^b Better absolute mean difference for comparison algorithm.

On the other hand, the MODPSO consistently did not show any significant improvement over any algorithm for Spacing indicator. For Spread_max indicator, the proposed algorithm also did not show significant improvements in the low-level reference setting. However, when the reference setting is moved to a medium level, the MODPSO shows significant improvement over MOGA, ACO, and NSGA-II. Finally, in the problem with high-level reference setting, significant improvements are achieved by MODPSO over all other algorithms. From this result, the best performance of MODPSO is found in the problem with high reference setting. Meanwhile, the weakest performance is in the problem with low-level reference setting, even though the overall performance in this problem category is still better than other algorithms.

The superior performance of MODPSO in optimising integrated mixed-model ASP and ALB arises because this algorithm was specifically developed for discrete multi-objective optimisation problem. This algorithm uses a similar procedure for Initialization, Evaluation, and Selection strategies as in NSGA-II. The NSGA-II is another algorithm that specifically developed for multi-objective optimization problems that also performed well in this application. However, it does not have a fine tuning feature. The fine tuning feature means the ability of an algorithm to make small adjustments to the solution in order to achieve the best or a desired performance. This is an important feature for ASP and ALB, where small changes may lead to sudden improvement in results.

The discrete updating procedure in MODPSO is designed to enable fine tuning toward the end of iterations. According to discrete updating procedure [Subtraction operator (X _i – X _j)] in section “Update position and velocity”, zero velocity is given when a similar element in X _i and X _j is found (this is the case when all particles move toward the best solution at the end of iterations). When the majority of velocity elements are zero, only small changes occur in assembly sequence as presented by Addition operator (X _i + V _i) in section “Update Position and velocity”. This feature allows fine tuning of the assembly sequences in MODPSO.