Introduction
The challenges for designing a general-purpose parametric shape grammar application are numerous. Several accounts have been given in the literature (see, e.g., Krishnamurti, Reference Krishnamurti1981; Krishnamurti & Earl, Reference Krishnamurti and Earl1992; Chase, Reference Chase2002; Chau et al., Reference Chau, Chen, McKay, de Pennington and Gero2004; Duarte & Correia, Reference Duarte and Correia2006; Ertelt & Shea, Reference Ertelt and Shea2009; Trescak et al., Reference Trescak, Esteva, Rodriguez and Werner2009; Jowers & Earl, Reference Jowers and Earl2010; Hoisl & Shea, Reference Hoisl and Shea2011). Some of these accounts examine technical and/or expressive characteristics of interpreters, including underlying computing language, subshape recognition, the dimensionality of shapes, and so forth. Others concentrate on the tasks for programs that implement shape grammars, for example, generation, parsing, and inference tasks and their interactions with CAD modelers (Gips, Reference Gips1999). Then there are those that focus on usage in design, including general interpreters versus specific domain applications; schematic design versus design development; industrial strength interpreters versus proof-of-concept applications (Chase, Reference Chase2002).
Here a general parametric shape grammar interpreter, code-named GRAPE, is discussed. The first account of this work has been given in Grasl and Economou (Reference Grasl and Economou2013a). The interpreter uses graph grammars to carry out computations on part-relation graphs that encode maximal representations of shapes. In this work, it was further argued that what distinguishes GRAPE is that emergent shapes and general parametric rules are both supported – while fully acknowledging that parametric subshape recognition is NP-hard (Yue et al., Reference Yue, Krishnamurti, Grobler, Tidafi and Dorta2009).
The work here builds on this foundational work and reports on advances presented elsewhere since then (Grasl & Economou, Reference Grasl and Economou2013b, Reference Grasl and Economou2014). Extensions to the graph model are presented, some topics concerning a visual rule editor are discussed, and rule selection agents are introduced. Finally, some first results from the usage of GRAPE in a design curriculum in academia are reported.
Grape
GRAPE is a shape grammar system based on graph grammars. The implementation enables labeled parametric shape grammars (Stiny, Reference Stiny1980) defined in various algebras of shape and supports emergence (Knight, Reference Knight2003). It was originally described in Grasl and Economou (Reference Grasl and Economou2013a). Here the discussion will focus on the graph model, the intricacies of the visual rule editor, the automation of the rule selection process through agents, and some details concerning the various GRAPE applications (Fig. 1).

Fig. 1. The components of GRAPE.
Graph model
In GRAPE, a rule is applied by taking the current shape C, converting it to its graph representation G, applying the respective graph grammar rule in order to obtain the new graph G′, and convert the graph back to a shape C′ (Fig. 1). The graph model and the features of the graph grammar implementation have a strong influence on the capability of the system. Some of the details are introduced in the following.
Part-relation graph and emergence
The model is based on a so-called part-relation graph. In the implemented version, the maximal representations of shapes and their intersections are mapped to attribute part-relation graphs and shape rules are mapped to their equivalent graph rules. The subgraph-matching algorithm can then handle the problem of subshape detection and emergence. Geometric constraints are easily added to search patterns in form of geometric functions.
Elements
Different types of nodes and edges can be defined. These classes support inheritance and each class can hold attributes that are accessible from within a rule.
Points and labels
Due to the part-relation approach, all geometry elements are eventually described by points. Point nodes hold attributes for the X, Y, and Z coordinates (Fig. 2a). This information is used for all geometric calculations from determining the length of line segments to deciding whether two segments are parallel or not.

Fig. 2. A point node (a) and a labeled point (b).
Labeled points are represented by a label node, holding a label value attribute, connected to a point node by a label edge (Fig. 2b).
Line segments
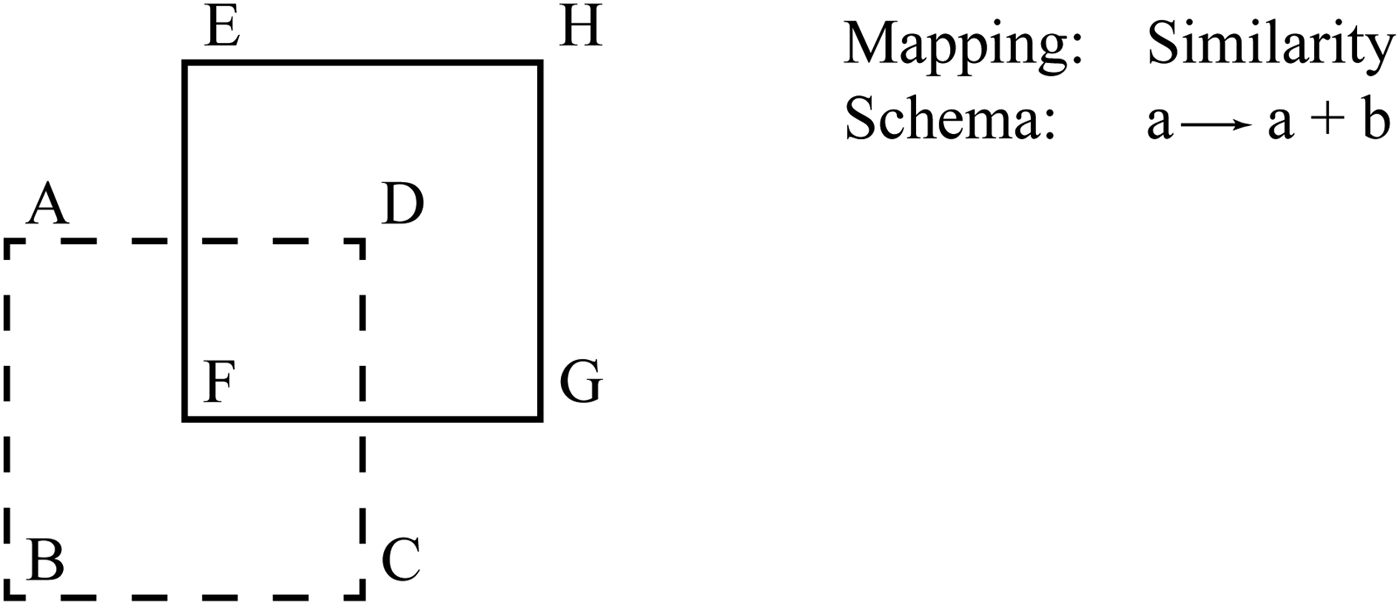
Line nodes are connected to the lines endpoints and to present intersection points. The part-relation graph of the classic example of the two overlapping squares is shown in Figure 3. In this diagram, white nodes are line nodes and black nodes are point nodes. Through Figure 4, which shows embeddings of a graph representing a square, it becomes evident that the intersections are necessary to enable emergence.

Fig. 3. Part-relation graph of two overlapping squares. The geometry is shown dashed for convenience.

Fig. 4. Different embeddings of the search pattern that will find the original squares (a) as well as the emergent square (b) of the graph in Figure 1.
One common issue while dealing with shape grammar systems is the handling of isomorphisms. A shape rule, can apply to the same subshape in a number of ways and more specifically in as many ways as the order of the symmetry point group of the left-hand side (LHS; Stiny, Reference Stiny2006). Note that the graph grammar engine will return all permutations of a match (Grasl & Economou, Reference Grasl and Economou2013a, Reference Grasl and Economou2013b), and the geometric interpretations of these subgraphs correspond to the required isomorphisms. Finding all these matches is important for shape grammars as the formalism allows rules to be applied under symmetry transformations.
The rule shown in Figure 5a has an LHS symmetry of D4 which is of the order of eight. Figure 5b shows eight different ways in which the rule can be applied to a square.

Fig. 5. A rule with LHS symmetry of D 4 (a), and the eight possible ways to apply the rule to a square (b).
Circles and circular arcs
It is straightforward to add an arc node to connect two or more points of an arc. Still, this alone is not sufficient to unambiguously represent an arc. Two points on a circle split the circle into two segments the minor arc and the major arc, so some additional information is required. In CAD programs, this is often solved by requesting two endpoints and an intermediate point to create an arc. The three points define the base circle, and in addition, the intermediate point defines whether to use the minor or major arc (Fig. 6).

Fig. 6. A circular arc with two intermediate points I1 and I2 as well as a breakpoint B.
For a shape grammar application that supports emergence, it is important that the arc is defined using any two of its points and it is inconvenient to have to calculate an appropriate third point for each pair of points. Hence instead of an intermediate point, the model uses a breakpoint from the opposite side of the base circle as the third point. The same breakpoint can then be used in combination with any two of the arcs points. In Figure 6, for example, breakpoint B can be used for the arc P1P2 as well as for P2I1. This model works well for arcs, but it cannot handle circles. For a circle, all three defining points fall together; hence, neither the center point nor the circles plane can be derived. So in order to be able to use the same model for both arcs and circles, both a center point and the plane normal have been added to the model. For arcs this means that there is some redundant information in the model, which is never ideal, but in general, it solves more problems than it creates. Figure 7a shows the graph representation of an arc and a circle. Here white nodes are arc nodes and black nodes are point nodes. The part-relation edges are shown as thin edges. The edge to the center point is drawn as a thick line, and the one to the breakpoint is dashed. Figure 7b depicts a search pattern that will find all of the nine arcs and circles embedded in Figure 7a.

Fig. 7. (a) Part-relation graph of an arc and a circle, and (b) search pattern for an arc segment. The geometry is shown dashed for convenience.
Figure 8 shows a simple sample derivation using circles and emergent arcs. The first rule copies and moves the initial circle along the x-axis, another takes the emergent lentil shape and rotates it at 90°. The example was computed using the Rhino version of GRAPE, the only version that currently supports circles and arcs.

Fig. 8. Derivation using circles and emergent arcs.
Faces
Here the main question was whether to model faces based on indices or loops. An index-based approach results in a central face node connected to each point by an edge holding an index attribute, such a model offers direct access to the faces points much like an array. A loop-based model results in each point being linked to its two neighbors, like a circular linked list. Additionally connecting face nodes directly to point nodes can only support planar, straight-edged faces. For non-planar faces, face nodes would have to connect to line nodes instead.
This is an area in which the model requires some improvements. For the time being a simple version based on indices and points has been implemented, and it does not support emergence. Figure 9 shows some results from a Fröbel exercise investigating one spatial relation of two oblongs.

Fig. 9. A Fröbel exercise using oblongs based on faces.
Objects
Realizing that most of the more extensive grammars in the literature do not require emergence, some objects have been added to the model that can be manipulated as set grammars. This is computationally simpler and enables the user to work with objects she may be used to from other object-orientated applications. The same basic framework can be used for these kinds of computation, the main differences being that no intersections are computed and that in general fewer nodes are required, which again improve performance during the subgraph matching process.
The Rhino version has been extended to support some primitives such as spheres, cylinders, and boxes. Each primitive is represented by a single node, which holds all the required information in its attributes, this includes a base-point and two coordinates to define a local coordinate system (Fig. 10a). The Dirksen grammar presented below makes use of these kinds of objects.

Fig. 10. A box node along with a symmetry construct (a) and a wall node based on a line segment (b).
Since an object like a box is represented by a single node, search patterns cannot return isomorphisms as would be the case for a part-relation representation. If isomorphisms are important for the respective grammar symmetry constructs can be added to the graph (Fig. 10a). Search patterns can then be designed to return the transformation under which it is to be applied.
Some architectural objects are special cases. Here additional architectural object nodes are connected to geometry nodes to the represented point, line, and polygon-based objects such as columns, walls, and slabs (Fig. 10b). The object nodes hold the information required in addition to the information extracted from the basic geometry nodes. The symmetry of the underlying geometry can be used to return some isomorphisms.
Edge hierarchy
Using inheritance the edge classes can be arranged in a hierarchy. Now a search for an edge of a specific class will return all instances of any of its subclasses. Using the hierarchy shown in Figure 11, searching for real-part edges will return all boundary and all interior edges. This feature can be used to exert more control over which shapes are matched by an LHS. For example, a rule using real-part edges will support emergence, while a rule using only boundary edges will not.
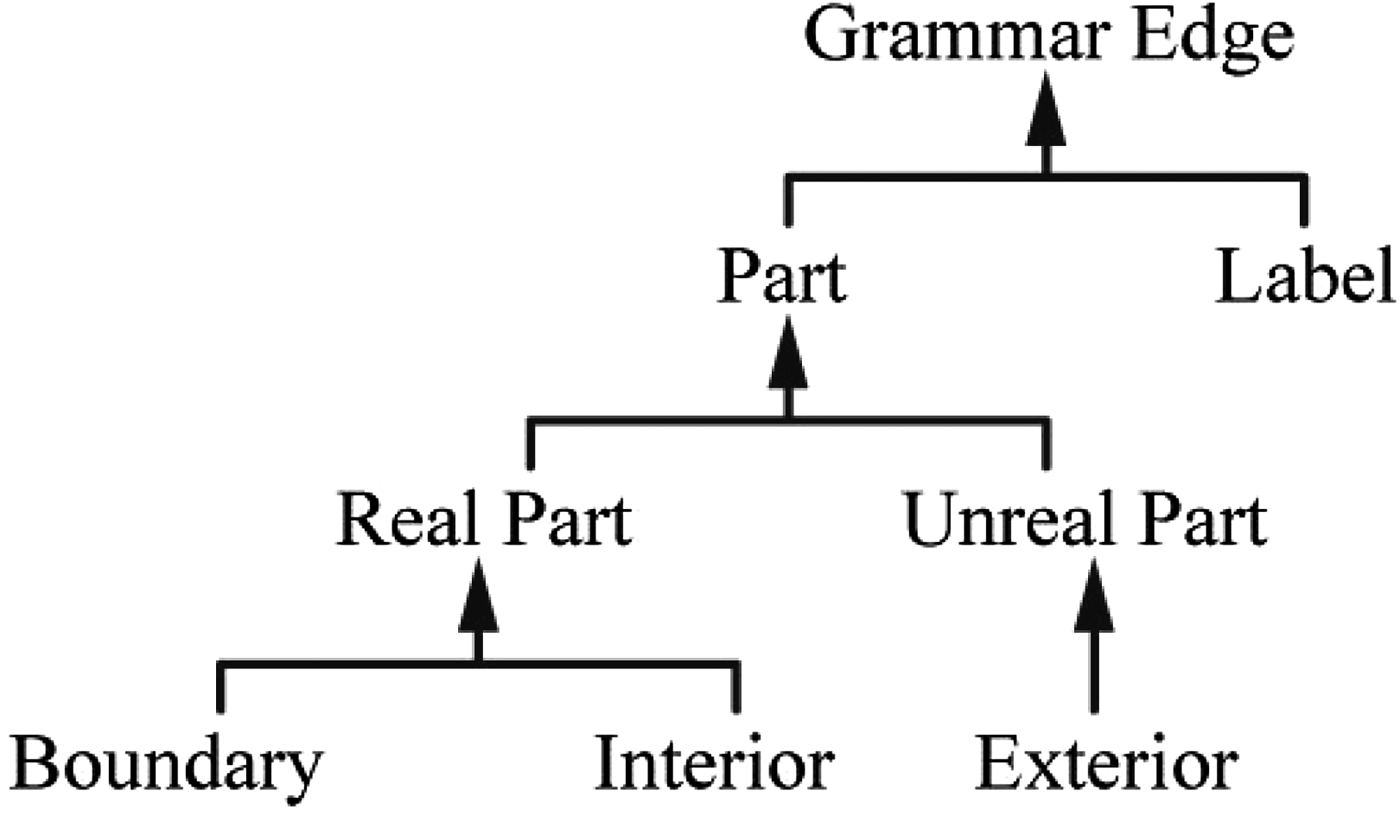
Fig. 11. Hierarchy of edges.
Exterior edges can be used to keep note of intersections beyond a line segments current boundary. Sub-shapes that are implied but not fully present within a shape can be used for rules.
Parametric rules
So far, it has not been mentioned that sometimes too many matches are returned. While the search pattern shown in Figure 4 will find the squares represented by the graph in Figure 3, in another graph it would also find parallelograms, trapezoids, and other quadrilaterals. This behavior enables parametric rules. The unrestricted graph pattern will match any shape with the corresponding topology. Since such uncontrolled behavior is mostly not desirable constraints can be added to make the search pattern more rigid. Constraints are geometric functions that are based on the graphs attributes and return a Boolean value. Figure 12 shows such a constrained graph that will return only isosceles trapezoids.
Fig. 12. A restricted search pattern.
Variables
Sometimes it can be useful to provide additional variables to parametric rules or to maintain and manipulate some non-geometric information. For this, the model has been extended to support variables. These are organized in a dedicated subgraph. The general target is to support all types and operations described by Stouffs (Reference Stouffs2018) in order to build on a robust theoretical model and provide some comparability and interoperability. To this extent, a parser has been written to deal with strings in the proposed format. The model currently supports unordered lists of floating point and integer value variables. These can be used within search conditions on LHS of the rule or as parameters on the right-hand side (RHS) of the rule. An example of using variables in search patterns is given in Figure 13. Given a state where the model contains some arbitrary geometry and the list of floating point numbers A = {1.5, 3.0, 7.5}, the search pattern will return all triangles where one of the sides is 1.5, 3.0, or 7.5 units long.

Fig. 13. Variables and search patterns in the LHS.
The same variables can be used as parameters on the RHS of the rule. Figure 14 gives a simple example. A square is created around the origin. Because the list A contains three values, the rule will return three matches, creating a square with sides either 3.0, 6.0, or 15.0 units in length.

Fig. 14. Variables and parameters in the RHS.
Editor
Creating a visual editor for parametric shape grammar rules is not as straightforward as one might assume. Some ambiguity is possible while translating the drawn shapes to their graph equivalents.
Assigning specific geometric mappings and rule schemas can support the rule interpreter.
Mappings
The mappings determine the geometric operations that are permissible while transforming the LHS to fit a subshape. The transformations under which the rules may apply follow the hierarchy of transformations outlined in March and Steadman (Reference March and Steadman1974) and are shown in Table 1. The original intention was to distinguish between rigid (Euclidean or non-parametric) rules and parametric rules. Non-parametric rules can, for example, be assigned a similarity mapping so the LHS could be translated, rotated, reflected, and scaled. This is the most common interpretation of a shape grammar rule. Parametric rules require the more flexible topology mapping, which requires only that the neighborliness criterion is met.
Table 1. Possible mappings and what they constrain

An unconstrained subgraph search over a part-relation graph will already reflect neighborliness and thus can be used for parametric rules. For non-parametric rules, the graph has to be constrained using appropriate geometric conditions. This can be either done manually by specifying the conditions in the editor of the application or automatically by specifying the mapping under which the rule applies and have the corresponding constraints added to the rule by the application.
Hence, a topology mapping does not require any constraints at all. A similarity mapping is ascertained by triangulating the shapes on the LHS and placing constraints on the proportions of the triangles. For an isometry mapping, it is then sufficient to place a single length constraint on any two of the vertices of the shape. An identity mapping could build on an isometry mapping, but in practice, it has proven more stable to simply constrain the positions of all vertices of such a rule. Rules using identity mappings can be used to draw initial rules because they do not require an LHS. In all other cases, the RHS has to be expressed in terms of elements found on the LHS; this mostly requires at least three non-collinear points.
Schemas
Schemas have proven to be valuable in structuring rules for both the human and the machine. For example, distinguishing between the schemas x → y and x → x + y provides a simple way to determine whether the LHS is deleted. Currently, few schemas are supported as an initial step to test their usability within the editor. Significantly, the schemas x → t(x) and x → x + t(x) have been added to resolve ambiguities that can occur with parametric rules. The rule in Figure 15a depicts a parametric rule that must be interpreted differently depending on the chosen schema. Applying the rule to a rectangle under the schema x → x + y will result in the shape shown in Figure 15b, while under the schema a → x + t(x) the result will be as shown in Figure 15c.

Fig. 15. Ambiguous parametric rule (a) and its application to a rectangle as (b) x → x + y and (c) x → x + t(x).
Symmetry reduction
As was demonstrated by the rule in Figure 5 the graph grammar engine will return all permutations of a pattern, and these can be interpreted as the isomorphism of the LHS shape. In general, this is a welcomed feature, but if a rule has not all symmetry on the LHS, but an overall symmetry too (Fig. 16a), applying the rule to all matches will result in duplicate results. In order to reduce the number of possible rule applications, these redundant results have to be filtered out (Fig. 16b). This could be done in a straightforward way by computing all the returned solutions and comparing them to one another but it would be unnecessarily expensive. Here instead an alternative solution is proposed where the graph rules are modified so that the corresponding subgraphs are filtered out during the search. The approach utilizes insight into the symmetric structure of the rules and computationally makes use of the constraints system that is already in place. The disadvantage is that it cannot be applied to rules using the topology mapping since in these cases the symmetry of the match is not known at design time and thus the corresponding constraints cannot be applied to the rule.

Fig. 16. A rule with LHS symmetry of D 4 and overall symmetry of D 2 (a), and the two possible ways to apply the rule to a square (b).
If the overall symmetry group H is a subgroup of the LHS symmetry group G, then in order to return each solution only once the search pattern has to be reduced from G to a complement group of H in G. So first a method of detecting point symmetry groups is required. Here the algorithm described by Wolter et al. (Reference Wolter, Woo and Volz1985) is used. For the rule in Figure 16a, the result is that the LHS has symmetry of D 4, while the overall rule has symmetry of D 2. A complement group of D 2 in D 4 is C 2. In order to reduce the LHS symmetry to C 2, the mirror symmetry and part of the rotation have to be restricted. This can be problematic because in order to do so one needs a suitable external reference point. Mirror symmetry can be restricted by adding a handedness or chirality constraint to the rule. Three non-collinear points are selected and their order of rotation (clockwise or counter-clockwise) around an appropriate vector is constrained. Restricting rotation is more complicated. To do so it requires a set of LHS points that together exhibit the rotational symmetry to be restricted, then a suitable constraint can be placed on those points to prevent them from mapping onto each other. This is done by requiring one or more of the points to have a distinction in relation to an external reference, such as being among the closest x points to the origin.
Overall this feature could be dropped because the redundant solutions are correct and there is something to be learned by displaying them, but some rules return a lot of matches, and filtering out redundant solutions can help in making the application more user-friendly. While Wolter et al. (Reference Wolter, Woo and Volz1985) describe the procedure for point symmetry detection in two- (2D) and three-dimensional (3D), currently only the 2D algorithm has been implemented.
Visual editor, advanced, macro
Currently, there are three modes of editing rules within the GRAPE web application. Firstly, the visual editor in which a rule is drawn using standard CAD functionality. The drawing is then interpreted and translated into a graph grammar rule automatically. Figure 17 shows a rule to copy and move a square diagonally. In the Editor, the LHS and the RHS are drawn on top of each other, where the LHS is shown dashed.

Fig. 17. The copy and move square diagonally rule as drawn in the visual editor. Labels are for reference only.
Secondly, using the advanced editor graph grammar rules can be written using the GrGEN.NET modeling language. This is the most capable method of defining a rule, but it also requires a thorough understanding of the underlying model and hence is reserved for advanced users. Listing 1 shows the rule from Figure 17 in the modeling language.
rule copyMoveDiagonally {
// Search for quadrilateral topology
A:PointNode -:RealPartEdge- :LineNode -:RealPartEdge-
B:PointNode -:RealPartEdge- :LineNode -:RealPartEdge-
C:PointNode -:RealPartEdge- :LineNode -:RealPartEdge-
D:PointNode -:RealPartEdge- :LineNode -:RealPartEdge- A;
// Constrain to square
if {ABparallelToCD(A, B, D, C);}
if {ABparallelToCD(A, D, B, C);}
if {ABsameDistanceToCD(A, B, A, D);}
if {ABsameDistanceToCD(A, C, B, D);}
// Restrict isomorphisms
if {rightTurn(A, D, C);}
modify {
// Create new topology
E:PointNode -:BoundaryEdge- :LineNode -:BoundaryEdge-
F:PointNode -:BoundaryEdge- :LineNode -:BoundaryEdge-
G:PointNode -:BoundaryEdge- :LineNode -:BoundaryEdge-
H:PointNode -:BoundaryEdge- :LineNode -:BoundaryEdge- E;
// Set coordinates
eval {
E.x = A.x + 0.5 *(D.x - B.x);
E.y = A.y + 0.5 *(D.y - B.y);
E.z = 0;
F.x = 0.5 *(B.x + D.x);
F.y = 0.5 *(B.y + D.y);
F.z = 0;
G.x = 2 *D.x - E.x;
G.y = 2 *D.y - E.y;
G.z = 0;
H.x = 2 *D.x - F.x;
H.y = 2 *D.y - F.y;
H.z = 0;
}
}
}
Listing 1: The rule showed in Figure 17 in the GrGen.NET modeling language.
Thirdly, macro rules can be defined as a sequence of rule applications. These can be used to store specific derivations or other common rule sequences.
Agents
Once a grammar has been defined its expressive possibilities can be explored. This can be done in a variety of ways ranging from manually applying rules one by one to using automated decisions algorithms to choose sequences of any desired length. Strobbe et al. (Reference Strobbe, Pauwels, Verstraeten and De Meyer2015) demonstrate how the visual exploration of design spaces can be supported by grammars. A generous overview of the interface of grammars in design inquiry is given by Chase (Reference Chase2002). Here an agent-based extension for the systematic and automated exploration of the solution space is implemented (Grasl & Economou, Reference Grasl and Economou2014). The system follows the common sensor–actuator agent design described by Russell and Norvig (Reference Russell and Norvig2013). Such an agent (Fig. 18) can perceive its environment via its sensors. These perceptions are processed and may or may not result in the agent acting on the environment using its actuators. The kind of processing performed by the agent is not pre-determined. In GRAPE, the agents’ sensing abilities are restricted to analyzing the current state; this includes both the graph and the geometric representation. Their actuators are restricted to applying rules. Effectively they operate the application much like a user would. This agent system is expandable: agents following different agendas and using various processing techniques can be added at any time. Some of the agents currently available in GRAPE are described below and for comparative purposes, all use the rules of the Palladian grammar (Stiny & Mitchell, Reference Stiny and Mitchell1978).

Fig. 18. Common sensor–actuator agent design.
Probabilistic agents
One fairly easy way of selecting rules is to use a random number generator. The result of a naïve, purely random approach of selecting 15 rules for the Palladian grammar is shown in Figure 19a. The derivation cannot progress because certain obligatory rules are not executed or are called in the wrong order. The performance of such a rule selection strategy largely depends on the structure of the grammar. Given enough time and attempts at selecting rules the agent can improve upon Figure 19a, and will eventually select the required obligatory rules to continue the derivation. Nevertheless, this agent can be seen as the worst-case scenario; obviously, all following agents should outperform it.

Fig. 19. Exemplary results for probabilistic agents using (a) naïve randomness and (b) weighted randomness.
Two steps up are to use sequenced and weighted randomness (Fig. 19b), which means creating a sequence of pools out which to select rules and to assign a different probability to each rule (Fig. 20). The sequence will most likely be based on the structure of the grammar, the weights can be based on intuition or on an analysis of the body of work a grammar is attempting to model. The generation is then essentially to pick a variable number of rules from each pool. This approach can easily be formalized, to enable the designer to control the generation, either through a user interface or via a simple scripting language. The City Engine software uses a similar mechanism (Wonka et al., Reference Wonka, Wimmer, Sillion and Ribarsky2003).

Fig. 20. Pools for the sequenced and weighted random selection.
Such an approach, of course, has little intelligence above that embedded in the rules themselves. The derivation in Figure 19b is complete, and even better results can be achieved with this approach, but this is mainly thanks to the well-devised phasing of the Palladian grammar and its cleverly constructed rules. Still the derivation suffers from a lack of doors and an unconventional layout that most likely would not have pleased Andrea Palladio, things that are hard, if not impossible, to control with shape rules alone.
Tree traversal agent
Enumeration has been part of the shape grammar discourse since the beginning (Stiny & Mitchell, Reference Stiny and Mitchell1978; Flemming, Reference Flemming1981; Koning & Eizenberg, Reference Koning and Eizenberg1981). Here tree traversal agents search through the solution tree looking for derivations that fulfill certain criteria. Coming up with a definite number of derivations is however not always as straightforward as it might appear at first glance, even if the symmetry of the final derivation is disregarded and all isomorphisms are counted. There are two issues: firstly, there are mostly several ways to apply a rule at any given time, and secondly, results can be identical despite a different order of rule application. So applying the same rules twice can lead to different results, and applying different rules, or the same rules in a different order, can lead to the same result.
For a specific enumeration problem, it may be possible to exploit grammar-specific features to simplify the procedure. A general tool will have to use an extensive search to find solutions. The traversal agents use depth-first search (Cormen et al., Reference Cormen, Leiserson, Rivest and Stein2001). Such an approach will most likely lead to numerous duplicates, which have to be filtered out. It is a brute force approach and potentially computationally expensive, but perhaps the only viable one if it is to be applicable to all grammars. To configure the agent four bits of information must be passed:
(a) A sequence of rules to execute before starting the enumeration,
(b) A set of rules over which to enumerate,
(c) A condition that designates a solution, and
(d) One or more prune conditions that indicate that the current branch cannot lead to a valid solution anymore.
The agent then offers a mechanism for cycling through the solutions, generating the derivations on the fly. Comparing branches to a database of previously visited branches filters out duplicates.
As an example, Figure 21 shows the results returned by an agent configured to search for layouts based on a 5 × 4 grid with a T-shaped space and five spaces in total. The start sequence (a) constructed a 5 × 4 grid. The enumeration pool (b) contained all rules to merge spaces and create T-shaped spaces. The target condition (c) checked whether there were a T-shaped space and the layout consisted of exactly five spaces. Finally, the pruning conditions (d) abandoned a branch if there were less than six spaces left and no solution has been found. The results shown in Figure 21 are necessarily reminiscent of “Counting Palladian plans” by Stiny and Mitchell (Reference Stiny and Mitchell1978) but it is interesting to note that arbitrary conditions can be defined to filter the solutions even further. In general, the agent has proven to be a useful tool to quickly get an idea of the possibilities offered by a grammar, or by a subset of the rules of the grammar. Time complexity can be an issue, but by restricting the agent to the subset of interest, results can mostly be achieved within reasonable time frames. It is difficult to give concrete numbers because the conditions can vary immensely. On a t2.medium AWS instance, the first result in Figure 21 was found after 2.5 s, all 27 solutions were found in 24.3 min, and it took another 13.4 min to complete the search.

Fig. 21. All solutions for a 5 × 4 grid with a T-shaped space and five spaces in total.
Rule-based agents
Here we can distinguish between forwarding chaining agents and backward chaining agents. Both kinds of agents rely on a sequential list of IF-THEN rules. At every iteration, the agent steps through the list of rules, as soon as the conditions in the IF-clause of a rule are met, the THEN-clause is executed and a new iteration is started. The process is much like the one familiar from shape grammars, except that the rule selection mechanism is pre-determined.
Forward chaining agents can generate a derivation that fulfills a given set of target criteria. Unlike tree traversal agents they do not simply try all possible combinations looking for a solution, instead, their IF–THEN rules will return one shape rule to apply for each state of the derivation. They follow a more direct albeit deterministic path. Given an identical set of starting conditions, a rule-based agent will always return the same result.
Target criteria can determine things like the size of the grid, whether a portico should be attached and whether there should be an I-shaped space or not. These criteria are then used to guide the agent's actions. The creation of an I-shaped space requires several rules to be selected in the right order and to be applied to the right match. Backward chaining agents are given a finished shape and may attempt to find a path back to the initial shape, thereby proving that the given shape is a valid derivation of the grammar.
Rule-based agents follow the same computational paradigm as shape grammars. Generally, rule-based systems are used to determine a reaction to a given state. Here the state is that of the derivation in combination with the target values. This enables automated derivations with augmented control over the outcome.
Figure 22 shows some such derivations. Here a parallel, topological representation (Duarte, Reference Duarte2005) is maintained throughout the generation. It can be used to overcome some of the problems encountered by the weighted random generation. For example, this rule selection logic can guarantee that: (a) the doors added to the floor plan connect all the rooms; (b) the grid has an appropriate size; (c) the proportions are satisfying; and (d) the provisions formulated by Stiny and Gips (Reference Stiny and Gips1978) are satisfied.

Fig. 22. Some results from a rule-based agent.
Rule-based agents can maintain much better control over the derivation than the previously presented agents. This comes at the cost of requiring grammar-specific knowledge, essentially requiring a tailor-made solution for each grammar. In addition, a rule selection mechanism based solely on the maximal line representation is possible but did not seem feasible for this project. Hence, the shape grammar rules were augmented to create a parallel representation of the topological structure. Such rules are currently beyond the capabilities of the visual editor and have to be written in the modeling language. The requirement of such an effort does create a barrier. The inclusion of descriptions (Stiny, Reference Stiny1981; Stouffs, Reference Stouffs2018) could generalize the solution and mitigate the problem to a certain degree.
Applications
The described model has been implemented as the GRAPE shape grammar engine. It defines various interfaces, which have to be implemented to create an actual shape grammar application. Several plugins for commercial CAD packages and one web-application have been created using this approach. The GRAPE engine is designed to be independent of other packages and platforms. On the back-end, an interface is designed for the communication with a graph grammar engine for subshape detection, and on the front-end, two types of interfaces are included, one for editor functionality and one for the application functionality.
Backend
Currently, the only backend adaptor is for the GrGen.NET graph grammar engine (Jakumeit et al., Reference Jakumeit, Buchwald and Kroll2010). Significantly, this engine could be exchanged without breaking the existing applications should this ever become necessary. Although currently only one backend engine exists, and there are no intentions of expanding this. The adaptor approach was chosen in order to remain independent of other projects. It is unclear how the GrGen.NET engine will develop, and whether it will be more advantageous to switch to another library in the future.
Frontend
For the front-end, there are several implementations in varying degrees of completeness. Grammars can be executed in AutoCAD, Revit, Rhino, and the custom-made web interface. Rules can be declared either directly using the GrGen.NET graph grammar rule modeling language or via the visual editor implemented in the web interface. While these implementations all use the same interfaces to the GRAPE engine, most of them implement different subsets of the functionality and thus have different capabilities.
The geometries and objects supported by each implementation are shown in Table 2. In all these implementations lines are fully supported as parametric, labeled shapes and include emergence. One implementation supports arcs. Surfaces are currently supported in two implementations as parametric and labeled shapes, but do not support emergence. Solid primitives and architectural objects are supported in one implementation each as parametric and labeled shapes. An extended model should be able to support all these shapes and emergence up to U33 but a whole set of additional support functions would be necessary to handle conversion of shapes to their maximal representations as well as the detection and handling of relevant intersections. The majority of these functions are described in Stouffs and Krishnamurti (Reference Stouffs and Krishnamurti1993) and remain to be implemented in another iteration of the implementation.
Table 2. Geometries and objects supported in various implementations of the Grape core

Designs
The technical specification of shape rules and parametric shape rules has been the subject of this paper so far. The ways that these types of rules could begin to work in design practice and research is the subject of this part of our work. A detailed account of the usage of GRAPE in an academic setting and for design explorations in the formal composition has been given in Economou & Grasl (Reference Economou and Grasl2017). A very brief account is given below to give a sense of the work and provide an immediate context for the applicability of the software in practice and design.
The setting for the testing of the GRAPE involved a successive series of workshops having students trying out rules, known and new ones, and exploring on their own the expressiveness of the rules and the software itself. These workshops were informal in the sense that they did not take account of numbers of participants, abilities of participants, duration of the encounter with the software, and so forth. In fact, the results of the workshops varied widely as some students decided to pursue the design problems they were introduced to further for a project in an independent study to be pursued after the workshop itself.
The workshops were structured along two different trajectories: one starting from existing grammars and one starting from scratch, and both in a rising complexity in the specification of the rules and the ways they affect the design. The key idea in the first series of studies was the implementation of known rules in the literature – and there are many to admire – to produce the designs that have manually been produced in the original papers, additional ones that are in principle possible by the original grammars and new ones by purposefully playing with the rules, i.e. the transformations under which the rules apply, the assignment of values in the parametric shapes, the shapes themselves in the schema rules, and so on. The key idea in the second series of studies was the implementation of new rules designed from scratch, to produce the designs that were selected to provide the corpus for the grammar, additional ones that are in principle possible by the grammars and new ones by purposefully playing with the rules. A brief description of both experiments is given below followed by few examples from each case.
From rules to rules
The first series of studies foregrounds a hands-on constructive understanding of existing grammars in the literature. The students are encouraged to copy rules in the literature, see on their own how the rules were supposed to apply in the original design setting and what they can make, and once they get a command of their expressiveness and generative power, to start editing them in a variety of ways to make them their own. The range of techniques used to edit the rules is open-ended; once the copy and implementation of the rule have been considered successful, the students are encouraged to alter the rules in some way to accommodate design ideas and insights that might have emerged through the computations with the existing rules. A sample of three studies is given below to showcase some of the findings of the workshop in GRAPE. The authors of the grammars are specified in parentheses within the brief account of each project.
Rosette designs
The nested square and quad designs are perhaps the most popular designs in the shape grammar discourse because they illustrate nicely the compositional richness of recursive visual composition, where the inscription of a square within a square or a quadrilateral within a quadrilateral, and even more, the seamless shifting of vocabularies in shape recognition from squares, to triangles, pentagons, hexagons, and all sorts of other more exotic shapes (Stiny, Reference Stiny1980; Mitchell, Reference Mitchell, Antonsson and Cagan2002). The series of the rosette designs in Figure 23 showcase the expressive results that emerge out of the substitution of the spatial relation of the two squares by a series of spatial relations of whirling squares or pairs of regular polygons to explore natural growth exhibiting threefold, fourfold, fivefold, sixfold point symmetries, and so forth. All the designs shown are produced by versions of rules that erase the circumscribed square or the corresponding regular polygon every time they apply. The elimination of the bounding exterior squares or regular polygons foregrounds the emergent spatial relations in the center of the shape and the inward spiral growth of the pattern. The derivation of the first four members of the series is given in Figure 23a for the regular triangle, square, pentagon, and hexagon. The series in Figure 23b shows a language (set) of fourfold designs that combine polyrhythmic applications of the parametric rules to resemble bird-nests, flowers, and/or other biological formations with point symmetry. The iterations of the rule applications in GRAPE are all kept to a similar number of steps to render the similarities and the differences between the designs as evident as possible. Clearly, the compositional process outlined here for the fourfold symmetry can be generalized for all regular polygons and for other shapes as desired.

Fig. 23. Some designs in the rosette language (Hong Tzu-Chieh). (a) Designs showcasing threefold, fourfold, fivefold, and sixfold regular symmetries. (b) Designs featuring polyrhythmic fourfold symmetry.
Checkerboard lattice designs
The checkerboard lattice designs, a specific subset of the Chinese lattice designs that fill window frames (Stiny, Reference Stiny1977) provide a great initial framework to discuss key ideas in a formal composition, including repetition, recursion, modularity, grid, frame, boundary, proportion, symmetry, and many more. The additional constraint of a labeled grid that gets filled by different modules whose combinations make produce predictable or unpredictable results provides a rewarding visual context for taking on in a constructive way the idea of formal analysis and the specification of a whole series of diverse designs that all share a common framework. The two schemas typically used for the casting of the labeled shaped rules are the schema x → x + t(x) for the generation of the underlying rectangular lattice, and the schema x → y for the generation of the different substitute motifs upon the square or rectangular module. The series of designs in Figure 24 showcase nicely the substitution of the last rule of the original grammar with other shape rules that introduce new motifs to be inscribed within the cells of the checkerboard lattices to create very diverse designs. Significantly, the shape in the RHS of these rules was drawn and tested on the fly in GRAPE to see how the symmetries of the RHS partake of the overall symmetry of the design, and in different schemas too, to eliminate the frame of the square module and foreground other relations in the overall design, including quadrilaterals, pentagons, hexagons, octagons, and so forth, all in a variety of emergent spatial relations.
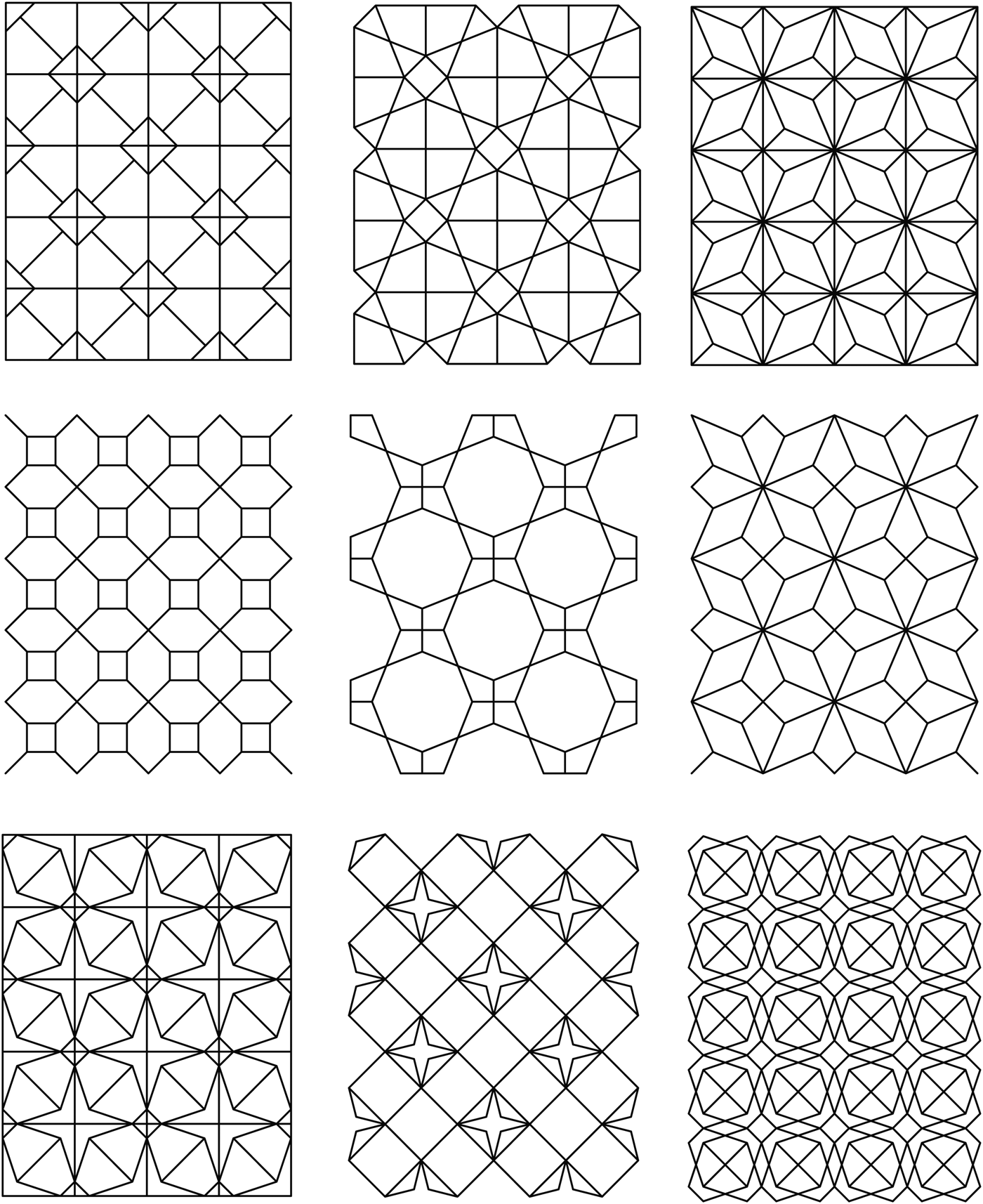
Fig. 24. Some designs in the checkerboard lattice language (Stephanie Douthitt).
Mughal designs
The Mughal gardens grammar is one of the earliest labeled parametric shape grammars in print (Stiny & Mitchell, Reference Stiny and Mitchell1978) and one of the most didactic showcasing in an exemplary way the layering of formal analysis in shape grammar discourse starting from the significance of an architectural concept and idea, here the concept of the paradise, to its history of design, its geometry, and finally the postulation of a formal grammar that can capture its salient features. The implementation of the Mughal garden grammar was by no means a simple feat as it relied extensively on parametric definitions of rules in GRAPE. Most rules in the grammar are defined in the schema rule x → Σ t(x) whereas t(x) is one of the transformations of the symmetry group of the square, the underlying framework of the garden. In this sense, a rule that may apply, say, in the upper left quadrant of the design, it also applies to all corresponding parts of the design and depending on the exact location of the part, the rule may apply in seven more locations (for a total of eight) or three more (for a total of four) if the rule has already some symmetry built in that aligns with the overall symmetry of the total design. The series of designs in Figure 25 show instances of the nine configurationally unique possibilities that can be produced by the grammar. Clearly, architectural elements such as the ornamentation of the reservoir of water at the center of the canals in a square or an octagonal form, the ornamentation of the endings of the water canals, and the parameterization of the dimensions of the borders and the canals can provide a rich palette for an expressive language with unique characteristics; and even more, the compositional subdivision based on the fourfold symmetry of the original grammar can be generalized for all regular polygons and shapes as desired.
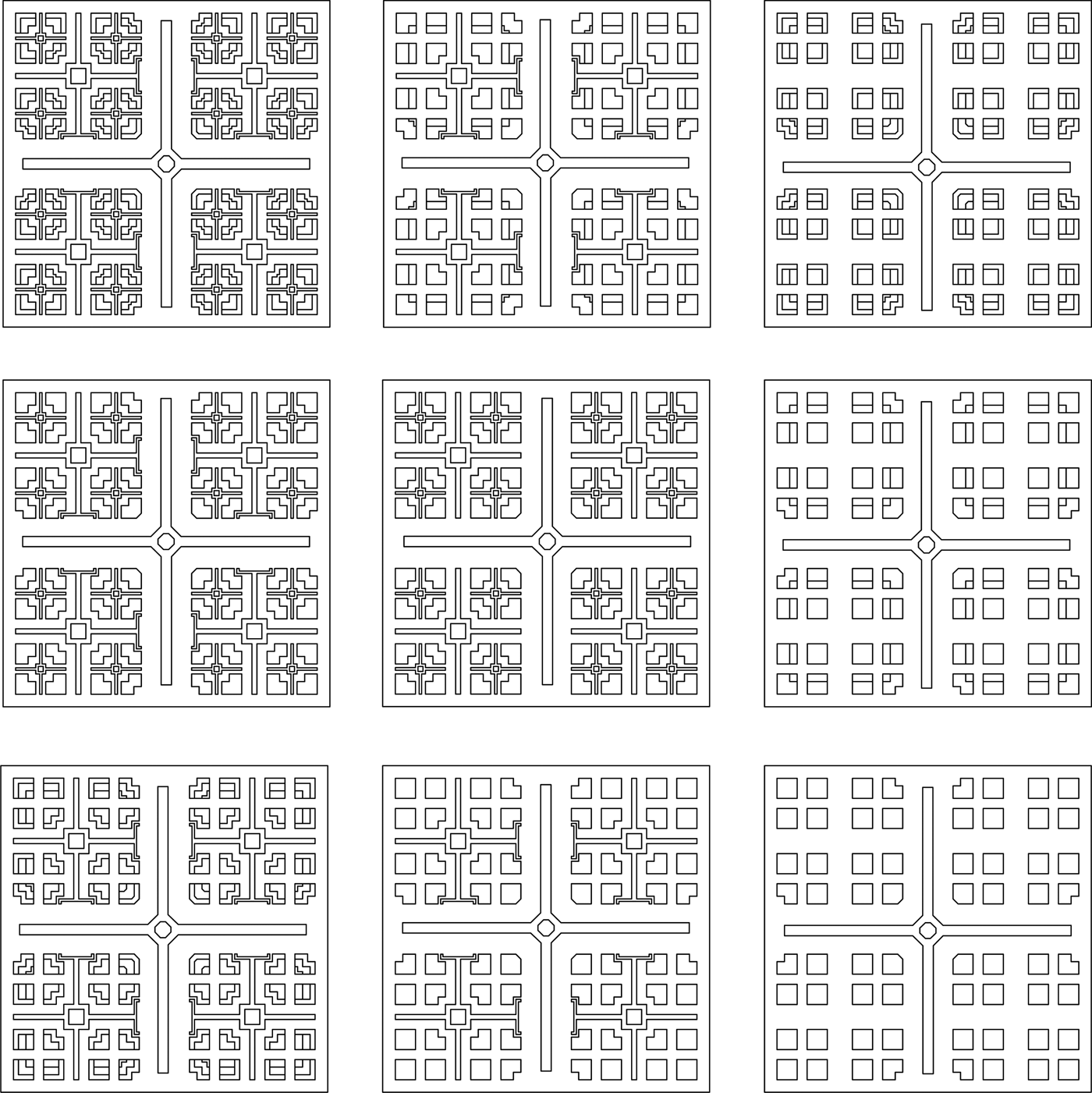
Fig. 25. Some designs in the Mughal garden language (Nirvik Saha).
From designs to rules
The second series of studies foregrounds a hands-on constructive inquiry on new grammars in the literature. The students are encouraged to come up with a list of existing artifacts or buildings they want to explore, or alternatively, a brief for the design of some new artifact or building. In either case, the rules for the generative description of the existing design works or the new ones do not exist and the students have to think them through, design and test them in GRAPE. The goal in this exercise is not the complete formal specification of a set of artifacts or buildings, existing or new; rather, it is the testing of how existing artifacts or briefs can be used constructively in the design of new rules. Again, the range of techniques used to design rules is open-ended; once a rule has been successfully implemented in GRAPE, the students make several productions to test its usefulness in the accommodation of additional requirements and constraints in the corpus or the brief. A sample of three studies is given below to showcase some of the findings of the workshop in GRAPE. The authors of the grammars are specified in parentheses within the brief account of each project.
Ad quadrant designs
The Speculation 8 (March 1972) and its range of nucleated and linear distributions of n% coverage within an abstract square configuration provide one of the most captivating schemata for the design of urban grids and blocks. The speculation is captured here in the definition of the subdivision of squares in terms of 4, 9, 16, 25, and in general n 2 squares. Clearly any subdivision of a square by n × n squares creates a simple division based on the square number sequence and any combination of such divisions nicely illustrates the ideas of recursion and emergence too, the two paramount characteristics of shape grammars, and the ability of GRAPE in capturing both in the application of the division algorithms in nested smaller copies of the square. The simplicity of the rules hides the delightful complexity they can generate once they apply recursively and at different scales within the design production. The straightforward application of each rule by itself creates familiar series of configurations, for example, the successive division to 22 creates the series 1, 4, 16, 64, 256, …, the successive division to 32 squares the series 1, 9, 81, 729, 6561, …, and so forth. More interestingly the combinations of any two subdivision rules A and B in various sequences, say, ABABAB…, BABABA…, AABBAA…, BBAABB…, AAABBB…, BBBAAA…, and so forth, and in other non-regular series too, immediately shows the inexhaustible possibilities that emerge out of the different sequence of rule applications and the corresponding designs all with their own visual characteristics. And clearly, the incorporation of specific ratios between the diminishing squares produces interesting densities and frit effects in the overall configuration. More importantly, the definition of the rules in the schema x → x + Σt(x) rather than the x → Σt(x) retain the original square and produce a whole new range of designs that show interesting and complex patterns of emergent spatial relations between squares at various scales. A sample of designs in the language of the ad quadrant grammar is shown in Figure 26. Additional designs utilizing square numbers for prime numbers using any of the techniques outlined above are readily available too.

Fig. 26. Some designs in the ad quadrant language (Abigail Smith). All designs use the ad quadrant subdivision rules in the schema x → x + ∑t(x).
MCE designs
M.C. Escher's recursive tilings are routinely used for interfaces between math and spatial design and for visual illustrations of symmetry, recursion, topology, and so on. The MCE grammar is not meant to be exhaustive for the corpus of the Dutch graphic artist but playfully uses his idea of the substitution of regular shapes with some spatial idea or motif that typically recalls a biomorphic association. Here the key shape is the isosceles Root2 (R2) triangle and the two main compositional ideas are its recursive substitution with three copies of itself, an identity R2 triangle and two smaller R2 triangles whose sum measures exactly the original one to produce a square and/or a nested R2 triangle respectively; and the recursive substitution of the R2 triangle with a complex shape featuring a weaving outline arranged around the edges of the triangle. Clearly, other shapes are possible and several were explored interactively in GRAPE before the designer committed to this final substitution. A catalog of some possible designs in the language is given in Figure 27. These designs showcase alternative ways of using the grammar either by applying shape rules manually to specific parts of the design or by applying a shape rule simultaneously to all possible matches within the design.
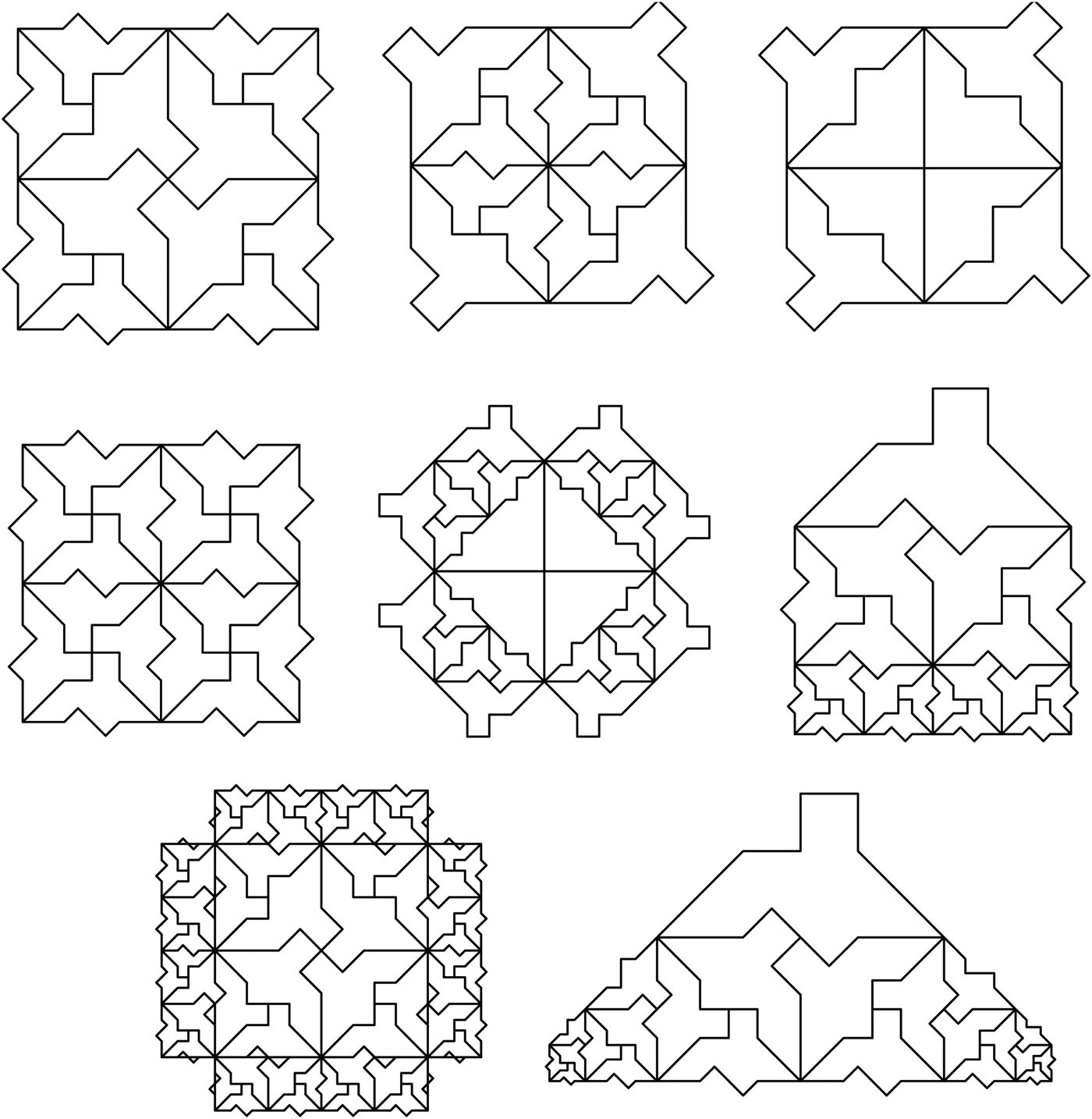
Fig. 27. Some designs in the MCE language (Kelsey Kurzeja).
Dirksen variations
The Everett McKinley Dirksen United States Courthouse in Chicago, designed and built by Mies van der Rohe during 1959–1964, is one of the most significant buildings of Mies’ output in the United States (Schulze, Reference Schulze1992). An initial proposal for an analog shape grammar for the design of the courtroom arrangements is given in Park and Economou (Reference Park, Economou, Martens, Wurzer, Grasl, Lorenz and Schaffranek2015). This iteration features the representation and implementation of the proposed parametric shape rules in GRAPE all in a truly 3D form. The project is quite ambitious and attempts to cast light in the design process of Mies’ office and more specifically, articulate the ways that Mies’ architectural language has been possibly deployed in this building type, foreground the sectional principles in the arrangement of the program, and more broadly speculate the aspects of this project that embodied Mies’ view on architecture and law. The Dirksen grammar is so far the most ambitious project in GRAPE taking on the complexities of writing new rules from scratch to specify given corpus, parameterizing them fully to be able to capture Mies’ proportional ideas, specify everything in three-dimensions in a uniform way and implement all directly in GRAPE. Clearly, these ambitions do not come without challenges. All rules here are implemented in the Rhino version and are encoded directly in the scripting environment, an interface quite distinct from the visual one in the web version of the software. Still, the current state of the work is very promising in that it manages to produce 3D models that can be exported and used in a variety of other applications for reviewing, rendering, slicing, printing and so forth. Interestingly the majority of the rules in the grammar follow the schema rule x + t(x) → [x + t(x)] + t 1 [x + t(x)], that is, a similar schema to the one used in the Palladian grammar capturing Mies’ desire for unilateral symmetry along the short axis of the courthouse. Furthermore, the grammar here provides a 3D analog for the Palladian one by modeling the spaces directly and having the walls emerge as poché walls in a specific state of the production. A set of six 3D courthouse models produced by the Dirksen grammar in GRAPE for Rhino are shown in Figure 28. All models feature a core of 24 courtrooms in various configurations per floor. The first three models (a–c) are models that are found in the archives of Mies’ office. The last three models (d–f) are theoretically possible designs in Mies’ language. All six models are derived from manual applications of the rules of the Dirksen grammar within the GRAPE for Rhino environment and are shown here in sectional axonometric projections manually prepared in Rhino for illustrative purposes.

Fig. 28. A set of six sectional axonometric models of Miesian courthouse designs (James Park). All models feature a total of 24 courtrooms in various arrangements. Models (a–c) showcase designs that are found in the archives of the design process. Models (d–f) showcase possible hypothetical designs in the language.
Discussion
A key motivation underlying the work described so far has been the speculation of a new design workflow whereas the designers seamlessly design and test their rules within their design processes. While shape grammars applications have been developed for over 40 years, still no parametric shape grammar interpreter has emerged to comprehensively address the range of issues that have emerged in the discourse over the years. The presented work describes a graph model intended as the backbone in tackling these issues and makes some progress toward the overall goal, especially concerning the description and execution of parametric rules for varying kinds of geometry. In addition, the layout of the software components is an attempt to keep the engine independent and extendible. The ability to attach the engine to various platforms does reduce the threshold for users. It allows users to work in environments they are acquainted with, but it does simultaneously place an additional burden on the development. If an important part of the engine is changed, then all implementations have to be updated.
For ease of distribution and maintenance, as well as due to the flexibility of the user interface the web version has received the most attention. This is also the version most users of the workshops were introduced to. Getting acquainted with the grammar-specific features was straightforward for most users; the biggest hindrance to the development of grammars was the lack of CAD functionality offered by the web version of GRAPE. The respective JavaScript libraries are tailor-made and enable only a limited set of operations. Meanwhile more extensive web CAD libraries have emerged and this issue could be addressed by switching to one of these.
Furthermore, the visual editor will probably never be able to support all available features offered by the GRAPE model in combination with a graph grammar engine. For advanced grammars it will thus remain necessary to be versed in some kind of scripting or modeling language, be it the GrGen.NET modeling language or something else.
The work here outlined the continuation of the work presented in the paper “From topologies to shapes” (Grasl & Economou, Reference Grasl and Economou2013a). The incorporation of additional geometries including curvilinear and 3D ones as well as variables in the graph model was discussed, some issues pertaining to the visual rule editor were highlighted, and rule selection agents were introduced.
Thomas Grasl is a founding member of SWAP Architects and leads their R&D department known simply as PLUS. His research focuses on computational design, CAAD, and the application of grammars in architecture. Previously he worked as assistant professor at the department of building theory and design, as lecturer at the department of spatial design, and as consultant master planner for the ad-m (airport design-management). Recently he took the lead in developing Eva, a CAD software that supports architects and planners during the early phases of design. Dr. Grasl holds a M.Sc. and a Doctor technicae in Architecture from TU Vienna as well as a Fulbright scholarship for advanced studies in architecture at Georgia Institute of Technology, USA.
Athanassios Economou is Professor in the College of Design at the Georgia Institute of Technology. Dr. Economou's teaching and research are in the areas of shape grammars, computational design, computer-aided design and design theory, with over forty published papers in these areas. Design projects from his studios at Georgia Tech have received prestigious awards in international and national architectural competitions. He is the Director of the Shape Computation Lab at Georgia Tech and the Director of the Art and Architecture in Greece and Italy Study Abroad Program at Georgia Tech. He has been invited to give talks, seminars, and workshops at several universities including MIT, Harvard, TU Vienna, U. Michigan, UCLA, NTUA, U. Thessaly, U. Aegean, among others. Dr. Economou holds a Diploma in Architecture from NTUA, Athens, Greece, an M.Arch from USC, and a Ph.D. in Architecture from UCLA.