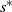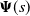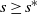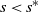1. Introduction
Let ![]() $\{ (\varphi(t)):t\geq 0\}$ be an irreducible, positive-recurrent, continuous-time Markov chain (CTMC) with some finite state space
$\{ (\varphi(t)):t\geq 0\}$ be an irreducible, positive-recurrent, continuous-time Markov chain (CTMC) with some finite state space ![]() $\mathcal{S}=\{1,2,\ldots ,n\}$ and infinitesimal generator T. Let
$\mathcal{S}=\{1,2,\ldots ,n\}$ and infinitesimal generator T. Let ![]() $\{(\varphi(t),X(t)):t\geq 0\}$ be a Markovian stochastic fluid model (SFM) [Reference Ahn and Ramaswami2, Reference Ahn and Ramaswami3, Reference Ahn and Ramaswami4, Reference Asmussen7, Reference Bean, O’Reilly and Taylor15, Reference Bean, O’Reilly and Taylor16, Reference Bean, O’Reilly and Taylor17, Reference Ramaswami43, Reference Ramaswami44], with phase variable
$\{(\varphi(t),X(t)):t\geq 0\}$ be a Markovian stochastic fluid model (SFM) [Reference Ahn and Ramaswami2, Reference Ahn and Ramaswami3, Reference Ahn and Ramaswami4, Reference Asmussen7, Reference Bean, O’Reilly and Taylor15, Reference Bean, O’Reilly and Taylor16, Reference Bean, O’Reilly and Taylor17, Reference Ramaswami43, Reference Ramaswami44], with phase variable ![]() $\varphi(t)\in\mathcal{S}$, level variable
$\varphi(t)\in\mathcal{S}$, level variable ![]() $X(t)\geq 0$, and constant rates
$X(t)\geq 0$, and constant rates ![]() $c_i\in\mathbb{R}$, for all
$c_i\in\mathbb{R}$, for all ![]() $i\in\mathcal{S}$. The model assumes that when
$i\in\mathcal{S}$. The model assumes that when ![]() $\varphi(t)=i$ and
$\varphi(t)=i$ and ![]() $X(t)>0$, the rate at which the level is changing is
$X(t)>0$, the rate at which the level is changing is ![]() $c_i$, and when
$c_i$, and when ![]() $\varphi(t)=i$ and
$\varphi(t)=i$ and ![]() $X(t)=0$, the rate at which the level is changing is
$X(t)=0$, the rate at which the level is changing is ![]() $max\{0,c_i\}$. Therefore, we refer to the CTMC
$max\{0,c_i\}$. Therefore, we refer to the CTMC ![]() $\{ (\varphi(t)):t\geq 0\}$ as the process that is driving (or modulating) the SFM
$\{ (\varphi(t)):t\geq 0\}$ as the process that is driving (or modulating) the SFM ![]() $\{(\varphi(t),X(t)):t\geq 0\}$.
$\{(\varphi(t),X(t)):t\geq 0\}$.
SFMs are a key class of models in the theory of matrix-analytic methods [Reference He29, Reference Latouche and Ramaswami36, Reference Latouche37], which comprises methodologies for the analysis of Markov chains and Markovian-modulated models that lead to efficient algorithms for numerical computation.
Let ![]() $\mathcal{S}_1=\{i\in\mathcal{S}:c_i>0\}$,
$\mathcal{S}_1=\{i\in\mathcal{S}:c_i>0\}$, ![]() $\mathcal{S}_2=\{i\in\mathcal{S}:c_i<0\}$,
$\mathcal{S}_2=\{i\in\mathcal{S}:c_i<0\}$, ![]() $\mathcal{S}_0=\{i\in\mathcal{S}:c_i=0\}$, and partition the generator as
$\mathcal{S}_0=\{i\in\mathcal{S}:c_i=0\}$, and partition the generator as
 \begin{align}{\textbf{T}}=\left[\begin{array}{c@{\quad}c@{\quad}c}{\textbf{T}}_{11} & {\textbf{T}}_{12} & {\textbf{T}}_{10}\\[4pt]{\textbf{T}}_{21} & {\textbf{T}}_{22} & {\textbf{T}}_{20}\\[4pt]{\textbf{T}}_{01} & {\textbf{T}}_{02} & {\textbf{T}}_{00}\end{array}\right],\end{align}
\begin{align}{\textbf{T}}=\left[\begin{array}{c@{\quad}c@{\quad}c}{\textbf{T}}_{11} & {\textbf{T}}_{12} & {\textbf{T}}_{10}\\[4pt]{\textbf{T}}_{21} & {\textbf{T}}_{22} & {\textbf{T}}_{20}\\[4pt]{\textbf{T}}_{01} & {\textbf{T}}_{02} & {\textbf{T}}_{00}\end{array}\right],\end{align}
according to ![]() $\mathcal{S}=\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$.
$\mathcal{S}=\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$.
We assume that the process is stable; that is,
where ![]() $\boldsymbol{\xi}=[\xi_i]_{i\in\mathcal{S}}$ is the stationary distribution vector of the Markov chain
$\boldsymbol{\xi}=[\xi_i]_{i\in\mathcal{S}}$ is the stationary distribution vector of the Markov chain ![]() $\{(\varphi(t)):t\geq 0\}$.
$\{(\varphi(t)):t\geq 0\}$.
So far, the analysis of SFMs has focused on the transient and stationary behaviour. In this paper, we are interested in the behaviour of the process conditional on absorption not having taken place, where absorption means that the busy period of the process has ended, that is, the process has not hit the level zero as yet. For ![]() $x\geq 0$, let
$x\geq 0$, let ![]() $\theta(x)=\inf\{t>0:X(t)=x\}$ be the first time at which the process reaches level x. To this end, we define the following quantity, referred to as the Yaglom limit.
$\theta(x)=\inf\{t>0:X(t)=x\}$ be the first time at which the process reaches level x. To this end, we define the following quantity, referred to as the Yaglom limit.
Definition 1. Define the matrix ![]() $\boldsymbol{\mu}(dy)^{(x)}=[\mu(dy)^{(x)}_{ij}]_{i,j\in\mathcal{S}}$,
$\boldsymbol{\mu}(dy)^{(x)}=[\mu(dy)^{(x)}_{ij}]_{i,j\in\mathcal{S}}$, ![]() $x,y> 0$, such that
$x,y> 0$, such that
and the matrix ![]() $\boldsymbol{\mu}(dy)^{(0)}=[\mu(dy)^{(0)}_{ij}]_{i\in\mathcal{S}_1,j\in\mathcal{S}}$,
$\boldsymbol{\mu}(dy)^{(0)}=[\mu(dy)^{(0)}_{ij}]_{i\in\mathcal{S}_1,j\in\mathcal{S}}$, ![]() $y> 0$, such that
$y> 0$, such that
whenever the limit exists. We refer to ![]() $\mu(dy)^{(x)}_{ij}$ as the limiting conditional distribution (Yaglom limit) of observing the process in level y and phase j, given that the process started from level x in phase i at time zero and has been evolving without hitting level zero.
$\mu(dy)^{(x)}_{ij}$ as the limiting conditional distribution (Yaglom limit) of observing the process in level y and phase j, given that the process started from level x in phase i at time zero and has been evolving without hitting level zero.
Remark 1. In general, for Markov processes there are no sufficient conditions that we can refer to under which the Yaglom limit or quasi-stationary distribution exists. Usually, the existence of the Yaglom limit is proved case by case. Here, we prove that it exists for our model.
We partition ![]() $\boldsymbol{\mu}(dy)^{(x)}$,
$\boldsymbol{\mu}(dy)^{(x)}$, ![]() $x>0$, according to
$x>0$, according to ![]() $\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0 \times \mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$ as
$\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0 \times \mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$ as
 \begin{equation}\boldsymbol{\mu}(dy)^{(x)}=\left[\begin{array}{c@{\quad}c@{\quad}c}\boldsymbol{\mu}(dy)^{(x)}_{11}&\boldsymbol{\mu}(dy)^{(x)}_{12}&\boldsymbol{\mu}(dy)^{(x)}_{10}\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{21}&\boldsymbol{\mu}(dy)^{(x)}_{22}&\boldsymbol{\mu}(dy)^{(x)}_{20}\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{01}&\boldsymbol{\mu}(dy)^{(x)}_{02}&\boldsymbol{\mu}(dy)^{(x)}_{00}\\[4pt]\end{array}\right],\end{equation}
\begin{equation}\boldsymbol{\mu}(dy)^{(x)}=\left[\begin{array}{c@{\quad}c@{\quad}c}\boldsymbol{\mu}(dy)^{(x)}_{11}&\boldsymbol{\mu}(dy)^{(x)}_{12}&\boldsymbol{\mu}(dy)^{(x)}_{10}\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{21}&\boldsymbol{\mu}(dy)^{(x)}_{22}&\boldsymbol{\mu}(dy)^{(x)}_{20}\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{01}&\boldsymbol{\mu}(dy)^{(x)}_{02}&\boldsymbol{\mu}(dy)^{(x)}_{00}\\[4pt]\end{array}\right],\end{equation}
and partition its row sums accordingly, as
 \begin{equation}\boldsymbol{\mu}(dy)^{(x)}{\boldsymbol{1}}=\left[\begin{array}{c}\boldsymbol{\mu}(dy)^{(x)}_{1}\\[4pt]\boldsymbol{\mu}(dy)^{(x)}_{2}\\[4pt]\boldsymbol{\mu}(dy)^{(x)}_{0}\\[4pt]\end{array}\right],\end{equation}
\begin{equation}\boldsymbol{\mu}(dy)^{(x)}{\boldsymbol{1}}=\left[\begin{array}{c}\boldsymbol{\mu}(dy)^{(x)}_{1}\\[4pt]\boldsymbol{\mu}(dy)^{(x)}_{2}\\[4pt]\boldsymbol{\mu}(dy)^{(x)}_{0}\\[4pt]\end{array}\right],\end{equation}
where ![]() ${\boldsymbol{1}}$ denotes a vector of ones of appropriate size, so that
${\boldsymbol{1}}$ denotes a vector of ones of appropriate size, so that ![]() $\boldsymbol{\mu}(dy)^{(x)}_{1}=\boldsymbol{\mu}(dy)^{(x)}_{11}{\boldsymbol{1}}+\boldsymbol{\mu}(dy)^{(x)}_{12}{\boldsymbol{1}}+\boldsymbol{\mu}(dy)^{(x)}_{10}{\boldsymbol{1}}$, and so on.
$\boldsymbol{\mu}(dy)^{(x)}_{1}=\boldsymbol{\mu}(dy)^{(x)}_{11}{\boldsymbol{1}}+\boldsymbol{\mu}(dy)^{(x)}_{12}{\boldsymbol{1}}+\boldsymbol{\mu}(dy)^{(x)}_{10}{\boldsymbol{1}}$, and so on.
We partition ![]() $\boldsymbol{\mu}(dy)^{(0)}$ according to
$\boldsymbol{\mu}(dy)^{(0)}$ according to ![]() $\mathcal{S}_1\times\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$ as
$\mathcal{S}_1\times\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$ as
and let
This paper is the first analysis of the Yaglom limit of SFMs. We derive expressions for the Yaglom limit, show its uniqueness, and illustrate the theory with simple examples. The Yaglom limit concerns some Markov process X(t) and some almost surely finite absorption time ![]() $\theta$ (usually the first exit time from some set, such as a positive half-line), and is defined by
$\theta$ (usually the first exit time from some set, such as a positive half-line), and is defined by
It describes the state of the Markov system conditioned on surviving killing coming from ![]() $\theta$ for a very long time. The Yaglom limit is strongly related to the so-called quasi-stationary distribution, which satisfies
$\theta$ for a very long time. The Yaglom limit is strongly related to the so-called quasi-stationary distribution, which satisfies
see for example [Reference Darroch and Seneta21]. In particular, the Yaglom limit ![]() $\mu$ (if it exists) is necessarily quasi-stationary, but it may be difficult to show its uniqueness [Reference Asmussen8, Section 3]. In other words, there might be more quasi-stationary laws, and the Yaglom limit might be one of them. It might be the case as well that there exists a quasi-stationary distribution but that the Yaglom limit is not well-defined.
$\mu$ (if it exists) is necessarily quasi-stationary, but it may be difficult to show its uniqueness [Reference Asmussen8, Section 3]. In other words, there might be more quasi-stationary laws, and the Yaglom limit might be one of them. It might be the case as well that there exists a quasi-stationary distribution but that the Yaglom limit is not well-defined.
A related class of models in the theory of matrix-analytic methods is that of quasi-birth-and-death processes (QBDs) [Reference Latouche and Ramaswami36], in which the level variable is discrete. The quasi-stationary analysis of QBDs has been provided in [Reference Bean10, Reference Bean, Pollett and Taylor11, Reference Bean, Pollett and Taylor12], along with several examples of areas of applications, which are relevant here as well, due to the similar application potential of QBDs and SFMs [Reference Bean and O’Reilly13].
Information on quasi-stationary distributions for other Markov processes can be found in the classical works of Seneta and Vere-Jones [Reference Seneta and Vere-Jones45], Tweedie [Reference Tweedie46], and Jacka and Roberts [Reference Jacka and Roberts32]. The bibliographic database of Pollet [Reference Pollett42] gives a detailed history of quasi-stationary distributions. In particular, Yaglom [Reference Yaglom48] was the first to explicitly identify quasi-stationary distributions for the subcritical Bienaymé–Galton–Watson branching process. Some of the results on quasi-stationary distributions concern Markov chains on the positive integers with an absorbing state at the origin [Reference Collet, Martnez and San Martn20, Reference Ferrari, Kesten, Martínez and Picco23, Reference Flaspohler and Holmes25, Reference Seneta and Vere-Jones45, Reference Van Doorn47, Reference Zhang, Li and Song49]. Other objects of study are the extinction probabilities for continuous-time branching processes and the Fleming–Viot processes [Reference Asselah, Ferrari, Groisman and Jonckheere9, Reference Ferrari and Marić24, Reference Lambert35]. A separate topic is that of Lévy processes exiting from the positive half-line or a cone. Here the case of the Brownian motion with drift was resolved by Martínez and San Martín [Reference Martnez and San Martn40], complementing the result for random walks obtained by Iglehart [Reference Iglehart31]. The case of more general Lévy processes was studied by [Reference Bogdan, Palmowski and Wang19, Reference Kyprianou and Palmowski33, Reference Kyprianou34, Reference Mandjes, Palmowski and Rolski39]. One-dimensional self-similar processes, including the symmetric ![]() $\alpha$-stable Lévy process, were subject of interest in [Reference Haas and Rivero28].
$\alpha$-stable Lévy process, were subject of interest in [Reference Haas and Rivero28].
The rest of the paper is structured as follows. In Section 2 we define the Laplace–Stieltjes transforms (LSTs) which form the key building blocks of the analysis, and in Section 3 we outline the approach based on the Heaviside principle. The key results of this paper are contained in Section 4. To illustrate the theory we construct a simple example with scalar parameters, which we analyse throughout the paper, as we introduce the theory. In Section 5 we analyse another example, with matrix parameters, where we provide some numerical output as well.
2. The Laplace–Stieltjes transforms
Note that by Definition 1, for ![]() $x\geq 0$,
$x\geq 0$,
 \begin{eqnarray}\mu(dy)^{(x)}_{ij}&\,=\,&\lim_{t\to\infty}\mathbb{P}(X(t)\in dy,\varphi(t)=j\ |\ \theta(0)>t,X(0)=x,\varphi(0)=i)\nonumber\\[4pt]
&\,=\,&\lim_{t\to\infty}\frac{\mathbb{P}(X(t)\in dy,\varphi(t)=j,\theta(0)>t\ |\ X(0)=x,\varphi(0)=i)}{\mathbb{P}(\theta(0)>t\ |\ X(0)=x,\varphi(0)=i)}.\end{eqnarray}
\begin{eqnarray}\mu(dy)^{(x)}_{ij}&\,=\,&\lim_{t\to\infty}\mathbb{P}(X(t)\in dy,\varphi(t)=j\ |\ \theta(0)>t,X(0)=x,\varphi(0)=i)\nonumber\\[4pt]
&\,=\,&\lim_{t\to\infty}\frac{\mathbb{P}(X(t)\in dy,\varphi(t)=j,\theta(0)>t\ |\ X(0)=x,\varphi(0)=i)}{\mathbb{P}(\theta(0)>t\ |\ X(0)=x,\varphi(0)=i)}.\end{eqnarray}
For all ![]() $x\geq 0$ and
$x\geq 0$ and ![]() $y>0$, define the matrix
$y>0$, define the matrix ![]() ${\textbf{E}}(dy)^{(x)}(s)=[E(dy)^{(x)}_{ij}(s)]_{i,j\in\mathcal{S}}$ and the vector
${\textbf{E}}(dy)^{(x)}(s)=[E(dy)^{(x)}_{ij}(s)]_{i,j\in\mathcal{S}}$ and the vector ![]() ${\textbf{E}}^{(x)}(s)=[E^{(x)}_i(s)]_{i\in\mathcal{S}}$, which record the corresponding Laplace–Stieltjes transforms (LSTs),
${\textbf{E}}^{(x)}(s)=[E^{(x)}_i(s)]_{i\in\mathcal{S}}$, which record the corresponding Laplace–Stieltjes transforms (LSTs),
 \begin{eqnarray}E(dy)^{(x)}_{ij}(s)&\,=\,&\int_0^\infty \mathbb{E}(e^{-s t} {\boldsymbol{1}}\{X(t)\in dy,\varphi(t)=j,\theta(0)>t\}\ |\ X(0)=x,\varphi(0)=i) dt,\nonumber\\[4pt]E^{(x)}_i(s)&\,=\,&\int_0^\infty \mathbb{E}(e^{-s t} {\boldsymbol{1}}\{\theta(0)>t\}\ |\ X(0)=x,\varphi(0)=i)dt,\end{eqnarray}
\begin{eqnarray}E(dy)^{(x)}_{ij}(s)&\,=\,&\int_0^\infty \mathbb{E}(e^{-s t} {\boldsymbol{1}}\{X(t)\in dy,\varphi(t)=j,\theta(0)>t\}\ |\ X(0)=x,\varphi(0)=i) dt,\nonumber\\[4pt]E^{(x)}_i(s)&\,=\,&\int_0^\infty \mathbb{E}(e^{-s t} {\boldsymbol{1}}\{\theta(0)>t\}\ |\ X(0)=x,\varphi(0)=i)dt,\end{eqnarray}
where ![]() ${\boldsymbol{1}}\{\cdot\}$ denotes an indicator function. We have
${\boldsymbol{1}}\{\cdot\}$ denotes an indicator function. We have
We partition ![]() ${\textbf{E}}(dy)^{(x)}(s)$,
${\textbf{E}}(dy)^{(x)}(s)$, ![]() $x>0$, according to
$x>0$, according to ![]() $\mathcal{S}\times \mathcal{S}$ for
$\mathcal{S}\times \mathcal{S}$ for ![]() $\mathcal{S}=\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$ as
$\mathcal{S}=\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$ as
 \begin{equation}{\textbf{E}}(dy)^{(x)}(s)=\left[\begin{array}{c@{\quad}c@{\quad}c}{\textbf{E}}(dy)^{(x)}(s)_{11}&{\textbf{E}}(dy)^{(x)}(s)_{12}&{\textbf{E}}(dy)^{(x)}(s)_{10}\\[4pt]{\textbf{E}}(dy)^{(x)}(s)_{21}&{\textbf{E}}(dy)^{(x)}(s)_{22}&{\textbf{E}}(dy)^{(x)}(s)_{20}\\[4pt]{\textbf{E}}(dy)^{(x)}(s)_{01}&{\textbf{E}}(dy)^{(x)}(s)_{02}&{\textbf{E}}(dy)^{(x)}(s)_{00}\\[4pt]\end{array}\right],\end{equation}
\begin{equation}{\textbf{E}}(dy)^{(x)}(s)=\left[\begin{array}{c@{\quad}c@{\quad}c}{\textbf{E}}(dy)^{(x)}(s)_{11}&{\textbf{E}}(dy)^{(x)}(s)_{12}&{\textbf{E}}(dy)^{(x)}(s)_{10}\\[4pt]{\textbf{E}}(dy)^{(x)}(s)_{21}&{\textbf{E}}(dy)^{(x)}(s)_{22}&{\textbf{E}}(dy)^{(x)}(s)_{20}\\[4pt]{\textbf{E}}(dy)^{(x)}(s)_{01}&{\textbf{E}}(dy)^{(x)}(s)_{02}&{\textbf{E}}(dy)^{(x)}(s)_{00}\\[4pt]\end{array}\right],\end{equation}
and ![]() ${\textbf{E}}^{(x)}(s)$,
${\textbf{E}}^{(x)}(s)$, ![]() $x>0$, as
$x>0$, as
 \begin{equation}{\textbf{E}}^{(x)}(s)=\left[\begin{array}{c}{\textbf{E}}^{(x)}(s)_1\\[4pt]{\textbf{E}}^{(x)}(s)_2\\[4pt]{\textbf{E}}^{(x)}(s)_0\end{array}\right].\end{equation}
\begin{equation}{\textbf{E}}^{(x)}(s)=\left[\begin{array}{c}{\textbf{E}}^{(x)}(s)_1\\[4pt]{\textbf{E}}^{(x)}(s)_2\\[4pt]{\textbf{E}}^{(x)}(s)_0\end{array}\right].\end{equation}
We partition ![]() ${\textbf{E}}(dy)^{(0)}(s)$ according to
${\textbf{E}}(dy)^{(0)}(s)$ according to ![]() $\mathcal{S}_1\times\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$ as
$\mathcal{S}_1\times\mathcal{S}_1\cup\mathcal{S}_2\cup\mathcal{S}_0$ as
and let
Define ![]() ${\textbf{C}}_1=diag(c_i)_{i\in\mathcal{S}_1}$,
${\textbf{C}}_1=diag(c_i)_{i\in\mathcal{S}_1}$, ![]() ${\textbf{C}}_2=diag(|c_i|)_{i\in\mathcal{S}_2}$, and let
${\textbf{C}}_2=diag(|c_i|)_{i\in\mathcal{S}_2}$, and let ![]() ${\textbf{Q}}(s)$ be the key fluid generator matrix
${\textbf{Q}}(s)$ be the key fluid generator matrix ![]() ${\textbf{Q}}(s)$ introduced in [Reference Bean, O’Reilly and Taylor16],
${\textbf{Q}}(s)$ introduced in [Reference Bean, O’Reilly and Taylor16],
 \begin{equation}{\textbf{Q}}(s)=\left[\begin{array}{c@{\quad}c}{\textbf{Q}}_{11}(s) & {\textbf{Q}}_{12}(s) \\[4pt]{\textbf{Q}}_{21}(s) & {\textbf{Q}}_{22}(s)\end{array}\right],\end{equation}
\begin{equation}{\textbf{Q}}(s)=\left[\begin{array}{c@{\quad}c}{\textbf{Q}}_{11}(s) & {\textbf{Q}}_{12}(s) \\[4pt]{\textbf{Q}}_{21}(s) & {\textbf{Q}}_{22}(s)\end{array}\right],\end{equation}
where the block matrices are given by
 \begin{eqnarray}{\textbf{Q}}_{22}(s)&\,=\,&{\textbf{C}}^{-1}_{2}\left({\textbf{T}}_{22}-s{\textbf{I}}-{\textbf{T}}_{20}({\textbf{T}}_{00}-s{\textbf{I}})^{-1}{\textbf{T}}_{02}\right),\nonumber\\[4pt]{\textbf{Q}}_{11}(s)&\,=\,&{\textbf{C}}^{-1}_{1}\left({\textbf{T}}_{11}-s{\textbf{I}}-{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-1}{\textbf{T}}_{01}\right),\nonumber\\[4pt]{\textbf{Q}}_{12}(s)&\,=\,&{\textbf{C}}^{-1}_{1}\left({\textbf{T}}_{12}-{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-1}{\textbf{T}}_{02}\right),\nonumber\\[4pt]{\textbf{Q}}_{21}(s)&\,=\,&{\textbf{C}}^{-1}_{2}\left({\textbf{T}}_{21}-{\textbf{T}}_{20}({\textbf{T}}_{00}-s{\textbf{I}})^{-1}{\textbf{T}}_{01}\right).\end{eqnarray}
\begin{eqnarray}{\textbf{Q}}_{22}(s)&\,=\,&{\textbf{C}}^{-1}_{2}\left({\textbf{T}}_{22}-s{\textbf{I}}-{\textbf{T}}_{20}({\textbf{T}}_{00}-s{\textbf{I}})^{-1}{\textbf{T}}_{02}\right),\nonumber\\[4pt]{\textbf{Q}}_{11}(s)&\,=\,&{\textbf{C}}^{-1}_{1}\left({\textbf{T}}_{11}-s{\textbf{I}}-{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-1}{\textbf{T}}_{01}\right),\nonumber\\[4pt]{\textbf{Q}}_{12}(s)&\,=\,&{\textbf{C}}^{-1}_{1}\left({\textbf{T}}_{12}-{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-1}{\textbf{T}}_{02}\right),\nonumber\\[4pt]{\textbf{Q}}_{21}(s)&\,=\,&{\textbf{C}}^{-1}_{2}\left({\textbf{T}}_{21}-{\textbf{T}}_{20}({\textbf{T}}_{00}-s{\textbf{I}})^{-1}{\textbf{T}}_{01}\right).\end{eqnarray}
Here, ![]() ${\textbf{Q}}(s)$ exists for all real s such that
${\textbf{Q}}(s)$ exists for all real s such that ![]() $({\textbf{T}}_{00}-s{\textbf{I}})^{-1}=\int_{t=0}^{\infty}e^{-st}e^{{\textbf{T}}_{00}t}dt<\infty$, or for all real s when
$({\textbf{T}}_{00}-s{\textbf{I}})^{-1}=\int_{t=0}^{\infty}e^{-st}e^{{\textbf{T}}_{00}t}dt<\infty$, or for all real s when ![]() $S_0=\emptyset$.
$S_0=\emptyset$.
Also, let ![]() ${\boldsymbol{\Psi}}(s)$ be the key matrix for SFMs [Reference Bean, O’Reilly and Taylor16] such that, for all
${\boldsymbol{\Psi}}(s)$ be the key matrix for SFMs [Reference Bean, O’Reilly and Taylor16] such that, for all ![]() $i\in\mathcal{S}_1, j\in\mathcal{S}_2$,
$i\in\mathcal{S}_1, j\in\mathcal{S}_2$,
is the LST of the first return time to the original level zero, with this occurring in phase j, given a start at level zero in phase i. Let ![]() $\boldsymbol{\psi}(t)$ be the corresponding density, so that
$\boldsymbol{\psi}(t)$ be the corresponding density, so that ![]() ${\boldsymbol{\Psi}}(s)=\int_{t=0}^{\infty}e^{-st}\boldsymbol{\psi}(t)dt$. Clearly,
${\boldsymbol{\Psi}}(s)=\int_{t=0}^{\infty}e^{-st}\boldsymbol{\psi}(t)dt$. Clearly, ![]() ${\boldsymbol{\Psi}}(s)>0$ for real s such that
${\boldsymbol{\Psi}}(s)>0$ for real s such that ![]() ${\boldsymbol{\Psi}}(s)<\infty$ exists.
${\boldsymbol{\Psi}}(s)<\infty$ exists.
Define matrices
and note that by the assumed stability of the process, the spectra of ![]() ${\textbf{K}}(s)$ and
${\textbf{K}}(s)$ and ![]() $({-}{\textbf{D}}(s))$ are separate for
$({-}{\textbf{D}}(s))$ are separate for ![]() $s\geq 0$ by [Reference Bean, O’Reilly and Taylor15, Reference Bean, O’Reilly and Taylor16, Reference Bean, O’Reilly and Taylor17]; that is,
$s\geq 0$ by [Reference Bean, O’Reilly and Taylor15, Reference Bean, O’Reilly and Taylor16, Reference Bean, O’Reilly and Taylor17]; that is, ![]() $sp({\textbf{K}}(s))\cap sp({-}{\textbf{D}}(s))=\varnothing$.
$sp({\textbf{K}}(s))\cap sp({-}{\textbf{D}}(s))=\varnothing$.
We extend the result in [Reference Bean, O’Reilly and Taylor16, Equation (23)] from ![]() $Re(s)\geq 0$ to all real s such that
$Re(s)\geq 0$ to all real s such that ![]() ${\boldsymbol{\Psi}}(s)<\infty$ exists.
${\boldsymbol{\Psi}}(s)<\infty$ exists.
Lemma 1. For all real s such that ![]() ${\boldsymbol{\Psi}}(s)<\infty$ exists, the matrix
${\boldsymbol{\Psi}}(s)<\infty$ exists, the matrix ![]() ${\boldsymbol{\Psi}}(s)$ is a solution of the Riccati equation,
${\boldsymbol{\Psi}}(s)$ is a solution of the Riccati equation,
Proof. Suppose s is real and ![]() ${\boldsymbol{\Psi}}(s)<\infty$. Then, by [Reference Bean, O’Reilly and Taylor16, Theorem 1] and [Reference Bean, O’Reilly and Taylor17, Algorithm 1 of Section 3.1],
${\boldsymbol{\Psi}}(s)<\infty$. Then, by [Reference Bean, O’Reilly and Taylor16, Theorem 1] and [Reference Bean, O’Reilly and Taylor17, Algorithm 1 of Section 3.1],
Then, letting
we have
and so
 \begin{eqnarray}{\textbf{Q}}_{11}(s){\boldsymbol{\Psi}}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{22}(s)&\,=\,&\int_{y=0}^{\infty}\frac{\partial}{\partial y}\left( {\boldsymbol{\Psi}}(s,y) \right)dy\nonumber\\[8pt]
&\,=\,&\lim_{y\to\infty}{\boldsymbol{\Psi}}(s,y)-{\boldsymbol{\Psi}}(s,0)\end{eqnarray}
\begin{eqnarray}{\textbf{Q}}_{11}(s){\boldsymbol{\Psi}}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{22}(s)&\,=\,&\int_{y=0}^{\infty}\frac{\partial}{\partial y}\left( {\boldsymbol{\Psi}}(s,y) \right)dy\nonumber\\[8pt]
&\,=\,&\lim_{y\to\infty}{\boldsymbol{\Psi}}(s,y)-{\boldsymbol{\Psi}}(s,0)\end{eqnarray}
and
which implies that ![]() ${\boldsymbol{\Psi}}(s)$ is a solution of (21).
${\boldsymbol{\Psi}}(s)$ is a solution of (21).
Below, we state expressions for ![]() ${\textbf{E}}(dy)^{(0)}(s)$ derived in [Reference Ahn and Ramaswami3, Theorem 3.1.1] and [Reference Bean and O’Reilly14, Theorem 2].
${\textbf{E}}(dy)^{(0)}(s)$ derived in [Reference Ahn and Ramaswami3, Theorem 3.1.1] and [Reference Bean and O’Reilly14, Theorem 2].
Lemma 2. We have
 \begin{eqnarray}{\textbf{E}}(dy)^{(0)}(s)_{10}&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{E}}(dy)^{(0)}(s)_{11}&{\textbf{E}}(dy)^{(0)}(s)_{12}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]{\textbf{T}}_{20}\end{array}\right] \times({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})dy.\end{eqnarray}
\begin{eqnarray}{\textbf{E}}(dy)^{(0)}(s)_{10}&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{E}}(dy)^{(0)}(s)_{11}&{\textbf{E}}(dy)^{(0)}(s)_{12}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]{\textbf{T}}_{20}\end{array}\right] \times({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})dy.\end{eqnarray}
In the next lemma, we derive expressions for ![]() ${\textbf{E}}(dy)^{(x)}(s)$,
${\textbf{E}}(dy)^{(x)}(s)$, ![]() $x>0$. The formal proof of this lemma was already given by Ahn and Ramaswami [Reference Ahn and Ramaswami5]. However, since the lemma is crucial to all of the remaining analysis, we include its proof for completeness.
$x>0$. The formal proof of this lemma was already given by Ahn and Ramaswami [Reference Ahn and Ramaswami5]. However, since the lemma is crucial to all of the remaining analysis, we include its proof for completeness.
Lemma 3. For ![]() $x>0$ we have
$x>0$ we have
 \begin{eqnarray}{\textbf{E}}(dy)^{(x)}(s)_{21}&\,=\,&\int_{z=0}^{\min\{x,y\}}e^{{\textbf{D}}(s)(x-z)}{\textbf{Q}}_{21}(s)e^{{\textbf{K}}(s)(y-z)}{\textbf{C}}_1^{-1}dzdy,\nonumber\\[7pt]
{\textbf{E}}(dy)^{(x)}(s)_{22}&\,=\,&{\textbf{E}}(dy)^{(x)}(s)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}+e^{{\textbf{D}}(s)(x-y)}{\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y<x\}dy,\nonumber\\[7pt]
{\textbf{E}}(dy)^{(x)}(s)_{20}&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{E}}(dy)^{(x)}(s)_{21}&{\textbf{E}}(dy)^{(x)}(s)_{22}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[7pt]
{\textbf{T}}_{20}\end{array}\right] \times({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})dy,\nonumber\\[7pt]
{\textbf{E}}(dy)^{(x)}(s)_{11}&\,=\,&{\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{21}+e^{{\textbf{K}}(s)(y-x)}{\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy,\nonumber\\[7pt]{\textbf{E}}(dy)^{(x)}(s)_{12}&\,=\,&{\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{22}+e^{{\textbf{K}}(s)(y-x)}{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y> x\}dy,\nonumber\\[7pt]{\textbf{E}}(dy)^{(x)}(s)_{10}&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{E}}(dy)^{(x)}(s)_{11}&{\textbf{E}}(dy)^{(x)}(s)_{12}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[7pt]{\textbf{T}}_{20}\end{array}\right] \times({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})dy.\end{eqnarray}
\begin{eqnarray}{\textbf{E}}(dy)^{(x)}(s)_{21}&\,=\,&\int_{z=0}^{\min\{x,y\}}e^{{\textbf{D}}(s)(x-z)}{\textbf{Q}}_{21}(s)e^{{\textbf{K}}(s)(y-z)}{\textbf{C}}_1^{-1}dzdy,\nonumber\\[7pt]
{\textbf{E}}(dy)^{(x)}(s)_{22}&\,=\,&{\textbf{E}}(dy)^{(x)}(s)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}+e^{{\textbf{D}}(s)(x-y)}{\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y<x\}dy,\nonumber\\[7pt]
{\textbf{E}}(dy)^{(x)}(s)_{20}&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{E}}(dy)^{(x)}(s)_{21}&{\textbf{E}}(dy)^{(x)}(s)_{22}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[7pt]
{\textbf{T}}_{20}\end{array}\right] \times({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})dy,\nonumber\\[7pt]
{\textbf{E}}(dy)^{(x)}(s)_{11}&\,=\,&{\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{21}+e^{{\textbf{K}}(s)(y-x)}{\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy,\nonumber\\[7pt]{\textbf{E}}(dy)^{(x)}(s)_{12}&\,=\,&{\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{22}+e^{{\textbf{K}}(s)(y-x)}{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y> x\}dy,\nonumber\\[7pt]{\textbf{E}}(dy)^{(x)}(s)_{10}&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{E}}(dy)^{(x)}(s)_{11}&{\textbf{E}}(dy)^{(x)}(s)_{12}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[7pt]{\textbf{T}}_{20}\end{array}\right] \times({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})dy.\end{eqnarray}
Proof. The expressions for ![]() ${\textbf{E}}(dy)^{(x)}(s)_{10}$ and
${\textbf{E}}(dy)^{(x)}(s)_{10}$ and ![]() ${\textbf{E}}(dy)^{(x)}(s)_{20}$ follow from the argument in the proof of Lemma 2. Furthermore, by partitioning the sample paths, since the process may visit level y after returning to level x first, or without hitting level x at all, we have
${\textbf{E}}(dy)^{(x)}(s)_{20}$ follow from the argument in the proof of Lemma 2. Furthermore, by partitioning the sample paths, since the process may visit level y after returning to level x first, or without hitting level x at all, we have
 \begin{eqnarray}{\textbf{E}}(dy)^{(x)}(s)_{11}&\,=\,&{\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{21}+{\textbf{E}}(d(y-x))^{(0)}(s)_{11}{\boldsymbol{1}}\{y>x\}dy,\nonumber\\[4pt]{\textbf{E}}(dy)^{(x)}(s)_{12}&\,=\,&{\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{22}+{\textbf{E}}(d(y-x))^{(0)}(s)_{12}{\boldsymbol{1}}\{y>x\}dy,\end{eqnarray}
\begin{eqnarray}{\textbf{E}}(dy)^{(x)}(s)_{11}&\,=\,&{\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{21}+{\textbf{E}}(d(y-x))^{(0)}(s)_{11}{\boldsymbol{1}}\{y>x\}dy,\nonumber\\[4pt]{\textbf{E}}(dy)^{(x)}(s)_{12}&\,=\,&{\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{22}+{\textbf{E}}(d(y-x))^{(0)}(s)_{12}{\boldsymbol{1}}\{y>x\}dy,\end{eqnarray}
and so the expressions for ![]() ${\textbf{E}}(dy)^{(x)}(s)_{11}$ and
${\textbf{E}}(dy)^{(x)}(s)_{11}$ and ![]() ${\textbf{E}}(dy)^{(x)}(s)_{12}$ follow from Lemma 2.
${\textbf{E}}(dy)^{(x)}(s)_{12}$ follow from Lemma 2.
Next, we consider ![]() ${\textbf{E}}(dy)^{(x)}(s)_{22}$. For
${\textbf{E}}(dy)^{(x)}(s)_{22}$. For ![]() $x>0$, define a matrix
$x>0$, define a matrix ![]() ${\textbf{G}}(x,t)=[G(x,t)_{kj}]$ such that for
${\textbf{G}}(x,t)=[G(x,t)_{kj}]$ such that for ![]() $k,j\in\mathcal{S}$,
$k,j\in\mathcal{S}$,
is the probability that, given that the process starts from level x in phase k, it first hits level zero by time t, and does so in phase j. We partition ![]() ${\textbf{G}}(x,t)$ according to
${\textbf{G}}(x,t)$ according to ![]() $\mathcal{S}_1\cup\mathcal{S}_2$ as
$\mathcal{S}_1\cup\mathcal{S}_2$ as
 \begin{equation}{\textbf{G}}(x,t)=\left[\begin{array}{c@{\quad}c}{\boldsymbol{0}}&{\textbf{G}}(x,t)_{12}\\[4pt]{\boldsymbol{0}}&{\textbf{G}}(x,t)_{22}\end{array}\right].\end{equation}
\begin{equation}{\textbf{G}}(x,t)=\left[\begin{array}{c@{\quad}c}{\boldsymbol{0}}&{\textbf{G}}(x,t)_{12}\\[4pt]{\boldsymbol{0}}&{\textbf{G}}(x,t)_{22}\end{array}\right].\end{equation}
Also, define ![]() $\widetilde{\textbf{G}}(x,s)=\int_{t=0}^{\infty}e^{-s t}d{\textbf{G}}(x,t)$, which we partition in an analogous manner.
$\widetilde{\textbf{G}}(x,s)=\int_{t=0}^{\infty}e^{-s t}d{\textbf{G}}(x,t)$, which we partition in an analogous manner.
The expression for ![]() ${\textbf{E}}(dy)^{(x)}(s)_{22}$ then follows from partitioning the sample paths. The process can visit level y in some phase in
${\textbf{E}}(dy)^{(x)}(s)_{22}$ then follows from partitioning the sample paths. The process can visit level y in some phase in ![]() $\mathcal{S}_2$ directly after a visit to level y in some phase in
$\mathcal{S}_2$ directly after a visit to level y in some phase in ![]() $\mathcal{S}_1$, or without visiting level y in some phase in
$\mathcal{S}_1$, or without visiting level y in some phase in ![]() $\mathcal{S}_1$ at all, and so we take the sum of expressions corresponding to these two possibilities, which gives
$\mathcal{S}_1$ at all, and so we take the sum of expressions corresponding to these two possibilities, which gives
The result follows since by [Reference Bean, O’Reilly and Taylor16], ![]() $\widetilde{\textbf{G}}(x-y,s)=e^{{\textbf{D}}(s)(x-y)}$.
$\widetilde{\textbf{G}}(x-y,s)=e^{{\textbf{D}}(s)(x-y)}$.
Finally, we consider ![]() ${\textbf{E}}(dy)^{(x)}(s)_{21}$. Define
${\textbf{E}}(dy)^{(x)}(s)_{21}$. Define
Note that, given that the process starts with ![]() $X(0)=x$,
$X(0)=x$, ![]() $\varphi(0)=i$, for the process to end with
$\varphi(0)=i$, for the process to end with ![]() $X(t)\in dy$,
$X(t)\in dy$, ![]() $\varphi(t)=j$, with a taboo
$\varphi(t)=j$, with a taboo ![]() $\theta(0)>t$, one of the following two alternatives must hold.
$\theta(0)>t$, one of the following two alternatives must hold.
The first alternative is that ![]() $y\geq x$. In this case, the following occurs:
$y\geq x$. In this case, the following occurs:
• First, given
 $X(0)=x$,
$X(0)=x$,  $\varphi(0)=i$, the process must reach some infimum
$\varphi(0)=i$, the process must reach some infimum  $\underline{X}(t)=z\in(0,x]$ at some time
$\underline{X}(t)=z\in(0,x]$ at some time  $u\in[0,t]$, in some phase in
$u\in[0,t]$, in some phase in  $\mathcal{S}_2$, with the corresponding density recorded by the matrix
$\mathcal{S}_2$, with the corresponding density recorded by the matrix  ${\textbf{G}}_{22}(x-z,u)$. This is followed by an instantaneous transition to some phase k in
${\textbf{G}}_{22}(x-z,u)$. This is followed by an instantaneous transition to some phase k in  $\mathcal{S}_1$ according to the rate recorded by the block matrix
$\mathcal{S}_1$ according to the rate recorded by the block matrix  ${\textbf{Q}}_{21}$ of the fluid generator Q, by the physical interpretation of Q in [Reference Bean, O’Reilly and Taylor16]. The corresponding density of this occurring is therefore
${\textbf{Q}}_{21}$ of the fluid generator Q, by the physical interpretation of Q in [Reference Bean, O’Reilly and Taylor16]. The corresponding density of this occurring is therefore  $[{\textbf{G}}_{22}(x-z,u){\textbf{Q}}_{21}]_{ik}$.
$[{\textbf{G}}_{22}(x-z,u){\textbf{Q}}_{21}]_{ik}$.-
• Next, starting from level z in phase k at time u, the process must remain above level z during the time interval [u,t], ending in some level y in phase j at time t. The corresponding density of this occurring is
 $[\boldsymbol{\phi}(y-z,t-u)]_{kj}$.
$[\boldsymbol{\phi}(y-z,t-u)]_{kj}$.
Consequently, the LST of this alternative is
 \begin{eqnarray*}&&{\int_{z=0}^x\int_{t=0}^{\infty}\int_{u=0}^te^{-s t}{\textbf{G}}_{22}(x-z,u){\textbf{Q}}_{21}(s)\boldsymbol{\phi}(y-z,t-u)_{11}dudtdz}\\[4pt]
&&\,=\,\int_{z=0}^x\int_{u=0}^{\infty}\int_{t=u}^{\infty}e^{-s u}{\textbf{G}}_{22}(x-z,u){\textbf{Q}}_{21}(s)e^{-s (t-u)}\boldsymbol{\phi}(y-z,t-u)_{11}dudtdz\\[4pt]
&&\,=\,\int_{z=0}^x\left(\int_{u=0}^{\infty}e^{-s u}{\textbf{G}}_{22}(x-z,u)du\right){\textbf{Q}}_{21}(s)\left(\int_{t=0}^{\infty}e^{-s t}\boldsymbol{\phi}(y-z,t)_{11}dt\right)dz\\[4pt]
&&\,=\,\int_{z=0}^xe^{{\textbf{D}}(s)(x-z)}{\textbf{Q}}_{21}(s)e^{{\textbf{K}}(s)(y-z)}dz.\end{eqnarray*}
\begin{eqnarray*}&&{\int_{z=0}^x\int_{t=0}^{\infty}\int_{u=0}^te^{-s t}{\textbf{G}}_{22}(x-z,u){\textbf{Q}}_{21}(s)\boldsymbol{\phi}(y-z,t-u)_{11}dudtdz}\\[4pt]
&&\,=\,\int_{z=0}^x\int_{u=0}^{\infty}\int_{t=u}^{\infty}e^{-s u}{\textbf{G}}_{22}(x-z,u){\textbf{Q}}_{21}(s)e^{-s (t-u)}\boldsymbol{\phi}(y-z,t-u)_{11}dudtdz\\[4pt]
&&\,=\,\int_{z=0}^x\left(\int_{u=0}^{\infty}e^{-s u}{\textbf{G}}_{22}(x-z,u)du\right){\textbf{Q}}_{21}(s)\left(\int_{t=0}^{\infty}e^{-s t}\boldsymbol{\phi}(y-z,t)_{11}dt\right)dz\\[4pt]
&&\,=\,\int_{z=0}^xe^{{\textbf{D}}(s)(x-z)}{\textbf{Q}}_{21}(s)e^{{\textbf{K}}(s)(y-z)}dz.\end{eqnarray*}
The second alternative is that ![]() $y<x$. The LST of this alternative, by an argument similar to the above, is
$y<x$. The LST of this alternative, by an argument similar to the above, is
Taking the sum of the expressions corresponding to the two alternatives and right-multiplying by ![]() ${\textbf{C}}_1^{-1}$ results in the integral expression for
${\textbf{C}}_1^{-1}$ results in the integral expression for ![]() ${\textbf{E}}(dy)^{(x)}(s)_{21}$.
${\textbf{E}}(dy)^{(x)}(s)_{21}$.
Remark 2. Consider
where ![]() ${\textbf{X}}=\int_{y=0}^{\infty}{\textbf{X}}(y)dy$, and
${\textbf{X}}=\int_{y=0}^{\infty}{\textbf{X}}(y)dy$, and
Then, by integration by parts in (39), ![]() ${\textbf{X}}(y)$ is the solution of
${\textbf{X}}(y)$ is the solution of
and by integrating (40), X is the solution of
 \begin{eqnarray} {\textbf{D}}(s){\textbf{X}}+{\textbf{X}}{\textbf{K}}(s)&\,=\,&e^{{\textbf{D}}(s)(x)}{\textbf{Q}}_{21}(s)({-}{\textbf{K}}(s)^{-1})-({-}{\textbf{D}}(s)^{-1}){\textbf{Q}}_{21}(s)\nonumber\\[4pt]
&&+\,({-}{\textbf{D}}(s)^{-1})e^{{\textbf{D}}(s)(x)}{\textbf{Q}}_{21}(s)+{\textbf{Q}}_{21}(s){\textbf{K}}(s)^{-1}. \end{eqnarray}
\begin{eqnarray} {\textbf{D}}(s){\textbf{X}}+{\textbf{X}}{\textbf{K}}(s)&\,=\,&e^{{\textbf{D}}(s)(x)}{\textbf{Q}}_{21}(s)({-}{\textbf{K}}(s)^{-1})-({-}{\textbf{D}}(s)^{-1}){\textbf{Q}}_{21}(s)\nonumber\\[4pt]
&&+\,({-}{\textbf{D}}(s)^{-1})e^{{\textbf{D}}(s)(x)}{\textbf{Q}}_{21}(s)+{\textbf{Q}}_{21}(s){\textbf{K}}(s)^{-1}. \end{eqnarray}
3. Approach
The key idea is to write each of ![]() ${\textbf{E}}(dy)^{(x)}(s)$ and
${\textbf{E}}(dy)^{(x)}(s)$ and ![]() ${\textbf{E}}^{(x)}(s)$ in the form
${\textbf{E}}^{(x)}(s)$ in the form
and then apply the Heaviside principle in order to evaluate (10). In this section, we summarise the relevant mathematical background required for this analysis.
Consider a function ![]() $f:\mathbb{R}\to\mathbb{R}$. Let
$f:\mathbb{R}\to\mathbb{R}$. Let ![]() $\tilde f(s):=\int_0^\infty e^{-s x}f(x)\ dx$ for
$\tilde f(s):=\int_0^\infty e^{-s x}f(x)\ dx$ for ![]() $s\in \mathbb{R}$ be its Laplace transform. Consider the singularities of
$s\in \mathbb{R}$ be its Laplace transform. Consider the singularities of ![]() $\tilde{f}(s)$. We assume that one with the largest strictly negative real part is real, and we denote it by
$\tilde{f}(s)$. We assume that one with the largest strictly negative real part is real, and we denote it by ![]() $s^*<0$. Notice that this yields the integrability of
$s^*<0$. Notice that this yields the integrability of ![]() $\int_0^\infty|f(x)|\ dx$. The inversion formula reads
$\int_0^\infty|f(x)|\ dx$. The inversion formula reads
for some (and then any) ![]() $a>s^*$.
$a>s^*$.
We now focus on a class of theorems that infer the tail behaviour of a function from its Laplace transform, commonly referred to as Tauberian theorems. Importantly, the behaviour of the Laplace transform around the singularity ![]() $s^*$ plays a crucial role here. The following heuristic principle given in [Reference Abate and Whitt1] is often relied upon. Suppose that for
$s^*$ plays a crucial role here. The following heuristic principle given in [Reference Abate and Whitt1] is often relied upon. Suppose that for ![]() $s^*$, some constants K and C, and a non-integer
$s^*$, some constants K and C, and a non-integer ![]() $q > 0$,
$q > 0$,
Then
where ![]() $\Gamma(\cdot)$ is the gamma function. Below we specify conditions under which this relation can be rigorously proven. Later in our paper we apply it in the specific case that
$\Gamma(\cdot)$ is the gamma function. Below we specify conditions under which this relation can be rigorously proven. Later in our paper we apply it in the specific case that ![]() $q=1/2$; recall that
$q=1/2$; recall that ![]() $\Gamma({-}1/2)=-2\sqrt{\pi}$.
$\Gamma({-}1/2)=-2\sqrt{\pi}$.
A formal justification of the above relation can be found in Doetsch [Reference Doetsch22, Theorem 37.1]. Following Miyazawa and Rolski [Reference Miyazawa and Rolski41], we consider the following specific form. For this we first recall the concept of the ![]() $\mathfrak{W}$-contour with a half-angle of opening
$\mathfrak{W}$-contour with a half-angle of opening ![]() $\pi/2<\psi\le \pi$, as depicted in [Reference Doetsch22, Figure 30, p. 240]; also,
$\pi/2<\psi\le \pi$, as depicted in [Reference Doetsch22, Figure 30, p. 240]; also, ![]() ${\mathscr G}_{\alpha}(\psi)$ is the region between the contour
${\mathscr G}_{\alpha}(\psi)$ is the region between the contour ![]() $\mathfrak W$ and the line
$\mathfrak W$ and the line ![]() $\Re(z)=0$. More precisely,
$\Re(z)=0$. More precisely,
where ![]() $\arg z$ is the principal part of the argument of the complex number z. In the following theorem, conditions are identified such that the above principle holds; we refer to this as Heaviside’s operational principle, or simply the Heaviside principle.
$\arg z$ is the principal part of the argument of the complex number z. In the following theorem, conditions are identified such that the above principle holds; we refer to this as Heaviside’s operational principle, or simply the Heaviside principle.
Theorem 1. (Heaviside principle) Suppose that for ![]() $\tilde f:\mathbb{C}\to \mathbb{C}$ and
$\tilde f:\mathbb{C}\to \mathbb{C}$ and ![]() $s^* < 0$ the following three conditions hold:
$s^* < 0$ the following three conditions hold:
(A1)
 $\tilde f(\cdot)$ is analytic in a region
$\tilde f(\cdot)$ is analytic in a region  ${\mathscr G}_{s^*}(\psi)$ for some
${\mathscr G}_{s^*}(\psi)$ for some  $\pi/2<\psi\le \pi$;
$\pi/2<\psi\le \pi$;(A2)
 $\tilde f(s) \to 0$ as
$\tilde f(s) \to 0$ as  $|s| \to \infty$ with
$|s| \to \infty$ with  $s \in {\mathscr G}_{s^*}(\psi)$;
$s \in {\mathscr G}_{s^*}(\psi)$;(A3) for some constants K and C, and a non-integer
 $q>0$,
(47)where
$q>0$,
(47)where \begin{eqnarray} \tilde f(s)=K - C (s-s^*)^{q}+o((s-s^*)^{q}), \end{eqnarray}
\begin{eqnarray} \tilde f(s)=K - C (s-s^*)^{q}+o((s-s^*)^{q}), \end{eqnarray}
 ${\mathscr G}_{s^*}(\psi)\ni s \to s^*$.
${\mathscr G}_{s^*}(\psi)\ni s \to s^*$.
Then
as ![]() $x\to\infty$.
$x\to\infty$.
We now discuss when the assumption (A1) is satisfied. To check that the Laplace transform ![]() $\tilde{f}(\cdot)$ is analytic in the region
$\tilde{f}(\cdot)$ is analytic in the region ![]() $\mathscr G_{s^*}(\psi)$, we can use the concept of semiexponentiality of f (see [30, p. 314]).
$\mathscr G_{s^*}(\psi)$, we can use the concept of semiexponentiality of f (see [30, p. 314]).
Definition 2. (Semiexponentiality) f is said to be semiexponential if for some ![]() $0< \phi\le\pi/2$ and all
$0< \phi\le\pi/2$ and all ![]() $-\phi\le {\vartheta}\le \phi$ there exists finite and strictly negative
$-\phi\le {\vartheta}\le \phi$ there exists finite and strictly negative ![]() $\gamma({\vartheta})$, defined as the infimum of all a such that
$\gamma({\vartheta})$, defined as the infimum of all a such that
for all sufficiently large r.
Relying on this concept, the following sufficient condition for (A1) applies.
Proposition 1. [Reference Henrici30, Theorem 10.9f] Suppose that f is semiexponential with ![]() $\gamma({\vartheta})$ fulfilling the following conditions: (i)
$\gamma({\vartheta})$ fulfilling the following conditions: (i) ![]() $\gamma=\gamma(0)<0$, (ii)
$\gamma=\gamma(0)<0$, (ii) ![]() $\gamma({\vartheta})\geq\gamma(0)$ in a neighborhood of
$\gamma({\vartheta})\geq\gamma(0)$ in a neighborhood of ![]() ${\vartheta}=0$, and (iii)
${\vartheta}=0$, and (iii) ![]() $\gamma({\vartheta})$ is smooth. Then (A1) is satisfied.
$\gamma({\vartheta})$ is smooth. Then (A1) is satisfied.
Note that by Lemma 3, all assumptions of Proposition 1 are satisfied, and we can apply the Heaviside principle given in Theorem 1 for ![]() ${\textbf{E}}(dy)^{(x)}(s)$ and
${\textbf{E}}(dy)^{(x)}(s)$ and ![]() ${\textbf{E}}^{(x)}(s)$.
${\textbf{E}}^{(x)}(s)$.
4. Application of the Heaviside principle
By Section 2, ![]() ${\textbf{E}}(dy)^{(x)}(s)$ and
${\textbf{E}}(dy)^{(x)}(s)$ and ![]() ${\textbf{E}}^{(x)}(s)$ are expressed in terms of
${\textbf{E}}^{(x)}(s)$ are expressed in terms of ![]() ${\textbf{Q}}(s)$ and
${\textbf{Q}}(s)$ and ![]() ${\boldsymbol{\Psi}}(s)$, and so we derive the expansion around
${\boldsymbol{\Psi}}(s)$, and so we derive the expansion around ![]() $s^*$ for each of them first.
$s^*$ for each of them first.
Consider ![]() ${\boldsymbol{\Psi}}(s)$ as defined in (19). We have
${\boldsymbol{\Psi}}(s)$ as defined in (19). We have ![]() ${\boldsymbol{\Psi}}(s)=\int_{t=0}^{\infty}e^{-st}\boldsymbol{\psi}(t)dt<\infty$ for all
${\boldsymbol{\Psi}}(s)=\int_{t=0}^{\infty}e^{-st}\boldsymbol{\psi}(t)dt<\infty$ for all ![]() $s\geq 0$ by [Reference Bean, O’Reilly and Taylor16, Reference Bean, O’Reilly and Taylor17]. Define the singularity
$s\geq 0$ by [Reference Bean, O’Reilly and Taylor16, Reference Bean, O’Reilly and Taylor17]. Define the singularity
where the existence of ![]() $s^*$ follows from [Reference Doetsch22, Theorem 3.3, p. 15].
$s^*$ follows from [Reference Doetsch22, Theorem 3.3, p. 15].
Consider matrices ![]() ${\textbf{K}}(s)$ and
${\textbf{K}}(s)$ and ![]() ${\textbf{D}}(s)$ as defined in (20), and recall that
${\textbf{D}}(s)$ as defined in (20), and recall that ![]() $sp({\textbf{K}}(s))\cap sp({-}{\textbf{D}}(s))=\varnothing$ for all
$sp({\textbf{K}}(s))\cap sp({-}{\textbf{D}}(s))=\varnothing$ for all ![]() $s\geq 0$. Define
$s\geq 0$. Define
whenever the maximum exists. The definition implies that ![]() ${\textbf{K}}(\delta^*)$ and
${\textbf{K}}(\delta^*)$ and ![]() $({-}{\textbf{D}}(\delta^*))$ have a common eigenvalue.
$({-}{\textbf{D}}(\delta^*))$ have a common eigenvalue.
Lemma 4. We have ![]() $s^*=\delta^*$.
$s^*=\delta^*$.
Proof. Consider Equation (21), and for all s for which ![]() ${\textbf{Q}}(s)$ exists, define the following function of
${\textbf{Q}}(s)$ exists, define the following function of ![]() ${\textbf{X}}=[x_{ij}]_{i\in\mathcal{S}_1,j\in\mathcal{S}_2}$:
${\textbf{X}}=[x_{ij}]_{i\in\mathcal{S}_1,j\in\mathcal{S}_2}$:
For ![]() ${\textbf{X}}\geq {\boldsymbol{0}}$,
${\textbf{X}}\geq {\boldsymbol{0}}$, ![]() ${\textbf{X}}\not= {\boldsymbol{0}}$, we have
${\textbf{X}}\not= {\boldsymbol{0}}$, we have
 \begin{eqnarray} \frac{d}{ds}g_s({\textbf{X}})&\,=\,& -{\textbf{C}}^{-1}_1{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-2}{\textbf{T}}_{02} {\textbf{X}} -{\textbf{C}}^{-1}_1\left({\textbf{I}}+{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-2}{\textbf{T}}_{01}\right) {\textbf{X}} \nonumber\\[4pt] && -{\textbf{X}} {\textbf{C}}^{-1}_2\left({\textbf{I}}+{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-2}{\textbf{T}}_{02}\right) - {\textbf{X}} {\textbf{C}}^{-1}_2{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-2}{\textbf{T}}_{01} {\textbf{X}} \nonumber\\[4pt] &<&{\boldsymbol{0}}, \end{eqnarray}
\begin{eqnarray} \frac{d}{ds}g_s({\textbf{X}})&\,=\,& -{\textbf{C}}^{-1}_1{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-2}{\textbf{T}}_{02} {\textbf{X}} -{\textbf{C}}^{-1}_1\left({\textbf{I}}+{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-2}{\textbf{T}}_{01}\right) {\textbf{X}} \nonumber\\[4pt] && -{\textbf{X}} {\textbf{C}}^{-1}_2\left({\textbf{I}}+{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-2}{\textbf{T}}_{02}\right) - {\textbf{X}} {\textbf{C}}^{-1}_2{\textbf{T}}_{10}({\textbf{T}}_{00}-s{\textbf{I}})^{-2}{\textbf{T}}_{01} {\textbf{X}} \nonumber\\[4pt] &<&{\boldsymbol{0}}, \end{eqnarray}
since ![]() $({\textbf{T}}_{00}-s{\textbf{I}})^{-2}=\left(\int_{t=0}^{\infty}e^{-st}e^{{\textbf{T}}_{00}t}dy\right)^2>{\boldsymbol{0}}$, and so
$({\textbf{T}}_{00}-s{\textbf{I}})^{-2}=\left(\int_{t=0}^{\infty}e^{-st}e^{{\textbf{T}}_{00}t}dy\right)^2>{\boldsymbol{0}}$, and so ![]() $g_s({\textbf{X}})$ is a decreasing function of s.
$g_s({\textbf{X}})$ is a decreasing function of s.
Also, define the functions ![]() $g_s^{(u,v)}({\textbf{X}})=[g_s({\textbf{X}})]_{uv}$, for
$g_s^{(u,v)}({\textbf{X}})=[g_s({\textbf{X}})]_{uv}$, for ![]() $u\in\mathcal{S}_1$,
$u\in\mathcal{S}_1$, ![]() $v\in\mathcal{S}_2$, by
$v\in\mathcal{S}_2$, by
each of these corresponds to an ![]() $|\mathcal{S}_1|\times|\mathcal{S}_2|$-dimensional smooth quadratic surface. The matrix equation (21) is equivalent to the system of
$|\mathcal{S}_1|\times|\mathcal{S}_2|$-dimensional smooth quadratic surface. The matrix equation (21) is equivalent to the system of ![]() $|\mathcal{S}_1|\times|\mathcal{S}_2|$ quadratic polynomial equations given by
$|\mathcal{S}_1|\times|\mathcal{S}_2|$ quadratic polynomial equations given by
each corresponding to the (u,v)th level curve.
Now, by Lemma 1, for all ![]() $s\geq s^*$,
$s\geq s^*$, ![]() ${\boldsymbol{\Psi}}(s)$ is a solution of
${\boldsymbol{\Psi}}(s)$ is a solution of ![]() $g_{s}({\textbf{X}})={\boldsymbol{0}}$ and so is an intersection point of all level curves (53).
$g_{s}({\textbf{X}})={\boldsymbol{0}}$ and so is an intersection point of all level curves (53).
Some other solutions to ![]() $g_{s}({\textbf{X}})={\boldsymbol{0}}$ may exist. For all real s, we denote by
$g_{s}({\textbf{X}})={\boldsymbol{0}}$ may exist. For all real s, we denote by ![]() ${\textbf{X}}(s)$ the family of solutions that correspond to the intersection point
${\textbf{X}}(s)$ the family of solutions that correspond to the intersection point ![]() ${\boldsymbol{\Psi}}(s)$. That is, when
${\boldsymbol{\Psi}}(s)$. That is, when ![]() $s\geq s^*$,
$s\geq s^*$, ![]() ${\textbf{X}}(s)={\boldsymbol{\Psi}}(s)$, and if
${\textbf{X}}(s)={\boldsymbol{\Psi}}(s)$, and if ![]() ${\textbf{X}}(s)$ exists for
${\textbf{X}}(s)$ exists for ![]() $s<s^*$ in some neighbourhood of
$s<s^*$ in some neighbourhood of ![]() $s^*$, then
$s^*$, then ![]() ${\textbf{X}}(s)$ must be a continuous function of s in this neighbourhood, by the monotonicity and continuity of
${\textbf{X}}(s)$ must be a continuous function of s in this neighbourhood, by the monotonicity and continuity of ![]() $g_s({\textbf{X}})$.
$g_s({\textbf{X}})$.
So suppose that there exist solutions ![]() ${\textbf{X}}(s)$ to
${\textbf{X}}(s)$ to ![]() $g_{s}({\textbf{X}})={\boldsymbol{0}}$ for
$g_{s}({\textbf{X}})={\boldsymbol{0}}$ for ![]() $s<s^*$ in some neighbourhood of
$s<s^*$ in some neighbourhood of ![]() $s^*$, and that
$s^*$, and that ![]() $\lim_{s\uparrow s^*}{\textbf{X}}(s)={\boldsymbol{\Psi}}(s^*)$. Then, since
$\lim_{s\uparrow s^*}{\textbf{X}}(s)={\boldsymbol{\Psi}}(s^*)$. Then, since ![]() ${\boldsymbol{\Psi}}(s^*)>{\boldsymbol{0}}$, there exists
${\boldsymbol{\Psi}}(s^*)>{\boldsymbol{0}}$, there exists ![]() ${\textbf{W}}>{\boldsymbol{0}}$ with
${\textbf{W}}>{\boldsymbol{0}}$ with ![]() $g_{s}({\textbf{W}})={\boldsymbol{0}}$ for some
$g_{s}({\textbf{W}})={\boldsymbol{0}}$ for some ![]() $s<s^*$ with
$s<s^*$ with ![]() $sp({\textbf{Q}}_{11}(s))\cap sp({-}{\textbf{Q}}_{22}(s))=\varnothing$ (since the spectra
$sp({\textbf{Q}}_{11}(s))\cap sp({-}{\textbf{Q}}_{22}(s))=\varnothing$ (since the spectra ![]() $sp({\textbf{Q}}_{11}(s))$ and
$sp({\textbf{Q}}_{11}(s))$ and ![]() $sp({-}{\textbf{Q}}_{22}(s))$ are discrete).
$sp({-}{\textbf{Q}}_{22}(s))$ are discrete).
Therefore, by [Reference Guo27, Theorem 2.3] and [Reference Bean, O’Reilly and Taylor17, Algorithm 1], we have ![]() ${\boldsymbol{\Psi}}(s)<\infty$ for such
${\boldsymbol{\Psi}}(s)<\infty$ for such ![]() $s<s^*$, and this contradicts the definition of
$s<s^*$, and this contradicts the definition of ![]() $s^*$. Consequently,
$s^*$. Consequently, ![]() ${\textbf{X}}(s)$ does not exist for
${\textbf{X}}(s)$ does not exist for ![]() $s<s^*$, and so the level curves (53) must touch (have a common tangent line) at
$s<s^*$, and so the level curves (53) must touch (have a common tangent line) at ![]() $s=s^*$, but not at
$s=s^*$, but not at ![]() $s>s^*$.
$s>s^*$.
Define
and note that
 \begin{eqnarray} && { \nabla g_{s^*}^{(u,v)}(x_{ij},[x_{ij}^*]) = \frac{\partial}{\partial x_{ij}}g_{s^*}^{(u,v)}([x_{ij}])\Big|_{[x_{ij}^*]} } \nonumber \\[2pt]
&&\,=\, [{\textbf{Q}}_{11}(s^*)]_{ui}{\boldsymbol{1}}\{j=v\} +[{\textbf{Q}}_{22}(s^*)]_{jv}{\boldsymbol{1}}\{i=u\} +\sum_{k\in\mathcal{S}_2} [{\textbf{Q}}_{21}(s^*)]_{ki}\times x_{uk}^* {\boldsymbol{1}}\{j=v\} \nonumber\\
&&\quad \,+ \sum_{\ell\in\mathcal{S}_1}[{\textbf{Q}}_{21}(s^*)]_{j\ell}\times x_{\ell v}^*{\boldsymbol{1}}\{i=u\} \nonumber\\[2pt]
&&\,=\, [{\textbf{K}}(s^*)]_{ui}{\boldsymbol{1}}\{j=v\} +[{\textbf{D}}(s^*)]_{jv}{\boldsymbol{1}}\{i=u\} . \end{eqnarray}
\begin{eqnarray} && { \nabla g_{s^*}^{(u,v)}(x_{ij},[x_{ij}^*]) = \frac{\partial}{\partial x_{ij}}g_{s^*}^{(u,v)}([x_{ij}])\Big|_{[x_{ij}^*]} } \nonumber \\[2pt]
&&\,=\, [{\textbf{Q}}_{11}(s^*)]_{ui}{\boldsymbol{1}}\{j=v\} +[{\textbf{Q}}_{22}(s^*)]_{jv}{\boldsymbol{1}}\{i=u\} +\sum_{k\in\mathcal{S}_2} [{\textbf{Q}}_{21}(s^*)]_{ki}\times x_{uk}^* {\boldsymbol{1}}\{j=v\} \nonumber\\
&&\quad \,+ \sum_{\ell\in\mathcal{S}_1}[{\textbf{Q}}_{21}(s^*)]_{j\ell}\times x_{\ell v}^*{\boldsymbol{1}}\{i=u\} \nonumber\\[2pt]
&&\,=\, [{\textbf{K}}(s^*)]_{ui}{\boldsymbol{1}}\{j=v\} +[{\textbf{D}}(s^*)]_{jv}{\boldsymbol{1}}\{i=u\} . \end{eqnarray}
The tangent plane to the (u,v)th level curve (53) at ![]() ${\boldsymbol{\Psi}}(s^*)=[x_{ij}^*]$ is the solution to the equation
${\boldsymbol{\Psi}}(s^*)=[x_{ij}^*]$ is the solution to the equation
 \begin{eqnarray} 0&\,=\,& \sum_{i,j} \nabla g^{(u,v)}_{s^*}(x_{ij},[x_{ij}^*]) (x_{ij}-x_{ij}^*) \nonumber\\
&\,=\,&\sum_{i,j} \Big( [{\textbf{K}}(s^*)]_{ui}{\boldsymbol{1}}\{j=v\} +[{\textbf{D}}(s^*)]_{jv}{\boldsymbol{1}}\{i=u\} \Big) (x_{ij}-x_{ij}^*) \nonumber\\
&\,=\,& \sum_i[{\textbf{K}}(s^*)]_{ui}[{\textbf{X}}-{\boldsymbol{\Psi}}(s^*)]_{iv} +\sum_j [{\textbf{X}}-{\boldsymbol{\Psi}}(s^*)]_{uj}[{\textbf{D}}(s^*)]_{jv} \nonumber\\
&\,=\,& \left[ {\textbf{K}}(s^*)({\textbf{X}}-{\boldsymbol{\Psi}}(s^*)) +({\textbf{X}}-{\boldsymbol{\Psi}}(s^*)){\textbf{D}}(s^*)\right]_{uv}. \end{eqnarray}
\begin{eqnarray} 0&\,=\,& \sum_{i,j} \nabla g^{(u,v)}_{s^*}(x_{ij},[x_{ij}^*]) (x_{ij}-x_{ij}^*) \nonumber\\
&\,=\,&\sum_{i,j} \Big( [{\textbf{K}}(s^*)]_{ui}{\boldsymbol{1}}\{j=v\} +[{\textbf{D}}(s^*)]_{jv}{\boldsymbol{1}}\{i=u\} \Big) (x_{ij}-x_{ij}^*) \nonumber\\
&\,=\,& \sum_i[{\textbf{K}}(s^*)]_{ui}[{\textbf{X}}-{\boldsymbol{\Psi}}(s^*)]_{iv} +\sum_j [{\textbf{X}}-{\boldsymbol{\Psi}}(s^*)]_{uj}[{\textbf{D}}(s^*)]_{jv} \nonumber\\
&\,=\,& \left[ {\textbf{K}}(s^*)({\textbf{X}}-{\boldsymbol{\Psi}}(s^*)) +({\textbf{X}}-{\boldsymbol{\Psi}}(s^*)){\textbf{D}}(s^*)\right]_{uv}. \end{eqnarray}
From linear algebra, a matrix equation of the form ![]() ${\boldsymbol{0}}={\textbf{A}}{\textbf{X}}+{\textbf{X}}{\textbf{B}}$ has a nonzero solution if and only if A and
${\boldsymbol{0}}={\textbf{A}}{\textbf{X}}+{\textbf{X}}{\textbf{B}}$ has a nonzero solution if and only if A and ![]() $({-}{\textbf{B}})$ have a common eigenvalue (e.g. see [Reference Bhatia and Rosenthal18]). Therefore, the equation
$({-}{\textbf{B}})$ have a common eigenvalue (e.g. see [Reference Bhatia and Rosenthal18]). Therefore, the equation
has a solution ![]() ${\textbf{Z}}=[z_{ij}]\not= {\boldsymbol{\Psi}}(s^*)$ if and only if
${\textbf{Z}}=[z_{ij}]\not= {\boldsymbol{\Psi}}(s^*)$ if and only if ![]() ${\textbf{K}}(s^*)$ and
${\textbf{K}}(s^*)$ and ![]() $({-}{\textbf{D}}(s^*))$ have a common eigenvalue, in which case the tangent planes (56) to all level curves (53) at
$({-}{\textbf{D}}(s^*))$ have a common eigenvalue, in which case the tangent planes (56) to all level curves (53) at ![]() ${\boldsymbol{\Psi}}(s^*)$ intersect one another at a tangent line that goes through Z and
${\boldsymbol{\Psi}}(s^*)$ intersect one another at a tangent line that goes through Z and ![]() ${\boldsymbol{\Psi}}(s^*)$.
${\boldsymbol{\Psi}}(s^*)$.
That is, the level curves (53) touch if and only if ![]() $sp({\textbf{K}}(s^*))\cap sp({-}{\textbf{D}}(s^*))\not=\varnothing$. Hence,
$sp({\textbf{K}}(s^*))\cap sp({-}{\textbf{D}}(s^*))\not=\varnothing$. Hence, ![]() $s^*=\delta^*$.
$s^*=\delta^*$.
We now extend the result for ![]() $s>0$ in [Reference Bean, O’Reilly and Taylor16, Theorem 1] to all
$s>0$ in [Reference Bean, O’Reilly and Taylor16, Theorem 1] to all ![]() $s\geq s^*$.
$s\geq s^*$.
Corollary 4.1. For all ![]() $s\geq s^*$,
$s\geq s^*$, ![]() ${\boldsymbol{\Psi}}(s)$ is the minimum nonnegative solution of the Riccati equation (21).
${\boldsymbol{\Psi}}(s)$ is the minimum nonnegative solution of the Riccati equation (21).
Proof. Suppose ![]() $s\geq s^*$. Then
$s\geq s^*$. Then ![]() ${\textbf{Q}}_{11}(s)\leq {\textbf{K}}(s)={\textbf{Q}}_{11}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s)$ and
${\textbf{Q}}_{11}(s)\leq {\textbf{K}}(s)={\textbf{Q}}_{11}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s)$ and ![]() ${\textbf{Q}}_{22}(s)\leq {\textbf{D}}(s)={\textbf{Q}}_{22}(s)+{\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s)$, and so
${\textbf{Q}}_{22}(s)\leq {\textbf{D}}(s)={\textbf{Q}}_{22}(s)+{\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s)$, and so ![]() $sp({\textbf{Q}}_{11}(s))\cap sp({-}{\textbf{Q}}_{22}(s))=\varnothing$.
$sp({\textbf{Q}}_{11}(s))\cap sp({-}{\textbf{Q}}_{22}(s))=\varnothing$.
Therefore, by [Reference Guo27, Theorem 2.3] and [Reference Bean, O’Reilly and Taylor17, Algorithm 1], ![]() ${\boldsymbol{\Psi}}(s)$ is the minimum nonnegative solution of (21).
${\boldsymbol{\Psi}}(s)$ is the minimum nonnegative solution of (21).
In order to illustrate the theory, we consider the following simple example, which we will analyse as we develop the results throughout the paper.
Example 1. Let ![]() $\mathcal{S}=\{1,2\}$,
$\mathcal{S}=\{1,2\}$, ![]() $\mathcal{S}_1=\{1\}$,
$\mathcal{S}_1=\{1\}$, ![]() $\mathcal{S}_2=\{2\}$,
$\mathcal{S}_2=\{2\}$, ![]() $c_1=1$,
$c_1=1$, ![]() $c_2=-1$, and
$c_2=-1$, and
 \begin{eqnarray} {\textbf{T}} &\,=\,&\left[ \begin{array}{c@{\quad}c} {\textbf{T}}_{11}&{\textbf{T}}_{12}\\[4pt] {\textbf{T}}_{21}&{\textbf{T}}_{22} \end{array} \right] =\left[ \begin{array}{c@{\quad}c} -a&a\\[4pt] b&-b \end{array} \right], \end{eqnarray}
\begin{eqnarray} {\textbf{T}} &\,=\,&\left[ \begin{array}{c@{\quad}c} {\textbf{T}}_{11}&{\textbf{T}}_{12}\\[4pt] {\textbf{T}}_{21}&{\textbf{T}}_{22} \end{array} \right] =\left[ \begin{array}{c@{\quad}c} -a&a\\[4pt] b&-b \end{array} \right], \end{eqnarray}
 \begin{eqnarray} {\textbf{Q}}(s) &\,=\,&\left[ \begin{array}{c@{\quad}c} {\textbf{Q}}_{11}(s)&{\textbf{Q}}_{12}(s)\\[4pt] {\textbf{Q}}_{21}(s)&{\textbf{Q}}_{22}(s) \end{array} \right] =\left[ \begin{array}{c@{\quad}c} -a-s&a\\[4pt] b&-b-s \end{array} \right], \end{eqnarray}
\begin{eqnarray} {\textbf{Q}}(s) &\,=\,&\left[ \begin{array}{c@{\quad}c} {\textbf{Q}}_{11}(s)&{\textbf{Q}}_{12}(s)\\[4pt] {\textbf{Q}}_{21}(s)&{\textbf{Q}}_{22}(s) \end{array} \right] =\left[ \begin{array}{c@{\quad}c} -a-s&a\\[4pt] b&-b-s \end{array} \right], \end{eqnarray}
with ![]() $a>b>0$ so that the process is stable.
$a>b>0$ so that the process is stable.
Then ![]() ${\boldsymbol{\Psi}}(s)$ is the minimum nonnegative solution of (21), here equivalent to
${\boldsymbol{\Psi}}(s)$ is the minimum nonnegative solution of (21), here equivalent to
which has solutions provided ![]() $\Delta(s)=(a+b+2s)^2-4ab \geq 0$, that is, for all
$\Delta(s)=(a+b+2s)^2-4ab \geq 0$, that is, for all
 \begin{eqnarray} s\in \left({-}\infty, \frac{-(a+b)-2\sqrt{ab}}{2} \right] \cup\left[ \frac{-(a+b)+2\sqrt{ab}}{2}, +\infty\right) . \end{eqnarray}
\begin{eqnarray} s\in \left({-}\infty, \frac{-(a+b)-2\sqrt{ab}}{2} \right] \cup\left[ \frac{-(a+b)+2\sqrt{ab}}{2}, +\infty\right) . \end{eqnarray}
Since
it follows that ![]() ${\boldsymbol{\Psi}}(s)$ exists for all
${\boldsymbol{\Psi}}(s)$ exists for all ![]() $s\geq \frac{-(a+b)+2\sqrt{ab}}{2}$, and
$s\geq \frac{-(a+b)+2\sqrt{ab}}{2}$, and
Therefore,
and
Note that ![]() $s^*=\delta^*$.
$s^*=\delta^*$.
Lemma 5. For all ![]() $s>s^*$,
$s>s^*$,
where, for all ![]() $s> s^*$,
$s> s^*$,
and ![]() ${\textbf{A}}_{22}(s^*)=\lim_{s\downarrow s^*}{\textbf{A}}_{22}(s)<\infty$,
${\textbf{A}}_{22}(s^*)=\lim_{s\downarrow s^*}{\textbf{A}}_{22}(s)<\infty$, ![]() ${\textbf{A}}_{11}(s^*)=\lim_{s\downarrow s^*}{\textbf{A}}_{11}(s)<\infty$,
${\textbf{A}}_{11}(s^*)=\lim_{s\downarrow s^*}{\textbf{A}}_{11}(s)<\infty$, ![]() ${\textbf{A}}_{12}(s^*)=\lim_{s\downarrow s^*}$
${\textbf{A}}_{12}(s^*)=\lim_{s\downarrow s^*}$ ![]() ${\textbf{A}}_{12}(s)<\infty$, and
${\textbf{A}}_{12}(s)<\infty$, and ![]() ${\textbf{A}}_{21}(s^*)=\lim_{s\downarrow s^*}{\textbf{A}}_{21}(s)<\infty$.
${\textbf{A}}_{21}(s^*)=\lim_{s\downarrow s^*}{\textbf{A}}_{21}(s)<\infty$.
Proof. For all ![]() $s>s^*$,
$s>s^*$,
and so by (18),
which, with the notation ![]() ${\textbf{A}}_{22}(s)=-\frac{d}{ds}{\textbf{Q}}_{22}(s)$, implies
${\textbf{A}}_{22}(s)=-\frac{d}{ds}{\textbf{Q}}_{22}(s)$, implies
Next, since ![]() ${\boldsymbol{\Psi}}(s^*)<\infty$ by Lemma 4, we have
${\boldsymbol{\Psi}}(s^*)<\infty$ by Lemma 4, we have ![]() $\left({-}({\textbf{T}}_{00}-s^*{\textbf{I}})^{-1} \right)<\infty$ and
$\left({-}({\textbf{T}}_{00}-s^*{\textbf{I}})^{-1} \right)<\infty$ and ![]() $({\textbf{T}}_{00}-s^*{\textbf{I}})^{-2}<\infty$, which implies that
$({\textbf{T}}_{00}-s^*{\textbf{I}})^{-2}<\infty$, which implies that ![]() ${\textbf{A}}_{22}(s^*)<\infty$. Taking the limits as
${\textbf{A}}_{22}(s^*)<\infty$. Taking the limits as ![]() $s\downarrow s^*$ in (80) and substituting
$s\downarrow s^*$ in (80) and substituting ![]() $h=(s-s^*)$ gives
$h=(s-s^*)$ gives
The proofs for the remaining expressions are analogous.
For ![]() $s>s^*$, let
$s>s^*$, let
and, for ![]() $s\geq s^*$, let
$s\geq s^*$, let
noting that ![]() ${\textbf{U}}(s^*)$ exists by Lemma 5.
${\textbf{U}}(s^*)$ exists by Lemma 5.
Lemma 6. For ![]() $s>s^*$,
$s>s^*$, ![]() ${\boldsymbol{\Phi}}(s)$ is the unique solution of the equation
${\boldsymbol{\Phi}}(s)$ is the unique solution of the equation
Furthermore, ![]() ${\boldsymbol{\Phi}}(s^*)=\lim_{s\downarrow s^*}{\boldsymbol{\Phi}}(s)=-\infty$.
${\boldsymbol{\Phi}}(s^*)=\lim_{s\downarrow s^*}{\boldsymbol{\Phi}}(s)=-\infty$.
Proof. By Lemma 4, for all ![]() $s>s^*$,
$s>s^*$, ![]() ${\textbf{K}}(s)$ and
${\textbf{K}}(s)$ and ![]() $({-}{\textbf{D}}(s))$ have no common eigenvalues, and so by [Reference Laub38, Theorem 13.18], Equation (84) has a unique solution. We now show that
$({-}{\textbf{D}}(s))$ have no common eigenvalues, and so by [Reference Laub38, Theorem 13.18], Equation (84) has a unique solution. We now show that ![]() ${\boldsymbol{\Phi}} (s)$ is the solution of (84). Also see [Reference Bean, O’Reilly and Taylor16, Corollary 3]. Indeed, by taking derivatives with respect to s in Equation (21) for
${\boldsymbol{\Phi}} (s)$ is the solution of (84). Also see [Reference Bean, O’Reilly and Taylor16, Corollary 3]. Indeed, by taking derivatives with respect to s in Equation (21) for ![]() ${\boldsymbol{\Psi}}(s)$, we have
${\boldsymbol{\Psi}}(s)$, we have
 \begin{eqnarray}{\boldsymbol{0}}&\,=\,&\frac{d}{ds}\Big({\textbf{Q}}_{12}(s)+{\textbf{Q}}_{11}(s){\boldsymbol{\Psi}}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{22}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s)\Big)\nonumber\\[4pt]&\,=\,&-{\textbf{A}}_{12}(s)-{\textbf{A}}_{11}(s){\boldsymbol{\Psi}}(s)+{\textbf{Q}}_{11}(s){\boldsymbol{\Phi}}(s)-{\boldsymbol{\Psi}}(s){\textbf{A}}_{22}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{22}(s)\nonumber\\[4pt]&&+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s){\textbf{A}}_{21}(s){\boldsymbol{\Psi}}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Phi}}(s)\nonumber\\[4pt]&\,=\,&-{\textbf{U}}(s)+{\textbf{K}}(s){\boldsymbol{\Phi}} (s)+{\boldsymbol{\Phi}} (s){\textbf{D}}(s).\end{eqnarray}
\begin{eqnarray}{\boldsymbol{0}}&\,=\,&\frac{d}{ds}\Big({\textbf{Q}}_{12}(s)+{\textbf{Q}}_{11}(s){\boldsymbol{\Psi}}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{22}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s)\Big)\nonumber\\[4pt]&\,=\,&-{\textbf{A}}_{12}(s)-{\textbf{A}}_{11}(s){\boldsymbol{\Psi}}(s)+{\textbf{Q}}_{11}(s){\boldsymbol{\Phi}}(s)-{\boldsymbol{\Psi}}(s){\textbf{A}}_{22}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{22}(s)\nonumber\\[4pt]&&+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s){\textbf{A}}_{21}(s){\boldsymbol{\Psi}}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Phi}}(s)\nonumber\\[4pt]&\,=\,&-{\textbf{U}}(s)+{\textbf{K}}(s){\boldsymbol{\Phi}} (s)+{\boldsymbol{\Phi}} (s){\textbf{D}}(s).\end{eqnarray}
Also, ![]() ${\boldsymbol{\Phi}}(s)<{\boldsymbol{0}}$, since
${\boldsymbol{\Phi}}(s)<{\boldsymbol{0}}$, since
When ![]() $s=s^*$, however, by Lemma 4,
$s=s^*$, however, by Lemma 4, ![]() ${\textbf{K}}(s)$ and
${\textbf{K}}(s)$ and ![]() $({-}{\textbf{D}}(s))$ have a common eigenvalue, and so by [Reference Laub38, Theorem 13.18], Equation (84) does not have a unique solution.
$({-}{\textbf{D}}(s))$ have a common eigenvalue, and so by [Reference Laub38, Theorem 13.18], Equation (84) does not have a unique solution.
Finally, we show that ![]() $\lim_{s\downarrow s^*}{\boldsymbol{\Phi}}(s)=-\infty$. By standard methodology [Reference Laub38, Section 13.3], for
$\lim_{s\downarrow s^*}{\boldsymbol{\Phi}}(s)=-\infty$. By standard methodology [Reference Laub38, Section 13.3], for ![]() $s>s^*$, the unique solution to Equation (84) can be written in the form
$s>s^*$, the unique solution to Equation (84) can be written in the form
where ![]() $vec({\boldsymbol{\Phi}}(s))$ and
$vec({\boldsymbol{\Phi}}(s))$ and ![]() $vec({\textbf{U}}(s))$ are column vectors obtained by stacking the columns (from left to right) of the original matrices one under another,
$vec({\textbf{U}}(s))$ are column vectors obtained by stacking the columns (from left to right) of the original matrices one under another,
and the eigenvalues of ![]() ${\textbf{Z}}(s)$ are
${\textbf{Z}}(s)$ are ![]() $(\lambda_i-\mu_j)$, where
$(\lambda_i-\mu_j)$, where ![]() $\lambda_i$ are eigenvalues of
$\lambda_i$ are eigenvalues of ![]() ${\textbf{K}}(s)$ and
${\textbf{K}}(s)$ and ![]() $\mu_j$ are eigenvalues of
$\mu_j$ are eigenvalues of ![]() $({-}{\textbf{D}}(s))$. Because
$({-}{\textbf{D}}(s))$. Because ![]() $det({\textbf{Z}}(s))$ is the product of the eigenvalues of
$det({\textbf{Z}}(s))$ is the product of the eigenvalues of ![]() ${\textbf{Z}}(s)$, and because, as
${\textbf{Z}}(s)$, and because, as ![]() $s\downarrow s^*$, one of the eigenvalues will approach zero since
$s\downarrow s^*$, one of the eigenvalues will approach zero since ![]() $s^*=\delta^*$ by Lemma 4, we have
$s^*=\delta^*$ by Lemma 4, we have ![]() $\lim_{s\downarrow s^*}det({\textbf{Z}}(s))=0$ and so
$\lim_{s\downarrow s^*}det({\textbf{Z}}(s))=0$ and so ![]() ${\boldsymbol{\Phi}}(s^*)=\lim_{s\downarrow s^*}{\boldsymbol{\Phi}}(s)=-\infty$, where the negative sign is due to the fact that
${\boldsymbol{\Phi}}(s^*)=\lim_{s\downarrow s^*}{\boldsymbol{\Phi}}(s)=-\infty$, where the negative sign is due to the fact that ![]() ${\boldsymbol{\Phi}}(s)<{\boldsymbol{0}}$ for all
${\boldsymbol{\Phi}}(s)<{\boldsymbol{0}}$ for all ![]() $s>s^*$.
$s>s^*$.
We now state the key result of this paper.
Theorem 2. For all ![]() $s>s^*$,
$s>s^*$,
where ![]() ${\boldsymbol{0}}<{\textbf{B}}(s^*)<\infty$ solves
${\boldsymbol{0}}<{\textbf{B}}(s^*)<\infty$ solves
and
Proof. Note that for any function ![]() $h(\cdot)$ with
$h(\cdot)$ with ![]() $h(s-s^*)=o(s-s^*)$ or
$h(s-s^*)=o(s-s^*)$ or ![]() $h(s-s^*)=c\cdot (s-s^*)$ for some constant c, we have
$h(s-s^*)=c\cdot (s-s^*)$ for some constant c, we have
Consider ![]() $h(s-s^*)=(s-s^*)/|| {\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*) ||$. We have
$h(s-s^*)=(s-s^*)/|| {\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*) ||$. We have
which implies ![]() $(s-s^*)=o(h(s-s^*))$, and
$(s-s^*)=o(h(s-s^*))$, and
 \begin{equation} \lim_{s\downarrow s^*} \Bigg|\Bigg| \frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{s-s^*}h(s-s^*) \Bigg|\Bigg| =1\not= 0.\end{equation}
\begin{equation} \lim_{s\downarrow s^*} \Bigg|\Bigg| \frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{s-s^*}h(s-s^*) \Bigg|\Bigg| =1\not= 0.\end{equation}
Therefore, there exists a continuous, positive-valued function ![]() $h(\cdot)$ such that
$h(\cdot)$ such that ![]() $(s-s^*)=$
$(s-s^*)=$ ![]() $o(h(s-s^*))$ and
$o(h(s-s^*))$ and
for some constant matrix ![]() ${\boldsymbol{0}}<{\textbf{B}}(s^*)<\infty$. For such
${\boldsymbol{0}}<{\textbf{B}}(s^*)<\infty$. For such ![]() $h(\cdot)$, define the function
$h(\cdot)$, define the function ![]() $g(\cdot)$ by
$g(\cdot)$ by
clearly ![]() $\lim_{s\downarrow s^*}g(s-s^*)=0$ since
$\lim_{s\downarrow s^*}g(s-s^*)=0$ since ![]() $(s-s^*)=o(h(s-s^*))$.
$(s-s^*)=o(h(s-s^*))$.
Consequently, we have
which implies that
We now solve for ![]() ${\textbf{B}}(s^*)$ and
${\textbf{B}}(s^*)$ and ![]() $g(s-s^*)$. By (21) and Lemma 5, since
$g(s-s^*)$. By (21) and Lemma 5, since
we have
 \begin{eqnarray}{\boldsymbol{0}}&\,=\,& {\textbf{Q}}_{12}(s) +{\textbf{Q}}_{11}(s){\boldsymbol{\Psi}}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{22}(s) +{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s)\nonumber \\[4pt] &\,=\,&\left({\textbf{Q}}_{12}(s^*)-{\textbf{A}}_{12}(s^*)(s-s^*)\right) \nonumber\\[4pt] && + \left( {\textbf{Q}}_{11}(s^*)-{\textbf{A}}_{11}(s^*)(s-s^*) \right) \left( {\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)g(s-s^*) \right) \nonumber\\[4pt] && + \left( {\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)g(s-s^*) \right) \left( {\textbf{Q}}_{22}(s^*)-{\textbf{A}}_{22}(s^*)(s-s^*) \right) \nonumber\\[4pt] && + \left( {\boldsymbol{\Psi}}(s^*) - {\textbf{B}}(s^*)g(s-s^*) \right) \left( {\textbf{Q}}_{21}(s^*)-{\textbf{A}}_{21}(s^*)(s-s^*) \right) \left( {\boldsymbol{\Psi}}(s^*) - {\textbf{B}}(s^*)g(s-s^*) \right) \nonumber\\[4pt] && +o(s-s^*)+o(g(s-s^*)),\end{eqnarray}
\begin{eqnarray}{\boldsymbol{0}}&\,=\,& {\textbf{Q}}_{12}(s) +{\textbf{Q}}_{11}(s){\boldsymbol{\Psi}}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{22}(s) +{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s)\nonumber \\[4pt] &\,=\,&\left({\textbf{Q}}_{12}(s^*)-{\textbf{A}}_{12}(s^*)(s-s^*)\right) \nonumber\\[4pt] && + \left( {\textbf{Q}}_{11}(s^*)-{\textbf{A}}_{11}(s^*)(s-s^*) \right) \left( {\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)g(s-s^*) \right) \nonumber\\[4pt] && + \left( {\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)g(s-s^*) \right) \left( {\textbf{Q}}_{22}(s^*)-{\textbf{A}}_{22}(s^*)(s-s^*) \right) \nonumber\\[4pt] && + \left( {\boldsymbol{\Psi}}(s^*) - {\textbf{B}}(s^*)g(s-s^*) \right) \left( {\textbf{Q}}_{21}(s^*)-{\textbf{A}}_{21}(s^*)(s-s^*) \right) \left( {\boldsymbol{\Psi}}(s^*) - {\textbf{B}}(s^*)g(s-s^*) \right) \nonumber\\[4pt] && +o(s-s^*)+o(g(s-s^*)),\end{eqnarray}
and so
where ![]() ${\textbf{U}}(s^*)$ is as defined in (83), and
${\textbf{U}}(s^*)$ is as defined in (83), and
 \begin{eqnarray} {\textbf{W}}(s^*)&\,=\,& \left( {\textbf{Q}}_{11}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{Q}}_{21}(s^*) \right) {\textbf{B}}(s^*) +{\textbf{B}}(s^*) \left( {\textbf{Q}}_{22}(s^*)+{\textbf{Q}}_{21}(s^*){\boldsymbol{\Psi}}(s^*) \right) \nonumber\\[4pt] &\,=\,& {\textbf{K}}(s^*){\textbf{B}}(s^*)+{\textbf{B}}(s^*){\textbf{D}}(s^*) , \nonumber\\[4pt] {\textbf{V}}(s^*) &\,=\,& {\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*){\textbf{B}}(s^*) .\end{eqnarray}
\begin{eqnarray} {\textbf{W}}(s^*)&\,=\,& \left( {\textbf{Q}}_{11}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{Q}}_{21}(s^*) \right) {\textbf{B}}(s^*) +{\textbf{B}}(s^*) \left( {\textbf{Q}}_{22}(s^*)+{\textbf{Q}}_{21}(s^*){\boldsymbol{\Psi}}(s^*) \right) \nonumber\\[4pt] &\,=\,& {\textbf{K}}(s^*){\textbf{B}}(s^*)+{\textbf{B}}(s^*){\textbf{D}}(s^*) , \nonumber\\[4pt] {\textbf{V}}(s^*) &\,=\,& {\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*){\textbf{B}}(s^*) .\end{eqnarray}
We now use (102) to solve for ![]() ${\textbf{B}}(s^*)$ and
${\textbf{B}}(s^*)$ and ![]() $g(s-s^*)$. We note that
$g(s-s^*)$. We note that ![]() ${\textbf{V}}(s^*)\not= {\boldsymbol{0}}$ and
${\textbf{V}}(s^*)\not= {\boldsymbol{0}}$ and ![]() ${\textbf{U}}(s^*)\not= {\boldsymbol{0}}$. Indeed,
${\textbf{U}}(s^*)\not= {\boldsymbol{0}}$. Indeed, ![]() ${\textbf{V}}(s^*)\not= {\boldsymbol{0}}$, since
${\textbf{V}}(s^*)\not= {\boldsymbol{0}}$, since ![]() ${\textbf{V}}(s^*)> {\boldsymbol{0}}$ because
${\textbf{V}}(s^*)> {\boldsymbol{0}}$ because ![]() ${\textbf{B}}(s^*)>{\boldsymbol{0}}$,
${\textbf{B}}(s^*)>{\boldsymbol{0}}$, ![]() ${\textbf{Q}}_{21}(s^*)\geq {\boldsymbol{0}}$, and
${\textbf{Q}}_{21}(s^*)\geq {\boldsymbol{0}}$, and ![]() ${\textbf{Q}}_{21}(s^*)\not= {\boldsymbol{0}}$. Furthermore,
${\textbf{Q}}_{21}(s^*)\not= {\boldsymbol{0}}$. Furthermore, ![]() ${\textbf{U}}(s^*)\not= {\boldsymbol{0}}$ since
${\textbf{U}}(s^*)\not= {\boldsymbol{0}}$ since ![]() ${\textbf{U}}(s^*)> {\boldsymbol{0}}$. Indeed, in the case
${\textbf{U}}(s^*)> {\boldsymbol{0}}$. Indeed, in the case ![]() $\mathcal{S}_0=\varnothing$, since
$\mathcal{S}_0=\varnothing$, since ![]() ${\textbf{C}}_1,{\textbf{C}}_2>{\boldsymbol{0}}$ and
${\textbf{C}}_1,{\textbf{C}}_2>{\boldsymbol{0}}$ and ![]() ${\boldsymbol{\Psi}}(s^*)>{\boldsymbol{0}}$, we have
${\boldsymbol{\Psi}}(s^*)>{\boldsymbol{0}}$, we have ![]() ${\textbf{U}}(s^*)={\textbf{C}}_1^{-1}{\boldsymbol{\Psi}}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}>{\boldsymbol{0}}$. In the case
${\textbf{U}}(s^*)={\textbf{C}}_1^{-1}{\boldsymbol{\Psi}}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}>{\boldsymbol{0}}$. In the case ![]() $\mathcal{S}_0\not=\varnothing$, we have
$\mathcal{S}_0\not=\varnothing$, we have ![]() $-({\textbf{T}}_{00}-s^*{\textbf{I}})^{-1}=\int_{t=0}^{\infty}e^{-s^*t}e^{{\textbf{T}}_{00}t}dt>{\boldsymbol{0}}$, and
$-({\textbf{T}}_{00}-s^*{\textbf{I}})^{-1}=\int_{t=0}^{\infty}e^{-s^*t}e^{{\textbf{T}}_{00}t}dt>{\boldsymbol{0}}$, and ![]() $({\textbf{T}}_{00}-s^*{\textbf{I}})^{-2}=({-}({\textbf{T}}_{00}-s^*{\textbf{I}})^{-1})^2>0$. Therefore
$({\textbf{T}}_{00}-s^*{\textbf{I}})^{-2}=({-}({\textbf{T}}_{00}-s^*{\textbf{I}})^{-1})^2>0$. Therefore ![]() ${\textbf{A}}_{11}(s^*),{\textbf{A}}_{22}(s^*)>{\boldsymbol{0}}$,
${\textbf{A}}_{11}(s^*),{\textbf{A}}_{22}(s^*)>{\boldsymbol{0}}$, ![]() ${\textbf{A}}_{12}(s^*),{\textbf{A}}_{21}(s^*)\geq 0$, and
${\textbf{A}}_{12}(s^*),{\textbf{A}}_{21}(s^*)\geq 0$, and ![]() ${\boldsymbol{\Psi}}(s^*)>{\boldsymbol{0}}$, so that
${\boldsymbol{\Psi}}(s^*)>{\boldsymbol{0}}$, so that ![]() ${\textbf{U}}(s^*)={\textbf{A}}_{12}(s^*)+{\textbf{A}}_{11}(s^*){\boldsymbol{\Psi}}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{A}}_{22}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{A}}_{21}(s^*){\boldsymbol{\Psi}}(s^*)>{\boldsymbol{0}}$.
${\textbf{U}}(s^*)={\textbf{A}}_{12}(s^*)+{\textbf{A}}_{11}(s^*){\boldsymbol{\Psi}}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{A}}_{22}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{A}}_{21}(s^*){\boldsymbol{\Psi}}(s^*)>{\boldsymbol{0}}$.
Consequently, below we consider the two cases ![]() ${\textbf{W}}(s^*)\not= {\boldsymbol{0}}$ and
${\textbf{W}}(s^*)\not= {\boldsymbol{0}}$ and ![]() ${\textbf{W}}(s^*)= {\boldsymbol{0}}$, respectively labelled Case I and Case II.
${\textbf{W}}(s^*)= {\boldsymbol{0}}$, respectively labelled Case I and Case II.
Case I. Suppose ![]() ${\textbf{W}}(s^*)\not= {\boldsymbol{0}}$. Then
${\textbf{W}}(s^*)\not= {\boldsymbol{0}}$. Then
Consider ![]() $(s-s^*)$ and
$(s-s^*)$ and ![]() $g(s-s^*)$. Either one of them dominates the other, or one is a multiple of the other.
$g(s-s^*)$. Either one of them dominates the other, or one is a multiple of the other.
(i) If
 $g(s-s^*)=o(s-s^*)$, then dividing Equation (104) by
$g(s-s^*)=o(s-s^*)$, then dividing Equation (104) by  $(s-s^*)$ and taking limits as
$(s-s^*)$ and taking limits as  $s\downarrow s^*$ gives
$s\downarrow s^*$ gives  ${\boldsymbol{0}}={\textbf{U}}(s^*)$, a contradiction.
${\boldsymbol{0}}={\textbf{U}}(s^*)$, a contradiction.-
(ii) If
 $(s-s^*)=o(g(s-s^*))$, then dividing Equation (104) by
$(s-s^*)=o(g(s-s^*))$, then dividing Equation (104) by  $g(s-s^*)$ and taking limits as
$g(s-s^*)$ and taking limits as  $s\downarrow s^*$ gives
$s\downarrow s^*$ gives  ${\boldsymbol{0}}={\textbf{W}}(s^*)$, a contradiction.
${\boldsymbol{0}}={\textbf{W}}(s^*)$, a contradiction. -
(iii) If
 $g(s-s^*)=c\cdot (s-s^*)$ for some constant
$g(s-s^*)=c\cdot (s-s^*)$ for some constant  $c>0$, then without loss of generality we may assume
$c>0$, then without loss of generality we may assume  $c=1$, since
$c=1$, since  ${\textbf{B}}(s^*)g(s-s^*)=({\textbf{B}}(s^*)c )(s-s^*)$ suggests the substitution
${\textbf{B}}(s^*)g(s-s^*)=({\textbf{B}}(s^*)c )(s-s^*)$ suggests the substitution  $\tilde {\textbf{B}}(s^*)\equiv {\textbf{B}}(s^*)c$. We then have
(105)with
$\tilde {\textbf{B}}(s^*)\equiv {\textbf{B}}(s^*)c$. We then have
(105)with \begin{eqnarray} {\boldsymbol{\Psi}}(s)&\,=\,&{\boldsymbol{\Psi}}(s^*)-\tilde{\textbf{B}}(s^*)(s-s^*) +o(s-s^*),\end{eqnarray}
\begin{eqnarray} {\boldsymbol{\Psi}}(s)&\,=\,&{\boldsymbol{\Psi}}(s^*)-\tilde{\textbf{B}}(s^*)(s-s^*) +o(s-s^*),\end{eqnarray}
 $\tilde {\textbf{B}}(s^*)<\infty$. However, dividing Equation (105) by
$\tilde {\textbf{B}}(s^*)<\infty$. However, dividing Equation (105) by  $(s-s^*)$ and taking limits as
$(s-s^*)$ and taking limits as  $s\downarrow s^*$ gives, by Lemma 6,
(106)a contradiction.
$s\downarrow s^*$ gives, by Lemma 6,
(106)a contradiction. \begin{eqnarray} \tilde{\textbf{B}}(s^*)=-\lim_{s\downarrow s^*}\frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{s-s^*}=\infty,\end{eqnarray}
\begin{eqnarray} \tilde{\textbf{B}}(s^*)=-\lim_{s\downarrow s^*}\frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{s-s^*}=\infty,\end{eqnarray}
That is, the assumption ![]() ${\textbf{W}}(s^*)\not= {\boldsymbol{0}}$ leads to a contradiction.
${\textbf{W}}(s^*)\not= {\boldsymbol{0}}$ leads to a contradiction.
Case II. By the above, we must have ![]() ${\textbf{W}}(s^*)= {\boldsymbol{0}}$, or equivalently,
${\textbf{W}}(s^*)= {\boldsymbol{0}}$, or equivalently,
and so,
We note that ![]() $g^2(s-s^*)=o(g(s-s^*))$, and consider the following.
$g^2(s-s^*)=o(g(s-s^*))$, and consider the following.
(i) First, we show that ![]() $(s-s^*)=o(g(s-s^*))$. Indeed, if
$(s-s^*)=o(g(s-s^*))$. Indeed, if ![]() $g(s-s^*)=o(s-s^*)$ or
$g(s-s^*)=o(s-s^*)$ or ![]() $g(s-s^*)=c\cdot (s-s^*)$ for some
$g(s-s^*)=c\cdot (s-s^*)$ for some ![]() $c\not= 0$, then dividing Equation (108) by
$c\not= 0$, then dividing Equation (108) by ![]() $(s-s^*)$ and taking limits as
$(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\textbf{U}}(s^*)={\boldsymbol{0}}$, a contradiction. Therefore we must have
${\textbf{U}}(s^*)={\boldsymbol{0}}$, a contradiction. Therefore we must have ![]() $(s-s^*)=o(g(s-s^*))$. That is,
$(s-s^*)=o(g(s-s^*))$. That is, ![]() $g(s-s^*)$ dominates both
$g(s-s^*)$ dominates both ![]() $g^2(s-s^*)$ and
$g^2(s-s^*)$ and ![]() $(s-s^*)$.
$(s-s^*)$.
Then,
which gives ![]() $o(s-s^*)=o(g(s-s^*))$, and so we write (108) in the form
$o(s-s^*)=o(g(s-s^*))$, and so we write (108) in the form
Since ![]() $(s-s^*)=o(g(s-s^*))$, we consider two cases,
$(s-s^*)=o(g(s-s^*))$, we consider two cases, ![]() $o(g(s-s^*))={\boldsymbol{0}}$ and
$o(g(s-s^*))={\boldsymbol{0}}$ and ![]() $o(g(s-s^*))\not ={\boldsymbol{0}}$, respectively labelled (A) and (B) below.
$o(g(s-s^*))\not ={\boldsymbol{0}}$, respectively labelled (A) and (B) below.
(A) Suppose ![]() $o(g(s-s^*))={\boldsymbol{0}}$. Then (110) reduces to
$o(g(s-s^*))={\boldsymbol{0}}$. Then (110) reduces to
If ![]() $(s-s^*)=o(g^2(s-s^*))$, we divide (111) by
$(s-s^*)=o(g^2(s-s^*))$, we divide (111) by ![]() $g^2(s-s^*)$ and take limits as
$g^2(s-s^*)$ and take limits as ![]() $s\downarrow s^*$ to get
$s\downarrow s^*$ to get ![]() ${\textbf{V}}(s^*)={\boldsymbol{0}}$, a contradiction. If
${\textbf{V}}(s^*)={\boldsymbol{0}}$, a contradiction. If ![]() $g^2(s-s^*)=o(s-s^*)$, we divide (111) by
$g^2(s-s^*)=o(s-s^*)$, we divide (111) by ![]() $(s-s^*)$ and take limits as
$(s-s^*)$ and take limits as ![]() $s\downarrow s^*$ to get
$s\downarrow s^*$ to get ![]() ${\textbf{U}}(s^*)={\boldsymbol{0}}$, a contradiction. So we must have
${\textbf{U}}(s^*)={\boldsymbol{0}}$, a contradiction. So we must have ![]() $(s-s^*)=c\cdot g^2(s-s^*)$ for some constant
$(s-s^*)=c\cdot g^2(s-s^*)$ for some constant ![]() $c>0$, and without loss of generality we may assume
$c>0$, and without loss of generality we may assume ![]() $c=1$. Then dividing (111) by
$c=1$. Then dividing (111) by ![]() $(s-s^*)$ and taking limits as
$(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\textbf{U}}(s^*)={\textbf{V}}(s^*)$, or equivalently,
${\textbf{U}}(s^*)={\textbf{V}}(s^*)$, or equivalently,
That is, Case (A) gives ![]() $g(s-s^*)=\sqrt{s-s^*}$.
$g(s-s^*)=\sqrt{s-s^*}$.
(B) Suppose ![]() $o(g(s-s^*))\not={\boldsymbol{0}}$. Then we write the term
$o(g(s-s^*))\not={\boldsymbol{0}}$. Then we write the term ![]() $o(g(s-s^*))$ in the form
$o(g(s-s^*))$ in the form
for some function ![]() $L(\cdot)\not= 0$ such that
$L(\cdot)\not= 0$ such that ![]() $L(s-s^*)=o(g(s-s^*))$ and some constant
$L(s-s^*)=o(g(s-s^*))$ and some constant ![]() ${\textbf{Y}}(s^*)\not= {\boldsymbol{0}}$.
${\textbf{Y}}(s^*)\not= {\boldsymbol{0}}$.
We then have
In relation to the terms ![]() $(s-s^*)$,
$(s-s^*)$, ![]() $g^2(s-s^*)$, and
$g^2(s-s^*)$, and ![]() $L(s-s^*)$, we consider three cases, labelled (B)(ii)–(B)(iv). We will show that Case (B)(ii) gives a contradiction and Cases (B)(iii) and (B)(iv) give
$L(s-s^*)$, we consider three cases, labelled (B)(ii)–(B)(iv). We will show that Case (B)(ii) gives a contradiction and Cases (B)(iii) and (B)(iv) give ![]() $g(s-s^*)=\sqrt{s-s^*}$.
$g(s-s^*)=\sqrt{s-s^*}$.
(B)(ii) Suppose one of ![]() $(s-s^*)$,
$(s-s^*)$, ![]() $g^2(s-s^*)$, and
$g^2(s-s^*)$, and ![]() $L(s-s^*)$ dominates the other two.
$L(s-s^*)$ dominates the other two.
If ![]() $(s-s^*)$ dominates the other terms, that is,
$(s-s^*)$ dominates the other terms, that is, ![]() $g^2(s-s^*)=o(s-s^*)$ and
$g^2(s-s^*)=o(s-s^*)$ and ![]() $L(s-s^*)=$
$L(s-s^*)=$ ![]() $o(s-s^*)$, then dividing Equation (114) by
$o(s-s^*)$, then dividing Equation (114) by ![]() $(s-s^*)$ and taking limits as
$(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\textbf{U}}(s^*)={\boldsymbol{0}}$, a contradiction.
${\textbf{U}}(s^*)={\boldsymbol{0}}$, a contradiction.
If ![]() $g^2(s-s^*)$ dominates the other terms, that is,
$g^2(s-s^*)$ dominates the other terms, that is, ![]() $(s-s^*)=o(g^2(s-s^*))$ and
$(s-s^*)=o(g^2(s-s^*))$ and ![]() $L(s-s^*)=o(g^2(s-s^*))$, then dividing Equation (114) by
$L(s-s^*)=o(g^2(s-s^*))$, then dividing Equation (114) by ![]() $g^2(s-s^*)$ and taking limits as
$g^2(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\textbf{V}}(s^*)={\boldsymbol{0}}$, a contradiction.
${\textbf{V}}(s^*)={\boldsymbol{0}}$, a contradiction.
If ![]() $L(s-s^*)$ dominates the other terms, that is,
$L(s-s^*)$ dominates the other terms, that is, ![]() $(s-s^*)=o(L(s-s^*))$ and
$(s-s^*)=o(L(s-s^*))$ and ![]() $g^2(s-s^*)=o(L(s-s^*))$, then dividing Equation (114) by
$g^2(s-s^*)=o(L(s-s^*))$, then dividing Equation (114) by ![]() $L(s-s^*)$ and taking limits as
$L(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\textbf{Y}}(s^*)={\boldsymbol{0}}$, a contradiction.
${\textbf{Y}}(s^*)={\boldsymbol{0}}$, a contradiction.
That is, Case (B)(ii) gives a contradiction. Therefore at least two of ![]() $(s-s^*)$,
$(s-s^*)$, ![]() $g^2(s-s^*)$, and
$g^2(s-s^*)$, and ![]() $L(s-s^*)$ must be multiples of each other.
$L(s-s^*)$ must be multiples of each other.
(B)(iii) Suppose each of ![]() $(s-s^*)$,
$(s-s^*)$, ![]() $g^2(s-s^*)$ and
$g^2(s-s^*)$ and ![]() $L(s-s^*)$ is a multiple of the others. Then
$L(s-s^*)$ is a multiple of the others. Then ![]() $(s-s^*)=c\cdot g^2(s-s^*)=d\cdot L(s-s^*)$, and without loss of generality we may assume
$(s-s^*)=c\cdot g^2(s-s^*)=d\cdot L(s-s^*)$, and without loss of generality we may assume ![]() $c=1$,
$c=1$, ![]() $d=1$, by an argument analogous to the one used before. Therefore, dividing Equation (114) by
$d=1$, by an argument analogous to the one used before. Therefore, dividing Equation (114) by ![]() $(s-s^*)$ and taking limits as
$(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\boldsymbol{0}}=-{\textbf{U}}(s^*)+{\textbf{V}}(s^*)+{\textbf{Y}}(s^*)$, or equivalently,
${\boldsymbol{0}}=-{\textbf{U}}(s^*)+{\textbf{V}}(s^*)+{\textbf{Y}}(s^*)$, or equivalently,
That is, Case (B)(iii) gives ![]() $g(s-s^*)=\sqrt{s-s^*}$.
$g(s-s^*)=\sqrt{s-s^*}$.
(B)(iv) Suppose exactly two of ![]() $(s-s^*)$,
$(s-s^*)$, ![]() $g^2(s-s^*)$, and
$g^2(s-s^*)$, and ![]() $L(s-s^*)$ are multiples of one another. Then these two terms must dominate the third term, or we have a contradiction by Part (i) of Case II above.
$L(s-s^*)$ are multiples of one another. Then these two terms must dominate the third term, or we have a contradiction by Part (i) of Case II above.
If ![]() $(s-s^*)=c\cdot g^2(s-s^*)$ for some
$(s-s^*)=c\cdot g^2(s-s^*)$ for some ![]() $c>0$, then without loss of generality we may assume
$c>0$, then without loss of generality we may assume ![]() $c=1$. Also, we must have
$c=1$. Also, we must have ![]() $L(s-s^*)=o(s-s^*)$. Therefore,
$L(s-s^*)=o(s-s^*)$. Therefore, ![]() $g(s-s^*)=\sqrt{s-s^*}$, and dividing Equation (114) by
$g(s-s^*)=\sqrt{s-s^*}$, and dividing Equation (114) by ![]() $(s-s^*)$ and taking limits as
$(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\textbf{U}}(s^*)={\textbf{V}}(s^*)$, or equivalently,
${\textbf{U}}(s^*)={\textbf{V}}(s^*)$, or equivalently,
If ![]() $L(s-s^*)=c\cdot (s-s^*)$ for some
$L(s-s^*)=c\cdot (s-s^*)$ for some ![]() $c\not= 0$, then dividing Equation (114) by
$c\not= 0$, then dividing Equation (114) by ![]() $(s-s^*)$ and taking limits as
$(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\textbf{V}}(s^*)={\boldsymbol{0}}$, a contradiction.
${\textbf{V}}(s^*)={\boldsymbol{0}}$, a contradiction.
If ![]() $L(s-s^*)=c\cdot g^2(s-s^*)$ for some
$L(s-s^*)=c\cdot g^2(s-s^*)$ for some ![]() $c> 0$, then without loss of generality we may assume
$c> 0$, then without loss of generality we may assume ![]() $c=1$. Also, we must have
$c=1$. Also, we must have ![]() $L(s-s^*)=o(s-s^*)$. Therefore, Equation (114) becomes
$L(s-s^*)=o(s-s^*)$. Therefore, Equation (114) becomes
In this case, if ![]() $g^2(s-s^*)=o(s-s^*)$, then dividing Equation (117) by
$g^2(s-s^*)=o(s-s^*)$, then dividing Equation (117) by ![]() $(s-s^*)$ and taking limits as
$(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\textbf{U}}(s^*)={\boldsymbol{0}}$, a contradiction. If
${\textbf{U}}(s^*)={\boldsymbol{0}}$, a contradiction. If ![]() $(s-s^*)=o(g^2(s-s^*))$, then dividing Equation (117) by
$(s-s^*)=o(g^2(s-s^*))$, then dividing Equation (117) by ![]() $g^2(s-s^*)$ and taking limits as
$g^2(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives ![]() ${\textbf{U}}(s^*)+{\textbf{Y}}(s^*)={\boldsymbol{0}}$, a contradiction. Therefore, we must have
${\textbf{U}}(s^*)+{\textbf{Y}}(s^*)={\boldsymbol{0}}$, a contradiction. Therefore, we must have ![]() $g^2(s-s^*)=c\cdot (s-s^*)$ for some
$g^2(s-s^*)=c\cdot (s-s^*)$ for some ![]() $c> 0$. Without loss of generality we may assume
$c> 0$. Without loss of generality we may assume ![]() $c=1$. Therefore,
$c=1$. Therefore, ![]() $g(s-s^*)=\sqrt{s-s^*}$, and dividing Equation (117) by
$g(s-s^*)=\sqrt{s-s^*}$, and dividing Equation (117) by ![]() $g^2(s-s^*)$ and taking limits as
$g^2(s-s^*)$ and taking limits as ![]() $s\downarrow s^*$ gives
$s\downarrow s^*$ gives
That is, Case (B)(iv) gives ![]() $g(s-s^*)=\sqrt{s-s^*}$.
$g(s-s^*)=\sqrt{s-s^*}$.
By the above arguments, we must have
and
and ![]() $-\infty<{\textbf{Y}}(s^*)\leq {\textbf{U}}(s^*)$. Here,
$-\infty<{\textbf{Y}}(s^*)\leq {\textbf{U}}(s^*)$. Here, ![]() ${\textbf{Y}}(s^*)= {\boldsymbol{0}}$ whenever the term
${\textbf{Y}}(s^*)= {\boldsymbol{0}}$ whenever the term ![]() $o(g(s-s^*))$ in (110) satisfies
$o(g(s-s^*))$ in (110) satisfies ![]() $o(g(s-s^*))=o(s-s^*)$, and
$o(g(s-s^*))=o(s-s^*)$, and ![]() ${\textbf{Y}}(s^*)\not= {\boldsymbol{0}}$ when
${\textbf{Y}}(s^*)\not= {\boldsymbol{0}}$ when ![]() $o(g(s-s^*))=(s-s^*){\textbf{Y}}(s^*)+o(s-s^*)$.
$o(g(s-s^*))=(s-s^*){\textbf{Y}}(s^*)+o(s-s^*)$.
Finally, we show (92). By L’Hospital’s rule,
and so, by taking limits as ![]() $s\downarrow s^*$ in (85),
$s\downarrow s^*$ in (85),
 \begin{eqnarray}&&{{\textbf{B}}(s^*){\textbf{Q}}_{21} (s^*){\textbf{B}}(s^*)+{\textbf{Y}}(s^*)= {\textbf{U}}(s^*)}\nonumber\\[4pt]
&&\,=\, \lim_{s\downarrow s^*} \Big[ {\textbf{K}}(s){\boldsymbol{\Phi}}(s) +{\boldsymbol{\Phi}}(s){\textbf{D}}(s) \Big]\nonumber\\[4pt]
&&\,=\,\lim_{s\downarrow s^*}\Big[({\textbf{Q}}_{11}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s)){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s)({\textbf{Q}}_{22}(s)+{\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s))\Big]\nonumber
&&\,=\,\lim_{s\downarrow s^*}\Bigg[\frac{1}{2}\left(\frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{\sqrt{s-s^*}}\right){\textbf{Q}}_{21}(s)\left({\boldsymbol{\Phi}}(s)2\sqrt{s-s^*}\right)\nonumber\\[4pt]
&&+\frac{1}{2}\left({\boldsymbol{\Phi}}(s)2\sqrt{s-s^*}\right){\textbf{Q}}_{21}(s)\left(\frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{\sqrt{s-s^*}}\right)\nonumber\\[4pt]&&+{\textbf{Q}}_{11}(s){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{22}(s)+{\boldsymbol{\Psi}}(s^*){\textbf{Q}}_{21}(s){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s^*)\Bigg]\nonumber\\[4pt]&\,=\,&\frac{1}{2}{\textbf{B}}(s^*){\textbf{Q}}_{21} (s^*){\textbf{B}}(s^*)+\frac{1}{2}{\textbf{B}}(s^*){\textbf{Q}}_{21} (s^*){\textbf{B}}(s^*)\nonumber\\[4pt]&&+\lim_{s\downarrow s^*}\Bigg[\left(\frac{{\textbf{Q}}_{11}(s)-{\textbf{Q}}_{11}(s^*)}{\sqrt{s-s^*}}\right)({\boldsymbol{\Phi}}(s)\sqrt{s-s^*})+(\sqrt{s-s^*}{\boldsymbol{\Phi}}(s))\left(\frac{{\textbf{Q}}_{22}(s)-{\textbf{Q}}_{22}(s^*)}{\sqrt{s-s^*}} \right)\nonumber\\[4pt]&&+{\textbf{Q}}_{11}(s^*){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{22}(s^*)\nonumber\\[4pt]&&+{\boldsymbol{\Psi}}(s^*)\left(\frac{{\textbf{Q}}_{21}(s)-{\textbf{Q}}_{21}(s^*)}{\sqrt{s-s^*}}\right)({\boldsymbol{\Phi}}(s)\sqrt{s-s^*})+({\boldsymbol{\Phi}}(s)\sqrt{s-s^*})\left(\frac{{\textbf{Q}}_{21}(s)-{\textbf{Q}}_{21}(s^*)}{\sqrt{s-s^*}}\right){\boldsymbol{\Psi}}(s^*)\nonumber\\[4pt]&&+{\boldsymbol{\Psi}}(s^*){\textbf{Q}}_{21}(s^*){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{21}(s^*){\boldsymbol{\Psi}}(s^*)\Bigg]\nonumber\\[4pt]&\,=\,&{\textbf{B}}(s^*){\textbf{Q}}_{21} (s^*){\textbf{B}}(s^*)+ {\boldsymbol{0}}+\lim_{s\downarrow s^*}\Big[{\textbf{K}}(s^*){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{D}}(s^*)\Big],\end{eqnarray}
\begin{eqnarray}&&{{\textbf{B}}(s^*){\textbf{Q}}_{21} (s^*){\textbf{B}}(s^*)+{\textbf{Y}}(s^*)= {\textbf{U}}(s^*)}\nonumber\\[4pt]
&&\,=\, \lim_{s\downarrow s^*} \Big[ {\textbf{K}}(s){\boldsymbol{\Phi}}(s) +{\boldsymbol{\Phi}}(s){\textbf{D}}(s) \Big]\nonumber\\[4pt]
&&\,=\,\lim_{s\downarrow s^*}\Big[({\textbf{Q}}_{11}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s)){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s)({\textbf{Q}}_{22}(s)+{\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s))\Big]\nonumber
&&\,=\,\lim_{s\downarrow s^*}\Bigg[\frac{1}{2}\left(\frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{\sqrt{s-s^*}}\right){\textbf{Q}}_{21}(s)\left({\boldsymbol{\Phi}}(s)2\sqrt{s-s^*}\right)\nonumber\\[4pt]
&&+\frac{1}{2}\left({\boldsymbol{\Phi}}(s)2\sqrt{s-s^*}\right){\textbf{Q}}_{21}(s)\left(\frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{\sqrt{s-s^*}}\right)\nonumber\\[4pt]&&+{\textbf{Q}}_{11}(s){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{22}(s)+{\boldsymbol{\Psi}}(s^*){\textbf{Q}}_{21}(s){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{21}(s){\boldsymbol{\Psi}}(s^*)\Bigg]\nonumber\\[4pt]&\,=\,&\frac{1}{2}{\textbf{B}}(s^*){\textbf{Q}}_{21} (s^*){\textbf{B}}(s^*)+\frac{1}{2}{\textbf{B}}(s^*){\textbf{Q}}_{21} (s^*){\textbf{B}}(s^*)\nonumber\\[4pt]&&+\lim_{s\downarrow s^*}\Bigg[\left(\frac{{\textbf{Q}}_{11}(s)-{\textbf{Q}}_{11}(s^*)}{\sqrt{s-s^*}}\right)({\boldsymbol{\Phi}}(s)\sqrt{s-s^*})+(\sqrt{s-s^*}{\boldsymbol{\Phi}}(s))\left(\frac{{\textbf{Q}}_{22}(s)-{\textbf{Q}}_{22}(s^*)}{\sqrt{s-s^*}} \right)\nonumber\\[4pt]&&+{\textbf{Q}}_{11}(s^*){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{22}(s^*)\nonumber\\[4pt]&&+{\boldsymbol{\Psi}}(s^*)\left(\frac{{\textbf{Q}}_{21}(s)-{\textbf{Q}}_{21}(s^*)}{\sqrt{s-s^*}}\right)({\boldsymbol{\Phi}}(s)\sqrt{s-s^*})+({\boldsymbol{\Phi}}(s)\sqrt{s-s^*})\left(\frac{{\textbf{Q}}_{21}(s)-{\textbf{Q}}_{21}(s^*)}{\sqrt{s-s^*}}\right){\boldsymbol{\Psi}}(s^*)\nonumber\\[4pt]&&+{\boldsymbol{\Psi}}(s^*){\textbf{Q}}_{21}(s^*){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{Q}}_{21}(s^*){\boldsymbol{\Psi}}(s^*)\Bigg]\nonumber\\[4pt]&\,=\,&{\textbf{B}}(s^*){\textbf{Q}}_{21} (s^*){\textbf{B}}(s^*)+ {\boldsymbol{0}}+\lim_{s\downarrow s^*}\Big[{\textbf{K}}(s^*){\boldsymbol{\Phi}}(s)+{\boldsymbol{\Phi}}(s){\textbf{D}}(s^*)\Big],\end{eqnarray}
which completes the proof.
The next result follows immediately by Theorem 1.
Corollary 1. We have
Example 1. Since ![]() $\lim_{s\downarrow s^*} \Delta(s)=\Delta(s^*)=0$, we have
$\lim_{s\downarrow s^*} \Delta(s)=\Delta(s^*)=0$, we have
 \begin{eqnarray}\lim_{s\downarrow s^*}\frac{d}{ds}{\boldsymbol{\Psi}}(s)&\,=\,& \lim_{s\downarrow s^*}\frac{d}{ds} \frac{(a+b+2s)-\sqrt{\Delta(s)}}{2b}\nonumber\\[4pt]&\,=\,& \lim_{s\downarrow s^*}\frac{d}{ds}\left(\frac{1}{b}-\frac{1}{4b \sqrt{\Delta(s)}}(8s+4(a+b))\right)\nonumber\\[4pt]&\,=\,&-\infty,\end{eqnarray}
\begin{eqnarray}\lim_{s\downarrow s^*}\frac{d}{ds}{\boldsymbol{\Psi}}(s)&\,=\,& \lim_{s\downarrow s^*}\frac{d}{ds} \frac{(a+b+2s)-\sqrt{\Delta(s)}}{2b}\nonumber\\[4pt]&\,=\,& \lim_{s\downarrow s^*}\frac{d}{ds}\left(\frac{1}{b}-\frac{1}{4b \sqrt{\Delta(s)}}(8s+4(a+b))\right)\nonumber\\[4pt]&\,=\,&-\infty,\end{eqnarray}
as expected. Furthermore,
 \begin{eqnarray}\lim_{s\downarrow (s^*)}\frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{\sqrt{s-s^*}}&\,=\,&\lim_{s\downarrow (s^*)}\left(\frac{(a+b+2s)-\sqrt{\Delta(s)}}{2b\sqrt{s-s^*}}-\frac{(a+b+2s^*)-\sqrt{\Delta(s^*)}}{2b\sqrt{s-s^*}}\right)\nonumber\\[4pt]&\,=\,& \frac{\sqrt{2\sqrt{ab}}}{-b},\end{eqnarray}
\begin{eqnarray}\lim_{s\downarrow (s^*)}\frac{{\boldsymbol{\Psi}}(s)-{\boldsymbol{\Psi}}(s^*)}{\sqrt{s-s^*}}&\,=\,&\lim_{s\downarrow (s^*)}\left(\frac{(a+b+2s)-\sqrt{\Delta(s)}}{2b\sqrt{s-s^*}}-\frac{(a+b+2s^*)-\sqrt{\Delta(s^*)}}{2b\sqrt{s-s^*}}\right)\nonumber\\[4pt]&\,=\,& \frac{\sqrt{2\sqrt{ab}}}{-b},\end{eqnarray}
which implies
where
Therefore, by Theorem 1,
 \begin{equation}\boldsymbol{\psi}(t)=\frac{\sqrt{2\sqrt{ab}}}{2b\sqrt{\pi}}t^{-3/2}\exp\left(\left(\frac{-(a+b)+2\sqrt{ab}}{2}\right)t\right)(1+o(1)).\end{equation}
\begin{equation}\boldsymbol{\psi}(t)=\frac{\sqrt{2\sqrt{ab}}}{2b\sqrt{\pi}}t^{-3/2}\exp\left(\left(\frac{-(a+b)+2\sqrt{ab}}{2}\right)t\right)(1+o(1)).\end{equation}
Also, ![]() ${\textbf{A}}_{12}(s^*)=0$,
${\textbf{A}}_{12}(s^*)=0$, ![]() ${\textbf{A}}_{21}(s^*)=0$,
${\textbf{A}}_{21}(s^*)=0$, ![]() ${\textbf{A}}_{11}(s^*)=1$,
${\textbf{A}}_{11}(s^*)=1$, ![]() ${\textbf{A}}_{22}(s^*)=1$, so
${\textbf{A}}_{22}(s^*)=1$, so
 \begin{eqnarray}{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*){\textbf{B}}(s^*)&\,=\,&b\left(\frac{\sqrt{2\sqrt{ab}}}{b}\right)^2= \ 2\sqrt{\frac{a}{b}}\ = \ {\textbf{U}}(s^*),\end{eqnarray}
\begin{eqnarray}{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*){\textbf{B}}(s^*)&\,=\,&b\left(\frac{\sqrt{2\sqrt{ab}}}{b}\right)^2= \ 2\sqrt{\frac{a}{b}}\ = \ {\textbf{U}}(s^*),\end{eqnarray}
and
 \begin{eqnarray}{\textbf{K}}(s^*){\textbf{B}}(s^*)+{\textbf{B}}(s^*){\textbf{D}}(s^*)&\,=\,&\left( \frac{b-a}{2}+\frac{a-b}{2} \right)\left(\frac{\sqrt{2\sqrt{ab}}}{b}\right)={\boldsymbol{0}},\end{eqnarray}
\begin{eqnarray}{\textbf{K}}(s^*){\textbf{B}}(s^*)+{\textbf{B}}(s^*){\textbf{D}}(s^*)&\,=\,&\left( \frac{b-a}{2}+\frac{a-b}{2} \right)\left(\frac{\sqrt{2\sqrt{ab}}}{b}\right)={\boldsymbol{0}},\end{eqnarray}
For ![]() $n\geq 1$, define the matrices
$n\geq 1$, define the matrices
 \begin{eqnarray}{\textbf{H}}_{1,n}(s^*)&\,=\,&\sum_{i=0}^{n-1}\left({\textbf{K}}(s^*) \right)^i\times{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*)\times\left({\textbf{K}}(s^*) \right)^{n-1-i}\end{eqnarray}
\begin{eqnarray}{\textbf{H}}_{1,n}(s^*)&\,=\,&\sum_{i=0}^{n-1}\left({\textbf{K}}(s^*) \right)^i\times{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*)\times\left({\textbf{K}}(s^*) \right)^{n-1-i}\end{eqnarray}
and
and define a column vector
 \begin{eqnarray}\widetilde{\textbf{H}}(s^*)&\,=\,&{\textbf{H}}(s^*){\textbf{C}}_1^{-1}{\boldsymbol{1}}+\left({-}({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}{\boldsymbol{1}}\nonumber\\[4pt]&&+\left[\begin{array}{c@{\quad}c}{\textbf{H}}(s^*)&-({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\end{array}\right]\left[\begin{array}{c}{\textbf{C}}_1^{-1}{\textbf{T}}_{10}\\[4pt]{\textbf{C}}_2^{-1}{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}){\boldsymbol{1}}.\nonumber\\[4pt]\end{eqnarray}
\begin{eqnarray}\widetilde{\textbf{H}}(s^*)&\,=\,&{\textbf{H}}(s^*){\textbf{C}}_1^{-1}{\boldsymbol{1}}+\left({-}({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}{\boldsymbol{1}}\nonumber\\[4pt]&&+\left[\begin{array}{c@{\quad}c}{\textbf{H}}(s^*)&-({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\end{array}\right]\left[\begin{array}{c}{\textbf{C}}_1^{-1}{\textbf{T}}_{10}\\[4pt]{\textbf{C}}_2^{-1}{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}){\boldsymbol{1}}.\nonumber\\[4pt]\end{eqnarray}
Below, we derive the expressions for ![]() $\boldsymbol{\mu}(dy)^{(0)}$.
$\boldsymbol{\mu}(dy)^{(0)}$.
Theorem 3. The matrix ![]() $\boldsymbol{\mu}(dy)^{(0)}$ is unique, and
$\boldsymbol{\mu}(dy)^{(0)}$ is unique, and
 \begin{eqnarray}\boldsymbol{\mu}(dy)^{(0)}_{11}&\,=\,&diag({\widetilde{\textbf{H}}(s^*)})^{-1}{ {\textbf{H}}(s^*,y){\textbf{C}}_1^{-1}}dy,\nonumber\\[4pt]\boldsymbol{\mu}(dy)^{(0)}_{12}&\,=\,&diag({\widetilde{\textbf{H}}(s^*)})^{-1}\left(e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*)+{\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}dy,\nonumber\\[4pt]\boldsymbol{\mu}(dy)^{(0)}_{10}&\,=\,& \left[\begin{array}{c@{\quad}c}\boldsymbol{\mu}(dy)^{(0)}_{11} &\boldsymbol{\mu}(dy)^{(0)}_{12}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}).\end{eqnarray}
\begin{eqnarray}\boldsymbol{\mu}(dy)^{(0)}_{11}&\,=\,&diag({\widetilde{\textbf{H}}(s^*)})^{-1}{ {\textbf{H}}(s^*,y){\textbf{C}}_1^{-1}}dy,\nonumber\\[4pt]\boldsymbol{\mu}(dy)^{(0)}_{12}&\,=\,&diag({\widetilde{\textbf{H}}(s^*)})^{-1}\left(e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*)+{\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}dy,\nonumber\\[4pt]\boldsymbol{\mu}(dy)^{(0)}_{10}&\,=\,& \left[\begin{array}{c@{\quad}c}\boldsymbol{\mu}(dy)^{(0)}_{11} &\boldsymbol{\mu}(dy)^{(0)}_{12}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}).\end{eqnarray}
Remark 3. From Theorem 3 it follows that the crucial step in identifying the Yaglom limit given above is identification of ![]() $s^*$. Unfortunately, this must be done for each stochastic fluid queue separately.
$s^*$. Unfortunately, this must be done for each stochastic fluid queue separately.
Proof. By Lemma 2, Lemma 5, and Theorem 2, we have
 \begin{eqnarray}e^{{\textbf{K}}(s)y}&\,=\,&\lim_{K\to\infty}\sum_{n=0}^{K}\frac{y^n}{n!}\left({\textbf{Q}}_{11}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s)\right)^n\nonumber\qquad\ \\[4pt]
&\,=\,&\lim_{K\to\infty}\sum_{n=0}^{K}\frac{y^n}{n!}\left({\textbf{Q}}_{11}(s^*)+\left( {\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)\sqrt{s-s^*} \right){\textbf{Q}}_{21}(s^*)+o(\sqrt{s-s^*})\right)^n\nonumber\\[4pt]
&\,=\,&\lim_{K\to\infty}\sum_{n=0}^{K}\frac{y^n}{n!}\left({\textbf{Q}}_{11}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{Q}}_{21}(s^*)\right)^n-\lim_{K\to\infty}\sqrt{s-s^*}\sum_{n=1}^{K }\frac{y^n}{n!}{\textbf{H}}_{1,n}+o(\sqrt{s-s^*})\nonumber\\[4pt]
&\,=\,&e^{{\textbf{K}}(s^*)y}-\sqrt{s-s^*}{\textbf{H}}(s^*,y)+o(\sqrt{s-s^*}),\end{eqnarray}
\begin{eqnarray}e^{{\textbf{K}}(s)y}&\,=\,&\lim_{K\to\infty}\sum_{n=0}^{K}\frac{y^n}{n!}\left({\textbf{Q}}_{11}(s)+{\boldsymbol{\Psi}}(s){\textbf{Q}}_{21}(s)\right)^n\nonumber\qquad\ \\[4pt]
&\,=\,&\lim_{K\to\infty}\sum_{n=0}^{K}\frac{y^n}{n!}\left({\textbf{Q}}_{11}(s^*)+\left( {\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)\sqrt{s-s^*} \right){\textbf{Q}}_{21}(s^*)+o(\sqrt{s-s^*})\right)^n\nonumber\\[4pt]
&\,=\,&\lim_{K\to\infty}\sum_{n=0}^{K}\frac{y^n}{n!}\left({\textbf{Q}}_{11}(s^*)+{\boldsymbol{\Psi}}(s^*){\textbf{Q}}_{21}(s^*)\right)^n-\lim_{K\to\infty}\sqrt{s-s^*}\sum_{n=1}^{K }\frac{y^n}{n!}{\textbf{H}}_{1,n}+o(\sqrt{s-s^*})\nonumber\\[4pt]
&\,=\,&e^{{\textbf{K}}(s^*)y}-\sqrt{s-s^*}{\textbf{H}}(s^*,y)+o(\sqrt{s-s^*}),\end{eqnarray}
which gives
 \begin{eqnarray}{\textbf{E}}(dy)^{(0)}(s)_{11}&\,=\,&e^{{\textbf{K}}(s)y}{\textbf{C}}_1^{-1}dy\nonumber\\[4pt]&\,=\,&{\textbf{E}}(dy)^{(0)}(s^*)_{11}-\sqrt{s-s^*}{\textbf{H}}(s^*,y){\textbf{C}}_1^{-1}dy+o(\sqrt{s-s^*})\end{eqnarray}
\begin{eqnarray}{\textbf{E}}(dy)^{(0)}(s)_{11}&\,=\,&e^{{\textbf{K}}(s)y}{\textbf{C}}_1^{-1}dy\nonumber\\[4pt]&\,=\,&{\textbf{E}}(dy)^{(0)}(s^*)_{11}-\sqrt{s-s^*}{\textbf{H}}(s^*,y){\textbf{C}}_1^{-1}dy+o(\sqrt{s-s^*})\end{eqnarray}
and
 \begin{eqnarray}
{\textbf{E}}(dy)^{(0)}(s)_{12}& = & e^{{\textbf{K}}(s)y}{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}dy\nonumber\\[4pt]
&=\,&\left(e^{{\textbf{K}}(s^*)y}-\sqrt{s-s^*}{\textbf{H}}(s^*,y)\right)({\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)\sqrt{s-s^*}){\textbf{C}}_2^{-1}dy+o(\sqrt{s-s^*})\nonumber\\[4pt]
&=\,&{\textbf{E}}(dy)^{(0)}(s^*)_{12}-\sqrt{s-s^*}\left(e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*)+{\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}dy+o(\sqrt{s-s^*}).\nonumber\\[5pt]\end{eqnarray}
\begin{eqnarray}
{\textbf{E}}(dy)^{(0)}(s)_{12}& = & e^{{\textbf{K}}(s)y}{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}dy\nonumber\\[4pt]
&=\,&\left(e^{{\textbf{K}}(s^*)y}-\sqrt{s-s^*}{\textbf{H}}(s^*,y)\right)({\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)\sqrt{s-s^*}){\textbf{C}}_2^{-1}dy+o(\sqrt{s-s^*})\nonumber\\[4pt]
&=\,&{\textbf{E}}(dy)^{(0)}(s^*)_{12}-\sqrt{s-s^*}\left(e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*)+{\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}dy+o(\sqrt{s-s^*}).\nonumber\\[5pt]\end{eqnarray}
Also, noting that ![]() $({\textbf{T}}_{00}-s{\textbf{I}})^{-1}-({\textbf{T}}_{00}-s^*{\textbf{I}})^{-1}=(s-s^*)({\textbf{T}}_{00}-s^*{\textbf{I}})^{-2}+o(s-s^*)$, which gives
$({\textbf{T}}_{00}-s{\textbf{I}})^{-1}-({\textbf{T}}_{00}-s^*{\textbf{I}})^{-1}=(s-s^*)({\textbf{T}}_{00}-s^*{\textbf{I}})^{-2}+o(s-s^*)$, which gives ![]() $({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1}=({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}+o(\sqrt{s-s^*})$, we have
$({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1}=({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}+o(\sqrt{s-s^*})$, we have
 \begin{eqnarray}&& {{\textbf{E}}(dy)^{(0)}(s)_{10}=\left[\begin{array}{c@{\quad}c} e^{{\textbf{K}}(s)y} {\textbf{C}}_1^{-1}&e^{{\textbf{K}}(s)y}{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})}\nonumber\\[4pt]
&&\,=\,{\textbf{E}}(dy)^{(0)}(s^*)_{10}-\sqrt{s-s^*}\left[\begin{array}{c@{\quad}c}{\textbf{H}}(s^*,y)&\left(e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*)+{\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*)\right)\end{array}\right]\nonumber\\[4pt]
&&\quad\times\left[\begin{array}{c}{\textbf{C}}_1^{-1}{\textbf{T}}_{10}\\[4pt]{\textbf{C}}_2^{-1}{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1})dy+o(\sqrt{s-s^*}).\end{eqnarray}
\begin{eqnarray}&& {{\textbf{E}}(dy)^{(0)}(s)_{10}=\left[\begin{array}{c@{\quad}c} e^{{\textbf{K}}(s)y} {\textbf{C}}_1^{-1}&e^{{\textbf{K}}(s)y}{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})}\nonumber\\[4pt]
&&\,=\,{\textbf{E}}(dy)^{(0)}(s^*)_{10}-\sqrt{s-s^*}\left[\begin{array}{c@{\quad}c}{\textbf{H}}(s^*,y)&\left(e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*)+{\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*)\right)\end{array}\right]\nonumber\\[4pt]
&&\quad\times\left[\begin{array}{c}{\textbf{C}}_1^{-1}{\textbf{T}}_{10}\\[4pt]{\textbf{C}}_2^{-1}{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1})dy+o(\sqrt{s-s^*}).\end{eqnarray}
Furthermore,
 \begin{eqnarray}{\textbf{E}}^{(0)}(s)_1&\,=\,&\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(0)}(s)_{11}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(0)}(s)_{12}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(0)}(s)_{10}{\boldsymbol{1}}\nonumber\\[8pt]
&\,=\,&{\textbf{E}}^{(0)}(s^*)_1-\sqrt{s-s^*}{\textbf{H}}(s^*){\textbf{C}}_1^{-1}{\boldsymbol{1}}-\sqrt{s-s^*}\left({-}({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right){\boldsymbol{1}}\nonumber\\[8pt]
&&-\sqrt{s-s^*}\left[\begin{array}{c@{\quad}c}{\textbf{H}}(s^*)&\left({-}({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right)\end{array}\right]\nonumber\\[9pt]
&&\times\left[\begin{array}{c}{\textbf{C}}_1^{-1}{\textbf{T}}_{10}\\[10pt]
{\textbf{C}}_2^{-1}{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}){\boldsymbol{1}}+o(\sqrt{s-s^*})\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(0)}(s^*)_1-\sqrt{s-s^*}\widetilde{\textbf{H}}(s^*)+o(\sqrt{s-s^*}).\end{eqnarray}
\begin{eqnarray}{\textbf{E}}^{(0)}(s)_1&\,=\,&\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(0)}(s)_{11}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(0)}(s)_{12}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(0)}(s)_{10}{\boldsymbol{1}}\nonumber\\[8pt]
&\,=\,&{\textbf{E}}^{(0)}(s^*)_1-\sqrt{s-s^*}{\textbf{H}}(s^*){\textbf{C}}_1^{-1}{\boldsymbol{1}}-\sqrt{s-s^*}\left({-}({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right){\boldsymbol{1}}\nonumber\\[8pt]
&&-\sqrt{s-s^*}\left[\begin{array}{c@{\quad}c}{\textbf{H}}(s^*)&\left({-}({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right)\end{array}\right]\nonumber\\[9pt]
&&\times\left[\begin{array}{c}{\textbf{C}}_1^{-1}{\textbf{T}}_{10}\\[10pt]
{\textbf{C}}_2^{-1}{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}){\boldsymbol{1}}+o(\sqrt{s-s^*})\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(0)}(s^*)_1-\sqrt{s-s^*}\widetilde{\textbf{H}}(s^*)+o(\sqrt{s-s^*}).\end{eqnarray}
The result follows from Theorem 1 and (10), since the relevant terms cancel out. Indeed, for ![]() $i,j\in\mathcal{S}_1$, by (138)–(141), Theorem 1, and (10),
$i,j\in\mathcal{S}_1$, by (138)–(141), Theorem 1, and (10),
 \begin{eqnarray} \mu(dy)^{(0)}_{ij} &\,=\,& \lim_{t\to\infty} \frac{ \mathbb{P}(X(t)\in dy,\varphi(t)=j,\theta(0)>t\, |\, X(0)=0,\varphi(0)=i) } { \mathbb{P}(\theta(0)>t\, |\, X(0)=0,\varphi(0)=i) } \nonumber\\[8pt]
&\,=\,& \frac{ \lim_{t\to\infty} ([{\textbf{H}}(s^*,y) {\textbf{C}}_1^{-1}]_{ij}\Gamma(1/2)^{-1}t^{-1/2-1}e^{s^*t}(1+o(1)) } { \lim_{t\to\infty} ([\widetilde{\textbf{H}}(s^*)]_{i}\Gamma(1/2)^{-1}t^{-1/2-1}e^{s^*t}(1+o(1)) }dy \nonumber\\[8pt]
&\,=\,& \frac{[{\textbf{H}}(s^*,y){\textbf{C}}_1^{-1}]_{ij} } { [\widetilde{\textbf{H}}(s^*)]_{i} }dy, \end{eqnarray}
\begin{eqnarray} \mu(dy)^{(0)}_{ij} &\,=\,& \lim_{t\to\infty} \frac{ \mathbb{P}(X(t)\in dy,\varphi(t)=j,\theta(0)>t\, |\, X(0)=0,\varphi(0)=i) } { \mathbb{P}(\theta(0)>t\, |\, X(0)=0,\varphi(0)=i) } \nonumber\\[8pt]
&\,=\,& \frac{ \lim_{t\to\infty} ([{\textbf{H}}(s^*,y) {\textbf{C}}_1^{-1}]_{ij}\Gamma(1/2)^{-1}t^{-1/2-1}e^{s^*t}(1+o(1)) } { \lim_{t\to\infty} ([\widetilde{\textbf{H}}(s^*)]_{i}\Gamma(1/2)^{-1}t^{-1/2-1}e^{s^*t}(1+o(1)) }dy \nonumber\\[8pt]
&\,=\,& \frac{[{\textbf{H}}(s^*,y){\textbf{C}}_1^{-1}]_{ij} } { [\widetilde{\textbf{H}}(s^*)]_{i} }dy, \end{eqnarray}
which gives the result for ![]() $\boldsymbol{\mu}(dy)^{(0)}_{11}$. The expressions for
$\boldsymbol{\mu}(dy)^{(0)}_{11}$. The expressions for ![]() $\boldsymbol{\mu}(dy)^{(0)}_{12}$ and
$\boldsymbol{\mu}(dy)^{(0)}_{12}$ and ![]() $\boldsymbol{\mu}(dy)^{(0)}_{10}$ follow in a similar manner.
$\boldsymbol{\mu}(dy)^{(0)}_{10}$ follow in a similar manner.
Example 1. Finally,
 \begin{eqnarray}{\textbf{H}}(s^*,y)&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}{\textbf{H}}_{1,n}(s^*)\nonumber\\[4pt]&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}\sum_{i=0}^{n-1}\left({\textbf{K}}(s^*) \right)^i\times{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*)\times\left({\textbf{K}}(s^*) \right)^{n-1-i}\nonumber\\[4pt]&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}\sum_{i=0}^{n-1}\left( -(a-b)/2\right)^{n-1}\sqrt{2\sqrt{ab}}\nonumber\\[4pt]&\,=\,&ye^{\left( -(a-b)/2 \right)y}\sqrt{2\sqrt{ab}},\end{eqnarray}
\begin{eqnarray}{\textbf{H}}(s^*,y)&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}{\textbf{H}}_{1,n}(s^*)\nonumber\\[4pt]&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}\sum_{i=0}^{n-1}\left({\textbf{K}}(s^*) \right)^i\times{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*)\times\left({\textbf{K}}(s^*) \right)^{n-1-i}\nonumber\\[4pt]&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}\sum_{i=0}^{n-1}\left( -(a-b)/2\right)^{n-1}\sqrt{2\sqrt{ab}}\nonumber\\[4pt]&\,=\,&ye^{\left( -(a-b)/2 \right)y}\sqrt{2\sqrt{ab}},\end{eqnarray}
and
 \begin{eqnarray}{\textbf{H}}(s^*)&\,=\,&\int_{y=0}^{\infty}ye^{\left( -(a-b)/2 \right)y}\sqrt{2\sqrt{ab}}\ dy\nonumber\\[4pt]
&\,=\,&\frac{\sqrt{2\sqrt{ab}}}{(a-b)^2/4},\nonumber\\[4pt]
\widetilde{\textbf{H}}(s^*)&\,=\,&{\textbf{H}}(s^*)+\left({-}({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right)\nonumber\\[4pt]
&\,=\,&\frac{\sqrt{2\sqrt{ab}}}{(a-b)^2/4} \left(1+\sqrt{\frac{a}{b}} \right)+\frac{2}{a-b}\left(\frac{\sqrt{2\sqrt{ab}}}{b}\right),\end{eqnarray}
\begin{eqnarray}{\textbf{H}}(s^*)&\,=\,&\int_{y=0}^{\infty}ye^{\left( -(a-b)/2 \right)y}\sqrt{2\sqrt{ab}}\ dy\nonumber\\[4pt]
&\,=\,&\frac{\sqrt{2\sqrt{ab}}}{(a-b)^2/4},\nonumber\\[4pt]
\widetilde{\textbf{H}}(s^*)&\,=\,&{\textbf{H}}(s^*)+\left({-}({\textbf{K}}(s^*))^{-1}{\textbf{B}}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right)\nonumber\\[4pt]
&\,=\,&\frac{\sqrt{2\sqrt{ab}}}{(a-b)^2/4} \left(1+\sqrt{\frac{a}{b}} \right)+\frac{2}{a-b}\left(\frac{\sqrt{2\sqrt{ab}}}{b}\right),\end{eqnarray}
so
 \begin{eqnarray}\boldsymbol{\mu}(dy)^{(0)}_{11}&\,=\,& diag({\widetilde{\textbf{H}}(s^*)})^{-1} { {\textbf{H}}(s^*,y)} dy \nonumber\\[4pt]
&\,=\,&\left(\frac{1}{(a-b)^2/4}\, \left(1+\sqrt{\frac{a}{b}} \right) +\frac{2}{a-b} \left( \frac{1}{b} \right)\right)^{-1}ye^{({-}(a-b)/2)y}dy,\nonumber\\[4pt]
\boldsymbol{\mu}(dy)^{(0)}_{12}&\,=\,&diag({\widetilde{\textbf{H}}(s^*)})^{-1}\left(e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*)+{\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*)\right)dy\nonumber\\[4pt]
&\,=\,& \left(\frac{1}{(a-b)^2/4}\, \left(1+\sqrt{\frac{a}{b}} \right) +\frac{2}{a-b} \left( \frac{1}{b} \right) \right)^{-1} \left( \frac{1}{b}+y\sqrt{\frac{a}{b}} \right) e^{({-}(a-b)/2)y} dy.\nonumber\\[4pt]
\end{eqnarray}
\begin{eqnarray}\boldsymbol{\mu}(dy)^{(0)}_{11}&\,=\,& diag({\widetilde{\textbf{H}}(s^*)})^{-1} { {\textbf{H}}(s^*,y)} dy \nonumber\\[4pt]
&\,=\,&\left(\frac{1}{(a-b)^2/4}\, \left(1+\sqrt{\frac{a}{b}} \right) +\frac{2}{a-b} \left( \frac{1}{b} \right)\right)^{-1}ye^{({-}(a-b)/2)y}dy,\nonumber\\[4pt]
\boldsymbol{\mu}(dy)^{(0)}_{12}&\,=\,&diag({\widetilde{\textbf{H}}(s^*)})^{-1}\left(e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*)+{\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*)\right)dy\nonumber\\[4pt]
&\,=\,& \left(\frac{1}{(a-b)^2/4}\, \left(1+\sqrt{\frac{a}{b}} \right) +\frac{2}{a-b} \left( \frac{1}{b} \right) \right)^{-1} \left( \frac{1}{b}+y\sqrt{\frac{a}{b}} \right) e^{({-}(a-b)/2)y} dy.\nonumber\\[4pt]
\end{eqnarray}
We plot the values of ![]() $\boldsymbol{\mu}(dy)^{(0)}_{11}$ and
$\boldsymbol{\mu}(dy)^{(0)}_{11}$ and ![]() $\boldsymbol{\mu}(dy)^{(0)}_{12}$ in Figure 1.
$\boldsymbol{\mu}(dy)^{(0)}_{12}$ in Figure 1.

Figure 1: The values of ![]() $\boldsymbol{\mu}(dy)^{(0)}_{11}/dy$ and
$\boldsymbol{\mu}(dy)^{(0)}_{11}/dy$ and ![]() $\boldsymbol{\mu}(dy)^{(0)}_{12}/dy$ in Example 4 for
$\boldsymbol{\mu}(dy)^{(0)}_{12}/dy$ in Example 4 for ![]() $b=1$,
$b=1$, ![]() $a=4,3,2$ (dotted, solid, and dashed lines, respectively).
$a=4,3,2$ (dotted, solid, and dashed lines, respectively).
We will now find the Yaglom limit for a strictly positive initial position of ![]() $X(0)=x>0$. For
$X(0)=x>0$. For ![]() $n\geq 1$, define the matrices
$n\geq 1$, define the matrices
 \begin{eqnarray} \mathbf{W}(s^*, x-z)&\,=\,&\sum_{n=1}^\infty \frac{(x-z)^n}{n!}\sum_{i=1}^{n-1}\mathbf{D}(s^*)^i \times\mathbf{Q}_{21}(s^*) \mathbf{B}(s^*) \times\mathbf{D}(s^*)^{n-1-i}, \nonumber\\[4pt] \mathbf{W}_x(s^*)&\,=\,&\int_{z=0}^x \mathbf{W}(s^*, x-z)dz, \nonumber\\[4pt] \mathbf{Z}_x(s^*,y)&\,=\,&\int_{z=0}^{\min\{x,y\}}\left(\mathbf{W}(s^*, x-z){\textbf{Q}}_{21}(s^*)e^{{\textbf{K}}(s^*)(y-z)}\right. \nonumber\\[4pt] &&\left.+e^{{\textbf{D}}(s^*)(x-z)}{\textbf{Q}}_{21}(s^*)\mathbf{H}(s^*, y-z) \right)dz, \nonumber\\[4pt] {\mathbf{Z}}_x(s^*)&\,=\,&\int_{y=0}^\infty \mathbf{Z}_x(s^*,y)\;dy, \end{eqnarray}
\begin{eqnarray} \mathbf{W}(s^*, x-z)&\,=\,&\sum_{n=1}^\infty \frac{(x-z)^n}{n!}\sum_{i=1}^{n-1}\mathbf{D}(s^*)^i \times\mathbf{Q}_{21}(s^*) \mathbf{B}(s^*) \times\mathbf{D}(s^*)^{n-1-i}, \nonumber\\[4pt] \mathbf{W}_x(s^*)&\,=\,&\int_{z=0}^x \mathbf{W}(s^*, x-z)dz, \nonumber\\[4pt] \mathbf{Z}_x(s^*,y)&\,=\,&\int_{z=0}^{\min\{x,y\}}\left(\mathbf{W}(s^*, x-z){\textbf{Q}}_{21}(s^*)e^{{\textbf{K}}(s^*)(y-z)}\right. \nonumber\\[4pt] &&\left.+e^{{\textbf{D}}(s^*)(x-z)}{\textbf{Q}}_{21}(s^*)\mathbf{H}(s^*, y-z) \right)dz, \nonumber\\[4pt] {\mathbf{Z}}_x(s^*)&\,=\,&\int_{y=0}^\infty \mathbf{Z}_x(s^*,y)\;dy, \end{eqnarray}
and define the column vectors
 \begin{eqnarray*} \widetilde{\mathbf{Z}}_x(s^*) &\,=\,&\widetilde{\mathbf{Z}}_x(s^*)_{11}{\boldsymbol{1}} + \widetilde{\mathbf{Z}}_x(s^*)_{12}{\boldsymbol{1}} \nonumber\\[4pt]
&& + \left[ \begin{array}{c@{\quad}c} \widetilde{\mathbf{Z}}_x(s^*)_{11} & \widetilde{\mathbf{Z}}_x(s^*)_{12} \end{array} \right] \left[ \begin{array}{c} {\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20} \end{array} \right] ({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}) {\boldsymbol{1}}, \widetilde{\widetilde{\mathbf{Z}}}_x(s^*) &\,=\,&\widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{21}{\boldsymbol{1}} + \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{22}{\boldsymbol{1}} \nonumber\\[4pt]
&& + \left[ \begin{array}{c@{\quad}c} \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{21} & \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_x(s^*)_{22} \end{array} \right] \left[ \begin{array}{c} {\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20} \end{array} \right] ({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}) {\boldsymbol{1}},\end{eqnarray*}
\begin{eqnarray*} \widetilde{\mathbf{Z}}_x(s^*) &\,=\,&\widetilde{\mathbf{Z}}_x(s^*)_{11}{\boldsymbol{1}} + \widetilde{\mathbf{Z}}_x(s^*)_{12}{\boldsymbol{1}} \nonumber\\[4pt]
&& + \left[ \begin{array}{c@{\quad}c} \widetilde{\mathbf{Z}}_x(s^*)_{11} & \widetilde{\mathbf{Z}}_x(s^*)_{12} \end{array} \right] \left[ \begin{array}{c} {\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20} \end{array} \right] ({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}) {\boldsymbol{1}}, \widetilde{\widetilde{\mathbf{Z}}}_x(s^*) &\,=\,&\widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{21}{\boldsymbol{1}} + \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{22}{\boldsymbol{1}} \nonumber\\[4pt]
&& + \left[ \begin{array}{c@{\quad}c} \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{21} & \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_x(s^*)_{22} \end{array} \right] \left[ \begin{array}{c} {\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20} \end{array} \right] ({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}) {\boldsymbol{1}},\end{eqnarray*}
where
 \begin{eqnarray} \widetilde{\mathbf{Z}}_x(s^*)_{11}&\,=\,& {\mathbf{Z}}_x(s^*){\textbf{C}}_1^{-1}, \nonumber\\[4pt] \widetilde{\mathbf{Z}}_x(s^*)_{12}&\,=\,& \left( {\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1 \mathbf{B}(s^*) +{\mathbf{Z}}_x(s^*){\boldsymbol{\Psi}}(s^*)+\mathbf{W}_x(s^*) \right) {\textbf{C}}_2^{-1}, \nonumber\\[4pt] \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{21} &\,=\,& \mathbf{B}(s^*){\textbf{E}}^{(x)}(s^*)_{21} +{\boldsymbol{\Psi}}(s^*)\mathbf{Z}_x(s^*){\textbf{C}}_1^{-1} +\mathbf{H}(s^*){\textbf{C}}_1^{-1}, \nonumber\\[4pt] \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{22}&\,=\,& \mathbf{B}(s^*){\textbf{E}}^{(x)}(s^*)_{22} +{\boldsymbol{\Psi}}(s^*) \Big( {\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1} +\mathbf{Z}_x(s^*){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1} + \mathbf{W}(s^*){\textbf{C}}_2^{-1} \Big) \nonumber\\[4pt] && + \left( ({-}{{\textbf{K}}(s^*))^{-1}}\mathbf{B}(s^*) + {\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*) \right){\textbf{C}}_2^{-1}, \end{eqnarray}
\begin{eqnarray} \widetilde{\mathbf{Z}}_x(s^*)_{11}&\,=\,& {\mathbf{Z}}_x(s^*){\textbf{C}}_1^{-1}, \nonumber\\[4pt] \widetilde{\mathbf{Z}}_x(s^*)_{12}&\,=\,& \left( {\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1 \mathbf{B}(s^*) +{\mathbf{Z}}_x(s^*){\boldsymbol{\Psi}}(s^*)+\mathbf{W}_x(s^*) \right) {\textbf{C}}_2^{-1}, \nonumber\\[4pt] \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{21} &\,=\,& \mathbf{B}(s^*){\textbf{E}}^{(x)}(s^*)_{21} +{\boldsymbol{\Psi}}(s^*)\mathbf{Z}_x(s^*){\textbf{C}}_1^{-1} +\mathbf{H}(s^*){\textbf{C}}_1^{-1}, \nonumber\\[4pt] \widetilde{\widetilde{\mathbf{Z}}}_x(s^*)_{22}&\,=\,& \mathbf{B}(s^*){\textbf{E}}^{(x)}(s^*)_{22} +{\boldsymbol{\Psi}}(s^*) \Big( {\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1} +\mathbf{Z}_x(s^*){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1} + \mathbf{W}(s^*){\textbf{C}}_2^{-1} \Big) \nonumber\\[4pt] && + \left( ({-}{{\textbf{K}}(s^*))^{-1}}\mathbf{B}(s^*) + {\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*) \right){\textbf{C}}_2^{-1}, \end{eqnarray}
with ![]() ${\textbf{E}}^{(x)}(s^*)_{21}=\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s^*)_{21}$ as considered in Remark 2, and
${\textbf{E}}^{(x)}(s^*)_{21}=\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s^*)_{21}$ as considered in Remark 2, and
 \begin{eqnarray}{\textbf{E}}^{(x)}(s^*)_{22}&\,=\,&{\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}+\int_{y=0}^xe^{{\textbf{D}}(s^*)(x-y)}{\textbf{C}}_2^{-1}dy\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}-\int_{w=0}^xe^{{\textbf{D}}(s^*)w}{\textbf{C}}_2^{-1}dw\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}-({\textbf{D}}(s^*))^{-1}\left(e^{{\textbf{D}}(s^*)x}-{\textbf{I}}\right){\textbf{C}}_2^{-1}.\end{eqnarray}
\begin{eqnarray}{\textbf{E}}^{(x)}(s^*)_{22}&\,=\,&{\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}+\int_{y=0}^xe^{{\textbf{D}}(s^*)(x-y)}{\textbf{C}}_2^{-1}dy\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}-\int_{w=0}^xe^{{\textbf{D}}(s^*)w}{\textbf{C}}_2^{-1}dw\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(x)}(s^*)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}-({\textbf{D}}(s^*))^{-1}\left(e^{{\textbf{D}}(s^*)x}-{\textbf{I}}\right){\textbf{C}}_2^{-1}.\end{eqnarray}
Theorem 4. For ![]() $x>0$, the matrix
$x>0$, the matrix ![]() $\boldsymbol{\mu}(dy)^{(x)}$ is unique, and
$\boldsymbol{\mu}(dy)^{(x)}$ is unique, and
 \begin{eqnarray*}\boldsymbol{\mu}(dy)^{(x)}_{21}&\,=\,&diag({\widetilde{\textbf{Z}}_x(s^*)})^{-1}{{\textbf{Z}}_x(s^*,y){\textbf{C}}_1^{-1}}dy,\nonumber\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{22}&\,=\,&diag({\widetilde{\textbf{Z}}_x(s^*)})^{-1}\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1}+\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy\nonumber\\[8pt]
&&+ \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big),\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{20}&\,=\,&\left[\begin{array}{c@{\quad}c}\boldsymbol{\mu}(dy)^{(x)}_{21}&\boldsymbol{\mu}(dy)^{(x)}_{22}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}),\nonumber\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{11}&\,=\,&diag({\widetilde{\widetilde{\textbf{Z}}}_x(s^*)})^{-1}\Big(\mathbf{B}(s^*){\textbf{E}}(dy)^{(x)}(s^*)_{21}+{\boldsymbol{\Psi}}(s^*)\mathbf{Z}_x(s^*,y){\textbf{C}}_1^{-1} dy\\[4pt]
&&+\mathbf{H}(s^*, y-x){\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy\Big),\boldsymbol{\mu}(dy)^{(x)}_{12}&\,=\,&diag({\widetilde{\widetilde{\textbf{Z}}}_x(s^*)})^{-1}\Big\{\Big(\mathbf{B}(s^*){\textbf{E}}(dy)^{(x)}(s^*)_{22}+{\boldsymbol{\Psi}}(s^*)\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1}\nonumber\\[4pt]&&+\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy+ \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big)\Big)\nonumber\\[4pt]&&+\left(e^{{\textbf{K}}(s^*)(y-x)}\mathbf{B}(s^*)+{\textbf{H}}(s^*,y-x){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y>x\}dy\Big\},\nonumber\\[4pt]\boldsymbol{\mu}(dy)^{(x)}_{10}&\,=\,&\left[\begin{array}{c@{\quad}c}\boldsymbol{\mu}(dy)^{(x)}_{11}&\boldsymbol{\mu}(dy)^{(x)}_{12}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}).
\end{eqnarray*}
\begin{eqnarray*}\boldsymbol{\mu}(dy)^{(x)}_{21}&\,=\,&diag({\widetilde{\textbf{Z}}_x(s^*)})^{-1}{{\textbf{Z}}_x(s^*,y){\textbf{C}}_1^{-1}}dy,\nonumber\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{22}&\,=\,&diag({\widetilde{\textbf{Z}}_x(s^*)})^{-1}\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1}+\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy\nonumber\\[8pt]
&&+ \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big),\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{20}&\,=\,&\left[\begin{array}{c@{\quad}c}\boldsymbol{\mu}(dy)^{(x)}_{21}&\boldsymbol{\mu}(dy)^{(x)}_{22}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}),\nonumber\\[8pt]
\boldsymbol{\mu}(dy)^{(x)}_{11}&\,=\,&diag({\widetilde{\widetilde{\textbf{Z}}}_x(s^*)})^{-1}\Big(\mathbf{B}(s^*){\textbf{E}}(dy)^{(x)}(s^*)_{21}+{\boldsymbol{\Psi}}(s^*)\mathbf{Z}_x(s^*,y){\textbf{C}}_1^{-1} dy\\[4pt]
&&+\mathbf{H}(s^*, y-x){\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy\Big),\boldsymbol{\mu}(dy)^{(x)}_{12}&\,=\,&diag({\widetilde{\widetilde{\textbf{Z}}}_x(s^*)})^{-1}\Big\{\Big(\mathbf{B}(s^*){\textbf{E}}(dy)^{(x)}(s^*)_{22}+{\boldsymbol{\Psi}}(s^*)\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1}\nonumber\\[4pt]&&+\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy+ \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big)\Big)\nonumber\\[4pt]&&+\left(e^{{\textbf{K}}(s^*)(y-x)}\mathbf{B}(s^*)+{\textbf{H}}(s^*,y-x){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y>x\}dy\Big\},\nonumber\\[4pt]\boldsymbol{\mu}(dy)^{(x)}_{10}&\,=\,&\left[\begin{array}{c@{\quad}c}\boldsymbol{\mu}(dy)^{(x)}_{11}&\boldsymbol{\mu}(dy)^{(x)}_{12}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1}).
\end{eqnarray*}
The next corollary follows from Theorems 3 and 4.
Corollary 2. The Yaglom limit depends on the initial position of the fluid level ![]() $X(0)=x$ in the model.
$X(0)=x$ in the model.
Remark 4. There has been a conjecture that the Yaglom limit does not depend on the initial position of the Markov process. However, a counterexample to this conjecture has already been provided by Foley and McDonald [Reference Foley and McDonald26]. Our model produces another counterexample of the same kind.
Proof. Our proof is again based on Theorem 1 and (10). Note that
 \begin{align}e^{\mathbf{D}(s)(x-z)}& =\lim_{K\to+\infty}\sum_{n=0}^K\frac{(x-z)^n}{n!}\left(\mathbf{Q}_{22}(s)+\mathbf{Q}_{21}(s){\boldsymbol{\Psi}}(s)\right)^n\nonumber\\[4pt]
& =\lim_{K\to+\infty}\sum_{n=0}^k\frac{(x-z)^n}{n!}\left(\mathbf{Q}_{22}(s^*)+\mathbf{Q}_{21}(s^*)({\boldsymbol{\Psi}}(s^*)-\mathbf{B}(s^*)\sqrt{s-s^*}+o(\sqrt{s-s^*})))\right)^n\nonumber\\[4pt]
& = e^{\mathbf{D}(s^*)(x-z)}- \sqrt{s-s^*}\mathbf{W}(s^*, x-z)+o(\sqrt{s-s^*}).\end{align}
\begin{align}e^{\mathbf{D}(s)(x-z)}& =\lim_{K\to+\infty}\sum_{n=0}^K\frac{(x-z)^n}{n!}\left(\mathbf{Q}_{22}(s)+\mathbf{Q}_{21}(s){\boldsymbol{\Psi}}(s)\right)^n\nonumber\\[4pt]
& =\lim_{K\to+\infty}\sum_{n=0}^k\frac{(x-z)^n}{n!}\left(\mathbf{Q}_{22}(s^*)+\mathbf{Q}_{21}(s^*)({\boldsymbol{\Psi}}(s^*)-\mathbf{B}(s^*)\sqrt{s-s^*}+o(\sqrt{s-s^*})))\right)^n\nonumber\\[4pt]
& = e^{\mathbf{D}(s^*)(x-z)}- \sqrt{s-s^*}\mathbf{W}(s^*, x-z)+o(\sqrt{s-s^*}).\end{align}
By (137), (150), Lemmas 5 and 3, and Theorem 2, we have
 \begin{eqnarray}{\textbf{E}}(dy)^{(x)}(s)_{21}&\,=\,&\int_{z=0}^{\min\{x,y\}}e^{{\textbf{D}}(s)(x-z)}{\textbf{Q}}_{21}(s)e^{{\textbf{K}}(s)(y-z)}{\textbf{C}}_1^{-1}dzdy\nonumber\\[4pt]&\,=\,&\int_{z=0}^{\min\{x,y\}}\left(e^{\mathbf{D}(s^*)(x-z)}- \sqrt{s-s^*}\mathbf{W}^*(s^*, x-z)\right)\mathbf{Q}_{21}(s^*)\nonumber\\[4pt]&&\times \left(e^{\mathbf{K}(s^*)(y-z)}- \sqrt{s-s^*}\mathbf{H}(s^*, y-z)\right){\textbf{C}}_1^{-1}dz dy+o(\sqrt{s-s^*})\nonumber\\[4pt]&\,=\,&{\textbf{E}}(dy)^{(x)}(s^*)_{21}- \sqrt{s-s^*}\mathbf{Z}_x(s^*,y){\textbf{C}}_1^{-1} dy +o(\sqrt{s-s^*}),\end{eqnarray}
\begin{eqnarray}{\textbf{E}}(dy)^{(x)}(s)_{21}&\,=\,&\int_{z=0}^{\min\{x,y\}}e^{{\textbf{D}}(s)(x-z)}{\textbf{Q}}_{21}(s)e^{{\textbf{K}}(s)(y-z)}{\textbf{C}}_1^{-1}dzdy\nonumber\\[4pt]&\,=\,&\int_{z=0}^{\min\{x,y\}}\left(e^{\mathbf{D}(s^*)(x-z)}- \sqrt{s-s^*}\mathbf{W}^*(s^*, x-z)\right)\mathbf{Q}_{21}(s^*)\nonumber\\[4pt]&&\times \left(e^{\mathbf{K}(s^*)(y-z)}- \sqrt{s-s^*}\mathbf{H}(s^*, y-z)\right){\textbf{C}}_1^{-1}dz dy+o(\sqrt{s-s^*})\nonumber\\[4pt]&\,=\,&{\textbf{E}}(dy)^{(x)}(s^*)_{21}- \sqrt{s-s^*}\mathbf{Z}_x(s^*,y){\textbf{C}}_1^{-1} dy +o(\sqrt{s-s^*}),\end{eqnarray}
 \begin{align}& {\textbf{E}}(dy)^{(x)}(s)_{22}={\textbf{E}}(dy)^{(x)}(s)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}+e^{{\textbf{D}}(s)(x-y)}{\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y<x\}dy\nonumber\\[4pt]
& = \left({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1- \sqrt{s-s^*}\mathbf{Z}_x(s^*,y) dy\right)\left({\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)\sqrt{s-s^*}\right){\textbf{C}}_2^{-1}\nonumber\\[4pt]
& \quad +\left(e^{\mathbf{D}(s^*)(x-y)}- \sqrt{s-s^*}\mathbf{W}(s^*, x-y)\right){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y<x\}dy+o(\sqrt{s-s^*})\nonumber\\[4pt]
& ={\textbf{E}}(dy)^{(x)}(s^*)_{22}- \sqrt{s-s^*}\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1({-}\mathbf{B}(s^*)){\textbf{C}}_2^{-1}+\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy\nonumber\\[4pt]
& \quad + \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big)+o(\sqrt{s-s^*}),\end{align}
\begin{align}& {\textbf{E}}(dy)^{(x)}(s)_{22}={\textbf{E}}(dy)^{(x)}(s)_{21}{\textbf{C}}_1{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}+e^{{\textbf{D}}(s)(x-y)}{\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y<x\}dy\nonumber\\[4pt]
& = \left({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1- \sqrt{s-s^*}\mathbf{Z}_x(s^*,y) dy\right)\left({\boldsymbol{\Psi}}(s^*)-{\textbf{B}}(s^*)\sqrt{s-s^*}\right){\textbf{C}}_2^{-1}\nonumber\\[4pt]
& \quad +\left(e^{\mathbf{D}(s^*)(x-y)}- \sqrt{s-s^*}\mathbf{W}(s^*, x-y)\right){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y<x\}dy+o(\sqrt{s-s^*})\nonumber\\[4pt]
& ={\textbf{E}}(dy)^{(x)}(s^*)_{22}- \sqrt{s-s^*}\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1({-}\mathbf{B}(s^*)){\textbf{C}}_2^{-1}+\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy\nonumber\\[4pt]
& \quad + \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big)+o(\sqrt{s-s^*}),\end{align}
 \begin{align}& {{\textbf{E}}(dy)^{(x)}(s)_{20}=\left[\begin{array}{c@{\quad}c}{\textbf{E}}(dy)^{(x)}(s)_{21}&{\textbf{E}}(dy)^{(x)}(s)_{22}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})}\nonumber\\[4pt]
& = {\textbf{E}}(dy)^{(x)}(s^*)_{20}\nonumber\\[4pt]
& \quad - \sqrt{s-s^*} \left[ \begin{array}{c@{\quad}c} {\mathbf{Z}}_x(s^*,y) & {\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1 \mathbf{B}(s^*) +{\mathbf{Z}}_x(s^*){\boldsymbol{\Psi}}(s^*)dy+\mathbf{W}(s^*,x-y){\boldsymbol{1}}\{y<x\}dy \end{array} \right] \nonumber\\[4pt]
& \quad\times \left[ \begin{array}{c} {\textbf{C}}_1^{-1}{\textbf{T}}_{10}\\[4pt]
{\textbf{C}}_2^{-1}{\textbf{T}}_{20} \end{array} \right] ({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1})+o(\sqrt{s-s^*}),\end{align}
\begin{align}& {{\textbf{E}}(dy)^{(x)}(s)_{20}=\left[\begin{array}{c@{\quad}c}{\textbf{E}}(dy)^{(x)}(s)_{21}&{\textbf{E}}(dy)^{(x)}(s)_{22}\end{array}\right]\left[\begin{array}{c}{\textbf{T}}_{10}\\[4pt]
{\textbf{T}}_{20}\end{array}\right]({-}({{\textbf{T}}}_{00}-s{\textbf{I}})^{-1})}\nonumber\\[4pt]
& = {\textbf{E}}(dy)^{(x)}(s^*)_{20}\nonumber\\[4pt]
& \quad - \sqrt{s-s^*} \left[ \begin{array}{c@{\quad}c} {\mathbf{Z}}_x(s^*,y) & {\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1 \mathbf{B}(s^*) +{\mathbf{Z}}_x(s^*){\boldsymbol{\Psi}}(s^*)dy+\mathbf{W}(s^*,x-y){\boldsymbol{1}}\{y<x\}dy \end{array} \right] \nonumber\\[4pt]
& \quad\times \left[ \begin{array}{c} {\textbf{C}}_1^{-1}{\textbf{T}}_{10}\\[4pt]
{\textbf{C}}_2^{-1}{\textbf{T}}_{20} \end{array} \right] ({-}({{\textbf{T}}}_{00}-s^*{\textbf{I}})^{-1})+o(\sqrt{s-s^*}),\end{align}
and
 \begin{eqnarray}{\textbf{E}}^{(x)}(s)_2&\,=\,&\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{21}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{22}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{20}{\boldsymbol{1}}\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(x)}(s^*)_1- \sqrt{s-s^*}\widetilde{\textbf{Z}}_x(s^*)+o(\sqrt{s-s^*}).\end{eqnarray}
\begin{eqnarray}{\textbf{E}}^{(x)}(s)_2&\,=\,&\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{21}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{22}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{20}{\boldsymbol{1}}\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(x)}(s^*)_1- \sqrt{s-s^*}\widetilde{\textbf{Z}}_x(s^*)+o(\sqrt{s-s^*}).\end{eqnarray}
Thus, the expressions for ![]() $\boldsymbol{\mu}(dy)^{(x)}_{21}$,
$\boldsymbol{\mu}(dy)^{(x)}_{21}$, ![]() $\boldsymbol{\mu}(dy)^{(x)}_{22}$, and
$\boldsymbol{\mu}(dy)^{(x)}_{22}$, and ![]() $\boldsymbol{\mu}(dy)^{(x)}_{20}$ follow from arguments similar to those in the proof of Theorem 3.
$\boldsymbol{\mu}(dy)^{(x)}_{20}$ follow from arguments similar to those in the proof of Theorem 3.
Furthermore, by (137), Lemmas 5 and 3, and Theorem 2, we have
 \begin{align}&{{\textbf{E}}(dy)^{(x)}(s)_{11}={\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{21}+e^{{\textbf{K}}(s)(y-x)}{\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy}\nonumber\\[4pt]
& = ({\boldsymbol{\Psi}}(s^*)-\mathbf{B}(s^*)\sqrt{s-s^*})({\textbf{E}}(dy)^{(x)}(s^*)_{21}- \sqrt{s-s^*}\mathbf{Z}_x(s^*,y){\textbf{C}}_1^{-1} dy)\nonumber\\[4pt]
& \quad +\left(e^{\mathbf{K}(s^*)(y-x)}- \sqrt{s-s^*}\mathbf{H}(s^*, y-x)\right){\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy+o(\sqrt{s-s^*})\nonumber\\[4pt]
& = {\textbf{E}}(dy)^{(x)}(s^*)_{11}- \sqrt{s-s^*}\Big(\mathbf{B}(s^*){\textbf{E}}(dy)^{(x)}(s^*)_{21}+{\boldsymbol{\Psi}}(s^*)\mathbf{Z}_x(s^*,y){\textbf{C}}_1^{-1} dy\nonumber\\[4pt]
& \quad +\mathbf{H}(s^*, y-x){\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy\Big)+o(\sqrt{s-s^*})\end{align}
\begin{align}&{{\textbf{E}}(dy)^{(x)}(s)_{11}={\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{21}+e^{{\textbf{K}}(s)(y-x)}{\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy}\nonumber\\[4pt]
& = ({\boldsymbol{\Psi}}(s^*)-\mathbf{B}(s^*)\sqrt{s-s^*})({\textbf{E}}(dy)^{(x)}(s^*)_{21}- \sqrt{s-s^*}\mathbf{Z}_x(s^*,y){\textbf{C}}_1^{-1} dy)\nonumber\\[4pt]
& \quad +\left(e^{\mathbf{K}(s^*)(y-x)}- \sqrt{s-s^*}\mathbf{H}(s^*, y-x)\right){\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy+o(\sqrt{s-s^*})\nonumber\\[4pt]
& = {\textbf{E}}(dy)^{(x)}(s^*)_{11}- \sqrt{s-s^*}\Big(\mathbf{B}(s^*){\textbf{E}}(dy)^{(x)}(s^*)_{21}+{\boldsymbol{\Psi}}(s^*)\mathbf{Z}_x(s^*,y){\textbf{C}}_1^{-1} dy\nonumber\\[4pt]
& \quad +\mathbf{H}(s^*, y-x){\textbf{C}}_1^{-1}{\boldsymbol{1}}\{y>x\}dy\Big)+o(\sqrt{s-s^*})\end{align}
and
 \begin{align}& {{\textbf{E}}(dy)^{(x)}(s)_{12}={\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{22}+e^{{\textbf{K}}(s)(y-x)}{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y> x\}dy}\nonumber\\[4pt]
& = \left({\boldsymbol{\Psi}}(s^*)-\mathbf{B}(s^*)\sqrt{s-s^*}\right)\Big( {\textbf{E}}(dy)^{(x)}(s^*)_{22}- \sqrt{s-s^*}\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1}\nonumber\\[4pt]
& \quad +\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy+ \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big)\nonumber\\[4pt]
& \quad +\Big(e^{{\textbf{K}}(s^*)(y-x)}{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y>x\}dy\nonumber\\[4pt]
& \quad - \sqrt{s-s^*}\left(e^{{\textbf{K}}(s^*)(y-x)}\mathbf{B}(s^*)+{\textbf{H}}(s^*,y-x){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}dy\Big)+o(\sqrt{s-s^*})\nonumber\\[4pt]
& = {\textbf{E}}(dy)^{(x)}(s^*)_{12}- \sqrt{s-s^*}\Big(\mathbf{B}(s^*){\textbf{E}}(dy)^{(x)}(s^*)_{22}+{\boldsymbol{\Psi}}(s^*)\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1}\nonumber\\[4pt]
& \quad +\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy+ \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big)\Big)\nonumber\\[4pt]
& \quad - \sqrt{s-s^*}\left(e^{{\textbf{K}}(s^*)(y-x)}\mathbf{B}(s^*)+{\textbf{H}}(s^*,y-x){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y>x\}dy+o(\sqrt{s-s^*}).\nonumber\\[4pt]
\end{align}
\begin{align}& {{\textbf{E}}(dy)^{(x)}(s)_{12}={\boldsymbol{\Psi}}(s){\textbf{E}}(dy)^{(x)}(s)_{22}+e^{{\textbf{K}}(s)(y-x)}{\boldsymbol{\Psi}}(s){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y> x\}dy}\nonumber\\[4pt]
& = \left({\boldsymbol{\Psi}}(s^*)-\mathbf{B}(s^*)\sqrt{s-s^*}\right)\Big( {\textbf{E}}(dy)^{(x)}(s^*)_{22}- \sqrt{s-s^*}\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1}\nonumber\\[4pt]
& \quad +\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy+ \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big)\nonumber\\[4pt]
& \quad +\Big(e^{{\textbf{K}}(s^*)(y-x)}{\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y>x\}dy\nonumber\\[4pt]
& \quad - \sqrt{s-s^*}\left(e^{{\textbf{K}}(s^*)(y-x)}\mathbf{B}(s^*)+{\textbf{H}}(s^*,y-x){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}dy\Big)+o(\sqrt{s-s^*})\nonumber\\[4pt]
& = {\textbf{E}}(dy)^{(x)}(s^*)_{12}- \sqrt{s-s^*}\Big(\mathbf{B}(s^*){\textbf{E}}(dy)^{(x)}(s^*)_{22}+{\boldsymbol{\Psi}}(s^*)\Big({\textbf{E}}(dy)^{(x)}(s^*)_{21}{\textbf{C}}_1\mathbf{B}(s^*){\textbf{C}}_2^{-1}\nonumber\\[4pt]
& \quad +\mathbf{Z}_x(s^*,y){\boldsymbol{\Psi}}(s^*){\textbf{C}}_2^{-1}dy+ \mathbf{W}(s^*, x-y){\boldsymbol{1}}\{y<x\}{\textbf{C}}_2^{-1}dy\Big)\Big)\nonumber\\[4pt]
& \quad - \sqrt{s-s^*}\left(e^{{\textbf{K}}(s^*)(y-x)}\mathbf{B}(s^*)+{\textbf{H}}(s^*,y-x){\boldsymbol{\Psi}}(s^*)\right){\textbf{C}}_2^{-1}{\boldsymbol{1}}\{y>x\}dy+o(\sqrt{s-s^*}).\nonumber\\[4pt]
\end{align}
Thus, the expressions for ![]() $\boldsymbol{\mu}(dy)^{(x)}_{11}$,
$\boldsymbol{\mu}(dy)^{(x)}_{11}$, ![]() $\boldsymbol{\mu}(dy)^{(x)}_{12}$, and
$\boldsymbol{\mu}(dy)^{(x)}_{12}$, and ![]() $\boldsymbol{\mu}(dy)^{(x)}_{10}$ follow from a similar argument, with
$\boldsymbol{\mu}(dy)^{(x)}_{10}$ follow from a similar argument, with
 \begin{eqnarray}{\textbf{E}}^{(x)}(s)_1&\,=\,&\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{11}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{12}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{10}{\boldsymbol{1}}\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(x)}(s^*)_1- \sqrt{s-s^*}\widetilde{\widetilde{\textbf{Z}}}_x(s^*)+o(\sqrt{s-s^*}).\end{eqnarray}
\begin{eqnarray}{\textbf{E}}^{(x)}(s)_1&\,=\,&\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{11}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{12}{\boldsymbol{1}}+\int_{y=0}^{\infty}{\textbf{E}}(dy)^{(x)}(s)_{10}{\boldsymbol{1}}\nonumber\\[4pt]&\,=\,&{\textbf{E}}^{(x)}(s^*)_1- \sqrt{s-s^*}\widetilde{\widetilde{\textbf{Z}}}_x(s^*)+o(\sqrt{s-s^*}).\end{eqnarray}
5. Example with non-scalar  ${\boldsymbol{\Psi}}(s)$
${\boldsymbol{\Psi}}(s)$
Below we construct an example where, unlike in Example 1, key quantities are matrices, rather than scalars. We derive expressions for this example analytically and illustrate these results with some numerical output as well.
Example 2. Consider a system with ![]() $N=2$ sources based on an example analysed in [Reference Anick, Mitra and Sondhi6]. Let
$N=2$ sources based on an example analysed in [Reference Anick, Mitra and Sondhi6]. Let ![]() $\mathcal{S}=\{1,2,3\}$,
$\mathcal{S}=\{1,2,3\}$, ![]() $\mathcal{S}_1=\{1\}$,
$\mathcal{S}_1=\{1\}$, ![]() $\mathcal{S}_2=\{2,3\}$,
$\mathcal{S}_2=\{2,3\}$, ![]() $c_1=1$,
$c_1=1$, ![]() $c_2=c_3=-1$, and
$c_2=c_3=-1$, and
 \begin{eqnarray}{\textbf{T}}&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{T}}_{11}&{\textbf{T}}_{12}\\[4pt]
{\textbf{T}}_{21}&{\textbf{T}}_{22}\end{array}\right]=\left[\begin{array}{c|cc}-2\lambda&2\lambda&0\\[4pt]
\hline 1&-(1+\lambda)&\lambda\\[4pt]
0&2&-2\end{array}\right],\nonumber\\[4pt]{\textbf{Q}}(s)&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{Q}}_{11}(s)&{\textbf{Q}}_{12}(s)\\[4pt]{\textbf{Q}}_{21}(s)&{\textbf{Q}}_{22}(s)\end{array}\right]=\left[\begin{array}{c|cc}-(2\lambda +s)&2\lambda&0\\[4pt]\hline1&-(1+\lambda +s)&\lambda\\[4pt]0&2&-(2+s)\end{array}\right],\nonumber\end{eqnarray}
\begin{eqnarray}{\textbf{T}}&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{T}}_{11}&{\textbf{T}}_{12}\\[4pt]
{\textbf{T}}_{21}&{\textbf{T}}_{22}\end{array}\right]=\left[\begin{array}{c|cc}-2\lambda&2\lambda&0\\[4pt]
\hline 1&-(1+\lambda)&\lambda\\[4pt]
0&2&-2\end{array}\right],\nonumber\\[4pt]{\textbf{Q}}(s)&\,=\,&\left[\begin{array}{c@{\quad}c}{\textbf{Q}}_{11}(s)&{\textbf{Q}}_{12}(s)\\[4pt]{\textbf{Q}}_{21}(s)&{\textbf{Q}}_{22}(s)\end{array}\right]=\left[\begin{array}{c|cc}-(2\lambda +s)&2\lambda&0\\[4pt]\hline1&-(1+\lambda +s)&\lambda\\[4pt]0&2&-(2+s)\end{array}\right],\nonumber\end{eqnarray}
with some parameter ![]() $\lambda>\sqrt{2}-1$ such that the process is stable. In our plots of the output below, we will assume the value
$\lambda>\sqrt{2}-1$ such that the process is stable. In our plots of the output below, we will assume the value ![]() $\lambda=2.5$.
$\lambda=2.5$.
Denote by ![]() $[x\ z]={\boldsymbol{\Psi}}(s)=\int_{t=0}^{\infty}e^{-st}\boldsymbol{\psi}(t)dt$ the minimum nonnegative solution of (21), here equivalent to
$[x\ z]={\boldsymbol{\Psi}}(s)=\int_{t=0}^{\infty}e^{-st}\boldsymbol{\psi}(t)dt$ the minimum nonnegative solution of (21), here equivalent to
 \begin{eqnarray}[0\ 0]&\,=\,&[2\lambda\ 0]-(2\lambda+s)[x\ z]+[x\ z]\left[\begin{array}{c@{\quad}c}-(1+\lambda+s)&\lambda\\[4pt]2&-(2+s)\end{array}\right]\nonumber\\[4pt]&&+[x\ z]\left[\begin{array}{c}1\\[4pt]0\end{array}\right][x\ z],\end{eqnarray}
\begin{eqnarray}[0\ 0]&\,=\,&[2\lambda\ 0]-(2\lambda+s)[x\ z]+[x\ z]\left[\begin{array}{c@{\quad}c}-(1+\lambda+s)&\lambda\\[4pt]2&-(2+s)\end{array}\right]\nonumber\\[4pt]&&+[x\ z]\left[\begin{array}{c}1\\[4pt]0\end{array}\right][x\ z],\end{eqnarray}
which we write as a system of equations
The minimum nonnegative solution ![]() $[x\ z]$ of (159)–(160) must be strictly positive, satisfy
$[x\ z]$ of (159)–(160) must be strictly positive, satisfy ![]() $2+2\lambda+2s-x> 0$, and occur at the intersection of the two curves
$2+2\lambda+2s-x> 0$, and occur at the intersection of the two curves
To facilitate the analysis that follows, we consider the shape of the curves in (161)–(162); see Figure 2. It is a straightforward exercise to verify that, when ![]() $s=0$, we have
$s=0$, we have ![]() $z_1(x,0)<-\lambda<z_2(x,0)$ for all
$z_1(x,0)<-\lambda<z_2(x,0)$ for all ![]() $x< 0$, and so the two curves may only intersect at some point (x, z) with
$x< 0$, and so the two curves may only intersect at some point (x, z) with ![]() $x>0$.
$x>0$.
Furthermore, when ![]() $2+2\lambda+2s-x> 0$, we have
$2+2\lambda+2s-x> 0$, we have
and so, when ![]() $s=0$, the minimum nonnegative solution
$s=0$, the minimum nonnegative solution ![]() $[x\ z]$ of (159)–(160) is in fact the minimum real-valued solution of (159)–(160).
$[x\ z]$ of (159)–(160) is in fact the minimum real-valued solution of (159)–(160).
Also, when ![]() $x>0$ and
$x>0$ and ![]() $2+2\lambda+2s-x> 0$, we have
$2+2\lambda+2s-x> 0$, we have
 \begin{eqnarray}\frac{\partial z_1(x,s)}{\partial s}=x&\ >\ &0,\nonumber\\[4pt]
\frac{\partial z_2(x,s)}{\partial s}=\frac{-2\lambda x}{(2+2\lambda+2s-x)^2}&\ <\ &0,\end{eqnarray}
\begin{eqnarray}\frac{\partial z_1(x,s)}{\partial s}=x&\ >\ &0,\nonumber\\[4pt]
\frac{\partial z_2(x,s)}{\partial s}=\frac{-2\lambda x}{(2+2\lambda+2s-x)^2}&\ <\ &0,\end{eqnarray}
and so as ![]() $s\downarrow s^*$ we have
$s\downarrow s^*$ we have ![]() $z_1(x,s)\downarrow$ while
$z_1(x,s)\downarrow$ while ![]() $z_2(x,s)\uparrow$, until the two curves touch when
$z_2(x,s)\uparrow$, until the two curves touch when ![]() $s=s^*$, and then move apart when
$s=s^*$, and then move apart when ![]() $s<s^*$. Therefore, by the argument about the continuity of
$s<s^*$. Therefore, by the argument about the continuity of ![]() ${\boldsymbol{\Psi}}(s)$ which was used in the proof of Lemma 4, for all
${\boldsymbol{\Psi}}(s)$ which was used in the proof of Lemma 4, for all ![]() $s\in [s^*,0]$,
$s\in [s^*,0]$, ![]() ${\boldsymbol{\Psi}}(s)=[x\ z]$ is the minimum real-valued solution of (159)–(160).
${\boldsymbol{\Psi}}(s)=[x\ z]$ is the minimum real-valued solution of (159)–(160).
Instead of looking at the problem in terms of two intersecting curves ![]() $z_1(x,s)$ and
$z_1(x,s)$ and ![]() $z_2(x,s)$, we now look at it in terms of one cubic curve
$z_2(x,s)$, we now look at it in terms of one cubic curve ![]() $g_s(x)$. Substitute (162) into (159) and multiply by
$g_s(x)$. Substitute (162) into (159) and multiply by ![]() $(2+2\lambda+2s-x)$ to get
$(2+2\lambda+2s-x)$ to get
 \begin{eqnarray}0&\,=\,&-x^3+(3+5\lambda+4s)x^2-(2+2\lambda+2s)(1+3\lambda+2s)x+(2+2\lambda+2s)2\lambda\nonumber\\[4pt]&\,=\,&g_s(x),\end{eqnarray}
\begin{eqnarray}0&\,=\,&-x^3+(3+5\lambda+4s)x^2-(2+2\lambda+2s)(1+3\lambda+2s)x+(2+2\lambda+2s)2\lambda\nonumber\\[4pt]&\,=\,&g_s(x),\end{eqnarray}
which is of the form
with ![]() $g_s(0)=d>0$ (we have
$g_s(0)=d>0$ (we have ![]() $d>0$ because
$d>0$ because ![]() $0<x<2+2\lambda+2s$, since
$0<x<2+2\lambda+2s$, since ![]() $z>0$ in (162)). (See the plots of
$z>0$ in (162)). (See the plots of ![]() $g_s(x)$ in Figure 3 for the case
$g_s(x)$ in Figure 3 for the case ![]() $\lambda=2.5$.) Noting that
$\lambda=2.5$.) Noting that ![]() $a=-1<0$, we conclude that when
$a=-1<0$, we conclude that when ![]() $s=s^*$, the solution
$s=s^*$, the solution ![]() $[x\ z]$ corresponds to the local minimum,
$[x\ z]$ corresponds to the local minimum,
 \begin{equation}x=\min \left\{ \frac{-b+ \sqrt{b^2-3ac}}{3a},\frac{-b - \sqrt{b^2-3ac}}{3a} \right\}=\frac{-b+ \sqrt{b^2-3ac}}{3a},\end{equation}
\begin{equation}x=\min \left\{ \frac{-b+ \sqrt{b^2-3ac}}{3a},\frac{-b - \sqrt{b^2-3ac}}{3a} \right\}=\frac{-b+ \sqrt{b^2-3ac}}{3a},\end{equation}
where

Figure 3: The plot of (165) for ![]() $s=0$ (top left),
$s=0$ (top left), ![]() $s=-2$ (top right), and
$s=-2$ (top right), and ![]() $s=-1.1178$ (bottom), when
$s=-1.1178$ (bottom), when ![]() $\lambda=2.5$.
$\lambda=2.5$.
We transform the cubic equation (166) into the form
using the substitution
with
for suitable ![]() $c_p^{(1)}$,
$c_p^{(1)}$, ![]() $c_p^{(2)}$,
$c_p^{(2)}$, ![]() $c_p$, and
$c_p$, and
for suitable ![]() $c_q^{(1)}$,
$c_q^{(1)}$, ![]() $c_q^{(2)}$,
$c_q^{(2)}$, ![]() $c_q^{(3)}$,
$c_q^{(3)}$, ![]() $c_q$.
$c_q$.
Below, we choose the convention of writing p(s) to demonstrate that p is a function of s, with similar notation applied for other quantities such as q, x, y, and so on. Observe that
 \begin{eqnarray*}s^3-(s^*)^3&\,=\,&(s-s^*)(s^2+ss^*+(s^*)^2)=C_3\times (s-s^*)+o(s-s^*),\\[4pt]s^2-(s^*)^2&\,=\,&(s-s^*)(s+s^*)=C_2\times (s-s^*)+o(s-s^*),\end{eqnarray*}
\begin{eqnarray*}s^3-(s^*)^3&\,=\,&(s-s^*)(s^2+ss^*+(s^*)^2)=C_3\times (s-s^*)+o(s-s^*),\\[4pt]s^2-(s^*)^2&\,=\,&(s-s^*)(s+s^*)=C_2\times (s-s^*)+o(s-s^*),\end{eqnarray*}
where ![]() $C_3=3(s^*)^2$ and
$C_3=3(s^*)^2$ and ![]() $C_2=2s^*$, and so by (171)–(172),
$C_2=2s^*$, and so by (171)–(172),
where the constants ![]() $C_p$ and
$C_p$ and ![]() $C_q$ are given by
$C_q$ are given by
 \begin{eqnarray}C_p&\,=\,& c_p^{(1)}+C_2\times c_p^{(2)},\nonumber\\[4pt]C_q&\,=\,&c_q^{(1)}+C_2\times c_q^{(2)}+C_3\times c_q^{(3)}.\end{eqnarray}
\begin{eqnarray}C_p&\,=\,& c_p^{(1)}+C_2\times c_p^{(2)},\nonumber\\[4pt]C_q&\,=\,&c_q^{(1)}+C_2\times c_q^{(2)}+C_3\times c_q^{(3)}.\end{eqnarray}
Consider (169) and apply Vieta’s substitution,
where ![]() $u^3$ solves the quadratic equation
$u^3$ solves the quadratic equation
The two solutions are
with
where ![]() $\Delta(s)<0$ for
$\Delta(s)<0$ for ![]() $s>s^*$, and the repeated root requires
$s>s^*$, and the repeated root requires
When ![]() $s>s^*$, the three (real) solutions of (169) are the three cube roots
$s>s^*$, the three (real) solutions of (169) are the three cube roots
and we choose the minimum,
which corresponds to the minimum ![]() $x(s)={\boldsymbol{\Psi}}(s)_1$, where
$x(s)={\boldsymbol{\Psi}}(s)_1$, where ![]() ${\boldsymbol{\Psi}}(s)_i$ denotes the ith element of
${\boldsymbol{\Psi}}(s)_i$ denotes the ith element of ![]() ${\boldsymbol{\Psi}}(s)$.
${\boldsymbol{\Psi}}(s)$.
Therefore, by (174),
 \begin{eqnarray}u^3(s)-u^3(s^*)&\,=\,&\frac{-q(s) + \sqrt{\Delta (s)}}{2}+ \frac{q(s^*)}{2}\nonumber\\[4pt]&\,=\,&-\frac{1}{2}C_q\times (s-s^*) + \frac{1}{2}\sqrt{\Delta(s)}+o(s-s^*).\end{eqnarray}
\begin{eqnarray}u^3(s)-u^3(s^*)&\,=\,&\frac{-q(s) + \sqrt{\Delta (s)}}{2}+ \frac{q(s^*)}{2}\nonumber\\[4pt]&\,=\,&-\frac{1}{2}C_q\times (s-s^*) + \frac{1}{2}\sqrt{\Delta(s)}+o(s-s^*).\end{eqnarray}
Now,
 \begin{align}\Delta(s) & =\Delta(s)-\Delta(s^*)\nonumber\\[4pt]
& = \frac{1}{2}(q(s)-q(s^*))(q(s)+q(s^*))+\frac{4}{27} (p(s)-p(s^*))(p(s)^2+p(s)p(s^*)+p(s^*)^2),\nonumber\\[4pt]\end{align}
\begin{align}\Delta(s) & =\Delta(s)-\Delta(s^*)\nonumber\\[4pt]
& = \frac{1}{2}(q(s)-q(s^*))(q(s)+q(s^*))+\frac{4}{27} (p(s)-p(s^*))(p(s)^2+p(s)p(s^*)+p(s^*)^2),\nonumber\\[4pt]\end{align}
where the constant ![]() $C_\Delta<0$ is given by
$C_\Delta<0$ is given by
Therefore,
 \begin{eqnarray*}\lim_{s\downarrow s^*}\left(\frac{u^3(s)-u^3(s^*)}{\sqrt{s-s^*}}\right)&\,=\,&\lim_{s\downarrow s^*}\left({-}\frac{1}{2} C_q\sqrt{s-s^*}+\frac{1}{2}\sqrt{\frac{C_\Delta\times (s-s^*)+o(s-s^*)}{s-s^*}}\right)\\[4pt]&\,=\,&\frac{1}{2}\sqrt{C_\Delta},\end{eqnarray*}
\begin{eqnarray*}\lim_{s\downarrow s^*}\left(\frac{u^3(s)-u^3(s^*)}{\sqrt{s-s^*}}\right)&\,=\,&\lim_{s\downarrow s^*}\left({-}\frac{1}{2} C_q\sqrt{s-s^*}+\frac{1}{2}\sqrt{\frac{C_\Delta\times (s-s^*)+o(s-s^*)}{s-s^*}}\right)\\[4pt]&\,=\,&\frac{1}{2}\sqrt{C_\Delta},\end{eqnarray*}
and
 \begin{eqnarray*}\lim_{s\downarrow s^*}\left(\frac{u(s)-u(s^*)}{\sqrt{s-s^*}}\right)&\,=\,&\lim_{s\downarrow s^*}\left(\frac{u(s)-u(s^*)}{\sqrt{s-s^*}}\times\frac{u^2(s)+u(s)u(s^*)+u^2(s^*)}{u^2(s)+u(s)u(s^*)+u^2(s^*)}\right)\nonumber\\[4pt]&\,=\,&\lim_{s\downarrow s^*}\left(\frac{u^3(s)-u^3(s^*)}{\sqrt{s-s^*}}\times\frac{1}{u^2(s)+u(s)u(s^*)+u^2(s^*)}\right)\nonumber\\[4pt]&\,=\,&\frac{1}{6u^2(s^*)}\sqrt{C_\Delta},\end{eqnarray*}
\begin{eqnarray*}\lim_{s\downarrow s^*}\left(\frac{u(s)-u(s^*)}{\sqrt{s-s^*}}\right)&\,=\,&\lim_{s\downarrow s^*}\left(\frac{u(s)-u(s^*)}{\sqrt{s-s^*}}\times\frac{u^2(s)+u(s)u(s^*)+u^2(s^*)}{u^2(s)+u(s)u(s^*)+u^2(s^*)}\right)\nonumber\\[4pt]&\,=\,&\lim_{s\downarrow s^*}\left(\frac{u^3(s)-u^3(s^*)}{\sqrt{s-s^*}}\times\frac{1}{u^2(s)+u(s)u(s^*)+u^2(s^*)}\right)\nonumber\\[4pt]&\,=\,&\frac{1}{6u^2(s^*)}\sqrt{C_\Delta},\end{eqnarray*}
where ![]() $u(s^*)\neq 0$ by (177), since
$u(s^*)\neq 0$ by (177), since ![]() $p(s^*)\neq 0$ by (168) and (171).
$p(s^*)\neq 0$ by (168) and (171).
From the above we conclude that by (176),
 \begin{align*} & {\lim_{s\downarrow s^*}\left(\frac{y(s)-y(s^*)}{\sqrt{s-s^*}}\right)=\lim_{s\downarrow s^*}\left(\frac{u(s)-u(s^*)}{\sqrt{s-s^*}} -\frac{1}{3\sqrt{s-s^*}}\left(\frac{p(s)}{u(s)}-\frac{p(s^*)}{u(s^*)}\right)\right)}\\[4pt]
& = \lim_{s\downarrow s^*}\left(\frac{u(s)-u(s^*)}{\sqrt{s-s^*}}-\frac{(p(s)-p(s^*))u(s^*)}{3\sqrt{s-s^*}u(s)u(s^*)}+\frac{p(s^*)(u(s)-u(s^*))}{3\sqrt{s-s^*}u(s)u(s^*)}\right)\\[4pt]
& = \pm \frac{1}{6u^2(s^*)}\sqrt{C_\Delta}-0 \frac{1}{6u^2(s^*)}\sqrt{C_\Delta}\frac{p(s^*)}{3u^2(s^*)}\\[4pt]
& = \frac{1}{6u^2(s^*)}\sqrt{C_\Delta}\left(1+\frac{p(s^*)}{3u^2(s^*)}\right). \end{align*}
\begin{align*} & {\lim_{s\downarrow s^*}\left(\frac{y(s)-y(s^*)}{\sqrt{s-s^*}}\right)=\lim_{s\downarrow s^*}\left(\frac{u(s)-u(s^*)}{\sqrt{s-s^*}} -\frac{1}{3\sqrt{s-s^*}}\left(\frac{p(s)}{u(s)}-\frac{p(s^*)}{u(s^*)}\right)\right)}\\[4pt]
& = \lim_{s\downarrow s^*}\left(\frac{u(s)-u(s^*)}{\sqrt{s-s^*}}-\frac{(p(s)-p(s^*))u(s^*)}{3\sqrt{s-s^*}u(s)u(s^*)}+\frac{p(s^*)(u(s)-u(s^*))}{3\sqrt{s-s^*}u(s)u(s^*)}\right)\\[4pt]
& = \pm \frac{1}{6u^2(s^*)}\sqrt{C_\Delta}-0 \frac{1}{6u^2(s^*)}\sqrt{C_\Delta}\frac{p(s^*)}{3u^2(s^*)}\\[4pt]
& = \frac{1}{6u^2(s^*)}\sqrt{C_\Delta}\left(1+\frac{p(s^*)}{3u^2(s^*)}\right). \end{align*}
Therefore, by (170), we have
 \begin{eqnarray}\lim_{s\downarrow s^*}\left(\frac{{\boldsymbol{\Psi}}(s)_1-{\boldsymbol{\Psi}}(s^*)_1}{\sqrt{s-s^*}}\right)&\,=\,&\lim_{s\downarrow s^*}\left(\frac{x(s)-x(s^*)}{\sqrt{s-s^*}}\right)\nonumber\\[4pt]&\,=\,&\lim_{s\downarrow s^*}\left(\frac{y(s)-y(s^*)}{\sqrt{s-s^*}} +o(1)\right)\nonumber\\[4pt]&\,=\,&\frac{1}{6u^2(s^*)}\sqrt{C_\Delta}\left(1+\frac{p(s^*)}{3u^2(s^*)}\right)\nonumber\\[4pt]&\,=\,&-\mathbf{B}(s^*)_1.\end{eqnarray}
\begin{eqnarray}\lim_{s\downarrow s^*}\left(\frac{{\boldsymbol{\Psi}}(s)_1-{\boldsymbol{\Psi}}(s^*)_1}{\sqrt{s-s^*}}\right)&\,=\,&\lim_{s\downarrow s^*}\left(\frac{x(s)-x(s^*)}{\sqrt{s-s^*}}\right)\nonumber\\[4pt]&\,=\,&\lim_{s\downarrow s^*}\left(\frac{y(s)-y(s^*)}{\sqrt{s-s^*}} +o(1)\right)\nonumber\\[4pt]&\,=\,&\frac{1}{6u^2(s^*)}\sqrt{C_\Delta}\left(1+\frac{p(s^*)}{3u^2(s^*)}\right)\nonumber\\[4pt]&\,=\,&-\mathbf{B}(s^*)_1.\end{eqnarray}
Furthermore, by (162),
 \begin{align}& { \lim_{s\downarrow s^*} \left(\frac{{\boldsymbol{\Psi}}(s)_2-{\boldsymbol{\Psi}}(s^*)_2}{\sqrt{s-s^*}}\right)= \lim_{s\downarrow s^*} \left( \frac{z(s)-z(s^*)}{\sqrt{s-s^*}} \right)}\nonumber\\[4pt]
& = \lim_{s\downarrow s^*} \left(\frac{1}{\sqrt{s-s^*}}\left(\frac{\lambda x(s)}{2+2\lambda+2s-x(s)}-\frac{\lambda x(s^*)}{2+2\lambda+2s^*-x(s^*)}\right)\right)\nonumber\\[4pt]
& =\frac{2\lambda(1+\lambda+s^*)}{(2+2\lambda+2s^*-x(s^*))^2}\mathbf{B}(s^*)_1\nonumber\\[4pt]
& = -\mathbf{B}(s^*)_2,\end{align}
\begin{align}& { \lim_{s\downarrow s^*} \left(\frac{{\boldsymbol{\Psi}}(s)_2-{\boldsymbol{\Psi}}(s^*)_2}{\sqrt{s-s^*}}\right)= \lim_{s\downarrow s^*} \left( \frac{z(s)-z(s^*)}{\sqrt{s-s^*}} \right)}\nonumber\\[4pt]
& = \lim_{s\downarrow s^*} \left(\frac{1}{\sqrt{s-s^*}}\left(\frac{\lambda x(s)}{2+2\lambda+2s-x(s)}-\frac{\lambda x(s^*)}{2+2\lambda+2s^*-x(s^*)}\right)\right)\nonumber\\[4pt]
& =\frac{2\lambda(1+\lambda+s^*)}{(2+2\lambda+2s^*-x(s^*))^2}\mathbf{B}(s^*)_1\nonumber\\[4pt]
& = -\mathbf{B}(s^*)_2,\end{align}
which gives
as expected (cf. (89)).
Now, assuming ![]() $\lambda=2.5$, we solve (180) numerically, obtaining
$\lambda=2.5$, we solve (180) numerically, obtaining
We evaluate ![]() $[x\ z]={\boldsymbol{\Psi}}(s^*)$, using (167) to get x and then (162) to get z,
$[x\ z]={\boldsymbol{\Psi}}(s^*)$, using (167) to get x and then (162) to get z,
We obtain ![]() ${\textbf{K}}(s^*)$ and
${\textbf{K}}(s^*)$ and ![]() $({-}{\textbf{D}}(s^*))$ using (20):
$({-}{\textbf{D}}(s^*))$ using (20):
 \begin{eqnarray}-{\textbf{D}}(s^*) \approx \left[\begin{array}{c@{\quad}c}-0.5944 & 4.0016\\[4pt]
2.0000 & -0.8822\end{array}\right],\end{eqnarray}
\begin{eqnarray}-{\textbf{D}}(s^*) \approx \left[\begin{array}{c@{\quad}c}-0.5944 & 4.0016\\[4pt]
2.0000 & -0.8822\end{array}\right],\end{eqnarray}
which have common eigenvalue ![]() $\gamma \approx -2.0944$. Also, we use (83) to obtain
$\gamma \approx -2.0944$. Also, we use (83) to obtain
Finally, we evaluate ![]() ${\textbf{B}}(s^*)$ using (187) and
${\textbf{B}}(s^*)$ using (187) and ![]() ${\textbf{Y}}(s^*)$ using (90):
${\textbf{Y}}(s^*)$ using (90):
This yields
which is approximately zero, as expected (cf. (91)).
Finally,
 \begin{eqnarray}{\textbf{H}}(s^*,y)&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}{\textbf{H}}_{1,n}(s^*)\nonumber\\[4pt]&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}\sum_{i=0}^{n-1}\left({\textbf{K}}(s^*) \right)^i\times\mathbf{B}(s^*){\textbf{Q}}_{21}(s^*)\times\left({\textbf{K}}(s^*) \right)^{n-1-i}\nonumber\\[4pt]&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}\sum_{i=0}^{n-1}\left( {\textbf{K}}(s^*)\right)^{n-1}\left(\mathbf{B}(s^*){\textbf{Q}}_{21}(s^*)\right)\nonumber\\[4pt]&\,=\,&ye^{{\textbf{K}}(s^*)y}\mathbf{B}(s^*){\textbf{Q}}_{21}(s^*)\nonumber\\[4pt]&\approx&1.6416 ye^{-2.0944\times y},\end{eqnarray}
\begin{eqnarray}{\textbf{H}}(s^*,y)&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}{\textbf{H}}_{1,n}(s^*)\nonumber\\[4pt]&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}\sum_{i=0}^{n-1}\left({\textbf{K}}(s^*) \right)^i\times\mathbf{B}(s^*){\textbf{Q}}_{21}(s^*)\times\left({\textbf{K}}(s^*) \right)^{n-1-i}\nonumber\\[4pt]&\,=\,&\sum_{n=1}^{\infty}\frac{y^n}{n!}\sum_{i=0}^{n-1}\left( {\textbf{K}}(s^*)\right)^{n-1}\left(\mathbf{B}(s^*){\textbf{Q}}_{21}(s^*)\right)\nonumber\\[4pt]&\,=\,&ye^{{\textbf{K}}(s^*)y}\mathbf{B}(s^*){\textbf{Q}}_{21}(s^*)\nonumber\\[4pt]&\approx&1.6416 ye^{-2.0944\times y},\end{eqnarray}
and
 \begin{eqnarray}{\textbf{H}}(s^*)&\,=\,&\int_{y=0}^{\infty}ye^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*)dy\nonumber\\[4pt]&\,=\,&({\textbf{K}}(s^*))^{-2}{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*),\nonumber\\[4pt]\widetilde{\textbf{H}}(s^*)&\,=\,&{\textbf{H}}(s^*)+\left({-}({\textbf{K}}(s^*))^{-1}\mathbf{B}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right){\boldsymbol{1}}\nonumber\\[4pt]&\approx& 3.4428,\end{eqnarray}
\begin{eqnarray}{\textbf{H}}(s^*)&\,=\,&\int_{y=0}^{\infty}ye^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*)dy\nonumber\\[4pt]&\,=\,&({\textbf{K}}(s^*))^{-2}{\textbf{B}}(s^*){\textbf{Q}}_{21}(s^*),\nonumber\\[4pt]\widetilde{\textbf{H}}(s^*)&\,=\,&{\textbf{H}}(s^*)+\left({-}({\textbf{K}}(s^*))^{-1}\mathbf{B}(s^*)+{\textbf{H}}(s^*){\boldsymbol{\Psi}}(s^*)\right){\boldsymbol{1}}\nonumber\\[4pt]&\approx& 3.4428,\end{eqnarray}
so
 \begin{eqnarray} \boldsymbol{\mu}(dy)^{(0)}_{11}&\,=\,& diag({\widetilde{\textbf{H}}(s^*)})^{-1} { {\textbf{H}}(s^*,y)} dy \nonumber\\[4pt] &\approx& 0.2905\times 1.6416 ye^{-2.0944\times y} dy ,\nonumber\\[4pt] \boldsymbol{\mu}(dy)^{(0)}_{12}&\,=\,& diag({\widetilde{\textbf{H}}(s^*)})^{-1} \left( e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*) + {\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*) \right) dy \nonumber\\[4pt] &\approx& 0.2905\times \left( [1.6416\quad 2.2069] +1.6416 y [1.7878\quad 1.5016] \right) e^{-2.0944\times y} dy , \nonumber\\[4pt] \end{eqnarray}
\begin{eqnarray} \boldsymbol{\mu}(dy)^{(0)}_{11}&\,=\,& diag({\widetilde{\textbf{H}}(s^*)})^{-1} { {\textbf{H}}(s^*,y)} dy \nonumber\\[4pt] &\approx& 0.2905\times 1.6416 ye^{-2.0944\times y} dy ,\nonumber\\[4pt] \boldsymbol{\mu}(dy)^{(0)}_{12}&\,=\,& diag({\widetilde{\textbf{H}}(s^*)})^{-1} \left( e^{{\textbf{K}}(s^*)y}{\textbf{B}}(s^*) + {\textbf{H}}(s^*,y){\boldsymbol{\Psi}}(s^*) \right) dy \nonumber\\[4pt] &\approx& 0.2905\times \left( [1.6416\quad 2.2069] +1.6416 y [1.7878\quad 1.5016] \right) e^{-2.0944\times y} dy , \nonumber\\[4pt] \end{eqnarray}
where ![]() $\mu(dy)^{(0)}_{ij}$ is the limiting conditional distribution (Yaglom limit) of observing the process in level y and phase j, given that the process started from level zero in phase i at time zero, and has been evolving without hitting level zero.
$\mu(dy)^{(0)}_{ij}$ is the limiting conditional distribution (Yaglom limit) of observing the process in level y and phase j, given that the process started from level zero in phase i at time zero, and has been evolving without hitting level zero.
Acknowledgements
We would like to thank the Australian Research Council for funding this research through Linkage Project LP140100152. Zbigniew Palmowski was partially supported by the National Science Centre (Poland) under the grant 2018/29/B/ST1/00756.