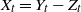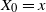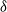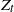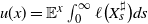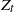1. Introduction
Let
![]() $(X_t)_{t\geq 0}$
be a càdlàg strong Markov process with values in
$(X_t)_{t\geq 0}$
be a càdlàg strong Markov process with values in
![]() ${\unicode{x211D}^d}$
, defined on the probability space
${\unicode{x211D}^d}$
, defined on the probability space
![]() $\big(\Omega, \mathcal{F}, (\mathcal{F}_t)_{t\geq 0},\big(\mathbb{P}^x\big)_{x\in {\unicode{x211D}^d}}\big)$
, where
$\big(\Omega, \mathcal{F}, (\mathcal{F}_t)_{t\geq 0},\big(\mathbb{P}^x\big)_{x\in {\unicode{x211D}^d}}\big)$
, where
![]() $\mathbb{P}^x (X_0=x)=1$
,
$\mathbb{P}^x (X_0=x)=1$
,
![]() $(\mathcal{F}_t)_{t\geq 0}$
is a right-continuous natural filtration satisfying the usual conditions, and
$(\mathcal{F}_t)_{t\geq 0}$
is a right-continuous natural filtration satisfying the usual conditions, and
![]() $\mathcal{F}\,:\!=\,\sigma\big(\bigcup_{t\geq 0} \mathcal{F}_t\big)$
.
$\mathcal{F}\,:\!=\,\sigma\big(\bigcup_{t\geq 0} \mathcal{F}_t\big)$
.
In this note we study the behaviour of the potential u(x) of the process X, killed at some terminal time, when the starting point
![]() $x\in {\unicode{x211D}^d}$
tends to infinity in the sense that
$x\in {\unicode{x211D}^d}$
tends to infinity in the sense that
![]() $x^0\to \infty$
, where
$x^0\to \infty$
, where
![]() $x^0\,:\!=\,\min_{1 \leq i \leq d} x_i$
. A particular case of this model is the behaviour of the ruin probability if the initial capital x is big. In the case when the claims are heavy-tailed, this probability can still be quite large. The other example where the function u(x) appears comes from mathematical finance, where u(x) describes the discounted utility of consumption; see [Reference Asmussen and Albrecher2, Reference Mikosch31, Reference Rolski, Schmidli, Schmidt and Teugels36] and references therein. We show that in some cases one can still calculate the asymptotic behaviour of u(x) for large x, and discuss some practical examples.
$x^0\,:\!=\,\min_{1 \leq i \leq d} x_i$
. A particular case of this model is the behaviour of the ruin probability if the initial capital x is big. In the case when the claims are heavy-tailed, this probability can still be quite large. The other example where the function u(x) appears comes from mathematical finance, where u(x) describes the discounted utility of consumption; see [Reference Asmussen and Albrecher2, Reference Mikosch31, Reference Rolski, Schmidli, Schmidt and Teugels36] and references therein. We show that in some cases one can still calculate the asymptotic behaviour of u(x) for large x, and discuss some practical examples.
Let us introduce some necessary notions and notation. Assume that X is of the form
where
![]() $Y_t$
is a càdlàg
$Y_t$
is a càdlàg
![]() ${\unicode{x211D}^d}$
-valued strong Markov process with jumps of size strictly smaller than some
${\unicode{x211D}^d}$
-valued strong Markov process with jumps of size strictly smaller than some
![]() $\delta>0$
, and
$\delta>0$
, and
![]() $Z_t$
is a compound Poisson process independent of
$Z_t$
is a compound Poisson process independent of
![]() $Y_t$
with jumps of size bigger than
$Y_t$
with jumps of size bigger than
![]() $\delta$
. That is,
$\delta$
. That is,
 \begin{equation}Z_t\,:\!=\, \sum_{k=1}^{N_t}U_k,\end{equation}
\begin{equation}Z_t\,:\!=\, \sum_{k=1}^{N_t}U_k,\end{equation}
where
![]() $\{U_k\}$
is a sequence of independent and identically distributed (i.i.d.) random variables with a distribution function F,
$\{U_k\}$
is a sequence of independent and identically distributed (i.i.d.) random variables with a distribution function F,
and
![]() $N_t$
is an independent Poisson process with intensity
$N_t$
is an independent Poisson process with intensity
![]() $\lambda$
. In this set-up we have
$\lambda$
. In this set-up we have
![]() $\mathbb{P}^x (Y_0=x)=1$
.
$\mathbb{P}^x (Y_0=x)=1$
.
Let T be an
![]() $\mathcal{F}_t$
-terminal time; i.e. for any
$\mathcal{F}_t$
-terminal time; i.e. for any
![]() $\mathcal{F}_t$
-stopping time S it satisfies the relation
$\mathcal{F}_t$
-stopping time S it satisfies the relation
see [Reference Sharpe38, Section 12] or [Reference Bass4, Section 22.1]. Among the examples of terminal times are the following:
-
The first exit time
 $\tau_D$
from a Borel set D:
$\tau_D$
from a Borel set D:
 $\tau_D\,:\!=\, \inf\{t>0\,:\, \, X_t \notin D\}$
.
$\tau_D\,:\!=\, \inf\{t>0\,:\, \, X_t \notin D\}$
. -
The exponential (with some parameter
 $\mu$
) random variable independent of X.
$\mu$
) random variable independent of X. -
 $T\,:\!=\, \inf\big\{t>0\,:\, \int_0^t f(X_s)\, ds\geq 1\big\}$
, where f is a nonnegative function.
$T\,:\!=\, \inf\big\{t>0\,:\, \int_0^t f(X_s)\, ds\geq 1\big\}$
, where f is a nonnegative function.
See [Reference Sharpe38] for more examples.
For
![]() $t\geq 0$
we define the killed process
$t\geq 0$
we define the killed process
 \begin{equation}X^\sharp_t\,:\!=\, \left\{\begin{array}{l@{\quad}r}X_{t}, & t<T, \\[5pt]\partial, & t\geq T,\end{array}\right.\end{equation}
\begin{equation}X^\sharp_t\,:\!=\, \left\{\begin{array}{l@{\quad}r}X_{t}, & t<T, \\[5pt]\partial, & t\geq T,\end{array}\right.\end{equation}
where
![]() $\partial$
is a fixed cemetery state. Note that the killed process
$\partial$
is a fixed cemetery state. Note that the killed process
![]() $\big(X^\sharp_t, \mathcal{F}_t\big)$
is still strongly Markov (cf. [Reference Bass4, Proposition 22.1]).
$\big(X^\sharp_t, \mathcal{F}_t\big)$
is still strongly Markov (cf. [Reference Bass4, Proposition 22.1]).
Denote by
![]() $\mathcal{B}_b\big({\unicode{x211D}^d}\big)$
$\mathcal{B}_b\big({\unicode{x211D}^d}\big)$
![]() $\big($
resp.,
$\big($
resp.,
![]() $\mathcal{B}_b^+\big({\unicode{x211D}^d}\big)\big)$
the class of bounded
$\mathcal{B}_b^+\big({\unicode{x211D}^d}\big)\big)$
the class of bounded
![]() $\big($
resp., bounded such that the infimum is nonnegative on
$\big($
resp., bounded such that the infimum is nonnegative on
![]() ${\unicode{x211D}^d}$
and it is strictly positive on
${\unicode{x211D}^d}$
and it is strictly positive on
![]() ${\unicode{x211D}_+^d}\big)$
Borel functions on
${\unicode{x211D}_+^d}\big)$
Borel functions on
![]() ${\unicode{x211D}^d}$
.
${\unicode{x211D}^d}$
.
We investigate the asymptotic properties of the potential of
![]() $X^\sharp$
:
$X^\sharp$
:
where
![]() $\ell \in \mathcal{B}_b^+\big({\unicode{x211D}^d}\big)$
and throughout the paper we assume that
$\ell \in \mathcal{B}_b^+\big({\unicode{x211D}^d}\big)$
and throughout the paper we assume that
![]() $\ell(\partial)=0$
. From the assumption
$\ell(\partial)=0$
. From the assumption
![]() $\ell(\partial)=0$
we have
$\ell(\partial)=0$
we have
![]() $u(\partial)=0$
. This function u(x) is a particular example of a Gerber–Shiu function (see [Reference Asmussen and Albrecher2]), which relates the ruin time and the penalty function and appears often in insurance mathematics when one needs to calculate the risk of a ruin. We assume that the function u(x) is well-defined and bounded. For example this is true if
$u(\partial)=0$
. This function u(x) is a particular example of a Gerber–Shiu function (see [Reference Asmussen and Albrecher2]), which relates the ruin time and the penalty function and appears often in insurance mathematics when one needs to calculate the risk of a ruin. We assume that the function u(x) is well-defined and bounded. For example this is true if
![]() $\mathbb{E}^x T=\int_0^\infty \mathbb{P}^x (T>s)ds<\infty$
, because
$\mathbb{E}^x T=\int_0^\infty \mathbb{P}^x (T>s)ds<\infty$
, because
![]() $\ell \in \mathcal{B}_b^+\big({\unicode{x211D}^d}\big)$
.
$\ell \in \mathcal{B}_b^+\big({\unicode{x211D}^d}\big)$
.
Having appropriate upper and lower bounds on the transition probability density of
![]() $X_t$
makes it possible to estimate u(x). However, in some cases one can get the asymptotic behaviour of u(x). In fact, using the strong Markov property, one can show that u(x) satisfies the following renewal-type equation:
$X_t$
makes it possible to estimate u(x). However, in some cases one can get the asymptotic behaviour of u(x). In fact, using the strong Markov property, one can show that u(x) satisfies the following renewal-type equation:
with some
![]() $h\in\mathcal{B}_b^+\big({\unicode{x211D}^d}\big)$
and a (sub-)probability measure
$h\in\mathcal{B}_b^+\big({\unicode{x211D}^d}\big)$
and a (sub-)probability measure
![]() $\mathfrak{G}(x,dz)$
on
$\mathfrak{G}(x,dz)$
on
![]() ${\unicode{x211D}^d}$
that can be identified explicitly. Note that under the assumptions made above, this equation has a unique bounded solution (cf. Remark 1). In the case when
${\unicode{x211D}^d}$
that can be identified explicitly. Note that under the assumptions made above, this equation has a unique bounded solution (cf. Remark 1). In the case when
![]() $Y_t$
has independent increments, this is a typical renewal equation, i.e. (7) becomes
$Y_t$
has independent increments, this is a typical renewal equation, i.e. (7) becomes
for some (sub-)probability measure G(dz).
In the case when T is an independent killing, the measure
![]() $\mathfrak{G}(x,dz)$
is a sub-probability measure with
$\mathfrak{G}(x,dz)$
is a sub-probability measure with
![]() $\rho\,:\!=\,\mathfrak{G}\big(x,{\unicode{x211D}^d}\big)<1$
(note that
$\rho\,:\!=\,\mathfrak{G}\big(x,{\unicode{x211D}^d}\big)<1$
(note that
![]() $\rho$
does not depend on x; see (27) below). This makes it possible to give precisely the asymptotic behaviour of u if F is
$\rho$
does not depend on x; see (27) below). This makes it possible to give precisely the asymptotic behaviour of u if F is
![]() $\big({\unicode{x211D}^d}\big)$
-subexponential. The case when F is subexponential corresponds to the situation when the impact of the claim is rather big, e.g.,
$\big({\unicode{x211D}^d}\big)$
-subexponential. The case when F is subexponential corresponds to the situation when the impact of the claim is rather big, e.g.,
![]() $U_i$
does not have finite variance. Such a situation appears in many insurance models; see, for example, Mikosch [Reference Mikosch31], as well as the monographs of Asmussen [Reference Asmussen1] and Asmussen and Albrecher [Reference Asmussen and Albrecher2]. We discuss several practical examples in Section 5.
$U_i$
does not have finite variance. Such a situation appears in many insurance models; see, for example, Mikosch [Reference Mikosch31], as well as the monographs of Asmussen [Reference Asmussen1] and Asmussen and Albrecher [Reference Asmussen and Albrecher2]. We discuss several practical examples in Section 5.
The case when the time T depends on the process may be different, however. We discuss this problem in Example 4, where X is a one-dimensional risk process with
![]() $Y_t= at$
,
$Y_t= at$
,
![]() $a>0$
, and T is a ruin time, that is, the first time at which the process goes below zero. In this case we suggest rewriting Equation (8) in a different way in order to deduce the asymptotic of u(x).
$a>0$
, and T is a ruin time, that is, the first time at which the process goes below zero. In this case we suggest rewriting Equation (8) in a different way in order to deduce the asymptotic of u(x).
The asymptotic behaviour of the solution to the renewal equation of type (7) has been studied quite a lot; see the monograph of Feller [Reference Feller21], and also Çinlar [Reference Çinlar12] and Asmussen [Reference Asmussen1]. The behaviour of the solution depends heavily on the integrability of h and the behaviour of the tails of G. We refer to [Reference Feller21] for the classical situation, where the Cramér–Lundberg condition holds, i.e. where there exists a solution
![]() $\alpha=\alpha(\rho, G)$
to the equation
$\alpha=\alpha(\rho, G)$
to the equation
![]() $\rho\int e^{\alpha x} G(dx)=1$
; see also Stone [Reference Stone39] for a moment condition. In the multidimensional case under the generalization of the Cramér–Lundberg or moment assumptions, the asymptotic behaviour of the solution is studied in Chung [Reference Chung10], Doney [Reference Doney16], Nagaev [Reference Nagaev32], Carlsson and Wainger [Reference Carlsson and Wainger6, Reference Carlsson and Wainger7], and Höglund [Reference Höglund25] (see also the reference therein for the multidimensional renewal theorem). In Chover, Nei, and Wainger [Reference Chover, Ney and Wainger8, Reference Chover, Ney and Wainger9] and Embrecht and Goldie [Reference Embrechts and Goldie19, Reference Embrechts and Goldie20] the asymptotic behaviour of the tails of the measure
$\rho\int e^{\alpha x} G(dx)=1$
; see also Stone [Reference Stone39] for a moment condition. In the multidimensional case under the generalization of the Cramér–Lundberg or moment assumptions, the asymptotic behaviour of the solution is studied in Chung [Reference Chung10], Doney [Reference Doney16], Nagaev [Reference Nagaev32], Carlsson and Wainger [Reference Carlsson and Wainger6, Reference Carlsson and Wainger7], and Höglund [Reference Höglund25] (see also the reference therein for the multidimensional renewal theorem). In Chover, Nei, and Wainger [Reference Chover, Ney and Wainger8, Reference Chover, Ney and Wainger9] and Embrecht and Goldie [Reference Embrechts and Goldie19, Reference Embrechts and Goldie20] the asymptotic behaviour of the tails of the measure
![]() $\sum_{j=1}^\infty c_j G^{*j}$
on
$\sum_{j=1}^\infty c_j G^{*j}$
on
![]() $\unicode{x211D}$
is investigated under the subexponentiality condition on the tails of G, e.g. when the moment condition is not necessarily satisfied. These results are further extended in the works of Cline [Reference Cline13, Reference Cline14], Cline and Resnik [Reference Cline and Resnick15], Omey [Reference Omey33], Omey, Mallor, and Santos [Reference Omey, Mallor and Santos34], and Yin and Zhao [Reference Yin and Zhao41]; see also the monographs of Embrechts, Klüppelberg, and Mikosh [Reference Embrechts, Klüppelberg and Mikosch18], and of Foss, Korshunov, and Zahary [Reference Foss, Korshunov and Zachary23].
$\unicode{x211D}$
is investigated under the subexponentiality condition on the tails of G, e.g. when the moment condition is not necessarily satisfied. These results are further extended in the works of Cline [Reference Cline13, Reference Cline14], Cline and Resnik [Reference Cline and Resnick15], Omey [Reference Omey33], Omey, Mallor, and Santos [Reference Omey, Mallor and Santos34], and Yin and Zhao [Reference Yin and Zhao41]; see also the monographs of Embrechts, Klüppelberg, and Mikosh [Reference Embrechts, Klüppelberg and Mikosch18], and of Foss, Korshunov, and Zahary [Reference Foss, Korshunov and Zachary23].
The main tools used in this paper to derive the above-mentioned asymptotics of the potential u(x) given in (6) are based on the properties of subexponential distributions in
![]() ${\unicode{x211D}^d}$
introduced and discussed in [Reference Omey33, Reference Omey, Mallor and Santos34].
${\unicode{x211D}^d}$
introduced and discussed in [Reference Omey33, Reference Omey, Mallor and Santos34].
The paper is organized as follows. In Section 2 we construct the renewal equation for the potential function u. In Section 3 we give the main results. Some particular examples and extensions are described in Section 4. Finally, in Section 5 we give some possible applications of the results proved.
We use the following notation. We write
![]() $f (x)\asymp g(x)$
when
$f (x)\asymp g(x)$
when
![]() $C_1g(x) \leq f(x) \leq C_2g(x)$
for some constants
$C_1g(x) \leq f(x) \leq C_2g(x)$
for some constants
![]() $C_1, C_2> 0$
. We write
$C_1, C_2> 0$
. We write
![]() $y<x$
for
$y<x$
for
![]() $x,y\in {\unicode{x211D}^d}$
, if all components of y are less than the respective components of x.
$x,y\in {\unicode{x211D}^d}$
, if all components of y are less than the respective components of x.
2. Renewal-type equation: general case
Let
![]() $\zeta\sim \operatorname{Exp}(\lambda)$
be the moment of the first big jump of size
$\zeta\sim \operatorname{Exp}(\lambda)$
be the moment of the first big jump of size
![]() $\geq \delta$
of the process
$\geq \delta$
of the process
![]() $Z_t$
. Define
$Z_t$
. Define
For a Borel-measurable set
![]() $A\subset {\unicode{x211D}^d}$
,
$A\subset {\unicode{x211D}^d}$
,
In the case when
![]() $Y_s$
is not a deterministic function of s, the kernel
$Y_s$
is not a deterministic function of s, the kernel
![]() $\mathfrak{G}(x,dz)$
can be rewritten in the following way:
$\mathfrak{G}(x,dz)$
can be rewritten in the following way:
In the theorem below we derive the renewal(-type) equation for u.
For the kernels
![]() $H_i(x,dy)$
,
$H_i(x,dy)$
,
![]() $i=1,2$
, define the convolution
$i=1,2$
, define the convolution
Note that if the
![]() $H_i$
are of the type
$H_i$
are of the type
![]() $H_i(x,dy)= h_i(y)dy$
,
$H_i(x,dy)= h_i(y)dy$
,
![]() $i=1,2$
, then this convolution reduces to the ordinary convolution of the functions
$i=1,2$
, then this convolution reduces to the ordinary convolution of the functions
![]() $h_1$
and
$h_1$
and
![]() $h_2$
:
$h_2$
:
Similarly, if only
![]() $H_1(x,dy)$
is of the form
$H_1(x,dy)$
is of the form
![]() $H_1(x,dy)= h_1(y)dy$
, then by
$H_1(x,dy)= h_1(y)dy$
, then by
![]() $\big(h_1* H_2\big)(z,x)$
we understand
$\big(h_1* H_2\big)(z,x)$
we understand
Theorem 1. Assume that the terminal time T satisfies
![]() $\mathbb{E} T<\infty$
. Then the function u(x) given by (6) is a solution to the equation (7) and admits the representation
$\mathbb{E} T<\infty$
. Then the function u(x) given by (6) is a solution to the equation (7) and admits the representation
where
![]() $\mathfrak{G}^{* 0 }(x,dz)=\delta_0(dz)$
and
$\mathfrak{G}^{* 0 }(x,dz)=\delta_0(dz)$
and
![]() $\mathfrak{G}^{* n }(x,dz) \,:\!=\, \int_{\unicode{x211D}^d} \mathfrak{G}^{* (n-1) }(x,dy)\mathfrak{G}(x-y,dz-y)$
for
$\mathfrak{G}^{* n }(x,dz) \,:\!=\, \int_{\unicode{x211D}^d} \mathfrak{G}^{* (n-1) }(x,dy)\mathfrak{G}(x-y,dz-y)$
for
![]() $n\geq 1$
.
$n\geq 1$
.
If
![]() $Y_t$
has independent increments, then
$Y_t$
has independent increments, then
and
 \begin{equation}u(x)= \Bigg(h* \sum_{n=0}^\infty G^{* n }\Bigg)(x,x).\end{equation}
\begin{equation}u(x)= \Bigg(h* \sum_{n=0}^\infty G^{* n }\Bigg)(x,x).\end{equation}
Remark 1. Recall that u(x) is assumed to be bounded. Then, since
![]() $\ell\in \mathcal{B}_b^+(\unicode{x211D})$
, u(x) is the unique bounded solution to (7). The proof of this fact is similar to that in Feller [Reference Feller21, XI.1, Lemma 1]. Indeed, suppose that v(x) is another bounded solution to (7). Take
$\ell\in \mathcal{B}_b^+(\unicode{x211D})$
, u(x) is the unique bounded solution to (7). The proof of this fact is similar to that in Feller [Reference Feller21, XI.1, Lemma 1]. Indeed, suppose that v(x) is another bounded solution to (7). Take
![]() $x\in {\unicode{x211D}^d}\backslash \partial$
. Then
$x\in {\unicode{x211D}^d}\backslash \partial$
. Then
![]() $w(x)\,:\!=\, u(x)-v(x)$
satisfies the equation
$w(x)\,:\!=\, u(x)-v(x)$
satisfies the equation
Note that for any Borel-measurable
![]() $A\subset {\unicode{x211D}^d} $
we have
$A\subset {\unicode{x211D}^d} $
we have
![]() $ \mathfrak{G} (x,A) < 1$
by (10). Then
$ \mathfrak{G} (x,A) < 1$
by (10). Then
Hence,
![]() $w(x)\equiv 0$
for
$w(x)\equiv 0$
for
![]() $x\in A$
for any A as above.
$x\in A$
for any A as above.
Before we proceed to the proof of Theorem 2, recall the definition of the strong Markov property, which is crucial for the proof. Recall (cf. [Reference Chung11, Section 2.3]) that the process
![]() $\big(X_t,\mathcal{F}_t\big)$
is called strongly Markov if, for any optional time S and any real-valued function f that is continuous on
$\big(X_t,\mathcal{F}_t\big)$
is called strongly Markov if, for any optional time S and any real-valued function f that is continuous on
![]() $\overline{{\unicode{x211D}^d}}\,:\!=\,{\unicode{x211D}^d}\cup \{\infty\}$
and such that
$\overline{{\unicode{x211D}^d}}\,:\!=\,{\unicode{x211D}^d}\cup \{\infty\}$
and such that
![]() $\underset{x\in\overline{{\unicode{x211D}^d}}}{\sup}|f(x)|<\infty$
,
$\underset{x\in\overline{{\unicode{x211D}^d}}}{\sup}|f(x)|<\infty$
,
Here
![]() $\mathcal{F}_{S}\,:\!=\, \{ A\in \mathcal{F}| \, A \cap \{S \leq t\}\in \mathcal{F}_{t+}\equiv\mathcal{F}_{t}\,\quad \forall t\geq 0\}$
, and since
$\mathcal{F}_{S}\,:\!=\, \{ A\in \mathcal{F}| \, A \cap \{S \leq t\}\in \mathcal{F}_{t+}\equiv\mathcal{F}_{t}\,\quad \forall t\geq 0\}$
, and since
![]() $\mathcal{F}_t$
is assumed to be right-continuous, the notions of the stopping and optional times coincide. Sometimes it is convenient to reformulate the strong Markov property in terms of the shift operator: let
$\mathcal{F}_t$
is assumed to be right-continuous, the notions of the stopping and optional times coincide. Sometimes it is convenient to reformulate the strong Markov property in terms of the shift operator: let
![]() $\theta_t\,:\, \Omega\to \Omega$
be such that for all
$\theta_t\,:\, \Omega\to \Omega$
be such that for all
![]() $r>0$
,
$r>0$
,
![]() $(X_r \circ \theta_t)(\omega) = X_{r+s}(\omega)$
. This operator naturally extends to
$(X_r \circ \theta_t)(\omega) = X_{r+s}(\omega)$
. This operator naturally extends to
![]() $\theta_S$
for an optional time S as follows:
$\theta_S$
for an optional time S as follows:
![]() $(X_r \circ \theta_S)(\omega) = X_{r+S}(\omega)$
. Then one can rewrite (16) as
$(X_r \circ \theta_S)(\omega) = X_{r+S}(\omega)$
. Then one can rewrite (16) as
and for any
![]() $Z\in \mathcal{F}$
,
$Z\in \mathcal{F}$
,
The definition (4) of the terminal time T allows us to use the strong Markov property (18) to ‘separate’ the future of the process from its past.
Proof of Theorem 1. Using the strong Markov property we get
We estimate the two terms
![]() $I_1$
and
$I_1$
and
![]() $I_2$
separately. Note that
$I_2$
separately. Note that
![]() $X_s^\sharp= Y_s^\sharp$
for
$X_s^\sharp= Y_s^\sharp$
for
![]() $s \leq \zeta$
. Therefore by the Fubini theorem we have
$s \leq \zeta$
. Therefore by the Fubini theorem we have
 \begin{align*}I_1 &= \mathbb{E}^x \int_0^\infty \lambda e^{-\lambda s} \int_0^s \ell\big(Y_r^\sharp\big)\, dr ds= \mathbb{E}^x \int_0^\infty \left( \int_r^\infty \lambda e^{-\lambda s} \, ds \right) \ell \big(Y_r^\sharp\big) \, dr \\&= \mathbb{E}^x \int_0^\infty e^{-\lambda r} \ell\big(Y_r^\sharp\big)\, dr= \int_{\unicode{x211D}^d} \ell(w) \int_0^\infty e^{-\lambda r} \mathbb{P}^x (Y_r \in dw, T>r)dr\\&=h(x).\end{align*}
\begin{align*}I_1 &= \mathbb{E}^x \int_0^\infty \lambda e^{-\lambda s} \int_0^s \ell\big(Y_r^\sharp\big)\, dr ds= \mathbb{E}^x \int_0^\infty \left( \int_r^\infty \lambda e^{-\lambda s} \, ds \right) \ell \big(Y_r^\sharp\big) \, dr \\&= \mathbb{E}^x \int_0^\infty e^{-\lambda r} \ell\big(Y_r^\sharp\big)\, dr= \int_{\unicode{x211D}^d} \ell(w) \int_0^\infty e^{-\lambda r} \mathbb{P}^x (Y_r \in dw, T>r)dr\\&=h(x).\end{align*}
To transform
![]() $I_2$
, we use the fact that T is the terminal time, the strong Markov property (18) of X, and the fact that
$I_2$
, we use the fact that T is the terminal time, the strong Markov property (18) of X, and the fact that
![]() $X_\zeta^\sharp= Y_\zeta^\sharp$
. Let
$X_\zeta^\sharp= Y_\zeta^\sharp$
. Let
![]() $Z= \int_0^\infty \ell\big(X_r^\sharp\big) \,dr$
. Then by the definition (4) of the terminal time we get
$Z= \int_0^\infty \ell\big(X_r^\sharp\big) \,dr$
. Then by the definition (4) of the terminal time we get
 \begin{align*}I_2&= \mathbb{E}^x \int_0^\infty \ell\Big(X_r^\sharp\circ \theta_\zeta\Big)dr=\mathbb{E}^x\left[ \mathbb{E}^x \left[\int_0^\infty \ell\Big(X_r^\sharp\circ \theta_\zeta\Big) \,dr \Big| \mathcal{F}_\zeta \right]\right] \\[3pt]&= \mathbb{E}^x \left[ \mathbb{E}^x \left[Z \circ \theta_\zeta \Big| \mathcal{F}_\zeta \right] \right]= \mathbb{E}^x \Big[\mathbb{E}^{X_\zeta^\sharp} Z\Big]= \mathbb{E}^x u\Big(X_\zeta^\sharp\Big)=\mathbb{E}^x u\Big(Y_\zeta^\sharp\Big) \\[3pt] &= \int_{\unicode{x211D}^d} \int_{\unicode{x211D}^d} u(w-y) \left[\int_0^\infty \lambda e^{-\lambda s } F(dy) \mathbb{P}^x( Y_s \in dw, T>s) ds\right] \\[3pt] &= \int_{\unicode{x211D}^d} \int_{\unicode{x211D}^d} u(v-(y-x))\left[ \int_0^\infty \lambda e^{-\lambda s } F(dy) \mathbb{P}^x( Y_s \in dv+x, T>s) ds\right]\\[3pt] &= \int_{\unicode{x211D}^d} u(x-z) \left[\int_{\unicode{x211D}^d} \int_0^\infty \lambda e^{-\lambda s } F(dz+v) \mathbb{P}^x( Y_s \in dv+x, T>s) ds\right],\end{align*}
\begin{align*}I_2&= \mathbb{E}^x \int_0^\infty \ell\Big(X_r^\sharp\circ \theta_\zeta\Big)dr=\mathbb{E}^x\left[ \mathbb{E}^x \left[\int_0^\infty \ell\Big(X_r^\sharp\circ \theta_\zeta\Big) \,dr \Big| \mathcal{F}_\zeta \right]\right] \\[3pt]&= \mathbb{E}^x \left[ \mathbb{E}^x \left[Z \circ \theta_\zeta \Big| \mathcal{F}_\zeta \right] \right]= \mathbb{E}^x \Big[\mathbb{E}^{X_\zeta^\sharp} Z\Big]= \mathbb{E}^x u\Big(X_\zeta^\sharp\Big)=\mathbb{E}^x u\Big(Y_\zeta^\sharp\Big) \\[3pt] &= \int_{\unicode{x211D}^d} \int_{\unicode{x211D}^d} u(w-y) \left[\int_0^\infty \lambda e^{-\lambda s } F(dy) \mathbb{P}^x( Y_s \in dw, T>s) ds\right] \\[3pt] &= \int_{\unicode{x211D}^d} \int_{\unicode{x211D}^d} u(v-(y-x))\left[ \int_0^\infty \lambda e^{-\lambda s } F(dy) \mathbb{P}^x( Y_s \in dv+x, T>s) ds\right]\\[3pt] &= \int_{\unicode{x211D}^d} u(x-z) \left[\int_{\unicode{x211D}^d} \int_0^\infty \lambda e^{-\lambda s } F(dz+v) \mathbb{P}^x( Y_s \in dv+x, T>s) ds\right],\end{align*}
where in the third and the last lines we used the Fubini theorem, and in the last two lines we made the changes of variables
![]() $w\rightsquigarrow v+x$
and
$w\rightsquigarrow v+x$
and
![]() $y\rightsquigarrow v+z$
, respectively. The integral in the square brackets in the last line is equal to
$y\rightsquigarrow v+z$
, respectively. The integral in the square brackets in the last line is equal to
![]() $\mathfrak{G}(x,dz)$
. Thus u satisfies the renewal equation (7). Iterating this equation we get (13).
$\mathfrak{G}(x,dz)$
. Thus u satisfies the renewal equation (7). Iterating this equation we get (13).
3. Asymptotic behaviour in case of independent killing
In this section we show that under certain conditions one can get the asymptotic behaviour of u(x) for large x. We begin with a short subsection where we collect the necessary auxiliary notions.
3.1. Subexponential distributions on
 ${\unicode{x211D}_+^d}$
and
${\unicode{x211D}_+^d}$
and
 ${\unicode{x211D}^d}$
${\unicode{x211D}^d}$
Recall the notation
![]() ${\unicode{x211D}_+^d}= (0,\infty)^d$
and
${\unicode{x211D}_+^d}= (0,\infty)^d$
and
![]() $x^0=\min_{1 \leq i \leq d} x_i<\infty$
for
$x^0=\min_{1 \leq i \leq d} x_i<\infty$
for
![]() $x\in {\unicode{x211D}^d}$
.
$x\in {\unicode{x211D}^d}$
.
Definition 1.
-
1. A function
 $f\,:\, {\unicode{x211D}_+^d}\to [0,\infty)$
is called weakly long-tailed
$f\,:\, {\unicode{x211D}_+^d}\to [0,\infty)$
is called weakly long-tailed
 $\big($
notation:
$\big($
notation:
 $f\in WL\big({\unicode{x211D}_+^d}\big)$
$f\in WL\big({\unicode{x211D}_+^d}\big)$
 $\big)$
if (19)
$\big)$
if (19) \begin{equation}\lim_{x^0\to \infty} \frac{f(x-a)}{f(x)} =1 \quad \forall a>0.\end{equation}
\begin{equation}\lim_{x^0\to \infty} \frac{f(x-a)}{f(x)} =1 \quad \forall a>0.\end{equation}
-
2. We say that a distribution function F on
 ${\unicode{x211D}_+^d}$
is weakly subexponential
${\unicode{x211D}_+^d}$
is weakly subexponential
 $\big($
notation:
$\big($
notation:
 $F\in WS\big({\unicode{x211D}_+^d}\big)\big)$
if (20)
$F\in WS\big({\unicode{x211D}_+^d}\big)\big)$
if (20) \begin{equation}\lim_{x^0\to \infty}\frac{\overline{F^{*2}}(x)}{\overline{F}(x)} =2.\end{equation}
\begin{equation}\lim_{x^0\to \infty}\frac{\overline{F^{*2}}(x)}{\overline{F}(x)} =2.\end{equation}
-
3. We say that a distribution function F on
 ${\unicode{x211D}^d}$
is weakly subexponential
${\unicode{x211D}^d}$
is weakly subexponential
 $\big($
notation:
$\big($
notation:
 $F\in WS\big({\unicode{x211D}^d}\big)\big)$
if it is long-tailed and (20) holds.
$F\in WS\big({\unicode{x211D}^d}\big)\big)$
if it is long-tailed and (20) holds.
Remark 2.
-
1. If
 $F\in WS\big({\unicode{x211D}_+^d}\big)$
then
$F\in WS\big({\unicode{x211D}_+^d}\big)$
then
 $\overline{F}$
is long-tailed.
$\overline{F}$
is long-tailed. -
2. For
 $F\in WS\big({\unicode{x211D}_+^d}\big)$
we have (cf. [Reference Omey33, Corollary 11])
$F\in WS\big({\unicode{x211D}_+^d}\big)$
we have (cf. [Reference Omey33, Corollary 11])  \begin{equation*}\lim_{x^0\to \infty}\frac{\overline{F^{*n}}(x)}{\overline{F}(x)} =n.\end{equation*}
\begin{equation*}\lim_{x^0\to \infty}\frac{\overline{F^{*n}}(x)}{\overline{F}(x)} =n.\end{equation*}
-
3. Rewriting [Reference Foss, Korshunov and Zachary23, Lemma 2.17, p. 19] in the multivariate set-up, we conclude that any weakly subexponential distribution function is heavy-tailed; that is, for any
 $\varsigma$
with
$\varsigma$
with
 $\varsigma^0 >0$
, (21)where
$\varsigma^0 >0$
, (21)where \begin{equation}\lim_{x^0\to \infty}\overline{F}(x) e^{\varsigma x } =+\infty, \end{equation}
\begin{equation}\lim_{x^0\to \infty}\overline{F}(x) e^{\varsigma x } =+\infty, \end{equation}
 $\varsigma x\,:\!=\,(\varsigma_1x_1,\dots, \varsigma_dx_d)$
.
$\varsigma x\,:\!=\,(\varsigma_1x_1,\dots, \varsigma_dx_d)$
.
-
4. We have extended the definition of the whole-line subexponentiality from [Reference Foss, Korshunov and Zachary23, Definition 3.5] to the multidimensional case. Note that even on the real line the assumption (20) alone does not imply that the distribution is long-tailed; see [Reference Foss, Korshunov and Zachary23, Section 3.2].
An important property of a long-tailed function f is the existence of an insensitive function.
Definition 2. We say that a function f is
![]() $\phi$
-insensitive as
$\phi$
-insensitive as
![]() $x^0\to\infty$
, where
$x^0\to\infty$
, where
![]() $\phi\,:\,{\unicode{x211D}_+^d}\to {\unicode{x211D}_+^d}$
is a nonnegative function that is increasing in each coordinate, if
$\phi\,:\,{\unicode{x211D}_+^d}\to {\unicode{x211D}_+^d}$
is a nonnegative function that is increasing in each coordinate, if
Remark 3. Suppose that the function
![]() $\phi$
in Definition 2 is such that
$\phi$
in Definition 2 is such that
![]() $x-\phi(x)^0 \to \infty $
if and only if
$x-\phi(x)^0 \to \infty $
if and only if
![]() $x^0\rightarrow +\infty$
. Then for a
$x^0\rightarrow +\infty$
. Then for a
![]() $\phi$
-insensitive function f we also have
$\phi$
-insensitive function f we also have
Remark 4. In the one-dimensional case if f is long-tailed then such a function
![]() $\phi$
exists. If f is regularly varying, then it is
$\phi$
exists. If f is regularly varying, then it is
![]() $\phi$
-insensitive with respect to any function
$\phi$
-insensitive with respect to any function
![]() $\phi(t)= o(t)$
as
$\phi(t)= o(t)$
as
![]() $t\to \infty$
. The observation below shows that this property can be extended to the multidimensional case.
$t\to \infty$
. The observation below shows that this property can be extended to the multidimensional case.
Let
![]() $\phi(x)= (\phi_1(x_1), \dots, \phi_d(x_d))$
, where
$\phi(x)= (\phi_1(x_1), \dots, \phi_d(x_d))$
, where
![]() $\phi_i \,:\, [0,\infty)\to [0,\infty)$
,
$\phi_i \,:\, [0,\infty)\to [0,\infty)$
,
![]() $1 \leq i \leq d$
, are increasing functions,
$1 \leq i \leq d$
, are increasing functions,
![]() $\phi_i(t)= o(t)$
as
$\phi_i(t)= o(t)$
as
![]() $t\to \infty$
. If f is regularly varying in each component (and, hence, long-tailed in each component), then it is
$t\to \infty$
. If f is regularly varying in each component (and, hence, long-tailed in each component), then it is
![]() $\phi(x)$
-insensitive. Indeed,
$\phi(x)$
-insensitive. Indeed,
 \begin{equation}\begin{split}&\lim_{x^0 \to \infty} \frac{f(x+\phi(x))}{f(x)} = \lim_{x^0 \to \infty}\left\{ \frac{f(x_1+ \phi_1(x_1), \dots, x_d+ \phi_d(x_d))}{f(x_1+\phi_1(x_1), \dots, x_{d-1}+ \phi_{d-1}(x_{d-1}), x_d)} \right.\\&\quad \cdot \left.\frac{f(x_1+ \phi_1(x_1), \dots,x_{d-1}+ \phi_{d-1}(x_{d-1}), x_d)}{f(x_1+\phi_1(x_1), \dots, x_{d-1}, x_d)} \dots \frac{f(x_1+ \phi_1(x_1), x_2,\dots, x_d)}{f(x_1, x_2, \dots, x_d)}\right\} \\&\quad =1.\end{split}\end{equation}
\begin{equation}\begin{split}&\lim_{x^0 \to \infty} \frac{f(x+\phi(x))}{f(x)} = \lim_{x^0 \to \infty}\left\{ \frac{f(x_1+ \phi_1(x_1), \dots, x_d+ \phi_d(x_d))}{f(x_1+\phi_1(x_1), \dots, x_{d-1}+ \phi_{d-1}(x_{d-1}), x_d)} \right.\\&\quad \cdot \left.\frac{f(x_1+ \phi_1(x_1), \dots,x_{d-1}+ \phi_{d-1}(x_{d-1}), x_d)}{f(x_1+\phi_1(x_1), \dots, x_{d-1}, x_d)} \dots \frac{f(x_1+ \phi_1(x_1), x_2,\dots, x_d)}{f(x_1, x_2, \dots, x_d)}\right\} \\&\quad =1.\end{split}\end{equation}
Remark 5. Note that if a function is regularly varying in each component, it is long-tailed in the sense of the definition (19), which follows from (22). However, the class of long-tailed functions is larger than that of multivariate regularly varying functions. There are several definitions of multivariate regular variation; see e.g. [Reference Basrak, Davis and Mikosch3, Reference Omey33]. According to [Reference Omey33], a function
![]() $f\,:\, {\unicode{x211D}_+^d}\to [0,\infty)$
is called regularly varying if, for any
$f\,:\, {\unicode{x211D}_+^d}\to [0,\infty)$
is called regularly varying if, for any
![]() $x\in {\unicode{x211D}_+^d}$
,
$x\in {\unicode{x211D}_+^d}$
,
where
![]() $\kappa \in \unicode{x211D}$
,
$\kappa \in \unicode{x211D}$
,
![]() $r({\cdot})$
is slowly varying at infinity, and
$r({\cdot})$
is slowly varying at infinity, and
![]() $\psi({\cdot})\geq 0$
(see [Reference Basrak, Davis and Mikosch3] for the definition of multivariate regular variation of a distribution tail); it is called weakly regularly varying with respect to h if, for any
$\psi({\cdot})\geq 0$
(see [Reference Basrak, Davis and Mikosch3] for the definition of multivariate regular variation of a distribution tail); it is called weakly regularly varying with respect to h if, for any
![]() $x,b\in {\unicode{x211D}_+^d}$
,
$x,b\in {\unicode{x211D}_+^d}$
,
where
![]() $b x\,:\!=\,\big(b_1x_1,\dots, b_dx_d\big)$
. Note that the function of the form
$b x\,:\!=\,\big(b_1x_1,\dots, b_dx_d\big)$
. Note that the function of the form
![]() $f(x_1,x_2)= c_1\big(1+x_1^{\alpha_1}\big)^{-1} + c_2 \big(1+x_1^{\alpha_2}\big)^{-1}$
(where
$f(x_1,x_2)= c_1\big(1+x_1^{\alpha_1}\big)^{-1} + c_2 \big(1+x_1^{\alpha_2}\big)^{-1}$
(where
![]() $c_i, \alpha_i>0$
,
$c_i, \alpha_i>0$
,
![]() $i=1,2$
) is regularly varying in each variable, but is not regularly varying in the sense of (23) or (24) unless
$i=1,2$
) is regularly varying in each variable, but is not regularly varying in the sense of (23) or (24) unless
![]() $\alpha_1=\alpha_2$
.
$\alpha_1=\alpha_2$
.
3.2. Asymptotic behaviour of u(x)
Let T be an independent exponential killing with parameter
![]() $\mu$
. We assume that the law
$\mu$
. We assume that the law
![]() $P_s(x,dw)$
of
$P_s(x,dw)$
of
![]() $Y_s$
is absolutely continuous with respect to the Lebesgue measure, and denote the respective transition probability density function by
$Y_s$
is absolutely continuous with respect to the Lebesgue measure, and denote the respective transition probability density function by
![]() $\mathfrak{p}_s(x,w)$
.
$\mathfrak{p}_s(x,w)$
.
Rewrite
![]() $\mathfrak{G}(x,dz)$
as
$\mathfrak{G}(x,dz)$
as
where
Observe that in the case of independent killing we have (cf. (25))
For
![]() $z\in {\unicode{x211D}^d}$
, define
$z\in {\unicode{x211D}^d}$
, define
Theorem 2. Assume that T is an independent exponential killing with parameter
![]() $\mu$
and
$\mu$
and
![]() $\ell(x)\to 0$
as
$\ell(x)\to 0$
as
![]() $x^0\to -\infty$
. Let
$x^0\to -\infty$
. Let
![]() $F\in WS\big({\unicode{x211D}_+^d}\big)$
and suppose that the function q(x,w) defined in (25) satisfies the estimate
$F\in WS\big({\unicode{x211D}_+^d}\big)$
and suppose that the function q(x,w) defined in (25) satisfies the estimate
for some
![]() $\theta, C>0$
. Suppose the following:
$\theta, C>0$
. Suppose the following:
-
(a)
 $\ell$
is long-tailed and
$\ell$
is long-tailed and
 $\phi$
-insensitive for some
$\phi$
-insensitive for some
 $\phi$
such that
$\phi$
such that
 $\phi(x)^0\rightarrow +\infty$
and
$\phi(x)^0\rightarrow +\infty$
and
 $(x-\phi(x))^0\rightarrow +\infty$
as
$(x-\phi(x))^0\rightarrow +\infty$
as
 $x^0\to \infty$
;
$x^0\to \infty$
; -
(b) for any
 $c>0$
, (29)
$c>0$
, (29) \begin{equation}\lim_{x^0\to \infty}\min\big(\overline{F}(x), \ell(x)\big) e^{c|\phi(x)|}= \infty;\end{equation}
\begin{equation}\lim_{x^0\to \infty}\min\big(\overline{F}(x), \ell(x)\big) e^{c|\phi(x)|}= \infty;\end{equation}
-
(c) there exists
 $B\in [0,\infty]$
such that (30)
$B\in [0,\infty]$
such that (30) \begin{equation} \lim_{x^0\to\infty} \frac{\ell(x)}{\overline{F}(x) }=B; \end{equation}
\begin{equation} \lim_{x^0\to\infty} \frac{\ell(x)}{\overline{F}(x) }=B; \end{equation}
-
(d) if
 $B=\infty$
, we assume in addition that
$B=\infty$
, we assume in addition that
 $\ell(x)$
is regularly varying in each component.
$\ell(x)$
is regularly varying in each component.
Then
 \begin{equation}u(x) =\begin{cases}\frac{B \rho }{1-\rho}\overline{F}(x) (1+ o(1)), & B \in (0,\infty),\\[4pt]o(1) \overline{F}(x), & B =0,\\[4pt]\frac{ \rho \ell(x)}{1-\rho} (1+ o(1)), & B=\infty,\end{cases}\quad \text{as $x^0\to \infty.$}\end{equation}
\begin{equation}u(x) =\begin{cases}\frac{B \rho }{1-\rho}\overline{F}(x) (1+ o(1)), & B \in (0,\infty),\\[4pt]o(1) \overline{F}(x), & B =0,\\[4pt]\frac{ \rho \ell(x)}{1-\rho} (1+ o(1)), & B=\infty,\end{cases}\quad \text{as $x^0\to \infty.$}\end{equation}
Remark 6. If we consider the one-dimensional case and
![]() $Y_t$
is a Lévy process, the proof follows from [Reference Embrechts, Goldie and Veraverbeke17, Corollary 3], [Reference Embrechts, Klüppelberg and Mikosch18, Theorem A.3.20], or [Reference Foss, Korshunov and Zachary23, Corollaries 3.16–3.19].
$Y_t$
is a Lévy process, the proof follows from [Reference Embrechts, Goldie and Veraverbeke17, Corollary 3], [Reference Embrechts, Klüppelberg and Mikosch18, Theorem A.3.20], or [Reference Foss, Korshunov and Zachary23, Corollaries 3.16–3.19].
Remark 7. One can relax the condition of existence of the limit (30) replacing it by the existence of
![]() $\underset{x^0\to\infty}{\limsup}$
and
$\underset{x^0\to\infty}{\limsup}$
and
![]() $\underset{x^0\to\infty}{\liminf}$
and the assumption that
$\underset{x^0\to\infty}{\liminf}$
and the assumption that
![]() $\ell$
is regularly varying in each component by
$\ell$
is regularly varying in each component by
Since this extension is straightforward, we do not go into details.
Remark 8. Note that
By (28) and the dominated convergence theorem, the assumption
![]() $\ell(x)\to 0$
as
$\ell(x)\to 0$
as
![]() $x^0\to -\infty$
implies that
$x^0\to -\infty$
implies that
![]() $h(x)\to 0$
as
$h(x)\to 0$
as
![]() $x^0\to -\infty$
.
$x^0\to -\infty$
.
For the proof of Theorem 2 we need the following auxiliary lemmas.
Lemma 1. Under the assumptions of Theorem 2 we have
and there exists
![]() $C>0$
such that
$C>0$
such that
Proof. The proof is similar to that of [Reference Foss, Korshunov and Zachary23, Theorem 3.34]. The idea is that the parametric dependence on x is hidden in the function
![]() $q(x,x+w)$
, which decays much faster than
$q(x,x+w)$
, which decays much faster than
![]() $\overline{F}$
because of (21).
$\overline{F}$
because of (21).
Take
![]() $\phi$
such that
$\phi$
such that
![]() $\overline{F}$
is
$\overline{F}$
is
![]() $\phi$
-insensitive and
$\phi$
-insensitive and
![]() $(x-\phi(x))^0\rightarrow +\infty$
as
$(x-\phi(x))^0\rightarrow +\infty$
as
![]() $x^0\to \infty$
.
$x^0\to \infty$
.
We split:
 \begin{align*}\overline{G}_\rho(z,x)&= \rho^{-1}\int_{\unicode{x211D}^d} \overline{F}(x+w) q(z,w+z)dw\\&= \rho^{-1}\Bigg( \int_{ w \leq -\phi(x) } +\int_{ |w| \leq |\phi(x)| } + \int_{w > \phi(x)} \Bigg) \overline{F}(x+ w) q(z,w+z)dw \\&\,:\!=\, K_1(z,x)+ K_2(z,x)+K_3(z,x).\end{align*}
\begin{align*}\overline{G}_\rho(z,x)&= \rho^{-1}\int_{\unicode{x211D}^d} \overline{F}(x+w) q(z,w+z)dw\\&= \rho^{-1}\Bigg( \int_{ w \leq -\phi(x) } +\int_{ |w| \leq |\phi(x)| } + \int_{w > \phi(x)} \Bigg) \overline{F}(x+ w) q(z,w+z)dw \\&\,:\!=\, K_1(z,x)+ K_2(z,x)+K_3(z,x).\end{align*}
We have by (28)
and
From (29) it follows that the left-hand sides of the above inequalities are
![]() $o\big(\overline{F}(x)\big)$
as
$o\big(\overline{F}(x)\big)$
as
![]() $x^0 \to \infty$
.
$x^0 \to \infty$
.
Note that
![]() $K_2(z,x) \leq \sup_{|w| \leq \phi(x)} \overline{F}(x -w)$
. Hence by Definition 2, Remark 4, and
$K_2(z,x) \leq \sup_{|w| \leq \phi(x)} \overline{F}(x -w)$
. Hence by Definition 2, Remark 4, and
![]() $\phi$
-insensitivity of
$\phi$
-insensitivity of
![]() $\overline{F}$
we can conclude that
$\overline{F}$
we can conclude that
Thus, (33) holds for
![]() $n=1$
. By the same argument we get that
$n=1$
. By the same argument we get that
![]() $\overline{G_\rho} (z,x)$
is long-tailed as
$\overline{G_\rho} (z,x)$
is long-tailed as
![]() $x\to \infty$
, uniformly in z.
$x\to \infty$
, uniformly in z.
Thus, there exist
![]() $ 0<C_5<C_6<\infty$
such that
$ 0<C_5<C_6<\infty$
such that
uniformly in z.
Consider the second convolution
![]() $\overline{G^{* 2}_\rho} (z,x)$
. By the definition of the convolution given in Theorem 1 we have
$\overline{G^{* 2}_\rho} (z,x)$
. By the definition of the convolution given in Theorem 1 we have
 \begin{align*}\overline{G^{* 2}_\rho} (z,x)&= \left( \int_{ w< -\phi(x) }+ \int_{-\phi(x) \leq w \leq \phi(x)}+ \int_{\phi(x)< w \leq x-\phi(x)}\right.\\[3pt]&\left. \quad + \int_{ w >x-\phi(x)}\right) \overline{G}_\rho(z- w,x- w)G_\rho(z,d w) \\[3pt]&\,:\!=\, K_{21}( z,x )+ K_{22}( z,x)+ K_{23}( z,x)+K_{24}( z,x ).\end{align*}
\begin{align*}\overline{G^{* 2}_\rho} (z,x)&= \left( \int_{ w< -\phi(x) }+ \int_{-\phi(x) \leq w \leq \phi(x)}+ \int_{\phi(x)< w \leq x-\phi(x)}\right.\\[3pt]&\left. \quad + \int_{ w >x-\phi(x)}\right) \overline{G}_\rho(z- w,x- w)G_\rho(z,d w) \\[3pt]&\,:\!=\, K_{21}( z,x )+ K_{22}( z,x)+ K_{23}( z,x)+K_{24}( z,x ).\end{align*}
Similarly to the argument for
![]() $K_{1}(z,x)$
, we get
$K_{1}(z,x)$
, we get
![]() $\sup_z K_{21} (z,x)= o \big(\overline{F}(x)\big)$
as
$\sup_z K_{21} (z,x)= o \big(\overline{F}(x)\big)$
as
![]() $x^0\to \infty$
.
$x^0\to \infty$
.
The relations (37) allow us to derive the bound
which is
![]() $o(\overline{F}(x))$
as
$o(\overline{F}(x))$
as
![]() $x^0\to \infty$
(see [Reference Foss, Korshunov and Zachary23, Theorem 3.7] for the one-dimensional case; the argument in the multidimensional case is the same). By the same argument as for
$x^0\to \infty$
(see [Reference Foss, Korshunov and Zachary23, Theorem 3.7] for the one-dimensional case; the argument in the multidimensional case is the same). By the same argument as for
![]() $K_2(z,x)$
, we conclude that
$K_2(z,x)$
, we conclude that
![]() $K_{22}(z,x)= \overline{F}(x)(1+o(1))$
,
$K_{22}(z,x)= \overline{F}(x)(1+o(1))$
,
![]() $x^0\to \infty$
. Finally, by
$x^0\to \infty$
. Finally, by
![]() $\phi$
-insensitivity of
$\phi$
-insensitivity of
![]() $\overline{F}$
, Remark 4, and (37) we have
$\overline{F}$
, Remark 4, and (37) we have
 \begin{align*}K_{24}(z,x)& \geq \int_{ w\geq x+ \phi(x)} \overline{G}_\rho(z- w,x- w)G_\rho(z,d w) \geq\inf_y \overline{G}_\rho(y,-\phi(x)) \overline{G}_\rho(z,x+\phi(x))\\&= \overline{F}(x) (1+o(1)).\end{align*}
\begin{align*}K_{24}(z,x)& \geq \int_{ w\geq x+ \phi(x)} \overline{G}_\rho(z- w,x- w)G_\rho(z,d w) \geq\inf_y \overline{G}_\rho(y,-\phi(x)) \overline{G}_\rho(z,x+\phi(x))\\&= \overline{F}(x) (1+o(1)).\end{align*}
Thus,
![]() $K_{24}(z,x)= \overline{F}(x)(1+o(1))$
. For general n the proof follows by induction and an argument similar to that for
$K_{24}(z,x)= \overline{F}(x)(1+o(1))$
. For general n the proof follows by induction and an argument similar to that for
![]() $n=2$
.
$n=2$
.
To prove Kesten’s bound (34) we follow again [Reference Foss, Korshunov and Zachary23, Chapter 3.10] and [Reference Omey33, p. 5439]. Note that
 \begin{equation*}\overline{G^{* n}_\rho}( z,x) \leq \sum_{i=1}^d \overline{G^{* n}_{\rho,i}}( z, x),\end{equation*}
\begin{equation*}\overline{G^{* n}_\rho}( z,x) \leq \sum_{i=1}^d \overline{G^{* n}_{\rho,i}}( z, x),\end{equation*}
where
![]() $G^{* n}_{\rho,i}(z, x)\,:\!=\, G^{* n}_{\rho}(z, \unicode{x211D} \times \ldots \times ({-}\infty, x_i)\times \ldots \times \unicode{x211D})$
are marginals of
$G^{* n}_{\rho,i}(z, x)\,:\!=\, G^{* n}_{\rho}(z, \unicode{x211D} \times \ldots \times ({-}\infty, x_i)\times \ldots \times \unicode{x211D})$
are marginals of
![]() $G^{* n}_{\rho}$
. Now, generalizing [Reference Foss, Korshunov and Zachary23, Chapter 3.10] to our set-up of
$G^{* n}_{\rho}$
. Now, generalizing [Reference Foss, Korshunov and Zachary23, Chapter 3.10] to our set-up of
![]() $G^{* n}_{\rho,i}$
, we can conclude that for each
$G^{* n}_{\rho,i}$
, we can conclude that for each
![]() $\epsilon >0$
there exists a constant C such that
$\epsilon >0$
there exists a constant C such that
 \begin{equation*}\overline{G^{* n}_\rho}( z,x) \leq C (1+\epsilon)^n \sum_{i=1}^d \overline{G}_{\rho,i}( z, x),\end{equation*}
\begin{equation*}\overline{G^{* n}_\rho}( z,x) \leq C (1+\epsilon)^n \sum_{i=1}^d \overline{G}_{\rho,i}( z, x),\end{equation*}
implying
Proof of Theorem 2.1. Case
![]() $B\in [0,\infty)$
. Let
$B\in [0,\infty)$
. Let
Applying (34) with
![]() $\epsilon< \frac{1-\rho}{\rho}$
, we can pass to the limit
$\epsilon< \frac{1-\rho}{\rho}$
, we can pass to the limit
We prove that (cf. (32))
We use (28) and the fact that
![]() $\ell \in \mathcal{B}_b^+\big({\unicode{x211D}^d}\big)$
and is long-tailed. Indeed, by the same idea as that used in the proof of Lemma 1, we split the integral as follows:
$\ell \in \mathcal{B}_b^+\big({\unicode{x211D}^d}\big)$
and is long-tailed. Indeed, by the same idea as that used in the proof of Lemma 1, we split the integral as follows:
 \begin{align*}\int_{\unicode{x211D}^d} \frac{\ell(x+w)q(x,w+x)}{\ell(x)} dw &= \left(\int_{|w| \leq |\phi(x)| } + \int_{|w|>|\phi(x)|} \right) \frac{\ell(x+w)q(x,w+x)}{\ell(x)} dw \\&\,:\!=\, I_1(x)+ I_2(x),\end{align*}
\begin{align*}\int_{\unicode{x211D}^d} \frac{\ell(x+w)q(x,w+x)}{\ell(x)} dw &= \left(\int_{|w| \leq |\phi(x)| } + \int_{|w|>|\phi(x)|} \right) \frac{\ell(x+w)q(x,w+x)}{\ell(x)} dw \\&\,:\!=\, I_1(x)+ I_2(x),\end{align*}
where the function
![]() $\phi(x)=(\phi_1(x),\dots,\phi_d(x))$
,
$\phi(x)=(\phi_1(x),\dots,\phi_d(x))$
,
![]() $\phi_i(x)>0$
, is such that
$\phi_i(x)>0$
, is such that
![]() $\ell$
is
$\ell$
is
![]() $\phi$
-insensitive.
$\phi$
-insensitive.
For any
![]() $\epsilon=\epsilon \big(b^0\big)>0$
and large enough
$\epsilon=\epsilon \big(b^0\big)>0$
and large enough
![]() $x^0\geq b^0$
we get
$x^0\geq b^0$
we get
and similarly
Thus,
![]() $\lim_{x^0\to \infty} I_1(x)=\rho$
. By (29) we get
$\lim_{x^0\to \infty} I_1(x)=\rho$
. By (29) we get
Now we investigate the asymptotic behaviour of
![]() $\int_{\unicode{x211D}^d} h(x-y) \mathcal{G}(z,dy)$
(at the moment we assume that
$\int_{\unicode{x211D}^d} h(x-y) \mathcal{G}(z,dy)$
(at the moment we assume that
![]() $z\in {\unicode{x211D}^d}$
is fixed; as we will see, it does not affect the asymptotic behaviour of the convolution). From now on,
$z\in {\unicode{x211D}^d}$
is fixed; as we will see, it does not affect the asymptotic behaviour of the convolution). From now on,
![]() $\phi$
is such that both
$\phi$
is such that both
![]() $\ell$
and
$\ell$
and
![]() $\overline{F}$
are
$\overline{F}$
are
![]() $\phi$
-insensitive. Split the integral:
$\phi$
-insensitive. Split the integral:
 \begin{align*}\int_{\unicode{x211D}^d} h(x-y) \mathcal{G}(z,dy)&= \left(\int_{y \leq -\phi(x)} + \int_{-\phi(x) \leq y \leq \phi(x)} + \int_{\phi(x)<y<x-\phi(x)}\right.\\&\qquad \left.+ \int_{x-\phi(x)}^{x+\phi(x)}+ \int_{x+\phi(x)}^\infty \right) h(x-y) \mathcal{G}(z,dy)\\&\,:\!=\, J_1(z,x)+ J_2(z,x)+ J_3(z,x)+ J_4(z,x) + J_5(z,x).\end{align*}
\begin{align*}\int_{\unicode{x211D}^d} h(x-y) \mathcal{G}(z,dy)&= \left(\int_{y \leq -\phi(x)} + \int_{-\phi(x) \leq y \leq \phi(x)} + \int_{\phi(x)<y<x-\phi(x)}\right.\\&\qquad \left.+ \int_{x-\phi(x)}^{x+\phi(x)}+ \int_{x+\phi(x)}^\infty \right) h(x-y) \mathcal{G}(z,dy)\\&\,:\!=\, J_1(z,x)+ J_2(z,x)+ J_3(z,x)+ J_4(z,x) + J_5(z,x).\end{align*}
Observe that
![]() $B\in [0,\infty)$
implies that
$B\in [0,\infty)$
implies that
![]() $\ell(x)$
is either comparable with the monotone function
$\ell(x)$
is either comparable with the monotone function
![]() $\overline{F}(x)$
, or
$\overline{F}(x)$
, or
![]() $\ell(x)= o\big(\overline{F}(x)\big)$
as
$\ell(x)= o\big(\overline{F}(x)\big)$
as
![]() $x^0\to \infty$
. By (39), this allows us to estimate
$x^0\to \infty$
. By (39), this allows us to estimate
![]() $J_1$
as
$J_1$
as
 \begin{align*}J_1(z,x)& \leq \sup_{w\geq \phi(x)} h(x+w) \mathcal{G}(z,({-}\infty,-\phi(x)]) \leq C_1 \ell(x) \mathcal{G}(z, ({-}\infty,-\phi(x)]) \\&= o(\ell(x))= o \big(\overline{F}(x)\big), \quad x^0\to \infty,\end{align*}
\begin{align*}J_1(z,x)& \leq \sup_{w\geq \phi(x)} h(x+w) \mathcal{G}(z,({-}\infty,-\phi(x)]) \leq C_1 \ell(x) \mathcal{G}(z, ({-}\infty,-\phi(x)]) \\&= o(\ell(x))= o \big(\overline{F}(x)\big), \quad x^0\to \infty,\end{align*}
uniformly in z. From (39) we have
uniformly in z. Let us estimate
![]() $J_3(z,x)$
. Under the assumption
$J_3(z,x)$
. Under the assumption
![]() $B\in [0,\infty)$
we have
$B\in [0,\infty)$
we have
Since F is subexponential, the right-hand side of (41) is
![]() $o\big(\overline{F}(x)\big)$
as
$o\big(\overline{F}(x)\big)$
as
![]() $x^0\to \infty$
. In the one-dimensional case this is stated in [Reference Foss, Korshunov and Zachary23, Theorem 3.7]; the proof in the multidimensional case is literally the same.
$x^0\to \infty$
. In the one-dimensional case this is stated in [Reference Foss, Korshunov and Zachary23, Theorem 3.7]; the proof in the multidimensional case is literally the same.
For
![]() $J_4$
we have
$J_4$
we have
uniformly in z. Finally, for
![]() $J_5$
we have
$J_5$
we have
Thus, in the case
![]() $B\in [0,\infty)$
we get the first and second relations in (31).
$B\in [0,\infty)$
we get the first and second relations in (31).
2. Case
![]() $B =\infty$
. The argument for
$B =\infty$
. The argument for
![]() $J_1$
and
$J_1$
and
![]() $J_2$
remains the same. For
$J_2$
remains the same. For
![]() $J_3$
we have
$J_3$
we have
By Remark 4 we can chose
![]() $\phi$
such that
$\phi$
such that
![]() $|\phi(x)|\asymp |x| \ln^{-2} |x|$
as
$|\phi(x)|\asymp |x| \ln^{-2} |x|$
as
![]() $x^0 \to \infty$
. Since in the case when
$x^0 \to \infty$
. Since in the case when
![]() $B=\infty$
the function
$B=\infty$
the function
![]() $\ell$
is assumed to be regularly varying, it has a power decay,
$\ell$
is assumed to be regularly varying, it has a power decay,
![]() $J_3(z,x)= o (\ell(x))$
,
$J_3(z,x)= o (\ell(x))$
,
![]() $x^0\to \infty$
. By the same argument,
$x^0\to \infty$
. By the same argument,
![]() $J_i(z,x)= o(\ell(x))$
,
$J_i(z,x)= o(\ell(x))$
,
![]() $i=4,5$
, which proves the last relation in (31).
$i=4,5$
, which proves the last relation in (31).
In the next section we provide examples in which (28) is satisfied.
Remark 9. In the case when Y is degenerate, e.g.
![]() $Y_t=x+at$
, one can derive the asymptotic behaviour of u(x) by a much simpler procedure. For example, let
$Y_t=x+at$
, one can derive the asymptotic behaviour of u(x) by a much simpler procedure. For example, let
![]() $d=1$
,
$d=1$
,
![]() $T\sim \operatorname{Exp}(\mu)$
,
$T\sim \operatorname{Exp}(\mu)$
,
![]() $\mu>0$
,
$\mu>0$
,
![]() $Y_t=at$
with
$Y_t=at$
with
![]() $a>0$
,
$a>0$
,
![]() $\ell(x)= \overline{F}(x)$
,
$\ell(x)= \overline{F}(x)$
,
![]() $x\geq 0$
, and
$x\geq 0$
, and
![]() $\ell(x)=0$
for
$\ell(x)=0$
for
![]() $x<0$
. This special type of the function
$x<0$
. This special type of the function
![]() $\ell$
appears in the multivariate ruin problem; see also (71) below. In this case
$\ell$
appears in the multivariate ruin problem; see also (71) below. In this case
![]() $\rho=\frac{\lambda}{\lambda+\mu}$
. Then
$\rho=\frac{\lambda}{\lambda+\mu}$
. Then
Direct calculation gives
![]() $ \overline{G}(z)= \overline{F}(x)(1+ o(1))$
as
$ \overline{G}(z)= \overline{F}(x)(1+ o(1))$
as
![]() $x^0\to \infty$
, implying that
$x^0\to \infty$
, implying that
4. Examples
We begin with a simple example which illustrates Theorem 2. Note that in the Lévy case,
![]() $\mathfrak{p}_s(x,w)$
depends on the difference
$\mathfrak{p}_s(x,w)$
depends on the difference
![]() $w-x$
; in order to simplify the notation we write in this case
$w-x$
; in order to simplify the notation we write in this case
![]() $ \mathfrak{p}_s(x,w) = p_s(w-x)$
,
$ \mathfrak{p}_s(x,w) = p_s(w-x)$
,
and
We prove below a technical lemma, which provides the necessary estimate for
![]() $\mathfrak{p}_s(x,w)$
in the following cases:
$\mathfrak{p}_s(x,w)$
in the following cases:
-
(a)
 $Y_t = x +at + Z^{\text{small}}_t$
, where
$Y_t = x +at + Z^{\text{small}}_t$
, where
 $a\in {\unicode{x211D}^d}$
and
$a\in {\unicode{x211D}^d}$
and
 $Z^{\text{small}}$
is a Lévy process with jump sizes smaller than
$Z^{\text{small}}$
is a Lévy process with jump sizes smaller than
 $\delta$
, i.e. its characteristic exponent is of the form (44)where
$\delta$
, i.e. its characteristic exponent is of the form (44)where \begin{equation}\psi^{\text{small}}(\xi) \,:\!=\, \int_{|u| \leq \delta} \big(1-e^{i\xi u} + i \xi u\big) \nu(du), \end{equation}
\begin{equation}\psi^{\text{small}}(\xi) \,:\!=\, \int_{|u| \leq \delta} \big(1-e^{i\xi u} + i \xi u\big) \nu(du), \end{equation}
 $\nu$
is a Lévy measure;
$\nu$
is a Lévy measure;
-
(b)
 $Y_t= x + at +V_t$
, where
$Y_t= x + at +V_t$
, where
 $V_t$
is an Ornstein–Uhlenbeck process driven by
$V_t$
is an Ornstein–Uhlenbeck process driven by
 $Z^{\text{small}}_t$
, i.e.
$Z^{\text{small}}_t$
, i.e.
 $V_t$
satisfies the stochastic differential equation We assume that
$V_t$
satisfies the stochastic differential equation We assume that \begin{equation*}dV_t = \vartheta V_t dt + d Z_t^{\text{small}}.\end{equation*}
\begin{equation*}dV_t = \vartheta V_t dt + d Z_t^{\text{small}}.\end{equation*}
 $\vartheta <0$
and that
$\vartheta <0$
and that
 $Z_t^{\text{small}}$
in this model has only positive jumps.
$Z_t^{\text{small}}$
in this model has only positive jumps.
Assume that for some
![]() $\alpha\in (0,2)$
and
$\alpha\in (0,2)$
and
![]() $c>0$
,
$c>0$
,
where
![]() $\mathbb{S}^d$
is the sphere in
$\mathbb{S}^d$
is the sphere in
![]() ${\unicode{x211D}^d}$
. Under this condition, there exists (cf. [Reference Knopova26]) the transition probability density of
${\unicode{x211D}^d}$
. Under this condition, there exists (cf. [Reference Knopova26]) the transition probability density of
![]() $Y_t$
in both cases. Let
$Y_t$
in both cases. Let
where
![]() $f(t,s)= {\unicode{x1D7D9}}_{s \leq t} $
in Case (a), and
$f(t,s)= {\unicode{x1D7D9}}_{s \leq t} $
in Case (a), and
![]() $f(t,s)= e^{(t-s)\vartheta} {\unicode{x1D7D9}}_{0 \leq s \leq t} $
in Case (b). Note that since
$f(t,s)= e^{(t-s)\vartheta} {\unicode{x1D7D9}}_{0 \leq s \leq t} $
in Case (b). Note that since
![]() $\vartheta<0$
we have
$\vartheta<0$
we have
![]() $0<f(t,s) \leq 1$
. Moreover, in Case (b),
$0<f(t,s) \leq 1$
. Moreover, in Case (b),
![]() $\mathfrak{p}_t(0,x)=k_t(x)$
.
$\mathfrak{p}_t(0,x)=k_t(x)$
.
Observe that we always have
where in the second inequality we used (45).
Lemma 2. Suppose that (45) is satisfied. We have
 \begin{equation}k_t(x) \leq \begin{cases} C e^{ - (1-\epsilon) \theta_\nu |x-at| } & {if} \quad t>0, \, |x-at|\gg t\vee 1,\\ C t^{-d/\alpha} & {if} \quad t>0, \, x\in {\unicode{x211D}^d}, \end{cases}\end{equation}
\begin{equation}k_t(x) \leq \begin{cases} C e^{ - (1-\epsilon) \theta_\nu |x-at| } & {if} \quad t>0, \, |x-at|\gg t\vee 1,\\ C t^{-d/\alpha} & {if} \quad t>0, \, x\in {\unicode{x211D}^d}, \end{cases}\end{equation}
in Case (a), and
 \begin{equation}k_t(x) \leq \begin{cases}C e^{- (1-\epsilon) \theta_\nu |x-at|} & {if} \quad t>0, \, x\in {\unicode{x211D}^d},\, |x-at|\gg 1,\\C & {if} \quad t>0, \, x\in {\unicode{x211D}^d},\end{cases}\end{equation}
\begin{equation}k_t(x) \leq \begin{cases}C e^{- (1-\epsilon) \theta_\nu |x-at|} & {if} \quad t>0, \, x\in {\unicode{x211D}^d},\, |x-at|\gg 1,\\C & {if} \quad t>0, \, x\in {\unicode{x211D}^d},\end{cases}\end{equation}
in Case (b). Here
![]() $\theta_\nu>0$
is a constant depending on the support of
$\theta_\nu>0$
is a constant depending on the support of
![]() $\nu$
and
$\nu$
and
![]() $\epsilon>0$
is arbitrarily small.
$\epsilon>0$
is arbitrarily small.
Proof. For simplicity, we assume that in Case (b) we have
![]() $\vartheta=-1$
.
$\vartheta=-1$
.
Without loss of generality assume that
![]() $x>0$
. Rewrite
$x>0$
. Rewrite
![]() $\mathfrak{p}_t(x)$
as
$\mathfrak{p}_t(x)$
as
where
It is shown in Knopova [Reference Knopova26, p. 38] that the function
![]() $\xi\mapsto H(t,x,i\xi)$
,
$\xi\mapsto H(t,x,i\xi)$
,
![]() $\xi\in {\unicode{x211D}^d}$
, is convex; there exists a solution to
$\xi\in {\unicode{x211D}^d}$
, is convex; there exists a solution to
![]() $\nabla_\xi H(t,x,i\xi)=0$
, which we denote by
$\nabla_\xi H(t,x,i\xi)=0$
, which we denote by
![]() $\xi=\xi(t,x)$
; and by the non-degeneracy condition (45) we have
$\xi=\xi(t,x)$
; and by the non-degeneracy condition (45) we have
![]() $x\cdot \xi>0$
and
$x\cdot \xi>0$
and
![]() $|\xi(t,x)|\to\infty$
,
$|\xi(t,x)|\to\infty$
,
![]() $|x|\to \infty$
. Furthermore, in the same way as in [Reference Knopova26] (see also Knopova and Schilling [Reference Knopova and Schilling28] and Knopova and Kulik [Reference Knopova and Kulik27] for the one-dimensional version), one can apply the Cauchy–Poincaré theorem and get
$|x|\to \infty$
. Furthermore, in the same way as in [Reference Knopova26] (see also Knopova and Schilling [Reference Knopova and Schilling28] and Knopova and Kulik [Reference Knopova and Kulik27] for the one-dimensional version), one can apply the Cauchy–Poincaré theorem and get
 \begin{equation}\begin{split}k_t(x)&= (2\pi)^{-d} \int_{i\xi (t,x)+ {\unicode{x211D}^d}} e^{H(t,x,z)} dz\\&= (2\pi)^{-d} \int_{ {\unicode{x211D}^d}} e^{H(t,x,i\xi(t,x)+ \eta)} d\eta\\&= (2\pi)^{-d} \int_{ {\unicode{x211D}^d}} e^{{\text{Re}}\, H(t,x,i\xi(t,x)+ \eta)} \cos \big(\text{Im}\, H(t,x,i\xi(t,x)+ \eta)\big)d\eta\\& \leq (2\pi)^{-d} \int_{ {\unicode{x211D}^d}} e^{{\text{Re}}\, H(t,x,i\xi(t,x)+ \eta)}d\eta.\end{split}\end{equation}
\begin{equation}\begin{split}k_t(x)&= (2\pi)^{-d} \int_{i\xi (t,x)+ {\unicode{x211D}^d}} e^{H(t,x,z)} dz\\&= (2\pi)^{-d} \int_{ {\unicode{x211D}^d}} e^{H(t,x,i\xi(t,x)+ \eta)} d\eta\\&= (2\pi)^{-d} \int_{ {\unicode{x211D}^d}} e^{{\text{Re}}\, H(t,x,i\xi(t,x)+ \eta)} \cos \big(\text{Im}\, H(t,x,i\xi(t,x)+ \eta)\big)d\eta\\& \leq (2\pi)^{-d} \int_{ {\unicode{x211D}^d}} e^{{\text{Re}}\, H(t,x,i\xi(t,x)+ \eta)}d\eta.\end{split}\end{equation}
We have
 \begin{align*}{\text{Re}}\, H(t,x,i\xi+ \eta) &= H(t,x,i\xi) -\int_0^t\int_{|u| \leq \delta} e^{f(t,s)\xi \cdot u} \big( 1-\cos( f(t,s) \eta \cdot u) \big)\nu(du)\,ds\\& \leq H(t,x,i\xi) -\int_0^t \int_{|u| \leq \delta,\,\xi \cdot u>0} \big( 1-\cos( f(t,s) \eta \cdot u) \big)\nu(du)\,ds\\& \leq H(t,x,i\xi) - c |\eta|^\alpha\int_0^t |f(t,s)|^\alpha ds,\end{align*}
\begin{align*}{\text{Re}}\, H(t,x,i\xi+ \eta) &= H(t,x,i\xi) -\int_0^t\int_{|u| \leq \delta} e^{f(t,s)\xi \cdot u} \big( 1-\cos( f(t,s) \eta \cdot u) \big)\nu(du)\,ds\\& \leq H(t,x,i\xi) -\int_0^t \int_{|u| \leq \delta,\,\xi \cdot u>0} \big( 1-\cos( f(t,s) \eta \cdot u) \big)\nu(du)\,ds\\& \leq H(t,x,i\xi) - c |\eta|^\alpha\int_0^t |f(t,s)|^\alpha ds,\end{align*}
where
and in the last inequality we used (45). Hence,
Now we estimate the function
![]() $H(t,x,i\xi)$
. Differentiating, we get
$H(t,x,i\xi)$
. Differentiating, we get
 \begin{align*}\partial_\xi H(t,x,i\xi)& = -(x-at)\cdot e_\xi + \int_0^t\int_{|u| \leq \delta} \Big( e^{f(t,s) \xi\cdot u} -1\Big)f(t,s) u \cdot e_\xi \nu(du) ds\\&=\!: -(x-at)\cdot e_\xi + I(t,x,\xi),\end{align*}
\begin{align*}\partial_\xi H(t,x,i\xi)& = -(x-at)\cdot e_\xi + \int_0^t\int_{|u| \leq \delta} \Big( e^{f(t,s) \xi\cdot u} -1\Big)f(t,s) u \cdot e_\xi \nu(du) ds\\&=\!: -(x-at)\cdot e_\xi + I(t,x,\xi),\end{align*}
where
![]() $e_\xi = \xi /|\xi|$
. For large
$e_\xi = \xi /|\xi|$
. For large
![]() $|\xi|$
we can estimate
$|\xi|$
we can estimate
![]() $I(t,x,\xi)$
as follows:
$I(t,x,\xi)$
as follows:
 \begin{align*}I(t,x,\xi)& \leq C_1 \int_0^t \int_{|u| \leq \delta} |f(t,s) u|^2 e^{f(t,s) \xi \cdot u} \nu(du)\,ds\\& \leq C_1 e^{\delta |\xi| \max_{s\in[0,t]}f(t,s)} \int_0^t f^2(t,s) ds\end{align*}
\begin{align*}I(t,x,\xi)& \leq C_1 \int_0^t \int_{|u| \leq \delta} |f(t,s) u|^2 e^{f(t,s) \xi \cdot u} \nu(du)\,ds\\& \leq C_1 e^{\delta |\xi| \max_{s\in[0,t]}f(t,s)} \int_0^t f^2(t,s) ds\end{align*}
for some constant
![]() $C_1$
. For the lower bound we get
$C_1$
. For the lower bound we get
 \begin{align*}I(t,x,\xi)&\geq C_2 \int^t_{(1-\epsilon_0)t} \int_{ |u| \leq \delta, \, \xi \cdot u > |\xi|(\delta-\epsilon)} |f(t,s) u|^2 e^{f(t,s) \xi \cdot u} \nu(du)\,ds\\&\geq C_3 e^{(\delta-\epsilon) |\xi| \min_{s\in[(1-\epsilon_0)t,t]}f(t,s)} \int_{(1-\epsilon_0)t}^t f^2(t,s) ds,\end{align*}
\begin{align*}I(t,x,\xi)&\geq C_2 \int^t_{(1-\epsilon_0)t} \int_{ |u| \leq \delta, \, \xi \cdot u > |\xi|(\delta-\epsilon)} |f(t,s) u|^2 e^{f(t,s) \xi \cdot u} \nu(du)\,ds\\&\geq C_3 e^{(\delta-\epsilon) |\xi| \min_{s\in[(1-\epsilon_0)t,t]}f(t,s)} \int_{(1-\epsilon_0)t}^t f^2(t,s) ds,\end{align*}
where
![]() $C_2,C_3>0$
are some constant,
$C_2,C_3>0$
are some constant,
![]() $\epsilon_0,\epsilon\in (0,1)$
. Thus, we get
$\epsilon_0,\epsilon\in (0,1)$
. Thus, we get
in Case (a), and
in Case (b). In particular, this estimate implies that there exists
![]() $c_0>0$
such that
$c_0>0$
such that
![]() $(x-at)\cdot e_\xi\geq c_0$
; i.e.,
$(x-at)\cdot e_\xi\geq c_0$
; i.e.,
![]() $e_\xi$
is directed towards
$e_\xi$
is directed towards
![]() $x-at$
. Thus, for example, it cannot be orthogonal to
$x-at$
. Thus, for example, it cannot be orthogonal to
![]() $x-at$
.
$x-at$
.
We now treat each case separately.
Case (a). If
![]() $|x-at|/t\to \infty$
, we get for any
$|x-at|/t\to \infty$
, we get for any
![]() $\zeta\in (0,1)$
$\zeta\in (0,1)$
where the constant
![]() $\theta_\nu>0$
depends on the support
$\theta_\nu>0$
depends on the support
![]() $\operatorname{supp} \nu$
. Therefore,
$\operatorname{supp} \nu$
. Therefore,
for
![]() $ t>0$
,
$ t>0$
,
![]() $|x-at|\gg t$
, and some constant
$|x-at|\gg t$
, and some constant
![]() $C_4$
.
$C_4$
.
It remains to estimate the integral term in (51). We have
![]() $\int_0^t f^\alpha (t,s) ds= t $
; hence
$\int_0^t f^\alpha (t,s) ds= t $
; hence
Thus, we get
For
![]() $t\geq 1$
, the first estimate in (48) follows from (56), because
$t\geq 1$
, the first estimate in (48) follows from (56), because
![]() $t^{-d/\alpha} \leq 1$
.
$t^{-d/\alpha} \leq 1$
.
Consider now the case
![]() $t\in (0,1]$
. For
$t\in (0,1]$
. For
![]() $t\in (0,1]$
and
$t\in (0,1]$
and
![]() $|x|\gg 1$
(otherwise we do not have
$|x|\gg 1$
(otherwise we do not have
![]() $|x-ta|\gg t$
) we have for K big enough and some constant
$|x-ta|\gg t$
) we have for K big enough and some constant
![]() $C_7$
$C_7$
Without loss of generality, assume that
![]() $K>d/\alpha$
. Then
$K>d/\alpha$
. Then
 \begin{align*}k_t(x)& \leq C_8 t^{-d/\alpha} e^{ - (1-\zeta)^2 \theta_\nu |x-at| \ln (|x-at|/t)- \zeta(1-\zeta) \theta_\nu |x-at| \ln (|x-at|/t)}\\& \leq C_9 t^{-d/\alpha} \left(\frac{t}{|x-at|}\right)^K e^{ - (1-\zeta)^2 \theta_\nu|x-at| } \\& \leq C_{10} e^{- (1-\zeta)^3 \theta_\nu|x-at| },\end{align*}
\begin{align*}k_t(x)& \leq C_8 t^{-d/\alpha} e^{ - (1-\zeta)^2 \theta_\nu |x-at| \ln (|x-at|/t)- \zeta(1-\zeta) \theta_\nu |x-at| \ln (|x-at|/t)}\\& \leq C_9 t^{-d/\alpha} \left(\frac{t}{|x-at|}\right)^K e^{ - (1-\zeta)^2 \theta_\nu|x-at| } \\& \leq C_{10} e^{- (1-\zeta)^3 \theta_\nu|x-at| },\end{align*}
which proves the first estimate of (48) if we take
![]() $1-\epsilon =(1-\zeta)^3$
. For the third estimate in (48), observe that
$1-\epsilon =(1-\zeta)^3$
. For the third estimate in (48), observe that
![]() $H(t,x,i\xi) \leq 0$
. Then the bound follows from (55).
$H(t,x,i\xi) \leq 0$
. Then the bound follows from (55).
Case (b). If
![]() $|x-at|\to \infty$
, we get for any
$|x-at|\to \infty$
, we get for any
![]() $\zeta\in (0,1)$
$\zeta\in (0,1)$
where
![]() $\theta_\nu$
is a constant which depends on the support
$\theta_\nu$
is a constant which depends on the support
![]() $\operatorname{supp} \nu$
.
$\operatorname{supp} \nu$
.
Now we estimate the right-hand side of (55) in Case (b). Since
![]() $\int_0^t f^\alpha(t,s) ds= \alpha^{-1} (1- e^{-\alpha t}) $
, we get
$\int_0^t f^\alpha(t,s) ds= \alpha^{-1} (1- e^{-\alpha t}) $
, we get
for some constant
![]() $C_{11}$
. Thus, there exist
$C_{11}$
. Thus, there exist
![]() $C_{12}>0$
and
$C_{12}>0$
and
![]() $\epsilon\in (0,1)$
such that for
$\epsilon\in (0,1)$
such that for
![]() $x\in {\unicode{x211D}^d}$
and
$x\in {\unicode{x211D}^d}$
and
![]() $t>0$
satisfying
$t>0$
satisfying
![]() $|x-at|\gg 1 $
,
$|x-at|\gg 1 $
,
which proves (49) for large
![]() $|x-at|$
. Finally, the boundedness of
$|x-at|$
. Finally, the boundedness of
![]() $\kappa_t(x)$
follows from (47) and the fact that in Case (b) we have
$\kappa_t(x)$
follows from (47) and the fact that in Case (b) we have
![]() $c \leq \int_0^t f^\alpha(t,s) ds \leq C$
for all
$c \leq \int_0^t f^\alpha(t,s) ds \leq C$
for all
![]() $t>0$
.
$t>0$
.
Remark 10. (a) The same estimates can also be proved for the model
![]() $Y_t = x+ at+ \sigma B_t + Z^{\text{small}}_t$
.
$Y_t = x+ at+ \sigma B_t + Z^{\text{small}}_t$
.
(b) Note that
![]() $\epsilon>0$
in the exponent in (48) and (49) can be chosen arbitrarily close to 0; i.e., the estimates are in a sense sharp.
$\epsilon>0$
in the exponent in (48) and (49) can be chosen arbitrarily close to 0; i.e., the estimates are in a sense sharp.
Lemma 3. Let Y be as in Case (a). There exist
![]() $C>0$
and
$C>0$
and
![]() $\epsilon\in (0,1)$
such that the estimate
$\epsilon\in (0,1)$
such that the estimate
holds true, where
Proof. We use Lemma 2. We have
For
![]() $I_1$
we use the triangle inequality:
$I_1$
we use the triangle inequality:
 \begin{align*}I_1 & \leq C_1 e^{-(1-\epsilon)\theta_\nu |x| } \int_{\{t\,:\, |x|>|a|t\}} e^{-(\lambda- (1-\epsilon) \theta_\nu |a|) t} dt \\[4pt] & \leq C_1 e^{-(1-\epsilon)\theta_\nu |x| } \begin{cases} C_2 & \text{if} \quad \lambda> (1-\epsilon) \theta_\nu |a|,\\[9pt] C_2 e^{\frac{(1-\epsilon) \theta_\nu |a|-\lambda}{ |a|} |x|} & \text{if} \quad \lambda< (1-\epsilon) \theta_\nu |a|, \end{cases} \end{align*}
\begin{align*}I_1 & \leq C_1 e^{-(1-\epsilon)\theta_\nu |x| } \int_{\{t\,:\, |x|>|a|t\}} e^{-(\lambda- (1-\epsilon) \theta_\nu |a|) t} dt \\[4pt] & \leq C_1 e^{-(1-\epsilon)\theta_\nu |x| } \begin{cases} C_2 & \text{if} \quad \lambda> (1-\epsilon) \theta_\nu |a|,\\[9pt] C_2 e^{\frac{(1-\epsilon) \theta_\nu |a|-\lambda}{ |a|} |x|} & \text{if} \quad \lambda< (1-\epsilon) \theta_\nu |a|, \end{cases} \end{align*}
where
![]() $C_1,C_2>0$
are certain constants and we exclude the equality case by choosing appropriate
$C_1,C_2>0$
are certain constants and we exclude the equality case by choosing appropriate
![]() $\epsilon>0$
. Hence,
$\epsilon>0$
. Hence,
 \begin{equation*} I_1 \leq \begin{cases} C_3e^{-(1-\epsilon)\theta_\nu |x| }, & \lambda> (1-\epsilon) \theta_\nu |a|,\\[5pt] C_3 e^{- \frac{\lambda}{|a|} |x|}, & \lambda< (1-\epsilon) \theta_\nu |a|, \end{cases}\end{equation*}
\begin{equation*} I_1 \leq \begin{cases} C_3e^{-(1-\epsilon)\theta_\nu |x| }, & \lambda> (1-\epsilon) \theta_\nu |a|,\\[5pt] C_3 e^{- \frac{\lambda}{|a|} |x|}, & \lambda< (1-\epsilon) \theta_\nu |a|, \end{cases}\end{equation*}
for some
![]() $C_3>0$
.
$C_3>0$
.
For
![]() $I_2$
we get, since
$I_2$
we get, since
![]() $|x|\gg 1$
,
$|x|\gg 1$
,
Thus, there exist
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $C>0$
such that
$C>0$
such that
This completes the proof.
Consider now the estimate in Case (b). Recall that we assumed that the process Y has only positive jumps. This means, in particular, that in the transition probability density
![]() $\mathfrak{p}_t(x,y)$
we only have
$\mathfrak{p}_t(x,y)$
we only have
![]() $y\geq x$
(in the coordinate sense). Under this assumption, it is possible to show that q(x,y) (cf. (25)) decays exponentially fast as
$y\geq x$
(in the coordinate sense). Under this assumption, it is possible to show that q(x,y) (cf. (25)) decays exponentially fast as
![]() $|y-x|\to \infty$
.
$|y-x|\to \infty$
.
Lemma 4. In Case (b) there exist
![]() $C>0$
and
$C>0$
and
![]() $\epsilon\in (0,1)$
such that
$\epsilon\in (0,1)$
such that
where
![]() $\theta_q$
is the same as in Lemma 3.
$\theta_q$
is the same as in Lemma 3.
Proof. From the representation
![]() $Y_t = e^{-t}\big(x+ \int_0^t e^s dZ_s^{\text{small}}\big)$
and (49) we get
$Y_t = e^{-t}\big(x+ \int_0^t e^s dZ_s^{\text{small}}\big)$
and (49) we get
Similarly to the proof of Lemma 3, we have
 \begin{align*}q(x,y)& \leq C_1 \int_{\{t\,:\, |y-x|> |a| t\}} e^{-\lambda t} e^{-(1-\epsilon)\theta_\nu |y-e^{-t}x-at|} dt + C_2\int_{\{t\,:\, |y-x| \leq |a| t\}} e^{-\lambda t} dt\\&\,:\!=\, I_1 + I_2.\end{align*}
\begin{align*}q(x,y)& \leq C_1 \int_{\{t\,:\, |y-x|> |a| t\}} e^{-\lambda t} e^{-(1-\epsilon)\theta_\nu |y-e^{-t}x-at|} dt + C_2\int_{\{t\,:\, |y-x| \leq |a| t\}} e^{-\lambda t} dt\\&\,:\!=\, I_1 + I_2.\end{align*}
Since
![]() $y>x$
, we have
$y>x$
, we have
![]() $|y-e^{-t}x|= y- e^{-t}x> y-x>0$
and therefore
$|y-e^{-t}x|= y- e^{-t}x> y-x>0$
and therefore
 \begin{align*}M_1 & \leq C_1 \int_{\{t\,:\, |y-x|> |a| t\}} e^{-(\lambda- (1-\epsilon) \theta_\nu |y-e^{-t}x|- (1-\epsilon) \theta_\nu |a|) t} dt \\[5pt]& \leq C_1 e^{-(1-\epsilon)\theta_\nu |y-x| } \int_{\{t\,:\, |y-x|> |a| t\}} e^{-(\lambda- (1-\epsilon) \theta_\nu |a|) t} dt \\ & \leq C_1 e^{-(1-\epsilon)\theta_\nu |y-x| } \begin{cases} C_3, & \lambda> (1-\epsilon) \theta_\nu |a|,\\ C_3 e^{\frac{(1-\epsilon) \theta_\nu |a|-\lambda}{ |a|} |y-x|}, & \lambda< (1-\epsilon) \theta_\nu |a|. \end{cases} \end{align*}
\begin{align*}M_1 & \leq C_1 \int_{\{t\,:\, |y-x|> |a| t\}} e^{-(\lambda- (1-\epsilon) \theta_\nu |y-e^{-t}x|- (1-\epsilon) \theta_\nu |a|) t} dt \\[5pt]& \leq C_1 e^{-(1-\epsilon)\theta_\nu |y-x| } \int_{\{t\,:\, |y-x|> |a| t\}} e^{-(\lambda- (1-\epsilon) \theta_\nu |a|) t} dt \\ & \leq C_1 e^{-(1-\epsilon)\theta_\nu |y-x| } \begin{cases} C_3, & \lambda> (1-\epsilon) \theta_\nu |a|,\\ C_3 e^{\frac{(1-\epsilon) \theta_\nu |a|-\lambda}{ |a|} |y-x|}, & \lambda< (1-\epsilon) \theta_\nu |a|. \end{cases} \end{align*}
Hence,
 \begin{equation*} I_1 \leq \begin{cases} Ce^{-(1-\epsilon)\theta_\nu |y-x| } & \text{if} \quad\lambda> (1-\epsilon) \theta_\nu |a|,\\[5pt] C e^{- \frac{\lambda}{|a|} |y-x|} & \text{if} \quad \lambda< (1-\epsilon) \theta_\nu |a|. \end{cases}\end{equation*}
\begin{equation*} I_1 \leq \begin{cases} Ce^{-(1-\epsilon)\theta_\nu |y-x| } & \text{if} \quad\lambda> (1-\epsilon) \theta_\nu |a|,\\[5pt] C e^{- \frac{\lambda}{|a|} |y-x|} & \text{if} \quad \lambda< (1-\epsilon) \theta_\nu |a|. \end{cases}\end{equation*}
Clearly,
which completes the proof.
Remark 11. Direct calculation shows that the estimate (28) is not satisfied for the Ornstein–Uhlenbeck process driven by a Brownian motion, unless
![]() $\lambda>\theta$
.
$\lambda>\theta$
.
Consider an example in
![]() $\unicode{x211D}^2$
, which illustrates how one can get the asymptotic of u(x) along curves.
$\unicode{x211D}^2$
, which illustrates how one can get the asymptotic of u(x) along curves.
Example 1. Let
![]() $d=2$
and
$d=2$
and
![]() $x=(x_1(t), x_2(t))$
. We assume that
$x=(x_1(t), x_2(t))$
. We assume that
![]() $x_i=x_i(t)\to \infty$
as
$x_i=x_i(t)\to \infty$
as
![]() $t\to \infty$
in such a way that
$t\to \infty$
in such a way that
![]() $x(t)\in \mathbb{R}^2\backslash \partial$
. Suppose that
$x(t)\in \mathbb{R}^2\backslash \partial$
. Suppose that
![]() $F\in WS\big(\unicode{x211D}^2_+\big)$
and factors as
$F\in WS\big(\unicode{x211D}^2_+\big)$
and factors as
![]() $F(x)= F_1(x_1) F_2(x_2)$
. Suppose also that the assumptions of Theorem 2 are satisfied with
$F(x)= F_1(x_1) F_2(x_2)$
. Suppose also that the assumptions of Theorem 2 are satisfied with
![]() $B\in (0,\infty)$
. Since
$B\in (0,\infty)$
. Since
we get in Theorem 2 for
![]() $B\in (0,\infty)$
the relations
$B\in (0,\infty)$
the relations
Thus, taking different (admissible)
![]() $x_i(t)$
,
$x_i(t)$
,
![]() $i=1,2$
, we can achieve different effects in the asymptotic of u(x). For example, assume that for
$i=1,2$
, we can achieve different effects in the asymptotic of u(x). For example, assume that for
![]() $z\geq 1$
$z\geq 1$
where
![]() $c_i, \alpha_i>0$
, are suitable constants. Direct calculation shows that the
$c_i, \alpha_i>0$
, are suitable constants. Direct calculation shows that the
![]() $F_i(x)$
are subexponential and the relations in (20) hold true. Note that the behaviour of F depends on the constants
$F_i(x)$
are subexponential and the relations in (20) hold true. Note that the behaviour of F depends on the constants
![]() $\alpha_i$
and on the coordinates of x. We have
$\alpha_i$
and on the coordinates of x. We have
 \begin{equation}\overline{F}(x(t))= \begin{cases} \frac{c_1(1+o(1))}{(x_1(t))^{1+\alpha_1}} & \text{if} \quad \lim_{t\to\infty} \frac{x_1^{1+\alpha_1}(t)}{x_2^{1+\alpha_2}(t)}=0,\\[12pt] \frac{c_2(1+o(1))}{(x_2(t))^{1+\alpha_2}} & \text{if} \quad \lim_{t\to\infty} \frac{x_1^{1+\alpha_1}(t)}{x_2^{1+\alpha_2}(t)}=\infty,\\[12pt] (1+o(1))\Big( \frac{c_1}{x_1(t)^{1+\alpha_1}}+\frac{c_2 }{x_2(t)^{1+\alpha_2}}\Big) & \text{if} \quad \lim_{t\to\infty} \frac{x_1^{1+\alpha_1}(t)}{x_2^{1+\alpha_2}(t)}=c\in (0,\infty).\\ \end{cases} \end{equation}
\begin{equation}\overline{F}(x(t))= \begin{cases} \frac{c_1(1+o(1))}{(x_1(t))^{1+\alpha_1}} & \text{if} \quad \lim_{t\to\infty} \frac{x_1^{1+\alpha_1}(t)}{x_2^{1+\alpha_2}(t)}=0,\\[12pt] \frac{c_2(1+o(1))}{(x_2(t))^{1+\alpha_2}} & \text{if} \quad \lim_{t\to\infty} \frac{x_1^{1+\alpha_1}(t)}{x_2^{1+\alpha_2}(t)}=\infty,\\[12pt] (1+o(1))\Big( \frac{c_1}{x_1(t)^{1+\alpha_1}}+\frac{c_2 }{x_2(t)^{1+\alpha_2}}\Big) & \text{if} \quad \lim_{t\to\infty} \frac{x_1^{1+\alpha_1}(t)}{x_2^{1+\alpha_2}(t)}=c\in (0,\infty).\\ \end{cases} \end{equation}
Taking, for example,
![]() $x=(t,t)$
or
$x=(t,t)$
or
![]() $x=\big(t,t^2\big)$
, we get the behaviour of u(x) along the line
$x=\big(t,t^2\big)$
, we get the behaviour of u(x) along the line
![]() $y=x$
or along the parabola
$y=x$
or along the parabola
![]() $y=x^2$
, respectively.
$y=x^2$
, respectively.
Example 2. Let
![]() $d=2$
and suppose that the generic jump is of the form
$d=2$
and suppose that the generic jump is of the form
![]() $U=(\varrho \Xi, (1-\varrho)\Xi)$
, where
$U=(\varrho \Xi, (1-\varrho)\Xi)$
, where
![]() $\varrho \in (0,1)$
and the distribution function H of the random variable
$\varrho \in (0,1)$
and the distribution function H of the random variable
![]() $\Xi$
is subexponential on
$\Xi$
is subexponential on
![]() $[0,\infty)$
. Then
$[0,\infty)$
. Then
![]() $\overline F (x)= \overline{H}\left(\frac{x_1}{\varrho}\wedge \frac{x_2}{1-\varrho}\right)$
,
$\overline F (x)= \overline{H}\left(\frac{x_1}{\varrho}\wedge \frac{x_2}{1-\varrho}\right)$
,
![]() $F\in WS \big(\unicode{x211D}_+^2\big)$
, and
$F\in WS \big(\unicode{x211D}_+^2\big)$
, and
 \begin{equation*}\overline{F}(x(t))=\left\{\begin{array}{l@{\quad}r}\overline{H}\left(\frac{x_1(t)}{\varrho}\right)(1+o(1))& \text{if} \quad \lim_{t\rightarrow\infty} \frac{x_1(t)(1-\rho)}{x_2(t)\varrho} \leq 1,\\[9pt]\overline{H}\left(\frac{x_2(t)}{1-\varrho}\right)(1+o(1))& \text{if} \quad \lim_{t\rightarrow \infty} \frac{x_1(t)(1-\rho)}{x_2(t)\varrho}> 1.\end{array}\right.\end{equation*}
\begin{equation*}\overline{F}(x(t))=\left\{\begin{array}{l@{\quad}r}\overline{H}\left(\frac{x_1(t)}{\varrho}\right)(1+o(1))& \text{if} \quad \lim_{t\rightarrow\infty} \frac{x_1(t)(1-\rho)}{x_2(t)\varrho} \leq 1,\\[9pt]\overline{H}\left(\frac{x_2(t)}{1-\varrho}\right)(1+o(1))& \text{if} \quad \lim_{t\rightarrow \infty} \frac{x_1(t)(1-\rho)}{x_2(t)\varrho}> 1.\end{array}\right.\end{equation*}
Thus, one can get the asymptotic behaviour of u(x) provided that the assumptions of Theorem 2 are satisfied with
![]() $B\in (0,\infty)$
.
$B\in (0,\infty)$
.
Example 3. Let
![]() $x\in {\unicode{x211D}^d}$
, and assume that the stopping time
$x\in {\unicode{x211D}^d}$
, and assume that the stopping time
![]() $T\sim \operatorname{Exp}(\mu)$
is independent of X and that Y is as in Case (a) or (b). Recall that in this case
$T\sim \operatorname{Exp}(\mu)$
is independent of X and that Y is as in Case (a) or (b). Recall that in this case
![]() $\rho=\frac{\lambda}{\lambda+ \mu}$
. Let
$\rho=\frac{\lambda}{\lambda+ \mu}$
. Let
![]() $\ell(x) = {\unicode{x1D7D9}}_{|x| \leq r}$
. Then
$\ell(x) = {\unicode{x1D7D9}}_{|x| \leq r}$
. Then
Then the assumptions of Theorem 2 are satisfied with
![]() $B=0$
; therefore,
$B=0$
; therefore,
If
![]() $\ell(x)= {\unicode{x1D7D9}}_{\min x_i\geq r}$
then
$\ell(x)= {\unicode{x1D7D9}}_{\min x_i\geq r}$
then
Then we are in the situation of Theorem 2 with
![]() $B=\infty$
, so
$B=\infty$
, so
Example 4. At the end of this section we consider a simple example where T is not independent of X. We consider the well-known one-dimensional case
![]() $X_t = x+ at - Z_t$
with
$X_t = x+ at - Z_t$
with
![]() $a>0$
,
$a>0$
,
![]() $\mathbb{E} U_1=\mu$
,
$\mathbb{E} U_1=\mu$
,
![]() $N_t \sim \operatorname{Pois}(\lambda)$
, and
$N_t \sim \operatorname{Pois}(\lambda)$
, and
![]() $T=\inf\{t\geq 0\,:\, X_t<0\}$
being a ruin time. We put
$T=\inf\{t\geq 0\,:\, X_t<0\}$
being a ruin time. We put
Then the renewal equation (7) for u(x) is
Changing variables we get
with
![]() $h(x)= \int_0^\infty \lambda e^{-\lambda t} \overline{F} (x+at)dt $
and
$h(x)= \int_0^\infty \lambda e^{-\lambda t} \overline{F} (x+at)dt $
and
Note that
![]() $\operatorname{supp} G = \unicode{x211D}$
and
$\operatorname{supp} G = \unicode{x211D}$
and
![]() $G(\unicode{x211D})=1$
; hence, the result of Theorem 2 cannot be applied directly. In this situation the well-known approach is more suitable; below we recall this approach.
$G(\unicode{x211D})=1$
; hence, the result of Theorem 2 cannot be applied directly. In this situation the well-known approach is more suitable; below we recall this approach.
Taking
and starting from (61), we end up with
 \begin{align*}&v(x)=-\int_0^\infty \lambda e^{-\lambda t} \overline{F} (x+at)dt \\&\qquad\qquad +\int_0^\infty \lambda e^{-\lambda t} \left(\int_0^{x+at}F(dy) +\overline{F} (x+at)-\int_0^{x+at} u(x+at-y) F(dy) \right)\, dt\\&\qquad = \int_0^\infty \lambda e^{-\lambda t} \int_0^{x+at} v(x+at-y) F(dy) \, dt,\end{align*}
\begin{align*}&v(x)=-\int_0^\infty \lambda e^{-\lambda t} \overline{F} (x+at)dt \\&\qquad\qquad +\int_0^\infty \lambda e^{-\lambda t} \left(\int_0^{x+at}F(dy) +\overline{F} (x+at)-\int_0^{x+at} u(x+at-y) F(dy) \right)\, dt\\&\qquad = \int_0^\infty \lambda e^{-\lambda t} \int_0^{x+at} v(x+at-y) F(dy) \, dt,\end{align*}
where we used the equality
![]() $\int_0^{x+at}F(dy) +\overline{F} (x+at)=1$
. Hence, v satisfies the equation
$\int_0^{x+at}F(dy) +\overline{F} (x+at)=1$
. Hence, v satisfies the equation
which coincides with [Reference Embrechts, Klüppelberg and Mikosch18, (1.19)]. On the other hand, (63) can be written in the form [Reference Embrechts, Klüppelberg and Mikosch18, (1.22)]
where
![]() $F_I (x) =\frac{1}{\mu} \int_0^x \overline{F}(y)dy$
is the integrated tail of F,
$F_I (x) =\frac{1}{\mu} \int_0^x \overline{F}(y)dy$
is the integrated tail of F,
![]() $\theta\,:\!=\, \frac{a}{\lambda \mu} -1$
. Equivalently,
$\theta\,:\!=\, \frac{a}{\lambda \mu} -1$
. Equivalently,
where
![]() $\rho= \frac{1}{1+\theta}$
. Note that we can apply to the above equation Theorem 2 with
$\rho= \frac{1}{1+\theta}$
. Note that we can apply to the above equation Theorem 2 with
![]() $F_I$
instead of F. Note also that this model is defined for
$F_I$
instead of F. Note also that this model is defined for
![]() $x>0$
; i.e., we restrict
$x>0$
; i.e., we restrict
![]() $h(x)= \rho \overline{F}_I(x)$
to
$h(x)= \rho \overline{F}_I(x)$
to
![]() $[0,\infty)$
. Under the stronger assumption that
$[0,\infty)$
. Under the stronger assumption that
![]() $F_I$
is subexponential, the asymptotic behaviour of the solution to this equation is well known (cf. [Reference Asmussen and Albrecher2, Theorem 2.1, p. 302]):
$F_I$
is subexponential, the asymptotic behaviour of the solution to this equation is well known (cf. [Reference Asmussen and Albrecher2, Theorem 2.1, p. 302]):
5. Applications
Properties of potentials of type (6) are important in many applied probability models, such as branching processes, queueing theory, insurance ruin theory, reliability theory, and demography.
The renewal equation (8) and the one-dimensional random walk. Most applications concern the renewal function
![]() $u(x)=\mathbb{E}^0L_x$
where L is a renewal process with the distribution G of inter-arrival times. In this case, the renewal equation (8) holds true with
$u(x)=\mathbb{E}^0L_x$
where L is a renewal process with the distribution G of inter-arrival times. In this case, the renewal equation (8) holds true with
![]() $ h(x)=G(x)$
. For example, in demographic models used in branching theory,
$ h(x)=G(x)$
. For example, in demographic models used in branching theory,
![]() $L_x$
corresponds to the number of organisms/particles alive at time x; see for example [Reference Willmot, Cai and Lin40, Reference Yin and Zhao41].
$L_x$
corresponds to the number of organisms/particles alive at time x; see for example [Reference Willmot, Cai and Lin40, Reference Yin and Zhao41].
Other applications use the distribution of the all-time supremum
![]() $S=\max_{n\geq 1} S_n$
of a one-dimensional random walk
$S=\max_{n\geq 1} S_n$
of a one-dimensional random walk
![]() $S_n=\sum_{k=1}^n \eta_k$
(and
$S_n=\sum_{k=1}^n \eta_k$
(and
![]() $S_0=0$
) with
$S_0=0$
) with
![]() $\eta_k\geq 0$
and
$\eta_k\geq 0$
and
In this case the function
![]() $v(x)=\mathbb{P}^0(S \leq x)$
for
$v(x)=\mathbb{P}^0(S \leq x)$
for
![]() $x\geq 0$
satisfies the following equation (cf. [Reference Asmussen1, Proposition 2.9, p. 149]):
$x\geq 0$
satisfies the following equation (cf. [Reference Asmussen1, Proposition 2.9, p. 149]):
with
![]() $G(dy)=\mathbb{P}(\eta_1\in dy)$
and the proper distribution function
$G(dy)=\mathbb{P}(\eta_1\in dy)$
and the proper distribution function
![]() $G_\rho(dy)=G(dy)/\rho$
. Hence
$G_\rho(dy)=G(dy)/\rho$
. Hence
![]() $u(x)=1-v(x)=\mathbb{P}^0(S>x)$
satisfies the equation
$u(x)=1-v(x)=\mathbb{P}^0(S>x)$
satisfies the equation
which is (8) with
![]() $h(x)= \rho\overline{G}_\rho(x)$
. As is proved in [Reference Asmussen1, Theorem 2.2, p. 224], in the case of a general non-defective random walk with negative drift, one can take the first ascending ladder height for the distribution of
$h(x)= \rho\overline{G}_\rho(x)$
. As is proved in [Reference Asmussen1, Theorem 2.2, p. 224], in the case of a general non-defective random walk with negative drift, one can take the first ascending ladder height for the distribution of
![]() $\eta_1$
. In particular, in the case of a single-server GI/GI/1 queue, the quantity S corresponds to the steady-state workload; see [Reference Asmussen1, Equation (1.5), p. 268]. Then
$\eta_1$
. In particular, in the case of a single-server GI/GI/1 queue, the quantity S corresponds to the steady-state workload; see [Reference Asmussen1, Equation (1.5), p. 268]. Then
![]() $\eta_k$
is the kth ascending ladder height of the random walk
$\eta_k$
is the kth ascending ladder height of the random walk
![]() $\sum_{k=1}^n\chi_k$
for
$\sum_{k=1}^n\chi_k$
for
![]() $\chi_k$
being the difference between successive i.i.d. service times
$\chi_k$
being the difference between successive i.i.d. service times
![]() $U_k$
and i.i.d. inter-arrival times
$U_k$
and i.i.d. inter-arrival times
![]() $E_k$
. In the case of an M/G/1 queue we have
$E_k$
. In the case of an M/G/1 queue we have
![]() $\chi_k=U_k-E_k$
, where
$\chi_k=U_k-E_k$
, where
![]() $E_k$
is exponentially distributed with intensity, say,
$E_k$
is exponentially distributed with intensity, say,
![]() $\lambda$
. Then
$\lambda$
. Then
see [Reference Asmussen1, Theorem 5.7, p. 237]. Note that by (67), in this case
![]() $\rho=\lambda \mathbb{E} U_1$
. By duality (see e.g. [Reference Asmussen1, Theorem 4.2, p. 261]), in risk theory the tail distribution of S corresponds to the ruin probability of a classical Cramér–Lundberg process defined by
$\rho=\lambda \mathbb{E} U_1$
. By duality (see e.g. [Reference Asmussen1, Theorem 4.2, p. 261]), in risk theory the tail distribution of S corresponds to the ruin probability of a classical Cramér–Lundberg process defined by
where
![]() $Z_t=\sum_{i=1}^{N_t}U_k$
is given in (2) and describes the cumulative amount of the claims up to time t,
$Z_t=\sum_{i=1}^{N_t}U_k$
is given in (2) and describes the cumulative amount of the claims up to time t,
![]() $N_t$
is a Poisson process with intensity
$N_t$
is a Poisson process with intensity
![]() $\lambda$
, and
$\lambda$
, and
![]() $U_k$
is the claim size reached at the kth epoch of the Poisson process N. Here x describes the initial capital of the insurance company and a is a premium intensity. Indeed, taking
$U_k$
is the claim size reached at the kth epoch of the Poisson process N. Here x describes the initial capital of the insurance company and a is a premium intensity. Indeed, taking
![]() $\chi_k=U_k-E_k$
with exponentially distributed
$\chi_k=U_k-E_k$
with exponentially distributed
![]() $E_k$
with intensity
$E_k$
with intensity
![]() $\lambda$
, one can prove that for the ruin time
$\lambda$
, one can prove that for the ruin time
we have
Note that, by duality, the service times
![]() $U_k$
in the GI/GI/1 queue correspond to the claim sizes, and therefore we use the same letter to denote them. Similarly, the inter-arrival times
$U_k$
in the GI/GI/1 queue correspond to the claim sizes, and therefore we use the same letter to denote them. Similarly, the inter-arrival times
![]() $E_k$
in the single-server queue correspond to the times between Poisson epochs of the process
$E_k$
in the single-server queue correspond to the times between Poisson epochs of the process
![]() $N_t$
in the risk process (69). Assume that
$N_t$
in the risk process (69). Assume that
![]() $\delta=0$
in (3) and that
$\delta=0$
in (3) and that
![]() $Y_s=s$
, that is,
$Y_s=s$
, that is,
![]() $a=1$
in Example 4. If the net profit condition
$a=1$
in Example 4. If the net profit condition
![]() $\rho<1$
holds true (under which the above ruin probability is strictly less than one), we can conclude that the ruin probability satisfies (65). From [Reference Foss, Korshunov and Zachary23, Theorem 5.2, p. 106], under the assumption that
$\rho<1$
holds true (under which the above ruin probability is strictly less than one), we can conclude that the ruin probability satisfies (65). From [Reference Foss, Korshunov and Zachary23, Theorem 5.2, p. 106], under the assumption that
![]() $F_I\in \mathcal{S}$
(which is equivalent to the assumption that
$F_I\in \mathcal{S}$
(which is equivalent to the assumption that
![]() $G\in \mathcal{S}$
), we derive the asymptotic of the ruin probability given in (66).
$G\in \mathcal{S}$
), we derive the asymptotic of the ruin probability given in (66).
Multivariate risk process. There is an obvious need to understand the heavy-tailed asymptotic for the ruin probability in the multidimensional set-up. Consider the multivariate risk process
![]() $X_t=\big(X_t^1, \ldots, X_t^d\big)$
with possibly dependent components
$X_t=\big(X_t^1, \ldots, X_t^d\big)$
with possibly dependent components
![]() $X_t^i$
describing the reserves of the ith insurance company which covers incoming claims. We assume that the claims arrive simultaneously to all companies, that is,
$X_t^i$
describing the reserves of the ith insurance company which covers incoming claims. We assume that the claims arrive simultaneously to all companies, that is,
![]() $X_t$
is a multivariate Lévy risk process with
$X_t$
is a multivariate Lévy risk process with
![]() $a\in \mathbb{R}^d$
, and
$a\in \mathbb{R}^d$
, and
![]() $Z_t$
is a compound Poisson process as given in (2) with arrival intensity
$Z_t$
is a compound Poisson process as given in (2) with arrival intensity
![]() $\lambda$
and the generic claim size
$\lambda$
and the generic claim size
![]() $U \in \mathbb{R}^d$
. We assume that
$U \in \mathbb{R}^d$
. We assume that
![]() $\delta=0$
and
$\delta=0$
and
![]() $Y_s=as$
. Each company can have its own claims process as well. Indeed, to do so, it suffices to merge the separate independent Poisson arrival processes with the simultaneous arrival process (hence constructing a new Poisson arrival process) and allow the claim size to have atoms in one of the axis directions. Consider now the ruin time
$Y_s=as$
. Each company can have its own claims process as well. Indeed, to do so, it suffices to merge the separate independent Poisson arrival processes with the simultaneous arrival process (hence constructing a new Poisson arrival process) and allow the claim size to have atoms in one of the axis directions. Consider now the ruin time
which is the first exit time of X from a nonnegative quadrant; that is, T is the first time at which at least one company is ruined. Assume the net profit condition
![]() $\lambda \mathbb{E} U^{(k)}<1$
(
$\lambda \mathbb{E} U^{(k)}<1$
(
![]() $k=1,2,\ldots, d$
) for the kth coordinate
$k=1,2,\ldots, d$
) for the kth coordinate
![]() $U^{(k)}$
of the generic claim size
$U^{(k)}$
of the generic claim size
![]() $U_1$
. Then from the compensation formula given in [29, Theorem 3.4, p. 18] (see also [29, Equation (5.5), p. 42]) it follows that
$U_1$
. Then from the compensation formula given in [29, Theorem 3.4, p. 18] (see also [29, Equation (5.5), p. 42]) it follows that
with
![]() $x=(x_1,\ldots, x_d)\in {\unicode{x211D}_+^d}$
and
$x=(x_1,\ldots, x_d)\in {\unicode{x211D}_+^d}$
and
where F is the claim size distribution. In fact, a more general Gerber–Shiu function
can be represented as a potential function with
see [Reference Feng and Shimizu22]. The so-called penalty function w in (72) is applied to the deficit
![]() $X_T$
at the ruin moment and position
$X_T$
at the ruin moment and position
![]() $X_{T-}$
prior to the ruin time.
$X_{T-}$
prior to the ruin time.
If
![]() $d=1$
, then by (60) and (71) we recover the heavy-tailed asymptotic of u from Example 4.
$d=1$
, then by (60) and (71) we recover the heavy-tailed asymptotic of u from Example 4.
If
![]() $d=2$
(we have two companies), then using arguments similar to those in Example 4 for
$d=2$
(we have two companies), then using arguments similar to those in Example 4 for
![]() $v(x)=1-u(x)$
and
$v(x)=1-u(x)$
and
![]() $x=(x_1, x_2)\in \mathbb{R}^2_+$
we get
$x=(x_1, x_2)\in \mathbb{R}^2_+$
we get
where
![]() $a=(a_1,a_2)$
and
$a=(a_1,a_2)$
and
![]() $y=(y_1,y_2)$
.
$y=(y_1,y_2)$
.
Assume now that the claims coming simultaneously to both companies are independent of each other; that is,
![]() $U_1=\big(U^{(1)}, U^{(2)}\big)$
and
$U_1=\big(U^{(1)}, U^{(2)}\big)$
and
![]() $U^{(k)}\sim F_k $
,
$U^{(k)}\sim F_k $
,
![]() $k=1,2$
, are mutually independent. Then (73) is equivalent to
$k=1,2$
, are mutually independent. Then (73) is equivalent to
Following Foss et al. [Reference Foss, Korshunov, Palmowski and Rolski24], we can also consider the proportional reinsurance where the generic claim U is divided into fixed proportions between the two companies; that is,
![]() $U^{(1)}=\beta Z$
and
$U^{(1)}=\beta Z$
and
![]() $U^{(2)}=(1-\beta) Z$
for some random variable with distribution
$U^{(2)}=(1-\beta) Z$
for some random variable with distribution
![]() $F_Z$
and
$F_Z$
and
![]() $\beta\in (0,1)$
. In this case,
$\beta\in (0,1)$
. In this case,
Let
![]() $a_1>a_2$
and
$a_1>a_2$
and
![]() $x_1<x_2$
. In this case, by [Reference Foss, Korshunov, Palmowski and Rolski24, Corollaries 2.1 and 2.2], we have
$x_1<x_2$
. In this case, by [Reference Foss, Korshunov, Palmowski and Rolski24, Corollaries 2.1 and 2.2], we have
as
![]() $x^0\to\infty$
, where Z is strong subexponential, that is,
$x^0\to\infty$
, where Z is strong subexponential, that is,
![]() $F_Z\in \mathcal{S}$
and
$F_Z\in \mathcal{S}$
and
Mathematical finance. Other applications of the potential function (6) come from mathematical finance. For example, the renewal equation (7) can be used in pricing a perpetual put option; see Yin and Zhao [Reference Yin and Zhao41, Ex. 4.2] for details.
The potential function also appears in a consumption–investment problem initiated by Merton [Reference Merton30]. Consider a very simple model where on the market we have d assets
![]() $S_t^i=e^{-X_t^i}$
,
$S_t^i=e^{-X_t^i}$
,
![]() $1 \leq i \leq d$
, governed by exponential Lévy processes
$1 \leq i \leq d$
, governed by exponential Lévy processes
![]() $X_t^i$
(which may depend on each other). In fact, take
$X_t^i$
(which may depend on each other). In fact, take
![]() $X_t=x+W_t-Z_t$
with
$X_t=x+W_t-Z_t$
with
![]() $W_t$
being a d-dimensional Wiener process and Z as defined in (2). Let
$W_t$
being a d-dimensional Wiener process and Z as defined in (2). Let
![]() $\big(\pi_1,\pi_2,\ldots,\pi_d\big)$
be the strictly positive proportions of the total wealth that are invested in each of the d stocks. Then the wealth process equals
$\big(\pi_1,\pi_2,\ldots,\pi_d\big)$
be the strictly positive proportions of the total wealth that are invested in each of the d stocks. Then the wealth process equals
![]() $\sum_{i=1}^d \pi_iS_t^i.$
Assume that the investor withdraws the proportion
$\sum_{i=1}^d \pi_iS_t^i.$
Assume that the investor withdraws the proportion
![]() $\varpi$
of his funds for consumption. The discounted utility of consumption is measured by the function
$\varpi$
of his funds for consumption. The discounted utility of consumption is measured by the function
where
![]() $q>0$
, T is an independent killing time exponentially distributed with parameter q, and
$q>0$
, T is an independent killing time exponentially distributed with parameter q, and
 \begin{equation*}\ell(x_1,x_2,\ldots,x_d)=L\left(\varpi\sum_{i=1}^d \pi_i e^{-x_i}\right)\end{equation*}
\begin{equation*}\ell(x_1,x_2,\ldots,x_d)=L\left(\varpi\sum_{i=1}^d \pi_i e^{-x_i}\right)\end{equation*}
for some utility function L; see [Reference Cadenillas5] for details. We take the power utility
![]() $L(z)=z^\alpha$
for
$L(z)=z^\alpha$
for
![]() $\alpha \in (0,1)$
and
$\alpha \in (0,1)$
and
![]() $z>0$
. Assume that
$z>0$
. Assume that
![]() $F\in WS\big({\unicode{x211D}^d}\big)$
. Since
$F\in WS\big({\unicode{x211D}^d}\big)$
. Since
![]() $\ell (b x) \leq C\sum_{i=1}^d e^{-\alpha b_i x_i}$
for a sufficiently large constant C, we have
$\ell (b x) \leq C\sum_{i=1}^d e^{-\alpha b_i x_i}$
for a sufficiently large constant C, we have
and since
![]() $Y_t$
is a Wiener process,
$Y_t$
is a Wiener process,
Hence by Theorem 2 the asymptotic behaviour of the discounted utility consumption is
![]() $u(x)=o(1)\overline{F}(x)$
as
$u(x)=o(1)\overline{F}(x)$
as
![]() $x^0\to \infty$
(that is, as the initial asset prices go to zero).
$x^0\to \infty$
(that is, as the initial asset prices go to zero).
We have chosen only a few examples where the subexponential asymptotic can be used; the set of possible applications is much wider.
Funding information
This work is partially supported by Polish National Science Centre Grant No. 2018/29/B/ST1/00756, 2019–2022.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process for this article.