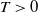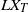1. Introduction
Let  $X=(X_t,\, t\in [0, T])$
be a d-dimensional diffusion process satisfying the stochastic differential equation (SDE)
$X=(X_t,\, t\in [0, T])$
be a d-dimensional diffusion process satisfying the stochastic differential equation (SDE)
 \begin{equation} {\mathrm{d}} X_t = b(t,X_t) \,{\mathrm{d}} t + {\sigma}(t,X_t) \,{\mathrm{d}} W_t,\quad X_0=x_0,\quad t\in [0,T].\end{equation}
\begin{equation} {\mathrm{d}} X_t = b(t,X_t) \,{\mathrm{d}} t + {\sigma}(t,X_t) \,{\mathrm{d}} W_t,\quad X_0=x_0,\quad t\in [0,T].\end{equation}
Here  $b\colon [0,\infty)\times {\mathbb{R}}^d \to {\mathbb{R}}^d$
,
$b\colon [0,\infty)\times {\mathbb{R}}^d \to {\mathbb{R}}^d$
,  ${\sigma}\colon [0,\infty)\times {\mathbb{R}}^d \to {\mathbb{R}}^{d\times d'}$
and W is a d′-dimensional Wiener process with all components independent. Stochastic differential equations are widely used for modelling in engineering, finance, and biology, to name a few fields of applications. In this paper we will not only consider uniformly elliptic models, where it is assumed that there exists an
${\sigma}\colon [0,\infty)\times {\mathbb{R}}^d \to {\mathbb{R}}^{d\times d'}$
and W is a d′-dimensional Wiener process with all components independent. Stochastic differential equations are widely used for modelling in engineering, finance, and biology, to name a few fields of applications. In this paper we will not only consider uniformly elliptic models, where it is assumed that there exists an  ${\varepsilon} >0$
such that for all
${\varepsilon} >0$
such that for all  ${(t,x) \in [0,T] \times {\mathbb{R}}^d}$
and
${(t,x) \in [0,T] \times {\mathbb{R}}^d}$
and  $y\in {\mathbb{R}}^d$
we have
$y\in {\mathbb{R}}^d$
we have  $\|{\sigma}(t,x)^{\prime} y\|^2 \ge {\varepsilon} \|y\|^2$
, but also hypo-elliptic models. These are models where the randomness spreads through all components, ensuring the existence of smooth transition densities of the diffusion, even though the diffusion is possibly not uniformly elliptic (for example because the Wiener noise only affects certain components). Such models appear frequently in application areas; many examples are given in the introductory section of [Reference Clairon and Samson9]. A rich subclass of non-linear hypo-elliptic diffusions that is included in our set-up is specified by a drift of the form
$\|{\sigma}(t,x)^{\prime} y\|^2 \ge {\varepsilon} \|y\|^2$
, but also hypo-elliptic models. These are models where the randomness spreads through all components, ensuring the existence of smooth transition densities of the diffusion, even though the diffusion is possibly not uniformly elliptic (for example because the Wiener noise only affects certain components). Such models appear frequently in application areas; many examples are given in the introductory section of [Reference Clairon and Samson9]. A rich subclass of non-linear hypo-elliptic diffusions that is included in our set-up is specified by a drift of the form
 \begin{equation}b(t,x) = B x + \beta(t,x),\end{equation}
\begin{equation}b(t,x) = B x + \beta(t,x),\end{equation}
where
 \begin{equation} B=\begin{bmatrix} 0_{k\times k'} &\quad I_{k\times k} \\[5pt] 0_{k'\times k'} &\quad 0_{k'\times k}\end{bmatrix}, \quad \beta(t,x)=\begin{bmatrix} 0_{k\times 1} \\[5pt] \underline{\beta}(t,x)\end{bmatrix}, \quad {\sigma} =\begin{bmatrix} 0_{k\times d'} \\[5pt] \underline{\sigma}(t) \end{bmatrix} {,}\end{equation}
\begin{equation} B=\begin{bmatrix} 0_{k\times k'} &\quad I_{k\times k} \\[5pt] 0_{k'\times k'} &\quad 0_{k'\times k}\end{bmatrix}, \quad \beta(t,x)=\begin{bmatrix} 0_{k\times 1} \\[5pt] \underline{\beta}(t,x)\end{bmatrix}, \quad {\sigma} =\begin{bmatrix} 0_{k\times d'} \\[5pt] \underline{\sigma}(t) \end{bmatrix} {,}\end{equation}
and  $\underline{{\sigma}} \colon [0,\infty) \to {\mathbb{R}}^{k'\times d'}$
,
$\underline{{\sigma}} \colon [0,\infty) \to {\mathbb{R}}^{k'\times d'}$
,  $\underline{\beta}\colon[0,\infty) \times {\mathbb{R}}^d \to {\mathbb{R}}^{k'}$
, and
$\underline{\beta}\colon[0,\infty) \times {\mathbb{R}}^d \to {\mathbb{R}}^{k'}$
, and  $k+k'=d$
. This includes several forms of integrated diffusions.
$k+k'=d$
. This includes several forms of integrated diffusions.
Suppose L is a  $m\times d$
matrix with
$m\times d$
matrix with  $m \le d$
. We aim to simulate the process X, conditioned on the random variable
$m \le d$
. We aim to simulate the process X, conditioned on the random variable
 \[V = L X_T.\]
\[V = L X_T.\]
The conditional process is termed a diffusion bridge, although its paths do not necessarily end at a fixed point but in the set  $\{x\colon V = L x\}$
. Besides being an interesting mathematical problem in its own right, simulation of such diffusion bridges is key to parameter estimation of diffusions from discrete observations. If the process is observed at discrete times directly or through an observation operator L, data-augmentation is routinely used to perform Bayesian inference (see e.g. [Reference Golightly and Wilkinson16], [Reference Papaspiliopoulos, Roberts and Stramer30], and [Reference van der Meulen and Schauer38]). Here, a key step consists of the simulation of the ‘missing’ data, which amounts to simulation of diffusion bridges.
$\{x\colon V = L x\}$
. Besides being an interesting mathematical problem in its own right, simulation of such diffusion bridges is key to parameter estimation of diffusions from discrete observations. If the process is observed at discrete times directly or through an observation operator L, data-augmentation is routinely used to perform Bayesian inference (see e.g. [Reference Golightly and Wilkinson16], [Reference Papaspiliopoulos, Roberts and Stramer30], and [Reference van der Meulen and Schauer38]). Here, a key step consists of the simulation of the ‘missing’ data, which amounts to simulation of diffusion bridges.
Another application is non-linear filtering, where at time t the state  $X_t$
was observed and at time
$X_t$
was observed and at time  ${t+T}$
a new observation
${t+T}$
a new observation  $L X_{t+T}$
comes in. Interest then lies in sampling from the distribution on
$L X_{t+T}$
comes in. Interest then lies in sampling from the distribution on  $X_{t+T}$
, conditional on
$X_{t+T}$
, conditional on  ${(X_t, L X_{t+T})}$
. The simulation method developed in this paper can then be used to construct efficient particle filters. We leave the application of our methods to estimation and filtering to future research, although it is clear that our results can be used directly within the algorithms given in [Reference van der Meulen and Schauer38]. Finally, rare-event simulation is a third application area for which our results are useful.
${(X_t, L X_{t+T})}$
. The simulation method developed in this paper can then be used to construct efficient particle filters. We leave the application of our methods to estimation and filtering to future research, although it is clear that our results can be used directly within the algorithms given in [Reference van der Meulen and Schauer38]. Finally, rare-event simulation is a third application area for which our results are useful.
We aim for a unified approach, by which we mean that the bridge simulation method applies simultaneously to uniformly elliptic and hypo-elliptic models. This is important, as in the aforementioned estimation problems either one of the two types of ellipticity may apply to the data. While the sample paths of uniformly elliptic and hypo-elliptic diffusions are very different, the corresponding distributions of the observations can be very similar if the diffusion coefficients are close. Algorithms which are invalid for hypo-elliptic diffusions will therefore be numerically unstable if the model is close to being hypo-elliptic, and it may be a priori unknown if this is the case.
1.1. Literature review
When the diffusion is uniformly elliptic and the endpoint is fully observed, i.e.  $L=I$
, the problem has been studied extensively; see [Reference Clark10], [Reference Durham and Gallant15], [Reference Beskos, Papaspiliopoulos, Roberts and Fearnhead4], [Reference Delyon and Hu13], [Reference Beskos, Roberts, Stuart and Voss5], [Reference Hairer, Stuart and Voss17], [Reference Lin, Chen and Mykland21], [Reference LindstrÖm22], [Reference Bayer and Schoenmakers3], [Reference Bladt, Finch and SØrensen7], [Reference Schauer, van der Meulen and van Zanten35], and [Reference Whitaker, Golightly, Boys and Sherlock42].
$L=I$
, the problem has been studied extensively; see [Reference Clark10], [Reference Durham and Gallant15], [Reference Beskos, Papaspiliopoulos, Roberts and Fearnhead4], [Reference Delyon and Hu13], [Reference Beskos, Roberts, Stuart and Voss5], [Reference Hairer, Stuart and Voss17], [Reference Lin, Chen and Mykland21], [Reference LindstrÖm22], [Reference Bayer and Schoenmakers3], [Reference Bladt, Finch and SØrensen7], [Reference Schauer, van der Meulen and van Zanten35], and [Reference Whitaker, Golightly, Boys and Sherlock42].
Much less is known when either  $L\neq I$
or when the diffusion is not assumed to be uniformly elliptic. In [Reference Beskos, Roberts, Stuart and Voss5] and [Reference Hairer, Stuart and Voss17] a Langevin MCMC sampler was constructed to sample diffusion bridges when the drift is of the form
$L\neq I$
or when the diffusion is not assumed to be uniformly elliptic. In [Reference Beskos, Roberts, Stuart and Voss5] and [Reference Hairer, Stuart and Voss17] a Langevin MCMC sampler was constructed to sample diffusion bridges when the drift is of the form  $b(x) =B x + {\sigma} {\sigma}^{\prime} \nabla V(x)$
and
$b(x) =B x + {\sigma} {\sigma}^{\prime} \nabla V(x)$
and  ${\sigma}$
is constant, assuming uniform ellipticity. Subsequently, in [Reference Hairer, Stuart and Voss18], this approach was extended to hypo-elliptic diffusions of the form
${\sigma}$
is constant, assuming uniform ellipticity. Subsequently, in [Reference Hairer, Stuart and Voss18], this approach was extended to hypo-elliptic diffusions of the form
 \[\begin{bmatrix} X_t \\[5pt] Y_t \end{bmatrix} = \begin{bmatrix} Y_t \\[5pt] f(X_t) - Y_t\end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 \\[5pt] 1\end{bmatrix} \,{\mathrm{d}} W_t {.}\]
\[\begin{bmatrix} X_t \\[5pt] Y_t \end{bmatrix} = \begin{bmatrix} Y_t \\[5pt] f(X_t) - Y_t\end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 \\[5pt] 1\end{bmatrix} \,{\mathrm{d}} W_t {.}\]
However, no simulation results were included in the paper, as ‘these simulations proved prohibitively slow and the resulting method does not seem like a useful approach to sampling’ [Reference Hairer, Stuart and Voss18, page 671].
We will shortly review in more detail the works [Reference Delyon and Hu13], [Reference Marchand27], and [Reference van der Meulen and Schauer40], as the present paper builds upon these. The first of these papers includes some forms of hypo-elliptic diffusions, whereas the latter two papers consider uniformly elliptic diffusions with  $L\neq I$
.
$L\neq I$
.
Stramer and Roberts [Reference Stramer and Roberts37] considered Bayesian estimation of non-linear continuous-time autoregressive (NLCAR) processes using a data-augmentation scheme. This is a specific class of hypo-elliptic models included by the specification (1.2)–(1.3). The method of imputation, however, is different from that proposed here.
Estimation of discretely observed hypo-elliptic diffusions has been an active field over the past 10 years. As we stated earlier, within the Bayesian approach a data-augmentation strategy where diffusion bridges are imputed is natural. However, this is by no means the only way to do estimation. Frequentist approaches to the estimation problem include [Reference SØrensen36], [Reference Ditlevsen and Samson14], [Reference Lu, Lin and Chorin24], [Reference Comte, Prieur and Samson11], [Reference Samson and Thieullen33], [Reference Pokern, Stuart and Wiberg31], [Reference Clairon and Samson9], and [Reference Melnykova28].
1.2. Review of [Reference Delyon and Hu13] and [Reference Schauer, van der Meulen and van Zanten35]
To motivate and explain our approach, it is useful to review briefly the methods developed by Delyon and Hu [Reference Delyon and Hu13] and Schauer, van der Meulen, and van Zanten [Reference Schauer, van der Meulen and van Zanten35]. The method we propose in this article builds on their papers. Both are restricted to the setting  $L=I$
(full observation of the diffusion at time T) and uniform ellipticity. Their common starting point is that under mild conditions the diffusion bridge, obtained by conditioning on
$L=I$
(full observation of the diffusion at time T) and uniform ellipticity. Their common starting point is that under mild conditions the diffusion bridge, obtained by conditioning on  $L X_t = v$
, is itself a diffusion process, governed by the SDE
$L X_t = v$
, is itself a diffusion process, governed by the SDE
 \begin{equation} {{\mathrm d}} X^\star_t = (b(t,X^\star_t) + a(t,X^\star_t)r(t,X^\star_t) ) \,{\mathrm{d}} t + {\sigma}(t,X^\star_t) \,{\mathrm{d}} W_t,\quad X^\star_0=x_0.\end{equation}
\begin{equation} {{\mathrm d}} X^\star_t = (b(t,X^\star_t) + a(t,X^\star_t)r(t,X^\star_t) ) \,{\mathrm{d}} t + {\sigma}(t,X^\star_t) \,{\mathrm{d}} W_t,\quad X^\star_0=x_0.\end{equation}
Here  $a={\sigma} {\sigma}^{\prime}$
and
$a={\sigma} {\sigma}^{\prime}$
and  $r(t,x) = \nabla_x \log p(t,x;\ T,v)$
. We have implicitly assumed the existence of transition densities p such that
$r(t,x) = \nabla_x \log p(t,x;\ T,v)$
. We have implicitly assumed the existence of transition densities p such that
 \[ {\mathbb{P}}^{(t,\ x)}(X_T \in A)=\int_A p(t,x;\ {T},\xi) \,{\mathrm{d}} \xi\]
\[ {\mathbb{P}}^{(t,\ x)}(X_T \in A)=\int_A p(t,x;\ {T},\xi) \,{\mathrm{d}} \xi\]
and r(t, x) is well-defined. The SDE for  $X^\star$
can be derived from Doob’s h-transform or the theory of initial enlargement of the filtration. Unfortunately, the ‘guiding’ term
$X^\star$
can be derived from Doob’s h-transform or the theory of initial enlargement of the filtration. Unfortunately, the ‘guiding’ term  $a(t,X^\star_t) r(t,X^\star_t)$
appearing in the drift of
$a(t,X^\star_t) r(t,X^\star_t)$
appearing in the drift of  $X^\star$
is intractable, as the transition densities p are not available in closed form. Henceforth, as direct simulation of
$X^\star$
is intractable, as the transition densities p are not available in closed form. Henceforth, as direct simulation of  $X^\star$
is infeasible, a common feature of both [Reference Delyon and Hu13] and [Reference Schauer, van der Meulen and van Zanten35] is to simulate a tractable process
$X^\star$
is infeasible, a common feature of both [Reference Delyon and Hu13] and [Reference Schauer, van der Meulen and van Zanten35] is to simulate a tractable process  $X^\circ$
instead of
$X^\circ$
instead of  $X^\star$
, that resembles
$X^\star$
, that resembles  $X^\star$
. Next, the mismatch can be corrected for by a Metropolis–Hastings step or weighting. The proposal
$X^\star$
. Next, the mismatch can be corrected for by a Metropolis–Hastings step or weighting. The proposal  $X^\circ$
(the terminology is inherited from
$X^\circ$
(the terminology is inherited from  $X^\circ$
being a proposal for a Metropolis–Hastings step) is assumed to solve the SDE
$X^\circ$
being a proposal for a Metropolis–Hastings step) is assumed to solve the SDE
 \begin{equation}{\mathrm{d}} X^\circ_t = b^\circ(t, X^\circ_t) \,{\mathrm{d}} t + \sigma(t, X^\circ_t) \,{\mathrm{d}} W_t, \quad X^\circ_0 = x_0, \quad t\in [0,T],\end{equation}
\begin{equation}{\mathrm{d}} X^\circ_t = b^\circ(t, X^\circ_t) \,{\mathrm{d}} t + \sigma(t, X^\circ_t) \,{\mathrm{d}} W_t, \quad X^\circ_0 = x_0, \quad t\in [0,T],\end{equation}
where the drift  $b^\circ$
is chosen such that the process
$b^\circ$
is chosen such that the process  $ X_t^\circ$
hits the correct endpoint (say v) at the final time T. Delyon and Hu [Reference Delyon and Hu13] proposed taking
$ X_t^\circ$
hits the correct endpoint (say v) at the final time T. Delyon and Hu [Reference Delyon and Hu13] proposed taking
 \begin{equation} b^\circ(t,x) = {\lambda} b(t,x) + (v-x)/(T-t),\end{equation}
\begin{equation} b^\circ(t,x) = {\lambda} b(t,x) + (v-x)/(T-t),\end{equation}
where either  ${\lambda}=0$
or
${\lambda}=0$
or  ${\lambda}=1$
, the choice
${\lambda}=1$
, the choice  ${\lambda}=1$
requiring the drift b to be bounded. If
${\lambda}=1$
requiring the drift b to be bounded. If  ${\lambda}=0$
, a popular discretisation of this SDE is the modified diffusion bridge introduced in [Reference Durham and Gallant15]. A drawback of this method is that the drift is not taken into account. Schauer, van der Meulen, and van Zanten [Reference Schauer, van der Meulen and van Zanten35] proposed taking
${\lambda}=0$
, a popular discretisation of this SDE is the modified diffusion bridge introduced in [Reference Durham and Gallant15]. A drawback of this method is that the drift is not taken into account. Schauer, van der Meulen, and van Zanten [Reference Schauer, van der Meulen and van Zanten35] proposed taking
 \begin{equation}b^\circ(t, x) = b(t,x) + a(t, x) \tilde{r}(t,x) {.}\end{equation}
\begin{equation}b^\circ(t, x) = b(t,x) + a(t, x) \tilde{r}(t,x) {.}\end{equation}
Here  $\tilde{r}(t,x)=\nabla_x \log \tilde{p}(t,x;\ T,v)$
, where
$\tilde{r}(t,x)=\nabla_x \log \tilde{p}(t,x;\ T,v)$
, where  $\tilde p(t,x)$
is the transition density of an auxiliary diffusion process
$\tilde p(t,x)$
is the transition density of an auxiliary diffusion process  $\tilde{X}$
that has tractable transition densities. In this paper, we always assume
$\tilde{X}$
that has tractable transition densities. In this paper, we always assume  $\tilde{X}$
to be a linear process, i.e. a diffusion satisfying the SDE
$\tilde{X}$
to be a linear process, i.e. a diffusion satisfying the SDE
 \begin{equation}{\mathrm{d}} \tilde{X}_t =\tilde{b}(t,\tilde{X}_t) \,{\mathrm{d}} t + \tilde\sigma(t) \,{\mathrm{d}} W_t, \quad\text{where } \tilde{b}(t,x)=\tilde{B}(t) x +\tilde\beta(t).\end{equation}
\begin{equation}{\mathrm{d}} \tilde{X}_t =\tilde{b}(t,\tilde{X}_t) \,{\mathrm{d}} t + \tilde\sigma(t) \,{\mathrm{d}} W_t, \quad\text{where } \tilde{b}(t,x)=\tilde{B}(t) x +\tilde\beta(t).\end{equation}
The process  $X^\circ$
obtained in this way will be referred to as a guided proposal.
$X^\circ$
obtained in this way will be referred to as a guided proposal.
We denote the laws of X,  $X^\star$
, and
$X^\star$
, and  $X^\circ$
viewed as measures on the space
$X^\circ$
viewed as measures on the space  $C([0,t], {\mathbb{R}}^d)$
of continuous functions from [0,t] to
$C([0,t], {\mathbb{R}}^d)$
of continuous functions from [0,t] to  ${\mathbb{R}}^d$
equipped with its Borel-
${\mathbb{R}}^d$
equipped with its Borel- $\sigma$
-algebra by
$\sigma$
-algebra by  ${\mathbb{P}}_t$
,
${\mathbb{P}}_t$
,  ${\mathbb{P}}^\star_t$
, and
${\mathbb{P}}^\star_t$
, and  ${\mathbb{P}}^\circ_t$
respectively. Delyon and Hu [Reference Delyon and Hu13] provided sufficient conditions such that
${\mathbb{P}}^\circ_t$
respectively. Delyon and Hu [Reference Delyon and Hu13] provided sufficient conditions such that  ${\mathbb{P}}^\star_T$
is absolutely continuous with respect to
${\mathbb{P}}^\star_T$
is absolutely continuous with respect to  ${\mathbb{P}}^\circ_T$
for the proposals derived from (1.6). Moreover, closed-form expressions for the Radon–Nikodým derivative were derived. For the proposals derived from (1.7), Schauer et al. [Reference Schauer, van der Meulen and van Zanten35] proved that the condition
${\mathbb{P}}^\circ_T$
for the proposals derived from (1.6). Moreover, closed-form expressions for the Radon–Nikodým derivative were derived. For the proposals derived from (1.7), Schauer et al. [Reference Schauer, van der Meulen and van Zanten35] proved that the condition  $\tilde\sigma(T)^{\prime} \tilde\sigma(T) = a(T,v)$
is necessary for absolute continuity of
$\tilde\sigma(T)^{\prime} \tilde\sigma(T) = a(T,v)$
is necessary for absolute continuity of  ${\mathbb{P}}^\star_T$
with respect to
${\mathbb{P}}^\star_T$
with respect to  ${\mathbb{P}}^\circ_T$
. We refer to this condition as the matching condition, as the diffusivity of X and
${\mathbb{P}}^\circ_T$
. We refer to this condition as the matching condition, as the diffusivity of X and  $\tilde X$
need to match at the conditioning point. Under that condition (and some additional technical conditions), it was derived that
$\tilde X$
need to match at the conditioning point. Under that condition (and some additional technical conditions), it was derived that
 $$\frac{{\mathrm{d}} {\mathbb{P}}^\star_T}{{\mathrm{d}} {\mathbb{P}}^\circ_T}(X^\circ) =\frac{\tilde{p}(0,x_0;\ T,v)}{p(0,x_0, T,v)} \exp\bigg(\int_0^T \mathcal{G}(s,X^\circ_s) \,{\mathrm{d}} s\bigg),$$
$$\frac{{\mathrm{d}} {\mathbb{P}}^\star_T}{{\mathrm{d}} {\mathbb{P}}^\circ_T}(X^\circ) =\frac{\tilde{p}(0,x_0;\ T,v)}{p(0,x_0, T,v)} \exp\bigg(\int_0^T \mathcal{G}(s,X^\circ_s) \,{\mathrm{d}} s\bigg),$$
where  $\mathcal{G}(s,x)$
is tractable. A great deal of work in the proof is concerned with proving that
$\mathcal{G}(s,x)$
is tractable. A great deal of work in the proof is concerned with proving that  $\|X^\circ_t -v\| \to 0$
at the ‘correct’ rate.
$\|X^\circ_t -v\| \to 0$
at the ‘correct’ rate.
1.3. Approach
We aim to extend the results in [Reference Delyon and Hu13] and [Reference Schauer, van der Meulen and van Zanten35] by lifting the restrictions of
(1) uniform ellipticity,
(2) L being the identity matrix.
1.3.1. Extending [Reference Delyon and Hu13]
We first explain the difficulty in extending this approach beyond uniform ellipticity. To see the problem, we fix  $t<T$
. Absolute continuity of
$t<T$
. Absolute continuity of  ${\mathbb{P}}^\star_t$
with respect to
${\mathbb{P}}^\star_t$
with respect to  ${\mathbb{P}}^\circ$
requires the existence of a mapping
${\mathbb{P}}^\circ$
requires the existence of a mapping  $\eta(s,x)$
such that
$\eta(s,x)$
such that
 \begin{equation}{\sigma}(s,x) \eta(s,x) = b^\star(s,x)-b^\circ(s,x),\quad s\in [0,t], \quad x\in {\mathbb{R}}^d,\end{equation}
\begin{equation}{\sigma}(s,x) \eta(s,x) = b^\star(s,x)-b^\circ(s,x),\quad s\in [0,t], \quad x\in {\mathbb{R}}^d,\end{equation}
which follows from Girsanov’s theorem [Reference Liptser and Shiryaev23, Section 7.6.4]. However, for the choice of [Reference Delyon and Hu13] (as given in equation (1.6)) this mapping  $\eta$
need not exist for
$\eta$
need not exist for  ${\lambda}=0$
and
${\lambda}=0$
and  ${\lambda}=1$
. If
${\lambda}=1$
. If  ${\lambda}=1$
, then we have
${\lambda}=1$
, then we have
 $$b^\star(s,x)-b^\circ(s,x)=\frac{v-x}{T-s},$$
$$b^\star(s,x)-b^\circ(s,x)=\frac{v-x}{T-s},$$
and therefore  $\eta(s,x)$
only exists if
$\eta(s,x)$
only exists if  $v-x$
is in the column space of
$v-x$
is in the column space of  ${\sigma}(s,x)$
. A similar argument applies to the case
${\sigma}(s,x)$
. A similar argument applies to the case  ${\lambda}=0$
. From these considerations, it is not surprising that Delyon and Hu [Reference Delyon and Hu13] need additional assumptions on the form of the drift to deal with the hypo-elliptic case. More specifically, they consider
${\lambda}=0$
. From these considerations, it is not surprising that Delyon and Hu [Reference Delyon and Hu13] need additional assumptions on the form of the drift to deal with the hypo-elliptic case. More specifically, they consider
 \begin{equation} {{\mathrm d}} X_t = ( {\sigma}(t) h(t,X_t) + B(t) x + \beta(t)) \,{\mathrm{d}} t + \sigma(t) \,{\mathrm{d}} W_t,\end{equation}
\begin{equation} {{\mathrm d}} X_t = ( {\sigma}(t) h(t,X_t) + B(t) x + \beta(t)) \,{\mathrm{d}} t + \sigma(t) \,{\mathrm{d}} W_t,\end{equation}
with  ${\sigma}(t)$
admitting a left-inverse. Then they show that bridges can be obtained by simulating bridges corresponding to this SDE with
${\sigma}(t)$
admitting a left-inverse. Then they show that bridges can be obtained by simulating bridges corresponding to this SDE with  $h\equiv 0$
, followed by correcting for the discrepancy by weighting according to their likelihood ratio. Clearly, the form of the drift in the above display is restrictive, but necessary for absolute continuity.
$h\equiv 0$
, followed by correcting for the discrepancy by weighting according to their likelihood ratio. Clearly, the form of the drift in the above display is restrictive, but necessary for absolute continuity.
Whereas lifting the assumption of uniform ellipticity seems hard, lifting the assumption that  $L=I$
is possible. Indeed, Marchand [Reference Marchand27] showed in a clever way how this can be done by using the guiding term
$L=I$
is possible. Indeed, Marchand [Reference Marchand27] showed in a clever way how this can be done by using the guiding term
 \begin{equation}v(t,x)\coloneqq a(t,x) L^{\prime} (L a(t,x) L^{\prime})^{-1} \frac{v-Lx}{T-t}\end{equation}
\begin{equation}v(t,x)\coloneqq a(t,x) L^{\prime} (L a(t,x) L^{\prime})^{-1} \frac{v-Lx}{T-t}\end{equation}
to be superimposed on the drift of the original diffusion. Hence, the proposal satisfies the SDE
 $${\mathrm{d}} X^{\triangle}_t = b(t,X^{\triangle}_t) \,{\mathrm{d}} t + v(t,X^{\triangle}_t) \,{\mathrm{d}} t + {\sigma}(t,X^{\triangle}_t) \,{\mathrm{d}} W_t, \quad X^{\triangle}_0 =x_0.$$
$${\mathrm{d}} X^{\triangle}_t = b(t,X^{\triangle}_t) \,{\mathrm{d}} t + v(t,X^{\triangle}_t) \,{\mathrm{d}} t + {\sigma}(t,X^{\triangle}_t) \,{\mathrm{d}} W_t, \quad X^{\triangle}_0 =x_0.$$
By applying Itô’s lemma to  ${(T-t)^{-1} (LX^{\triangle}(t)-v)}$
, followed by the law of the iterated logarithm for Brownian motion, the rate at which
${(T-t)^{-1} (LX^{\triangle}(t)-v)}$
, followed by the law of the iterated logarithm for Brownian motion, the rate at which  $L X^{\triangle}(t)$
converges to v can be derived. Interestingly, the same guiding term as in (1.11) was used in a specific setting in [Reference Arnaudon, Holm and Sommer2], where the guiding term was rewritten as
$L X^{\triangle}(t)$
converges to v can be derived. Interestingly, the same guiding term as in (1.11) was used in a specific setting in [Reference Arnaudon, Holm and Sommer2], where the guiding term was rewritten as  ${\sigma}(t,x) (L{\sigma}(t,x))^+ (v-Lx)/(T-t)$
, assuming that
${\sigma}(t,x) (L{\sigma}(t,x))^+ (v-Lx)/(T-t)$
, assuming that  $L{\sigma}$
has linearly independent rows. Here
$L{\sigma}$
has linearly independent rows. Here  $A^+$
denotes the Moore–Penrose inverse of the matrix A. The form of the guiding term in (1.11) suggests that invertibility of
$A^+$
denotes the Moore–Penrose inverse of the matrix A. The form of the guiding term in (1.11) suggests that invertibility of  $La(t,x)L^{\prime}$
suffices, which, depending on the precise form of L, would allow for some forms of hypo-ellipticity. However, we believe there are fundamental problems when one wants to include for example integrated diffusions. We return to this in the discussion in Section 7.
$La(t,x)L^{\prime}$
suffices, which, depending on the precise form of L, would allow for some forms of hypo-ellipticity. However, we believe there are fundamental problems when one wants to include for example integrated diffusions. We return to this in the discussion in Section 7.
1.3.2. Extending [Reference Schauer, van der Meulen and van Zanten35]
When L is not the identity matrix, the conditioned diffusion also satisfies the SDE (1.4), albeit with an adjusted definition of r(t, x). To find the right form of r(t, x), assume without loss of generality that  $\textrm{rank}\ L = m<d$
. Let
$\textrm{rank}\ L = m<d$
. Let  ${(f_1, \ldots, f_m)}$
denote an orthonormal basis of
${(f_1, \ldots, f_m)}$
denote an orthonormal basis of  $\mathrm{Col}\,(L^{\prime})$
, and let
$\mathrm{Col}\,(L^{\prime})$
, and let  ${(f_{m+1},\ldots,f_d)}$
denote an orthonormal basis of
${(f_{m+1},\ldots,f_d)}$
denote an orthonormal basis of  $\ker L$
. Then for
$\ker L$
. Then for  $A\subset {\mathbb{R}}^m$
$A\subset {\mathbb{R}}^m$
 \begin{equation*}{\mathbb{P}}^{(t,x)}(X_T \in A \times {\mathbb{R}}^{d-m}) = \int_A \Bigg(\int_{{\mathbb{R}}^{d-m}} p\Bigg(t,x;\ T,\ \sum_{i=1}^d \xi_i f_i\Bigg) \,{\mathrm{d}} \xi_{m+1},\ldots ,{\mathrm{d}} \xi_d \Bigg) \,{\mathrm{d}} \xi_1,\ldots,{\mathrm{d}} \xi_m.\end{equation*}
\begin{equation*}{\mathbb{P}}^{(t,x)}(X_T \in A \times {\mathbb{R}}^{d-m}) = \int_A \Bigg(\int_{{\mathbb{R}}^{d-m}} p\Bigg(t,x;\ T,\ \sum_{i=1}^d \xi_i f_i\Bigg) \,{\mathrm{d}} \xi_{m+1},\ldots ,{\mathrm{d}} \xi_d \Bigg) \,{\mathrm{d}} \xi_1,\ldots,{\mathrm{d}} \xi_m.\end{equation*}
Suppose  $x=\sum_{i=1}^d \xi_i f_i$
is such that
$x=\sum_{i=1}^d \xi_i f_i$
is such that  $Lx=v$
. This is equivalent to
$Lx=v$
. This is equivalent to
 \begin{equation}\sum_{i=1}^m \xi_i L f_i = v,\end{equation}
\begin{equation}\sum_{i=1}^m \xi_i L f_i = v,\end{equation}
since  $f_{m+1},\ldots, f_d \in \ker L$
. Hence if
$f_{m+1},\ldots, f_d \in \ker L$
. Hence if  $\xi_1,\ldots, \xi_m$
are determined by (1.12) and if we define
$\xi_1,\ldots, \xi_m$
are determined by (1.12) and if we define
 $$\rho(t,x) = \int_{{\mathbb{R}}^{d-m}} p\Bigg(t,x;\ T, \sum_{i=1}^d \xi_i f_i\Bigg) \,{\mathrm{d}} \xi_{m+1},\ldots,{\mathrm{d}} \xi_d,$$
$$\rho(t,x) = \int_{{\mathbb{R}}^{d-m}} p\Bigg(t,x;\ T, \sum_{i=1}^d \xi_i f_i\Bigg) \,{\mathrm{d}} \xi_{m+1},\ldots,{\mathrm{d}} \xi_d,$$
then this is the density of  $X_T \mid X_t$
, concentrated on the subspace
$X_T \mid X_t$
, concentrated on the subspace  $LX_T=v$
.
$LX_T=v$
.
When  $\textrm{rank}\ L=d$
, we can assume without loss of generality that
$\textrm{rank}\ L=d$
, we can assume without loss of generality that  $L=I$
, which is the situation of fully observing
$L=I$
, which is the situation of fully observing  $X_T$
. Summarising, we define
$X_T$
. Summarising, we define
 \begin{equation*} \rho(t,x)= \begin{cases} p(t,x;\ T, v) & \text{if } m=d, \\[3pt] \int_{{\mathbb{R}}^{d-m}} p(t,x;\ T, \sum_{i=1}^d \xi_i f_i) \,{\mathrm{d}} \xi_{m+1},\ldots,{\mathrm{d}} \xi_d\, & \text{if } m<d,\end{cases}\end{equation*}
\begin{equation*} \rho(t,x)= \begin{cases} p(t,x;\ T, v) & \text{if } m=d, \\[3pt] \int_{{\mathbb{R}}^{d-m}} p(t,x;\ T, \sum_{i=1}^d \xi_i f_i) \,{\mathrm{d}} \xi_{m+1},\ldots,{\mathrm{d}} \xi_d\, & \text{if } m<d,\end{cases}\end{equation*}
and let  $r(t,x) =\nabla_x \rho(t,x)$
. The definition of guided proposals in the partially observed hypo-elliptic case is then just as in the uniformly elliptic case with a full observation: replace the intractable transition density p appearing in the definition of
$r(t,x) =\nabla_x \rho(t,x)$
. The definition of guided proposals in the partially observed hypo-elliptic case is then just as in the uniformly elliptic case with a full observation: replace the intractable transition density p appearing in the definition of  $\rho$
by
$\rho$
by  $\tilde{p}$
to yield
$\tilde{p}$
to yield  $\tilde\rho$
. Then define
$\tilde\rho$
. Then define
 $$\tilde{r}(t,x)=\nabla_x \log \tilde\rho(t,x)$$
$$\tilde{r}(t,x)=\nabla_x \log \tilde\rho(t,x)$$
and let the process  $X^\circ$
be defined by equation (1.5) with
$X^\circ$
be defined by equation (1.5) with  $b^\circ(t,x)=b(t,x) + a(t,x) \tilde{r}(t,x)$
. For
$b^\circ(t,x)=b(t,x) + a(t,x) \tilde{r}(t,x)$
. For  $t<T$
, it is conceivable that
$t<T$
, it is conceivable that  ${\mathbb{P}}^\star_t$
is absolutely continuous with respect to
${\mathbb{P}}^\star_t$
is absolutely continuous with respect to  ${\mathbb{P}}^\circ_t$
because clearly equation (1.9) is solved by
${\mathbb{P}}^\circ_t$
because clearly equation (1.9) is solved by  $ \eta(s,x) ={\sigma}(s,x) (r(s,x)-\tilde{r}(s,x)).$
Contrary to the hypo-elliptic setting in [Reference Delyon and Hu13], no specific form of the drift needs to be imposed here. However, it is not clear whether
$ \eta(s,x) ={\sigma}(s,x) (r(s,x)-\tilde{r}(s,x)).$
Contrary to the hypo-elliptic setting in [Reference Delyon and Hu13], no specific form of the drift needs to be imposed here. However, it is not clear whether
 $\|L X^\circ_t - v\|$
tends to zero as
$\|L X^\circ_t - v\|$
tends to zero as  $t\uparrow T$
,
$t\uparrow T$
, ${\mathbb{P}}^\star_T \ll {\mathbb{P}}^\circ_T$
.
${\mathbb{P}}^\star_T \ll {\mathbb{P}}^\circ_T$
.
The two main results of this paper (Proposition 2.2 and Theorem 2.6) provide conditions such that this is indeed the case. Interestingly, in the hypo-elliptic case the necessary ‘matching condition’ on the parameters of the auxiliary process  $\tilde{X}$
involves not only its diffusion coefficient
$\tilde{X}$
involves not only its diffusion coefficient  $\tilde{\sigma}(t)$
but also its drift
$\tilde{\sigma}(t)$
but also its drift  $\tilde{b}(t,x)$
. In particular, simply equating
$\tilde{b}(t,x)$
. In particular, simply equating  $\tilde{b}$
to zero makes the measures
$\tilde{b}$
to zero makes the measures  ${\mathbb{P}}^\star_T$
and
${\mathbb{P}}^\star_T$
and  ${\mathbb{P}}^\circ_T$
mutually singular. To derive the rate at which
${\mathbb{P}}^\circ_T$
mutually singular. To derive the rate at which  $\|L X^\circ_t - v\|$
decays we employ a completely different method of proof compared to the analogous result in [Reference Schauer, van der Meulen and van Zanten35], using techniques detailed in [Reference Mao26]. While the proof of the absolute continuity result is along the lines of that in [Reference Schauer, van der Meulen and van Zanten35], having a partial observation and hypo-ellipticity requires non-trivial adaptations of that proof.
$\|L X^\circ_t - v\|$
decays we employ a completely different method of proof compared to the analogous result in [Reference Schauer, van der Meulen and van Zanten35], using techniques detailed in [Reference Mao26]. While the proof of the absolute continuity result is along the lines of that in [Reference Schauer, van der Meulen and van Zanten35], having a partial observation and hypo-ellipticity requires non-trivial adaptations of that proof.
Put briefly, our results show that guided proposals can be defined for partially observed hypo-elliptic diffusions exactly as in [Reference Schauer, van der Meulen and van Zanten35], if an extra restriction on the drift  $\tilde{b}$
of the auxiliary process
$\tilde{b}$
of the auxiliary process  $\tilde{X}$
is taken into account.
$\tilde{X}$
is taken into account.
Whereas most of the results are derived for  ${\sigma}$
depending on the state x, the applicability of our methods is mostly confined to the case where
${\sigma}$
depending on the state x, the applicability of our methods is mostly confined to the case where  ${\sigma}$
is only allowed to depend on t. The difficulty lies in checking the fourth inequality of Assumption 2.4 appearing in Section 2. On the other hand, numerical experiments can give insight as to whether the law of a particular proposal process and the law of the conditional process are equivalent.
${\sigma}$
is only allowed to depend on t. The difficulty lies in checking the fourth inequality of Assumption 2.4 appearing in Section 2. On the other hand, numerical experiments can give insight as to whether the law of a particular proposal process and the law of the conditional process are equivalent.
Examples of hypo-elliptic diffusion processes that fall into our set-up include:
(1) integrated diffusions, when either the rough, smooth, or both components are observed,
(2) higher-order integrated diffusions,
(3) NLCAR models,
(4) the class of hypo-elliptic diffusions considered in [Reference Hairer, Stuart and Voss18].
These examples are listed here for the sake of illustration. We stress that the derived results are more general.
Whereas some examples that we discuss can be treated by the approach of [Reference Delyon and Hu13] (which is restricted to SDEs of the form (1.10)), our approach extends well beyond this class of models (see e.g. Example 3.8). Moreover, the hypo-elliptic bridges proposed in [Reference Delyon and Hu13] are bridges of a linear process, whereas the bridges we propose only use a linear process to derive the guiding term that is superimposed on the true drift. This means that only our approach is able to incorporate non-linearity in the drift of the proposal.
1.4. A toy problem
Here we first consider a two-dimensional uniformly elliptic diffusion with unit diffusion coefficient, which is fully observed. Upon taking  $\tilde{b}\equiv 0$
and
$\tilde{b}\equiv 0$
and  $\tilde{\sigma}={\sigma}$
, we have
$\tilde{\sigma}={\sigma}$
, we have
 $${\mathrm{d}} X^\circ_t = b(t,X^\circ_t) \,{\mathrm{d}} t + \frac{v-X^\circ_t}{T-t} \,{\mathrm{d}} t + \,{\mathrm{d}} W_t.$$
$${\mathrm{d}} X^\circ_t = b(t,X^\circ_t) \,{\mathrm{d}} t + \frac{v-X^\circ_t}{T-t} \,{\mathrm{d}} t + \,{\mathrm{d}} W_t.$$
The guiding term can be viewed as the distance left to be covered,  $v-X^\circ_t$
, divided by the remaining time
$v-X^\circ_t$
, divided by the remaining time  $T-t$
. This simple expression is to be contrasted with a hypo-elliptic diffusion, perhaps the simplest example being an integrated diffusion, with both components observed, i.e. a diffusion with
$T-t$
. This simple expression is to be contrasted with a hypo-elliptic diffusion, perhaps the simplest example being an integrated diffusion, with both components observed, i.e. a diffusion with
 $$b(t,x)=\begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad 0 \end{bmatrix} x \eqqcolon B x \quad \text{and} \quad {\sigma}=\begin{bmatrix} 0 \\[3pt] 1\end{bmatrix}.$$
$$b(t,x)=\begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad 0 \end{bmatrix} x \eqqcolon B x \quad \text{and} \quad {\sigma}=\begin{bmatrix} 0 \\[3pt] 1\end{bmatrix}.$$
It follows from the results in this paper that using guided proposals we obtain an ‘exact’ proposal, i.e.  $X_t^{\circ} = X_t^{\star}$
, upon taking
$X_t^{\circ} = X_t^{\star}$
, upon taking  $\tilde{B}=B$
,
$\tilde{B}=B$
,  $\tilde\beta\equiv 0$
and
$\tilde\beta\equiv 0$
and  $\tilde{\sigma}={\sigma}$
. The SDE for
$\tilde{\sigma}={\sigma}$
. The SDE for  $X^\circ$
takes the form
$X^\circ$
takes the form
 $${\mathrm{d}} X^\circ_t = \begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad 0 \end{bmatrix} X^\circ_t \,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] 18 {{({v_1-X^\circ_{t,1}})}/{{(T-t)^2}}} + {{({10v_2-28 X^\circ_{t,2}})}/{({T-t})}}\end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] 1 \end{bmatrix} \,{\mathrm{d}} W_t{,}$$
$${\mathrm{d}} X^\circ_t = \begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad 0 \end{bmatrix} X^\circ_t \,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] 18 {{({v_1-X^\circ_{t,1}})}/{{(T-t)^2}}} + {{({10v_2-28 X^\circ_{t,2}})}/{({T-t})}}\end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] 1 \end{bmatrix} \,{\mathrm{d}} W_t{,}$$
where  $X_{t,i}$
and
$X_{t,i}$
and  $v_i$
denote the ith component of
$v_i$
denote the ith component of  $X_t$
and v respectively. This is an elementary consequence of the process being Gaussian, and follows for example directly as a special case of either Lemma 2.1 or equation (1.10).
$X_t$
and v respectively. This is an elementary consequence of the process being Gaussian, and follows for example directly as a special case of either Lemma 2.1 or equation (1.10).
Even for this relatively simple case the guiding term’s behaviour is radically different compared with the uniformly elliptic case. The pulling term only acts on the rough coordinate and is no longer inversely proportional to the remaining time. This illustrates the inherent difficulty of the problem and explains the centering and scaling of  $X^\circ$
that we will introduce to study its behaviour.
$X^\circ$
that we will introduce to study its behaviour.
1.5. Outline
In Section 2 we present the main results of the paper. We illustrate the main theorems by applying them to various forms of partially conditioned hypo-elliptic diffusions in Section 3. In Section 4 we illustrate our work with simulation examples for the FitzHugh–Nagumo model and a twice-integrated diffusion model. The proof of the proposition on the behaviour of  $X^\circ$
near the endpoint is given in Section 5 and the proof of the theorem on absolute continuity is given in Section 6. We end with a discussion in Section 7. Some technical and additional results are gathered in the Appendix.
$X^\circ$
near the endpoint is given in Section 5 and the proof of the theorem on absolute continuity is given in Section 6. We end with a discussion in Section 7. Some technical and additional results are gathered in the Appendix.
1.6. Frequently used notation
1.6.1. Inequalities
We use the following notation to compare two sequences  $\{a_n\}$
and
$\{a_n\}$
and  $\{b_n\}$
of positive real numbers:
$\{b_n\}$
of positive real numbers:  $a_n\lesssim b_n$
(or
$a_n\lesssim b_n$
(or  $b_n\gtrsim a_n$
) means that there exists a constant
$b_n\gtrsim a_n$
) means that there exists a constant  $C>0$
that is independent of n and is such that
$C>0$
that is independent of n and is such that  $a_n\leq C b_n.$
As a combination of the two we write
$a_n\leq C b_n.$
As a combination of the two we write  $a_n\asymp b_n$
if both
$a_n\asymp b_n$
if both  $a_n\lesssim b_n$
and
$a_n\lesssim b_n$
and  $a_n\gtrsim b_n$
. We will also write
$a_n\gtrsim b_n$
. We will also write  $a_n \gg b_n$
to indicate that
$a_n \gg b_n$
to indicate that  $a_n/b_n\rightarrow\infty$
as
$a_n/b_n\rightarrow\infty$
as  $n\rightarrow\infty$
. By
$n\rightarrow\infty$
. By  $a \vee b$
and
$a \vee b$
and  $a \wedge b$
we denote the maximum and minimum of two numbers a and b respectively.
$a \wedge b$
we denote the maximum and minimum of two numbers a and b respectively.
1.6.2. Linear algebra
We denote the smallest and largest eigenvalue of a square matrix A by  ${\lambda_{\rm min}}(A)$
and
${\lambda_{\rm min}}(A)$
and  ${\lambda_{\rm max}}(A)$
respectively. The
${\lambda_{\rm max}}(A)$
respectively. The  $p\times p$
identity matrix is denoted by
$p\times p$
identity matrix is denoted by  $I_p$
. The
$I_p$
. The  $p\times q$
matrix with all entries equal to zero is denoted by
$p\times q$
matrix with all entries equal to zero is denoted by  $0_{p\times q}$
. For matrices we use the spectral norm, which equals the largest singular value of the matrix. The determinant of the matrix A is denoted by
$0_{p\times q}$
. For matrices we use the spectral norm, which equals the largest singular value of the matrix. The determinant of the matrix A is denoted by  $|A|$
and the trace by
$|A|$
and the trace by  $\mathrm{tr}(A)$
.
$\mathrm{tr}(A)$
.
1.6.3. Stochastic processes
For easy reference, Table 1 summarises the various processes around. The rightmost three columns give the drift, diffusion coefficient, and measure on  $C([0,t], {\mathbb{R}}^d)$
respectively. We write
$C([0,t], {\mathbb{R}}^d)$
respectively. We write
 $$ a(t,x) = {\sigma}(t,x){\sigma}(t,x)^{\prime} \quad \text{and}\quad \tilde{a}(t) = \tilde{\sigma}(t) \tilde{\sigma}(t)^{\prime}.$$
$$ a(t,x) = {\sigma}(t,x){\sigma}(t,x)^{\prime} \quad \text{and}\quad \tilde{a}(t) = \tilde{\sigma}(t) \tilde{\sigma}(t)^{\prime}.$$
The state-space of X,  $X^\star$
, and
$X^\star$
, and  $X^\circ$
is
$X^\circ$
is  ${\mathbb{R}}^d$
. The Wiener process lives on
${\mathbb{R}}^d$
. The Wiener process lives on  ${\mathbb{R}}^{d'}$
. The observation is determined by the
${\mathbb{R}}^{d'}$
. The observation is determined by the  $m\times d$
matrix L. Finally, the orthonormal basis
$m\times d$
matrix L. Finally, the orthonormal basis  $\{f_1,\ldots, f_d\}$
for
$\{f_1,\ldots, f_d\}$
for  ${\mathbb{R}}^d$
defined in Section 1.3.2 is fixed throughout, as are the numbers
${\mathbb{R}}^d$
defined in Section 1.3.2 is fixed throughout, as are the numbers  $\xi_1,\ldots, \xi_m$
defined via equation (1.12).
$\xi_1,\ldots, \xi_m$
defined via equation (1.12).
Table 1. Stochastic processes.

2. Main results
Throughout, we assume the following.
Assumption 2.1. Both b and  ${\sigma}$
are globally Lipschitz-continuous in both arguments.
${\sigma}$
are globally Lipschitz-continuous in both arguments.
This ensures that a strong solution to the SDE (1.1) exists. We define the conditioned process, denoted by  $X^{\star}$
, to be a diffusion process satisfying the SDE
$X^{\star}$
, to be a diffusion process satisfying the SDE
 \begin{equation}{\mathrm{d}} X^\star_t = b(t,X^\star_t) \,{\mathrm{d}} t + a(t,X^\star_t) r(t,X^\star_t) \,{\mathrm{d}} t + {\sigma}(t,X^\star_t) \,{\mathrm{d}} W_t, \quad X^\star_0=x_0.\end{equation}
\begin{equation}{\mathrm{d}} X^\star_t = b(t,X^\star_t) \,{\mathrm{d}} t + a(t,X^\star_t) r(t,X^\star_t) \,{\mathrm{d}} t + {\sigma}(t,X^\star_t) \,{\mathrm{d}} W_t, \quad X^\star_0=x_0.\end{equation}
Here  $r(t,x)=\nabla_x \log \rho(t,x)$
. A derivation is given in Appendix D.
$r(t,x)=\nabla_x \log \rho(t,x)$
. A derivation is given in Appendix D.
Assumption 2.2. The process X has transition densities such that the mapping  $ \rho \colon {\mathbb{R}}_+ \times {\mathbb{R}}^d \to {\mathbb{R}}$
is
$ \rho \colon {\mathbb{R}}_+ \times {\mathbb{R}}^d \to {\mathbb{R}}$
is  $C^{\infty,\infty}$
and strictly positive for all
$C^{\infty,\infty}$
and strictly positive for all  $s< T$
and
$s< T$
and  $x\in {\mathbb{R}}^d$
.
$x\in {\mathbb{R}}^d$
.
For fixed  $x\in {\mathbb{R}}^d$
, s, and
$x\in {\mathbb{R}}^d$
, s, and  $t>s+{\varepsilon}$
, the mapping
$t>s+{\varepsilon}$
, the mapping  ${(t,y) \to p(s,x;\ t,y)}$
is continuous and bounded.
${(t,y) \to p(s,x;\ t,y)}$
is continuous and bounded.
In general Assumption 2.2 is established by verifying Hörmander’s hypo-ellipticity conditions: see [Reference Williams43]. The assumption is satisfied in particular under suitable conditions for the diffusion as described by equations (1.2) and (1.3). Note that the results in this paper are not limited to this special case.
Proposition 2.1. Suppose that the matrix-valued function  $t,x \mapsto \underline{\sigma}$
in the hypo-elliptic model given by (1.2) and (1.3) has rank k’ for all (t, x). Furthermore, suppose that
$t,x \mapsto \underline{\sigma}$
in the hypo-elliptic model given by (1.2) and (1.3) has rank k’ for all (t, x). Furthermore, suppose that  $\underline \sigma$
and
$\underline \sigma$
and  $\underline \beta$
are infinitely often differentiable with respect to (t, x). Then the process
$\underline \beta$
are infinitely often differentiable with respect to (t, x). Then the process  ${(X_t)}$
admits a smooth (i.e.
${(X_t)}$
admits a smooth (i.e.  $C^{\infty}$
) density which is also smooth with respect to the initial condition.
$C^{\infty}$
) density which is also smooth with respect to the initial condition.
Proof.This is a special case of Proposition C.1 in Appendix C.
2.1. Existence of guided proposals
The guiding term of  $X^\circ$
involves
$X^\circ$
involves  $\tilde{r}\colon [0,\infty) \times {\mathbb{R}}^d \to {\mathbb{R}}$
. In the uniformly elliptic case it is easily verified that this mapping is well-defined. This need not be the case in the hypo-elliptic setting.
$\tilde{r}\colon [0,\infty) \times {\mathbb{R}}^d \to {\mathbb{R}}$
. In the uniformly elliptic case it is easily verified that this mapping is well-defined. This need not be the case in the hypo-elliptic setting.
Let  $\Phi(t)$
denote the fundamental matrix solution of the ODE
$\Phi(t)$
denote the fundamental matrix solution of the ODE  ${\mathrm{d}} \Phi(t) = \tilde{B}(t) \Phi(t) \,{\mathrm{d}} t$
,
${\mathrm{d}} \Phi(t) = \tilde{B}(t) \Phi(t) \,{\mathrm{d}} t$
,  $\Phi(0)=I$
and set
$\Phi(0)=I$
and set  $\Phi(t,s)=\Phi(t)\Phi(s)^{-1}$
. Define
$\Phi(t,s)=\Phi(t)\Phi(s)^{-1}$
. Define
 \begin{equation*} L(t) \coloneqq L \Phi(T,t).\end{equation*}
\begin{equation*} L(t) \coloneqq L \Phi(T,t).\end{equation*}
Assumption 2.3. The matrix
 $$ \int_t^T \Phi(T,s) \tilde{a}(s) \Phi(T,s)^{\prime} \,{\mathrm{d}} s $$
$$ \int_t^T \Phi(T,s) \tilde{a}(s) \Phi(T,s)^{\prime} \,{\mathrm{d}} s $$
is strictly positive definite for  $t<T$
.
$t<T$
.
In the uniformly elliptic setting, this assumption is always satisfied. Under this assumption, the matrix
 $$ {M^\dagger}(t) \coloneqq \int_t^T L(s) \tilde{a}(s) L(s)^{\prime} \,{\mathrm{d}} s$$
$$ {M^\dagger}(t) \coloneqq \int_t^T L(s) \tilde{a}(s) L(s)^{\prime} \,{\mathrm{d}} s$$
is also strictly positive definite for all  $t\in [0,T)$
and, in particular, invertible.
$t\in [0,T)$
and, in particular, invertible.
Lemma 2.1. If Assumption 2.3 holds, then
 \begin{equation}\tilde{r}(t,x)=L(t)^{\prime} M(t) ( v -\mu(t)-L(t)x), \quad t\in [0,T],\end{equation}
\begin{equation}\tilde{r}(t,x)=L(t)^{\prime} M(t) ( v -\mu(t)-L(t)x), \quad t\in [0,T],\end{equation}
where
 $$\mu(t)=\int_t^T L(s) \tilde\beta(s) \,{\mathrm{d}} s$$
$$\mu(t)=\int_t^T L(s) \tilde\beta(s) \,{\mathrm{d}} s$$
and
 \begin{equation*} M(t) = [{M^\dagger}(t)]^{-1}.\end{equation*}
\begin{equation*} M(t) = [{M^\dagger}(t)]^{-1}.\end{equation*}
Proof.The solution to the SDE for  $\tilde{X}_u$
is given by
$\tilde{X}_u$
is given by
 $$\tilde{X}_u = \Phi(u,t) x + \int_t^u \Phi(u,s) \tilde\beta(s) \,{\mathrm{d}} s + \int_t^u \Phi(u,s) \tilde{\sigma}(s) \,{\mathrm{d}} W_s, \quad u\ge t ,\quad \tilde{X}_t =x.$$
$$\tilde{X}_u = \Phi(u,t) x + \int_t^u \Phi(u,s) \tilde\beta(s) \,{\mathrm{d}} s + \int_t^u \Phi(u,s) \tilde{\sigma}(s) \,{\mathrm{d}} W_s, \quad u\ge t ,\quad \tilde{X}_t =x.$$
See [23, Theorem 4.10]. The result now follows directly upon taking  $u=T$
, multiplying both sides by L, and using the definition of L(t). □
$u=T$
, multiplying both sides by L, and using the definition of L(t). □
In Appendix A easily verifiable conditions for the existence of  $\tilde{p}$
are given for the case
$\tilde{p}$
are given for the case  $L=I$
.
$L=I$
.
Since  $t\mapsto \mu(t)$
and
$t\mapsto \mu(t)$
and  $t\mapsto M(t)$
are continuous and
$t\mapsto M(t)$
are continuous and  $x\mapsto \tilde{r}(t,x)$
is linear in x for fixed t, the process
$x\mapsto \tilde{r}(t,x)$
is linear in x for fixed t, the process  $X^\circ$
is well-defined on intervals bounded away from T.
$X^\circ$
is well-defined on intervals bounded away from T.
Lemma 2.2. Under Assumptions 2.1 and 2.3 we have that for any  $t<T$
, the SDE for
$t<T$
, the SDE for  $X^\circ$
has a unique strong solution on [0, t].
$X^\circ$
has a unique strong solution on [0, t].
Throughout, without explicitly stating it in lemmas and theorems, we will assume that Assumptions 2.1, 2.2, and 2.3hold true.
2.2. Behaviour of guided proposals near the endpoint
Let  $\Delta(t)$
be an invertible
$\Delta(t)$
be an invertible  $m\times m$
diagonal matrix-valued measurable function on [0,T). Define
$m\times m$
diagonal matrix-valued measurable function on [0,T). Define
 \begin{equation}{Z_{\Delta,t}}=\Delta(t) ( v- \mu(t)-L(t) X^\circ_t )\end{equation}
\begin{equation}{Z_{\Delta,t}}=\Delta(t) ( v- \mu(t)-L(t) X^\circ_t )\end{equation}
and
 \begin{equation}{L_{\Delta}}(t)=\Delta(t) L(t) {,} \quad {M_{\Delta}}(t)=\Delta(t)^{-1} M(t) \Delta(t)^{-1}.\end{equation}
\begin{equation}{L_{\Delta}}(t)=\Delta(t) L(t) {,} \quad {M_{\Delta}}(t)=\Delta(t)^{-1} M(t) \Delta(t)^{-1}.\end{equation}
Note that for  $t\approx T$
we have
$t\approx T$
we have  $\Phi(T,t)\approx I$
and hence
$\Phi(T,t)\approx I$
and hence  ${Z_{\Delta,t}} \approx \Delta(t)(v-L X^\circ_t)$
. The matrix
${Z_{\Delta,t}} \approx \Delta(t)(v-L X^\circ_t)$
. The matrix  $\Delta(t)$
is a scaling matrix which in the hypo-elliptic case incorporates the difference in rate of convergence for smooth and rough components of
$\Delta(t)$
is a scaling matrix which in the hypo-elliptic case incorporates the difference in rate of convergence for smooth and rough components of  $L X^\circ_t$
to v, when
$L X^\circ_t$
to v, when  $t\uparrow T$
. In the uniformly elliptic case, we can always take
$t\uparrow T$
. In the uniformly elliptic case, we can always take  $\Delta(t)=I_{m}$
.
$\Delta(t)=I_{m}$
.
The following assumption is of key importance.
Assumption 2.4. There exists an invertible  $m\times m$
diagonal matrix-valued function
$m\times m$
diagonal matrix-valued function  $\Delta(t)$
, which is measurable on [0,T), a
$\Delta(t)$
, which is measurable on [0,T), a  $t_0<T$
,
$t_0<T$
,  $\alpha \in (0,1]$
and positive constants
$\alpha \in (0,1]$
and positive constants  $\underline{c}$
,
$\underline{c}$
,  $\overline{c}$
,
$\overline{c}$
,  $c_1$
,
$c_1$
,  $c_2$
, and
$c_2$
, and  $c_3$
such that, for all
$c_3$
such that, for all  $t \in [t_0,T)$
,
$t \in [t_0,T)$
,
 \begin{align}\underline{c}\, (T-t)^{-1}\le {\lambda_{\rm min}}({M_{\Delta}}(t)) &\le {\lambda_{\rm max}}({M_{\Delta}}(t)) \le \overline{c}\, (T-t)^{-1}, \notag\\[3pt]\| {L_{\Delta}}(t) (\tilde{b}(t,x) - b(t,x)) \| &\le c_1 {,} \notag \\[3pt] \mathrm{tr}({L_{\Delta}}(t)\, a(t,x)\, {L_{\Delta}}(t)^{\prime} )&\le c_2 {,} \notag\\[3pt] \|{L_{\Delta}}(t) (\tilde{a}(t)-a(t,x)) {L_{\Delta}}(t)^{\prime}\| &\le c_3 (T-t)^\alpha.\end{align}
\begin{align}\underline{c}\, (T-t)^{-1}\le {\lambda_{\rm min}}({M_{\Delta}}(t)) &\le {\lambda_{\rm max}}({M_{\Delta}}(t)) \le \overline{c}\, (T-t)^{-1}, \notag\\[3pt]\| {L_{\Delta}}(t) (\tilde{b}(t,x) - b(t,x)) \| &\le c_1 {,} \notag \\[3pt] \mathrm{tr}({L_{\Delta}}(t)\, a(t,x)\, {L_{\Delta}}(t)^{\prime} )&\le c_2 {,} \notag\\[3pt] \|{L_{\Delta}}(t) (\tilde{a}(t)-a(t,x)) {L_{\Delta}}(t)^{\prime}\| &\le c_3 (T-t)^\alpha.\end{align}
Proposition 2.2. Under Assumption 2.4, there exists a positive number C such that
 $$\limsup_{t\uparrow T} \frac{\|{Z_{\Delta,t}}\|}{\sqrt{(T-t) \log(1/(T-t))}} \le C \quad \text{a.s.}$$
$$\limsup_{t\uparrow T} \frac{\|{Z_{\Delta,t}}\|}{\sqrt{(T-t) \log(1/(T-t))}} \le C \quad \text{a.s.}$$
Remark 2.1. If  ${\sigma}$
is state-dependent, it is particularly difficult to ensure that the fourth inequality in (2.5) is satisfied. There is at least one non-trivial example where this inequality can be assured (see Example 2.1). In Section 7 we further discuss the case of state-dependent diffusivity. In the simpler case where
${\sigma}$
is state-dependent, it is particularly difficult to ensure that the fourth inequality in (2.5) is satisfied. There is at least one non-trivial example where this inequality can be assured (see Example 2.1). In Section 7 we further discuss the case of state-dependent diffusivity. In the simpler case where  ${\sigma}$
only depends on t, we can always take
${\sigma}$
only depends on t, we can always take  $\tilde{\sigma}(t)={\sigma}(t)$
and then the fourth inequality is trivially satisfied. In Section 3 we verify (2.5) for a wide range of examples. As a prelude: for the SDE system specified by (1.2) and (1.3) one takes
$\tilde{\sigma}(t)={\sigma}(t)$
and then the fourth inequality is trivially satisfied. In Section 3 we verify (2.5) for a wide range of examples. As a prelude: for the SDE system specified by (1.2) and (1.3) one takes  $\tilde{B}=B$
and
$\tilde{B}=B$
and  $\tilde{\sigma}={\sigma}$
. Then
$\tilde{\sigma}={\sigma}$
. Then  $\Delta(t)$
can be chosen such that the first inequality is satisfied. The second condition of (2.5) encapsulates a matching condition on the drift which induces some restrictions on
$\Delta(t)$
can be chosen such that the first inequality is satisfied. The second condition of (2.5) encapsulates a matching condition on the drift which induces some restrictions on  $\tilde\beta$
and
$\tilde\beta$
and  $\underline\beta$
. The third inequality is then usually satisfied automatically.
$\underline\beta$
. The third inequality is then usually satisfied automatically.
The uniformly elliptic case is particularly simple.
Corollary 2.1. (Uniformly elliptic case.) Assume that either (i) the diffusivity  ${\sigma}$
is constant and
${\sigma}$
is constant and  $\tilde{\sigma}={\sigma}$
or (ii)
$\tilde{\sigma}={\sigma}$
or (ii)  ${\sigma}$
depends on t and
${\sigma}$
depends on t and  $\tilde{\sigma}(t)={\sigma}(t)$
. Assume a is strictly positive definite and that
$\tilde{\sigma}(t)={\sigma}(t)$
. Assume a is strictly positive definite and that  $b(t,x)-\tilde{b}(t,x)$
is bounded on
$b(t,x)-\tilde{b}(t,x)$
is bounded on  $[0,T]\times {\mathbb{R}}^d$
. Then the conclusion of Proposition 2.2 holds true with
$[0,T]\times {\mathbb{R}}^d$
. Then the conclusion of Proposition 2.2 holds true with  $\Delta(t)=I_m$
.
$\Delta(t)=I_m$
.
Remark 2.2. The behaviour of  $\|{Z_{\Delta,t}}\|$
that we obtain agrees with the results of [Reference Schauer, van der Meulen and van Zanten35]. That paper is confined to
$\|{Z_{\Delta,t}}\|$
that we obtain agrees with the results of [Reference Schauer, van der Meulen and van Zanten35]. That paper is confined to  $L=I$
and the uniformly elliptic case, but includes the case of state-dependent diffusion coefficient. Under this assumption, it suffices that
$L=I$
and the uniformly elliptic case, but includes the case of state-dependent diffusion coefficient. Under this assumption, it suffices that  $\tilde\sigma(T)^{\prime} \tilde\sigma(T) = a(T,v)$
, a condition that can always be satisfied.
$\tilde\sigma(T)^{\prime} \tilde\sigma(T) = a(T,v)$
, a condition that can always be satisfied.
The proofs of Theorem 2.2 and Corollary 2.1 are given in Section 5.
In Section 3 we give a set of tractable hypo-elliptic models for which the conclusion of Theorem 2.2 is valid. The appropriate choice of the scaling matrix  $\Delta(t)$
is really problem-specific. Moreover, the assumptions on the auxiliary process depend on the choice of L.
$\Delta(t)$
is really problem-specific. Moreover, the assumptions on the auxiliary process depend on the choice of L.
In most cases it will not be possible to satisfy the fourth inequality of Assumption 2.4 when the diffusion coefficient is state-dependent. The following example shows an exception.
Example 2.1. Suppose the diffusion is uniformly elliptic and  $L=[ \underline{L}\ \ 0_{m\times k'}]$
, where
$L=[ \underline{L}\ \ 0_{m\times k'}]$
, where  $L \in {\mathbb{R}}^{m\times k}$
and
$L \in {\mathbb{R}}^{m\times k}$
and  $d=k+k'$
. Now suppose a(t, x) is of block form
$d=k+k'$
. Now suppose a(t, x) is of block form
 $$a(t,x) =\begin{bmatrix} a_{11}(t) & 0_{k\times k'} \\ 0_{k'\times k} & \quad a_{22}(t,x) \end{bmatrix}{,}$$
$$a(t,x) =\begin{bmatrix} a_{11}(t) & 0_{k\times k'} \\ 0_{k'\times k} & \quad a_{22}(t,x) \end{bmatrix}{,}$$
and that we take  $\tilde{a}$
to be of the same block form. Upon taking
$\tilde{a}$
to be of the same block form. Upon taking  $\tilde{B} =0_{d\times d}$
and
$\tilde{B} =0_{d\times d}$
and  $\Delta(t)=I_d$
, we see that
$\Delta(t)=I_d$
, we see that  ${L_{\Delta}}(t)=L$
and hence
${L_{\Delta}}(t)=L$
and hence
 $${L_{\Delta}}(t) (\tilde{a}(t)-a(t,x)) {L_{\Delta}}(t)^{\prime} = \underline{L} (\tilde{a}_{11}(t)-a_{11}(t)) \underline{L}^{\prime}.$$
$${L_{\Delta}}(t) (\tilde{a}(t)-a(t,x)) {L_{\Delta}}(t)^{\prime} = \underline{L} (\tilde{a}_{11}(t)-a_{11}(t)) \underline{L}^{\prime}.$$
Therefore, if we choose  $\tilde{a}_{11}(t)$
to be equal to
$\tilde{a}_{11}(t)$
to be equal to  $a_{11}(t)$
the fourth inequality in Assumption 2.4 is trivially satisfied.
$a_{11}(t)$
the fourth inequality in Assumption 2.4 is trivially satisfied.
Empirically, however, it appears that Assumption 2.4 is stronger than needed for valid guided proposals; see Example 4.4.
2.3. Absolute continuity
The following theorem gives sufficient conditions for absolute continuity of  ${\mathbb{P}}_T^\star$
with respect to
${\mathbb{P}}_T^\star$
with respect to  ${\mathbb{P}}_T^\circ$
. First we introduce an assumption.
${\mathbb{P}}_T^\circ$
. First we introduce an assumption.
Assumption 2.5. There exists a constant C such that
 \begin{equation*} p(s,x;\ t,y) \le C \tilde{p}(s,x;\ t,y){,} \quad 0\le s<t<T\end{equation*}
\begin{equation*} p(s,x;\ t,y) \le C \tilde{p}(s,x;\ t,y){,} \quad 0\le s<t<T\end{equation*}
for all  $x, y \in {\mathbb{R}}^d$
.
$x, y \in {\mathbb{R}}^d$
.
Theorem 2.6. Assume there exists a positive  $\delta$
such that
$\delta$
such that  $|\Delta(t)| \lesssim (T-t)^{-\delta}$
. If Assumptions 2.4 and 2.5 hold true, then
$|\Delta(t)| \lesssim (T-t)^{-\delta}$
. If Assumptions 2.4 and 2.5 hold true, then
 $$\frac{{\mathrm{d}} {\mathbb{P}}_T^\star}{{\mathrm{d}} {\mathbb{P}}_T^\circ}(X^\circ) = \frac{\tilde \rho(0,x_0)}{ \rho(0,x_0)}\Psi_T(X^\circ),$$
$$\frac{{\mathrm{d}} {\mathbb{P}}_T^\star}{{\mathrm{d}} {\mathbb{P}}_T^\circ}(X^\circ) = \frac{\tilde \rho(0,x_0)}{ \rho(0,x_0)}\Psi_T(X^\circ),$$
where
 \begin{equation}\Psi_t(X^\circ)=\exp\bigg(\int_0^t \mathcal{G}(s,X^\circ_s) \,{\mathrm{d}} s\bigg),\end{equation}
\begin{equation}\Psi_t(X^\circ)=\exp\bigg(\int_0^t \mathcal{G}(s,X^\circ_s) \,{\mathrm{d}} s\bigg),\end{equation}
 \begin{equation*} \mathcal{G}(s,x) = (b(s,x) - \tilde b(s,x))^{\prime} \tilde r(s,x) - \frac12 \mathrm{tr}([a(s,x) - \tilde a(s)] [\tilde H(s)-\tilde{r}(s,x)\tilde{r}(s,x)^{\prime}]){,}\end{equation*}
\begin{equation*} \mathcal{G}(s,x) = (b(s,x) - \tilde b(s,x))^{\prime} \tilde r(s,x) - \frac12 \mathrm{tr}([a(s,x) - \tilde a(s)] [\tilde H(s)-\tilde{r}(s,x)\tilde{r}(s,x)^{\prime}]){,}\end{equation*}
and  $\tilde{H}(s)=L(s)^{\prime} M(s) L(s)$
.
$\tilde{H}(s)=L(s)^{\prime} M(s) L(s)$
.
The proof is given in Section 6.
Remark 2.3. The expression for the Radon–Nikodým derivative depends on the intractable transition densities p via the term  $\rho(0,x_0)$
. This is a multiplicative term that only shows up in the denominator and therefore cancels in the acceptance probability for sampling diffusion bridges using the Metropolis–Hastings algorithm.
$\rho(0,x_0)$
. This is a multiplicative term that only shows up in the denominator and therefore cancels in the acceptance probability for sampling diffusion bridges using the Metropolis–Hastings algorithm.
The following lemma is useful for verifying Assumption 2.5. Its proof is located in Section 6.
Lemma 2.3. Assume  $\eta(s,x)$
satisfies the equation
$\eta(s,x)$
satisfies the equation
 $${\sigma}(s,x) \eta(s,x) = b(s,x)-\tilde{b}(s,x)$$
$${\sigma}(s,x) \eta(s,x) = b(s,x)-\tilde{b}(s,x)$$
and that  $\eta$
is bounded. Then there exists a constant C such that
$\eta$
is bounded. Then there exists a constant C such that
 $$p(s,x;\ t,y) \le C \tilde{p}(s,x;\ t,y)$$
$$p(s,x;\ t,y) \le C \tilde{p}(s,x;\ t,y)$$
for all  $x, y \in {\mathbb{R}}^d$
and
$x, y \in {\mathbb{R}}^d$
and  $0\le s<t\le T $
.
$0\le s<t\le T $
.
3. Tractable hypo-elliptic models
In this section we give several examples of hypo-elliptic models that satisfy Assumption 2.4. In the following we write  $X_t=[ X_{t,1} \ \ \cdots\ \ X_{t,d}]^{\prime}$
.
$X_t=[ X_{t,1} \ \ \cdots\ \ X_{t,d}]^{\prime}$
.
In each of the examples we choose an appropriate scaling matrix  $\Delta(t)$
and verify the conditions of Assumption 2.4. For this, we need to evaluate
$\Delta(t)$
and verify the conditions of Assumption 2.4. For this, we need to evaluate  ${L_{\Delta}}(t)$
and
${L_{\Delta}}(t)$
and  ${M_{\Delta}}(t)$
. The computations are somewhat tedious by hand (though straightforward), and for that reason we used the computer algebra system Maple® for this. Ideally, instead of the conditions appearing in Assumption 2.4, one would like to have conditions only containing b,
${M_{\Delta}}(t)$
. The computations are somewhat tedious by hand (though straightforward), and for that reason we used the computer algebra system Maple® for this. Ideally, instead of the conditions appearing in Assumption 2.4, one would like to have conditions only containing b,  $\tilde b$
,
$\tilde b$
,  ${\sigma}$
, and
${\sigma}$
, and  $\tilde {\sigma}$
. This, however, seems hard to obtain and maybe a bit too much to ask for, given the wide diversity in behaviour of hypo-elliptic diffusions and the generality of the matrix L. In each of the examples, we state the model and the conditions on
$\tilde {\sigma}$
. This, however, seems hard to obtain and maybe a bit too much to ask for, given the wide diversity in behaviour of hypo-elliptic diffusions and the generality of the matrix L. In each of the examples, we state the model and the conditions on  $\tilde{b}$
and
$\tilde{b}$
and  $\tilde{\sigma}$
such that Assumption 2.4 is satisfied.
$\tilde{\sigma}$
such that Assumption 2.4 is satisfied.
Example 3.1. (Integrated diffusion, fully observed.) Suppose
 \begin{equation*} \begin{split}{\mathrm{d}} X_{t,1} & = X_{t,2} \,{\mathrm{d}} t {,} \\[3pt] {\mathrm{d}} X_{t,2} & = \underline\beta(t,X_t) \,{\mathrm{d}} t + {\gamma} \,{\mathrm{d}} W_t, \end{split}\end{equation*}
\begin{equation*} \begin{split}{\mathrm{d}} X_{t,1} & = X_{t,2} \,{\mathrm{d}} t {,} \\[3pt] {\mathrm{d}} X_{t,2} & = \underline\beta(t,X_t) \,{\mathrm{d}} t + {\gamma} \,{\mathrm{d}} W_t, \end{split}\end{equation*}
where  $\underline\beta\colon [0,T] \times {\mathbb{R}}^2 \to {\mathbb{R}}$
is bounded and globally Lipschitz in both arguments. If
$\underline\beta\colon [0,T] \times {\mathbb{R}}^2 \to {\mathbb{R}}$
is bounded and globally Lipschitz in both arguments. If  $L=I_2$
, and the coefficients of the auxiliary process
$L=I_2$
, and the coefficients of the auxiliary process  $\tilde{X}$
satisfy
$\tilde{X}$
satisfy
 $$\tilde{B}(t) = \begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad 0 \end{bmatrix}, \quad \tilde\beta_1(t) = 0, \quad \tilde\sigma =\begin{bmatrix} 0 \\[3pt] \gamma\end{bmatrix} {,}$$
$$\tilde{B}(t) = \begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad 0 \end{bmatrix}, \quad \tilde\beta_1(t) = 0, \quad \tilde\sigma =\begin{bmatrix} 0 \\[3pt] \gamma\end{bmatrix} {,}$$
then Assumption 2.4 is satisfied.
Proof.As we expect the rate of the first component, which is smooth, to converge to the endpoint one order faster than the second component, which is rough, we take
 $$\Delta(t)=\begin{bmatrix} (T-t)^{-1} &\quad 0 \\[3pt] 0 &\quad 1 \end{bmatrix}.$$
$$\Delta(t)=\begin{bmatrix} (T-t)^{-1} &\quad 0 \\[3pt] 0 &\quad 1 \end{bmatrix}.$$
We have
 $$b(t,x)-\tilde{b}(t,x) = \begin{bmatrix} 0 \\[3pt] \underline\beta(t,x)\end{bmatrix}.$$
$$b(t,x)-\tilde{b}(t,x) = \begin{bmatrix} 0 \\[3pt] \underline\beta(t,x)\end{bmatrix}.$$
By choice of  $\tilde{B}$
and
$\tilde{B}$
and  $\Delta$
we get
$\Delta$
we get
 $${L_{\Delta}}(t)=\Delta(t) L \Phi(T,t) =\Delta(t) \Phi(T,t)= \begin{bmatrix} 1/(T-t) &\quad 1 \\[3pt] 0 &\quad 1 \end{bmatrix}$$
$${L_{\Delta}}(t)=\Delta(t) L \Phi(T,t) =\Delta(t) \Phi(T,t)= \begin{bmatrix} 1/(T-t) &\quad 1 \\[3pt] 0 &\quad 1 \end{bmatrix}$$
and
 $$M(t) = \frac1{{\gamma}^2} \begin{bmatrix} 12/(T-t)^3 &\quad 6/(T-t)^2 \\[3pt] 6/(T-t)^2 &\quad 4/(T-t) \end{bmatrix} \quad \Longrightarrow\quad {M_{\Delta}}(t) = \frac1{{\gamma}^2} (T-t)^{-1} \begin{bmatrix} 12 &\quad 6 \\[3pt] 6 &\quad 4\end{bmatrix}.$$
$$M(t) = \frac1{{\gamma}^2} \begin{bmatrix} 12/(T-t)^3 &\quad 6/(T-t)^2 \\[3pt] 6/(T-t)^2 &\quad 4/(T-t) \end{bmatrix} \quad \Longrightarrow\quad {M_{\Delta}}(t) = \frac1{{\gamma}^2} (T-t)^{-1} \begin{bmatrix} 12 &\quad 6 \\[3pt] 6 &\quad 4\end{bmatrix}.$$
Now it is trivial to verify that Assumption 2.4 is satisfied.
Example 3.2. (Integrated diffusion, smooth component observed.) Consider the same setting as in the previous example, but now with  $L=[ 1 \ \ 0]$
. That is, only the smooth (integrated) component is observed. Then Assumption 2.4 is satisfied.
$L=[ 1 \ \ 0]$
. That is, only the smooth (integrated) component is observed. Then Assumption 2.4 is satisfied.
Proof.Upon taking  $\Delta(t)=(T-t)^{-1}$
, we get
$\Delta(t)=(T-t)^{-1}$
, we get
 \begin{equation}{M_{\Delta}}(t)=3{\gamma}^{-2}(T-t)^{-1} \quad \text{and} \quad {L_{\Delta}}(t)=[ 1/(T-t) \ \ 1 ] {,}\end{equation}
\begin{equation}{M_{\Delta}}(t)=3{\gamma}^{-2}(T-t)^{-1} \quad \text{and} \quad {L_{\Delta}}(t)=[ 1/(T-t) \ \ 1 ] {,}\end{equation}
from which the claim easily follows.
Example 3.3. (Integrated diffusion, rough component observed.) Consider the same setting as in Example 3.1, but now with  $L=[ 0\ \ 1]$
. That is, only the rough component is observed. Then Assumption 2.4 is satisfied.
$L=[ 0\ \ 1]$
. That is, only the rough component is observed. Then Assumption 2.4 is satisfied.
Proof.Taking  $\Delta(t)=1$
we get
$\Delta(t)=1$
we get  $ {M_{\Delta}}(t)={\gamma}^{-2}(T-t)^{-1}$
and
$ {M_{\Delta}}(t)={\gamma}^{-2}(T-t)^{-1}$
and  ${L_{\Delta}}(t)=[ 0\ \ 1 ]$
, from which the claim easily follows.
${L_{\Delta}}(t)=[ 0\ \ 1 ]$
, from which the claim easily follows.
The guiding term is completely independent of the first component. This is not surprising, as this example is equivalent to fully observing a one-dimensional uniformly elliptic diffusion (described by the second component).
Example 3.4. (NLCAR(p)-model.) The integrated diffusion model is a special case of the class of continuous-time non-linear autoregressive models (see [Reference Stramer and Roberts37]). The real-valued process Y is called a pth-order NLCAR model if it solves the pth-order SDE
 $${\mathrm{d}} Y^{(p-1)}_t = \underline\beta(t,Y_t) \,{\mathrm{d}} t + {\gamma} \,{\mathrm{d}} W_t.$$
$${\mathrm{d}} Y^{(p-1)}_t = \underline\beta(t,Y_t) \,{\mathrm{d}} t + {\gamma} \,{\mathrm{d}} W_t.$$
We assume  $\underline\beta\colon [0,T] \times {\mathbb{R}}^2 \to {\mathbb{R}}$
is bounded and globally Lipschitz in both arguments. This example corresponds to the model specified by (1.2)–(1.3) with
$\underline\beta\colon [0,T] \times {\mathbb{R}}^2 \to {\mathbb{R}}$
is bounded and globally Lipschitz in both arguments. This example corresponds to the model specified by (1.2)–(1.3) with  $d=p$
,
$d=p$
,  $d'=1$
, and
$d'=1$
, and  $k=p-1$
. Integrated diffusions correspond to
$k=p-1$
. Integrated diffusions correspond to  $p=2$
. Observing only the smoothest component means that we have
$p=2$
. Observing only the smoothest component means that we have  $L=[ 1\ \ 0_{1\times d-1} ]$
. This class of models includes in particular continuous-time autoregressive and continuous-time threshold autoregressive models, as defined in [Reference Brockwell8].
$L=[ 1\ \ 0_{1\times d-1} ]$
. This class of models includes in particular continuous-time autoregressive and continuous-time threshold autoregressive models, as defined in [Reference Brockwell8].
We consider the NCLAR(3)-model more specifically, which can be written explicitly as a diffusion in  ${\mathbb{R}}^3$
with
${\mathbb{R}}^3$
with
 \begin{equation*} b(t,x) = \begin{bmatrix} 0 &\quad 1 &\quad 0 \\[3pt] 0 &\quad 0 &\quad 1 \\[3pt] 0 &\quad 0 &\quad 0 \end{bmatrix} x + \begin{bmatrix} 0 \\[3pt] 0 \\[3pt] \underline{\beta}(t,x)\end{bmatrix}{,} \quad {\sigma}=\begin{bmatrix} 0 \\[3pt] 0 \\[3pt] {\gamma}\end{bmatrix}.\end{equation*}
\begin{equation*} b(t,x) = \begin{bmatrix} 0 &\quad 1 &\quad 0 \\[3pt] 0 &\quad 0 &\quad 1 \\[3pt] 0 &\quad 0 &\quad 0 \end{bmatrix} x + \begin{bmatrix} 0 \\[3pt] 0 \\[3pt] \underline{\beta}(t,x)\end{bmatrix}{,} \quad {\sigma}=\begin{bmatrix} 0 \\[3pt] 0 \\[3pt] {\gamma}\end{bmatrix}.\end{equation*}
If either  $L=I_3$
or
$L=I_3$
or  $L=[ 1\ \ 0\ \ 0]$
, Assumption 2.4 is satisfied if the coefficients of the auxiliary process
$L=[ 1\ \ 0\ \ 0]$
, Assumption 2.4 is satisfied if the coefficients of the auxiliary process  $\tilde{X}$
satisfy
$\tilde{X}$
satisfy
 \begin{equation}\tilde{B}(t) = \begin{bmatrix} 0 &\quad 1&\quad 0 \\[3pt] 0 &\quad 0&\quad 1 \\[3pt] 0 &\quad 0 &\quad 0 \end{bmatrix}, \quad \tilde\beta_1(t)=\tilde\beta_2(t) = 0, \quad \tilde\sigma =\begin{bmatrix} 0 \\[3pt] 0\\[3pt] \gamma\end{bmatrix}.\end{equation}
\begin{equation}\tilde{B}(t) = \begin{bmatrix} 0 &\quad 1&\quad 0 \\[3pt] 0 &\quad 0&\quad 1 \\[3pt] 0 &\quad 0 &\quad 0 \end{bmatrix}, \quad \tilde\beta_1(t)=\tilde\beta_2(t) = 0, \quad \tilde\sigma =\begin{bmatrix} 0 \\[3pt] 0\\[3pt] \gamma\end{bmatrix}.\end{equation}
Proof.If  $L=I_3$
, we take the scaling matrix
$L=I_3$
, we take the scaling matrix
 $$\Delta(t)=\begin{bmatrix} (T-t)^{-2} &\quad 0&\quad 0 \\[3pt] 0 &\quad (T-t)^{-1}&\quad 0\\[3pt] 0 &\quad 0 &\quad 1 \end{bmatrix}$$
$$\Delta(t)=\begin{bmatrix} (T-t)^{-2} &\quad 0&\quad 0 \\[3pt] 0 &\quad (T-t)^{-1}&\quad 0\\[3pt] 0 &\quad 0 &\quad 1 \end{bmatrix}$$
to account for the different degrees of smoothness of the paths of the diffusion. Then, defining  $w(t)=(T-t)^{-1}$
, we obtain
$w(t)=(T-t)^{-1}$
, we obtain
 $${M_{\Delta}}(t)= \frac{3w(t)}{{\gamma}^2}\begin{bmatrix} 240 &\quad -120 &\quad 20 \\[3pt] -120 &\quad 64 &\quad -12 \\[3pt] 20 &\quad -12 &\quad 3\end{bmatrix}\quad \text{and} \quad {L_{\Delta}}(t)=\begin{bmatrix} w(t)^2 &\quad w(t) &\quad 1/2 \\[3pt] 0 &\quad w(t) &\quad 1 \\[3pt] 0 &\quad 0 &\quad 1\end{bmatrix}\!,$$
$${M_{\Delta}}(t)= \frac{3w(t)}{{\gamma}^2}\begin{bmatrix} 240 &\quad -120 &\quad 20 \\[3pt] -120 &\quad 64 &\quad -12 \\[3pt] 20 &\quad -12 &\quad 3\end{bmatrix}\quad \text{and} \quad {L_{\Delta}}(t)=\begin{bmatrix} w(t)^2 &\quad w(t) &\quad 1/2 \\[3pt] 0 &\quad w(t) &\quad 1 \\[3pt] 0 &\quad 0 &\quad 1\end{bmatrix}\!,$$
from which the claim is easily verified.
For  $L=[ 1\ \ 0 \ \ 0]$
we take
$L=[ 1\ \ 0 \ \ 0]$
we take  $\Delta(t)=(T-t)^{-2}$
, and since
$\Delta(t)=(T-t)^{-2}$
, and since
 $${M_{\Delta}}(t) = \frac{20}{{\gamma}^2} (T-t)^{-1} \quad \text{and}\quad {L_{\Delta}}(t)=[ (T-t)^{-2}\ \ (T-t)^{-1} \ \ 1/2]{,}$$
$${M_{\Delta}}(t) = \frac{20}{{\gamma}^2} (T-t)^{-1} \quad \text{and}\quad {L_{\Delta}}(t)=[ (T-t)^{-2}\ \ (T-t)^{-1} \ \ 1/2]{,}$$
Assumption 2.4 is satisfied. See Example 4.1 for a numerical illustration of this example.
Example 3.5. Assume the following model for FM-demodulation:
 $${\mathrm{d}} \begin{bmatrix} X_{t,1} \\[3pt] X_{t,2}\\[3pt] X_{t,2}\end{bmatrix} =\begin{bmatrix} X_{t,2} \\[3pt] -\alpha X_{t,2} \\[3pt] \sqrt{2{\gamma}} \sin(\omega t + X_{t,1}) \end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 &\quad 0 \\[3pt] \sqrt{2{\gamma} \alpha} &\quad 0 \\[3pt] 0 &\quad \psi \end{bmatrix} \,{\mathrm{d}} \begin{bmatrix} W_{t,1} \\[3pt] W_{t,2} \end{bmatrix}.$$
$${\mathrm{d}} \begin{bmatrix} X_{t,1} \\[3pt] X_{t,2}\\[3pt] X_{t,2}\end{bmatrix} =\begin{bmatrix} X_{t,2} \\[3pt] -\alpha X_{t,2} \\[3pt] \sqrt{2{\gamma}} \sin(\omega t + X_{t,1}) \end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 &\quad 0 \\[3pt] \sqrt{2{\gamma} \alpha} &\quad 0 \\[3pt] 0 &\quad \psi \end{bmatrix} \,{\mathrm{d}} \begin{bmatrix} W_{t,1} \\[3pt] W_{t,2} \end{bmatrix}.$$
Here, the observation is determined by  $L=[ 0\ \ 0\ \ 1]$
. Motivated by this example, we check our results for a diffusion with coefficients
$L=[ 0\ \ 0\ \ 1]$
. Motivated by this example, we check our results for a diffusion with coefficients
 $$b(t,x) = B x + \begin{bmatrix} 0 \\[3pt] \underline\beta_2(t,x) \\[3pt] \,\underline\beta_3(t,x) \end{bmatrix}, \quad B=\begin{bmatrix} 0 &\quad 1 &\quad 0 \\[3pt] 0 &\quad -\alpha &\quad 0 \\[3pt] 0 &\quad 0 &\quad 0 \end{bmatrix}{,}\quad{\sigma} = \begin{bmatrix} 0 &\quad 0 \\[3pt] {\gamma}_1 &\quad {\gamma}_2 \\[3pt] {\gamma}_3 &\quad {\gamma}_4\end{bmatrix}.$$
$$b(t,x) = B x + \begin{bmatrix} 0 \\[3pt] \underline\beta_2(t,x) \\[3pt] \,\underline\beta_3(t,x) \end{bmatrix}, \quad B=\begin{bmatrix} 0 &\quad 1 &\quad 0 \\[3pt] 0 &\quad -\alpha &\quad 0 \\[3pt] 0 &\quad 0 &\quad 0 \end{bmatrix}{,}\quad{\sigma} = \begin{bmatrix} 0 &\quad 0 \\[3pt] {\gamma}_1 &\quad {\gamma}_2 \\[3pt] {\gamma}_3 &\quad {\gamma}_4\end{bmatrix}.$$
Note that this is a slight generalisation of the FM-demodulation model. We will assume that  ${\gamma}_3^2+{\gamma}_4^2\neq 0$
and
${\gamma}_3^2+{\gamma}_4^2\neq 0$
and  $\underline\beta_3$
are bounded. If
$\underline\beta_3$
are bounded. If  $\tilde{B}(t)=B$
and
$\tilde{B}(t)=B$
and  $\tilde{\sigma}=\sigma$
, then Assumption 2.4 is satisfied.
$\tilde{\sigma}=\sigma$
, then Assumption 2.4 is satisfied.
Proof.As the observation is on the rough component, we choose  $\Delta(t)=1$
. We have
$\Delta(t)=1$
. We have
 $${M_{\Delta}}(t)=(T-t)^{-1}({\gamma}_3^2+{\gamma}_4^2)^{-1}$$
$${M_{\Delta}}(t)=(T-t)^{-1}({\gamma}_3^2+{\gamma}_4^2)^{-1}$$
and  ${L_{\Delta}}(t)=[ 0\ \ 0\ \ 1]$
. Hence
${L_{\Delta}}(t)=[ 0\ \ 0\ \ 1]$
. Hence  $ {L_{\Delta}}(t)(\tilde{b}(t)-b(t,x)) = \tilde\beta_3(t)-\underline\beta_3(t,x) $
and the other conditions are easily verified.
$ {L_{\Delta}}(t)(\tilde{b}(t)-b(t,x)) = \tilde\beta_3(t)-\underline\beta_3(t,x) $
and the other conditions are easily verified.
Example 3.6. Assume  $[ X_{t,1}\ \ X_{t,2}]^{\prime}$
gives the position in the plane of a particle at time t. Suppose the velocity vector of the particle at time t, denoted by
$[ X_{t,1}\ \ X_{t,2}]^{\prime}$
gives the position in the plane of a particle at time t. Suppose the velocity vector of the particle at time t, denoted by  $[ X_{t,3}\ \ X_{t,4}]^{\prime}$
, satisfies an SDE driven by a two-dimensional Wiener process. The evolution of
$[ X_{t,3}\ \ X_{t,4}]^{\prime}$
, satisfies an SDE driven by a two-dimensional Wiener process. The evolution of  $X_t=[ X_{t,1}\ \ X_{t,2}\ \ X_{t,3}\ \ X_{t,4}]^{\prime}$
is then described by the SDE
$X_t=[ X_{t,1}\ \ X_{t,2}\ \ X_{t,3}\ \ X_{t,4}]^{\prime}$
is then described by the SDE
 \begin{align*}{\mathrm{d}} X_{t,1} & = X_{t,3} \,{\mathrm{d}} t {,} \\[3pt]{\mathrm{d}} X_{t,2} & = X_{t,4} \,{\mathrm{d}} t {,} \\[3pt]{\mathrm{d}} \begin{bmatrix} X_{t,3}\\[3pt] X_{t,4}\end{bmatrix} & = \begin{bmatrix} \underline\beta_3(t,X_t) \\[3pt] \underline\beta_4(t,X_t)\end{bmatrix} \,{\mathrm{d}} t + {\gamma} \,{\mathrm{d}} W_t,\end{align*}
\begin{align*}{\mathrm{d}} X_{t,1} & = X_{t,3} \,{\mathrm{d}} t {,} \\[3pt]{\mathrm{d}} X_{t,2} & = X_{t,4} \,{\mathrm{d}} t {,} \\[3pt]{\mathrm{d}} \begin{bmatrix} X_{t,3}\\[3pt] X_{t,4}\end{bmatrix} & = \begin{bmatrix} \underline\beta_3(t,X_t) \\[3pt] \underline\beta_4(t,X_t)\end{bmatrix} \,{\mathrm{d}} t + {\gamma} \,{\mathrm{d}} W_t,\end{align*}
where  $W_t \in {\mathbb{R}}^2$
. This example corresponds to the case
$W_t \in {\mathbb{R}}^2$
. This example corresponds to the case  $d=4$
,
$d=4$
,  $d'=2$
, and
$d'=2$
, and  $k=2$
in the model specified by (1.2)–(1.3). Observing only the location corresponds to
$k=2$
in the model specified by (1.2)–(1.3). Observing only the location corresponds to
 $$L=\begin{bmatrix} 1 &\quad 0 &\quad 0&\quad 0 \\[3pt] 0 &\quad 1 &\quad 0 &\quad 0 \end{bmatrix}.$$
$$L=\begin{bmatrix} 1 &\quad 0 &\quad 0&\quad 0 \\[3pt] 0 &\quad 1 &\quad 0 &\quad 0 \end{bmatrix}.$$
In matrix–vector notation the drift of the diffusion is given by  $b(t,x) = B x + \beta(t,x)$
, where
$b(t,x) = B x + \beta(t,x)$
, where
 $$B=\begin{bmatrix} 0 &\quad 0 &\quad 1 &\quad 0\\[3pt] 0 &\quad 0 &\quad 0&\quad 1 \\[3pt] 0 &\quad 0 &\quad 0 &\quad 0\\[3pt]0 &\quad 0 &\quad 0 &\quad 0\end{bmatrix} \quad\text{and}\quad \beta(t,x) =\begin{bmatrix} 0 \\[3pt] 0 \\[3pt] \underline\beta_3(t,X_t)\\[3pt] \underline\beta_4(t,X_t)\end{bmatrix}.$$
$$B=\begin{bmatrix} 0 &\quad 0 &\quad 1 &\quad 0\\[3pt] 0 &\quad 0 &\quad 0&\quad 1 \\[3pt] 0 &\quad 0 &\quad 0 &\quad 0\\[3pt]0 &\quad 0 &\quad 0 &\quad 0\end{bmatrix} \quad\text{and}\quad \beta(t,x) =\begin{bmatrix} 0 \\[3pt] 0 \\[3pt] \underline\beta_3(t,X_t)\\[3pt] \underline\beta_4(t,X_t)\end{bmatrix}.$$
We will assume diffusion coefficient
 $$ {\sigma}=\begin{bmatrix} 0 &\quad 0 &\quad {\gamma}_1 &\quad {\gamma}_3\\[3pt] 0&\quad 0&\quad {\gamma}_2 &\quad {\gamma}_4\end{bmatrix}^{\prime}, $$
$$ {\sigma}=\begin{bmatrix} 0 &\quad 0 &\quad {\gamma}_1 &\quad {\gamma}_3\\[3pt] 0&\quad 0&\quad {\gamma}_2 &\quad {\gamma}_4\end{bmatrix}^{\prime}, $$
where  ${\gamma}_1{\gamma}_4-{\gamma}_2{\gamma}_3 \neq 0$
. If
${\gamma}_1{\gamma}_4-{\gamma}_2{\gamma}_3 \neq 0$
. If  $\tilde\beta_1(t)=\tilde\beta_2(t)=0$
,
$\tilde\beta_1(t)=\tilde\beta_2(t)=0$
,  $\tilde{B}(t)=B$
, and
$\tilde{B}(t)=B$
, and  $\tilde{\sigma}={\sigma}$
, then Assumption 2.4 is satisfied.
$\tilde{\sigma}={\sigma}$
, then Assumption 2.4 is satisfied.
Proof.As we observed the first two coordinates, which are both smooth, we take  $\Delta(t)=(T-t)^{-1}I_2$
. The claim now follows from
$\Delta(t)=(T-t)^{-1}I_2$
. The claim now follows from
 $${M_{\Delta}}(t)=(T-t)^{-1}\frac{3}{({\gamma}_1{\gamma}_4-{\gamma}_2{\gamma}_3)^2}\begin{bmatrix}-{\gamma}_3^2-{\gamma}_4^2 &\quad {\gamma}_1{\gamma}_3+{\gamma}_2{\gamma}_4\\[3pt] {\gamma}_1{\gamma}_3+{\gamma}_2{\gamma}_4&\quad -{\gamma}_1^2-{\gamma}_2^2.\end{bmatrix}$$
$${M_{\Delta}}(t)=(T-t)^{-1}\frac{3}{({\gamma}_1{\gamma}_4-{\gamma}_2{\gamma}_3)^2}\begin{bmatrix}-{\gamma}_3^2-{\gamma}_4^2 &\quad {\gamma}_1{\gamma}_3+{\gamma}_2{\gamma}_4\\[3pt] {\gamma}_1{\gamma}_3+{\gamma}_2{\gamma}_4&\quad -{\gamma}_1^2-{\gamma}_2^2.\end{bmatrix}$$
and
 $${L_{\Delta}}(t) = \begin{bmatrix} (T-t)^{-1} &\quad 0 &\quad 1 &\quad 0 \\[3pt] 0 &\quad (T-t)^{-1} &\quad 0 &\quad 1 \end{bmatrix}.$$
$${L_{\Delta}}(t) = \begin{bmatrix} (T-t)^{-1} &\quad 0 &\quad 1 &\quad 0 \\[3pt] 0 &\quad (T-t)^{-1} &\quad 0 &\quad 1 \end{bmatrix}.$$
Example 3.7. Hairer, Stuart, and Voss [Reference Hairer, Stuart and Voss18] consider SDEs of the form
 $${\mathrm{d}} X_t = \begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad \theta\end{bmatrix} X_t\,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] \underline\beta(t,X_t) \end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] \gamma \end{bmatrix} \,{\mathrm{d}} W_t, $$
$${\mathrm{d}} X_t = \begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad \theta\end{bmatrix} X_t\,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] \underline\beta(t,X_t) \end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] \gamma \end{bmatrix} \,{\mathrm{d}} W_t, $$
where  $X_t=[ X_{t,1}\ \ X_{t,2}]^{\prime}$
,
$X_t=[ X_{t,1}\ \ X_{t,2}]^{\prime}$
,  $\theta >0$
and the conditioning is specified by
$\theta >0$
and the conditioning is specified by  $L=[ 1 \ \ 0]$
. As explained in [Reference Hairer, Stuart and Voss18], the solution to this SDE can be viewed as the time evolution of the state of a mechanical system with friction under the influence of noise. Assume
$L=[ 1 \ \ 0]$
. As explained in [Reference Hairer, Stuart and Voss18], the solution to this SDE can be viewed as the time evolution of the state of a mechanical system with friction under the influence of noise. Assume  ${(t,x) \mapsto \underline\beta(t,x)}$
is bounded and Lipschitz in both arguments. Note that this hypo-elliptic SDE is not of the form given in (1.2) and (1.3). However, if
${(t,x) \mapsto \underline\beta(t,x)}$
is bounded and Lipschitz in both arguments. Note that this hypo-elliptic SDE is not of the form given in (1.2) and (1.3). However, if
 $$\tilde{B}(t)= B_{\theta}= \begin{bmatrix} 0 &\quad 1\\[3pt] 0 &\quad \theta\end{bmatrix}, \quad \tilde\beta_1(t)=0{,}\quad \tilde{\sigma}=\begin{bmatrix} 0 \\[3pt] \gamma \end{bmatrix},$$
$$\tilde{B}(t)= B_{\theta}= \begin{bmatrix} 0 &\quad 1\\[3pt] 0 &\quad \theta\end{bmatrix}, \quad \tilde\beta_1(t)=0{,}\quad \tilde{\sigma}=\begin{bmatrix} 0 \\[3pt] \gamma \end{bmatrix},$$
then Assumption 2.4 is satisfied.
Proof.Upon taking  $\Delta(t)=(T-t)^{-1}$
, we find that
$\Delta(t)=(T-t)^{-1}$
, we find that
 $$\lim_{t\uparrow T} (T-t) {M_{\Delta}}(t) = 3{\gamma}^{-2} \quad\text{and} \quad {L_{\Delta}}(t) =\begin{bmatrix} \frac1{T-t} &\quad \frac{{\mathrm{e}}^{\theta (T-t)}-1}{\theta (T-t)}\end{bmatrix}.$$
$$\lim_{t\uparrow T} (T-t) {M_{\Delta}}(t) = 3{\gamma}^{-2} \quad\text{and} \quad {L_{\Delta}}(t) =\begin{bmatrix} \frac1{T-t} &\quad \frac{{\mathrm{e}}^{\theta (T-t)}-1}{\theta (T-t)}\end{bmatrix}.$$
This is to be compared with the expressions in (3.1). We conclude as in Example 3.2 that the conditions in Assumption 2.4 are satisfied.
Example 3.8. This is an example to illustrate that our approach applies beyond equations of the form (1.10). We assume
 $${\mathrm{d}} X_t = B X_t\,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] \underline\beta(t,X_t) \end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 1 \\[3pt] 1 \end{bmatrix} \,{\mathrm{d}} W_t {,}$$
$${\mathrm{d}} X_t = B X_t\,{\mathrm{d}} t + \begin{bmatrix} 0 \\[3pt] \underline\beta(t,X_t) \end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 1 \\[3pt] 1 \end{bmatrix} \,{\mathrm{d}} W_t {,}$$
with  $\underline\beta\colon [0,T] \times {\mathbb{R}}^2 \to {\mathbb{R}}$
bounded and globally Lipschitz in both arguments. Suppose
$\underline\beta\colon [0,T] \times {\mathbb{R}}^2 \to {\mathbb{R}}$
bounded and globally Lipschitz in both arguments. Suppose  $L=[ 1\ \ 0]$
. If
$L=[ 1\ \ 0]$
. If
 $$\tilde{B} =B\coloneqq \begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad 0\end{bmatrix}, \quad \tilde\beta=\begin{bmatrix} 0 \\[3pt] 0 \end{bmatrix}, \quad \tilde{\sigma} = \begin{bmatrix} 1\\[3pt] 1 \end{bmatrix},$$
$$\tilde{B} =B\coloneqq \begin{bmatrix} 0 &\quad 1 \\[3pt] 0 &\quad 0\end{bmatrix}, \quad \tilde\beta=\begin{bmatrix} 0 \\[3pt] 0 \end{bmatrix}, \quad \tilde{\sigma} = \begin{bmatrix} 1\\[3pt] 1 \end{bmatrix},$$
then Assumption 2.4 holds.
Proof.Using  $\Delta(t)=1$
, we have
$\Delta(t)=1$
, we have  $L_{\Delta}(t)=[ 1\ \ T-t]$
,
$L_{\Delta}(t)=[ 1\ \ T-t]$
,  $\lim_{t\uparrow T} (T-t) {M_{\Delta}}(t)=1$
and the claim follows as in the previous examples.
$\lim_{t\uparrow T} (T-t) {M_{\Delta}}(t)=1$
and the claim follows as in the previous examples.
4. Numerical illustrations
In this section we will discuss implementational aspects of our sampling method, and we will illustrate the method by some representative numerical examples. We implemented the examples in our software package Bridge [Reference Schauer34], written in the programming language Julia [Reference Bezanson, Karpinski, Shah and Edelman6]. The corresponding code is available in [Reference van der Meulen and Schauer41].
To compute the guiding term and likelihood ratio, we have the following backward ordinary differential equations:
 \begin{alignat*}{3}{\mathrm{d}} L(t) &= -L(t) \tilde{B}(t)\,{\mathrm{d}} t,&L(T)&= L {,} \\[3pt]{\mathrm{d}} {M^\dagger}(t)&=- L(t) \tilde{a}(t) L(t)^{\prime}\,{\mathrm{d}} t,\quad& {M^\dagger}(T)&=0_{m\times m} {,} \\[3pt]{\mathrm{d}} \mu(t) &=-L(t) \tilde\beta(t)\,{\mathrm{d}} t,& \mu(T)&=0_{m\times 1},\end{alignat*}
\begin{alignat*}{3}{\mathrm{d}} L(t) &= -L(t) \tilde{B}(t)\,{\mathrm{d}} t,&L(T)&= L {,} \\[3pt]{\mathrm{d}} {M^\dagger}(t)&=- L(t) \tilde{a}(t) L(t)^{\prime}\,{\mathrm{d}} t,\quad& {M^\dagger}(T)&=0_{m\times m} {,} \\[3pt]{\mathrm{d}} \mu(t) &=-L(t) \tilde\beta(t)\,{\mathrm{d}} t,& \mu(T)&=0_{m\times 1},\end{alignat*}
where  $t\in [0,T]$
. These are easily derived: see [Reference van der Meulen and Schauer39, Lemma 2.4]. These backward differential equations need only be solved once. Next, Algorithm 1 from [Reference van der Meulen and Schauer38] can be applied. This algorithm describes a Metropolis–Hastings sampler for simulating diffusion bridges using guided proposals. We briefly recap the steps of this algorithm; more details can be found in [Reference van der Meulen and Schauer38]. As we assume
$t\in [0,T]$
. These are easily derived: see [Reference van der Meulen and Schauer39, Lemma 2.4]. These backward differential equations need only be solved once. Next, Algorithm 1 from [Reference van der Meulen and Schauer38] can be applied. This algorithm describes a Metropolis–Hastings sampler for simulating diffusion bridges using guided proposals. We briefly recap the steps of this algorithm; more details can be found in [Reference van der Meulen and Schauer38]. As we assume  $X^\circ$
to be a strong solution to the SDE specified by (1.5) and (1.7), there is a measurable mapping
$X^\circ$
to be a strong solution to the SDE specified by (1.5) and (1.7), there is a measurable mapping  $\mathcal{G}\mathcal{P}$
such that
$\mathcal{G}\mathcal{P}$
such that  $X^\circ=\mathcal{G}\mathcal{P}(x_0, W)$
, where
$X^\circ=\mathcal{G}\mathcal{P}(x_0, W)$
, where  $x_0$
is the starting point and W a
$x_0$
is the starting point and W a  ${\mathbb{R}}^{d'}$
-valued Wiener process (
${\mathbb{R}}^{d'}$
-valued Wiener process ( $\mathcal{G}\mathcal{P}$
stands for ‘guided proposal’). As
$\mathcal{G}\mathcal{P}$
stands for ‘guided proposal’). As  $x_0$
is fixed, we will write, with slight abuse of notation,
$x_0$
is fixed, we will write, with slight abuse of notation,  $X^\circ=\mathcal{G}\mathcal{P}(W)$
. The algorithm requires us to choose a tuning parameter
$X^\circ=\mathcal{G}\mathcal{P}(W)$
. The algorithm requires us to choose a tuning parameter  $\rho\in [0,1)$
and proceeds according to the following steps.
$\rho\in [0,1)$
and proceeds according to the following steps.
(1) Draw a Wiener process Z on [0, T]. Set
 $X=g(Z)$
.
$X=g(Z)$
.(2) Propose a Wiener process W on [0, T]. Set
and \begin{equation}Z^\circ = \rho Z + \sqrt{1-\rho^2} W\end{equation}
\begin{equation}Z^\circ = \rho Z + \sqrt{1-\rho^2} W\end{equation}
 $X^\circ=\mathcal{G}\mathcal{P}(Z^\circ)$
.
$X^\circ=\mathcal{G}\mathcal{P}(Z^\circ)$
.(3) Compute
 $A=\Psi_T(X^\circ)/\Psi_T(X)$
(where
$A=\Psi_T(X^\circ)/\Psi_T(X)$
(where  $\Psi_T$
is as defined in (2.6)). Sample
$\Psi_T$
is as defined in (2.6)). Sample  $U\sim \mbox{Uniform}(0,1)$
. If
$U\sim \mbox{Uniform}(0,1)$
. If  $U<A$
then set
$U<A$
then set  $Z=Z^\circ$
and
$Z=Z^\circ$
and  $X=X^\circ$
.
$X=X^\circ$
.(4) Repeat steps (2) and (3).
The invariant distribution of this chain is precisely  ${\mathbb{P}}^\star_T$
. If the guided proposal is good, then we may use
${\mathbb{P}}^\star_T$
. If the guided proposal is good, then we may use  $\rho=0$
, which yields an independence sampler. However, for difficult bridge simulation schemes, possibly caused by a large value of T or strong non-linearity in the drift or diffusion coefficient, a value of
$\rho=0$
, which yields an independence sampler. However, for difficult bridge simulation schemes, possibly caused by a large value of T or strong non-linearity in the drift or diffusion coefficient, a value of  $\rho$
close to 1 may be required. The proposal in (4.1) is precisely the pCN method; see e.g. [Reference Cotter, Roberts, Stuart and White12].
$\rho$
close to 1 may be required. The proposal in (4.1) is precisely the pCN method; see e.g. [Reference Cotter, Roberts, Stuart and White12].
In the implementation we use a fine equidistant grid, which is transformed by the mapping  $\tau\colon [0,T] \to [0,T]$
given by
$\tau\colon [0,T] \to [0,T]$
given by  $\tau(s)=s(2-s/T)$
. Motivation for this choice is given in Section 5 of [Reference van der Meulen and Schauer38]. Intuitively, the guiding term gets stronger near T, and therefore we use a finer grid the closer we get to T. The guided proposal is simulated on this grid, and using the values obtained,
$\tau(s)=s(2-s/T)$
. Motivation for this choice is given in Section 5 of [Reference van der Meulen and Schauer38]. Intuitively, the guiding term gets stronger near T, and therefore we use a finer grid the closer we get to T. The guided proposal is simulated on this grid, and using the values obtained,  $\Psi_T(X^\circ)$
is approximated by Riemann approximation. Furthermore, for numerical stability we solve the equation for
$\Psi_T(X^\circ)$
is approximated by Riemann approximation. Furthermore, for numerical stability we solve the equation for  ${M^\dagger}(t)$
using
${M^\dagger}(t)$
using  ${M^\dagger}(T)= 10^{-10} I_{m\times m}$
instead of
${M^\dagger}(T)= 10^{-10} I_{m\times m}$
instead of  ${M^\dagger}(T)=0_{m\times m}$
.
${M^\dagger}(T)=0_{m\times m}$
.
Example 4.1. Assume the NCLAR(3)-model, as described in Example 3.4 with  $\underline\beta(t,x) =-6\sin(2\pi x)$
and
$\underline\beta(t,x) =-6\sin(2\pi x)$
and  $x_0=[ 0 \ \ 0 \ \ 0]^{\prime}$
. We first condition the process on hitting
$x_0=[ 0 \ \ 0 \ \ 0]^{\prime}$
. We first condition the process on hitting
 $$ v=[ 1/32\ \ 1/4\ \ 1]^{\prime} $$
$$ v=[ 1/32\ \ 1/4\ \ 1]^{\prime} $$
at time  $T=0.5$
, assuming
$T=0.5$
, assuming  $L=I_3$
(full observation at time T). The idea of this example is that sample paths of the rough component are mean-reverting at levels
$L=I_3$
(full observation at time T). The idea of this example is that sample paths of the rough component are mean-reverting at levels  $k \in {\mathbb{Z}}$
, with occasional noise-driven shifts from one level to another. The given conditioning then forces the process to move halfway along the interval (at about time
$k \in {\mathbb{Z}}$
, with occasional noise-driven shifts from one level to another. The given conditioning then forces the process to move halfway along the interval (at about time  $0.25$
) from level 0 to level 1, remaining at approximately level 1 up to time T. Such paths are rare events and obtaining these by forward simulation is computationally extremely intensive.
$0.25$
) from level 0 to level 1, remaining at approximately level 1 up to time T. Such paths are rare events and obtaining these by forward simulation is computationally extremely intensive.
We constructed guided proposals according to (3.2) with  $\tilde\beta_3(t)=0$
. Iterates of the sampler using
$\tilde\beta_3(t)=0$
. Iterates of the sampler using  $\rho=0.85$
are shown in Figure 1. The average Metropolis–Hastings acceptance percentage was 43%. We need a value of
$\rho=0.85$
are shown in Figure 1. The average Metropolis–Hastings acceptance percentage was 43%. We need a value of  $\rho$
close to 1 as we cannot easily incorporate the strong non-linearity into the guiding term of the guided proposal. We repeated the simulation, this time only conditioning on
$\rho$
close to 1 as we cannot easily incorporate the strong non-linearity into the guiding term of the guided proposal. We repeated the simulation, this time only conditioning on  $LX_T=1/32$
, where
$LX_T=1/32$
, where  $L=[ 1\ \ 0\ \ 0]$
. We again took
$L=[ 1\ \ 0\ \ 0]$
. We again took  $\rho=0.95$
, leading to an average Metropolis–Hastings acceptance percentage of 24%. The results are shown in Figure 2. The distribution of bridges turns out to be bimodal. The latter is confirmed by extensive forward simulation and only keeping those paths which approximately satisfy the conditioning.
$\rho=0.95$
, leading to an average Metropolis–Hastings acceptance percentage of 24%. The results are shown in Figure 2. The distribution of bridges turns out to be bimodal. The latter is confirmed by extensive forward simulation and only keeping those paths which approximately satisfy the conditioning.
Example 4.2. Ditlevsen and Samson [Reference Ditlevsen and Samson14] consider the stochastic hypo-elliptic FitzHugh–Nagumo model, which is specified by the SDE
 \begin{equation}{\mathrm{d}} X_t = \begin{bmatrix} 1/{\varepsilon} &\quad -1/{\varepsilon} \\ {\gamma} &\quad -1 \end{bmatrix} X_t \,{\mathrm{d}} t + \begin{bmatrix} -X_{t,1}^3/{\varepsilon} +s/{\varepsilon} \\ \beta\end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 \\ {\sigma}\end{bmatrix} \,{\mathrm{d}} W_t,\quad X_0=x(0).\end{equation}
\begin{equation}{\mathrm{d}} X_t = \begin{bmatrix} 1/{\varepsilon} &\quad -1/{\varepsilon} \\ {\gamma} &\quad -1 \end{bmatrix} X_t \,{\mathrm{d}} t + \begin{bmatrix} -X_{t,1}^3/{\varepsilon} +s/{\varepsilon} \\ \beta\end{bmatrix} \,{\mathrm{d}} t + \begin{bmatrix} 0 \\ {\sigma}\end{bmatrix} \,{\mathrm{d}} W_t,\quad X_0=x(0).\end{equation}
Only the first component is observed, hence  $L=[ 1\ \ 0]$
. We consider the same parameter values as in [Reference Ditlevsen and Samson14]:
$L=[ 1\ \ 0]$
. We consider the same parameter values as in [Reference Ditlevsen and Samson14]:
 \begin{equation}[ {\varepsilon}\ \ s\ \ {\gamma}\ \ \beta\ \ \sigma] =[ 0.1\ \ 0\ \ 1.5\ \ 0.8\ \ 0.3].\end{equation}
\begin{equation}[ {\varepsilon}\ \ s\ \ {\gamma}\ \ \beta\ \ \sigma] =[ 0.1\ \ 0\ \ 1.5\ \ 0.8\ \ 0.3].\end{equation}
A realisation of a sample path on [0, 10] is given in Figure 3.

Figure 1. Sampled guided diffusion bridges when conditioning on  $X_T=[ 1/32 \ \ 1/4 \ \ 1]^{\prime}$
in Example 4.1.
$X_T=[ 1/32 \ \ 1/4 \ \ 1]^{\prime}$
in Example 4.1.

Figure 2. Sampled guided diffusion bridges when conditioning on  $L X_T=1/32$
with
$L X_T=1/32$
with  $L=[ 1\ \ 0\ \ 0]^{{\prime}}$
in Example 4.1.
$L=[ 1\ \ 0\ \ 0]^{{\prime}}$
in Example 4.1.
While this example formally does not fall into our set-up, the conditions of Assumption 2.4 strongly suggest that the component of the drift with smooth path, i.e. the first component of b, certainly needs to match at the observed endpoint. We construct guided proposals by linearising the drift term  $X_{t,1}$
at the observed endpoint v. Hence, using
$X_{t,1}$
at the observed endpoint v. Hence, using  $-x^3\approx 2 a^3 -3 a^2 x$
for x near a, we take
$-x^3\approx 2 a^3 -3 a^2 x$
for x near a, we take
 $$\tilde{B}(t)= \begin{bmatrix} 1/{\varepsilon}-3 v^2/{\varepsilon} &\quad -1/{\varepsilon} \\ {\gamma} &\quad -1 \end{bmatrix}, \quad \tilde\beta(t) = \begin{bmatrix} 2v^3/{\varepsilon} +s/{\varepsilon} \\ \beta\end{bmatrix}{,}\quad \tilde\sigma= \begin{bmatrix} 0 \\ {\sigma}\end{bmatrix}.$$
$$\tilde{B}(t)= \begin{bmatrix} 1/{\varepsilon}-3 v^2/{\varepsilon} &\quad -1/{\varepsilon} \\ {\gamma} &\quad -1 \end{bmatrix}, \quad \tilde\beta(t) = \begin{bmatrix} 2v^3/{\varepsilon} +s/{\varepsilon} \\ \beta\end{bmatrix}{,}\quad \tilde\sigma= \begin{bmatrix} 0 \\ {\sigma}\end{bmatrix}.$$
To illustrate the performance of our method, we take a rather challenging, strongly non-linear problem. We consider bridges over the time-interval [0, T] with  $T=2$
, starting at
$T=2$
, starting at  $x(0)=[\!-0.5\ \ -0.6]$
. In Figure 4 we forward-simulated 100 paths, to access the behaviour of the process. Next, we consider two cases.
$x(0)=[\!-0.5\ \ -0.6]$
. In Figure 4 we forward-simulated 100 paths, to access the behaviour of the process. Next, we consider two cases.
(a) Conditioning on the first coordinate at the endpoint of a ‘typical’ path; we took
 $v=-1$
.
$v=-1$
.(b) 2. Conditioning on the first coordinate at the endpoint of an ‘extreme’ path; we took
 $v=1.1$
.
$v=1.1$
.

Figure 5. Sampled guided diffusion bridges when conditioning on  $v=-1$
(typical case).
$v=-1$
(typical case).

Figure 6. Sampled guided diffusion bridges when conditioning on  $v=1.1$
(extreme case). The ‘outlying’ green curve corresponds to the initialisation of the algorithm.
$v=1.1$
(extreme case). The ‘outlying’ green curve corresponds to the initialisation of the algorithm.
We ran the sampler for  $50\,000$
iterations, using
$50\,000$
iterations, using  $\rho=0$
and
$\rho=0$
and  $\rho=0.9$
in cases (a) and (b) respectively. The percentage of accepted proposals in the Metropolis–Hastings step equals 64% and 21% respectively. In Figures 5 and 6 we plotted every 1000th sampled path out of the
$\rho=0.9$
in cases (a) and (b) respectively. The percentage of accepted proposals in the Metropolis–Hastings step equals 64% and 21% respectively. In Figures 5 and 6 we plotted every 1000th sampled path out of the  $50\,000$
iterations for the ‘typical’ and ‘extreme’ cases respectively. Figure 5 immediately demonstrates that for a typical path, guided proposals very closely resemble true bridges (using Figure 4 as comparison). To assess whether in the ‘extreme’ case the sampled bridges resemble true bridges, we also forward-simulated the process, only keeping those paths for which
$50\,000$
iterations for the ‘typical’ and ‘extreme’ cases respectively. Figure 5 immediately demonstrates that for a typical path, guided proposals very closely resemble true bridges (using Figure 4 as comparison). To assess whether in the ‘extreme’ case the sampled bridges resemble true bridges, we also forward-simulated the process, only keeping those paths for which  $|L x_T-v| <0.01$
. The resulting paths are shown in Figure 7 and resemble those in Figure 6 quite well.
$|L x_T-v| <0.01$
. The resulting paths are shown in Figure 7 and resemble those in Figure 6 quite well.
This example is extremely challenging in the sense that we take a rather long time horizon ( $T=2$
), the noise-level on the second coordinate is small, and the drift of the diffusion is highly non-linear. As a result, the true distribution of bridges is multimodal. Even in much simpler settings, sampling from a multimodal distribution using MCMC constitutes a difficult problem. Here, the multimodality is recovered remarkably well by our method, as can be seen in Figure 6.
$T=2$
), the noise-level on the second coordinate is small, and the drift of the diffusion is highly non-linear. As a result, the true distribution of bridges is multimodal. Even in much simpler settings, sampling from a multimodal distribution using MCMC constitutes a difficult problem. Here, the multimodality is recovered remarkably well by our method, as can be seen in Figure 6.
Remark 4.1. We have chosen  $50\,000$
iterations in the examples. However, qualitatively the same figures of simulating bridges can be obtained by reducing the number of iterations to approximately
$50\,000$
iterations in the examples. However, qualitatively the same figures of simulating bridges can be obtained by reducing the number of iterations to approximately  $10\,000$
.
$10\,000$
.
4.1. Numerical checks on the validity of guided proposals
In this section we first investigate the quality of guided proposals over long time spans. Next, we empirically demonstrate that the conditions of our main theorem, especially Assumption 2.4, are stronger than actually needed. In each numerical experiment we compare two histogram estimators for  $v \mapsto \rho(0,x_0;\ T,v)$
. The first estimator is obtained by making a histogram of a large number of forward simulations of the unconditioned diffusion process. Let
$v \mapsto \rho(0,x_0;\ T,v)$
. The first estimator is obtained by making a histogram of a large number of forward simulations of the unconditioned diffusion process. Let  $\{A_k\}$
denote the bins of this histogram. A second estimator is obtained by using the equality
$\{A_k\}$
denote the bins of this histogram. A second estimator is obtained by using the equality
 $$\rho(0,x_0;\ T, v) = \tilde \rho(0, x_0;\ T, v) {{\mathbb{E}}}[{\Psi_T(X^{\circ, T, v}) }] {,}$$
$$\rho(0,x_0;\ T, v) = \tilde \rho(0, x_0;\ T, v) {{\mathbb{E}}}[{\Psi_T(X^{\circ, T, v}) }] {,}$$
which is a direct consequence of Theorem 2.6. Note that we extended the notation to highlight that  $\rho$
,
$\rho$
,  $\tilde \rho$
, and
$\tilde \rho$
, and  $X^\circ$
depend on T and v. We use the relation in the previous display as follows: for each bin
$X^\circ$
depend on T and v. We use the relation in the previous display as follows: for each bin  $A_k$
,
$A_k$
,
 $$\int_{A_k} \rho(0,x_0;\ T, v) \,{\mathrm{d}} v ={{\mathbb{E}}}\bigg[{{\textbf{1}}_{A_k}(\tilde V) \frac{\tilde \rho(0, x_0;\ T, \tilde V)}{q( \tilde V)} \Psi_T(X^{T, \tilde V,\circ}) }\bigg]{,}$$
$$\int_{A_k} \rho(0,x_0;\ T, v) \,{\mathrm{d}} v ={{\mathbb{E}}}\bigg[{{\textbf{1}}_{A_k}(\tilde V) \frac{\tilde \rho(0, x_0;\ T, \tilde V)}{q( \tilde V)} \Psi_T(X^{T, \tilde V,\circ}) }\bigg]{,}$$
where  $\tilde V$
is sampled from the density q. Hence,
$\tilde V$
is sampled from the density q. Hence,  $\int_{A_k} \rho(0,x_0;\ T, v) \,{\mathrm{d}} v$
can be approximated using importance sampling, where repeatedly first the endpoint v is sampled from q and subsequently a guided proposal is simulated that is conditioned to hit v at time T. In our experiments we took the importance sampling density q to be the Gaussian density with mean and covariance obtained from the unconditioned forward-simulated endpoint values.
$\int_{A_k} \rho(0,x_0;\ T, v) \,{\mathrm{d}} v$
can be approximated using importance sampling, where repeatedly first the endpoint v is sampled from q and subsequently a guided proposal is simulated that is conditioned to hit v at time T. In our experiments we took the importance sampling density q to be the Gaussian density with mean and covariance obtained from the unconditioned forward-simulated endpoint values.
Note that the set-up is such that this is feasible, at least when estimating the entire histogram, but of course it would be prohibitively expensive to use forward sampling to compute the density in a single small bin or at a single point.
Example 4.3. Consider the non-linear hypo-elliptic two-dimensional system determined by drift  $b(t, x) = B x + \beta(t) + [ 0;\ \frac12 \sin(x_2) ]$
with
$b(t, x) = B x + \beta(t) + [ 0;\ \frac12 \sin(x_2) ]$
with  $B =\frac{1}{10} [ -1\ \ 1;\ \ 0\ \ {-1}] $
,
$B =\frac{1}{10} [ -1\ \ 1;\ \ 0\ \ {-1}] $
,  $\beta(t) = [ 0\ \ \frac12\sin(t/4) ]$
, and dispersion
$\beta(t) = [ 0\ \ \frac12\sin(t/4) ]$
, and dispersion  $\sigma \equiv [ 0;\ 2]$
(with a semicolon separating matrix rows). Starting at
$\sigma \equiv [ 0;\ 2]$
(with a semicolon separating matrix rows). Starting at  $X_0 = [ 0 ;\ {-\pi/2}]$
, we expect to observe
$X_0 = [ 0 ;\ {-\pi/2}]$
, we expect to observe  $V = L X_T + Z$
with
$V = L X_T + Z$
with  $L = [ 1\ \ 1]$
,
$L = [ 1\ \ 1]$
,  $Z \sim N(0, 10^{-6})$
. We consider both
$Z \sim N(0, 10^{-6})$
. We consider both  $T=4\pi$
and
$T=4\pi$
and  $T=40\pi$
, the latter to check how guided proposals perform over a very long time span. We take guided proposals derived from
$T=40\pi$
, the latter to check how guided proposals perform over a very long time span. We take guided proposals derived from  $\tilde b(t, x) = B x + \beta(t)$
and
$\tilde b(t, x) = B x + \beta(t)$
and  $\tilde\sigma=\sigma$
.
$\tilde\sigma=\sigma$
.
In Figure 8 the two histograms are contrasted. Interestingly, the results show no degradation in performance when increasing T by an order. For the simulations we took  $K = 70$
bins and
$K = 70$
bins and  $100\,000$
samples of V respective draws from
$100\,000$
samples of V respective draws from  $\tilde V$
(thus on average approximately 1500 draws per bin) and time grid
$\tilde V$
(thus on average approximately 1500 draws per bin) and time grid  $t_i = s_i (2 - s_i/T)$
with
$t_i = s_i (2 - s_i/T)$
with  $s_i = h \, i$
,
$s_i = h \, i$
,  $h= 0.01$
, therefore decreasing step-size towards T while keeping the number of grid points equal to
$h= 0.01$
, therefore decreasing step-size towards T while keeping the number of grid points equal to  $T/h$
, as suggested in [Reference van der Meulen and Schauer38]. The implementation is based on our Julia package [Reference Mider and Schauer29] with package co-author Marcin Mider. The figures also serve to verify the correctness of the implementation.
$T/h$
, as suggested in [Reference van der Meulen and Schauer38]. The implementation is based on our Julia package [Reference Mider and Schauer29] with package co-author Marcin Mider. The figures also serve to verify the correctness of the implementation.
Example 4.4. It is interesting to ask if – numerically speaking – the change of measure is successful in cases where  $\sigma$
depends on x and the fourth inequality of Assumption 2.4
cannot be verified. For that purpose, we slightly adjust the setting of the previous example by now taking
$\sigma$
depends on x and the fourth inequality of Assumption 2.4
cannot be verified. For that purpose, we slightly adjust the setting of the previous example by now taking  $L = [ 1\ \ 0 ]$
and
$L = [ 1\ \ 0 ]$
and  $\sigma(t, x) = [ 0;\ 2 + \frac12\cos(x_2) ]$
and repeating the experiment. In this case we chose
$\sigma(t, x) = [ 0;\ 2 + \frac12\cos(x_2) ]$
and repeating the experiment. In this case we chose  $\tilde \sigma = \sigma(0, [ 0;\,0])$
. As the problem is more difficult, we took fewer bins (
$\tilde \sigma = \sigma(0, [ 0;\,0])$
. As the problem is more difficult, we took fewer bins ( $K = 50$
) and set
$K = 50$
) and set  $h = 0.005$
(otherwise keeping our previous choices). The resulting Figure 9 shows no indication of lack of absolute continuity or loss of probability mass. This strongly indicates that guided proposals can perform perfectly well for the present complex setting that includes state-dependent diffusion coefficient and hypo-ellipticity.
$h = 0.005$
(otherwise keeping our previous choices). The resulting Figure 9 shows no indication of lack of absolute continuity or loss of probability mass. This strongly indicates that guided proposals can perform perfectly well for the present complex setting that includes state-dependent diffusion coefficient and hypo-ellipticity.

Figure 8. Dark orange: histogram baseline estimate of the density of observation  $V = L X_T + Z$
,
$V = L X_T + Z$
,  $Z \sim N(0, 10^{-6})$
from forward simulation. Dashed blue: observation density estimate using weighted histogram of points
$Z \sim N(0, 10^{-6})$
from forward simulation. Dashed blue: observation density estimate using weighted histogram of points  $\tilde V$
sampled from Gaussian distribution weighted with importance weights from guided proposals steered towards those points. Top:
$\tilde V$
sampled from Gaussian distribution weighted with importance weights from guided proposals steered towards those points. Top:  $T = 4\pi$
. Bottom:
$T = 4\pi$
. Bottom:  $T = 40\pi$
. Pink: difference between histograms.
$T = 40\pi$
. Pink: difference between histograms.

Figure 9. As Figure 8, but estimates for the model with observation operator  $L =[1\ \ 0]$
and
$L =[1\ \ 0]$
and  $\sigma(t, x) = [ 0;\ 2 + \frac12\cos(x_2) ]$
, at
$\sigma(t, x) = [ 0;\ 2 + \frac12\cos(x_2) ]$
, at  $T = 4\pi$
.
$T = 4\pi$
.
However, care is needed. In Figure 10 we show the result for the same experiment but with L changed to  $L = [ 1\ \ 1]$
. Here, the loss of probability mass indicates violation of absolute continuity. We conjecture that
$L = [ 1\ \ 1]$
. Here, the loss of probability mass indicates violation of absolute continuity. We conjecture that  $L a(T,v) L^{\prime} = L \tilde{a}(T) L^{\prime}$
may be the ‘right’ restriction on choosing
$L a(T,v) L^{\prime} = L \tilde{a}(T) L^{\prime}$
may be the ‘right’ restriction on choosing  $\tilde{a}(T)$
. To obtain empirical evidence, we redid the experiment with
$\tilde{a}(T)$
. To obtain empirical evidence, we redid the experiment with  $L = [ 1\ \ 1]$
but now
$L = [ 1\ \ 1]$
but now  $\sigma(t, x) = [ 0;\ 2 + \frac12\cos(Lx) ]$
. In this case one can match the diffusivity at time T by taking
$\sigma(t, x) = [ 0;\ 2 + \frac12\cos(Lx) ]$
. In this case one can match the diffusivity at time T by taking  $\tilde\sigma = [ 0;\ 2 + \frac12\cos(v) ]$
. The resulting figure (Figure 11) indicates no loss of absolute continuity, supporting the conjecture.
$\tilde\sigma = [ 0;\ 2 + \frac12\cos(v) ]$
. The resulting figure (Figure 11) indicates no loss of absolute continuity, supporting the conjecture.

Figure 10. As Figure 8, but estimates for the model with observation operator  $L =[1\ \ 1]$
and
$L =[1\ \ 1]$
and  $\sigma(t, x) = [ 0;\ 2 + \frac12\cos(x_2) ]$
, at
$\sigma(t, x) = [ 0;\ 2 + \frac12\cos(x_2) ]$
, at  $T = 4\pi$
. Note the loss of probability mass indicating lack of absolute continuity.
$T = 4\pi$
. Note the loss of probability mass indicating lack of absolute continuity.

Figure 11. As Figure 8, but estimates for the model with observation operator  $L =[1\ \ 1]$
and
$L =[1\ \ 1]$
and  $\sigma(t, x) = [ 0; \ 2 + \frac12\cos(x_1 + x_2) ]$
, at
$\sigma(t, x) = [ 0; \ 2 + \frac12\cos(x_1 + x_2) ]$
, at  $T = 4\pi$
.
$T = 4\pi$
.
5. Proofs of Proposition 2.2 and Corollary 2.1
In this section we give proofs of the results from Section 2.2 on the behaviour of guided proposals near the conditioning point. For clarity, the proof of Proposition 2.2 is split up over Sections 5.1, 5.2, and 5.3. The proof of Corollary 2.1 is in Section 5.4.
5.1. Centering and scaling of the guided proposal
To reduce notational overheads, we write  $a_t\equiv a(t,X^\circ_t)$
. Then
$a_t\equiv a(t,X^\circ_t)$
. Then  $\tilde{b}_t$
,
$\tilde{b}_t$
,  $b_t$
, and
$b_t$
, and  ${\sigma}_t$
are defined similarly. Our starting point is the expression for
${\sigma}_t$
are defined similarly. Our starting point is the expression for  $\tilde{r}$
in (2.2).
$\tilde{r}$
in (2.2).
Lemma 5.1. If we define
 $$ Z_t = v- \mu(t)-L(t) X^\circ_t ,$$
$$ Z_t = v- \mu(t)-L(t) X^\circ_t ,$$
then
 $$ {\mathrm{d}} Z_t = L(t) (\tilde{b}_t-b_t)\,{\mathrm{d}} t + L(t){\sigma}_t \,{\mathrm{d}} W_t - L(t)a_t L(t)^{\prime} M(t) Z_t \,{\mathrm{d}} t.$$
$$ {\mathrm{d}} Z_t = L(t) (\tilde{b}_t-b_t)\,{\mathrm{d}} t + L(t){\sigma}_t \,{\mathrm{d}} W_t - L(t)a_t L(t)^{\prime} M(t) Z_t \,{\mathrm{d}} t.$$
Proof.We have
 $${\mathrm{d}} Z_t = -\bigg(\frac{{\mathrm{d}} }{{\mathrm{d}} t} L(t)\bigg) X^\circ_t \,{\mathrm{d}} t -\frac{{\mathrm{d}} }{{\mathrm{d}} t} \mu(t)-L(t) \,{\mathrm{d}} X^\circ_t.$$
$${\mathrm{d}} Z_t = -\bigg(\frac{{\mathrm{d}} }{{\mathrm{d}} t} L(t)\bigg) X^\circ_t \,{\mathrm{d}} t -\frac{{\mathrm{d}} }{{\mathrm{d}} t} \mu(t)-L(t) \,{\mathrm{d}} X^\circ_t.$$
The results now follow because the first two terms on the right-hand side together equal  $L(t) \tilde{b}(t,X^\circ_t)$
.
$L(t) \tilde{b}(t,X^\circ_t)$
.
Lemma 5.2. We have
 \begin{align*} \frac12 {\mathrm{d}} (Z_t^{\prime} M(t) Z_t) & = \frac12 Z_t^{\prime} M(t) L(t) (\tilde{a}(t)-a_t) L(t)^{\prime} M(t) Z_t \,{\mathrm{d}} t \\[3pt] & \quad\, +Z_t^{\prime} M(t) L(t) (\tilde{b}_t-b_t) \,{\mathrm{d}} t \\[3pt]& \quad\, + Z_t^{\prime} M(t) L(t) {\sigma}_t \,{\mathrm{d}} W_t -\frac12 Z_t^{\prime} M(t) L(t) a_t L(t)^{\prime} M(t) Z_t \,{\mathrm{d}} t \\[3pt]& \quad\, +\mathrm{tr}(L(t) a_t L(t)^{\prime} M(t))\,{\mathrm{d}} t.\end{align*}
\begin{align*} \frac12 {\mathrm{d}} (Z_t^{\prime} M(t) Z_t) & = \frac12 Z_t^{\prime} M(t) L(t) (\tilde{a}(t)-a_t) L(t)^{\prime} M(t) Z_t \,{\mathrm{d}} t \\[3pt] & \quad\, +Z_t^{\prime} M(t) L(t) (\tilde{b}_t-b_t) \,{\mathrm{d}} t \\[3pt]& \quad\, + Z_t^{\prime} M(t) L(t) {\sigma}_t \,{\mathrm{d}} W_t -\frac12 Z_t^{\prime} M(t) L(t) a_t L(t)^{\prime} M(t) Z_t \,{\mathrm{d}} t \\[3pt]& \quad\, +\mathrm{tr}(L(t) a_t L(t)^{\prime} M(t))\,{\mathrm{d}} t.\end{align*}
Proof.By Itô’s lemma,
 $$\frac12 {\mathrm{d}} (Z_t^{\prime} M(t) Z_t) = \frac12 Z_t^{\prime} \frac{{\mathrm{d}} M(t)}{{\mathrm{d}} t} Z_t \,{\mathrm{d}} t +Z_t^{\prime} M(t) \,{\mathrm{d}} Z_t +\mathrm{tr}(L(t) a_t L(t)^{\prime} M(t))\,{\mathrm{d}} t.$$
$$\frac12 {\mathrm{d}} (Z_t^{\prime} M(t) Z_t) = \frac12 Z_t^{\prime} \frac{{\mathrm{d}} M(t)}{{\mathrm{d}} t} Z_t \,{\mathrm{d}} t +Z_t^{\prime} M(t) \,{\mathrm{d}} Z_t +\mathrm{tr}(L(t) a_t L(t)^{\prime} M(t))\,{\mathrm{d}} t.$$
Next, substitute the SDE for  $Z_t$
from Lemma 5.1 and use
$Z_t$
from Lemma 5.1 and use
 $$\frac{{\mathrm{d}} M(t)}{{\mathrm{d}} t} = -M(t) \frac{{\mathrm{d}} M(t)^{-1}}{{\mathrm{d}} t} M(t) =M(t) L(t) \tilde{a}(t) L(t)^{\prime} M(t).$$
$$\frac{{\mathrm{d}} M(t)}{{\mathrm{d}} t} = -M(t) \frac{{\mathrm{d}} M(t)^{-1}}{{\mathrm{d}} t} M(t) =M(t) L(t) \tilde{a}(t) L(t)^{\prime} M(t).$$
The final equality follows from the fact that  ${M^\dagger}(t)=M(t)^{-1}$
satisfies the ordinary differential equation
${M^\dagger}(t)=M(t)^{-1}$
satisfies the ordinary differential equation  ${\mathrm{d}} {M^\dagger}(t)=- L(t) \tilde{a}(t) L(t)^{\prime}\,{\mathrm{d}} t.$
The result follows upon reorganising terms.
${\mathrm{d}} {M^\dagger}(t)=- L(t) \tilde{a}(t) L(t)^{\prime}\,{\mathrm{d}} t.$
The result follows upon reorganising terms.
Whereas in the uniformly elliptic case all elements of  $Z_t$
and M(t) behave in the same way as a function of
$Z_t$
and M(t) behave in the same way as a function of  $T-t$
, this is not so in the hypo-elliptic case. For this reason, we introduce a diagonal scaling matrix
$T-t$
, this is not so in the hypo-elliptic case. For this reason, we introduce a diagonal scaling matrix  $\Delta(t)$
.
$\Delta(t)$
.
Lemma 5.3. Let  $\Delta(t)$
be an invertible
$\Delta(t)$
be an invertible  $m\times m$
diagonal matrix. If
$m\times m$
diagonal matrix. If  ${Z_{\Delta,t}}$
,
${Z_{\Delta,t}}$
,  ${L_{\Delta}}(t)$
and
${L_{\Delta}}(t)$
and  ${M_{\Delta}}(t)$
are as defined in (2.3) and (2.4), then
${M_{\Delta}}(t)$
are as defined in (2.3) and (2.4), then
 \begin{align}\frac12 {\mathrm{d}} ({Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {Z_{\Delta,t}})& = \frac12 {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {L_{\Delta}}(t) (\tilde{a}(t)-a_t) {L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}} \,{\mathrm{d}} t \notag \\[3pt] & \quad\, + {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {L_{\Delta}}(t) (\tilde{b}_t-b_t) \,{\mathrm{d}} t \notag \\[3pt] & \quad\, + {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {L_{\Delta}}(t) {\sigma}_t \,{\mathrm{d}} W_t -\frac12 {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {L_{\Delta}}(t) a_t {L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}} \,{\mathrm{d}} t \notag \\* & \quad\, +\mathrm{tr}({L_{\Delta}}(t) a_t {L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t))\,{\mathrm{d}} t.\end{align}
\begin{align}\frac12 {\mathrm{d}} ({Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {Z_{\Delta,t}})& = \frac12 {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {L_{\Delta}}(t) (\tilde{a}(t)-a_t) {L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}} \,{\mathrm{d}} t \notag \\[3pt] & \quad\, + {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {L_{\Delta}}(t) (\tilde{b}_t-b_t) \,{\mathrm{d}} t \notag \\[3pt] & \quad\, + {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {L_{\Delta}}(t) {\sigma}_t \,{\mathrm{d}} W_t -\frac12 {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {L_{\Delta}}(t) a_t {L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}} \,{\mathrm{d}} t \notag \\* & \quad\, +\mathrm{tr}({L_{\Delta}}(t) a_t {L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t))\,{\mathrm{d}} t.\end{align}
Moreover,
 \begin{equation}\tilde{r}(t,X^\circ_t)={L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}}{.}\end{equation}
\begin{equation}\tilde{r}(t,X^\circ_t)={L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}}{.}\end{equation}
Proof.This is a straightforward consequence of Lemma 5.2. The expression for  $\tilde{r}$
follows from equation (2.2).
$\tilde{r}$
follows from equation (2.2).
5.2. Recap on notation and results
For clarity we summarise our notation, some of which was already defined in Section 1.6. The auxiliary process is defined by the SDE  ${\mathrm{d}} \tilde{X}_t = (\tilde{B}(t) \tilde{X}_t + \tilde\beta(t)) \,{\mathrm{d}} t + \tilde{\sigma}(t) \,{\mathrm{d}} W_t$
. The matrix
${\mathrm{d}} \tilde{X}_t = (\tilde{B}(t) \tilde{X}_t + \tilde\beta(t)) \,{\mathrm{d}} t + \tilde{\sigma}(t) \,{\mathrm{d}} W_t$
. The matrix  $\Phi(t)$
satisfies the ODE
$\Phi(t)$
satisfies the ODE  ${\mathrm{d}} \Phi(t) =\tilde{B}(t) \Phi(t) \,{\mathrm{d}} t$
and we set
${\mathrm{d}} \Phi(t) =\tilde{B}(t) \Phi(t) \,{\mathrm{d}} t$
and we set  $\Phi(T,t)=\Phi(T) \Phi(t)^{-1}$
. A realisation v of
$\Phi(T,t)=\Phi(T) \Phi(t)^{-1}$
. A realisation v of  $V=LX_T$
is observed. The scaled process is defined by
$V=LX_T$
is observed. The scaled process is defined by
 $${Z_{\Delta,t}}=\Delta(t) \bigg( v- \int_t^T L(\tau) \tilde\beta(\tau) \,{\mathrm{d}} \tau-L(t) X^\circ_t \bigg),$$
$${Z_{\Delta,t}}=\Delta(t) \bigg( v- \int_t^T L(\tau) \tilde\beta(\tau) \,{\mathrm{d}} \tau-L(t) X^\circ_t \bigg),$$
where  $ L(t)= L \Phi(T,t)$
and
$ L(t)= L \Phi(T,t)$
and  ${L_{\Delta}}(t)=\Delta(t)L(t). $
Furthermore, we defined
${L_{\Delta}}(t)=\Delta(t)L(t). $
Furthermore, we defined
 $$ M(t)= \bigg(\int_t^T L(\tau) \tilde{a}(\tau) L(\tau)^{\prime} \,{\mathrm{d}} \tau\bigg)^{-1}\quad\text{and}\quad {M_{\Delta}}(t) = \Delta(t)^{-1} M(t) \Delta(t)^{-1},$$
$$ M(t)= \bigg(\int_t^T L(\tau) \tilde{a}(\tau) L(\tau)^{\prime} \,{\mathrm{d}} \tau\bigg)^{-1}\quad\text{and}\quad {M_{\Delta}}(t) = \Delta(t)^{-1} M(t) \Delta(t)^{-1},$$
where  $\tilde{a}(t)=\tilde{\sigma}(t) \tilde{\sigma}(t)^{\prime}$
. Finally, the guiding term in the SDE for the guided proposal
$\tilde{a}(t)=\tilde{\sigma}(t) \tilde{\sigma}(t)^{\prime}$
. Finally, the guiding term in the SDE for the guided proposal  $X^\circ_t$
is given by
$X^\circ_t$
is given by  $a(t,X^\circ_t) {L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}}$
. The process
$a(t,X^\circ_t) {L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}}$
. The process  $t\mapsto {Z_{\Delta,t}}$
is the key object to be studied in this section.
$t\mapsto {Z_{\Delta,t}}$
is the key object to be studied in this section.
5.3. Proof of Proposition 2.2
The line of proof is exactly as suggested in [Reference Mao25, page 341], as follows.
(1) Start with the Lyapunov function
 $V(t,{Z_{\Delta,t}})=\frac12 {Z_{\Delta,t}}{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}}$
.
$V(t,{Z_{\Delta,t}})=\frac12 {Z_{\Delta,t}}{\prime} {M_{\Delta}}(t) {Z_{\Delta,t}}$
.(2) Apply Itô’s lemma to
 $V(t,{Z_{\Delta,t}})$
.
$V(t,{Z_{\Delta,t}})$
.(3) Use martingale inequalities to bound the stochastic integral.
(4) Apply a Gronwall-type inequality.
We bound all terms appearing in equation (5.1). Note that the first term on the right-hand side vanishes. We start with the Wiener integral term. To this end, fix  $t_0 \in [0,T)$
and let
$t_0 \in [0,T)$
and let
 $$N_t= \int_{t_0}^t {Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) {\sigma} \,{\mathrm{d}} W_s.$$
$$N_t= \int_{t_0}^t {Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) {\sigma} \,{\mathrm{d}} W_s.$$
Then
 $$\int_{t_0}^t {Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) {\sigma}_s \,{\mathrm{d}} W_s -\frac12 \int_{t_0}^t {Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s) {Z_{\Delta,s}} \,{\mathrm{d}} s =N_t -\frac12[N]_t.$$
$$\int_{t_0}^t {Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) {\sigma}_s \,{\mathrm{d}} W_s -\frac12 \int_{t_0}^t {Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s) {Z_{\Delta,s}} \,{\mathrm{d}} s =N_t -\frac12[N]_t.$$
Now  $N_t$
can be bounded using an exponential martingale inequality. Let
$N_t$
can be bounded using an exponential martingale inequality. Let  $\{{\gamma}_n\}$
be a sequence of positive numbers. For
$\{{\gamma}_n\}$
be a sequence of positive numbers. For  $n\in {\mathbb{N}}$
, define
$n\in {\mathbb{N}}$
, define  $t_n=T-1/n$
and
$t_n=T-1/n$
and
 $$E_n=\bigg\{ \sup_{0\le t \le t_{n+1}} \bigg( N_t- \frac{1}{2} [N]_t \bigg) > {\gamma}_n\bigg\}.$$
$$E_n=\bigg\{ \sup_{0\le t \le t_{n+1}} \bigg( N_t- \frac{1}{2} [N]_t \bigg) > {\gamma}_n\bigg\}.$$
By the exponential martingale inequality of [Reference Mao26, Theorem 1.7.4], we obtain that  $P(E_n) \le {\mathrm{e}}^{-{\gamma}_n}$
. If we assume
$P(E_n) \le {\mathrm{e}}^{-{\gamma}_n}$
. If we assume  $\sum_{n=1}^\infty {\mathrm{e}}^{-{\gamma}_n}<\infty$
, then by the Borel–Cantelli lemma
$\sum_{n=1}^\infty {\mathrm{e}}^{-{\gamma}_n}<\infty$
, then by the Borel–Cantelli lemma  $ P(\limsup_{n\to \infty} E_n)=0. $
Hence, for almost all
$ P(\limsup_{n\to \infty} E_n)=0. $
Hence, for almost all  $\omega$
, there exists
$\omega$
, there exists  $ n_0(\omega)$
such that, for all
$ n_0(\omega)$
such that, for all  $n\ge n_0(\omega)$
,
$n\ge n_0(\omega)$
,
 \begin{equation} \sup_{t_0\le t \le t_{n+1}} \bigg( N_t -\frac{1}{2}\int_0^t [N]_t \bigg)\le{\gamma}_n.\end{equation}
\begin{equation} \sup_{t_0\le t \le t_{n+1}} \bigg( N_t -\frac{1}{2}\int_0^t [N]_t \bigg)\le{\gamma}_n.\end{equation}
Let  ${\varepsilon}>0$
. Upon taking
${\varepsilon}>0$
. Upon taking  ${\gamma}_n=(1+2{\varepsilon}) \log n$
, we get
${\gamma}_n=(1+2{\varepsilon}) \log n$
, we get
 $$\sum_{n=1}^\infty {\mathrm{e}}^{-{\gamma}_n}=\sum_{n=1}^\infty n^{-1-2{\varepsilon}} <\infty.$$
$$\sum_{n=1}^\infty {\mathrm{e}}^{-{\gamma}_n}=\sum_{n=1}^\infty n^{-1-2{\varepsilon}} <\infty.$$
Since  ${M_{\Delta}}(t)$
is strictly positive definite,
${M_{\Delta}}(t)$
is strictly positive definite,
 $${\lambda_{\rm min}}({M_{\Delta}}(t)) \|{Z_{\Delta,t}}\|^2 \le {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {Z_{\Delta,t}}.$$
$${\lambda_{\rm min}}({M_{\Delta}}(t)) \|{Z_{\Delta,t}}\|^2 \le {Z_{\Delta,t}^{\prime}} {M_{\Delta}}(t) {Z_{\Delta,t}}.$$
Assume  $t_0 < t< t_{n+1}$
. Combining the inequality of the above display with Lemma 5.3 and substituting the bound in (5.3), we obtain, for any
$t_0 < t< t_{n+1}$
. Combining the inequality of the above display with Lemma 5.3 and substituting the bound in (5.3), we obtain, for any  ${\varepsilon}>0$
,
${\varepsilon}>0$
,
 \begin{align*}\frac12{\lambda_{\rm min}}({M_{\Delta}}(t)) \|{Z_{\Delta,t}}\|^2 &\le \frac12 {Z_{\Delta,t_0}} {M_{\Delta}}(t_0) {Z_{\Delta,t_0}}\\ &\quad\, +\int_{t_0}^t \|{Z_{\Delta,s}}\| \| {M_{\Delta}}(s)\| \| {L_{\Delta}}(s) (\tilde{b}_s-b_s)\| \,{\mathrm{d}} s \\ & \quad\, +{\gamma}_n + \int_{t_0}^t \mathrm{tr}({L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s)) \,{\mathrm{d}} s \\ & \quad\, + \frac12 \int_{t_0}^t{Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) (\tilde{a}(s)-a_s) {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s) {Z_{\Delta,s}} \,{\mathrm{d}} s {.}\end{align*}
\begin{align*}\frac12{\lambda_{\rm min}}({M_{\Delta}}(t)) \|{Z_{\Delta,t}}\|^2 &\le \frac12 {Z_{\Delta,t_0}} {M_{\Delta}}(t_0) {Z_{\Delta,t_0}}\\ &\quad\, +\int_{t_0}^t \|{Z_{\Delta,s}}\| \| {M_{\Delta}}(s)\| \| {L_{\Delta}}(s) (\tilde{b}_s-b_s)\| \,{\mathrm{d}} s \\ & \quad\, +{\gamma}_n + \int_{t_0}^t \mathrm{tr}({L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s)) \,{\mathrm{d}} s \\ & \quad\, + \frac12 \int_{t_0}^t{Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) (\tilde{a}(s)-a_s) {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s) {Z_{\Delta,s}} \,{\mathrm{d}} s {.}\end{align*}
Recall that for positive semidefinite matrices A and C we have
 $$|\mathrm{tr}(AC)| \le \mathrm{tr}(A) \mathrm{tr}(C)\le \mathrm{tr}(A) p {\lambda}_{\rm max}(C)$$
$$|\mathrm{tr}(AC)| \le \mathrm{tr}(A) \mathrm{tr}(C)\le \mathrm{tr}(A) p {\lambda}_{\rm max}(C)$$
if  $C \in {\mathbb{R}}^{p\times p}$
. Hence
$C \in {\mathbb{R}}^{p\times p}$
. Hence
 \begin{equation}\mathrm{tr}({L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s)) \le\mathrm{tr}({L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime}) m {\lambda}_{\rm max}({M_{\Delta}}(s)) {.}\end{equation}
\begin{equation}\mathrm{tr}({L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s)) \le\mathrm{tr}({L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime}) m {\lambda}_{\rm max}({M_{\Delta}}(s)) {.}\end{equation}
Furthermore, as
 \begin{equation}\|{M_{\Delta}}(s)\|=\sqrt{ {\lambda}_{\rm max}({M_{\Delta}}(s)^2)} = {\lambda}_{\rm max}({M_{\Delta}}(s)){,}\end{equation}
\begin{equation}\|{M_{\Delta}}(s)\|=\sqrt{ {\lambda}_{\rm max}({M_{\Delta}}(s)^2)} = {\lambda}_{\rm max}({M_{\Delta}}(s)){,}\end{equation}
we can combine the preceding three inequalities to obtain
 \begin{align*} \frac12{\lambda_{\rm min}}({M_{\Delta}}(t)) \|{Z_{\Delta,t}}\|^2 &\le \frac12 {Z_{\Delta,t_0}} {M_{\Delta}}(t_0) {Z_{\Delta,t_0}} \notag\\[3pt] &\quad\, +\int_{t_0}^t \|{Z_{\Delta,s}}\| {\lambda}_{\rm max}({M_{\Delta}}(s)) \| {L_{\Delta}}(s) (\tilde{b}_s-b_s)\| \,{\mathrm{d}} s \notag \\[3pt] & \quad\, +{\gamma}_n + m\int_{t_0}^t \mathrm{tr}({L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime}){\lambda}_{\rm max}({M_{\Delta}}(s)) \,{\mathrm{d}} s \notag \\[3pt] & \quad\, + \frac12 \int_{t_0}^t{Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) (\tilde{a}(s)-a_s) {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s) {Z_{\Delta,s}} \,{\mathrm{d}} s .\end{align*}
\begin{align*} \frac12{\lambda_{\rm min}}({M_{\Delta}}(t)) \|{Z_{\Delta,t}}\|^2 &\le \frac12 {Z_{\Delta,t_0}} {M_{\Delta}}(t_0) {Z_{\Delta,t_0}} \notag\\[3pt] &\quad\, +\int_{t_0}^t \|{Z_{\Delta,s}}\| {\lambda}_{\rm max}({M_{\Delta}}(s)) \| {L_{\Delta}}(s) (\tilde{b}_s-b_s)\| \,{\mathrm{d}} s \notag \\[3pt] & \quad\, +{\gamma}_n + m\int_{t_0}^t \mathrm{tr}({L_{\Delta}}(s)\, a_s\, {L_{\Delta}}(s)^{\prime}){\lambda}_{\rm max}({M_{\Delta}}(s)) \,{\mathrm{d}} s \notag \\[3pt] & \quad\, + \frac12 \int_{t_0}^t{Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) (\tilde{a}(s)-a_s) {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s) {Z_{\Delta,s}} \,{\mathrm{d}} s .\end{align*}
Upon substituting the bounds in (2.5), for certain positive constants  $C_0$
,
$C_0$
,  $C_1$
,
$C_1$
,  $C_2$
,
$C_2$
,  $C_3$
, and
$C_3$
, and  $C_4$
we obtain
$C_4$
we obtain
 \begin{align} (T-t)^{-1} \|{Z_{\Delta,t}}\|^2 &\le C_0+ C_1 \int_{t_0}^t \|{Z_{\Delta,s}}\| (T-s)^{-1} \,{\mathrm{d}} s \notag \\[3pt]& \quad\, +C_2 {\gamma}_n +C_3 \int_{t_0}^t (T-s)^{-1} \,{\mathrm{d}} + C_4 \int_{t_0}^t \|{Z_{\Delta,s}}\|^2 (T-s)^{\alpha-2}.\end{align}
\begin{align} (T-t)^{-1} \|{Z_{\Delta,t}}\|^2 &\le C_0+ C_1 \int_{t_0}^t \|{Z_{\Delta,s}}\| (T-s)^{-1} \,{\mathrm{d}} s \notag \\[3pt]& \quad\, +C_2 {\gamma}_n +C_3 \int_{t_0}^t (T-s)^{-1} \,{\mathrm{d}} + C_4 \int_{t_0}^t \|{Z_{\Delta,s}}\|^2 (T-s)^{\alpha-2}.\end{align}
If we define  $\xi_t=(T-t)^{-1} \|{Z_{\Delta,t}}\|^2$
, then this inequality can be rewritten as
$\xi_t=(T-t)^{-1} \|{Z_{\Delta,t}}\|^2$
, then this inequality can be rewritten as
 \begin{align*} \xi_t &\le C_0 +C_2 {\gamma}_n + C_3 \log\bigg(\frac{T-t_0}{T-t}\bigg) \notag \\[3pt] & \quad\, + C_1 \int_{t_0}^t (T-s)^{-1/2} \sqrt{\xi_s}\,{\mathrm{d}} s + C_4 \int_{t_0}^t (T-s)^{\alpha-1} \xi_s \,{\mathrm{d}} s .\end{align*}
\begin{align*} \xi_t &\le C_0 +C_2 {\gamma}_n + C_3 \log\bigg(\frac{T-t_0}{T-t}\bigg) \notag \\[3pt] & \quad\, + C_1 \int_{t_0}^t (T-s)^{-1/2} \sqrt{\xi_s}\,{\mathrm{d}} s + C_4 \int_{t_0}^t (T-s)^{\alpha-1} \xi_s \,{\mathrm{d}} s .\end{align*}
By Lemma B.1 in the Appendix this implies
 \begin{align*} \xi_t & \leq \bigg( \sqrt{C_0 +C_2 {\gamma}_n + C_3 \log\bigg(\!\frac{T-t_0}{T-t}\!\bigg)} + \frac12 C_1 \big( \sqrt{T- t_0} - \sqrt{T-t} \big)\bigg)^2 \exp\bigg(\!C_4 \int_{t_0}^t (T-s)^{\alpha-1}\!\bigg).\end{align*}
\begin{align*} \xi_t & \leq \bigg( \sqrt{C_0 +C_2 {\gamma}_n + C_3 \log\bigg(\!\frac{T-t_0}{T-t}\!\bigg)} + \frac12 C_1 \big( \sqrt{T- t_0} - \sqrt{T-t} \big)\bigg)^2 \exp\bigg(\!C_4 \int_{t_0}^t (T-s)^{\alpha-1}\!\bigg).\end{align*}
Now divide both sides of this inequality by  $\log(1/(T-t))$
and consider
$\log(1/(T-t))$
and consider  $t_n < t < t_{n+1}$
. Then
$t_n < t < t_{n+1}$
. Then  $\log n \le \log(1/(T-t))$
. It then follows that
$\log n \le \log(1/(T-t))$
. It then follows that
 $$\limsup_{t\uparrow T} \frac{\|{Z_{\Delta,t}}\|^2}{(T-t)\log(1/(T-t))} \le C_2(1+2{\varepsilon}) +C_3.$$
$$\limsup_{t\uparrow T} \frac{\|{Z_{\Delta,t}}\|^2}{(T-t)\log(1/(T-t))} \le C_2(1+2{\varepsilon}) +C_3.$$
Now let  ${\varepsilon}\downarrow 0$
.
${\varepsilon}\downarrow 0$
.
5.4. Proof of Corollary 2.1
As  $\Delta(t)=I_m$
it is easy to see that
$\Delta(t)=I_m$
it is easy to see that  $M(t)={\mathrm{O}} (1/(T-t)$
and
$M(t)={\mathrm{O}} (1/(T-t)$
and  ${L_{\Delta}}(t)={\mathrm{O}} (1)$
. This behaviour of M(t) is also contained in the first inequality of [Reference Schauer, van der Meulen and van Zanten35, Lemma 8] (in that paper,
${L_{\Delta}}(t)={\mathrm{O}} (1)$
. This behaviour of M(t) is also contained in the first inequality of [Reference Schauer, van der Meulen and van Zanten35, Lemma 8] (in that paper,  $\tilde{H}$
corresponds to M as defined here). Now it is easy to see that the conditions of Theorem 2.2 are satisfied.
$\tilde{H}$
corresponds to M as defined here). Now it is easy to see that the conditions of Theorem 2.2 are satisfied.
6. Absolute continuity with respect to the guided proposal distribution
6.1. Proof of Theorem 2.6
We start with a result that gives the Radon–Nikodým derivative of  ${\mathbb{P}}^\star_t$
relative to
${\mathbb{P}}^\star_t$
relative to  ${\mathbb{P}}^\circ_t$
for
${\mathbb{P}}^\circ_t$
for  $t<T$
.
$t<T$
.
Proposition 6.1. For  $t<T$
we have
$t<T$
we have
 \begin{equation*} \frac{{\mathrm{d}} {\mathbb{P}}_t^\star}{{\mathrm{d}} {\mathbb{P}}_t^\circ}(X^\circ) = \frac{\tilde \rho(0,x_0)}{ \rho(0,x_0)}\frac{ \rho(t,X^\circ_t)}{\tilde \rho(t,X^\circ_t)} \Psi_t(X^\circ),\end{equation*}
\begin{equation*} \frac{{\mathrm{d}} {\mathbb{P}}_t^\star}{{\mathrm{d}} {\mathbb{P}}_t^\circ}(X^\circ) = \frac{\tilde \rho(0,x_0)}{ \rho(0,x_0)}\frac{ \rho(t,X^\circ_t)}{\tilde \rho(t,X^\circ_t)} \Psi_t(X^\circ),\end{equation*}
where  $\Psi_t$
is defined in (2.6).
$\Psi_t$
is defined in (2.6).
Proof.Although this result is not a special case of [35, Proposition 1] (where it is assumed that  $L=I$
and that the diffusion is uniformly elliptic), the arguments for deriving the likelihood ratio of
$L=I$
and that the diffusion is uniformly elliptic), the arguments for deriving the likelihood ratio of  ${\mathbb{P}}^\star_t$
with respect to
${\mathbb{P}}^\star_t$
with respect to  ${\mathbb{P}}^\circ_t$
are the same and therefore omitted. The only thing that needs to be checked is that
${\mathbb{P}}^\circ_t$
are the same and therefore omitted. The only thing that needs to be checked is that  $\tilde\rho(t,x)$
satisfies the Kolmogorov backward equation associated with
$\tilde\rho(t,x)$
satisfies the Kolmogorov backward equation associated with  $\tilde X$
. This can be proved along the lines of Lemma 3.4 and Corollary 3.5 of [Reference van der Meulen and Schauer40]. Let
$\tilde X$
. This can be proved along the lines of Lemma 3.4 and Corollary 3.5 of [Reference van der Meulen and Schauer40]. Let  $\tilde{\mathcal{F}}_t ={\sigma}(\tilde{X}_s,\, 0\le s \le t)$
and set
$\tilde{\mathcal{F}}_t ={\sigma}(\tilde{X}_s,\, 0\le s \le t)$
and set  $\tilde{Y}_t =\tilde\rho(t,\tilde{X}_t)$
. Now
$\tilde{Y}_t =\tilde\rho(t,\tilde{X}_t)$
. Now
 \begin{align*} {{\mathbb{E}}}[{\tilde{Y}_t \mid \tilde{\mathcal{F}}_s}] & = \int_{{\mathbb{R}}^d} \tilde\rho(t,x) \tilde{p}(s,\tilde{X}_s;\ t,x) \,{\mathrm{d}} x \\[3pt] & = \int_{{\mathbb{R}}^d} \tilde{p}(s,\tilde{X}_s;\ t,x) \int_{{\mathbb{R}}^{d-m}} \Bigg(\tilde{p}t,x;\ T, \sum_{j=1}^d \xi_j f_j\Bigg) \,{\mathrm{d}} \xi_{m+1},\ldots, {\mathrm{d}} \xi_d \\[3pt] & =\int_{{\mathbb{R}}^{d-m}} \tilde{p}\Bigg(s,\tilde{X}_s;\ T, \sum_{j=1}^d \xi_j f_j\Bigg)\,{\mathrm{d}} \xi_{m+1},\ldots, {\mathrm{d}} \xi_d = \tilde\rho(s,\tilde{X}_s)=\tilde{Y}_s.\end{align*}
\begin{align*} {{\mathbb{E}}}[{\tilde{Y}_t \mid \tilde{\mathcal{F}}_s}] & = \int_{{\mathbb{R}}^d} \tilde\rho(t,x) \tilde{p}(s,\tilde{X}_s;\ t,x) \,{\mathrm{d}} x \\[3pt] & = \int_{{\mathbb{R}}^d} \tilde{p}(s,\tilde{X}_s;\ t,x) \int_{{\mathbb{R}}^{d-m}} \Bigg(\tilde{p}t,x;\ T, \sum_{j=1}^d \xi_j f_j\Bigg) \,{\mathrm{d}} \xi_{m+1},\ldots, {\mathrm{d}} \xi_d \\[3pt] & =\int_{{\mathbb{R}}^{d-m}} \tilde{p}\Bigg(s,\tilde{X}_s;\ T, \sum_{j=1}^d \xi_j f_j\Bigg)\,{\mathrm{d}} \xi_{m+1},\ldots, {\mathrm{d}} \xi_d = \tilde\rho(s,\tilde{X}_s)=\tilde{Y}_s.\end{align*}
That is,  ${(\tilde{Y}_t, \tilde{\mathcal{F}}_t)}$
is a martingale. If
${(\tilde{Y}_t, \tilde{\mathcal{F}}_t)}$
is a martingale. If  $\tilde{\mathcal{L}}$
denotes the infinitesimal generator of
$\tilde{\mathcal{L}}$
denotes the infinitesimal generator of  $\tilde{X}_t$
, then
$\tilde{X}_t$
, then  $\mathcal{K}=\partial / (\partial t) + \tilde{\mathcal{L}}$
is the infinitesimal generator of the space–time process
$\mathcal{K}=\partial / (\partial t) + \tilde{\mathcal{L}}$
is the infinitesimal generator of the space–time process  ${(t,\tilde{Y}_t)}$
. Since
${(t,\tilde{Y}_t)}$
. Since  $\tilde{Y}_t$
is a martingale, the mapping
$\tilde{Y}_t$
is a martingale, the mapping  ${(t,x) \mapsto \tilde\rho(t,x)}$
is space–time harmonic. Then by Proposition 1.7 in Chapter VII of [Reference Revuz and Yor32],
${(t,x) \mapsto \tilde\rho(t,x)}$
is space–time harmonic. Then by Proposition 1.7 in Chapter VII of [Reference Revuz and Yor32],  $\mathcal{K} \tilde\rho(t,x)=0$
. That is,
$\mathcal{K} \tilde\rho(t,x)=0$
. That is,  $\tilde{\rho}(t,x)$
satisfies Kolmogorov’s backward equation.
$\tilde{\rho}(t,x)$
satisfies Kolmogorov’s backward equation.
This absolute continuity result is only useful for simulating conditioned diffusions if it can be shown to hold in the limit  $t\uparrow T$
as well. The main line of proof is the same as in the proof of [Reference Schauer, van der Meulen and van Zanten35, Theorem 1], where at various places p and
$t\uparrow T$
as well. The main line of proof is the same as in the proof of [Reference Schauer, van der Meulen and van Zanten35, Theorem 1], where at various places p and  $\tilde{p}$
need to be replaced with
$\tilde{p}$
need to be replaced with  $\rho$
and
$\rho$
and  $\tilde\rho$
. However, some of the auxiliary results that are used require new arguments in the present setting. Moreover, the assumed Aronson-type bounds are not suitable for hypo-elliptic diffusions.
$\tilde\rho$
. However, some of the auxiliary results that are used require new arguments in the present setting. Moreover, the assumed Aronson-type bounds are not suitable for hypo-elliptic diffusions.
6.2. Proof of Theorem 2.6
We start by introducing some notation. Define the mapping  $g_{\Delta}\colon [0,\infty) \times {\mathbb{R}}^d \to {\mathbb{R}}^m$
by
$g_{\Delta}\colon [0,\infty) \times {\mathbb{R}}^d \to {\mathbb{R}}^m$
by
 $$g_{\Delta}(t,x) = \Delta(t) ( v-\mu(t) - L(t) x)$$
$$g_{\Delta}(t,x) = \Delta(t) ( v-\mu(t) - L(t) x)$$
and note that  ${Z_{\Delta,t}} = g_{\Delta}(t,X^\circ_t)$
. For a diffusion process Y we define the stopping time
${Z_{\Delta,t}} = g_{\Delta}(t,X^\circ_t)$
. For a diffusion process Y we define the stopping time
 $${\sigma}_k(Y) = T \wedge \inf_{t\in [0,T]} \big\{ \|g_{\Delta}(t,Y_t)\| \ge k \sqrt{(T-t) \log(1/(T-t))}\big\},$$
$${\sigma}_k(Y) = T \wedge \inf_{t\in [0,T]} \big\{ \|g_{\Delta}(t,Y_t)\| \ge k \sqrt{(T-t) \log(1/(T-t))}\big\},$$
where  $k\in {\mathbb{N}}$
. We write
$k\in {\mathbb{N}}$
. We write
 $${\sigma}_k^\circ = {\sigma}_k(X^\circ) \quad {\sigma}_k = {\sigma}_k(X)\quad {\sigma}_k^\star = {\sigma}_k(X^\star).$$
$${\sigma}_k^\circ = {\sigma}_k(X^\circ) \quad {\sigma}_k = {\sigma}_k(X)\quad {\sigma}_k^\star = {\sigma}_k(X^\star).$$
Define  $\bar\rho = \tilde\rho(0,x_0)/\rho(0,x_0)$
. By Proposition 6.1, for any
$\bar\rho = \tilde\rho(0,x_0)/\rho(0,x_0)$
. By Proposition 6.1, for any  $t<T$
and bounded,
$t<T$
and bounded,  $\mathcal F_t$
-measurable f, we have
$\mathcal F_t$
-measurable f, we have
 \begin{equation}{{\mathbb{E}}}\bigg[{ f(X^\star) \frac{ \tilde \rho(t, X^\star_t)}{\rho(t, X^\star_t)}}\bigg] ={{\mathbb{E}}}[{ f(X^\circ) \bar{\rho} \: \Psi_t(X^\circ)}].\end{equation}
\begin{equation}{{\mathbb{E}}}\bigg[{ f(X^\star) \frac{ \tilde \rho(t, X^\star_t)}{\rho(t, X^\star_t)}}\bigg] ={{\mathbb{E}}}[{ f(X^\circ) \bar{\rho} \: \Psi_t(X^\circ)}].\end{equation}
By taking  $f_t(x)={\textbf{1}}\{t\le {\sigma}_k(x)\}$
, we get
$f_t(x)={\textbf{1}}\{t\le {\sigma}_k(x)\}$
, we get
 \begin{equation}\bar\rho\, {\mathbb{E}}[ \Psi_t(X^\circ) {\textbf{1}}\{t\le {\sigma}^\circ_k\}] = {\mathbb{E}}\bigg[ \frac{\tilde\rho(t,X^\star_t)}{\rho(t,X^\star_t)} {\textbf{1}}\{t\le {\sigma}^\star_k\}\bigg].\end{equation}
\begin{equation}\bar\rho\, {\mathbb{E}}[ \Psi_t(X^\circ) {\textbf{1}}\{t\le {\sigma}^\circ_k\}] = {\mathbb{E}}\bigg[ \frac{\tilde\rho(t,X^\star_t)}{\rho(t,X^\star_t)} {\textbf{1}}\{t\le {\sigma}^\star_k\}\bigg].\end{equation}
Next, we take  $\lim_{k\to\infty} \lim_{t\uparrow T}$
on both sides. We start with the left-hand side. By Lemma 6.1, for each
$\lim_{k\to\infty} \lim_{t\uparrow T}$
on both sides. We start with the left-hand side. By Lemma 6.1, for each  $k\in{\mathbb{N}}$
,
$k\in{\mathbb{N}}$
,  $\sup_{0\le t\le T}\Psi_t(X^\circ)$
is uniformly bounded on the event
$\sup_{0\le t\le T}\Psi_t(X^\circ)$
is uniformly bounded on the event  $\{T={\sigma}_k^\circ\}$
. Hence, by the dominated convergence theorem we obtain
$\{T={\sigma}_k^\circ\}$
. Hence, by the dominated convergence theorem we obtain
 $$\lim_{k\to\infty} \lim_{t\uparrow T}{\mathbb{E}}[ \Psi_t(X^\circ) {\textbf{1}}\{t\le {\sigma}^\circ_k\}] = \lim_{k\to \infty} {\mathbb{E}}[ \Psi_T(X^\circ) {\textbf{1}}\{T\le {\sigma}^\circ_k\}].$$
$$\lim_{k\to\infty} \lim_{t\uparrow T}{\mathbb{E}}[ \Psi_t(X^\circ) {\textbf{1}}\{t\le {\sigma}^\circ_k\}] = \lim_{k\to \infty} {\mathbb{E}}[ \Psi_T(X^\circ) {\textbf{1}}\{T\le {\sigma}^\circ_k\}].$$
Since by definition  ${\sigma}^\circ_k\le T$
, we have
${\sigma}^\circ_k\le T$
, we have  $\{T\le {\sigma}^\circ_k\}=\{T= {\sigma}^\circ_k\}$
. Furthermore,
$\{T\le {\sigma}^\circ_k\}=\{T= {\sigma}^\circ_k\}$
. Furthermore,
 $${\textbf{1}}\{T={\sigma}^\circ_k\} = {\textbf{1}}\big\{\|Z^\circ_{\Delta,t}\| \le k \sqrt{(T-t) \log(1/(T-t))} \big\} \uparrow 1 \quad \text{as } k \to \infty,$$
$${\textbf{1}}\{T={\sigma}^\circ_k\} = {\textbf{1}}\big\{\|Z^\circ_{\Delta,t}\| \le k \sqrt{(T-t) \log(1/(T-t))} \big\} \uparrow 1 \quad \text{as } k \to \infty,$$
by Proposition 2.2. Therefore, by monotone convergence,
 $$\lim_{k\to\infty} \lim_{t\uparrow T}{\mathbb{E}}[ \Psi_t(X^\circ) {\textbf{1}}\{t\le {\sigma}^\circ_k\}] = {\mathbb{E}}[ \Psi_T(X^\circ)].$$
$$\lim_{k\to\infty} \lim_{t\uparrow T}{\mathbb{E}}[ \Psi_t(X^\circ) {\textbf{1}}\{t\le {\sigma}^\circ_k\}] = {\mathbb{E}}[ \Psi_T(X^\circ)].$$
It remains to show that the right-hand side of (6.2) tends to 1. We write
 \begin{align*} \rho(0,x_0) {\mathbb{E}}\bigg[ \frac{\tilde\rho(t,X^\star_t)}{\rho(t,X^\star_t)} {\textbf{1}}\{t\le {\sigma}^\star_k\}\bigg] &= {\mathbb{E}}[ \tilde\rho(t,X_t) {\textbf{1}}\{t\le {\sigma}_k\}] \\[3pt] & ={\mathbb{E}}[ \tilde\rho(t,X_t)] - {\mathbb{E}}[ \tilde\rho(t,X_t) {\textbf{1}}\{t> {\sigma}_k\}]{.}\end{align*}
\begin{align*} \rho(0,x_0) {\mathbb{E}}\bigg[ \frac{\tilde\rho(t,X^\star_t)}{\rho(t,X^\star_t)} {\textbf{1}}\{t\le {\sigma}^\star_k\}\bigg] &= {\mathbb{E}}[ \tilde\rho(t,X_t) {\textbf{1}}\{t\le {\sigma}_k\}] \\[3pt] & ={\mathbb{E}}[ \tilde\rho(t,X_t)] - {\mathbb{E}}[ \tilde\rho(t,X_t) {\textbf{1}}\{t> {\sigma}_k\}]{.}\end{align*}
By Lemma 6.3 the first of the terms on the right-hand side tends to  $\rho(0,x_0)$
when
$\rho(0,x_0)$
when  $t\uparrow T$
. The second term tends to zero by Lemma 6.4.
$t\uparrow T$
. The second term tends to zero by Lemma 6.4.
To complete the proof we note that by equation (6.1) and Lemma 6.3 we have  $\bar \rho\, {{\mathbb{E}}}[{\Psi_t(X^\circ)}] \to 1$
as
$\bar \rho\, {{\mathbb{E}}}[{\Psi_t(X^\circ)}] \to 1$
as  $t\uparrow T$
. In view of the preceding and Scheffé’s lemma this implies that
$t\uparrow T$
. In view of the preceding and Scheffé’s lemma this implies that  $\Psi_t(X^\circ) \to \Psi_T(X^\circ)$
in the
$\Psi_t(X^\circ) \to \Psi_T(X^\circ)$
in the  $L^1$
-sense as
$L^1$
-sense as  $t \uparrow T$
. Hence for
$t \uparrow T$
. Hence for  $s< T$
and a bounded,
$s< T$
and a bounded,  $\mathcal{F}_s$
-measurable, continuous functional g,
$\mathcal{F}_s$
-measurable, continuous functional g,
 $${{\mathbb{E}}}[{g(X^\circ) \bar \rho \Psi_T(X^\circ)}] = \lim_{t \uparrow T} {{\mathbb{E}}}\bigg[{g(X^\star)\frac{\tilde \rho(t, X^\star_{t})}{\rho(t, X^\star_{t})}}\bigg].$$
$${{\mathbb{E}}}[{g(X^\circ) \bar \rho \Psi_T(X^\circ)}] = \lim_{t \uparrow T} {{\mathbb{E}}}\bigg[{g(X^\star)\frac{\tilde \rho(t, X^\star_{t})}{\rho(t, X^\star_{t})}}\bigg].$$
By Lemma 6.3 this converges to  ${\mathbb{E}}\, g (X^\star)$
as
${\mathbb{E}}\, g (X^\star)$
as  $t \uparrow T$
and we find that
$t \uparrow T$
and we find that  ${\mathbb{E}}\, g(X^\circ) \bar \rho \Psi_T(X^\circ) = {\mathbb{E}}\, g (X^\star)$
.
${\mathbb{E}}\, g(X^\circ) \bar \rho \Psi_T(X^\circ) = {\mathbb{E}}\, g (X^\star)$
.
Lemma 6.1. Under Assumption 2.4there exists a positive constant K (not depending on k) such that
 $$\Psi_t(X^\circ) {\textbf{1}}_{t\le {\sigma}^\circ_m} \le \exp(Kk^2).$$
$$\Psi_t(X^\circ) {\textbf{1}}_{t\le {\sigma}^\circ_m} \le \exp(Kk^2).$$
Proof.To bound  $\Psi_t(X^\circ)$
, we will first rewrite
$\Psi_t(X^\circ)$
, we will first rewrite  $\mathcal{G}(s,X^\circ)$
in terms of
$\mathcal{G}(s,X^\circ)$
in terms of  ${Z_{\Delta,t}}$
,
${Z_{\Delta,t}}$
,  ${L_{\Delta}}(t)$
and
${L_{\Delta}}(t)$
and  ${M_{\Delta}}(t)$
, as defined in (2.3) and (2.4). By (5.2), we have
${M_{\Delta}}(t)$
, as defined in (2.3) and (2.4). By (5.2), we have
 $$\tilde{r}(t,X^\circ_t)={L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t){Z_{\Delta,t}} \quad \text{and} \quad \tilde{H}(t)={L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {L_{\Delta}}(t).$$
$$\tilde{r}(t,X^\circ_t)={L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t){Z_{\Delta,t}} \quad \text{and} \quad \tilde{H}(t)={L_{\Delta}}(t)^{\prime} {M_{\Delta}}(t) {L_{\Delta}}(t).$$
Here, the expression for  $\tilde{H}(t)$
was obtained from
$\tilde{H}(t)$
was obtained from
 $$\tilde{H}(t)= -{\,\mathrm D} L(t)^{\prime} M(t) (v-\mu(t)-L(t)x)={\,\mathrm D} (L(t)^{\prime} M(t) L(t) x)= L(t)^{\prime} M(t) L(t).$$
$$\tilde{H}(t)= -{\,\mathrm D} L(t)^{\prime} M(t) (v-\mu(t)-L(t)x)={\,\mathrm D} (L(t)^{\prime} M(t) L(t) x)= L(t)^{\prime} M(t) L(t).$$
Hence
 \begin{align*} \mathcal{G}(s,X^\circ_s) &= (b(s,X^\circ_s) - \tilde b(s,X^\circ_s))^{\prime} {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s){Z_{\Delta,s}} \notag \\[3pt] & \quad\, - \frac12 \mathrm{tr}([a_s - \tilde a(s)] {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s)) \notag \\[3pt] & \quad\, +\frac12 {Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) [a_s - \tilde a(s)] {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s){Z_{\Delta,s}} .\end{align*}
\begin{align*} \mathcal{G}(s,X^\circ_s) &= (b(s,X^\circ_s) - \tilde b(s,X^\circ_s))^{\prime} {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s){Z_{\Delta,s}} \notag \\[3pt] & \quad\, - \frac12 \mathrm{tr}([a_s - \tilde a(s)] {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s)) \notag \\[3pt] & \quad\, +\frac12 {Z_{\Delta,s}}^{\prime} {M_{\Delta}}(s) {L_{\Delta}}(s) [a_s - \tilde a(s)] {L_{\Delta}}(s)^{\prime} {M_{\Delta}}(s){Z_{\Delta,s}} .\end{align*}
On the event  $\{t \le {\sigma}_k^\circ\}$
we have
$\{t \le {\sigma}_k^\circ\}$
we have
 $$\|{Z_{\Delta,t}}\| \le k \sqrt{(T-t) \log(1/(T-t))}.$$
$$\|{Z_{\Delta,t}}\| \le k \sqrt{(T-t) \log(1/(T-t))}.$$
The absolute value of the first term of  $\mathcal{G}$
can be bounded by
$\mathcal{G}$
can be bounded by
 \begin{align*} & \| {M_{\Delta}}(s)\|\!\| {L_{\Delta}}(s)( \tilde{b}(s,X^\circ_s)-b(s,X^\circ_s) )\|\!\|{Z_{\Delta,s}}\| \\[3pt] & \quad \le (T-s)^{-1} \|{Z_{\Delta,s}}\| \\[3pt] &\quad \le c_1 m (T-s)^{-1/2} \sqrt{\log(1/(T-s))}.\end{align*}
\begin{align*} & \| {M_{\Delta}}(s)\|\!\| {L_{\Delta}}(s)( \tilde{b}(s,X^\circ_s)-b(s,X^\circ_s) )\|\!\|{Z_{\Delta,s}}\| \\[3pt] & \quad \le (T-s)^{-1} \|{Z_{\Delta,s}}\| \\[3pt] &\quad \le c_1 m (T-s)^{-1/2} \sqrt{\log(1/(T-s))}.\end{align*}
Here we bounded  $\|{M_{\Delta}}(t)\| \le {\lambda_{\rm max}}({M_{\Delta}}(t))$
, as in (5.5). The absolute value of twice the second term of
$\|{M_{\Delta}}(t)\| \le {\lambda_{\rm max}}({M_{\Delta}}(t))$
, as in (5.5). The absolute value of twice the second term of  $\mathcal{G}$
can be bounded by
$\mathcal{G}$
can be bounded by
 $$\mathrm{tr}({L_{\Delta}}(s) (a_s-\tilde{a}(s)) {L_{\Delta}}(s)^{\prime} ) k {\lambda}_{\rm max}({M_{\Delta}}(s)),$$
$$\mathrm{tr}({L_{\Delta}}(s) (a_s-\tilde{a}(s)) {L_{\Delta}}(s)^{\prime} ) k {\lambda}_{\rm max}({M_{\Delta}}(s)),$$
just as in (5.4). As for a  $p\times p$
matrix A we have
$p\times p$
matrix A we have  $\mathrm{tr}(A)\le p {\lambda_{\rm max}}(A) = p \|A\|^2$
(recall we assume the spectral norm on matrices throughout), this can be bounded by
$\mathrm{tr}(A)\le p {\lambda_{\rm max}}(A) = p \|A\|^2$
(recall we assume the spectral norm on matrices throughout), this can be bounded by
 $$m\|{L_{\Delta}}(s) (a_s-\tilde{a}(s)) {L_{\Delta}}(s)^{\prime}\|^2 m {\lambda}_{\rm max}({M_{\Delta}}(s)) \le m^2 c_3 \bar{c}(T-s)^{2\alpha-1} {.}$$
$$m\|{L_{\Delta}}(s) (a_s-\tilde{a}(s)) {L_{\Delta}}(s)^{\prime}\|^2 m {\lambda}_{\rm max}({M_{\Delta}}(s)) \le m^2 c_3 \bar{c}(T-s)^{2\alpha-1} {.}$$
The absolute value of twice the third term of  $\mathcal{G}$
can be bounded by
$\mathcal{G}$
can be bounded by
 \begin{align*} & \|{Z_{\Delta,s}}\|^2 \|{M_{\Delta}}(s)\|^2 \|{L_{\Delta}}(s) (a(s)-\tilde{a}(s)) {L_{\Delta}}(s)^{\prime}\| \\[3pt] & \quad \le k^2 (T-s) \log(1/(T-s)) \bar{c}^2 (T-s)^{-2} c_3 (T-s)^\alpha\\[3pt] & \quad \le k^2 \bar{c}^2 c_3 (T-s)^{\alpha-1} \log(1/(T-s)).\end{align*}
\begin{align*} & \|{Z_{\Delta,s}}\|^2 \|{M_{\Delta}}(s)\|^2 \|{L_{\Delta}}(s) (a(s)-\tilde{a}(s)) {L_{\Delta}}(s)^{\prime}\| \\[3pt] & \quad \le k^2 (T-s) \log(1/(T-s)) \bar{c}^2 (T-s)^{-2} c_3 (T-s)^\alpha\\[3pt] & \quad \le k^2 \bar{c}^2 c_3 (T-s)^{\alpha-1} \log(1/(T-s)).\end{align*}
We conclude that all three terms in  $\mathcal{G}$
are integrable on [0, T].
$\mathcal{G}$
are integrable on [0, T].
Lemma 6.2. For all bounded, continuous  $f\colon [0,T] \times {\mathbb{R}}^d \to {\mathbb{R}}$
,
$f\colon [0,T] \times {\mathbb{R}}^d \to {\mathbb{R}}$
,
 $$\lim_{t\uparrow T} \int f(t,x) \tilde{p}(t,x;\ T,v) \,{\mathrm{d}} x = f(T,v).$$
$$\lim_{t\uparrow T} \int f(t,x) \tilde{p}(t,x;\ T,v) \,{\mathrm{d}} x = f(T,v).$$
Proof.The proof is just as in Lemma 7 of [Reference Schauer, van der Meulen and van Zanten35].
Lemma 6.3. If Assumption 2.5 holds true,  $0<t_1 < t_2 < \dots < t_N< t < T$
, and
$0<t_1 < t_2 < \dots < t_N< t < T$
, and  $g \in C_b({\mathbb{R}}^{Nd})$
, then
$g \in C_b({\mathbb{R}}^{Nd})$
, then
 $$\lim_{t \uparrow T} {{\mathbb{E}}}\bigg[{g(X^\star_{t_1}, \ldots, X^\star_{t_N}) \frac{\tilde \rho(t, X^\star_{t})}{ \rho(t, X^\star_{t})}}\bigg] = {{\mathbb{E}}}[{g(X^\star_{t_1}, \ldots, X^\star_{t_N})}].$$
$$\lim_{t \uparrow T} {{\mathbb{E}}}\bigg[{g(X^\star_{t_1}, \ldots, X^\star_{t_N}) \frac{\tilde \rho(t, X^\star_{t})}{ \rho(t, X^\star_{t})}}\bigg] = {{\mathbb{E}}}[{g(X^\star_{t_1}, \ldots, X^\star_{t_N})}].$$
Proof.The joint density q of  ${(X_{t_1}, \ldots, X_{t_N})}$
, conditional on
${(X_{t_1}, \ldots, X_{t_N})}$
, conditional on  $X_{t_0}=x_0$
, is given by
$X_{t_0}=x_0$
, is given by
 $$q(x_1,\ldots, x_N) = \prod_{i=1}^N p(t_{i-1}, x_{i-1};\ t_i, x_i) .$$
$$q(x_1,\ldots, x_N) = \prod_{i=1}^N p(t_{i-1}, x_{i-1};\ t_i, x_i) .$$
Hence
 \begin{align}& {{\mathbb{E}}}\bigg[{g(X^\star_{t_1}, \ldots, X^\star_{t_N}) \frac{\tilde \rho(t, X^\star_{t})}{ \rho(t, X^\star_{t})}}\bigg] \notag \\* & \quad = \int g(x_1,\ldots,x_N) \frac{\tilde{ \rho}(t,x)}{ \rho(t,x)} q(x_1,\ldots,x_N) \frac{p(t_N,x_N;\ t,x) \rho(t,x)}{ \rho(0,x_0)} \,{\mathrm{d}} x_1\ldots {\mathrm{d}} x_N \,{\mathrm{d}} x \notag \\* & \quad = \frac{1}{\rho(0,x_0)} \int g(x_1,\ldots,x_N) q(x_1,\ldots, x_N) F(t;\ t_N, x_N) \,{\mathrm{d}} x_1\ldots {\mathrm{d}} x_N,\end{align}
\begin{align}& {{\mathbb{E}}}\bigg[{g(X^\star_{t_1}, \ldots, X^\star_{t_N}) \frac{\tilde \rho(t, X^\star_{t})}{ \rho(t, X^\star_{t})}}\bigg] \notag \\* & \quad = \int g(x_1,\ldots,x_N) \frac{\tilde{ \rho}(t,x)}{ \rho(t,x)} q(x_1,\ldots,x_N) \frac{p(t_N,x_N;\ t,x) \rho(t,x)}{ \rho(0,x_0)} \,{\mathrm{d}} x_1\ldots {\mathrm{d}} x_N \,{\mathrm{d}} x \notag \\* & \quad = \frac{1}{\rho(0,x_0)} \int g(x_1,\ldots,x_N) q(x_1,\ldots, x_N) F(t;\ t_N, x_N) \,{\mathrm{d}} x_1\ldots {\mathrm{d}} x_N,\end{align}
where for  $t_N<t<T$
$t_N<t<T$
 $$F(t;\ t_N, x_N)=\int p(t_N, x_N;\ t,x) \tilde{\rho}(t,x) \,{\mathrm{d}} x.$$
$$F(t;\ t_N, x_N)=\int p(t_N, x_N;\ t,x) \tilde{\rho}(t,x) \,{\mathrm{d}} x.$$
We can assume  $t\ge (T+t_N)/2$
. For fixed
$t\ge (T+t_N)/2$
. For fixed  $t_N$
and
$t_N$
and  $x_N$
, the mapping
$x_N$
, the mapping  ${(t,x) \mapsto p(t_N, x_N;\ t,x)}$
is continuous and bounded, for t bounded away from
${(t,x) \mapsto p(t_N, x_N;\ t,x)}$
is continuous and bounded, for t bounded away from  $t_N$
. By Lemma 6.2 it follows that
$t_N$
. By Lemma 6.2 it follows that  $F(t;\ t_N, x_N) \to \rho(t_N,x_N)$
when
$F(t;\ t_N, x_N) \to \rho(t_N,x_N)$
when  $t\uparrow T$
. The argument is finished by taking the limit
$t\uparrow T$
. The argument is finished by taking the limit  $t\uparrow T$
on both sides of equation (6.3), interchanging limit and integral on the right-hand side and noting that the limit on the right-hand side coincides with
$t\uparrow T$
on both sides of equation (6.3), interchanging limit and integral on the right-hand side and noting that the limit on the right-hand side coincides with  ${{\mathbb{E}}}[{g(X^\star_{t_1}, \ldots, X^\star_{t_N})}]$
.
${{\mathbb{E}}}[{g(X^\star_{t_1}, \ldots, X^\star_{t_N})}]$
.
The interchange is permitted by dominated convergence. To see this, first note that g is assumed to be bounded. Next,
 $$\int \Bigg(\prod_{i=1}^n p(t_{i-1}, x_{i-1};\ t_i, x_i)\Bigg) p(t_N,x_N;\ t,x) \tilde\rho(t,x) \,{\mathrm{d}} x \,{\mathrm{d}} x_1\ldots {\mathrm{d}} x_N \le C^{N+1} \tilde\rho(t_0,x_0),$$
$$\int \Bigg(\prod_{i=1}^n p(t_{i-1}, x_{i-1};\ t_i, x_i)\Bigg) p(t_N,x_N;\ t,x) \tilde\rho(t,x) \,{\mathrm{d}} x \,{\mathrm{d}} x_1\ldots {\mathrm{d}} x_N \le C^{N+1} \tilde\rho(t_0,x_0),$$
which follows from repeated application of Assumption 2.5.
Lemma 6.4. Assume that there exists a positive  $\delta$
such that
$\delta$
such that  $|\Delta(t)| \lesssim (T-t)^{-\delta}$
. If Assumption 2.5 holds true, then
$|\Delta(t)| \lesssim (T-t)^{-\delta}$
. If Assumption 2.5 holds true, then
 $$\lim_{k\to \infty} \lim_{t \uparrow T}{{\mathbb{E}}}[{ \tilde\rho(t,X_t) {\textbf{1}}\{t> {\sigma}_k\}}] .$$
$$\lim_{k\to \infty} \lim_{t \uparrow T}{{\mathbb{E}}}[{ \tilde\rho(t,X_t) {\textbf{1}}\{t> {\sigma}_k\}}] .$$
Proof.As in the proof of [Reference Schauer, van der Meulen and van Zanten35, Lemma 5], it suffices to show that
 \begin{equation*} \lim_{k\to \infty} \lim_{t \uparrow T} {{\mathbb{E}}}\bigg[{ {\textbf{1}}_{\{t >\sigma_k\}} \int p(\sigma_k,X_{\sigma_k};\ t,z) \tilde \rho(t ,z) \,{\mathrm{d}} z }\bigg] =0 .\end{equation*}
\begin{equation*} \lim_{k\to \infty} \lim_{t \uparrow T} {{\mathbb{E}}}\bigg[{ {\textbf{1}}_{\{t >\sigma_k\}} \int p(\sigma_k,X_{\sigma_k};\ t,z) \tilde \rho(t ,z) \,{\mathrm{d}} z }\bigg] =0 .\end{equation*}
Applying Assumption 2.5 and using the Chapman–Kolmogorov relations, we obtain
 $$\int p(\sigma_k,X_{\sigma_k};\ t,z) \tilde \rho(t ,z) \,{\mathrm{d}} z \le C \tilde\rho(\sigma_k,X_{\sigma_k}).$$
$$\int p(\sigma_k,X_{\sigma_k};\ t,z) \tilde \rho(t ,z) \,{\mathrm{d}} z \le C \tilde\rho(\sigma_k,X_{\sigma_k}).$$
Define  $\tilde{Z}_t=v-\mu(t) - L(t) \tilde{X}_t$
. If we denote its transition density by
$\tilde{Z}_t=v-\mu(t) - L(t) \tilde{X}_t$
. If we denote its transition density by  $\tilde{q}$
, then
$\tilde{q}$
, then
 $$\tilde\rho(t,y) = \tilde{q}(t,v-\mu(t)-L(t) y;\ T, 0), \quad y \in {\mathbb{R}}^d \quad \text{and}\quad t\in [0,T),$$
$$\tilde\rho(t,y) = \tilde{q}(t,v-\mu(t)-L(t) y;\ T, 0), \quad y \in {\mathbb{R}}^d \quad \text{and}\quad t\in [0,T),$$
since  $\tilde{r}(t,x)$
depends on x only via L(t)x. Define the set
$\tilde{r}(t,x)$
depends on x only via L(t)x. Define the set
 $$\mathcal{A}_k = \{(t,y) \in [0,T) \times {\mathbb{R}}^d \colon \|\Delta(t)(v-\mu(t)-L(t)y)\| = k \eta(t)\},$$
$$\mathcal{A}_k = \{(t,y) \in [0,T) \times {\mathbb{R}}^d \colon \|\Delta(t)(v-\mu(t)-L(t)y)\| = k \eta(t)\},$$
where  $\eta(t) = \sqrt{(T-t)\log(1/(T-t))}$
. Then
$\eta(t) = \sqrt{(T-t)\log(1/(T-t))}$
. Then
 $${{\mathbb{E}}}\bigg[{ {\textbf{1}}_{\{t >\sigma_k\}} \int p(\sigma_k,X_{\sigma_k};\ t,z) \tilde \rho(t ,z) \,{\mathrm{d}} z }\bigg] \le {{\mathbb{E}}}\bigg[{\sup_{(t,y) \in \mathcal{A}_k}\tilde\rho(t,y)}\bigg],$$
$${{\mathbb{E}}}\bigg[{ {\textbf{1}}_{\{t >\sigma_k\}} \int p(\sigma_k,X_{\sigma_k};\ t,z) \tilde \rho(t ,z) \,{\mathrm{d}} z }\bigg] \le {{\mathbb{E}}}\bigg[{\sup_{(t,y) \in \mathcal{A}_k}\tilde\rho(t,y)}\bigg],$$
since by definition of  ${\sigma}_k$
,
${\sigma}_k$
,  $\|\Delta({\sigma}_k)(v-\mu({\sigma}_k)-L({\sigma}_k)X_{{\sigma}_k})\| = k \eta({\sigma}_k)$
. The expectation on the right-hand side is now superfluous. It is easily derived that
$\|\Delta({\sigma}_k)(v-\mu({\sigma}_k)-L({\sigma}_k)X_{{\sigma}_k})\| = k \eta({\sigma}_k)$
. The expectation on the right-hand side is now superfluous. It is easily derived that  $\tilde{Z}_t$
satisfies the SDE
$\tilde{Z}_t$
satisfies the SDE
 $${\mathrm{d}} \tilde{Z}_t = L(t)\tilde{\sigma}(t) \,{\mathrm{d}} W_t$$
$${\mathrm{d}} \tilde{Z}_t = L(t)\tilde{\sigma}(t) \,{\mathrm{d}} W_t$$
and hence for  $x\in {\mathbb{R}}^m$
$x\in {\mathbb{R}}^m$
 $$\tilde{q}(t,x;\ T,0) = \phi_m(0;\ x, {M^\dagger}(t)),$$
$$\tilde{q}(t,x;\ T,0) = \phi_m(0;\ x, {M^\dagger}(t)),$$
where we denote the density of the multivariate normal distribution in  ${\mathbb{R}}^m$
with mean vector
${\mathbb{R}}^m$
with mean vector  $\nu$
and covariance matrix
$\nu$
and covariance matrix  $\Upsilon$
, evaluated in u by
$\Upsilon$
, evaluated in u by  $\phi_m(u;\ \nu,\Upsilon)$
. Hence, stitching the previous derivations together we obtain
$\phi_m(u;\ \nu,\Upsilon)$
. Hence, stitching the previous derivations together we obtain
 $${{\mathbb{E}}}\bigg[{ {\textbf{1}}_{\{t >\sigma_k\}} \int p(\sigma_k,X_{\sigma_k};\ t,z) \tilde \rho(t ,z) \,{\mathrm{d}} z }\bigg] \le \sup_{(t,y) \in \mathcal{A}_k} \phi_m(0;\ x, {M^\dagger}(t)).$$
$${{\mathbb{E}}}\bigg[{ {\textbf{1}}_{\{t >\sigma_k\}} \int p(\sigma_k,X_{\sigma_k};\ t,z) \tilde \rho(t ,z) \,{\mathrm{d}} z }\bigg] \le \sup_{(t,y) \in \mathcal{A}_k} \phi_m(0;\ x, {M^\dagger}(t)).$$
The right-hand side multiplied by  ${(2\pi)^{m/2}}$
equals
${(2\pi)^{m/2}}$
equals
 $$|M(t)|^{1/2} \exp\bigg( -\frac12(v-\mu(t)-L(t)y)^{\prime} M(t)(v-\mu(t)-L(t)y)\bigg){,}$$
$$|M(t)|^{1/2} \exp\bigg( -\frac12(v-\mu(t)-L(t)y)^{\prime} M(t)(v-\mu(t)-L(t)y)\bigg){,}$$
which can be further bounded by
 \begin{align*}& \sup_{(t,y) \in \mathcal{A}_k} |\Delta(t)| |{M_{\Delta}}(t)|^{1/2}\exp\bigg( -\frac12(v-\mu(t)-L(t)y)^{\prime} \Delta(t) {M_{\Delta}}(t) \Delta(t) (v-\mu(t)-L(t)y)\bigg)\\[3pt] &\quad \le \sup_{(t,y) \in \mathcal{A}_k} |\Delta(t)| ( {\lambda_{\rm max}}({M_{\Delta}}(t))^{m/2} \exp\bigg(-\frac12\|\Delta(t)(v-\mu(t)-L(t)y))\|^2 {\lambda_{\rm min}}({M_{\Delta}}(t))\bigg)\\[3pt] & \quad\le \sup_{t\in [0,T)} |\Delta(t)| \bigg(\frac{\bar{c}}{T-t}\bigg)^{m/2} \exp\bigg(-\frac{\underline{c} k^2\eta(t)^2}{2(T-t)}\bigg)\\[3pt]& \quad \lesssim \sup_{t\in [0,T)} (T-t)^{-\delta-m/2} \exp\bigg(-\frac{\underline{c} k^2\eta(t)^2}{2(T-t)}\bigg).\end{align*}
\begin{align*}& \sup_{(t,y) \in \mathcal{A}_k} |\Delta(t)| |{M_{\Delta}}(t)|^{1/2}\exp\bigg( -\frac12(v-\mu(t)-L(t)y)^{\prime} \Delta(t) {M_{\Delta}}(t) \Delta(t) (v-\mu(t)-L(t)y)\bigg)\\[3pt] &\quad \le \sup_{(t,y) \in \mathcal{A}_k} |\Delta(t)| ( {\lambda_{\rm max}}({M_{\Delta}}(t))^{m/2} \exp\bigg(-\frac12\|\Delta(t)(v-\mu(t)-L(t)y))\|^2 {\lambda_{\rm min}}({M_{\Delta}}(t))\bigg)\\[3pt] & \quad\le \sup_{t\in [0,T)} |\Delta(t)| \bigg(\frac{\bar{c}}{T-t}\bigg)^{m/2} \exp\bigg(-\frac{\underline{c} k^2\eta(t)^2}{2(T-t)}\bigg)\\[3pt]& \quad \lesssim \sup_{t\in [0,T)} (T-t)^{-\delta-m/2} \exp\bigg(-\frac{\underline{c} k^2\eta(t)^2}{2(T-t)}\bigg).\end{align*}
Next, the maximum can be bounded, followed by taking the limit  $k\to \infty$
, to see that this tends to zero. This is exactly as in the proof of [Reference Schauer, van der Meulen and van Zanten35, Lemma 5].
$k\to \infty$
, to see that this tends to zero. This is exactly as in the proof of [Reference Schauer, van der Meulen and van Zanten35, Lemma 5].
6.3. Proof of Lemma 2.3
By absolute continuity of the laws of  $\tilde X$
and X and the abstract Bayes’ formula, for bounded
$\tilde X$
and X and the abstract Bayes’ formula, for bounded  $\mathcal{F}_T$
-measurable f we have
$\mathcal{F}_T$
-measurable f we have
 $${{\mathbb{E}}} [{f(X) \mid X_T=v}] = \frac{\tilde{p}(0,x_0;\ T,v)}{p(0,x_0;\ T,v)} {{\mathbb{E}}}\bigg[{f(\tilde{X}) \frac{{\mathrm{d}} {\mathbb{P}}_T}{{\mathrm{d}} \tilde{{\mathbb{P}}}_T}(\tilde{X} ) \biggm| \tilde{X}_T=v}\bigg].$$
$${{\mathbb{E}}} [{f(X) \mid X_T=v}] = \frac{\tilde{p}(0,x_0;\ T,v)}{p(0,x_0;\ T,v)} {{\mathbb{E}}}\bigg[{f(\tilde{X}) \frac{{\mathrm{d}} {\mathbb{P}}_T}{{\mathrm{d}} \tilde{{\mathbb{P}}}_T}(\tilde{X} ) \biggm| \tilde{X}_T=v}\bigg].$$
Hence, upon taking  $f\equiv 1$
and applying Girsanov’s theorem, we get
$f\equiv 1$
and applying Girsanov’s theorem, we get
 $$p(0,x_0;\ T,v) = \tilde{p}(0,x_0;\ T,v) {{\mathbb{E}}}\bigg[{\exp\bigg(\int_0^T \eta(\tilde{X}_s)^{\prime} \,{\mathrm{d}} W_s - \frac12 \int_0^T\|\eta(\tilde{X}_s)\|^2 \,{\mathrm{d}} s \bigg) \biggm| \tilde{X}_T=v}\bigg].$$
$$p(0,x_0;\ T,v) = \tilde{p}(0,x_0;\ T,v) {{\mathbb{E}}}\bigg[{\exp\bigg(\int_0^T \eta(\tilde{X}_s)^{\prime} \,{\mathrm{d}} W_s - \frac12 \int_0^T\|\eta(\tilde{X}_s)\|^2 \,{\mathrm{d}} s \bigg) \biggm| \tilde{X}_T=v}\bigg].$$
Since  $\eta$
is bounded, this implies
$\eta$
is bounded, this implies
 $$p(0,x_0;\ T,v) \propto \tilde{p}(0,x_0;\ T,v) {{\mathbb{E}}}\bigg[{\exp\bigg(\int_0^T \eta(\tilde{X}_s)' \,{\mathrm{d}} W_s \bigg) \biggm| \tilde{X}_T=v}\bigg].$$
$$p(0,x_0;\ T,v) \propto \tilde{p}(0,x_0;\ T,v) {{\mathbb{E}}}\bigg[{\exp\bigg(\int_0^T \eta(\tilde{X}_s)' \,{\mathrm{d}} W_s \bigg) \biggm| \tilde{X}_T=v}\bigg].$$
Upon defining  $\tau_j =\int_0^T \eta_j(\tilde{X}_s)^2 \,{\mathrm{d}} s $
, the Dambis–Dubins–Schwarz theorem implies that the expectation on the right-hand side equals
$\tau_j =\int_0^T \eta_j(\tilde{X}_s)^2 \,{\mathrm{d}} s $
, the Dambis–Dubins–Schwarz theorem implies that the expectation on the right-hand side equals
 $${{\mathbb{E}}}\big[{{\mathrm{e}}^{-\sum_{j=1}^{d'} \int_0^T \eta_j(\tilde{X}_s) \,{\mathrm{d}} W_s^j} \mid \tilde{X}_T=v}\big] ={{\mathbb{E}}}\big[{{\mathrm{e}}^{\sum_{j=1}^{d'} {W}_{\tau_j}^j} \mid \tilde{X}_T=v}\big] .$$
$${{\mathbb{E}}}\big[{{\mathrm{e}}^{-\sum_{j=1}^{d'} \int_0^T \eta_j(\tilde{X}_s) \,{\mathrm{d}} W_s^j} \mid \tilde{X}_T=v}\big] ={{\mathbb{E}}}\big[{{\mathrm{e}}^{\sum_{j=1}^{d'} {W}_{\tau_j}^j} \mid \tilde{X}_T=v}\big] .$$
By boundedness of  $\eta$
there exist constants
$\eta$
there exist constants  $\{K_j\}_{j=1}^{d'}$
such that
$\{K_j\}_{j=1}^{d'}$
such that  $\tau_j\le K_j$
. Hence the right-hand side of the above display can be bounded by
$\tau_j\le K_j$
. Hence the right-hand side of the above display can be bounded by
 $${{\mathbb{E}}}\big[{{\mathrm{e}}^{\sum_{j=1}^{d'} \sup_{0\le s \le K_j}{W}_s^j } \mid \tilde{X}_T=v}\big] = {{\mathbb{E}}}\big[{{\mathrm{e}}^{\sum_{j=1}^{d'} \sup_{0\le s \le K_j} {W}_s^j}}\big] = \prod_{j=1}^{d'} {{\mathbb{E}}}[{{\mathrm{e}}^{\sup_{0\le s \le K_j} {W}_s^j}}],$$
$${{\mathbb{E}}}\big[{{\mathrm{e}}^{\sum_{j=1}^{d'} \sup_{0\le s \le K_j}{W}_s^j } \mid \tilde{X}_T=v}\big] = {{\mathbb{E}}}\big[{{\mathrm{e}}^{\sum_{j=1}^{d'} \sup_{0\le s \le K_j} {W}_s^j}}\big] = \prod_{j=1}^{d'} {{\mathbb{E}}}[{{\mathrm{e}}^{\sup_{0\le s \le K_j} {W}_s^j}}],$$
where the final equality follows from the components of  $\bar{W}$
being independent. The expectation on the right-hand side is finite, the constant only depending on T. To see this, if
$\bar{W}$
being independent. The expectation on the right-hand side is finite, the constant only depending on T. To see this, if  $B_t$
is a one-dimensional Brownian motion, then
$B_t$
is a one-dimensional Brownian motion, then  $\bar{B}_t =\sup_{0\le s\le t} B_s$
has density
$\bar{B}_t =\sup_{0\le s\le t} B_s$
has density  $f_{\bar{B}_t}(x)=\sqrt{2/(\pi t)} {\mathrm{e}}^{-x^2/(2t)}{\textbf{1}}_{[0,\infty)}(x)$
, which implies that
$f_{\bar{B}_t}(x)=\sqrt{2/(\pi t)} {\mathrm{e}}^{-x^2/(2t)}{\textbf{1}}_{[0,\infty)}(x)$
, which implies that  ${{\mathbb{E}}}[{\exp(\bar{B}_t)}]<\infty$
.
${{\mathbb{E}}}[{\exp(\bar{B}_t)}]<\infty$
.
The statement of the theorem now follows by considering the processes X and  $\tilde{X}$
started in x at time s and noting that the derived constant only depends on T.
$\tilde{X}$
started in x at time s and noting that the derived constant only depends on T.
7. Discussion
7.1. Extending the approach in [Reference Marchand27] to hypo-elliptic diffusions
A potential advantage of the approach of Marchand [Reference Marchand27] is that, at least in the uniformly elliptic case, there is no matching condition for the diffusion coefficient to be satisfied. Inspecting the guiding term in (1.11), it can be seen that it is also well-defined when  ${\ker }({\sigma}(t,x)^{\prime} L^{\prime})=\{0\}$
, since this ensures that the inverse of
${\ker }({\sigma}(t,x)^{\prime} L^{\prime})=\{0\}$
, since this ensures that the inverse of  $La(t,x) L^{\prime}$
exists for all
$La(t,x) L^{\prime}$
exists for all  $t\ge 0$
and
$t\ge 0$
and  $x\in {\mathbb{R}}^d$
. Unfortunately, this excludes, for example, the case where the smooth component of an integrated diffusion process is observed (Example 3.2). Here, the guiding term is given by
$x\in {\mathbb{R}}^d$
. Unfortunately, this excludes, for example, the case where the smooth component of an integrated diffusion process is observed (Example 3.2). Here, the guiding term is given by
 $${\rm guid}_1(t,x)\coloneqq a L(t)^{\prime} \bigg(\int_t^T L(\tau) \tilde{a} L(\tau)^{\prime} \,{\mathrm{d}} \tau\bigg)^{-1} (v-L(t)x).$$
$${\rm guid}_1(t,x)\coloneqq a L(t)^{\prime} \bigg(\int_t^T L(\tau) \tilde{a} L(\tau)^{\prime} \,{\mathrm{d}} \tau\bigg)^{-1} (v-L(t)x).$$
Now it is tempting to adjust the proposals of [Reference Marchand27] in (1.11) in the same way as was done for guided proposals, by replacing L with L(t). This leads to the guiding term
 $$ {\rm guid}_2(t,x)\coloneqq a L(t)^{\prime} (L(t) a L(t)^{\prime})^{-1} \frac{v-L(t)x}{T-t}.$$
$$ {\rm guid}_2(t,x)\coloneqq a L(t)^{\prime} (L(t) a L(t)^{\prime})^{-1} \frac{v-L(t)x}{T-t}.$$
This guiding term will not give correct bridges, though. To see this, if  $\underline\beta\equiv 0$
then
$\underline\beta\equiv 0$
then  $X^\circ=X^\star$
, but
$X^\circ=X^\star$
, but
 \begin{equation*} {\rm guid}_2(t,x)=\frac13 {\rm guid}_1(t,x) \quad \text{with} \quad {\rm guid}_1(t,x)=\begin{bmatrix} 0 \\ 3{{({v-x_1-(T-t)x_2})}/{{(T-t)^2}}}\end{bmatrix}\end{equation*}
\begin{equation*} {\rm guid}_2(t,x)=\frac13 {\rm guid}_1(t,x) \quad \text{with} \quad {\rm guid}_1(t,x)=\begin{bmatrix} 0 \\ 3{{({v-x_1-(T-t)x_2})}/{{(T-t)^2}}}\end{bmatrix}\end{equation*}
(here  $x_i$
denotes the ith component of the vector x). We stress that
$x_i$
denotes the ith component of the vector x). We stress that  ${\rm guid}_2(t,x)$
was never proposed in [Reference Marchand27] and that the guiding term in (1.11) is perfectly valid in the uniformly elliptic case. The point we make here is that it is far from straightforward to generalise the work of [Reference Marchand27] to the hypo-elliptic setting. Possibly, the correct generalisation of [Reference Marchand27] to the hypo-elliptic case is to take the guiding term of the form
${\rm guid}_2(t,x)$
was never proposed in [Reference Marchand27] and that the guiding term in (1.11) is perfectly valid in the uniformly elliptic case. The point we make here is that it is far from straightforward to generalise the work of [Reference Marchand27] to the hypo-elliptic setting. Possibly, the correct generalisation of [Reference Marchand27] to the hypo-elliptic case is to take the guiding term of the form
 $$a(t,X^\circ_t) L(t)^{\prime} \bigg(\int_t^T L(\tau) a(\tau,X^\circ_{\tau}) L(\tau)^{\prime} \,{\mathrm{d}} \tau\bigg)^{-1} (v-L(t)X^\circ_t).$$
$$a(t,X^\circ_t) L(t)^{\prime} \bigg(\int_t^T L(\tau) a(\tau,X^\circ_{\tau}) L(\tau)^{\prime} \,{\mathrm{d}} \tau\bigg)^{-1} (v-L(t)X^\circ_t).$$
This term, however, is unattractive from a computational point of view.
7.2. State-dependent diffusion coefficient
We have formulated our results for state-dependent diffusion coefficients  ${\sigma}$
. The main difficulty, however, resides in checking the fourth inequality of Assumption 2.4. We conjecture that the ‘right’ way to deal with this term is to bound
${\sigma}$
. The main difficulty, however, resides in checking the fourth inequality of Assumption 2.4. We conjecture that the ‘right’ way to deal with this term is to bound
 $$\| {L_{\Delta}}(t) (\tilde{a}(t)-a(t,X^\circ_t)) {L_{\Delta}}(t)^{\prime}\| \lesssim \|{Z_{\Delta,t}}\|.$$
$$\| {L_{\Delta}}(t) (\tilde{a}(t)-a(t,X^\circ_t)) {L_{\Delta}}(t)^{\prime}\| \lesssim \|{Z_{\Delta,t}}\|.$$
Then the final term in inequality (5.6) would be replaced with  $C_4 \int_{t_0}^t (T-s)^{-2} \|{Z_{\Delta,s}}\|^3 \,{\mathrm{d}} s$
. The conjecture is motivated by the proof of [Reference Schauer, van der Meulen and van Zanten35, Theorem 2]. Obtaining such an inequality is not straightforward, as is the corresponding Gronwall-type argument. We postpone such investigations to future research.
$C_4 \int_{t_0}^t (T-s)^{-2} \|{Z_{\Delta,s}}\|^3 \,{\mathrm{d}} s$
. The conjecture is motivated by the proof of [Reference Schauer, van der Meulen and van Zanten35, Theorem 2]. Obtaining such an inequality is not straightforward, as is the corresponding Gronwall-type argument. We postpone such investigations to future research.
Appendix A. Existence of  $\tilde{r}$
if
$\tilde{r}$
if  $L=I$
$L=I$
When  $L=I$
, the existence problem of transition densities has been studied in control theory as well.
$L=I$
, the existence problem of transition densities has been studied in control theory as well.
Definition A.1. The pair  ${(\tilde{B}, \tilde{{\sigma}})}$
is called completely controllable at s if, for any
${(\tilde{B}, \tilde{{\sigma}})}$
is called completely controllable at s if, for any  $t>s$
and
$t>s$
and  $x, y \in {\mathbb{R}}^d$
, there exists a function
$x, y \in {\mathbb{R}}^d$
, there exists a function  $v \in L^2[s,t]$
and corresponding solution Y of
$v \in L^2[s,t]$
and corresponding solution Y of
 $${\mathrm{d}} Y(u) = ( \tilde{B}(u) Y(u) + \tilde{{\sigma}}(u) v(u) ) \,{\mathrm{d}} u, \quad Y(s)=x$$
$${\mathrm{d}} Y(u) = ( \tilde{B}(u) Y(u) + \tilde{{\sigma}}(u) v(u) ) \,{\mathrm{d}} u, \quad Y(s)=x$$
such that  $Y(t)=y$
.
$Y(t)=y$
.
The following lemma is proved in [Reference Hermes19].
Lemma A.1. The following are equivalent:
(1)
 ${(\tilde{B},\tilde{\sigma})}$
is completely controllable at s,
${(\tilde{B},\tilde{\sigma})}$
is completely controllable at s,(2) non-degenerate Gaussian transition densities
 $\tilde{p}(s,x;\ t,y)$
exist,
$\tilde{p}(s,x;\ t,y)$
exist,(3) for arbitrary Gaussian initial data
 $\tilde{X}_s$
, the random vector
$\tilde{X}_s$
, the random vector  $\tilde{X}_t$
is non-degenerate Gaussian for
$\tilde{X}_t$
is non-degenerate Gaussian for  $t>s$
.
$t>s$
.
If  $\tilde{B}$
,
$\tilde{B}$
,  $\tilde{\sigma}$
in (1.8) are constant matrices, complete controllability is equivalent to
$\tilde{\sigma}$
in (1.8) are constant matrices, complete controllability is equivalent to  $\mbox{rank}(C)=d$
, where the controllability matrix C is defined by
$\mbox{rank}(C)=d$
, where the controllability matrix C is defined by
 $$C\coloneqq [\tilde{\sigma},\: \tilde{B}\tilde{\sigma},\ldots, \tilde{B}^{d-1} \tilde{\sigma} ]$$
$$C\coloneqq [\tilde{\sigma},\: \tilde{B}\tilde{\sigma},\ldots, \tilde{B}^{d-1} \tilde{\sigma} ]$$
(see [Reference Hermes19, page 74] or [Reference Karatzas and Shreve20, Proposition 6.5]). This provides an easily verifiable condition for complete controllability.
Appendix B. Gronwall-type inequality
In the proof of Theorem 2.2 we used the following Gronwall-type inequality.
Lemma B.1. Assume  $t\mapsto \zeta(t)$
is continuously differentiable and non-negative on
$t\mapsto \zeta(t)$
is continuously differentiable and non-negative on  $[t_0,t_1)$
. Assume
$[t_0,t_1)$
. Assume  $t\mapsto f_1(t)$
and
$t\mapsto f_1(t)$
and  $t\mapsto f_2(t)$
are continuous and non-negative on
$t\mapsto f_2(t)$
are continuous and non-negative on  $[t_0,t_1)$
. Suppose
$[t_0,t_1)$
. Suppose  $t\mapsto u(t)$
is a continuous and non-negative function on
$t\mapsto u(t)$
is a continuous and non-negative function on  $[t_0, t_1)$
satisfying the inequality
$[t_0, t_1)$
satisfying the inequality
 $$u(t) \le \zeta(t)+ \int_{t_0}^t f_1(s) \sqrt{u(s)} \,{\mathrm{d}} s +\int_{t_0}^t f_2(s) u(s) \,{\mathrm{d}} s , \quad t\in [t_0, t_1).$$
$$u(t) \le \zeta(t)+ \int_{t_0}^t f_1(s) \sqrt{u(s)} \,{\mathrm{d}} s +\int_{t_0}^t f_2(s) u(s) \,{\mathrm{d}} s , \quad t\in [t_0, t_1).$$
Then
 $$u(t) \le \bigg(\sqrt{\zeta(t_0) + \int_{t_0}^t |\zeta'(s)| \,{\mathrm{d}} s}+ \frac12\int_{t_0}^t f_1(s) \,{\mathrm{d}} s \bigg)^2 \exp\bigg(\int_{t_0}^t f_2(s) \,{\mathrm{d}} s\bigg).$$
$$u(t) \le \bigg(\sqrt{\zeta(t_0) + \int_{t_0}^t |\zeta'(s)| \,{\mathrm{d}} s}+ \frac12\int_{t_0}^t f_1(s) \,{\mathrm{d}} s \bigg)^2 \exp\bigg(\int_{t_0}^t f_2(s) \,{\mathrm{d}} s\bigg).$$
Proof.This is a special case of [Reference Agarwal, Deng and Zhang1, Theorem 2.1]. In their notation, we have  $n=2$
,
$n=2$
,  $w_1(x)=\sqrt{x}$
,
$w_1(x)=\sqrt{x}$
,  $W_1(x)=2\sqrt{x}$
(taking
$W_1(x)=2\sqrt{x}$
(taking  $u_1=0$
),
$u_1=0$
),  $w_2(x)=x$
,
$w_2(x)=x$
,  $W_2(x)=\log x$
(taking
$W_2(x)=\log x$
(taking  $u_2=1$
).
$u_2=1$
).
Appendix C. Hypo-ellipticity
Proposition C.1. Consider the diffusion (1.1) with  $ b(t,x) = B x + \beta(t,x)$
for
$ b(t,x) = B x + \beta(t,x)$
for  $B \in {\mathbb{R}}^{d \times d}$
and
$B \in {\mathbb{R}}^{d \times d}$
and  $\beta \in C^{\infty}([0,T] \times {\mathbb{R}}^d, {\mathbb{R}}^d)$
, and with
$\beta \in C^{\infty}([0,T] \times {\mathbb{R}}^d, {\mathbb{R}}^d)$
, and with  $\sigma \in C^{\infty}([0,T] \times {\mathbb{R}}^d, {\mathbb{R}}^{d \times d'})$
. Suppose that, for all
$\sigma \in C^{\infty}([0,T] \times {\mathbb{R}}^d, {\mathbb{R}}^{d \times d'})$
. Suppose that, for all  ${(t,x) \in (0,T) \times {\mathbb{R}}^d}$
, the pair
${(t,x) \in (0,T) \times {\mathbb{R}}^d}$
, the pair  ${(B, \sigma(t,x))}$
is controllable, that is, the rank of the matrix concatenation
${(B, \sigma(t,x))}$
is controllable, that is, the rank of the matrix concatenation
 $$[ \sigma(t,x)\ \ B \sigma(t,x) \ \ \cdots \ \ B^{d-1} \sigma(t,x) ]$$
$$[ \sigma(t,x)\ \ B \sigma(t,x) \ \ \cdots \ \ B^{d-1} \sigma(t,x) ]$$
is equal to d. Further, suppose that for all  ${(t,x) \in (0,T) \times {\mathbb{R}}^d}$
and all tuples
${(t,x) \in (0,T) \times {\mathbb{R}}^d}$
and all tuples  ${(n_0, n_1, \ldots, n_d) \in \{0, 1, \ldots, d-1\}^{d+1}}$
,
${(n_0, n_1, \ldots, n_d) \in \{0, 1, \ldots, d-1\}^{d+1}}$
,
 $$(\partial_{t})^{n_0} \prod_{i=1}^d (\partial_{x_i})^{n_i} \beta(t,x) \in \mathrm{Col}\, \sigma(t,x)$$
$$(\partial_{t})^{n_0} \prod_{i=1}^d (\partial_{x_i})^{n_i} \beta(t,x) \in \mathrm{Col}\, \sigma(t,x)$$
and
 $$\mathrm{Col}\, \Bigg( (\partial_{t})^{n_0} \prod_{i=1}^d (\partial_{x_i})^{n_i} \sigma(t,x) \Bigg) \subset \mathrm{Col}\, \sigma(t,x),$$
$$\mathrm{Col}\, \Bigg( (\partial_{t})^{n_0} \prod_{i=1}^d (\partial_{x_i})^{n_i} \sigma(t,x) \Bigg) \subset \mathrm{Col}\, \sigma(t,x),$$
that is, the column spaces of all partial derivatives of  $\beta(t,x)$
and
$\beta(t,x)$
and  $\sigma(t,x)$
, including
$\sigma(t,x)$
, including  $\beta(t,x)$
itself, belong to the column space of
$\beta(t,x)$
itself, belong to the column space of  $\sigma(t,x)$
. Finally, suppose there exists at most one strong solution to (1.1) (which is the case if, for example,
$\sigma(t,x)$
. Finally, suppose there exists at most one strong solution to (1.1) (which is the case if, for example,  $\beta$
and
$\beta$
and  $\sigma$
satisfy a linear growth condition). Then, for all initial conditions
$\sigma$
satisfy a linear growth condition). Then, for all initial conditions  $x_0$
and all
$x_0$
and all  $t \geq 0$
, the distribution of
$t \geq 0$
, the distribution of  $X_t$
admits a density function p(t, x, y):
$X_t$
admits a density function p(t, x, y):
 $${\mathbb{E}}_{x_0}[f(X_t)] = \int_{{\mathbb{R}}^d} p(t,x_0,y) f(y) \,{\mathrm{d}} y, \quad f \in C_0({\mathbb{R}}^d),$$
$${\mathbb{E}}_{x_0}[f(X_t)] = \int_{{\mathbb{R}}^d} p(t,x_0,y) f(y) \,{\mathrm{d}} y, \quad f \in C_0({\mathbb{R}}^d),$$
and p is a smooth (infinitely often continuously differentiable) function on  ${(0,\infty) \times {\mathbb{R}}^d \times {\mathbb{R}}^d}$
.
${(0,\infty) \times {\mathbb{R}}^d \times {\mathbb{R}}^d}$
.
Proof.Write  ${(\sigma_j)_{j=1}^{d'}}$
for the columns of
${(\sigma_j)_{j=1}^{d'}}$
for the columns of  $\sigma$
so that
$\sigma$
so that
 $$\sigma(t,x) =[ \sigma_1(t,x) \ \ \cdots \ \ \sigma_{d'}(t,x) ].$$
$$\sigma(t,x) =[ \sigma_1(t,x) \ \ \cdots \ \ \sigma_{d'}(t,x) ].$$
The Stratonovich form of (1.1) is given by
 $${\mathrm{d}} X_t = \widetilde b(t,X_t) \,{\mathrm{d}} t + {\sigma}(t,X_t) \circ \,{\mathrm{d}} W_t,\quad X_0=x_0,\quad t\in [0,T],$$
$${\mathrm{d}} X_t = \widetilde b(t,X_t) \,{\mathrm{d}} t + {\sigma}(t,X_t) \circ \,{\mathrm{d}} W_t,\quad X_0=x_0,\quad t\in [0,T],$$
where  $\widetilde b(t,x) = B x + \widetilde \beta(t,x)$
with coordinates of
$\widetilde b(t,x) = B x + \widetilde \beta(t,x)$
with coordinates of  $\widetilde \beta$
given by
$\widetilde \beta$
given by
 $$\widetilde \beta^i(t,x) = \beta^i(t,x) - \frac 1 2 \sum_{j=1}^{d'} \sum_{l=1}^d \sigma_j^l (\partial_l \sigma^i_j)(t,x).$$
$$\widetilde \beta^i(t,x) = \beta^i(t,x) - \frac 1 2 \sum_{j=1}^{d'} \sum_{l=1}^d \sigma_j^l (\partial_l \sigma^i_j)(t,x).$$
Observe that  $\widetilde \beta(t,x) \in \mathrm{Col}\, \sigma(t,x)$
, just like
$\widetilde \beta(t,x) \in \mathrm{Col}\, \sigma(t,x)$
, just like  $\beta(t,x)$
.
$\beta(t,x)$
.
In particular, the generator of the diffusion (1.1) can be given in terms of the first-order differential operators
 $$\mathcal A_0 \,f(t,x) = \partial_t f(t,x) + \langle \widetilde b(t,x), \nabla_x\, f(t,x) \rangle, \quad \mathcal A_j\, f(t,x) = \langle \sigma_j(t,x), \nabla_x\, f(t,x) \rangle, \quad j = 1, \ldots, d',$$
$$\mathcal A_0 \,f(t,x) = \partial_t f(t,x) + \langle \widetilde b(t,x), \nabla_x\, f(t,x) \rangle, \quad \mathcal A_j\, f(t,x) = \langle \sigma_j(t,x), \nabla_x\, f(t,x) \rangle, \quad j = 1, \ldots, d',$$
as  $\mathcal L = \mathcal A_0 + \frac 1 2 \sum_{j=1}^{d'} \mathcal A_j^2$
. In this proof, without further comment, we will use (i) Einstein’s summation convention, and (ii) the canonical identification of first-order partial differential operators
$\mathcal L = \mathcal A_0 + \frac 1 2 \sum_{j=1}^{d'} \mathcal A_j^2$
. In this proof, without further comment, we will use (i) Einstein’s summation convention, and (ii) the canonical identification of first-order partial differential operators  $\mathcal A = a^i \partial_i = a^0(t,x) \partial_t + \sum_{i=1}^d a^i(x) \partial_{x_i}$
(acting on functions
$\mathcal A = a^i \partial_i = a^0(t,x) \partial_t + \sum_{i=1}^d a^i(x) \partial_{x_i}$
(acting on functions  $f \colon [0,\infty) \times {\mathbb{R}}^d \rightarrow {\mathbb{R}}$
) with vector fields
$f \colon [0,\infty) \times {\mathbb{R}}^d \rightarrow {\mathbb{R}}$
) with vector fields  $[ a^0(t,x) \quad a^1(t,x) \ \ \cdots \ \ a^d(t,x) ]^T \in C^{\infty} ([0,\infty) \times {\mathbb{R}}^d;\ {\mathbb{R}} \times {\mathbb{R}}^d)$
. The commutator
$[ a^0(t,x) \quad a^1(t,x) \ \ \cdots \ \ a^d(t,x) ]^T \in C^{\infty} ([0,\infty) \times {\mathbb{R}}^d;\ {\mathbb{R}} \times {\mathbb{R}}^d)$
. The commutator  $[\mathcal U_1, \mathcal U_2]$
of two vector fields
$[\mathcal U_1, \mathcal U_2]$
of two vector fields  $\mathcal U_1$
,
$\mathcal U_1$
,  $\mathcal U_2$
is as usual defined by
$\mathcal U_2$
is as usual defined by
 $$[ \mathcal U_1, \mathcal U_2] f(t,x) = \mathcal U_1 \mathcal U_2 f(t,x) - \mathcal U_2 \mathcal U_1 f(t,x).$$
$$[ \mathcal U_1, \mathcal U_2] f(t,x) = \mathcal U_1 \mathcal U_2 f(t,x) - \mathcal U_2 \mathcal U_1 f(t,x).$$
For  $l = 0, \ldots, d-1$
, write
$l = 0, \ldots, d-1$
, write
 $$V^l \coloneqq \mathrm{Col}\,[ \sigma(t,x)\ \ B \sigma(t,x)\ \ \cdots \ \ B^l \sigma(t,x) ].$$
$$V^l \coloneqq \mathrm{Col}\,[ \sigma(t,x)\ \ B \sigma(t,x)\ \ \cdots \ \ B^l \sigma(t,x) ].$$
Write  $[\cdot, \mathcal A_0]^l$
for taking the Lie bracket with
$[\cdot, \mathcal A_0]^l$
for taking the Lie bracket with  $\mathcal A_0$
repeatedly, that is, recursively we define
$\mathcal A_0$
repeatedly, that is, recursively we define
 $$[\mathcal U,\mathcal A_0]^0 f = \mathcal U f \quad \mbox{and} \quad [\mathcal U, \mathcal A_0]^{l+1} = [ [\mathcal U, \mathcal A_0]^l, \mathcal A_0 ], \quad l=0,1,2, \ldots.$$
$$[\mathcal U,\mathcal A_0]^0 f = \mathcal U f \quad \mbox{and} \quad [\mathcal U, \mathcal A_0]^{l+1} = [ [\mathcal U, \mathcal A_0]^l, \mathcal A_0 ], \quad l=0,1,2, \ldots.$$
We first compute
 \begin{equation*}[\mathcal A_j, \mathcal A_0] f = \sigma_j^k B_k^i \partial_i f -(\partial_t \sigma_j^k)\partial_k f - B^i_l x^l (\partial_i \sigma_j^k) \partial_k f - \widetilde \beta^i(\partial_i \sigma_j^k)\partial_k f + \sigma_j^k (\partial_k \widetilde \beta^i) \partial_i f.\end{equation*}
\begin{equation*}[\mathcal A_j, \mathcal A_0] f = \sigma_j^k B_k^i \partial_i f -(\partial_t \sigma_j^k)\partial_k f - B^i_l x^l (\partial_i \sigma_j^k) \partial_k f - \widetilde \beta^i(\partial_i \sigma_j^k)\partial_k f + \sigma_j^k (\partial_k \widetilde \beta^i) \partial_i f.\end{equation*}
Observe that the first term represents the operator  $\langle B \sigma_j, \nabla f\rangle$
, and the remaining terms assume values in
$\langle B \sigma_j, \nabla f\rangle$
, and the remaining terms assume values in  $V^0 = \mathrm{Col}\, \sigma(t,x)$
. By iterating we obtain
$V^0 = \mathrm{Col}\, \sigma(t,x)$
. By iterating we obtain  $[\mathcal A_j, \mathcal A_0]^l = B^{l} \sigma + \mathcal U$
, where
$[\mathcal A_j, \mathcal A_0]^l = B^{l} \sigma + \mathcal U$
, where  $\mathcal U(t,x) \in V^{l-1}$
for all (t, x). By the controllability assumption on B and
$\mathcal U(t,x) \in V^{l-1}$
for all (t, x). By the controllability assumption on B and  $\sigma$
, the vectors
$\sigma$
, the vectors
 $$\{ [\mathcal A_j, \mathcal A_0]^l(t,x) \colon l = 1, \ldots, d-1, j = 1, \ldots, d' \}$$
$$\{ [\mathcal A_j, \mathcal A_0]^l(t,x) \colon l = 1, \ldots, d-1, j = 1, \ldots, d' \}$$
span  ${\mathbb{R}}^d$
for all (t, x). Adding
${\mathbb{R}}^d$
for all (t, x). Adding  $\mathcal A_0$
to the collection of vectors gives that
$\mathcal A_0$
to the collection of vectors gives that
 $$\operatorname{span} \{ \mathcal A_0, [\mathcal A_j, \mathcal A_0]^l(t,x) \colon l = 1, \ldots, d-1, j = 1, \ldots, d' \}$$
$$\operatorname{span} \{ \mathcal A_0, [\mathcal A_j, \mathcal A_0]^l(t,x) \colon l = 1, \ldots, d-1, j = 1, \ldots, d' \}$$
has dimension  $d+1$
, for all
$d+1$
, for all  ${(t,x) \in (0,T) \times {\mathbb{R}}^d}$
. The result now follows from Hörmander’s theorem lifted to
${(t,x) \in (0,T) \times {\mathbb{R}}^d}$
. The result now follows from Hörmander’s theorem lifted to  ${(0,T) \times {\mathbb{R}}^d}$
, for example [Reference Williams43, Corollary 5.8].
${(0,T) \times {\mathbb{R}}^d}$
, for example [Reference Williams43, Corollary 5.8].
Appendix D. Derivation of the conditioned process
The SDE for the conditioned process, given in (2.1), can be derived using Doob’s h-transform.
Assumption D.1. The mapping  $ \rho \colon {\mathbb{R}}_+ \times {\mathbb{R}}^d \to {\mathbb{R}}$
is
$ \rho \colon {\mathbb{R}}_+ \times {\mathbb{R}}^d \to {\mathbb{R}}$
is  $C^{1,2}$
and strictly positive.
$C^{1,2}$
and strictly positive.
Suppose  $0\le s<t<T$
. By the Chapman–Kolmogorov equations, for a compactly supported
$0\le s<t<T$
. By the Chapman–Kolmogorov equations, for a compactly supported  $C^\infty$
-function
$C^\infty$
-function  $f\colon {\mathbb{R}}^d \to {\mathbb{R}}$
we have
$f\colon {\mathbb{R}}^d \to {\mathbb{R}}$
we have
 $${\mathbb{E}}[ f(X_t) \mid X_s=x, LX_T=v] = \int f(y) p(s,x;\ t,y) \frac{\rho(t,y)}{\rho(s,x)}\,{\mathrm{d}} y.$$
$${\mathbb{E}}[ f(X_t) \mid X_s=x, LX_T=v] = \int f(y) p(s,x;\ t,y) \frac{\rho(t,y)}{\rho(s,x)}\,{\mathrm{d}} y.$$
Define  $g(t,x)=f(x) \rho(t,x)$
. Using the above display we find that the infinitesimal generator of the conditioned process, say
$g(t,x)=f(x) \rho(t,x)$
. Using the above display we find that the infinitesimal generator of the conditioned process, say  $\mathcal{L}^\star$
, equals
$\mathcal{L}^\star$
, equals
 \begin{align*}\mathcal{L}^\star f(x)&=\lim_{\Delta \downarrow 0} \Delta^{-1}( {\mathbb{E}}[ f(X_{s+\Delta}) \mid X_s=x, LX_T=v] - f(x) )\\[3pt] &=\frac1{\rho(s,x)} \lim_{\Delta \downarrow 0} \Delta^{-1}\bigg( \int g(s+\Delta,y) p(s,x;\ s+\Delta,y) \,{\mathrm{d}} y -g(s,x) \bigg)\\[3pt] &=\frac1{\rho(s,x)} \lim_{\Delta \downarrow 0} \Delta^{-1}( {\mathbb{E}} [ g(s+\Delta,X_{s+\Delta}) \mid X_s=x] -g(s,x)).\end{align*}
\begin{align*}\mathcal{L}^\star f(x)&=\lim_{\Delta \downarrow 0} \Delta^{-1}( {\mathbb{E}}[ f(X_{s+\Delta}) \mid X_s=x, LX_T=v] - f(x) )\\[3pt] &=\frac1{\rho(s,x)} \lim_{\Delta \downarrow 0} \Delta^{-1}\bigg( \int g(s+\Delta,y) p(s,x;\ s+\Delta,y) \,{\mathrm{d}} y -g(s,x) \bigg)\\[3pt] &=\frac1{\rho(s,x)} \lim_{\Delta \downarrow 0} \Delta^{-1}( {\mathbb{E}} [ g(s+\Delta,X_{s+\Delta}) \mid X_s=x] -g(s,x)).\end{align*}
By Assumption D.1, g is a compactly supported  $C^\infty$
-function in the domain of the infinitesimal generator
$C^\infty$
-function in the domain of the infinitesimal generator  $\mathcal{K}$
of the space–time process
$\mathcal{K}$
of the space–time process  ${(t,X_t)}$
. Therefore
${(t,X_t)}$
. Therefore
 $$\mathcal{L}^\star f(x) = \frac1{\rho(s,x)} (\mathcal{K}g)(s,x),$$
$$\mathcal{L}^\star f(x) = \frac1{\rho(s,x)} (\mathcal{K}g)(s,x),$$
where
 $$\mathcal{K} \phi(s,x)= \frac{\partial}{\partial s} \phi(s,x) + \sum_i b_i(s,x) {\,\mathrm D}_i \phi(s,x) +\frac12 \sum_{i,j} a_{ij}(s,x) {\,\mathrm D}^2_{ij} \phi(s,x). $$
$$\mathcal{K} \phi(s,x)= \frac{\partial}{\partial s} \phi(s,x) + \sum_i b_i(s,x) {\,\mathrm D}_i \phi(s,x) +\frac12 \sum_{i,j} a_{ij}(s,x) {\,\mathrm D}^2_{ij} \phi(s,x). $$
Here (and in the following) all summations run over  $1,\ldots, d$
:
$1,\ldots, d$
:
 $$ {\mathrm D}_i=\frac{\partial}{\partial x_i}\quad\text{and}\quad{\mathrm D}^2_{ij}=\frac{\partial^2}{\partial x_i\partial x_j}. $$
$$ {\mathrm D}_i=\frac{\partial}{\partial x_i}\quad\text{and}\quad{\mathrm D}^2_{ij}=\frac{\partial^2}{\partial x_i\partial x_j}. $$
Using the definition of g, we get
 \begin{align*} \mathcal{L}^\star f(x)&= \sum_i\Bigg(b_i(s,x) + \sum_j a_{ij}(s,x) \frac{{\,\mathrm D}_j \rho(s,x)}{\rho(s,x)}\Bigg) {\,\mathrm D}_i f(x) \\* & \quad\, + \frac12 \sum_{i,j} a_{ij}(s,x) {\,\mathrm D}^2_{ij} f(x)+\frac{f(x)}{\rho(s,x)} (\mathcal{K}\rho)(s,x) .\end{align*}
\begin{align*} \mathcal{L}^\star f(x)&= \sum_i\Bigg(b_i(s,x) + \sum_j a_{ij}(s,x) \frac{{\,\mathrm D}_j \rho(s,x)}{\rho(s,x)}\Bigg) {\,\mathrm D}_i f(x) \\* & \quad\, + \frac12 \sum_{i,j} a_{ij}(s,x) {\,\mathrm D}^2_{ij} f(x)+\frac{f(x)}{\rho(s,x)} (\mathcal{K}\rho)(s,x) .\end{align*}
We claim  ${(\mathcal{K}\rho)(s,x)=0}$
(i.e.
${(\mathcal{K}\rho)(s,x)=0}$
(i.e.  $\rho(t,x)$
satisfies Kolmogorov’s backward equation). The drift and diffusion coefficients of the conditioned process can then be identified from the infinitesimal generator
$\rho(t,x)$
satisfies Kolmogorov’s backward equation). The drift and diffusion coefficients of the conditioned process can then be identified from the infinitesimal generator  $\mathcal{L}^\star$
. To verify the claim, first note that
$\mathcal{L}^\star$
. To verify the claim, first note that  $Z_t=\rho(t,X_t)$
defines a martingale: if
$Z_t=\rho(t,X_t)$
defines a martingale: if  $\mathcal{F}_s$
is the natural filtration of X, then
$\mathcal{F}_s$
is the natural filtration of X, then
 $${\mathbb{E}} [Z_t \mid \mathcal{F}_s] = \int p(s,X_s;\ t,x) \rho(t,x) \,{\mathrm{d}} x =Z_s{,}$$
$${\mathbb{E}} [Z_t \mid \mathcal{F}_s] = \int p(s,X_s;\ t,x) \rho(t,x) \,{\mathrm{d}} x =Z_s{,}$$
where we used the Chapman–Kolmogorov equations. Therefore  ${(t,x)\mapsto \rho(t,x)}$
is space–time harmonic and then the claim follows from [Reference Revuz and Yor32, Proposition 1.7, Chapter VII].
${(t,x)\mapsto \rho(t,x)}$
is space–time harmonic and then the claim follows from [Reference Revuz and Yor32, Proposition 1.7, Chapter VII].
Acknowledgements
We thank O. Papaspiliopoulos (Universitat Pompeu Fabra Barcelona), S. Sommer (University of Copenhagen), and M. Mider (University of Warwick) for stimulating discussions on diffusion bridge simulation.
J. Bierkens acknowledges support by the Dutch Research Council (NWO) for the research project ‘Zigzagging through computational barriers’ via project number 016.Vidi.189.043.