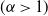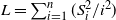1. Model and summary of results
Consider two urns, each of which initially has one ball. Balls come sequentially. When there are i balls in the first urn and j balls in the second urn, the next ball is placed in the first urn with probability ![]() $i^{{\alpha}}/(i^{{\alpha}}+j^{{\alpha}})$ and in the second urn with probability
$i^{{\alpha}}/(i^{{\alpha}}+j^{{\alpha}})$ and in the second urn with probability ![]() $j^{{\alpha}}/(i^{{\alpha}}+j^{{\alpha}})$. Here
$j^{{\alpha}}/(i^{{\alpha}}+j^{{\alpha}})$. Here ![]() ${\alpha}$ is a constant. In this work we shall consider only
${\alpha}$ is a constant. In this work we shall consider only ![]() ${\alpha} > 1$, though we note that the case
${\alpha} > 1$, though we note that the case ![]() ${\alpha}=1$ is the classic Pólya urn model [Reference Eggenberger and Pólya10, Reference Pólya23]; see Remark 1.1. Equivalently, we define a Markov chain
${\alpha}=1$ is the classic Pólya urn model [Reference Eggenberger and Pólya10, Reference Pólya23]; see Remark 1.1. Equivalently, we define a Markov chain ![]() $\{(X_n,Y_n)\colon n \geq 2\}$ with states
$\{(X_n,Y_n)\colon n \geq 2\}$ with states ![]() $\mathbb{N}\times \mathbb{N}$ and initial state
$\mathbb{N}\times \mathbb{N}$ and initial state ![]() $ (X_2,Y_2)=(1, 1) $, and transition probabilities
$ (X_2,Y_2)=(1, 1) $, and transition probabilities
(We have chosen the notation such that ![]() $X_n+Y_n=n$; we thus start with
$X_n+Y_n=n$; we thus start with ![]() $n=2$.)
$n=2$.)
In this model the rich get richer. It is highly unstable, as demonstrated by Theorems 2.1 and 2.3 below. We examine the (rare) event that the urn populations remain stable. For definiteness we concentrate on the event that state (n, n) is reached, i.e. ![]() $ (X_{2n},Y_{2n})=(n,n) $, which we denote
$ (X_{2n},Y_{2n})=(n,n) $, which we denote ![]() $\operatorname{BINGO}(n,n)$.
$\operatorname{BINGO}(n,n)$.
This work has three interrelated goals. First, we find the asymptotic probability of the urn population remaining stable, more precisely that it reaches the state (n, n) (see Theorem 2.3). Second, we study the typical behavior of the urn process ![]() $\{ (X_n, Y_n) \colon n \geq 2\}$, conditional on the rare event that state (n, n) is reached. We find that the typical walk from (1, 1) to (n, n) is given asymptotically by a distorted Brownian bridge (see Theorem 1.2 below) and locally, suitably scaled, by an Ornstein–Uhlenbeck process, stated in Theorem 1.4. The technique of continuous-time embedding, as described in Section 2, is crucially utilized in deriving these results. Finally, as an independent application of these ideas, we provide a lower-tail large deviation principle (LDP) for a quadratic functional of simple symmetric random walk, defined formally in (1.3).
$\{ (X_n, Y_n) \colon n \geq 2\}$, conditional on the rare event that state (n, n) is reached. We find that the typical walk from (1, 1) to (n, n) is given asymptotically by a distorted Brownian bridge (see Theorem 1.2 below) and locally, suitably scaled, by an Ornstein–Uhlenbeck process, stated in Theorem 1.4. The technique of continuous-time embedding, as described in Section 2, is crucially utilized in deriving these results. Finally, as an independent application of these ideas, we provide a lower-tail large deviation principle (LDP) for a quadratic functional of simple symmetric random walk, defined formally in (1.3).
For the convenience of the reader, we start with a high-level description of the connection of our urn process to the random walk statistic L defined below. Note that a sequence ![]() $\xi_1,\ldots,\xi_{2n-2}=\pm 1$ corresponds bijectively to a path P of length
$\xi_1,\ldots,\xi_{2n-2}=\pm 1$ corresponds bijectively to a path P of length ![]() $2n-2$ on
$2n-2$ on ![]() $\mathbb{N} \times \mathbb{N}$ starting at (1, 1), with
$\mathbb{N} \times \mathbb{N}$ starting at (1, 1), with ![]() $\pm 1$ representing horizontal and vertical moves respectively.
$\pm 1$ representing horizontal and vertical moves respectively. ![]() ${\mathbb{P}}[{\bf P}]$ represents the probability the Markov chain follows the path P.
${\mathbb{P}}[{\bf P}]$ represents the probability the Markov chain follows the path P. ![]() ${\mathbb{P}}[\!\operatorname{BINGO}(n,n)]$ is then the sum of
${\mathbb{P}}[\!\operatorname{BINGO}(n,n)]$ is then the sum of ![]() ${\mathbb{P}}[{\bf P}]$ over all paths from (1, 1) to (n, n). The values
${\mathbb{P}}[{\bf P}]$ over all paths from (1, 1) to (n, n). The values ![]() ${\mathbb{P}}[{\bf P}]$ vary considerably. The further P is from the main diagonal the lower is
${\mathbb{P}}[{\bf P}]$ vary considerably. The further P is from the main diagonal the lower is ![]() ${\mathbb{P}}[{\bf P}]$. Set
${\mathbb{P}}[{\bf P}]$. Set ![]() $S_t=\sum_{i=1}^t \xi_i$.
$S_t=\sum_{i=1}^t \xi_i$. ![]() $S_t$ then measures how far the path is from the main diagonal after t steps. The exact relationship between the
$S_t$ then measures how far the path is from the main diagonal after t steps. The exact relationship between the ![]() $S_t$ and
$S_t$ and ![]() ${\mathbb{P}}[{\bf P}]$ is given by a somewhat complex formula. Perhaps surprisingly, the asymptotic relationship is well captured by a single statistic,
${\mathbb{P}}[{\bf P}]$ is given by a somewhat complex formula. Perhaps surprisingly, the asymptotic relationship is well captured by a single statistic, ![]() $L \,:\!= \sum_{t=1}^{2n-2}t^{-2}S_t^2$. This relationship is captured in Section 4.
$L \,:\!= \sum_{t=1}^{2n-2}t^{-2}S_t^2$. This relationship is captured in Section 4. ![]() ${\mathbb{P}}[{\bf P}]$ is given by a term
${\mathbb{P}}[{\bf P}]$ is given by a term ![]() $\operatorname{BASE}$, common to all paths, and an expression
$\operatorname{BASE}$, common to all paths, and an expression ![]() $\operatorname{FIT}$, defined in (4.3) and (4.5).
$\operatorname{FIT}$, defined in (4.3) and (4.5). ![]() $\operatorname{FIT}$, in turn, will be approximated by
$\operatorname{FIT}$, in turn, will be approximated by ![]() $\exp[-{\lambda} L]$,
$\exp[-{\lambda} L]$, ![]() ${\lambda}$ given by (4.2).
${\lambda}$ given by (4.2). ![]() ${\mathbb{P}}[\!\operatorname{BINGO}(n,n)]$ is then given by the number of paths times
${\mathbb{P}}[\!\operatorname{BINGO}(n,n)]$ is then given by the number of paths times ![]() $\operatorname{BASE}$ times the expected value of
$\operatorname{BASE}$ times the expected value of ![]() $\operatorname{FIT}$. The expectation of
$\operatorname{FIT}$. The expectation of ![]() $\operatorname{FIT}$, critically, is approximated by the Laplace transform
$\operatorname{FIT}$, critically, is approximated by the Laplace transform ![]() ${\mathbb E}[\exp[-{\lambda} L]]$. An approximation for
${\mathbb E}[\exp[-{\lambda} L]]$. An approximation for ![]() ${\mathbb{P}}[\!\operatorname{BINGO}(n,n)]$ thus provides tight estimates of the Laplace transform of L, which in turn governs the lower-tail large deviations of L, given by Theorem 1.1 below.
${\mathbb{P}}[\!\operatorname{BINGO}(n,n)]$ thus provides tight estimates of the Laplace transform of L, which in turn governs the lower-tail large deviations of L, given by Theorem 1.1 below.
We return to a more formal presentation. Let ![]() $\xi_1,\ldots,\xi_n=\pm 1$, uniformly and independently, and set
$\xi_1,\ldots,\xi_n=\pm 1$, uniformly and independently, and set ![]() $S_t \,:\!= \sum_{i=1}^t \xi_i$. That is,
$S_t \,:\!= \sum_{i=1}^t \xi_i$. That is, ![]() $S_t$ is the position of the simple symmetric random walk at time t. (Note that we are not conditioning on
$S_t$ is the position of the simple symmetric random walk at time t. (Note that we are not conditioning on ![]() $\sum\xi_i=0$.) We set
$\sum\xi_i=0$.) We set
As ![]() ${\mathbb E}[S_i^2]=i$,
${\mathbb E}[S_i^2]=i$,
and, as will be seen later, ![]() $L_n$ is typically about
$L_n$ is typically about ![]() $\ln n$.
$\ln n$.
Our concern is with the lower tail of the distribution of ![]() $L_n$, and we prove the following. (See Theorem 8.4 for a corresponding result for the upper tail.)
$L_n$, and we prove the following. (See Theorem 8.4 for a corresponding result for the upper tail.)
Theorem 1.1. For any fixed ![]() $c \in (0, 1)$,
$c \in (0, 1)$,
with
The connection between the urn process and the random walk statistic L, alluded to above, provided the original motivation for our investigations. In pursuing these investigations we have found ![]() $L_n$ to have quite subtle properties.
$L_n$ to have quite subtle properties.
In studying ![]() $L_n$ it is helpful to parametrize
$L_n$ it is helpful to parametrize ![]() $S_i=\sqrt{i}N_i$; the
$S_i=\sqrt{i}N_i$; the ![]() $N_i$ are asymptotically (in i) standard Gaussian and
$N_i$ are asymptotically (in i) standard Gaussian and ![]() $L=\sum N_i^2/i$. The harmonic series suggests a logarithmic scaling,
$L=\sum N_i^2/i$. The harmonic series suggests a logarithmic scaling, ![]() $t=\ln i$. Note that under this scaling we have strong correlation when t, t’ are close, which fades as the distance increases. That is,
$t=\ln i$. Note that under this scaling we have strong correlation when t, t’ are close, which fades as the distance increases. That is, ![]() $S_i,S_{i{\lambda}}$ are closely correlated when
$S_i,S_{i{\lambda}}$ are closely correlated when ![]() ${\lambda}$ is close to one and have positive asymptotic correlation for any fixed
${\lambda}$ is close to one and have positive asymptotic correlation for any fixed ![]() ${\lambda}$, but that correlation approaches zero as
${\lambda}$, but that correlation approaches zero as ![]() ${\lambda}$ approaches infinity.
${\lambda}$ approaches infinity.
We give two very different arguments for Theorem 1.1. In Sections 4–6 we employ the Markov process ![]() $(X_n,Y_n)$ and the continuous-time argument for it in Section 2 to derive the Laplace transform of L, and from that deduce the large deviation Theorem 1.1. In Sections 7–8 we provide a more traditional proof, which turns out to be quite challenging. We couple the random walk to a standard Brownian motion via the celebrated KMT (Komlós–Major–Tusnády) coupling, and establish that it suffices to derive the corresponding LDP for a Brownian analog of L. Subsequently, we derive the LDP by the general theory for quadratic functionals of Brownian motion.
$(X_n,Y_n)$ and the continuous-time argument for it in Section 2 to derive the Laplace transform of L, and from that deduce the large deviation Theorem 1.1. In Sections 7–8 we provide a more traditional proof, which turns out to be quite challenging. We couple the random walk to a standard Brownian motion via the celebrated KMT (Komlós–Major–Tusnády) coupling, and establish that it suffices to derive the corresponding LDP for a Brownian analog of L. Subsequently, we derive the LDP by the general theory for quadratic functionals of Brownian motion.
Theorem 1.1 establishes a rigorous lower-tail LDP for a quadratic functional of the simple symmetric random walk. Large deviations for non-linear functions of ![]() $\{\pm 1\}$ variables have been an active research area in recent years. In a breakthrough paper, Chatterjee and Dembo [Reference Chatterjee and Dembo7] initiated a systematic study of LDPs of non-linear functionals of
$\{\pm 1\}$ variables have been an active research area in recent years. In a breakthrough paper, Chatterjee and Dembo [Reference Chatterjee and Dembo7] initiated a systematic study of LDPs of non-linear functionals of ![]() $\{\pm 1\}$ variables. The theory was subsequently extended by Eldan [Reference Eldan11], and has been applied to numerous problems in probability and combinatorics (see e.g. [Reference Bhattacharya, Ganguly, Lubetzky and Zhao3], [Reference Bhattacharya, Ganguly, Shao and Zhao4], [Reference Eldan and Gross12], [Reference Eldan and Gross13], and [Reference Lubetzky and Zhao20]). We emphasize that Theorem 1.1 does not follow using the general theory established in these prior works, and that our approaches are entirely different. We elaborate more on this in Remark 8.2.
$\{\pm 1\}$ variables. The theory was subsequently extended by Eldan [Reference Eldan11], and has been applied to numerous problems in probability and combinatorics (see e.g. [Reference Bhattacharya, Ganguly, Lubetzky and Zhao3], [Reference Bhattacharya, Ganguly, Shao and Zhao4], [Reference Eldan and Gross12], [Reference Eldan and Gross13], and [Reference Lubetzky and Zhao20]). We emphasize that Theorem 1.1 does not follow using the general theory established in these prior works, and that our approaches are entirely different. We elaborate more on this in Remark 8.2.
In Section 9 we return to the Markov process ![]() $(X_k,Y_k)$ defined above, conditioned on the rare event
$(X_k,Y_k)$ defined above, conditioned on the rare event ![]() $\operatorname{BINGO}(n,n)$, and examine the typical path from (1, 1) to (n, n). We define
$\operatorname{BINGO}(n,n)$, and examine the typical path from (1, 1) to (n, n). We define ![]() ${\Delta}_k \,:\!=X_k-Y_k$, so that
${\Delta}_k \,:\!=X_k-Y_k$, so that
and define, for completeness, ![]() ${\Delta}_0={\Delta}_1 \,:\!=0$. (For typographical reasons, we sometimes write
${\Delta}_0={\Delta}_1 \,:\!=0$. (For typographical reasons, we sometimes write ![]() ${\Delta}(k)$.) Note that the event
${\Delta}(k)$.) Note that the event ![]() $\operatorname{BINGO}(n,n)$ can be written
$\operatorname{BINGO}(n,n)$ can be written ![]() ${\Delta}_{2n}=0$. We provide a functional limit law which shows that conditioned on
${\Delta}_{2n}=0$. We provide a functional limit law which shows that conditioned on ![]() $\operatorname{BINGO}(n,n)$,
$\operatorname{BINGO}(n,n)$, ![]() ${\Delta}_k$ is typically of order
${\Delta}_k$ is typically of order ![]() $\sqrt n$ for
$\sqrt n$ for ![]() $2<k<2n$, and that suitably rescaled,
$2<k<2n$, and that suitably rescaled, ![]() $ ({\Delta}_k)_{k=2}^{2n} $ converges to a distorted Brownian bridge.
$ ({\Delta}_k)_{k=2}^{2n} $ converges to a distorted Brownian bridge.
Theorem 1.2. Let ![]() ${G_{\alpha}}(t)$,
${G_{\alpha}}(t)$, ![]() $t\in{[0, 1]}$, be the continuous Gaussian process with mean 0 and covariance function
$t\in{[0, 1]}$, be the continuous Gaussian process with mean 0 and covariance function
Then, as ![]() ${{n\to\infty}}$, conditioned on
${{n\to\infty}}$, conditioned on ![]() $\operatorname{BINGO}(n,n)$ (i.e.
$\operatorname{BINGO}(n,n)$ (i.e. ![]() ${\Delta}_{2n}=0)$,
${\Delta}_{2n}=0)$,
in ![]() ${\mathcal{D}}{[0, 1]}$ with the Skorokhod topology.
${\mathcal{D}}{[0, 1]}$ with the Skorokhod topology.
![]() ${G_{\alpha}}(t)$ can be constructed from a standard Brownian bridge
${G_{\alpha}}(t)$ can be constructed from a standard Brownian bridge ![]() ${\operatorname{{Br}}}(t)$ as
${\operatorname{{Br}}}(t)$ as
with ![]() ${G_{\alpha}}(0) \,:\!=0$. Related constructions from a Brownian motion are given in (9.16)–(9.17).
${G_{\alpha}}(0) \,:\!=0$. Related constructions from a Brownian motion are given in (9.16)–(9.17).
We give also a version of this theorem for ![]() $k={\mathrm{o}}(n)$. Now a Brownian motion B(t) appears instead of a Brownian bridge.
$k={\mathrm{o}}(n)$. Now a Brownian motion B(t) appears instead of a Brownian bridge.
Theorem 1.3. Let ![]() $m_n\to\infty$ be real numbers with
$m_n\to\infty$ be real numbers with ![]() $m_n={\mathrm{o}}(n)$. Then, as
$m_n={\mathrm{o}}(n)$. Then, as ![]() ${{n\to\infty}}$, conditioned on
${{n\to\infty}}$, conditioned on ![]() $\operatorname{BINGO}(n,n)$ (i.e.
$\operatorname{BINGO}(n,n)$ (i.e. ![]() ${\Delta}_{2n}=0$),
${\Delta}_{2n}=0$),
in ![]() ${{\mathcal{D}}[0,\infty)}$ with the Skorokhod topology.
${{\mathcal{D}}[0,\infty)}$ with the Skorokhod topology.
In particular, taking ![]() $m_n$ integers and
$m_n$ integers and ![]() $t=1$, it follows that for any integers
$t=1$, it follows that for any integers ![]() $m=m_n\to\infty$ with
$m=m_n\to\infty$ with ![]() $m={\mathrm{o}}(n)$, conditioned on
$m={\mathrm{o}}(n)$, conditioned on ![]() $\operatorname{BINGO}(n,n)$,
$\operatorname{BINGO}(n,n)$,
For ![]() $m<n$ with
$m<n$ with ![]() $m=\Theta(n)$, we obtain from Theorem 1.2 a similar result with a correction factor for the variance. Thus,
$m=\Theta(n)$, we obtain from Theorem 1.2 a similar result with a correction factor for the variance. Thus, ![]() ${\Delta}_m$ is typically of order
${\Delta}_m$ is typically of order ![]() $\sqrt m$ for
$\sqrt m$ for ![]() $m<n$.
$m<n$.
Under a suitable logarithmic scaling, we have in the limit a stationary Ornstein–Uhlenbeck process, defined by (1.11) below.
Theorem 1.4. Fix any sequence ![]() $t_n$ such that
$t_n$ such that ![]() $t_n \to \infty$ and
$t_n \to \infty$ and ![]() $\log n - \log t_n \to\infty$. Then we have, as
$\log n - \log t_n \to\infty$. Then we have, as ![]() $n \to \infty$, conditional on
$n \to \infty$, conditional on ![]() $\operatorname{BINGO}(n,n)$,
$\operatorname{BINGO}(n,n)$,
in ![]() $\mathcal{D}(-\infty, \infty)$ with the Skorokhod topology, where Z(s) is a centered Gaussian process with covariance function
$\mathcal{D}(-\infty, \infty)$ with the Skorokhod topology, where Z(s) is a centered Gaussian process with covariance function
Remark 1.1. As said above, we consider in this paper only ![]() $\alpha>1$, which is necessary for Theorem 2.1, for example. However, it would also be interesting to study
$\alpha>1$, which is necessary for Theorem 2.1, for example. However, it would also be interesting to study ![]() $\alpha\in{[0, 1]}$, when
$\alpha\in{[0, 1]}$, when ![]() $(X_k,Y_k)$ behaves quite differently. Note that
$(X_k,Y_k)$ behaves quite differently. Note that ![]() $\alpha=0$ yields
$\alpha=0$ yields ![]() ${\Delta}_k$ as a simple symmetric random walk, and then it is well known that (1.7) holds with
${\Delta}_k$ as a simple symmetric random walk, and then it is well known that (1.7) holds with ![]() $G_0(t) \,:\!=\sqrt2 {\operatorname{{Br}}}(t)$ (see e.g. [Reference Billingsley5, Theorem 24.1]). (The factor
$G_0(t) \,:\!=\sqrt2 {\operatorname{{Br}}}(t)$ (see e.g. [Reference Billingsley5, Theorem 24.1]). (The factor ![]() $\sqrt2$ is because of our choice of normalization.) Furthermore, for
$\sqrt2$ is because of our choice of normalization.) Furthermore, for ![]() $\alpha=1$, when, as mentioned above,
$\alpha=1$, when, as mentioned above, ![]() $(X_k,Y_k)$ is the classical Pólya urn, it is well known that the increments are exchangeable, and thus, conditioned on
$(X_k,Y_k)$ is the classical Pólya urn, it is well known that the increments are exchangeable, and thus, conditioned on ![]() $\operatorname{BINGO}(n,n)$, all paths to (n, n) have the same probability. This can be seen from (4.5)–(4.7) below, noting that for
$\operatorname{BINGO}(n,n)$, all paths to (n, n) have the same probability. This can be seen from (4.5)–(4.7) below, noting that for ![]() $\alpha=0$ or
$\alpha=0$ or ![]() $\alpha=1$,
$\alpha=1$, ![]() $\operatorname{FIT}_i$ in (4.3) is constant 1. Thus, conditioned on
$\operatorname{FIT}_i$ in (4.3) is constant 1. Thus, conditioned on ![]() $\operatorname{BINGO}(n,n)$,
$\operatorname{BINGO}(n,n)$, ![]() $\alpha=1$ and
$\alpha=1$ and ![]() $\alpha=0$ coincide, and therefore (1.7) holds for
$\alpha=0$ coincide, and therefore (1.7) holds for ![]() $\alpha=1$ too, with
$\alpha=1$ too, with ![]() $G_1(t) =G_0(t)=\sqrt2 {\operatorname{{Br}}}(t)$. Note further that this agrees with (1.6). However, for (1.8), it holds for
$G_1(t) =G_0(t)=\sqrt2 {\operatorname{{Br}}}(t)$. Note further that this agrees with (1.6). However, for (1.8), it holds for ![]() $\alpha=1$ but not for
$\alpha=1$ but not for ![]() $\alpha=0$. Similarly, (1.9) and (1.10)–(1.11) hold for
$\alpha=0$. Similarly, (1.9) and (1.10)–(1.11) hold for ![]() $\alpha=1$, with
$\alpha=1$, with ![]() $H_1(t)=B(t)$. It would be interesting to find an analog of Theorem 1.2 for
$H_1(t)=B(t)$. It would be interesting to find an analog of Theorem 1.2 for ![]() $0<\alpha<1$.
$0<\alpha<1$.
2. Continuous time
In this section we examine the Markov chain defined in Section 1 (1.1)–(1.2) with initial state (1, 1).
Definition 2.1. ![]() $\operatorname{BINGO}(i,j)$ denotes the event that state (i, j) is reached.
$\operatorname{BINGO}(i,j)$ denotes the event that state (i, j) is reached.
In this section, we study asymptotic probabilities of various ![]() $\operatorname{BINGO}$ events. These probabilities will turn out to be extremely crucial in our proof of Theorem 1.1 in Sections 4, 5, and 6.
$\operatorname{BINGO}$ events. These probabilities will turn out to be extremely crucial in our proof of Theorem 1.1 in Sections 4, 5, and 6.
This preferential attachment model is best tackled (see Remark 2.1) via continuous time. Let ![]() ${V}_i,{W}_i$,
${V}_i,{W}_i$, ![]() $i\geq 1$, denote exponential distributions with rate parameter
$i\geq 1$, denote exponential distributions with rate parameter ![]() $i^{{\alpha}}$. That is,
$i^{{\alpha}}$. That is, ![]() ${V}_i,{W}_i$ have probability density function
${V}_i,{W}_i$ have probability density function ![]() ${\lambda} \,{\mathrm{e}}^{-{\lambda} x}$ with
${\lambda} \,{\mathrm{e}}^{-{\lambda} x}$ with ![]() ${\lambda}=i^{{\alpha}}$. The
${\lambda}=i^{{\alpha}}$. The ![]() ${V}_i,{W}_i$ are all chosen mutually independently. Begin the urn model, as before, with each urn having one ball. Begin time at zero. When an urn has i balls it waits time
${V}_i,{W}_i$ are all chosen mutually independently. Begin the urn model, as before, with each urn having one ball. Begin time at zero. When an urn has i balls it waits time ![]() ${V}_i$ until it receives its next ball. The forgetfulness property of the exponential distribution (plus a little calculus) gives that when the bins have i, j balls, respectively, the probability that
${V}_i$ until it receives its next ball. The forgetfulness property of the exponential distribution (plus a little calculus) gives that when the bins have i, j balls, respectively, the probability that ![]() ${V}_i < {W}_j$ is
${V}_i < {W}_j$ is ![]() $i^{{\alpha}}/(i^{{\alpha}}+j^{{\alpha}})$ as desired. This leads to a remarkable theorem ([Reference Davis8], but see Remark 2.1) with what is surely a Proof from The Book.
$i^{{\alpha}}/(i^{{\alpha}}+j^{{\alpha}})$ as desired. This leads to a remarkable theorem ([Reference Davis8], but see Remark 2.1) with what is surely a Proof from The Book.
Theorem 2.1. With probability 1, one of the bins gets all but a finite number of the balls.
Proof. Let ![]() ${V}=\sum_{i=1}^{\infty}{V}_i$,
${V}=\sum_{i=1}^{\infty}{V}_i$, ![]() ${W}=\sum_{i=1}^{\infty}{W}_i$. As
${W}=\sum_{i=1}^{\infty}{W}_i$. As ![]() $\sum i^{-{\alpha}}$ is finite (here using that
$\sum i^{-{\alpha}}$ is finite (here using that ![]() ${\alpha} > 1$), both V and W are finite a.s. (almost surely). As the distribution is non-atomic,
${\alpha} > 1$), both V and W are finite a.s. (almost surely). As the distribution is non-atomic, ![]() ${V}\neq {W}$ a.s. Say
${V}\neq {W}$ a.s. Say ![]() ${V} < {W}$. Then bin one receives all its balls before bin two does. When bin one has all its balls the process stops (a countable number of balls have been placed) and bin two has only a finite number of balls.
${V} < {W}$. Then bin one receives all its balls before bin two does. When bin one has all its balls the process stops (a countable number of balls have been placed) and bin two has only a finite number of balls.
 \begin{equation} \lim_{M{\rightarrow}\infty}\lim_{k{\rightarrow}\infty}\sum_{i=M}^{k-M}{\mathbb{P}}[\!\operatorname{BINGO}(i,k-i)]=0 . \end{equation}
\begin{equation} \lim_{M{\rightarrow}\infty}\lim_{k{\rightarrow}\infty}\sum_{i=M}^{k-M}{\mathbb{P}}[\!\operatorname{BINGO}(i,k-i)]=0 . \end{equation}
Proof. For M fixed let ![]() $\operatorname{FENCE}(k)$ denote the union of the
$\operatorname{FENCE}(k)$ denote the union of the ![]() $\operatorname{BINGO}$
$\operatorname{BINGO}$ ![]() $(i,k-i)$ over
$(i,k-i)$ over ![]() $M\leq i\leq k-M$; this is the event that at the time when there are k balls in the urns, there are at least M balls in each urn. As these
$M\leq i\leq k-M$; this is the event that at the time when there are k balls in the urns, there are at least M balls in each urn. As these ![]() $\operatorname{BINGO}(i,k-i)$ are disjoint (a path can only hit one state with a given sum of coefficients),
$\operatorname{BINGO}(i,k-i)$ are disjoint (a path can only hit one state with a given sum of coefficients), ![]() $\Pr[\!\operatorname{FENCE}(k)]$ is given by the sum in (2.1). Further,
$\Pr[\!\operatorname{FENCE}(k)]$ is given by the sum in (2.1). Further, ![]() $\operatorname{FENCE}(k)$ implies
$\operatorname{FENCE}(k)$ implies ![]() $\operatorname{FENCE}(k')$ for all
$\operatorname{FENCE}(k')$ for all ![]() $k'\geq k$, as once a path hits the fence at k it cannot escape the fence at k’. Thus the union of all
$k'\geq k$, as once a path hits the fence at k it cannot escape the fence at k’. Thus the union of all ![]() $\operatorname{FENCE}(k)$ has probability
$\operatorname{FENCE}(k)$ has probability ![]() $\lim_{k{\rightarrow}\infty}$ of the sum. But the union is the event that both bins eventually get at least M balls. From Theorem 2.1, this has limiting value (in M) of zero.
$\lim_{k{\rightarrow}\infty}$ of the sum. But the union is the event that both bins eventually get at least M balls. From Theorem 2.1, this has limiting value (in M) of zero.
Remark 2.1. The use of continuous time appears to be due to Herman Rubin, as attributed by Burgess Davis in [Reference Davis8]. A thorough study of preferential attachment (in a far more general setting) via continuous time was given in the PhD thesis of Roberto Oliveira. Many of the results of Oliveira’s thesis are given in [Reference Oliveira and Spencer22]. Theorem 2.1 and Corollary 2.1 provided the original motivation for our current research. The senior author (JS) searched for a combinatorial proof, appropriately counting paths with their respective probabilities, for Corollary 2.1. This in turn led to attempts to estimate ![]() $\operatorname{BINGO}(i,j)$ without using continuous time. Somewhat surprisingly, one result is in the opposite direction. The estimates on
$\operatorname{BINGO}(i,j)$ without using continuous time. Somewhat surprisingly, one result is in the opposite direction. The estimates on ![]() $\operatorname{BINGO}(i,j)$ given by continuous time have given a fairly roundabout argument for the large deviation results for the random variable L given by Theorem 1.1.
$\operatorname{BINGO}(i,j)$ given by continuous time have given a fairly roundabout argument for the large deviation results for the random variable L given by Theorem 1.1.
Continuous time gives us excellent asymptotics on ![]() $\operatorname{BINGO}$. We first provide the bridge between continuous time and
$\operatorname{BINGO}$. We first provide the bridge between continuous time and ![]() $\operatorname{BINGO}$.
$\operatorname{BINGO}$.
Theorem 2.2. Set
 \begin{equation*} \Xi \,:\!= \sum_{s=1}^{i-1}{V}_i - \sum_{t=1}^{j-1}{W}_j {.}\end{equation*}
\begin{equation*} \Xi \,:\!= \sum_{s=1}^{i-1}{V}_i - \sum_{t=1}^{j-1}{W}_j {.}\end{equation*}
Then ![]() $\operatorname{BINGO}(i,j)$ occurs if and only if either
$\operatorname{BINGO}(i,j)$ occurs if and only if either ![]() $0 \le \Xi < {W}_j$ or
$0 \le \Xi < {W}_j$ or ![]() $0 \le -\Xi< {V}_i$.
$0 \le -\Xi< {V}_i$.
Proof. ![]() $\Xi$ is the time difference between when urn one receives its ith ball and urn two receives its jth ball. Suppose
$\Xi$ is the time difference between when urn one receives its ith ball and urn two receives its jth ball. Suppose ![]() $\Xi \le 0$. At time
$\Xi \le 0$. At time ![]() $T=\sum_{s=1}^{i-1}$
$T=\sum_{s=1}^{i-1}$ ![]() ${V}_i$, urn one receives its ith ball. Urn two will receive its jth ball at time
${V}_i$, urn one receives its ith ball. Urn two will receive its jth ball at time ![]() $T-\Xi$.
$T-\Xi$. ![]() $\operatorname{BINGO}(i,j)$ occurs when urn one has not yet received its
$\operatorname{BINGO}(i,j)$ occurs when urn one has not yet received its ![]() $(i+1)$th ball, which it does at time
$(i+1)$th ball, which it does at time ![]() $T+{V}_i$. This occurs if and only if
$T+{V}_i$. This occurs if and only if ![]() ${V}_i > -\Xi$. The case
${V}_i > -\Xi$. The case ![]() $\Xi \ge 0$ is similar.
$\Xi \ge 0$ is similar.
Theorem 2.3. There is a positive constant ![]() $\beta$, dependent only on
$\beta$, dependent only on ![]() ${\alpha}$, so that when
${\alpha}$, so that when ![]() $i,j{\rightarrow}\infty$
$i,j{\rightarrow}\infty$
In particular,
Remark 2.2. Set ![]() $\Xi^{\dagger} \,:\!= \sum_{i=1}^{\infty} ({V}_i-{W}_i)$. Basically
$\Xi^{\dagger} \,:\!= \sum_{i=1}^{\infty} ({V}_i-{W}_i)$. Basically ![]() $\Xi$ is estimated by
$\Xi$ is estimated by ![]() $\Xi^{\dagger}$ and
$\Xi^{\dagger}$ and ![]() $\beta$ is the probability density function of
$\beta$ is the probability density function of ![]() $\Xi^{\dagger}$ at 0.
$\Xi^{\dagger}$ at 0. ![]() ${W}_j$ is almost always
${W}_j$ is almost always ![]() ${\mathrm{o}}(1)$ (as
${\mathrm{o}}(1)$ (as ![]() $j{\rightarrow}\infty$) so that
$j{\rightarrow}\infty$) so that ![]() $0 \le \Xi < {W}_j$ should occur with asymptotic probability
$0 \le \Xi < {W}_j$ should occur with asymptotic probability ![]() $\beta {\mathbb E}[{W}_j] = \beta j^{-{\alpha}}$. However, the validity of the approximation is non-trivial and has forced our somewhat technical calculations.
$\beta {\mathbb E}[{W}_j] = \beta j^{-{\alpha}}$. However, the validity of the approximation is non-trivial and has forced our somewhat technical calculations.
Proof of Theorem 2.3. We analyze ![]() ${\mathbb{P}}[0\le \Xi < {W}_{j}]$ as
${\mathbb{P}}[0\le \Xi < {W}_{j}]$ as ![]() $ i,j \to \infty$. The analysis of the other term is similar, and is thus omitted. Note that
$ i,j \to \infty$. The analysis of the other term is similar, and is thus omitted. Note that ![]() $\Xi=\Xi_{ij}$ is the sum of independent random variables, each with a density with respect to Lebesgue measure. Thus
$\Xi=\Xi_{ij}$ is the sum of independent random variables, each with a density with respect to Lebesgue measure. Thus ![]() $\Xi_{ij}$ has a probability density function, which we denote as
$\Xi_{ij}$ has a probability density function, which we denote as ![]() $f_{ij}$.
$f_{ij}$.
We will use characteristic functions to study the density ![]() $f_{ij}$. We set
$f_{ij}$. We set ![]() $\phi_{ij}(t) = {\mathbb E}[ \exp({\mathrm{i}} t \Xi_{ij})]$. Upon direct computation, we have
$\phi_{ij}(t) = {\mathbb E}[ \exp({\mathrm{i}} t \Xi_{ij})]$. Upon direct computation, we have
 \begin{align*}\phi_{ij}(t) = \prod_{k=1}^{i-1} \dfrac{k^{\alpha}}{k^{\alpha} - {\mathrm{i}} t}\prod_{k=1}^{j-1} \dfrac{k^{\alpha}}{k^{\alpha} + {\mathrm{i}} t }.\end{align*}
\begin{align*}\phi_{ij}(t) = \prod_{k=1}^{i-1} \dfrac{k^{\alpha}}{k^{\alpha} - {\mathrm{i}} t}\prod_{k=1}^{j-1} \dfrac{k^{\alpha}}{k^{\alpha} + {\mathrm{i}} t }.\end{align*}
Using the Fourier inversion theorem, the density may be related to the characteristic function. Thus, provided ![]() $i+j\ge4$,
$i+j\ge4$, ![]() $\phi_{ij}(t)$ is integrable with respect to Lebesgue measure and then
$\phi_{ij}(t)$ is integrable with respect to Lebesgue measure and then
In particular,
Further, note that for each ![]() $t \in {\mathbb{R}}$ as
$t \in {\mathbb{R}}$ as ![]() $i,j \to \infty$,
$i,j \to \infty$,
and thus by dominated convergence,
This establishes the pointwise convergence of the density. Moreover, the same argument shows that for any convergent sequence ![]() $x_{ij}\to x$,
$x_{ij}\to x$, ![]() $f_{ij}(x_{ij})\to f_\infty(x)$. In particular, we define
$f_{ij}(x_{ij})\to f_\infty(x)$. In particular, we define ![]() $\beta \,:\!= f_{\infty}(0)$. We have, since
$\beta \,:\!= f_{\infty}(0)$. We have, since ![]() ${W}_j$ is independent of
${W}_j$ is independent of ![]() $\Xi_{ij}$, and has the same distribution as
$\Xi_{ij}$, and has the same distribution as ![]() $j^{-\alpha}{W}_1$,
$j^{-\alpha}{W}_1$,
and hence, by dominated convergence,
as ![]() $i,j \to \infty$. This establishes the required asymptotics of
$i,j \to \infty$. This establishes the required asymptotics of ![]() ${\mathbb{P}}[ 0 \leq \Xi_{ij} < {W}_{j} ] $.
${\mathbb{P}}[ 0 \leq \Xi_{ij} < {W}_{j} ] $.
3. More continuous time
We generalize ![]() $\operatorname{BINGO}$ to allow for arbitrary initial states. These results will be used crucially to establish finite-dimensional convergence in Section 9.
$\operatorname{BINGO}$ to allow for arbitrary initial states. These results will be used crucially to establish finite-dimensional convergence in Section 9.
Definition 3.1. ![]() $\operatorname{BINGO}(a,b;\,c,d)$ denotes the event that the Markov chain
$\operatorname{BINGO}(a,b;\,c,d)$ denotes the event that the Markov chain ![]() $(X_k,Y_k)$ given by (1.1)–(1.2) with initial state (a, b) reaches state (c, d).
$(X_k,Y_k)$ given by (1.1)–(1.2) with initial state (a, b) reaches state (c, d).
As before, let ![]() ${V}_i,{W}_j$ be exponentials at rate
${V}_i,{W}_j$ be exponentials at rate ![]() $i^{{\alpha}},j^{{\alpha}}$ but now restrict to
$i^{{\alpha}},j^{{\alpha}}$ but now restrict to ![]() $i\geq a, j\geq b$. Again we have a bridge.
$i\geq a, j\geq b$. Again we have a bridge.
Theorem 3.1. Let ![]() $a\le c$ and
$a\le c$ and ![]() $b\le d$, and set
$b\le d$, and set
 \begin{equation*} \Xi \,:\!= \sum_{i=a}^{c-1}{V}_i - \sum_{j=b}^{d-1} {W}_j .\end{equation*}
\begin{equation*} \Xi \,:\!= \sum_{i=a}^{c-1}{V}_i - \sum_{j=b}^{d-1} {W}_j .\end{equation*}
![]() $\operatorname{BINGO}(a,b;\,c,d)$ occurs if and only if either
$\operatorname{BINGO}(a,b;\,c,d)$ occurs if and only if either ![]() $0 \le -\Xi < {V}_c$ or
$0 \le -\Xi < {V}_c$ or ![]() $0 \le \Xi < {W}_d$.
$0 \le \Xi < {W}_d$.
Proof. The same as for Theorem 2.2.
Continuous time gives the asymptotics of ![]() $\operatorname{BINGO}$ for a wide variety of the parameters. We derive accurate estimates for various
$\operatorname{BINGO}$ for a wide variety of the parameters. We derive accurate estimates for various ![]() $\operatorname{BINGO}$ events, which will be used in our subsequent discussions.
$\operatorname{BINGO}$ events, which will be used in our subsequent discussions.
We begin with the simplest case, starting and ending on the diagonal. (See (2.2), when starting at (1, 1).)
Theorem 3.2. For any sequence ![]() $A = A(n) \to \infty$ with
$A = A(n) \to \infty$ with ![]() $A(n) = {\mathrm{o}}(n)$, as
$A(n) = {\mathrm{o}}(n)$, as ![]() $n \to \infty$,
$n \to \infty$,
In the proof of Theorem 1.1, we will use only the weaker
Before proving Theorem 3.2 we state a generalization, where we allow initial and final points that are off the diagonal (but not too far away; we consider only what will turn out to be the typical cases: see Theorems 1.2 and 1.3). Also, for later use in Section 9, we allow ![]() $A=\Theta(n)$ as long as
$A=\Theta(n)$ as long as ![]() $n-A=\Theta(n)$ (and in this connection we change the notation from n to B).
$n-A=\Theta(n)$ (and in this connection we change the notation from n to B).
Theorem 3.3. Fix ![]() $M >0$, and
$M >0$, and ![]() ${\theta}>1$. Then, uniformly for all
${\theta}>1$. Then, uniformly for all ![]() $A,B,{\Lambda},{\Gamma}\in\frac12{\mathbb Z}$ with
$A,B,{\Lambda},{\Gamma}\in\frac12{\mathbb Z}$ with ![]() $A\pm{\Lambda}\in{\mathbb Z}$,
$A\pm{\Lambda}\in{\mathbb Z}$, ![]() $B\pm{\Gamma}\in{\mathbb Z}$ such that
$B\pm{\Gamma}\in{\mathbb Z}$ such that ![]() $A>0$,
$A>0$, ![]() $B\ge {\theta} A$,
$B\ge {\theta} A$, ![]() $|{\Lambda}| \leq M \sqrt{A}$, and
$|{\Lambda}| \leq M \sqrt{A}$, and ![]() $|{\Gamma}| \leq M \sqrt{B}$,
$|{\Gamma}| \leq M \sqrt{B}$,
 \begin{align}& {\mathbb{P}}[\!\operatorname{BINGO}(A+ {\Lambda},A - {\Lambda};\, B + {\Gamma}, B - {\Gamma})] \\ &\qquad={({1+o_{A}(1)})}\sqrt{\dfrac{2\alpha-1}{\pi}}\dfrac{A^{\alpha-1/2}}{B^\alpha\sqrt{1-(A/B)^{2\alpha-1}}} \\&\qquad\quad\,\times\exp{\biggl({-\dfrac{2\alpha-1}{1-(A/B)^{2\alpha-1}} {\bigg({\dfrac{{\Lambda}}{A^{1/2}}-\dfrac{{\Gamma}}{B^{\alpha} A^{1/2-\alpha}}}\bigg)}^2}\biggr)},\end{align}
\begin{align}& {\mathbb{P}}[\!\operatorname{BINGO}(A+ {\Lambda},A - {\Lambda};\, B + {\Gamma}, B - {\Gamma})] \\ &\qquad={({1+o_{A}(1)})}\sqrt{\dfrac{2\alpha-1}{\pi}}\dfrac{A^{\alpha-1/2}}{B^\alpha\sqrt{1-(A/B)^{2\alpha-1}}} \\&\qquad\quad\,\times\exp{\biggl({-\dfrac{2\alpha-1}{1-(A/B)^{2\alpha-1}} {\bigg({\dfrac{{\Lambda}}{A^{1/2}}-\dfrac{{\Gamma}}{B^{\alpha} A^{1/2-\alpha}}}\bigg)}^2}\biggr)},\end{align}
where ![]() $o_A(1)$ is a quantity that tends to 0 as
$o_A(1)$ is a quantity that tends to 0 as ![]() $A\to\infty$, uniformly in the other variables; that is,
$A\to\infty$, uniformly in the other variables; that is, ![]() $|o_A(1)|\le {\varepsilon}(A)$ for some function
$|o_A(1)|\le {\varepsilon}(A)$ for some function ![]() ${\varepsilon}(A)\to0$ as
${\varepsilon}(A)\to0$ as ![]() $A\to\infty$.
$A\to\infty$.
Remark 3.1. The right-hand side of (3.3), omitting the ![]() $o_{A}$ term, is the density function at
$o_{A}$ term, is the density function at ![]() ${\Gamma}$ for a normal distribution
${\Gamma}$ for a normal distribution ![]() $N(\mu,{\sigma^2})$ with parameters
$N(\mu,{\sigma^2})$ with parameters
 \begin{align*}\mu&=(B/A)^\alpha {\Lambda},\\ {\sigma^2}&=\dfrac{ A^{1-2\alpha}B^{2\alpha}{({1-(A/B)^{2\alpha-1}})}}{2(2\alpha-1)}.\end{align*}
\begin{align*}\mu&=(B/A)^\alpha {\Lambda},\\ {\sigma^2}&=\dfrac{ A^{1-2\alpha}B^{2\alpha}{({1-(A/B)^{2\alpha-1}})}}{2(2\alpha-1)}.\end{align*}
The two main cases of interest to us are ![]() $A\ll B=n$, as in Theorem 3.2, and
$A\ll B=n$, as in Theorem 3.2, and ![]() $B/A$ constant (at least up to rounding errors). For convenience, we state immediate corollaries covering these cases.
$B/A$ constant (at least up to rounding errors). For convenience, we state immediate corollaries covering these cases.
Corollary 3.1. Suppose ![]() $A=A(n)\to\infty$ with
$A=A(n)\to\infty$ with ![]() $A={\mathrm{o}}(n)$. Then, for all
$A={\mathrm{o}}(n)$. Then, for all ![]() ${\Lambda}={\Lambda}(n)$ and
${\Lambda}={\Lambda}(n)$ and ![]() ${\Gamma}={\Gamma}(n)$ with
${\Gamma}={\Gamma}(n)$ with ![]() ${\Lambda}={\mathrm{O}}({\sqrt A})$ and
${\Lambda}={\mathrm{O}}({\sqrt A})$ and ![]() ${\Gamma}={\mathrm{O}}({\sqrt n})$,
${\Gamma}={\mathrm{O}}({\sqrt n})$,
In Section 5 we use only the rougher asymptotics, extending (3.2):
Corollary 3.2. Suppose ![]() $A=A(n)$ and
$A=A(n)$ and ![]() $B=B(n)$ with
$B=B(n)$ with ![]() $A\to\infty$ and
$A\to\infty$ and ![]() $B/A\to{\theta}>1$ as
$B/A\to{\theta}>1$ as ![]() ${{n\to\infty}}$. Then, for all
${{n\to\infty}}$. Then, for all ![]() ${\Lambda}={\Lambda}(n)$ and
${\Lambda}={\Lambda}(n)$ and ![]() ${\Gamma}={\Gamma}(n)$ with
${\Gamma}={\Gamma}(n)$ with ![]() ${\Lambda}={\mathrm{O}}({\sqrt A})$ and
${\Lambda}={\mathrm{O}}({\sqrt A})$ and ![]() ${\Gamma}={\mathrm{O}}({\sqrt B})$,
${\Gamma}={\mathrm{O}}({\sqrt B})$,
 \begin{align*} & {\mathbb{P}}[\!\operatorname{BINGO}(A+ {\Lambda},A - {\Lambda};\, B + {\Gamma}, B - {\Gamma})] \\ &\qquad \sim\sqrt{\dfrac{2\alpha-1}{\pi}}\dfrac{A^{\alpha-1/2}}{B^\alpha\sqrt{1-{\theta} ^{1-2\alpha}}}\exp{\biggl({-\dfrac{(2\alpha-1)}{{({1-{\theta}^{1-2\alpha}})}A} {({{\Lambda}-{\theta}^{-\alpha}{\Gamma}})}^2}\biggr)}.\end{align*}
\begin{align*} & {\mathbb{P}}[\!\operatorname{BINGO}(A+ {\Lambda},A - {\Lambda};\, B + {\Gamma}, B - {\Gamma})] \\ &\qquad \sim\sqrt{\dfrac{2\alpha-1}{\pi}}\dfrac{A^{\alpha-1/2}}{B^\alpha\sqrt{1-{\theta} ^{1-2\alpha}}}\exp{\biggl({-\dfrac{(2\alpha-1)}{{({1-{\theta}^{1-2\alpha}})}A} {({{\Lambda}-{\theta}^{-\alpha}{\Gamma}})}^2}\biggr)}.\end{align*}
The proofs of Theorems 3.2 and 3.3 are similar to the proof of Theorem 2.3. We begin with a proof of the simpler Theorem 3.2, to show the main features of the proof. We then show the modifications needed for the more general Theorem 3.3.
Remark 3.2. Theorem 3.2 is basically a local CLT for ![]() $\Xi$; see Remark 2.2. Set
$\Xi$; see Remark 2.2. Set
 \[\Xi_n \,:\!= \sum_{k=A}^{n-1}({V}_k-{W}_k).\]
\[\Xi_n \,:\!= \sum_{k=A}^{n-1}({V}_k-{W}_k).\]
Then ![]() $\Xi_n$ is asymptotically Gaussian with mean
$\Xi_n$ is asymptotically Gaussian with mean ![]() $\mu=0$ and variance
$\mu=0$ and variance
 \begin{equation}{\sigma}_n^2 \,:\!= \mathrm{Var}[\Xi_n]=2\sum_{k=A}^{n-1}k^{-2{\alpha}} \sim \dfrac{2}{2{\alpha}-1}A^{1-2{\alpha}} .\end{equation}
\begin{equation}{\sigma}_n^2 \,:\!= \mathrm{Var}[\Xi_n]=2\sum_{k=A}^{n-1}k^{-2{\alpha}} \sim \dfrac{2}{2{\alpha}-1}A^{1-2{\alpha}} .\end{equation}
Approximating ![]() $\Xi_n$ by this Gaussian, its probability density function at zero is asymptotically
$\Xi_n$ by this Gaussian, its probability density function at zero is asymptotically
The probability that ![]() $0 \le -\Xi_n < {V}_n$ is then
$0 \le -\Xi_n < {V}_n$ is then ![]() $\sim {\mathbb E}[{V}_{n}]= n^{-{\alpha}}$ times this, and
$\sim {\mathbb E}[{V}_{n}]= n^{-{\alpha}}$ times this, and ![]() ${\mathbb{P}}[\!\operatorname{BINGO}]$ is twice that.
${\mathbb{P}}[\!\operatorname{BINGO}]$ is twice that.
Note that in Corollary 3.1, the probability has an extra factor of ![]() $\exp[-(2{\alpha}-1)({\Lambda}/\sqrt A)^2]$ over the basic
$\exp[-(2{\alpha}-1)({\Lambda}/\sqrt A)^2]$ over the basic ![]() ${\lambda}=0$ case of Theorem 3.2. Roughly, while
${\lambda}=0$ case of Theorem 3.2. Roughly, while ![]() $\Xi$ is still asymptotically Gaussian, the mean has moved
$\Xi$ is still asymptotically Gaussian, the mean has moved ![]() $\sim 2{\Lambda} A^{-{\alpha}}$ from zero.
$\sim 2{\Lambda} A^{-{\alpha}}$ from zero.
As before, the validity of the approximations is non-trivial and has forced our somewhat technical calculations.
Proof of Theorem 3.2. We assume ![]() $A\le n-1$ and define, as in Remark 3.2,
$A\le n-1$ and define, as in Remark 3.2,
 \[ \Xi_n \,:\!= \sum_{k=A}^{n-1} ({V}_k - {W}_k). \]
\[ \Xi_n \,:\!= \sum_{k=A}^{n-1} ({V}_k - {W}_k). \]
We note that ![]() $\Xi_n$ is centered with variance
$\Xi_n$ is centered with variance ![]() ${\sigma^2_n}$ given by (3.5), and, by the same argument as in the proof of Theorem 2.3, it has a probability density function, which we denote as
${\sigma^2_n}$ given by (3.5), and, by the same argument as in the proof of Theorem 2.3, it has a probability density function, which we denote as ![]() $f_n$.
$f_n$.
We set the characteristic function ![]() $\phi_n(t) \,:\!= {\mathbb E}[\exp({\mathrm{i}} t\, \Xi_n) ] $ and note that, by direct computation,
$\phi_n(t) \,:\!= {\mathbb E}[\exp({\mathrm{i}} t\, \Xi_n) ] $ and note that, by direct computation,
 \begin{equation}\phi_n(t) = \prod_{k=A}^{n-1} \dfrac{k^{2\alpha}}{k^{2 \alpha} + t^2}.\end{equation}
\begin{equation}\phi_n(t) = \prod_{k=A}^{n-1} \dfrac{k^{2\alpha}}{k^{2 \alpha} + t^2}.\end{equation}
As in our earlier analysis, we use the Fourier inversion formula to conclude that
This again implies that ![]() $f_n(x) \leq f_n(0)$. Note that (3.7) implies
$f_n(x) \leq f_n(0)$. Note that (3.7) implies
Using the change of variables ![]() $v = \sigma_n t$, we have, by (3.6),
$v = \sigma_n t$, we have, by (3.6),
 \begin{equation}\sigma_n f_n(0)= \dfrac{1}{\pi} \int_0^{\infty} \phi_n\bigg(\dfrac{v}{\sigma_n} \bigg) {\,\mathrm{d}} v= \dfrac{1}{\pi} \int_0^{\infty} \prod_{k=A}^{n-1} \dfrac{k^{2 \alpha}}{k^{2 \alpha} + {v^2}/{\sigma_n^2}} {\,\mathrm{d}} v.\end{equation}
\begin{equation}\sigma_n f_n(0)= \dfrac{1}{\pi} \int_0^{\infty} \phi_n\bigg(\dfrac{v}{\sigma_n} \bigg) {\,\mathrm{d}} v= \dfrac{1}{\pi} \int_0^{\infty} \prod_{k=A}^{n-1} \dfrac{k^{2 \alpha}}{k^{2 \alpha} + {v^2}/{\sigma_n^2}} {\,\mathrm{d}} v.\end{equation}
We use the dominated convergence theorem, and begin by noting that for ![]() $k \ge A$, we have, using (3.5) and letting C and c denote unspecified positive constants,
$k \ge A$, we have, using (3.5) and letting C and c denote unspecified positive constants,
In particular, for any fixed real v, recalling again (3.6) and (3.5),
 \begin{equation}\ln \phi_n \bigg(\dfrac{v}{\sigma_n} \bigg)=-\sum_{k=A}^{n-1}\ln\bigg(1+ \dfrac{v^2/\sigma_n^2}{k^{2 \alpha}}\bigg)\sim-\sum_{k=A}^{n-1} \dfrac{v^2/\sigma_n^2}{k^{2 \alpha}}=-\dfrac{v^2}{2}\end{equation}
\begin{equation}\ln \phi_n \bigg(\dfrac{v}{\sigma_n} \bigg)=-\sum_{k=A}^{n-1}\ln\bigg(1+ \dfrac{v^2/\sigma_n^2}{k^{2 \alpha}}\bigg)\sim-\sum_{k=A}^{n-1} \dfrac{v^2/\sigma_n^2}{k^{2 \alpha}}=-\dfrac{v^2}{2}\end{equation}
and thus
Furthermore, if ![]() $|v|\le\sqrt A$, then (3.9) shows
$|v|\le\sqrt A$, then (3.9) shows ![]() $k^{-2{\alpha}}v^2/\sigma_n^2={\mathrm{O}}(1)$ and thus, for some
$k^{-2{\alpha}}v^2/\sigma_n^2={\mathrm{O}}(1)$ and thus, for some ![]() $c>0$,
$c>0$, ![]() $\ln(1+k^{-2{\alpha}}v^2/\sigma_n^2)\ge ck^{-2{\alpha}}v^2/\sigma_n^2$ and, similarly to (3.10),
$\ln(1+k^{-2{\alpha}}v^2/\sigma_n^2)\ge ck^{-2{\alpha}}v^2/\sigma_n^2$ and, similarly to (3.10), ![]() $\ln \phi_n ({v}/{\sigma_n})\le -c{v^2}/{2}$ and thus
$\ln \phi_n ({v}/{\sigma_n})\le -c{v^2}/{2}$ and thus
If ![]() $|v|>\sqrt A$, we instead have, when
$|v|>\sqrt A$, we instead have, when ![]() $k\le 2A$, using again (3.5),
$k\le 2A$, using again (3.5),
Thus, crudely, by (3.6) and (3.5), for large enough n and ![]() $|v|>\sqrt A$,
$|v|>\sqrt A$,
 \begin{equation} \phi_n \bigg(\dfrac{v}{\sigma_n} \bigg)\le\prod_{A}^{2A} \dfrac{k^{2{\alpha}}}{k^{2{\alpha}}+v^2/\sigma_n^2}\le \dfrac{A^{2{\alpha}}}{A^{2{\alpha}}+v^2/\sigma_n^2}\prod_{A+1}^{2A} c_2\le \dfrac{A^{2{\alpha}}\sigma_n^2}{v^2}c_2^A.\end{equation}
\begin{equation} \phi_n \bigg(\dfrac{v}{\sigma_n} \bigg)\le\prod_{A}^{2A} \dfrac{k^{2{\alpha}}}{k^{2{\alpha}}+v^2/\sigma_n^2}\le \dfrac{A^{2{\alpha}}}{A^{2{\alpha}}+v^2/\sigma_n^2}\prod_{A+1}^{2A} c_2\le \dfrac{A^{2{\alpha}}\sigma_n^2}{v^2}c_2^A.\end{equation}
For convenience, we combine (3.12) and (3.13) into the (far from sharp) estimate, valid for large n and all v,
Consequently, dominated convergence yields, using (3.8), (3.11), and (3.14),
Moreover, for any sequence ![]() $x_n={\mathrm{o}}(\sigma_n)$, we obtain in the same way from (3.7)
$x_n={\mathrm{o}}(\sigma_n)$, we obtain in the same way from (3.7)
We again use the fact that ![]() ${W}_{j}$ has the same distribution as
${W}_{j}$ has the same distribution as ![]() $j^{-{\alpha}}{W}_1$, and obtain
$j^{-{\alpha}}{W}_1$, and obtain
Recall also that ![]() $f_n(x)\le f_n(0)$ for every x, and thus (3.15) implies that
$f_n(x)\le f_n(0)$ for every x, and thus (3.15) implies that ![]() $\sigma_n f_n(x)$ is uniformly bounded for all n and x.
$\sigma_n f_n(x)$ is uniformly bounded for all n and x.
Since, for every fixed y, ![]() $y/n^{{\alpha}}={\mathrm{o}}(\sigma_n)$ by (3.5), we can use (3.16) and dominated convergence (twice) in (3.17) and obtain
$y/n^{{\alpha}}={\mathrm{o}}(\sigma_n)$ by (3.5), we can use (3.16) and dominated convergence (twice) in (3.17) and obtain
Thus,
The probability ![]() ${\mathbb{P}}[ 0\le -\Xi_n < {V}_{n}] $ is the same, and (3.1) follows.
${\mathbb{P}}[ 0\le -\Xi_n < {V}_{n}] $ is the same, and (3.1) follows.
Proof of Theorem 3.3. The proof is similar to that of Theorem 3.2 and thus we detail only the novelties and omit some parts which are similar to the earlier proof.
Let ![]() $p(A,B,{\Lambda},{\Gamma})$ denote the left-hand side of (3.3), and let
$p(A,B,{\Lambda},{\Gamma})$ denote the left-hand side of (3.3), and let ![]() $q(A,B,{\Lambda},{\Gamma})$ denote the right-hand side without the factor
$q(A,B,{\Lambda},{\Gamma})$ denote the right-hand side without the factor ![]() $1+o_A(1)$. First, note that if the asserted uniform estimate does not hold, then there exist
$1+o_A(1)$. First, note that if the asserted uniform estimate does not hold, then there exist ![]() ${\varepsilon}>0$ and
${\varepsilon}>0$ and ![]() $A=A(n)\to\infty$,
$A=A(n)\to\infty$, ![]() $B=B(n)$,
$B=B(n)$, ![]() ${\Lambda}={\Lambda}(n)$, and
${\Lambda}={\Lambda}(n)$, and ![]() ${\Gamma}={\Gamma}(n)$ that satisfy the conditions such that
${\Gamma}={\Gamma}(n)$ that satisfy the conditions such that ![]() $|p(A,B,{\Lambda},{\Gamma})/q(A,B,{\Lambda},{\Gamma})-1|>{\varepsilon}$ for every n. By selecting a subsequence, we may furthermore assume that
$|p(A,B,{\Lambda},{\Gamma})/q(A,B,{\Lambda},{\Gamma})-1|>{\varepsilon}$ for every n. By selecting a subsequence, we may furthermore assume that
for some ![]() $\zeta\in[0, 1)$ and
$\zeta\in[0, 1)$ and ![]() ${\lambda},{\gamma}\in{\mathbb R}$. Hence, to obtain the desired contradiction, it suffices to prove that
${\lambda},{\gamma}\in{\mathbb R}$. Hence, to obtain the desired contradiction, it suffices to prove that ![]() $p(A,B,{\Lambda},{\Gamma})\sim q(A,B,{\Lambda},{\Gamma})$ under the extra assumption (3.20). (This assumption is convenient below, but not essential.)
$p(A,B,{\Lambda},{\Gamma})\sim q(A,B,{\Lambda},{\Gamma})$ under the extra assumption (3.20). (This assumption is convenient below, but not essential.)
We assume (3.20) and define
 \begin{equation*}\Xi_n = \sum_{k= A + \Lambda }^{B + \Gamma-1 } {V}_k - \sum_{k=A- \Lambda }^{B- \Gamma-1 } {W}_k.\end{equation*}
\begin{equation*}\Xi_n = \sum_{k= A + \Lambda }^{B + \Gamma-1 } {V}_k - \sum_{k=A- \Lambda }^{B- \Gamma-1 } {W}_k.\end{equation*}
From Theorem 3.1, ![]() $\operatorname{BINGO}(A + \Lambda, A - \Lambda;\, B + \Gamma, B - \Gamma)$ occurs if either
$\operatorname{BINGO}(A + \Lambda, A - \Lambda;\, B + \Gamma, B - \Gamma)$ occurs if either ![]() $\{ 0\le - \Xi_n <{V}_{B+\Gamma } \}$ or if
$\{ 0\le - \Xi_n <{V}_{B+\Gamma } \}$ or if ![]() $\{ 0\le \Xi_n < {W}_{B-\Gamma } \}$. We analyze
$\{ 0\le \Xi_n < {W}_{B-\Gamma } \}$. We analyze ![]() ${\mathbb{P}}[ 0 \le \Xi_n < {W}_{B- \Gamma }]$.
${\mathbb{P}}[ 0 \le \Xi_n < {W}_{B- \Gamma }]$.
We first compute the variance of ![]() $\Xi_n$ and observe that, using (3.20),
$\Xi_n$ and observe that, using (3.20),
 \begin{align}\sigma_n^2& \,:\!= \mathrm{Var}(\Xi_n) \\ &= \sum_{k= A + \Lambda }^{B + \Gamma-1 } \mathrm{Var} {V}_k + \sum_{k=A- \Lambda}^{B- \Gamma-1 }\mathrm{Var} {W}_k \\ &=\sum_{k= A + \Lambda }^{B + \Gamma-1 } k^{-2{\alpha}} + \sum_{k=A- \Lambda}^{B- \Gamma-1 } k^{-2{\alpha}} \\ &\sim \dfrac{2}{2 \alpha -1}{({A^{-(2 \alpha -1)}-B^{-(2\alpha-1)}})} \\ & \sim \dfrac{2}{2 \alpha -1} A^{-(2 \alpha -1)}{({1-\zeta^{2\alpha-1}})}.\end{align}
\begin{align}\sigma_n^2& \,:\!= \mathrm{Var}(\Xi_n) \\ &= \sum_{k= A + \Lambda }^{B + \Gamma-1 } \mathrm{Var} {V}_k + \sum_{k=A- \Lambda}^{B- \Gamma-1 }\mathrm{Var} {W}_k \\ &=\sum_{k= A + \Lambda }^{B + \Gamma-1 } k^{-2{\alpha}} + \sum_{k=A- \Lambda}^{B- \Gamma-1 } k^{-2{\alpha}} \\ &\sim \dfrac{2}{2 \alpha -1}{({A^{-(2 \alpha -1)}-B^{-(2\alpha-1)}})} \\ & \sim \dfrac{2}{2 \alpha -1} A^{-(2 \alpha -1)}{({1-\zeta^{2\alpha-1}})}.\end{align}
We continue with the characteristic function
 \begin{equation*}\phi_n(t) \,:\!= {\mathbb E}[{\mathrm{e}}^{{\mathrm{i}} t \Xi_n}]= \prod_{k= A + \Lambda }^{B + \Gamma-1 } \dfrac{k^{{\alpha}}}{k^{{\alpha}}-{\mathrm{i}} t} \prod_{k=A- \Lambda}^{B- \Gamma-1 } \dfrac{k^{{\alpha}}}{k^{{\alpha}}+{\mathrm{i}} t}.\end{equation*}
\begin{equation*}\phi_n(t) \,:\!= {\mathbb E}[{\mathrm{e}}^{{\mathrm{i}} t \Xi_n}]= \prod_{k= A + \Lambda }^{B + \Gamma-1 } \dfrac{k^{{\alpha}}}{k^{{\alpha}}-{\mathrm{i}} t} \prod_{k=A- \Lambda}^{B- \Gamma-1 } \dfrac{k^{{\alpha}}}{k^{{\alpha}}+{\mathrm{i}} t}.\end{equation*}
This is no longer real, but we can still estimate its absolute value as in (3.12) and (3.13), with minor modifications, and obtain (3.14). Furthermore,
 \begin{equation*}\ln\phi_n(t)= -\sum_{k= A + \Lambda }^{B + \Gamma-1 }\ln \bigg(1-\dfrac{{\mathrm{i}} t}{k^{{\alpha}}}\bigg)- \sum_{k=A- \Lambda}^{B- \Gamma-1 }\ln \bigg(1+\dfrac{{\mathrm{i}} t}{k^{{\alpha}}}\bigg).\end{equation*}
\begin{equation*}\ln\phi_n(t)= -\sum_{k= A + \Lambda }^{B + \Gamma-1 }\ln \bigg(1-\dfrac{{\mathrm{i}} t}{k^{{\alpha}}}\bigg)- \sum_{k=A- \Lambda}^{B- \Gamma-1 }\ln \bigg(1+\dfrac{{\mathrm{i}} t}{k^{{\alpha}}}\bigg).\end{equation*}
We consider ![]() $t=v/\sigma_n$ for a fixed real v, and obtain by Taylor expansions, recalling (3.9) (with a trivial modification), (3.21) and (3.20),
$t=v/\sigma_n$ for a fixed real v, and obtain by Taylor expansions, recalling (3.9) (with a trivial modification), (3.21) and (3.20),
 \begin{align}\ln\phi_n{\bigg({\dfrac{v}{\sigma_n}}\bigg)}&=\bigg( \sum_{k= A + \Lambda }^{B + \Gamma-1 } - \sum_{k=A- \Lambda}^{B- \Gamma-1 }\bigg)\dfrac{{\mathrm{i}} v/\sigma_n}{k^{{\alpha}}}-\bigg( \sum_{k= A + \Lambda }^{B + \Gamma-1 } + \sum_{k=A- \Lambda}^{B- \Gamma-1 }\bigg)\dfrac{ v^2/\sigma_n^2}{2k^{2{\alpha}}}{({1+{\mathrm{o}}(1)})} \\ &=-2{\Lambda}\dfrac{{\mathrm{i}} v/\sigma_n}{A^{{\alpha}}}+2{\Gamma}\dfrac{{\mathrm{i}} v/\sigma_n}{B^{{\alpha}}}-\dfrac{v^2}{2}+{\mathrm{o}}(1) \\ &\to\sqrt{\dfrac{2(2{\alpha}-1)}{1-\zeta^{2\alpha-1}}}{({-\lambda+\zeta^{\alpha-1/2}{\gamma}})} v\,{\mathrm{i}} -\dfrac{v^2}{2}.\end{align}
\begin{align}\ln\phi_n{\bigg({\dfrac{v}{\sigma_n}}\bigg)}&=\bigg( \sum_{k= A + \Lambda }^{B + \Gamma-1 } - \sum_{k=A- \Lambda}^{B- \Gamma-1 }\bigg)\dfrac{{\mathrm{i}} v/\sigma_n}{k^{{\alpha}}}-\bigg( \sum_{k= A + \Lambda }^{B + \Gamma-1 } + \sum_{k=A- \Lambda}^{B- \Gamma-1 }\bigg)\dfrac{ v^2/\sigma_n^2}{2k^{2{\alpha}}}{({1+{\mathrm{o}}(1)})} \\ &=-2{\Lambda}\dfrac{{\mathrm{i}} v/\sigma_n}{A^{{\alpha}}}+2{\Gamma}\dfrac{{\mathrm{i}} v/\sigma_n}{B^{{\alpha}}}-\dfrac{v^2}{2}+{\mathrm{o}}(1) \\ &\to\sqrt{\dfrac{2(2{\alpha}-1)}{1-\zeta^{2\alpha-1}}}{({-\lambda+\zeta^{\alpha-1/2}{\gamma}})} v\,{\mathrm{i}} -\dfrac{v^2}{2}.\end{align}
It follows by Fourier inversion and dominated convergence, using (3.22) and (3.14), that, for any sequence ![]() $x_n={\mathrm{o}}(\sigma_n)$, with
$x_n={\mathrm{o}}(\sigma_n)$, with ![]() $c_1 \,:\!=\sqrt{2(2{\alpha}-1)/(1-\zeta^{2\alpha-1})}$,
$c_1 \,:\!=\sqrt{2(2{\alpha}-1)/(1-\zeta^{2\alpha-1})}$,
 \begin{align}\sigma_n f_n(x_n) &= \dfrac{\sigma_n}{2\pi} \int_{-\infty}^{\infty} \,{\mathrm{e}}^{-{\mathrm{i}} x_n t}\phi_n (t){\,\mathrm{d}} t \\ &= \dfrac{1}{2\pi} \int_{-\infty}^{\infty} \,{\mathrm{e}}^{-{\mathrm{i}} v x_n/\sigma_n}\phi_n\bigg(\dfrac{v}{\sigma_n} \bigg) {\,\mathrm{d}} v \\ &\to\dfrac{1}{2\pi} \int_{-\infty}^{\infty} \,{\mathrm{e}}^{-c_1(\lambda-\zeta^{\alpha-1/2}{\gamma}) v\,{\mathrm{i}} -v^2/2} {\,\mathrm{d}} v \\ &= \dfrac{1}{\sqrt{2\pi}} \,{\mathrm{e}}^{-c_1^2(\lambda-\zeta^{\alpha-1/2}{\gamma})^2/2}.\end{align}
\begin{align}\sigma_n f_n(x_n) &= \dfrac{\sigma_n}{2\pi} \int_{-\infty}^{\infty} \,{\mathrm{e}}^{-{\mathrm{i}} x_n t}\phi_n (t){\,\mathrm{d}} t \\ &= \dfrac{1}{2\pi} \int_{-\infty}^{\infty} \,{\mathrm{e}}^{-{\mathrm{i}} v x_n/\sigma_n}\phi_n\bigg(\dfrac{v}{\sigma_n} \bigg) {\,\mathrm{d}} v \\ &\to\dfrac{1}{2\pi} \int_{-\infty}^{\infty} \,{\mathrm{e}}^{-c_1(\lambda-\zeta^{\alpha-1/2}{\gamma}) v\,{\mathrm{i}} -v^2/2} {\,\mathrm{d}} v \\ &= \dfrac{1}{\sqrt{2\pi}} \,{\mathrm{e}}^{-c_1^2(\lambda-\zeta^{\alpha-1/2}{\gamma})^2/2}.\end{align}
Furthermore, using (3.14) again, we have the uniform bound, for all real x,
We complete the proof as in (3.17)–(3.19), now obtaining
![]() ${\mathbb{P}}[ 0< - \Xi_n < {V}_{B+ \Gamma }]$ is similar, and thus
${\mathbb{P}}[ 0< - \Xi_n < {V}_{B+ \Gamma }]$ is similar, and thus
If we use (3.20) in (3.3), a simple calculation shows that the same asymptotics hold for ![]() $q(A,B,{\Lambda},{\Gamma})$, and thus
$q(A,B,{\Lambda},{\Gamma})$, and thus ![]() $p(A,B,{\Lambda},{\Gamma})\sim q(A,B,{\Lambda},{\Gamma})$. As explained at the beginning of the proof, this implies the theorem.
$p(A,B,{\Lambda},{\Gamma})\sim q(A,B,{\Lambda},{\Gamma})$. As explained at the beginning of the proof, this implies the theorem.
We end this section with two less precise estimates that are useful because they do not require the condition ![]() $B\ge{\theta} A$ in Theorem 3.3.
$B\ge{\theta} A$ in Theorem 3.3.
Lemma 3.1. Suppose that ![]() $0<A<B$, and that
$0<A<B$, and that ![]() ${\Lambda},{\Gamma}\ge0$ with
${\Lambda},{\Gamma}\ge0$ with ![]() ${\Lambda}< A$,
${\Lambda}< A$, ![]() $B-{\Gamma}\ge A$, and
$B-{\Gamma}\ge A$, and ![]() ${\Gamma}/B\le \frac{1}{8}{\Lambda}/A$. Then, for some constant
${\Gamma}/B\le \frac{1}{8}{\Lambda}/A$. Then, for some constant ![]() $c>0$ depending on
$c>0$ depending on ![]() $\alpha$ only,
$\alpha$ only,
Proof. Denote the event on the left-hand side of (3.24) by ![]() ${\mathcal{E}}$. We may assume
${\mathcal{E}}$. We may assume ![]() $B+{\Gamma}\ge A+{\Lambda}$, since otherwise
$B+{\Gamma}\ge A+{\Lambda}$, since otherwise ![]() ${\mathcal{E}}$ is empty. By an argument similar to the proof of Theorem 2.2, the event
${\mathcal{E}}$ is empty. By an argument similar to the proof of Theorem 2.2, the event ![]() ${\mathcal{E}}$ occurs if and only if
${\mathcal{E}}$ occurs if and only if
 \[\sum_{i=A+{\Lambda}}^{B+{\Gamma}}{V}_i \ge \sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}{W}_j.\]
\[\sum_{i=A+{\Lambda}}^{B+{\Gamma}}{V}_i \ge \sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}{W}_j.\]
Note that this event is monotonically decreasing in ![]() ${\Lambda}$; hence it suffices to prove (3.24) for
${\Lambda}$; hence it suffices to prove (3.24) for ![]() ${\Lambda}\le A/2$ (and
${\Lambda}\le A/2$ (and ![]() ${\Gamma}/B\le\frac{1}4{\Lambda}/A$), since we may otherwise decrease
${\Gamma}/B\le\frac{1}4{\Lambda}/A$), since we may otherwise decrease ![]() ${\Lambda}$ to
${\Lambda}$ to ![]() $A/2$ (changing c); we make these assumptions.
$A/2$ (changing c); we make these assumptions.
By Markov’s inequality and independence, for every ![]() $t\ge0$,
$t\ge0$,
 \begin{align} \Pr[{\mathcal{E}}]&={\mathbb{P}}{\Bigg[{\sum_{i=A+{\Lambda}}^{B+{\Gamma}}{V}_i - \sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}{W}_j\ge0}\Bigg]} \\ &\le {\mathbb E} \,{\mathrm{e}}^{t\sum_{i=A+{\Lambda}}^{B+{\Gamma}}{V}_i - t\sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}{W}_j} \\ & =\prod_{i=A+{\Lambda}}^{B+{\Gamma}}{\mathbb E} \,{\mathrm{e}}^{t {V}_i} \prod_{j=A-{\Lambda}}^{B-{\Gamma}-1}{\mathbb E} \,{\mathrm{e}}^{-t{W}_j}.\end{align}
\begin{align} \Pr[{\mathcal{E}}]&={\mathbb{P}}{\Bigg[{\sum_{i=A+{\Lambda}}^{B+{\Gamma}}{V}_i - \sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}{W}_j\ge0}\Bigg]} \\ &\le {\mathbb E} \,{\mathrm{e}}^{t\sum_{i=A+{\Lambda}}^{B+{\Gamma}}{V}_i - t\sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}{W}_j} \\ & =\prod_{i=A+{\Lambda}}^{B+{\Gamma}}{\mathbb E} \,{\mathrm{e}}^{t {V}_i} \prod_{j=A-{\Lambda}}^{B-{\Gamma}-1}{\mathbb E} \,{\mathrm{e}}^{-t{W}_j}.\end{align}
Furthermore, when ![]() $-\infty < t < i^\alpha$,
$-\infty < t < i^\alpha$,
Consequently, (3.25) implies, for ![]() $0\le t\le \frac12A^{-\alpha}$ and some constant
$0\le t\le \frac12A^{-\alpha}$ and some constant ![]() $C\ge1$ (depending on
$C\ge1$ (depending on ![]() $\alpha$), using the convexity of
$\alpha$), using the convexity of ![]() $j \mapsto j^{-\alpha}$ in the fourth inequality,
$j \mapsto j^{-\alpha}$ in the fourth inequality,
 \begin{align}\ln \Pr[{\mathcal{E}}]&\le-\sum_{i=A+{\Lambda}}^{B+{\Gamma}}\ln(1-ti^{-\alpha})-\sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}\ln(1+tj^{-\alpha}) \\ &\le\sum_{i=A+{\Lambda}}^{B+{\Gamma}}{({ti^{-\alpha}+t^2i^{-2\alpha}})}-\sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}{({tj^{-\alpha}-t^2j^{-2\alpha}})} \\ &\le-\sum_{j=A-{\Lambda}}^{A+{\Lambda}-1} tj^{-\alpha}+\sum_{i=B-{\Gamma}}^{B+{\Gamma}} ti^{-\alpha}+2\sum_{i=A-{\Lambda}}^{\infty}t^2i^{-2\alpha} \\ &\le-2{\Lambda} t A^{-\alpha} + (2{\Gamma}+1)t(B-{\Gamma})^{-\alpha}+C t^2 A^{1-2\alpha} \\ &\le-t{\Lambda} A^{-\alpha} +C t^2 A^{1-2\alpha},\end{align}
\begin{align}\ln \Pr[{\mathcal{E}}]&\le-\sum_{i=A+{\Lambda}}^{B+{\Gamma}}\ln(1-ti^{-\alpha})-\sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}\ln(1+tj^{-\alpha}) \\ &\le\sum_{i=A+{\Lambda}}^{B+{\Gamma}}{({ti^{-\alpha}+t^2i^{-2\alpha}})}-\sum_{j=A-{\Lambda}}^{B-{\Gamma}-1}{({tj^{-\alpha}-t^2j^{-2\alpha}})} \\ &\le-\sum_{j=A-{\Lambda}}^{A+{\Lambda}-1} tj^{-\alpha}+\sum_{i=B-{\Gamma}}^{B+{\Gamma}} ti^{-\alpha}+2\sum_{i=A-{\Lambda}}^{\infty}t^2i^{-2\alpha} \\ &\le-2{\Lambda} t A^{-\alpha} + (2{\Gamma}+1)t(B-{\Gamma})^{-\alpha}+C t^2 A^{1-2\alpha} \\ &\le-t{\Lambda} A^{-\alpha} +C t^2 A^{1-2\alpha},\end{align}
where the last inequality follows because the assumptions imply ![]() $(2{\Gamma}+1)/(B-{\Gamma}) \le {\Lambda}/A$.
$(2{\Gamma}+1)/(B-{\Gamma}) \le {\Lambda}/A$.
Now choose ![]() $t \,:\!=(2C){^{-1}}{\Lambda} A^{\alpha-1}$; then (3.26) yields (3.24), with
$t \,:\!=(2C){^{-1}}{\Lambda} A^{\alpha-1}$; then (3.26) yields (3.24), with ![]() $c=1/4C$.
$c=1/4C$.
Lemma 3.2. For any ![]() $A<n$ and
$A<n$ and ![]() ${\Lambda}$ with
${\Lambda}$ with ![]() $|{\Lambda}|\le A-1$, for some universal constants C,C´,
$|{\Lambda}|\le A-1$, for some universal constants C,C´,
Proof. Consider the Markov chain ![]() $(X_k,Y_k)_{2A}^\infty$, started at
$(X_k,Y_k)_{2A}^\infty$, started at ![]() $(X_{2A},Y_{2A})=(A+{\Lambda},A-{\Lambda})$. We couple the chain with a simple random walk
$(X_{2A},Y_{2A})=(A+{\Lambda},A-{\Lambda})$. We couple the chain with a simple random walk ![]() $(X^*_k,Y^*_k)_{2A}^\infty$, also started at
$(X^*_k,Y^*_k)_{2A}^\infty$, also started at ![]() $(A+{\Lambda},A-{\Lambda})$, such that, for every
$(A+{\Lambda},A-{\Lambda})$, such that, for every ![]() $k\ge 2A$,
$k\ge 2A$,
This can be achieved as follows. If strict inequality holds in (3.28), so ![]() $ |X_k-Y_k|\ge |X_k^*-Y_k^*|+2$ since both sides have the same parity, we may couple the next steps for the two chains arbitrarily. The same holds if
$ |X_k-Y_k|\ge |X_k^*-Y_k^*|+2$ since both sides have the same parity, we may couple the next steps for the two chains arbitrarily. The same holds if ![]() $|X_k-Y_k|=|X_k^*-Y_k^*|=0$. Finally, if
$|X_k-Y_k|=|X_k^*-Y_k^*|=0$. Finally, if ![]() $|X_k-Y_k|=|X_k^*-Y_k^*|>0$, we have to couple such that if
$|X_k-Y_k|=|X_k^*-Y_k^*|>0$, we have to couple such that if ![]() $|X^*_{k+1}-Y^*_{k+1}|=|X_k^*-Y_k^*|+1$, then
$|X^*_{k+1}-Y^*_{k+1}|=|X_k^*-Y_k^*|+1$, then ![]() $|X_{k+1}-Y_{k+1}|=|X_k-Y_k|+1$; this is always possible, since the first event has probability
$|X_{k+1}-Y_{k+1}|=|X_k-Y_k|+1$; this is always possible, since the first event has probability ![]() $1/2$, and the second has probability
$1/2$, and the second has probability ![]() $\max\{{X_k^\alpha,Y_k^\alpha}\}/(X_k^{\alpha}+Y_k^\alpha)>1/2$.
$\max\{{X_k^\alpha,Y_k^\alpha}\}/(X_k^{\alpha}+Y_k^\alpha)>1/2$.
Using this coupling, (3.28) shows ![]() $ |X_{2n}-Y_{2n}|\ge |X_{2n}^*-Y_{2n}^*|$, and thus
$ |X_{2n}-Y_{2n}|\ge |X_{2n}^*-Y_{2n}^*|$, and thus
 \begin{align*} {\mathbb{P}}{[{\operatorname{BINGO}(A+{\Lambda},A-{\Lambda};\,n,n)}]}& = {\mathbb{P}}{[{X_{2n}=Y_{2n}=n}]} \\ &\le {\mathbb{P}}{[{X^*_{2n}=Y^*_{2n}}]} \\&= {\mathbb{P}}{[{\mathrm{Bin}(2n-2A,1/2)=n-A-{\Lambda}}]} \\ &=2^{-(2n-2A)}\binom{2n-2A}{n-A-{\Lambda}} {,}\end{align*}
\begin{align*} {\mathbb{P}}{[{\operatorname{BINGO}(A+{\Lambda},A-{\Lambda};\,n,n)}]}& = {\mathbb{P}}{[{X_{2n}=Y_{2n}=n}]} \\ &\le {\mathbb{P}}{[{X^*_{2n}=Y^*_{2n}}]} \\&= {\mathbb{P}}{[{\mathrm{Bin}(2n-2A,1/2)=n-A-{\Lambda}}]} \\ &=2^{-(2n-2A)}\binom{2n-2A}{n-A-{\Lambda}} {,}\end{align*}
and (3.27) follows by standard calculations using Stirling’s formula.
4. A basic case
Here we prove a modified version of Theorem 1.1. Initially ![]() $\xi_1,\ldots,\xi_{2n-2}=\pm 1$ are uniform and independent. We set
$\xi_1,\ldots,\xi_{2n-2}=\pm 1$ are uniform and independent. We set
We shall be splitting the walk into an initial part, until time ![]() $2A-2$, and the main part, in the time interval
$2A-2$, and the main part, in the time interval ![]() $2A-2\leq i \leq 2n-2$. See Remark 4.1 for further comments.
$2A-2\leq i \leq 2n-2$. See Remark 4.1 for further comments.
We condition on ![]() $S_{2A-2}=0$ and
$S_{2A-2}=0$ and ![]() $S_{2n-2}=0$. We may and shall consider the
$S_{2n-2}=0$. We may and shall consider the ![]() $S_i$ in two regimes. For
$S_i$ in two regimes. For ![]() $0\leq i\leq 2A-2$ the
$0\leq i\leq 2A-2$ the ![]() $S_i$ form a random excursion, beginning (
$S_i$ form a random excursion, beginning (![]() $i=0$) and ending (
$i=0$) and ending (![]() $i=2A-2$) at zero. For
$i=2A-2$) at zero. For ![]() $2A-2 \leq i \leq 2n-2$ the
$2A-2 \leq i \leq 2n-2$ the ![]() $S_i$ form a random excursion beginning (
$S_i$ form a random excursion beginning (![]() $i=2A-2$) and ending (
$i=2A-2$) and ending (![]() $i=2n-2$) at zero. We note, importantly, that the two sides of the walk are mutually independent excursions. Let
$i=2n-2$) at zero. We note, importantly, that the two sides of the walk are mutually independent excursions. Let ![]() $ \operatorname{{COND}}$ denote this condition. The function
$ \operatorname{{COND}}$ denote this condition. The function ![]() $L=L_{2n-2}$ splits naturally into two parts:
$L=L_{2n-2}$ splits naturally into two parts:
 \begin{align*} L^{\mathrm{init}}& = \sum_{i=1}^{2A-2} \dfrac{S_i^2}{i^2},\\ L^{\mathrm{main}} &= \sum_{i=2A-1}^{2n-2} \dfrac{S_i^2}{i^2}.\end{align*}
\begin{align*} L^{\mathrm{init}}& = \sum_{i=1}^{2A-2} \dfrac{S_i^2}{i^2},\\ L^{\mathrm{main}} &= \sum_{i=2A-1}^{2n-2} \dfrac{S_i^2}{i^2}.\end{align*}
Theorem 4.1. Under ![]() $\operatorname{{COND}}$, for
$\operatorname{{COND}}$, for ![]() $c \in (0, 1)$,
$c \in (0, 1)$,
with (as in Theorem 1.1)
Remark 4.1. There is considerable flexibility in the choice of the breakpoint A. The basic object is to protect against rare events. Our basic argument will break down when, say, ![]() $|S_i|\geq 0.01i$. This occurs with probability exponentially small in i. However, Theorem 1.1 deals with polynomially small (in n) probabilities. Thus a priori, for small i, the probability of this rare event is not automatically negligible on the scale of interest. Restricting to
$|S_i|\geq 0.01i$. This occurs with probability exponentially small in i. However, Theorem 1.1 deals with polynomially small (in n) probabilities. Thus a priori, for small i, the probability of this rare event is not automatically negligible on the scale of interest. Restricting to ![]() $i\geq A$, exponentially small probabilities in i are less than polynomially small in n, and hence negligible. The split at A should be considered an artifact of the proof and it is quite possible that an argument exists that does not use this artificial split. Both the restriction to
$i\geq A$, exponentially small probabilities in i are less than polynomially small in n, and hence negligible. The split at A should be considered an artifact of the proof and it is quite possible that an argument exists that does not use this artificial split. Both the restriction to ![]() $i\geq A$ and the restriction to a random excursion will be removed later.
$i\geq A$ and the restriction to a random excursion will be removed later.
We shall actually find the asymptotics of the Laplace transform of ![]() $L^{\mathrm{main}}$. For notational convenience, given
$L^{\mathrm{main}}$. For notational convenience, given ![]() ${\alpha} > 1$ we define
${\alpha} > 1$ we define
Theorem 4.2. For any ![]() ${\alpha} > 1$,
${\alpha} > 1$,
As ![]() ${\alpha}$ ranges over
${\alpha}$ ranges over ![]() $(1,\infty)$,
$(1,\infty)$, ![]() $t \,:\!=-{\lambda}$ ranges over the negative reals. Theorem 4.2 then gives the asymptotics of the Laplace transform of
$t \,:\!=-{\lambda}$ ranges over the negative reals. Theorem 4.2 then gives the asymptotics of the Laplace transform of ![]() $L^{\mathrm{main}}\mid{\operatorname{{COND}}}$: letting
$L^{\mathrm{main}}\mid{\operatorname{{COND}}}$: letting ![]() ${\hat L}_n$ be
${\hat L}_n$ be ![]() $L^{\mathrm{main}}\mid{\operatorname{{COND}}}$ for a particular value of n,
$L^{\mathrm{main}}\mid{\operatorname{{COND}}}$ for a particular value of n,
Then (as done in more detail in Section 8.3), the Legendre transform of ![]() ${\Lambda}(t)$ is, by a simple calculation,
${\Lambda}(t)$ is, by a simple calculation,
and the Gärtner–Ellis theorem [Reference Dembo and Zeitouni9, Theorem 2.3.6] yields the asymptotics of ![]() ${\mathbb{P}}[{\hat L}_n\leq c\ln n]$ of Theorem 4.1.
${\mathbb{P}}[{\hat L}_n\leq c\ln n]$ of Theorem 4.1.
Remark 4.2. The main contribution to ![]() ${\mathbb E}[{\mathrm{e}}^{-{\lambda} L^{\mathrm{main}}}\mid{\operatorname{{COND}}}]$ comes when
${\mathbb E}[{\mathrm{e}}^{-{\lambda} L^{\mathrm{main}}}\mid{\operatorname{{COND}}}]$ comes when ![]() $L^{\mathrm{main}}\approx c \ln n$ with
$L^{\mathrm{main}}\approx c \ln n$ with ![]() $c=(2{\alpha} -1)^{-1}$, i.e.
$c=(2{\alpha} -1)^{-1}$, i.e. ![]() ${\alpha} ={(c+1)}/{(2c)}$.
${\alpha} ={(c+1)}/{(2c)}$.
Now we study ![]() ${\mathbb{P}}[\!\operatorname{BINGO}(A,A;\,n,n)]$ as the sum of the probabilities of all paths P from (A, A) to (n, n). Let
${\mathbb{P}}[\!\operatorname{BINGO}(A,A;\,n,n)]$ as the sum of the probabilities of all paths P from (A, A) to (n, n). Let ![]() $P_{2A}=(A,A),\ldots,P_{2n}=(n,n)$ denote the points of path P,
$P_{2A}=(A,A),\ldots,P_{2n}=(n,n)$ denote the points of path P, ![]() $P_i$ having sum of coordinates i,
$P_i$ having sum of coordinates i, ![]() $2A\leq i \leq 2n$. Let
$2A\leq i \leq 2n$. Let ![]() $P_i=(x_i,y_i)$. Critically, we parametrize, as in (1.5),
$P_i=(x_i,y_i)$. Critically, we parametrize, as in (1.5),
Here ![]() ${\delta}_i$ reflects the ‘distance’ of the path from the main diagonal. By
${\delta}_i$ reflects the ‘distance’ of the path from the main diagonal. By ![]() $\Pr({\bf P})$ we mean the probability of following precisely the path P. The
$\Pr({\bf P})$ we mean the probability of following precisely the path P. The ![]() ${\mathbb{P}}({\bf P})$ vary in an interesting way. The numerators multiply out the same with factors
${\mathbb{P}}({\bf P})$ vary in an interesting way. The numerators multiply out the same with factors ![]() $i^{{\alpha}}$ for
$i^{{\alpha}}$ for ![]() $A\leq i < n$ and
$A\leq i < n$ and ![]() $j^{{\alpha}}$ for
$j^{{\alpha}}$ for ![]() $A\leq j < n$. The denominator factor
$A\leq j < n$. The denominator factor ![]() $x_i^{{\alpha}}+y_i^{{\alpha}}$ is minimal when
$x_i^{{\alpha}}+y_i^{{\alpha}}$ is minimal when ![]() $x_i=y_i={i}/{2}$. We define
$x_i=y_i={i}/{2}$. We define
Then ![]() $\operatorname{FIT}_i= f({\varepsilon})$, where
$\operatorname{FIT}_i= f({\varepsilon})$, where ![]() ${\varepsilon}= {\delta}_i/i$ and
${\varepsilon}= {\delta}_i/i$ and
We shall make critical use of the asymptotics
Set
 \begin{equation} \operatorname{FIT}= \operatorname{FIT}({\bf P}) = \prod_{i=2A}^{2n-1} \operatorname{FIT}_i {.}\end{equation}
\begin{equation} \operatorname{FIT}= \operatorname{FIT}({\bf P}) = \prod_{i=2A}^{2n-1} \operatorname{FIT}_i {.}\end{equation}
Each ![]() $\operatorname{FIT}_i\leq 1$ and hence
$\operatorname{FIT}_i\leq 1$ and hence ![]() $\operatorname{FIT}\leq 1$. A low
$\operatorname{FIT}\leq 1$. A low ![]() $\operatorname{FIT}$ tells us that the path P is relatively unlikely. Roughly, paths P which stay close to the main diagonal will have a high
$\operatorname{FIT}$ tells us that the path P is relatively unlikely. Roughly, paths P which stay close to the main diagonal will have a high ![]() $\operatorname{FIT}$, meaning they will be more likely than those that stray far from the main diagonal. We now split
$\operatorname{FIT}$, meaning they will be more likely than those that stray far from the main diagonal. We now split
Here ![]() $\operatorname{BASE}$ is what P would be if the terms
$\operatorname{BASE}$ is what P would be if the terms ![]() $x_i^{{\alpha}}+y_i^{{\alpha}}$ were replaced with
$x_i^{{\alpha}}+y_i^{{\alpha}}$ were replaced with ![]() $2(i/2)^{{\alpha}}$ and
$2(i/2)^{{\alpha}}$ and ![]() $\operatorname{FIT}$ is the additional factor with the actual
$\operatorname{FIT}$ is the additional factor with the actual ![]() $x_i,y_i$,
$x_i,y_i$, ![]() $2A\leq i < 2n$. Then the denominator would be precisely the product of
$2A\leq i < 2n$. Then the denominator would be precisely the product of ![]() $2(i/2)^{{\alpha}}$ over
$2(i/2)^{{\alpha}}$ over ![]() $2A\leq i < 2n$. That is,
$2A\leq i < 2n$. That is,
 \begin{equation} \operatorname{BASE} = \dfrac{\prod_{i=A}^{n-1}i^{{\alpha}}\prod_{j=A}^{n-1}j^{{\alpha}}} {\prod_{i=2A}^{2n-1} 2(i/2)^{{\alpha}}} {.}\end{equation}
\begin{equation} \operatorname{BASE} = \dfrac{\prod_{i=A}^{n-1}i^{{\alpha}}\prod_{j=A}^{n-1}j^{{\alpha}}} {\prod_{i=2A}^{2n-1} 2(i/2)^{{\alpha}}} {.}\end{equation}
![]() $\operatorname{BINGO}(A,A;\,n,n)$ is the sum of
$\operatorname{BINGO}(A,A;\,n,n)$ is the sum of ![]() $\operatorname{BASE}\cdot \operatorname{FIT}({\bf P})$ over all
$\operatorname{BASE}\cdot \operatorname{FIT}({\bf P})$ over all ![]() $\binom{2(n-A)} {n-A}$ paths from (A, A) to (n, n). Summing over all paths P, we rewrite (4.6) with the exact formula
$\binom{2(n-A)} {n-A}$ paths from (A, A) to (n, n). Summing over all paths P, we rewrite (4.6) with the exact formula
where expectation is over a uniformly chosen path from (A, A) to (n, n). Equation (4.8) is of fundamental importance in our analysis; indeed, this relation connects the study of the reinforced urn model with the random walk. Stirling’s formula asymptotics give
and
Applying (3.2) we deduce
Remark 4.3. We had originally hoped to apply (4.9) in reverse. That is, a combinatorial (or other) argument for the asymptotics of ![]() ${\mathbb E}[\!\operatorname{FIT}({\bf P})]$ would yield an alternative proof, a non-Book Proof, for
${\mathbb E}[\!\operatorname{FIT}({\bf P})]$ would yield an alternative proof, a non-Book Proof, for ![]() ${\mathbb{P}}[\!\operatorname{BINGO}]$. It was surprising that the continuous-time approach led to (4.10), which is quite difficult to prove directly.
${\mathbb{P}}[\!\operatorname{BINGO}]$. It was surprising that the continuous-time approach led to (4.10), which is quite difficult to prove directly.
Now we try to estimate ![]() $\operatorname{FIT}$ using (4.4). The technical difficulty is that we do not have
$\operatorname{FIT}$ using (4.4). The technical difficulty is that we do not have ![]() ${\varepsilon} = {\delta}_i/i = {\mathrm{o}}(1)$ tautologically. Call a walk P weird if
${\varepsilon} = {\delta}_i/i = {\mathrm{o}}(1)$ tautologically. Call a walk P weird if ![]() $|S_i|>i^{0.99}$ for some
$|S_i|>i^{0.99}$ for some ![]() $A\leq i \leq n$. Otherwise call P normal. Large deviation results give that the probability P is weird for a particular i is at most
$A\leq i \leq n$. Otherwise call P normal. Large deviation results give that the probability P is weird for a particular i is at most ![]() $\exp[-i^{0.98}/2]$. We only look at
$\exp[-i^{0.98}/2]$. We only look at ![]() $i\geq A$. We have selected A so that this probability is sub-polynomial. As
$i\geq A$. We have selected A so that this probability is sub-polynomial. As ![]() $\operatorname{FIT}({\bf P})\leq 1$ tautologically, the effect on
$\operatorname{FIT}({\bf P})\leq 1$ tautologically, the effect on ![]() ${\mathbb E}[\!\operatorname{FIT}({\bf P})]$ of weird P is negligible. Hence in calculating
${\mathbb E}[\!\operatorname{FIT}({\bf P})]$ of weird P is negligible. Hence in calculating ![]() ${\mathbb E}[\!\operatorname{FIT}({\bf P})]$ we can restrict ourselves to normal P. Normal P have
${\mathbb E}[\!\operatorname{FIT}({\bf P})]$ we can restrict ourselves to normal P. Normal P have ![]() ${\varepsilon} = |S_i|/i < i^{-0.01} = {\mathrm{o}}(1)$ uniformly. We apply (4.4), each
${\varepsilon} = |S_i|/i < i^{-0.01} = {\mathrm{o}}(1)$ uniformly. We apply (4.4), each ![]() $\ln(\operatorname{FIT}_i)\sim -{\lambda} S_i^2i^{-2}$ so that
$\ln(\operatorname{FIT}_i)\sim -{\lambda} S_i^2i^{-2}$ so that ![]() $\ln(\operatorname{FIT}) \sim -{\lambda} L^{\mathrm{main}}$. Therefore
$\ln(\operatorname{FIT}) \sim -{\lambda} L^{\mathrm{main}}$. Therefore
as desired, giving Theorem 4.2 and hence Theorem 4.1.
We now extend Theorem 4.1 to ![]() $L=L^{\mathrm{init}}+L^{\mathrm{main}}$. As
$L=L^{\mathrm{init}}+L^{\mathrm{main}}$. As ![]() $L^{\mathrm{init}}\geq 0$,
$L^{\mathrm{init}}\geq 0$,
Now we show ![]() $L^{\mathrm{init}}$ under
$L^{\mathrm{init}}$ under ![]() $\operatorname{{COND}}$ is appropriately negligible. We have
$\operatorname{{COND}}$ is appropriately negligible. We have ![]() $\xi_1,\ldots,\xi_{2A-2}=\pm 1$ conditioned on their sum being zero.
$\xi_1,\ldots,\xi_{2A-2}=\pm 1$ conditioned on their sum being zero. ![]() $S_i=\xi_1+\cdots+\xi_i$. A standard second moment calculation gives the precise value
$S_i=\xi_1+\cdots+\xi_i$. A standard second moment calculation gives the precise value ![]() $E[S_i^2] = i - i(i-1)(2A-3)^{-1}$ but we shall only use
$E[S_i^2] = i - i(i-1)(2A-3)^{-1}$ but we shall only use ![]() $E[S_i^2]\leq i$. (That is, the conditioning lowers the variance.) Then, using (4.1),
$E[S_i^2]\leq i$. (That is, the conditioning lowers the variance.) Then, using (4.1),
 \begin{equation*} {\mathbb E}[L^{\mathrm{init}} \mid{\operatorname{{COND}}}] \leq \sum_{i=1}^{2A-2} \dfrac{i}{i^2} \leq (10+{\mathrm{o}}(1))\ln\ln n .\end{equation*}
\begin{equation*} {\mathbb E}[L^{\mathrm{init}} \mid{\operatorname{{COND}}}] \leq \sum_{i=1}^{2A-2} \dfrac{i}{i^2} \leq (10+{\mathrm{o}}(1))\ln\ln n .\end{equation*}
By Markov’s inequality, with n sufficiently large, ![]() $L^{\mathrm{init}}\leq 21\ln\ln n$ with probability at least
$L^{\mathrm{init}}\leq 21\ln\ln n$ with probability at least ![]() $0.5$. We have created
$0.5$. We have created ![]() $L^{\mathrm{init}},L^{\mathrm{main}}$ to be independent, so with probability at least
$L^{\mathrm{init}},L^{\mathrm{main}}$ to be independent, so with probability at least ![]() $0.5\cdot {\mathrm{e}}^{-(K(c)+{\mathrm{o}}(1))\ln n}$ both
$0.5\cdot {\mathrm{e}}^{-(K(c)+{\mathrm{o}}(1))\ln n}$ both ![]() $L^{\mathrm{init}}\leq 21\ln\ln n$ and
$L^{\mathrm{init}}\leq 21\ln\ln n$ and ![]() $L^{\mathrm{main}}\leq c\ln n$. Hence
$L^{\mathrm{main}}\leq c\ln n$. Hence
The multiplicative factor of ![]() ${1}/{2}$ and the additive factor of
${1}/{2}$ and the additive factor of ![]() $21\ln\ln n$ get absorbed in the asymptotics, giving
$21\ln\ln n$ get absorbed in the asymptotics, giving
We have shown the following.
Theorem 4.3. Under ![]() $\operatorname{{COND}}$,
$\operatorname{{COND}}$,
5. The lower bound
Let ![]() $|{\Lambda}|\leq \sqrt{A}$,
$|{\Lambda}|\leq \sqrt{A}$, ![]() $|{\Gamma}| \leq \sqrt{n}$. We generalize the Basic Case. Initially
$|{\Gamma}| \leq \sqrt{n}$. We generalize the Basic Case. Initially ![]() $\xi_1,\ldots,\xi_{2n-2}=\pm 1$ are uniform and independent. Here we condition on
$\xi_1,\ldots,\xi_{2n-2}=\pm 1$ are uniform and independent. Here we condition on ![]() $S_{2A-2}=2{\Lambda}$ and
$S_{2A-2}=2{\Lambda}$ and ![]() $S_{2n-2}=2{\Gamma}$. We may and shall consider the
$S_{2n-2}=2{\Gamma}$. We may and shall consider the ![]() $S_i$ in two regimes. For
$S_i$ in two regimes. For ![]() $0\leq i\leq 2A-2$, the
$0\leq i\leq 2A-2$, the ![]() $S_i$ form a random excursion, beginning (
$S_i$ form a random excursion, beginning (![]() $i=0$) at 0 and ending (
$i=0$) at 0 and ending (![]() $i=2A-2$) at
$i=2A-2$) at ![]() $2{\Lambda}$. For
$2{\Lambda}$. For ![]() $2A-2 \leq i \leq 2n-2$, the
$2A-2 \leq i \leq 2n-2$, the ![]() $S_i$ form a random excursion beginning (
$S_i$ form a random excursion beginning (![]() $i=2A-2$) at
$i=2A-2$) at ![]() $2{\Lambda}$ and ending (
$2{\Lambda}$ and ending (![]() $i=2n-2$) at
$i=2n-2$) at ![]() $2{\Gamma}$. As in Section 4, the two excursions are independent. Let
$2{\Gamma}$. As in Section 4, the two excursions are independent. Let ![]() $\operatorname{{COND}}({\Lambda},{\Gamma})$ denote this condition.
$\operatorname{{COND}}({\Lambda},{\Gamma})$ denote this condition.
Theorem 5.1. Uniformly in ![]() $|{\Lambda}|\leq \sqrt{A}$,
$|{\Lambda}|\leq \sqrt{A}$, ![]() $|{\Gamma}| \leq \sqrt{n}$, under
$|{\Gamma}| \leq \sqrt{n}$, under ![]() $\operatorname{{COND}} ({\Lambda},{\Gamma})$,
$\operatorname{{COND}} ({\Lambda},{\Gamma})$,
Proof. This follows the same lines as Theorem 4.3. The critical preferential attachment Theorem 3.2 and (3.2) are replaced by Corollary 3.1 and (3.4).
From Theorem 5.1 we derive the lower bound of Theorem 1.1.
Theorem 5.2. For ![]() $c \in (0, 1)$,
$c \in (0, 1)$,
with
Proof. We split (sum over ![]() $|{\Lambda}|\leq \sqrt{A}$,
$|{\Lambda}|\leq \sqrt{A}$, ![]() $|{\Gamma}| \leq \sqrt{n}$)
$|{\Gamma}| \leq \sqrt{n}$)
These conditionings are disjoint. An unrestricted random walk has probability ![]() $\Omega(1)$ of having these ‘reasonable’ values at
$\Omega(1)$ of having these ‘reasonable’ values at ![]() $2A-2$ and
$2A-2$ and ![]() $2n-2$, so the sum of the probabilities of
$2n-2$, so the sum of the probabilities of ![]() $\operatorname{{COND}}$ is
$\operatorname{{COND}}$ is ![]() $\Omega(1)$. From Theorem 5.1 the conditional probabilities of
$\Omega(1)$. From Theorem 5.1 the conditional probabilities of ![]() $L\leq c\ln n$ are all bounded from below.
$L\leq c\ln n$ are all bounded from below.
6. The upper bound
We employ coupling arguments to give upper bounds on the large deviation of L.
Theorem 6.1. For any ![]() ${\Lambda}$ with
${\Lambda}$ with ![]() $|{\Lambda}|\leq A$ and any z,
$|{\Lambda}|\leq A$ and any z,
Proof. We couple paths
with paths
Determine the random paths ![]() $P,P^*$ sequentially, starting at 2A. Let t be the first value (if any) for which, setting
$P,P^*$ sequentially, starting at 2A. Let t be the first value (if any) for which, setting ![]() $P_t=(a,b)$, either
$P_t=(a,b)$, either ![]() $P_t^*=(a,b)$ or
$P_t^*=(a,b)$ or ![]() $P_t^*=(b,a)$. In the first case couple
$P_t^*=(b,a)$. In the first case couple ![]() $P_s=P_s^*$ for all
$P_s=P_s^*$ for all ![]() $t\leq s \leq 2n$. In the second case couple
$t\leq s \leq 2n$. In the second case couple ![]() $P_s^*$ to be
$P_s^*$ to be ![]() $P_s$ with coordinates reversed (i.e. flip the path on the diagonal) for all
$P_s$ with coordinates reversed (i.e. flip the path on the diagonal) for all ![]() $t\leq s\leq 2n$. For any paired
$t\leq s\leq 2n$. For any paired ![]() $P,P^*$,
$P,P^*$, ![]() $|S_i|> |S_i^*|$ for
$|S_i|> |S_i^*|$ for ![]() $2A\leq i < t$ and
$2A\leq i < t$ and ![]() $|S_i|=|S_i^*|$ for
$|S_i|=|S_i^*|$ for ![]() $t\leq i \leq 2n$. Thus
$t\leq i \leq 2n$. Thus ![]() $L^{\mathrm{main}}(P) \geq L^{\mathrm{main}}(P^*)$ and (6.1) follows.
$L^{\mathrm{main}}(P) \geq L^{\mathrm{main}}(P^*)$ and (6.1) follows.
Corollary 6.1. For any ![]() ${\Lambda}$ with
${\Lambda}$ with ![]() $|{\Lambda}|\leq A$ and any z,
$|{\Lambda}|\leq A$ and any z,
Proof. ![]() $L^{\mathrm{main}}\leq L$ so
$L^{\mathrm{main}}\leq L$ so ![]() ${\mathbb{P}}[L\leq z] \leq {\mathbb{P}}[L^{\mathrm{main}}\leq z]$.
${\mathbb{P}}[L\leq z] \leq {\mathbb{P}}[L^{\mathrm{main}}\leq z]$.
Corollary 6.2. For any z,
Proof. The event ![]() $P_{2n}=(n,n)$ is the disjoint union of the events
$P_{2n}=(n,n)$ is the disjoint union of the events ![]() ${\operatorname{{COND}}} ({\Lambda},0)$. Since, from (6.2),
${\operatorname{{COND}}} ({\Lambda},0)$. Since, from (6.2), ![]() ${\mathbb{P}}[L\leq z]$ is uniformly bounded conditional under each of the events
${\mathbb{P}}[L\leq z]$ is uniformly bounded conditional under each of the events ![]() ${\operatorname{{COND}}} ({\Lambda},0)$, it has the same bound conditional on their union.
${\operatorname{{COND}}} ({\Lambda},0)$, it has the same bound conditional on their union.
Theorem 6.2. For any ![]() ${\Gamma}$ with
${\Gamma}$ with ![]() $|{\Gamma}|\leq n$,
$|{\Gamma}|\leq n$,
Proof. We reverse time, and consider the random walk starting at ![]() $P_{2n}^*=(n+{\Gamma},n-{\Gamma})$ and ending at
$P_{2n}^*=(n+{\Gamma},n-{\Gamma})$ and ending at ![]() $P_2^*=(1, 1)$. That is, at a state (a, b) one moves to either
$P_2^*=(1, 1)$. That is, at a state (a, b) one moves to either ![]() $(a-1,b)$ or
$(a-1,b)$ or ![]() $(a,b-1)$ with the probabilities that the random walk from (1, 1) to (a, b) goes through those states. We couple walks
$(a,b-1)$ with the probabilities that the random walk from (1, 1) to (a, b) goes through those states. We couple walks ![]() $P_{2n}^*,\ldots, P_2^*$ with walks
$P_{2n}^*,\ldots, P_2^*$ with walks ![]() $P_{2n},\ldots,P_2$. Let t be the first value (here, highest index value) so that, with
$P_{2n},\ldots,P_2$. Let t be the first value (here, highest index value) so that, with ![]() $P_t^*=(a,b)$, either
$P_t^*=(a,b)$, either ![]() $P_t=(a,b)$ or
$P_t=(a,b)$ or ![]() $P_t=(b,a)$. In the first case we couple
$P_t=(b,a)$. In the first case we couple ![]() $P_s^*=P_s$ for
$P_s^*=P_s$ for ![]() $2\leq s\leq t$ and in the second case
$2\leq s\leq t$ and in the second case ![]() $P_s$ is
$P_s$ is ![]() $P_s^*$ with coordinates reversed for
$P_s^*$ with coordinates reversed for ![]() $2\leq s\leq t$. For any paired paths
$2\leq s\leq t$. For any paired paths ![]() $P^*,P$,
$P^*,P$, ![]() $L(P^*)\geq L(P)$ and so the lower-tail inequality (6.3) follows.
$L(P^*)\geq L(P)$ and so the lower-tail inequality (6.3) follows.
Corollary 6.3. For any ![]() ${\Gamma}$ with
${\Gamma}$ with ![]() $|{\Gamma}|\leq n$,
$|{\Gamma}|\leq n$,
Theorem 6.3. Let ![]() $\xi_3,\ldots,\xi_{2n}=\pm 1$ independently and uniformly. Let
$\xi_3,\ldots,\xi_{2n}=\pm 1$ independently and uniformly. Let ![]() $S_t$ be the walk with initial value
$S_t$ be the walk with initial value ![]() $S_2=0$ and step
$S_2=0$ and step ![]() $S_t=S_{t-1}+\xi_t$. Set
$S_t=S_{t-1}+\xi_t$. Set ![]() $L = \sum_{i=2}^{2n} S_i^2/i^2$. Then
$L = \sum_{i=2}^{2n} S_i^2/i^2$. Then
Proof. The unrestricted walk is the disjoint union of the excursions ending at ![]() $P_{2n}=(n+{\Gamma},n-{\Gamma})$. Corollary 6.3 gives the upper bound under any of these conditions, so the upper bound holds under their union.
$P_{2n}=(n+{\Gamma},n-{\Gamma})$. Corollary 6.3 gives the upper bound under any of these conditions, so the upper bound holds under their union.
We set ![]() $z=c\ln n$. Theorems 6.3 and 4.1 yield the upper bound to Theorem 1.1 and hence, together with Theorem 5.2, prove Theorem 1.1.
$z=c\ln n$. Theorems 6.3 and 4.1 yield the upper bound to Theorem 1.1 and hence, together with Theorem 5.2, prove Theorem 1.1.
7. Brownian approximations
In this section we introduce a Brownian analog for L, and establish that for the purposes of establishing Theorem 1.1, it is enough to establish the corresponding statement for the Brownian analog. To this end, let ![]() $\{B_t \colon t \geq 0\}$ be a standard Brownian motion (with
$\{B_t \colon t \geq 0\}$ be a standard Brownian motion (with ![]() $B_0=0$). Thus
$B_0=0$). Thus ![]() $B_n$ is a natural approximation of
$B_n$ is a natural approximation of ![]() $S_n$.
$S_n$.
Recall ![]() $L=L_n$ from (1.3) and define the two natural approximations
$L=L_n$ from (1.3) and define the two natural approximations
We introduce a cut-off A; ![]() $A \,:\!={\lfloor{\ln^{10}n}\rfloor}$ as in (4.1) works in this case as well, except that we assume that A is an even integer (this is convenient and simplifies the argument in Lemma 7.2 below, but is not essential). Define
$A \,:\!={\lfloor{\ln^{10}n}\rfloor}$ as in (4.1) works in this case as well, except that we assume that A is an even integer (this is convenient and simplifies the argument in Lemma 7.2 below, but is not essential). Define
 \begin{align}L' &= L'_{n} = \sum_{i=A+1}^n \dfrac{S_i^2}{i^2} , \\ {\widetilde L}' &= {\widetilde L}'_{n} = \sum_{i=A+1}^n \dfrac{B_i^2}{i^2} , \\ {\widehat L}' &= {\widehat L}'_{n} = \int_A^n \dfrac{B_t^2}{t^2}{\,\mathrm{d}} t \end{align}
\begin{align}L' &= L'_{n} = \sum_{i=A+1}^n \dfrac{S_i^2}{i^2} , \\ {\widetilde L}' &= {\widetilde L}'_{n} = \sum_{i=A+1}^n \dfrac{B_i^2}{i^2} , \\ {\widehat L}' &= {\widehat L}'_{n} = \int_A^n \dfrac{B_t^2}{t^2}{\,\mathrm{d}} t \end{align}
and
 \begin{align}L'' &= L''_{n} = \sum_{i=A+1}^n \dfrac{(S_i-S_A)^2}{i^2} ,\\ {\widetilde L}'' &= {\widetilde L}''_{n} = \sum_{i=A+1}^n \dfrac{(B_i-B_A)^2}{i^2} ,\end{align}
\begin{align}L'' &= L''_{n} = \sum_{i=A+1}^n \dfrac{(S_i-S_A)^2}{i^2} ,\\ {\widetilde L}'' &= {\widetilde L}''_{n} = \sum_{i=A+1}^n \dfrac{(B_i-B_A)^2}{i^2} ,\end{align}
and
Note that
and
Throughout this discussion, C denotes some unspecified finite constants, changing from one occurrence to the next (in contrast to c, which is our main parameter). We implicitly assume that n is large. At least, assume ![]() $n\ge 8$ throughout, so
$n\ge 8$ throughout, so ![]() $\ln\ln n\ge1$.
$\ln\ln n\ge1$.
Lemmas 7.1–7.4 establish that the random variable ![]() $L_n$ and those defined in (7.1)–(7.5) are equivalent for our purposes.
$L_n$ and those defined in (7.1)–(7.5) are equivalent for our purposes.
Lemma 7.1. For any ![]() $c>0$ and
$c>0$ and ![]() ${\varepsilon}>0$, for n large enough,
${\varepsilon}>0$, for n large enough,
Proof. The proofs of all three parts are identical, up to obvious (notational) changes. Hence we consider only (7.7).
By Minkowski’s inequality (the triangle inequality in ![]() $\ell^2$),
$\ell^2$),
and thus
Furthermore, ![]() ${\mathbb E} S_A^2=A$ and
${\mathbb E} S_A^2=A$ and ![]() ${\mathbb E} L_A = {\mathrm{O}}{({\ln A})}={\mathrm{O}}{({\ln\ln n})}$ by (7.6); hence, by Chebyshev’s and Markov’s inequalities, for a suitable C,
${\mathbb E} L_A = {\mathrm{O}}{({\ln A})}={\mathrm{O}}{({\ln\ln n})}$ by (7.6); hence, by Chebyshev’s and Markov’s inequalities, for a suitable C,
 \begin{align*}{\mathbb{P}}{\bigg({\dfrac{|S_A|}{\sqrt{A}}> C}\bigg)} &\le \dfrac{1}4,\\ {\mathbb{P}}{({{L_A}> C \ln\ln n})} &\le \dfrac{1}4,\end{align*}
\begin{align*}{\mathbb{P}}{\bigg({\dfrac{|S_A|}{\sqrt{A}}> C}\bigg)} &\le \dfrac{1}4,\\ {\mathbb{P}}{({{L_A}> C \ln\ln n})} &\le \dfrac{1}4,\end{align*}
and thus
Since ![]() $L_n''$ is independent of
$L_n''$ is independent of ![]() $S_A$ and
$S_A$ and ![]() $L_A$, it follows from (7.10) and (7.11) that
$L_A$, it follows from (7.10) and (7.11) that
 \begin{align*} {\mathbb{P}}{({L_n\le c\ln n})}&\ge {\mathbb{P}}{({L_n''\le (c-{\varepsilon})\ln n})}{\mathbb{P}}{\bigg({\dfrac{|S_A|}{\sqrt{A}}+\sqrt{L_A}\le C\sqrt{\ln\ln n}}\bigg)} \\ &\geq \dfrac{1}{2}{\mathbb{P}} \{L_n''\le (c-\varepsilon)\log n \}.\end{align*}
\begin{align*} {\mathbb{P}}{({L_n\le c\ln n})}&\ge {\mathbb{P}}{({L_n''\le (c-{\varepsilon})\ln n})}{\mathbb{P}}{\bigg({\dfrac{|S_A|}{\sqrt{A}}+\sqrt{L_A}\le C\sqrt{\ln\ln n}}\bigg)} \\ &\geq \dfrac{1}{2}{\mathbb{P}} \{L_n''\le (c-\varepsilon)\log n \}.\end{align*}
Obviously, ![]() $L_n\ge L_n'$,
$L_n\ge L_n'$, ![]() ${\widetilde L}_n\ge{\widetilde L}_n'$ and
${\widetilde L}_n\ge{\widetilde L}_n'$ and ![]() ${\widehat L}_n\ge{\widehat L}_n'$. The next lemma says that
${\widehat L}_n\ge{\widehat L}_n'$. The next lemma says that ![]() $L_n'$ is stochastically larger than
$L_n'$ is stochastically larger than ![]() $L_n''$, and so on.
$L_n''$, and so on.
Lemma 7.2. For any ![]() $y\ge0$,
$y\ge0$,
Proof. Consider first (7.12). Define ![]() ${\overline S}_i \,:\!=S_i-S_A$ for
${\overline S}_i \,:\!=S_i-S_A$ for ![]() $i\ge A$. Then
$i\ge A$. Then ![]() ${\overline S}_i$,
${\overline S}_i$, ![]() $i\ge A$, is a simple random walk starting at
$i\ge A$, is a simple random walk starting at ![]() ${\overline S}_A=0$.
${\overline S}_A=0$.
If we condition ![]() $ (S_i)_{i\ge A} $ on
$ (S_i)_{i\ge A} $ on ![]() $S_A=x$, we obtain a simple random walk starting at x. This has the same distribution as
$S_A=x$, we obtain a simple random walk starting at x. This has the same distribution as ![]() $x+{\overline S}_i$, but we shall use a different coupling defined as follows. Recall that A is chosen to be even, and thus
$x+{\overline S}_i$, but we shall use a different coupling defined as follows. Recall that A is chosen to be even, and thus ![]() $S_A$ is an even integer.
$S_A$ is an even integer.
For a given even integer x, define the stopping time ![]() $\tau \,:\!=\inf\{{k\ge A\colon {\overline S}_k=x/2}\}$, and
$\tau \,:\!=\inf\{{k\ge A\colon {\overline S}_k=x/2}\}$, and
 \begin{equation*} {{\overline S}{^{(x)}_i}} \,:\!= \begin{cases} x-{\overline S}_i & A\le i\le \tau,\\{\overline S}_i & i>\tau. \end{cases}\end{equation*}
\begin{equation*} {{\overline S}{^{(x)}_i}} \,:\!= \begin{cases} x-{\overline S}_i & A\le i\le \tau,\\{\overline S}_i & i>\tau. \end{cases}\end{equation*}
Then ![]() ${{\overline S}{^{(x)}_i}}$ is a simple random walk, started at
${{\overline S}{^{(x)}_i}}$ is a simple random walk, started at ![]() ${{\overline S}{^{(x)}_A}}=x$, and thus
${{\overline S}{^{(x)}_A}}=x$, and thus ![]() $ ({{\overline S}{^{(x)}_i}})_A^\infty $ has the same distribution as
$ ({{\overline S}{^{(x)}_i}})_A^\infty $ has the same distribution as ![]() $ (x+{\overline S}_i)_A^\infty $. Furthermore, it is easily seen that, for all
$ (x+{\overline S}_i)_A^\infty $. Furthermore, it is easily seen that, for all ![]() $i\ge A$,
$i\ge A$,
(To see this, we may by symmetry assume ![]() $x\ge0$. It suffices to consider
$x\ge0$. It suffices to consider ![]() $A\le i\le \tau$, and then
$A\le i\le \tau$, and then ![]() ${\overline S}_i\le x/2$, and thus either
${\overline S}_i\le x/2$, and thus either ![]() ${\overline S}_i\le 0$ and
${\overline S}_i\le 0$ and ![]() ${{\overline S}{^{(x)}_i}}=x+|{\overline S}_i|$, or
${{\overline S}{^{(x)}_i}}=x+|{\overline S}_i|$, or ![]() $0<{\overline S}_i\le x/2 \le {{\overline S}{^{(x)}_i}}$.)
$0<{\overline S}_i\le x/2 \le {{\overline S}{^{(x)}_i}}$.)
Consequently, for every even integer x and every ![]() $y\ge0$,
$y\ge0$,
 \begin{equation*} \begin{split}{\mathbb{P}}{({L''_n \le y})}&={\mathbb{P}}{\bigg({\sum_{i=A+1}^n \dfrac{{\overline S}_i^2}{i^2} \le y}\bigg)}\\ &\ge{\mathbb{P}}{\bigg({\sum_{i=A+1}^n \dfrac{{({{{\overline S}{^{(x)}_i}}})}^2}{i^2} \le y}\bigg)}\\ &={\mathbb{P}}{\bigg({\sum_{i=A+1}^n \dfrac{S_i^2}{i^2} \le y \biggm| S_A=x}\bigg)}\\ &={\mathbb{P}}{({L'_n \le y \mid S_A=x})}. \end{split}\end{equation*}
\begin{equation*} \begin{split}{\mathbb{P}}{({L''_n \le y})}&={\mathbb{P}}{\bigg({\sum_{i=A+1}^n \dfrac{{\overline S}_i^2}{i^2} \le y}\bigg)}\\ &\ge{\mathbb{P}}{\bigg({\sum_{i=A+1}^n \dfrac{{({{{\overline S}{^{(x)}_i}}})}^2}{i^2} \le y}\bigg)}\\ &={\mathbb{P}}{\bigg({\sum_{i=A+1}^n \dfrac{S_i^2}{i^2} \le y \biggm| S_A=x}\bigg)}\\ &={\mathbb{P}}{({L'_n \le y \mid S_A=x})}. \end{split}\end{equation*}
Thus, ![]() ${\mathbb{P}}{ ({L''_n \le y})}\ge {\mathbb{P}}{ ({L'_n \le y\mid S_A})}$, and we obtain (7.12) by taking the expectation.
${\mathbb{P}}{ ({L''_n \le y})}\ge {\mathbb{P}}{ ({L'_n \le y\mid S_A})}$, and we obtain (7.12) by taking the expectation.
The proofs of (7.13) and (7.14) are the same, with ![]() $S_n$ replaced by
$S_n$ replaced by ![]() $B_t$.
$B_t$.
Lemma 7.3. For every ![]() ${\varepsilon}>0$,
${\varepsilon}>0$, ![]() $c>0$, and
$c>0$, and ![]() $a<\infty$,
$a<\infty$,
Proof. By [Reference Komlós, Major and Tusnády18], there exists a coupling (the ‘dyadic coupling’) of the simple random walk ![]() $ (S_i)_{i\ge0} $ and the Brownian motion
$ (S_i)_{i\ge0} $ and the Brownian motion ![]() $ (B_t)_{t\ge0} $ such that, with probability
$ (B_t)_{t\ge0} $ such that, with probability ![]() $1-{\mathrm{O}}(n^{-a})$, for some constant
$1-{\mathrm{O}}(n^{-a})$, for some constant ![]() $C_a$,
$C_a$,
(see also [Reference Lawler and Limic19, Chapter 7]). If (7.19) holds, then ![]() $|(S_i-S_A)-(B_i-B_A)|\le 2C_a\ln n$ for
$|(S_i-S_A)-(B_i-B_A)|\le 2C_a\ln n$ for ![]() $A\le i\le n$, and thus, by Minkowski’s inequality,
$A\le i\le n$, and thus, by Minkowski’s inequality,
 \begin{equation} \begin{split}| \sqrt{L_n''}-\sqrt{{\widetilde L}_n''}|&\le{\bigg({\sum_{i=A+1}^n \dfrac{{ ({(S_i-S_A)-(B_i-B_A)})}^2}{i^2}}\bigg)}^{1/2}\\ & \le 2C_a\dfrac{\ln n}{\sqrt A}\\ &={\mathrm{o}}(1). \end{split}\end{equation}
\begin{equation} \begin{split}| \sqrt{L_n''}-\sqrt{{\widetilde L}_n''}|&\le{\bigg({\sum_{i=A+1}^n \dfrac{{ ({(S_i-S_A)-(B_i-B_A)})}^2}{i^2}}\bigg)}^{1/2}\\ & \le 2C_a\dfrac{\ln n}{\sqrt A}\\ &={\mathrm{o}}(1). \end{split}\end{equation}
Hence, (7.15) and (7.16) follow.
In order to prove (7.17)–(7.18), we introduce yet another version of ![]() $L_n$:
$L_n$:
Then (see (7.4)),
Moreover, by simple standard properties of Brownian motion,
 \begin{align*}{\mathbb{P}}{\Big({\sup_{t\le n} |B_{\lceil t\rceil}-B_t|>\ln n}\Big)}&\le n{\mathbb{P}}{\Big({\sup_{0\le t\le 1} |B_{1}-B_t|>\ln n}\Big)} \\ &\le n{\mathbb{P}}{\bigg({\sup_{0\le t\le 1} |B_t|>\dfrac12\ln n}\bigg)} \\ &\le 4n{\mathbb{P}}{\biggl({B_1>\dfrac12\ln n}\biggr)} \\ &\le C n \,{\mathrm{e}}^{-\ln^2n/8} \\ &={\mathrm{O}}{ ({n^{-a}})}.\end{align*}
\begin{align*}{\mathbb{P}}{\Big({\sup_{t\le n} |B_{\lceil t\rceil}-B_t|>\ln n}\Big)}&\le n{\mathbb{P}}{\Big({\sup_{0\le t\le 1} |B_{1}-B_t|>\ln n}\Big)} \\ &\le n{\mathbb{P}}{\bigg({\sup_{0\le t\le 1} |B_t|>\dfrac12\ln n}\bigg)} \\ &\le 4n{\mathbb{P}}{\biggl({B_1>\dfrac12\ln n}\biggr)} \\ &\le C n \,{\mathrm{e}}^{-\ln^2n/8} \\ &={\mathrm{O}}{ ({n^{-a}})}.\end{align*}
Hence, similarly to (7.20), with probability ![]() $1-{\mathrm{O}}{ ({n^{-a}})}$,
$1-{\mathrm{O}}{ ({n^{-a}})}$,
Lemma 7.4. For every ![]() ${\varepsilon}>0$,
${\varepsilon}>0$, ![]() $c>0$, and
$c>0$, and ![]() $a<\infty$,
$a<\infty$,
Proof. By (7.12), (7.15), (7.17), and (7.9),
 \begin{align*}{\mathbb{P}}(L_n\le c\ln n)&\le{\mathbb{P}}(L_n''\le c\ln n) \\ &\le {\mathbb{P}}{ ({{\widetilde L}_n''\le (c+{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})} \\ &\le {\mathbb{P}}{ ({{\widehat L}_n''\le (c+2{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})} \\ &\le 2{\mathbb{P}}{ ({{\widehat L}_n\le (c+3{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})}, \end{align*}
\begin{align*}{\mathbb{P}}(L_n\le c\ln n)&\le{\mathbb{P}}(L_n''\le c\ln n) \\ &\le {\mathbb{P}}{ ({{\widetilde L}_n''\le (c+{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})} \\ &\le {\mathbb{P}}{ ({{\widehat L}_n''\le (c+2{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})} \\ &\le 2{\mathbb{P}}{ ({{\widehat L}_n\le (c+3{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})}, \end{align*}
which yields (7.23) after replacing ![]() ${\varepsilon}$ with
${\varepsilon}$ with ![]() ${\varepsilon}/3$.
${\varepsilon}/3$.
Similarly, (7.14), (7.18), (7.16), and (7.7) yield
 \begin{align*}{\mathbb{P}}({\widehat L}_n\le c\ln n)&\le{\mathbb{P}}({\widehat L}_n''\le c\ln n) \\ &\le {\mathbb{P}}{ ({{\widetilde L}_n''\le (c+{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})} \\ &\le {\mathbb{P}}{ ({L_n''\le (c+2{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})} \\ &\le 2{\mathbb{P}}{ ({L_n\le (c+3{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})}.\end{align*}
\begin{align*}{\mathbb{P}}({\widehat L}_n\le c\ln n)&\le{\mathbb{P}}({\widehat L}_n''\le c\ln n) \\ &\le {\mathbb{P}}{ ({{\widetilde L}_n''\le (c+{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})} \\ &\le {\mathbb{P}}{ ({L_n''\le (c+2{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})} \\ &\le 2{\mathbb{P}}{ ({L_n\le (c+3{\varepsilon})\ln n})} + {\mathrm{O}}{ ({n^{-a}})}.\end{align*}
Consequently, it does not matter whether we use ![]() $L_n$ or
$L_n$ or ![]() ${\widehat L}_n$ (or
${\widehat L}_n$ (or ![]() ${\widetilde L}_n$) in Theorem 1.1: the different versions are equivalent.
${\widetilde L}_n$) in Theorem 1.1: the different versions are equivalent.
8. Analysis of the Brownian versions
Note from (7.1)–(7.2) that both ![]() ${\widetilde L}_n$ and
${\widetilde L}_n$ and ![]() ${\widehat L}_n$ are quadratic functionals of Gaussian variables. There is a general theory for such studying large deviation for such variables. This facilitates a direct analysis of the moment generating function of (7.2).
${\widehat L}_n$ are quadratic functionals of Gaussian variables. There is a general theory for such studying large deviation for such variables. This facilitates a direct analysis of the moment generating function of (7.2).
8.1. Moment generating function of  ${\widehat L}$
${\widehat L}$
We utilize the general theory of Gaussian Hilbert spaces to compute the moment generating function of ![]() ${\widehat L}_n$. For the convenience of the reader, we include a brief summary, relevant for this application, in Appendix A, and refer the interested reader to [Reference Janson16, Chapters VII and VI] for further details.
${\widehat L}_n$. For the convenience of the reader, we include a brief summary, relevant for this application, in Appendix A, and refer the interested reader to [Reference Janson16, Chapters VII and VI] for further details.
By Theorem A.2 and Lemma A.1, for every ![]() $t<(2\max{\lambda}_j){^{-1}}$,
$t<(2\max{\lambda}_j){^{-1}}$,
where ![]() $({\lambda}_j)$ are the non-zero eigenvalues of the integral operator
$({\lambda}_j)$ are the non-zero eigenvalues of the integral operator
acting in ![]() $L^2{(0,n)}$. As shown in Appendix A (see Remark A.1),
$L^2{(0,n)}$. As shown in Appendix A (see Remark A.1), ![]() $T=T_n$ is a positive compact operator, and thus
$T=T_n$ is a positive compact operator, and thus ![]() ${\lambda}_j>0$; furthermore,
${\lambda}_j>0$; furthermore, ![]() $\sum_j{\lambda}_j={\mathbb E}{\widehat L}_n=\ln n<\infty$.
$\sum_j{\lambda}_j={\mathbb E}{\widehat L}_n=\ln n<\infty$.
Suppose that f is an eigenfunction with a non-zero eigenvalue ![]() ${\lambda}$. Thus
${\lambda}$. Thus ![]() $f\in L^2{(0,n)}$ is not identically 0, and
$f\in L^2{(0,n)}$ is not identically 0, and ![]() $Tf={\lambda} f$. It follows from (8.2) by dominated convergence that Tf(x) is continuous in
$Tf={\lambda} f$. It follows from (8.2) by dominated convergence that Tf(x) is continuous in ![]() $x\in{[0,n]}$; thus
$x\in{[0,n]}$; thus ![]() $f={\lambda}{^{-1}} Tf$ is continuous on [0, n]. Similarly,
$f={\lambda}{^{-1}} Tf$ is continuous on [0, n]. Similarly, ![]() $f={\lambda}{^{-1}} Tf$ is constant on [0, 1], and
$f={\lambda}{^{-1}} Tf$ is constant on [0, 1], and ![]() $f(n)=0$. By (8.2), we have
$f(n)=0$. By (8.2), we have
and it follows that f is continuously differentiable on (1, n), with
Conversely, if f is continuous on [0, n], constant on [0, 1] and satisfies (8.3) on (1, n) with the boundary condition ![]() $f(n)=0$, then
$f(n)=0$, then ![]() $Tf={\lambda} f$.
$Tf={\lambda} f$.
Letting ![]() $F(x) \,:\!=\int_0^x f(\kern1pty){\,\mathrm{d}} y$, we have
$F(x) \,:\!=\int_0^x f(\kern1pty){\,\mathrm{d}} y$, we have ![]() $F'(x)=f(x)$, and thus (8.3) yields the differential equation
$F'(x)=f(x)$, and thus (8.3) yields the differential equation
Furthermore, ![]() $F(1)={\int_0^1} f(x){\,\mathrm{d}} x = f(1)=F'(1)$ and
$F(1)={\int_0^1} f(x){\,\mathrm{d}} x = f(1)=F'(1)$ and ![]() $ F'(n)=f(n)=0$. Hence, we have the boundary conditions (with derivatives at the endpoints 1 and n interpreted by continuity)
$ F'(n)=f(n)=0$. Hence, we have the boundary conditions (with derivatives at the endpoints 1 and n interpreted by continuity)
Conversely, if F solves (8.4) on (1, n) with the boundary conditions (8.5)–(8.1), then ![]() $f(x) \,:\!=F'(x\lor 1)$ solves (8.3) and
$f(x) \,:\!=F'(x\lor 1)$ solves (8.3) and ![]() ${\lambda}$ is an eigenvalue of T.
${\lambda}$ is an eigenvalue of T.
For a given ![]() ${\lambda}>0$, the differential equation (8.4) has the solutions
${\lambda}>0$, the differential equation (8.4) has the solutions
where ![]() $\alpha_\pm$ are the solutions of
$\alpha_\pm$ are the solutions of ![]() $\alpha(\alpha-1)=-{\lambda}{^{-1}}$, and thus
$\alpha(\alpha-1)=-{\lambda}{^{-1}}$, and thus
If ![]() ${\lambda}=4$, so we have a double root
${\lambda}=4$, so we have a double root ![]() $\alpha_+=\alpha_-=1/2$, we instead have the solutions
$\alpha_+=\alpha_-=1/2$, we instead have the solutions
Suppose that ![]() ${\lambda}>0$ with
${\lambda}>0$ with ![]() ${\lambda}\neq4$. It is easily verified that the solutions (8.7) that satisfy (8.5) are multiples of
${\lambda}\neq4$. It is easily verified that the solutions (8.7) that satisfy (8.5) are multiples of ![]() $F(x) \,:\!=\alpha_+x^{\alpha_+}-\alpha_-x^{\alpha_-}$. Hence,
$F(x) \,:\!=\alpha_+x^{\alpha_+}-\alpha_-x^{\alpha_-}$. Hence, ![]() ${\lambda}$ is an eigenvalue of T if and only if this function satisfies (8.6), that is, if and only if
${\lambda}$ is an eigenvalue of T if and only if this function satisfies (8.6), that is, if and only if
Furthermore, this eigenvalue is simple.
Consider first the case ![]() $0<{\lambda}<4$. Then (8.8) yields the complex roots
$0<{\lambda}<4$. Then (8.8) yields the complex roots ![]() $\alpha_\pm=\frac12\pm {\omega}\,{\mathrm{i}} $, with
$\alpha_\pm=\frac12\pm {\omega}\,{\mathrm{i}} $, with ![]() ${\omega}=\sqrt{1/{\lambda}-1/4}$ and thus
${\omega}=\sqrt{1/{\lambda}-1/4}$ and thus
We rewrite (8.10) as
or, taking logarithms,
The left-hand side of (8.13) is a continuous increasing function of ![]() ${\omega}\in{[0,\infty)}$, with the value 0 for
${\omega}\in{[0,\infty)}$, with the value 0 for ![]() ${\omega}=0$. Hence, for a given
${\omega}=0$. Hence, for a given ![]() $n\ge2$, there is for each integer
$n\ge2$, there is for each integer ![]() $k\ge1$ exactly one solution
$k\ge1$ exactly one solution ![]() ${\omega}_k>0$ with
${\omega}_k>0$ with
and it follows, by (8.11), that the eigenvalues of T in (0, 4) are
In fact, these are all the non-zero eigenvalues, since if ![]() ${\lambda}>4$, so
${\lambda}>4$, so ![]() $\alpha_\pm$ are real with
$\alpha_\pm$ are real with ![]() $\alpha_+>\alpha_-$, then (8.10) cannot hold, and a similar argument shows that no non-zero F of the form (8.9) satisfies (8.5)–(8.6). (This also follows from Remark 8.1 below.) Hence, (8.1) shows that, for every
$\alpha_+>\alpha_-$, then (8.10) cannot hold, and a similar argument shows that no non-zero F of the form (8.9) satisfies (8.5)–(8.6). (This also follows from Remark 8.1 below.) Hence, (8.1) shows that, for every ![]() $t>-1/8$, at least,
$t>-1/8$, at least,
Note that ![]() $ {\rm Im} \ln(1+2{\omega}_k\,{\mathrm{i}} )\in(0,\pi/2)$, and thus (8.14) yields
$ {\rm Im} \ln(1+2{\omega}_k\,{\mathrm{i}} )\in(0,\pi/2)$, and thus (8.14) yields
Remark 8.1. The norm of ![]() $T=T_n$ is
$T=T_n$ is ![]() ${\lambda}_1=4/(1+4{\omega}_1^2)=4-{\mathrm{O}}(1/\ln^2 n)$ (see (8.15) and (8.17)). If we replace the lower cut-off 1 in (8.2) with a, which by homogeneity and a change of variables is equivalent to considering
${\lambda}_1=4/(1+4{\omega}_1^2)=4-{\mathrm{O}}(1/\ln^2 n)$ (see (8.15) and (8.17)). If we replace the lower cut-off 1 in (8.2) with a, which by homogeneity and a change of variables is equivalent to considering ![]() $T_{n/a}$, and then let
$T_{n/a}$, and then let ![]() $a\to0$ and
$a\to0$ and ![]() $n\to\infty$, we obtain as a weak limit of T the integral operator on
$n\to\infty$, we obtain as a weak limit of T the integral operator on ![]() $L^2$ with kernel
$L^2$ with kernel ![]() $1/(x\lor y)$. This limiting operator
$1/(x\lor y)$. This limiting operator ![]() ${T_\infty}$ is bounded on
${T_\infty}$ is bounded on ![]() $L^2{[0,\infty)}$ with norm 4, but it is not compact and has no eigenvectors. That the norm is 4 follows from the result for
$L^2{[0,\infty)}$ with norm 4, but it is not compact and has no eigenvectors. That the norm is 4 follows from the result for ![]() $T_n$ above; that it is at most 4 follows also from [Reference Hardy, Littlewood and Pólya14, Theorem 319]; that there are no eigenvectors in
$T_n$ above; that it is at most 4 follows also from [Reference Hardy, Littlewood and Pólya14, Theorem 319]; that there are no eigenvectors in ![]() $L^2{[0,\infty)}$ is seen by a direct calculation similar to the one above; that
$L^2{[0,\infty)}$ is seen by a direct calculation similar to the one above; that ![]() ${T_\infty}$ is bounded but not compact follows also from [Reference Aleksandrov, Janson, Peller and Rochberg2, Theorems 3.1 and 3.2], where a class of integral operators (including both
${T_\infty}$ is bounded but not compact follows also from [Reference Aleksandrov, Janson, Peller and Rochberg2, Theorems 3.1 and 3.2], where a class of integral operators (including both ![]() ${T_\infty}$ and
${T_\infty}$ and ![]() $T_n$) is studied.
$T_n$) is studied.
8.2. Asymptotics of the moment generating function
So far we have kept n fixed. Now consider asymptotics as ![]() ${{n\to\infty}}$. Taking logarithms in (8.16), and using (8.17), we obtain for
${{n\to\infty}}$. Taking logarithms in (8.16), and using (8.17), we obtain for ![]() $t>0$
$t>0$
For ![]() $-1/8<t<0$, (8.18) holds with the inequalities reversed. Hence, for a fixed
$-1/8<t<0$, (8.18) holds with the inequalities reversed. Hence, for a fixed ![]() $t>-1/8$, uniformly in n,
$t>-1/8$, uniformly in n,
 \begin{equation} \begin{split}\ln {\mathbb E} \,{\mathrm{e}}^{-t{\widehat L}_n}&= -\dfrac12 {\sum_{k=1}^\infty} \ln {\bigg({1+\dfrac{8t}{1+(4\pi^2/\ln^2 n)k^2}}\bigg)} + {\mathrm{O}}(1)\\ &= -\dfrac12{\int_0^\infty} \ln {\bigg({1+\dfrac{8t}{1+(4\pi^2/\ln^2 n)x^2}}\bigg)}{\,\mathrm{d}} x + {\mathrm{O}}(1).\\ &= -\dfrac{\ln n}{4\pi} {\int_0^\infty} \ln {\bigg({1+\dfrac{8t}{1+ y^2}}\bigg)}{\,\mathrm{d}} y + {\mathrm{O}}(1). \end{split}\end{equation}
\begin{equation} \begin{split}\ln {\mathbb E} \,{\mathrm{e}}^{-t{\widehat L}_n}&= -\dfrac12 {\sum_{k=1}^\infty} \ln {\bigg({1+\dfrac{8t}{1+(4\pi^2/\ln^2 n)k^2}}\bigg)} + {\mathrm{O}}(1)\\ &= -\dfrac12{\int_0^\infty} \ln {\bigg({1+\dfrac{8t}{1+(4\pi^2/\ln^2 n)x^2}}\bigg)}{\,\mathrm{d}} x + {\mathrm{O}}(1).\\ &= -\dfrac{\ln n}{4\pi} {\int_0^\infty} \ln {\bigg({1+\dfrac{8t}{1+ y^2}}\bigg)}{\,\mathrm{d}} y + {\mathrm{O}}(1). \end{split}\end{equation}
Furthermore,
 \begin{align}& {\int_0^\infty} \ln {\bigg({1+\dfrac{8t}{1+ y^2}}\bigg)}{\,\mathrm{d}} y \\ & \qquad = {\int_0^\infty} {({\ln {({1+8t+ y^2})}- \ln {({1+ y^2})}})}{\,\mathrm{d}} y \\ & \qquad= [y{ ({\ln(1+8t+y^2)-\ln(1+y^2)})}+2\sqrt{1+8t}\arctan(\kern1pty/\sqrt{1+8t})-2\arctan(\kern1pty)]_0^\infty \\ &\qquad=\pi{ ({\sqrt{1+8t}-1})}.\end{align}
\begin{align}& {\int_0^\infty} \ln {\bigg({1+\dfrac{8t}{1+ y^2}}\bigg)}{\,\mathrm{d}} y \\ & \qquad = {\int_0^\infty} {({\ln {({1+8t+ y^2})}- \ln {({1+ y^2})}})}{\,\mathrm{d}} y \\ & \qquad= [y{ ({\ln(1+8t+y^2)-\ln(1+y^2)})}+2\sqrt{1+8t}\arctan(\kern1pty/\sqrt{1+8t})-2\arctan(\kern1pty)]_0^\infty \\ &\qquad=\pi{ ({\sqrt{1+8t}-1})}.\end{align}
Consequently, by (8.19) and (8.20), we have shown the following.
Theorem 8.1. For any fixed ![]() $t>-1/8$, and all
$t>-1/8$, and all ![]() $n\ge2$,
$n\ge2$,
For ![]() $t=-1/8$, a little extra work shows that (8.19) holds with the error term
$t=-1/8$, a little extra work shows that (8.19) holds with the error term ![]() ${\mathrm{O}}(\ln \ln n)$. If
${\mathrm{O}}(\ln \ln n)$. If ![]() $t<-1/8$, then
$t<-1/8$, then ![]() $-2t{\lambda}_1>1$ for large n, and thus
$-2t{\lambda}_1>1$ for large n, and thus ![]() ${\mathbb E} \,{\mathrm{e}}^{-t{\widehat L}_n}=\infty$.
${\mathbb E} \,{\mathrm{e}}^{-t{\widehat L}_n}=\infty$.
8.3. A second proof of Theorem 1.1
By Theorem 8.1 (and the comments after it, for completeness),
 \begin{equation} \lim_{{n\to\infty}}\dfrac{1}{\ln n} \ln {\mathbb E} \,{\mathrm{e}}^{t {\widehat L}_n}={\Lambda}(t) \,:\!=\begin{cases}\dfrac{1-\sqrt{1-8t}}4 & t\le {1}/{8},\\+\infty & t \gt 1/8.\end{cases}\end{equation}
\begin{equation} \lim_{{n\to\infty}}\dfrac{1}{\ln n} \ln {\mathbb E} \,{\mathrm{e}}^{t {\widehat L}_n}={\Lambda}(t) \,:\!=\begin{cases}\dfrac{1-\sqrt{1-8t}}4 & t\le {1}/{8},\\+\infty & t \gt 1/8.\end{cases}\end{equation}
The Legendre transform of ![]() ${\Lambda}(t)$ is, by a simple calculation,
${\Lambda}(t)$ is, by a simple calculation,
 \begin{equation} {{\Lambda}^*}(x) \,:\!=\sup_{t\in{\mathbb R}} { ({tx-{\Lambda}(t)})}=\begin{cases} \dfrac{1}{8x}(x-1)^2 = \dfrac{x}{8}+\dfrac{1}{8x}-\dfrac{1}4 & x>0,\\+\infty & x\le 0.\end{cases}\end{equation}
\begin{equation} {{\Lambda}^*}(x) \,:\!=\sup_{t\in{\mathbb R}} { ({tx-{\Lambda}(t)})}=\begin{cases} \dfrac{1}{8x}(x-1)^2 = \dfrac{x}{8}+\dfrac{1}{8x}-\dfrac{1}4 & x>0,\\+\infty & x\le 0.\end{cases}\end{equation}
By (8.21) and the Gärtner–Ellis theorem (see e.g. [Reference Dembo and Zeitouni9, Theorem 2.3.6], and Remark (a) after it), the large deviation principle holds for the variables ![]() ${\widehat L}_n/\ln n$ with rate function
${\widehat L}_n/\ln n$ with rate function ![]() ${{\Lambda}^*}(x)$ in (8.22), in the sense that, for example,
${{\Lambda}^*}(x)$ in (8.22), in the sense that, for example,
Note that ![]() ${{\Lambda}^*}(c)=K(c)$ given by (1.4). Consequently, we have shown the following Brownian analog of Theorem 1.1.
${{\Lambda}^*}(c)=K(c)$ given by (1.4). Consequently, we have shown the following Brownian analog of Theorem 1.1.
Theorem 8.2. For every ![]() $c\in(0, 1]$,
$c\in(0, 1]$,
Second proof of Theorem 1.1. We use Theorem 8.2 and Lemma 7.4.
Moreover, (8.21) and the Gärtner–Ellis theorem also give a corresponding result for the upper tail.
Theorem 8.3. For every ![]() $c\in [1,\infty)$,
$c\in [1,\infty)$,
This result too transfers from the Brownian version to the random walk.
Theorem 8.4. For every ![]() $c\in [1,\infty)$,
$c\in [1,\infty)$,
Proof. This follows by Theorem 8.3 and an upper-tail version of Lemma 7.4 with ![]() ${\mathbb{P}}(L_n \le c\ln n)$ replaced by
${\mathbb{P}}(L_n \le c\ln n)$ replaced by ![]() ${\mathbb{P}}(L_n\ge c\ln n)$, and so on; this version is proved in the same way as above, so we omit the details.
${\mathbb{P}}(L_n\ge c\ln n)$, and so on; this version is proved in the same way as above, so we omit the details.
Remark 8.2. In their original paper, Chatterjee and Dembo [Reference Chatterjee and Dembo7] considered ![]() $f\colon [0, 1]^n \to \mathbb{R}$, and
$f\colon [0, 1]^n \to \mathbb{R}$, and ![]() $\mathbf{Y} = (Y_1, \ldots, Y_n)$, with
$\mathbf{Y} = (Y_1, \ldots, Y_n)$, with ![]() $Y_i \sim^{\textrm{i.i.d.}} \mathrm{Ber}(p)$ random variables. For each
$Y_i \sim^{\textrm{i.i.d.}} \mathrm{Ber}(p)$ random variables. For each ![]() $t>0$, they derived explicit non-asymptotic bounds for the upper-tail probability
$t>0$, they derived explicit non-asymptotic bounds for the upper-tail probability ![]() ${\mathbb{P}}[\kern1.5ptf(Y) > tn]$. For functions f satisfying a ‘complexity’ condition on its gradient, these bounds are asymptotically tight, and establish an LDP for this non-linear functional.
${\mathbb{P}}[\kern1.5ptf(Y) > tn]$. For functions f satisfying a ‘complexity’ condition on its gradient, these bounds are asymptotically tight, and establish an LDP for this non-linear functional.
Our setting differs from that of [Reference Chatterjee and Dembo7] in certain crucial ways. First, the relevant deviations for us occur on the ![]() $\log n$ scale, rather than the n scale. Second, the approach of [Reference Chatterjee and Dembo7] is inherently based on Taylor approximation, and works for a wide number of examples, for example sub-graph counts, random arithmetic progressions etc. On the other hand, our approach is tailored to analyzing the specific quadratic functional under consideration.
$\log n$ scale, rather than the n scale. Second, the approach of [Reference Chatterjee and Dembo7] is inherently based on Taylor approximation, and works for a wide number of examples, for example sub-graph counts, random arithmetic progressions etc. On the other hand, our approach is tailored to analyzing the specific quadratic functional under consideration.
9. Conditional functional limit laws
In this section we study the preferential attachment process ![]() $\{(X_k,Y_k)\colon k \geq 2\}$ defined in Section 1, and establish functional limit theorems for the trajectories, conditional on the event
$\{(X_k,Y_k)\colon k \geq 2\}$ defined in Section 1, and establish functional limit theorems for the trajectories, conditional on the event ![]() $\operatorname{BINGO}(n,n)$. We define
$\operatorname{BINGO}(n,n)$. We define ![]() ${\Delta}_k \,:\!=X_k-Y_k$, so that the process is given by (1.5), and state the results in terms of the stochastic process
${\Delta}_k \,:\!=X_k-Y_k$, so that the process is given by (1.5), and state the results in terms of the stochastic process ![]() $\{ \Delta_k \colon 2 \leq k \leq 2n \}$, conditional on
$\{ \Delta_k \colon 2 \leq k \leq 2n \}$, conditional on ![]() $\operatorname{BINGO}(n,n)$; recall that
$\operatorname{BINGO}(n,n)$; recall that ![]() $\operatorname{BINGO}(n,n)$ in this notation is the event
$\operatorname{BINGO}(n,n)$ in this notation is the event ![]() ${\Delta}_{2n}=0$.
${\Delta}_{2n}=0$.
In particular, we prove Theorem 1.2 stated in Section 1. We also state and prove related functional limit results for the process at times ![]() ${\mathrm{o}}(n)$. We establish the results using the usual two-step approach: first we establish finite-dimensional convergence and then we establish tightness (see e.g. [Reference Billingsley5]). The proofs proceed using the local CLT estimates in Section 3, in particular Theorem 3.3. Finite-dimensional convergence follows by straightforward calculations, but our proof of tightness is rather complicated, and uses several lemmas. We base the proof of tightness on a theorem by Aldous [Reference Aldous1] (see Section 9.1 below), but for technical reasons discussed there, we do not use Aldous’s result directly. Instead, in Section 9.1 we state and prove a variant that is convenient in our situation. We then prove Theorem 1.2 in Section 9.2, and give corresponding results for small times in Section 9.3.
${\mathrm{o}}(n)$. We establish the results using the usual two-step approach: first we establish finite-dimensional convergence and then we establish tightness (see e.g. [Reference Billingsley5]). The proofs proceed using the local CLT estimates in Section 3, in particular Theorem 3.3. Finite-dimensional convergence follows by straightforward calculations, but our proof of tightness is rather complicated, and uses several lemmas. We base the proof of tightness on a theorem by Aldous [Reference Aldous1] (see Section 9.1 below), but for technical reasons discussed there, we do not use Aldous’s result directly. Instead, in Section 9.1 we state and prove a variant that is convenient in our situation. We then prove Theorem 1.2 in Section 9.2, and give corresponding results for small times in Section 9.3.
Note that the processes ![]() $(X_k,Y_k)$,
$(X_k,Y_k)$, ![]() ${\Delta}_k$, and
${\Delta}_k$, and ![]() $n{^{-1/2}}{\Delta}_{{\lfloor{2nt}\rfloor}}$ are Markov processes, and so they are (by a simple, general, calculation) also conditioned on
$n{^{-1/2}}{\Delta}_{{\lfloor{2nt}\rfloor}}$ are Markov processes, and so they are (by a simple, general, calculation) also conditioned on ![]() $\operatorname{BINGO}(n,n)$.
$\operatorname{BINGO}(n,n)$.
9.1. A general criterion for tightness
Our proof uses a tightness criterion by Aldous [Reference Aldous1] (and, in a slightly different formulation, Mackevičius [Reference Mackevičius21]); see also [Reference Whitt24, Lemma 3.12]. Recall that a sequence of ![]() ${{\mathcal{D}}[0,\infty)}$-valued stochastic processes
${{\mathcal{D}}[0,\infty)}$-valued stochastic processes ![]() $\{ Z_n(t) \colon n \geq 1 \}$ is stochastically bounded if, for every
$\{ Z_n(t) \colon n \geq 1 \}$ is stochastically bounded if, for every ![]() $T >0$,
$T >0$,
It is well known, and easy to see, that it suffices to show (9.1) with ![]() $\sup_n$ replaced by
$\sup_n$ replaced by ![]() $\limsup_{{n\to\infty}}$.
$\limsup_{{n\to\infty}}$.
Lemma 9.1. ([Reference Aldous1, Reference Mackevičius21, Reference Whitt24].) Suppose that ![]() $Z_n(t)$ is a sequence of stochastic processes in
$Z_n(t)$ is a sequence of stochastic processes in ![]() ${{\mathcal{D}}[0,\infty)}$ satisfying the following conditions.
${{\mathcal{D}}[0,\infty)}$ satisfying the following conditions.
(i)
 $\{{Z_n(t)\colon n\ge1}\}$ is stochastically bounded.
$\{{Z_n(t)\colon n\ge1}\}$ is stochastically bounded.(ii) For each
 $n\ge1$,
$n\ge1$,  $T >0$,
$T >0$,  $\varepsilon >0$,
$\varepsilon >0$,  $\lambda < \infty$, and
$\lambda < \infty$, and  ${\delta}>0$, there exists a number
${\delta}>0$, there exists a number  $\alpha_n(\lambda, \varepsilon, \delta, T)$ such that
(9.2)a.s. on the event
$\alpha_n(\lambda, \varepsilon, \delta, T)$ such that
(9.2)a.s. on the event \begin{equation}{\mathbb{P}}{ [{ | Z_n(u) - Z_n(t_m)| > \varepsilon \mid Z_n(t_1), \ldots, Z_n(t_m) }]}\leq \alpha_n(\lambda, \varepsilon, \delta, T)\end{equation}
\begin{equation}{\mathbb{P}}{ [{ | Z_n(u) - Z_n(t_m)| > \varepsilon \mid Z_n(t_1), \ldots, Z_n(t_m) }]}\leq \alpha_n(\lambda, \varepsilon, \delta, T)\end{equation}
 $\{\max_i |Z_n(t_i)| \leq \lambda \}$, for every finite sequence
$\{\max_i |Z_n(t_i)| \leq \lambda \}$, for every finite sequence  $\{t_i \colon 1 \leq i \leq m\}$ and u with
$\{t_i \colon 1 \leq i \leq m\}$ and u with  $0 \leq t_1 \leq t_2 \leq \cdots \leq t_m \leq u \leq T$ and
$0 \leq t_1 \leq t_2 \leq \cdots \leq t_m \leq u \leq T$ and  $u - t_m \le \delta$. Furthermore, these numbers
$u - t_m \le \delta$. Furthermore, these numbers  $\alpha_n({\lambda},{\varepsilon},{\delta},T)$ satisfy
(9.3)for every
$\alpha_n({\lambda},{\varepsilon},{\delta},T)$ satisfy
(9.3)for every \begin{equation}\lim_{\delta \downarrow 0} \limsup_{n \to \infty} \alpha_n (\lambda, \varepsilon, \delta, T) =0,\end{equation}
\begin{equation}\lim_{\delta \downarrow 0} \limsup_{n \to \infty} \alpha_n (\lambda, \varepsilon, \delta, T) =0,\end{equation}
 ${\lambda},T,{\varepsilon}$.
${\lambda},T,{\varepsilon}$.
Then the sequence ![]() $Z_n(t)$ is tight in
$Z_n(t)$ is tight in ![]() ${{\mathcal{D}}[0,\infty)}$.
${{\mathcal{D}}[0,\infty)}$.
For Markov processes (as in our case), the condition (9.2) simplifies: by the Markov property, it suffices to consider the case ![]() $m=1$.
$m=1$.
A technical problem that prevents us from a direct application of Lemma 9.1 to our processes, using Theorem 3.3 to verify the condition, is that in (9.2), ![]() $u-t_m$ may be arbitrarily small, while in Theorem 3.3,
$u-t_m$ may be arbitrarily small, while in Theorem 3.3, ![]() $B/A$ is supposed to be bounded below by some
$B/A$ is supposed to be bounded below by some ![]() ${\theta}>1$. We thus first prove the following variant of Lemma 9.1, where we have a lower bound on
${\theta}>1$. We thus first prove the following variant of Lemma 9.1, where we have a lower bound on ![]() $u-t_m$. For simplicity, we state the lemma only in the Markov case. We assume also, again for simplicity, that the processes are strong Markov; recall that this means, informally, that the Markov property holds not only at fixed times but also at stopping times. A discrete-time Markov process, or a process such as our
$u-t_m$. For simplicity, we state the lemma only in the Markov case. We assume also, again for simplicity, that the processes are strong Markov; recall that this means, informally, that the Markov property holds not only at fixed times but also at stopping times. A discrete-time Markov process, or a process such as our ![]() $n{^{-1/2}}{\Delta}_{{\lfloor{2nt}\rfloor}}$ that essentially has discrete time, is automatically strong Markov.
$n{^{-1/2}}{\Delta}_{{\lfloor{2nt}\rfloor}}$ that essentially has discrete time, is automatically strong Markov.
The main difference from Lemma 9.1 is that the condition ![]() $0\le u-t_m\le{\delta}$ is replaced by
$0\le u-t_m\le{\delta}$ is replaced by ![]() ${\delta}\le u-t\le 2{\delta}$. We also add a condition that the jumps are uniformly bounded (which trivially holds in our case); we do not know whether this condition really is needed. (The condition can presumably be weakened to stochastic boundedness of the jumps, as in [Reference Billingsley6], but we have not pursued this.)
${\delta}\le u-t\le 2{\delta}$. We also add a condition that the jumps are uniformly bounded (which trivially holds in our case); we do not know whether this condition really is needed. (The condition can presumably be weakened to stochastic boundedness of the jumps, as in [Reference Billingsley6], but we have not pursued this.)
Lemma 9.2. Suppose that ![]() $Z_n(t)$ is a sequence of strong Markov processes in
$Z_n(t)$ is a sequence of strong Markov processes in ![]() ${{\mathcal{D}}[0,\infty)}$ satisfying the following conditions.
${{\mathcal{D}}[0,\infty)}$ satisfying the following conditions.
(i)
 $\{{Z_n(t)\colon n\ge1}\}$ is stochastically bounded.
$\{{Z_n(t)\colon n\ge1}\}$ is stochastically bounded.(ii) For each
 $n\ge1$,
$n\ge1$,  $T >0$,
$T >0$,  $\varepsilon >0$,
$\varepsilon >0$,  $\lambda < \infty$, and
$\lambda < \infty$, and  ${\delta}>0$, there exists a number
${\delta}>0$, there exists a number  $\alpha_n(\lambda, \varepsilon, \delta, T)$ such that
(9.4)a.s. on the event
$\alpha_n(\lambda, \varepsilon, \delta, T)$ such that
(9.4)a.s. on the event \begin{equation}{\mathbb{P}}{ [{| Z_n(u) - Z_n(t)| > \varepsilon \bigm|Z_n(t) }]}\leq \alpha_n(\lambda, \varepsilon, \delta, T)\end{equation}
\begin{equation}{\mathbb{P}}{ [{| Z_n(u) - Z_n(t)| > \varepsilon \bigm|Z_n(t) }]}\leq \alpha_n(\lambda, \varepsilon, \delta, T)\end{equation}
 $\{{ |Z_n(t)| \leq \lambda }\}$, for every t and u with
$\{{ |Z_n(t)| \leq \lambda }\}$, for every t and u with  $0\le t\le u\le T$ and
$0\le t\le u\le T$ and  $t+{\delta}\le u\le t+2{\delta}$. Furthermore, these numbers
$t+{\delta}\le u\le t+2{\delta}$. Furthermore, these numbers  $\alpha_n$ satisfy
(9.5)for every
$\alpha_n$ satisfy
(9.5)for every \begin{equation}\lim_{\delta \downarrow 0} \limsup_{n \to \infty} \alpha_n (\lambda, \varepsilon, \delta, T) =0,\end{equation}
\begin{equation}\lim_{\delta \downarrow 0} \limsup_{n \to \infty} \alpha_n (\lambda, \varepsilon, \delta, T) =0,\end{equation}
 ${\lambda},T,{\varepsilon}$.
${\lambda},T,{\varepsilon}$.(iii) The jumps are bounded by 1:
(9.6)for all n and t. \begin{equation}| Z_n(t)-Z_n(t-)|\le1\end{equation}
\begin{equation}| Z_n(t)-Z_n(t-)|\le1\end{equation}
Then the sequence ![]() $Z_n(t)$ is tight in
$Z_n(t)$ is tight in ![]() ${{\mathcal{D}}[0,\infty)}$.
${{\mathcal{D}}[0,\infty)}$.
We reduce to Lemma 9.1 using the following lemma.
Lemma 9.3. Suppose that Z(t) is a strong Markov process in ![]() ${{\mathcal{D}}[0,\infty)}$, such that, for some given numbers
${{\mathcal{D}}[0,\infty)}$, such that, for some given numbers ![]() ${\lambda},T,{\varepsilon},{\delta},\alpha>0$,
${\lambda},T,{\varepsilon},{\delta},\alpha>0$,
a.s. on the event ![]() $\{{|Z(t)|\le{\lambda}+2{\varepsilon}+1}\}$, for each t and u with
$\{{|Z(t)|\le{\lambda}+2{\varepsilon}+1}\}$, for each t and u with ![]() $0\le t\le u\le T+2{\delta}$ with
$0\le t\le u\le T+2{\delta}$ with ![]() $t+{\delta}\le u\le t+2{\delta}$. Suppose further that the jumps in Z(t) are bounded by 1, that is,
$t+{\delta}\le u\le t+2{\delta}$. Suppose further that the jumps in Z(t) are bounded by 1, that is,
for all ![]() $t\ge0$. Then, for each
$t\ge0$. Then, for each ![]() $t\le T$,
$t\le T$,
a.s. on the event ![]() $\{{|Z(t)|\le{\lambda}}\}$.
$\{{|Z(t)|\le{\lambda}}\}$.
Proof. Let ![]() ${\mathcal F}_t$ be the
${\mathcal F}_t$ be the ![]() ${\sigma}$-field generated by
${\sigma}$-field generated by ![]() $\{{Z(s)\colon s\le t}\}$, and define a stopping time by
$\{{Z(s)\colon s\le t}\}$, and define a stopping time by
using the definition ![]() $\inf\emptyset \,:\!=\infty$ if there is no such u.
$\inf\emptyset \,:\!=\infty$ if there is no such u.
Let ![]() $v \,:\!=t+2{\delta}$. If
$v \,:\!=t+2{\delta}$. If ![]() $\tau<\infty$, then
$\tau<\infty$, then ![]() $\tau\in[t,t+{\delta}]$, and thus
$\tau\in[t,t+{\delta}]$, and thus ![]() $\tau+{\delta}\le v\le \tau+2{\delta}$; hence, by (9.7) and the strong Markov property,
$\tau+{\delta}\le v\le \tau+2{\delta}$; hence, by (9.7) and the strong Markov property,
a.s. on the event ![]() $\{{\tau<\infty}\}\cap\{{|Z(\tau)|\le {\lambda}+2{\varepsilon}+1}\}$. Furthermore,
$\{{\tau<\infty}\}\cap\{{|Z(\tau)|\le {\lambda}+2{\varepsilon}+1}\}$. Furthermore, ![]() $\tau<\infty$ implies, by the definition (9.9) and right-continuity,
$\tau<\infty$ implies, by the definition (9.9) and right-continuity,
and thus also ![]() $\tau>t$ and, by (9.7) again,
$\tau>t$ and, by (9.7) again,
Let ![]() ${\mathcal{E}}$ be any event with
${\mathcal{E}}$ be any event with ![]() ${\mathcal{E}}\in{\mathcal F}_t$ and
${\mathcal{E}}\in{\mathcal F}_t$ and ![]() ${\mathcal{E}}\subseteq \{{|Z(t)|\le {\lambda}}\}$. Then, on the event
${\mathcal{E}}\subseteq \{{|Z(t)|\le {\lambda}}\}$. Then, on the event ![]() ${\mathcal{E}}\cap\{{\tau<\infty}\}$, by (9.8) and (9.12),
${\mathcal{E}}\cap\{{\tau<\infty}\}$, by (9.8) and (9.12),
Hence, (9.10) applies, and thus, since ![]() ${\mathcal F}_t\subseteq{\mathcal F}_\tau$,
${\mathcal F}_t\subseteq{\mathcal F}_\tau$,
In other words, recalling that ![]() ${\mathcal{E}}$ can be any event in
${\mathcal{E}}$ can be any event in ![]() ${\mathcal F}_t$ with
${\mathcal F}_t$ with ![]() ${\mathcal{E}}\subseteq \{{|Z(t)|\le {\lambda}}\}$,
${\mathcal{E}}\subseteq \{{|Z(t)|\le {\lambda}}\}$,
a.s. on the event ![]() $\{{|Z(t)|\le {\lambda}}\}$.
$\{{|Z(t)|\le {\lambda}}\}$.
Furthermore, ![]() $\tau<\infty$ and
$\tau<\infty$ and ![]() $|Z(v)-Z(\tau)|\le{\varepsilon}$ imply, using (9.11),
$|Z(v)-Z(\tau)|\le{\varepsilon}$ imply, using (9.11), ![]() $|Z(v)-Z(t)|\ge{\varepsilon}$. Consequently, (9.7) implies (using the Markov property)
$|Z(v)-Z(t)|\ge{\varepsilon}$. Consequently, (9.7) implies (using the Markov property)
a.s. on the event ![]() $\{{|Z(t)|\le {\lambda}}\}$.
$\{{|Z(t)|\le {\lambda}}\}$.
Assume first ![]() $\alpha\le1/2$. Combining (9.13) and (9.14), we obtain
$\alpha\le1/2$. Combining (9.13) and (9.14), we obtain
a.s. on the event ![]() $\{{|Z(t)|\le {\lambda}}\}$. Since the event satisfies
$\{{|Z(t)|\le {\lambda}}\}$. Since the event satisfies
the result follows. The case ![]() $\alpha>1/2$ is trivial.
$\alpha>1/2$ is trivial.
Proof of Lemma 9.2. Lemma 9.3 applies to each ![]() $Z_n$ with
$Z_n$ with ![]() ${\varepsilon}$ replaced by
${\varepsilon}$ replaced by ![]() ${\varepsilon}/2$ and
${\varepsilon}/2$ and ![]() $\alpha \,:\!=\alpha_n({\lambda}+{\varepsilon}+1,{\varepsilon}/2,{\delta},T+2{\delta})$. This shows that, for each
$\alpha \,:\!=\alpha_n({\lambda}+{\varepsilon}+1,{\varepsilon}/2,{\delta},T+2{\delta})$. This shows that, for each ![]() $t\le T$,
$t\le T$,
a.s. on the event ![]() $\{{|Z_n(t)|\le{\lambda}}\}$. Hence, assumption (ii) holds with
$\{{|Z_n(t)|\le{\lambda}}\}$. Hence, assumption (ii) holds with ![]() $\alpha_n$ replaced by
$\alpha_n$ replaced by ![]() $\alpha_n'$; note that (9.3) holds for
$\alpha_n'$; note that (9.3) holds for ![]() $\alpha_n'$ by (9.5) and (9.15) (since it suffices to consider
$\alpha_n'$ by (9.5) and (9.15) (since it suffices to consider ![]() ${\delta}\le1$).
${\delta}\le1$).
Hence, Lemma 9.1 applies and the result follows.
9.2. Proof of Theorem 1.2
Note first that if we define ![]() ${G_{\alpha}}(t)$ by (1.8), then its covariance function agrees with (1.6); this shows that the Gaussian process
${G_{\alpha}}(t)$ by (1.8), then its covariance function agrees with (1.6); this shows that the Gaussian process ![]() ${G_{\alpha}}(t)$ in Theorem 1.2 really exists and is continuous on [0, 1] (also at
${G_{\alpha}}(t)$ in Theorem 1.2 really exists and is continuous on [0, 1] (also at ![]() $t=0$, since
$t=0$, since ![]() ${\operatorname{{Br}}}(t)$ is Hölder
${\operatorname{{Br}}}(t)$ is Hölder![]() $(\frac12-{\varepsilon})$ for every
$(\frac12-{\varepsilon})$ for every ![]() ${\varepsilon}>0$). Equivalently, we can define
${\varepsilon}>0$). Equivalently, we can define ![]() ${G_{\alpha}}(t)$ from a Brownian motion B(t) by either
${G_{\alpha}}(t)$ from a Brownian motion B(t) by either
or (reversing the flow of time)
Again, these are verified by calculating the covariances. Note that ![]() ${G_{\alpha}}(0)={G_{\alpha}}(1)=0$, for example by (1.8).
${G_{\alpha}}(0)={G_{\alpha}}(1)=0$, for example by (1.8).
Lemma 9.4. Finite-dimensional convergence holds in (1.7), that is, if ![]() $0\le t_1<\cdots<t_m\le 1$ are fixed, then, conditioned on
$0\le t_1<\cdots<t_m\le 1$ are fixed, then, conditioned on ![]() $\operatorname{BINGO}(n,n)$, as
$\operatorname{BINGO}(n,n)$, as ![]() ${{n\to\infty}}$,
${{n\to\infty}}$,
Proof. Since ![]() ${\Delta}_0={\Delta}_{2n}=0$ and
${\Delta}_0={\Delta}_{2n}=0$ and ![]() ${G_{\alpha}}(0)={G_{\alpha}}(1)=0$ by definition, we may assume
${G_{\alpha}}(0)={G_{\alpha}}(1)=0$ by definition, we may assume ![]() $0<t_1<\cdots <t_m<1$. We also fix some
$0<t_1<\cdots <t_m<1$. We also fix some ![]() $M>0$. Let
$M>0$. Let ![]() $n_{i} \,:\!={\lfloor{2nt_i}\rfloor}$, and let
$n_{i} \,:\!={\lfloor{2nt_i}\rfloor}$, and let ![]() $k_1,\ldots,k_m\in{\mathbb Z}$ with
$k_1,\ldots,k_m\in{\mathbb Z}$ with ![]() $n_{i}+k_i\in2{\mathbb Z}$ and
$n_{i}+k_i\in2{\mathbb Z}$ and ![]() $|k_i|\le M \sqrt n$. (Assume n so large that each
$|k_i|\le M \sqrt n$. (Assume n so large that each ![]() $n_i\ge2$.) Then
$n_i\ge2$.) Then ![]() $\operatorname{BINGO}(n,n)$ holds together with
$\operatorname{BINGO}(n,n)$ holds together with ![]() ${\Delta}(n_i)=k_i$ for
${\Delta}(n_i)=k_i$ for ![]() $i=1,\ldots,m$, if and only if the events
$i=1,\ldots,m$, if and only if the events ![]() ${\mathcal{A}}_1,\ldots {\mathcal{A}}_{m+1}$ occur, where we set
${\mathcal{A}}_1,\ldots {\mathcal{A}}_{m+1}$ occur, where we set
![]() \begin{align}{\rm and}\; {\rm for}\; 2 \le i\le m+1,\; {\rm with}\; n_{m+1} \,:=2n\; {\rm and}\; k_{m+1} \,:=0,\end{align}
\begin{align}{\rm and}\; {\rm for}\; 2 \le i\le m+1,\; {\rm with}\; n_{m+1} \,:=2n\; {\rm and}\; k_{m+1} \,:=0,\end{align}
The events ![]() ${\mathcal{A}}_1,\ldots,{\mathcal{A}}_{m+1}$ are independent, and thus
${\mathcal{A}}_1,\ldots,{\mathcal{A}}_{m+1}$ are independent, and thus
 \begin{align} &{\mathbb{P}}{ [{\Delta( n_{1}) = k_1,\ldots, \Delta(n_{m}) = k_m \mid \operatorname{BINGO}(n,n)}]} \\ &\qquad = \dfrac{\prod_{i=1}^{m+1} {\mathbb{P}}[ \mathcal{A}_i] }{{\mathbb{P}} [\!\operatorname{BINGO}(n,n) ]} \\ &\qquad = \dfrac{{\mathbb{P}}[ \mathcal{A}_1] }{{\mathbb{P}} [\!\operatorname{BINGO}(n,n) ]}\prod_{i=2}^{m+1} {\mathbb{P}}[ \mathcal{A}_i] .\end{align}
\begin{align} &{\mathbb{P}}{ [{\Delta( n_{1}) = k_1,\ldots, \Delta(n_{m}) = k_m \mid \operatorname{BINGO}(n,n)}]} \\ &\qquad = \dfrac{\prod_{i=1}^{m+1} {\mathbb{P}}[ \mathcal{A}_i] }{{\mathbb{P}} [\!\operatorname{BINGO}(n,n) ]} \\ &\qquad = \dfrac{{\mathbb{P}}[ \mathcal{A}_1] }{{\mathbb{P}} [\!\operatorname{BINGO}(n,n) ]}\prod_{i=2}^{m+1} {\mathbb{P}}[ \mathcal{A}_i] .\end{align}
By Theorem 2.3, and ![]() $|k_1|\le M\sqrt n \le M'\sqrt{n_1}$,
$|k_1|\le M\sqrt n \le M'\sqrt{n_1}$,
 \begin{align}\dfrac{{\mathbb{P}}[ \mathcal{A}_1] }{{\mathbb{P}} [\!\operatorname{BINGO}(n,n) ]}&=\frac{\bigg({\mathbb{P}}{\bigg[{\operatorname{BINGO}{\biggl({\dfrac{n_1 + k_1 }{2}, \dfrac{ n_1-k_1 }{2}}\biggr)}}\bigg]} \bigg)}{{\mathbb{P}} [\!\operatorname{BINGO}(n,n) ]} \\ &\sim\frac{\bigg({\biggl({\dfrac{n_1+k_1}{2}}\biggr)}^{-\alpha}+{\biggl({\dfrac{n_1-k_1}{2}}\biggr)}^{-\alpha}\bigg)}{2n^{-\alpha}} \\ &\sim\dfrac{2(n_1/2)^{-\alpha}}{2n^{-\alpha}} \\ &\sim t_1^{-\alpha},\end{align}
\begin{align}\dfrac{{\mathbb{P}}[ \mathcal{A}_1] }{{\mathbb{P}} [\!\operatorname{BINGO}(n,n) ]}&=\frac{\bigg({\mathbb{P}}{\bigg[{\operatorname{BINGO}{\biggl({\dfrac{n_1 + k_1 }{2}, \dfrac{ n_1-k_1 }{2}}\biggr)}}\bigg]} \bigg)}{{\mathbb{P}} [\!\operatorname{BINGO}(n,n) ]} \\ &\sim\frac{\bigg({\biggl({\dfrac{n_1+k_1}{2}}\biggr)}^{-\alpha}+{\biggl({\dfrac{n_1-k_1}{2}}\biggr)}^{-\alpha}\bigg)}{2n^{-\alpha}} \\ &\sim\dfrac{2(n_1/2)^{-\alpha}}{2n^{-\alpha}} \\ &\sim t_1^{-\alpha},\end{align}
where, as in the estimates below, the implicit factors ![]() $1+{\mathrm{o}}(1)$ tend to 1 as
$1+{\mathrm{o}}(1)$ tend to 1 as ![]() ${{n\to\infty}}$, uniformly for all
${{n\to\infty}}$, uniformly for all ![]() $k_1,\ldots,k_m$ as above, for fixed
$k_1,\ldots,k_m$ as above, for fixed ![]() $t_1,\ldots,t_m$ and M.
$t_1,\ldots,t_m$ and M.
Denote the probability density function of the normal distribution N(0, t) by
Furthermore, let
Note that ![]() $n_i/2\sim t_in$, where we define
$n_i/2\sim t_in$, where we define ![]() $t_{m+1} \,:\!=1$. Thus (9.20) and Corollary 3.2 yield, for
$t_{m+1} \,:\!=1$. Thus (9.20) and Corollary 3.2 yield, for ![]() $2\le i\le m+1$,
$2\le i\le m+1$,
 \begin{align} {\mathbb{P}}[ {\mathcal{A}}_i]&\sim\sqrt{\dfrac{2\alpha-1}{\pi}}\dfrac{1}{n{^{1/2}} t_i^{\alpha}\sqrt{t_{i-1}^{1-2\alpha}-t_i^{1-2\alpha}}}\exp{\biggl({-\dfrac{{ ({y_{i-1}-y_i})}^2}{2(t_{i-1}^{1-2\alpha}-t_i^{1-2\alpha})} }\biggr)} \\&=\dfrac{2{\kappa}}{t_i^{\alpha}\sqrt n}\phi_{T_{i-1}-T_i}(\kern1pty_{i-1}-y_i) .\end{align}
\begin{align} {\mathbb{P}}[ {\mathcal{A}}_i]&\sim\sqrt{\dfrac{2\alpha-1}{\pi}}\dfrac{1}{n{^{1/2}} t_i^{\alpha}\sqrt{t_{i-1}^{1-2\alpha}-t_i^{1-2\alpha}}}\exp{\biggl({-\dfrac{{ ({y_{i-1}-y_i})}^2}{2(t_{i-1}^{1-2\alpha}-t_i^{1-2\alpha})} }\biggr)} \\&=\dfrac{2{\kappa}}{t_i^{\alpha}\sqrt n}\phi_{T_{i-1}-T_i}(\kern1pty_{i-1}-y_i) .\end{align}
Consequently, (9.21), (9.22), and (9.27) yield, uniformly for ![]() $|k_i|\le M\sqrt n$,
$|k_i|\le M\sqrt n$,
 \begin{align}&{\mathbb{P}}{ [{\Delta( n_{1}) = k_1,\ldots, \Delta(n_{m})= k_m \mid \operatorname{BINGO}(n,n)}]} \\ &\qquad\sim t_1^{-\alpha} \prod_{j=1}^m \dfrac{2{\kappa}}{t_{j+1}^{\alpha}\sqrt n}\phi_{T_j-T_{j+1}}(\kern1pty_j-y_{j+1}) \\ &\qquad= \prod_{j=1}^m \dfrac{2{\kappa}}{t_{j}^{\alpha}\sqrt n}\phi_{T_j-T_{j+1}}(\kern1pty_j-y_{j+1}).\end{align}
\begin{align}&{\mathbb{P}}{ [{\Delta( n_{1}) = k_1,\ldots, \Delta(n_{m})= k_m \mid \operatorname{BINGO}(n,n)}]} \\ &\qquad\sim t_1^{-\alpha} \prod_{j=1}^m \dfrac{2{\kappa}}{t_{j+1}^{\alpha}\sqrt n}\phi_{T_j-T_{j+1}}(\kern1pty_j-y_{j+1}) \\ &\qquad= \prod_{j=1}^m \dfrac{2{\kappa}}{t_{j}^{\alpha}\sqrt n}\phi_{T_j-T_{j+1}}(\kern1pty_j-y_{j+1}).\end{align}
Note that ![]() $T_1>\cdots>T_m>T_{m+1}=0$, and thus (recalling
$T_1>\cdots>T_m>T_{m+1}=0$, and thus (recalling ![]() $y_{m+1}=0$)
$y_{m+1}=0$) ![]() $\prod_{i=1}^m\phi_{T_j-T_{j+1}}(\kern1pty_j-y_{j+1})$ is the joint density function of
$\prod_{i=1}^m\phi_{T_j-T_{j+1}}(\kern1pty_j-y_{j+1})$ is the joint density function of ![]() ${ ({B(T_1),\ldots,B(T_m)})}$ for a Brownian motion B(t). Since M is arbitrary, it follows easily, recalling the scaling (9.26) and noting that
${ ({B(T_1),\ldots,B(T_m)})}$ for a Brownian motion B(t). Since M is arbitrary, it follows easily, recalling the scaling (9.26) and noting that ![]() $k_i+n_i\in 2{\mathbb Z}$, so
$k_i+n_i\in 2{\mathbb Z}$, so ![]() $k_i$ takes values spaced by 2, and thus
$k_i$ takes values spaced by 2, and thus ![]() $y_i$ takes values spaced by
$y_i$ takes values spaced by ![]() $2{\kappa} t_i^{-\alpha}n^{-1/2}$, that
$2{\kappa} t_i^{-\alpha}n^{-1/2}$, that
Hence,
which, using (9.25) and the construction (9.17), is the same as (9.18).
Remark 9.1. We assumed in the proof above that ![]() $t_1,\ldots,t_m$ are fixed. In fact, the proof shows, using the uniformity assertion in Theorem 3.3, that the estimates, in particular (9.28), hold uniformly for all
$t_1,\ldots,t_m$ are fixed. In fact, the proof shows, using the uniformity assertion in Theorem 3.3, that the estimates, in particular (9.28), hold uniformly for all ![]() $0<t_1<\cdots<t_m<1$ with
$0<t_1<\cdots<t_m<1$ with ![]() $\min\{{t_1,t_{i+1}-t_i, 1-t_m}\}\ge\delta$, for any fixed
$\min\{{t_1,t_{i+1}-t_i, 1-t_m}\}\ge\delta$, for any fixed ![]() $M<\infty$ and
$M<\infty$ and ![]() $\delta>0$.
$\delta>0$.
We let ![]() $Z_n$ denote the processes
$Z_n$ denote the processes ![]() $Z_n(t) \,:\!=n{^{-1/2}} {{\Delta}_{{\lfloor{2nt}\rfloor}}}$, always conditioned on
$Z_n(t) \,:\!=n{^{-1/2}} {{\Delta}_{{\lfloor{2nt}\rfloor}}}$, always conditioned on ![]() $\operatorname{BINGO}(n,n)$. We also let
$\operatorname{BINGO}(n,n)$. We also let ![]() ${\widehat{{\mathbb{P}}}}$ denote probabilities conditional on
${\widehat{{\mathbb{P}}}}$ denote probabilities conditional on ![]() $\operatorname{BINGO}(n,n)$.
$\operatorname{BINGO}(n,n)$.
We proceed to tightness and functional convergence. Our proof requires special arguments for t close to the endpoints 0 and 1, mainly because of the lack of uniformity in Theorem 3.3 when A is close to 0 or B. We first prove that the sequence ![]() $Z_n(t)$ is stochastically bounded on a sub-interval
$Z_n(t)$ is stochastically bounded on a sub-interval ![]() $[a,b]\subset(0, 1)$.
$[a,b]\subset(0, 1)$.
Lemma 9.5. Let ![]() $0<a<b<1$. Then, conditioned on
$0<a<b<1$. Then, conditioned on ![]() $\operatorname{BINGO}(n,n)$, the sequence of stochastic processes
$\operatorname{BINGO}(n,n)$, the sequence of stochastic processes ![]() $Z_n(t) \,:\!=n{^{-1/2}}{\Delta}_{{\lfloor{2nt}\rfloor}}$ is stochastically bounded on [a,b].
$Z_n(t) \,:\!=n{^{-1/2}}{\Delta}_{{\lfloor{2nt}\rfloor}}$ is stochastically bounded on [a,b].
Proof. Let ![]() $A_0 \,:\!={\lfloor{2na}\rfloor}$ and
$A_0 \,:\!={\lfloor{2na}\rfloor}$ and ![]() $B_0 \,:\!={\lfloor{2nb}\rfloor}$. Further, let
$B_0 \,:\!={\lfloor{2nb}\rfloor}$. Further, let ![]() $K>0$ be a large number. Define (for each n) the stopping time
$K>0$ be a large number. Define (for each n) the stopping time
as always with ![]() $\inf\emptyset \,:\!=\infty$. Then
$\inf\emptyset \,:\!=\infty$. Then
 \begin{equation} \Pr{ [{\{{A_0 \lt \tau_K\le B_0 }\}\land \operatorname{BINGO}(n,n)}]} =\sum_{k=A_0+1}^{B_0}{\mathbb{P}}[\tau_K=k] \Pr{ [{\operatorname{BINGO}(n,n)\!\mid\! \tau_K=k}]}.\end{equation}
\begin{equation} \Pr{ [{\{{A_0 \lt \tau_K\le B_0 }\}\land \operatorname{BINGO}(n,n)}]} =\sum_{k=A_0+1}^{B_0}{\mathbb{P}}[\tau_K=k] \Pr{ [{\operatorname{BINGO}(n,n)\!\mid\! \tau_K=k}]}.\end{equation}
If ![]() $\tau_K=k>A_0$, then
$\tau_K=k>A_0$, then ![]() $|{\Delta}_k|={\lceil {Kn{^{1/2}}} \rceil}$ or
$|{\Delta}_k|={\lceil {Kn{^{1/2}}} \rceil}$ or ![]() ${\lceil {Kn{^{1/2}}} \rceil}+1$ (depending on the parity of k). Denoting this number by
${\lceil {Kn{^{1/2}}} \rceil}+1$ (depending on the parity of k). Denoting this number by ![]() ${\hat{\Delta}_k}$, and assuming
${\hat{\Delta}_k}$, and assuming ![]() $A_0<k\le B_0$, we have by Corollary 3.2, for all
$A_0<k\le B_0$, we have by Corollary 3.2, for all ![]() $n\ge n_0$ for some
$n\ge n_0$ for some ![]() $n_0$ not depending on k, and some C not depending on n, k, or K (but perhaps on
$n_0$ not depending on k, and some C not depending on n, k, or K (but perhaps on ![]() $a,b,\alpha$),
$a,b,\alpha$),
 \begin{align}{\mathbb{P}}{ [{\operatorname{BINGO}(n,n)\mid \tau_K=k}]}&= {\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{k\pm{\hat{\Delta}_k}}2,\dfrac{k\mp{\hat{\Delta}_k}}2 ;\,n,n}\bigg)}}\bigg]} \\ &\le C n{^{-1/2}} \,{\mathrm{e}}^{-{\hat{\Delta}_k}^2/2k} \\ &\le C n{^{-1/2}} \,{\mathrm{e}}^{-K^2 n/2k} \\ &\le C n{^{-1/2}} \,{\mathrm{e}}^{-K^2/4}.\end{align}
\begin{align}{\mathbb{P}}{ [{\operatorname{BINGO}(n,n)\mid \tau_K=k}]}&= {\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{k\pm{\hat{\Delta}_k}}2,\dfrac{k\mp{\hat{\Delta}_k}}2 ;\,n,n}\bigg)}}\bigg]} \\ &\le C n{^{-1/2}} \,{\mathrm{e}}^{-{\hat{\Delta}_k}^2/2k} \\ &\le C n{^{-1/2}} \,{\mathrm{e}}^{-K^2 n/2k} \\ &\le C n{^{-1/2}} \,{\mathrm{e}}^{-K^2/4}.\end{align}
Note also that ![]() $\tau_K=k>A_0$ implies
$\tau_K=k>A_0$ implies ![]() $|{\Delta}_{A_0}|<Kn{^{1/2}}$ by (9.30). Hence, (9.31) and (9.32) yield, for
$|{\Delta}_{A_0}|<Kn{^{1/2}}$ by (9.30). Hence, (9.31) and (9.32) yield, for ![]() $n\ge n_0$,
$n\ge n_0$,
 \begin{align} {\mathbb{P}}{ [{\{{A_0 \lt \tau_K\le B_0 }\}\land \operatorname{BINGO}(n,n)}]} &\le\sum_{k=A_0+1}^{B_0}{\mathbb{P}}[\tau_K=k] Cn{^{-1/2}} \,{\mathrm{e}}^{-K^2/4} \\ &= Cn{^{-1/2}} \,{\mathrm{e}}^{-K^2/4} {\mathbb{P}}{ [{A_0 \lt \tau_K\le B_0}]} \\ &\le C n{^{-1/2}} \,{\mathrm{e}}^{-K^2/4} {\mathbb{P}}{ [{|{\Delta}_{A_0}| \lt Kn{^{1/2}}}]}.\end{align}
\begin{align} {\mathbb{P}}{ [{\{{A_0 \lt \tau_K\le B_0 }\}\land \operatorname{BINGO}(n,n)}]} &\le\sum_{k=A_0+1}^{B_0}{\mathbb{P}}[\tau_K=k] Cn{^{-1/2}} \,{\mathrm{e}}^{-K^2/4} \\ &= Cn{^{-1/2}} \,{\mathrm{e}}^{-K^2/4} {\mathbb{P}}{ [{A_0 \lt \tau_K\le B_0}]} \\ &\le C n{^{-1/2}} \,{\mathrm{e}}^{-K^2/4} {\mathbb{P}}{ [{|{\Delta}_{A_0}| \lt Kn{^{1/2}}}]}.\end{align}
Furthermore, by Theorem 2.3, as ![]() ${{n\to\infty}}$,
${{n\to\infty}}$,
 \begin{align} {\mathbb{P}}{ [{|{\Delta}_{A_0}| \lt Kn{^{1/2}}}]}&=\sum_{|\:j| \lt Kn{^{1/2}}} \Pr{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{A_0+j}2,\dfrac{A_0-j}2 }\bigg)}}\bigg]} \\ &\sim 2Kn{^{1/2}}\cdot2{\beta} (A_0/2)^{-\alpha} \\ &\sim 4{\beta} K a^{-\alpha} n^{1/2-\alpha}.\end{align}
\begin{align} {\mathbb{P}}{ [{|{\Delta}_{A_0}| \lt Kn{^{1/2}}}]}&=\sum_{|\:j| \lt Kn{^{1/2}}} \Pr{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{A_0+j}2,\dfrac{A_0-j}2 }\bigg)}}\bigg]} \\ &\sim 2Kn{^{1/2}}\cdot2{\beta} (A_0/2)^{-\alpha} \\ &\sim 4{\beta} K a^{-\alpha} n^{1/2-\alpha}.\end{align}
By the same theorem, ![]() ${\mathbb{P}}{ [{\operatorname{BINGO}(n,n)}]}\sim 2{\beta} n^{-\alpha}$. Consequently, (9.33) implies
${\mathbb{P}}{ [{\operatorname{BINGO}(n,n)}]}\sim 2{\beta} n^{-\alpha}$. Consequently, (9.33) implies
 \begin{align*}\limsup_{{n\to\infty}}{\widehat{{\mathbb{P}}}}{ [{\{{A_0 \lt \tau_K\le B_0 }\}}]} &=\limsup_{{n\to\infty}}\dfrac{ {\mathbb{P}}{ [{\{{A_0 \lt \tau_K\le B_0 }\}\land \operatorname{BINGO}(n,n)}]}}{{\mathbb{P}}{ [{\operatorname{BINGO}(n,n)}]}} \\ &\le\limsup_{{n\to\infty}}\dfrac{C n{^{-1/2}} \,{\mathrm{e}}^{-K^2/4} \cdot4{\beta} K a^{-\alpha} n^{1/2-\alpha}}{2{\beta} n^{-\alpha}} \\ &= C_1 K \,{\mathrm{e}}^{-K^2/4}.\end{align*}
\begin{align*}\limsup_{{n\to\infty}}{\widehat{{\mathbb{P}}}}{ [{\{{A_0 \lt \tau_K\le B_0 }\}}]} &=\limsup_{{n\to\infty}}\dfrac{ {\mathbb{P}}{ [{\{{A_0 \lt \tau_K\le B_0 }\}\land \operatorname{BINGO}(n,n)}]}}{{\mathbb{P}}{ [{\operatorname{BINGO}(n,n)}]}} \\ &\le\limsup_{{n\to\infty}}\dfrac{C n{^{-1/2}} \,{\mathrm{e}}^{-K^2/4} \cdot4{\beta} K a^{-\alpha} n^{1/2-\alpha}}{2{\beta} n^{-\alpha}} \\ &= C_1 K \,{\mathrm{e}}^{-K^2/4}.\end{align*}
We have also, by Lemma 9.4, as ![]() ${{n\to\infty}}$,
${{n\to\infty}}$,
Consequently, conditioned on ![]() $\operatorname{BINGO}(n,n)$,
$\operatorname{BINGO}(n,n)$,
 \begin{align*}\limsup_{{n\to\infty}} {\widehat{{\mathbb{P}}}}{ \Big[{\sup_{a\le t\le b}|Z_n(t)|\ge K}\Big]}&=\limsup_{{n\to\infty}} {\widehat{{\mathbb{P}}}}{ [{A_0\le \tau_k\le B_0 }]} \\ &\le C_1 K \,{\mathrm{e}}^{-K^2/4} + {\mathbb{P}}{[{G_\alpha(a)\ge K}]}.\end{align*}
\begin{align*}\limsup_{{n\to\infty}} {\widehat{{\mathbb{P}}}}{ \Big[{\sup_{a\le t\le b}|Z_n(t)|\ge K}\Big]}&=\limsup_{{n\to\infty}} {\widehat{{\mathbb{P}}}}{ [{A_0\le \tau_k\le B_0 }]} \\ &\le C_1 K \,{\mathrm{e}}^{-K^2/4} + {\mathbb{P}}{[{G_\alpha(a)\ge K}]}.\end{align*}
The right-hand side tends to 0 as ![]() $K\to\infty$, and the result follows.
$K\to\infty$, and the result follows.
We next prove that ![]() $Z_n(t)$ is (with large probability) uniformly small for small t.
$Z_n(t)$ is (with large probability) uniformly small for small t.
Lemma 9.6. For every ![]() ${\varepsilon}>0$ and
${\varepsilon}>0$ and ![]() $\eta>0$, there exists
$\eta>0$, there exists ![]() ${\delta}>0$ such that
${\delta}>0$ such that
Proof. The argument is similar to the proof of Lemma 9.5, but with some differences. Define (for each n) the stopping time
Let ![]() $A_0 \,:\!={\lceil {{\varepsilon} n{^{1/2}}} \rceil}$ and fix also some
$A_0 \,:\!={\lceil {{\varepsilon} n{^{1/2}}} \rceil}$ and fix also some ![]() $M\ge {\varepsilon}$. Note that if
$M\ge {\varepsilon}$. Note that if ![]() $k\le A_0$, then
$k\le A_0$, then ![]() $|{\Delta}_k|\le k-2<{\varepsilon} n{^{1/2}}$. Thus,
$|{\Delta}_k|\le k-2<{\varepsilon} n{^{1/2}}$. Thus, ![]() ${\tau_{{\varepsilon}}}>A_0$.
${\tau_{{\varepsilon}}}>A_0$.
Suppose that
Then, with ![]() ${\hat{\Delta}_k}$ as in the proof of Lemma 9.5 (with
${\hat{\Delta}_k}$ as in the proof of Lemma 9.5 (with ![]() ${\varepsilon}$ instead of K),
${\varepsilon}$ instead of K),
 \begin{align}& {\mathbb{P}}{ [{\{{A \lt {\tau_{{\varepsilon}}}\le 2A }\}\land\{{|{\Delta}_n|\le Mn{^{1/2}}}\}\land \operatorname{BINGO}(n,n)}]} \\ &\qquad=\sum_{k=A+1}^{2A}\sum_{|\:j|\le Mn{^{1/2}}}{\mathbb{P}}[{\tau_{{\varepsilon}}}=k] {\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{k\pm{\hat{\Delta}_k}}2,\dfrac{k\mp{\hat{\Delta}_k}}2 ;\,\dfrac{n+j}2,\dfrac{n-j}2}\bigg)}}\bigg]} \\ &\qquad\quad\, \times {\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{n+j}2,\dfrac{n-j}2;\,n,n}\bigg)}}\bigg]}.\end{align}
\begin{align}& {\mathbb{P}}{ [{\{{A \lt {\tau_{{\varepsilon}}}\le 2A }\}\land\{{|{\Delta}_n|\le Mn{^{1/2}}}\}\land \operatorname{BINGO}(n,n)}]} \\ &\qquad=\sum_{k=A+1}^{2A}\sum_{|\:j|\le Mn{^{1/2}}}{\mathbb{P}}[{\tau_{{\varepsilon}}}=k] {\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{k\pm{\hat{\Delta}_k}}2,\dfrac{k\mp{\hat{\Delta}_k}}2 ;\,\dfrac{n+j}2,\dfrac{n-j}2}\bigg)}}\bigg]} \\ &\qquad\quad\, \times {\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{n+j}2,\dfrac{n-j}2;\,n,n}\bigg)}}\bigg]}.\end{align}
Let c and C denote positive constants, not depending on n, A, ![]() ${\varepsilon}$, or M, but possibly varying from one occurrence to another. Lemma 3.1 applies by (9.36), provided
${\varepsilon}$, or M, but possibly varying from one occurrence to another. Lemma 3.1 applies by (9.36), provided ![]() $n\ge n_1(M)$ for some
$n\ge n_1(M)$ for some ![]() $n_1(M)$ depending on M only, and yields, for every k in the sum in (9.37),
$n_1(M)$ depending on M only, and yields, for every k in the sum in (9.37),
 \begin{align*}\sum_{|\:j|\le Mn{^{1/2}}}& {\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{k+{\hat{\Delta}_k}}2,\dfrac{k-{\hat{\Delta}_k}}2 ;\,\dfrac{n+j}2,\dfrac{n-j}2}\bigg)}}\bigg]}\le {\mathrm{e}}^{-c {\varepsilon}^2 n /2k}\le {\mathrm{e}}^{-c {\varepsilon}^2 n /A}.\end{align*}
\begin{align*}\sum_{|\:j|\le Mn{^{1/2}}}& {\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{k+{\hat{\Delta}_k}}2,\dfrac{k-{\hat{\Delta}_k}}2 ;\,\dfrac{n+j}2,\dfrac{n-j}2}\bigg)}}\bigg]}\le {\mathrm{e}}^{-c {\varepsilon}^2 n /2k}\le {\mathrm{e}}^{-c {\varepsilon}^2 n /A}.\end{align*}
By symmetry the same holds with ![]() ${\hat{\Delta}_k}$ replaced by
${\hat{\Delta}_k}$ replaced by ![]() $-{\hat{\Delta}_k}$. Similarly, Corollary 3.2 yields, provided
$-{\hat{\Delta}_k}$. Similarly, Corollary 3.2 yields, provided ![]() $n\ge n_2(M)$,
$n\ge n_2(M)$,
Hence, (9.37) implies, assuming from now on that ![]() $n\ge n_1(M)\lor n_2(M)$,
$n\ge n_1(M)\lor n_2(M)$,
If ![]() $A\ge 2A_0$, we use Theorem 2.3 similarly to (9.34) and obtain
$A\ge 2A_0$, we use Theorem 2.3 similarly to (9.34) and obtain
Combining (9.38) and (9.39), and recalling (2.2), we then obtain
If ![]() $A_0\le A<2A_0$, we instead use
$A_0\le A<2A_0$, we instead use ![]() $ {\mathbb{P}}{ [{A<{\tau_{{\varepsilon}}}\le 2A}]}\le1$ and obtain from (9.38) similarly
$ {\mathbb{P}}{ [{A<{\tau_{{\varepsilon}}}\le 2A}]}\le1$ and obtain from (9.38) similarly
 \begin{align} {\widehat{{\mathbb{P}}}}{ [{\{{A \lt {\tau_{{\varepsilon}}}\le 2A }\}\land\{{|{\Delta}_n| \le Mn{^{1/2}}}\}}]} &\le C \,{\mathrm{e}}^{-c{\varepsilon}^2 n/A} n{^{-1/2}} n^{\alpha} \\ &\le C \,{\mathrm{e}}^{-c{\varepsilon} n{^{1/2}}} n^{\alpha-1/2} \\ &\le C {\varepsilon}^{-2\alpha-1} A_0/n,\end{align}
\begin{align} {\widehat{{\mathbb{P}}}}{ [{\{{A \lt {\tau_{{\varepsilon}}}\le 2A }\}\land\{{|{\Delta}_n| \le Mn{^{1/2}}}\}}]} &\le C \,{\mathrm{e}}^{-c{\varepsilon}^2 n/A} n{^{-1/2}} n^{\alpha} \\ &\le C \,{\mathrm{e}}^{-c{\varepsilon} n{^{1/2}}} n^{\alpha-1/2} \\ &\le C {\varepsilon}^{-2\alpha-1} A_0/n,\end{align}
yielding the same conclusion as (9.40).
Assume ![]() $0<{\delta}\le {\varepsilon}/32 M$ and sum (9.40) or (9.41) with
$0<{\delta}\le {\varepsilon}/32 M$ and sum (9.40) or (9.41) with ![]() $A=A_j \,:\!=2^jA_0$, for
$A=A_j \,:\!=2^jA_0$, for ![]() $0\le j\le j_0 \,:\!= {\lfloor{\log_2(2{\delta} n/A_0)}\rfloor}$; note that
$0\le j\le j_0 \,:\!= {\lfloor{\log_2(2{\delta} n/A_0)}\rfloor}$; note that ![]() ${\delta} n < A_{j_0}\le 2{\delta} n$, and that (9.36) holds for each
${\delta} n < A_{j_0}\le 2{\delta} n$, and that (9.36) holds for each ![]() $A_j$. This yields, with
$A_j$. This yields, with ![]() $C({\varepsilon})$ denoting constants that may depend on
$C({\varepsilon})$ denoting constants that may depend on ![]() ${\varepsilon}$,
${\varepsilon}$,
 \begin{equation*} {\widehat{{\mathbb{P}}}}{ [{\{{A_0<{\tau_{{\varepsilon}}}\le 2{\delta} n }\}\land\{{|{\Delta}_n|\le Mn{^{1/2}}}\}}]}\le C({\varepsilon})\sum_{j=0}^{j_0} \dfrac{A_{j}}n\le C({\varepsilon}){\delta}\end{equation*}
\begin{equation*} {\widehat{{\mathbb{P}}}}{ [{\{{A_0<{\tau_{{\varepsilon}}}\le 2{\delta} n }\}\land\{{|{\Delta}_n|\le Mn{^{1/2}}}\}}]}\le C({\varepsilon})\sum_{j=0}^{j_0} \dfrac{A_{j}}n\le C({\varepsilon}){\delta}\end{equation*}
and thus, recalling that ![]() ${\tau_{{\varepsilon}}}>A_0$,
${\tau_{{\varepsilon}}}>A_0$,
The right-hand side can be made smaller than ![]() $\eta$, uniformly in n, by choosing M large and
$\eta$, uniformly in n, by choosing M large and ![]() ${\delta}$ small. We assumed above that
${\delta}$ small. We assumed above that ![]() $n\ge n_1(M)\lor n_2(M)$. The result extends trivially to all n as stated in (9.35) by decreasing
$n\ge n_1(M)\lor n_2(M)$. The result extends trivially to all n as stated in (9.35) by decreasing ![]() ${\delta}$.
${\delta}$.
Lemma 9.7. For every ![]() ${\varepsilon}>0$ and
${\varepsilon}>0$ and ![]() $\eta>0$, there exists
$\eta>0$, there exists ![]() ${\delta}>0$ such that
${\delta}>0$ such that
Unlike in Lemma 9.6, we cannot replace ![]() $\limsup_n$ with
$\limsup_n$ with ![]() $\sup_n$, since trivially
$\sup_n$, since trivially
for every n and ![]() ${\delta}$.
${\delta}$.
Proof. Assume ![]() $0<{\delta}\lt 1/2$, let
$0<{\delta}\lt 1/2$, let ![]() $A_0 \,:\!={\lfloor{(1-{\delta})2 n}\rfloor}$ and define (for each n) the stopping time
$A_0 \,:\!={\lfloor{(1-{\delta})2 n}\rfloor}$ and define (for each n) the stopping time
Let ![]() ${\hat{\Delta}_k}$, C, and
${\hat{\Delta}_k}$, C, and ![]() $C({\varepsilon})$ be as in the proof of Lemma 9.6. Then, using Lemma 3.2,
$C({\varepsilon})$ be as in the proof of Lemma 9.6. Then, using Lemma 3.2,
 \begin{align}& {\mathbb{P}}{ [{\{{A_0 \lt {\tau_{{\varepsilon}}} \lt 2n }\}\land \operatorname{BINGO}(n,n)}]} \\ &\qquad=\sum_{k=A_0+1}^{2n-1}{\mathbb{P}}[{\tau_{{\varepsilon}}}=k]{\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{k\pm{\hat{\Delta}_k}}2,\dfrac{k\mp{\hat{\Delta}_k}}2 ;\,n,n}\bigg)}}\bigg]} \\ &\qquad\le\sum_{k=A_0+1}^{2n-1}{\mathbb{P}}[{\tau_{{\varepsilon}}}=k]\dfrac{C}{{\hat{\Delta}_k}}\,{\mathrm{e}}^{-{\varepsilon}^2 n/4(2n-k)} \\ &\qquad\le C({\varepsilon})n{^{-1/2}} \,{\mathrm{e}}^{-{\varepsilon}^2/8{\delta}}{\mathbb{P}}[{\tau_{{\varepsilon}}}>A_0].\end{align}
\begin{align}& {\mathbb{P}}{ [{\{{A_0 \lt {\tau_{{\varepsilon}}} \lt 2n }\}\land \operatorname{BINGO}(n,n)}]} \\ &\qquad=\sum_{k=A_0+1}^{2n-1}{\mathbb{P}}[{\tau_{{\varepsilon}}}=k]{\mathbb{P}}{\bigg[{\operatorname{BINGO}{\bigg({\dfrac{k\pm{\hat{\Delta}_k}}2,\dfrac{k\mp{\hat{\Delta}_k}}2 ;\,n,n}\bigg)}}\bigg]} \\ &\qquad\le\sum_{k=A_0+1}^{2n-1}{\mathbb{P}}[{\tau_{{\varepsilon}}}=k]\dfrac{C}{{\hat{\Delta}_k}}\,{\mathrm{e}}^{-{\varepsilon}^2 n/4(2n-k)} \\ &\qquad\le C({\varepsilon})n{^{-1/2}} \,{\mathrm{e}}^{-{\varepsilon}^2/8{\delta}}{\mathbb{P}}[{\tau_{{\varepsilon}}}>A_0].\end{align}
Furthermore, similarly to (9.34), Theorem 2.3 yields
Combining (9.43) and (9.44) and recalling (2.2), we obtain
Moreover, as ![]() ${{n\to\infty}}$, by Lemma 9.4,
${{n\to\infty}}$, by Lemma 9.4,
Hence, combining (9.45) and (9.46),
 \begin{align*}\limsup_{{n\to\infty}} {\widehat{{\mathbb{P}}}}{\Big[{\sup_{t\ge{1-{\delta}}}|Z_n(t)|\ge{\varepsilon}}\Big]}&= \limsup_{{n\to\infty}}{\widehat{{\mathbb{P}}}}{ [{\{{A_0 \le {\tau_{{\varepsilon}}} \lt 2n }\}}]} \\ &\le C({\varepsilon}) \,{\mathrm{e}}^{-{\varepsilon}^2/8{\delta}} + \Pr{ [{|G_{1-{\delta}}|\ge{\varepsilon}}]}.\end{align*}
\begin{align*}\limsup_{{n\to\infty}} {\widehat{{\mathbb{P}}}}{\Big[{\sup_{t\ge{1-{\delta}}}|Z_n(t)|\ge{\varepsilon}}\Big]}&= \limsup_{{n\to\infty}}{\widehat{{\mathbb{P}}}}{ [{\{{A_0 \le {\tau_{{\varepsilon}}} \lt 2n }\}}]} \\ &\le C({\varepsilon}) \,{\mathrm{e}}^{-{\varepsilon}^2/8{\delta}} + \Pr{ [{|G_{1-{\delta}}|\ge{\varepsilon}}]}.\end{align*}
The right-hand side can be made less than ![]() $\eta$ by choosing
$\eta$ by choosing ![]() ${\delta}$ small, which yields (9.42).
${\delta}$ small, which yields (9.42).
Next, consider the processes only on an interval [a,1), for some fixed ![]() $a\in(0, 1)$.
$a\in(0, 1)$.
Lemma 9.8. Let ![]() $0<a<1$. Then
$0<a<1$. Then ![]() $Z_n(t){\overset{\mathrm{d}}{{\longrightarrow}}} {G_{\alpha}}(t)$ in
$Z_n(t){\overset{\mathrm{d}}{{\longrightarrow}}} {G_{\alpha}}(t)$ in ![]() ${\mathcal{D}}[a,1)$ as
${\mathcal{D}}[a,1)$ as ![]() ${{n\to\infty}}$.
${{n\to\infty}}$.
Proof. The space ![]() ${\mathcal{D}}[a,1)$ of functions, equipped with the Skorokhod topology, is homeomorphic to the space
${\mathcal{D}}[a,1)$ of functions, equipped with the Skorokhod topology, is homeomorphic to the space ![]() ${{\mathcal{D}}[0,\infty)}$ by a change of variable. (Any continuous increasing bijection
${{\mathcal{D}}[0,\infty)}$ by a change of variable. (Any continuous increasing bijection ![]() $[a,1)\to[0,\infty)$ will do; we pick one, for example
$[a,1)\to[0,\infty)$ will do; we pick one, for example ![]() $t\mapsto(t-a)/(1-t)$.) It follows that Lemma 9.2 applies to
$t\mapsto(t-a)/(1-t)$.) It follows that Lemma 9.2 applies to ![]() ${\mathcal{D}}[a,1)$ as well, considering only
${\mathcal{D}}[a,1)$ as well, considering only ![]() $T<1$ in (i), (9.1) and (ii), and
$T<1$ in (i), (9.1) and (ii), and ![]() $t\ge a$ in (ii).
$t\ge a$ in (ii).
The stochastic boundedness on [a,1) is given by Lemma 9.5. The condition (9.6) is satisfied, because trivially each jump in ![]() $Z_n(t)$ is
$Z_n(t)$ is ![]() $n{^{-1/2}}$.
$n{^{-1/2}}$.
It remains to verify (ii) in Lemma 9.2. Let ![]() $\alpha_n({\lambda},{\varepsilon},{\delta},T)$ be the smallest number such that (9.4) holds, i.e. the supremum of the left-hand side over all t, u and
$\alpha_n({\lambda},{\varepsilon},{\delta},T)$ be the smallest number such that (9.4) holds, i.e. the supremum of the left-hand side over all t, u and ![]() $Z_n(t)$ satisfying the conditions.
$Z_n(t)$ satisfying the conditions.
Let ![]() $n_1 \,:\!={\lfloor{2nt}\rfloor}$,
$n_1 \,:\!={\lfloor{2nt}\rfloor}$, ![]() $n_2 \,:\!={\lfloor{2nu}\rfloor}$ and let k be an integer with
$n_2 \,:\!={\lfloor{2nu}\rfloor}$ and let k be an integer with ![]() $|k|\le{\lambda} n{^{1/2}}$. Then
$|k|\le{\lambda} n{^{1/2}}$. Then
 \begin{align} {{\widehat{{\mathbb{P}}}}{ [{|Z_n(u)-Z_n(t)|\le{\varepsilon}\mid Z_n(t)=kn{^{-1/2}}}]}}&= {{\widehat{{\mathbb{P}}}}{ [{{|{{\Delta}({n_2})}-{{\Delta}({n_1})}|\le{\varepsilon} n{^{1/2}}\mid {{\Delta}({n_1})}=k}}]}} \\ &=\sum_{|\:j-k|\le {\varepsilon} n{^{1/2}}} \dfrac{{{\mathbb{P}}[{{\mathcal{A}}_1(\:j)}]}{{\mathbb{P}}[{{\mathcal{A}}_2(\:j)}]}}{{{\mathbb{P}}[{{\mathcal{A}}_0}]}},\end{align}
\begin{align} {{\widehat{{\mathbb{P}}}}{ [{|Z_n(u)-Z_n(t)|\le{\varepsilon}\mid Z_n(t)=kn{^{-1/2}}}]}}&= {{\widehat{{\mathbb{P}}}}{ [{{|{{\Delta}({n_2})}-{{\Delta}({n_1})}|\le{\varepsilon} n{^{1/2}}\mid {{\Delta}({n_1})}=k}}]}} \\ &=\sum_{|\:j-k|\le {\varepsilon} n{^{1/2}}} \dfrac{{{\mathbb{P}}[{{\mathcal{A}}_1(\:j)}]}{{\mathbb{P}}[{{\mathcal{A}}_2(\:j)}]}}{{{\mathbb{P}}[{{\mathcal{A}}_0}]}},\end{align}
where we define the events
 \begin{align*} {\mathcal{A}}_1(\:j) & \,:\!=\operatorname{BINGO}{\bigg({\dfrac{n_1+k}2,\dfrac{n_1-k}2;\,\dfrac{n_2+j}2,\dfrac{n_2-j}2}\bigg)},\\{\mathcal{A}}_2(\:j) & \,:\!=\operatorname{BINGO}{\bigg({\dfrac{n_2+j}2,\dfrac{n_2-j}2;\,n,n}\bigg)},\\{\mathcal{A}}_0 & \,:\!=\operatorname{BINGO}{\bigg({\dfrac{n_1+k}2,\dfrac{n_1-k}2;\,n,n}\bigg)}.\end{align*}
\begin{align*} {\mathcal{A}}_1(\:j) & \,:\!=\operatorname{BINGO}{\bigg({\dfrac{n_1+k}2,\dfrac{n_1-k}2;\,\dfrac{n_2+j}2,\dfrac{n_2-j}2}\bigg)},\\{\mathcal{A}}_2(\:j) & \,:\!=\operatorname{BINGO}{\bigg({\dfrac{n_2+j}2,\dfrac{n_2-j}2;\,n,n}\bigg)},\\{\mathcal{A}}_0 & \,:\!=\operatorname{BINGO}{\bigg({\dfrac{n_1+k}2,\dfrac{n_1-k}2;\,n,n}\bigg)}.\end{align*}
Let ![]() $\phi_t(x)$ and
$\phi_t(x)$ and ![]() ${\kappa}$ be as in (9.23) and (9.24). Further (see (9.25)–(9.26)), let
${\kappa}$ be as in (9.23) and (9.24). Further (see (9.25)–(9.26)), let ![]() $T_1 \,:\!=t^{1-2\alpha}-1$,
$T_1 \,:\!=t^{1-2\alpha}-1$, ![]() $T_2 \,:\!=u^{1-2\alpha}-1$,
$T_2 \,:\!=u^{1-2\alpha}-1$, ![]() $x \,:\!={\kappa} t^{-\alpha} k/\sqrt n$, and
$x \,:\!={\kappa} t^{-\alpha} k/\sqrt n$, and ![]() $y \,:\!={\kappa} u^{-\alpha} j/\sqrt n$. By calculations as in the proof of Lemma 9.4 (see (9.27)), we obtain
$y \,:\!={\kappa} u^{-\alpha} j/\sqrt n$. By calculations as in the proof of Lemma 9.4 (see (9.27)), we obtain
 \begin{align} \dfrac{{{\mathbb{P}}[{{\mathcal{A}}_1(\:j)}]}{{\mathbb{P}}[{{\mathcal{A}}_2(\:j)}]}}{{{\mathbb{P}}[{{\mathcal{A}}_0}]}}&\sim \dfrac{2{\kappa}}{u^\alpha\sqrt n}\dfrac{\phi_{T_1-T_2}(x-y)\phi_{T_2}(\kern1pty)}{\phi_{T_1}(x)} \\ &=\dfrac{2{\kappa}}{u^\alpha\sqrt n}\phi_{{(T_1-T_2)T_2}/{T_1}}{\bigg({y-\dfrac{T_2}{T_1}x}\bigg)},\end{align}
\begin{align} \dfrac{{{\mathbb{P}}[{{\mathcal{A}}_1(\:j)}]}{{\mathbb{P}}[{{\mathcal{A}}_2(\:j)}]}}{{{\mathbb{P}}[{{\mathcal{A}}_0}]}}&\sim \dfrac{2{\kappa}}{u^\alpha\sqrt n}\dfrac{\phi_{T_1-T_2}(x-y)\phi_{T_2}(\kern1pty)}{\phi_{T_1}(x)} \\ &=\dfrac{2{\kappa}}{u^\alpha\sqrt n}\phi_{{(T_1-T_2)T_2}/{T_1}}{\bigg({y-\dfrac{T_2}{T_1}x}\bigg)},\end{align}
uniformly in all t, u, k, j, satisfying the conditions above (see Remark 9.1). Using (9.47) and summing (9.48) over all j with ![]() $|\:j-k|\le {\varepsilon} n{^{1/2}}$ and
$|\:j-k|\le {\varepsilon} n{^{1/2}}$ and ![]() $j\equiv n_2\pmod 2$, y takes values with step
$j\equiv n_2\pmod 2$, y takes values with step ![]() $2{\kappa} u^{-\alpha}/\sqrt n$, we obtain, with
$2{\kappa} u^{-\alpha}/\sqrt n$, we obtain, with ![]() $Z\sim N(0, 1)$ a standard normal variable,
$Z\sim N(0, 1)$ a standard normal variable,
 \begin{align*} & {{\widehat{{\mathbb{P}}}}{ [{{|Z_n(u)-Z_n(t)|\le{\varepsilon}\mid Z_n(t)=kn{^{-1/2}}}}]}} \\ &\qquad\sim \int_{|u^\alpha y -t^{\alpha} x|\le{\kappa} {\varepsilon}}\phi_{{(T_1-T_2)T_2}/{T_1}}{\bigg({y-\dfrac{T_2}{T_1}x}\bigg)}{\,\mathrm{d}} y \\ &\qquad={{\mathbb{P}}{\bigg[{{ {\bigg|{{\bigg({\dfrac{(T_1-T_2)T_2}{T_1}}\bigg)}^{1/2} Z +\dfrac{T_2}{T_1}x -\dfrac{t^\alpha}{u^\alpha}x}\bigg|}\le {\kappa}{\varepsilon} u^{-\alpha}}}\bigg]}},\end{align*}
\begin{align*} & {{\widehat{{\mathbb{P}}}}{ [{{|Z_n(u)-Z_n(t)|\le{\varepsilon}\mid Z_n(t)=kn{^{-1/2}}}}]}} \\ &\qquad\sim \int_{|u^\alpha y -t^{\alpha} x|\le{\kappa} {\varepsilon}}\phi_{{(T_1-T_2)T_2}/{T_1}}{\bigg({y-\dfrac{T_2}{T_1}x}\bigg)}{\,\mathrm{d}} y \\ &\qquad={{\mathbb{P}}{\bigg[{{ {\bigg|{{\bigg({\dfrac{(T_1-T_2)T_2}{T_1}}\bigg)}^{1/2} Z +\dfrac{T_2}{T_1}x -\dfrac{t^\alpha}{u^\alpha}x}\bigg|}\le {\kappa}{\varepsilon} u^{-\alpha}}}\bigg]}},\end{align*}
uniformly in t and u satisfying the conditions. Hence, taking complements and recalling the definition of ![]() $\alpha_n$,
$\alpha_n$,
taking the supremum over t, u, x with ![]() $a\le t\le u\le T$,
$a\le t\le u\le T$, ![]() $t+{\delta}\le u\le t+2{\delta}$ and
$t+{\delta}\le u\le t+2{\delta}$ and ![]() $|x|\le {\kappa} t^{-\alpha}{\lambda}\le{\kappa} a^{-\alpha}{\lambda}$. For fixed
$|x|\le {\kappa} t^{-\alpha}{\lambda}\le{\kappa} a^{-\alpha}{\lambda}$. For fixed ![]() ${\varepsilon},{\lambda}>0$ and
${\varepsilon},{\lambda}>0$ and ![]() $T<1$, if
$T<1$, if ![]() ${\delta}\to0$, then
${\delta}\to0$, then ![]() $t/u\to 1$,
$t/u\to 1$, ![]() $T_2/T_1\to1$ and
$T_2/T_1\to1$ and ![]() $T_1-T_2\to 0$, uniformly for all t and u satisfying these conditions. It follows from (9.49) that
$T_1-T_2\to 0$, uniformly for all t and u satisfying these conditions. It follows from (9.49) that
which verifies (ii) in Lemma 9.2.
We have verified the conditions in Lemma 9.2, and the lemma thus shows that the sequence ![]() $Z_n(t)$ is tight in
$Z_n(t)$ is tight in ![]() ${\mathcal{D}}[a,1)$. Combined with the finite-dimensional convergence in Lemma 9.4, this shows convergence to
${\mathcal{D}}[a,1)$. Combined with the finite-dimensional convergence in Lemma 9.4, this shows convergence to ![]() $G_\alpha(t)$ in
$G_\alpha(t)$ in ![]() ${\mathcal{D}}[a,1)$.
${\mathcal{D}}[a,1)$.
Proof of Theorem 1.2. Lemma 9.8 shows ![]() $Z_n(t){\overset{\mathrm{d}}{{\longrightarrow}}} {G_{\alpha}}(t)$ in
$Z_n(t){\overset{\mathrm{d}}{{\longrightarrow}}} {G_{\alpha}}(t)$ in ![]() ${\mathcal{D}}[a,1)$ for every
${\mathcal{D}}[a,1)$ for every ![]() $a\in(0, 1)$. This can equivalently be expressed as convergence in
$a\in(0, 1)$. This can equivalently be expressed as convergence in ![]() ${\mathcal{D}}(0, 1)$, considering the open interval (0, 1), and this can be improved to convergence in D[0, 1] using Lemmas 9.6 and 9.7 (see e.g. [Reference Janson15, Proposition 2.4]).
${\mathcal{D}}(0, 1)$, considering the open interval (0, 1), and this can be improved to convergence in D[0, 1] using Lemmas 9.6 and 9.7 (see e.g. [Reference Janson15, Proposition 2.4]).
A direct proof can be made as follows. Let ![]() ${\varepsilon},\eta>0$ be given. Find
${\varepsilon},\eta>0$ be given. Find ![]() ${\delta}>0$ such that (9.35) and (9.42) hold, and furthermore
${\delta}>0$ such that (9.35) and (9.42) hold, and furthermore
By Lemma 9.8 with ![]() $a={\delta}$,
$a={\delta}$, ![]() $Z_n(t){\overset{\mathrm{d}}{{\longrightarrow}}} {G_{\alpha}}(t)$ in
$Z_n(t){\overset{\mathrm{d}}{{\longrightarrow}}} {G_{\alpha}}(t)$ in ![]() ${\mathcal{D}}[{\delta},1)$, and thus in
${\mathcal{D}}[{\delta},1)$, and thus in ![]() ${\mathcal{D}}[{\delta},1-{\delta}]$. By the Skorokhod coupling theorem [Reference Kallenberg17, Theorem 4.30], we may assume that
${\mathcal{D}}[{\delta},1-{\delta}]$. By the Skorokhod coupling theorem [Reference Kallenberg17, Theorem 4.30], we may assume that ![]() $Z_n(t)\to {G_{\alpha}}(t)$ uniformly on
$Z_n(t)\to {G_{\alpha}}(t)$ uniformly on ![]() $[{\delta},1-{\delta}]$. Then, now writing
$[{\delta},1-{\delta}]$. Then, now writing ![]() $\Pr$ instead of
$\Pr$ instead of ![]() ${\widehat{{\mathbb{P}}}}$,
${\widehat{{\mathbb{P}}}}$,
 \begin{align*}&\limsup_{{n\to\infty}} {{\mathbb{P}}{\Big[{{\sup_{0\le t\le 1}|Z_n(t)-{G_{\alpha}}(t)|>2{\varepsilon}}}\Big]}} \\ &\qquad\le 4\eta + \limsup_{{n\to\infty}} {{\mathbb{P}}{\Big[{{\sup_{{\delta}\le t\le 1-{\delta}}|Z_n(t)-{G_{\alpha}}(t)|>2{\varepsilon}}}\Big]}} \\ &\qquad= 4 \eta.\end{align*}
\begin{align*}&\limsup_{{n\to\infty}} {{\mathbb{P}}{\Big[{{\sup_{0\le t\le 1}|Z_n(t)-{G_{\alpha}}(t)|>2{\varepsilon}}}\Big]}} \\ &\qquad\le 4\eta + \limsup_{{n\to\infty}} {{\mathbb{P}}{\Big[{{\sup_{{\delta}\le t\le 1-{\delta}}|Z_n(t)-{G_{\alpha}}(t)|>2{\varepsilon}}}\Big]}} \\ &\qquad= 4 \eta.\end{align*}
Since ![]() $\eta$ and
$\eta$ and ![]() ${\varepsilon}$ are arbitrary, this shows
${\varepsilon}$ are arbitrary, this shows ![]() $Z_n(t)\to{G_{\alpha}}(t)$ in
$Z_n(t)\to{G_{\alpha}}(t)$ in ![]() ${\mathcal{D}}{[0, 1]}$ in probability, and thus in distribution.
${\mathcal{D}}{[0, 1]}$ in probability, and thus in distribution.
9.3. The initial part of the process
Proof of Theorem 1.3. The proof is very similar to the proof of Theorem 1.2, and we only point out the differences. For convenience, we change the notation by replacing n with N and ![]() $m_n$ with 2n. Note that the normalization is then by
$m_n$ with 2n. Note that the normalization is then by ![]() $(2n){^{-1/2}}$, differing by a factor
$(2n){^{-1/2}}$, differing by a factor ![]() $2{^{-1/2}}$ from the one in Theorem 1.2.
$2{^{-1/2}}$ from the one in Theorem 1.2.
Finite-dimensional convergence is proved as in Lemma 9.4. The main difference is that the probability of the last event ![]() ${\mathcal{A}}_{m+1}$ is estimated using Corollary 3.1 instead of Corollary 3.2, and that we define
${\mathcal{A}}_{m+1}$ is estimated using Corollary 3.1 instead of Corollary 3.2, and that we define ![]() $T_i \,:\!=t_i^{1-2\alpha}$, where now
$T_i \,:\!=t_i^{1-2\alpha}$, where now ![]() $t_i\in(0,\infty)$. Then the same calculations as before show that (9.29) holds, which yields finite-dimensional convergence in (1.9).
$t_i\in(0,\infty)$. Then the same calculations as before show that (9.29) holds, which yields finite-dimensional convergence in (1.9).
Stochastic boundedness on any interval [a, b] with ![]() $0<a<b<\infty$ follows as in Lemma 9.5, again using Corollary 3.1.
$0<a<b<\infty$ follows as in Lemma 9.5, again using Corollary 3.1.
The convergence (1.9) in the space ![]() ${\mathcal{D}}[a,\infty)$ for any
${\mathcal{D}}[a,\infty)$ for any ![]() $a>0$ now follows as in Lemma 9.8, again using Lemma 9.2. This is equivalent to convergence in
$a>0$ now follows as in Lemma 9.8, again using Lemma 9.2. This is equivalent to convergence in ![]() ${\mathcal{D}}(0,\infty)$.
${\mathcal{D}}(0,\infty)$.
Finally, the analog of Lemma 9.6 holds, by the same proof with trivial modifications, which yields convergence also in ![]() ${\mathcal{D}}{[0,\infty)}$.
${\mathcal{D}}{[0,\infty)}$.
Proof of Theorem 1.4. Apply Theorem 1.3 with ![]() $m_n \,:\!={\mathrm{e}}^{t_n}$. Then (1.9) holds in
$m_n \,:\!={\mathrm{e}}^{t_n}$. Then (1.9) holds in ![]() ${{\mathcal{D}}[0,\infty)}$, and thus in
${{\mathcal{D}}[0,\infty)}$, and thus in ![]() ${\mathcal{D}}(0,\infty)$. The change of variables
${\mathcal{D}}(0,\infty)$. The change of variables ![]() $t={\mathrm{e}}^s$ yields
$t={\mathrm{e}}^s$ yields
in ![]() ${\mathcal{D}}(-\infty,\infty)$. Multiplying (9.50) by the continuous function
${\mathcal{D}}(-\infty,\infty)$. Multiplying (9.50) by the continuous function ![]() ${\mathrm{e}}^{-s/2}$ yields
${\mathrm{e}}^{-s/2}$ yields
in ![]() ${\mathcal{D}}(-\infty,\infty)$, which is (1.10). The covariance (1.11) follows from the definition of Z(s) in (9.51).
${\mathcal{D}}(-\infty,\infty)$, which is (1.10). The covariance (1.11) follows from the definition of Z(s) in (9.51).
Acknowledgement
SJ was partly supported by the Knut and Alice Wallenberg Foundation.
Appendix A. Quadratic functionals of Gaussian variables
A Gaussian Hilbert space is a closed subspace H of ![]() $L^2{({\Omega},{\mathcal F},P)}$, for some probability space
$L^2{({\Omega},{\mathcal F},P)}$, for some probability space ![]() ${({\Omega},{\mathcal F},P)}$, such that every element f of H is a random variable with a centered Gaussian distribution
${({\Omega},{\mathcal F},P)}$, such that every element f of H is a random variable with a centered Gaussian distribution ![]() $N(0,{\sigma^2})$ (where
$N(0,{\sigma^2})$ (where ![]() ${\sigma^2}=\|\:{f}\|_2^2$). (In this appendix, we consider real vector spaces and real-valued functions; thus
${\sigma^2}=\|\:{f}\|_2^2$). (In this appendix, we consider real vector spaces and real-valued functions; thus ![]() $L^2=L^2_{\mathbb R}$ is the space of real-valued square-integrable functions.) Here, for the readers’ and our own convenience, we review some basic and more or less well-known facts; further details can be found in [16], for example. In our application above, H is the closed linear span of
$L^2=L^2_{\mathbb R}$ is the space of real-valued square-integrable functions.) Here, for the readers’ and our own convenience, we review some basic and more or less well-known facts; further details can be found in [16], for example. In our application above, H is the closed linear span of ![]() $\{{B_t\colon 0\le t\le n}\}$, as usual defined on some anonymous probability space
$\{{B_t\colon 0\le t\le n}\}$, as usual defined on some anonymous probability space ![]() ${({\Omega},{\mathcal F},P)}$, but we state the results generally.
${({\Omega},{\mathcal F},P)}$, but we state the results generally.
If ![]() $\xi,\eta\in H$, define their Wick product by
$\xi,\eta\in H$, define their Wick product by ![]() ${:\,\xi\eta\,:} \,:\!=\xi\eta-{\mathbb E}(\xi\eta)$, i.e. the centered product. Let
${:\,\xi\eta\,:} \,:\!=\xi\eta-{\mathbb E}(\xi\eta)$, i.e. the centered product. Let ![]() ${H^{:2:}}$ be the closed linear span of all Wick products
${H^{:2:}}$ be the closed linear span of all Wick products ![]() ${:\,\xi\eta\,:}$,
${:\,\xi\eta\,:}$, ![]() $\xi,\eta\in H$. Hence, if
$\xi,\eta\in H$. Hence, if ![]() $X=Q(\xi_1,\ldots,\xi_N)$ is a quadratic form in Gaussian random variables
$X=Q(\xi_1,\ldots,\xi_N)$ is a quadratic form in Gaussian random variables ![]() $\xi_1,\ldots,\xi_N\in H$, then
$\xi_1,\ldots,\xi_N\in H$, then ![]() $X-{\mathbb E} X\in {H^{:2:}}$, and conversely, every element of
$X-{\mathbb E} X\in {H^{:2:}}$, and conversely, every element of ![]() ${H^{:2:}}$ is a limit of such centered quadratic forms, and can be written as a quadratic form in (in general) infinitely many variables. Moreover, this form can be diagonalized by a suitable choice of orthonormal basis in H, leading to the following representation theorem. (Note that every
${H^{:2:}}$ is a limit of such centered quadratic forms, and can be written as a quadratic form in (in general) infinitely many variables. Moreover, this form can be diagonalized by a suitable choice of orthonormal basis in H, leading to the following representation theorem. (Note that every ![]() $X\in{H^{:2:}}$ has
$X\in{H^{:2:}}$ has ![]() ${\mathbb E} X=0$ as a consequence of the definition.)
${\mathbb E} X=0$ as a consequence of the definition.)
Theorem A.1. ([16, Theorem 6.1].) If ![]() $X\in{H^{:2:}}$, then there exists a finite or infinite sequence
$X\in{H^{:2:}}$, then there exists a finite or infinite sequence ![]() $ ({\lambda}_j)_{j=1}^N $,
$ ({\lambda}_j)_{j=1}^N $, ![]() $0\le N\le \infty$, of non-zero real numbers such that
$0\le N\le \infty$, of non-zero real numbers such that ![]() $\sum_j{\lambda}_j^2<\infty$ and
$\sum_j{\lambda}_j^2<\infty$ and
 \begin{equation} X{\overset{\mathrm{d}}{=}} \sum_{j=1}^N {\lambda}_j{ ({\xi_j^2-1})},\end{equation}
\begin{equation} X{\overset{\mathrm{d}}{=}} \sum_{j=1}^N {\lambda}_j{ ({\xi_j^2-1})},\end{equation}
where ![]() $\xi_j$ are independent, identically distributed (i.i.d.) N(0, 1) random variables. The numbers
$\xi_j$ are independent, identically distributed (i.i.d.) N(0, 1) random variables. The numbers ![]() ${\lambda}_j$ are the non-zero eigenvalues (counted with multiplicities) of the compact symmetric bilinear form
${\lambda}_j$ are the non-zero eigenvalues (counted with multiplicities) of the compact symmetric bilinear form
or, equivalently, of the corresponding compact symmetric operator ![]() ${T}_X$ on H defined by
${T}_X$ on H defined by
In particular, (A.1) yields the moment generating function, for all real t such that ![]() $2{\lambda}_j t<1$ for every j,
$2{\lambda}_j t<1$ for every j,
In our application, we deal with non-centered quadratic functionals, and then the following version is more directly applicable. (See the more general but less specific [16, Theorem 6.2]. We do not know a reference for the precise statements in Theorem A.2, so we give a complete proof.)
Theorem A.2. Suppose the following.
(i) X is a random variable such that
 $X-{\mathbb E} X\in{H^{:2:}}$.
$X-{\mathbb E} X\in{H^{:2:}}$.(ii)
 $X\ge 0$ a.s., and
$X\ge 0$ a.s., and  ${\mathbb{P}}(X<{\varepsilon})>0$ for every
${\mathbb{P}}(X<{\varepsilon})>0$ for every  ${\varepsilon}>0$, that is, the lower bound of the support of X is 0.
${\varepsilon}>0$, that is, the lower bound of the support of X is 0.(iii) The bilinear form
 ${Q}={Q}_{X-{\mathbb E} X}$ is positive, that is,
for every
${Q}={Q}_{X-{\mathbb E} X}$ is positive, that is,
for every \begin{equation*}{Q}_{X-{\mathbb E} X}(\xi,\xi)= \dfrac12{\mathbb E} { ({(X-{\mathbb E} X)\xi^2})}\ge0\end{equation*}
\begin{equation*}{Q}_{X-{\mathbb E} X}(\xi,\xi)= \dfrac12{\mathbb E} { ({(X-{\mathbb E} X)\xi^2})}\ge0\end{equation*}
 $\xi\in H$.
$\xi\in H$.
Then
 \begin{equation} X{\overset{\mathrm{d}}{=}} \sum_{j=1}^N {\lambda}_j\xi_j^2,\end{equation}
\begin{equation} X{\overset{\mathrm{d}}{=}} \sum_{j=1}^N {\lambda}_j\xi_j^2,\end{equation}
where ![]() $\xi_j$ are i.i.d. N(0, 1) random variables and the coefficients
$\xi_j$ are i.i.d. N(0, 1) random variables and the coefficients ![]() ${\lambda}_j>0$ are the non-zero eigenvalues (counted with multiplicities) of Q. Furthermore,
${\lambda}_j>0$ are the non-zero eigenvalues (counted with multiplicities) of Q. Furthermore,
 \begin{equation} {\mathbb E} X= \sum_{j=1}^N {\lambda}_j \lt \infty\end{equation}
\begin{equation} {\mathbb E} X= \sum_{j=1}^N {\lambda}_j \lt \infty\end{equation}
and, for ![]() $-\infty<t<(2 \max_j{\lambda}_j){^{-1}}$,
$-\infty<t<(2 \max_j{\lambda}_j){^{-1}}$,
Proof. Theorem A.1 yields the representation
where ![]() ${\lambda}_j>0$ since the positive form Q has only non-negative eigenvalues. Hence, (A.2) applies for any
${\lambda}_j>0$ since the positive form Q has only non-negative eigenvalues. Hence, (A.2) applies for any ![]() $t<0$, and thus, replacing t with
$t<0$, and thus, replacing t with ![]() $-t$, for every
$-t$, for every ![]() $t>0$,
$t>0$,
 \begin{equation} \dfrac1t\ln{\mathbb E} \,{\mathrm{e}}^{-t(X-{\mathbb E} X)}=\sum_j \dfrac{t{\lambda}_j-\frac12\ln(1+2{\lambda}_j t)}{t}.\end{equation}
\begin{equation} \dfrac1t\ln{\mathbb E} \,{\mathrm{e}}^{-t(X-{\mathbb E} X)}=\sum_j \dfrac{t{\lambda}_j-\frac12\ln(1+2{\lambda}_j t)}{t}.\end{equation}
Now let ![]() $t\to\infty$. By (ii),
$t\to\infty$. By (ii), ![]() ${\mathbb E} \,{\mathrm{e}}^{-tX}\le1$, but
${\mathbb E} \,{\mathrm{e}}^{-tX}\le1$, but
and thus
In the sum on the right-hand side of (A.7), each term is positive, and increases to ![]() ${\lambda}_j$ as
${\lambda}_j$ as ![]() ${{t\to\infty}}$ (because
${{t\to\infty}}$ (because ![]() $\ln$ is concave); hence the sum tends to
$\ln$ is concave); hence the sum tends to ![]() $\sum_j{\lambda}_j$ by monotone convergence. Consequently,
$\sum_j{\lambda}_j$ by monotone convergence. Consequently, ![]() ${\mathbb E} X=\sum_j{\lambda}_j$, and since
${\mathbb E} X=\sum_j{\lambda}_j$, and since ![]() ${\mathbb E} X<\infty$, (A.4) holds.
${\mathbb E} X<\infty$, (A.4) holds.
The representation (A.3) follows from (A.6) and (A.4), and (A.5) is an immediate consequence.
Remark A.1. The operator T in Theorem A.1 is a Hilbert–Schmidt operator, since ![]() $\sum_j{\lambda}_j^2<\infty$. Similarly, in Theorem A.2, T is a trace class operator, with trace and trace norm
$\sum_j{\lambda}_j^2<\infty$. Similarly, in Theorem A.2, T is a trace class operator, with trace and trace norm ![]() $\sum_j{\lambda}_j={\mathbb E} X$.
$\sum_j{\lambda}_j={\mathbb E} X$.
If ![]() $Y\in H$, then
$Y\in H$, then ![]() $X \,:\!=Y^2$ satisfies (i) and (ii) in Theorem A.2. Furthermore, for
$X \,:\!=Y^2$ satisfies (i) and (ii) in Theorem A.2. Furthermore, for ![]() $\xi,\eta\in H$, since
$\xi,\eta\in H$, since ![]() $X-{\mathbb E} X= Y^2-{\mathbb E} Y^2={:\,Y^2\,:}$, by [16, Theorem 3.9],
$X-{\mathbb E} X= Y^2-{\mathbb E} Y^2={:\,Y^2\,:}$, by [16, Theorem 3.9],
Taking ![]() $\eta=\xi$, we see that Q is a positive form. Hence the conditions (i)–(iii) hold for
$\eta=\xi$, we see that Q is a positive form. Hence the conditions (i)–(iii) hold for ![]() $X=Y^2$, and it follows that they also hold for any finite sum of squares
$X=Y^2$, and it follows that they also hold for any finite sum of squares ![]() $\sum_i Y_i^2$ with
$\sum_i Y_i^2$ with ![]() $Y_i\in H$, for example
$Y_i\in H$, for example ![]() ${\widetilde L}_n$ in (7.1). Moreover, we can take limits, and conclude that the conditions also hold for the integral
${\widetilde L}_n$ in (7.1). Moreover, we can take limits, and conclude that the conditions also hold for the integral ![]() ${\widehat L}_n$ in (7.2), for example. (Note that (ii) is obvious for
${\widehat L}_n$ in (7.2), for example. (Note that (ii) is obvious for ![]() ${\widehat L}_n$.) Hence, Theorem A.2 applies to
${\widehat L}_n$.) Hence, Theorem A.2 applies to ![]() ${\widehat L}_n$.
${\widehat L}_n$.
A.1. Stochastic integration
In order to find the eigenvalues ![]() ${\lambda}_i$ in Theorem A.2 in our application to
${\lambda}_i$ in Theorem A.2 in our application to ![]() ${\widehat L}_n$, it is convenient to transfer from the Gaussian Hilbert space H to the function space
${\widehat L}_n$, it is convenient to transfer from the Gaussian Hilbert space H to the function space ![]() $L^2{(0,n)}$ by means of stochastic integrals.
$L^2{(0,n)}$ by means of stochastic integrals.
The stochastic integral ![]() ${\int_0^n} f(t){\,\mathrm{d}} B_t$ can be defined for every (deterministic) function
${\int_0^n} f(t){\,\mathrm{d}} B_t$ can be defined for every (deterministic) function ![]() $f\in L^2{(0,n)}$ as follows. (This is a simple form of stochastic integrals; we have no need for the general theory of random integrands here.)
$f\in L^2{(0,n)}$ as follows. (This is a simple form of stochastic integrals; we have no need for the general theory of random integrands here.)
First, ![]() ${\int_0^n} {\boldsymbol1}_{(0,a)}(t){\,\mathrm{d}} B_t=B_a$ for every
${\int_0^n} {\boldsymbol1}_{(0,a)}(t){\,\mathrm{d}} B_t=B_a$ for every ![]() $a\in[0,n]$. This and linearity define
$a\in[0,n]$. This and linearity define ![]() ${\int_0^n} f(t){\,\mathrm{d}} B_t$ for every step function f (in the obvious, naive way). A simple calculation shows that
${\int_0^n} f(t){\,\mathrm{d}} B_t$ for every step function f (in the obvious, naive way). A simple calculation shows that
Hence, the mapping ![]() $I\colon f\mapsto \int f{\,\mathrm{d}} B_t$ is an isometry from the subspace of step functions in
$I\colon f\mapsto \int f{\,\mathrm{d}} B_t$ is an isometry from the subspace of step functions in ![]() $L^2{(0,n)}$ to the linear span of the random variables
$L^2{(0,n)}$ to the linear span of the random variables ![]() $B_t$,
$B_t$, ![]() $t\in{[0,n]}$. We let H be the closure of the latter space, regarded as a subspace of
$t\in{[0,n]}$. We let H be the closure of the latter space, regarded as a subspace of ![]() $L^2{({\Omega},{\mathcal F},P)}$; then I extends by continuity to an isometry
$L^2{({\Omega},{\mathcal F},P)}$; then I extends by continuity to an isometry ![]() $I\colon L^2{(0,n)}\to H$. We may write
$I\colon L^2{(0,n)}\to H$. We may write ![]() $I(\kern1.7ptf)={\int_0^n} f(t){\,\mathrm{d}} B_t$. This isometry enables us to regard the bilinear form Q and operator T as defined on
$I(\kern1.7ptf)={\int_0^n} f(t){\,\mathrm{d}} B_t$. This isometry enables us to regard the bilinear form Q and operator T as defined on ![]() $L^2{(0,n)}$.
$L^2{(0,n)}$.
If ![]() $Y=I(\kern1.7ptf)$,
$Y=I(\kern1.7ptf)$, ![]() $\xi=I(g)$ and
$\xi=I(g)$ and ![]() $\eta=I(h)$, for some
$\eta=I(h)$, for some ![]() $f,g,h\in L^2{(0,n)}$, and
$f,g,h\in L^2{(0,n)}$, and ![]() $X=Y^2$, then (A.8) yields
$X=Y^2$, then (A.8) yields
which shows that T, regarded as an operator on ![]() $L^2{(0,n)}$, is the integral operator with kernel
$L^2{(0,n)}$, is the integral operator with kernel ![]() $f(x)f(\kern1pty)$.
$f(x)f(\kern1pty)$.
Example A.1. For any ![]() $t\in{[0,n]}$,
$t\in{[0,n]}$, ![]() $B_t=I({\boldsymbol1}_{(0,t)})$, and thus
$B_t=I({\boldsymbol1}_{(0,t)})$, and thus ![]() $X=B_t^2$ corresponds to the integral operator T with kernel
$X=B_t^2$ corresponds to the integral operator T with kernel ![]() ${\boldsymbol1}_{(0,t)}(x){\boldsymbol1}_{(0,t)}(\kern1pty)$. It follows easily that
${\boldsymbol1}_{(0,t)}(x){\boldsymbol1}_{(0,t)}(\kern1pty)$. It follows easily that ![]() ${\widehat L}_n=\int_1^n { ({B_t^2/t^2})} {\,\mathrm{d}} t$ corresponds to the integral operator with kernel
${\widehat L}_n=\int_1^n { ({B_t^2/t^2})} {\,\mathrm{d}} t$ corresponds to the integral operator with kernel
We summarize as follows.
Lemma A.1. Theorem A.2 applies to ![]() $X={\widehat L}_n$, with
$X={\widehat L}_n$, with ![]() ${\lambda}_j$ the non-zero eigenvalues of the symmetric integral operator on
${\lambda}_j$ the non-zero eigenvalues of the symmetric integral operator on ![]() $L^2{(0,n)}$ with kernel
$L^2{(0,n)}$ with kernel ![]() $K_n$ given by (A.9).
$K_n$ given by (A.9).