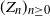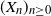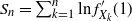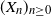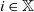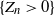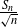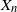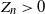1. Introduction and main results
One of the most used models in the dynamic of populations is the Galton–Watson branching process, which has numerous applications in different areas, including physics, biology, medicine, and economics. We refer the reader to the books of Harris [Reference Harris17] and Athreya and Ney [Reference Athreya and Ney6] for an introduction. Branching processes in random environments were first considered by Smith and Wilkinson [Reference Smith and Wilkinson24] and by Athreya and Karlin [Reference Athreya and Karlin4, Reference Athreya and Karlin5]. The subject has been further studied by Kozlov [Reference Kozlov20, Reference Kozlov21], Dekking [Reference Dekking7], Liu [Reference Liu22], D’Souza and Hambly [Reference D’Souza and Hambly8], Geiger and Kersting [Reference Geiger and Kersting9], Guivarc’h and Liu [Reference Guivarc’h and Liu16], Geiger, Kersting and Vatutin [Reference Geiger, Kersting and Vatutin10], Afanasyev [Reference Afanasyev1], and Kersting and Vatutin [Reference Kersting and Vatutin19], to name only a few. Recently, in [Reference Grama, Lauvergnat and Le Page13], based on new conditioned limit theorems for sums of functions defined on Markov chains in [Reference Grama, Lauvergnat and Le Page11, Reference Grama, Lauvergnat and Le Page12, Reference Grama, Lauvergnat and Le Page14, Reference Grama, Le Page and Peigné15], exact asymptotic results for the survival probability when the environment is a Markov chain have been obtained for branching processes in Markovian environment (BPMEs). In this paper we complement these by new results, such as a limit theorem for the normalized number of particles and a Yaglom-type theorem for BPMEs.
We start by introducing the Markovian environment, which is given on the probability space
$\left( \Omega, \mathscr{F}, \mathbb{P} \right)$
by a homogeneous Markov chain
$\left( X_n \right)_{n\geq 0}$
with values in the finite state space
$\mathbb{X}$
and with the matrix of transition probabilities
$\textbf{P} = (\textbf{P} (i,j))_{i,j\in \mathbb{X}}$
. We suppose the following.
Condition 1. The Markov chain
$\left( X_n \right)_{n\geq 0}$
is irreducible and aperiodic.
Condition 1 implies a spectral gap property for the transition operator
$\textbf{P}$
of
$\left( X_n \right)_{n\geq 0}$
, defined by the relation
$\textbf{P} g (i) = \sum_{j\in \mathbb{X}} g(\,j) \textbf{P}(i,j)$
for any g in the space
$\mathscr{C} (\mathbb X)$
of complex functions g on
$\mathbb{X}$
endowed with the norm
$\left\lVert{g}\right\rVert_{\infty} = \sup_{x\in \mathbb{X}} \left\lvert{g(x)}\right\rvert$
. Indeed, Condition 1 is necessary and sufficient for the matrix
$(\textbf{P} (i,j))_{i,j\in \mathbb X}$
to be primitive (all entries of
$\textbf{P}^{k_0}$
are positive for some
$k_0 \geq 1$
). By the Perron–Frobenius theorem, there exist positive constants
$c_1$
,
$c_2$
, a unique positive
$\textbf{P}$
-invariant probability
$\boldsymbol{\nu}$
on
$\mathbb{X}$
(
$\boldsymbol{\nu}(\textbf{P})=\boldsymbol{\nu}$
), and an operator Q on
$\mathscr{C}(\mathbb X)$
such that, for any
$g \in \mathscr{C}(\mathbb X)$
and
$n \geq 1$
,
$i \in \mathbb{X}$
,
\begin{align} \textbf{P}g(i) = \boldsymbol{\nu}(g) + Q(g)(i) \quad \text{and} \quad \left\lVert{Q^n(g)}\right\rVert_{\infty} \leq c_1 e^{-c_2n} \left\lVert{g}\right\rVert_{\infty},\end{align}
where
$Q \left(1 \right) = 0$
and
$\boldsymbol{\nu} \left(Q(g) \right) = 0$
with
$\boldsymbol{\nu}(g) \,{:\!=}\, \sum_{i \in \mathbb{X}} g(i) \boldsymbol{\nu}(i)$
. In particular, from (1.1), it follows that, for any
$(i,j) \in \mathbb{X}^2$
,
\begin{equation} {}\left\lvert{\textbf{P}^n(i,j) - \boldsymbol{\nu}(\,j)}\right\rvert \leq c_1e^{-c_2 n}.\end{equation}
Set
$\mathbb N \,{:\!=}\, \left\{0,1,2,\ldots\right\}$
. For any
$i\in \mathbb X$
, let
$\mathbb{P}_i$
be the probability law on
$ \mathbb X^{\mathbb N} $
and
$\mathbb{E}_i$
the associated expectation generated by the finite-dimensional distributions of the Markov chain
$\left( X_n \right)_{n\geq 0}$
starting at
$X_0 = i$
. Note that
$\textbf{P}^ng(i) = \mathbb{E}_i \left( g(X_n) \right)$
, for any
$g \in \mathscr{C}(\mathbb X)$
,
$i \in \mathbb{X}$
, and
$n\geq 1.$
Assume that on the same probability space
$\left( \Omega, \mathscr{F}, \mathbb{P} \right)$
, for any
$i \in \mathbb{X}$
, we are given a random variable
$\xi_i$
with the probability generating function
\begin{equation} {} {}f_i(s) \,{:\!=}\, \mathbb{E} \left( s^{\xi_i} \right), \quad s \in [0,1].\end{equation}
Consider a collection of independent and identically distributed random variables
$( \xi_i^{n,j} )_{j,n \geq 1}$
having the same law as the generic variable
$\xi_i$
. The variable
$\xi_{i}^{n,j}$
represents the number of children generated by the parent
$j\in \{1, 2, \dots\}$
at time n when the environment is i. Throughout the paper, the sequences
$( \xi_i^{n,j} )_{j,n \geq 1}$
,
$i\in \mathbb{X}$
, and the Markov chain
$\left( X_n \right)_{n\geq 0}$
are supposed to be independent.
Denote by
$\mathbb E$
the expectation associated to
$\mathbb P.$
We assume that the variables
$\xi_i$
have positive means and finite second moments.
Condition 2. For any
$i \in \mathbb{X}$
, the random variable
$\xi_i$
satisfies the following:
$\mathbb{E} \left( \xi_i \right)>0$
and
$\mathbb{E} ( \xi_i^2 ) < +\infty.$
From Condition 2 it follows that
$0< f_i^{\prime}(1) < +\infty$
and
$f_i^{\prime\prime}(1) < +\infty.$
We are now prepared to introduce the branching process
$\left( Z_n \right)_{n\geq 0}$
in the Markovian environment
$\left( X_n \right)_{n\geq 0}$
. The initial population size is
$Z_0 = z \in \mathbb N$
. For
$n\geq 1$
, we let
$Z_{n-1}$
be the population size at time
$n-1$
and assume that at time n the parent
$j\in \{1, \dots Z_{n-1} \}$
generates
$\xi_{X_n}^{n,j}$
children. Then the population size at time n is given by
\begin{equation*}Z_{n} = \sum_{j=1}^{Z_{n-1}} \xi_{X_{n}}^{n,j}, \end{equation*}
where the empty sum is equal to 0. In particular, when
$Z_0=0$
, it follows that
$Z_n=0$
for any
$n\geq 1$
. We note that for any
$n\geq 1$
the variables
$\xi_{i}^{n,j}$
,
$j\geq 1$
,
$i\in \mathbb X$
, are independent of
$Z_{0},\ldots, Z_{n-1}$
.
Introduce the function
$\rho: \mathbb X \mapsto \mathbb R$
satisfying
\begin{equation*} {}\rho(i) = \ln f_i^{\prime}(1) , \quad i \in \mathbb{X}.\end{equation*}
Along with
$\left( Z_n \right)_{n\geq 0}$
consider the Markov walk
$\left( S_n \right)_{n\geq 0}$
such that
$S_0 = 0$
and, for
$n\geq 1$
,
\begin{equation}S_n = \ln \left( f_{X_1}^{\prime}(1) \cdots f_{X_n}^{\prime}(1) \right)= \sum_{k=1}^n \rho\left( X_k \right).\end{equation}
The couple
$\left( X_n, Z_n\right)_{n\geq 0}$
is a Markov chain with values in
$\mathbb X \times \mathbb N $
, whose transition operator
$\widetilde{\textbf{P}} $
is defined by the following relation: for any
$i\in \mathbb X$
,
$z\in \mathbb N,$
$\ s\in [0,1]$
, and
$h: \mathbb X \mapsto \mathbb R$
bounded measurable,
\begin{align} \widetilde{\textbf{P}} (h_s)(i,z) = \sum_{j \in \mathbb X} \textbf{P}(i,j) h(\,j) [f_j(s)]^z,\end{align}
where
$h_s(i,z)= h(i) s^z$
. Let
$\mathbb{P}_{i,z}$
be the probability law on
$ (\mathbb X \times \mathbb N )^{\mathbb N}$
and
$\mathbb{E}_{i,z}$
the associated expectation generated by the finite-dimensional distributions of the Markov chain
$\left( X_n, Z_n \right)_{n\geq 0}$
starting at
$X_0 = i$
and
$Z_0=z$
. By straightforward calculations, for any
$i\in \mathbb X$
,
$z\in \mathbb N$
,
\begin{align} \mathbb E_{i,z} (Z_n) = z \mathbb E_{i} (e^{S_n}).\end{align}
The following non-lattice condition is used indirectly in the proofs in the present paper; it is needed to ensure that the local limit theorem for the Markov walk (1.4) holds true.
Condition 3. For any
$\theta, a \in \mathbb{R}$
, there exist
$m\geq 0$
and a path
$x_0, \dots, x_m$
in
$\mathbb{X}$
such that
$\textbf{P}(x_0,x_1) \cdots \textbf{P}(x_{m-1},x_m) {\textbf{P}}(x_m,x_0) > 0$
and
\begin{equation*}\rho(x_0) + \cdots + \rho(x_m) - (m+1)\theta \notin a\mathbb{Z}.\end{equation*}
Condition 3 is an extension of the corresponding non-lattice condition for independent and identically distributed random variables
$X_0, X_1, \ldots $
, which can be stated as follows: there exists
$m\geq 0$
such that
$X_0 + \cdots + X_m$
does not take values in the lattice
$(m+1)\theta + a\mathbb{Z}$
with some positive probability, whatever
$\theta, a \in \mathbb{R}$
. Usually, the latter is formulated in an equivalent way with
$m=0$
. For Markov chains, Condition 3 is equivalent to the condition that the Fourier transform operator
\begin{equation} {} {}\textbf{P}_{i t}g(i) \,{:\!=}\, \textbf{P}\left( e^{i t \rho} g \right)(i) = \mathbb{E}_{i} \left( e^{it S_1} g(X_1) \right), {}\qquad g \in \mathscr{C}(\mathbb X), \ i \in \mathbb{X},\end{equation}
has a spectral radius strictly less than 1 for
$t\not= 0$
; see Lemma 4.1 of [Reference Grama, Lauvergnat and Le Page14]. Non-latticity for Markov chains with not necessarily finite state spaces is considered, for instance, in Shurenkov [Reference Shurenkov23] and Alsmeyer [Reference Alsmeyer3].
For the following facts and definitions we refer to [Reference Grama, Lauvergnat and Le Page13]. Under Condition 1, from the spectral gap property of the operator
$\textbf{P}$
it follows that, for any
$\lambda \in \mathbb{R}$
and any
$i \in \mathbb{X}$
, the limit
\begin{align*}k(\lambda) \,{:\!=}\, \lim_{n\to +\infty} \mathbb{E}_{i}^{1/n} \left( e^{\lambda S_n} \right)\end{align*}
exists and does not depend on the initial state of the Markov chain
$X_0=i$
. Moreover, the number
$k(\lambda)$
is the spectral radius of the transfer operator
$\textbf{P}_{\lambda}$
:
\begin{equation} {} {}\textbf{P}_{\lambda}g(i) \,{:\!=}\, \textbf{P}\left( e^{\lambda \rho} g \right)(i) = \mathbb{E}_{i} \left( e^{\lambda S_1} g(X_1) \right), {} {}\qquad g \in \mathscr{C}(\mathbb X), \ i \in \mathbb{X}. \end{equation}
In particular, under Conditions 1 and 3,
$k(\lambda)$
is a simple eigenvalue of the operator
$\textbf{P}_{\lambda}$
and there is no other eigenvalue of modulus
$k(\lambda)$
. In addition, the function
$k(\lambda)$
is analytic on
$\mathbb R.$
The BPME is said to be subcritical if
$k'(0)<0$
, critical if
$k'(0)=0$
, and supercritical if
$k'(0)>0$
. The following identity has been established in [Reference Grama, Lauvergnat and Le Page13]:
\begin{equation} k'(0) = \boldsymbol{\nu}(\rho) = \mathbb{E}_{\boldsymbol{\nu}} \left( \rho(X_1) \right) = \mathbb{E}_{\boldsymbol{\nu}} \left( \ln f_{X_1}^{\prime}(1) \right) =\phi' (0), \end{equation}
where
$\mathbb E_{\boldsymbol{\nu}} $
is the expectation generated by the finite-dimensional distributions of the Markov chain
$\left( X_n \right)_{n\geq 0}$
in the stationary regime, and
$\phi (\lambda)=\mathbb{E}_{\boldsymbol{\nu}} ( \exp\{\lambda\ln f_{X_1}^{\prime}(1)\} )$
,
$\lambda \in \mathbb{R}.$
The relation (1.9) proves that the classification made in the case of BPMEs and that for independent and identically distributed environment are coherent: when the random variables
$\left( X_n \right)_{n\geq 1}$
are independent and identically distributed with common law
$\boldsymbol{\nu}$
, from (1.9) it follows that the two classifications coincide.
In the present paper we will focus on the critical case:
$k'(0)=0$
. Our first result establishes the exact asymptotic of the survival probability of
$Z_n$
jointly with the event
$\{X_n=j\}$
when the branching process starts with z particles.
Theorem 1.1. Assume Conditions 1–3 and
$k'(0) = 0.$
Then there exists a positive function
$u(i,z): \mathbb{X} \times \mathbb{N} \mapsto \mathbb R_{+}^{*}$
such that for any
$(i,j) \in \mathbb{X}^2$
and
$z \in \mathbb{N}$
,
$z\not=0,$
\begin{equation*} \mathbb{P}_{i,z} \left( Z_n > 0 \,,\, X_n = j \right) \underset{n \to +\infty}{\sim} \frac {u(i,z) \boldsymbol{\nu} (\,j) } {\sqrt{n}}. \end{equation*}
An explicit formula for u(i,z) is given in Proposition 3.4. In the case
$z=1$
, Theorem 1.1 has been proved in [Reference Grama, Lauvergnat and Le Page13, Theorem 1.1]. The proof for the case
$z>1$
, which is not a direct consequence of the case
$z=1$
, will be given in Proposition 2.3.
We shall complement the previous statement by studying the asymptotic behavior of
$Z_n$
given
$Z_n>0$
under the following condition.
Condition 4. The random variables
$\xi_i$
,
$i\in \mathbb X$
, satisfy
\begin{align*} \inf_{ i\in\mathbb X} \mathbb P (\xi_i \geq 2) >0. \end{align*}
Condition 4 is quite natural—it says that each parent can generate more than one child with positive probability. In the present paper is used to prove the nondegeneracy of the limit of the martingale
\begin{equation*}\left(\frac{Z_{n}}{e^{S_{n}}} \right)_{n\geq0}\end{equation*}
in the key result Lemma 4.1.
The next result concerns the nondegeneracy of the limit law of the properly normalized number of particles
$Z_n$
at time n jointly with the event
$\{X_n=j\}$
.
Theorem 1.2. Assume Conditions 1–4 and
$k'(0) = 0.$
Then, for any
$i \in \mathbb{X}$
,
$z \in \mathbb{N}$
,
$z\not=0,$
there exists a probability measure
$\mu_{i,z}$
on
$\mathbb{R}_{+}$
such that, for any continuity point
$t\geq0$
of the distribution function
$\mu_{i,z} ([0,\cdot])$
and
$j \in \mathbb{X}$
, it holds that
\begin{equation*} \lim_{n\to\infty} \sqrt{n} \mathbb{P}_{i,z} \left( \frac{Z_n}{e^{S_n}} \leq t, X_n = j, Z_n>0 \right) = \mu_{i,z} ([0,t]) \boldsymbol{\nu} (\,j) u(i,z) \end{equation*}
and
\begin{equation*} \lim_{n\to\infty} \mathbb{P}_{i,z} \left( \frac{Z_n}{e^{S_n}} \leq t, X_n = j \big| Z_n>0 \right) = \mu_{i,z} ([0,t]) \boldsymbol{\nu} (\,j). \end{equation*}
Moreover, it holds that
$\mu_{i,z} (\{0\})=0$
.
From [Reference Grama, Lauvergnat and Le Page14, Lemma 10.3] it follows that, under Conditions 1 and 3, the quantity
\begin{equation} \sigma^2 \,{:\!=}\, \boldsymbol{\nu} \left( \rho^2 \right) - \boldsymbol{\nu} \left( \rho \right)^2 + 2 \sum_{n=1}^{+\infty} \left[ \boldsymbol{\nu} \left( \rho \textbf{P}^n \rho \right) - \boldsymbol{\nu} \left( \rho \right)^2 \right] \end{equation}
is finite and positive, i.e.
$0< \sigma <\infty$
. Let
\begin{equation*}\Phi^{+} (t) = \bigg(1 - e^{-\frac{t^2}{2}}\bigg) \unicode{x1D7D9}(t\geq 0), \qquad t\in \mathbb R,\end{equation*}
be the Rayleigh distribution function. The following assertion gives the asymptotic behavior of the normalized Markov walk
$S_n$
jointly with
$X_n$
provided
$Z_n>0$
.
Theorem 1.3. Assume Conditions 1–4 and
$k'(0) = 0.$
Then, for any
$i,j \in \mathbb{X}$
,
$z \in \mathbb{N}$
,
$z\not=0$
, and
$t \in \mathbb R$
,
\begin{equation*} \lim_{n\to\infty} \sqrt{n} \mathbb{P}_{i,z} \left( \frac{ S_n}{\sigma\sqrt{n}} \leq t, X_n = j, Z_n>0 \right) = \Phi^{+} (t) \boldsymbol{\nu} (\,j) u(i,z) \end{equation*}
and
\begin{equation*} \lim_{n\to\infty} \mathbb{P}_{i,z} \left( \frac{ S_n}{\sigma\sqrt{n}} \leq t, X_n = j \big| Z_n>0 \right) = \Phi^{+} (t) \boldsymbol{\nu} (\,j). \end{equation*}
The following assertion is the Yaglom-type limit theorem for
$\log Z_n$
jointly with
$X_n$
.
Theorem 1.4. Assume Conditions 1–4 and
$k'(0) = 0.$
Then, for any
$i, j \in \mathbb{X}$
,
$z \in \mathbb{N}$
,
$z\not=0$
, and
$t \geq 0$
,
\begin{equation*} \lim_{n\to\infty} \sqrt{n} \mathbb{P}_{i,z}\left( \frac{\log Z_n}{\sigma\sqrt{n}} \leq t, X_n = j, Z_n>0 \right) = \Phi^{+} (t) \boldsymbol{\nu} (\,j) u(i,z) \end{equation*}
and
\begin{equation*} \lim_{n\to\infty} \mathbb{P}_{i,z} \left( \frac{\log Z_n}{\sigma\sqrt{n}} \leq t, X_n = j \big| Z_n>0 \right) = \Phi^{+} (t) \boldsymbol{\nu} (\,j). \end{equation*}
As mentioned before, in the proofs of the stated results we make use of the previous developments in the papers [Reference Grama, Lauvergnat and Le Page13, Reference Grama, Lauvergnat and Le Page14]. These studies are based heavily on the existence of the harmonic function and the study of the asymptotic of the probability of the exit time for Markov chains which were performed recently in [Reference Grama, Lauvergnat and Le Page12, Reference Grama, Le Page and Peigné15]; these are recalled in the next section. For recurrent Markov chains, alternative approaches based on renewal arguments are possible. The advantage of the harmonic function approach proposed here is that it could be extended to more general Markov environments which are not recurrent. In particular, with these methods one could treat multi-type branching processes in random environments.
The outline of the paper is as follows. In Section 2 we give a series of assertions for walks on Markov chains conditioned to stay positive and prove Theorem 1.1 for
$z>1$
. In Section 3 we state some preparatory results for branching processes. The proofs of Theorems 1.2, 1.3, and 1.4 are given in Sections 4 and 5.
We end this section by fixing some notation. As usual the symbol c will denote a positive constant depending on all previously introduced constants. In the same way the symbol c equipped with subscripts will denote a positive constant depending only on the indices and all previously introduced constants. All these constants will change in value at every occurrence. By
$f \circ g$
we mean the composition of two functions f and g:
$f \circ g (\cdot)=f(g(\cdot))$
. The indicator of an event A is denoted by
$\unicode{x1D7D9}_A$
. For any bounded measurable function f on
$\mathbb{X}$
, random variable X in some measurable space
$\mathbb{X}$
, and event A, we define
\begin{equation*}\int_{\mathbb{X}} f(x) \mathbb{P} (X \in dx, A) = \mathbb{E}\left( f(X)\,{;}\, A\right) \,{:\!=}\, \mathbb{E} \left(f(X) \unicode{x1D7D9}_A\right).\end{equation*}
2. Facts about Markov walks conditioned to stay positive
2.1. Conditioned limit theorems
We start by formulating two propositions which are consequences of the results in [Reference Grama, Lauvergnat and Le Page12], [Reference Grama, Lauvergnat and Le Page13], and Reference Grama, Lauvergnat and Le Page14].
We introduce the first time when the Markov walk
$\left(y+ S_n \right)_{n\geq 0}$
becomes nonpositive: for any
$y \in \mathbb{R}$
, set
\begin{align} \tau_y \,{:\!=}\, \inf \left\{ k \geq 1 : y+S_k \leq 0 \right\}, \end{align}
where
$\inf \emptyset = 0.$
Conditions 1 and 3 together with
$\boldsymbol{\nu}(\rho) = 0$
ensure that the stopping time
$\tau_y$
is well defined and finite
$\mathbb{P}_i$
-almost surely (-a.s.), for any
$i \in \mathbb{X}$
.
The following important proposition is a direct consequence of the results in [Reference Grama, Lauvergnat and Le Page12] adapted to the case of a finite Markov chain. It proves the existence of the harmonic function related to the Markov walk
$\left(y+ S_n \right)_{n\geq 0}$
and states some of its properties that will be used in the proofs of the main results of the paper.
Proposition 2.1. Assume Conditions 1 and 3 and
$k'(0) = 0$
. There exists a nonnegative function V on
$\mathbb{X} \times \mathbb{R}$
such that the following hold:
-
1. For any
$(i,y) \in \mathbb{X} \times \mathbb{R}$
and
$n \geq 1$
,
\begin{equation*} {}\mathbb{E}_i \left( V \left( X_n, y+S_n \right) \,;\, \tau_y > n \right) = V(i,y). {}\end{equation*}
-
2. For any
$i\in \mathbb{X}$
, the function
$V(i,\cdot)$
is nondecreasing, and for any
$(i,y) \in \mathbb{X} \times \mathbb{R}$
,
\begin{equation*} {}V(i,y) \leq c \left( 1+\max(y,0) \right). {}\end{equation*}
-
3. For any
$i \in \mathbb{X}$
,
$y > 0$
, and
$\delta \in (0,1)$
,
\begin{equation*} {}\left( 1- \delta \right)y - c_{\delta} \leq V(i,y) \leq \left(1+\delta \right)y + c_{\delta}. {}\end{equation*}
We need the asymptotic of the probability of the event
$\{ \tau_y > n\}$
jointly with the state of the Markov chain
$(X_n)_{n\geq 1}$
.
Proposition 2.2. Assume Conditions 1 and 3 and
$k'(0)=0$
.
-
1. For any
$(i,y) \in \mathbb{X} \times \mathbb{R}$
and
$j \in \mathbb{X}$
, we have
\begin{align*}\lim_{n\to +\infty} \sqrt{n} \mathbb{P}_{i} \left( X_n = j \,,\, \tau_y > n \right) = \frac{2V(i,y) \boldsymbol{\nu} (\,j)}{\sqrt{2\pi} \sigma}.\end{align*}
-
2. For any
$(i,y) \in \mathbb{X} \times \mathbb{R}$
,
$j\in \mathbb{X}$
, and
$n\geq 1$
,
$${\mathbb{P}_i}\left( {{X_n} = j,{\tau _y} > n} \right) \le c{{1 + \max (y,0)} \over {\sqrt n }}.$$
For a proof of the first assertion of Proposition 2.2, see Lemma 2.11 in [Reference Grama, Lauvergnat and Le Page13]. The second is deduced from the point (b) of Theorem 2.3 of [Reference Grama, Lauvergnat and Le Page12].
Denote by
$ \textrm{supp}(V) = \left\{ (i,y) \in \mathbb{X} \times \mathbb{R} : \right.$
$\left. V(i,y) > 0 \right\}$
the support of the function V. By the point 3 of Theorem 1.1, the harmonic function V satisfies the following property: for any
$i\in \mathbb X$
there exists
$y_i\geq 0$
such that
$(i,y)\in \text{supp}\ V$
for any
$y>y_i$
.
In addition to the previous two propositions we need the following result, which gives the asymptotic behavior of the conditioned limit law of the Markov walk
$\left(y+ S_n \right)_{n\geq 0}$
jointly with the Markov chain
$\left(X_n \right)_{n\geq 0}$
. It extends Theorem 2.5 of [Reference Grama, Lauvergnat and Le Page12], which considers the asymptotic of
\begin{equation*}\frac{y+S_n}{\sigma \sqrt{n}}\end{equation*}
given the event
$\{\tau_y >n\}$
.
Proposition 2.3. Assume Conditions 1 and 3 and
$k'(0)=0$
.
-
1. For any
$(i,y) \in \textrm{supp}(V)$
,
$ j\in \mathbb{X} $
, and
$t\geq 0$
,
\begin{align*} {}\mathbb{P}_i \left( \left.{\frac{y+S_n}{\sigma \sqrt{n}} \leq t, X_n=j } \,\middle|\,{\tau_y >n}\right. \right) \underset{n\to+\infty}{\longrightarrow} {} \Phi^+(t) \boldsymbol{\nu} (\,j).\end{align*}
-
2. There exists
$\varepsilon_0 >0$
such that, for any
$\varepsilon \in (0,\varepsilon_0)$
,
$n\geq 1$
,
$t_0 > 0$
,
$t\in[0,t_0]$
,
$(i,y) \in \mathbb{X} \times \mathbb{R}$
, and
$ j \in \mathbb{X}$
,
\begin{align*} {}&\left\lvert{ \mathbb{P}_i \left(\frac{y+S_n}{\sqrt{n} \sigma} \leq t, X_n=j, \tau_y > n \right) - \frac{2V(i,y)}{\sqrt{2\pi n}\sigma} \Phi^+(t) \boldsymbol{\nu} (\,j) }\right\rvert \\[3pt] {}&\hskip6cm \leq c_{\varepsilon,t_0} \frac{\left( 1+\max(y,0)^2 \right)}{n^{1/2+\varepsilon}}.\end{align*}
Proof. It is enough to prove the point 2 of the proposition. This will be derived from the corresponding result in Theorem 2.5 of [Reference Grama, Lauvergnat and Le Page12]. We first establish an upper bound. Let
$k=\big[n^{1/4}\big]$
and
$\| \rho \|_{\infty}=\max_{i\in \mathbb X } | \rho(i) |$
. Since
\begin{equation*}S_n=S_{n-k}+ \sum_{i=n-k+1}^{n} \rho(X_i),\end{equation*}
we have
\begin{align} &\mathbb{P}_i \left(\frac{y+S_n}{\sqrt{n} \sigma} \leq t, X_n=j, \tau_y > n \right) \nonumber \\[3pt]&\leq\mathbb{P}_i \left(\frac{y+S_{n-k}}{\sqrt{n} \sigma} \leq t + \frac{k}{\sigma\sqrt{n}} \| \rho \|, X_n=j, \tau_y > n-k \right) \nonumber \\[2pt] &\,{:\!=}\,I (k,n).\end{align}
By the Markov property
\begin{align*} I (k,n)= \mathbb{E}_i \left( P^k(X_{n-k},j); \frac{y+S_{n-k}}{\sqrt{n} \sigma} \leq t + \frac{k}{\sigma\sqrt{n}} \| \rho \|, \tau_y > n-k \right). \end{align*}
Now, using (1.2) and setting
\begin{equation*}t_{n,k}=\frac{\sqrt{n}}{\sqrt{n-k}}\left(t + \frac{k}{\sigma\sqrt{n}} \right) \| \rho \|,\end{equation*}
we have
\begin{align} I(k,n) \leq (\boldsymbol{\nu}(\,j) + c_1e^{-c_2 k}) \mathbb{P}_i \left(\frac{y+S_{n-k}}{\sqrt{n-k} \sigma} \leq t_{n,k}, \tau_y > n-k \right). \end{align}
By Theorem 2.5 and Remark 2.10 of [Reference Grama, Lauvergnat and Le Page12], there exists
$\varepsilon_0>0$
such that for any
$\varepsilon \in (0, \varepsilon_0)$
and
$t_0>0$
,
$n\geq1$
, we have, for
$t_{n,k}\leq t_0 $
,
\begin{align} &\mathbb{P}_i \left(\frac{y+S_{n-k}}{\sqrt{n-k} \sigma} \leq t_{n,k}, \tau_y > n-k \right) \nonumber \\[3pt] &\leq \frac{2V(i,y)}{\sqrt{2\pi (n-k)}\sigma} \Phi^{+}(t_{n,k}) t_0\frac{(1+\max\{0,y\})^2 }{ (n-k)^{1/2+\varepsilon/16}}. \end{align}
Since
$| t_{n,k} - t| \leq c_{t_0}\frac{1}{n^{1/4}}$
and
$\Phi^+$
is smooth, we obtain
\begin{align} \frac{2V(i,y)}{\sqrt{2\pi (n-k)}\sigma} \Phi^+(t_{n,k}) \leq \frac{2V(i,y)}{\sqrt{2\pi n}\sigma} \Phi^+(t) + c_{t_0}\frac{(1+\max\{0,y\})^2}{n^{1/2 +1/4}}. \end{align}
From (2.2), (2.3), (2.4), and (2.5) it follows that
\begin{align} \mathbb{P}_i &\left(\frac{y+S_n}{\sqrt{n} \sigma} \leq t, X_n=j, \tau_y > n \right) \nonumber \\[3pt]&\leq \boldsymbol \nu(j) \frac{2V(i,y)}{\sqrt{2\pi n}\sigma} \Phi^+(t)+ c_{\varepsilon, t_0}\frac{(1+\max\{0,y\})^2 }{ n^{1/2+\varepsilon/16}}. \end{align}
Now we shall establish a lower bound. With the notation introduced above, we have
\begin{align} &\mathbb{P}_i \left(\frac{y+S_n}{\sqrt{n} \sigma} \leq t, X_n=j, \tau_y > n \right) \nonumber \\[3pt] &\geq \mathbb{P}_i \left(\frac{y+S_{n-k}}{\sqrt{n} \sigma} \leq t - \frac{k}{\sigma\sqrt{n}} \| \rho \|, X_n=j, \tau_y > n-k \right) \nonumber \\[3pt] & -\mathbb{P}_i \left( n-k < \tau_y \leq n \right) \nonumber \\[3pt] &\,{:\!=}\,I_1 (k,n) - I_2(k,n). \end{align}
As in the proof of (2.6), we establish the lower bound
\begin{align} I_1(k,n)\geq \boldsymbol{\nu}(\,j) \frac{2V(i,y)}{\sqrt{2\pi n}\sigma} \Phi^+(t)- c_{\varepsilon, t_0}\frac{(1+\max\{0,y\})^2 }{ n^{1/2+\varepsilon/16}}. \end{align}
Note that
$0 \geq \min_{n-k < i \leq n} \{ y+S_i \} \geq y+S_{n-k} - k \| \rho \|_{\infty}$
, on the set
$\{ n-k < \tau_y \leq n \}$
. Set
\begin{equation*}t_{n,k}=\frac{k \| \rho \|_{\infty} }{\sigma\sqrt{n-k}}.\end{equation*}
Then
\begin{align} I_2(k,n) &= \mathbb{P}_i \left( n-k < \tau_y \leq n \right) \nonumber\\[3pt]&\leq \mathbb P_i \left( \frac{y+S_{n-k}}{\sigma\sqrt{n-k}} \leq t_{n,k}, n-k < \tau_y \leq n \right) \nonumber\\[3pt]&\leq \mathbb P_i \left( \frac{y+S_{n-k}}{\sigma\sqrt{n-k}} \leq t_{n,k}, \tau_y \geq n -k \right). \end{align}
Again by Theorem 2.5 and Remark 2.10 of [Reference Grama, Lauvergnat and Le Page12], there exists
$\varepsilon_0>0$
such that for any
$\varepsilon \in (0, \varepsilon_0)$
and
$t_0>0$
,
$n\geq1$
, we have, for
$t_{n,k}\leq t_0 $
,
\begin{align} &\mathbb{P}_i \left(\frac{y+S_{n-k}}{\sqrt{n-k} \sigma} \leq t_{n,k}, \tau_y > n-k \right) \nonumber \\&\leq \frac{2V(i,y)}{\sqrt{2\pi (n-k)}\sigma} \Phi^+(t_{n,k}) + c_{\varepsilon, t_0}\frac{(1+\max\{0,y\})^2 }{ (n-k)^{1/2+\varepsilon/16}}. \end{align}
Since
$| t_{n,k} | \leq c_{t_0}\frac{1}{n^{1/4}}$
and
$\Phi^+(0)=0$
, we obtain
\begin{align} \frac{2V(i,y)}{\sqrt{2\pi (n-k)}\sigma} \Phi^+(t_{n,k}) &\leq \frac{2V(i,y)}{\sqrt{2\pi n}\sigma} \Phi^+(0) + c_{t_0}\frac{(1+\max\{0,y\})^2}{n^{1/2 +1/4}} \nonumber \\[3pt] &=c_{t_0}\frac{(1+\max\{0,y\})^2}{n^{1/2 +1/4}}. \end{align}
From (2.9), (2.10), and (2.11), we deduce that
\begin{align} I_2(k,n) \leq c_{\varepsilon, t_0}\frac{(1+\max\{0,y\})^2 }{ n^{1/2+\varepsilon/16}}. \end{align}
Using (2.7), (2.8), and (2.12), one gets
\begin{align*} \mathbb P_i &\left(\frac{y+S_n}{\sqrt{n} \sigma} \leq t, X_n=j, \tau_y > n \right) \\[3pt]&\geq \boldsymbol \nu(j) \frac{2V(i,y)}{\sqrt{2\pi n}\sigma} \Phi^+(t)- c_{\varepsilon, t_0}\frac{(1+\max\{0,y\})^2 }{ n^{1/2+\varepsilon/16}}, \end{align*}
which together with (2.6) ends the proof of the point 2 of the proposition. The point 1 follows from the point 2.
We need the following estimate, whose proof can be found in [Reference Grama, Lauvergnat and Le Page14].
Proposition 2.4. Assume Conditions 1 and 4 and
$k'(0)=0$
. Then there exists
$c > 0$
such that for any
$a>0$
, nonnegative function
$\psi \in \mathscr{C}(\mathbb X)$
,
$y \in \mathbb{R}$
,
$t \geq 0$
, and
$n \geq 1$
,
\begin{align*} \sup_{i\in \mathbb{X}} \mathbb{E}_{i} &\left( \psi \left( X_{n} \right) \,;\, y+S_{n} \in [t,t+a] \,,\, \tau_y > n \right) \\ &\leq \frac{c \left\lVert{\psi}\right\rVert_{\infty}}{n^{3/2}} \left( 1+a^3 \right)\left( 1+t \right)\left( 1+\max(y,0) \right). \end{align*}
2.2. Change of probability measure
Fix any
$(i,y) \in \textrm{supp}(V)$
and
$z\in \mathbb N$
. The harmonic function V from Proposition 2.1 allows us to introduce the probability measure
$\mathbb{P}_{i,y,z}^+$
on
${(\mathbb X \times \mathbb N})^{\mathbb{N}}$
and the corresponding expectation
$\mathbb{E}_{i,y,z}^+$
, by the following relation: for any
$n\geq 1$
and any bounded measurable g:
${(\mathbb X \times \mathbb N )}^{n} \mapsto \mathbb{R}$
,
\begin{align} {} {}&\mathbb{E}_{i,y,z}^+ \left( g \left( X_1,Z_1, \dots, X_n,Z_n \right) \right) \nonumber\\ {}&\,{:\!=}\, \frac{1}{V(i,y)} \mathbb{E}_{i,z} \big( g\left( X_1,Z_1, \dots, X_n,Z_n \right) \nonumber\\ {}&\qquad\qquad\qquad \times V\left( X_n, y+S_n \right) \,;\, \tau_y > n \big). \end{align}
The fact that the function V is harmonic (by point 1 of Proposition 2.1) ensures the applicability of the Kolmogorov extension theorem and shows that
$\mathbb{P}_{i,z,y}^+$
is a probability measure. In the same way we define the probability measure
$\mathbb{P}_{i,y}^+$
and the corresponding expectation
$\mathbb{E}_{i,y}^+$
: for any
$(i,y) \in \textrm{supp}(V)$
,
$n \geq 1$
, and any bounded measurable g:
$\mathbb{X}^n \to \mathbb{R}$
,
\begin{align} &\mathbb{E}_{i,y}^+ \left( g \left( X_1, \dots, X_n \right) \right) \nonumber\\ &\,{:\!=}\, \frac{1}{V(i,y)} \mathbb{E}_{i} \left( g\left( X_1, \dots, X_n \right) V\left( X_n, y+S_n \right) \,;\, \tau_y > n \right). \end{align}
The relation between the expectations
$\mathbb{E}_{i,y,z}^+$
and
$\mathbb{E}_{i,y}^+$
is given by the following identity: for any
$n \geq 1$
and any bounded measurable g:
$\mathbb{X}^n \to \mathbb{R}$
,
\begin{align} {} {}\mathbb{E}_{i,y,z}^+ \left( g \left( X_1, \dots, X_n \right) \right) = \mathbb{E}_{i,y}^+ \left( g \left( X_1, \dots, X_n \right) \right). \end{align}
With the help of Proposition 2.4, we have the following bounds.
Lemma 2.5. Assume Conditions 1 and 3 and
$k'(0)=0$
. For any
$(i,y) \in \textrm{supp}(V)$
, we have, for any
$k \geq 1$
,
\begin{equation*} \mathbb{E}_{i,y}^+ \left( e^{-S_k}\right) \leq \frac{c \left( 1+\max(y,0) \right)e^{y}}{k^{3/2} V(i,y)}. \end{equation*}
In particular,
\begin{equation*} \mathbb{E}_{i,y}^+ \left( \sum_{k=0}^{+\infty} e^{-S_k} \right) \leq \frac{c \left( 1+\max(y,0) \right)e^{y}}{V(i,y)}. \end{equation*}
The proof, being similar to that in [Reference Grama, Lauvergnat and Le Page13], is left to the reader.
We need the following statements. Let
$ \mathscr F_n = \sigma \{ X_0,Z_0, \ldots, X_n, Z_n \} $
and
$(Y_n)_{n\geq 0}$
a bounded
$(\mathscr F_n)_{n\geq 0}$
-adapted sequence.
Lemma 2.6. Assume Conditions 1–3 and
$k'(0)=0$
. For any
$k \geq 1$
,
$(i,y) \in \textrm{supp}(V)$
,
$z\in \mathbb N$
, and
$j \in \mathbb{X}$
,
\begin{equation*} \lim_{n\to +\infty} \mathbb{E}_{i,z} \left( \left.{ Y_k \,;\, X_n = j} \,\middle|\,{ \tau_y > n }\right. \right) = \mathbb{E}_{i,y,z}^+ ( Y_k ) \boldsymbol{\nu} (\,j). \end{equation*}
Proof. For the sake of brevity, for any
$(i,j) \in \mathbb{X}^2$
,
$y \in \mathbb{R}$
, and
$n \geq 1$
, we set
\begin{equation*} P_n(i,y,j) \,{:\!=}\, \mathbb{P}_i \left( X_n = j \,,\, \tau_y > n \right). \end{equation*}
Fix
$k \geq 1$
. By the point 1 of Proposition 2.2, it is clear that for any
$(i,y) \in \textrm{supp}(V)$
and n large enough,
$\mathbb{P}_i \left( \tau_y > n \right) > 0$
. By the Markov property, for any
$j \in \mathbb{X}$
and
$n \geq k+1$
large enough,
\begin{align*} I_0 &\,{:\!=}\, \mathbb{E}_{i,z} \left( \left.{ Y_k \,;\, X_n = j} \,\middle|\,{ \tau_y > n }\right. \right)\\[3pt] &= \mathbb{E}_{i,z} \left( Y_k \frac{P_{n-k} \left( X_k,y+S_k, j \right)}{\mathbb{P}_i \left( \tau_y > n \right)} \,;\, \tau_y > m \right). \end{align*}
Using the point 1 of Proposition 2.2, by the Lebesgue dominated convergence theorem,
\begin{align*} {}\lim_{n\to+\infty} I_0 &= {}\mathbb{E}_{i,z} \left( Y_k \frac{V \left( X_k,y+S_m \right)}{V(i,y)} \,;\, \tau_y > k \right) \boldsymbol{\nu}(\,j) \\[3pt] {}&= \mathbb{E}_{i,y,z}^+ \left( Y_k \right) \boldsymbol{\nu} (\,j).\\[-35pt] \end{align*}
Lemma 2.7. Assume that
$(i,y) \in \text{supp}\ V $
and
$z\in \mathbb N$
. For any bounded
$(\mathscr F_n)_{n\geq 0}$
-adapted sequence
$(Y_n)_{n\geq 0}$
such that
$Y_n\to Y_{\infty}$
$\mathbb P_{i,y,z}^{+}$
-a.s.,
\begin{align*} \limsup_{k\to \infty} \limsup_{n\to \infty} \sqrt{n} \mathbb E_{i,z} \big( \big| Y_n-Y_k \big|; \tau_y > n \big) =0. \end{align*}
Proof. Let
$k\geq1$
and
$\theta>1$
. Then
\begin{align} \mathbb E_{i,z} \big( \big| Y_n-Y_k \big|; \tau_y > n \big) &= \mathbb E_{i,z} \big( \big|Y_n-Y_k \big|; \tau_y > \theta n \big) \nonumber \\[3pt] & + \mathbb E_{i,z} \big( \big|Y_n-Y_k \big|; n< \tau_y \leq \theta n \big). \end{align}
We bound the second term in the right-hand side of (2.16):
\begin{align} &\mathbb E_{i,z} \big( \big|Y_n-Y_k \big|;\ n< \tau_y \leq \theta n \big) \leq C \mathbb P_{i,z} \big( n< \tau_y \leq \theta n \big) \end{align}
By the point 1 of Proposition 2.2, we have
\begin{align} &\lim_{n\to \infty} \sqrt{n} \mathbb P_{i,z} \big( n< \tau_y \leq \theta n \big) \nonumber \\[3pt] &= \lim_{n\to \infty} \sqrt{n} \mathbb P_{i,z} \big( \tau_y >n \big) - \lim_{n\to \infty} \sqrt{n} \mathbb P_{i,z} \big( \tau_y > \theta n \big) \nonumber\\[3pt] &= \frac{2V(i,y)}{\sqrt{2\pi}\sigma} \Big(1-\frac{1}{\sqrt{\theta}}\Big). \end{align}
Now we shall prove that
\begin{align} \limsup_{k\to \infty} \limsup_{n\to \infty} \sqrt{n} \mathbb E_{i,z} \big( \big|Y_n-Y_k \big|; \tau_y > \theta n \big) =0. \end{align}
Recall that
$\theta >1$
. By the Markov property (conditioning on
$\mathscr F_n$
),
\begin{align} &\mathbb E_{i,z} \big( \big|Y_n-Y_k \big|; \tau_y > \theta n \big)\nonumber \\[3pt] &\qquad = \mathbb E_{i,z} \big( \left\lvert{Y_n-Y_k}\right\rvert P_{[(\theta-1)n]}(X_n,y+S_n) ; \tau_y > n \big), \end{align}
where we use the notation
$P_{n'}(i',y') \,{:\!=}\, \mathbb P_{i',y'} \big( \tau_y^{\prime} > n' \big).$
By the point 2 of Proposition 2.2 and the point 3 of Proposition 2.1, there exists
$y_0>0$
such that for
$i' \in \mathbb X$
,
$y' > y_0$
, and
$n'\in\mathbb N$
,
\begin{align} P_{n'}(i',y') \leq \frac{c}{\sqrt{n'}} \left(1+\max\{0,y'\} \right) \leq c\frac{V(i',y')}{\sqrt{n'}}. \end{align}
Representing the right-hand side of (2.20) as a sum of two terms and using (2.21) gives
\begin{align} &\sqrt{n}\mathbb E_{i,z} \big( \big|Y_n-Y_k \big|;\ \tau_y > \theta n \big)\nonumber \\[3pt] & = \sqrt{n}\mathbb E_{i,z} \big( \left\lvert{Y_n-Y_k}\right\rvert P_{[(\theta-1)n]}(X_n,y+S_n) ;\ y+S_n \leq y_0, \tau_y > n \big) \nonumber \\[3pt] & \quad + \sqrt{n}\mathbb E_{i,z} \big( \left\lvert{Y_n-Y_k}\right\rvert P_{[(\theta-1)n]}(X_n,y+S_n) ;\ y+S_n > y_0, \tau_y > n \big) \nonumber \\[3pt] &\leq c \sqrt{n}\mathbb P_{i} \big( y+S_n \leq y_0, \tau_y > n \big) \nonumber \\[3pt] &\quad + \frac{c}{\sqrt{\theta-1}} \mathbb E_{i,z} \big( \left\lvert{Y_n-Y_k}\right\rvert V(X_n, y+S_n);\ \tau_y > n \big). \end{align}
Using the point 1 of Proposition 2.3 and the point 1 of Proposition 2.2, we have
\begin{align} \lim_{n\to\infty}\sqrt{n}\mathbb P_{i} \big( y+S_n \leq y_0, \tau_y > n \big)=0. \end{align}
By the change-of-measure formula (2.13),
\begin{align} \mathbb E_{i,z} \big( \left\lvert{Y_n-Y_k}\right\rvert V(X_n, y+S_n);\ \tau_y > n \big) = V(i,y) \mathbb E_{i,y,z}^{+} \big( \left\lvert{Y_n-Y_k}\right\rvert \big). \end{align}
Letting first
$n\to\infty$
and then
$k\to\infty$
, by the Lebesgue dominated convergence theorem,
\begin{align} \limsup_{k\to \infty} \limsup_{n\to \infty} \mathbb E_{i,y,z}^{+} \big( \left\lvert{Y_n-Y_k}\right\rvert \big) =0. \end{align}
From (2.22)–(2.25) we deduce (2.19). Now (2.16)–(2.19) imply that, for any
$\theta>1$
,
\begin{align*} \limsup_{k\to \infty} \limsup_{n\to \infty} \sqrt{n} \mathbb E_{i,z} \big( \big| Y_n-Y_k \big|;\ \tau_y > n \big) \leq \frac{2V(i,y)}{\sqrt{2\pi}\sigma} \Big(1-\frac{1}{\sqrt{\theta}}\Big). \end{align*}
Since
$\theta $
can be taken arbitrarily close to 1, we conclude the claim of the lemma.
The next assertion is an easy consequence of Lemmata 2.6 and 2.7.
Lemma 2.8. Assume that
$(i,y) \in \text{supp}\ V $
,
$j\in \mathbb{X}$
, and
$z\in \mathbb N$
. For any bounded
$(\mathscr F_n)_{n\geq 0}$
-adapted sequence
$(Y_n)_{n\geq 0}$
such that
$Y_n\to Y_{\infty}$
$\mathbb P_{i,y,z}^{+}$
-a.s.,
\begin{align*} \lim_{n\to +\infty} \mathbb E_{i,z} \big( Y_n;\ X_n=j \big| \tau_y > n \big) = \mathbb E_{i,y,z}^{+} \big( Y_{\infty}\big) \boldsymbol{\nu} (\,j). \end{align*}
Proof. For any
$n > k \geq1$
, we have
\begin{align} &\lim_{n\to \infty} \sqrt{n} \mathbb E_{i,z} \big( Y_n;\ X_n=j, \tau_y > n \big) \nonumber \\[3pt] &= \sqrt{n} \mathbb E_{i,z} \big( Y_k;\ X_n=j, \tau_y > n \big) + \sqrt{n} \mathbb E_{i,z} \big( Y_n-Y_k;\ X_n=j, \tau_y > n \big). \end{align}
By Lemma 2.6, the first term in the right-hand side of (2.26) converges to
\begin{equation*}\frac{2V(i,y)}{\sqrt{2\pi}\sigma} \boldsymbol{\nu} (\,j) \mathbb E_{i,y,z}^{+} Y_{k}\end{equation*}
as
$n\to\infty$
, where
$ \lim_{k\to \infty} \mathbb E_{i,z,y}^{+} Y_{k} = \mathbb E_{i,y,z}^{+} Y_{\infty}.$
By Lemma 2.7, the second term in the right-hand side of (2.26) vanishes, which completes the proof.
2.3. The dual Markov chain
Note that the invariant measure
$\boldsymbol{\nu}$
is positive on
$\mathbb{X}$
. Therefore the dual Markov kernel
\begin{equation} \textbf{P}^* \left( i,j \right) = \frac{\boldsymbol{\nu} \left( j \right)}{\boldsymbol{\nu} (i)} \textbf{P} \left( j,i \right), \qquad i,j \in \mathbb{X}, \end{equation}
is well defined. On an extension of the probability space
$(\Omega, \mathscr{F}, \mathbb{P})$
we consider the dual Markov chain
$\left( X_n^* \right)_{n\geq 0}$
with values in
$\mathbb{X}$
and with transition probability
$\textbf{P}^*$
. The dual chain
$\left( X_n^* \right)_{n\geq 0}$
can be chosen to be independent of the chain
$\left( X_n \right)_{n\geq 0}$
. Accordingly, the dual Markov walk
$\left(S_n^* \right)_{n\geq 0}$
is defined by setting
\begin{equation} S_0^* = 0 \quad \text{and} \quad S_n^* = -\sum_{k=1}^n \rho \left( X_k^* \right), \qquad n \geq 1. \end{equation}
For any
$y \in \mathbb{R}$
define the first time when the Markov walk
$\left(y+ S_n^* \right)_{n\geq 0}$
becomes nonpositive:
\begin{equation} \tau_y^* \,{:\!=}\, \inf \left\{ k \geq 1\,{:}\, y+S_k^* \leq 0 \right\}. \end{equation}
For any
$i\in \mathbb{X}$
, denote by
$\mathbb{P}_i^*$
and
$\mathbb{E}_i^*$
the probability and the associated expectation generated by the finite-dimensional distributions of the Markov chain
$( X_n^* )_{n\geq 0}$
starting at
$X_0^* = i$
.
It is easy to verify (see [Reference Grama, Lauvergnat and Le Page13]) that
$\boldsymbol{\nu}$
is also
$\textbf{P}^*$
invariant and that Conditions 1 and 3 are satisfied for
$\textbf{P}^*$
. This implies that Propositions 2.1–2.4, formulated in Subsection 2.1, hold also for the dual Markov chain
$(X_n^*)_{n\geq 0}$
and the Markov walk
$\left(y+ S_n^* \right)_{n\geq 0}$
, with the harmonic function
$V^*$
such that, for any
$(i,y) \in \mathbb{X} \times \mathbb{R}$
and
$n \geq 1$
,
\begin{align*} \mathbb{E}_i \left( V^* \left( X_n, y+S_n^* \right) \,;\, \tau^*_y > n \right) = V^*(i,y). \end{align*}
The following duality property is obvious (see [Reference Grama, Lauvergnat and Le Page13]).
Lemma 2.9. (Duality.) For any
$n\geq 1$
and any function g:
$\mathbb{X}^n \to \mathbb{C}$
,
\begin{equation*} \mathbb{E}_i \left( g \left( X_1, \dots, X_n \right) \,;\, X_{n+1} = j \right) = \mathbb{E}_j^* \left( g \left( X_n^*, \dots, X_1^* \right) \,;\, X_{n+1}^* = i \right) \frac{\boldsymbol{\nu}(\,j)}{\boldsymbol{\nu}(i)}. \end{equation*}
3. Preparatory results for branching processes
Throughout the remainder of the paper we will use the following notation. For
$ s \in [0,1)$
, let
\begin{align*} \varphi_{X_k}(s) =\frac{1}{1-f_{X_k}(s)} - \frac{1}{f^{\prime}_{X_k}(1)(1-s)}, \end{align*}
and, by continuity,
\begin{align*} \varphi_{X_k}(1) = \lim_{s\to 1} \varphi_{X_k}(s) = \frac{ f^{\prime\prime}_{X_k}(1) }{2 f^{\prime}_{X_k}(1)^2}. \end{align*}
In addition, for
$s \in [0,1),\ z\in \mathbb{N},\ z\neq 0$
, let
$g_{z}(s)=s^z$
and
\begin{align*} \psi_{z}(s) =\frac{1}{1-g_{z}(s)} - \frac{1}{g^{\prime}_{z}(1)(1-s)} = \frac{1}{1-s^z} - \frac{1}{z(1-s)}, \end{align*}
and, by continuity,
\begin{align*} \psi_{z}(1) = \lim_{s\to 1} \psi_{z}(s) = \frac{ z(z-1) }{2 z^2}= \frac{1}{2}\frac{ z-1 }{z}. \end{align*}
For any
$n\geq 1$
,
$z\in \mathbb{N},\ z\not= 0$
, and
$s\in [0,1]$
, the following quantity will play an important role in our study:
\begin{align*} q_{n,z} (s) = 1-\big( f_{X_1}\circ \cdots \circ f_{X_n} (s)\big)^z. \end{align*}
Under Condition 2, for any
$i\in \mathbb X$
and
$s\in [0,1]$
we have
$f_i(s)\in [0,1]$
and
$f_{X_1}\circ \cdots \circ f_{X_n} (s) \in [0,1]$
. This implies that, for any
$s\in [0,1]$
,
\begin{align} q_{n,z} (s) \in [0,1]. \end{align}
For any
$n\geq 1$
and
$z\in \mathbb{N},\ z\neq 0$
, the function
$s\mapsto q_{n,z} (s) $
is convex on [0,1]. Since the sequence
$( \xi_i^{n,j} )_{j,n \geq 1}$
is independent of the Markov chain
$\left( X_n \right)_{n\geq 0},$
with
$s=0$
, we have,
$\mathbb P_{i,y,z}^{+}$
-a.s.,
\begin{align} q_{n,z} (0) = \mathbb P_{i,y,z}^{+} ( Z_n >0 \big| (X_k)_{k\geq 0} ). \end{align}
Note also that
$\{ Z_{n} >0\} \supset \{ Z_{n+1} >0\}$
and therefore, for
$n\geq 1$
,
\begin{align} q_{n,z} (0) \geq q_{n+1,z} (0). \end{align}
Taking the limit as
$n\to\infty$
,
$\mathbb P_{i,y,z}^{+}$
-a.s.,
\begin{align} \lim_{n\to \infty} q_{n,z} (0) &= \lim_{n\to \infty} \mathbb P_{i,y,z}^{+} (Z_n >0 \big| (X_k)_{k\geq 0} ) \nonumber \\[3pt] &= \mathbb P_{i,y,z}^{+} ( \cap_{n\geq 1} \{ Z_n >0\} \big| (X_k)_{k\geq 0} ). \end{align}
Moreover, by convexity of the function
$q_{n,z}(s)$
we have
\begin{align} q_{n,z}(0) \leq z e^{S_n}. \end{align}
The following formula (whose proof is left to the reader) is similar to the well-known statements from the papers by Agresti [Reference Agresti2] and Geiger and Kersting [Reference Geiger and Kersting9]: for any
$s \in [0,1)$
and
$n \geq 1$
,
\begin{align} \frac{1}{q_{n,z} (s)} &= \frac{1}{z f^{\prime}_{X_1}(1) \cdots f^{\prime}_{X_n}(1) (1-s) } \nonumber \\[3pt] &+ \frac{1}{z}\sum_{k=1}^{n} \frac{\varphi_{X_{k}} \circ f_{X_{k+1}} \circ \cdots \circ f_{X_n} (s)}{f^{\prime}_{X_1}(1) \cdots f^{\prime}_{X_{k-1}}(1) } \nonumber\\[3pt] &+ \psi_{z} \circ f_{X_{1}} \circ \cdots \circ f_{X_n} (s). \end{align}
We can rewrite (3.6) in the following more convenient form: for any
$s \in [0,1)$
and
$n \geq 1$
,
\begin{align} q_{n,z} (s)^{-1} &= \frac{1}{z}\bigg( \frac{e^{-S_n}}{1-s} + \sum_{k=0}^{n-1} e^{-S_{k}} \eta_{k+1,n}(s) \bigg) \nonumber\\[3pt] {}&+ \psi_{z} \circ f_{X_{1}} \circ \cdots \circ f_{X_n} (s), \end{align}
where
\begin{equation*} \eta_{k,n}(s) = \varphi_{X_{k}} \circ f_{X_{k+1}} \circ \cdots \circ f_{X_n} (s). \end{equation*}
Since
$\frac{1}{2}\varphi(0) \leq \varphi(s) \leq 2 \varphi(1) $
, for any
$k \in \{ 1, \dots, m \}$
,
\begin{equation} 0 \leq \eta_{k,m}(s) \leq \frac{f^{\prime\prime}_{X_{k}}(1)}{f^{\prime}_{X_{k}}(1)^2} \leq \eta\,{:\!=}\,\max_{i\in \mathbb X} \frac{f^{\prime\prime}_{i}(1)}{f^{\prime}_i (1)^2}. \end{equation}
By Theorem 5 of [Reference Athreya and Karlin4], for any
$(i,y) \in \textrm{supp}(V)$
,
$s \in[0,1)$
,
$m\geq 1$
, and
$k \in \{ 1, \dots, m \}$
, there exists a random variable
$\eta_{k,\infty}(s)$
such that
\begin{align} \lim_{n\to+\infty} \eta_{k,n}(s) = \eta_{k,\infty}(s) \end{align}
everywhere, and by (3.8), for any
$s \in[0,1)$
and
$k \geq 1 $
,
\begin{equation} {} {}\eta_{k,\infty}(s) \in [0,\eta].\end{equation}
In the same way,
\begin{align} \lim_{n\to+\infty} \psi_{z} \circ f_{X_{1}} \circ \cdots \circ f_{X_n} (s) = \psi_{z,\infty}(s) \in \left[0,\frac{z-1}{2} \right]\end{align}
everywhere. For any
$s \in [0,1)$
, define
$q_{\infty,z}(s)$
by setting
\begin{equation} {} {}q_{\infty,z}(s)^{-1} \,{:\!=}\, \frac{1}{z}\left[ \sum_{k=0}^{+\infty} e^{-S_k} \eta_{k+1,\infty}(s) \right] + \psi_{z,\infty}(s). \end{equation}
By Lemma 2.5, we have that
\begin{align} \mathbb{E}_{i,y}^+ q_{\infty,z}(s)^{-1} <+\infty. \end{align}
Lemma 3.1. Assume Conditions 1 and 3 and
$k'(0)=0$
. For any
$(i,y) \in \text{supp}\ V$
,
$z\in \mathbb{N},\ z\neq 0$
, and
$s\in [0,1)$
,
\begin{align*} \lim_{n\to+\infty} \mathbb{E}_{i,y}^+ \left|\frac{1}{q_{n,z}(s) } - \frac{1}{q_{\infty,z}(s) } \right| = 0 \end{align*}
and
\begin{align*} \lim_{n\to+\infty} \mathbb{E}_{i,y}^+ \left| q_{n,z}(s) - q_{\infty,z}(s) \right| = 0. \end{align*}
Proof. We give a sketch only. Following the proof of Lemma 3.2 in [Reference Grama, Lauvergnat and Le Page13], for any
$(i,y) \in \text{supp}\ V$
, by (3.7), (3.8), and (3.10), we obtain
\begin{align} \mathbb{E}_{i,y}^+ \left( \left\lvert{q_{n,z}^{-1}(s) - q_{\infty,z}^{-1}(s)}\right\rvert \right) &\leq \frac{1}{z(1-s)}\mathbb{E}_{i,y}^+ \left( e^{-S_n} \right) \nonumber\\[3pt] &+ \frac{1}{z} \mathbb{E}_{i,y}^+ \left( \sum_{k=0}^{l} e^{-S_k} \left\lvert{\eta_{k+1,n}(s) - \eta_{k+1,\infty}(s) }\right\rvert \right) \nonumber\\[3pt] &+ \frac{2\eta}{z} \mathbb{E}_{i,y}^+ \left( \sum_{k=l+1}^{+\infty} e^{-S_k} \right) \nonumber\\[3pt] {}&+ \mathbb{E}_{i,y}^+ \big|\psi_{z}\circ f_{X_1} \circ\dots \circ f_{X_n}(s) - \psi_{z,\infty}(s)\big|. \end{align}
The last term in the right-hand side of (3.14) converges to 0 as
$n\to \infty$
by (3.11). By Lemma 2.5 and the Lebesgue dominated convergence theorem, we have
\begin{align*} {}\limsup_{n\to\infty} \mathbb{E}_{i,y}^+ \left( \left\lvert{q_{n,z}^{-1}(s) - q_{\infty,z}^{-1}(s)}\right\rvert \right) {}\leq \frac{2\eta}{z} \mathbb{E}_{i,y}^+ \left( \sum_{k=l+1}^{+\infty} e^{-S_k} \right). \end{align*}
Taking the limit as
$l\to \infty$
, again by Lemma 2.5, we conclude the first assertion of the lemma. The second assertion follows from the first one, since
$q_{n,z}(s) \leq 1$
and
$q_{\infty,z}(s)\leq 1$
.
Lemma 3.2. Assume Conditions 1 and 3 and
$k'(0)=0$
. For any
$(i,y)\in \text{supp}\ V$
and
$z\in \mathbb N$
,
$z\not=0$
, we have, for any
$k \geq 1$
,
$\mathbb P_{i,y,z}^{+}$
-a.s.,
\begin{align*} \mathbb P_{i,y,z}^{+} ( \cup_{k\geq 1} \{ Z_k =0\} \big| (X_k)_{k\geq 1} ) <1. \end{align*}
Proof. By (3.4) we have,
$\mathbb P_{i,z,y}^{+}$
-a.s.,
\begin{align*} 1- \mathbb P_{i,z,y}^{+} ( \cup_{k\geq 1} \{ Z_k =0\} \big| (X_k)_{k\geq 1} ) = \lim_{n\to \infty} q_{n,z} (0). \end{align*}
\begin{align} \mathbb E_{i,y}^{+} q_{n,z} (0)^{-1} &\leq \frac{1}{z} \mathbb E_{i,y}^{+} \bigg( e^{-S_n} + \eta \sum_{k=0}^{n} e^{-S_{k-1}} \bigg) + 1. \end{align}
By Lemma 2.5 and a monotone convergence argument,
\begin{align} \mathbb E_{i,y}^{+} \lim_{n\to\infty} q_{n,z} (0)^{-1} = \lim_{n\to\infty}\mathbb E_{i,y}^{+} q_{n,z} (0)^{-1} < \infty. \end{align}
Thus,
$\mathbb P_{i,y}^{+}$
-a.s.,
\begin{align*} \lim_{n\to\infty} q_{n,z} (0) >0, \end{align*}
which ends the proof of the lemma.
We will make use of the following lemma.
Lemma 3.3. There exists a constant c such that, for any
$z\in \mathbb N$
,
$z\not=0,$
and
$y\geq 0$
sufficiently large,
\begin{align*} \sup_{i\in \mathbb X}\mathbb P_{i,z} \bigg( Z_n >0, \tau_{y} \leq n \bigg) \leq c z\frac{ e^{-y} (1+ \max\{y,0 \})}{\sqrt{n}}. \end{align*}
Proof. We follow the same line as the proof of Theorem 1.1 in [Reference Grama, Lauvergnat and Le Page13]. First, we have
\begin{align*} \mathbb P_{i,z}(Z_n>0, \tau_y \leq n) = \mathbb P_i(q_{n,z}(0);\ \tau_y \leq n). \end{align*}
Using (3.5) and the fact that
$q_{n,z}(0)$
is nonincreasing in n, we have
\begin{equation*} q_{n,z}(0) \leq z e^{\min_{1\leq k\leq n} S_k}. \end{equation*}
Setting
$B_{n,j}=\{ -(\,j+1) < \min_{1\leq k\leq n} (y+S_k) \leq -j \}$
, this implies
\begin{align*} &\mathbb P_{i,z}(Z_n>0, \tau_y \leq n) \\[3pt]& \leq z \mathbb E_{i,0}(e^{\min_{1\leq k\leq n} S_k};\ \tau_y \leq n) \\[3pt]&\leq z e^{-y}\sum_{j=1}^{\infty} \mathbb E_{i,0}(e^{\min_{1\leq k\leq n} (y+S_k)};\ B_{n,j}, \tau_y \leq n)\\[3pt]&\leq z e^{-y}\sum_{j=1}^{\infty} e^{-j} \mathbb P_{i,0}( \tau_{y+j+1} > n). \end{align*}
Using the point 2 of Proposition 2.2 we obtain the assertion of the lemma.
It is known from the results in [Reference Grama, Lauvergnat and Le Page12] that when y is sufficiently large,
$(i,y) \in \text{supp}\ V$
. For
$(i,y) \in \text{supp}\ V$
, set
\begin{align} U(i,y,z) \,{:\!=}\, \mathbb E_{i,y}^{+} q_{\infty,z}(0) = \mathbb P_{i,z,y}^{+} (\cap_{n\geq1} \{ Z_n>0\}). \end{align}
Theorem 1.1 is a direct consequence of the following proposition, which extends Theorem 1.1 in [Reference Grama, Lauvergnat and Le Page13] to the case
$z>1$
.
Proposition 3.4. Assume Conditions 1–4. Suppose that
$i\in \mathbb X$
and
$z\in \mathbb N, z \neq 0$
. Then for any
$i \in \mathbb X$
the limit as
$y\to \infty$
of V(i,y) U(i,y,z) exists and satisfies
\begin{align*} u(i,z ) \,{:\!=}\, \lim_{y\to \infty} \frac{2}{\sqrt{2\pi} \sigma} V(i,y) U(i,y,z) >0. \end{align*}
Moreover,
\begin{align*} \lim_{y\to \infty} \sqrt{n} \mathbb P_{i,z} (Z_n>0, X_n=j) = u(i,z ) \boldsymbol \nu (j). \end{align*}
Proof. By Lemma 2.8 and (3.17), for
$(i,y)\in \text{supp}\ V$
and
$j \in \mathbb X, $
\begin{align} &\lim_{n\to\infty}\sqrt{n} \mathbb P_{i,z} \left( Z_n > 0 \,,\, X_n = j \,,\, \tau_y > n \right) \nonumber \\[3pt]&= \frac{2V(i,y)}{\sqrt{2\pi}\sigma} \boldsymbol \nu (j)\mathbb P_{i,y,z}^{+} (\cap_{n\geq1} \{ Z_n>0\}) \nonumber \\[3pt]&= \frac{2V(i,y)}{\sqrt{2\pi}\sigma} U(i,y,z) \boldsymbol \nu (j), \end{align}
and
\begin{align} \sqrt{n} \mathbb P_{i,z} (Z_n>0, X_n=j)& = \sqrt{n} \mathbb P_{i,z} (Z_n>0, X_n=j, \tau_y > n) \nonumber \\[3pt] & +\sqrt{n} \mathbb P_{i,z} (Z_n>0, X_n=j, \tau_y \leq n) \nonumber \\[3pt] &= J_1(n,y) + J_2(n,y). \end{align}
By Lemma 3.3,
\begin{align} J_2(n,y) \leq c z e^{-y} (1+ \max\{y,0 \}). \end{align}
From (3.18), (3.19), and (3.20), when y is sufficiently large,
\begin{align} \limsup_{n\to\infty} \sqrt{n} \mathbb P_{i,z} (Z_n>0, X_n=j)&\leq\frac{2V(i,y)}{\sqrt{2\pi}\sigma} U(i,y,z) \boldsymbol \nu (j) \nonumber \\[3pt]&+ c z e^{-y} (1+ \max\{y,0 \}) <\infty. \end{align}
Similarly, when y is sufficiently large,
\begin{align} L_0=\liminf_{n\to\infty} \sqrt{n} \mathbb P_{i,z} (Z_n>0, X_n=j) &\geq \frac{2V(i,y)}{\sqrt{2\pi}\sigma} U(i,y,z) \boldsymbol{\nu} (\,j). \end{align}
Since
$\mathbb{P}_{i,z} \left( Z_n > 0 \,,\, X_n = j \,,\, \tau_y > n \right)$
is nondecreasing in y, from (3.18) it follows that the function
\begin{align} u(i,y,z ) \,{:\!=}\, \frac{2V(i,y)}{\sqrt{2\pi}\sigma} U(i,y,z) \end{align}
is nondecreasing in y. Moreover, by (3.21) and (3.22), we deduce that u(i, y, z) as a function of y is bounded by
$L_0$
. Therefore its limit as
$y \to \infty$
exists:
$ u(i,z)= \lim_{y\to \infty } u(i,y,z). $
To prove that
$U(i,y,z)=\mathbb E_{i,y}^{+} q_{\infty,z}(0) >0$
, it is enough to remark that, by (3.13), it holds that
$\mathbb E_{i,y}^{+} q^{-1}_{\infty,z}(0) <\infty$
. On the other hand,
$V(i,y)>0$
for large enough y. Therefore
$u(i,z)>0$
, which proves the first assertion. The second assertion follows immediately from (3.21) and (3.22) by letting
$y\to\infty$
.
4. Proof of Theorem 1.2
Throughout this section we write, for
$n\geq 1$
,
\begin{align*} T_n=\sup\{ 0\leq k \leq n\,{:}\, S_k =\inf \{ S_0,\ldots,S_n \} \}, \end{align*}
and, for
$0 \leq k \leq n$
,
\begin{align*} L_{k,n} = \inf_{k\leq j\leq n} \big( S_{j} - S_{k}\big). \end{align*}
Recall the following identities, which will be useful in the proofs:
\begin{align} \{T_k=k \}&= \{S_0\geq S_k, S_1\geq S_k,\ldots, S_{k-1}\geq S_{k} \} , \end{align}
\begin{align} \{L_{k,n} > 0 \}&= \{S_{k+1}\geq S_k, S_{k+2} \geq S_k,\ldots, S_n\geq S_k \}, \end{align}
\begin{align} \{T_n=k \} &= \{T_k=k \} \cap \{L_{k,n} >0 \}. \end{align}
For any
$n\geq 1,$
set
\begin{align} P_{n}(i,s,z)=\mathbb E_{i,z} \left(e^{-e^{-s}\frac{Z_{n}}{e^{S_{n}}} };\ Z_{n}>0, L_{0,n} >0 \right)\!. \end{align}
It is easy to see that, by the definition (2.1) of
$\tau_y$
, we have
$\{\tau_0>n\}=\{L_{0,n}>0\}$
, so that (4.4) is equivalent to
\begin{align} P_{n}(i,s,z) = \mathbb E_{i,z} \left(e^{-e^{-s}\frac{Z_{n}}{e^{S_{n}}} };\ Z_{n}>0, \tau_{0} >n \right)\!. \end{align}
We first prove a series of auxiliary statements.
Lemma 4.1. Assume Conditions 1–4. Let
$s\geq 0$
. For any
$(i,0)\in \text{supp}\, V$
and
$z\in \mathbb N$
,
$z\not=0$
, there exists a positive random variable
$W_{i,z}$
such that
\begin{align*} \lim_{n\to \infty} \sqrt{n}P_{n}(i,s,z) =2\frac{V(i,0)}{\sqrt{2\pi}\sigma} P_{\infty}(i,s,z), \end{align*}
where
\begin{align*} P_{\infty}(i,s,z) \,{:\!=}\, \mathbb E^{+}_{i,0,z} \big(e^{-W_{i,z}e^{-s}}; \cap_{p\geq 1} \{ Z_p >0\} \big)\leq 1. \end{align*}
Moreover, for any
$(i,0)\in \text{supp}\ V$
and
$z\in \mathbb N$
,
$z\not=0$
, it holds
$\mathbb P^{+}_{i,0,z}$
-a.s. that
\begin{align*} \cap_{p\geq 1} \{ Z_p >0\} = \{ W_{i,z} >0\}. \end{align*}
For any
$(i,0)\not\in \text{supp}\ V$
and
$z\in \mathbb N$
,
$z\not=0$
,
\begin{align*} \lim_{n\to \infty} \sqrt{n}P_{n}(i,s,z) = 0. \end{align*}
Proof. Define
\begin{equation*}Y_n= e^{-e^{-s}\frac{Z_{n}}{e^{S_{n}}} } \textbf{1} \{ Z_n>0\}.\end{equation*}
Since
\begin{equation*}\left(\frac{Z_{n}}{e^{S_{n}}}\right)_{n\geq0}\end{equation*}
is a positive
$((\mathscr F_n)_{n\geq0}, \mathbb P^{+}_{i,0,z} )$
-martingale, its limit, say
\begin{equation*}W_{i,z}=\lim_{n\to\infty}\frac{Z_{n}}{e^{S_{n}}},\end{equation*}
exists
$\mathbb P^{+}_{i,0,z}$
-a.s. and is nonnegative. Therefore,
$\mathbb P^{+}_{i,0,z}$
-a.s.
\begin{align*} \lim_{n\to \infty} Y_n = e^{-e^{-s} W_{i,z} } \textbf{1} \{ \cap_{p\geq 1} \{ Z_p >0\} \}. \end{align*}
Now the first assertion follows from Lemma 2.8.
For the second assertion we use a result from Kersting [Reference Kersting18] stated in a more general setting of branching processes with varying environment. To apply it we shall condition with respect to the environment
$(X_n)_{n\geq 0}$
, so that one can consider that the environment is fixed. The condition (A) in [Reference Kersting18] is obviously satisfied because of Condition 4. Moreover, according to Lemma 3.2, the extinction probability satisfies,
$P_{i,0,z}^{+}$
-a.s.,
\begin{align*} \mathbb P_{i,0,z}^{+} ( \cup_{p\geq 1} \{ Z_p =0\} \big| (X_n)_{n\geq 1} ) <1. \end{align*}
By Theorem 2 in [Reference Kersting18], this implies that,
$P_{i,0,z}^{+}$
-a.s.,
\begin{align*} \mathbb P_{i,0,z}^{+} ( \cup_{p\geq 1} \{ Z_p =0\} \big| (X_n)_{n\geq 1} )=\mathbb P_{i,0,z}^{+} ( W_{i,z} =0 \big| (X_n)_{n\geq 1} ). \end{align*}
Since
$P_{i,0,z}^{+}$
-a.s. we have
$ \cup_{p\geq 1} \{ Z_p =0\} \subset \{ W_{i,z} = 0\},$
we obtain the second assertion.
The third assertion follows from the point 1 of Proposition 2.2, since
$V(i,0)=0$
. This ends the proof of the lemma.
Notice that
$P_{\infty}(i,s,z)$
can be rewritten as
\begin{align*} P_{\infty}(i,s,z) = \mathbb E^{+}_{i,0,z} \big(e^{-W_{i,z}e^{-s}};\ W_{i,z} >0 \big). \end{align*}
This shows that
$P_{\infty}(i,s,z)$
is the Laplace transformation at
$e^{-s}$
of a measure on
$\mathbb R_{+}$
which assigns the mass
$0$
to the set
$\{0\}$
.
We will need the following lemma.
Lemma 4.2. There exists a constant
$c $
such that, for any
$n\geq 1, z\in \mathbb{N}, z\neq 0$
,
\begin{align*} \sup_{i\in \mathbb X}\mathbb P_{i,z} \big( T_n=n, Z_n >0 \big) \leq c\frac{ z}{n^{3/2}}. \end{align*}
Proof. Since
$T_n$
is a function only on the environment
$\left( X_k \right)_{k\geq 0}$
, conditioning with respect to
$\left( X_k \right)_{k\geq 0}$
, we have
\begin{align*} \mathbb P_{i,z} \big( T_n=n, Z_n >0 \big) = \mathbb E_{i,z} \big( q_{n,z}(0);\ T_n=n \big), \end{align*}
with
$q_{n,z}(0)$
defined by (3.2). Using the bound (3.5) we obtain
\begin{align} \mathbb P_{i,z} \big( T_n=n, Z_n >0 \big) \leq z \mathbb E_{i} \big( e^{S_n};\ T_n=n \big). \end{align}
By (4.1) and the duality (Lemma 2.9),
\begin{align} \mathbb E_{i} \big( e^{S_n};\ T_n=n \big) &= \mathbb E_{\boldsymbol{\nu}}^* \big( e^{-S_n^*};\ \tau^*_0>n \big) \frac{1}{\boldsymbol{\nu}(i)} \nonumber \\[3pt] &\leq c \mathbb E_{\boldsymbol{\nu}}^* \big( e^{-S_n^*};\ \tau^*_0>n \big). \end{align}
Using the local limit theorem for the dual Markov chain (see Proposition 2.4) and following the proof of Lemma 2.5, we obtain
\begin{align} \mathbb E_{\boldsymbol{\nu}}^* \big( e^{-S_n^*};\ \tau^*_0>n \big) \leq \frac{c}{n^{3/2}}. \end{align}
The key point of the proof of Theorem 1.2 is the following statement.
Proposition 4.3. Assume Conditions 1–4. For any
$i\in \mathbb X$
,
$s\in \mathbb R$
, and
$z\in \mathbb N$
,
$z\not=0$
,
\begin{align*} &\lim_{n\to \infty} \sqrt{n}\mathbb E_{i,z} \left( e^{-e^{-s}\frac{Z_n}{e^{S_n}} };\ Z_n>0\right) \\[3pt] &=\frac{2}{\sqrt{2\pi}\sigma}\sum_{k=1}^{\infty} \mathbb E_{i,z} \big(V(X_k,0) \textbf{1}_{ \text{supp}\ V} (X_k,0) P_{\infty}(X_k,s+S_k,Z_k); \\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad Z_k>0, T_k=k \big)\\ & \,{=\!:}\, u(i,z, e^{-s}). \end{align*}
With
$s=+\infty$
,
\begin{align*} &\lim_{n\to \infty} \sqrt{n}\mathbb P_{i,z} ( Z_n>0) = u(i,z),\\ \end{align*}
where
\begin{align*} &u(i,z)=\frac{2}{\sqrt{2\pi}\sigma}\sum_{k=1}^{\infty} \mathbb E_{i,z} \big( V(X_k,0) \textbf{1}_{ \text{supp}\ V} (X_k,0) \mathbb P^{+}_{X_k,0,Z_k} ( W_{i,z} >0 ); \\&\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\quad Z_k>0, T_k=k\big) >0 \end{align*}
is defined in Theorem 1.1.
Proof. Using (4.3), one has
\begin{align} \mathbb E_{i,z} (e^{-e^{-s}\frac{Z_n}{e^{S_n}} };\ Z_n>0)& =\sum_{k=0}^{n-1} \mathbb E_{i,z} \big( e^{-e^{-s}\frac{Z_n}{e^{S_n}} };\ Z_n>0, T_k=k, L_{k,n} >0 \big) \nonumber\\ &\quad + \mathbb E_{i,z} \big( e^{-e^{-s}\frac{Z_n}{e^{S_n}} };\ Z_n>0, T_n=n \big)\nonumber\\[3pt] &=J_1(n) + J_2(n). \end{align}
By Lemma 4.2,
\begin{align} \limsup_{n\to\infty}\sqrt{n} J_2(n) \leq \lim_{n\to\infty} \sqrt{n} \mathbb P_{i,z} \big( T_n=n, Z_n >0 \big) = 0. \end{align}
We now deal with the term
$J_1(n)$
. We shall make use of the notation
$P_{n}(i,y,z)$
defined in (4.5). By the Markov property (conditioning with respect to
$\mathscr F_k = \sigma \{ X_0,Z_0, \ldots, X_k, Z_k \}$
), and using (4.2), we obtain
\begin{align*} &\mathbb E_{i,z} \big( e^{-e^{-s}\frac{Z_n}{e^{S_n}} };\ Z_n>0, T_k=k, L_{k,n} >0 \big) \\[3pt] &\qquad = \mathbb E_{i,z} \big( P_{n-k}(X_{k},s+S_k,Z_{k}) ;\ T_k=k, Z_k >0 \big). \end{align*}
Therefore
\begin{align*} J_1(n) =\sum_{k=0}^{n-1} \frac{1}{\sqrt{n-k}} \mathbb E_{i,z} \big( \sqrt{n-k} P_{n-k}(X_{k},s+S_k,Z_{k}) ;\ T_k=k, Z_k >0 \big). \end{align*}
For brevity, write
\begin{align*} E_k= \mathbb E_{i,z} \big( \sqrt{n-k} P_{n-k}(X_{k},s+S_k,Z_{k}) ;\ T_k=k, Z_k >0 \big). \end{align*}
It is easy to see that, with some
$ l\leq n$
,
\begin{align} \sqrt{n}J_1(n) &= \sum_{k=0}^{l} \frac{\sqrt{n}}{\sqrt{n-k}} E_k + \sum_{k=l+1}^{n-1} \frac{\sqrt{n}}{\sqrt{n-k}} E_k \nonumber\\&= J_{11}(n,l) + J_{12}(n,l). \end{align}
For
$J_{12}(n,l)$
, we have, using (4.5),
\begin{align*} J_{12}(n,l) &= \sum_{k=l+1}^{n-1} \frac{\sqrt{n}}{\sqrt{n-k}} E_k \\ &\leq \sum_{k=l+1}^{n-1} \frac{\sqrt{n}}{\sqrt{n-k}} \mathbb E_{i,z} \big( \sqrt{n-k} \mathbb P_{X_{k}} (\tau_0>n-k) ;\ T_k=k, Z_k >0 \big). \end{align*}
Using the point 2 of Proposition 2.2 and Lemma 4.2,
\begin{align*} J_{12}(n,l) &\leq c\sum_{k=l+1}^{n-1} \frac{\sqrt{n}}{\sqrt{n-k}} \mathbb P_{i,z} \big( T_k=k, Z_k >0 \big) \\[3pt] &\leq c z\sum_{k=l+1}^{n-1} \frac{\sqrt{n}}{\sqrt{n-k}} \frac{ 1}{k^{3/2}}\\[3pt] &\leq c z\bigg( \frac{1}{\sqrt{n}} + \frac{2}{\sqrt{l}} \bigg), \end{align*}
where to bound the second line we split the summation into two parts, for
$k > n/2$
and
$k\leq n/2$
. Let
$\varepsilon >0$
be arbitrary. Then there exists
$n_{\varepsilon, z}$
such that, for
$n\geq l\geq n_{\varepsilon, z}$
,
\begin{align} J_{12}(n,l) \leq \varepsilon. \end{align}
For
$J_{11}(n,l)$
, we have
\begin{align*} J_{11}(n,l) = \sum_{k=0}^{l} \frac{\sqrt{n}}{\sqrt{n-k}} \mathbb E_{i,z} \big( \sqrt{n-k} P_{n-k}(X_{k},s+S_k,Z_{k}) ;\ T_k=k, Z_k >0 \big). \end{align*}
Since l is fixed, taking the limit as
$n\to \infty$
, by Lemmata 4.1 and 4.2,
\begin{align} \lim_{n\to\infty} J_{11}(n,l) &= \sum_{k=0}^{l} \mathbb E_{i,z} \big( P_{\infty}(X_k,s+S_k,Z_k) ;\ T_k=k, Z_k >0 \big) \nonumber\\ &\leq \sum_{k=0}^{l} \mathbb P_{i,z} \big( T_k=k, Z_k >0 \big) \nonumber\\ &\leq \sum_{k=0}^{\infty} \frac{cz}{k^{3/2}} \leq c z. \end{align}
Since
$\varepsilon$
is arbitrary, from (4.11), (4.12), and (4.13), taking the limit as
$l\to\infty$
, we deduce that
\begin{align*} \lim_{n\to\infty} \sqrt{n}J_{1}(n) &= \sum_{k=0}^{\infty} \mathbb E_{i,z} \big( P_{\infty}(X_k,s+S_k,Z_k) ;\ T_k=k, Z_k >0 \big). \end{align*}
From this and (4.9)–(4.10) we deduce the first assertion of the proposition. The second one is proved in the same way.
Now we proceed to prove Theorem 1.2. Denote by
\begin{equation*} \mu_{n,i,z,j} (B) = \mathbb P_{i,z} \left( Z_ne^{-S_n} \in B, X_n=j \big| Z_n>0 \right)\end{equation*}
the joint law law of
$\frac{Z_n}{e^{S_n}}$
and
$X_n=j$
given
$Z_n>0$
under
$\mathbb P_i$
, where B is any Borel set of
$\mathbb R_+.$
Set for short
\begin{equation*}\mu_{n,i,z} (B) = \mathbb P_{i,z} \left( Z_ne^{-S_n} \in B \big| Z_n>0 \right).\end{equation*}
We shall prove that the sequence
$(\mu_{n,i,z})_{n\geq1}$
is convergent in law. For this we use the convergence of the corresponding Laplace transformations:
\begin{align*} \mathbb E_{i,z} ( e^{-t\frac{Z_n}{e^{S_n}} } \big| Z_n>0) &= \frac{\sqrt{n}\mathbb E_{i,z} ( e^{-t\frac{Z_n}{e^{S_n}} };\ Z_n>0)} {\sqrt{n}\mathbb P_{i,z} ( Z_n>0)}. \end{align*}
By Proposition 4.3, we see that, with
$t=e^{-s}$
,
\begin{align*} \lim_{n\to \infty} \mathbb E_{i,z} ( e^{-e^{-s}\frac{Z_n}{e^{S_n}} } \big| Z_n>0) = \frac{u(i,z, e^{-s}) } {u(i,z) }.\end{align*}
It is obvious that
$u(i,z, e^{-s})$
is also a Laplace transformation at
$t=e^{-s}$
of a measure on
$\mathbb R_{+}$
which assigns the mass 0 to the set
$\{0\}$
and that u(i,z) is the total mass of this measure. Therefore the ratio
\begin{equation*} \frac{u(i,z, e^{-s}) } {u(i,z) }\end{equation*}
is the Laplace transformation of a probability measure
$\mu_{i,z}$
on
$R_{+}$
such that
$\mu_{i,z}(\{0\})=0.$
5. Proof of Theorems 1.3 and 1.4
Recall that by the properties of the harmonic function, for any
$i\in \mathbb X$
there exists
$y_i\geq 0$
such that
$(i,y)\in \text{supp}\ V$
for any
$y\geq y_i.$
First we prove the following auxiliary statement.
Lemma 5.1. Assume Conditions 1–4. Let
$i\in \mathbb X$
and
$z\in \mathbb N$
,
$z\not = 0$
. For any
$\theta \in (0,1)$
and
$y\geq 0$
large enough such that
$(i,y)\in \text{supp}\ V$
,
\begin{align*} \lim_{m\to\infty}\lim_{n\to\infty} \sqrt{n} \mathbb P_{i,z} \left( Z_m>0, Z_{[\theta n]}=0, \tau_y>n \right) = 0. \end{align*}
Proof. Let
$m, n\geq 1$
be such that
$[\theta n] >m$
. Then
\begin{align*} J_{m,n}(\theta,y)&\,{:\!=}\,\mathbb P_{i,z} \left( Z_m>0, Z_{[\theta n]}=0, \tau_y>n \right) \\[3pt] &= \mathbb P_{i,z} \left( Z_m>0, \tau_y>n \right) -\mathbb P_{i,z} \left(Z_{[\theta n]}>0, \tau_y>n \right)\\[3pt] &= \mathbb E_{i,z} \big( \mathbb P_{i,z} \left( Z_m>0 | X_1,\ldots, X_m \right) \\[3pt] &\qquad\qquad - \mathbb P_{i,z} \left(Z_{[\theta n]}>0 | X_1,\ldots, X_{[\theta n]} \right);\ \tau_y>n \big)\\[3pt] &\leq \mathbb E_{i,z} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right|;\ \tau_y>n \big). \end{align*}
Let
$P_n(i,y)=\mathbb P_{i}(\tau_y>n).$
By the Markov property
\begin{align*} &\mathbb E_{i,z} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right|;\ \tau_y>n \big)\\[3pt] &=\mathbb E_{i} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right| P_{n-[\theta n]}(X_{[\theta n]}, y+ S_{[\theta n]});\ \tau_y>[\theta n] \big). \end{align*}
Using the point 2 of Proposition 2.2 and the point 3 of Proposition 2.1, on the set
$\{ \tau_y>[\theta n] \}$
,
\begin{align*} P_{n-[\theta n]}(X_{[\theta n]}, y+ S_{[\theta n]},z)\leq c\frac{1+y+ S_{[\theta n]}}{\sqrt{n-[\theta n]}} \leq c\frac{1+ V(X_{[\theta n]}, y+ S_{[\theta n]}) }{\sqrt{(1-\theta) n} }.\end{align*}
Therefore
\begin{align*}&\sqrt{n} J_{m,n}(\theta,y) \\[3pt] &\leq\mathbb E_{i} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right|\sqrt{n}P_{n-[\theta n]}(X_{[\theta n]}, y+ S_{[\theta n]});\ \tau_y>[\theta n] \big)\\[3pt] &\leq \frac{c}{\sqrt{1-\theta} } \mathbb E_{i} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right| ;\ \tau_y>[\theta n] \big) \\[3pt] &\quad + \frac{c}{\sqrt{1-\theta} } \mathbb E_{i} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right|V(X_{[\theta n]}, y+ S_{[\theta n]}) ;\ \tau_y>[\theta n] \big). \end{align*}
Using the bound (3.1) and again the point 2 of Proposition 2.2,
\begin{align*} \limsup_{n\to\infty}\mathbb E_{i} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right| ;\ \tau_y>[\theta n] \big) \leq \lim_{n\to\infty} \mathbb P_{i} \big( \tau_y>[\theta n] \big) = 0. \end{align*}
If
$(i,y)\not\in \text{supp}\ V$
,
\begin{align*} & \mathbb E_{i} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right| V(X_{[\theta n]}, y+ S_{[\theta n]}) ;\ \tau_y>[\theta n] \big) \\[3pt] &\leq \mathbb E_{i} \big( V(X_{[\theta n]}, y+ S_{[\theta n]}) ;\ \tau_y>[\theta n] \big) \\[3pt] &= V(i,y)=0. \end{align*}
If
$(i,y)\in \text{supp}\ V$
, changing the measure by (2.14), we have
\begin{align*} & \mathbb E_{i} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right| V(X_{[\theta n]}, y+ S_{[\theta n]}) ;\ \tau_y>[\theta n] \big) \\[3pt] &= V(i,y) \mathbb E_{i,y}^+ \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right|. \end{align*}
Taking the limit as
$n\to\infty$
and then as
$m\to\infty$
, by Lemma 3.1,
\begin{align*} &\lim_{m\to\infty}\lim_{n\to\infty} \mathbb E_{i} \big( \left| q_{m,z}(0) - q_{[\theta n],z}(0) \right| V(X_{[\theta n]}, y+ S_{[\theta n]}) ; \tau_y>[\theta n] \big) =0. \end{align*}
Taking into account the previous bounds we obtain the assertion of the lemma.
Proof of Theorem 1.3. Let
$i,j\in \mathbb X$
,
$y\geq 0$
,
$z\in \mathbb N$
,
$z\not=0$
,
$t\in \mathbb R$
. Then, for any
$n\geq 1$
and
$y \geq 0,$
\begin{align} &\mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_n>0 \right) \nonumber \\[3pt]&= \mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_n>0, \tau_y>n \right)\nonumber \\[3pt]&+ \mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_n>0, \tau_y\leq n \right)\nonumber \\[3pt]&=I_{1}(n,y) + I_{2}(n,y). \end{align}
By Lemma 3.3,
\begin{align} \sqrt{n} I_{2}(n,y) \leq \sqrt{n} P_{i,z}(Z_n>0, \tau_y \leq n) \leq c z e^{-y}(1+y). \end{align}
In the sequel we study
$I_{1}(n,y)$
. Let
$\theta \in (0,1)$
be arbitrary. We decompose
$I_{1}(n,y)$
into two parts:
\begin{align} I_{1}(n,y) &=\mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_{[\theta n]}>0, Z_n>0, \tau_y>n \right) \nonumber \\[3pt] &=\mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_{[\theta n]}>0, \tau_y>n \right) \nonumber \\[3pt] &- \mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_{[\theta n]}>0, Z_n=0, \tau_y>n \right) \nonumber \\[3pt] &=I_{11}(n,\theta,y) - I_{12}(n,\theta,y). \end{align}
In the following lemma we prove that the second term
$\sqrt{n}I_{12}(n,\theta,y)$
vanishes as
$n\to \infty.$
Lemma 5.2. Assume Conditions 1–4. For any
$i,j\in \mathbb X$
,
$z\in \mathbb N$
,
$z\not= 0$
, and
$y\geq 0$
sufficiently large,
\begin{align} \lim_{n\to \infty} \sqrt{n} \mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_{[\theta n]}>0, Z_n=0, \tau_y>n \right) = 0. \end{align}
Proof. Obviously,
\begin{align} | I_{12}(n,\theta,y)| &=\left| \mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_{[\theta n]}>0, Z_n=0, \tau_y>n \right) \right| \nonumber \\[3pt] &\leq \mathbb P_{i,z} \left( X_n=j, Z_{[\theta n]}>0, Z_n=0, \tau_y>n \right) \nonumber \\[3pt] &=\mathbb P_{i,z} \left( X_n=j, Z_{[\theta n]}>0, \tau_y>n \right) \nonumber \\[3pt] &\quad - \mathbb P_{i,z} \left( X_n=j, Z_n>0, \tau_y>n \right). \end{align}
As in (3.18), choosing
$y\geq 0$
such that
$(i,y) \in \text{supp}\ V$
, we have
\begin{align} \lim _{n\to\infty} \sqrt{n} \mathbb P_{i,z} \left( X_n=j, Z_n>0, \tau_y>n \right) = \frac{2V(i,y)}{\sqrt{2\pi}\sigma} U(i,y,z) \boldsymbol{\nu} (\,j). \end{align}
We shall prove that for any
$\theta \in (0,1)$
,
\begin{align} \lim _{n\to\infty} \sqrt{n} \mathbb P_{i,z} \left( X_n=j, Z_{[\theta n]}>0, \tau_y>n \right) = \frac{2V(i,y)}{\sqrt{2\pi}\sigma} U(i,y,z) \boldsymbol{\nu} (\,j). \end{align}
For any
$m\geq 1$
and n such that
$[\theta n] >m$
,
\begin{align} &\mathbb P_{i,z} \left( X_n=j, Z_{[\theta n]}>0, \tau_y>n \right) \nonumber \\[3pt] &=\mathbb P_{i,z} \left( X_n=j, Z_m>0, Z_{[\theta n]}>0, \tau_y>n \right) \nonumber \\[3pt] &=\mathbb P_{i,z} \left( X_n=j, Z_m>0, \tau_y>n \right) \nonumber \\[3pt] &\quad - \mathbb P_{i,z} \left( X_n=j, Z_m>0, Z_{[\theta n]}=0, \tau_y>n \right). \end{align}
By Lemma 2.6,
\begin{align*} &\lim_{n\to\infty} \sqrt{n} \mathbb P_{i,z} \left( X_n=j, Z_m>0, \tau_y>n \right) \nonumber \\[3pt]&= \frac{2V(i,y)}{\sqrt{2\pi}\sigma} \mathbb P_{i,z,y}^+ \left( Z_m>0 \right) \boldsymbol\nu (j). \end{align*}
Taking the limit as
$m\to\infty$
, by (3.17), we have
\begin{align} &\lim_{m\to\infty} \lim_{n\to\infty} \sqrt{n} \mathbb P_{i,z} \left( X_n=j, Z_m>0, \tau_y>n \right) \nonumber \\[3pt] &= \frac{2V(i,y)}{\sqrt{2\pi}\sigma} \mathbb P_{i,z,y}^{+} (\cap_{m\geq1} \{ Z_m>0\}) \boldsymbol{\nu} (\,j) \nonumber \\ &= \frac{2V(i,y)}{\sqrt{2\pi}\sigma} U(i,y,z) \boldsymbol{\nu} (\,j). \end{align}
By Lemma 5.1,
\begin{align*} & \limsup_{m\to\infty} \limsup_{n\to\infty} \sqrt{n} \mathbb P_{i,z} \left( X_n=j, Z_m>0, Z_{[\theta n]}=0, \tau_y>n \right) \\[3pt] &\leq \limsup_{m\to\infty} \lim_{n\to\infty} \sqrt{n} \mathbb P_{i,z} \left( Z_m>0, Z_{[\theta n]}=0, \tau_y>n \right) = 0, \end{align*}
which together with (5.8) and (5.9) proves (5.7). From (5.5), (5.6), and (5.7) we obtain the assertion of the lemma.
To handle the term
$I_{11}(n,\theta,y)$
we choose any m satisfying
$1\leq m \leq [\theta n]$
and split it into two parts:
\begin{align} I_{11}(n,\theta,y) &= \mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_m>0, \tau_y>n \right) \nonumber \\[3pt] &- \mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_m>0, Z_{[\theta n]}=0, \tau_y>n \right) \nonumber \\[3pt] & = I_{111}(n,m,y) - I_{112}(n,m,\theta,y). \end{align}
By Lemma 5.1, we have
\begin{align} &\limsup_{m\to\infty} \limsup_{n\to\infty} \sqrt{n} I_{112}(n,m,\theta,y) \nonumber \\[3pt] &\leq \lim_{m\to\infty} \lim_{n\to\infty} \sqrt{n}\mathbb P_{i,z} \left(Z_m>0, Z_{[\theta n]}=0, \tau_y>n \right) =0. \end{align}
The following lemma gives a limit for
$\sqrt{n}I_{111}(n,m,y)$
as
$n\to\infty$
and
$m\to\infty$
.
Lemma 5.3. Assume Conditions 1–4. Suppose that
$i,j\in \mathbb X$
,
$z\in \mathbb N$
,
$z\not = 0$
, and
$t\in \mathbb R.$
Then, for any
$y\geq 0$
sufficiently large,
\begin{align} \lim_{m\to \infty} & \lim_{n\to \infty} \sqrt{n} \mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_m>0, \tau_y>n \right) \nonumber \\[3pt] &= \frac{2\Phi^{+} (t)}{\sqrt{2\pi} \sigma} V(i,y) U(i,y,z) \boldsymbol{\nu} (\,j). \end{align}
Proof. Without loss of generality we can assume that
$n\geq2m.$
Let
$y \geq 0$
be so large that
$(i,y)\in \text{supp}\ V.$
Set
\begin{equation*}t_{n,y}=t+\frac{y}{\sqrt{n}\sigma}.\end{equation*}
Then
$I_{111}(n,m,y)$
can be rewritten as
\begin{align*} I_{111}(n,m,y)= \mathbb P_{i,z} \left( \frac{y+S_n}{\sqrt{n}\sigma} \leq t_{n,y}, X_n=j, Z_m>0, \tau_y>n \right). \end{align*}
If
$t<0$
, we have
$t_{n,y}<0$
for n large enough, and the assertion of the lemma becomes obvious since
$I_{111}(n,m,y)= 0 =\Phi^{+} (t)$
. Therefore, it is enough to assume that
$t \geq 0$
. To find the asymptotic of
$I_{111}(n,m,y)$
we introduce the following notation: for
$y',t'\in \mathbb R$
and
$1\leq k=n-m\leq n$
,
\begin{align*} \Phi_{k}(i,y',t') = \mathbb P_{i}\Big(\frac{y'+S_k}{\sigma\sqrt{k}} \leq t'; \tau_{y'}>k \Big). \end{align*}
Set
\begin{equation*}t_{n,m,y}=t_{n,y}\frac{\sqrt{n}}{\sqrt{n-m}}= \left(t+\frac{y}{\sqrt{n}\sigma} \right)\frac{\sqrt{n}}{\sqrt{n-m}}.\end{equation*}
By the Markov property,
\begin{align*} I_{111}(n,m,y)= \mathbb E_{i,z} \big( \Phi_{n-m}(X_m,y+S_m, t_{n,m,y}) ;\ Z_m>0, \tau_y>m\big). \end{align*}
Since
$t_{n,m,y} \leq \sqrt{2} (t +y/\sigma)$
, by Proposition 2.3, there exists an
$\varepsilon>0$
such that for any
$(i,y')\in \mathbb X\times \mathbb R$
,
\begin{align} & \sqrt{n-m}\left\lvert{\Phi_{n-m}(i,y',t_{n,m,y}) -\frac{2V(i,y')}{\sqrt{2\pi (n-m)} \sigma}\Phi^{+} \Big(t_{n,m,y} \Big) }\right\rvert \nonumber \\[3pt] &\leq c_{\varepsilon,t,y}\frac{1+\max\{ y',0 \}^2 }{(n-m)^{\varepsilon}}. \end{align}
Therefore, using (5.13),
\begin{align*} &A_n(m,y)\,{:\!=}\,\\ &\left\lvert{I_{111}(n,m,y) - \mathbb E_{i,z} \left( \frac{2V(X_m,y+S_m)}{\sqrt{2\pi (n-m)} \sigma}\Phi^{+} \big(t_{n,m,y}\big) ;\ Z_m>0, \tau_y>m\right)}\right\rvert \\ &\leq c_{\varepsilon,t,y}\frac{1+\mathbb E_{i,z} \max\{ y+S_m,0 \}^2 }{(n-m)^{1/2+\varepsilon}}.\end{align*}
This implies that
\begin{align} \lim_{n\to \infty} \sqrt{n} A_n(m,y) = 0. \end{align}
Note that with m and
$y\geq 0$
fixed, we have
$t_{n,m,y} \to t$
as
$n\to\infty$
. Therefore
\begin{align} \lim_{n\to +\infty} &\sqrt{n} \mathbb E_{i,z} \left( \frac{2V(X_m,y+S_m)}{\sqrt{2\pi k} \sigma}\Phi^{+} \big(t_{n,m}\big) ; Z_m>0, \tau_y>m\right) \nonumber \\ &= \frac{2\Phi^{+} (t)}{\sqrt{2\pi} \sigma} \mathbb E_{i,z} \big( V(X_m,y+S_m) ;\ Z_m>0, \tau_y>m\big). \end{align}
When
$(i,y) \in \text{supp}\ V$
, the change of measure (2.13) gives
\begin{align} \mathbb E_{i,z} & \big( V(X_m,y+S_m) ;\ Z_m>0, \tau_y>m\big) \nonumber \\ &\qquad\qquad\qquad\qquad\qquad = V(i,y)\mathbb P_{i,y,z}^{+} (Z_m>0). \end{align}
Since
$\mathbb P_{i,y,z}^{+} (Z_m>0) = \mathbb E_{i,y}^{+} q_{m,z}(0)$
, using Lemma 2.7,
\begin{align*} \lim_{m\to +\infty} \mathbb P_{i,y,z}^{+} (Z_m>0) = \lim_{m\to +\infty} \mathbb E_{i,y}^{+} q_{m,z}(0)= \mathbb E_{i,y}^{+} q_{\infty,z}(0) = U(i,y,z), \end{align*}
which, together with (5.14), (5.15), and (5.16), gives
\begin{align*} \lim_{m\to \infty} \lim_{n\to \infty} \sqrt{n} I_{111}(n,m,y) = \frac{2\Phi^{+} (t)}{\sqrt{2\pi} \sigma} V(i,y) U(i,y,z) \boldsymbol{\nu} (\,j). \end{align*}
This proves the assertion of the lemma for
$t\geq 0$
.
We now perform the final assembly. From (5.1), (5.2), (5.3), and (5.4), we have, for any
$i,j\in \mathbb X$
,
$z\in \mathbb N$
,
$z\not= 0$
,
$t\in \mathbb R$
, and y sufficiently large,
\begin{align} &\lim_{n\to \infty}\bigg| \sqrt{n}\mathbb P_{i,z} \left( \frac{S_n}{\sqrt{n}\sigma} \leq t, X_n=j, Z_n>0 \right)- \sqrt{n} I_{11}(n,\theta,y) \bigg| \nonumber\\[3pt]& \leq c z e^{-y}(1+y). \end{align}
From (5.10), (5.11), and (5.12) we obtain
\begin{align} \lim_{m\to \infty}\lim_{n\to \infty} \sqrt{n} I_{11}(n,\theta,y) = \frac{2\Phi^{+} (t)}{\sqrt{2\pi} \sigma} V(i,y) U(i,y,z) \boldsymbol{\nu} (\,j). \end{align}
From (5.17) and (5.18), taking consecutively the limits as
$n\to \infty$
and
$m\to \infty$
, we obtain, for any
$i,j \in \mathbb{X}$
,
$z \in \mathbb{N}$
,
$z\not = 0$
,
$t \in \mathbb R$
, and
$y\geq 0$
sufficiently large so that
$(i,y)\in \text{supp}\ V$
,
\begin{align*} \lim_{n\to\infty} \bigg|&\sqrt{n} \mathbb P_{i,z}\left( \frac{ S_n}{\sigma\sqrt{n}} \leq t, X_n=j, Z_n>0 \right) - \frac{2\Phi^{+} (t)}{\sqrt{2\pi} \sigma} V(i,y) U(i,y,z) \boldsymbol \nu (j) \bigg| \\&\leq c z e^{-y}(1+y). \end{align*}
Taking the limit as
$y\to \infty$
, we obtain, for any
$i,j \in \mathbb{X}$
,
$z \in \mathbb{N}$
,
$z\not = 0$
, and
$t \in \mathbb R$
,
\begin{equation*} \lim_{n\to\infty} \sqrt{n} \mathbb{P}_{i,z} \left( \frac{ S_n}{\sigma\sqrt{n}} \leq t, X_n=j, Z_n>0 \right) = \Phi^{+} (t) \boldsymbol{\nu} (\,j) u(i,z), \end{equation*}
where
$u(i,z)>0$
is defined in Proposition 3.4. This proves the first assertion of the theorem. The second assertion is obtained from the first one by using Theorem 1.1.
Proof of Theorem 1.4. The assertion of Theorem 1.4 is easily obtained from Theorem 1.3. Let
$\varepsilon>0$
be arbitrary. By simple computations,
\begin{align*} \mathbb{P}_{i,z} &\left( \left\lvert{ \frac{\log Z_n}{\sigma\sqrt{n}} - \frac{S_n}{\sqrt{n}\sigma} } \right\rvert\geq \varepsilon , X_n = j, Z_n>0 \right) \\[3pt] &=\mathbb{P}_{i,z} \left( \frac{Z_n}{e^{S_n}} \geq e^{\varepsilon\sqrt{n}\sigma} , X_n = j, Z_n>0 \right) \\[3pt] &+\mathbb{P}_{i,z} \left( \frac{Z_n}{e^{S_n}} \leq e^{-\varepsilon\sqrt{n}\sigma} , X_n = j, Z_n>0 \right). \end{align*}
Fix some
$A>1$
. Then, for n sufficiently large so that
$e^{\varepsilon \sqrt{n}}>A$
,
\begin{align*} \mathbb{P}_{i,z} &\left( \left\lvert{ \frac{\log Z_n}{\sigma\sqrt{n}} - \frac{S_n}{\sqrt{n}\sigma} }\right\rvert \geq \varepsilon , X_n = j, Z_n>0 \right) \\[3pt] &\leq \mathbb{P}_{i,z} \left( \frac{Z_n}{e^{S_n}} \geq A , X_n = j, Z_n>0 \right) \\[3pt] &+\mathbb{P}_{i,z} \left( \frac{Z_n}{e^{S_n}} \leq 1/A , X_n = j, Z_n>0 \right), \end{align*}
where, by Theorem 1.2,
\begin{align*} \limsup_{n\to+\infty}\sqrt{n} \mathbb{P}_{i,z} \left( \frac{Z_n}{e^{S_n}} \geq A , X_n = j, Z_n>0 \right) \leq \mu_{i,z} ([A,+\infty]) \boldsymbol{\nu} (\,j) u(i,z), \end{align*}
and
\begin{align*} \limsup_{n\to+\infty}\sqrt{n} \mathbb{P}_{i,z} \left( \frac{Z_n}{e^{S_n}} \leq 1/A , X_n = j, Z_n>0 \right) \leq \mu_{i,z} ([0,1/A]) \boldsymbol{\nu} (\,j) u(i,z). \end{align*}
Since
$\mu_{i,z}$
is a probability measure of mass 0 in 0, taking the limit as
$A\to +\infty$
, we have that
\begin{align*} \lim_{n\to+\infty}\sqrt{n}\mathbb{P}_{i,z} \left( \left\lvert{ \frac{\log Z_n}{\sigma\sqrt{n}} - \frac{S_n}{\sqrt{n}\sigma} }\right\rvert \geq \varepsilon , X_n = j, Z_n>0 \right) =0. \end{align*}
As
$\varepsilon$
is arbitrary, using Theorem 1.3 we conclude the proof.
Acknowledgements
We wish to thank the editor and two referees for their remarks and comments, which helped to improve the presentation of the paper. Two of the authors wish to pay tribute to Emile Le Page, who was the initiator of this article and who, to our great regret, passed away this year.
Funding Information
There are no funding bodies to thank in relation to the creation of this article.
Competing Interests
There are no competing interests to declare which arose during the preparation or publication process for this article.
