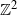1. Introduction
We analyse the dynamics of a stochastic process with dependent coordinates, commonly referred to as the cat-and-mouse (CM) Markov chain (MC), and of its generalisations. Let
![]() $\mathcal{S}$
be a directed graph. Let
$\mathcal{S}$
be a directed graph. Let
![]() $\{(C_n, M_n)\}_{n=0}^\infty$
denote the CM MC on
$\{(C_n, M_n)\}_{n=0}^\infty$
denote the CM MC on
![]() $\mathcal{S}^2$
, defined as follows. We assume that
$\mathcal{S}^2$
, defined as follows. We assume that
![]() $\{C_n\}_{n=0}^\infty$
, the location of the cat, is a MC on
$\{C_n\}_{n=0}^\infty$
, the location of the cat, is a MC on
![]() $\mathcal{S}$
with transition matrix
$\mathcal{S}$
with transition matrix
![]() $P = (p(x, y),x, y \in \mathcal{S})$
. The second coordinate, the location of the mouse,
$P = (p(x, y),x, y \in \mathcal{S})$
. The second coordinate, the location of the mouse,
![]() $\{M_n\}_{n=0}^\infty$
, has the following dynamics:
$\{M_n\}_{n=0}^\infty$
, has the following dynamics:
-
If
 $M_n \neq C_n$
, then
$M_n \neq C_n$
, then
 $M_{n+1} = M_n$
.
$M_{n+1} = M_n$
. -
If
 $M_n = C_n$
, then, conditionally on
$M_n = C_n$
, then, conditionally on
 $M_n$
, the random variable (RV)
$M_n$
, the random variable (RV)
 $M_{n+1}$
has distribution
$M_{n+1}$
has distribution
 $(p(M_n, y), y \in \mathcal{S})$
and is independent of
$(p(M_n, y), y \in \mathcal{S})$
and is independent of
 $C_{n+1}$
.
$C_{n+1}$
.
In our model the cat is trying to catch the mouse. The mouse is usually in hiding and not moving, but if the cat hits the same location of the graph, the mouse jumps. The cat does not notice where the mouse jumps to, so it proceeds independently.
The CM MC is an example of a class of models called CM games. CM games are common in game theory. We refer to [Reference Coppersmith, Doyle, Raghavan and Snir9], where the authors showed that a CM game is at the core of many online algorithms and, in particular, may be used in settings considered by [Reference Borodin, Linial and Saks7, Reference Manasse, McGeoch and Sleator28]. Some special cases of CM games on the plane have been studied by [Reference Baeza-Yates, Culberson and Rawlins4]. Two examples of CM games are discussed in [Reference Aldous and Fill1] in the context of reversible MCs.
There are many related models in applied probability in which time evolution of the process may be represented as a multi-component MC where one of the components has independent dynamics and forms an MC itself (see, e.g., [Reference Borst, Jonckheere and Leskela8, Reference Foss, Shneer and Tyurlikov16–Reference Gamarnik and Squillante18]). Typically such dependence is modelled using Markov modulation. In this paper we consider the case where the first component is a random walk. Thus, our model can be viewed as a random-walk-modulated random walk. We consider null-recurrent and transient cases where we find proper scaling for the components.
We are mainly motivated by the results of the paper by [Reference Litvak and Robert26], where the authors analyse scaling properties of the (non-Markovian) sequence
![]() $\{M_n\}_{n=0}^\infty$
for a specific transition matrix P when
$\{M_n\}_{n=0}^\infty$
for a specific transition matrix P when
![]() $\mathcal{S}$
is either
$\mathcal{S}$
is either
![]() $\mathbb{Z}$
,
$\mathbb{Z}$
,
![]() $\mathbb{Z}^2$
, or
$\mathbb{Z}^2$
, or
![]() $\mathbb{Z}^+$
. Although it deals with a relatively simple case of the CM MC, it clearly illustrates a certain phenomenon related to this type of Markov modulation. We will focus on the case
$\mathbb{Z}^+$
. Although it deals with a relatively simple case of the CM MC, it clearly illustrates a certain phenomenon related to this type of Markov modulation. We will focus on the case
![]() $\mathcal{S} = \mathbb{Z}$
. In addition, we assume that the transition matrix P satisfies
$\mathcal{S} = \mathbb{Z}$
. In addition, we assume that the transition matrix P satisfies
![]() $p(x, x+1) = p(x, x-1) = 1/2$
. It was proven in Theorem 3 of [Reference Litvak and Robert26] that the convergence in distribution
$p(x, x+1) = p(x, x-1) = 1/2$
. It was proven in Theorem 3 of [Reference Litvak and Robert26] that the convergence in distribution
holds, where
![]() $B_1(t)$
and
$B_1(t)$
and
![]() $B_2(t)$
are independent standard Brownian motions on
$B_2(t)$
are independent standard Brownian motions on
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $L_{B_2}(t)$
is the local time process of
$L_{B_2}(t)$
is the local time process of
![]() $B_2(t)$
at 0. By convergence in distribution of càdlàg stochastic processes we mean convergence in the
$B_2(t)$
at 0. By convergence in distribution of càdlàg stochastic processes we mean convergence in the
![]() ${\mathcal J}_1$
-topology (see Appendix A for further explanation).
${\mathcal J}_1$
-topology (see Appendix A for further explanation).
This result looks natural, since the mouse, observed at the meeting times with the cat, is a simple random walk. The time intervals between meeting times are independent and identically distributed (i.i.d.). They have the same distribution as the time needed for the cat (also a simple random walk) to get from 1 to 0, which has a regularly varying tail with parameter
![]() $1/2$
(see, e.g., [Reference Spitzer32]). Thus, the scaling for the location of the mouse is
$1/2$
(see, e.g., [Reference Spitzer32]). Thus, the scaling for the location of the mouse is
![]() $\sqrt[4]{n} = (n^{1/2})^{1/2}$
. Local time
$\sqrt[4]{n} = (n^{1/2})^{1/2}$
. Local time
![]() $L_{B_2}(t)$
can be interpreted as the scaled duration of time the cat and the mouse spend together.
$L_{B_2}(t)$
can be interpreted as the scaled duration of time the cat and the mouse spend together.
This leads us to ask to what extent such a phenomenon holds, for what kinds of distributions of jumps, and for which types of Markov modulation. In this paper we show that similar behaviour holds when jump-size distributions of both components have zero mean and finite variance. The behaviour changes slightly when we introduce heavier tails for the jump-size distribution of the mouse. For this case we develop a more general approach based on the work of [Reference Jurlewicz, Kern, Meerschaert and Scheffler23]. In parallel, we introduce additional components while applying an analogue of the aforementioned Markov modulation. Here, through the analysis of dynamical structural properties, we demonstrate a similar phenomenon for additional components.
More specifically, we provide two generalisations of the CM MC introduced above. The first generalisation relates to the jump distribution of the mouse. Given
![]() $C_{n} = M_{n}$
, the RV
$C_{n} = M_{n}$
, the RV
![]() $M_{n+1} - M_n$
has a general distribution which has a finite first moment and belongs to the strict domain of attraction of a stable law with index
$M_{n+1} - M_n$
has a general distribution which has a finite first moment and belongs to the strict domain of attraction of a stable law with index
![]() $\alpha \in [1, 2]$
, with a normalising function
$\alpha \in [1, 2]$
, with a normalising function
![]() $\{b(n)\}_{n=1}^\infty$
(note that distributions with a finite second moment belong to the domain of attraction of a normal distribution) and a centring function
$\{b(n)\}_{n=1}^\infty$
(note that distributions with a finite second moment belong to the domain of attraction of a normal distribution) and a centring function
![]() $n\mathbb{E}(M_{n+1} - M_n)$
. We find a weak limit of
$n\mathbb{E}(M_{n+1} - M_n)$
. We find a weak limit of
![]() ${\{b^{-1}(\sqrt{n}) M_{[nt + 1]}\}_{t\geq 0}}$
, as
${\{b^{-1}(\sqrt{n}) M_{[nt + 1]}\}_{t\geq 0}}$
, as
![]() $n\to\infty$
. This model is more challenging than the classical setting because, when the mouse jumps, the value of this jump and the time until the next jump may be dependent. Also, if the jump distribution of the mouse has an infinite second moment, we cannot use classical results for regenerative jump processes such as Theorem 5.1 from [Reference Kasahara24]. Next, we consider the case where both components have general distributions with finite second moments. Here our results take into account the approach developed by [Reference Uchiyama33].
$n\to\infty$
. This model is more challenging than the classical setting because, when the mouse jumps, the value of this jump and the time until the next jump may be dependent. Also, if the jump distribution of the mouse has an infinite second moment, we cannot use classical results for regenerative jump processes such as Theorem 5.1 from [Reference Kasahara24]. Next, we consider the case where both components have general distributions with finite second moments. Here our results take into account the approach developed by [Reference Uchiyama33].
In the second generalisation we add more components to the system (we will refer to the objects whose dynamics these components describe as ‘agents’), while keeping the chain ‘hierarchy’. For instance, the addition of one extra agent (which we refer to as the dog), acting on the cat in the same way as the cat acts on the mouse, slows down the cat and, therefore, also the mouse. We are interested in the effect of this on the scaling properties of the process. Recursive addition of further agents will slow the mouse down further. For the system with three agents we investigate the dynamical structural properties and find a weak limit of
![]() $\{n^{-1/8} M_{[nt]}\}_{t\geq 0}$
, as
$\{n^{-1/8} M_{[nt]}\}_{t\geq 0}$
, as
![]() $n\to\infty$
. The system regenerates when all the agents are at the same point. Therefore, if we find the tail asymptotics of the time intervals between these events, we can split the process into i.i.d. cycles and use a limit theorem for regenerative processes by [Reference Kasahara24].
$n\to\infty$
. The system regenerates when all the agents are at the same point. Therefore, if we find the tail asymptotics of the time intervals between these events, we can split the process into i.i.d. cycles and use a limit theorem for regenerative processes by [Reference Kasahara24].
We also consider systems with an arbitrary finite number of agents, for which we provide a relatively simple result on weak convergence, for a fixed
![]() $t>0$
. The path analysis in this case turns out to be difficult, and we have only partial results. Namely, we have studied the relation between the numbers of jumps of different agents and obtained the limiting law for the last agent. We have not succeeded in finding the asymptotics for the time intervals between regeneration points, which remains an open question.
$t>0$
. The path analysis in this case turns out to be difficult, and we have only partial results. Namely, we have studied the relation between the numbers of jumps of different agents and obtained the limiting law for the last agent. We have not succeeded in finding the asymptotics for the time intervals between regeneration points, which remains an open question.
We note that our paper is devoted to limit theorems for the above-mentioned Markov-modulated MCs. It is worth noting that there are other interesting questions for such models not covered here: stability problems are studied in, e.g., [Reference Foss, Shneer, Thomas and Worrall15, Reference Georgiou and Wade19, Reference Shah and Shin30], while large deviations problems are studied in, e.g., [Reference Alsmeyer and Sgibnev2, Reference Asmussen, Henriksen and Kloppelberg3, Reference Foss, Konstantopoulos and Zachary14, Reference Hansen and Jensen20, Reference Jelenkovic and Lazar22, Reference Lu and Li27].
The paper is structured as follows. In Section 2 we define our models and formulate our results. In Sections 3 and 4 we analyse the trajectories of the CM MC and dog-and-cat-and-mouse (DCM) MC, respectively. This analysis gives the main idea of the proof of our result on scaling properties of the DCM MC (Theorem 3). In Section 5.1, we prove our results on scaling properties of general CM MCs (Theorem 1 and Theorem 2). We shift the time of our process and use characteristic functions to show that the conditions of Theorem 3.1 from [Reference Jurlewicz, Kern, Meerschaert and Scheffler23] hold. In Section 5.2, we prove Theorem 3. We approximate the dynamics of the mouse by considering only the values of the process at times when all agents are at the same point of the integer line, and then use Theorem 5.1 from [Reference Kasahara24] to obtain the result. In Section 5.3, we prove our result on scaling properties for the system with an arbitrary finite number N of agents. We approximate the Nth component of the system
![]() $X^{(N)}$
(which describes the behaviour of the Nth agent) by the component
$X^{(N)}$
(which describes the behaviour of the Nth agent) by the component
![]() $X^{(N-1)}$
, slowed down by an independent renewal process.
$X^{(N-1)}$
, slowed down by an independent renewal process.
The appendix includes definitions and proofs of supplementary results. In Appendix A, we define weak convergence of stochastic processes. Appendix B clarifies the asymptotic closeness of two scaled processes related to Theorem 1. Finally, in Appendix C we provide auxiliary results on randomly stopped sums with positive summands having a regularly varying tail distribution and infinite mean.
Throughout the paper we use the following conventions and notation. For two ultimately positive functions f(t) and g(t) we write
![]() $f(t) \sim g(t)$
if
$f(t) \sim g(t)$
if
![]() $\lim_{t\to\infty} f(t)/g(t) = 1$
. For any event A, its indicator function I[A] is an RV that takes the value 1 if the event occurs, and the value 0 otherwise. We use the symbol
$\lim_{t\to\infty} f(t)/g(t) = 1$
. For any event A, its indicator function I[A] is an RV that takes the value 1 if the event occurs, and the value 0 otherwise. We use the symbol
![]() ${\Rightarrow}$
for the weak convergence of distributions of RVs or vectors, and
${\Rightarrow}$
for the weak convergence of distributions of RVs or vectors, and
![]() $\overset{\mathcal{D}}{\Rightarrow}$
for convergence of trajectories of random processes in the
$\overset{\mathcal{D}}{\Rightarrow}$
for convergence of trajectories of random processes in the
![]() ${\mathcal J}_1$
-topology (see Appendix A). Next,
${\mathcal J}_1$
-topology (see Appendix A). Next,
![]() $X\overset{d}{=}Y$
means that the RVs X and Y are identically distributed. Finally we use the following abbreviations: CM (cat-and-mouse), DCM (dog-and-cat-and-mouse), MC (Markov chain), i.i.d. (independent and identically distributed), RV (random variable), a.s. (almost surely), w.p. (with probability).
$X\overset{d}{=}Y$
means that the RVs X and Y are identically distributed. Finally we use the following abbreviations: CM (cat-and-mouse), DCM (dog-and-cat-and-mouse), MC (Markov chain), i.i.d. (independent and identically distributed), RV (random variable), a.s. (almost surely), w.p. (with probability).
2. Models and results
In this section we recall the CM MC on the integers and introduce several of its generalisations.
2.1. ‘Standard’ cat-and-mouse Markov chain on
 $\mathbb{Z}$
$\mathbb{Z}$
 $(C\to M)$
$(C\to M)$
Let
![]() $\xi = \pm 1$
w.p.
$\xi = \pm 1$
w.p.
![]() $1/2$
. Let
$1/2$
. Let
![]() $\big\{\xi^{(1)}_n\big\}_{n=1}^\infty$
and
$\big\{\xi^{(1)}_n\big\}_{n=1}^\infty$
and
![]() $\big\{\xi^{(2)}_n\big\}_{n=1}^\infty$
be two mutually independent sequences of independent copies of
$\big\{\xi^{(2)}_n\big\}_{n=1}^\infty$
be two mutually independent sequences of independent copies of
![]() $\xi$
. Given
$\xi$
. Given
![]() $C_0 = M_0 = 0$
, we define the dynamics of CM MC
$C_0 = M_0 = 0$
, we define the dynamics of CM MC
![]() $(C_n, M_n)$
as follows:
$(C_n, M_n)$
as follows:
 \begin{equation*}M_n = M_{n-1} + \begin{cases}0, & \text{if $C_{n-1} \neq M_{n-1},$}\\ \\[-7pt] \xi^{(2)}_n, & \text{if $C_{n-1} = M_{n-1},$}\end{cases}\end{equation*}
\begin{equation*}M_n = M_{n-1} + \begin{cases}0, & \text{if $C_{n-1} \neq M_{n-1},$}\\ \\[-7pt] \xi^{(2)}_n, & \text{if $C_{n-1} = M_{n-1},$}\end{cases}\end{equation*}
for
![]() $n \geq 1$
.
$n \geq 1$
.
Let
![]() $D[[0,\infty), \mathbb{R}]$
denote the space of all right-continuous functions on
$D[[0,\infty), \mathbb{R}]$
denote the space of all right-continuous functions on
![]() $[0, \infty)$
having left limits (RCLL or càdlàg functions).
$[0, \infty)$
having left limits (RCLL or càdlàg functions).
Let
![]() $M(nt) = M_{[nt]}$
,
$M(nt) = M_{[nt]}$
,
![]() $t\geq0$
, be a continuous-time stochastic process taking values
$t\geq0$
, be a continuous-time stochastic process taking values
![]() $M_k$
,
$M_k$
,
![]() $k\geq 0$
, for
$k\geq 0$
, for
![]() $t\in[k/n, (k+1)/n)$
. Clearly, it is piecewise constant and its trajectories belong to
$t\in[k/n, (k+1)/n)$
. Clearly, it is piecewise constant and its trajectories belong to
![]() $D[[0,\infty), \mathbb{R}]$
.
$D[[0,\infty), \mathbb{R}]$
.
[Reference Litvak and Robert26] have proved convergence of trajectories
where
![]() $B_1(t)$
and
$B_1(t)$
and
![]() $B_2(t)$
are independent standard Brownian motions on
$B_2(t)$
are independent standard Brownian motions on
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $L_{B_2}(t)$
is the local time process of
$L_{B_2}(t)$
is the local time process of
![]() $B_2(t)$
at 0.
$B_2(t)$
at 0.
2.2. Cat-and-mouse model with a general jump distribution of the mouse
 $(C \to M)$
$(C \to M)$
In this subsection we introduce our results for CM MCs with more general distributions of RVs
![]() $\xi^{(1)}_n$
and
$\xi^{(1)}_n$
and
![]() $\xi^{(2)}_n$
. We start with the same distribution of
$\xi^{(2)}_n$
. We start with the same distribution of
![]() $\xi^{(1)}_n$
and generalise the distribution of
$\xi^{(1)}_n$
and generalise the distribution of
![]() $\xi^{(2)}_n$
. Thus, the cat is a simple random walk and the mouse is a general random walk. We then proceed to generalise the distribution of
$\xi^{(2)}_n$
. Thus, the cat is a simple random walk and the mouse is a general random walk. We then proceed to generalise the distribution of
![]() $\xi^{(1)}_n$
as well.
$\xi^{(1)}_n$
as well.
2.2.1.
We continue to assume that the dynamics of the cat is described by a simple random walk on
![]() $\mathbb{Z}$
. Let
$\mathbb{Z}$
. Let
![]() $\xi = \pm 1$
w.p.
$\xi = \pm 1$
w.p.
![]() $1/2$
. Let
$1/2$
. Let
![]() $C_0 = 0, \ C_{n} = C_{n-1} + \xi^{(1)}_n$
, where
$C_0 = 0, \ C_{n} = C_{n-1} + \xi^{(1)}_n$
, where
![]() $\xi, \xi^{(1)}_1, \xi^{(1)}_2, \ldots$
are i.i.d. RVs.
$\xi, \xi^{(1)}_1, \xi^{(1)}_2, \ldots$
are i.i.d. RVs.
Let
![]() $M_0 = 0, \ M_n = M_{n-1} + \xi^{(2)}_n I[C_{n-1} = M_{n-1}]$
, where
$M_0 = 0, \ M_n = M_{n-1} + \xi^{(2)}_n I[C_{n-1} = M_{n-1}]$
, where
![]() $\big\{\xi^{(2)}_n\big\}_{n=1}^\infty$
are i.i.d. RVs independent of
$\big\{\xi^{(2)}_n\big\}_{n=1}^\infty$
are i.i.d. RVs independent of
![]() $\big\{\xi^{(1)}_n\big\}_{n=1}^\infty$
. Assume that
$\big\{\xi^{(1)}_n\big\}_{n=1}^\infty$
. Assume that
and that the distribution of
![]() $\xi_1^{(2)}$
belongs to the domain of attraction of a strictly stable distribution, i.e. there exist a function
$\xi_1^{(2)}$
belongs to the domain of attraction of a strictly stable distribution, i.e. there exist a function
![]() $b(c) >0$
,
$b(c) >0$
,
![]() $c\geq0$
, and an RV
$c\geq0$
, and an RV
![]() $A^{(2)}$
having a strictly stable distribution with index
$A^{(2)}$
having a strictly stable distribution with index
![]() $\alpha \in [1,2]$
such that the weak convergence
$\alpha \in [1,2]$
such that the weak convergence
 \begin{equation}\frac{\sum_{k=1}^{n} \Big(\xi^{(2)}_k - \mu\Big)}{b(n)} \Rightarrow A^{(2)}, \ \text{as $n\to\infty$}\end{equation}
\begin{equation}\frac{\sum_{k=1}^{n} \Big(\xi^{(2)}_k - \mu\Big)}{b(n)} \Rightarrow A^{(2)}, \ \text{as $n\to\infty$}\end{equation}
holds. Define
Given (1), we show that the tail-distribution of
![]() $\tau(1)$
is regularly varying with index
$\tau(1)$
is regularly varying with index
![]() $1/2$
. It follows then that there exists an RV
$1/2$
. It follows then that there exists an RV
![]() $D^{(2)}$
having a strictly stable distribution with index
$D^{(2)}$
having a strictly stable distribution with index
![]() $1/2$
such that
$1/2$
such that
In the proof of Theorem 2 we show that in fact there is a weak convergence of two-dimensional random vectors
 \begin{align*}\left(\frac{\sum_{k=1}^{n} \Big(\xi^{(2)}_k - \mu\Big)}{b(n)}, \ \frac{\tau(n)}{n^2}\right) \ \Rightarrow \big(A^{(2)}, D^{(2)}\big), \ \text{as $n\to\infty$,}\end{align*}
\begin{align*}\left(\frac{\sum_{k=1}^{n} \Big(\xi^{(2)}_k - \mu\Big)}{b(n)}, \ \frac{\tau(n)}{n^2}\right) \ \Rightarrow \big(A^{(2)}, D^{(2)}\big), \ \text{as $n\to\infty$,}\end{align*}
where the RVs on the right-hand side are independent. Further, let
![]() $\big\{\big(A^{(2)}(t), D^{(2)}(t)\big)\big\}_{t\geq 0}$
denote a stochastic process with independent increments such that
$\big\{\big(A^{(2)}(t), D^{(2)}(t)\big)\big\}_{t\geq 0}$
denote a stochastic process with independent increments such that
![]() $\big(A^{(2)}(1), D^{(2)}(1)\big)$
has the same distribution as
$\big(A^{(2)}(1), D^{(2)}(1)\big)$
has the same distribution as
![]() $\big(A^{(2)}, D^{(2)}\big)$
, or, equivalently, the Lévy process generated by
$\big(A^{(2)}, D^{(2)}\big)$
, or, equivalently, the Lévy process generated by
![]() $\big(A^{(2)}, D^{(2)}\big)$
. Let
$\big(A^{(2)}, D^{(2)}\big)$
. Let
![]() $E^{(2)}(s) = \inf\big\{t\geq0 \,{:}\,D^{(2)}(t)> s\big\}$
, which is a multiple of
$E^{(2)}(s) = \inf\big\{t\geq0 \,{:}\,D^{(2)}(t)> s\big\}$
, which is a multiple of
![]() $L_{B_2}(s)$
, the local time at zero of a standard Brownian motion. Thus, the following result is a natural extension of the result by [Reference Litvak and Robert26]; see remark below.
$L_{B_2}(s)$
, the local time at zero of a standard Brownian motion. Thus, the following result is a natural extension of the result by [Reference Litvak and Robert26]; see remark below.
Theorem 1. Assume that (1) and (2) hold. Then
-
if
 $\mu = 0$
, we have (4)
$\mu = 0$
, we have (4) \begin{equation} \left\lbrace \frac{M(nt + 1)}{b(\sqrt{n})}, \ t\geq 0\right\rbrace \overset{\mathcal{D}}{\Rightarrow} \big\{A^{(2)}\big(E^{(2)}(t)\big), t\geq 0\big\}, \ \text{as $n\to\infty$;}\end{equation}
\begin{equation} \left\lbrace \frac{M(nt + 1)}{b(\sqrt{n})}, \ t\geq 0\right\rbrace \overset{\mathcal{D}}{\Rightarrow} \big\{A^{(2)}\big(E^{(2)}(t)\big), t\geq 0\big\}, \ \text{as $n\to\infty$;}\end{equation}
-
if
 $\mu \neq 0$
, we have (5)
$\mu \neq 0$
, we have (5) \begin{equation}\left\lbrace \frac{M(nt + 1)}{\sqrt{n}}, \ t\geq 0\right\rbrace \overset{\mathcal{D}}{\Rightarrow} \big\{\mu E^{(2)}(t), t\geq 0\big\}, \ \text{as $n\to\infty$.}\end{equation}
\begin{equation}\left\lbrace \frac{M(nt + 1)}{\sqrt{n}}, \ t\geq 0\right\rbrace \overset{\mathcal{D}}{\Rightarrow} \big\{\mu E^{(2)}(t), t\geq 0\big\}, \ \text{as $n\to\infty$.}\end{equation}
Remark. If the RVs
![]() $\xi_n^{(2)}$
are bounded, then the function b(n) is proportional to
$\xi_n^{(2)}$
are bounded, then the function b(n) is proportional to
![]() $\sqrt{n}$
, and it is easy to show that the processes
$\sqrt{n}$
, and it is easy to show that the processes
are equivalent (see Appendix B for details). Then the results of Theorem 1 may be reformulated for the scaled process M(nt) in place of
![]() $M(nt + 1)$
.
$M(nt + 1)$
.
2.2.2.
Assume now that both
![]() $\xi^{(1)}_1$
and
$\xi^{(1)}_1$
and
![]() $\xi^{(2)}_1$
have general distributions on the integer lattice. The main difference for the mouse is that we now need to assume that the second moment of
$\xi^{(2)}_1$
have general distributions on the integer lattice. The main difference for the mouse is that we now need to assume that the second moment of
![]() $\xi^{(2)}_1$
is finite. Our main result in this setting is that replacing the simple random walk with a general random walk does not change the scaling if we assume aperiodicity and finite second moments for the increments. By aperiodicity (strong aperiodicity in the sense of [Reference Spitzer32]) we mean here that
$\xi^{(2)}_1$
is finite. Our main result in this setting is that replacing the simple random walk with a general random walk does not change the scaling if we assume aperiodicity and finite second moments for the increments. By aperiodicity (strong aperiodicity in the sense of [Reference Spitzer32]) we mean here that
where ‘G.C.D.’ stands for ‘greatest common divisor’.
Theorem 2. Assume that
![]() $\mathbb{E} \xi^{(1)} =0$
,
$\mathbb{E} \xi^{(1)} =0$
,
![]() $0 <\mathbf{Var} \xi^{(1)}_1 < \infty$
and
$0 <\mathbf{Var} \xi^{(1)}_1 < \infty$
and
![]() $\xi^{(1)}_1$
has an aperiodic distribution. Assume
$\xi^{(1)}_1$
has an aperiodic distribution. Assume
![]() $0< \mathbf{Var} \xi^{(2)}_1 < \infty$
and, therefore, (2) holds with
$0< \mathbf{Var} \xi^{(2)}_1 < \infty$
and, therefore, (2) holds with
![]() $b(n) = \sqrt{n\mathbf{Var} \xi^{(2)}_1}$
and a standard normal RV
$b(n) = \sqrt{n\mathbf{Var} \xi^{(2)}_1}$
and a standard normal RV
![]() $A^{(2)}$
. Then the statements (4) and (5) of Theorem 1 continue to hold, with
$A^{(2)}$
. Then the statements (4) and (5) of Theorem 1 continue to hold, with
![]() $b(\sqrt{n}) = n^{1/4}\sqrt{\mathbf{Var} \xi^{(2)}_1}$
in (4).
$b(\sqrt{n}) = n^{1/4}\sqrt{\mathbf{Var} \xi^{(2)}_1}$
in (4).
2.3. Dog-and-cat-and-mouse model (
 $D \to C \to M$
)
$D \to C \to M$
)
In this subsection we present a generalisation of the CM MC to the case of three dimensions. Let
![]() $\xi = \pm 1$
w.p.
$\xi = \pm 1$
w.p.
![]() $1/2$
. Let
$1/2$
. Let
![]() $\big\{\xi^{(1)}_n\big\}_{n=1}^\infty$
,
$\big\{\xi^{(1)}_n\big\}_{n=1}^\infty$
,
![]() $\big\{\xi^{(2)}_n\big\}_{n=1}^\infty$
, and
$\big\{\xi^{(2)}_n\big\}_{n=1}^\infty$
, and
![]() $\big\{\xi^{(3)}_n\big\}_{n=1}^\infty$
be mutually independent sequences of independent copies of
$\big\{\xi^{(3)}_n\big\}_{n=1}^\infty$
be mutually independent sequences of independent copies of
![]() $\xi$
. Given
$\xi$
. Given
![]() $D_0 = C_0 = M_0 = 0$
, we can define the dynamics of the DCM MC
$D_0 = C_0 = M_0 = 0$
, we can define the dynamics of the DCM MC
![]() $\{(D_n, C_n, M_n)_n\}_{n=1}^\infty$
as follows: for
$\{(D_n, C_n, M_n)_n\}_{n=1}^\infty$
as follows: for
![]() $n\ge 1$
,
$n\ge 1$
,
 \begin{equation*}C_n = C_{n-1} + \begin{cases}0, & \text{if $D_{n-1} \neq C_{n-1},$}\\ \\[-7pt] \xi^{(2)}_n, & \text{if $D_{n-1} = C_{n-1},$}\end{cases}\end{equation*}
\begin{equation*}C_n = C_{n-1} + \begin{cases}0, & \text{if $D_{n-1} \neq C_{n-1},$}\\ \\[-7pt] \xi^{(2)}_n, & \text{if $D_{n-1} = C_{n-1},$}\end{cases}\end{equation*}
 \begin{equation*}M_n = M_{n-1} + \begin{cases}0, & \text{if $C_{n-1} \neq M_{n-1},$}\\ \\[-7pt] \xi^{(3)}_n, & \text{if $C_{n-1} = M_{n-1}.$}\end{cases}\end{equation*}
\begin{equation*}M_n = M_{n-1} + \begin{cases}0, & \text{if $C_{n-1} \neq M_{n-1},$}\\ \\[-7pt] \xi^{(3)}_n, & \text{if $C_{n-1} = M_{n-1}.$}\end{cases}\end{equation*}
Let
![]() $T^{(3)}(0) = 0$
and
$T^{(3)}(0) = 0$
and
![]() $T^{(3)}(k) = \min\{n >T^{(3)}(k-1): \ D_n = C_n = M_n\}$
, for
$T^{(3)}(k) = \min\{n >T^{(3)}(k-1): \ D_n = C_n = M_n\}$
, for
![]() $k\geq 1$
. We show that the tail-distribution of
$k\geq 1$
. We show that the tail-distribution of
![]() $T^{(3)}(1)$
is regularly varying with index
$T^{(3)}(1)$
is regularly varying with index
![]() $1/4$
. Further, we show that there exists a positive RV
$1/4$
. Further, we show that there exists a positive RV
![]() $D^{(3)}$
with a stable distribution and Laplace transform
$D^{(3)}$
with a stable distribution and Laplace transform
![]() $\exp\big(\!-s^{1/4}\big)$
such that
$\exp\big(\!-s^{1/4}\big)$
such that
Let
![]() $\big\{D^{(3)}(t)\big\}_{t\geq 0}$
be a Lévy process generated by
$\big\{D^{(3)}(t)\big\}_{t\geq 0}$
be a Lévy process generated by
![]() $D^{(3)}$
and
$D^{(3)}$
and
![]() $E^{(3)}(s) = \inf\big\{t\geq0 : \ D^{(3)}(t)> s\big\}$
.
$E^{(3)}(s) = \inf\big\{t\geq0 : \ D^{(3)}(t)> s\big\}$
.
Theorem 3. We have
![]() $\mathbb{E} M\big(T^{(3)}(1)\big) = 0$
,
$\mathbb{E} M\big(T^{(3)}(1)\big) = 0$
,
![]() $\sigma^2 = \mathbf{Var} M\big(T^{(3)}(1)\big) = 2$
, and
$\sigma^2 = \mathbf{Var} M\big(T^{(3)}(1)\big) = 2$
, and
where B(t) is a standard Brownian motion, independent of
![]() $E^{(3)}(t)$
.
$E^{(3)}(t)$
.
2.4. Linear hierarchical chains
 $\big(\boldsymbol{X}^{(1)} \to \boldsymbol{X}^{(2)} \to \ldots \to \boldsymbol{X}^{(\boldsymbol{N})}\big)$
of length N
$\big(\boldsymbol{X}^{(1)} \to \boldsymbol{X}^{(2)} \to \ldots \to \boldsymbol{X}^{(\boldsymbol{N})}\big)$
of length N
In this subsection we consider a generalisation of the CM MC to the case of N dimensions. Owing to the complexity of sample paths for
![]() $N>3$
, it does not seem to be possible to prove an analogue of (3) and (6). For this setting, we prove the convergence for every fixed
$N>3$
, it does not seem to be possible to prove an analogue of (3) and (6). For this setting, we prove the convergence for every fixed
![]() $t>0$
.
$t>0$
.
Let
![]() $\xi = \pm 1$
w.p.
$\xi = \pm 1$
w.p.
![]() $1/2$
. Let
$1/2$
. Let
![]() $\big\{\big\{\xi^{(j)}_n\big\}_{n=1}^\infty\big\}_{j=1}^N$
be mutually independent sequences of independent copies of
$\big\{\big\{\xi^{(j)}_n\big\}_{n=1}^\infty\big\}_{j=1}^N$
be mutually independent sequences of independent copies of
![]() $\xi$
. Assume
$\xi$
. Assume
![]() $X^{(1)}_0 = \ldots = X^{(N)}_0 = 0$
. Then MC
$X^{(1)}_0 = \ldots = X^{(N)}_0 = 0$
. Then MC
![]() $\big(X^{(1)}_n, \ldots, X^{(N)}_n\big)$
is defined as follows:
$\big(X^{(1)}_n, \ldots, X^{(N)}_n\big)$
is defined as follows:
 \begin{equation*}X^{(j)}_n = X^{(j)}_{n-1} + \begin{cases}0, & \text{if $X^{(j-1)}_{n-1} \neq X^{(j)}_{n-1},$}\\ \\[-6pt]\xi^{(j)}_n, & \text{if $X^{(j-1)}_{n-1} = X^{(j)}_{n-1},$}\end{cases}\end{equation*}
\begin{equation*}X^{(j)}_n = X^{(j)}_{n-1} + \begin{cases}0, & \text{if $X^{(j-1)}_{n-1} \neq X^{(j)}_{n-1},$}\\ \\[-6pt]\xi^{(j)}_n, & \text{if $X^{(j-1)}_{n-1} = X^{(j)}_{n-1},$}\end{cases}\end{equation*}
for
![]() $j \in \{2, \ldots, N\}$
and for
$j \in \{2, \ldots, N\}$
and for
![]() $n \geq 1$
.
$n \geq 1$
.
For the result below we need the following distribution. Let
![]() $G_\alpha$
be the distribution function of a one-sided strictly stable law satisfying the condition
$G_\alpha$
be the distribution function of a one-sided strictly stable law satisfying the condition
![]() $x^\alpha (1- G_\alpha(x)) \to (2-\alpha) / \alpha$
, as
$x^\alpha (1- G_\alpha(x)) \to (2-\alpha) / \alpha$
, as
![]() $x\to\infty$
.
$x\to\infty$
.
Theorem 4. Let
![]() $\{\zeta_i\}_{i=1}^\infty$
be i.i.d. RVs satisfying
$\{\zeta_i\}_{i=1}^\infty$
be i.i.d. RVs satisfying
![]() $\mathbb{P}\{\zeta_i \geq y\} = G_{1/2}(9/y^2)$
. Let
$\mathbb{P}\{\zeta_i \geq y\} = G_{1/2}(9/y^2)$
. Let
![]() $\psi$
be an RV with a standard normal distribution and independent of
$\psi$
be an RV with a standard normal distribution and independent of
![]() $\{\zeta_i\}_{i=1}^\infty$
. Then, for any fixed
$\{\zeta_i\}_{i=1}^\infty$
. Then, for any fixed
![]() $t>0$
, we have
$t>0$
, we have
 \begin{equation*}\frac{X^{(N)}_{[nt]}}{n^{1/2^N}} \Rightarrow t^{1/2^N} \psi \prod_{i=1}^{N} \sqrt{\sqrt{\frac{\pi}{2}}\zeta_i}, \ \text{as $n\to\infty$.}\end{equation*}
\begin{equation*}\frac{X^{(N)}_{[nt]}}{n^{1/2^N}} \Rightarrow t^{1/2^N} \psi \prod_{i=1}^{N} \sqrt{\sqrt{\frac{\pi}{2}}\zeta_i}, \ \text{as $n\to\infty$.}\end{equation*}
3. Trajectories of the ‘standard’ cat-and-mouse model
In order to prove Theorems 1–3, we first revisit the ‘standard’ CM model and highlight a number of properties that are of use in the analysis of the more general CM and DCM models discussed here.
We assume that
![]() $C_0 = M_0 = 0$
. Let
$C_0 = M_0 = 0$
. Let
![]() $V_n = |C_n - M_n|$
, for
$V_n = |C_n - M_n|$
, for
![]() $n\geq 0$
. We can write
$n\geq 0$
. We can write
![]() $M_{n+1} = M_{n} + \xi^{(2)}_{n+1}I[V_{n} = 0]$
, for
$M_{n+1} = M_{n} + \xi^{(2)}_{n+1}I[V_{n} = 0]$
, for
![]() $n\geq 1$
. Then
$n\geq 1$
. Then
We can further observe that
 \begin{equation*}V_{n+1} = \begin{cases}\Big|\xi^{(1)}_{n+1} - \xi^{(2)}_{n+1}\Big|\overset{d}{=} 1 + \xi^{(1)}_{n+1}, \ \text{ if $V_n = 0$,} \\ \\[-7pt] \Big|C_n - M_n + \xi^{(1)}_{n+1}\Big| \overset{d}{=} V_n + \xi^{(1)}_{n+1}, \ \text{ if $V_n \neq 0$.}\end{cases}\end{equation*}
\begin{equation*}V_{n+1} = \begin{cases}\Big|\xi^{(1)}_{n+1} - \xi^{(2)}_{n+1}\Big|\overset{d}{=} 1 + \xi^{(1)}_{n+1}, \ \text{ if $V_n = 0$,} \\ \\[-7pt] \Big|C_n - M_n + \xi^{(1)}_{n+1}\Big| \overset{d}{=} V_n + \xi^{(1)}_{n+1}, \ \text{ if $V_n \neq 0$.}\end{cases}\end{equation*}
Thus,
![]() $V_n$
forms a MC. Let
$V_n$
forms a MC. Let
![]() $p_i(j) = \mathbb{P}\{V_{n+1}=j | V_n = i\}$
, for
$p_i(j) = \mathbb{P}\{V_{n+1}=j | V_n = i\}$
, for
![]() $i,j\geq 0$
. Note that
$i,j\geq 0$
. Note that
![]() $p_0(j) = p_1(j)$
for any j.
$p_0(j) = p_1(j)$
for any j.
Let
Since
![]() $p_0(j) = p_1(j)$
for any j, we have that the RVs
$p_0(j) = p_1(j)$
for any j, we have that the RVs
![]() $\big\{U^{(2)}(k) - U^{(2)}(k-1)\big\}_{k=1}^\infty$
are i.i.d., and the RV
$\big\{U^{(2)}(k) - U^{(2)}(k-1)\big\}_{k=1}^\infty$
are i.i.d., and the RV
![]() $\big(U^{(2)}(k) - U^{(2)}(k-1)\big)$
does not depend on
$\big(U^{(2)}(k) - U^{(2)}(k-1)\big)$
does not depend on
![]() $V_{U^{(2)}(k-1)}$
, for
$V_{U^{(2)}(k-1)}$
, for
![]() $k\ge 1$
. From the Markov property we have
$k\ge 1$
. From the Markov property we have
 \begin{align*}V_{U^{(2)}(k) + 1} \overset{d}{=} 1 + \xi^{(1)}_{1} = \begin{cases}0, & \text{w.p. $\frac{1}{2}$,}\\ \\[-7pt] 2, & \text{w.p. $\frac{1}{2}$.}\end{cases}\end{align*}
\begin{align*}V_{U^{(2)}(k) + 1} \overset{d}{=} 1 + \xi^{(1)}_{1} = \begin{cases}0, & \text{w.p. $\frac{1}{2}$,}\\ \\[-7pt] 2, & \text{w.p. $\frac{1}{2}$.}\end{cases}\end{align*}
Thus, after each time instant
![]() $U^{(2)}(k)$
the cat and the mouse jump with equal probabilities either to the same point or to two different points at distance 2 from each other. In the latter case,
$U^{(2)}(k)$
the cat and the mouse jump with equal probabilities either to the same point or to two different points at distance 2 from each other. In the latter case,
![]() $V_{U^{(2)}(k+1)} = 1$
, since the cat’s jumps are 1 or
$V_{U^{(2)}(k+1)} = 1$
, since the cat’s jumps are 1 or
![]() $-1$
. For the cat, let
$-1$
. For the cat, let
![]() $\tau^{(1)}_m = \min \big\{n: \sum_{k=1}^n \xi^{(1)}_k = m\big\}$
denote the hitting time of the state m. Then
$\tau^{(1)}_m = \min \big\{n: \sum_{k=1}^n \xi^{(1)}_k = m\big\}$
denote the hitting time of the state m. Then
 \begin{align*}U^{(2)}(1) \overset{d}{=} 1 + \begin{cases}0, & \text{w.p. $\frac{1}{2}$,}\\ \\[-7pt] \tau^{(1)}_1, & \text{w.p. $\frac{1}{2}$.}\end{cases}\end{align*}
\begin{align*}U^{(2)}(1) \overset{d}{=} 1 + \begin{cases}0, & \text{w.p. $\frac{1}{2}$,}\\ \\[-7pt] \tau^{(1)}_1, & \text{w.p. $\frac{1}{2}$.}\end{cases}\end{align*}
The tail asymptotics for
![]() $\tau^{(1)}_1$
are known:
$\tau^{(1)}_1$
are known:
![]() $\mathbb{P}\{\tau^{(1)}_1>n\} \sim \sqrt{2/(\pi n)}$
, as
$\mathbb{P}\{\tau^{(1)}_1>n\} \sim \sqrt{2/(\pi n)}$
, as
![]() $n\to \infty$
(see, e.g., Section III.2 in [Reference Feller12] for a related result). Since
$n\to \infty$
(see, e.g., Section III.2 in [Reference Feller12] for a related result). Since
![]() $\tau^{(1)}_1$
has a distribution with a regularly varying tail, for any
$\tau^{(1)}_1$
has a distribution with a regularly varying tail, for any
![]() $m=2, 3, \ldots$
we have
$m=2, 3, \ldots$
we have
4. Trajectories in the dog-and-cat-and-mouse model
In this section we study structural properties of the DCM MC on
![]() $\mathbb{Z}$
. We describe the main idea of the analysis, which may be of independent interest, as we believe it may be applied to other multi-component MCs.
$\mathbb{Z}$
. We describe the main idea of the analysis, which may be of independent interest, as we believe it may be applied to other multi-component MCs.
As before, let
![]() $\big\{T^{(3)}(n)\big\}_{n=0}^\infty$
be the meeting-time instants, when all three agents meet at a certain point of
$\big\{T^{(3)}(n)\big\}_{n=0}^\infty$
be the meeting-time instants, when all three agents meet at a certain point of
![]() $\mathbb{Z}$
, and let
$\mathbb{Z}$
, and let
![]() $\big\{J_k^{(3)}\big\}_{k=1}^\infty = \big\{T^{(3)}(k) - T^{(3)}(k-1)\big\}_{k=1}^\infty$
be the times between such events. Let
$\big\{J_k^{(3)}\big\}_{k=1}^\infty = \big\{T^{(3)}(k) - T^{(3)}(k-1)\big\}_{k=1}^\infty$
be the times between such events. Let
![]() $M_{T^{(3)}(n)}$
,
$M_{T^{(3)}(n)}$
,
![]() $n=0, 1, \ldots$
, be the locations of the mouse (and, therefore, the common locations of the agents) at the embedded epochs
$n=0, 1, \ldots$
, be the locations of the mouse (and, therefore, the common locations of the agents) at the embedded epochs
![]() $T^{(3)}(n)$
, and let
$T^{(3)}(n)$
, and let
![]() $\big\{Y_k^{(3)}\big\}_{k=1}^\infty = \big\{M_{T^{(3)}(k)} - M_{T^{(3)}(k-1)}\big\}_{k=1}^\infty$
be the corresponding jump sizes between the embedded epochs. Because of time homogeneity, random vectors
$\big\{Y_k^{(3)}\big\}_{k=1}^\infty = \big\{M_{T^{(3)}(k)} - M_{T^{(3)}(k-1)}\big\}_{k=1}^\infty$
be the corresponding jump sizes between the embedded epochs. Because of time homogeneity, random vectors
![]() $\big\{\big(Y_k^{(3)}, J_k^{(3)}\big)\big\}$
are i.i.d.
$\big\{\big(Y_k^{(3)}, J_k^{(3)}\big)\big\}$
are i.i.d.
Let
![]() $N(t) = \max\big\{n: \ T^{(3)}(n) = \sum_{k=1}^n J_k^{(3)} \leq t\big\}$
, for
$N(t) = \max\big\{n: \ T^{(3)}(n) = \sum_{k=1}^n J_k^{(3)} \leq t\big\}$
, for
![]() $t\geq0$
. Let
$t\geq0$
. Let
![]() $S_0 = 0$
and
$S_0 = 0$
and
![]() $S_n = \sum_{k=1}^n Y_k^{(3)}$
. We show that the statement of Theorem 3 holds if we replace
$S_n = \sum_{k=1}^n Y_k^{(3)}$
. We show that the statement of Theorem 3 holds if we replace
![]() $M_n$
with a continuous-time process
$M_n$
with a continuous-time process
 \begin{equation*}\widetilde{M}(t) = S_{N(t)} = \sum_{k=1}^{N(t)} Y_k, \ \text{for $t\geq 0$}.\end{equation*}
\begin{equation*}\widetilde{M}(t) = S_{N(t)} = \sum_{k=1}^{N(t)} Y_k, \ \text{for $t\geq 0$}.\end{equation*}
The process
![]() $\widetilde{M}(t)$
is a so-called coupled continuous-time random walk (see [Reference Becker-Kern, Meerschaert and Scheffler5]), and we use Theorem 5.1 from [Reference Kasahara24] to obtain its scaling properties.
$\widetilde{M}(t)$
is a so-called coupled continuous-time random walk (see [Reference Becker-Kern, Meerschaert and Scheffler5]), and we use Theorem 5.1 from [Reference Kasahara24] to obtain its scaling properties.
4.1. Distribution of the random variable
 $J^{(3)}_1$
$J^{(3)}_1$
We assume that
![]() $D_0 = C_0 = M_0 = 0$
. Let
$D_0 = C_0 = M_0 = 0$
. Let
![]() $V_n = (V_{n1}, V_{n2}) = (|D_n - C_n|, |C_n - M_n|)$
. Then the following recursion holds:
$V_n = (V_{n1}, V_{n2}) = (|D_n - C_n|, |C_n - M_n|)$
. Then the following recursion holds:
Note further that
 \begin{equation}V_{n+1} \overset{d}{=} \begin{cases}\Big(1 + \xi^{(1)}_{n+1}, 1+\xi^{(2)}_{n+1}\Big), \ \text{if $V_{n1} = V_{n2} = 0$,} \\ \\[-7pt] \Big(1 + \xi^{(1)}_{n+1}, V_{n2} + \xi^{(2)}_{n+1}\Big), \ \text{if $V_{n1} = 0$ and $V_{n2} \neq 0$,}\\ \\[-7pt] \Big(V_{n1} + \xi^{(1)}_{n+1}, 1\Big), \ \text{if $V_{n1} \neq 0$ and $V_{n2} = 0$,}\\ \\[-7pt]\Big(V_{n1} + \xi^{(1)}_{n+1}, V_{n2}\Big), \ \text{if $V_{n1} \neq 0$ and $V_{n2} \neq 0$.}\end{cases}\end{equation}
\begin{equation}V_{n+1} \overset{d}{=} \begin{cases}\Big(1 + \xi^{(1)}_{n+1}, 1+\xi^{(2)}_{n+1}\Big), \ \text{if $V_{n1} = V_{n2} = 0$,} \\ \\[-7pt] \Big(1 + \xi^{(1)}_{n+1}, V_{n2} + \xi^{(2)}_{n+1}\Big), \ \text{if $V_{n1} = 0$ and $V_{n2} \neq 0$,}\\ \\[-7pt] \Big(V_{n1} + \xi^{(1)}_{n+1}, 1\Big), \ \text{if $V_{n1} \neq 0$ and $V_{n2} = 0$,}\\ \\[-7pt]\Big(V_{n1} + \xi^{(1)}_{n+1}, V_{n2}\Big), \ \text{if $V_{n1} \neq 0$ and $V_{n2} \neq 0$.}\end{cases}\end{equation}
Thus,
![]() $\{V_n\}_{n=0}^\infty$
is a MC. Let
$\{V_n\}_{n=0}^\infty$
is a MC. Let
![]() $p_{ij}(k,l) = \mathbb{P}\{V_{n+1}=(k, l) | V_n = (i, j)\}$
, for
$p_{ij}(k,l) = \mathbb{P}\{V_{n+1}=(k, l) | V_n = (i, j)\}$
, for
![]() $i,j, k,l\geq 0$
. Note that
$i,j, k,l\geq 0$
. Note that
![]() $p_{00}(k,l) = p_{01}(k,l)$
for any
$p_{00}(k,l) = p_{01}(k,l)$
for any
![]() $k,l \ge 0$
.
$k,l \ge 0$
.
Let
Since
![]() $p_{00}(m,l) = p_{01}(m,l)$
for any m,l, we have that the RVs
$p_{00}(m,l) = p_{01}(m,l)$
for any m,l, we have that the RVs
![]() $\big\{U^{(3)}(k) - U^{(3)}(k-1)\big\}_{k=1}^\infty$
are i.i.d., and the RV
$\big\{U^{(3)}(k) - U^{(3)}(k-1)\big\}_{k=1}^\infty$
are i.i.d., and the RV
![]() $\big(U^{(3)}(k) - U^{(3)}(k-1)\big)$
does not depend on
$\big(U^{(3)}(k) - U^{(3)}(k-1)\big)$
does not depend on
![]() $V_{U^{(3)}(k-1)}$
, for
$V_{U^{(3)}(k-1)}$
, for
![]() $k\ge 1$
.
$k\ge 1$
.
In other words, each time
![]() $n=U^{(3)}(k)$
, the DCM process visits either a state on the ‘main diagonal’
$n=U^{(3)}(k)$
, the DCM process visits either a state on the ‘main diagonal’
![]() $D_n=C_n=M_n$
or an auxiliary state
$D_n=C_n=M_n$
or an auxiliary state
![]() $D_n = C_n = M_n \pm 1$
. To find the tail asymptotics for
$D_n = C_n = M_n \pm 1$
. To find the tail asymptotics for
![]() $T^{(3)}_1$
, we find tail asymptotics for
$T^{(3)}_1$
, we find tail asymptotics for
![]() $U^{(3)}(1)$
and then use the natural link between time instants
$U^{(3)}(1)$
and then use the natural link between time instants
![]() $T^{(3)}(1)$
and
$T^{(3)}(1)$
and
![]() $\big\{U^{(3)}(k)\big\}_{k=1}^\infty$
.
$\big\{U^{(3)}(k)\big\}_{k=1}^\infty$
.
Lemma 1. Let
![]() $V_0 \in \{(0,0), (0,1)\}$
. Then we have
$V_0 \in \{(0,0), (0,1)\}$
. Then we have
Further,
![]() $U^{(3)}(1) = 1$
if and only if
$U^{(3)}(1) = 1$
if and only if
![]() $V_{U^{(3)}(1)} = (0,0)$
.
$V_{U^{(3)}(1)} = (0,0)$
.
Proof. Let
![]() $V_0 = (0,0)$
. It is apparent from the first line of Equation (7) that
$V_0 = (0,0)$
. It is apparent from the first line of Equation (7) that
Since
![]() $p_{00}(k,l) = p_{01}(k,l)$
, the RV
$p_{00}(k,l) = p_{01}(k,l)$
, the RV
![]() $V_1$
has the same distribution given
$V_1$
has the same distribution given
![]() $V_0 = (0, 1)$
.
$V_0 = (0, 1)$
.
Let
![]() $V_1 = (0, 2)$
(Figure 1c). From the second and the fourth lines of Equation (7) we know that
$V_1 = (0, 2)$
(Figure 1c). From the second and the fourth lines of Equation (7) we know that
![]() $|V_{(k+1)2} - V_{k2}| \in \{0, 1\}$
, for
$|V_{(k+1)2} - V_{k2}| \in \{0, 1\}$
, for
![]() $k\ge 1$
, given
$k\ge 1$
, given
![]() $V_{k2} \neq 0$
. Therefore
$V_{k2} \neq 0$
. Therefore
![]() $V_{k2}$
arrives at 1 before hitting 0, and
$V_{k2}$
arrives at 1 before hitting 0, and
![]() $V_{U^{(3)}(1)} = (0, 1)$
. Let
$V_{U^{(3)}(1)} = (0, 1)$
. Let
![]() $\tau, \tau_1, \tau_2, \ldots$
be independent copies of
$\tau, \tau_1, \tau_2, \ldots$
be independent copies of
![]() $\tau^{(1)}_1$
. Then
$\tau^{(1)}_1$
. Then
![]() $U^{(3)}(1)$
has the same distribution as
$U^{(3)}(1)$
has the same distribution as
![]() $\sum_{k=1}^\tau \tau_k$
, and we have that
$\sum_{k=1}^\tau \tau_k$
, and we have that
 \begin{equation*}\mathbb{P}\bigg\{\sum_{k=1}^\tau \tau_k > n\bigg\} \sim n^{-1/4} \frac{\Gamma^{1/2}(1/2) \Gamma(1/2)}{\Gamma(3/4)} \sqrt{\sqrt{\frac{2}{\pi}}} \sqrt{\frac{2}{\pi}} = \frac{2^{3/4}}{\Gamma(3/4) n^{1/4}},\end{equation*}
\begin{equation*}\mathbb{P}\bigg\{\sum_{k=1}^\tau \tau_k > n\bigg\} \sim n^{-1/4} \frac{\Gamma^{1/2}(1/2) \Gamma(1/2)}{\Gamma(3/4)} \sqrt{\sqrt{\frac{2}{\pi}}} \sqrt{\frac{2}{\pi}} = \frac{2^{3/4}}{\Gamma(3/4) n^{1/4}},\end{equation*}
as
![]() $n\to\infty$
(see Appendix C).
$n\to\infty$
(see Appendix C).

Figure 1. The positioning after the first jump.
Let
![]() $V_1 = (2,2)$
(Figure 1d). From the fourth line of Equation (7),
$V_1 = (2,2)$
(Figure 1d). From the fourth line of Equation (7),
![]() $V_{k2}$
remains at 2 (the cat and the mouse do not move) until
$V_{k2}$
remains at 2 (the cat and the mouse do not move) until
![]() $V_{k1}$
reaches 0. This happens after a time which has the same distribution as
$V_{k1}$
reaches 0. This happens after a time which has the same distribution as
![]() $\tau^{(1)}_2 = \min\big\{n > 0: \ \sum_{k=1}^n \xi^{(1)}_k = 2\big\}$
. Thus, we travel from (2,2) to (0, 2) while never hitting (0,0). We also know that the tail asymptotics of the travel time are
$\tau^{(1)}_2 = \min\big\{n > 0: \ \sum_{k=1}^n \xi^{(1)}_k = 2\big\}$
. Thus, we travel from (2,2) to (0, 2) while never hitting (0,0). We also know that the tail asymptotics of the travel time are
![]() $\mathbb{P}\big\{\tau^{(1)}_2 > n\big\} \sim \sqrt{8/\pi n}$
, as
$\mathbb{P}\big\{\tau^{(1)}_2 > n\big\} \sim \sqrt{8/\pi n}$
, as
![]() $n\to\infty$
. Therefore, we travel from (2, 2) to (0, 2) much faster than from (0, 2) to (0, 1), and given
$n\to\infty$
. Therefore, we travel from (2, 2) to (0, 2) much faster than from (0, 2) to (0, 1), and given
![]() $V_1 = (2,2)$
, we again have
$V_1 = (2,2)$
, we again have
![]() $\mathbb{P}\big\{U^{(3)}(1) > n\big\} \sim \mathbb{P}\big\{\sum_{k=1}^\tau \tau_k > n\big\}$
, as
$\mathbb{P}\big\{U^{(3)}(1) > n\big\} \sim \mathbb{P}\big\{\sum_{k=1}^\tau \tau_k > n\big\}$
, as
![]() $n\to\infty$
.
$n\to\infty$
.
Finally, let
![]() $V_1 = (2, 0)$
(Figure 1b). From the third line of Equation (7) we have
$V_1 = (2, 0)$
(Figure 1b). From the third line of Equation (7) we have
![]() $V_{2} \overset{d}{=} \big(2+ \xi^{(1)}_{2}, 1\big)$
and
$V_{2} \overset{d}{=} \big(2+ \xi^{(1)}_{2}, 1\big)$
and
![]() $V_{U^{(3)}(1)} = (0, 1)$
, where, given
$V_{U^{(3)}(1)} = (0, 1)$
, where, given
![]() $V_1 = (2, 0)$
,
$V_1 = (2, 0)$
,
![]() $\mathbb{P}\big\{U^{(3)}(1)>n\big\} \sim \sqrt{8/\pi n}$
, as
$\mathbb{P}\big\{U^{(3)}(1)>n\big\} \sim \sqrt{8/\pi n}$
, as
![]() $n\to\infty$
.
$n\to\infty$
.
Thus,
We note the following relation between time instants
![]() $T^{(3)}(1)$
and
$T^{(3)}(1)$
and
![]() $\big\{U^{(3)}(k)\big\}_{k=1}^\infty$
. At each time n when we are at the auxiliary state (when
$\big\{U^{(3)}(k)\big\}_{k=1}^\infty$
. At each time n when we are at the auxiliary state (when
![]() $V_n = (0, 1)$
), we have a probability of
$V_n = (0, 1)$
), we have a probability of
![]() $1/4$
of jumping into the state
$1/4$
of jumping into the state
![]() $D_{n+1} = C_{n+1} = M_{n+1}$
, independently of anything else. Using Lemma 1 and the results in Section XIII.6 of [Reference Feller13], we get the following result.
$D_{n+1} = C_{n+1} = M_{n+1}$
, independently of anything else. Using Lemma 1 and the results in Section XIII.6 of [Reference Feller13], we get the following result.
Proposition 1. Let
Then
![]() $\nu$
has a geometric distribution with parameter
$\nu$
has a geometric distribution with parameter
![]() $1/4$
,
$1/4$
,
![]() $T^{(3)}\equiv J^{(3)}=U^{(3)}(\nu)$
a.s., and
$T^{(3)}\equiv J^{(3)}=U^{(3)}(\nu)$
a.s., and
Therefore, there exists a positive RV
![]() $D^{(3)}$
having a stable distribution with Laplace transform
$D^{(3)}$
having a stable distribution with Laplace transform
![]() $\exp\big(\!-s^{1/4}\big)$
such that
$\exp\big(\!-s^{1/4}\big)$
such that
4.2. Distribution of the random variable
 $Y^{(3)}_1$
$Y^{(3)}_1$
In the previous subsection we analysed the time our process spends between auxiliary states. In this subsection we analyse the total displacement of the mouse by time
![]() $T_1^{(3)}$
. Note that the mouse may have zero, one, or two jumps between consecutive visits to auxiliary states; therefore, the total number of jumps of the mouse by time
$T_1^{(3)}$
. Note that the mouse may have zero, one, or two jumps between consecutive visits to auxiliary states; therefore, the total number of jumps of the mouse by time
![]() $T_1^{(3)}$
, say
$T_1^{(3)}$
, say
![]() $\varkappa$
, admits the following simple upper bound:
$\varkappa$
, admits the following simple upper bound:
It follows that the sequence
![]() $Z_k = M_{U^{(3)}(k)} - C_{U^{(3)}(k)}$
,
$Z_k = M_{U^{(3)}(k)} - C_{U^{(3)}(k)}$
,
![]() $k=0,1,\ldots$
, forms a time-homogeneous MC, and
$k=0,1,\ldots$
, forms a time-homogeneous MC, and
![]() $Z_k \in \{-1, 0, 1\}$
a.s. Further,
$Z_k \in \{-1, 0, 1\}$
a.s. Further,
![]() $Z_0 = Z_\nu = 0$
, and for any
$Z_0 = Z_\nu = 0$
, and for any
![]() $k \in \{1, \nu - 1\}$
, we have
$k \in \{1, \nu - 1\}$
, we have
![]() $Z_k = \pm 1$
.
$Z_k = \pm 1$
.
Let
Our analysis of trajectories of the DCM MC in Section 4.1 shows that the
![]() $\gamma^{(3)}_k$
are conditionally independent given values of the auxiliary MC
$\gamma^{(3)}_k$
are conditionally independent given values of the auxiliary MC
![]() $\{Z_k\}_{k = 0}^\infty$
. Clearly,
$\{Z_k\}_{k = 0}^\infty$
. Clearly,
We now find the first and second moments of
![]() $Y_1^{(3)}$
and show that it has a light-tailed distribution.
$Y_1^{(3)}$
and show that it has a light-tailed distribution.
Since
![]() $D_0 = C_0 = M_0 = 0$
, we get
$D_0 = C_0 = M_0 = 0$
, we get
![]() $\nu=1$
if and only if
$\nu=1$
if and only if
![]() $Z_1 = 0$
and
$Z_1 = 0$
and
![]() $\gamma^{(3)}_1 = \pm 1$
. Additionally, we have
$\gamma^{(3)}_1 = \pm 1$
. Additionally, we have
Another case of exactly one jump is when the cat and the mouse jump in different directions. Here we have
Further, the mouse can have two jumps in the same direction w.p.
or two jumps in opposite directions w.p.
Thus, given
![]() $Z_0 = 0$
we have
$Z_0 = 0$
we have
From the above, we get that
![]() $\mathbb{E} \gamma^{(3)}_1 = 0$
and
$\mathbb{E} \gamma^{(3)}_1 = 0$
and
![]() $\mathbf{Var} \gamma^{(3)}_1 = 5/4$
.
$\mathbf{Var} \gamma^{(3)}_1 = 5/4$
.
We now analyse the distribution of
![]() $\gamma^{(3)}_k$
,
$\gamma^{(3)}_k$
,
![]() $k\ge 2$
. So as not to make the notation cumbersome, we assume that
$k\ge 2$
. So as not to make the notation cumbersome, we assume that
![]() $D_0 = C_0 = 0$
and
$D_0 = C_0 = 0$
and
![]() $M_0 = 1$
, so
$M_0 = 1$
, so
![]() $Z_0 = 1$
. The case
$Z_0 = 1$
. The case
![]() $Z_0 = -1$
is analogous by symmetry. Then the mouse can make either zero jumps or exactly one jump before the next visit of the process to an auxiliary state. In the case of zero jumps we have
$Z_0 = -1$
is analogous by symmetry. Then the mouse can make either zero jumps or exactly one jump before the next visit of the process to an auxiliary state. In the case of zero jumps we have
In the case of exactly one jump we have
Thus, given
![]() $Z_0 = 1$
we have
$Z_0 = 1$
we have
Thus,
![]() $\mathbb{E} \left( \gamma^{(3)}_1 \big| Z_0 = 1\right) = 0$
and
$\mathbb{E} \left( \gamma^{(3)}_1 \big| Z_0 = 1\right) = 0$
and
![]() $\mathbf{Var} \left( \gamma^{(3)}_1\big| Z_0 =1\right) = 1/4$
.
$\mathbf{Var} \left( \gamma^{(3)}_1\big| Z_0 =1\right) = 1/4$
.
Let us return to the case
![]() $D_0 = C_0 = M_0 = 0$
. Combining the results
$D_0 = C_0 = M_0 = 0$
. Combining the results
![]() $(8)$
and
$(8)$
and
![]() $(9)$
we get
$(9)$
we get
 \begin{align*}\mathbb{E} Y^{(3)}_1 = \mathbb{E} \sum_{k=1}^\nu \gamma^{(3)}_k = \mathbb{E} \sum_{k = 1}^\infty \left( \gamma^{(3)}_k I[\nu \ge k]\right) = \mathbb{E} \gamma^{(3)}_1 + \sum_{k = 2}^\infty \mathbb{E} \left( \gamma^{(3)}_k I[\nu \ge k]\right)& \\ & \kern-164pt = \sum_{k = 2}^\infty \mathbb{E} \left( \gamma^{(3)}_k I[Z_{k-1} = 1] + \gamma^{(3)}_kI[Z_{k-1} = -1]\right) = 0.\end{align*}
\begin{align*}\mathbb{E} Y^{(3)}_1 = \mathbb{E} \sum_{k=1}^\nu \gamma^{(3)}_k = \mathbb{E} \sum_{k = 1}^\infty \left( \gamma^{(3)}_k I[\nu \ge k]\right) = \mathbb{E} \gamma^{(3)}_1 + \sum_{k = 2}^\infty \mathbb{E} \left( \gamma^{(3)}_k I[\nu \ge k]\right)& \\ & \kern-164pt = \sum_{k = 2}^\infty \mathbb{E} \left( \gamma^{(3)}_k I[Z_{k-1} = 1] + \gamma^{(3)}_kI[Z_{k-1} = -1]\right) = 0.\end{align*}
In a similar manner we transform the second moment:
If we fix the values of
![]() $\{Z_k\}_{k=0}^\infty$
, the RVs
$\{Z_k\}_{k=0}^\infty$
, the RVs
![]() $ \gamma^{(3)}_k$
and
$ \gamma^{(3)}_k$
and
![]() $ \gamma^{(3)}_m$
become independent. Combined with the fact that
$ \gamma^{(3)}_m$
become independent. Combined with the fact that
![]() $\mathbb{E} \left( \gamma^{(3)}_m \big| Z_{m-1} = \pm 1 \right) = 0$
, we get that the second sum in
$\mathbb{E} \left( \gamma^{(3)}_m \big| Z_{m-1} = \pm 1 \right) = 0$
, we get that the second sum in
![]() $(10)$
equals zero. Now we can use the conditional second moments obtained above and the fact that the RV
$(10)$
equals zero. Now we can use the conditional second moments obtained above and the fact that the RV
![]() $\nu$
has a geometric distribution with parameter
$\nu$
has a geometric distribution with parameter
![]() $1/4$
. We obtain
$1/4$
. We obtain
 \begin{align*}\mathbb{E} \Big(Y^{(3)}_1\Big)^2 = \mathbb{E} \Big(\gamma^{(3)}_1\Big)^2 + \sum_{k=2}^\infty \mathbb{E}\left( \Big(\gamma^{(3)}_k\Big)^2\Bigg| \ Z_{k-1} = \pm 1\right) \mathbb{P}\{\nu\ge k\} = \frac{5}{4} + \frac{1}{4}(\mathbb{E} \nu -1) = 2.\end{align*}
\begin{align*}\mathbb{E} \Big(Y^{(3)}_1\Big)^2 = \mathbb{E} \Big(\gamma^{(3)}_1\Big)^2 + \sum_{k=2}^\infty \mathbb{E}\left( \Big(\gamma^{(3)}_k\Big)^2\Bigg| \ Z_{k-1} = \pm 1\right) \mathbb{P}\{\nu\ge k\} = \frac{5}{4} + \frac{1}{4}(\mathbb{E} \nu -1) = 2.\end{align*}
Finally, we observe that
![]() $\big|\gamma^{(3)}_1\big| \le 2$
. Therefore,
$\big|\gamma^{(3)}_1\big| \le 2$
. Therefore,
![]() $\big|Y^{(3)}_1\big| = \Big|M_{J^{(3)}_1}\Big| \le 2\nu$
a.s. and
$\big|Y^{(3)}_1\big| = \Big|M_{J^{(3)}_1}\Big| \le 2\nu$
a.s. and
![]() $|Y^{(3)}|$
has a finite exponential moment. In particular, the following holds.
$|Y^{(3)}|$
has a finite exponential moment. In particular, the following holds.
Proposition 2. We have
![]() $\mathbb{E} Y^{(3)}_1 = 0$
,
$\mathbb{E} Y^{(3)}_1 = 0$
,
![]() $\mathbf{Var} Y^{(3)}_1 = 2$
, and
$\mathbf{Var} Y^{(3)}_1 = 2$
, and
![]() $\mathbb{E} \big|Y^{(3)}_1\big|^m < \infty$
, for any
$\mathbb{E} \big|Y^{(3)}_1\big|^m < \infty$
, for any
![]() $m\geq 3$
.
$m\geq 3$
.
5. Proofs of main results
In this section we provide proofs of our main results.
5.1. Proofs of Theorems 1 and 2
We start with the general idea of the proofs of Theorems 1 and 2. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $S^{(i)}_0 = 0$
and
$S^{(i)}_0 = 0$
and
![]() $S^{(i)}_n = \sum_{k=1}^n \xi^{(i)}_k$
, for
$S^{(i)}_n = \sum_{k=1}^n \xi^{(i)}_k$
, for
![]() $n\geq1$
. Let
$n\geq1$
. Let
Since
![]() $\big\{\xi^{(1)}_k\big\}_{k=1}^\infty$
and
$\big\{\xi^{(1)}_k\big\}_{k=1}^\infty$
and
![]() $\big\{\xi^{(2)}_k\big\}_{k=1}^\infty$
are independent sequences of i.i.d. RVs, we have that
$\big\{\xi^{(2)}_k\big\}_{k=1}^\infty$
are independent sequences of i.i.d. RVs, we have that
![]() $\tau(n) - \tau(n-1) \overset{d}{=} \tau(1)$
, for
$\tau(n) - \tau(n-1) \overset{d}{=} \tau(1)$
, for
![]() $n \ge 1$
.
$n \ge 1$
.
Let
![]() $\eta(t) = \max\{k\geq 0 :\ \tau(k) \leq t\}$
for
$\eta(t) = \max\{k\geq 0 :\ \tau(k) \leq t\}$
for
![]() $t\geq 0$
. Define a continuous-time process M
$t\geq 0$
. Define a continuous-time process M
![]() $^{\prime}$
(t) by
$^{\prime}$
(t) by
 \begin{align*}M'(t) = 0 \ \text{for $t\in [0, 1)$, } \qquad M'(t) = S^{(2)}_{\eta(t-1) + 1} = \sum_{k=1}^{\eta(t-1)+1} \xi^{(2)}_k \ \text{for $t\geq 1$.}\end{align*}
\begin{align*}M'(t) = 0 \ \text{for $t\in [0, 1)$, } \qquad M'(t) = S^{(2)}_{\eta(t-1) + 1} = \sum_{k=1}^{\eta(t-1)+1} \xi^{(2)}_k \ \text{for $t\geq 1$.}\end{align*}
It is straightforward to verify that
![]() $\{M'(n), \ n\ge 0\} \overset{d}{=} \{M(n), \ n\ge 0\}$
. In the rest of the section we will omit the prime symbol and simply write M(t). The process
$\{M'(n), \ n\ge 0\} \overset{d}{=} \{M(n), \ n\ge 0\}$
. In the rest of the section we will omit the prime symbol and simply write M(t). The process
![]() $\{\widehat{M}(t)\}_{t\geq 0} = \{M'(t+1)\}_{t\geq 0}$
is a so-called oracle continuous-time random walk (see, e.g., [Reference Jurlewicz, Kern, Meerschaert and Scheffler23].
$\{\widehat{M}(t)\}_{t\geq 0} = \{M'(t+1)\}_{t\geq 0}$
is a so-called oracle continuous-time random walk (see, e.g., [Reference Jurlewicz, Kern, Meerschaert and Scheffler23].
First, consider the case
![]() $\mathbb{E}\xi^{(2)}_1 = 0$
. We want to show that
$\mathbb{E}\xi^{(2)}_1 = 0$
. We want to show that
 \begin{equation}\left(\frac{S^{(2)}_n}{b(n)}, \frac{\tau(n)}{n^2} \right) \Rightarrow \big(A^{(2)}, D^{(2)}\big), \ \text{as $n\to\infty$.}\end{equation}
\begin{equation}\left(\frac{S^{(2)}_n}{b(n)}, \frac{\tau(n)}{n^2} \right) \Rightarrow \big(A^{(2)}, D^{(2)}\big), \ \text{as $n\to\infty$.}\end{equation}
Given that, we will show that the first part of Theorem 1 follows from the next proposition.
Proposition 3. (Theorem 3.1, [Reference Jurlewicz, Kern, Meerschaert and Scheffler23].) Assume (11) holds. Then
A similar result is proven in Theorem 3.6 of [Reference Henry and Straka21].
We will now show that the relation (11) holds and that the RVs
![]() $A^{(2)}$
and
$A^{(2)}$
and
![]() $D^{(2)}$
are independent. We show that for certain functions
$D^{(2)}$
are independent. We show that for certain functions
![]() $f_1$
and
$f_1$
and
![]() $f_2$
,
$f_2$
,
 \begin{align}\mathbb{E} \exp\left( i\left(\lambda_1\frac{S^{(2)}_n}{b(n)} + \lambda_2 \frac{\tau(n)}{n^2}\right) \right) &= \mathbb{E} \exp\left( i\left(\lambda_1\frac{\xi^{(2)}_1}{b(n)} + \lambda_2 \frac{\tau(1)}{n^2}\right)\right)^n\\ &\qquad\qquad\qquad = \left(1 + \frac{f_1(\lambda_1) + f_2(\lambda_2)}{n} + o\left(\frac{1}{n} \right) \right)^n,\end{align}
\begin{align}\mathbb{E} \exp\left( i\left(\lambda_1\frac{S^{(2)}_n}{b(n)} + \lambda_2 \frac{\tau(n)}{n^2}\right) \right) &= \mathbb{E} \exp\left( i\left(\lambda_1\frac{\xi^{(2)}_1}{b(n)} + \lambda_2 \frac{\tau(1)}{n^2}\right)\right)^n\\ &\qquad\qquad\qquad = \left(1 + \frac{f_1(\lambda_1) + f_2(\lambda_2)}{n} + o\left(\frac{1}{n} \right) \right)^n,\end{align}
as
![]() $n\to\infty$
, for any
$n\to\infty$
, for any
![]() $\lambda_1, \lambda_2 \in \mathbb{R}$
. Indeed, convergence of characteristic functions is equivalent to weak convergence of RVs, and for independence of RVs it is sufficient to verify that the characteristic function of the sum is equal to the product of the respective characteristic functions. Since the right-hand side of (12) converges to
$\lambda_1, \lambda_2 \in \mathbb{R}$
. Indeed, convergence of characteristic functions is equivalent to weak convergence of RVs, and for independence of RVs it is sufficient to verify that the characteristic function of the sum is equal to the product of the respective characteristic functions. Since the right-hand side of (12) converges to
![]() $\exp(f_1(\lambda_1))\exp(f_2(\lambda_2))$
, this will prove the convergence and the independence of the limits
$\exp(f_1(\lambda_1))\exp(f_2(\lambda_2))$
, this will prove the convergence and the independence of the limits
![]() $A^{(2)}$
and
$A^{(2)}$
and
![]() $D^{(2)}$
.
$D^{(2)}$
.
5.1.1. Proof of Theorem 1
From the condition (2) we have the weak convergence of
![]() $S_n^{(2)} / b(n)$
to the RV
$S_n^{(2)} / b(n)$
to the RV
![]() $A^{(2)}$
. Again, this is equivalent to the convergence of the characteristic functions. Thus, (2) implies
$A^{(2)}$
. Again, this is equivalent to the convergence of the characteristic functions. Thus, (2) implies
 \begin{align*}\mathbb{E}\exp\left(i\lambda_1\frac{\sum_{k=1}^n\xi^{(2)}_k}{b(n)} \right) = \left[ \mathbb{E}\exp\left(i\lambda_1\frac{\xi^{(2)}_1}{b(n)} \right)\right]^n \to \mathbb{E}\exp\left(i\lambda_1 A^{(2)}\right), \ \text{as $n\to\infty$.}\end{align*}
\begin{align*}\mathbb{E}\exp\left(i\lambda_1\frac{\sum_{k=1}^n\xi^{(2)}_k}{b(n)} \right) = \left[ \mathbb{E}\exp\left(i\lambda_1\frac{\xi^{(2)}_1}{b(n)} \right)\right]^n \to \mathbb{E}\exp\left(i\lambda_1 A^{(2)}\right), \ \text{as $n\to\infty$.}\end{align*}
Additionally, if
![]() $B^n(n) \to z$
as
$B^n(n) \to z$
as
![]() $n\to\infty$
, then
$n\to\infty$
, then
![]() $n\log B(n) \to \log z$
, which leads to
$n\log B(n) \to \log z$
, which leads to
![]() $\log B(n) \sim n^{-1}\log z $
and hence, finally,
$\log B(n) \sim n^{-1}\log z $
and hence, finally,
![]() $B(n) \sim 1 + n^{-1}\log z$
, as
$B(n) \sim 1 + n^{-1}\log z$
, as
![]() $n\to\infty$
. Thus, we have the following:
$n\to\infty$
. Thus, we have the following:
 \begin{equation}\mathbb{E}\exp\left(i\lambda_1\frac{\xi^{(2)}_1}{b(n)} \right) \sim 1 + \frac{l_1(\lambda_1)}{n}, \ \text{as $n\to\infty$,}\end{equation}
\begin{equation}\mathbb{E}\exp\left(i\lambda_1\frac{\xi^{(2)}_1}{b(n)} \right) \sim 1 + \frac{l_1(\lambda_1)}{n}, \ \text{as $n\to\infty$,}\end{equation}
where
![]() $l_1(\lambda) = \log \mathbb{E} \exp\big(i\lambda A^{(2)}\big)$
, the logarithmic characteristic function of
$l_1(\lambda) = \log \mathbb{E} \exp\big(i\lambda A^{(2)}\big)$
, the logarithmic characteristic function of
![]() $A^{(2)}$
.
$A^{(2)}$
.
As in Section 3, we reformulate the distribution of the RV
![]() $\tau(1)$
using the time needed for the simple random walk to hit a fixed point. Let
$\tau(1)$
using the time needed for the simple random walk to hit a fixed point. Let
![]() $\big\{\tau^{(1)}_k\big\}_{k=1}^\infty$
be independent copies of
$\big\{\tau^{(1)}_k\big\}_{k=1}^\infty$
be independent copies of
![]() $\tau$
, the time needed for the simple random walk to hit 0 if it starts from 1, independent of
$\tau$
, the time needed for the simple random walk to hit 0 if it starts from 1, independent of
![]() $\big\{\xi^{(2)}_n\big\}_{n=1}^\infty$
. Given
$\big\{\xi^{(2)}_n\big\}_{n=1}^\infty$
. Given
![]() $\xi^{(2)}_1 = m \neq 0$
, the RV
$\xi^{(2)}_1 = m \neq 0$
, the RV
![]() $\tau(1)$
is the time needed for the random walk
$\tau(1)$
is the time needed for the random walk
![]() $S^{(1)}_n$
to reach m from zero, and thus,
$S^{(1)}_n$
to reach m from zero, and thus,
![]() $\tau(1) \overset{d}{=} \sum_{k=1}^{|m| } \tau^{(1)}_k$
. Given
$\tau(1) \overset{d}{=} \sum_{k=1}^{|m| } \tau^{(1)}_k$
. Given
![]() $\xi^{(2)}_1 = 0$
, we have
$\xi^{(2)}_1 = 0$
, we have
![]() $\tau(1) \overset{d}{=} 1 + \tau^{(1)}_1$
. Then we have the following relation for
$\tau(1) \overset{d}{=} 1 + \tau^{(1)}_1$
. Then we have the following relation for
![]() $\tau(1)$
:
$\tau(1)$
:
 \begin{align*}\tau(1) \overset{d}{=} I\Big[\xi^{(2)}_1 \neq 0\Big] \sum_{k=1}^{\big|\xi^{(2)}_1\big| } \tau^{(1)}_k + I\Big[\xi^{(2)}_1 = 0\Big]\Big(1 + \tau^{(1)}_1\Big).\end{align*}
\begin{align*}\tau(1) \overset{d}{=} I\Big[\xi^{(2)}_1 \neq 0\Big] \sum_{k=1}^{\big|\xi^{(2)}_1\big| } \tau^{(1)}_k + I\Big[\xi^{(2)}_1 = 0\Big]\Big(1 + \tau^{(1)}_1\Big).\end{align*}
Since
![]() $\mathbb{P}\big\{\tau^{(1)}_1 > n\big\} \sim \sqrt{2/(\pi n)}$
, as
$\mathbb{P}\big\{\tau^{(1)}_1 > n\big\} \sim \sqrt{2/(\pi n)}$
, as
![]() $n\to\infty$
, we conclude from Proposition 8 (see appendix) that
$n\to\infty$
, we conclude from Proposition 8 (see appendix) that
Thus, there exists an RV
![]() $D^{(2)}$
having a stable distribution with index
$D^{(2)}$
having a stable distribution with index
![]() $1/2$
such that
$1/2$
such that
Using the same argument as for (13), we get
where
![]() $\lambda_2(\lambda) = \log \mathbb{E} \exp\big(i\lambda D^{(2)}/ \big(\mathbb{E}|\xi^{(2)}_1 \big| + \mathbb{P}\big\{\xi^{(2)}_1 = 0\big\}\big)\big)$
, the logarithmic characteristic function of
$\lambda_2(\lambda) = \log \mathbb{E} \exp\big(i\lambda D^{(2)}/ \big(\mathbb{E}|\xi^{(2)}_1 \big| + \mathbb{P}\big\{\xi^{(2)}_1 = 0\big\}\big)\big)$
, the logarithmic characteristic function of
![]() $D^{(2)}/ \big(\mathbb{E}|\xi^{(2)}_1\big| + \mathbb{P}\big\{\xi^{(2)}_1 = 0\big\}\big)$
. We proceed as follows:
$D^{(2)}/ \big(\mathbb{E}|\xi^{(2)}_1\big| + \mathbb{P}\big\{\xi^{(2)}_1 = 0\big\}\big)$
. We proceed as follows:
 \begin{align*}\mathbb{E} \exp &\left( i\left[\lambda_1\frac{\xi^{(2)}_1}{b(n)} + \lambda_2\frac{ \tau(1)}{n^2}\right]\right)\\& =\sum_{-\infty}^{\infty} \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\}\mathbb{E} \exp\left( \left. i\lambda_2\frac{\tau(1)}{n^2} \right| \xi^{(2)}_1 = k \right) \\& = \mathbb{P}\Big\{\xi^{(2)}_1 = 0\Big\}\mathbb{E} \exp\left( i\lambda_2 \frac{1 + \tau}{n^2}\right) \\& + \sum_{k\neq 0} \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\}\left(\mathbb{E} \exp\left( i\lambda_2\frac{\tau}{n^2} \right)\right)^{|k|}.\end{align*}
\begin{align*}\mathbb{E} \exp &\left( i\left[\lambda_1\frac{\xi^{(2)}_1}{b(n)} + \lambda_2\frac{ \tau(1)}{n^2}\right]\right)\\& =\sum_{-\infty}^{\infty} \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\}\mathbb{E} \exp\left( \left. i\lambda_2\frac{\tau(1)}{n^2} \right| \xi^{(2)}_1 = k \right) \\& = \mathbb{P}\Big\{\xi^{(2)}_1 = 0\Big\}\mathbb{E} \exp\left( i\lambda_2 \frac{1 + \tau}{n^2}\right) \\& + \sum_{k\neq 0} \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\}\left(\mathbb{E} \exp\left( i\lambda_2\frac{\tau}{n^2} \right)\right)^{|k|}.\end{align*}
In order to transform the last sum in the last equation, we use (14) and get that, uniformly in
![]() $m>0$
,
$m>0$
,
 \begin{align*}\left(\mathbb{E} \exp\left( i\lambda_2\frac{\tau}{n^2} \right)\right)^m & = \left( 1 + \frac{l_2(\lambda_2)}{n} + o\left(\frac{1}{n}\right)\right)^m \notag \\[3pt]& = \exp\left( m\ln\bigg(1 + \frac{l_2(\lambda_2)+o(1)}{n}\bigg)\right) \notag \\[3pt] & = \exp\left( \frac{m l_2(\lambda_2)}{n}(1 + o(1)) \right) \notag \\[3pt] & = 1 + \frac{m l_2(\lambda_2)(1 + o(1))}{n} + \frac{1}{n^2}\sum_{j=2}^\infty \frac{(m l_2(\lambda_2)(1 + o(1)))^j}{n^{j-2} j!},\end{align*}
\begin{align*}\left(\mathbb{E} \exp\left( i\lambda_2\frac{\tau}{n^2} \right)\right)^m & = \left( 1 + \frac{l_2(\lambda_2)}{n} + o\left(\frac{1}{n}\right)\right)^m \notag \\[3pt]& = \exp\left( m\ln\bigg(1 + \frac{l_2(\lambda_2)+o(1)}{n}\bigg)\right) \notag \\[3pt] & = \exp\left( \frac{m l_2(\lambda_2)}{n}(1 + o(1)) \right) \notag \\[3pt] & = 1 + \frac{m l_2(\lambda_2)(1 + o(1))}{n} + \frac{1}{n^2}\sum_{j=2}^\infty \frac{(m l_2(\lambda_2)(1 + o(1)))^j}{n^{j-2} j!},\end{align*}
as
![]() $n\to\infty$
. Since the latter equation is uniform in
$n\to\infty$
. Since the latter equation is uniform in
![]() $m>0$
, we get
$m>0$
, we get
 \begin{align*}\sum_{k\neq 0} & \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\}\left(\mathbb{E} \exp\left( i\lambda_2\frac{\tau}{n^2} \right)\right)^{|k|}\\[3pt] & = \left(\mathbb{E}\exp\left(i\lambda_1\frac{\xi^{(2)}_1}{b(n)} \right) -\mathbb{P}\Big\{\xi^{(2)}_1 = 0\Big\}\right)\\ & + \frac{l_2(\lambda_2)}{n} \sum_{k\neq 0} |k| \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\} + \frac{1}{n^2}\sum_{k\neq 0}\sum_{j=2}^\infty \frac{(k l_2(\lambda_2)(1 + o(1)))^j}{n^{j-2} j!}+o\left(\frac{1}{n}\right),\end{align*}
\begin{align*}\sum_{k\neq 0} & \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\}\left(\mathbb{E} \exp\left( i\lambda_2\frac{\tau}{n^2} \right)\right)^{|k|}\\[3pt] & = \left(\mathbb{E}\exp\left(i\lambda_1\frac{\xi^{(2)}_1}{b(n)} \right) -\mathbb{P}\Big\{\xi^{(2)}_1 = 0\Big\}\right)\\ & + \frac{l_2(\lambda_2)}{n} \sum_{k\neq 0} |k| \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\} + \frac{1}{n^2}\sum_{k\neq 0}\sum_{j=2}^\infty \frac{(k l_2(\lambda_2)(1 + o(1)))^j}{n^{j-2} j!}+o\left(\frac{1}{n}\right),\end{align*}
as
![]() $n\to\infty$
. Now we use the fact that if
$n\to\infty$
. Now we use the fact that if
![]() $\sum_{-\infty}^{\infty} A_n = \sum_{-\infty}^{\infty} B_n + \sum_{-\infty}^{\infty} C_n$
and if the series
$\sum_{-\infty}^{\infty} A_n = \sum_{-\infty}^{\infty} B_n + \sum_{-\infty}^{\infty} C_n$
and if the series
![]() $\sum_{-\infty}^{\infty}A_n$
and
$\sum_{-\infty}^{\infty}A_n$
and
![]() $\sum_{-\infty}^{\infty}B_n$
converge, then
$\sum_{-\infty}^{\infty}B_n$
converge, then
![]() $\sum_{-\infty}^{\infty} C_n$
converges too. Thus,
$\sum_{-\infty}^{\infty} C_n$
converges too. Thus,
 \begin{equation*}\frac{1}{n^2}\sum_{k\neq 0}\sum_{j=2}^\infty \frac{(k l_2(\lambda_2)(1 + o(1)))^j}{n^{j-2} j!} = o\left(\frac{1}{n}\right)\end{equation*}
\begin{equation*}\frac{1}{n^2}\sum_{k\neq 0}\sum_{j=2}^\infty \frac{(k l_2(\lambda_2)(1 + o(1)))^j}{n^{j-2} j!} = o\left(\frac{1}{n}\right)\end{equation*}
and
 \begin{align*}\sum_{k\neq 0} & \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\}\left(\mathbb{E} \exp\left( i\lambda_2\frac{\tau}{n^2} \right)\right)^{|k|}\\& =\left(\mathbb{E}\exp\left(i\lambda_1\frac{\xi^{(2)}_1}{b(n)} \right) -\mathbb{P}\Big\{\xi^{(2)}_1 = 0\Big\}\right) +\mathbb{E}\Big|\xi^{(2)}_1\Big| \frac{l_2(\lambda_2)}{n} + o\left(\frac{1}{n}\right),\end{align*}
\begin{align*}\sum_{k\neq 0} & \exp\left(i\lambda_1\frac{k}{b(n)} \right)\mathbb{P}\Big\{\xi^{(2)}_1 = k\Big\}\left(\mathbb{E} \exp\left( i\lambda_2\frac{\tau}{n^2} \right)\right)^{|k|}\\& =\left(\mathbb{E}\exp\left(i\lambda_1\frac{\xi^{(2)}_1}{b(n)} \right) -\mathbb{P}\Big\{\xi^{(2)}_1 = 0\Big\}\right) +\mathbb{E}\Big|\xi^{(2)}_1\Big| \frac{l_2(\lambda_2)}{n} + o\left(\frac{1}{n}\right),\end{align*}
as
![]() $n\to\infty$
. Using (13) and (14), we have
$n\to\infty$
. Using (13) and (14), we have
 \begin{align*}\mathbb{E} \exp\left( i\left[\lambda_1\frac{\xi^{(2)}_1}{b(n)} + \lambda_2\frac{ \tau(1)}{n^2}\right]\right)& \\ &\kern-10pt = 1 + \frac{l_1(\lambda_1)}{n} + \Big(\mathbb{E}\Big|\xi^{(2)}_1\Big| + \mathbb{P}\Big\{\xi^{(2)}_1 = 0\Big\}\Big) \frac{l_2(\lambda_2)}{n} + o\left(\frac{1}{n}\right),\end{align*}
\begin{align*}\mathbb{E} \exp\left( i\left[\lambda_1\frac{\xi^{(2)}_1}{b(n)} + \lambda_2\frac{ \tau(1)}{n^2}\right]\right)& \\ &\kern-10pt = 1 + \frac{l_1(\lambda_1)}{n} + \Big(\mathbb{E}\Big|\xi^{(2)}_1\Big| + \mathbb{P}\Big\{\xi^{(2)}_1 = 0\Big\}\Big) \frac{l_2(\lambda_2)}{n} + o\left(\frac{1}{n}\right),\end{align*}
as
![]() $n\to\infty$
. We have proved that Equation (12) holds with
$n\to\infty$
. We have proved that Equation (12) holds with
![]() $f_1(\lambda_1) = l_1(\lambda_1)$
and
$f_1(\lambda_1) = l_1(\lambda_1)$
and
![]() $f_2(\lambda_2) = \big(\mathbb{E}\big|\xi^{(2)}_1\big| + \mathbb{P}\big\{\xi^{(2)}_1 = 0\big\}\big) l_2(\lambda_2)$
. Therefore, Equation (11) holds and we can use Proposition 3 to prove the first part of Theorem 1.
$f_2(\lambda_2) = \big(\mathbb{E}\big|\xi^{(2)}_1\big| + \mathbb{P}\big\{\xi^{(2)}_1 = 0\big\}\big) l_2(\lambda_2)$
. Therefore, Equation (11) holds and we can use Proposition 3 to prove the first part of Theorem 1.
We now turn to the second part and assume
![]() $\mathbb{E}\xi^{(2)} = \mu\neq 0$
. Then the above arguments are applicable to
$\mathbb{E}\xi^{(2)} = \mu\neq 0$
. Then the above arguments are applicable to
![]() $\sum_{k=1}^{\eta(t) + 1} \big(\xi^{(2)}_k - \mu\big)$
. Thus, we have shown that the process
$\sum_{k=1}^{\eta(t) + 1} \big(\xi^{(2)}_k - \mu\big)$
. Thus, we have shown that the process
![]() $\left( \left(\sum_{k=1}^{\eta(nt) + 1} \big(\xi^{(2)}_k - \mu\big) \right)/ b(\sqrt{n}), \ t\ge 0 \right) $
weakly converges to the limiting one (see Appendix A for the corresponding definitions). Since
$\left( \left(\sum_{k=1}^{\eta(nt) + 1} \big(\xi^{(2)}_k - \mu\big) \right)/ b(\sqrt{n}), \ t\ge 0 \right) $
weakly converges to the limiting one (see Appendix A for the corresponding definitions). Since
![]() $\mu < \infty$
, we have
$\mu < \infty$
, we have
![]() $b(n) = o(n)$
, as
$b(n) = o(n)$
, as
![]() $n\to\infty$
. Indeed, by the strong law of large numbers,
$n\to\infty$
. Indeed, by the strong law of large numbers,
Since
![]() $A^{(2)}$
in (2) is not deterministic, the denominator in the left-hand side of (2) must be an o(n) function. Therefore the process
$A^{(2)}$
in (2) is not deterministic, the denominator in the left-hand side of (2) must be an o(n) function. Therefore the process
 \begin{align*}\left( \frac{\sum_{k=1}^{\eta(nt) + 1} \Big(\xi^{(2)}_k - \mu\Big)}{\sqrt{n}}, \ t\ge 0 \right) =\left( \frac{\sum_{k=1}^{\eta(nt) + 1} \Big(\xi^{(2)}_k - \mu\Big)}{b(\sqrt{n})} \frac{b(\sqrt{n})}{\sqrt{n}} , \ t\ge 0\right)\end{align*}
\begin{align*}\left( \frac{\sum_{k=1}^{\eta(nt) + 1} \Big(\xi^{(2)}_k - \mu\Big)}{\sqrt{n}}, \ t\ge 0 \right) =\left( \frac{\sum_{k=1}^{\eta(nt) + 1} \Big(\xi^{(2)}_k - \mu\Big)}{b(\sqrt{n})} \frac{b(\sqrt{n})}{\sqrt{n}} , \ t\ge 0\right)\end{align*}
converges to the zero-valued process. Thus, it follows from the representation
 \begin{align*}\frac{\widehat{M}(nt)}{\sqrt{n}} = \frac{\sum_{k=1}^{\eta(nt)+1} \Big(\xi^{(2)}_k - \mu\Big)}{\sqrt{n}} + \frac{\mu (\eta(nt) +1)}{\sqrt{n}}\end{align*}
\begin{align*}\frac{\widehat{M}(nt)}{\sqrt{n}} = \frac{\sum_{k=1}^{\eta(nt)+1} \Big(\xi^{(2)}_k - \mu\Big)}{\sqrt{n}} + \frac{\mu (\eta(nt) +1)}{\sqrt{n}}\end{align*}
and from the corollary to Theorem 3.2 of [Reference Meerschaert and Scheffler29] that
5.1.2. Proof of Theorem 2
Under the assumption of the finiteness of second moments, we can extend our result to the case where both
![]() $\xi^{(1)}$
and
$\xi^{(1)}$
and
![]() $\xi^{(2)}$
have general distributions. Assume now that
$\xi^{(2)}$
have general distributions. Assume now that
![]() $\{S^{(1)}_n\}_{n=0}^\infty = \{\sum_{k=1}^n \xi^{(1)}_k\}_{n=0}^\infty$
is an aperiodic random walk with zero-mean and finite-variance-
$\{S^{(1)}_n\}_{n=0}^\infty = \{\sum_{k=1}^n \xi^{(1)}_k\}_{n=0}^\infty$
is an aperiodic random walk with zero-mean and finite-variance-
![]() $\sigma_1^2$
increments. The theory of general random walks and their hitting times is well developed. Nevertheless, results that are uniform in terms of the hitting point are rather scarce. It follows from Section 3.3 of [Reference Uchiyama33] that, uniformly in x,
$\sigma_1^2$
increments. The theory of general random walks and their hitting times is well developed. Nevertheless, results that are uniform in terms of the hitting point are rather scarce. It follows from Section 3.3 of [Reference Uchiyama33] that, uniformly in x,
where
Following steps similar to those used in the previous part, we take
![]() $t = \lambda_2 / n^2$
and, eventually, let n become large. A very important relation here is (18). When we take the characteristic function
$t = \lambda_2 / n^2$
and, eventually, let n become large. A very important relation here is (18). When we take the characteristic function
 \begin{equation*}\mathbb{E} \exp\left( i\left[ \lambda_1\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} + \lambda_2 \frac{\tau(1)}{n^2}\right]\right)\end{equation*}
\begin{equation*}\mathbb{E} \exp\left( i\left[ \lambda_1\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} + \lambda_2 \frac{\tau(1)}{n^2}\right]\right)\end{equation*}
and start to separate it into different summands, the relation (18) leads to the summand (see details below)
and this is the main reason we need to assume that
![]() $\xi^{(2)}_1$
has a finite second moment.
$\xi^{(2)}_1$
has a finite second moment.
Assume now that
![]() $\mathbb{E} \xi^{(2)}_1 = 0$
and
$\mathbb{E} \xi^{(2)}_1 = 0$
and
![]() $\sigma_2 = \mathbf{Var} \xi^{(2)}_1 < \infty$
. We have (see, e.g., Proposition 7.2 of [Reference Uchiyama34])
$\sigma_2 = \mathbf{Var} \xi^{(2)}_1 < \infty$
. We have (see, e.g., Proposition 7.2 of [Reference Uchiyama34])
As a consequence, we get
![]() $\mathbb{E} a^*\big(\xi^{(2)}_1\big) < \infty$
. Let
$\mathbb{E} a^*\big(\xi^{(2)}_1\big) < \infty$
. Let
![]() $p^{(2)}(x) = \mathbb{P}\big\{\xi^{(2)}_1 = x\big\}$
. Then the total probability formula gives us
$p^{(2)}(x) = \mathbb{P}\big\{\xi^{(2)}_1 = x\big\}$
. Then the total probability formula gives us
 \begin{align*}\mathbb{E} \exp\left( i\left[ \lambda_1\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} + \lambda_2 \frac{\tau(1)}{n^2}\right]\right)& \\ &\kern-50pt = \sum_{x\in\mathbb{Z}}\exp\left( i\lambda_1 \left[\frac{x}{\sigma_2\sqrt{n}} \right] \right)\mathbb{E}\left[ \exp\left.\left( i\left[\lambda_2 \frac{\tau(1)}{n^2}\right]\right) \right| \ \xi^{(2)}_1= x\right] p^{(2)}(x).\end{align*}
\begin{align*}\mathbb{E} \exp\left( i\left[ \lambda_1\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} + \lambda_2 \frac{\tau(1)}{n^2}\right]\right)& \\ &\kern-50pt = \sum_{x\in\mathbb{Z}}\exp\left( i\lambda_1 \left[\frac{x}{\sigma_2\sqrt{n}} \right] \right)\mathbb{E}\left[ \exp\left.\left( i\left[\lambda_2 \frac{\tau(1)}{n^2}\right]\right) \right| \ \xi^{(2)}_1= x\right] p^{(2)}(x).\end{align*}
 \begin{align*}\mathbb{E} \exp\left( i\left[ \lambda_1\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} + \lambda_2 \frac{\tau(1)}{n^2}\right]\right) & = \mathbb{E} \left[\exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right] \\[3pt] & \quad - \frac{\sigma_1 \sqrt{-2i\lambda_2}}{n} \mathbb{E} \left[a^*\Big(\xi^{(2)}_1\Big) \exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right] \\[3pt] &\quad + O\left( \frac{1}{n^2} \mathbb{E} \left[\left( \xi^{(2)}_1\right)^2 \exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right]\right) \\[3pt] &\quad + o\left( \frac{1}{n} \mathbb{E} \left[\xi^{(2)}_1 \exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right]\right) + o\left(\frac{1}{n} \right),\end{align*}
\begin{align*}\mathbb{E} \exp\left( i\left[ \lambda_1\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} + \lambda_2 \frac{\tau(1)}{n^2}\right]\right) & = \mathbb{E} \left[\exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right] \\[3pt] & \quad - \frac{\sigma_1 \sqrt{-2i\lambda_2}}{n} \mathbb{E} \left[a^*\Big(\xi^{(2)}_1\Big) \exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right] \\[3pt] &\quad + O\left( \frac{1}{n^2} \mathbb{E} \left[\left( \xi^{(2)}_1\right)^2 \exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right]\right) \\[3pt] &\quad + o\left( \frac{1}{n} \mathbb{E} \left[\xi^{(2)}_1 \exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right]\right) + o\left(\frac{1}{n} \right),\end{align*}
as
![]() $n\to\infty$
. Next, we use the relation (20) and the Taylor expansion for the exponent to get
$n\to\infty$
. Next, we use the relation (20) and the Taylor expansion for the exponent to get
 \begin{align*} \mathbb{E} \left[a^*\Big(\xi^{(2)}_1\Big) \exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right] = \mathbb{E} \left[a^*\Big(\xi^{(2)}_1\Big) \right] + o(1), \ \text{as $n\to\infty$.}\end{align*}
\begin{align*} \mathbb{E} \left[a^*\Big(\xi^{(2)}_1\Big) \exp\left( i\lambda_1 \left[\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} \right]\right)\right] = \mathbb{E} \left[a^*\Big(\xi^{(2)}_1\Big) \right] + o(1), \ \text{as $n\to\infty$.}\end{align*}
Since
![]() $\mathbb{E} \xi^{(2)}_1 = 0$
and
$\mathbb{E} \xi^{(2)}_1 = 0$
and
![]() $\mathbf{Var} \xi^{(2)}_1 < \infty$
, the central limit theorem holds. Thus, we have the analogue of (14) with
$\mathbf{Var} \xi^{(2)}_1 < \infty$
, the central limit theorem holds. Thus, we have the analogue of (14) with
![]() $l_1$
being a logarithmic characteristic function of an RV with a standard normal distribution. Finally, we get
$l_1$
being a logarithmic characteristic function of an RV with a standard normal distribution. Finally, we get
 \begin{multline*}\mathbb{E} \exp\left( i\left[ \lambda_1\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} + \lambda_2 \frac{\tau(1)}{n^2}\right]\right) = 1 + \frac{l_1(\lambda_1)}{n} - \frac{\sigma_1 \sqrt{-2i\lambda_2}}{n} \mathbb{E} \left[a^*\Big(\xi^{(2)}_1\Big) \right] + o\left(\frac{1}{n}\right).\end{multline*}
\begin{multline*}\mathbb{E} \exp\left( i\left[ \lambda_1\frac{\xi^{(2)}_1}{\sigma_2\sqrt{n}} + \lambda_2 \frac{\tau(1)}{n^2}\right]\right) = 1 + \frac{l_1(\lambda_1)}{n} - \frac{\sigma_1 \sqrt{-2i\lambda_2}}{n} \mathbb{E} \left[a^*\Big(\xi^{(2)}_1\Big) \right] + o\left(\frac{1}{n}\right).\end{multline*}
Thus, we have proved Equation (12) for this case. The rest of the proof follows the same argument as in the previous case.
5.2. Proof of Theorem 3
Recall that the random vectors
![]() $\big\{Y^{(3)}_n, J^{(3)}_n\big\}_{n=1}^\infty$
are i.i.d., where
$\big\{Y^{(3)}_n, J^{(3)}_n\big\}_{n=1}^\infty$
are i.i.d., where
![]() $Y^{(3)}_1 = \sum_{k=1}^\nu \gamma^{(3)}_k$
and
$Y^{(3)}_1 = \sum_{k=1}^\nu \gamma^{(3)}_k$
and
![]() $J^{(3)}_1 = T^{(3)}(1) = U^{(3)}(\nu)$
. We have
$J^{(3)}_1 = T^{(3)}(1) = U^{(3)}(\nu)$
. We have
 \begin{align*}N(t) = \max\!\left\{n> 0: \ \sum_{k=1}^n J^{(3)}_k \leq t\right\} \text{and} \ \widetilde{M}(t) = \sum_{k = 1}^{N(t)} Y^{(3)}_k.\end{align*}
\begin{align*}N(t) = \max\!\left\{n> 0: \ \sum_{k=1}^n J^{(3)}_k \leq t\right\} \text{and} \ \widetilde{M}(t) = \sum_{k = 1}^{N(t)} Y^{(3)}_k.\end{align*}
From Propositions 1 and 2 we have
as
![]() $n\to\infty$
. From Theorem 5.1 from [Reference Kasahara24] we have
$n\to\infty$
. From Theorem 5.1 from [Reference Kasahara24] we have
 \begin{equation}\left\lbrace \frac{\widetilde{M}(nt)}{2^{-7/8}n^{1/8}\sqrt{\mathbf{Var} Y^{(3)}_1}}, t\geq 0\right\rbrace \overset{\mathcal{D}}{\Rightarrow} \{B(E^{(3)}(t)), t\geq 0\}, \ \text{as $n\to\infty$,}\end{equation}
\begin{equation}\left\lbrace \frac{\widetilde{M}(nt)}{2^{-7/8}n^{1/8}\sqrt{\mathbf{Var} Y^{(3)}_1}}, t\geq 0\right\rbrace \overset{\mathcal{D}}{\Rightarrow} \{B(E^{(3)}(t)), t\geq 0\}, \ \text{as $n\to\infty$,}\end{equation}
where B(t) is a standard Brownian motion, independent of
![]() $E^{(3)}(t)$
.
$E^{(3)}(t)$
.
We show now that (21) holds with M(nt) in the place of
![]() $\widetilde{M}(nt)$
. It is sufficient to prove that, for any fixed
$\widetilde{M}(nt)$
. It is sufficient to prove that, for any fixed
![]() $T>0$
,
$T>0$
,
For
![]() $k=1,2,\ldots$
, let
$k=1,2,\ldots$
, let
![]() $\nu_k$
be the number of visits to the set
$\nu_k$
be the number of visits to the set
![]() $\{(0,0),(0,1)\}$
by the MC
$\{(0,0),(0,1)\}$
by the MC
![]() $V_n$
within the time interval
$V_n$
within the time interval
![]() $\big(T_{k-1}^{(3)}, T_k^{(3)}\big]$
, and let
$\big(T_{k-1}^{(3)}, T_k^{(3)}\big]$
, and let
![]() $\varkappa_k$
be the total number of jumps of the mouse within this time interval. Further, let
$\varkappa_k$
be the total number of jumps of the mouse within this time interval. Further, let
The triples
![]() $(\nu_k,\varkappa_k,R_k)$
are i.i.d., the pairs
$(\nu_k,\varkappa_k,R_k)$
are i.i.d., the pairs
![]() $(\nu_k,\varkappa_k)$
are i.i.d. copies of the pair
$(\nu_k,\varkappa_k)$
are i.i.d. copies of the pair
![]() $(\nu,\varkappa)$
introduced earlier, and
$(\nu,\varkappa)$
introduced earlier, and
Further, all RVs in (22) have a finite exponential moment,
![]() ${\mathbb E} \exp (cR_1)<\infty$
for some
${\mathbb E} \exp (cR_1)<\infty$
for some
![]() $c>0$
.
$c>0$
.
For
![]() $K>0$
, let
$K>0$
, let
![]() $\widehat{J}_j = \min \big(J^{(3)}_j, K\big)$
. Since
$\widehat{J}_j = \min \big(J^{(3)}_j, K\big)$
. Since
![]() ${\mathbb E} J^{(3)}_1=\infty$
, one can choose K such that
${\mathbb E} J^{(3)}_1=\infty$
, one can choose K such that
![]() $A:={\mathbb E} \widehat{J}_1> T$
. Let
$A:={\mathbb E} \widehat{J}_1> T$
. Let
![]() $\widehat{S}_n=\sum_{i=1}^n \widehat{J}_i$
. Then, for any
$\widehat{S}_n=\sum_{i=1}^n \widehat{J}_i$
. Then, for any
![]() $C>0$
,
$C>0$
,
where the term in the parentheses on the right-hand side may be made less than 1 for
![]() $C>0$
sufficiently small. Next,
$C>0$
sufficiently small. Next,
Then, for any
![]() $\varepsilon >0$
,
$\varepsilon >0$
,
 \begin{align*}{\mathbb P} \left(\frac{\max_{1 \leq k \leq [nT]}\left\lbrace \widetilde{M}_{k} - M_{k}\right\rbrace}{n^{1/8}}\ge \varepsilon\right)\le{\mathbb P}\bigg( \max_{1\le k \le n} R_k \ge n^{1/8}\varepsilon \bigg) +{\mathbb P} (\eta (nT)\ge n),\end{align*}
\begin{align*}{\mathbb P} \left(\frac{\max_{1 \leq k \leq [nT]}\left\lbrace \widetilde{M}_{k} - M_{k}\right\rbrace}{n^{1/8}}\ge \varepsilon\right)\le{\mathbb P}\bigg( \max_{1\le k \le n} R_k \ge n^{1/8}\varepsilon \bigg) +{\mathbb P} (\eta (nT)\ge n),\end{align*}
where both terms on the right-hand side are summable in n. Therefore, by the 0–1 law and by the arbitrariness of
![]() $\varepsilon >0$
, (22) follows. This completes the proof of Theorem 3.
$\varepsilon >0$
, (22) follows. This completes the proof of Theorem 3.
5.3. Proof of Theorem 4
The random process
![]() $X^{(1)}$
is a simple random walk on
$X^{(1)}$
is a simple random walk on
![]() $\mathbb{Z}$
, and for
$\mathbb{Z}$
, and for
![]() $j \in [2, N]$
we have
$j \in [2, N]$
we have
 \begin{align*}\mathbb{P}\big\{X^{(j)}(n) - X^{(j)}(n-1) &= 1\big| \ X^{(j)}(n-1) = X^{(j-1)}(n-1)\big\}\\[2pt] &= \mathbb{P}\big\{X^{(j)}(n) - X^{(j)}(n-1) = - 1\big| \ X^{(j)}(n-1) = X^{(j-1)}(n-1)\big\} = \frac{1}{2}.\end{align*}
\begin{align*}\mathbb{P}\big\{X^{(j)}(n) - X^{(j)}(n-1) &= 1\big| \ X^{(j)}(n-1) = X^{(j-1)}(n-1)\big\}\\[2pt] &= \mathbb{P}\big\{X^{(j)}(n) - X^{(j)}(n-1) = - 1\big| \ X^{(j)}(n-1) = X^{(j-1)}(n-1)\big\} = \frac{1}{2}.\end{align*}
Let us give a new representation of such a process. Let
![]() $X^{(1)}(0) = X^{(2)}(0) = \ldots = X^{(N)}(0) = 0$
, and let the RV
$X^{(1)}(0) = X^{(2)}(0) = \ldots = X^{(N)}(0) = 0$
, and let the RV
![]() $T_j(n)$
denote the time when
$T_j(n)$
denote the time when
![]() $X^{(j)}$
takes the nth step. Let
$X^{(j)}$
takes the nth step. Let
![]() $T_j(0) = 0$
. Note the difference between
$T_j(0) = 0$
. Note the difference between
![]() $T_j$
and
$T_j$
and
![]() $T^{(3)}$
. Thus,
$T^{(3)}$
. Thus,
![]() $\big\{X^{(j)}\big(T_j(k)\big)\big\}_{k=0}^\infty$
is a simple random walk on
$\big\{X^{(j)}\big(T_j(k)\big)\big\}_{k=0}^\infty$
is a simple random walk on
![]() $\mathbb{Z}$
, and if
$\mathbb{Z}$
, and if
![]() $X^{(j)}(n) \neq X^{(j)}(n-1)$
, then
$X^{(j)}(n) \neq X^{(j)}(n-1)$
, then
![]() $n\in \{T_j(k)\}_{k=1}^\infty$
. Let
$n\in \{T_j(k)\}_{k=1}^\infty$
. Let
for
![]() $j\geq 1$
and
$j\geq 1$
and
![]() $k\geq 1$
. By definition,
$k\geq 1$
. By definition,
![]() $\big\{\big\{\xi^{(j)}_k\big\}_{k=0}^\infty\big\}_{j=1}^N$
are mutually independent and equal
$\big\{\big\{\xi^{(j)}_k\big\}_{k=0}^\infty\big\}_{j=1}^N$
are mutually independent and equal
![]() $\pm 1$
w.p.
$\pm 1$
w.p.
![]() $1/2$
.
$1/2$
.
Since
![]() $X^{(1)}$
jumps every time,
$X^{(1)}$
jumps every time,
![]() $T_1(k) = k$
for
$T_1(k) = k$
for
![]() $k\geq 0$
. Let
$k\geq 0$
. Let
![]() $\tau$
be the time at which the simple random walk goes from the point 1 to 0. From Section 3 it is easy to deduce that the time between the meeting-time instants of the cat and the mouse has the same distribution as
$\tau$
be the time at which the simple random walk goes from the point 1 to 0. From Section 3 it is easy to deduce that the time between the meeting-time instants of the cat and the mouse has the same distribution as
![]() $\tau$
. Thus, if we look at the system only at the times
$\tau$
. Thus, if we look at the system only at the times
![]() $\{T_j(k)\}_{k=0}^\infty$
the time between meeting-time instants of
$\{T_j(k)\}_{k=0}^\infty$
the time between meeting-time instants of
![]() $X^{(j)}$
and
$X^{(j)}$
and
![]() $X^{(j+1)}$
has the same distribution as
$X^{(j+1)}$
has the same distribution as
![]() $\tau$
.
$\tau$
.
Let us define
![]() $\nu_j(n) = \max\{k\ge 0: \ T_j(k) \le n\}$
, the number of time instants up to time n at which
$\nu_j(n) = \max\{k\ge 0: \ T_j(k) \le n\}$
, the number of time instants up to time n at which
![]() $X^{(j)}$
changes its value. Then we can rewrite the dynamics of the jth coordinate as
$X^{(j)}$
changes its value. Then we can rewrite the dynamics of the jth coordinate as
 \begin{equation*}X^{(j)}(n) = \sum_{k=1}^{\nu_j(n)} \xi^{(j)}_{T_j(k)}.\end{equation*}
\begin{equation*}X^{(j)}(n) = \sum_{k=1}^{\nu_j(n)} \xi^{(j)}_{T_j(k)}.\end{equation*}
Our assumptions on the distribution of the increments
![]() $\xi^{(j)}_k$
, for
$\xi^{(j)}_k$
, for
![]() $k\ge 1$
, provide us with the next important property of our process.
$k\ge 1$
, provide us with the next important property of our process.
Proposition 4. The sequences
![]() $\{T_j(k)\}_{k=0}^\infty$
and
$\{T_j(k)\}_{k=0}^\infty$
and
![]() $\big\{\xi^{(j)}_k\big\}_{k=1}^\infty$
are independent for any
$\big\{\xi^{(j)}_k\big\}_{k=1}^\infty$
are independent for any
![]() $j\in\{1, \ldots, N\}$
.
$j\in\{1, \ldots, N\}$
.
This property comes from the space-symmetry of the model. Indeed, for
![]() $j=1$
the result is trivial, since
$j=1$
the result is trivial, since
![]() $\nu_1(n) = n$
. We show the result for
$\nu_1(n) = n$
. We show the result for
![]() $j=2$
and then extend it onto
$j=2$
and then extend it onto
![]() $j>2$
. Define
$j>2$
. Define
One can see that in our model
![]() $T_2(k) = 1 + {}^1\tau(k-1)$
, for
$T_2(k) = 1 + {}^1\tau(k-1)$
, for
![]() $k\ge 1$
. In the time interval
$k\ge 1$
. In the time interval
![]() $[1, {}^1\tau(1)]$
the second coordinate changes its value only at the time
$[1, {}^1\tau(1)]$
the second coordinate changes its value only at the time
![]() $T_2(1) = 1$
. Thus, the time
$T_2(1) = 1$
. Thus, the time
![]() ${}^1\tau(1)$
does not depend on
${}^1\tau(1)$
does not depend on
![]() $\xi^{(2)}_k$
, for
$\xi^{(2)}_k$
, for
![]() $k\ge 2$
. Additionally, the trajectory
$k\ge 2$
. Additionally, the trajectory
![]() $\{X^{(1)}(n)\}_{n=0}^\infty$
has the same distribution as
$\{X^{(1)}(n)\}_{n=0}^\infty$
has the same distribution as
![]() $\{-X^{(1)}(n)\}_{n=0}^\infty$
. Thus,
$\{-X^{(1)}(n)\}_{n=0}^\infty$
. Thus,
As a corollary of the last equation, we get that
![]() ${}^1\tau(1)$
has the same distribution as the time that is needed for the simple random walk to hit 0 if it starts from 1. This implies that
${}^1\tau(1)$
has the same distribution as the time that is needed for the simple random walk to hit 0 if it starts from 1. This implies that
From the symmetry of our model, it further follows that the sequence
![]() $\{{}^1\tau(k)\}_{k=0}^\infty$
, and subsequently the sequences
$\{{}^1\tau(k)\}_{k=0}^\infty$
, and subsequently the sequences
![]() $\{T_2(k)\}_{k=0}^\infty$
and
$\{T_2(k)\}_{k=0}^\infty$
and
![]() $\{\nu_2(n)\}_{n=1}^\infty$
, do not depend on
$\{\nu_2(n)\}_{n=1}^\infty$
, do not depend on
![]() $\big\{\xi^{(2)}_k\big\}_{k=1}^\infty$
(or, therefore, on
$\big\{\xi^{(2)}_k\big\}_{k=1}^\infty$
(or, therefore, on
![]() $\big\{\xi^{(j)}_k\big\}_{k\ge 1, j\ge2}$
).
$\big\{\xi^{(j)}_k\big\}_{k\ge 1, j\ge2}$
).
For the analysis of
![]() $\{T_j(k)\}_{k=0}^\infty$
,
$\{T_j(k)\}_{k=0}^\infty$
,
![]() $j > 2$
, we need to define an ‘embedded version’ of
$j > 2$
, we need to define an ‘embedded version’ of
![]() ${}^1\tau(k)$
. Let
${}^1\tau(k)$
. Let
The process
![]() $\big\{{}^j\tau(k)\big\}_{k=0}^\infty$
counts the number of times that the process
$\big\{{}^j\tau(k)\big\}_{k=0}^\infty$
counts the number of times that the process
![]() $X^{(j)}$
changes its value between the time instants when
$X^{(j)}$
changes its value between the time instants when
![]() $X^{(j)}$
and
$X^{(j)}$
and
![]() $X^{(j+1)}$
have the same value. Using the same argument as before, we get that the sequence
$X^{(j+1)}$
have the same value. Using the same argument as before, we get that the sequence
![]() $\big\{{}^j\tau(k)\big\}_{k=0}^\infty$
does not depend on
$\big\{{}^j\tau(k)\big\}_{k=0}^\infty$
does not depend on
![]() $\big\{\xi^{(j+1)}_k\big\}_{k=1}^\infty$
.
$\big\{\xi^{(j+1)}_k\big\}_{k=1}^\infty$
.
The jth coordinate
![]() $X^{(j)}$
changes its value for the kth time at a time instant n if and only if, up to time
$X^{(j)}$
changes its value for the kth time at a time instant n if and only if, up to time
![]() $n-1$
, the processes
$n-1$
, the processes
![]() $X^{(j-1)}$
and
$X^{(j-1)}$
and
![]() $X^{(j)}$
have had the same value exactly
$X^{(j)}$
have had the same value exactly
![]() $k-1$
times (not including
$k-1$
times (not including
![]() $X^{(j-1)}(0) = X^{(j)}(0) = 0$
), with the last time being at the time instant
$X^{(j-1)}(0) = X^{(j)}(0) = 0$
), with the last time being at the time instant
![]() $n-1$
(which also means that at the time instant
$n-1$
(which also means that at the time instant
![]() $n-1$
the process
$n-1$
the process
![]() $X^{(j-1)}$
changes its value). This can be rewritten as
$X^{(j-1)}$
changes its value). This can be rewritten as
and thus
![]() $T_j(k) = 1 + T_{j-1}({}^{j-1}\tau(k-1))$
. Thus, since the sequences
$T_j(k) = 1 + T_{j-1}({}^{j-1}\tau(k-1))$
. Thus, since the sequences
![]() $\{T_2(k)\}_{k=0}^\infty$
and
$\{T_2(k)\}_{k=0}^\infty$
and
![]() $\big\{{}^2\tau(k)\big\}_{k=0}^\infty$
do not depend on
$\big\{{}^2\tau(k)\big\}_{k=0}^\infty$
do not depend on
![]() $\big\{\xi^{(j)}_k\big\}_{k\ge 1, j\ge 3}$
, the same holds for
$\big\{\xi^{(j)}_k\big\}_{k\ge 1, j\ge 3}$
, the same holds for
![]() $\{T_3(k)\}_{k=0}^\infty$
. Therefore, using induction, we get that the sequences
$\{T_3(k)\}_{k=0}^\infty$
. Therefore, using induction, we get that the sequences
![]() $\{T_j(k)\}_{k=0}^\infty$
and
$\{T_j(k)\}_{k=0}^\infty$
and
![]() $\big\{\xi^{(j)}_k\big\}_{k=1}^\infty$
are independent for any
$\big\{\xi^{(j)}_k\big\}_{k=1}^\infty$
are independent for any
![]() $j\ge 1$
.
$j\ge 1$
.
As a corollary of this result we get
 \begin{align*}X^{(j)}(n) = \sum_{k=1}^{\nu_j(n)} \xi^{(j)}_{T_j(k)} \overset{d}{=} \sum_{k=1}^{\nu_j(n)} \xi^{(j)}_k.\end{align*}
\begin{align*}X^{(j)}(n) = \sum_{k=1}^{\nu_j(n)} \xi^{(j)}_{T_j(k)} \overset{d}{=} \sum_{k=1}^{\nu_j(n)} \xi^{(j)}_k.\end{align*}
Let
![]() ${}^j\eta(n) = \max\{k\geq 0 :\ {}^j\tau(k) \leq n\}$
for
${}^j\eta(n) = \max\{k\geq 0 :\ {}^j\tau(k) \leq n\}$
for
![]() $n\geq 0$
and
$n\geq 0$
and
![]() $j \in [1, \ldots, N]$
. Since the sequence
$j \in [1, \ldots, N]$
. Since the sequence
![]() $\{{}^j\tau(k)\}_{k=0}^\infty$
depends only on the sequence
$\{{}^j\tau(k)\}_{k=0}^\infty$
depends only on the sequence
![]() $\big\{\xi^{(j)}_k\big\}_{k=1}^\infty$
, we have that
$\big\{\xi^{(j)}_k\big\}_{k=1}^\infty$
, we have that
![]() $\{{}^j\eta(n)\}_{j=1}^{N-1}$
are i.i.d. RVs. For
$\{{}^j\eta(n)\}_{j=1}^{N-1}$
are i.i.d. RVs. For
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $j \in \{1, \ldots, N\}$
we have
$j \in \{1, \ldots, N\}$
we have
 \begin{align*}\nu_j(n) = \max\{k\geq 0:\ T_j(k) \leq n\} & = \max\Big\{k\geq 1:\ 1 + T_{j-1}\big({}^{j-1}\tau(k-1)\big) \leq n\Big\}\notag\\[2pt] & = 1 + \max\Big\{k\geq 0:\ T_{j-1}\big({}^{j-1}\tau(k)\big) \leq n - 1\Big\}\notag\\[2pt] & = 1 + \max\Big\{k\geq 0:\ {}^{j-1}\tau(k) \leq \nu_{j-1}(n - 1)\Big\}\notag\\[2pt] & = 1 + {}^{j-1}\eta\big(\nu_{j-1}(n-1)\big).\end{align*}
\begin{align*}\nu_j(n) = \max\{k\geq 0:\ T_j(k) \leq n\} & = \max\Big\{k\geq 1:\ 1 + T_{j-1}\big({}^{j-1}\tau(k-1)\big) \leq n\Big\}\notag\\[2pt] & = 1 + \max\Big\{k\geq 0:\ T_{j-1}\big({}^{j-1}\tau(k)\big) \leq n - 1\Big\}\notag\\[2pt] & = 1 + \max\Big\{k\geq 0:\ {}^{j-1}\tau(k) \leq \nu_{j-1}(n - 1)\Big\}\notag\\[2pt] & = 1 + {}^{j-1}\eta\big(\nu_{j-1}(n-1)\big).\end{align*}
For
![]() $n < N-1$
we can iterate the process and get
$n < N-1$
we can iterate the process and get
 \begin{align*}\nu_N(n) & = 1 + {}^{N-1}\eta\Big(1 + {}^{N-2}\eta\Big(\ldots \Big(1 + {}^{N-n}\eta(0)\Big)\ldots\Big)\Big)\notag\\[2pt] & = 1 + {}^{N-1}\eta\Big(1 + {}^{N-2}\eta\Big(\ldots \Big(1 + {}^{N-n+1}\eta(1)\Big)\ldots\Big)\Big)\notag\\[2pt] & \overset{d}{=} 1 + {}^{n-1}\eta\Big(1 + {}^{n-2}\eta(\ldots \Big(1 + {}^{1}\eta(1)\Big)\ldots\Big)\Big)\notag\\[2pt] & = \nu_n(n).\end{align*}
\begin{align*}\nu_N(n) & = 1 + {}^{N-1}\eta\Big(1 + {}^{N-2}\eta\Big(\ldots \Big(1 + {}^{N-n}\eta(0)\Big)\ldots\Big)\Big)\notag\\[2pt] & = 1 + {}^{N-1}\eta\Big(1 + {}^{N-2}\eta\Big(\ldots \Big(1 + {}^{N-n+1}\eta(1)\Big)\ldots\Big)\Big)\notag\\[2pt] & \overset{d}{=} 1 + {}^{n-1}\eta\Big(1 + {}^{n-2}\eta(\ldots \Big(1 + {}^{1}\eta(1)\Big)\ldots\Big)\Big)\notag\\[2pt] & = \nu_n(n).\end{align*}
For
![]() $n \ge N-1$
we have
$n \ge N-1$
we have
We want to construct a process with the same distribution as
![]() $\{\nu_N(n)\}_{n=0}^\infty$
in a form of
$\{\nu_N(n)\}_{n=0}^\infty$
in a form of
![]() $\nu_{N-1}(\varphi(n))$
, where the process
$\nu_{N-1}(\varphi(n))$
, where the process
![]() $\{\varphi(n)\}_{n=0}^\infty$
is independent of everything else. Define the process
$\{\varphi(n)\}_{n=0}^\infty$
is independent of everything else. Define the process
![]() $\{\eta(n)\}_{n=0}^\infty \overset{d}{=} \big\{{}^{N-1}\eta(n)\big\}_{n=0}^\infty$
, which is independent of everything else. Then, for
$\{\eta(n)\}_{n=0}^\infty \overset{d}{=} \big\{{}^{N-1}\eta(n)\big\}_{n=0}^\infty$
, which is independent of everything else. Then, for
![]() $n \ge N-1$
, we have
$n \ge N-1$
, we have
Using the same formula for
![]() $\nu_{N-1}(m)$
with m such that
$\nu_{N-1}(m)$
with m such that
![]() $m- (N\,{-}\,1) + 1 = 1 + {}^{N-1}\eta(n-N\,{+}\,1)$
, we get
$m- (N\,{-}\,1) + 1 = 1 + {}^{N-1}\eta(n-N\,{+}\,1)$
, we get
Then, for
![]() $n\geq N$
, we have
$n\geq N$
, we have
![]() $X^{(N)}(n) \overset{d}{=} X^{(N-1)}(N -1 + \eta(n-N+1))$
. There exists a nondegenerate RV
$X^{(N)}(n) \overset{d}{=} X^{(N-1)}(N -1 + \eta(n-N+1))$
. There exists a nondegenerate RV
![]() $\zeta$
(see Section XI.5 in [Reference Feller13]) such that
$\zeta$
(see Section XI.5 in [Reference Feller13]) such that
![]() $\mathbb{P}\{\zeta_i \geq y\} = G_{1/2}\big(9/y^2\big)$
and
$\mathbb{P}\{\zeta_i \geq y\} = G_{1/2}\big(9/y^2\big)$
and
Therefore, using (23) we get
as
![]() $n\to\infty$
, for
$n\to\infty$
, for
![]() $j\ge 1$
. We now present a known result that we utilise to prove Theorem 4.
$j\ge 1$
. We now present a known result that we utilise to prove Theorem 4.
Proposition 5. ([Reference Dobrushin11], (v).) Let Y(t) and
![]() $\tau_n$
be independent sequences of RVs such that
$\tau_n$
be independent sequences of RVs such that
Then for independent Y and
![]() $\tau$
we have
$\tau$
we have
Indeed, by the central limit theorem,
![]() $X^{(1)}(n) / \sqrt{n}$
weakly converges to a normally distributed RV
$X^{(1)}(n) / \sqrt{n}$
weakly converges to a normally distributed RV
![]() $\psi$
(we assume that
$\psi$
(we assume that
![]() $\psi$
and
$\psi$
and
![]() $\zeta$
are independent). Together with (24) and the independence of
$\zeta$
are independent). Together with (24) and the independence of
![]() $X^{(1)}(n)$
and
$X^{(1)}(n)$
and
![]() $\eta(n)$
, this ensures that the condition (25) holds with
$\eta(n)$
, this ensures that the condition (25) holds with
![]() $Y(t) = X^{(1)}([t])$
,
$Y(t) = X^{(1)}([t])$
,
![]() $\tau_n = 1 + \eta(n-1)$
, and
$\tau_n = 1 + \eta(n-1)$
, and
![]() $\beta = \delta = 1/2$
. By Proposition 5,
$\beta = \delta = 1/2$
. By Proposition 5,
 \begin{align*}\frac{X^{(2)}(n)}{n^{1/4}} \overset{d}{=} \frac{X^{(1)}(1 + \eta(n-1))}{n^{1/4}} \Rightarrow \psi \sqrt{\sqrt{\frac{\pi}{2}}\zeta}, \ \text{as $n\to\infty$.}\end{align*}
\begin{align*}\frac{X^{(2)}(n)}{n^{1/4}} \overset{d}{=} \frac{X^{(1)}(1 + \eta(n-1))}{n^{1/4}} \Rightarrow \psi \sqrt{\sqrt{\frac{\pi}{2}}\zeta}, \ \text{as $n\to\infty$.}\end{align*}
Let
![]() $\{\zeta_j\}_{j=2}^{N}$
be independent copies of
$\{\zeta_j\}_{j=2}^{N}$
be independent copies of
![]() $\zeta$
which are independent of
$\zeta$
which are independent of
![]() $\psi$
. Next, we use the induction argument. For some
$\psi$
. Next, we use the induction argument. For some
![]() $j\ge 1$
, the condition (25) holds with
$j\ge 1$
, the condition (25) holds with
![]() $Y(t) = X^{(j)}([t])$
,
$Y(t) = X^{(j)}([t])$
,
![]() $\tau_n = j-1 + \eta(n-j+1)$
,
$\tau_n = j-1 + \eta(n-j+1)$
,
![]() $\beta = 2^{-j}$
, and
$\beta = 2^{-j}$
, and
![]() $\delta = 2^{-1}$
. By Proposition 5, we get
$\delta = 2^{-1}$
. By Proposition 5, we get
 \begin{align*}\frac{X^{(j+1)}(n)}{n^{2^{-(j+1)}}}\overset{d}{=} \frac{X^{(j)}(j-1 + \eta(n-j+1))}{n^{2^{-(j+1)}}} \Rightarrow \psi \prod_{i=2}^{j+1}\sqrt{\sqrt{\frac{\pi}{2}}\zeta_i}, \quad \text{as $n\to\infty$.}\end{align*}
\begin{align*}\frac{X^{(j+1)}(n)}{n^{2^{-(j+1)}}}\overset{d}{=} \frac{X^{(j)}(j-1 + \eta(n-j+1))}{n^{2^{-(j+1)}}} \Rightarrow \psi \prod_{i=2}^{j+1}\sqrt{\sqrt{\frac{\pi}{2}}\zeta_i}, \quad \text{as $n\to\infty$.}\end{align*}
This concludes the proof of Theorem 4.
Appendix A. Weak convergence for processes from
 $D[[0,\infty), \mathbb{R}]$
$D[[0,\infty), \mathbb{R}]$
To make the paper self-contained, we recall the definition of the
![]() $\mathcal{J}_1$
-topology (see, e.g., [Reference Skorokhod31]). Let
$\mathcal{J}_1$
-topology (see, e.g., [Reference Skorokhod31]). Let
![]() $D[[0,T], \mathbb{R}]$
denote the space of all right-continuous functions on [0, T] having left limits (RCLL or càdlàg functions). For any
$D[[0,T], \mathbb{R}]$
denote the space of all right-continuous functions on [0, T] having left limits (RCLL or càdlàg functions). For any
![]() $g \in D[[0,T], \mathbb{R}]$
let
$g \in D[[0,T], \mathbb{R}]$
let
![]() $\bigl\|g\bigr\| = \sup_{t\in[0, T]} |g(t)|$
.
$\bigl\|g\bigr\| = \sup_{t\in[0, T]} |g(t)|$
.
Let
![]() $\Lambda_T$
be the set of increasing continuous functions
$\Lambda_T$
be the set of increasing continuous functions
![]() $\lambda: [0, T] \to [0, T]$
such that
$\lambda: [0, T] \to [0, T]$
such that
![]() $\lambda(0) = 0$
and
$\lambda(0) = 0$
and
![]() $\lambda(T) = T$
. Let
$\lambda(T) = T$
. Let
![]() $\lambda_{id, T}$
denote the identity function. Then
$\lambda_{id, T}$
denote the identity function. Then
defines a metric inducing
![]() $\mathcal{J}_1$
.
$\mathcal{J}_1$
.
Let
![]() $D[[0,\infty), \mathbb{R}]$
be the space of all RCLL functions on the positive half-line. On the space
$D[[0,\infty), \mathbb{R}]$
be the space of all RCLL functions on the positive half-line. On the space
![]() $D[[0, \infty), \mathbb{R}]$
, the
$D[[0, \infty), \mathbb{R}]$
, the
![]() $\mathcal{J}_1$
-topology is defined by the metric
$\mathcal{J}_1$
-topology is defined by the metric
where, for
![]() $i=1,2$
,
$i=1,2$
,
![]() $g_{i,T}$
is the restriction of function
$g_{i,T}$
is the restriction of function
![]() $g_i$
on the interval [0,T].
$g_i$
on the interval [0,T].
Convergence
![]() $g_n \to g$
in
$g_n \to g$
in
![]() $(D[[0, \infty), \mathbb{R}], \tau)$
means that
$(D[[0, \infty), \mathbb{R}], \tau)$
means that
![]() $d_{\tau, T}(g_n, g) \to 0$
for every continuity point T of g (see [Reference Whitt35]).
$d_{\tau, T}(g_n, g) \to 0$
for every continuity point T of g (see [Reference Whitt35]).
Let
![]() $\{\{X_n(t)\}_{t\geq 0}\}_{n=1}^\infty$
and
$\{\{X_n(t)\}_{t\geq 0}\}_{n=1}^\infty$
and
![]() $\{X(t)\}_{t\geq 0}$
be stochastic processes with trajectories from
$\{X(t)\}_{t\geq 0}$
be stochastic processes with trajectories from
![]() $D[[0,\infty), \mathbb{R}]$
. We say that weak convergence
$D[[0,\infty), \mathbb{R}]$
. We say that weak convergence
holds if
for any continuous and bounded function f on
![]() $D[[0,\infty), \mathbb{R}]$
endowed with the
$D[[0,\infty), \mathbb{R}]$
endowed with the
![]() $\mathcal{J}_1$
-topology.
$\mathcal{J}_1$
-topology.
Proposition 6. Let
![]() $\{X_n\}_{n=1}^\infty$
and
$\{X_n\}_{n=1}^\infty$
and
![]() $\{Y_n\}_{n=1}^\infty$
be two sequences of stochastic processes with trajectories from
$\{Y_n\}_{n=1}^\infty$
be two sequences of stochastic processes with trajectories from
![]() $D[[0, \infty), \mathbb{R}]$
. Given
$D[[0, \infty), \mathbb{R}]$
. Given
![]() $d_{\mathcal{J}_1, \infty}(X_n, Y_n) \overset{a.s.}{\to} 0$
, we have
$d_{\mathcal{J}_1, \infty}(X_n, Y_n) \overset{a.s.}{\to} 0$
, we have
B Asymptotic closeness of two scaled processes
In this section we prove the remark following Theorem 1. We consider a general CM MC
![]() $(C_n, M_n)$
,
$(C_n, M_n)$
,
![]() $n \ge 0$
, and the jumps
$n \ge 0$
, and the jumps
![]() $\xi^{(2)}_k$
of the second component are bounded RVs. Then for the process
$\xi^{(2)}_k$
of the second component are bounded RVs. Then for the process
![]() $M(nt) = M_{[nt]}$
we have the same functional limit theorem as for the process
$M(nt) = M_{[nt]}$
we have the same functional limit theorem as for the process
![]() $\widehat{M}(nt) = M(nt +1)$
. Thanks to Proposition 6, it is sufficient to prove the following.
$\widehat{M}(nt) = M(nt +1)$
. Thanks to Proposition 6, it is sufficient to prove the following.
Proposition 7. We have
Proof. First, we restrict our processes to the time interval [0, T], with an arbitrary finite T, and investigate the convergence of the distance
![]() $d_{\mathcal{J}_1, T} (\cdot, \cdot)$
between our processes. Second, we bound the distance using the following function
$d_{\mathcal{J}_1, T} (\cdot, \cdot)$
between our processes. Second, we bound the distance using the following function
![]() $\lambda_n$
:
$\lambda_n$
:
 \begin{equation*}\lambda_n(t) = \begin{cases}0, \ t\in \left[0, \frac{1}{n}\right],\\ \\[-7pt] t-\frac{1}{n}, \ t\in \left[\frac{1}{n}, t_n\right],\\ \\[-7pt] t_n + (t-t_n)\frac{T-t_n + 1/n}{T-t_n},\end{cases} \ \text{where} \ t_n = \frac{[nT] - 1}{n}.\end{equation*}
\begin{equation*}\lambda_n(t) = \begin{cases}0, \ t\in \left[0, \frac{1}{n}\right],\\ \\[-7pt] t-\frac{1}{n}, \ t\in \left[\frac{1}{n}, t_n\right],\\ \\[-7pt] t_n + (t-t_n)\frac{T-t_n + 1/n}{T-t_n},\end{cases} \ \text{where} \ t_n = \frac{[nT] - 1}{n}.\end{equation*}
Thus,
![]() $M(nt) = M(n\lambda_n(t)+1)$
for
$M(nt) = M(n\lambda_n(t)+1)$
for
![]() $t\in [1/n, t_n]$
. Then the distance between processes on the time interval [0,T] can be bounded as follows:
$t\in [1/n, t_n]$
. Then the distance between processes on the time interval [0,T] can be bounded as follows:
 \begin{multline*}d_{\mathcal{J}_1, T}\left(\left\lbrace \frac{M(nt)}{b(\sqrt{n})}, t \in[0, T] \right\rbrace,\left\lbrace \frac{M(nt + 1)}{b(\sqrt{n})}, t \in[0, T] \right\rbrace\right) \\[3pt]\le \max\left( \frac{\max\Big(\Big|\xi^{(2)}_1\Big|, \Big|\xi^{(2)}_{\eta([nT]-2) +1}\Big|, \Big|\xi^{(2)}_{\eta([nT]-2) +1} + \xi^{(2)}_{\eta([nT]-1) +1}\Big|\Big)}{b(\sqrt{n})}, \frac{1}{n} \right)\\[3pt] \le \max\left( \frac{\max\Big(\Big|\xi^{(2)}_1\Big|, \Big|\xi^{(2)}_{\eta([nT]-2) +1}\Big|, \Big|\xi^{(2)}_{\eta([nT]-2) +1}\Big| + \Big|\xi^{(2)}_{\eta([nT]-2) +2}\Big|\Big)}{b(\sqrt{n})}, \frac{1}{n} \right).\end{multline*}
\begin{multline*}d_{\mathcal{J}_1, T}\left(\left\lbrace \frac{M(nt)}{b(\sqrt{n})}, t \in[0, T] \right\rbrace,\left\lbrace \frac{M(nt + 1)}{b(\sqrt{n})}, t \in[0, T] \right\rbrace\right) \\[3pt]\le \max\left( \frac{\max\Big(\Big|\xi^{(2)}_1\Big|, \Big|\xi^{(2)}_{\eta([nT]-2) +1}\Big|, \Big|\xi^{(2)}_{\eta([nT]-2) +1} + \xi^{(2)}_{\eta([nT]-1) +1}\Big|\Big)}{b(\sqrt{n})}, \frac{1}{n} \right)\\[3pt] \le \max\left( \frac{\max\Big(\Big|\xi^{(2)}_1\Big|, \Big|\xi^{(2)}_{\eta([nT]-2) +1}\Big|, \Big|\xi^{(2)}_{\eta([nT]-2) +1}\Big| + \Big|\xi^{(2)}_{\eta([nT]-2) +2}\Big|\Big)}{b(\sqrt{n})}, \frac{1}{n} \right).\end{multline*}
Since the
![]() $\xi^{(2)}_k$
are bounded and
$\xi^{(2)}_k$
are bounded and
![]() $b(n) \to \infty$
as
$b(n) \to \infty$
as
![]() $n\to\infty$
, the right-hand side of the last inequality converges to zero a.s.
$n\to\infty$
, the right-hand side of the last inequality converges to zero a.s.
Appendix C. Tail asymptotics for randomly stopped sum
Let
![]() $\xi_1, \xi_2, \ldots$
be positive i.i.d. RVs with a common distribution function F. Let
$\xi_1, \xi_2, \ldots$
be positive i.i.d. RVs with a common distribution function F. Let
![]() $S_0 = 0$
and
$S_0 = 0$
and
![]() $S_k = \xi_1 + \ldots \xi_k$
,
$S_k = \xi_1 + \ldots \xi_k$
,
![]() $k\geq 1$
. Let
$k\geq 1$
. Let
![]() $\tau$
be a counting RV with a distribution function G, independent of
$\tau$
be a counting RV with a distribution function G, independent of
![]() $\{\xi_k\}_{k=1}^\infty$
. For a general overview concerning tail asymptotics of
$\{\xi_k\}_{k=1}^\infty$
. For a general overview concerning tail asymptotics of
![]() $S_\tau$
, see e.g. [Reference Denisov, Foss and Korshunov10] and references therein. The next result follows from Theorem 1 of [Reference Korshunov25].
$S_\tau$
, see e.g. [Reference Denisov, Foss and Korshunov10] and references therein. The next result follows from Theorem 1 of [Reference Korshunov25].
Proposition 8. Assume that
![]() $\overline{F}(x) \sim l_1(x) /x^\alpha$
,
$\overline{F}(x) \sim l_1(x) /x^\alpha$
,
![]() $\alpha \in [0, 1)$
, and
$\alpha \in [0, 1)$
, and
![]() $\tau$
has any distribution with
$\tau$
has any distribution with
![]() $\mathbb{E}\tau < \infty$
. Then
$\mathbb{E}\tau < \infty$
. Then
The next result we use in Lemma 1; we prove it using Tauberian theorems.
Proposition 9. Assume that
![]() $\overline{F}(x) \sim l_1(x) /x^\alpha$
and
$\overline{F}(x) \sim l_1(x) /x^\alpha$
and
![]() $\overline{G}(x) \sim l_2(x) /x^\beta$
,
$\overline{G}(x) \sim l_2(x) /x^\beta$
,
![]() $\alpha, \beta \in (0,1)$
. Then
$\alpha, \beta \in (0,1)$
. Then
Proof. Denote the cumulative distribution function of
![]() $S_\tau$
by H. Let
$S_\tau$
by H. Let
Define
![]() $\overline{G}, \widehat{G}, \overline{H}$
, and
$\overline{G}, \widehat{G}, \overline{H}$
, and
![]() $\widehat{H}$
similarly. We use the following result.
$\widehat{H}$
similarly. We use the following result.
Proposition 10. (Part of Corollary 8.1.7, [Reference Bingham, Goldie and Teugels6].) For a constant
![]() $ \alpha \in [0, 1]$
, and for a function l that is slowly varying at infinity, the following are equivalent:
$ \alpha \in [0, 1]$
, and for a function l that is slowly varying at infinity, the following are equivalent:
 \begin{align*}1 - \widehat{F}(\lambda) \sim \lambda^\alpha l\left(\frac{1}{\lambda} \right), \ as\ &\text{$\lambda \downarrow 0$, }\\\overline{F}(x) \sim \frac{l(x)}{x^\alpha \Gamma(1-\alpha)}, \ as\ &\text{$x\to \infty$,} \text{ if $0\le\alpha < 1.$}\end{align*}
\begin{align*}1 - \widehat{F}(\lambda) \sim \lambda^\alpha l\left(\frac{1}{\lambda} \right), \ as\ &\text{$\lambda \downarrow 0$, }\\\overline{F}(x) \sim \frac{l(x)}{x^\alpha \Gamma(1-\alpha)}, \ as\ &\text{$x\to \infty$,} \text{ if $0\le\alpha < 1.$}\end{align*}
Using this result, we get
Let us analyse
![]() $\widehat{H}$
:
$\widehat{H}$
:
Since
we have
 \begin{multline}1 - \widehat{H}(\lambda) \sim 1 - \widehat{G}\left(\lambda^\alpha \Gamma(1-\alpha)l_1\left(\frac{1}{\lambda} \right) \right)\\ \sim \lambda^{\alpha\beta}\Gamma^\beta(1-\alpha) \Gamma(1-\beta) l_1^\beta\left(\frac{1}{\lambda} \right) l_2 \left(\frac{1}{\lambda^\alpha \Gamma(1-\alpha)l_1\left(\frac{1}{\lambda} \right)} \right),\end{multline}
\begin{multline}1 - \widehat{H}(\lambda) \sim 1 - \widehat{G}\left(\lambda^\alpha \Gamma(1-\alpha)l_1\left(\frac{1}{\lambda} \right) \right)\\ \sim \lambda^{\alpha\beta}\Gamma^\beta(1-\alpha) \Gamma(1-\beta) l_1^\beta\left(\frac{1}{\lambda} \right) l_2 \left(\frac{1}{\lambda^\alpha \Gamma(1-\alpha)l_1\left(\frac{1}{\lambda} \right)} \right),\end{multline}
as
![]() $\lambda \downarrow 0$
, and finally
$\lambda \downarrow 0$
, and finally
Note that the function
![]() $l_2(h(\lambda))$
with
$l_2(h(\lambda))$
with
![]() $h(\lambda) = 1/ (\lambda^\alpha \Gamma(1-\alpha)l_1\left(\frac{1}{\lambda} \right))$
on the right-hand side of (26) is slowly varying at infinity. Indeed, for any constant
$h(\lambda) = 1/ (\lambda^\alpha \Gamma(1-\alpha)l_1\left(\frac{1}{\lambda} \right))$
on the right-hand side of (26) is slowly varying at infinity. Indeed, for any constant
![]() $c \neq 0$
, as
$c \neq 0$
, as
![]() $\lambda \downarrow 0$
,
$\lambda \downarrow 0$
,
 \begin{equation*}h(c\lambda) = \frac{1}{(c\lambda)^\alpha \Gamma(1-\alpha)l_1\left(\frac{1}{c\lambda} \right)} \sim c^{-\alpha}h(\lambda), \end{equation*}
\begin{equation*}h(c\lambda) = \frac{1}{(c\lambda)^\alpha \Gamma(1-\alpha)l_1\left(\frac{1}{c\lambda} \right)} \sim c^{-\alpha}h(\lambda), \end{equation*}
and therefore
![]() $l_2(h(c\lambda)) \sim l_2(c^{-\alpha} h(\lambda)) \sim l_2(h(\lambda))$
.
$l_2(h(c\lambda)) \sim l_2(c^{-\alpha} h(\lambda)) \sim l_2(h(\lambda))$
.
Acknowledgement
The authors would like to thank the two anonymous referees for their helpful and constructive comments.
Funding Information
Research was supported by the Mathematical Center in Akademgorodok under Agreement No. 075-15-2019-1613 with the Ministry of Science and Higher Education of the Russian Federation.
Competing Interests
There were no competing interests to declare which arose during the preparation or publication process for this article.