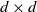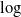1. Introduction
An affine process on the cone of symmetric positive semidefinite ![]() $d\times d$
matrices
$d\times d$
matrices ![]() $\mathbb{S}_{d}^{+}$
is a stochastically continuous Markov process taking values in
$\mathbb{S}_{d}^{+}$
is a stochastically continuous Markov process taking values in ![]() $\mathbb{S}_{d}^{+}$
, whose
$\mathbb{S}_{d}^{+}$
, whose ![]() $\log$
-Laplace transform depends in an affine way on the initial state of the process. Affine processes on the state space
$\log$
-Laplace transform depends in an affine way on the initial state of the process. Affine processes on the state space ![]() $\mathbb{S}_{d}^{+}$
were first systematically studied in the seminal article of Cuchiero et al. [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12]. In their work, the
$\mathbb{S}_{d}^{+}$
were first systematically studied in the seminal article of Cuchiero et al. [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12]. In their work, the ![]() $\mathbb{S}_{d}^{+}$
-valued affine process is constructed and completely characterized through a set of admissible parameters, and the related generalized Riccati equations are investigated. Subsequent developments complementing the results of [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12] can be found in [Reference Keller-Ressel and Mayerhofer33], [Reference Mayerhofer42], [Reference Mayerhofer, Pfaffel and Stelzer43], and [Reference Mayerhofer, Stelzer and Vestweber44]. Note that the notion of affine processes is not restricted to the state space
$\mathbb{S}_{d}^{+}$
-valued affine process is constructed and completely characterized through a set of admissible parameters, and the related generalized Riccati equations are investigated. Subsequent developments complementing the results of [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12] can be found in [Reference Keller-Ressel and Mayerhofer33], [Reference Mayerhofer42], [Reference Mayerhofer, Pfaffel and Stelzer43], and [Reference Mayerhofer, Stelzer and Vestweber44]. Note that the notion of affine processes is not restricted to the state space ![]() $\mathbb{S}_{d}^{+}$
. For affine processes on other finite-dimensional cones, particularly the canonical one
$\mathbb{S}_{d}^{+}$
. For affine processes on other finite-dimensional cones, particularly the canonical one ![]() $\mathbb{R}_{\geq0}^{m}\times\mathbb{R}^{n}$
, we refer the reader to [Reference Andersen and Piterbarg2], [Reference Barczy, Li and Pap5], [Reference Barczy, Li and Pap6], [Reference Dawson and Li15], [Reference Duffie, Filipović and Schachermayer16], [Reference Filipović and Mayerhofer17], [Reference Jena, Kim and Xing28], [Reference Keller-Ressel and Mayerhofer33], and [Reference Keller-Ressel, Schachermayer and Teichmann35]. We remark that the above list is far from complete.
$\mathbb{R}_{\geq0}^{m}\times\mathbb{R}^{n}$
, we refer the reader to [Reference Andersen and Piterbarg2], [Reference Barczy, Li and Pap5], [Reference Barczy, Li and Pap6], [Reference Dawson and Li15], [Reference Duffie, Filipović and Schachermayer16], [Reference Filipović and Mayerhofer17], [Reference Jena, Kim and Xing28], [Reference Keller-Ressel and Mayerhofer33], and [Reference Keller-Ressel, Schachermayer and Teichmann35]. We remark that the above list is far from complete.
The importance of ![]() $\mathbb{S}_{d}^{+}$
-valued affine processes has been demonstrated by the rapidly growing number of their applications in mathematical finance. In particular, they provide natural models for the evolution of the covariance matrix of multi-asset prices that exhibit random dependence, such as the Wishart process [Reference Bru10], the jump-type Wishart process [Reference Leippold and Trojani38], and a certain class of matrix-valued Ornstein–Uhlenbeck processes driven by Lévy subordinators [Reference Barndorff-Nielsen and Stelzer7]. Among these, the Wishart process is the most popular one, and it can be used as a multivariate covariance model that extends the well-known Heston model [Reference Heston26]; see also [Reference Baldeaux and Platen3], [Reference Biagini, Gnoatto and Härtel9], [Reference Chiarella, Da Fonseca and Grasselli11], [Reference Da Fonseca, Grasselli and Tebaldi14], [Reference Gnoatto21], [Reference Gnoatto and Grasselli22], [Reference Gourieroux and Sufana23], [Reference Gourieroux and Sufana24], and [Reference Grasselli and Miglietta25]. The jump-type Wishart process was introduced by Leippold and Trojani [Reference Leippold and Trojani38] to provide additional model flexibility. In [Reference Leippold and Trojani38] the jump-type Wishart process is used in multivariate option pricing, fixed-income models, and dynamic portfolio choice. For a more detailed review of financial applications of affine processes on
$\mathbb{S}_{d}^{+}$
-valued affine processes has been demonstrated by the rapidly growing number of their applications in mathematical finance. In particular, they provide natural models for the evolution of the covariance matrix of multi-asset prices that exhibit random dependence, such as the Wishart process [Reference Bru10], the jump-type Wishart process [Reference Leippold and Trojani38], and a certain class of matrix-valued Ornstein–Uhlenbeck processes driven by Lévy subordinators [Reference Barndorff-Nielsen and Stelzer7]. Among these, the Wishart process is the most popular one, and it can be used as a multivariate covariance model that extends the well-known Heston model [Reference Heston26]; see also [Reference Baldeaux and Platen3], [Reference Biagini, Gnoatto and Härtel9], [Reference Chiarella, Da Fonseca and Grasselli11], [Reference Da Fonseca, Grasselli and Tebaldi14], [Reference Gnoatto21], [Reference Gnoatto and Grasselli22], [Reference Gourieroux and Sufana23], [Reference Gourieroux and Sufana24], and [Reference Grasselli and Miglietta25]. The jump-type Wishart process was introduced by Leippold and Trojani [Reference Leippold and Trojani38] to provide additional model flexibility. In [Reference Leippold and Trojani38] the jump-type Wishart process is used in multivariate option pricing, fixed-income models, and dynamic portfolio choice. For a more detailed review of financial applications of affine processes on ![]() $\mathbb{S}_{d}^{+}$
we refer the reader to the introduction of [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12]; see also the references therein.
$\mathbb{S}_{d}^{+}$
we refer the reader to the introduction of [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12]; see also the references therein.
In this article, we investigate the long-time behavior of affine processes on ![]() $\mathbb{S}_{d}^{+}$
; i.e., we prove the existence, uniqueness, and convergence towards the limiting distribution. Such a problem was previously studied by Alfonsi et al. [Reference Alfonsi, Kebaier and Rey1] for the case of Wishart processes, using a fine analysis of the Laplace transform. The case of matrix-valued Ornstein–Uhlenbeck processes driven by Lévy subordinators was investigated by Barndorff-Nielsen and Stelzer [Reference Barndorff-Nielsen and Stelzer7], where also some results on the support of the invariant distribution were obtained; see also [Reference Pigorsch and Stelzer45] and [Reference Sato and Yamazato47]. Based on stochastic stability criteria of Meyn and Tweedie, convergence to the unique invariant distribution in total variation was then studied for a general class of Ornstein–Uhlenbeck processes in [Reference Masuda41], while generalized Ornstein–Uhlenbeck processes in dimension one have been investigated in [Reference Behme, Lindner and Maller8] and [Reference Kevei37]. First results on exponential ergodicity applicable to a class of affine processes on finite-dimensional cones were recently obtained by Mayerhofer et al. [Reference Mayerhofer, Stelzer and Vestweber44].
$\mathbb{S}_{d}^{+}$
; i.e., we prove the existence, uniqueness, and convergence towards the limiting distribution. Such a problem was previously studied by Alfonsi et al. [Reference Alfonsi, Kebaier and Rey1] for the case of Wishart processes, using a fine analysis of the Laplace transform. The case of matrix-valued Ornstein–Uhlenbeck processes driven by Lévy subordinators was investigated by Barndorff-Nielsen and Stelzer [Reference Barndorff-Nielsen and Stelzer7], where also some results on the support of the invariant distribution were obtained; see also [Reference Pigorsch and Stelzer45] and [Reference Sato and Yamazato47]. Based on stochastic stability criteria of Meyn and Tweedie, convergence to the unique invariant distribution in total variation was then studied for a general class of Ornstein–Uhlenbeck processes in [Reference Masuda41], while generalized Ornstein–Uhlenbeck processes in dimension one have been investigated in [Reference Behme, Lindner and Maller8] and [Reference Kevei37]. First results on exponential ergodicity applicable to a class of affine processes on finite-dimensional cones were recently obtained by Mayerhofer et al. [Reference Mayerhofer, Stelzer and Vestweber44].
In contrast, we study the existence of limit distributions for general conservative, subcritical affine processes on ![]() $\mathbb{S}_{d}^{+}$
satisfying an additional first-moment condition for the state-dependent jump measure and a
$\mathbb{S}_{d}^{+}$
satisfying an additional first-moment condition for the state-dependent jump measure and a ![]() $\log$
-moment condition for the state-independent jump measure, and therefore extend the aforementioned results of [Reference Alfonsi, Kebaier and Rey1] and [Reference Barndorff-Nielsen and Stelzer7] to a general class of affine processes on
$\log$
-moment condition for the state-independent jump measure, and therefore extend the aforementioned results of [Reference Alfonsi, Kebaier and Rey1] and [Reference Barndorff-Nielsen and Stelzer7] to a general class of affine processes on ![]() $\mathbb{S}_d^+$
. Our proofs are inspired by Sato and Yamazato [Reference Sato and Yamazato47] (for Ornstein–Uhlenbeck processes) and rely on some technical ideas taken from [Reference Jin, Kremer and Rüdiger30], where affine processes on the canonical state space
$\mathbb{S}_d^+$
. Our proofs are inspired by Sato and Yamazato [Reference Sato and Yamazato47] (for Ornstein–Uhlenbeck processes) and rely on some technical ideas taken from [Reference Jin, Kremer and Rüdiger30], where affine processes on the canonical state space ![]() $\mathbb{R}_{\geq0}^m \times \mathbb{R}^n$
were considered. However, compared to the canonical state space, the boundary of
$\mathbb{R}_{\geq0}^m \times \mathbb{R}^n$
were considered. However, compared to the canonical state space, the boundary of ![]() $\mathbb{S}_d^+$
is quite complicated and prevents us from directly applying the arguments in [Reference Jin, Kremer and Rüdiger30]. Additional details are explained in the next section. We would like to mention that our method to show stationarity could also be applied to affine processes on more general convex cones in the spirit of [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13] and [Reference Mayerhofer, Stelzer and Vestweber44]; however, this would require the introduction of additional notation which would make our key arguments less transparent, so we postpone the detailed discussion of this extension to Section 9.
$\mathbb{S}_d^+$
is quite complicated and prevents us from directly applying the arguments in [Reference Jin, Kremer and Rüdiger30]. Additional details are explained in the next section. We would like to mention that our method to show stationarity could also be applied to affine processes on more general convex cones in the spirit of [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13] and [Reference Mayerhofer, Stelzer and Vestweber44]; however, this would require the introduction of additional notation which would make our key arguments less transparent, so we postpone the detailed discussion of this extension to Section 9.
Finally, let us mention that the long-time behavior of affine processes has previously been studied in many different settings, either based on a detailed study of the characteristic function (see e.g. [Reference Pinsky46], [Reference Li39], [Reference Glasserman and Kim20], [Reference Sato and Yamazato47], [Reference Keller-Ressel and Mijatović34], [Reference Keller-Ressel32], [Reference Keller-Ressel and Steiner36], [Reference Jin, Kremer and Rüdiger30]), by stochastic stability criteria due to Meyn and Tweedie ([Reference Barczy, Döring, Li and Pap4], [Reference Jin, Kremer and Rüdiger29], [Reference Mayerhofer, Stelzer and Vestweber44]), or by coupling techniques ([Reference Friesen, Jin and Rüdiger19], [Reference Friesen, Jin, Kremer and Rüdiger18], [Reference Li and Ma40]). One application of such study is towards the estimation of parameters for affine models. In the case of the Wishart process, the maximum-likelihood estimator for the drift parameter was recently studied by Alfonsi et al. [Reference Alfonsi, Kebaier and Rey1]. As demonstrated in their article, ergodicity helps to derive strong consistency and asymptotic normality of the estimator.
This paper is organized as follows. In Section 2, we introduce ![]() $\mathbb{S}_{d}^{+}$
-valued affine processes, then formulate and discuss our main results. Section 3 is dedicated to applications of our results to specific affine models often used in finance. The proofs of the main results are then given in Sections 4–8. Finally, in Section 9 we provide an extension of our stationarity result to conservative affine processes on general convex cones.
$\mathbb{S}_{d}^{+}$
-valued affine processes, then formulate and discuss our main results. Section 3 is dedicated to applications of our results to specific affine models often used in finance. The proofs of the main results are then given in Sections 4–8. Finally, in Section 9 we provide an extension of our stationarity result to conservative affine processes on general convex cones.
2. Main results
In terms of terminology, we mainly follow the coordinate-free notation used in Mayerhofer [Reference Mayerhofer42] and Keller-Ressel and Mayerhofer [Reference Keller-Ressel and Mayerhofer33].
Let ![]() $d\geq2$
and denote by
$d\geq2$
and denote by ![]() $\mathbb{S}_{d}$
the space of symmetric
$\mathbb{S}_{d}$
the space of symmetric ![]() $d\times d$
matrices equipped with the scalar product
$d\times d$
matrices equipped with the scalar product ![]() $\langle x,y\rangle=\text{tr}(xy)$
and the Frobenius norm
$\langle x,y\rangle=\text{tr}(xy)$
and the Frobenius norm ![]() $\Vert x\Vert\,:\!=\langle x,x\rangle^{1/2}$
, where tr(.) denotes the trace of a matrix. We list in Appendix A some properties of the trace and its induced norm which are repeatedly used in the remainder of the article. Denote by
$\Vert x\Vert\,:\!=\langle x,x\rangle^{1/2}$
, where tr(.) denotes the trace of a matrix. We list in Appendix A some properties of the trace and its induced norm which are repeatedly used in the remainder of the article. Denote by ![]() $\mathbb{S}_{d}^{+}$
(resp.
$\mathbb{S}_{d}^{+}$
(resp. ![]() $\mathbb{S}_{d}^{++}$
) the cone of symmetric and positive semidefinite (resp. positive definite) real
$\mathbb{S}_{d}^{++}$
) the cone of symmetric and positive semidefinite (resp. positive definite) real ![]() $d\times d$
matrices. We write
$d\times d$
matrices. We write ![]() $x\preceq y$
if
$x\preceq y$
if ![]() $y-x\in\mathbb{S}_{d}^{+}$
and
$y-x\in\mathbb{S}_{d}^{+}$
and ![]() $x\prec y$
if
$x\prec y$
if ![]() $y-x\in\mathbb{S}_{d}^{++}$
for the natural partial and strict order relations introduced respectively by the cones
$y-x\in\mathbb{S}_{d}^{++}$
for the natural partial and strict order relations introduced respectively by the cones ![]() $\mathbb{S}_{d}^{+}$
and
$\mathbb{S}_{d}^{+}$
and ![]() $\mathbb{S}_{d}^{++}$
. Let
$\mathbb{S}_{d}^{++}$
. Let ![]() $\mathcal{B}(\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace)$
be the Borel-
$\mathcal{B}(\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace)$
be the Borel-![]() $\sigma$
-algebra on
$\sigma$
-algebra on ![]() $\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace$
. An
$\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace$
. An ![]() $\mathbb{S}_{d}^{+}$
-valued measure
$\mathbb{S}_{d}^{+}$
-valued measure ![]() $\eta$
on
$\eta$
on ![]() $\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace$
is a
$\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace$
is a ![]() $d\times d$
matrix of signed measures on
$d\times d$
matrix of signed measures on ![]() $\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace$
such that
$\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace$
such that ![]() $\eta(A)\in\mathbb{S}_{d}^{+}$
whenever
$\eta(A)\in\mathbb{S}_{d}^{+}$
whenever ![]() $A\in\mathcal{B}(\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace)$
with
$A\in\mathcal{B}(\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace)$
with ![]() $0\not\in\overline{A}$
.
$0\not\in\overline{A}$
.
In the following we present the notion of admissible parameters first introduced in Cuchiero et al. [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Definition 2.3]. Here we mainly follow the definition given in Mayerhofer [Reference Mayerhofer42, Definition 3.1], with a slightly stronger condition on the linear jump coefficient.
Definition 2.1. Let ![]() $d\geq2$
. An admissible parameter set
$d\geq2$
. An admissible parameter set ![]() $(\alpha,b,B,m,\mu)$
consists of the following:
$(\alpha,b,B,m,\mu)$
consists of the following:
(i) a linear diffusion coefficient
 $\alpha\in\mathbb{S}_{d}^{+}$
;
$\alpha\in\mathbb{S}_{d}^{+}$
;(ii) a constant drift
 $b\in\mathbb{S}_{d}^{+}$
satisfying
$b\in\mathbb{S}_{d}^{+}$
satisfying  $b\succeq(d-1)\alpha$
;
$b\succeq(d-1)\alpha$
;(iii) a constant jump term: a Borel measure m on
 $\mathbb{S}_{d}^{+}\backslash\{0\}$
satisfying
$\mathbb{S}_{d}^{+}\backslash\{0\}$
satisfying
 \begin{equation*}\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}\left(\left\Vert \xi\right\Vert \wedge1\right)m\left(\text{d}\xi\right)<\infty;\end{equation*}
\begin{equation*}\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}\left(\left\Vert \xi\right\Vert \wedge1\right)m\left(\text{d}\xi\right)<\infty;\end{equation*}
(iv) a linear jump coefficient
 $\mu$
which is an
$\mu$
which is an  $\mathbb{S}_{d}^{+}$
-valued, sigma-finite measure on
$\mathbb{S}_{d}^{+}$
-valued, sigma-finite measure on  $\mathbb{S}_{d}^{+}\backslash\{0\}$
satisfying
(1)where
$\mathbb{S}_{d}^{+}\backslash\{0\}$
satisfying
(1)where \begin{align}\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}\left\Vert \xi\right\Vert \text{tr}(\mu)\left(\text{d}\xi\right)
< \infty,\end{align}
\begin{align}\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}\left\Vert \xi\right\Vert \text{tr}(\mu)\left(\text{d}\xi\right)
< \infty,\end{align}
 $\text{tr}(\mu)$
denotes the measure induced by the relation
$\text{tr}(\mu)$
denotes the measure induced by the relation  $\text{tr}(\mu)(A)\,:\!=\text{tr}(\mu(A))$
for all
$\text{tr}(\mu)(A)\,:\!=\text{tr}(\mu(A))$
for all  $A\in\mathcal{B}(\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace)$
with
$A\in\mathcal{B}(\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace)$
with  $0\notin\bar{A}$
;
$0\notin\bar{A}$
;(v) a linear drift B, which is a linear map
 $B\,:\,\mathbb{S}_{d}\to\mathbb{S}_{d}$
satisfying
$B\,:\,\mathbb{S}_{d}\to\mathbb{S}_{d}$
satisfying
 \begin{equation*}\langle B(x),u\rangle\geq0\quad\text{for all }x,\thinspace u\in\mathbb{S}_{d}^{+}\text{ with }\langle x,u\rangle=0.\end{equation*}
\begin{equation*}\langle B(x),u\rangle\geq0\quad\text{for all }x,\thinspace u\in\mathbb{S}_{d}^{+}\text{ with }\langle x,u\rangle=0.\end{equation*}
According to our definition, a set of admissible parameters does not contain parameters corresponding to killing. In addition, compared with [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Definition 2.3], our definition involves an additional first-moment assumption on the linear jump coefficient ![]() $\mu$
. Thanks to this stronger assumption and [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Remark 2.5], the affine process we consider here is conservative.
$\mu$
. Thanks to this stronger assumption and [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Remark 2.5], the affine process we consider here is conservative.
Theorem 2.1. (Cuchiero et al. [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12].) Let ![]() $(\alpha,b,B,m,\mu)$
be admissible parameters in the sense of Definition 2.1. Then there exists a unique stochastically continuous transition kernel
$(\alpha,b,B,m,\mu)$
be admissible parameters in the sense of Definition 2.1. Then there exists a unique stochastically continuous transition kernel ![]() $p_{t}(x,\text{d}\xi)$
such that
$p_{t}(x,\text{d}\xi)$
such that ![]() $p_{t}(x,\mathbb{S}_{d}^{+})=1$
and
$p_{t}(x,\mathbb{S}_{d}^{+})=1$
and
where ![]() $\phi(t,u)$
and
$\phi(t,u)$
and ![]() $\psi(t,u)$
in (2) are the unique solutions to the generalized Riccati differential equations; that is, for
$\psi(t,u)$
in (2) are the unique solutions to the generalized Riccati differential equations; that is, for ![]() $u\in\mathbb{S}_{d}^{+}$
,
$u\in\mathbb{S}_{d}^{+}$
,
where the functions F and R are given by
 \begin{align*}F(u) & =\langle b,u\rangle-\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(\text{e}^{-\langle u,\xi\rangle}-1)m\left(\text{d}\xi\right)\!,\\[5pt]
R(u) & =-2u\alpha u+B{}^{\top}\left(u\right)-\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(\text{e}^{-\langle u,\xi\rangle}-1)\mu\left(\text{d}\xi\right)\!.\end{align*}
\begin{align*}F(u) & =\langle b,u\rangle-\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(\text{e}^{-\langle u,\xi\rangle}-1)m\left(\text{d}\xi\right)\!,\\[5pt]
R(u) & =-2u\alpha u+B{}^{\top}\left(u\right)-\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(\text{e}^{-\langle u,\xi\rangle}-1)\mu\left(\text{d}\xi\right)\!.\end{align*}
Here, ![]() $B^{\top}$
denotes the adjoint operator on
$B^{\top}$
denotes the adjoint operator on ![]() $\mathbb{S}_{d}$
defined by the relation
$\mathbb{S}_{d}$
defined by the relation ![]() $\langle u,B(\xi)\rangle=\langle B^{\top}(u),\xi\rangle$
for
$\langle u,B(\xi)\rangle=\langle B^{\top}(u),\xi\rangle$
for ![]() $u,\thinspace\xi\in\mathbb{S}_{d}$
. Under the additional moment condition (iv) of Definition 2.1, we will show in Lemma 4.2 below that R(u) is continuously differentiable and thus locally Lipschitz continuous on
$u,\thinspace\xi\in\mathbb{S}_{d}$
. Under the additional moment condition (iv) of Definition 2.1, we will show in Lemma 4.2 below that R(u) is continuously differentiable and thus locally Lipschitz continuous on ![]() $\mathbb{S}_{d}^{+}$
. This fact, together with the absence of parameters according to killing, implies that the affine process under consideration is indeed conservative (see [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Remark 2.5]) and, moreover, the Riccati equations have unique solutions for all
$\mathbb{S}_{d}^{+}$
. This fact, together with the absence of parameters according to killing, implies that the affine process under consideration is indeed conservative (see [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Remark 2.5]) and, moreover, the Riccati equations have unique solutions for all ![]() $u \in \mathbb{S}_d^+$
. Also, following [Reference Mayerhofer42], each affine process on
$u \in \mathbb{S}_d^+$
. Also, following [Reference Mayerhofer42], each affine process on ![]() $\mathbb{S}_d^+$
, when
$\mathbb{S}_d^+$
, when ![]() $d \geq 2$
, has jumps of finite variation, which is why we omitted, compared with [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12], additional compensation in the integral against
$d \geq 2$
, has jumps of finite variation, which is why we omitted, compared with [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12], additional compensation in the integral against ![]() $\mu$
.
$\mu$
.
2.1. First moment
Our first result provides existence and a precise formula for the first moment of conservative affine processes on ![]() $\mathbb{S}_{d}^{+}$
. For this purpose, we define the effective drift
$\mathbb{S}_{d}^{+}$
. For this purpose, we define the effective drift
Then note that ![]() $\widetilde{B}\,:\,\mathbb{S}_{d}\to\mathbb{S}_{d}$
is a linear map. We define the corresponding semigroup
$\widetilde{B}\,:\,\mathbb{S}_{d}\to\mathbb{S}_{d}$
is a linear map. We define the corresponding semigroup ![]() $(\exp(t\widetilde{B}))_{t\geq0}$
by its Taylor series
$(\exp(t\widetilde{B}))_{t\geq0}$
by its Taylor series ![]() $\exp(t\widetilde{B})(u)=\sum_{n=0}^{\infty}t^{n}/n!\widetilde{B}^{\circ n}(u)$
, where
$\exp(t\widetilde{B})(u)=\sum_{n=0}^{\infty}t^{n}/n!\widetilde{B}^{\circ n}(u)$
, where ![]() $\widetilde{B}^{\circ n}$
denotes the n-times composition of
$\widetilde{B}^{\circ n}$
denotes the n-times composition of ![]() $\widetilde{B}$
. For the remainder of the article we write
$\widetilde{B}$
. For the remainder of the article we write ![]() $\mathbbm{1}$
without an index for the
$\mathbbm{1}$
without an index for the ![]() $d\times d$
-identity matrix, while
$d\times d$
-identity matrix, while ![]() $\mathbbm{1}_{A}$
denotes the standard indicator function of a set A.
$\mathbbm{1}_{A}$
denotes the standard indicator function of a set A.
Theorem 2.2. Let ![]() $p_{t}(x,\text{d}\xi)$
be the transition kernel of an affine process on
$p_{t}(x,\text{d}\xi)$
be the transition kernel of an affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
satisfying
$(\alpha,b,B,m,\mu)$
satisfying
Then for each ![]() $t\geq0$
and
$t\geq0$
and ![]() $x\in\mathbb{S}_{d}^{+}$
, the first moment of
$x\in\mathbb{S}_{d}^{+}$
, the first moment of ![]() $p_{t}(x,\text{d}\xi)$
exists and equals
$p_{t}(x,\text{d}\xi)$
exists and equals
 \begin{equation}\int_{\mathbb{S}_{d}^{+}}\xi p_{t}(x,\text{d}\xi)=\text{e}^{t\widetilde{B}}x+\int_{0}^{t}\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\text{d}s.\end{equation}
\begin{equation}\int_{\mathbb{S}_{d}^{+}}\xi p_{t}(x,\text{d}\xi)=\text{e}^{t\widetilde{B}}x+\int_{0}^{t}\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\text{d}s.\end{equation}
Although this result is not very surprising, the proof of our main result (Theorem 2.3) crucially relies on (7). For the sake of completeness we therefore provide a full and detailed proof of Theorem 2.2 in Section 4.
Based on methods of stochastic calculus, similar results were obtained for affine processes with state-space ![]() $\mathbb{R}_{\geq0}^{m}$
in [Reference Barczy, Li and Pap5, Lemma 3.4] and on the canonical state space
$\mathbb{R}_{\geq0}^{m}$
in [Reference Barczy, Li and Pap5, Lemma 3.4] and on the canonical state space ![]() $\mathbb{R}_{\geq0}^{m}\times\mathbb{R}^{n}$
in [Reference Friesen, Jin and Rüdiger19, Lemma 5.2]. For affine processes on
$\mathbb{R}_{\geq0}^{m}\times\mathbb{R}^{n}$
in [Reference Friesen, Jin and Rüdiger19, Lemma 5.2]. For affine processes on ![]() $\mathbb{R}_{\geq0}$
, i.e., continuous-state branching processes with immigration, and also for the more general class of Dawson–Watanabe superprocesses, an alternative approach based on a fine analysis of the Laplace transform is provided in [Reference Li39]. The latter approach clearly has the advantage that it is purely analytical and does not rely on the use of stochastic equations and semimartingale representations for these processes. Our proof provided in Section 4 is also purely analytical and uses some ideas taken from [Reference Li39].
$\mathbb{R}_{\geq0}$
, i.e., continuous-state branching processes with immigration, and also for the more general class of Dawson–Watanabe superprocesses, an alternative approach based on a fine analysis of the Laplace transform is provided in [Reference Li39]. The latter approach clearly has the advantage that it is purely analytical and does not rely on the use of stochastic equations and semimartingale representations for these processes. Our proof provided in Section 4 is also purely analytical and uses some ideas taken from [Reference Li39].
Remark 2.1. Note that the transition kernel ![]() $p_{t}(x,\cdot)$
with admissible parameters
$p_{t}(x,\cdot)$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
is Feller by virtue of [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Theorem 2.4]. Therefore, there exists a canonical realization
$(\alpha,b,B,m,\mu)$
is Feller by virtue of [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Theorem 2.4]. Therefore, there exists a canonical realization ![]() $(X,(\mathbb{P}_{x})_{x\in\mathbb{S}_{d}^{+}})$
of the corresponding Markov process on the filtered space
$(X,(\mathbb{P}_{x})_{x\in\mathbb{S}_{d}^{+}})$
of the corresponding Markov process on the filtered space ![]() $(\Omega,\mathcal{F},(\mathcal{F}_{t})_{t\geq0})$
, where
$(\Omega,\mathcal{F},(\mathcal{F}_{t})_{t\geq0})$
, where ![]() $\Omega=\mathbb{D}(\mathbb{S}_{d}^{+})$
is the set of all càdlàg paths
$\Omega=\mathbb{D}(\mathbb{S}_{d}^{+})$
is the set of all càdlàg paths ![]() $\omega\,:\,\mathbb{R}_{\geq0}\to\mathbb{S}_{d}^{+}$
, and
$\omega\,:\,\mathbb{R}_{\geq0}\to\mathbb{S}_{d}^{+}$
, and ![]() $X_{t}(\omega)=\omega(t)$
for
$X_{t}(\omega)=\omega(t)$
for ![]() $\omega\in\Omega$
. Here
$\omega\in\Omega$
. Here ![]() $(\mathcal{F}_{t})_{t\geq0}$
is the natural filtration generated by X, and
$(\mathcal{F}_{t})_{t\geq0}$
is the natural filtration generated by X, and ![]() $\mathcal{F}=\bigvee_{t\geq0}\mathcal{F}_{t}$
. For
$\mathcal{F}=\bigvee_{t\geq0}\mathcal{F}_{t}$
. For ![]() $x\in\mathbb{S}_{d}^{+}$
, the probability measure
$x\in\mathbb{S}_{d}^{+}$
, the probability measure ![]() $\mathbb{P}_{x}$
on
$\mathbb{P}_{x}$
on ![]() $\Omega$
represents the law of the Markov process X given
$\Omega$
represents the law of the Markov process X given ![]() $X_{0}=x$
. With this notation, under the conditions of Theorem 2.2, the formula (7) reads
$X_{0}=x$
. With this notation, under the conditions of Theorem 2.2, the formula (7) reads
 \begin{equation*}\mathbb{E}_{x}\big[X_{t}\big]=\text{e}^{t\widetilde{B}}x+\int_{0}^{t}\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\text{d}s,\end{equation*}
\begin{equation*}\mathbb{E}_{x}\big[X_{t}\big]=\text{e}^{t\widetilde{B}}x+\int_{0}^{t}\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\text{d}s,\end{equation*}
where ![]() $\mathbb{E}_{x}$
denotes the expectation with respect to
$\mathbb{E}_{x}$
denotes the expectation with respect to ![]() $\mathbb{P}_{x}$
.
$\mathbb{P}_{x}$
.
2.2. Existence and convergence to the invariant distribution
In this subsection we formulate our main result. Let ![]() $p_{t}(x,\cdot)$
be the transition kernel of an affine process on
$p_{t}(x,\cdot)$
be the transition kernel of an affine process on ![]() $\mathbb{S}_{d}^{+}$
. Motivated by Theorem 2.2 it is reasonable to relate the long-time behavior of the process to the spectrum
$\mathbb{S}_{d}^{+}$
. Motivated by Theorem 2.2 it is reasonable to relate the long-time behavior of the process to the spectrum ![]() $\sigma(\widetilde{B})$
of
$\sigma(\widetilde{B})$
of ![]() $\widetilde{B}$
. More precisely, an affine process on
$\widetilde{B}$
. More precisely, an affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
is said to be subcritical if
$(\alpha,b,B,m,\mu)$
is said to be subcritical if
Under the condition (8), it is well-known that there exist constants ![]() $M\ge 1$
and
$M\ge 1$
and ![]() $\delta>0$
such that
$\delta>0$
such that
The next remark provides a sufficient condition for (9).
Remark 2.2. According to [Reference Mayerhofer, Stelzer and Vestweber44, Theorem 2.7], (9) is satisfied if and only if there exists a ![]() $v\in\mathbb{S}_{d}^{++}$
such that
$v\in\mathbb{S}_{d}^{++}$
such that ![]() $-\widetilde{B}^{\top}(v)\in\mathbb{S}_{d}^{++}$
. However, in many application the linear drift is of the form
$-\widetilde{B}^{\top}(v)\in\mathbb{S}_{d}^{++}$
. However, in many application the linear drift is of the form ![]() $\widetilde{B}(x)=\beta x+x\beta^{\top}$
, where
$\widetilde{B}(x)=\beta x+x\beta^{\top}$
, where ![]() $\beta$
is a real-valued
$\beta$
is a real-valued ![]() $d\times d$
matrix; see Section 3. In this case, it follows from [Reference Mayerhofer, Stelzer and Vestweber44, Corollary 5.1] that (9) is satisfied if and only if
$d\times d$
matrix; see Section 3. In this case, it follows from [Reference Mayerhofer, Stelzer and Vestweber44, Corollary 5.1] that (9) is satisfied if and only if
which in turn holds true if and only if there exists a ![]() $v\in\mathbb{S}_{d}^{++}$
such that
$v\in\mathbb{S}_{d}^{++}$
such that ![]() $-(\beta^{\top}v+v\beta)\in\mathbb{S}_{d}^{++}$
.
$-(\beta^{\top}v+v\beta)\in\mathbb{S}_{d}^{++}$
.
Let ![]() $\mathcal{P}(\mathbb{S}_{d}^{+})$
be the space of all Borel probability measures on
$\mathcal{P}(\mathbb{S}_{d}^{+})$
be the space of all Borel probability measures on ![]() $\mathbb{S}_{d}^{+}$
. We call
$\mathbb{S}_{d}^{+}$
. We call ![]() $\pi\in\mathcal{P}(\mathbb{S}_{d}^{+})$
an invariant distribution if
$\pi\in\mathcal{P}(\mathbb{S}_{d}^{+})$
an invariant distribution if
The following is our main result.
Theorem 2.3. Let ![]() $p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on
$p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
. Suppose that the measure m satisfies
$(\alpha,b,B,m,\mu)$
. Suppose that the measure m satisfies
Then there exists a unique invariant distribution ![]() $\pi$
. Moreover, for each
$\pi$
. Moreover, for each ![]() $x\in\mathbb{S}_{d}^{+}$
, one has
$x\in\mathbb{S}_{d}^{+}$
, one has ![]() $p_{t}(x,\cdot)\to\pi$
weakly as
$p_{t}(x,\cdot)\to\pi$
weakly as ![]() $t\to\infty$
, and
$t\to\infty$
, and ![]() $\pi$
has Laplace transform
$\pi$
has Laplace transform
The proof of Theorem 2.3 is postponed to Section 6. Let us make a few comments. Note that in dimension ![]() $d=1$
it holds that
$d=1$
it holds that ![]() $\mathbb{S}_{1}^{+}=\mathbb{R}_{\geq0}$
, and affine processes on this state space coincide with the class of continuous-state branching processes with immigration introduced by Kawazu and Watanabe [Reference Kawazu and Watanabe31]. In this case, the long-time behavior has been extensively studied in the articles [Reference Keller-Ressel and Steiner36, Theorem 3.16] and [Reference Keller-Ressel and Mijatović34, Theorem 2.6] and in the monograph [Reference Li39, Theorem 3.20 and Corollary 3.21]. This is why we restrict ourselves to the case
$\mathbb{S}_{1}^{+}=\mathbb{R}_{\geq0}$
, and affine processes on this state space coincide with the class of continuous-state branching processes with immigration introduced by Kawazu and Watanabe [Reference Kawazu and Watanabe31]. In this case, the long-time behavior has been extensively studied in the articles [Reference Keller-Ressel and Steiner36, Theorem 3.16] and [Reference Keller-Ressel and Mijatović34, Theorem 2.6] and in the monograph [Reference Li39, Theorem 3.20 and Corollary 3.21]. This is why we restrict ourselves to the case ![]() $d\geq2$
.
$d\geq2$
.
Theorem 2.3 establishes sufficient conditions for the existence, uniqueness, and convergence to the invariant distribution. For affine processes on the canonical state space ![]() $\mathbb{R}_{\geq0}^{m}\times\mathbb{R}^{n}$
a similar statement was recently shown in [Reference Jin, Kremer and Rüdiger30]. However, the method of [Reference Jin, Kremer and Rüdiger30] cannot be applied to the state space
$\mathbb{R}_{\geq0}^{m}\times\mathbb{R}^{n}$
a similar statement was recently shown in [Reference Jin, Kremer and Rüdiger30]. However, the method of [Reference Jin, Kremer and Rüdiger30] cannot be applied to the state space ![]() $\mathbb{S}_{d}^{+}$
. The reason is as follows. To apply the arguments of [Reference Jin, Kremer and Rüdiger30] to
$\mathbb{S}_{d}^{+}$
. The reason is as follows. To apply the arguments of [Reference Jin, Kremer and Rüdiger30] to ![]() $\mathbb{S}_{d}^{+}$
-valued affine processes requires the decomposition
$\mathbb{S}_{d}^{+}$
-valued affine processes requires the decomposition
where ![]() $r_{t}(x,\cdot)$
is the transition kernel of an affine process on
$r_{t}(x,\cdot)$
is the transition kernel of an affine process on ![]() $\mathbb{S}_{d}^{+}$
whose Laplace transform is given by
$\mathbb{S}_{d}^{+}$
whose Laplace transform is given by
that is, ![]() $r_{t}(x,\cdot)$
should have admissible parameters
$r_{t}(x,\cdot)$
should have admissible parameters ![]() $(\alpha,b=0,B,m=0,\mu)$
. Unfortunately, such a transition kernel
$(\alpha,b=0,B,m=0,\mu)$
. Unfortunately, such a transition kernel ![]() $r_{t}(x,\cdot)$
is well-defined if and only if
$r_{t}(x,\cdot)$
is well-defined if and only if ![]() $(\alpha,b=0,B,m=0,\mu)$
are admissible parameters in the sense of Definition 2.1. This in turn is true if and only if
$(\alpha,b=0,B,m=0,\mu)$
are admissible parameters in the sense of Definition 2.1. This in turn is true if and only if ![]() $\alpha=0$
, which is a consequence of the particular structure of the boundary
$\alpha=0$
, which is a consequence of the particular structure of the boundary ![]() $\partial \mathbb{S}_{d}^{+}$
. To overcome this difficulty, we use the cone structure to show that
$\partial \mathbb{S}_{d}^{+}$
. To overcome this difficulty, we use the cone structure to show that ![]() $\psi(t,u) \preceq \exp\{t \widetilde{B}^{\top}\}(u)$
, which requires us to study the first moment of the affine process with admissible parameters
$\psi(t,u) \preceq \exp\{t \widetilde{B}^{\top}\}(u)$
, which requires us to study the first moment of the affine process with admissible parameters ![]() $(\alpha,b,B, m = 0, \mu)$
; see (29). Note that the first moment of affine processes is already studied in Theorem 2.2, where the first moment condition for
$(\alpha,b,B, m = 0, \mu)$
; see (29). Note that the first moment of affine processes is already studied in Theorem 2.2, where the first moment condition for ![]() $\mu$
is also explicitly used. Uniform exponential stability for
$\mu$
is also explicitly used. Uniform exponential stability for ![]() $\psi(t,u)$
is then an immediate consequence of the assumption that the affine process is subcritical, i.e. that (9) holds. Compared with [Reference Jin, Kremer and Rüdiger30], our proof does not rely on stability results for ordinary differential equations; moreover, it has the advantage that it also applies to more general convex cones other than
$\psi(t,u)$
is then an immediate consequence of the assumption that the affine process is subcritical, i.e. that (9) holds. Compared with [Reference Jin, Kremer and Rüdiger30], our proof does not rely on stability results for ordinary differential equations; moreover, it has the advantage that it also applies to more general convex cones other than ![]() $\mathbb{S}_d^+$
(see Section 9). On the other hand, since this argument is crucially based on the proper closed convex cone structure, it cannot be applied to affine processes on the canonical state space
$\mathbb{S}_d^+$
(see Section 9). On the other hand, since this argument is crucially based on the proper closed convex cone structure, it cannot be applied to affine processes on the canonical state space ![]() $\mathbb{R}_{\geq0}^m \times \mathbb{R}^n$
.
$\mathbb{R}_{\geq0}^m \times \mathbb{R}^n$
.
Based on strong solutions to the stochastic equation and the construction of monotone couplings, an alternative approach for the study of the long-time behavior of affine processes on the canonical state space ![]() $\mathbb{R}_{\geq0}^m \times \mathbb{R}^n$
was recently given in [Reference Friesen, Jin and Rüdiger19]. This approach certainly does not apply here since it is still an open problem whether each affine process on
$\mathbb{R}_{\geq0}^m \times \mathbb{R}^n$
was recently given in [Reference Friesen, Jin and Rüdiger19]. This approach certainly does not apply here since it is still an open problem whether each affine process on ![]() $\mathbb{S}_{d}^{+}$
can be obtained as a strong solution to a certain stochastic equation driven by Brownian motions and Poisson random measures (it is actually not even known what such a stochastic equation in the general case should look like). We refer the reader to [Reference Mayerhofer, Pfaffel and Stelzer43] for some related results. In addition, we do not know if a comparison principle for such processes would be available.
$\mathbb{S}_{d}^{+}$
can be obtained as a strong solution to a certain stochastic equation driven by Brownian motions and Poisson random measures (it is actually not even known what such a stochastic equation in the general case should look like). We refer the reader to [Reference Mayerhofer, Pfaffel and Stelzer43] for some related results. In addition, we do not know if a comparison principle for such processes would be available.
For dimension ![]() $d=1$
it is known that (10) is not only sufficient, but also necessary for the convergence to some limiting distribution; see, e.g., [Reference Li39, Theorem 3.20 and Corollary 3.21]. To our knowledge, extensions of this result to higher-dimensional state spaces have not yet been obtained. In this context, we have the following partial result for subcritical affine processes on
$d=1$
it is known that (10) is not only sufficient, but also necessary for the convergence to some limiting distribution; see, e.g., [Reference Li39, Theorem 3.20 and Corollary 3.21]. To our knowledge, extensions of this result to higher-dimensional state spaces have not yet been obtained. In this context, we have the following partial result for subcritical affine processes on ![]() $\mathbb{S}_{d}^{+}$
.
$\mathbb{S}_{d}^{+}$
.
Proposition 2.1. Let ![]() $p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on
$p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
. Suppose that there exist
$(\alpha,b,B,m,\mu)$
. Suppose that there exist ![]() $x\in\mathbb{S}_{d}^{+}$
and
$x\in\mathbb{S}_{d}^{+}$
and ![]() $\pi\in\mathcal{P}(\mathbb{S}_{d}^{+})$
such that
$\pi\in\mathcal{P}(\mathbb{S}_{d}^{+})$
such that ![]() $p_{t}(x,\cdot)\to\pi$
weakly as
$p_{t}(x,\cdot)\to\pi$
weakly as ![]() $t\to\infty$
. If
$t\to\infty$
. If ![]() $\alpha=0$
and if there exists a constant
$\alpha=0$
and if there exists a constant ![]() $K>0$
satisfying
$K>0$
satisfying
then (10) holds.
In order to prove Proposition 2.1 we first establish in Section 5 a precise lower bound for ![]() $\psi(t,u)$
. Since in dimension
$\psi(t,u)$
. Since in dimension ![]() $d\geq2$
different components of the process interact through the drift B in a nontrivial manner on
$d\geq2$
different components of the process interact through the drift B in a nontrivial manner on ![]() $\mathbb{S}_{d}^{+}$
, the proof of the lower bound is deduced from the additional conditions
$\mathbb{S}_{d}^{+}$
, the proof of the lower bound is deduced from the additional conditions ![]() $\alpha=0$
and (14), which guarantee that these components are coupled in a well-behaved way. Let us remark that, in contrast to the proof of Theorem 2.3, the proof of Proposition 2.1 does not explicitly use the first moment condition for
$\alpha=0$
and (14), which guarantee that these components are coupled in a well-behaved way. Let us remark that, in contrast to the proof of Theorem 2.3, the proof of Proposition 2.1 does not explicitly use the first moment condition for ![]() $\mu$
. Indeed, it suffices to assume that
$\mu$
. Indeed, it suffices to assume that ![]() $\mu$
satisfies the condition
$\mu$
satisfies the condition ![]() $\int_{\mathbb{S}_d^+ \backslash \{0\}} ( 1 \wedge \| \xi \| ) \text{tr}(\mu)(\text{d}\xi) < \infty$
, which is weaker than (1), and, in addition, that the affine process is conservative.
$\int_{\mathbb{S}_d^+ \backslash \{0\}} ( 1 \wedge \| \xi \| ) \text{tr}(\mu)(\text{d}\xi) < \infty$
, which is weaker than (1), and, in addition, that the affine process is conservative.
We note that any linear map ![]() $B\,:\,\mathbb{S}_d\to\mathbb{S}_d$
with
$B\,:\,\mathbb{S}_d\to\mathbb{S}_d$
with ![]() $B(\mathbb{S}_d^+) \subset \mathbb{S}_d^+$
satisfies the condition (14) for each
$B(\mathbb{S}_d^+) \subset \mathbb{S}_d^+$
satisfies the condition (14) for each ![]() $K>0$
. As an example of such a map, let
$K>0$
. As an example of such a map, let ![]() $B(x)=\beta x\beta^{\top}$
for
$B(x)=\beta x\beta^{\top}$
for ![]() $x\in\mathbb{S}_d$
, where
$x\in\mathbb{S}_d$
, where ![]() $\beta$
is a real-valued
$\beta$
is a real-valued ![]() $d\times d$
matrix. Obviously, B defined in this way is admissible in the sense of Definition 2, and
$d\times d$
matrix. Obviously, B defined in this way is admissible in the sense of Definition 2, and ![]() $B(\mathbb{S}_d^+) \subset \mathbb{S}_d^+$
. However, such an example will not lead to a subcritical affine process. Just to understand this point, we can think of the simplest case when
$B(\mathbb{S}_d^+) \subset \mathbb{S}_d^+$
. However, such an example will not lead to a subcritical affine process. Just to understand this point, we can think of the simplest case when ![]() $d=1$
(although we always assume
$d=1$
(although we always assume ![]() $d\ge 2$
in the other parts of the paper):
$d\ge 2$
in the other parts of the paper): ![]() $B(x)=\beta^2 x$
and it is impossible for B to fulfill the subcritical condition (8).
$B(x)=\beta^2 x$
and it is impossible for B to fulfill the subcritical condition (8).
The simplest example of an admissible B that produces subcriticality and at the same time satisfies (14) is ![]() $B(x)=-x$
,
$B(x)=-x$
, ![]() $x\in S_{d}$
. However, there are also other examples like this one. For instance, consider
$x\in S_{d}$
. However, there are also other examples like this one. For instance, consider ![]() $d=2$
and the linear map B on
$d=2$
and the linear map B on ![]() $S_{2}$
defined by
$S_{2}$
defined by
 \begin{equation*}B\left(\left(\begin{array}{c@{\quad}c}x_{1} & x_{2}\\[3pt]
x_{2} & x_{3}\end{array}\right)\right)=\left(\begin{array}{c@{\quad}c}-x_{1} & -\kappa x_{2}\\[3pt]
-\kappa x_{2} & -x_{3}\end{array}\right)\!,\end{equation*}
\begin{equation*}B\left(\left(\begin{array}{c@{\quad}c}x_{1} & x_{2}\\[3pt]
x_{2} & x_{3}\end{array}\right)\right)=\left(\begin{array}{c@{\quad}c}-x_{1} & -\kappa x_{2}\\[3pt]
-\kappa x_{2} & -x_{3}\end{array}\right)\!,\end{equation*}
where ![]() $\kappa>1$
is a constant. First, such a B is admissible in the sense of Definition 2.1, since for
$\kappa>1$
is a constant. First, such a B is admissible in the sense of Definition 2.1, since for ![]() $u,x\in S_{2}^{+}$
with
$u,x\in S_{2}^{+}$
with ![]() $\left\langle x,u\right\rangle =0$
,
$\left\langle x,u\right\rangle =0$
,
 \begin{equation*}\left\langle B(x),u\right\rangle =-\kappa\left\langle x,u\right\rangle +(\kappa-1)\left\langle \left(\begin{array}{c@{\quad}c}x_{1} & 0\\[3pt]
0 & x_{3}\end{array}\right)\!,u\right\rangle =(\kappa-1)\left\langle \left(\begin{array}{c@{\quad}c}x_{1} & 0\\[3pt]
0 & x_{3}\end{array}\right)\!,u\right\rangle \ge0.\end{equation*}
\begin{equation*}\left\langle B(x),u\right\rangle =-\kappa\left\langle x,u\right\rangle +(\kappa-1)\left\langle \left(\begin{array}{c@{\quad}c}x_{1} & 0\\[3pt]
0 & x_{3}\end{array}\right)\!,u\right\rangle =(\kappa-1)\left\langle \left(\begin{array}{c@{\quad}c}x_{1} & 0\\[3pt]
0 & x_{3}\end{array}\right)\!,u\right\rangle \ge0.\end{equation*}
It is easy to see that the spectrum ![]() $\sigma(B)=\left\{ -1,-\kappa\right\} $
, so that we can choose a relatively small
$\sigma(B)=\left\{ -1,-\kappa\right\} $
, so that we can choose a relatively small ![]() $\mu$
to make
$\mu$
to make ![]() $\tilde{B}$
defined in (5) subcritical; moreover, (14) holds for
$\tilde{B}$
defined in (5) subcritical; moreover, (14) holds for ![]() $K=\kappa$
.
$K=\kappa$
.
We close this section with a useful moment result regarding the invariant distribution.
Corollary 2.1. Let ![]() $p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on
$p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
satisfying (6). Let
$(\alpha,b,B,m,\mu)$
satisfying (6). Let ![]() $\pi$
be the unique invariant distribution. Then
$\pi$
be the unique invariant distribution. Then
 \begin{equation*}\lim_{t\to\infty}\int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y)=\int_{\mathbb{S}_{d}^{+}}y\pi(\text{d}y)= -\widetilde{B}^{-1}\left( b + \int_{\mathbb{S}_d^+ \backslash \{0\}} \xi m(\text{d}\xi) \right)\!.\end{equation*}
\begin{equation*}\lim_{t\to\infty}\int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y)=\int_{\mathbb{S}_{d}^{+}}y\pi(\text{d}y)= -\widetilde{B}^{-1}\left( b + \int_{\mathbb{S}_d^+ \backslash \{0\}} \xi m(\text{d}\xi) \right)\!.\end{equation*}
2.3. Study of the convergence rate
Consider a subcritical affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
and let
$(\alpha,b,B,m,\mu)$
and let ![]() $\delta$
be defined by (9). In particular,
$\delta$
be defined by (9). In particular, ![]() $\delta$
is strictly positive, and we will see that it appears naturally in the convergence rate towards the invariant distribution. In order to measure this rate of convergence we introduce
$\delta$
is strictly positive, and we will see that it appears naturally in the convergence rate towards the invariant distribution. In order to measure this rate of convergence we introduce
 \begin{equation*}d_{L}(\eta,\nu)\,:\!=\sup_{u\in\mathbb{S}_{d}^{+}\setminus\{0\}}\frac{1}{\Vert u\Vert}\left|\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,x\rangle}\eta(\text{d}x)-\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,x\rangle}\nu(\text{d}x)\right|,\quad\eta,\thinspace\nu\in\mathcal{P}(\mathbb{S}_{d}^{+}).\end{equation*}
\begin{equation*}d_{L}(\eta,\nu)\,:\!=\sup_{u\in\mathbb{S}_{d}^{+}\setminus\{0\}}\frac{1}{\Vert u\Vert}\left|\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,x\rangle}\eta(\text{d}x)-\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,x\rangle}\nu(\text{d}x)\right|,\quad\eta,\thinspace\nu\in\mathcal{P}(\mathbb{S}_{d}^{+}).\end{equation*}
Note that this supremum is not necessarily finite. However, it is finite for elements from
 \begin{equation*}\mathcal{P}_{1}(\mathbb{S}_{d}^{+})=\left\lbrace \varrho\in\mathcal{P}(\mathbb{S}_{d}^{+})\thinspace:\thinspace\int_{\mathbb{S}_{d}^{+}}\Vert x\Vert\varrho(\text{d}x)<\infty\right\rbrace,\end{equation*}
\begin{equation*}\mathcal{P}_{1}(\mathbb{S}_{d}^{+})=\left\lbrace \varrho\in\mathcal{P}(\mathbb{S}_{d}^{+})\thinspace:\thinspace\int_{\mathbb{S}_{d}^{+}}\Vert x\Vert\varrho(\text{d}x)<\infty\right\rbrace,\end{equation*}
which essentially follows from
 \begin{align} \left|\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,x\rangle}\eta(\text{d}x)-\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,x\rangle}\nu(\text{d}x)\right| &= \left|\int_{\mathbb{S}_{d}^{+} \times \mathbb{S}_d^+}\left(\text{e}^{-\langle u,x\rangle} - \text{e}^{- \langle u,y \rangle} \right) \eta(\text{d}x)\nu(\text{d}y) \right|\\
&\leq \| u \| \int_{\mathbb{S}_d^+ \times \mathbb{S}_d^+} \| x -y\| \eta(\text{d}x) \nu(\text{d}y)\nonumber \\
& \leq \| u \| \left(\int_{\mathbb{S}_d^+} \| x \| \eta(\text{d}x)+ \int_{\mathbb{S}_d^+} \| y\| \nu(\text{d}y)\right)\!.\nonumber
\end{align}
\begin{align} \left|\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,x\rangle}\eta(\text{d}x)-\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,x\rangle}\nu(\text{d}x)\right| &= \left|\int_{\mathbb{S}_{d}^{+} \times \mathbb{S}_d^+}\left(\text{e}^{-\langle u,x\rangle} - \text{e}^{- \langle u,y \rangle} \right) \eta(\text{d}x)\nu(\text{d}y) \right|\\
&\leq \| u \| \int_{\mathbb{S}_d^+ \times \mathbb{S}_d^+} \| x -y\| \eta(\text{d}x) \nu(\text{d}y)\nonumber \\
& \leq \| u \| \left(\int_{\mathbb{S}_d^+} \| x \| \eta(\text{d}x)+ \int_{\mathbb{S}_d^+} \| y\| \nu(\text{d}y)\right)\!.\nonumber
\end{align}
It is easy to see that ![]() $d_L$
is a metric on
$d_L$
is a metric on ![]() $\mathcal{P}_1(\mathbb{S}_{d}^{+})$
; moreover,
$\mathcal{P}_1(\mathbb{S}_{d}^{+})$
; moreover, ![]() $\big(\mathcal{P}_1(\mathbb{S}_{d}^{+}),d_L\big)$
is complete. Using well-known properties of Laplace transforms, it can be shown that convergence with respect to
$\big(\mathcal{P}_1(\mathbb{S}_{d}^{+}),d_L\big)$
is complete. Using well-known properties of Laplace transforms, it can be shown that convergence with respect to ![]() $d_{L}$
implies weak convergence. The next result provides an exponential rate in
$d_{L}$
implies weak convergence. The next result provides an exponential rate in ![]() $d_{L}$
distance.
$d_{L}$
distance.
Theorem 2.4. Let ![]() $p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on
$p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
. Suppose that (10) holds and denote by
$(\alpha,b,B,m,\mu)$
. Suppose that (10) holds and denote by ![]() $\pi$
the unique invariant distribution. Then there exists a constant
$\pi$
the unique invariant distribution. Then there exists a constant ![]() $C>0$
such that
$C>0$
such that
The proof of this result is given in Section 7. Although under the given conditions ![]() $p_t(x,\cdot)$
and
$p_t(x,\cdot)$
and ![]() $\pi$
do not necessarily belong to
$\pi$
do not necessarily belong to ![]() $\mathcal{P}_1(\mathbb{S}_d^+)$
, the proof of (16) reveals that
$\mathcal{P}_1(\mathbb{S}_d^+)$
, the proof of (16) reveals that ![]() $d_L(p_t(x,\cdot), \pi)$
is well-defined. Let us mention that the main purpose of this work is dedicated to Theorem 2.3. The above convergence rate in the
$d_L(p_t(x,\cdot), \pi)$
is well-defined. Let us mention that the main purpose of this work is dedicated to Theorem 2.3. The above convergence rate in the ![]() $d_L$
distance is a simple byproduct of the estimates derived in the process of proving Theorem 2.3.
$d_L$
distance is a simple byproduct of the estimates derived in the process of proving Theorem 2.3.
We turn to investigate the convergence rate from the affine transition kernel to the invariant distribution in the Wasserstein-1-distance introduced below. Given ![]() $\varrho,\thinspace\widetilde{\varrho}\in\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
, a coupling H of
$\varrho,\thinspace\widetilde{\varrho}\in\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
, a coupling H of ![]() $(\varrho,\widetilde{\varrho})$
is a Borel probability measure on
$(\varrho,\widetilde{\varrho})$
is a Borel probability measure on ![]() $\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}$
which has marginals
$\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}$
which has marginals ![]() $\varrho$
and
$\varrho$
and ![]() $\widetilde{\varrho}$
, respectively. We denote by
$\widetilde{\varrho}$
, respectively. We denote by ![]() $\mathcal{H}(\varrho,\widetilde{\varrho})$
the collection of all such couplings. We define the Wasserstein distance on
$\mathcal{H}(\varrho,\widetilde{\varrho})$
the collection of all such couplings. We define the Wasserstein distance on ![]() $\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
by
$\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
by
 \begin{equation*}W_{1}\left(\varrho,\widetilde{\varrho}\right)=\inf\left\lbrace \int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}\Vert x-y\Vert H\left(\text{d}x,\text{d}y\right)\thinspace:\thinspace H\in\mathcal{H}\left(\varrho,\widetilde{\varrho}\right)\right\rbrace .\end{equation*}
\begin{equation*}W_{1}\left(\varrho,\widetilde{\varrho}\right)=\inf\left\lbrace \int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}\Vert x-y\Vert H\left(\text{d}x,\text{d}y\right)\thinspace:\thinspace H\in\mathcal{H}\left(\varrho,\widetilde{\varrho}\right)\right\rbrace .\end{equation*}
Since ![]() $\varrho$
and
$\varrho$
and ![]() $\widetilde{\varrho}$
belong to
$\widetilde{\varrho}$
belong to ![]() $\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
, it holds that
$\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
, it holds that ![]() $W_{1}(\varrho,\widetilde{\varrho})$
is finite. According to [Reference Villani48, Theorem 6.16], we have that
$W_{1}(\varrho,\widetilde{\varrho})$
is finite. According to [Reference Villani48, Theorem 6.16], we have that ![]() $(\mathcal{P}_1(\mathbb{S}_{d}^{+}),W_{1})$
is a complete separable metric space. Note that, by an argument similar to (15), one easily finds that
$(\mathcal{P}_1(\mathbb{S}_{d}^{+}),W_{1})$
is a complete separable metric space. Note that, by an argument similar to (15), one easily finds that ![]() $d_{L}(\eta,\nu) \leq W_1(\eta,\nu)$
for all
$d_{L}(\eta,\nu) \leq W_1(\eta,\nu)$
for all ![]() $\eta,\nu\in \mathcal{P}_1(\mathbb{S}_{d}^{+})$
. Exponential ergodicity in different Wasserstein distances for affine processes on the canonical state space
$\eta,\nu\in \mathcal{P}_1(\mathbb{S}_{d}^{+})$
. Exponential ergodicity in different Wasserstein distances for affine processes on the canonical state space ![]() $\mathbb{R}_{\geq0}^{m}\times\mathbb{R}^{n}$
was very recently studied in [Reference Friesen, Jin and Rüdiger19]. Below we provide a corresponding result for affine processes on
$\mathbb{R}_{\geq0}^{m}\times\mathbb{R}^{n}$
was very recently studied in [Reference Friesen, Jin and Rüdiger19]. Below we provide a corresponding result for affine processes on ![]() $\mathbb{S}_{d}^{+}$
.
$\mathbb{S}_{d}^{+}$
.
Theorem 2.5. Let ![]() $p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on
$p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
satisfying (6). If
$(\alpha,b,B,m,\mu)$
satisfying (6). If ![]() $\alpha=0$
, then
$\alpha=0$
, then
 \begin{equation}W_{1}\left(p_{t}(x,\cdot),\pi\right)\leq\sqrt{d}Me^{-\delta t}\left(\|x\|+\int_{\mathbb{S}_{d}^{+}}\|y\|\pi(\text{d}y)\right)\!,\quad t\geq0,\ \ x\in\mathbb{S}_{d}^{+}.\end{equation}
\begin{equation}W_{1}\left(p_{t}(x,\cdot),\pi\right)\leq\sqrt{d}Me^{-\delta t}\left(\|x\|+\int_{\mathbb{S}_{d}^{+}}\|y\|\pi(\text{d}y)\right)\!,\quad t\geq0,\ \ x\in\mathbb{S}_{d}^{+}.\end{equation}
The proof of Theorem 2.5, which is given in Section 8, largely follows some ideas of [Reference Friesen, Jin and Rüdiger19]. In contrast to the latter work, for the study of affine processes on ![]() $\mathbb{S}_{d}^{+}$
we encounter similar difficulties as in the proof of Theorem 2.3. Namely, the affine property allows us only to use the convolution argument (12) when
$\mathbb{S}_{d}^{+}$
we encounter similar difficulties as in the proof of Theorem 2.3. Namely, the affine property allows us only to use the convolution argument (12) when ![]() $\alpha = 0$
. Moreover, since it is still an open problem whether each affine process on
$\alpha = 0$
. Moreover, since it is still an open problem whether each affine process on ![]() $\mathbb{S}_{d}^{+}$
can be obtained as a strong solution to a certain stochastic equation driven by Brownian motions and Poisson random measures, we are not able to improve our Theorem 2.5 to other variants of Wasserstein distances as used in [Reference Friesen, Jin and Rüdiger19].
$\mathbb{S}_{d}^{+}$
can be obtained as a strong solution to a certain stochastic equation driven by Brownian motions and Poisson random measures, we are not able to improve our Theorem 2.5 to other variants of Wasserstein distances as used in [Reference Friesen, Jin and Rüdiger19].
3. Applications and examples
Let ![]() $(W_{t})_{t\geq0}$
be a
$(W_{t})_{t\geq0}$
be a ![]() $d\times d$
matrix of independent standard Brownian motions. Denote by
$d\times d$
matrix of independent standard Brownian motions. Denote by ![]() $(J_{t})_{t\geq0}$
an
$(J_{t})_{t\geq0}$
an ![]() $\mathbb{S}_{d}^{+}$
-valued Lévy subordinator with Lévy measure m. Suppose that these two processes are independent of each other. Following [Reference Mayerhofer, Pfaffel and Stelzer43], the stochastic differential equation
$\mathbb{S}_{d}^{+}$
-valued Lévy subordinator with Lévy measure m. Suppose that these two processes are independent of each other. Following [Reference Mayerhofer, Pfaffel and Stelzer43], the stochastic differential equation
 \begin{equation}\begin{cases}\text{d}X_{t}=\left(b+\beta X_{t}+X_{t}\beta^{\top}\right)\text{d}t+\sqrt{X_{t}}\text{d}W_{t}\Sigma+\Sigma^{\top}\text{d}W_{t}^{\top}\sqrt{X_{t}}+\text{d}J_{t}, & t\geq0,\\[5pt]
X_{0}=x\in\mathbb{S}_{d}^{+},\end{cases}\end{equation}
\begin{equation}\begin{cases}\text{d}X_{t}=\left(b+\beta X_{t}+X_{t}\beta^{\top}\right)\text{d}t+\sqrt{X_{t}}\text{d}W_{t}\Sigma+\Sigma^{\top}\text{d}W_{t}^{\top}\sqrt{X_{t}}+\text{d}J_{t}, & t\geq0,\\[5pt]
X_{0}=x\in\mathbb{S}_{d}^{+},\end{cases}\end{equation}
has a unique weak solution if ![]() $b\succeq(d-1)\Sigma^{\top}\Sigma$
and
$b\succeq(d-1)\Sigma^{\top}\Sigma$
and ![]() $\Sigma,\thinspace\beta$
are real-valued
$\Sigma,\thinspace\beta$
are real-valued ![]() $d\times d$
matrices. Moreover, according to [Reference Mayerhofer, Pfaffel and Stelzer43, Corollary 3.2], if
$d\times d$
matrices. Moreover, according to [Reference Mayerhofer, Pfaffel and Stelzer43, Corollary 3.2], if ![]() $b\succeq(d+1)\Sigma^{\top}\Sigma$
and
$b\succeq(d+1)\Sigma^{\top}\Sigma$
and ![]() $x \in \mathbb{S}_d^{++}$
, then there also exists an
$x \in \mathbb{S}_d^{++}$
, then there also exists an ![]() $\mathbb{S}_d^{++}$
-valued strong solution. The corresponding Markov process
$\mathbb{S}_d^{++}$
-valued strong solution. The corresponding Markov process ![]() $X=(X_{t})_{t\geq0}$
is a conservative affine process with admissible parameters
$X=(X_{t})_{t\geq0}$
is a conservative affine process with admissible parameters ![]() $(\alpha,b,B,m,0)$
with diffusion
$(\alpha,b,B,m,0)$
with diffusion ![]() $\alpha=\Sigma^{\top}\Sigma$
and linear drift
$\alpha=\Sigma^{\top}\Sigma$
and linear drift ![]() $B(x)=\beta x+x\beta^{\top}$
. The functions F and R are given by
$B(x)=\beta x+x\beta^{\top}$
. The functions F and R are given by
and
The generalized Riccati equations are now given by
 \begin{align*}\partial_{t}\phi(t,u) & =\langle b,\psi(t,u)\rangle+\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(1-\text{e}^{-\langle\psi(t,u),\xi\rangle})\,m(\text{d}\xi),\\[4pt]
\partial_{t}\psi(t,u) & =-2\psi(t,u)\alpha\psi(t,u)+\psi(t,u)\beta+\beta^{\top}\psi(t,u),\end{align*}
\begin{align*}\partial_{t}\phi(t,u) & =\langle b,\psi(t,u)\rangle+\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(1-\text{e}^{-\langle\psi(t,u),\xi\rangle})\,m(\text{d}\xi),\\[4pt]
\partial_{t}\psi(t,u) & =-2\psi(t,u)\alpha\psi(t,u)+\psi(t,u)\beta+\beta^{\top}\psi(t,u),\end{align*}
with initial conditions ![]() $\phi(0,u)=0$
and
$\phi(0,u)=0$
and ![]() $\psi(0,u)=u$
. Let
$\psi(0,u)=u$
. Let ![]() $\sigma_{t}^{\beta}\,:\,\mathbb{S}_{d}^{+}\to\mathbb{S}_{d}^{+}$
be given by
$\sigma_{t}^{\beta}\,:\,\mathbb{S}_{d}^{+}\to\mathbb{S}_{d}^{+}$
be given by
According to [Reference Mayerhofer42, Section 4.3], we have
 \begin{align*}\phi(t,u) & =\langle b,\int_{0}^{t}\psi(s,u)\text{d}s \rangle +\int_{0}^{t}\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(1-\text{e}^{-\langle\psi(s,u),\xi\rangle})\,m(\text{d}\xi)\text{d}s,\\[3pt]
\psi(t,u) & =\text{e}^{\beta^{\top}t}(u^{-1}+\sigma_{t}^{\beta}(\alpha))^{-1}\text{e}^{\beta t}.\end{align*}
\begin{align*}\phi(t,u) & =\langle b,\int_{0}^{t}\psi(s,u)\text{d}s \rangle +\int_{0}^{t}\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(1-\text{e}^{-\langle\psi(s,u),\xi\rangle})\,m(\text{d}\xi)\text{d}s,\\[3pt]
\psi(t,u) & =\text{e}^{\beta^{\top}t}(u^{-1}+\sigma_{t}^{\beta}(\alpha))^{-1}\text{e}^{\beta t}.\end{align*}
Since ![]() $\widetilde{B}(x)=B(x)$
, Remark 2.2 implies that X is subcritical, provided
$\widetilde{B}(x)=B(x)$
, Remark 2.2 implies that X is subcritical, provided ![]() $\beta$
has only eigenvalues with negative real parts. If the Lévy measure m satisfies (10), then Theorem 2.3 implies existence, uniqueness, and convergence to the invariant distribution
$\beta$
has only eigenvalues with negative real parts. If the Lévy measure m satisfies (10), then Theorem 2.3 implies existence, uniqueness, and convergence to the invariant distribution ![]() $\pi$
whose Laplace transform satisfies
$\pi$
whose Laplace transform satisfies
Moreover, if in addition ![]() $\int_{\lbrace\Vert\xi\Vert\geq1\rbrace}\Vert\xi\Vert m(\text{d}\xi)<\infty$
, then we infer from Corollary 2.1 that
$\int_{\lbrace\Vert\xi\Vert\geq1\rbrace}\Vert\xi\Vert m(\text{d}\xi)<\infty$
, then we infer from Corollary 2.1 that
 \begin{equation*}\lim_{t\to\infty}\mathbb{E}_{x}\!\left[X_{t}\right]=\int_{0}^{\infty}\text{e}^{s\beta^{\top}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\text{e}^{s\beta}\text{d}s=\int_{\mathbb{S}_{d}^{+}}y\pi(\text{d}y).\end{equation*}
\begin{equation*}\lim_{t\to\infty}\mathbb{E}_{x}\!\left[X_{t}\right]=\int_{0}^{\infty}\text{e}^{s\beta^{\top}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\text{e}^{s\beta}\text{d}s=\int_{\mathbb{S}_{d}^{+}}y\pi(\text{d}y).\end{equation*}
We end this section by considering the following examples.
Example 3.1. (The matrix-variate basic affine jump-diffusion and Wishart process.) Take ![]() $b=2k\Sigma^{\top}\Sigma$
with
$b=2k\Sigma^{\top}\Sigma$
with ![]() $k\geq d-1$
in (18). This process is called matrix-variate basic affine jump-diffusion on
$k\geq d-1$
in (18). This process is called matrix-variate basic affine jump-diffusion on ![]() $\mathbb{S}_{d}^{+}$
(MBAJD for short); see [Reference Mayerhofer42, Section 4]. Following [Reference Mayerhofer42, Section 4.3],
$\mathbb{S}_{d}^{+}$
(MBAJD for short); see [Reference Mayerhofer42, Section 4]. Following [Reference Mayerhofer42, Section 4.3], ![]() $\phi(t,u)$
is precisely given by
$\phi(t,u)$
is precisely given by
and Theorem 2.3 implies that the unique invariant distribution is given by
 \begin{align*}\int_{0}^{\infty}\text{e}^{-\langle u,x\rangle}\pi\left(\text{d}x\right) & =\left(\det\left(\mathbbm{1}+\sigma_{\infty}^{\beta}(\alpha)u\right)\right)^{-k}\exp\!\left({-}\int_{0}^{\infty}\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(1-\text{e}^{-\langle\psi(s,u),\xi\rangle})\,m(\text{d}\xi)\text{d}s\right)\!,\end{align*}
\begin{align*}\int_{0}^{\infty}\text{e}^{-\langle u,x\rangle}\pi\left(\text{d}x\right) & =\left(\det\left(\mathbbm{1}+\sigma_{\infty}^{\beta}(\alpha)u\right)\right)^{-k}\exp\!\left({-}\int_{0}^{\infty}\int_{\mathbb{S}_{d}^{+}\backslash\{0\}}(1-\text{e}^{-\langle\psi(s,u),\xi\rangle})\,m(\text{d}\xi)\text{d}s\right)\!,\end{align*}
where ![]() $\sigma_{\infty}^{\beta}(\alpha)=\int_{0}^{\infty}\exp(s\beta)\alpha\exp(s\beta^{\top})\text{d}s$
.
$\sigma_{\infty}^{\beta}(\alpha)=\int_{0}^{\infty}\exp(s\beta)\alpha\exp(s\beta^{\top})\text{d}s$
.
The well-known Wishart process, introduced by Bru [Reference Bru10], is a special case of the MBAJD with ![]() $m=0$
. Existence of a unique distribution was then obtained in [Reference Alfonsi, Kebaier and Rey1, Lemma C.1]. In this case
$m=0$
. Existence of a unique distribution was then obtained in [Reference Alfonsi, Kebaier and Rey1, Lemma C.1]. In this case ![]() $\pi$
is a Wishart distribution with shape parameter k and scale parameter
$\pi$
is a Wishart distribution with shape parameter k and scale parameter ![]() $\sigma_{\infty}^{\beta}(\alpha)$
.
$\sigma_{\infty}^{\beta}(\alpha)$
.
Example 3.2. (Matrix-variate Ornstein–Uhlenbeck-type processes.) For ![]() $b=0$
and
$b=0$
and ![]() $\Sigma=0$
, we call the solutions to the stochastic differential equation (18) matrix-variate Ornstein–Uhlenbeck-type (OU-type) processes; see [Reference Barndorff-Nielsen and Stelzer7]. Properties of the stationary matrix-variate OU-type processes were investigated in [Reference Pigorsch and Stelzer45]. Provided that
$\Sigma=0$
, we call the solutions to the stochastic differential equation (18) matrix-variate Ornstein–Uhlenbeck-type (OU-type) processes; see [Reference Barndorff-Nielsen and Stelzer7]. Properties of the stationary matrix-variate OU-type processes were investigated in [Reference Pigorsch and Stelzer45]. Provided that
Theorem 2.5 implies that the matrix-variate OU-type process is also exponentially ergodic in the Wasserstein-1-distance.
Note that in [Reference Masuda41] ergodicity in total variation was studied for matrix-variate OU-type processes. The proof crucially relies on particular properties of Ornstein–Uhlenbeck processes and hence cannot be extended to cases where the parameter ![]() $\mu$
for state-dependent jumps does not vanish. In contrast, our method would also apply for non-vanishing
$\mu$
for state-dependent jumps does not vanish. In contrast, our method would also apply for non-vanishing ![]() $\mu$
.
$\mu$
.
4. Proof of Theorem 2.2
In this section we study the first moment of a conservative affine process on ![]() $\mathbb{S}_{d}^{+}$
. In particular, we prove Theorem 2.2. Essential to the proof is the space-differentiability of the functions F and R as well as of
$\mathbb{S}_{d}^{+}$
. In particular, we prove Theorem 2.2. Essential to the proof is the space-differentiability of the functions F and R as well as of ![]() $\phi$
and
$\phi$
and ![]() $\psi$
. To simplify the notation we introduce
$\psi$
. To simplify the notation we introduce ![]() $L(\mathbb{S}_{d},\mathbb{S}_{d})$
as the space of all linear operators
$L(\mathbb{S}_{d},\mathbb{S}_{d})$
as the space of all linear operators ![]() $\mathbb{S}_{d}\to\mathbb{S}_{d}$
, and similarly
$\mathbb{S}_{d}\to\mathbb{S}_{d}$
, and similarly ![]() $L(\mathbb{S}_{d},\mathbb{R})$
stands for the space of all linear functionals
$L(\mathbb{S}_{d},\mathbb{R})$
stands for the space of all linear functionals ![]() $\mathbb{S}_{d}\to\mathbb{R}$
. For a function
$\mathbb{S}_{d}\to\mathbb{R}$
. For a function ![]() $G\,:\,\mathbb{S}_{d}\to\mathbb{S}_{d}$
we denote its derivative at
$G\,:\,\mathbb{S}_{d}\to\mathbb{S}_{d}$
we denote its derivative at ![]() $u\in\mathbb{S}_{d}$
, if it exists, by
$u\in\mathbb{S}_{d}$
, if it exists, by ![]() $DG(u)\in L(\mathbb{S}_{d},\mathbb{S}_{d})$
. Similarly, we denote the derivative of
$DG(u)\in L(\mathbb{S}_{d},\mathbb{S}_{d})$
. Similarly, we denote the derivative of ![]() $H\,:\,\mathbb{S}_{d}\to\mathbb{R}$
by
$H\,:\,\mathbb{S}_{d}\to\mathbb{R}$
by ![]() $DH(u)\in L(\mathbb{S}_{d},\mathbb{R})$
. We equip
$DH(u)\in L(\mathbb{S}_{d},\mathbb{R})$
. We equip ![]() $L(\mathbb{S}_{d},\mathbb{S}_{d})$
and
$L(\mathbb{S}_{d},\mathbb{S}_{d})$
and ![]() $L(\mathbb{S}_{d},\mathbb{R})$
with the corresponding norms
$L(\mathbb{S}_{d},\mathbb{R})$
with the corresponding norms
Let F and R be as in Theorem 2.1 According to [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Lemma 5.1] the function R is analytic on ![]() $\mathbb{S}_{d}^{++}$
. Below we study the differentiability of F and R on the entire cone
$\mathbb{S}_{d}^{++}$
. Below we study the differentiability of F and R on the entire cone ![]() $\mathbb{S}_{d}^{+}$
.
$\mathbb{S}_{d}^{+}$
.
We first give a lemma that slightly extends [Reference Mayerhofer42, Lemma 3.3].
Lemma 4.1. Let g be a measurable function on ![]() $\mathbb{S}_{d}^{+}$
with
$\mathbb{S}_{d}^{+}$
with ![]() $\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi)<\infty$
. Then
$\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi)<\infty$
. Then ![]() $\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g(\xi)\mu(\text{d}\xi)$
is finite and
$\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g(\xi)\mu(\text{d}\xi)$
is finite and
 \begin{equation*}\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g(\xi)\mu(\text{d}\xi)\right\Vert \le\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi).\end{equation*}
\begin{equation*}\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g(\xi)\mu(\text{d}\xi)\right\Vert \le\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi).\end{equation*}
Proof. Let ![]() $\mu=(\mu_{ij})$
and
$\mu=(\mu_{ij})$
and ![]() $\mu_{ij}=\mu_{ij}^{+}-\mu_{ij}^{-}$
be the Jordan decomposition of
$\mu_{ij}=\mu_{ij}^{+}-\mu_{ij}^{-}$
be the Jordan decomposition of ![]() $\mu_{ij}$
. Suppose
$\mu_{ij}$
. Suppose ![]() $\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi)<\infty$
. Then [Reference Mayerhofer42, Lemma 3.3] implies that
$\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi)<\infty$
. Then [Reference Mayerhofer42, Lemma 3.3] implies that ![]() $\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}|g(\xi)|\mu(\text{d}\xi)$
is finite and
$\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}|g(\xi)|\mu(\text{d}\xi)$
is finite and
 \begin{equation*}\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}|g(\xi)|\mu(\text{d}\xi)\right\Vert \le\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi).\end{equation*}
\begin{equation*}\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}|g(\xi)|\mu(\text{d}\xi)\right\Vert \le\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi).\end{equation*}
Since the ijth entry of ![]() $\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}|g(\xi)|\mu(\text{d}\xi)$
is given by
$\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}|g(\xi)|\mu(\text{d}\xi)$
is given by
which is finite, we must have
So ![]() $\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g(\xi)\mu(\text{d}\xi)$
is finite. Again by [Reference Mayerhofer42, Lemma 3.3],
$\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g(\xi)\mu(\text{d}\xi)$
is finite. Again by [Reference Mayerhofer42, Lemma 3.3],
 \begin{align*}\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g(\xi)\mu(\text{d}\xi)\right\Vert & =\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{+}(\xi)\mu(\text{d}\xi)-\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{-}(\xi)\mu(\text{d}\xi)\right\Vert \\[3pt]
& \le\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{+}(\xi)\mu(\text{d}\xi)\right\Vert +\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{-}(\xi)\mu(\text{d}\xi)\right\Vert \\[3pt]
& \le\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{+}(\xi)\text{tr}(\mu)(\text{d}\xi)+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{-}(\xi)\text{tr}(\mu)(\text{d}\xi)\\[3pt]
& \le\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi).\end{align*}
\begin{align*}\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g(\xi)\mu(\text{d}\xi)\right\Vert & =\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{+}(\xi)\mu(\text{d}\xi)-\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{-}(\xi)\mu(\text{d}\xi)\right\Vert \\[3pt]
& \le\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{+}(\xi)\mu(\text{d}\xi)\right\Vert +\left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{-}(\xi)\mu(\text{d}\xi)\right\Vert \\[3pt]
& \le\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{+}(\xi)\text{tr}(\mu)(\text{d}\xi)+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}g^{-}(\xi)\text{tr}(\mu)(\text{d}\xi)\\[3pt]
& \le\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert g(\xi)\right\vert \text{tr}(\mu)(\text{d}\xi).\end{align*}
The lemma is proved.
Lemma 4.2. The following statements hold:
(a) For
 $u\in\mathbb{S}_{d}^{++}$
,
$u\in\mathbb{S}_{d}^{++}$
,  $h\in\mathbb{S}_{d}$
, we have
(19)Moreover, through (19), DR(u) is continuously extended to
$h\in\mathbb{S}_{d}$
, we have
(19)Moreover, through (19), DR(u) is continuously extended to \begin{equation}DR(u)(h)=-2\left(u\alpha h+h\alpha u\right)+B^{\top}(h)+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\langle h,\xi\rangle\text{e}^{-\langle u,\xi\rangle}\mu(\text{d}\xi).\end{equation}
\begin{equation}DR(u)(h)=-2\left(u\alpha h+h\alpha u\right)+B^{\top}(h)+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\langle h,\xi\rangle\text{e}^{-\langle u,\xi\rangle}\mu(\text{d}\xi).\end{equation}
 $u\in\mathbb{S}_{d}^{+}$
. In particular,
$u\in\mathbb{S}_{d}^{+}$
. In particular,  $R\in C^{1}(\mathbb{S}_{d}^{+})$
and (19) holds true for all
$R\in C^{1}(\mathbb{S}_{d}^{+})$
and (19) holds true for all  $u\in\mathbb{S}_{d}^{+},h\in\mathbb{S}_{d}$
.
$u\in\mathbb{S}_{d}^{+},h\in\mathbb{S}_{d}$
.(b) If (6) is satisfied, then for
 $u\in\mathbb{S}_{d}^{++}$
,
$u\in\mathbb{S}_{d}^{++}$
,  $h\in\mathbb{S}_{d}$
,
(20)Moreover, through (20), DF(u) is continuously extended to
$h\in\mathbb{S}_{d}$
,
(20)Moreover, through (20), DF(u) is continuously extended to \begin{equation}DF(u)(h)=\langle b,h\rangle+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\langle h,\xi\rangle\text{e}^{-\langle u,\xi\rangle}m(\text{d}\xi).\end{equation}
\begin{equation}DF(u)(h)=\langle b,h\rangle+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\langle h,\xi\rangle\text{e}^{-\langle u,\xi\rangle}m(\text{d}\xi).\end{equation}
 $u\in\mathbb{S}_{d}^{+}$
. In particular,
$u\in\mathbb{S}_{d}^{+}$
. In particular,  $F\in C^{1}(\mathbb{S}_{d}^{+})$
and (20) holds true for all
$F\in C^{1}(\mathbb{S}_{d}^{+})$
and (20) holds true for all  $u\in\mathbb{S}_{d}^{+},h\in\mathbb{S}_{d}$
.
$u\in\mathbb{S}_{d}^{+},h\in\mathbb{S}_{d}$
.
Proof. (a) Let ![]() $u\in\mathbb{S}_{d}^{++}$
. Consider
$u\in\mathbb{S}_{d}^{++}$
. Consider ![]() $h\in\mathbb{S}_{d}$
with sufficiently small
$h\in\mathbb{S}_{d}$
with sufficiently small ![]() $\|h\|$
such that
$\|h\|$
such that ![]() $u+h\in\mathbb{S}_{d}^{+}$
. An easy calculation shows that
$u+h\in\mathbb{S}_{d}^{+}$
. An easy calculation shows that
where
Let us prove that ![]() $\lim_{0\not=\Vert h\Vert\to0}\Vert r(u,h)\Vert/\Vert h\Vert=0$
. Assume
$\lim_{0\not=\Vert h\Vert\to0}\Vert r(u,h)\Vert/\Vert h\Vert=0$
. Assume ![]() $\Vert h\Vert\not=0$
. First, note that
$\Vert h\Vert\not=0$
. First, note that
Let ![]() $M>0$
. For
$M>0$
. For ![]() $\Vert\xi\Vert\leq M$
, we have
$\Vert\xi\Vert\leq M$
, we have
 \begin{align}\left|\text{e}^{-\langle u,\xi\rangle}\left(1-\text{e}^{-\langle h,\xi\rangle}-\langle h,\xi\rangle\right)\right| & =\left|\langle h,\xi\rangle\left(\int_{0}^{1}\text{e}^{-\langle u+sh,\xi\rangle}\text{d}s-\text{e}^{-\langle u,\xi\rangle}\right)\right|\nonumber \\[4pt]
& =\left|\langle h,\xi\rangle\right|\cdot\left|\int_{0}^{1}\left(\text{e}^{-\langle u+sh,\xi\rangle}-\text{e}^{-\langle u,\xi\rangle}\right)\text{d}s\right|\nonumber \\[4pt]
& \le\left|\langle h,\xi\rangle\right|^{2},\end{align}
\begin{align}\left|\text{e}^{-\langle u,\xi\rangle}\left(1-\text{e}^{-\langle h,\xi\rangle}-\langle h,\xi\rangle\right)\right| & =\left|\langle h,\xi\rangle\left(\int_{0}^{1}\text{e}^{-\langle u+sh,\xi\rangle}\text{d}s-\text{e}^{-\langle u,\xi\rangle}\right)\right|\nonumber \\[4pt]
& =\left|\langle h,\xi\rangle\right|\cdot\left|\int_{0}^{1}\left(\text{e}^{-\langle u+sh,\xi\rangle}-\text{e}^{-\langle u,\xi\rangle}\right)\text{d}s\right|\nonumber \\[4pt]
& \le\left|\langle h,\xi\rangle\right|^{2},\end{align}
where we used the fact that ![]() $\langle u+sh,\xi\rangle\geq0$
and the Lipschitz continuity of
$\langle u+sh,\xi\rangle\geq0$
and the Lipschitz continuity of ![]() $[0,\infty)\in x\mapsto\exp({-}x)$
to get the last inequality. Similarly, for
$[0,\infty)\in x\mapsto\exp({-}x)$
to get the last inequality. Similarly, for ![]() $\Vert\xi\Vert>M$
,
$\Vert\xi\Vert>M$
,
Combining (21) and (22) and applying Lemma 4.1, we get
 \begin{align*}\frac{1}{\Vert h\Vert} & \left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\text{e}^{-\langle u,\xi\rangle}\left(1-\text{e}^{-\langle h,\xi\rangle}-\langle h,\xi\rangle\right)\mu(\text{d}\xi)\right\Vert \\[4pt]
& \quad\leq\frac{1}{\Vert h\Vert}\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert \text{e}^{-\langle u,\xi\rangle}\left(1-\text{e}^{-\langle h,\xi\rangle}-\langle h,\xi\rangle\right)\right\vert \text{tr}(\mu)(\text{d}\xi)\\[4pt]
& \quad\leq\Vert h\Vert\int_{\lbrace\Vert\xi\Vert\leq M\rbrace}\Vert\xi\Vert^{2}\text{tr}(\mu)(\text{d}\xi)+2\int_{\lbrace\Vert\xi\Vert>M\rbrace}\Vert\xi\Vert\text{tr}(\mu)(\text{d}\xi).\end{align*}
\begin{align*}\frac{1}{\Vert h\Vert} & \left\Vert \int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\text{e}^{-\langle u,\xi\rangle}\left(1-\text{e}^{-\langle h,\xi\rangle}-\langle h,\xi\rangle\right)\mu(\text{d}\xi)\right\Vert \\[4pt]
& \quad\leq\frac{1}{\Vert h\Vert}\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\left\vert \text{e}^{-\langle u,\xi\rangle}\left(1-\text{e}^{-\langle h,\xi\rangle}-\langle h,\xi\rangle\right)\right\vert \text{tr}(\mu)(\text{d}\xi)\\[4pt]
& \quad\leq\Vert h\Vert\int_{\lbrace\Vert\xi\Vert\leq M\rbrace}\Vert\xi\Vert^{2}\text{tr}(\mu)(\text{d}\xi)+2\int_{\lbrace\Vert\xi\Vert>M\rbrace}\Vert\xi\Vert\text{tr}(\mu)(\text{d}\xi).\end{align*}
So
Note that ![]() $\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\Vert\xi\Vert\text{tr}(\mu)(\text{d}\xi)<\infty$
by virtue of Definition 2.1(iv). Let
$\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\Vert\xi\Vert\text{tr}(\mu)(\text{d}\xi)<\infty$
by virtue of Definition 2.1(iv). Let ![]() $\varepsilon>0$
be arbitrary and fix some
$\varepsilon>0$
be arbitrary and fix some ![]() $M=M(\varepsilon)>0$
large enough so that
$M=M(\varepsilon)>0$
large enough so that ![]() $\int_{\lbrace\Vert\xi\Vert>M\rbrace}\Vert\xi\Vert\text{tr}(\mu)(\text{d}\xi)<\varepsilon/4$
. Define
$\int_{\lbrace\Vert\xi\Vert>M\rbrace}\Vert\xi\Vert\text{tr}(\mu)(\text{d}\xi)<\varepsilon/4$
. Define
Then, for ![]() $\Vert h\Vert\leq\delta$
, we see that
$\Vert h\Vert\leq\delta$
, we see that
This proves (19) for ![]() $u\in\mathbb{S}_{d}^{++}$
. Finally, the continuity of
$u\in\mathbb{S}_{d}^{++}$
. Finally, the continuity of ![]() $u\mapsto$
DR(u) in
$u\mapsto$
DR(u) in ![]() $\mathbb{S}_{d}^{+}$
can be easily obtained from the dominated convergence theorem.
$\mathbb{S}_{d}^{+}$
can be easily obtained from the dominated convergence theorem.
(b) Similarly as before, we derive ![]() $F(u+h)-F(u)=DF(u)(h)+r(u,h)$
with
$F(u+h)-F(u)=DF(u)(h)+r(u,h)$
with
Let ![]() $\Vert h\Vert\not=0$
. By essentially the same reasoning as in (a), we obtain that
$\Vert h\Vert\not=0$
. By essentially the same reasoning as in (a), we obtain that
and the second integral on the right-hand side is now finite by (6). Hence, we may follow the same steps as in (a) to see that ![]() $\Vert r(u,h)\Vert/\Vert h\Vert\to0$
as
$\Vert r(u,h)\Vert/\Vert h\Vert\to0$
as ![]() $\Vert h\Vert\to0$
and to obtain the continuity of DF(u) in
$\Vert h\Vert\to0$
and to obtain the continuity of DF(u) in ![]() $\mathbb{S}_{d}^{+}$
.
$\mathbb{S}_{d}^{+}$
.
Let ![]() $\phi$
and
$\phi$
and ![]() $\psi$
be as in Theorem 2.1. We know from [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Lemma 3.2 (iii)] that
$\psi$
be as in Theorem 2.1. We know from [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Lemma 3.2 (iii)] that ![]() $\phi(t,u)$
and
$\phi(t,u)$
and ![]() $\psi(t,u)$
are jointly continuous on
$\psi(t,u)$
are jointly continuous on ![]() $\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
and, moreover,
$\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
and, moreover, ![]() $u\mapsto\phi(t,u)$
and
$u\mapsto\phi(t,u)$
and ![]() $u\mapsto\psi(t,u)$
are analytic on
$u\mapsto\psi(t,u)$
are analytic on ![]() $\mathbb{S}_{d}^{++}$
for
$\mathbb{S}_{d}^{++}$
for ![]() $t\geq0$
.
$t\geq0$
.
Proposition 4.1. The following statements hold:
(a)
 $D\psi$
has a jointly continuous extension on
$D\psi$
has a jointly continuous extension on  $\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
.
$\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
.(b) If (6) is satisfied, then
 $D\phi$
has a jointly continuous extension on
$D\phi$
has a jointly continuous extension on  $\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
.
$\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
.
Proof. (a) Noting that ![]() $s\mapsto DR(\psi(s,u))\in L(\mathbb{S}_{d},\mathbb{S}_{d})$
is continuous, we may define
$s\mapsto DR(\psi(s,u))\in L(\mathbb{S}_{d},\mathbb{S}_{d})$
is continuous, we may define ![]() $f_{u}(t)$
as the unique solution in
$f_{u}(t)$
as the unique solution in ![]() $L(\mathbb{S}_{d},\mathbb{S}_{d})$
to
$L(\mathbb{S}_{d},\mathbb{S}_{d})$
to
Further, we then define the extension of ![]() $D\psi$
onto
$D\psi$
onto ![]() $\mathbb{R}_{\geq0}\times\partial\mathbb{S}_{d}^{+}$
simply by
$\mathbb{R}_{\geq0}\times\partial\mathbb{S}_{d}^{+}$
simply by
It remains to verify the joint continuity of ![]() $D\psi(t,u)$
on
$D\psi(t,u)$
on ![]() $\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
extended in this way. By the Riccati differential equation (4) we have
$\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
extended in this way. By the Riccati differential equation (4) we have
Using that ![]() $u\mapsto R(u)$
is continuous on
$u\mapsto R(u)$
is continuous on ![]() $\mathbb{S}_{d}^{+}$
and
$\mathbb{S}_{d}^{+}$
and ![]() $\psi$
is jointly continuous on
$\psi$
is jointly continuous on ![]() $\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
, we have that for all
$\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
, we have that for all ![]() $T>0$
and
$T>0$
and ![]() $M>0$
, there exists a constant
$M>0$
, there exists a constant ![]() $C(T,M)>0$
such that
$C(T,M)>0$
such that
Hence, for each ![]() $u\in\mathbb{S}_{d}^{+}$
with
$u\in\mathbb{S}_{d}^{+}$
with ![]() $\Vert u\Vert\leq M$
, we obtain
$\Vert u\Vert\leq M$
, we obtain
Applying Gronwall’s inequality yields
for all ![]() $t\in[0,T]$
and
$t\in[0,T]$
and ![]() $u\in\mathbb{S}_{d}^{+}$
with
$u\in\mathbb{S}_{d}^{+}$
with ![]() $\Vert u\Vert\leq M$
. Because
$\Vert u\Vert\leq M$
. Because ![]() $D\psi$
is jointly continuous in
$D\psi$
is jointly continuous in ![]() $\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{++}$
, it is enough to prove continuity at some fixed point
$\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{++}$
, it is enough to prove continuity at some fixed point ![]() $(t,u)\in\mathbb{R}_{\geq0}\times\partial\mathbb{S}_{d}^{+}$
, where
$(t,u)\in\mathbb{R}_{\geq0}\times\partial\mathbb{S}_{d}^{+}$
, where ![]() $\partial \mathbb{S}_d^+:=\mathbb{S}_d^+ \backslash \mathbb{S}_d^{++}$
.
$\partial \mathbb{S}_d^+:=\mathbb{S}_d^+ \backslash \mathbb{S}_d^{++}$
.
Without loss of generality we assume ![]() $t\in[0,T]$
and
$t\in[0,T]$
and ![]() $u\in\partial\mathbb{S}_{d}^{+}$
with
$u\in\partial\mathbb{S}_{d}^{+}$
with ![]() $\|u\|\le M$
. Let
$\|u\|\le M$
. Let ![]() $s\in\mathbb{R}_{\geq0}$
and
$s\in\mathbb{R}_{\geq0}$
and ![]() $v\in\mathbb{S}_{d}^{+}$
with
$v\in\mathbb{S}_{d}^{+}$
with ![]() $s\in[0,T]$
and
$s\in[0,T]$
and ![]() $\Vert v\Vert\leq M$
. We have
$\Vert v\Vert\leq M$
. We have
We estimate the first term on the right-hand side of (23) by
 \begin{align}\left\Vert D\psi(t,u)-D\psi(s,u)\right\Vert & \leq\left\Vert \int_{0}^{t}DR\left(\psi(r,u)\right)D\psi(r,u)\text{d}r-\int_{0}^{s}DR\left(\psi(r,u)\right)D\psi(r,u)\text{d}r\right\Vert \nonumber \\[3pt]
& \leq C(T,M)\int_{[s,t]\cup[t,s]}\left\Vert D\psi(r,u)\right\Vert \text{d}r\nonumber \\[3pt]
& \leq C(T,M)K(T,M)\vert t-s\vert.\end{align}
\begin{align}\left\Vert D\psi(t,u)-D\psi(s,u)\right\Vert & \leq\left\Vert \int_{0}^{t}DR\left(\psi(r,u)\right)D\psi(r,u)\text{d}r-\int_{0}^{s}DR\left(\psi(r,u)\right)D\psi(r,u)\text{d}r\right\Vert \nonumber \\[3pt]
& \leq C(T,M)\int_{[s,t]\cup[t,s]}\left\Vert D\psi(r,u)\right\Vert \text{d}r\nonumber \\[3pt]
& \leq C(T,M)K(T,M)\vert t-s\vert.\end{align}
Turning to the second term, for ![]() $v\in\mathbb{S}_{d}^{++}$
with
$v\in\mathbb{S}_{d}^{++}$
with ![]() $\Vert v\Vert\leq M$
,
$\Vert v\Vert\leq M$
, ![]() $D\psi(s,u)=f_{u}(s)$
, and
$D\psi(s,u)=f_{u}(s)$
, and ![]() $D\psi(r,u)=f_{u}(r)$
, we obtain
$D\psi(r,u)=f_{u}(r)$
, we obtain
 \begin{align*}\left\Vert D\psi(s,u)-D\psi(s,v)\right\Vert & \leq\int_{0}^{s}\left\Vert DR\left(\psi(r,u)\right)D\psi(r,u)-DR\left(\psi(r,v)\right)D\psi(r,v)\right\Vert \text{d}r\\[3pt]
& \leq\int_{0}^{s}\left\Vert DR(\psi(r,u))-DR\left(\psi(r,v)\right)\right\Vert \left\Vert D\psi(r,v)\right\Vert \text{d}r\\[3pt]
& \quad+\int_{0}^{s}\left\Vert DR\left(\psi(r,u)\right)\right\Vert \left\Vert D\psi(r,u)-D\psi(r,v)\right\Vert \text{d}r\\[3pt]
& \leq K(T,M)\int_{0}^{T}\left\Vert DR(\psi(r,u))-DR\left(\psi(r,v)\right)\right\Vert \text{d}r\\[3pt]
& \quad+C(T,M)\int_{0}^{s}\left\Vert D\psi(r,u)-D\psi(r,v)\right\Vert \text{d}r\\[3pt]
& =K(T,M)a_{T}(v,u)+C(T,M)\int_{0}^{s}\left\Vert D\psi(r,u)-D\psi(r,v)\right\Vert \text{d}r,\end{align*}
\begin{align*}\left\Vert D\psi(s,u)-D\psi(s,v)\right\Vert & \leq\int_{0}^{s}\left\Vert DR\left(\psi(r,u)\right)D\psi(r,u)-DR\left(\psi(r,v)\right)D\psi(r,v)\right\Vert \text{d}r\\[3pt]
& \leq\int_{0}^{s}\left\Vert DR(\psi(r,u))-DR\left(\psi(r,v)\right)\right\Vert \left\Vert D\psi(r,v)\right\Vert \text{d}r\\[3pt]
& \quad+\int_{0}^{s}\left\Vert DR\left(\psi(r,u)\right)\right\Vert \left\Vert D\psi(r,u)-D\psi(r,v)\right\Vert \text{d}r\\[3pt]
& \leq K(T,M)\int_{0}^{T}\left\Vert DR(\psi(r,u))-DR\left(\psi(r,v)\right)\right\Vert \text{d}r\\[3pt]
& \quad+C(T,M)\int_{0}^{s}\left\Vert D\psi(r,u)-D\psi(r,v)\right\Vert \text{d}r\\[3pt]
& =K(T,M)a_{T}(v,u)+C(T,M)\int_{0}^{s}\left\Vert D\psi(r,u)-D\psi(r,v)\right\Vert \text{d}r,\end{align*}
where ![]() $a_{T}(v,u)\,:\!=\int_{0}^{T}\Vert DR(\psi(r,u))-DR(\psi(r,v))\Vert\text{d}r$
. Using once again Gronwall’s inequality, we deduce
$a_{T}(v,u)\,:\!=\int_{0}^{T}\Vert DR(\psi(r,u))-DR(\psi(r,v))\Vert\text{d}r$
. Using once again Gronwall’s inequality, we deduce
Noting that ![]() $R\in C^{1}(\mathbb{S}_{d}^{+})$
and
$R\in C^{1}(\mathbb{S}_{d}^{+})$
and ![]() $\psi(r,0)=0$
by [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Remark 2.5], by the dominated convergence theorem we see that
$\psi(r,0)=0$
by [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Remark 2.5], by the dominated convergence theorem we see that ![]() $a_{T}(v,u)$
tends to zero as
$a_{T}(v,u)$
tends to zero as ![]() $v\to u$
. Consequently, the right-hand side of (25) tends to zero as
$v\to u$
. Consequently, the right-hand side of (25) tends to zero as ![]() $v\to u$
. Combining (23) with (24) and (25), we conclude that
$v\to u$
. Combining (23) with (24) and (25), we conclude that ![]() $D\psi$
extended in this way is jointly continuous in
$D\psi$
extended in this way is jointly continuous in ![]() $(t,u)\in\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
.
$(t,u)\in\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
.
(b) We know from the generalized Riccati equation (3) that ![]() $\phi(t,u)=\int_{0}^{t}F(\psi(s,u))\text{d}s$
. Noting that
$\phi(t,u)=\int_{0}^{t}F(\psi(s,u))\text{d}s$
. Noting that ![]() $F\in C^{1}(\mathbb{S}_{d}^{+})$
thanks to (6), the chain rule combined with the dominated convergence theorem implies the assertion.
$F\in C^{1}(\mathbb{S}_{d}^{+})$
thanks to (6), the chain rule combined with the dominated convergence theorem implies the assertion.
We are ready to prove Theorem 2.2.
Proof of Theorem 2.2. Let ![]() $\varepsilon>0$
. We have
$\varepsilon>0$
. We have
 \begin{align*}\frac{\partial}{\partial\varepsilon}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle\varepsilon u,\xi\rangle}p_{t}(x,\text{d}\xi) & =\frac{\partial}{\partial\varepsilon}\text{e}^{-\phi(t,\varepsilon u)-\langle x,\psi(t,\varepsilon u)\rangle}\\ & =-\left(D\phi(t,\varepsilon u)(u)+\langle x,D\psi(t,\varepsilon u)(u)\rangle\right)\text{e}^{-\phi(t,\varepsilon u)-\langle x,\psi(t,\varepsilon u)\rangle}\\ & \to-\left(D\phi(t,0)(u)+\langle x,D\psi(t,0)(u)\rangle\right)\quad\text{as }\varepsilon\to0,\end{align*}
\begin{align*}\frac{\partial}{\partial\varepsilon}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle\varepsilon u,\xi\rangle}p_{t}(x,\text{d}\xi) & =\frac{\partial}{\partial\varepsilon}\text{e}^{-\phi(t,\varepsilon u)-\langle x,\psi(t,\varepsilon u)\rangle}\\ & =-\left(D\phi(t,\varepsilon u)(u)+\langle x,D\psi(t,\varepsilon u)(u)\rangle\right)\text{e}^{-\phi(t,\varepsilon u)-\langle x,\psi(t,\varepsilon u)\rangle}\\ & \to-\left(D\phi(t,0)(u)+\langle x,D\psi(t,0)(u)\rangle\right)\quad\text{as }\varepsilon\to0,\end{align*}
where we used that the functions ![]() $D\phi$
and
$D\phi$
and ![]() $D\psi$
have a jointly continuous extension on
$D\psi$
have a jointly continuous extension on ![]() $\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
in accordance with Proposition 4.1. On the other hand, noting that
$\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
in accordance with Proposition 4.1. On the other hand, noting that
and applying the dominated convergence theorem, we get
Note that the limit on the right-hand side is finite. Indeed, using Fatou’s lemma, we obtain
for all ![]() $u\in\mathbb{S}_{d}^{+}$
. So
$u\in\mathbb{S}_{d}^{+}$
. So
In what follows, we compute the derivatives ![]() $D\phi(t,0)$
and
$D\phi(t,0)$
and ![]() $D\psi(t,0)$
explicitly. By means of the generalized Riccati equation (4), we have
$D\psi(t,0)$
explicitly. By means of the generalized Riccati equation (4), we have
According to Lemma 4.2 and Proposition 4.1 we are allowed to differentiate both sides of the latter equation with respect to ![]() $u\in\mathbb{S}_{d}^{+}$
and evaluate at
$u\in\mathbb{S}_{d}^{+}$
and evaluate at ![]() $u=0$
; thus, using the dominated convergence theorem,
$u=0$
; thus, using the dominated convergence theorem,
where Id denotes the identity map on ![]() $\mathbb{S}_{d}^{+}$
. From [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Lemma 3.2(iii)] we know that
$\mathbb{S}_{d}^{+}$
. From [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Lemma 3.2(iii)] we know that ![]() $\psi(t,u)$
is continuous in
$\psi(t,u)$
is continuous in ![]() $\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
, and noting that
$\mathbb{R}_{\geq0}\times\mathbb{S}_{d}^{+}$
, and noting that ![]() $\psi(s,0)=0$
(see [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Remark 2.5]), we get
$\psi(s,0)=0$
(see [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Remark 2.5]), we get
From this and the precise formula for ![]() $\phi(t,h)$
we deduce that
$\phi(t,h)$
we deduce that
We use Lemma 4.2 to get that
Finally, combining this with (26) yields
 \begin{align*}\int_{\mathbb{S}_{d}^{+}}\langle u,\xi\rangle p_{t}(x,\text{d}\xi) & =\int_{0}^{t}\left(DF(0)\right)\text{e}^{sDR(0)}(u)\text{d}s+\langle x,\text{e}^{tDR(0)}(u)\rangle\\ & =\int_{0}^{t}\langle\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\!,u\rangle\text{d}s+\langle\text{e}^{t\widetilde{B}}x,u\rangle.\end{align*}
\begin{align*}\int_{\mathbb{S}_{d}^{+}}\langle u,\xi\rangle p_{t}(x,\text{d}\xi) & =\int_{0}^{t}\left(DF(0)\right)\text{e}^{sDR(0)}(u)\text{d}s+\langle x,\text{e}^{tDR(0)}(u)\rangle\\ & =\int_{0}^{t}\langle\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\!,u\rangle\text{d}s+\langle\text{e}^{t\widetilde{B}}x,u\rangle.\end{align*}
Since the equality holds for each ![]() $u\in\mathbb{S}_{d}^{+}$
, the assertion is proved.
$u\in\mathbb{S}_{d}^{+}$
, the assertion is proved.
5. Estimates on  $\psi(t,u)$
$\psi(t,u)$
We fix an admissible parameter set ![]() $(\alpha,b,B,m,\mu)$
and let
$(\alpha,b,B,m,\mu)$
and let ![]() $\psi$
be the unique solution to (4). In this section we study upper and lower bounds for
$\psi$
be the unique solution to (4). In this section we study upper and lower bounds for ![]() $\psi$
. Let us start with an upper bound for
$\psi$
. Let us start with an upper bound for ![]() $\psi(t,u)$
.
$\psi(t,u)$
.
Propostion 5.1. Let ![]() $\psi$
be the unique solution to (4). Then
$\psi$
be the unique solution to (4). Then
where M and ![]() $\delta$
are given by (9).
$\delta$
are given by (9).
Proof. The proof is divided into three steps.
Step 1: Denote by ![]() $q_{t}(x,\text{d}\xi)$
the unique transition kernel of an affine process on
$q_{t}(x,\text{d}\xi)$
the unique transition kernel of an affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m=0,\mu)$
; that is, for each
$(\alpha,b,B,m=0,\mu)$
; that is, for each ![]() $u,\thinspace x\in\mathbb{S}_{d}^{+}$
, we have
$u,\thinspace x\in\mathbb{S}_{d}^{+}$
, we have
Applying Jensen’s inequality to the convex function ![]() $t\mapsto\exp({-}t)$
yields
$t\mapsto\exp({-}t)$
yields
 \begin{align}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}q_{t}(x,\text{d}\xi) & \geq\exp\!\left({-}\int_{\mathbb{S}_{d}^{+}}\langle u,\xi\rangle q_{t}(x,\text{d}\xi)\right) \notag\\ & =\exp\!\left({-}\int_{0}^{t}\langle\text{e}^{s\widetilde{B}}b,u\rangle\text{d}s-\langle\text{e}^{t\widetilde{B}}x,u\rangle\right)\!, \end{align}
\begin{align}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}q_{t}(x,\text{d}\xi) & \geq\exp\!\left({-}\int_{\mathbb{S}_{d}^{+}}\langle u,\xi\rangle q_{t}(x,\text{d}\xi)\right) \notag\\ & =\exp\!\left({-}\int_{0}^{t}\langle\text{e}^{s\widetilde{B}}b,u\rangle\text{d}s-\langle\text{e}^{t\widetilde{B}}x,u\rangle\right)\!, \end{align}
where the last identity is a special case of Theorem 2.2. Using (28) we obtain
Step 2: Let ![]() $\alpha \in \mathbb{S}_{d}^{+}$
be fixed. We claim that (30) holds not only for
$\alpha \in \mathbb{S}_{d}^{+}$
be fixed. We claim that (30) holds not only for ![]() $b\succeq(d-1)\alpha$
but also for any
$b\succeq(d-1)\alpha$
but also for any ![]() $b\in\mathbb{S}_{d}^{+}$
. Aiming for a contradiction, suppose that there exist
$b\in\mathbb{S}_{d}^{+}$
. Aiming for a contradiction, suppose that there exist ![]() $t_{0}>0$
and
$t_{0}>0$
and ![]() $\xi,\thinspace x_{0},\thinspace u_{0}\in\mathbb{S}_{d}^{+}$
such that
$\xi,\thinspace x_{0},\thinspace u_{0}\in\mathbb{S}_{d}^{+}$
such that
We now take an arbitrary but fixed ![]() $b_{0}\succeq(d-1)\alpha$
. Noting that
$b_{0}\succeq(d-1)\alpha$
. Noting that
is finite, we find a constant ![]() $K>0$
large enough so that
$K>0$
large enough so that ![]() $KI+\Delta>0$
, i.e.,
$KI+\Delta>0$
, i.e.,
Now, since ![]() $b_{0}+K\xi\succeq(d-1)\alpha$
, we see that (31) contradicts (30) if we choose
$b_{0}+K\xi\succeq(d-1)\alpha$
, we see that (31) contradicts (30) if we choose ![]() $b=b_{0}+K\xi$
,
$b=b_{0}+K\xi$
, ![]() $x=Kx_{0}$
,
$x=Kx_{0}$
, ![]() $u=u_{0}$
, and
$u=u_{0}$
, and ![]() $t=t_{0}$
. Hence (30) holds for all
$t=t_{0}$
. Hence (30) holds for all ![]() $b\in\mathbb{S}_{d}^{+}$
.
$b\in\mathbb{S}_{d}^{+}$
.
Step 3: According to Step 2, we are allowed to choose ![]() $b=0$
in (30), which implies
$b=0$
in (30), which implies
for all ![]() $t\geq0$
and
$t\geq0$
and ![]() $x,\thinspace u\in\mathbb{S}_{d}^{+}$
. This completes the proof.
$x,\thinspace u\in\mathbb{S}_{d}^{+}$
. This completes the proof.
We continue with a lower bound for ![]() $\psi(t,u)$
.
$\psi(t,u)$
.
Proposition 5.2. Let ![]() $\psi$
be the unique solution to (4) and suppose that
$\psi$
be the unique solution to (4) and suppose that ![]() $\alpha=0$
and (14) is satisfied. Then, for each
$\alpha=0$
and (14) is satisfied. Then, for each ![]() $u,\thinspace\xi\in\mathbb{S}_{d}^{+}$
,
$u,\thinspace\xi\in\mathbb{S}_{d}^{+}$
,
Proof. Fix ![]() $u\in\mathbb{S}_{d}^{+}$
and define
$u\in\mathbb{S}_{d}^{+}$
and define ![]() $W_{t}(u)\,:\!=\psi(t,u)-\exp({-}Kt)u$
. Using that
$W_{t}(u)\,:\!=\psi(t,u)-\exp({-}Kt)u$
. Using that ![]() $\exp({-}Kt)u=\psi(t,u)-W_{t}(u)$
we obtain
$\exp({-}Kt)u=\psi(t,u)-W_{t}(u)$
we obtain
Since ![]() $W_{0}(u)=0$
, the latter implies
$W_{0}(u)=0$
, the latter implies
Fix ![]() $\xi\in\mathbb{S}_{d}^{+}$
; then
$\xi\in\mathbb{S}_{d}^{+}$
; then
In the following we estimate the integrand. For this, we write ![]() $\langle\xi,R(\psi(s,u))\rangle=I_{1}+I_{2}$
, where
$\langle\xi,R(\psi(s,u))\rangle=I_{1}+I_{2}$
, where
and estimate ![]() $I_{1}$
and
$I_{1}$
and ![]() $I_{2}$
separately. For
$I_{2}$
separately. For ![]() $I_{1}$
, by (14) we get
$I_{1}$
, by (14) we get
where we used the self-duality of the cone ![]() $\mathbb{S}_d^+$
(see [Reference Horn and Johnson27, Theorem 7.5.4]). Turning to
$\mathbb{S}_d^+$
(see [Reference Horn and Johnson27, Theorem 7.5.4]). Turning to ![]() $I_{2}$
, we simply have
$I_{2}$
, we simply have
Collecting now the estimates for ![]() $I_{1}$
and
$I_{1}$
and ![]() $I_{2}$
, we see that
$I_{2}$
, we see that
and thus ![]() $\langle\xi,W_{t}(u)\rangle\geq0$
by (33). This proves the assertion.
$\langle\xi,W_{t}(u)\rangle\geq0$
by (33). This proves the assertion.
6. Proofs of the main results
In this section we will prove Theorem 2.2, Proposition 2.1, and Corollary 2.1. Let ![]() $p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on
$p_{t}(x,\text{d}\xi)$
be the transition kernel of a subcritical affine process on ![]() $\mathbb{S}_{d}^{+}$
with admissible parameters
$\mathbb{S}_{d}^{+}$
with admissible parameters ![]() $(\alpha,b,B,m,\mu)$
, and let
$(\alpha,b,B,m,\mu)$
, and let ![]() $\delta>0$
be given by (9).
$\delta>0$
be given by (9).
We note that ![]() $F(u)\geq0$
for all
$F(u)\geq0$
for all ![]() $u\in\mathbb{S}_{d}^{+}$
. Based on the estimates on
$u\in\mathbb{S}_{d}^{+}$
. Based on the estimates on ![]() $\psi(t,u)$
that we derived in the previous section, we easily obtain the following lemma.
$\psi(t,u)$
that we derived in the previous section, we easily obtain the following lemma.
Lemma 6.1. Suppose that (10) holds. Then there exists a constant ![]() $C>0$
such that
$C>0$
such that
Consequently,
Proof. We know that
 \begin{align*}F(\psi(s,u)) & =\langle b,\psi(s,u)\rangle+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\big(1-\text{e}^{-\langle\psi(s,u),\xi\rangle}\big)\,m(\text{d}\xi)\\ & =\!:\,\langle b,\psi(s,u)\rangle+I(u).\end{align*}
\begin{align*}F(\psi(s,u)) & =\langle b,\psi(s,u)\rangle+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\big(1-\text{e}^{-\langle\psi(s,u),\xi\rangle}\big)\,m(\text{d}\xi)\\ & =\!:\,\langle b,\psi(s,u)\rangle+I(u).\end{align*}
Now, first note that, by (27),
We turn to the estimate of I(u). Once again using (27), we obtain
 \begin{align*}I(u) & =\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\big(1-\text{e}^{-\langle\psi(s,u),\xi\rangle}\big)\,m(\text{d}\xi)\\
& \leq\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\min\left\lbrace 1,\langle\psi(s,u),\xi\rangle\right\rbrace m(\text{d}\xi)\\ & \leq\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\min\left\lbrace 1,\Vert\xi\Vert\Vert u\Vert\text{e}^{-s\delta}\right\rbrace m(\text{d}\xi).\end{align*}
\begin{align*}I(u) & =\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\big(1-\text{e}^{-\langle\psi(s,u),\xi\rangle}\big)\,m(\text{d}\xi)\\
& \leq\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\min\left\lbrace 1,\langle\psi(s,u),\xi\rangle\right\rbrace m(\text{d}\xi)\\ & \leq\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\min\left\lbrace 1,\Vert\xi\Vert\Vert u\Vert\text{e}^{-s\delta}\right\rbrace m(\text{d}\xi).\end{align*}
For all ![]() $a\geq0$
it holds that
$a\geq0$
it holds that ![]() $1\wedge a\leq\log(2)^{-1}\log(1+a)$
; hence
$1\wedge a\leq\log(2)^{-1}\log(1+a)$
; hence
 \begin{align*}I(u) & \leq\frac{1}{\log(2)}\int_{\lbrace\Vert\xi\Vert\leq1\rbrace}\Vert\xi\Vert\Vert u\Vert\text{e}^{-s\delta}m(\text{d}\xi)+\frac{1}{\log(2)}\int_{\lbrace\Vert\xi\Vert>1\rbrace}\log\left(1+\Vert\xi\Vert\Vert u\Vert\text{e}^{-s\delta}\right)m(\text{d}\xi)\\ & =\!:\,J_{1}(u)+J_{2}(u).\end{align*}
\begin{align*}I(u) & \leq\frac{1}{\log(2)}\int_{\lbrace\Vert\xi\Vert\leq1\rbrace}\Vert\xi\Vert\Vert u\Vert\text{e}^{-s\delta}m(\text{d}\xi)+\frac{1}{\log(2)}\int_{\lbrace\Vert\xi\Vert>1\rbrace}\log\left(1+\Vert\xi\Vert\Vert u\Vert\text{e}^{-s\delta}\right)m(\text{d}\xi)\\ & =\!:\,J_{1}(u)+J_{2}(u).\end{align*}
Let ![]() $C>0$
be a generic constant which may vary from line to line. Since
$C>0$
be a generic constant which may vary from line to line. Since ![]() $m(\text{d}\xi)$
integrates
$m(\text{d}\xi)$
integrates ![]() $\Vert\xi\Vert\mathbbm{1}_{\lbrace\Vert\xi\Vert\leq1\rbrace}$
by definition, we have
$\Vert\xi\Vert\mathbbm{1}_{\lbrace\Vert\xi\Vert\leq1\rbrace}$
by definition, we have
Moreover, noting that ![]() $m(\text{d}\xi)$
integrates
$m(\text{d}\xi)$
integrates ![]() $\log\Vert\xi\Vert\mathbbm{1}_{\lbrace\Vert\xi\Vert>1\rbrace}$
by assumption, for
$\log\Vert\xi\Vert\mathbbm{1}_{\lbrace\Vert\xi\Vert>1\rbrace}$
by assumption, for ![]() $J_{2}(u)$
we use the elementary inequality (see [Reference Friesen, Jin and Rüdiger19, Lemma 8.5])
$J_{2}(u)$
we use the elementary inequality (see [Reference Friesen, Jin and Rüdiger19, Lemma 8.5])
 \begin{align*}\log(1+a\cdot c) & \leq C\min\left\lbrace \log(1+a),\log(1+c)\right\rbrace +C\log(1+a)\log(1+c)\\ & \leq C\log(1+a)+Ca\log(1+c)\\ & \leq Ca\left(1+\log(1+c)\right)\end{align*}
\begin{align*}\log(1+a\cdot c) & \leq C\min\left\lbrace \log(1+a),\log(1+c)\right\rbrace +C\log(1+a)\log(1+c)\\ & \leq C\log(1+a)+Ca\log(1+c)\\ & \leq Ca\left(1+\log(1+c)\right)\end{align*}
for ![]() $a=\Vert u\Vert\exp({-}s\delta)$
and
$a=\Vert u\Vert\exp({-}s\delta)$
and ![]() $c=\Vert\xi\Vert$
to get
$c=\Vert\xi\Vert$
to get
Combining the estimates for ![]() $J_{1}(u)$
and
$J_{1}(u)$
and ![]() $J_{2}(u)$
yields
$J_{2}(u)$
yields
So, by (36) and (37), we have (34), which proves the assertion.
We are now able to prove Theorem 2.3.
Proof of Theorem 2.3. Fix ![]() $x\in\mathbb{S}_{d}^{+}$
. By means of Proposition 5.1, we see that
$x\in\mathbb{S}_{d}^{+}$
. By means of Proposition 5.1, we see that
 \begin{align*}\lim_{t\to\infty}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}p_{t}(x,\text{d}\xi) & =\lim_{t\to\infty}\exp\!\left({-}\int_{0}^{t}F(\psi(s,u))\text{d}s-\langle x,\psi(t,u)\rangle\right)\\[3pt]
& =\exp\!\left({-}\int_{0}^{\infty}F(\psi(s,u))\text{d}s\right)\!,\end{align*}
\begin{align*}\lim_{t\to\infty}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}p_{t}(x,\text{d}\xi) & =\lim_{t\to\infty}\exp\!\left({-}\int_{0}^{t}F(\psi(s,u))\text{d}s-\langle x,\psi(t,u)\rangle\right)\\[3pt]
& =\exp\!\left({-}\int_{0}^{\infty}F(\psi(s,u))\text{d}s\right)\!,\end{align*}
and the limit on the right-hand side is finite by Lemma 6. Clearly, by (35), we also have that ![]() $u\mapsto\int_{0}^{\infty}F(\psi(s,u)))\text{d}s$
is continuous at
$u\mapsto\int_{0}^{\infty}F(\psi(s,u)))\text{d}s$
is continuous at ![]() $u=0$
. Now, Lévy’s continuity theorem (cf. [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Lemma 4.5]) implies that
$u=0$
. Now, Lévy’s continuity theorem (cf. [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Lemma 4.5]) implies that ![]() $p_{t}(x,\cdot)\rightarrow\pi$
weakly as
$p_{t}(x,\cdot)\rightarrow\pi$
weakly as ![]() $t\to\infty$
. Moreover,
$t\to\infty$
. Moreover, ![]() $\pi$
has Laplace transform (11). It remains to verify that
$\pi$
has Laplace transform (11). It remains to verify that ![]() $\pi$
is the unique invariant distribution.
$\pi$
is the unique invariant distribution.
Invariance. Fix ![]() $u\in\mathbb{S}_{d}^{+}$
and let
$u\in\mathbb{S}_{d}^{+}$
and let ![]() $t\geq0$
be arbitrary. Then
$t\geq0$
be arbitrary. Then
 \begin{align*}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}\left(\int_{\mathbb{S}_{d}^{+}}p_{t}(x,\text{d}\xi)\pi(\text{d}x)\right) & =\int_{\mathbb{S}_{d}^{+}}\left(\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}p_{t}(x,\text{d}\xi)\right)\pi(\text{d}x)\\[3pt]
& =\text{e}^{-\phi(t,u)}\int_{\mathbb{S}_{d}^{+}}\exp\!\left({-}\langle x,\psi(t,u)\rangle\right)\pi(\text{d}x).\end{align*}
\begin{align*}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}\left(\int_{\mathbb{S}_{d}^{+}}p_{t}(x,\text{d}\xi)\pi(\text{d}x)\right) & =\int_{\mathbb{S}_{d}^{+}}\left(\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}p_{t}(x,\text{d}\xi)\right)\pi(\text{d}x)\\[3pt]
& =\text{e}^{-\phi(t,u)}\int_{\mathbb{S}_{d}^{+}}\exp\!\left({-}\langle x,\psi(t,u)\rangle\right)\pi(\text{d}x).\end{align*}
Note that ![]() $\psi$
satisfies the semi-flow equation by [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Lemma 3.2]; that is,
$\psi$
satisfies the semi-flow equation by [Reference Cuchiero, Filipović, Mayerhofer and Teichmann12, Lemma 3.2]; that is, ![]() $\psi(t+s,u)=\psi\left(s,\psi(t,u)\right)$
for all
$\psi(t+s,u)=\psi\left(s,\psi(t,u)\right)$
for all ![]() $t,\thinspace s\geq0$
. Using that the Laplace transform of
$t,\thinspace s\geq0$
. Using that the Laplace transform of ![]() $\pi$
is given by (11), for each
$\pi$
is given by (11), for each ![]() $u\in\mathbb{S}_{d}^{+}$
we obtain
$u\in\mathbb{S}_{d}^{+}$
we obtain
 \begin{align*}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}\left(\int_{\mathbb{S}_{d}^{+}}p_{t}(x,\text{d}\xi)\pi(\text{d}x)\right) & =\text{e}^{-\phi(t,u)}\exp\!\left({-}\int_{0}^{\infty}F\left(\psi\left(s,\psi(t,u)\right)\right)\text{d}s\right)\\[3pt]
& =\text{e}^{-\phi(t,u)}\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(t+s,u)\right)\text{d}s\right)\\[3pt]
& =\text{e}^{-\phi(t,u)}\exp\!\left({-}\int_{t}^{\infty}F\left(\psi(s,u)\right)\text{ds}\right)\\[3pt]
& =\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right)\\[3pt]
& =\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle x,u\rangle}\pi\left(\text{d}x\right)\!.\end{align*}
\begin{align*}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}\left(\int_{\mathbb{S}_{d}^{+}}p_{t}(x,\text{d}\xi)\pi(\text{d}x)\right) & =\text{e}^{-\phi(t,u)}\exp\!\left({-}\int_{0}^{\infty}F\left(\psi\left(s,\psi(t,u)\right)\right)\text{d}s\right)\\[3pt]
& =\text{e}^{-\phi(t,u)}\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(t+s,u)\right)\text{d}s\right)\\[3pt]
& =\text{e}^{-\phi(t,u)}\exp\!\left({-}\int_{t}^{\infty}F\left(\psi(s,u)\right)\text{ds}\right)\\[3pt]
& =\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right)\\[3pt]
& =\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle x,u\rangle}\pi\left(\text{d}x\right)\!.\end{align*}
Consequently, ![]() $\pi$
is invariant.
$\pi$
is invariant.
Uniqueness. Let ![]() $\pi'$
be another invariant distribution. For fixed
$\pi'$
be another invariant distribution. For fixed ![]() $u\in\mathbb{S}_{d}^{+}$
and
$u\in\mathbb{S}_{d}^{+}$
and ![]() $t\geq0$
we have
$t\geq0$
we have
 \begin{align*}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle x,u\rangle}\pi'(\text{d}x) & =\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}\left(\int_{\mathbb{S}_{d}^{+}}p_{t}(x,\text{d}\xi)\pi'(\text{d}x)\right)\\[3pt]
& =\int_{\mathbb{S}_{d}^{+}}\exp\!\left({-}\phi(t,u)-\langle x,\psi(t,u)\rangle\right)\pi'(\text{d}x).\end{align*}
\begin{align*}\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle x,u\rangle}\pi'(\text{d}x) & =\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}\left(\int_{\mathbb{S}_{d}^{+}}p_{t}(x,\text{d}\xi)\pi'(\text{d}x)\right)\\[3pt]
& =\int_{\mathbb{S}_{d}^{+}}\exp\!\left({-}\phi(t,u)-\langle x,\psi(t,u)\rangle\right)\pi'(\text{d}x).\end{align*}
Letting ![]() $t\to\infty$
shows that
$t\to\infty$
shows that ![]() $\pi'$
also satisfies (11). By uniqueness of the Laplace transforms, it holds that
$\pi'$
also satisfies (11). By uniqueness of the Laplace transforms, it holds that ![]() $\pi'=\pi$
.
$\pi'=\pi$
.
Proof of Proposition 2.1. Let ![]() $x\in\mathbb{S}_{d}^{+}$
and
$x\in\mathbb{S}_{d}^{+}$
and ![]() $\pi\in\mathcal{P}(\mathbb{S}_{d}^{+})$
be such that
$\pi\in\mathcal{P}(\mathbb{S}_{d}^{+})$
be such that ![]() $p_{t}(x,\cdot)\to\pi$
weakly as
$p_{t}(x,\cdot)\to\pi$
weakly as ![]() $t\to\infty$
. It follows that
$t\to\infty$
. It follows that
and we obtain from (2) that
In particular, this implies
Fix ![]() $u\in\mathbb{S}_{d}^{++}$
. Assume that
$u\in\mathbb{S}_{d}^{++}$
. Assume that ![]() $\alpha=0$
and (14) holds. By definition of F we have
$\alpha=0$
and (14) holds. By definition of F we have ![]() $F(u)\geq\int_{\mathbb{S}_{d}^{+}}(1-\exp({-}\langle u,\xi\rangle))m(\text{d}\xi)$
and thereby
$F(u)\geq\int_{\mathbb{S}_{d}^{+}}(1-\exp({-}\langle u,\xi\rangle))m(\text{d}\xi)$
and thereby
where we used (32). Integrating over ![]() $[0,\infty)$
and using a change of variable
$[0,\infty)$
and using a change of variable ![]() $r\,:\!=\exp({-}Ks)\langle\xi,u\rangle$
with
$r\,:\!=\exp({-}Ks)\langle\xi,u\rangle$
with ![]() $\text{d}s=-1/K\cdot\text{d}r/r$
yields
$\text{d}s=-1/K\cdot\text{d}r/r$
yields
 \begin{align*}\int_{0}^{\infty}F(\psi(s,u))\text{d}s & \geq\frac{1}{K}\int_{\lbrace\langle\xi,u\rangle>1\rbrace}\int_{0}^{\langle\xi,u\rangle}\frac{1-\text{e}^{-r}}{r}\text{d}rm(\text{d}\xi)\\[3pt]
& \geq\frac{1}{K}\int_{\lbrace\langle\xi,u\rangle>1\rbrace}\int_{1}^{\langle\xi,u\rangle}\frac{1-\text{e}^{-r}}{r}\text{d}rm(\text{d}\xi)\\[3pt]
& \geq\frac{1-\text{e}^{-1}}{K}\int_{\lbrace\langle\xi,u\rangle>1\rbrace}\log(\langle\xi,u\rangle)m(\text{d}\xi),\end{align*}
\begin{align*}\int_{0}^{\infty}F(\psi(s,u))\text{d}s & \geq\frac{1}{K}\int_{\lbrace\langle\xi,u\rangle>1\rbrace}\int_{0}^{\langle\xi,u\rangle}\frac{1-\text{e}^{-r}}{r}\text{d}rm(\text{d}\xi)\\[3pt]
& \geq\frac{1}{K}\int_{\lbrace\langle\xi,u\rangle>1\rbrace}\int_{1}^{\langle\xi,u\rangle}\frac{1-\text{e}^{-r}}{r}\text{d}rm(\text{d}\xi)\\[3pt]
& \geq\frac{1-\text{e}^{-1}}{K}\int_{\lbrace\langle\xi,u\rangle>1\rbrace}\log(\langle\xi,u\rangle)m(\text{d}\xi),\end{align*}
where we used in the last inequality that ![]() $1-\exp({-}r)\geq1-\exp({-}1)>0$
for
$1-\exp({-}r)\geq1-\exp({-}1)>0$
for ![]() $r\ge1$
. This leads to the estimate
$r\ge1$
. This leads to the estimate
Letting ![]() $u=\mathbbm{1}\in\mathbb{S}_{d}^{++}$
gives
$u=\mathbbm{1}\in\mathbb{S}_{d}^{++}$
gives ![]() $\langle\xi,\mathbbm{1}\rangle=\text{tr}(\xi)\geq\Vert\xi\Vert$
, so that
$\langle\xi,\mathbbm{1}\rangle=\text{tr}(\xi)\geq\Vert\xi\Vert$
, so that
This completes the proof.
Proof of Corollary 2.1. Using that ![]() $\Vert\exp(t\widetilde{B})\Vert\leq M\exp({-}\delta t)$
, where
$\Vert\exp(t\widetilde{B})\Vert\leq M\exp({-}\delta t)$
, where ![]() $\delta$
is given by (9), we have
$\delta$
is given by (9), we have
 \begin{align*}\lim_{t\to\infty}\int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y) & =\int_{0}^{\infty}\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}}\xi m(\text{d}\xi)\right)\text{d}s\in\mathbb{S}_{d}^{+}.\end{align*}
\begin{align*}\lim_{t\to\infty}\int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y) & =\int_{0}^{\infty}\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}}\xi m(\text{d}\xi)\right)\text{d}s\in\mathbb{S}_{d}^{+}.\end{align*}
By direct computation we find that
 \begin{equation*} \int_{0}^{\infty}\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\text{d}s = - \widetilde{B}^{-1}\left( b + \int_{\mathbb{S}_d^+ \backslash \{0\}} \xi m(\text{d}\xi) \right)\!,\end{equation*}
\begin{equation*} \int_{0}^{\infty}\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\text{d}s = - \widetilde{B}^{-1}\left( b + \int_{\mathbb{S}_d^+ \backslash \{0\}} \xi m(\text{d}\xi) \right)\!,\end{equation*}
and hence it suffices to prove that ![]() $\lim_{t\to\infty}\int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y)=\int_{\mathbb{S}_{d}^{+}}y\pi(\text{d}y)$
. To do so, we can proceed as in the proof of Theorem 2.2. Indeed, by Lemma A.1, we estimate
$\lim_{t\to\infty}\int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y)=\int_{\mathbb{S}_{d}^{+}}y\pi(\text{d}y)$
. To do so, we can proceed as in the proof of Theorem 2.2. Indeed, by Lemma A.1, we estimate
 \begin{equation*}\sup_{t\geq0}\int_{\mathbb{S}_{d}^{+}}\Vert y\Vert p_{t}(x,\text{d}y)\leq\sup_{t\geq0}\text{tr}\left(\int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y)\right)\leq\sqrt{d}\sup_{t\geq0}\left\Vert \int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y)\right\Vert <\infty.\end{equation*}
\begin{equation*}\sup_{t\geq0}\int_{\mathbb{S}_{d}^{+}}\Vert y\Vert p_{t}(x,\text{d}y)\leq\sup_{t\geq0}\text{tr}\left(\int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y)\right)\leq\sqrt{d}\sup_{t\geq0}\left\Vert \int_{\mathbb{S}_{d}^{+}}yp_{t}(x,\text{d}y)\right\Vert <\infty.\end{equation*}
Therefore, applying Fatou’s lemma yields
So ![]() $\pi\in\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
. Now, let
$\pi\in\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
. Now, let ![]() $\varepsilon>0$
. By the dominated convergence theorem, we see that
$\varepsilon>0$
. By the dominated convergence theorem, we see that
Moreover, noting that, by Proposition 5.1,
we can use once again the dominated convergence theorem to obtain
 \begin{align*}\lim_{\varepsilon\searrow0}\int_{\mathbb{S}_{d}^{+}}\frac{1-\text{e}^{-\langle\varepsilon u,y\rangle}}{\varepsilon}\pi(\text{d}y) & =\lim_{\varepsilon\searrow0}\frac{1}{\varepsilon}\int_{0}^{\infty}F(\psi(s,\varepsilon u))\text{d}s\\[4pt]
& =\lim_{\varepsilon\searrow0}\int_{0}^{\infty}\left(\langle b,\frac{\psi(s,\varepsilon u)}{\varepsilon}\rangle\text{d}s+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\frac{1-\text{e}^{-\langle\psi(s,\varepsilon u),\xi\rangle}}{\varepsilon}m(\text{d}\xi)\right)\text{d}s\\[4pt]
& =\int_{0}^{\infty}\langle b,D\psi(s,0)(u)\rangle\text{d}s+\int_{0}^{\infty}\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\langle D\psi(s,0)(u),\xi\rangle m(\text{d}\xi)\text{d}s\\[4pt]
& =\int_{0}^{\infty}\langle\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\!,u\rangle\text{d}s,\end{align*}
\begin{align*}\lim_{\varepsilon\searrow0}\int_{\mathbb{S}_{d}^{+}}\frac{1-\text{e}^{-\langle\varepsilon u,y\rangle}}{\varepsilon}\pi(\text{d}y) & =\lim_{\varepsilon\searrow0}\frac{1}{\varepsilon}\int_{0}^{\infty}F(\psi(s,\varepsilon u))\text{d}s\\[4pt]
& =\lim_{\varepsilon\searrow0}\int_{0}^{\infty}\left(\langle b,\frac{\psi(s,\varepsilon u)}{\varepsilon}\rangle\text{d}s+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\frac{1-\text{e}^{-\langle\psi(s,\varepsilon u),\xi\rangle}}{\varepsilon}m(\text{d}\xi)\right)\text{d}s\\[4pt]
& =\int_{0}^{\infty}\langle b,D\psi(s,0)(u)\rangle\text{d}s+\int_{0}^{\infty}\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\langle D\psi(s,0)(u),\xi\rangle m(\text{d}\xi)\text{d}s\\[4pt]
& =\int_{0}^{\infty}\langle\text{e}^{s\widetilde{B}}\left(b+\int_{\mathbb{S}_{d}^{+}\backslash\lbrace0\rbrace}\xi m(\text{d}\xi)\right)\!,u\rangle\text{d}s,\end{align*}
where we used that ![]() $D\psi(s,0)(u)=\exp(s\widetilde{B}^{\top})u$
(see the proof of Theorem 2.2). Since the latter identity holds for all
$D\psi(s,0)(u)=\exp(s\widetilde{B}^{\top})u$
(see the proof of Theorem 2.2). Since the latter identity holds for all ![]() $u\in\mathbb{S}_{d}^{+}$
, this concludes the proof.
$u\in\mathbb{S}_{d}^{+}$
, this concludes the proof.
7. Proof of Theorem 2.4
Proof of Theorem 2.4. Suppose that (10) holds. By definition of ![]() $d_{L}$
, we have
$d_{L}$
, we have
 \begin{align} & d_{L}\left(p_{t}(x,\text{d}\xi),\pi(\text{d}\xi)\right)\nonumber \\ & =\sup_{u\in\mathbb{S}_{d}^{+}\setminus\{0\}}\frac{1}{\Vert u\Vert}\left\vert \int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}p_{t}(x,\text{d}\xi)-\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}\pi(\text{d}\xi)\right\vert \nonumber \\ & =\sup_{u\in\mathbb{S}_{d}^{+}\setminus\{0\}}\frac{1}{\Vert u\Vert}\left\vert \exp\!\left({-}\int_{0}^{t}F\left(\psi(s,u)\right)\text{d}s-\langle x,\psi(t,u)\rangle\right)-\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right)\right\vert .\end{align}
\begin{align} & d_{L}\left(p_{t}(x,\text{d}\xi),\pi(\text{d}\xi)\right)\nonumber \\ & =\sup_{u\in\mathbb{S}_{d}^{+}\setminus\{0\}}\frac{1}{\Vert u\Vert}\left\vert \int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}p_{t}(x,\text{d}\xi)-\int_{\mathbb{S}_{d}^{+}}\text{e}^{-\langle u,\xi\rangle}\pi(\text{d}\xi)\right\vert \nonumber \\ & =\sup_{u\in\mathbb{S}_{d}^{+}\setminus\{0\}}\frac{1}{\Vert u\Vert}\left\vert \exp\!\left({-}\int_{0}^{t}F\left(\psi(s,u)\right)\text{d}s-\langle x,\psi(t,u)\rangle\right)-\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right)\right\vert .\end{align}
Let ![]() $C>0$
be a generic constant that may vary from line to line. Then, using (34), for each
$C>0$
be a generic constant that may vary from line to line. Then, using (34), for each ![]() $t\geq0$
we have
$t\geq0$
we have
 \begin{align*} & \left\vert \exp\!\left({-}\int_{0}^{t}F\left(\psi(s,u)\right)\text{d}s-\langle x,\psi(t,u)\rangle\right)-\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right)\right\vert \\ & \qquad\qquad\qquad\leq\left\vert \exp\!\left({-}\langle x\psi(t,u)\rangle\right)-1\right\vert \cdot\left|\exp\!\left({-}\int_{0}^{t}F\left(\psi(s,u)\right)\text{d}s\right)\right\vert \\ & \qquad\qquad\qquad\quad+\left\vert \exp\!\left({-}\int_{0}^{t}F\left(\psi(s,u)\right)\text{d}s\right)-\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right)\right\vert \\ & \qquad\qquad\qquad\leq\left\vert \langle x,\psi(s,u)\rangle\right|+\left|\int_{t}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right\vert \\ & \qquad\qquad\qquad\leq M\Vert x\Vert\Vert u\Vert\text{e}^{-t\delta}+C\Vert u\Vert\int_{t}^{\infty}\text{e}^{-s\delta}\text{d}s\\ & \qquad\qquad\qquad\leq C\left(1+\Vert x\Vert\right)\Vert u\Vert\text{e}^{-t\delta},\end{align*}
\begin{align*} & \left\vert \exp\!\left({-}\int_{0}^{t}F\left(\psi(s,u)\right)\text{d}s-\langle x,\psi(t,u)\rangle\right)-\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right)\right\vert \\ & \qquad\qquad\qquad\leq\left\vert \exp\!\left({-}\langle x\psi(t,u)\rangle\right)-1\right\vert \cdot\left|\exp\!\left({-}\int_{0}^{t}F\left(\psi(s,u)\right)\text{d}s\right)\right\vert \\ & \qquad\qquad\qquad\quad+\left\vert \exp\!\left({-}\int_{0}^{t}F\left(\psi(s,u)\right)\text{d}s\right)-\exp\!\left({-}\int_{0}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right)\right\vert \\ & \qquad\qquad\qquad\leq\left\vert \langle x,\psi(s,u)\rangle\right|+\left|\int_{t}^{\infty}F\left(\psi(s,u)\right)\text{d}s\right\vert \\ & \qquad\qquad\qquad\leq M\Vert x\Vert\Vert u\Vert\text{e}^{-t\delta}+C\Vert u\Vert\int_{t}^{\infty}\text{e}^{-s\delta}\text{d}s\\ & \qquad\qquad\qquad\leq C\left(1+\Vert x\Vert\right)\Vert u\Vert\text{e}^{-t\delta},\end{align*}
8. Proof of Theorem 2.5
Proof of Theorem 2.5. Note that ![]() $\pi\in\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
by Corollary 2.1. Let
$\pi\in\mathcal{P}_{1}(\mathbb{S}_{d}^{+})$
by Corollary 2.1. Let ![]() $q_{t}(x,\text{d}\xi)$
be a transition kernel for the conservative, subcritical affine process with admissible parameters
$q_{t}(x,\text{d}\xi)$
be a transition kernel for the conservative, subcritical affine process with admissible parameters ![]() $(\alpha=0,b=0,B,m=0,\mu)$
. Using the particular form of the Laplace transform for
$(\alpha=0,b=0,B,m=0,\mu)$
. Using the particular form of the Laplace transform for ![]() $p_{t}(x,\cdot)$
(see (2)), it is not difficult to see that
$p_{t}(x,\cdot)$
(see (2)), it is not difficult to see that ![]() $p_{t}(x,\cdot)=q_{t}(x,\cdot)\ast p_{t}(0,\cdot)$
, where ‘
$p_{t}(x,\cdot)=q_{t}(x,\cdot)\ast p_{t}(0,\cdot)$
, where ‘![]() $\ast$
’ denotes the convolution of measures. Let H be any coupling with marginals
$\ast$
’ denotes the convolution of measures. Let H be any coupling with marginals ![]() $\delta_{x}$
and
$\delta_{x}$
and ![]() $\pi$
, i.e.,
$\pi$
, i.e., ![]() $H\in\mathcal{H}(\delta_{x},\pi)$
. Using the invariance of
$H\in\mathcal{H}(\delta_{x},\pi)$
. Using the invariance of ![]() $\pi$
, together with the convexity of
$\pi$
, together with the convexity of ![]() $W_{1}$
(see [Reference Villani48, Theorem 4.8] and [Reference Friesen, Jin, Kremer and Rüdiger18, Lemma 2.3]), we find that
$W_{1}$
(see [Reference Villani48, Theorem 4.8] and [Reference Friesen, Jin, Kremer and Rüdiger18, Lemma 2.3]), we find that
 \begin{align*}W_{1}\left(p_{t}(x,\cdot),\pi\right) & =W_{1}\left(\int_{\mathbb{S}_{d}^{+}}p_{t}(y,\cdot)\delta_{x}(\text{d}y),\int_{\mathbb{S}_{d}^{+}}p_{t}(y',\cdot)\pi(\text{d}y')\right)\\[3pt]
& \leq\int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}W_{1}\left(p_{t}(y,\cdot),p_{t}(y',\cdot)\right)H(\text{d}y,\text{d}y')\\[3pt]
& \leq\int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}W_{1}\left(q_{t}(y,\cdot),q_{t}(y',\cdot)\right)H(\text{d}y,\text{d}y').\end{align*}
\begin{align*}W_{1}\left(p_{t}(x,\cdot),\pi\right) & =W_{1}\left(\int_{\mathbb{S}_{d}^{+}}p_{t}(y,\cdot)\delta_{x}(\text{d}y),\int_{\mathbb{S}_{d}^{+}}p_{t}(y',\cdot)\pi(\text{d}y')\right)\\[3pt]
& \leq\int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}W_{1}\left(p_{t}(y,\cdot),p_{t}(y',\cdot)\right)H(\text{d}y,\text{d}y')\\[3pt]
& \leq\int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}W_{1}\left(q_{t}(y,\cdot),q_{t}(y',\cdot)\right)H(\text{d}y,\text{d}y').\end{align*}
The integrand can now be estimated as follows:
 \begin{align*}W_{1}\left(q_{t}(y,\cdot),q_{t}(y',\cdot)\right) & \leq\int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}\|z-z'\|G(\text{d}z,\text{d}z')\\[3pt]
& \leq\int_{\mathbb{S}_{d}^{+}}\|z\|q_{t}(y,\text{d}z)+\int_{\mathbb{S}_{d}^{+}}\|z'\|q_{t}(y',\text{d}z')\\[3pt]
& \leq M\sqrt{d}\text{e}^{-t\delta}\left(\|y\|+\|y'\|\right)\!,\end{align*}
\begin{align*}W_{1}\left(q_{t}(y,\cdot),q_{t}(y',\cdot)\right) & \leq\int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}\|z-z'\|G(\text{d}z,\text{d}z')\\[3pt]
& \leq\int_{\mathbb{S}_{d}^{+}}\|z\|q_{t}(y,\text{d}z)+\int_{\mathbb{S}_{d}^{+}}\|z'\|q_{t}(y',\text{d}z')\\[3pt]
& \leq M\sqrt{d}\text{e}^{-t\delta}\left(\|y\|+\|y'\|\right)\!,\end{align*}
where G is any coupling of ![]() $(q_{t}(y,\cdot),q_{t}(y',\cdot))$
and we have used Lemma A.1 to obtain
$(q_{t}(y,\cdot),q_{t}(y',\cdot))$
and we have used Lemma A.1 to obtain
 \begin{align*}\int_{\mathbb{S}_{d}^{+}}\Vert z\Vert q_{t}(y,\text{d}z) & \leq\text{tr}\left(\int_{\mathbb{S}_{d}^{+}}zq_{t}(y,\text{d}z)\right)\\[3pt]
& =\text{tr}\left(\text{e}^{t\widetilde{B}}y\right)\\[3pt]
& \leq\sqrt{d}\left\Vert \text{e}^{t\widetilde{B}}y\right\Vert \\[3pt]
& \leq M\sqrt{d}\text{e}^{-t\delta}\Vert y\Vert.\end{align*}
\begin{align*}\int_{\mathbb{S}_{d}^{+}}\Vert z\Vert q_{t}(y,\text{d}z) & \leq\text{tr}\left(\int_{\mathbb{S}_{d}^{+}}zq_{t}(y,\text{d}z)\right)\\[3pt]
& =\text{tr}\left(\text{e}^{t\widetilde{B}}y\right)\\[3pt]
& \leq\sqrt{d}\left\Vert \text{e}^{t\widetilde{B}}y\right\Vert \\[3pt]
& \leq M\sqrt{d}\text{e}^{-t\delta}\Vert y\Vert.\end{align*}
Combining these estimates, we obtain
 \begin{align*}W_{1}(p_{t}(x,\cdot),\pi) & \leq M\sqrt{d}\text{e}^{-t\delta}\int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}\left(\|y\|+\|y'\|\right)H(\text{d}y,\text{d}y')\\ & \leq M\sqrt{d}\text{e}^{-t\delta}\left(\|x\|+\int_{\mathbb{S}_{d}^{+}}\Vert y\Vert\pi(\text{d}y)\right)\!,\end{align*}
\begin{align*}W_{1}(p_{t}(x,\cdot),\pi) & \leq M\sqrt{d}\text{e}^{-t\delta}\int_{\mathbb{S}_{d}^{+}\times\mathbb{S}_{d}^{+}}\left(\|y\|+\|y'\|\right)H(\text{d}y,\text{d}y')\\ & \leq M\sqrt{d}\text{e}^{-t\delta}\left(\|x\|+\int_{\mathbb{S}_{d}^{+}}\Vert y\Vert\pi(\text{d}y)\right)\!,\end{align*}
which yields (17).
9. Extension to affine processes on finite-dimensional convex cones
In this section we outline how our main result, Theorem 2.3, can be extended to the more general framework of affine processes on convex cones. Below we briefly introduce the necessary concepts, while additional details, proofs, and references can be found in [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13].
Let V be a finite-dimensional Euclidean space with scalar product ![]() $\langle\cdot,\cdot\rangle$
and associated norm
$\langle\cdot,\cdot\rangle$
and associated norm ![]() $\|\cdot\|$
. Let
$\|\cdot\|$
. Let ![]() $K\subset V$
be a closed convex cone and suppose that it is proper, i.e.
$K\subset V$
be a closed convex cone and suppose that it is proper, i.e. ![]() $K\cap({-}K)=\{0\}$
, and generating, i.e.
$K\cap({-}K)=\{0\}$
, and generating, i.e. ![]() $V=K-K$
. Note that its closed dual cone
$V=K-K$
. Note that its closed dual cone
is then also generating and proper. The partial order on V is, for ![]() $u,v\in V$
, defined by
$u,v\in V$
, defined by ![]() $u\preceq v\Longleftrightarrow v-u\in K^{*}$
. The following is the definition of affine transition semigroups due to [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Definition 2.1].
$u\preceq v\Longleftrightarrow v-u\in K^{*}$
. The following is the definition of affine transition semigroups due to [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Definition 2.1].
Definition 9.1. (Cuchiero et al. [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13].) A Markov transition kernel ![]() $(p_{t}(x,\text{d}\xi))_{t\geq0,x\in K}$
is called affine if the following hold:
$(p_{t}(x,\text{d}\xi))_{t\geq0,x\in K}$
is called affine if the following hold:
(i)
 $p_{t}(x,\cdot)\longrightarrow p_{s}(x,\cdot)$
weakly as
$p_{t}(x,\cdot)\longrightarrow p_{s}(x,\cdot)$
weakly as  $t\to s$
for every
$t\to s$
for every  $s\geq0$
and
$s\geq0$
and  $x\in K$
.
$x\in K$
.(ii) There exist functions
 $\phi\,:\,\mathbb{R}_{+}\times K^{*}\longrightarrow\mathbb{R}$
and
$\phi\,:\,\mathbb{R}_{+}\times K^{*}\longrightarrow\mathbb{R}$
and  $\psi\,:\,\mathbb{R}_{+}\times K^{*}\longrightarrow V$
such that
(39)
$\psi\,:\,\mathbb{R}_{+}\times K^{*}\longrightarrow V$
such that
(39) \begin{align}\int_{K}\text{e}^{-\langle u,\xi\rangle}p_{t}(x,\text{d}\xi)=\text{e}^{-\phi(t,u)-\langle\psi(t,u),x\rangle},\qquad x\in K,\ \ (t,u)\in\mathbb{R}_{+}\times K^{*}.\end{align}
\begin{align}\int_{K}\text{e}^{-\langle u,\xi\rangle}p_{t}(x,\text{d}\xi)=\text{e}^{-\phi(t,u)-\langle\psi(t,u),x\rangle},\qquad x\in K,\ \ (t,u)\in\mathbb{R}_{+}\times K^{*}.\end{align}
Note that this definition allows non-conservative affine transition kernels. However, having in mind that we investigate existence, uniqueness, and convergence of ![]() $p_{t}(x,\cdot)$
to the invariant distribution, we restrict our study to conservative kernels; that is,
$p_{t}(x,\cdot)$
to the invariant distribution, we restrict our study to conservative kernels; that is, ![]() $p_{t}(x,K)=1$
for all
$p_{t}(x,K)=1$
for all ![]() $t\geq0$
and
$t\geq0$
and ![]() $x\in K$
. The following is a summary of the main results obtained in [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13] on the existence and structure of conservative affine transition kernels. We emphasize that these results hold in a more general setting that allows killing and explosion of the process; see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13] for more details.
$x\in K$
. The following is a summary of the main results obtained in [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13] on the existence and structure of conservative affine transition kernels. We emphasize that these results hold in a more general setting that allows killing and explosion of the process; see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13] for more details.
Theorem 9.1. (Cuchiero et al. [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13])
(a) Let
 $p_{t}(x,\text{d}\xi)$
be a conservative affine transition kernel. Then the associated transition semigroup is
$p_{t}(x,\text{d}\xi)$
be a conservative affine transition kernel. Then the associated transition semigroup is  $C_{0}$
-Feller, and the functions
$C_{0}$
-Feller, and the functions  $\phi,\psi$
are differentiable with respect to t and satisfy the generalized Riccati equations for
$\phi,\psi$
are differentiable with respect to t and satisfy the generalized Riccati equations for  $u\in K^{*}$
; that is,
(40)
$u\in K^{*}$
; that is,
(40) \begin{align}\partial_{t}\phi(t,u) & =F(\psi(t,u)),\qquad\phi(0,u)=0,\end{align}
where
\begin{align}\partial_{t}\phi(t,u) & =F(\psi(t,u)),\qquad\phi(0,u)=0,\end{align}
where \begin{align}\qquad\partial_{t}\psi(t,u) & =R(\psi(t,u)),\qquad\psi(0,u)=u\in K^{*},\nonumber\end{align}
\begin{align}\qquad\partial_{t}\psi(t,u) & =R(\psi(t,u)),\qquad\psi(0,u)=u\in K^{*},\nonumber\end{align}
 $F(u)=\partial_{t}\phi(t,u)|_{t=0}$
and
$F(u)=\partial_{t}\phi(t,u)|_{t=0}$
and  $R(u)=\partial_{t}\psi(t,u)|_{t=0}$
. Moreover, there exists a parameter set
$R(u)=\partial_{t}\psi(t,u)|_{t=0}$
. Moreover, there exists a parameter set  $(Q,b,B,m,\mu)$
such that the functions F and R are of the form
$(Q,b,B,m,\mu)$
such that the functions F and R are of the form
 \begin{align*}F(u) & =\langle b,u\rangle-\int_{K\backslash\{0\}}\left(\text{e}^{-\langle u,\xi\rangle}-1\right)m(\text{d}\xi),\\[5pt]
R(u) & =-\frac{1}{2}Q(u,u)+B^{\top}(u)-\int_{K\backslash\{0\}}\left(\text{e}^{-\langle u,\xi\rangle}-1+\mathbbm{1}_{\{\|\xi\|\leq1\}}\langle\xi,u\rangle\right)\mu(\text{d}\xi),\end{align*}
\begin{align*}F(u) & =\langle b,u\rangle-\int_{K\backslash\{0\}}\left(\text{e}^{-\langle u,\xi\rangle}-1\right)m(\text{d}\xi),\\[5pt]
R(u) & =-\frac{1}{2}Q(u,u)+B^{\top}(u)-\int_{K\backslash\{0\}}\left(\text{e}^{-\langle u,\xi\rangle}-1+\mathbbm{1}_{\{\|\xi\|\leq1\}}\langle\xi,u\rangle\right)\mu(\text{d}\xi),\end{align*}
where
(i)
 $b\in K$
;
$b\in K$
;(ii) m is a Borel measure on
 $K\backslash\{0\}$
with
$K\backslash\{0\}$
with
 \begin{equation*}\int_{K\backslash\{0\}}\left(1\wedge\|\xi\|\right)m(\text{d}\xi)<\infty;\end{equation*}
\begin{equation*}\int_{K\backslash\{0\}}\left(1\wedge\|\xi\|\right)m(\text{d}\xi)<\infty;\end{equation*}
(iii)
 $Q:V\times V\longrightarrow V$
is a symmetric bilinear function such that for all
$Q:V\times V\longrightarrow V$
is a symmetric bilinear function such that for all  $v\in V$
,
$v\in V$
,  $Q(v,v)\in K^{*}$
, and
$Q(v,v)\in K^{*}$
, and  $\langle x,Q(u,v)\rangle=0$
whenever
$\langle x,Q(u,v)\rangle=0$
whenever  $\langle u,x\rangle=0$
for
$\langle u,x\rangle=0$
for  $u\in K^{*}$
and
$u\in K^{*}$
and  $x\in K$
;
$x\in K$
;(iv)
 $\mu$
is a
$\mu$
is a  $K^{*}$
-valued
$K^{*}$
-valued  $\sigma$
-finite Borel measure on
$\sigma$
-finite Borel measure on  $K\backslash\{0\}$
satisfying
$K\backslash\{0\}$
satisfying
 \begin{equation*}\int_{K\backslash\{0\}}\left(1\wedge\|\xi\|^{2}\right)\langle x,\mu(\text{d}\xi)\rangle<\infty,\qquad x\in K;\end{equation*}
\begin{equation*}\int_{K\backslash\{0\}}\left(1\wedge\|\xi\|^{2}\right)\langle x,\mu(\text{d}\xi)\rangle<\infty,\qquad x\in K;\end{equation*}
(v)
 $B:V\longrightarrow V$
is a linear map satisfying, for all
$B:V\longrightarrow V$
is a linear map satisfying, for all  $u\in K^{*}$
and
$u\in K^{*}$
and  $x\in K$
with
$x\in K$
with  $\langle u,x\rangle=0$
,
$\langle u,x\rangle=0$
,
 \begin{equation*}\int_{K\backslash\{0\}}\mathbbm{1}_{\{\|\xi\|\leq1\}}\langle\xi,u\rangle\langle x,\mu(\text{d}\xi)\rangle\leq\langle x,B^{\top}(u)\rangle<\infty.\end{equation*}
\begin{equation*}\int_{K\backslash\{0\}}\mathbbm{1}_{\{\|\xi\|\leq1\}}\langle\xi,u\rangle\langle x,\mu(\text{d}\xi)\rangle\leq\langle x,B^{\top}(u)\rangle<\infty.\end{equation*}
(b) Conversely, let
 $(Q=0,b,B,m,\mu)$
be a parameter set satisfying the above conditions, and suppose in addition that
(41)Then there exists a unique conservative affine transition semigroup on K such that (39) holds for all
$(Q=0,b,B,m,\mu)$
be a parameter set satisfying the above conditions, and suppose in addition that
(41)Then there exists a unique conservative affine transition semigroup on K such that (39) holds for all \begin{align}\int_{K\backslash\{0\}}\mathbbm{1}_{\{\|\xi\|>1\}}\|\xi\|\langle x,\mu(\text{d}\xi)\rangle<\infty,\qquad x\in K.\end{align}
\begin{align}\int_{K\backslash\{0\}}\mathbbm{1}_{\{\|\xi\|>1\}}\|\xi\|\langle x,\mu(\text{d}\xi)\rangle<\infty,\qquad x\in K.\end{align}
 $(t,u)\in\mathbb{R}_{+}\times K^{*}$
, where
$(t,u)\in\mathbb{R}_{+}\times K^{*}$
, where  $\phi(t,u)$
and
$\phi(t,u)$
and  $\psi(t,u)$
are given by (40).
$\psi(t,u)$
are given by (40).
Note that, for a given parameter set ![]() $(Q,b,B,m,\mu)$
, existence of an affine transition kernel is only shown for the case
$(Q,b,B,m,\mu)$
, existence of an affine transition kernel is only shown for the case ![]() $Q=0$
, while conservativeness is a consequence of the first moment condition (41) (see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, p. 373] and follow the argument given in [Reference Duffie, Filipović and Schachermayer16, Section 9]).
$Q=0$
, while conservativeness is a consequence of the first moment condition (41) (see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, p. 373] and follow the argument given in [Reference Duffie, Filipović and Schachermayer16, Section 9]).
Assuming, in addition, that K is an irreducible symmetric cone (see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Definition 2.6]), there exists a conservative affine transition semigroup for any parameter set ![]() $(Q,b,B,m,\mu)$
fulfilling the above conditions (i)–(v) and (41); see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Theorem 2.19]. Moreover, for dimensions larger than 2 it has been shown that the jumps are of finite variation and the drift satisfies
$(Q,b,B,m,\mu)$
fulfilling the above conditions (i)–(v) and (41); see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Theorem 2.19]. Moreover, for dimensions larger than 2 it has been shown that the jumps are of finite variation and the drift satisfies ![]() $b\succeq4^{-1}d(r-1)Q(e,e)$
, where e denotes the identity element for the multiplication on V, and r denotes the rank and d the Peirce invariant of V; see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Theorem 2.13] and [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Appendix] for additional details. Note that if we let
$b\succeq4^{-1}d(r-1)Q(e,e)$
, where e denotes the identity element for the multiplication on V, and r denotes the rank and d the Peirce invariant of V; see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Theorem 2.13] and [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Appendix] for additional details. Note that if we let ![]() $V=S_{d}$
and
$V=S_{d}$
and ![]() $K=S_{d}^{+}$
, we obtain the case of positive semidefinite matrices as a particular case of these results.
$K=S_{d}^{+}$
, we obtain the case of positive semidefinite matrices as a particular case of these results.
Below we provide an extension of Theorem 2.3 for a conservative affine transition kernel on a proper closed convex cone K, which is generating. Since we do not suppose that this cone is symmetric, existence of such a kernel is a priori not clear and should be established separately.
Theorem 9.2. Suppose that there exists an affine transition kernel ![]() $p_{t}(x,\text{d}\xi)$
with parameters
$p_{t}(x,\text{d}\xi)$
with parameters ![]() $(Q,b,B,m,\mu)$
satisfying (41) (which makes the kernel
$(Q,b,B,m,\mu)$
satisfying (41) (which makes the kernel ![]() $p_{t}$
necessarily conservative). Define
$p_{t}$
necessarily conservative). Define ![]() $\widetilde{B}:V\longrightarrow V$
by
$\widetilde{B}:V\longrightarrow V$
by
and suppose that ![]() $\sigma(\widetilde{B})\subset\{\lambda\in\mathbb{C}\ |\ \text{Re}(\lambda)<0\}$
. Moreover, assume that
$\sigma(\widetilde{B})\subset\{\lambda\in\mathbb{C}\ |\ \text{Re}(\lambda)<0\}$
. Moreover, assume that
Then the conservative affine transition kernel ![]() $p_{t}(x,\text{d}\xi)$
has a unique invariant distribution
$p_{t}(x,\text{d}\xi)$
has a unique invariant distribution ![]() $\pi$
. Moreover, for each
$\pi$
. Moreover, for each ![]() $x\in K$
, one has
$x\in K$
, one has ![]() $p_{t}(x,\cdot)\longrightarrow\pi$
weakly as
$p_{t}(x,\cdot)\longrightarrow\pi$
weakly as ![]() $t\to\infty$
, and
$t\to\infty$
, and ![]() $\pi$
has Laplace transform
$\pi$
has Laplace transform
where the latter integral is absolutely convergent.
Proof. We follow the proof of our main result, Theorem 2.3.
Step 1. Let us prove that there exist constants ![]() $M\geq1$
and
$M\geq1$
and ![]() $\delta>0$
such that
$\delta>0$
such that
Indeed, one could check that Theorem 2.2 also holds in this situation (provided that m has finite first moment). One may think of deducing the assertion by arguments similar to those for Proposition 5.1. Unfortunately, the latter is built on a convolution argument, and it requires the existence of a conservative affine transition kernel with parameters ![]() $(Q,b,B,m=0,\mu)$
, which is currently not known. So we provide below an alternative and direct proof which avoids the convolution trick.
$(Q,b,B,m=0,\mu)$
, which is currently not known. So we provide below an alternative and direct proof which avoids the convolution trick.
First observe that, for ![]() $u\in K^{*}$
, it holds that
$u\in K^{*}$
, it holds that
Let ![]() $y(t,u)=e^{t\widetilde{B}^{\top}}(u)$
be the unique solution to
$y(t,u)=e^{t\widetilde{B}^{\top}}(u)$
be the unique solution to
Note that R is quasi-monotone increasing on ![]() $K^{*}$
by [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Proposition 3.12]. Then
$K^{*}$
by [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Proposition 3.12]. Then
and hence by Volkmann’s comparison theorem for ordinary differential equations (see [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Theorem 3.13]) we conclude that
that is,
Now we can repeat the argument in [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, p. 387]: since ![]() $K^{*}$
is a finite-dimensional proper closed convex cone, it is normal; i.e., there exists a constant
$K^{*}$
is a finite-dimensional proper closed convex cone, it is normal; i.e., there exists a constant ![]() $\gamma_{K^{*}}$
such that for
$\gamma_{K^{*}}$
such that for ![]() $x,y\in K^{*}$
,
$x,y\in K^{*}$
,
We thus have
The property (42) is now an immediate consequence of the assumption that the spectrum of ![]() $\widetilde{B}$
is contained in the left half-plane of
$\widetilde{B}$
is contained in the left half-plane of ![]() $\mathbb{C}$
.
$\mathbb{C}$
.
Step 2. Following exactly the same arguments as in Lemma 6.1, we find a constant ![]() $C>0$
such that
$C>0$
such that
Step 3. Using [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Proposition 3.1(i)–(ii)] combined with a version of Lévy’s continuity theorem [Reference Cuchiero, Keller-Ressel, Mayerhofer and Teichmann13, Lemma 3.7], the assertion can be deduced by literally the same arguments as given in the proof of Theorem 2.3.
Appendix A. Matrix Calculus
For a ![]() $d\times d$
square matrix x, recall that
$d\times d$
square matrix x, recall that ![]() $\text{tr}(x)=\sum_{i=1}^{d}x_{ii}$
. The Frobenius norm of x is given by
$\text{tr}(x)=\sum_{i=1}^{d}x_{ii}$
. The Frobenius norm of x is given by ![]() $\Vert x\Vert=\text{tr}(xx)^{1/2}=(\sum_{i,j=1}^{d}\vert x_{ij}\vert^{2})^{1/2}$
. Let us recollect one property of this norm.
$\Vert x\Vert=\text{tr}(xx)^{1/2}=(\sum_{i,j=1}^{d}\vert x_{ij}\vert^{2})^{1/2}$
. Let us recollect one property of this norm.
Lemma A.1 Let ![]() $x\in\mathbb{S}_{d}^{+}$
; then
$x\in\mathbb{S}_{d}^{+}$
; then
Proof. Write ![]() $x=u^{\top}\kappa u$
, where u is orthogonal and
$x=u^{\top}\kappa u$
, where u is orthogonal and ![]() $\kappa$
is diagonal with its entries given by
$\kappa$
is diagonal with its entries given by ![]() $\lambda_{i}(x)$
,
$\lambda_{i}(x)$
, ![]() $i = 1,\ldots,d$
, the eigenvalues of x. We have
$i = 1,\ldots,d$
, the eigenvalues of x. We have
 \begin{equation*}\Vert x\Vert^{2}=\text{tr}\left(u^{\top}\kappa^{2}u\right)=\sum_{i=1}^{d}\lambda_{i}(x)^{2}.\end{equation*}
\begin{equation*}\Vert x\Vert^{2}=\text{tr}\left(u^{\top}\kappa^{2}u\right)=\sum_{i=1}^{d}\lambda_{i}(x)^{2}.\end{equation*}
Since ![]() $x\in\mathbb{S}_{d}^{+}$
, it holds that
$x\in\mathbb{S}_{d}^{+}$
, it holds that ![]() $\lambda_{i}(x)\geq0$
,
$\lambda_{i}(x)\geq0$
, ![]() $i=1,\ldots,d$
. Then
$i=1,\ldots,d$
. Then
 \begin{equation*}\left\Vert x\right\Vert =\left(\sum_{i=1}^{d}\lambda_{i}^{2}(x)\right)^{1/2}\leq\sum_{i=1}^{d}\lambda_{i}(x)\leq\sqrt{d}\left(\sum_{i=1}^{d}\lambda_{i}^{2}(x)\right)^{1/2}=\sqrt{d}\Vert x\Vert.\end{equation*}
\begin{equation*}\left\Vert x\right\Vert =\left(\sum_{i=1}^{d}\lambda_{i}^{2}(x)\right)^{1/2}\leq\sum_{i=1}^{d}\lambda_{i}(x)\leq\sqrt{d}\left(\sum_{i=1}^{d}\lambda_{i}^{2}(x)\right)^{1/2}=\sqrt{d}\Vert x\Vert.\end{equation*}
Acknowledgements
The authors would like to thank the referees for a careful reading of this work, useful comments, and pointing out the reference [Reference Masuda41]. Peng Jin is supported by the STU Scientific Research Foundation for Talents (No. NTF18023) and NFSC (No. 11861029).