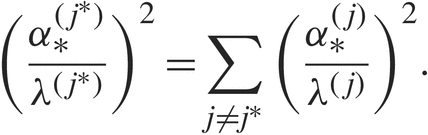1. Introduction
In the ranking and selection (R&S) problem, there are M ‘alternatives’ (or ‘systems’), and each alternative j ∈ {1 ,..., M} has an unknown value 
${\mu ^{\left( j \right)}} \in $ (for simplicity, suppose that μ (i) ≠ μ (j) for i ≠ j). We wish to identify the unique best alternative 
${j^*} = \arg \mathop {\max }\nolimits_j {\mu ^{(j)}}$. For any j, we have the ability to collect noisy samples of the form 
${W^{(j)}}N({\mu ^{(j)}},({\lambda ^{(j)}}{)^2})$, but we are limited to a total of N samples that have to be allocated among the alternatives, under independence assumptions ensuring that samples of j do not provide any information about i ≠ j . After the sampling budget has been consumed, we select the alternative with the highest sample mean. We say that ‘correct selection’ occurs if the selected alternative is identical to j * We seek to allocate the budget in a way that maximizes the probability of correct selection.
The R&S problem has a long history dating back to [Reference Bechhofer1], and continues to be an active area of research; see [Reference Chau, FU, QU and Ryzhov3] and [Reference Hong, Nelson and Rosetti11]. Most modern research on this problem considers sequential allocation strategies, in which the decision maker may spend part of the sampling budget, observe the results, and adjust the allocation of the remaining samples accordingly. The literature has developed various algorithmic approaches, including indifference-zone methods [Reference Kim and Nelson14], optimal computing budget allocation [Reference Chen, LIN, YüCesan and Chick4], and expected improvement [Reference Jones, Schonlau and Welch13]. The related literature on multiarmed bandits [Reference Gittins, Glazebrook and Weber8] has contributed other approaches, such as Thompson sampling [Reference Russo and Van Roy21], although the bandit problem uses a different objective function from the R&S problem and, thus, a good method for one problem may work poorly in the other [Reference Russo20].
Glynn and Juneja [Reference Glynn and Juneja9] gave a rigorous foundation for the notion of optimal budget allocation with regard to probability of correct selection. Denote by 0 ≤ N (j) ≤ N the number of samples assigned to alternative j (thus, 
$\sum\nolimits_j {N^{(j)}} = N),$ and take N → ∞ while keeping the proportion α (j) = N (j) / N constant. The optimal proportions 
$\mathop \alpha \nolimits_*^{\left( j \right)} $ (among all possible vectors 
$\alpha \in _{ + + }^M$ satisfying 
$\sum\nolimits_j {\alpha ^{(j)}} = 1$ satisfy the following conditions.
Proportion assigned to alternative j *:
$${({{\alpha _*^{({j^*})}} \over {{\lambda ^{({j^*})}}}})^2} = \sum\limits_{j \ne {j^*}} {({{\alpha _*^{(j)}} \over {{\lambda ^{(j)}}}})^2}.$$
(1.1)
Proportions assigned to arbitrary
$i,j \ne {j^*}$:
$${{{{({\mu ^{(i)}} - {\mu ^{({j^*})}})}^2}} \over {{{({\lambda ^{(i)}})}^2}/\alpha _*^{(i)} + {{({\lambda ^{({j^*})}})}^2}/\alpha _*^{({j^*})}}} = {{{{({\mu ^{(j)}} - {\mu ^{({j^*})}})}^2}} \over {{{({\lambda ^{(j)}})}^2}/\alpha _*^{(j)} + {{({\lambda ^{({j^*})}})}^2}/\alpha _*^{({j^*})}}}.$$
(1.2)
Under this allocation, the probability of incorrect selection will converge to 0 at the fastest possible rate (exponential with the best possible exponent). Of course, (1.1) and (1.2) themselves depend on the unknown performance values. A common work-around is to replace these values with plug-in estimators and repeatedly solve for the optimal proportions in a sequential manner. Even then, the optimality conditions are cumbersome to solve, which may explain why researchers and practitioners prefer suboptimal heuristics that are easier to implement. To give a recent example, Pasupathy et al. [Reference Pasupathy15] used large deviations theory to derive optimality conditions, analogous to (1.1) and (1.2), for a general class of simulation-based optimization problems, but advocated approximating the conditions to obtain a more tractable solution.
In this paper we focus on one particular class of heuristics, namely expected improvement (EI) methods, which have consistently demonstrated computational and practical advantages in a wide variety of problem classes [Reference Branke, Chick and Schmidt2], [Reference HAN, Ryzhov and Defourny10], [Reference Scott, Powell, Simão and Johansson24] ever since their introduction in [Reference Jones, Schonlau and Welch13]. Expected improvement is a Bayesian approach to the R&S problem that allocates samples in a purely sequential manner: each successive sample is used to update the posterior distributions of the values μ (j), and the next sample is adaptively assigned using the so-called value of information criterion. This notion will be formalized in Section 2; here we simply note that there are many competing definitions, such as the classic EI criterion of [Reference Jones, Schonlau and Welch13], the knowledge gradient criterion [Reference Powell and Ryzhov17], or the LL 1 criterion of [Reference Chick, Branke and Schmidt6]. Ryzhov [Reference Ryzhov22] showed that the seemingly minor differences between these variants produce very different asymptotic allocations, but also that all of these allocations are suboptimal.
Recently, however, Salemi et al. [Reference Salemi, Nelson, Staum and Tolk23] proposed a new criterion called complete expected improvement (CEI). The formal definition of CEI is given in Section 3, but the main idea is that, when we evaluate the potential of a seemingly suboptimal alternative to improve over the current-best value, we treat both of the values in this comparison as random variables (unlike classic EI, which only uses a plug-in estimate of the best value). Salemi et al. [Reference Salemi, Nelson, Staum and Tolk23] created and implemented this idea in the context of Gaussian Markov random fields, a more sophisticated Bayesian learning model than the version of the R&S problem with independent normal samples that we consider here. Although the Gaussian Markov model is far more scalable and practical, it also presents greater difficulties for theoretical analysis: for example, no analog of (1.1) and (1.2) is available for statistical models with a Gaussian Markov structure. In this paper we translate the CEI criterion to our simpler model, which enables us to study its theoretical convergence rate, and ultimately leads to strong new theoretical arguments in support of the CEI method.
Our main contribution in this paper is to prove that, with a slight modification to the method as it was originally laid out in [Reference Salemi, Nelson, Staum and Tolk23], this modified version of CEI achieves both (1.1) and (1.2) asymptotically as N →∞. Not only is this a new result for EI-type methods, it is also one of the strongest guarantees for any R&S problem heuristic to date. To compare it with state-of-the-art research, Russo [Reference Russo20] presented a class of heuristics, called ‘top-two methods’, which can also achieve optimal allocations, but only when a tuning parameter is set optimally. A more recent work by Qin et al. [Reference Qin, Klabjan and Russo18], which appeared while the present paper was under review, extended the top-two approach to use CEI calculations, but kept the requirement of a tunable parameter. From this work, it can be seen that top-two methods are structured similarly to our approach, but essentially deflect the calculation of 
$\mathop \alpha \nolimits_*^{\left( {j*} \right)} $ to the decision maker, whereas we develop a simple, adaptive scheme that learns this quantity with no tuning whatsoever. Also related is the work by Peng and Fu [Reference Peng and FU16], who found a way to reverse-engineer the EI calculations to optimize the rate, but this approach requires one to first solve (1.1) and (1.2) with plug-in estimators, and the procedure does not have a natural interpretation as an EI criterion. By contrast, CEI requires no additional computational effort compared to classic EI, and has a very simple and intuitive interpretation. In this way, our paper bridges the gap between convergence rate theory and the more practical concerns that motivate EI methods.
2 Preliminaries
We first provide some formal background for the optimality conditions (1.1)–(1.2) derived in [Reference Glynn and Juneja9], and then give an overview of EI-type methods. It is important to note that the theoretical framework of [Reference Glynn and Juneja9], as well as the theoretical analysis developed in this paper, relies on a frequentist interpretation of the R&S problem, in which the value of alternative i is treated as a fixed (though unknown) constant. On the other hand, EI methods are derived using Bayesian arguments; however, once the derivation is complete, one is free to apply and study the resulting algorithm in a frequentist setting (as we do in this paper). To avoid confusion, we first describe the frequentist model, then introduce details of the Bayesian model where necessary.
In the frequentist model the values μ (i) are fixed for i = 1 , ... , M. Let 
$\left\{ {{j_n}} \right\}_{n = 0}^\infty $ be a sequence of alternatives chosen for sampling. For each jn, we observe 
$W_{n + 1}^{({j_n})} \sim {\cal N}({\mu ^{({j_n})}},{\left( {{\lambda ^{({j_n})}}} \right)^2})$, where λ (j) > 0 is assumed to be known for all j. We let Fn be the σ-algebra generated by 
${j_0},W_1^{({j_0})},...,{j_{n - 1}},W_n^{({j_{n - 1}})}$. The allocation 
$\left\{ {{j_n}} \right\}_{n = 0}^\infty $ is said to be adaptive if each jn is Fn-measurable and static if all the jn are F 0 -measurable. We define 
$I_n^{(j)} = {1_{\left\{ {{j_n} = j} \right\}}},$ and let 
$N_n^{(j)} = \sum\nolimits_{m = 0}^{n - 1} I_m^{(j)}$ be the number of times that alternative j is sampled up to time index n = 1, 2, ....
At time n, we can calculate the statistics
$$\theta _n^{(j)} = {1 \over {N_n^{(j)}}}\sum\limits_{m = 0}^{n - 1} I_m^{(j)}W_{m + 1}^{(j)},$$
(2.1)
$${(\sigma _n^{(j)})^2} = {{{{({\lambda ^{(j)}})}^2}} \over {N_n^{(j)}}}.$$
(2.2)
If our sampling budget is limited to n samples then 
$j_n^* = \arg \mathop {\max }\nolimits_j \theta _n^{(j)}$ will be the final selected alternative. Correct selection occurs at time index n if 
$j_n^* = {j^*}$. The probability of correct selection (PCS), written as 
$\mathbb P( {j_n^* = {j^*}})$, depends on the rule used to allocate the samples. Glynn and Juneja [Reference Glynn and Juneja9] proved that, for any static allocation that assigns a proportion α (j) > 0 of the budget to each alternative j, the convergence rate of the PCS can be expressed in terms of the limit
$${\Gamma ^\alpha } = - \mathop {\lim }\limits_{n \to \infty } {1 \over n}\log {\kern 1pt} (j_n^* \ne {j^*}).$$
(2.3)
That is, the probability of incorrect selection converges to 0 at an exponential rate, where the exponent includes a constant Γα that depends on the vector α of proportions. Equations ( 1.1) and (1.2) characterize the proportions that optimize the rate (maximize Γα ) under the assumption of independent normal samples. Although Glynn and Juneja [Reference Glynn and Juneja9] only considered static allocations, nonetheless, to date, (2.3) continues to be one of the strongest rate results for the R&S problem. Optimal static allocations derived through this framework can be used as guidance for the design of dynamic allocations; see, for example, [Reference Hunter and Mc Closky12] and [Reference Pasupathy15].
We now describe EI, a prominent class of adaptive methods. EI uses a Bayesian model of the learning process, which is very similar to the model presented above, but makes the additional assumption that 
${\mu ^{(j)}} \sim {\cal N}(\theta _0^{(j)},(\sigma _0^{(j)}{)^2})$, where 
$\theta _0^{\left( j \right)}$ and 
$\sigma _0^{(j)}$ are prespecified prior parameters.
It is also assumed that μ (i) and μ (j) are independent for all i ≠ j. Under these assumptions, it is well known [Reference Degroot7] that the posterior distribution of μ (j) given Fn is 
${\cal N}(\theta _n^{(j)},(\sigma _n^{(j)}{)^2}),$ where the posterior mean and variance can be computed recursively. Under the noninformative prior 
$\sigma _0^{(j)} = \infty, $ the Bayesian posterior parameters 
$\theta _n^{(j)}$ and 
$\sigma _n^{(j)}$ are identical to the frequentist statistics defined in (2.1) and (2.2), and so we can use the same notation for both settings.
One of the first (and probably the best-known) EI algorithms was introduced by Jones et al. [ 13]. In this version of EI, as applied to our R&S model, we take 
${j_n} = \arg \mathop {\max }\nolimits_j v_n^{(j)}$, where
$$v_n^{(j)} = (\max \{ {\mu ^{(j)}} - \theta _n^{(j_n^*)},0\} {\kern 1pt} {\kern 1pt} |{\kern 1pt} {\kern 1pt} {{\cal F}_n}) = \sigma _n^{(j)}f( - {{\left| {\theta _n^{(j)} - \theta _n^{(j_n^*)}} \right|} \over {\sigma _n^{(j)}}}),$$
(2.4)
and 
$f\left( z \right) = z\Phi \left( z \right) + \phi \left( z \right),$ with ϕ and Φ being the standard Gaussian PDF and CDF, respectively. We can view (2.4) as a measure of the potential that the true value of j will improve upon the current-best estimate 
$\theta _n^{j_n^*}$. The EI criterion 
$v_n^{(j)}$ may be recomputed at each time stage n based on the most recent posterior parameters.
Ryzhov [Reference Ryzhov22] gave the first convergence rate analysis of this algorithm. Under EI, we have
$$\mathop {\lim }\limits_{n \to \infty } {{N_n^{({j^*})}} \over n} = 1,$$
(2.5)
$$\mathop {\lim }\limits_{n \to \infty } {{N_n^{(i)}} \over {N_n^{(j)}}} = {\left( {{{{\lambda ^{(i)}}|{\mu ^{(j)}} - {\mu ^{({j^*})}}|} \over {{\lambda ^{(j)}}\left| {{\mu ^{(i)}} - {\mu ^{({j^*})}}} \right|}}} \right)^2},\quad \quad i,j \ne {j^*},$$
(2.6)
where the limits hold almost surely. Clearly, (2.5) and (2.6) do not match (1.1) and (1.2) except in the limiting case where 
$\alpha _*^{({j^*})} \to 1$. Because 
${N^{(j)}}/n \to 0$ for 
$j \ne {j^*}$, EI will not achieve an exponential convergence rate for any finite M . Ryzhov [Reference Ryzhov22] also derived the limiting allocations for two other variants of EI, but they do not recover (1.1) and (1.2) either.
3 Algorithm and main results
Salemi et al. [Reference Salemi, Nelson, Staum and Tolk23] proposed to replace (2.4) with
$$v_n^{(j)} = (\max \{ {\mu ^{(j)}} - {\mu ^{(j_n^*)}},0\} {\kern 1pt} {\kern 1pt} |{\kern 1pt} {\kern 1pt} {{\cal F}_n}),$$
(3.1)
which can be written in closed form as
$$v_n^{(j)} = \sqrt {{{(\sigma _n^{(j)})}^2} + {{(\sigma _n^{(j_n^*)})}^2}} f\left( { - {{|\theta _n^{(j)} - \theta _n^{(j_n^*)}|} \over {\sqrt {{{(\sigma _n^{(j)})}^2} + {{(\sigma _n^{(j_n^*)})}^2}} {\kern 1pt} }}} \right)$$
(3.2)
for any 
$j \ne j_n^*$. In this way, the value of collecting information about j depends not only on our uncertainty about j, but also on our uncertainty about 
$j_n^*$. Salemi et al. [Reference Salemi, Nelson, Staum and Tolk23] considered a more general Gaussian Markov model with correlated beliefs, so the original presentation of CEI included a term representing the posterior covariance between μ (j) and 
${\mu ^{(j_n^*)}}$). In this paper we only consider independent priors, so we work with (3.2), which translates the CEI concept to our R&S model.
From (3.1), it follows that 
$v_n^{(j_n^*)} = 0$ for all n. Thus, we cannot simply assign 
${j_n} = \arg \mathop {\max }\nolimits_j v_n^{(j)}$ because, in that case, 
$j_n^*$ would never be chosen. It is necessary to modify the procedure by introducing some additional logic to handle samples assigned to 
$j_n^*$. To the best of our knowledge, this issue is not explicitly discussed in [Reference Salemi, Nelson, Staum and Tolk23]. In fact, many adaptive methods are unable to efficiently identify when 
$j_n^*$ should be measured; thus, both the classic EI method of [Reference Jones, Schonlau and Welch13], and the popular Thompson sampling algorithm [Reference Russo and Van Roy21], will sample 
$j_n^*$ too often. The class of top-two methods, first introduced in [Reference Russo20], addresses this problem by essentially assigning a fixed proportion β of samples to 
$j_n^*$, while using Thompson sampling or other means to choose between the other alternatives. Optimal allocations can be attained if β is tuned correctly, but the optimal choice of β is problem dependent and generally difficult to find.
Based on these considerations, we give a modified CEI (mCEI) procedure in Algorithm 3.1. The modification adds condition (3.3), which mimics (1.1) to decide whether 
$j_n^*$ should be sampled. This condition is trivial to implement, and the mCEI algorithm is completely free of tunable parameters. It was shown in [Reference Chen, Ryzhov and Chan5] that the mCEI algorithm samples every alternative infinitely often as n →∞.
Algorithm 3.1
(mCEI algorithm for the R&S problem.) Let n = 0 and repeat the following.
Check whether
$${\left( {{{N_n^{(j_n^*)}} \over {{\lambda ^{(j_n^*)}}}}} \right)^2} \lt \sum\limits_{j \ne j_n^*} {\left( {{{N_n^{(j)}} \over {{\lambda ^{(j)}}}}} \right)^2}.$$
(3.3)
If (3.3) holds, assign
${j_n} = j_n^*$. If( 3.3) does not hold, assign ${j_n} = \arg \mathop {\max }\nolimits_{j \ne j_n^*} v_n^{(j)}$, where $v_n^{(j)}$ is given by (3.2).Observe
$W_{n + 1}^{({j_n})}$, update posterior parameters, and increment n by 1.
We now state our main results on the asymptotic rate optimality of mCEI. Essentially, these theorems state that conditions (1.1) and (1.2) will hold in the limit as n →∞. Both theorems should be interpreted in the frequentist sense, that is, μ (j) is a fixed but unknown constant for each j.
Theorem 3.1
(Optimal alternative.) Let 
$\alpha _n^{(j)} = N_n^{(j)}/n$. Under the mCEI algorithm,
$$\mathop {\lim }\limits_{n \to \infty } {({{\alpha _n^{({j^*})}} \over {{\lambda ^{({j^*})}}}})^2} - \sum\limits_{j \ne j_n^*} {({{\alpha _n^{(j)}} \over {{\lambda ^{(j)}}}})^2} = 0\quad almost\,surely{\rm{.}}$$
Theorem 3.2
(Suboptimal alternatives.) For 
$j \ne {j^*}$$
, define
$$\tau _n^{(j)} = {{{{({\mu ^{(j)}} - {\mu ^{({j^*})}})}^2}} \over {{{({\lambda ^{(j)}})}^2}/\alpha _n^{(j)} + {{({\lambda ^{({j^*})}})}^2}/\alpha _n^{({j^*})}}},$$
where 
$\alpha _n^{(j)} = N_n^{(j)}/n$. Under the mCEI algorithm,
$$\mathop {\lim }\limits_{n \to \infty } {{\tau _n^{(i)}} \over {\tau _n^{(j)}}} = 1\quad almost\,surely$$
for any 
$i,j \ne {j^*}$.
4 Proofs of the main results
For notational convenience, we assume that 
${j^*} = 1$ is the unique optimal alternative. Since, under the mCEI algorithm, 
$N_n^{(j)} \to \infty $ for all j, on almost every sample path, we will always have 
$j_n^* = 1$ for all large enough n. It is therefore sufficient to prove Theorems 3.1 and 3.2 for a simplified version of the mCEI algorithm with (3.2) replaced by
$$v_n^{(j)} = \sqrt {{{{{({\lambda ^{(j)}})}^2}} \over {N_n^{(j)}}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}}} f\left( { - {{|\theta _n^{(j)} - \theta _n^{(1)}|} \over {\sqrt {{{({\lambda ^{(j)}})}^2}/N_n^{(j)} + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}} {\kern 1pt} }}} \right),$$
(4.1)
and (3.3) replaced by
$${({{N_n^{(1)}} \over {{\lambda ^{(1)}}}})^2} \lt \sum\limits_{j \gt 1} {({{N_n^{(j)}} \over {{\lambda ^{(j)}}}})^2}.$$
(4.2)
To simplify the presentation of the key arguments, we treat the noise parameters λ (j) as being known. If in (2.2) we replace λ (j) by the sample standard deviation (as recommended, e.g. in both [Reference Jones, Schonlau and Welch13] and [Reference Salemi, Nelson, Staum and Tolk23]) then simply plug the resulting approximation into (3.2), the limiting allocation will not be affected. Because the rate-optimality framework of Glynn and Juneja [Reference Glynn and Juneja9] is frequentist and assumes that selection is based only on sample means, it does not make any distinction between known and unknown variances in terms of characterizing an optimal allocation.
4.1 Proof of Theorem 3.1
First, we define the quantity
$${\Delta _n}{\kern 1pt} : = {\kern 1pt} {({{N_n^{(1)}/{\lambda ^{(1)}}} \over n})^2} - \sum\limits_{j = 2}^M {({{N_n^{(j)}/{\lambda ^{(j)}}} \over n})^2}$$
and prove the following technical lemma. We remind the reader that, in this and all subsequent proofs, we assume that sampling decisions are made by the mCEI algorithm with (4.1) and ( 4.2) replacing (3.2) and (3.3).
Lemma 4.1
If alternative 1 is sampled at time n then Δn+1 − Δn > 0. If any other alternative is sampled at time n then Δn+1 − Δn < 0.
Proof. Suppose that alternative 1 is sampled at time n . Then
$$\matrix{
{{\Delta _{n + 1}} - {\Delta _n}} \hfill \cr
{\quad \quad = {{\left( {{{(N_n^{(1)} + 1)/{\lambda ^{(1)}}} \over {n + 1}}} \right)}^2} - \sum\limits_{j = 2}^M {{\left( {{{N_n^{(j)}/{\lambda ^{(j)}}} \over {n + 1}}} \right)}^2} - \left( {{{\left( {{{N_n^{(1)}/{\lambda ^{(1)}}} \over n}} \right)}^2} - \sum\limits_{j = 2}^M {{\left( {{{N_n^{(j)}/{\lambda ^{(j)}}} \over n}} \right)}^2}} \right)} \hfill \cr
{\quad \quad = {1 \over {{{({\lambda ^{(1)}})}^2}}}\left( {{{\left( {{{(N_n^{(1)} + 1)} \over {n + 1}}} \right)}^2} - {{\left( {{{N_n^{(1)}} \over n}} \right)}^2}} \right) + \left( {\sum\limits_{j = 2}^M {{\left( {{{N_n^{(j)}/{\lambda ^{(j)}}} \over n}} \right)}^2} - \sum\limits_{j = 2}^M {{\left( {{{N_n^{(j)}/{\lambda ^{(j)}}} \over {n + 1}}} \right)}^2}} \right)} \hfill \cr
{\quad \quad \gt 0.} \hfill \cr
} $$
If some alternative 
$j' \gt 1$ is sampled, then Δn ≥ 0 and
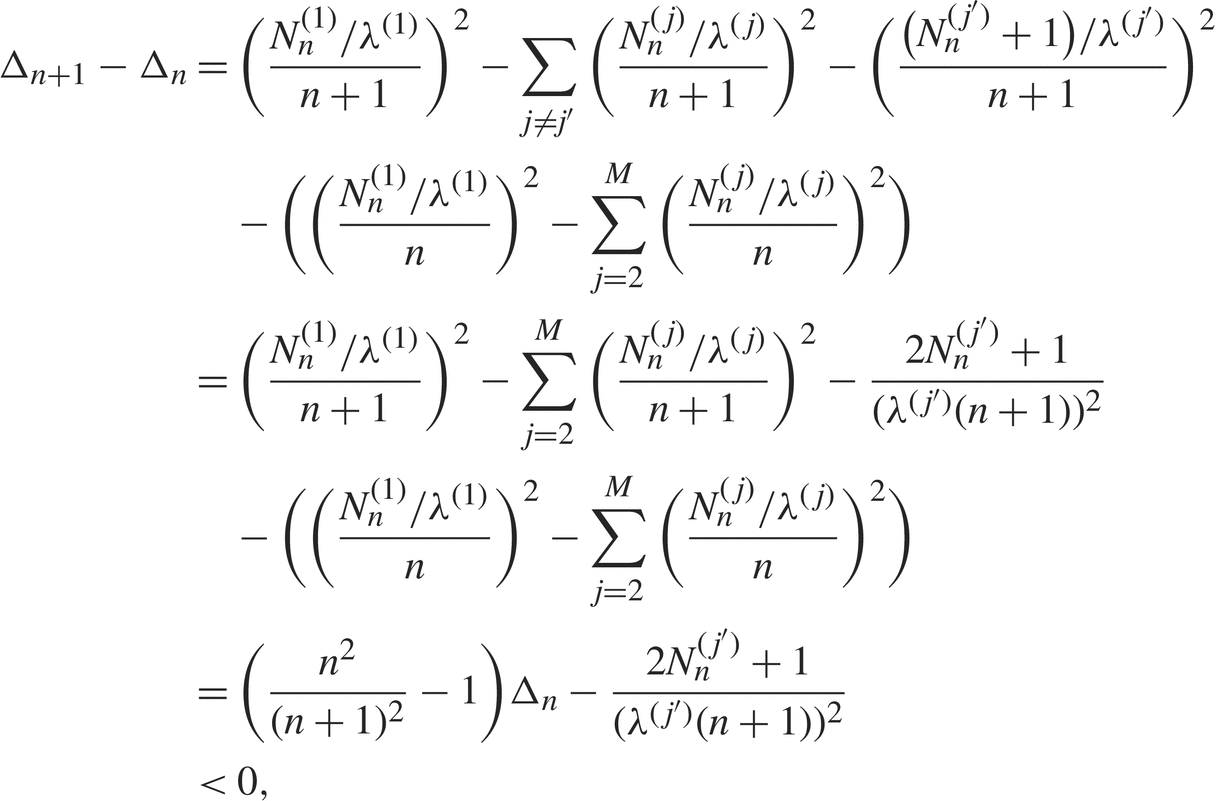$$\matrix{
{{\Delta _{n + 1}} - {\Delta _n} = ({{N_n^{(1)}/{\lambda ^{(1)}}} \over {n + 1}}{)^2} - \sum\limits_{j \ne j'} {{({{N_n^{(j)}/{\lambda ^{(j)}}} \over {n + 1}})}^2} - {{({{(N_n^{(j')} + 1)/{\lambda ^{(j')}}} \over {n + 1}})}^2}} \hfill \cr
{\quad {\rm{ }} - (({{N_n^{(1)}/{\lambda ^{(1)}}} \over n}{)^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}/{\lambda ^{(j)}}} \over n})}^2})} \hfill \cr
{{\rm{ }} = ({{N_n^{(1)}/{\lambda ^{(1)}}} \over {n + 1}}{)^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}/{\lambda ^{(j)}}} \over {n + 1}})}^2} - {{2N_n^{(j')} + 1} \over {{{({\lambda ^{(j')}}(n + 1))}^2}}}} \hfill \cr
{\quad {\rm{ }} - (({{N_n^{(1)}/{\lambda ^{(1)}}} \over n}{)^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}/{\lambda ^{(j)}}} \over n})}^2})} \hfill \cr
{{\rm{ }} = ({{{n^2}} \over {{{(n + 1)}^2}}} - 1){\Delta _n} - {{2N_n^{(j')} + 1} \over {{{({\lambda ^{(j')}}(n + 1))}^2}}}} \hfill \cr
{{\rm{ }} \lt 0,} \hfill \cr
} $$
which completes the proof.
Let 
$\ell = \mathop {\min }\nolimits_j {\lambda ^{(j)}}$ and recall that ℓ > 0 by assumption. Now, for all ɛ > 0, there exists a large enough n 1 such that 
${n_1} \gt 2/{\ell ^2}\varepsilon - 1$. Consider arbitrary n ≥ n 1 and suppose that Δn < 0. This means that alternative 1 is sampled at time n, whence Δn + 1 − Δn > 0 by Lemma 4.1.
Furthermore,
$$\matrix{
{{\Delta _{n + 1}} = ({{(N_n^{(1)} + 1)/{\lambda ^{(1)}}} \over {n + 1}}{)^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}/{\lambda ^{(j)}}} \over {n + 1}})}^2}} \hfill \cr
{{\rm{ }} = {\Delta _n} + {{2N_n^{(1)} + 1} \over {{{({\lambda ^{(1)}}(n + 1))}^2}}}} \hfill \cr
} $$
$$
{\quad {\rm{ }} \lt {{2n + 2} \over {{{({\lambda ^{(1)}}(n + 1))}^2}}}} \hfill \cr
{\quad {\rm{ }} \le {2 \over {{{({\lambda ^{(1)}})}^2}({n_1} + 1)}}} \hfill \cr
{\quad {\rm{ }} \lt {{{\ell ^2}} \over {{{({\lambda ^{(1)}})}^2}}}\varepsilon } \hfill \cr
{\quad {\rm{ }} \le \varepsilon .} \hfill \cr$$
Similarly, suppose that Δn ≥ 0. This means that some j > 1 is sampled, whence Δn+1 − Δn < 0 by Lemma 4.1. Using similar arguments as before, we find that
$$\matrix{
{{\Delta _{n + 1}} = ({{N_n^{(1)}/{\lambda ^{(1)}}} \over {n + 1}}{)^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}/{\lambda ^{(j)}}} \over {n + 1}})}^2} - {{2N_n^{(j')} + 1} \over {{{({\lambda ^{(j')}}(n + 1))}^2}}}} \hfill \cr
{{\rm{ }} = {\Delta _n} - {{2N_n^{(j')} + 1} \over {{{({\lambda ^{(j')}}(n + 1))}^2}}}} \hfill \cr
{{\rm{ }} \ge - {{2n + 2} \over {{{({\lambda ^{(j')}}(n + 1))}^2}}}} \hfill \cr
{{\rm{ }} \ge - \varepsilon .} \hfill \cr
} $$
Thus, if there exists some large enough n 2 satisfying n 2 ≥ n 1 and 
$ - \varepsilon \lt {\Delta _{{n_2}}} \lt \varepsilon $, then it follows that, for all n ≥ n 2 , we have Δn ∈ (−ɛ, ɛ ), which implies that 
$\mathop {\lim }\nolimits_{n \to \infty } {\Delta _n} = 0$ and completes the proof of Theorem 3.1. It only remains to show the existence of such n 2.
Again, we consider two cases. First, suppose that Δn1 < 0. Since the mCEI algorithm samples every alternative infinitely often, we can let n 2 = inf {n > n 1: Δn ≥ 0} . Since n 2 will be the first time after n 1 that any j′ > 1 is sampled, we have Δn2 − 1 < 0 and n 2 −1 ≥ n 1. From the previous arguments we have 0 ≤ Δn2 < ɛ. Similarly, in the second case where Δn1 ≥ 0, we let n 2 = inf {n > n 1: Δn < 0} , whence Δn2 −1 ≥ 0 and n 2 − 1 ≥ n 1. The previous arguments imply that −ɛ < Δn2 < 0. Thus, we can always find n 2 ≥ n 1 satisfying − ɛ < Δn2 < ɛ, as required.
4.2 Proof of Theorem 3.2
The proof relies on several technical lemmas. To present the main argument more clearly, these lemmas are stated here, and the full proofs are given in Appendix A. For notational convenience, we define 
$d_n^{(j)}{\kern 1pt} : = {\kern 1pt} |\theta _n^{(j)} - \theta _n^{(1)}|$ and 
$\delta _n^{(j)} = (d_n^{(j)}{)^2}$ for all j > 1. Furthermore, for any j and any positive integer m, we define
$$k_{(n,n + m)}^{(j)}{\kern 1pt} : = {\kern 1pt} N_{n + m}^{(j)} - N_n^{(j)}$$
to be the number of samples allocated to alternative j from stage n to stage n + m −1.
The first technical lemma implies that, for any two alternatives i and j, 
$N_n^{(i)} = \Theta (N_n^{(j)})$ and 
$N_n^{(i)} = \Theta (n)$.
Lemma 4.2
For any two alternatives i and j, 
$\mathop {\lim {\rm{ }}sup}\nolimits_{n \to \infty } N_n^{(i)}/N_n^{(j)} \lt \infty $.
Now let
$$z_n^{(j)}{\kern 1pt} : = {\kern 1pt} {{d_n^{(j)}} \over {\sqrt {{{({\lambda ^{(j)}})}^2}/N_n^{(j)} + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}} {\kern 1pt} }},\quad \quad t_n^{(j)}{\kern 1pt} : = {\kern 1pt} {(z_n^{(j)})^2} = {{\delta _n^{(j)}} \over {{{({\lambda ^{(j)}})}^2}/N_n^{(j)} + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}}}.$$
For any j, both 
$z_n^{(j)}$ and 
$t_n^{(j)}$ go to ∞ as n →∞. We apply an expansion of the Mills ratio [Reference Ruben19] to 
$v_n^{(j)}$. For all large enough n,
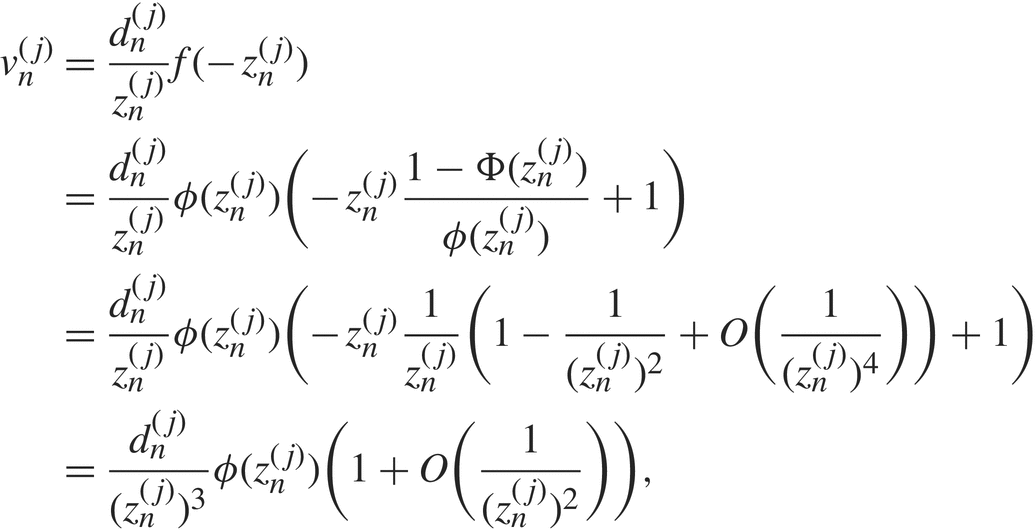$$\matrix{
{v_n^{(j)} = {{d_n^{(j)}} \over {z_n^{(j)}}}f( - z_n^{(j)})} \hfill \cr
{{\rm{ }} = {{d_n^{(j)}} \over {z_n^{(j)}}}\phi (z_n^{(j)})( - z_n^{(j)}{{1 - \Phi (z_n^{(j)})} \over {\phi (z_n^{(j)})}} + 1)} \hfill \cr
{{\rm{ }} = {{d_n^{(j)}} \over {z_n^{(j)}}}\phi (z_n^{(j)})( - z_n^{(j)}{1 \over {z_n^{(j)}}}(1 - {1 \over {{{(z_n^{(j)})}^2}}} + O({1 \over {{{(z_n^{(j)})}^4}}})) + 1)} \hfill \cr
{{\rm{ }} = {{d_n^{(j)}} \over {{{(z_n^{(j)})}^3}}}\phi (z_n^{(j)})(1 + O({1 \over {{{(z_n^{(j)})}^2}}})),} \hfill \cr
} $$
(4.3)
where (4.3) comes from the Mills ratio. Then
$$\matrix{
{2\log (v_n^{(j)}) = 2\log d_n^{(j)} - 6\log z_n^{(j)} + 2\log \phi (z_n^{(j)}) + 2\log (1 + O({1 \over {{{(z_n^{(j)})}^2}}}))} \hfill \cr
{{\rm{ }} = \log \delta _n^{(j)} - 3\log t_n^{(j)} - \log (2\pi ) - t_n^{(j)} + 2\log (1 + O({1 \over {t_n^{(j)}}}))} \hfill \cr
{{\rm{ }} = - t_n^{(j)}(1 + O({{\log t_n^{(j)}} \over {t_n^{(j)}}})).} \hfill \cr
} $$
For any two suboptimal alternatives i and j, define
$$r_n^{(i,j)}{\kern 1pt} : = {\kern 1pt} {{2\log (v_n^{(i)})} \over {2\log (v_n^{(j)})}} = {{t_n^{(i)}} \over {t_n^{(j)}}}{{1 + O(\log t_n^{(i)}/t_n^{(i)})} \over {1 + O(\log t_n^{(j)}/t_n^{(j)})}},$$
(4.4)
and note that both 
$1 + O(\log t_n^{(i)}/t_n^{(i)})$ and 
$1 + O(\log t_n^{(j)}/t_n^{(j)})$ converge to 1 as n →∞. We will show that 
$r_n^{(i,j)} \to 1$ for any suboptimal i and j ; then (4.4) will yield 
$t_n^{(i)}/t_n^{(j)} \to 1$, completing the proof of Theorem 3.2.
Note that, for any j, the CEI quantity 
$v_n^{\left( j \right)}$ can change when either j or the optimal alternative is sampled. Thus, it is necessary to characterize the relative frequency of such samples. This requires three other technical lemmas, which are stated below and proved in Appendix A.First, Lemma 4.3 shows that the number of samples that could be allocated to the optimal alternative between two samples of any suboptimal alternatives (not necessarily the same one) is O (1) and vice versa; next, Lemma 4.4 shows that 
$k_{(n,n + m)}^{(1)}$ is 
$O\left( {\sqrt {n\log \log n} } \right)$; finally, Lemma 4.5 bounds 
${n^{3/4}}|\delta _{n + 1}^{(i)} - \delta _n^{(i)}|$
Lemma 4.3
Between two samples assigned to any suboptimal alternatives (i.e. two time stages when condition (4.2) fails), the number of samples that could be allocated to the optimal alternative is at most equal to some fixed constant B 1 ; symmetrically, between two samples of alternative 1, the number of samples that could be allocated to any suboptimal alternatives is at most equal to some fixed constant B 2.
Lemma 4.4
On almost every sample path, there exists a fixed positive constant C < ∞ and time n 0 ≥ 3 such that, for any n ≥ n 0 in which some suboptimal alternative i is sampled and
$$m{\kern 1pt} : = {\rm{ }}\inf \{ l \gt 0:I_{n + l}^{(i)} = 1\} ,$$
we have 
$k_{(n,n + m)}^{(1)} \le C\sqrt {n\log \log n} $
Lemma 4.5
For any alternative i, 
${n^{3/4}}|\delta _{n + 1}^{(i)} - \delta _n^{(i)}| \to 0$ almost surely as n →∞.
Let i, j > 1, and suppose that i is sampled at stage n. We will first place an 
$O\left( {1/{n^{3/4}}} \right)$ bound on the increment 
$r_{n + 1}^{\left( {i,j} \right)} - r_n^{\left( {i,j} \right)}.$ We will then place a bound of 
$O(\sqrt {n\log \log n} /{n^{3/4}})$ on the growth of 
$(r_n^{(i,j)})$ in between two samples of i (note that, by definition, 
$r_n^{(i,j)} \le 1$ at any stage n when i is sampled). As this bound vanishes to 0 as n →∞, it will then be shown to follow that 
$r_n^{(i,j)} \to 1.$
If i is sampled at stage n then 
$r_n^{(i,j)} \le 1$ and
$$\matrix{
{r_{n + 1}^{(i,j)} - r_n^{(i,j)} = {{\log (v_{n + 1}^{(i)})} \over {\log (v_{n + 1}^{(j)})}} - {{\log (v_n^{(i)})} \over {\log (v_n^{(j)})}}} \hfill \cr
{{\rm{ }} = {{\log (v_{n + 1}^{(i)}) - \log (v_n^{(i)})} \over {\log (v_n^{(j)})}}} \hfill \cr
{{\rm{ }} \le {{|\log (v_{n + 1}^{(i)}) - \log (v_n^{(i)})|} \over {|\log (v_n^{(j)})|}}} \hfill \cr
{{\rm{ }} = {{{n^{1/4}}} \over {2|\log (v_n^{(j)})|}}{1 \over {{n^{1/4}}}}\left| {\left( {{{\delta _{n + 1}^{(i)}} \over {{{{{({\lambda ^{(i)}})}^2}} \over {N_n^{(i)} + 1}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}}}} - {{\delta _n^{(i)}} \over {{{{{({\lambda ^{(i)}})}^2}} \over {N_n^{(i)}}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}}}}} \right)} \right.} \hfill \cr
{\quad {\rm{ }} + 3\left( {\log {{\delta _{n + 1}^{(i)}} \over {{{{{\left( {{\lambda ^{(i)}}} \right)}^2}} \over {N_n^{(i)} + 1}} + {{{{\left( {{\lambda ^{(1)}}} \right)}^2}} \over {N_n^{(1)}}}}} - \log {{\delta _n^{(i)}} \over {{{{{\left( {{\lambda ^{(i)}}} \right)}^2}} \over {N_n^{(i)}}} + {{{{\left( {{\lambda ^{(1)}}} \right)}^2}} \over {N_n^{(1)}}}}}} \right)} \hfill \cr
{\quad {\rm{ }} - 2[\log (1 + O({{{{({\lambda ^{(i)}})}^2}} \over {N_n^{(i)} + 1}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}}))} \hfill \cr
{\quad {\rm{ }} - \log (1 + O({{{{({\lambda ^{(i)}})}^2}} \over {N_n^{(i)}}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}}))]} \hfill \cr
{\quad {\rm{ }} - (\log \delta _{n + 1}^{(i)} - \log \delta _n^{(i)})|.} \hfill \cr
} $$
(4.5)
By Lemma 4.2, there exists a positive constant C 1 such that, for all large enough n,
$$\matrix{
{{{2|\log (v_n^{(j)})|} \over {{n^{1/4}}}} = {{t_n^{(j)}} \over {{n^{1/4}}}}(1 + O({{\log t_n^{(j)}} \over {t_n^{(j)}}}))} \hfill \cr
{{\rm{ }} \gt {1 \over {2{n^{1/4}}}}{{\delta _n^{(j)}} \over {{{({\lambda ^{(j)}})}^2}/N_n^{(j)} + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}}}} \hfill \cr
} $$
$$
{{\rm{ }} \ge {C_1}{n \over {{n^{1/4}}}}} \hfill \cr
{{\rm{ }} = {C_1}{n^{3/4}}.} \hfill \cr
$$
On the other hand, for all large enough n, there also exists a positive constant C 2 such that
$$\matrix{
{{1 \over {{n^{1/4}}}}\left| {{{\delta _{n + 1}^{(i)}} \over {{{({\lambda ^{(i)}})}^2}/(N_n^{(i)} + 1) + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}}} - {{\delta _n^{(i)}} \over {{{({\lambda ^{(i)}})}^2}/N_n^{(i)} + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}}}} \right|} \hfill \cr
{ \le {1 \over {{n^{1/4}}}}(|{{\delta _{n + 1}^{(i)}} \over {{{({\lambda ^{(i)}})}^2}/(N_n^{(i)} + 1) + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}}} - {{\delta _{n + 1}^{(i)}} \over {{{({\lambda ^{(i)}})}^2}/N_n^{(i)} + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}}}|} \hfill \cr
{\quad + |{{\delta _{n + 1}^{(i)}} \over {{{({\lambda ^{(i)}})}^2}/N_n^{(i)} + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}}} - {{\delta _n^{(i)}} \over {{{({\lambda ^{(i)}})}^2}/N_n^{(i)} + {{({\lambda ^{(1)}})}^2}/N_n^{(1)}}}|)} \hfill \cr
{ = {1 \over {{n^{1/4}}}}(O(1) + O(n)|\delta _{n + 1}^{(i)} - \delta _n^{(i)}|)} \hfill \cr
{ = O(1)({1 \over {{n^{1/4}}}} + {n^{3/4}}|\delta _{n + 1}^{(i)} - \delta _n^{(i)}|)} \hfill \cr
{ = O\left( 1 \right)} \hfill \cr
{ \le {C_2},} \hfill \cr
} $$
where the first equality holds from Lemma 4.2 and the last equality holds from Lemma 4.5. Then, for all large enough n, we have
$$\matrix{
{{3 \over {{n^{1/4}}}}|\log {{\delta _{n + 1}^{(i)}} \over {{{\left( {{\lambda ^{(i)}}} \right)}^2}/(N_n^{(i)} + 1) + {{\left( {{\lambda ^{(1)}}} \right)}^2}/N_n^{(1)}}} - \log {{\delta _n^{(i)}} \over {{{\left( {{\lambda ^{(i)}}} \right)}^2}/N_n^{(i)} + {{\left( {{\lambda ^{(1)}}} \right)}^2}/N_n^{(1)}}}|} \hfill \cr
{ \le {3 \over {{n^{1/4}}}}|{{\delta _{n + 1}^{(i)}} \over {{{\left( {{\lambda ^{(i)}}} \right)}^2}/(N_n^{(i)} + 1) + {{\left( {{\lambda ^{(1)}}} \right)}^2}/N_n^{(1)}}} - {{\delta _n^{(i)}} \over {{{\left( {{\lambda ^{(i)}}} \right)}^2}/N_n^{(i)} + {{\left( {{\lambda ^{(1)}}} \right)}^2}/N_n^{(1)}}}|} \hfill \cr
{ \le 3{C_2},} \hfill \cr
} $$
and
$$\matrix{
{|{2 \over {{n^{1/4}}}}[\log (1 + O({{{{({\lambda ^{(i)}})}^2}} \over {N_n^{(i)} + 1}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}})) - \log (1 + O({{{{({\lambda ^{(i)}})}^2}} \over {N_n^{(i)}}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}}))]|} \hfill \cr
{\quad + {1 \over {{n^{1/4}}}}|\log \delta _{n + 1}^{(i)} - \log \delta _n^{(i)}|} \hfill \cr
{ \le {2 \over {{n^{1/4}}}}[|\log (1 + O({{{{({\lambda ^{(i)}})}^2}} \over {N_n^{(i)} + 1}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}}))| + |\log (1 + O({{{{({\lambda ^{(i)}})}^2}} \over {N_n^{(i)}}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}}))|]} \hfill \cr
{\quad + {1 \over {{n^{1/4}}}}|\log \delta _{n + 1}^{(i)} - \log \delta _n^{(i)}|} \hfill \cr
{ \le {C_2}.} \hfill \cr
} $$
We now have bounded all four terms in (4.5). Therefore, for all large enough n, we have
$$r_{n + 1}^{(i,j)} - r_n^{(i,j)} \le {{5{C_2}/{C_1}} \over {{n^{3/4}}}},$$
and
$$r_{n + 1}^{(i,j)} - 1 \le r_n^{(i,j)} - 1 + {{5{C_2}/{C_1}} \over {{n^{3/4}}}} \le {{5{C_2}/{C_1}} \over {{n^{3/4}}}}.$$
Thus, we have established a bound on the growth of 
$$r_n^{(i,j)}$ that can occur as a result of sampling i at time n.
We now consider the growth of the ratio between stages n and n + m, where
$$m{\kern 1pt} : = \inf \{ l \gt 0{\kern 1pt} :{\kern 1pt} I_{n + l}^{(i)} = 1\} ,$$
as in the statement of Lemma 4.4. In words, n + m is the index of the next time after n that we sample i. For any stage n + s with 0 < s ≤ m, the inequality 
$r_{n + s + 1}^{(i,j)} \gt r_{n + s}^{(i,j)}$ can only hold if alternative j or the optimal alternative is sampled at stage n + s.
If alternative j is sampled at stage n + s then
$$\matrix{
{r_{n + s + 1}^{(i,j)} - r_{n + s}^{(i,j)} = {{\log (v_{n + s + 1}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}} - {{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s}^{(j)})}}} \hfill \cr
{{\rm{ }} = {{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}} - {{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s}^{(j)})}}} \hfill \cr
{{\rm{ }} \le |{{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}}|{{|\log (v_{n + s + 1}^{(j)}) - \log (v_{n + s}^{(j)})|} \over {|\log (v_{n + s}^{(j)})|}}.} \hfill \cr
} $$
Using similar arguments as above, we have
$${{|\log (v_{n + s + 1}^{(j)}) - \log (v_{n + s}^{(j)})|} \over {|\log (v_{n + s}^{(j)})|}} = O((n + s{)^{ - 3/4}}) = O({n^{ - 3/4}}),$$
and, by Lemma 4.2,
$$|{{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}}| = O(1).$$
Thus, there exists a constant C 3 such that
$$r_{n + s + 1}^{(i,j)} - r_{n + s}^{(i,j)} \le {C_3}{n^{ - 3/4}}.$$
On the other hand, if alternative 1 is sampled at stage n + s then
$$\matrix{
{r_{n + s + 1}^{(i,j)} - r_{n + s}^{(i,j)} = {{\log (v_{n + s + 1}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}} - {{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s}^{(j)})}}} \hfill \cr
{ \le \left| {{{\log (v_{n + s + 1}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}} - {{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}}} \right| + \left| {{{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}} - {{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s}^{(j)})}}} \right|} \hfill \cr
{ = \left| {{{\log (v_{n + s + 1}^{(i)}) - \log (v_{n + s}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}}} \right| + \left| {{{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}}} \right|{{|\log (v_{n + s + 1}^{(j)}) - \log (v_{n + s}^{(j)})|} \over {|\log (v_{n + s}^{(j)})|}}.} \hfill \cr
} $$
Similarly as above, we have
$$\matrix{
{\left| {{{\log (v_{n + s + 1}^{(i)}) - \log (v_{n + s}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}}} \right| = O({n^{ - 3/4}}),} \cr
{\left| {{{\log (v_{n + s}^{(i)})} \over {\log (v_{n + s + 1}^{(j)})}}} \right|{{|\log (v_{n + s + 1}^{(j)}) - \log (v_{n + s}^{(j)})|} \over {|\log (v_{n + s}^{(j)})|}} = O({n^{ - 3/4}}).} \cr
} $$
Then there exists a constant C 4 such that
$$r_{n + s + 1}^{(i,j)} - r_{n + s}^{(i,j)} \le {C_4}{n^{ - 3/4}}.$$
Therefore, in all cases, for all large enough n, we have
$$r_{n + s + 1}^{(i,j)} - r_{n + s}^{(i,j)} \le {{{C_5}} \over {{n^{3/4}}}},$$
where 
${C_5} = \max \left\{ {5{C_2}/{C_1},{C_3},{C_4}} \right\}.$ It follows that
$$\matrix{
{r_{n + s + 1}^{(i,j)} - 1 \le r_{n + s}^{(i,j)} - 1 + {{{C_5}} \over {{n^{3/4}}}}} \hfill \cr
{{\rm{ }} \le r_n^{(i,j)} - 1 + (1 + k_s^{(j)} + k_s^{(1)}){{{C_5}} \over {{n^{3/4}}}}} \hfill \cr
{{\rm{ }} \le (1 + k_s^{(j)} + k_s^{(1)}){{{C_5}} \over {{n^{3/4}}}}.} \hfill \cr
} $$
However, from Lemma 4.4, we have 
$k_s^{(1)} \le k_m^{(1)} = O\left( {\sqrt {n\log \log n} } \right)$ for all 0 < s ≤ m, and at the same time, from Lemma 4.3, we know that at most B 2 samples could be allocated to any suboptimal alternatives between two samples of alternative 1. Then we also have 
$k_s^{(j)} \le k_m^{(j)} \le {B_2}(k_m^{(1)} + 1)$, whence 
$k_m^{(j)} = O\left( {\sqrt {n\log \log n} } \right).$ It follows that
$$r_{n + s + 1}^{(i,j)} - 1 \le (1 + k_m^{(j)} + k_m^{(1)}){{{C_5}} \over {{n^{3/4}}}} = O({{\sqrt {n\log \log n} } \over {{n^{3/4}}}}),$$
whence 
$\mathop {\lim {\rm{ }}sup}\nolimits_{n \to \infty } r_n^{(i,j)} = 1$. By symmetry,
$$\mathop {\lim {\rm{ }}inf}\limits_{n \to \infty } r_n^{(i,j)} = \mathop {\lim {\rm{ }}sup}\limits_{n \to \infty } r_n^{(j,i)} = 1,$$
whence 
$\mathop {\lim }\nolimits_{n \to \infty } r_n^{(i,j)} = 1.$ This completes the proof.
5 Conclusion
We have considered a ranking and selection problem with independent normal priors and samples, and shown that an EI-type method (a modified version of the CEI method of [Reference Salemi, Nelson, Staum and Tolk23]) achieves the rate-optimality conditions of [Reference Glynn and Juneja9] asymptotically. While convergence to the rate-optimal static allocation need not preserve the convergence rate of that allocation, nonetheless, the static framework of [Reference Glynn and Juneja9] is widely used by the simulation community as a guide for the development of dynamic algorithms, and from this viewpoint it is noteworthy that simple and efficient algorithms can learn optimal static allocations without tuning or approximations.
This paper strengthens the existing body of theoretical support for EI-type methods in general, and for the CEI method in particular. An interesting question is whether CEI would continue to perform optimally in, e.g. the more general Gaussian Markov framework of [Reference Salemi, Nelson, Staum and Tolk23]. However, the current theoretical understanding of such models is quite limited, and more fundamental questions (for example, how correlated Bayesian models impact the rate of convergence) should be answered before any particular algorithm can be analyzed.
Appendix A Additional proofs
Below, we give the full proofs of some technical lemmas that were stated in the main text.
A.1 Proof of Lemma 4.2
We proceed by contradiction. Suppose that i, j > 1 satisfy 
$\mathop {\lim {\rm{ }}sup}\nolimits_{n \to \infty } N_n^{(i)}/N_n^{(j)} = \infty $. Let 
$c = \mathop {\lim }\nolimits_{n \to \infty } \delta _n^{(j)}/\delta _n^{(i)} + 1 = ({\mu ^{(j)}} - {\mu ^{(1)}}{)^2}/({\mu ^{(i)}} - {\mu ^{(1)}}{)^2} + 1.$ Then, there must exist a large enough stage m such that
$${{N_m^{(i)}} \over {N_m^{(j)}}} \gt \max \{ c,1\} {{{{({\lambda ^{(i)}})}^2} + {\lambda ^{(1)}}{\lambda ^{(i)}}} \over {{{({\lambda ^{(j)}})}^2}}}$$
,
and we will sample alternative i to make 
$N_{m + 1}^{(i)}/N_{m + 1}^{(j)} \gt N_m^{(i)}/N_m^{(j)}$. But, at this stage m,
$$\matrix{
{v_m^{(i)} = \sqrt {{{{{({\lambda ^{(i)}})}^2}} \over {N_m^{(i)}}} + {{{{({\lambda ^{(1)}})}^2}} \over {N_m^{(1)}}}} f\left( { - {{d_m^{(i)}} \over {\sqrt {{{({\lambda ^{(i)}})}^2}/N_m^{(i)} + {{({\lambda ^{(1)}})}^2}/N_m^{(1)}} {\kern 1pt} }}} \right)} \cr
{{\rm{ }} \le \sqrt {{{{{\left( {{\lambda ^{(i)}}} \right)}^2}} \over {N_m^{(i)}}} + {{{\lambda ^{(1)}}{\lambda ^{(i)}}} \over {N_m^{(i)}}}} f\left( { - {{d_m^{(i)}} \over {\sqrt {{{({\lambda ^{(i)}})}^2}/N_m^{(i)} + {\lambda ^{(1)}}{\lambda ^{(i)}}/N_m^{(i)}} {\kern 1pt} }}} \right)} \cr
} $$
(A.1)
$$\matrix{
{ = \sqrt {{{{{\left( {{\lambda ^{(i)}}} \right)}^2} + {\lambda ^{(1)}}{\lambda ^{(i)}}} \over {N_m^{(i)}}}} f\left( { - {{d_m^{(i)}} \over {\sqrt {(({\lambda ^{(i)}}{)^2} + {\lambda ^{(1)}}{\lambda ^{(i)}})/N_m^{(i)}} {\kern 1pt} }}} \right)} \cr
{ \lt \sqrt {{{{{\left( {{\lambda ^{(j)}}} \right)}^2}} \over {N_m^{(j)}}}} f\left( { - {{d_m^{(j)}} \over {\sqrt {{{({\lambda ^{(j)}})}^2}/N_m^{(j)}} {\kern 1pt} }}} \right)} \cr
} $$
(A.2)
$$\matrix{
{ \lt \sqrt {{{{{\left( {{\lambda ^{(j)}}} \right)}^2}} \over {N_m^{(j)}}} + {{{{\left( {{\lambda ^{(1)}}} \right)}^2}} \over {N_m^{(1)}}}} f\left( { - {{d_m^{(j)}} \over {\sqrt {{{({\lambda ^{(j)}})}^2}/N_m^{(j)} + {{({\lambda ^{(1)}})}^2}/N_m^{(1)}} {\kern 1pt} }}} \right)} \cr
{ = v_m^{(j)},} \cr
} $$
(A.3)
where (A.1) holds because a suboptimal alternative is sampled at stage m, and (A.2) holds because 
$\mathop {\lim }\nolimits_{m \to \infty } d_m^{(j)}/d_m^{(i)} = |({\mu ^{(j)}} - {\mu ^{(1)}})|/|({\mu ^{(i)}} - {\mu ^{(1)}})|.$ From the definition of the mCEI algorithm, (A.3) implies that we cannot sample i at stage m. We conclude that 
$\mathop {\lim {\rm{ }}sup}\nolimits_{n \to \infty } N_n^{(i)}/N_n^{(j)} \lt \infty $ for any two suboptimal alternatives i and j.
From this result, we can see that, for i, j > 1, we have
$$0 \lt \mathop {\lim \,inf}\limits_{n \to \infty } {{N_n^{(i)}} \over {N_n^{(j)}}} \le \mathop {\lim \,sup}\limits_{n \to \infty } {{N_n^{(i)}} \over {N_n^{(j)}}} \lt \infty .$$
Together with Theorem 3.1, this implies that, for any i > 1, we have
$$0 \lt \mathop {\lim \,inf}\limits_{n \to \infty } {{N_n^{(i)}} \over {N_n^{(1)}}} \le \mathop {\lim \,sup}\limits_{n \to \infty } {{N_n^{(i)}} \over {N_n^{(1)}}} \lt \infty ,$$
completing the proof.
A.2 Proof of Lemma 4.3
Define 
${Q_n}{\kern 1pt} : = {\kern 1pt} {(N_n^{(1)}/{\lambda ^{(1)}})^2} - \sum\nolimits_{j = 2}^M {(N_n^{(j)}/{\lambda ^{(j)}})^2}.$ Suppose that, at some stage n, Qn < 0 and Q n + 1 ≥ 0, which means that the optimal alternative is sampled at time n and then a suboptimal alternative is sampled at time n + 1. Let 
$m{\kern 1pt} : = {\rm{ }}{\kern 1pt} \inf \left\{ {l \gt 0:{Q_{n + l}} \lt 0} \right\}$, i.e. stage n + m is the first time that alternative 1 is sampled after stage n. Then, in order to show that between two samples of alternative 1, the number of samples that could be allocated to suboptimal alternatives is O (1), it is sufficient to show that m = O (1).
To show this, first we can see that
$$\matrix{
{{Q_{n + 1}} = ({{N_n^{(1)} + 1} \over {{\lambda ^{(1)}}}}{)^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}} \over {{\lambda ^{(j)}}}})}^2}} \hfill \cr
{{\rm{ }} = ({{N_n^{(1)}} \over {{\lambda ^{(1)}}}}{)^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}} \over {{\lambda ^{(j)}}}})}^2} + {{2N_n^{(1)} + 1} \over {{{({\lambda ^{(1)}})}^2}}}} \hfill \cr
{{\rm{ }} = {Q_n} + {{2N_n^{(1)} + 1} \over {{{({\lambda ^{(1)}})}^2}}}} \hfill \cr
\matrix{
{\rm{ }} \lt {{2N_n^{(1)} + 1} \over {{{({\lambda ^{(1)}})}^2}}} \hfill \cr
{\rm{ }} \le {C_1}N_n^{(1)}, \hfill \cr} \hfill \cr
} $$
(A.4)
where C 1 is a suitable fixed positive constant and the first inequality holds because Qn < 0. Then, for any stage n + s, where 0 < s < m, we have
$$\matrix{
{{Q_{n + s}} = ({{N_{n + s}^{(1)}} \over {{\lambda ^{(1)}}}}{)^2} - \sum\limits_{j = 2}^M {{({{N_{n + s}^{(j)}} \over {{\lambda ^{(j)}}}})}^2}} \hfill \cr
{{\rm{ }} = ({{N_{n + 1}^{(1)}} \over {{\lambda ^{(1)}}}}{)^2} - \sum\limits_{j = 2}^M {{({{N_{n + s}^{(j)}} \over {{\lambda ^{(j)}}}})}^2}} \hfill \cr
{{\rm{ }} = ({{N_n^{(1)} + 1} \over {{\lambda ^{(1)}}}}{)^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}} \over {{\lambda ^{(j)}}}})}^2} - (\sum\limits_{j = 2}^M {{({{N_{n + s}^{(j)}} \over {{\lambda ^{(j)}}}})}^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}} \over {{\lambda ^{(j)}}}})}^2})} \hfill \cr
{{\rm{ }} \lt {C_1}N_n^{(1)} - (\sum\limits_{j = 2}^M {{({{N_{n + s}^{(j)}} \over {{\lambda ^{(j)}}}})}^2} - \sum\limits_{j = 2}^M {{({{N_n^{(j)}} \over {{\lambda ^{(j)}}}})}^2}),} \hfill \cr
} $$
where the inequality holds because of (A.4). We can also see that, after stage n, the increment of 
$\sum\nolimits_{j = 2}^M {(N_n^{(j)}/{\lambda ^{(j)}})^2}$ obtained by allocating a sample to alternative j is at least 
$2N_n^{(j)}/({\lambda ^{(j)}}{)^2}.$
Then, for all large enough n,
$$\sum\limits_{j = 2}^M {({{N_{n + s}^{(j)}} \over {{\lambda ^{(j)}}}})^2} - \sum\limits_{j = 2}^M {({{N_n^{(j)}} \over {{\lambda ^{(j)}}}})^2} \ge 2s{{\mathop {\min }\limits_{\{ j \gt 1\} } N_n^{(j)}} \over {\mathop {\max }\limits_{\{ j \gt 1\} } {{({\lambda ^{(j)}})}^2}}} \ge {C_2}sN_n^{(1)},$$
where C 2 is a suitable positive constant and the last inequality follows by Lemma 4.2. Therefore, for any 0 < s < m, we have 
${Q_{n + s}} \lt \left( {{C_1} - {C_2}s} \right)N_n^{(1)}$. But, from the definition of m, for any 0 < s < m, Q n+s ≥ 0 must hold. Thus, any 0 < s < m cannot be greater than C 1 / C 2; in other words, we must have m ≤ C 1 / C 2 + 1, which implies that m = O (1) for all large enough n. This proves the second claim of the lemma. The first claim of the lemma can be proved in a similar way due to symmetry.
A.3 Proof of Lemma 4.4
We first introduce a technical lemma, which establishes a relationship between 
$k_{(n,n + m)}^{(1)}$ and samples assigned to suboptimal alternatives. The lemma is proved in Appendix A.5.
Lemma A.1
Fix a sample path, and let C 1 be any positive constant. For a time stage n at which some suboptimal alternative i > 1 is sampled, define
$$m{\kern 1pt} : = {\kern 1pt} \inf \{ l \gt 0:I_{n + l}^{(i)} = 1\} ,\quad \quad s{\kern 1pt} : = {\kern 1pt} \sup \{ l \lt m:I_{n + l}^{(1)} = 0\} .$$
Suppose that there are infinitely many time stages n in which the condition
$${C_2}\sqrt {n\log \log n} \le k_{(n,n + s)}^{(1)} \le n$$
holds, where C 2 is a positive constant whose value does not depend on these values of n (but may depend on C 1). Then, for such large enough n, there exists some suboptimal alternative j ≠ i and a time stage n + u, where u ≤ s, such that j is sampled at stage n + u and
$$(1 + {C_1}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}} \lt {{N_n^{(j)} + k_{(n,n + u)}^{(j)}} \over {N_n^{(1)} + k_{(n,n + s)}^{(1)}}} \le {{N_n^{(j)} + k_{(n,n + u)}^{(j)}} \over {N_n^{(1)} + k_{(n,n + u)}^{(1)}}},$$
(A.5)
holds.
Essentially, Lemma A.1 will be used to prove the desired result by contradiction; we will show that (A.5) cannot arise, and, therefore, 
$k_{(n,n + m)}^{(j)}$ must be 
$O(\sqrt {n\log \log n} ).$
For convenience, we abbreviate 
$k_{(n,n + m)}^{(j)}$ by the notation 
$k_m^{(j)}$. We will prove the lemma by contradiction. Suppose that the conclusion of the lemma does not hold, that is, 
$k_m^{(1)}/\sqrt {n\log \log n} $ can be arbitrarily large. Since we sample i > 1 at stage n, then, for any other suboptimal alternative j ≠ i, we have
$$r_n^{(i,j)} = {{t_n^{(i)}} \over {t_n^{(j)}}}{{1 + O(\log t_n^{(i)}/t_n^{(i)})} \over {1 + O(\log t_n^{(j)}/t_n^{(j)})}} \le 1.$$
Then, by Lemma 4.2, there must exist positive constants C 1 and C 2 such that, for all large enough n,
$${{t_n^{(i)}} \over {t_n^{(j)}}} \le 1 + {C_1}({{\log t_n^{(j)}} \over {t_n^{(j)}}} + {{\log t_n^{(i)}} \over {t_n^{(i)}}}) \le 1 + {C_2}{{\log n} \over n},$$
that is, equivalently,
$${{\delta _n^{(i)}{{({\lambda ^{(j)}})}^2}} \over {N_n^{(j)}}} + {{\delta _n^{(i)}{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}} \le {{\delta _n^{(j)}{{({\lambda ^{(i)}})}^2}(1 + {C_2}(\log n)/n)} \over {N_n^{(i)}}} + {{\delta _n^{(j)}{{({\lambda ^{(1)}})}^2}(1 + {C_2}(\log n)/n)} \over {N_n^{(1)}}}.$$
(A.6)
Then, at stage n + u, where 0 < u < m, there must exist positive constants C 3 and C 4 such that, for all large enough n,
$$\matrix{
{r_{n + u}^{(i,j)}} = {{{t_{n + u}^{(i)}} \over {t_{n + u}^{(j)}}}{{1 + O(\log t_{n + u}^{(i)}/t_{n + u}^{(i)})} \over {1 + O(\log t_{n + u}^{(j)}/t_{n + u}^{(j)})}}} \cr
{} \le {{{t_{n + u}^{(i)}} \over {t_{n + u}^{(j)}}}{1 \over {1 - {C_3}(\log t_{n + u}^{(i)}/t_{n + u}^{(i)} + \log t_{n + u}^{(j)}/t_{n + u}^{(j)})}}} \cr
{} = {{{t_{n + u}^{(i)}} \over {t_{n + u}^{(j)}}}{1 \over {1 - {C_4}(\log n)/n}}.} \cr
} $$
Thus, for all large enough n, in order to have 
$r_{n + u}^{(i,j)} \lt 1,$ it is sufficient to require
$${{t_{n + u}^{(i)}} \over {t_{n + u}^{(j)}}} \le 1 - {C_4}{{\log n} \over n},$$
or, equivalently,
$$\matrix{
{{{\delta _{n + u}^{(i)}{{({\lambda ^{(j)}})}^2}} \over {N_n^{(j)} + k_u^{(j)}}} + {{\delta _{n + u}^{(i)}{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)} + k_u^{(1)}}}} \cr
{\quad \quad \le {{\delta _{n + u}^{(j)}{{({\lambda ^{(i)}})}^2}(1 - {C_4}(\log n)/n)} \over {N_n^{(i)} + k_u^{(i)}}} + {{\delta _{n + u}^{(j)}{{({\lambda ^{(1)}})}^2}(1 - {C_4}(\log n)/n)} \over {N_n^{(1)} + k_u^{(1)}}}.} \cr
} $$
(A.7)
Note that 
$k_u^{(i)} = 1.$ By the convergence of 
$\delta _n^{(i)}$ and 
$\delta _n^{(j)}$, an for all large enough n, we have
$$\matrix{
{(\delta _n^{(j)} - \delta _n^{(i)})(\delta _n^{(j)}(1 + {C_2}{{\log n} \over n}) - \delta _n^{(i)}) \gt 0,} \hfill \cr
{(\delta _n^{(j)} - \delta _n^{(i)})(\delta _n^{(j)}(1 - {C_4}{{\log n} \over n}) - \delta _n^{(i)}) \gt 0.} \hfill \cr
} $$
If 
$\mathop {\lim }\nolimits_{n \to \infty } {{\delta _n^{(j)}} \over {\delta _n^{(i)}}} \gt 1,$ i.e. μ (j) <μ (i), then by (A.6), we have
$$\matrix{
{{{\delta _{n + u}^{(i)}{{({\lambda ^{(j)}})}^2}} \over {N_n^{(j)} + k_u^{(j)}}} = {{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(i)}{{({\lambda ^{(j)}})}^2}} \over {N_n^{(j)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}} \hfill \cr
{ \le {{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}{{({\lambda ^{(i)}})}^2}(1 + {C_2}(\log n)/n)} \over {N_n^{(i)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}} \hfill \cr
{ + {{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}{{({\lambda ^{(1)}})}^2}(1 + {C_2}(\log n)/n) - \delta _n^{(i)}{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}} \hfill \cr}
{{ = {{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}{{({\lambda ^{(i)}})}^2}(1 - {C_4}(\log n)/n)} \over {N_n^{(i)} + 1}}{{(1 + {C_2}(\log n)/n)} \over {(1 - {C_4}(\log n)/n)}}{{N_n^{(i)} + 1} \over {N_n^{(i)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}} \hfill \cr
{ + {{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}{{({\lambda ^{(1)}})}^2}(1 + {C_2}(\log n)/n) - \delta _n^{(i)}{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)} + k_u^{(1)}}}{{N_n^{(1)} + k_u^{(1)}} \over {N_n^{(1)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}.} \hfill \cr } $$
It follows that there must exist a positive constant C 5 such that
$$\matrix{
{{{\delta _{n + u}^{(i)}{{({\lambda ^{(j)}})}^2}} \over {N_n^{(j)} + k_u^{(j)}}} \le {{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}{{({\lambda ^{(i)}})}^2}(1 - {C_4}(\log n)/n)} \over {N_n^{(i)} + 1}}(1 + {C_5}{{\log n} \over n}){{N_n^{(i)} + 1} \over {N_n^{(i)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}} \hfill \cr
{ + {{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}{{({\lambda ^{(1)}})}^2}(1 + {C_2}(\log n)/n) - \delta _n^{(i)}{{({\lambda ^{(1)}})}^2}} \over {N_n^{(1)} + k_u^{(1)}}}{{N_n^{(1)} + k_u^{(1)}} \over {N_n^{(1)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}.} \hfill \cr
} $$
Thus, to satisfy (A.7), it is sufficient to have
$${{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}} \over {\delta _{n + u}^{(j)}}}(1 + {C_5}{{\log n} \over n}){{N_n^{(i)} + 1} \over {N_n^{(i)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}} \le 1,$$
(A.8)
$${{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}(1 + {C_2}(\log n)/n) - \delta _n^{(i)}} \over {\delta _{n + u}^{(j)}(1 - {C_4}(\log n)/n) - \delta _{n + u}^{(i)}}}{{N_n^{(1)} + k_u^{(1)}} \over {N_n^{(1)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}} \le 1.$$
(A.9)
Note that, for all large enough n and any alternative i ≠ 1, by Lemma 4.2, we have
$$\matrix{
{|\delta _{n + u}^{(i)} - \delta _n^{(i)}| = |(d_{n + u}^{(i)}{)^2} - {{(d_n^{(i)})}^2}|} \hfill \cr
{ = |(\theta _{n + u}^{(i)} - \theta _{n + u}^{(1)}{)^2} - {{(\theta _n^{(i)} - \theta _n^{(1)})}^2}|} \hfill \cr
{ = |(\theta _{n + u}^{(i)} - \theta _{n + u}^{(1)}) + (\theta _n^{(i)} - \theta _n^{(1)})||(\theta _{n + u}^{(i)} - \theta _n^{(i)}) - (\theta _{n + u}^{(1)} - \theta _n^{(1)})|} \hfill \cr
{ \le |(\theta _{n + u}^{(i)} - \theta _{n + u}^{(1)}) + (\theta _n^{(i)} - \theta _n^{(1)})|} \hfill \cr
{\quad \cdot (|\theta _{n + u}^{(i)} - {\mu ^{(i)}}| + |\theta _n^{(i)} - {\mu ^{(i)}}| + |\theta _{n + u}^{(1)} - {\mu ^{(1)}}| + |\theta _n^{(1)} - {\mu ^{(1)}}|)} \hfill \cr
{ = O(\sqrt {{{\log \log N_n^{(i)}} \over {N_n^{(i)}}}} ) + O(\sqrt {{{\log \log N_n^{(1)}} \over {N_n^{(1)}}}} )} \hfill \cr
{ = O(\sqrt {{{\log \log n} \over n}} ),} \hfill \cr
} $$
where the fourth equality holds because of the law of the iterated logarithm, and the last equality holds by Lemma 4.2. Then, for all large enough n, we have
$$\matrix{
{{{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}} = {{\delta _{n + u}^{(i)} - \delta _n^{(i)} + \delta _n^{(i)}} \over {\delta _n^{(i)}}} = 1 + {{\delta _{n + u}^{(i)} - \delta _n^{(i)}} \over {\delta _n^{(i)}}} = 1 + O(\sqrt {{{\log \log n} \over n}} ),} \hfill \cr
{{{\delta _n^{(j)}} \over {\delta _{n + u}^{(j)}}} = 1 + O(\sqrt {{{\log \log n} \over n}} ),} \hfill \cr
} $$
and
$$\matrix{
{{{\delta _n^{(j)}(1 + {C_2}(\log n)/n) - \delta _n^{(i)}} \over {\delta _{n + u}^{(j)}(1 - {C_4}(\log n)/n) - \delta _{n + u}^{(i)}}}} \hfill \cr
{\quad \quad = 1 + {{\delta _n^{(j)}(1 + {C_2}(\log n)/n) - \delta _{n + u}^{(j)}(1 - {C_4}(\log n)/n) - (\delta _n^{(i)} - \delta _{n + u}^{(i)})} \over {\delta _{n + u}^{(j)}(1 - {C_4}(\log n)/n) - \delta _{n + u}^{(i)}}}} \hfill \cr
} $$
.
Then together with Lemma 4.2, there exists a positive constant C 6 such that, for all large enough n, the left-hand side of (A.8) satisfies
$$\matrix{
{{{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}} \over {\delta _{n + u}^{(j)}}}(1 + {C_5}{{\log n} \over n}){{N_n^{(i)} + 1} \over {N_n^{(i)}}}N_n^{(j)} - N_n^{(j)}} \hfill \cr
{ = (1 + O(\sqrt {{{\log \log n} \over n}} ))(1 + {C_5}{{\log n} \over n})(1 + O({1 \over n}))N_n^{(j)} - N_n^{(j)}} \hfill \cr
{ \le {C_6}\sqrt {n\log \log n} ,} \hfill \cr
} $$
while the left-hand side of (A.9) satisfies
$$\matrix{
{{{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}{{\delta _n^{(j)}\left( {1 + {C_2}(\log n)/n} \right) - \delta _n^{(i)}} \over {\delta _{n + u}^{(j)}\left( {1 - {C_4}(\log n)/n} \right) - \delta _{n + u}^{(i)}}}{{N_n^{(1)} + k_u^{(1)}} \over {N_n^{(1)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}} \hfill \cr
{ = (1 + O(\sqrt {{{\log \log n} \over n}} )){{N_n^{(1)} + k_u^{(1)}} \over {N_n^{(1)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}} \hfill \cr
{ \le (1 + {C_6}{{\sqrt {n\log \log n} } \over n}){{N_n^{(1)} + k_u^{(1)}} \over {N_n^{(1)}}}{{N_n^{(j)}} \over {N_n^{(j)} + k_u^{(j)}}}.} \hfill \cr
} $$
Therefore, to satisfy (A.8), it is sufficient to have
$${C_6}\sqrt {n\log \log n} \le k_u^{(j)}.$$
(A.10)
Now define
$$s{\kern 1pt} : = {\kern 1pt} \sup \{ l \lt m:I_{n + l}^{(1)} = 0\} .$$
(A.11)
Since 
$k_m^{(1)}/\sqrt {n\log \log n} $ can be arbitrarily large, we can suppose that 
$k_s^{(1)} \gt {C_7}\sqrt {n\log \log n},$ where C 7 is a positive constant to be specified. By Lemma A.1, since C 6 is a fixed positive constant, there must exist a constant C 8 such that, if C 7 ≥ C 8 , there exists a suboptimal j ≠ i, and a stage n + u with u ≤ s, such that j is sampled at stage n + u and
$$(1 + {C_6}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}} \lt {{N_n^{(j)} + k_u^{(j)}} \over {N_n^{(1)} + k_s^{(1)}}} \le {{N_n^{(j)} + k_u^{(j)}} \over {N_n^{(1)} + k_u^{(1)}}}.$$
Then, (A.9) holds at stage n + u. At the same time, since
$${{N_n^{(j)} + k_u^{(j)}} \over {N_n^{(1)} + k_s^{(1)}}} \gt (1 + {C_6}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}} \ge {{N_n^{(j)}} \over {N_n^{(1)}}},$$
we have 
$k_u^{(j)}/k_s^{(1)} \ge N_n^{(j)}/N_n^{(1)}.$ From Lemma 4.2, there must exist a positive constant C 9 such that, for all large enough n,
$$k_u^{(j)} \ge {C_9}k_s^{(1)} \ge {C_9}{C_7}\sqrt {n\log \log n} .$$
Now let C 7 = max {C 8, C 6 / C 9 }. Then, both (A.9) and (A.10) are satisfied at stage n + u,so (A.7) is satisfied, which means that
$$r_{n + u}^{(i,j)} \lt 1\quad \Rightarrow \quad v_{n + u}^{(i)} \gt v_{n + u}^{(j)}$$
.
But the alternative j is sampled at stage n + u, which means 
$v_{n + u}^{(i)} \le v_{n + u}^{(j)}.$ The desired contradiction follows.
Now, consider the other case where 
$\mathop {\lim }\nolimits_{n \to \infty } \delta _n^{(j)}/\delta _n^{(i)} \lt 1,$ i.e. μ (j) > μ (i). By (A.6), we have
$$\matrix{
{{{\delta _{n + u}^{(j)}{{({\lambda ^{(i)}})}^2}(1 - {C_4}(\log n)/n)} \over {N_n^{(i)} + 1}}} \hfill \cr
{\quad \quad = {{\delta _{n + u}^{(j)}} \over {\delta _n^{(j)}}}{{\delta _n^{(j)}{{({\lambda ^{(i)}})}^2}(1 + {C_2}(\log n)/n)} \over {N_n^{(i)}}}{{1 - {C_4}(\log n)/n} \over {1 + {C_2}(\log n)/n}}{{N_n^{(i)}} \over {N_n^{(i)} + 1}}} \hfill \cr
{\quad \quad \ge {{\delta _{n + u}^{(j)}} \over {\delta _n^{(j)}}}{{\delta _n^{(i)}{{({\lambda ^{(j)}})}^2}} \over {N_n^{(j)}}}{{1 - {C_4}(\log n)/n} \over {1 + {C_2}(\log n)/n}}{{N_n^{(i)}} \over {N_n^{(i)} + 1}}} \hfill \cr
{\quad \quad \quad {\kern 1pt} + {{\delta _{n + u}^{(j)}} \over {\delta _n^{(j)}}}{{\delta _n^{(i)}{{({\lambda ^{(1)}})}^2} - \delta _n^{(j)}{{({\lambda ^{(1)}})}^2}(1 + {C_2}(\log n)/n)} \over {N_n^{(1)}}}{{1 - {C_4}(\log n)/n} \over {1 + {C_2}(\log n)/n}}{{N_n^{(i)}} \over {N_n^{(i)} + 1}}.} \hfill \cr
} $$
Then, there must exist a positive constant C 10 such that, for all large enough n,
$$\matrix{
{{{\delta _{n + u}^{(j)}{{({\lambda ^{(i)}})}^2}\left( {1 - {C_4}(\log n)/n} \right)} \over {N_n^{(i)} + 1}}} \hfill \cr
{\quad \quad \ge {{\delta _{n + u}^{(j)}} \over {\delta _n^{(j)}}}{{\delta _n^{(i)}{{({\lambda ^{(j)}})}^2}} \over {N_n^{(j)}}}{1 \over {1 + {C_{10}}(\log n)/n}}{{N_n^{(i)}} \over {N_n^{(i)} + 1}}} \hfill \cr
{\quad \quad + {{\delta _{n + u}^{(j)}} \over {\delta _n^{(j)}}}{{\delta _n^{(i)}{{({\lambda ^{(1)}})}^2} - \delta _n^{(j)}{{({\lambda ^{(1)}})}^2}(1 + {C_2}(\log n)/n)} \over {N_n^{(1)}}}{1 \over {1 + {C_{10}}(\log n)/n}}{{N_n^{(i)}} \over {N_n^{(i)} + 1}}.} \hfill \cr
} $$
Thus, to satisfy (A.7), for all large enough n, it is sufficient to have
$$\matrix{
{\;\;{{\delta _{n + u}^{(j)}} \over {\delta _n^{(j)}}}{{\delta _n^{(i)}} \over {\delta _{n + u}^{(i)}}}{1 \over {N_n^{(j)}}}{1 \over {1 + {C_{10}}(\log n)/n}}{{N_n^{(i)}} \over {N_n^{(i)} + 1}} \ge {1 \over {N_n^{(j)} + k_u^{(j)}}},} \hfill \cr
{{{\delta _{n + u}^{(j)}} \over {\delta _n^{(j)}}}{{\delta _n^{(i)} - \delta _n^{(j)}\left( {1 + {C_2}(\log n)/n} \right)} \over {N_n^{(1)}}}{1 \over {1 + {C_{10}}(\log n)/n}}{{N_n^{(i)}} \over {N_n^{(i)} + 1}}} \hfill \cr
{\quad \quad \ge {{\delta _{n + u}^{(i)} - \delta _{n + u}^{(j)}\left( {1 - {C_4}(\log n)/n} \right)} \over {N_n^{(1)} + k_u^{(1)}}},} \hfill \cr
} $$
which can equivalently be rewritten as
$$\quad \quad \quad \quad \quad \quad \;k_u^{(j)} \ge {{\delta _n^{(j)}} \over {\delta _{n + u}^{(j)}}}{{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}(1 + {C_{10}}{{\log n} \over n}){{N_n^{(i)} + 1} \over {N_n^{(i)}}}N_n^{(j)} - N_n^{(j)},$$
(A.12)
$$k_u^{(1)} \ge {{\delta _n^{(j)}} \over {\delta _{n + u}^{(j)}}}(1 + {C_{10}}{{\log n} \over n}){{\delta _{n + u}^{(i)} - \delta _{n + u}^{(j)}\left( {1 - {C_4}(\log n)/n} \right)} \over {\delta _n^{(i)} - \delta _n^{(j)}\left( {1 + {C_2}(\log n)/n} \right)}}{{N_n^{(i)} + 1} \over {N_n^{(i)}}}N_n^{(1)} - N_n^{(1)}.$$
(A.13)
Similarly as above, by Lemma 4.2, there exist positive constants C 11, C 12, C 13, and C 14 such that, for all large enough n,
$${{\delta _n^{(j)}} \over {\delta _{n + u}^{(j)}}}{{\delta _{n + u}^{(i)}} \over {\delta _n^{(i)}}}(1 + {C_{10}}{{\log n} \over n}){{N_n^{(i)} + 1} \over {N_n^{(i)}}}N_n^{(j)} - N_n^{(j)} \le {C_{11}}\sqrt {n\log \log n} $$
and
$$\matrix{
{{{\delta _n^{(j)}} \over {\delta _{n + u}^{(j)}}}(1 + {C_{10}}{{\log n} \over n}){{\delta _{n + u}^{(i)} - \delta _{n + u}^{(j)}\left( {1 - {C_4}(\log n)/n} \right)} \over {\delta _n^{(i)} - \delta _n^{(j)}\left( {1 + {C_2}(\log n)/n} \right)}}{{N_n^{(i)} + 1} \over {N_n^{(i)}}}N_n^{(1)} - N_n^{(1)}} \hfill \cr
{ \le (1 + {C_{10}}{{\log n} \over n})(1 + {C_{12}}\sqrt {{{\log \log n} \over n}} ){{N_n^{(i)} + 1} \over {N_n^{(i)}}}N_n^{(1)} - N_n^{(1)}} \hfill \cr
{ \le (1 + {C_{13}}\sqrt {{{\log \log n} \over n}} ){{N_n^{(i)} + 1} \over {N_n^{(i)}}}N_n^{(1)} - N_n^{(1)}} \hfill \cr
{ \le {C_{14}}\sqrt {n\log \log n} .} \hfill \cr
} $$
Therefore, to satisfy (A.12) and (A.13), it is sufficient to have
$$k_u^{(j)} \ge {C_{11}}\sqrt {n\log \log n} ,$$
(A.14)
$$k_u^{(1)} \ge {C_{14}}\sqrt {n\log \log n} .$$
(A.15)
Again, define s as in (A.11). Since 
$k_m^{(1)}/\sqrt {n\log \log n} $ can be arbitrarily large, we can suppose that 
$k_s^{(1)} \gt {C_{15}}\sqrt {n\log \log n},$ where C 15 is a positive constant to be specified. By Lemma A.1, since C 11 is a fixed positive constant, there must exist a constant C 16 such that, if C 15 ≥ C 16, there exists a suboptimal alternative j ≠ i, and a stage n + u with u ≤ s, such that j is sampled at stage n + u and
$$(1 + {C_{11}}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}} \lt {{N_n^{(j)} + k_u^{(j)}} \over {N_n^{(1)} + k_s^{(1)}}} \le {{N_n^{(j)} + k_u^{(j)}} \over {N_n^{(1)} + k_u^{(1)}}},$$
whence
$${{N_n^{(j)} + k_u^{(j)}} \over {N_n^{(1)} + k_s^{(1)}}} \gt (1 + {C_{11}}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}} \ge {{N_n^{(j)}} \over {N_n^{(1)}}}.$$
Then, we have 
$k_u^{(j)}/k_s^{(1)} \ge N_n^{(j)}/N_n^{(1)}.$ From Lemma 4.2, there must exist a positive constant C 17 such that, for all large enough n,
$$k_u^{(j)} \ge {C_{17}}k_s^{(1)} \ge {C_{17}}{C_{15}}\sqrt {n\log \log n} .$$
At the same time, by Lemma 4.3, for all large enough n, we also have
$$k_u^{(1)} \ge {{k_u^{(j)} + 1} \over {{B_2}}} - 1 \ge {{{C_{17}}{C_{15}}\sqrt {n\log \log n} + 1} \over {{B_2}}} - 1 \ge {{{C_{17}}{C_{15}}\sqrt {n\log \log n} } \over {2{B_2}}}.$$]></tex-math>
</alternatives>
</disp-formula></p>
<p>Now, let <italic>C</italic><sub>15</sub> = max {<italic>C</italic><sub>16</sub>, <italic>C</italic><sub>11</sub> <italic>/ C</italic><sub>17</sub>, 2 <italic>B</italic><sub>2</sub> <italic>C</italic><sub>14</sub> <italic>/ C</italic><sub>17</sub> }. Then both (A.14) and (A.15) are satisfied at stage <italic>n</italic> + <italic>u</italic>, so (A.7) is satisfied, which means that</p>
<p>
<disp-formula id="udisp67">
<alternatives>
<graphic mime-subtype="gif" mimetype="image" xlink:href="S0001867819000090_eqn94" xlink:type="simple"/>
<tex-math><
$v_{n + u}^{(i)} \le v_{n + u}^{(j)}.$ Again, we have the desired contradiction.
A.4. Proof of Lemma 4.5
First, if an alternative j other than 1 or i is sampled at stage n, it is obvious that 
${n^{3/4}}|\delta _{n + 1}^{(i)} - \delta _n^{(i)}| = 0$
Second, if alternative i is sampled at stage n then, for all large enough n, there exists a constant C 1 such that
$${n^{3/4}}|\delta _{n + 1}^{(i)} - \delta _n^{(i)}| = {n^{3/4}}|(d_{n + 1}^{(i)}{)^2} - {(d_n^{(i)})^2}| \le {C_1}{n^{3/4}}|d_{n + 1}^{(i)} - d_n^{(i)}| = {{{C_1}} \over {{n^{1/4}}}}n|\theta _{n + 1}^{(i)} - \theta _n^{(i)}|,$$
where
$$\matrix{
{n|\theta _{n + 1}^{(i)} - \theta _n^{(i)}| = n|{1 \over {N_n^{(i)} + 1}}(N_n^{(i)}\theta _n^{(i)} + W_{n + 1}^{(i)}) - \theta _n^{(i)}|} \hfill \cr
{ \le {n \over {N_n^{(i)} + 1}}|\theta _n^{(i)}| + {n \over {N_n^{(i)} + 1}}|W_{n + 1}^{(i)}|} \hfill \cr
{ = O(1)(1 + |W_{n + 1}^{(i)}|);} \hfill \cr
} $$
thus, there exists a constant C 2 such that
$${n^{3/4}}|\delta _{n + 1}^{(i)} - \delta _n^{(i)}| \le {{{C_2}} \over {{n^{1/4}}}}(1 + |W_{n + 1}^{(i)}|).$$
Finally, if alternative 1 is sampled at stage n then, similarly as above, for all large enough n, there exist constants C 3 and C 4 such that
$${n^{3/4}}|\delta _{n + 1}^{(i)} - \delta _n^{(i)}| \le {{{C_3}} \over {{n^{1/4}}}}n|\theta _{n + 1}^{(1)} - \theta _n^{(1)}| \le {{{C_4}} \over {{n^{1/4}}}}(1 + |W_{n + 1}^{(1)}|).$$
Then it is sufficient to show that 
$|W_{n + 1}^{(i)}|/{n^{1/4}} \to 0$ and 
$|W_{n + 1}^{(1)}|/{n^{1/4}} \to 0$ almost surely. By Markov’s inequality, for all ɛ> 0,
$$({{|W_{n + 1}^{(i)}|} \over {{n^{1/4}}}} \ge \varepsilon ) \le ({{{{(W_{n + 1}^{(i)})}^8}} \over {{n^2}{\varepsilon ^8}}}) \le {{{C_5}} \over {{n^2}{\varepsilon ^8}}},$$
where C 5 is a fixed constant; thus, 
$|W_{n + 1}^{(i)}|/{n^{1/4}} \to 0$ in probability. Furthermore, by the Borel–Cantelli lemma, since
$$\sum\limits_n ({{|W_{n + 1}^{(i)}|} \over {{n^{1/4}}}} \ge \varepsilon ) \le \sum\limits_n {{{C_5}} \over {{n^2}{\varepsilon ^8}}} \lt \infty ,$$
then we have 
$|W_{n + 1}^{(i)}|/{n^{1/4}} \to 0$ almost surely. Using similar arguments, we also have 
$|W_{n + 1}^{(1)}|/{n^{1/4}} \to 0$ almost surely, completing the proof.
A.5 Proof of Lemma A.1
For convenience, we abbreviate 
$k_{(n,n + m)}^{(j)}$ by the notation 
$k_m^{(j)}$ for all j. First, since C 2 is a constant and 
$\mathop {\lim }\nolimits_{n \to \infty } \sqrt {n\log \log n} /n = 0,$ it follows that, for all large enough n, we must have 
${C_2}\sqrt {n\log \log n} \le n.$ Intuitively, from the definition of m and s, stage n + m is the first time that alternative i is sampled after stage n, and stage n + s is the last time that a suboptimal alternative is sampled before stage n + m. Recall that, by assumption, we must have 
${C_2}\sqrt {n\log \log n} \le k_s^{(1)} \le n$ for some positive constant C 2 to be specified.
At stage n, since we sample a suboptimal i by assumption, we must have
$${({{N_n^{(1)}} \over {{\lambda ^{(1)}}}})^2} \ge \sum\limits_{j = 2}^M {({{N_n^{(j)}} \over {{\lambda ^{(j)}}}})^2}.$$
(A.16)
At stage n + s, from the definition of s, it is also some suboptimal alternative that is sampled. Repeating the arguments in the proof of Theorem 3.1, we obtain
$${({{(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}} \over {n + s}})^2} - \sum\limits_{j = 2}^M {({{(N_n^{(j)} + k_s^{(j)})/{\lambda ^{(j)}}} \over {n + s}})^2} \le {{{C_3}} \over n}$$
for some fixed positive constant C 3. Note that 
$k_s^{(i)} = 1,$ whence
$$\sum\limits_{j \ge 2,{\kern 1pt} j \ne i} {({{(N_n^{(j)} + k_s^{(j)})/{\lambda ^{(j)}}} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}})^2} + {({{(N_n^{(i)} + 1)/{\lambda ^{(i)}}} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}})^2} + {{{C_3}} \over n}{({{n + s} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}})^2} \ge 1.$$
From Lemma 4.2, we know that 
$\mathop {\lim \,inf}\nolimits_{n \to \infty } N_n^{(1)}/n \gt 0.$ Then there must exist some constant C 4 such that
$${C_3}{({{n + s} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}})^2} \le {C_4},$$
whence
$$\sum\limits_{j \ge 2,j \ne i} {({{(N_n^{(j)} + k_s^{(j)})/{\lambda ^{(j)}}} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}})^2} \ge 1 - {({{(N_n^{(i)} + 1)/{\lambda ^{(i)}}} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}})^2} - {{{C_4}} \over n},$$
and, for all large enough n,
$$\matrix{
{\sum\limits_{j \ge 2,{\kern 1pt} j \ne i} [({{(N_n^{(j)} + k_s^{(j)})/{\lambda ^{(j)}}} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}}{)^2} - {{({{N_n^{(j)}/{\lambda ^{(j)}}} \over {N_n^{(1)}/{\lambda ^{(1)}}}})}^2}]} \hfill \cr
{\quad \quad \ge 1 - \sum\limits_{j \ge 2,{\kern 1pt} j \ne i} {{({{N_n^{(j)}/{\lambda ^{(j)}}} \over {N_n^{(1)}/{\lambda ^{(1)}}}})}^2} - {{({{(N_n^{(i)} + 1)/{\lambda ^{(i)}}} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}})}^2} - {{{C_4}} \over n}} \hfill \cr
} $$
$$\matrix{
{\quad \quad \ge {{({{N_n^{(i)}/{\lambda ^{(i)}}} \over {N_n^{(1)}/{\lambda ^{(1)}}}})}^2} - {{({{(N_n^{(i)} + 1)/{\lambda ^{(i)}}} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}})}^2} - {{{C_4}} \over n}} \hfill \cr
{\quad \quad = ({{{\lambda ^{(1)}}} \over {{\lambda ^{(i)}}}}{)^2}{{{{(N_n^{(i)})}^2}{{(N_n^{(1)} + k_s^{(1)})}^2} - {{(N_n^{(1)})}^2}{{(N_n^{(i)} + 1)}^2}} \over {{{(N_n^{(1)} + k_s^{(1)})}^2}{{(N_n^{(1)})}^2}}} - {{{C_4}} \over n}} \hfill \cr
{\quad \quad = ({{{\lambda ^{(1)}}} \over {{\lambda ^{(i)}}}}{)^2}{{{{(N_n^{(i)})}^2}(2N_n^{(1)}k_s^{(1)} + {{(k_s^{(1)})}^2}) - {{(N_n^{(1)})}^2}(2N_n^{(i)} + 1)} \over {{{(N_n^{(1)} + k_s^{(1)})}^2}{{(N_n^{(1)})}^2}}} - {{{C_4}} \over n}} \hfill \cr
{\quad \quad = ({{{\lambda ^{(1)}}} \over {{\lambda ^{(i)}}}}{)^2}{{{{(N_n^{(i)})}^2}(2N_n^{(1)}(k_s^{(1)} - N_n^{(1)}/N_n^{(i)}) + {{(k_s^{(1)})}^2} - {{(N_n^{(1)}/N_n^{(i)})}^2})} \over {{{(N_n^{(1)} + k_s^{(1)})}^2}{{(N_n^{(1)})}^2}}} - {{{C_4}} \over n}} \hfill \cr
} $$
(A.17)
$$\matrix{
{\quad \quad \gt ({{{\lambda ^{(1)}}} \over {{\lambda ^{(i)}}}}{)^2}{{{{(N_n^{(i)})}^2}(2N_n^{(1)}(k_s^{(1)}/2) + {{(k_s^{(1)})}^2}/2)} \over {{{(N_n^{(1)} + k_s^{(1)})}^2}{{(N_n^{(1)})}^2}}} - {{{C_4}} \over n}} \hfill \cr
{\quad \quad = {1 \over 2}{{({{{\lambda ^{(1)}}} \over {{\lambda ^{(i)}}}})}^2}{1 \over {{{(N_n^{(1)} + k_s^{(1)})}^2}}}{{({{N_n^{(i)}} \over {N_n^{(1)}}})}^2}(2N_n^{(1)}k_s^{(1)} + {{(k_s^{(1)})}^2}) - {{{C_4}} \over n},} \hfill \cr
} $$
(A.18)
where (A.17) holds due to (A.16), while (A.18) holds since 
$\mathop {\liminf}\nolimits_{n \to \infty } N_n^{(i)}/N_n^{(1)} \gt 0$ and 
$k_s^{(1)} \ge {C_2}\sqrt {n\log \log n} $ for a positive constant C 2. Since 
$\mathop {\liminf}\nolimits_{n \to \infty } N_n^{(i)}/N_n^{(1)} \gt 0$ and 
$\mathop {\liminf}\nolimits_{n \to \infty } N_n^{(1)}/n \gt 0,$ there must exist positive constants C 5, C 6, C 7, C 8, and C 9 such that, for all large enough n, we have
$$\matrix{
{{1 \over 2}{{({{{\lambda ^{(1)}}} \over {{\lambda ^{(i)}}}})}^2}{1 \over {{{(N_n^{(1)} + k_s^{(1)})}^2}}}{{({{N_n^{(i)}} \over {N_n^{(1)}}})}^2}(2N_n^{(1)}k_s^{(1)} + {{(k_s^{(1)})}^2}) - {{{C_4}} \over n}} \hfill \cr
{ \ge {C_5}{1 \over {{{(N_n^{(1)} + k_s^{(1)})}^2}}}(2N_n^{(1)}k_s^{(1)} + {{(k_s^{(1)})}^2}) - {{{C_4}} \over {N_n^{(1)}}}} \hfill \cr
{ = {{{C_5}} \over {{{(N_n^{(1)} + k_s^{(1)})}^2}}}(2N_n^{(1)}k_s^{(1)} + {{(k_s^{(1)})}^2} - {C_6}{{{{(N_n^{(1)} + k_s^{(1)})}^2}} \over {N_n^{(1)}}})} \hfill \cr
} $$
$$\matrix{
{ \ge {{{C_5}} \over {{{(N_n^{(1)} + k_s^{(1)})}^2}}}(2N_n^{(1)}k_s^{(1)} + {{(k_s^{(1)})}^2} - 2{C_7}N_n^{(1)})} \hfill \cr
{ \ge {{{C_5}} \over {{{(N_n^{(1)} + k_s^{(1)})}^2}}}2(k_s^{(1)} - {C_7})N_n^{(1)}} \hfill \cr
} $$
(A.19)
$$\matrix{
{ \ge {{{C_8}(k_s^{(1)} - {C_7})} \over {N_n^{(1)}}}} \hfill \cr
{ \ge {{{C_8}({C_2}\sqrt {n\log \log n} - {C_7})} \over n}} \hfill \cr
{ \ge {{{C_9}{C_2}\sqrt {n\log \log n} } \over n},} \hfill \cr
} $$
(A.20)
where (A.19) and (A.20) hold because 
$k_s^{(1)} \le n,$ Then
$$\sum\limits_{j \ge 2,{\kern 1pt} j \ne i} [({{(N_n^{(j)} + k_s^{(j)})/{\lambda ^{(j)}}} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}}{)^2} - {({{N_n^{(j)}/{\lambda ^{(j)}}} \over {N_n^{(1)}/{\lambda ^{(1)}}}})^2}] \gt {{{C_9}{C_2}\sqrt {n\log \log n} } \over n},$$
so there must be some suboptimal j such that
$${({{(N_n^{(j)} + k_s^{(j)})/{\lambda ^{(j)}}} \over {(N_n^{(1)} + k_s^{(1)})/{\lambda ^{(1)}}}})^2} - {({{N_n^{(j)}/{\lambda ^{(j)}}} \over {N_n^{(1)}/{\lambda ^{(1)}}}})^2} \gt {1 \over {M - 2}}{{{C_9}{C_2}\sqrt {n\log \log n} } \over n}.$$
Let C 10 = C 9 / (M −2) and C 11 = C 10 C 2 / 4. Then,
$${({{(N_n^{(j)} + k_s^{(j)})/(N_n^{(1)} + k_s^{(1)})} \over {N_n^{(j)}/N_n^{(1)}}})^2} \gt 1 + {{{C_{10}}{C_2}\sqrt {n\log \log n} } \over n},$$
and, for all large enough n, we have
$${{(N_n^{(j)} + k_s^{(j)})/(N_n^{(1)} + k_s^{(1)})} \over {N_n^{(j)}/N_n^{(1)}}} \gt 1 + {{{C_{11}}\sqrt {n\log \log n} } \over n},$$
whence
$${{N_n^{(j)} + k_s^{(j)}} \over {N_n^{(1)} + k_s^{(1)}}} \gt (1 + {C_{11}}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}}.$$
(A.21)
For the alternative j that satisfies (A.21), let
$$u{\kern 1pt} : = {\kern 1pt} \sup \{ l \le s:I_{n + l}^{(j)} = 1\} .$$
Then, stage n + u is the last time that alternative j is sampled before or at stage n + m. Since 
$k_s^{(j)}$ is monotonically increasing in s, we have
$$\matrix{
{{{N_n^{(j)} + k_u^{(j)}} \over {N_n^{(1)} + k_u^{(1)}}} \ge {{N_n^{(j)} + k_u^{(j)}} \over {N_n^{(1)} + k_s^{(1)}}}} \hfill \cr
{ \ge {{N_n^{(j)} + k_s^{(j)} - 1} \over {N_n^{(1)} + k_s^{(1)}}}} \hfill \cr
{ = (1 - {1 \over {N_n^{(j)} + k_s^{(j)}}}){{N_n^{(j)} + k_s^{(j)}} \over {N_n^{(1)} + k_s^{(1)}}}} \hfill \cr
{ \gt (1 - {1 \over {N_n^{(j)} + k_s^{(j)}}})(1 + {C_{11}}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}},} \hfill \cr
} $$
where the last line follows from (A.21). By Lemma 4.2, there must exist a positive constant C 12 such that, for all large enough n,
$$\matrix{
{(1 - {1 \over {N_n^{(j)} + k_s^{(j)}}})(1 + {C_{11}}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}}} \hfill \cr
{ \ge (1 - {{{C_{12}}} \over n})(1 + {C_{11}}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}}} \hfill \cr
{ = (1 + {C_{11}}{{\sqrt {n\log \log n} } \over n} - {{{C_{12}}} \over n} - {C_{12}}{C_{11}}{{\sqrt {n\log \log n} } \over {{n^2}}}){{N_n^{(j)}} \over {N_n^{(1)}}}} \hfill \cr
{ \ge (1 + {{{C_{11}}} \over 2}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}}} \hfill \cr
{ = (1 + {C_{13}}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}},} \hfill \cr
} $$
where C 13 = C 11 / 2 = C 10 C 2 / 8. Note that constants C 3 through C 10 are fixed and do not depend on C 1 or C 2. Thus, for all large enough n,if we take C 2 to be sufficiently large, i.e. C 2 ≥ 8 C 1 / C 10,to make C 13 ≥ C 1, then
$${{N_n^{(j)} + k_u^{(j)}} \over {N_n^{(1)} + k_s^{(1)}}} \gt (1 + {C_1}{{\sqrt {n\log \log n} } \over n}){{N_n^{(j)}} \over {N_n^{(1)}}},$$
which completes the proof.
Acknowledgement
The second author’s research was partially supported by the National Science Foundation (EAGER award CMMI-1745198).
