1.1 Introduction

Since the early days of computers and programming, humankind has been fascinated by the question whether machines can be intelligent. This is the domain of artificial intelligence (AI),Footnote ¹ a term first coined by John McCarthy when he organized the now legendary first summer project in Dartmouth in 1956. The field of AI seeks to answer this question by developing actual machines (robots or computers) that exhibit some kind of intelligent behavior.

Because intelligence encompasses many distinct aspects, one more complicated than the other, research toward AI is typically focused on one or only a few of these aspects. There exist many opinions and lengthy debates about how (artificial) intelligence should be defined. However, a reoccurring insight is that the capabilities of learning and reasoning are essential to achieve intelligence. While most practical AI systems rely on both learning and reasoning techniques, each of these techniques developed rather independently. One of the grand challenges of AI is achieving a truly integrated learning and reasoning mechanism.Footnote ² The difference between both can be thought of in terms of “System I” and “System II” thinking, as coined in cognitive psychology.Footnote ³ System I thinking concerns our instincts, reflexes, or fast thinking. In AI we can relate this to the subdomain of machine learning, which aims to develop machines that learn patterns from data (e.g., do I see a traffic light). System II thinking concerns our more deliberate, multistep, logical, slow thinking. It relates to the subdomain of reasoning and focuses on knowledge and (logical or probabilistic) inference (e.g., do I need to stop in this traffic situation). In this chapter, we dive deeper into both machine learning and machine reasoning and describe why they matter and how they function.

1.2 What Is Machine Learning?

To answer the question whether machines can learn and reason, we first need to define what is meant by a “machine” that can “learn” and “reason.” For “machine learning” we go to the, within the domain generally accepted, definition of machine learning by Tom Mitchell. A machine is said to learn if its performance at the specific task improves with experience.Footnote ⁴ The term machine herein refers to a robot, a computer, or even a computer program. The machine needs to perform a given task, which is typically a task with a narrow scope such that the performance can be measured numerically. The more the machine performs the task and gets feedback on its performance, the more it is exposed to experiences and the better its performance. A more informal definition by Arthur Samuel, an American computer scientist, isFootnote ⁵ “computers that have the ability to learn without being explicitly programmed.”Footnote ⁶

One of the original, but still fascinating, examples of machine learning is a computer program (the machine) developed by Arthur Samuel to play checkers (the task). After playing multiple games (the experience), the program became a stronger player. This was measured by counting the number of games won or the ranking the program achieved in tournaments (the performance). This computer program was developed in the 1950s and 1960s and was one of the first demonstrations of AI. Already then, the program succeeded in winning against one of the best US checkers players. By the early 1990s, the checkers program Chinook, developed at the University of Alberta, outperformed all human players.Footnote ⁷ Nowadays, checkers is a “solved” game. This means that a computer program can play optimally, and the best result an opponent, human or machine, can achieve is to draw. Since then, we have observed AI conquer increasingly complicated games. Playing chess at a human level was reached when Deep Blue won against world chess champion Gary Kasparov in 1997. The game of Go, for which playing strategies were considered too difficult to be even represented in computer memory, was conquered when the program AlphaGo won against Lee Sedol in 2016.Footnote ⁸ And recently also games where not all information is available to a player can be played by AI at the same level as top human players, such as the game of Stratego where DeepNash reached human expert level in 2022.Footnote ⁹

Another ubiquitous example of learning machines are mail filters (the machine) that automatically remove unwanted emails, categorize mails into folders, or automatically forward the mail to the relevant person within an organization (the task). Since email is customized to individuals and dependent on one’s context, mail handling should also be different from person to person and organization to organization. Therefore, mail filters ought to be adaptive, so that they can adapt to the needs and contexts of individual users. A user can correct undesired behavior or confirm desired behavior by moving and sorting emails manually, hereby indicating (lack) of performance. This feedback (the experiences) is used as examples from which the computer program can learn. Based on certain properties of those emails, such as sender, style, or word choice, the mail filter can learn to predict whether a new email is spam, needs to be deleted, moved, forwarded, or kept as is. Moreover, by analyzing the text and recognizing a question and intention, the mail filter can also learn to forward the mail to the person that previously answered a similar question successfully. The more examples or demonstrations are provided to the system, the more its performance improves.

A third example is a recommender system (the machine), which is used by shops to recommend certain products to their customers (the task). If, for example, it is observed that many of the customers who have watched Pulp Fiction by Quentin Tarantino also liked Kill Bill, this information can be used to recommend Kill Bill to customers that have watched Pulp Fiction. The experience is here the list of movies that customers have viewed (or rated), and the performance is measured by the revenue or customer retention, or customer satisfaction of the company.

These examples illustrate how machines need to process (digital) data to learn and thus perform machine learning. By analyzing previous experiences (e.g., games played, emails moved, and movies purchased), the system can extract relevant patterns and build models to improve the execution of their task according to the performance metric used. This also illustrates the inherent statistical nature of machine learning: It analyzes large datasets to identify patterns and then makes predictions, recommendations, or decisions based on those patterns. In that way, machine learning is also closely related to data science. Data science is a form of intelligent data analysis that allows us to reformat and merge data in order to extract novel and useful knowledge from large and possibly complex collections of data. Machine learning hence provides tools to conduct this analysis in a more intelligent and autonomous way. Machine learning allows machines to learn complicated tasks based on (large) datasets. While high performance is often achieved, it is not always easy to understand how the machine learning algorithm actually works and to provide explanations for the output of the algorithm. This is what is referred to as a “black box.”

1.3 What Is Machine Reasoning?

Machine learning has powered systems to identify spam emails, play advanced games, provide personalized recommendations, and chat like a human; the question remains whether these systems truly understand the concepts and the domain they are operating in. AI chatbots for instance generate dialogues that are human-like, but at the same time have been reported to invent facts and lack “reasoning” and “understanding.” ChatGPTFootnote ¹⁰ will, when asked to provide a route description between two addresses, confidently construct a route that includes a turn from street A to street B without these streets even being connected in reality or propose a route that is far from being the fastest or safest. The model underlying current versions of ChatGPT does not “understand” the concept of streets and connections between streets, and it is not fast and safe. Similarly, a recommender engine could recommend a book on Ethics in AI based on the books that friends in my social network have bought without “understanding” the concept of Ethics and AI and how they are related to my interests. The statistical patterns exploited in machine learning can be perceived as showing some form of reasoning because these patterns originate from (human) reasoning processes. Sentences generated with ChatGPT look realistic because the underlying large language models are learned from a huge dataset of real sentences, or driving directions can be correct because guidebooks used as training data contain these directions. A slightly different question may however cause ChatGPT to provide a wrong answer because directions for a changed or previously unseen situation cannot always be constructed only from linguistic patterns.

This is where reasoning comes into the picture. Léon Bottou put forward a plausible definition of reasoning in 2011: “[the] algebraic manipulation of previously acquired knowledge in order to answer a new question.”Footnote ¹¹ Just like in Mitchell’s definition, we can distinguish three elements. There is knowledge about the world that is represented, that knowledge can be used to answer (multiple) questions, and answering questions requires the manipulation of the available knowledge, a process that is often termed inference. A further characteristic of reasoning is that Bottou argues that his definition covers both logical and probabilistic reasoning, the two main paradigms in AI for representing and reasoning about knowledge.

Logical knowledge of a specific domain can be represented symbolically using rules, constraints, and facts. Subsequently, an inference engine can use deductive, abductive, or inductive inference to derive answers to questions about that domain. The logical approach to machine reasoning is well suited for solving complex problems that require a thorough understanding of multistep reasoning on the knowledge base. It is of particular interest for domains where understanding is crucial and the stakes are high, as deductive reasoning will lead to sound conclusions, thus conclusions that logically follow from the knowledge base. For example, to explore and predict optimal payroll policies, one needs to reason over the clauses or rules present in the tax legislation.Footnote ¹²

Probabilistic knowledge is often represented in graphical models.Footnote ¹³ These are graphical representations that represent not only the variables of interest but also the (in)dependencies between these variables. The variables are the nodes in the graphs and direct dependencies are specified using the edges (or arcs), and graphical models can be used to query the probability of some variables given that one knows the value of other variables.

Numerous contemporary expert systems are represented as graphical models. Expert systems are computer programs that mimic the decision-making ability of a human expert in a specific domain. Consider, for example, diagnosis in a medical domain such as predicting the preterm birth risk of pregnant womenFootnote ¹⁴ or the impact of combining medication (see Figure 1.1).Footnote ¹⁵ The variables would then include the symptoms, the possible tests that can be carried out, and the diseases that the patient could suffer from. Probabilistic inference then corresponds to computing the answers to questions such as what is the probability that the patient has pneumonia, given a positive X-ray and coughing. Probabilistic inference can reason from causes to effects (here: diseases to symptoms) and from effects to causes (diagnostic reasoning) or, in general, draw conclusions about the probability of variables given that the outcome of other variables is known. Furthermore, one can use the (in)dependencies modeled in the graphical model to infer which tests are relevant in the light of what is already known about the patient. Or in the domain of robotics, machine reasoning is used to determine the optimal sequence of actions to complete a manipulation or manufacturing task. An example is CRAM (Cognitive Robot Abstract Machine), equipping autonomous robots performing everyday manipulation with lightweight reasoning mechanisms that can automatically infer control decisions rather than requiring the decisions to be preprogrammed.Footnote ¹⁶

Figure 1.1 A (simple) Bayesian network to reason over the (joint) effects of two different medications that are commonly administered to patients suffering from epigastric pains because of pyrosis.

Logical and probabilistic knowledge can be created by knowledge experts encoding the domain knowledge elicited from domain experts, textbooks, and so on but can also be learned from data, hereby connecting the domain of reasoning to machine learning. Machine reasoning is, in contrast to machine learning, considered to be knowledge driven rather than data driven. It is also important to remark that logical and probabilistic inference naturally provides explanations for the answers to the questions it provides; therefore, machine reasoning is inherently explainable AI.

1.4 Why Machine Learning and Reasoning?

The interest in machine learning and reasoning can be explained from different perspectives. First, the domain of AI has a general interest in developing intelligent systems, and it is this interest that spurred the development of machine learning and reasoning. Second, it is hoped that a better understanding of machine learning and reasoning can provide novel insights into human behavior and intelligence more generally. Third, from a computer science point of view, it is very useful to have machines that learn and reason autonomously as not everything can be explicitly programmed or as the task may require answering questions that are hard to anticipate.

In this chapter, we focus on the third perspective. Our world is rapidly digitizing and programming machines manually is in the best case a tedious task, and in the worst case a nearly impossible endeavor. Data analysis requires a lot of laborious effort, as it is nowadays far easier to generate data than it is to interpret data, as also reflected by the popular phrase: “We are drowning in data but starving for knowledge.” As a result, machine learning and data mining are by now elementary tools in domains that deal with large amounts of data such as bio- and chem-informatics, medicine, computer linguistics, or prognostics. Increasingly, they are also finding their way into the analysis of data from social and economic sciences. Machine learning is also very useful to develop complex software that cannot be implemented manually. The mail filter mentioned earlier is a good example of this. It is impossible to write a custom computer program for each user or to write a new program every time a new type of message appears. We thus need computer programs that adapt automatically to their environment or user. Likewise, for complex control systems, such as autonomous cars or industrial machines, machine learning is essential. Whether it is to translate pixels into objects or a route into steering actions, it is not feasible to program all the subtleties that are required to successfully achieve this task. However, it is easy to provide ample examples of how this task can be carried out by gathering data while driving a car, or by annotating parts of the data.

In 2005, it was the first time that five teams succeeded in developing a car that could autonomously drive an entire predefined route over dust roads.Footnote ¹⁷ Translating all the measurements gathered from cameras, lasers, and sensors to steering would not have been possible if developers had to write down all computer code explicitly themselves. While there is still a significant work ahead to achieve a fully autonomous vehicle that safely operates in all possible environments and conditions, assisted driving and autonomous vehicles in constrained environments are nowadays operated daily thanks to advances in machine learning.

Machine reasoning is increasingly needed to support reasoning in complex domains, especially when the stakes are high, such as in health and robotics. When there is knowledge available about a particular domain and that knowledge can be used to flexibly answer multiple types of questions, it is much easier to infer the answer using a general-purpose reasoning technique than having to write programs for every type of question. So, machine reasoning allows us to reuse the same knowledge for multiple tasks. At the same time, when knowledge is already available, it does not make sense to still try to learn it from data. Consider applying the taxation rules in a particular country, we could directly encode this knowledge and it therefore does not make sense to try to learn these rules from tax declarations.

1.5 How Do Machine Learning and Reasoning Work?

The examples in the introduction illustrate that the goal of machine learning is to make machines more intelligent, thus allowing them to achieve a higher performance in executing their tasks by learning from experiences. To this end, they typically use input data (e.g., pixels, measurements, and descriptions) and produce an output (e.g., a move, a classification, and a prediction). Translating the input to the output is typically achieved by learning a mathematical function, also referred to as the machine learning model. For the game of checkers, this is a function that connects every possible game situation to a move. For mail filters, this is a function that takes an email and its metadata to output the categorization (spam or not). For recommender systems, the function links purchases of costumers to other products.

Within the domain of machine learning, we can distinguish different learning problems along two dimensions: (1) the type of function that needs to be learned and (2) the type of feedback or experiences that are available. While machine learning techniques typically cover multiple aspects of these dimensions, no technique covers all possible types of functions and feedback. Different methods exploit and sacrifice different properties or make different assumptions, resulting in a wide variety of machine learning techniques. Mapping the right technique to the right problem is already a challenge in itself.Footnote ¹⁸

1.5.1 Type of Function

Before explaining how different types of functions used in machine learning differ, it is useful to first point out what they all have in common. As indicated earlier, machine learning requires the machine learning function, or model, to improve when given feedback, often in the form of examples or experiences. This requires a mechanism that can adapt our model based on the performance of the model output for a new example or experience. If, for instance, the prediction of an algorithm differs from what is observed by the human (e.g., the prediction is a cat, while the picture shows a dog), the predictive model should be corrected. Correcting the model means that we need to be able to compute how we should change the function to better map the input to the output for the available examples, thus, to better fit the available observations. Computing an output such as a prediction from an input is referred to as forward inference, while computing how our function should be changed is referred to as backward inference. All types of functions have in common that a technique exists that allows us to perform backward inference. We can relate this to human intelligence by means of philosopher Søren Kierkegaard’s quote that says: “Life must be lived forward but can only be understood backwards.”

We will provide more details for three commonly used types of functions: Symbolic functions, Bayesian functions, and Deep functions. For each of these functions, the domain of machine learning studies how to efficiently learn the function (e.g., how much data is required), which classes of functions can be learned tractably (thus in a reasonable time), whether the function can represent the problem domain sufficiently accurate (e.g., a linear function cannot represent an ellipse), and whether the learned function can be interpreted or adheres to certain properties (e.g., feature importance and fairness constraints). We explain these types based on the supervised learning setting that will be introduced later. For now, it suffices to know that our feedback consists of observations that include a (target) label or an expected outcome (e.g., pictures with the label “cat” or “dog”).

1.5.1.1 Deep Functions

With deep functions we refer to neural network architectures which, in their simplest form, are combinations of many small (nonlinear or piecewise linear) functions. We can represent this combination of small functions as a graph where each node is one function that takes as input the output of previous nodes. The nodes are organized in layers where nodes in one layer use the outputs of the nodes in the previous layer as input and send their outputs to the nodes in the next layer. The term “deep” refers to the use of many consecutive layers. Individually, these small functions cannot accurately represent the desired function. However, together these small functions can represent any continuous function. The resulting function can fit the data very closely. This is depicted in Figure 1.2 where two simple functions can only linearly separate two halves of a flat plane, while the combination of two such functions already provides a more complicated separation.

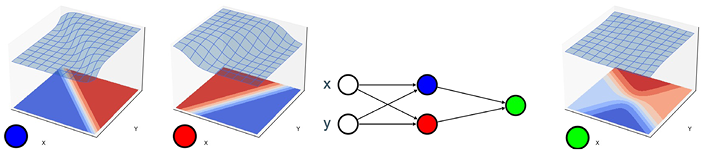
Figure 1.2 Each simple sigmoid function expresses a linear separation; together they form a more complicated function of two hyperbolas.

One way to think about this architecture is that nodes and layers introduce additional dimensions to look at the data and express chains of continuous transformations. Suppose we have a sheet of paper with two sets of points as depicted in Figure 1.3, and we want to learn a function that separates these two sets of points. We can now lift this piece of paper and introduce further dimensions in which we can rotate, stretch or twist the piece of paper.Footnote ¹⁹ This allows us to represent the data differently and ideally such that the points of the same group are close to each other and far away from the other group of points such that they are easier to distinguish (e.g., by a simple straight line). The analogy with a piece of paper does not hold completely when dealing with many layers, but we can intuitively still view it as stretching and twisting this paper until we find a combination of transformations for which the points of each class or close to each other but far apart from the other class. If we find such a set of transformations, we have learned a function that can now be used to classify any point that we would draw on this piece of paper. In Figure 1.3, one can observe that all points close to the (dark gray) circles would be labeled as a circle (like the question mark) and similarly for the (light gray) squares.

Figure 1.3 A geometric interpretation of adding layers and nodes to a neural network.

Computing the outcome of this function from the inputs is called forward inference. To update the parameters that define what functions we will combine and how (e.g., amount of rotation, stretching or folding of the paper, and which combinations of transformations), we need to perform backward inference to decide in what direction we should slightly alter the parameters based on the observed performance (e.g., a wrong prediction). This algorithm is often a variation of what is called the backpropagation algorithm. This refers to the propagation of results backward through the functions and adapting the parameters slightly to compensate for errors and reinforce correct results in order to improve the performance of the task. In our example of the classification of squares and circles (Figure 1.3), the observed wrong classification of a point as a square instead of a circle will require us to adapt the parameters of the neural network.

1.5.1.2 Symbolic Functions

Symbolic functions that are used in machine learning are in line with logic-based reasoning. The advantage is that the learned symbolic functions are typically tractable and that rigorous proof techniques can be used to learn and analyze the function. The disadvantage is that they cannot easily cope with uncertainty or fit numerical data. While classical logic is based on deductive inference, machine learning uses inductive inference. For deductive inference, one starts from a set of premises from which conclusions are derived. If the premises are true, then this guarantees that the conclusions are also true. For example, IF we know that all swans are white, and we know there is a swan, THEN we know this swan will also be white. For inductive reasoning, we start from specific observations, and derive generic rules. For example, if we see two white swans, then we can derive a rule that all swans are white. Inductive inference does not guarantee, in contrast to classical deductive inference, that all conclusions are true if the premises are true. It is possible that the next swan we observe, in contrast to the two observed earlier and our deductively inferred symbolic rule, is a black swan. This means that inductive inference does not necessarily return universally true rules. Therefore, inductively inferred rules are often combined with statistical interpretations. In our example, the rule that all swans are white would only be true with a certain probability.

Another form of inference that is sometimes used is abductive reasoning. In this case, possible explanations for observations (or experiments) are generated. For example, if we know the following rule: “IF stung by mosquito AND mosquito carries malaria THEN malaria is transferred” and we know that someone has malaria, then there is a possible explanation, which states that the person is stung by a mosquito with malaria. There might be also other explanations. For example, that the person has received a blood transfusion with infected blood. Thus, also abductive inference does not offer guarantees about the correctness of the conclusion. But we can again associate probabilities with the possible explanations. This form of inference is important when building tests of theories and has been used by systems such as the Robot Scientist to select the most relevant experiments.Footnote ²⁰ The goal of the Robot Scientist is to automate parts of the scientific method, notable the incremental design of a theory and to test hypotheses to (dis)prove this theory based on experiments. In the case of the Robot Scientist, an actual robot was built that operates in a microbiology laboratory. The robot starts from known theories about biological pathways for yeast. These known theories are altered on purpose to be incorrect, and the experiment was to verify whether the robot could retrieve the correct theories by autonomously designing experiments and executing these experiments in practice. When machine learning is not only learning from observations but also suggesting novel observations and asking for labels, this is called active learning.

1.5.1.3 Bayesian Functions

Some behaviors cannot be captured by logical if-then statements or by fitting a function because they are stochastic (e.g., rolling dice), thus the output or behavior of the system is uncertain. When learning the behavior of such systems, we need a function that can express and quantify stochasticity (e.g., the probability to get each side of a dice after a throw is 1/6). This can be expressed by a function using probability distributions. When dealing with multiple distributions that influence each other, one often uses Bayesian networks that model how different variables relate to each other probabilistically (Figure 1.1 shows a Bayesian network). These functions have as additional advantage that they allow us to easily incorporate domain knowledge and allow for insightful models (e.g., which variables influence or have a causal effect on another variable). For this type of function, we also need to perform forward and backward inference. In the forward direction these are conditional probabilities. In the spam example, forward inference entails calculating the probability that a mail spells your name correctly (correct) given that it is a spam email (spam): $P\left(correct|spam\right)$. For the backward direction we can use the rule of Bayes – therefore the name Bayesian networks – that tells us how to invert the reasoning: $P\left(spam|correct\right)=P\left(correct|spam\right)P\left(spam\right)/P\left(correct\right)$. For the example, if we know $P\left(correct|spam\right)$, that is, the probability that a spam email spells your name correctly, we can use Bayes rule to calculate $P\left(spam|correct\right)$, that is, the probability that a new mail with your name spelled correctly is a spam email.

Bayesian functions are most closely related to traditional statistics where one assumes that the type of distribution from which data is generated is known (e.g., a Gaussian or normal distribution) and then tries to identify the parameters of the distribution to fit the data. In machine learning, one can also start from the data and assume nothing is known about the distribution and thus needs to be learn as part of the machine learning. Furthermore, machine learning also does not require a generative view of the model – the model does not need to explain everything we observe. It suffices if it generates accurate predictions for our variable(s) of interest. However, finding this function is in both cases achieved by applying the laws of probability. Bayesian functions additionally suffer from limited expressional power: not all interactions between variables can be modeled with probability distributions alone.

1.6 Supervised Learning

As an example of a supervised learning technique, we discuss how decision trees can be derived from examples. Decision trees are useful for classification problems, which appear in numerous applications. The goal is to learn, in case of supervised learning, a function from a dataset with examples that are already categorized (or labeled) such that we can apply this function to predict the class of new, not yet classified examples. A good example concerns the classification of emails as spam or not spam.

Closely related with classification problems are regression problems where we want to predict a numerical value instead of a class. This is, for example, the case when the system is learning how to drive a car, and we want to predict the angle of the steering wheel and the desired speed that the car should maintain.

There is vast literature on supervised classification and regression tasks as it is the most studied problem in machine learning. The techniques cover all possible types of functions we have introduced before and combinations thereof. Here we use a simple but popular technique for classification that uses decision trees. In this example, we start from a table of examples, where each row is an example, and each column is an attribute (or feature) of an example. The class of each example can be found in a special column in that table. Take for example the table in Figure 1.4 containing (simplified) data about comic books. Each example expresses the properties of a comic book series: language, length, genre, and historical. The goal is to predict whether this customer would buy an album from a particular series. A decision tree is a tree-shaped structure where each node in the tree represents a decision made based on the value of a particular attribute. The branches emerging from a node represent the possible outcomes based on the values of that attribute. The leaves of this tree represent the predicted classification, in this example buy or not buy. When a new example is given, we traverse the tree following the branch that corresponds to the value that the attribute has in the example. Suppose there exists a series that the customer has not yet bought, with attribute values (NL/FR, Strip, Humor, Historical). When we traverse the tree, we follow the left branch (Strip) for the top node that splits on length. The next node selects based on language and we follow the left branch (NL/FR) ending in the prediction that the customer will buy this new series.

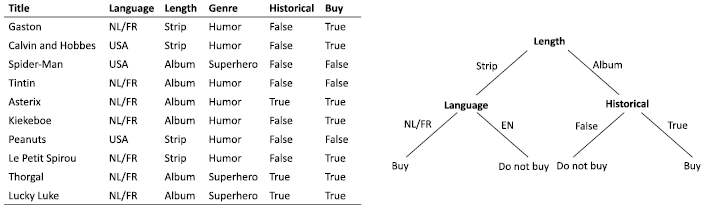
Figure 1.4 Table representing the dataset and the resulting decision tree

The algorithm to learn a decision tree works as follows: we start with a single node and all available examples. Next, we estimate by means of a heuristic which attribute differentiates best between the different classes. A simple heuristic would be to choose the attribute where, if we split the examples based on the possible values for this attribute, this split is most similar to when we would have split the examples based on their class values (buy or not buy). Once the attribute is decided, we create a branch and a new node per value of that attribute. The examples are split over the branches according to their value for that attribute. In each node we check if this new node contains (almost) only once class. If this is the case, we stop and make the node a leaf with as class the majority class. If not, we repeat the procedure on this smaller set of examples.

An advantage of decision trees is that they are easy and fast to learn and that they often deliver accurate predictions, especially if multiple trees are learned in an ensemble where each tree of the ensemble “votes” for a particular classification outcome. The accuracy of the predictions can be estimated from the data and is crucial for a user to decide whether the model is good enough to be used. Furthermore, decision trees are interpretable by users, which increases the user’s trust in the model. In general, their accuracy increases when more data is available and when the quality of this data increases. Defining what are good attributes for an observation, and being able to measure these, is one of the practical challenges that does not only apply for decision trees but for machine learning in general. Also, the heuristic that is used to decide which attribute to use first is central to the success of the method. Ideally, trees are compact by using the most informative attributes. Trying to achieve the most compact or simple tree aligns with the principle of parsimony from thirteenth-century philosopher William of Ockham. This is known as Ockham’s Razor and states that when multiple, alternative theories all explain a given set of observations, then the best theory is the simplest theory that makes the smallest number of assumptions. Empirical research in machine learning has shown that applying this principle often leads to more accurate decision trees that generalize better to unseen data. This principle has also led to concrete mathematical theories such as minimum description length used in machine learning.

1.7 Reinforcement Learning

Learning from rewards is used to decide which actions a system best takes given a certain situation. This technique was developed first by Arthur Samuel and has been further perfectioned since. We illustrate this technique using the Menace program developed by Donald Michie in 1961 to play the Tic-Tac-Toe game. While we illustrate this technique to learn from rewards using a game, these techniques are widely applied in industrial and scientific contexts (e.g., control strategies for elevators, robots, complex industrial processes, autonomous driving). Advances in this field are often showcased in games (e.g., checkers, chess, Go, Stratego) because these are controlled environments where performance is easily and objectively measured. Furthermore, it is a setting where human and machine performance are easily compared.

Tic-Tac-Toe is played on a board with three-by-three squares (see Figure 1.5: The Menace program playing Tic-Tac-Toe). There are two players, X and O, that play in turns. Player X can only put an X in an open square, and player O an O. The player that first succeeds in making a row, column, or diagonal that contains three identical letters wins the game. The task of the learning system is to decide which move to perform in any given situation on the board. The only feedback that is available is whether the game is eventually won or lost, not if a particular move is good or bad. For other strategy games such as checkers or chess, we can also devise rewards or penalties for winning or losing pieces on the board. Learning from rewards differs significantly from supervised learning for classification and regression problems because for every example, here a move, the category is not known. When learning from rewards, deriving whether an example (thus an individual move) is good or bad is part of the learning problem, as it must first be understood how credit is best assigned. This explains why learning from rewards is more difficult than supervised learning.

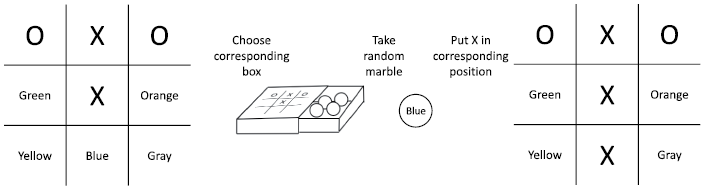
Figure 1.5 The Menace program playing Tic-Tac-Toe

Donald Michie has developed Menace from the observation that there are only 287 relevant positions for the game of Tic-Tac-Toe if one considers symmetry of the board. Because Donald Michie did not have access to computers as we have now, he developed the “hardware” himself. This consisted of 287 match boxes, one for each possible situation on the board. To represent each of the nine possible moves of player X – one for each open position on the board – he had many marbles in nine different colors. Each color represents one of the nine possible squares. These marbles were then divided equally over the match boxes, only excluding colors in those boxes representing a board situation where the move is not possible. Menace then decided on the move as follows:

1. a. Take the match box that represents the current situation on the board.

2. b. Randomly take a marble from the match box.

3. c. Play the move that corresponds to the color of the marble.

The Menace program thus represents a function that for every board situation and possible next moves returns a probability that this move should be played from this position. The probabilities are given by the relative number of marbles of a certain color in the corresponding match box. The learning then happens as follows. If the game is won by X, then for every match box from which one marble was taken, two marbles of that color are again added to these match boxes. If X loses the game, then no marbles are returned. The consequence of these actions is that the probability of winning moves in the relevant boxes (and thus board situations) is increased and that of losing moves is decreased. The more games that are played, the better the probabilities represent a good policy to follow to win a game. The rewards from which Menace learns are thus the won and lost games, where lost games are negative rewards or penalties.

When learning from rewards, it is important to find a good balance between exploration and exploitation. Exploration is important to explore the space of all possible strategies thoroughly, while exploitation is responsible for using the gained knowledge to improve performance. In the case of Menace, a stochastic strategy is used where a move is decided by randomly selecting a marble. Initially, the probability for any possible move in a particular situation is completely at random, which is important for exploration, as there are about an equal number of marbles for each (possible) color in each box. But after a while, the game converges to a good strategy when there are more marbles of colors that represent good moves, which is important for exploitation.

Today, learning from rewards does not use matchboxes anymore but still follows the same mathematical principles. These principles have been formalized as Markov Decision Processes and often a so-called Q-function $Q(s,a)$ is learned. Here $Q(s,a)$ represents the reward that is expected when an action a is taken in a state s. In the Tic-Tac-Toe example, the action is the next move a player takes and the state s is the current situation on the board. The Q-function is learned by using the famous Belmann equation, $Q\left(s,a\right)=R\left(s,a\right)+\gamma {\text{ max}}_{a^{\prime }}Q\left(s\prime ,a\prime \right)$, where $R\left(s,a\right)$ is the immediate reward received after taking action a in situation s, $\gamma$ is a number between 0 and 1 that indicates how future rewards relate to the immediate reward (rewards obtained in the future are less valuable than an equal immediate reward), and s′ the state that is reached after taking action a in situation s. The Q-function is also used to select the actions. The best action in a situation s is the action a for which $Q\left(s,a\right)$ is maximal. To illustrate Q-learning, consider again the Menace program. Each box can be considered as a state, and each color as an action that can be executed in that state. The Q-function then contains the probability of selecting a marble from that color in that box, and the best action is the one is that with the maximum probability (i.e., the color that occurs most in that box).

1.8 Unsupervised Learning

For the third type of feedback, we look at learning associations. Here we have no labels or direct feedback available. This technique became popular as part of recommender systems used by online shops such as Amazon and streaming platforms such as Netflix. Such companies sell products such as books or movies and advise their customers by recommending products they might like. These recommendations are often based on their previous consuming behavior (e.g., products bought or movies watched). Such associations can be expressed as rules like:

$\text{IF }X\text{ and }Y\text{ are being consumed},\text{THEN }Z\text{ will also be consumed}.$

X, Y, and Z represent specific items such as books or movies. For example, X = Pulp Fiction, Y = Kill Bill, and Z = Django Unchained. Such associations are derived from transaction data gathered about customers. From this data frequently occurring subsets of items are derived. This is expressed as a frequency of the number of times this combination of items occurs together. A collection of items is considered frequent if their frequency is at least x%, thus that it occurs in at least x% of all purchases. From these frequent collections, the associations are derived. Take for example a collection of items $\left(X,Y,Z\right)$ that is frequent since it appears in 15% of all purchases. In that case, we know that the collection $\left(X,Y\right)$ is also frequent and has a frequency of at least 15%. Say that the frequency of $\left(X,Y\right)$ is 20%, then we can assign some form of probability and build an association rule. The probability that Z will be consumed, if we know that X and Y have been consumed then:

$\text{Frequency}\left(\{X,Y,Z\}\right)/\text{frequency}\left(\{X,Y\}\right)=0.15/0.20=75\%$

The information on frequent collections and associations allows us to recommend products (e.g., books or movies). If we want to suggest products that fit with product X and Y, we can simply look at all frequent collections $\left(X,Y,Z\right)$ and recommend products Z based on increasing frequency of the collections $\left(X,Y,Z\right)$.

Learning associations are useful in various situations, for instance, when analyzing customer information in a grocery store. When the products X and Y are often bought together, then we can strategically position product Z in the store. The store owner can put the products close to each other to make it easy for customers to buy this combination or to be reminded of also buying this product. Or the owner can put them far apart and hope the customer picks up some additional products when traversing from one end of the store to the other end.

Another form of unsupervised learning is clustering. For clustering, one inspects the properties of the given set of items and tries to group them such that similar items are in the same group and dissimilar items are in other groups. Once a set of clusters is found, one can recommend items based on the most nearby group. For example, in a database of legal documents, clustering of related documents can be used to simplify locating similar or more relevant documents.

1.9 Reasoning

When considering reasoning, we often refer to knowledge as input to the system, as opposed to data for machine learning. Knowledge can be expressed in many ways, but logic and constraints are popular choices. We have already seen how logic can be used to express a function that is learned, but more deliberate, multi-step types of inference can be used when considering reasoning. As an example, consider a satisfiability problem, also known as a SAT problem. The goal of a SAT problem is to find, given a set of constraints, a solution that satisfies all these constraints. This type of problem is one of the most fundamental ones of computer science and AI. It is the prototypical hard computational problem and many other problems can be reduced to it. You also encounter SAT problems daily (e.g., suggesting a route to drive, which packages to pick up and when to deliver them, configuring a car). Say, we want to choose a restaurant with a group of people, and we know that Ann prefers Asian or Indian and is Vegan; Bob likes Italian or Asian, and if it is Vegan then he prefers Indian. Carry likes vegan or Indian but does not like Italian. We also know that Asian food includes Indian. We can express this knowledge using logic constraints:

$(\text{Asian}\vee \text{Indian})\wedge \text{Vegan}\wedge (\text{Italian}\vee \text{Asian})\wedge \left(\text{Vegan}\to \text{Indian}\right)\wedge (\text{Vegan}\vee \text{Indian})\wedge \neg \text{Italian}\wedge \left(\text{Indian}\to \text{Asian}\right)$

Observe that ∨ stands for OR (disjunction), and ∧ for AND (conjunction). Furthermore, A → B stands for IF A THEN B (implication).

When feeding these constraints to a solver, the computer will tell you the solution is to choose Vegan.Footnote ²¹ Actually, the solution that the solver would find is Vegan, Indian, not Italian, and Asian. It is easy that starting from the solution Vegan, then we can also derive Indian, and from Indian, we can derive Asian. Furthermore, the conjunction also specifies that not Italian should be true. With these, all elements of the conjunction are satisfied, and thus this provides a solution to the SAT problem.

While we presented an example that required pure reasoning, the integration of learning and reasoning is required in practice. For the previous example, this is the case when we also want to learn preferences. Similarly, when choosing a route to drive, we want to consider learned patterns of traffic jams; or when supplying stores, we want to consider learned customer buying patterns.

1.10 Trustworthy AI

Models learned by machine learning techniques are typically evaluated based on their predictive performance (e.g., accuracy, f1-score, AUC, squared error) on a test set – a held-aside portion of the data that was not used for learning the model. A good value on these performance metrics indicates that the learned model can also predict other unseen (i.e., not used for learning) examples accurately. While such an evaluation is crucial, in practice it is not sufficient. We illustrate this with three examples. (1) If a model achieves 99% accuracy, what do we know about the 1% that is not predicted accurately? If our training data is biased, the mistakes might not be distributed equally over our population. A well-known example is facial recognition where the training data contained less data about people of color causing more mistakes to be made on this subpopulation.Footnote ²² (2) If groups of examples in our population are not covered by our training data, will the model still predict accurately? If you train a medical prediction model on adults – because consent is easier to obtain – the model cannot be trusted for children because their physiology is different.Footnote ²³ Instead of incorrect predictions, more subtly this might lead to bias. If part of the population is not covered, say buildings in poor areas that are not yet digitized, should we then ignore such buildings in policies based on AI models? (3) Does our model conform to a set of given requirements? These can be legal requirements such as the prohibition to drive on the sidewalk, or ethical requirements such as fairness constraints.Footnote ²⁴

These questions are being tackled in the domain of trustworthy AI.Footnote ²⁵ AI researchers have been trying to answer questions about the trustworthiness and interpretability of their models since the early days of AI. Especially when systems were deployed in production like in the expert systems of the 1980s. But the recent explosion of deployed machine learning and reasoning systems together with the introduction of legislation such as the General Data Protection Regulation (GDPR) and the upcoming AI-act of the European Union has led to a renewed and much larger interest in all aspects related to trustworthy AI. Unfortunately, it is technically much more challenging to answer these questions as only forward and backward inference does not suffice. The field of trustworthy AI encompasses a few different questions that we will now discuss.

1.11 Explainable AI (XAI)

When an AI model, that is, a function, translates input information into an output (e.g., a prediction or recommendation), knowing only the output may not be acceptable for all persons or in all situations. When making a decision based on machine learning output, it is important to understand at least the crucial parts that led to the output. his is important to achieve appropriate trust in the model when these decisions impact humans or for instance the yield or efficiency of a production process. This is also reflected in the motivation behind legislation such as the GDPR.Footnote ²⁶ Often the need for explainability is driven by the realization that machine learning and reasoning models are prone to errors or bias. The training data might contain errors or bias that are replicated by the model, the model itself might have limitations in what it can express and induce errors or bias, inaccurate or even incorrect assumptions might have been made when modeling the problem, or there might simply be a programming error. On top of the mere output of a machine learning or reasoning algorithm, we thus need techniques to explain these outputs.

One can approach explaining AI models in two ways: only allowing white box models that can be inspected by looking at the model (e.g., a decision tree) or using and developing mechanisms to inspect black box models (e.g., neural networks). While the former is easier, there is also a trade-off with respect to accuracy.Footnote ²⁷ We thus need to be able to obtain explainability of black box models. However, full interpretability of the internal mechanisms of the algorithms or up to the sensory inputs might not be required. We also do not need to explain how our eyes and brain exactly translate light beams into objects and shapes such as a traffic light to explain that we stopped because the traffic light is red. Explainability could in these cases focus on generating a global understanding of how outputs follow from particular inputs (e.g., in the most relevant or most prominent cases that occur). For particular cases though, full explainability or a white box model might be a requirement. For example, when applying legislation to a situation where we need to explain which clauses are used where and why.

There have been great advances in explaining black box models. Model-specific explainers are explainers that work only on a particular type of black box models, such as explainers for neural networks. As these explainers are developed for particular models, the known underlying function can be reverse-engineered to explain model outputs for individual examples. Model-agnostic explainers (e.g., LIMEFootnote ²⁸ and SHAPFootnote ²⁹) on the other hand can be applied to any black box model and therefore cannot rely on the internal structure of the model. Their broad applicability often comes at the cost of precision: they can only rely on the black box model’s behavior between input and output and in contrast to the model-specific explainers cannot inspect the underlying function. Local explainers try to approximate the black box function around a given example and hereby generate the so-called “local explanations,” thus explanations of the behavior of the black box model in the neighborhood of the given example. One possibility is to use feature importance as explanations as it indicates which features are most important to explain the output (e.g., to decide whether a loan gets approved or not the model based its decision for similar clients most importantly on the family income and secondly on the health of the family). Another way to explain decisions is to search for counterfactual examplesFootnote ³⁰ that give us, for example, the most similar example that would have received a different categorization (e.g., what should I minimally change to get my loan approved?). Besides local explanations one could ideally also provide global explanations that hold for all instances, also those not yet covered by the training data. Global explanations are in general more difficult to obtain.

1.12 Robustness

Robustness is an assessment of whether our learned function meets the expected specifications. Its scope is broader than explanations in that it also requires certain guarantees to be met. A first aspect of robustness is to verify whether an adversarial example exists. An adversarial example is like a counterfactual example that flips the category, but one that is designed to deceive the model as a human would not observe a difference between the normal and the adversarial example (see Figure 1.6). For example, if by changing a few pixels in an image, changes that are meaningless to a human observer, the learned function can be convinced to change the predicted category (e.g., a picture that is clearly a stop sign for a human observer but deceives the model to be classified as a speed limit sign). A second popular analysis is about data privacy: does the learned function leak information about individual data examples (e.g., a patient)? A final aspect is that of fairness, sometimes also considered separately from robustness. It is vaguer by nature as it can differ for cultural or generational reasons. In general, it is an unjust advantage for one side. Remember the facial recognition example where the algorithm’s goal to optimize accuracy disadvantages people of color because they are a minority group in the data. Another example of fairness can be found in reinforcement learning where actions should not block something or somebody. A traffic light that never allows one to pass or an elevator that never stops on the third floor (because in our training data nobody was ever on the third floor) is considered unfair and to be avoided.

Figure 1.6 Adversarial examples for digits.Footnote ³¹

Robustness thus entails testing strategies to verify whether the AI system does what is expected under stress, when being deceived, and when confronted with anomalous or rare situations. This is also mentioned in the White Paper on Artificial Intelligence: A European approach to excellence and trust.Footnote ³² Offering such guarantees, however, is also the topic of many research projects since proving that the function adheres to certain statements or constraints is in many cases computationally intractable and only possible by approximation.

1.13 Conclusions

Machine learning and machine reasoning are domains within the larger field of AI and computer sciences that are still growing and evolving rapidly. AI studies how one can develop a machine that can learn from observations and what fundamental laws guide this process. There is consensus about the nature of machine learning, in that it can be formalized as learning of functions. There is also consensus that machine reasoning enables the exploitation of knowledge to infer answers to a wide range of queries. However, for now, there is neither a known set of universal laws that govern all AI and machine learning and reasoning, nor do we understand how machine learning and reasoning can be fully integrated. Therefore, many different approaches and techniques exist that push forward our insights and available technology. Despite the work ahead there are already many practical learning and reasoning systems and exciting applications that are being deployed and influence our daily life.