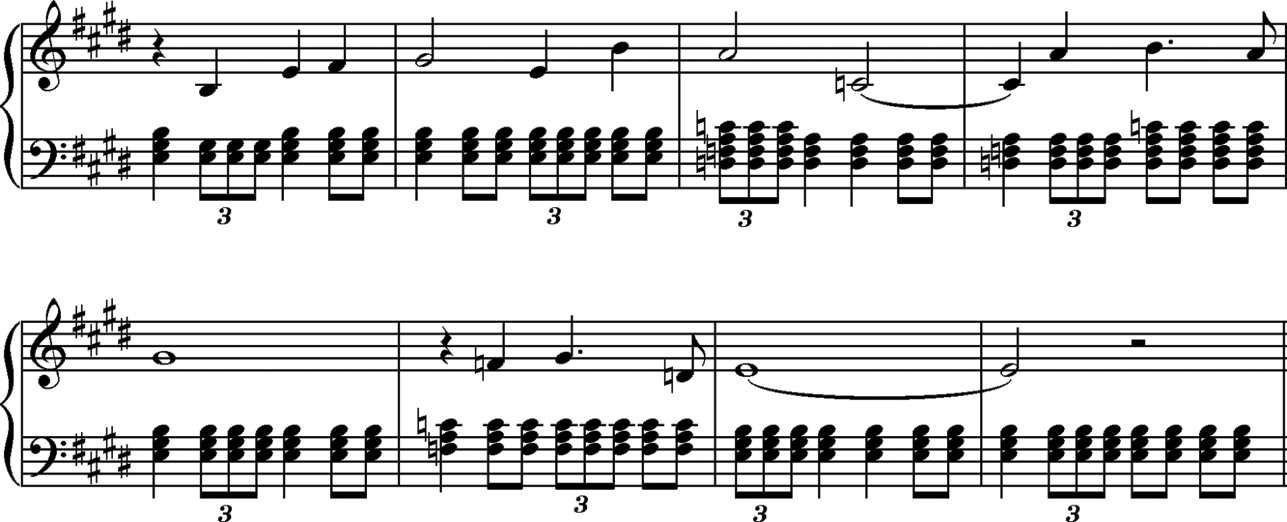Ludomusicologists generally agree that cinema and television represent the nearest siblings to video games, and so therefore adopt many methodologies familiar to film music scholarship in their work. For example, the influential concepts of diegetic and non-diegetic, which respectively describe sounds that exist either within or outside a narrative frame,Footnote 1 feature prominently in many accounts of game audio, and represent one axis of Karen Collins’s model for the uses of game audio, the other being dynamic and non-dynamic, where dynamic audio can be further subcategorized as adaptive or interactive.Footnote 2 Ludomusicologists generally also agree that the interactive nature of video games marks its primary distinction from other forms of multimedia, and so a fundamental point of entry into studying game audio is to examine how composers and sound designers create scores and soundtracks that can adapt to indeterminate player actions.
Indeterminacy, though, creates a challenge for modern music theory, which is founded on the close study of musical scores, subjecting to detailed analysis the dots, curves and lines inscribed on their pages to reveal the musical structures and organizational patterns that drive their composition. For music theorists, who may be most comfortable examining music that has been fixed into notation in the form of a musical score, indeterminacy raises additional questions and problems: how does one analyse music for which there is no single agreed-upon structure, and which may be realized in a fundamentally different way every time it is heard? Because of this problem, music theory, alongside historical musicology, has been vulnerable to criticism for its tendency to privilege the notated score above other forms and artefacts of musical creativity. Don Michael Randel has observed, for example, that in popular music, ‘“the work itself” is not so easily defined and certainly not in terms of musical notation’.Footnote 3 In that vein, Lydia Goehr’s study, The Imaginary Museum of Musical Works, has become a gold-standard critical handbook of philosophical approaches to the concept of ‘the musical work’, and one of her first tasks is to dispense with the notion that the work (if such a thing exists at all) can be fully encapsulated by the musical score – even in the case of a common-practice composition for which an authoritative score exists.Footnote 4 Other scholarship, such as Jean-Jacques Nattiez’s Music and Discourse,Footnote 5 has criticized the manner by which privileging the musical score presumes a direct communicative act between composer and listener that treats the role of the performer as ancillary. At worst, score-centric analysis may even suggest – or explicitly claim – that the need for musical performance reflects an unfortunate real-world compromise to an ideal situation in which musical ideas could be communicated from composer to listener without mediation. Heinrich Schenker’s opening line of The Art of Performance makes this argument in a particularly bold and provocative way: ‘Basically, a composition does not require a performance to exist.’Footnote 6 And what is more, some mid-twentieth-century composers embraced electronic music specifically for its potential to eliminate the need for human performance.Footnote 7
At best, music theorists might isolate single improvised performances as case studies, freezing them into musical notation to subject them to conventional analytical methodologies. But such strategies fail when applied to the analysis of ever-changing video game music. While a single performance of Charlie Parker and Dizzy Gillespie performing Tadd Dameron’s Hot House might achieve canonical heights worthy of transcription and close study, no single playthrough of a video game could ever be understood as definitive, and it is typically very difficult, if not impossible, to play a video game exactly the same way twice. A compelling analysis of a video game score, then, requires methodologies that are a bit alien to some assumptions that currently govern music-theoretical practice. We must heed David Lewin, who once described his analytic method ‘as a space of theoretical potentialities, rather than a compendium of musical practicalities’,Footnote 8 and yet go further, developing as we do approaches that can analyse music as both a set of theoretical potentialities and an adjoining set of practical musical potentialities, introduced whenever a video game score implements algorithmic solutions that provide satisfactory continuations to moments of musical indeterminacy. In short, many theoretical methodologies are not readily equipped to analyse game audio; existing toolsets must be reworked and new ones devised to grapple with this protean music.Footnote 9 This is a good thing: analytic methodologies are not destroyed but tempered and strengthened when reforged for use with new materials. This essay examines excerpts from Super Mario Galaxy (2007) through the lens of three music-theoretical methodologies in current practice – formal, reductive and transformational – demonstrating how the idiomatic nature of video game storytelling has a substantial impact on the utility of the analytical tools used to study its music.
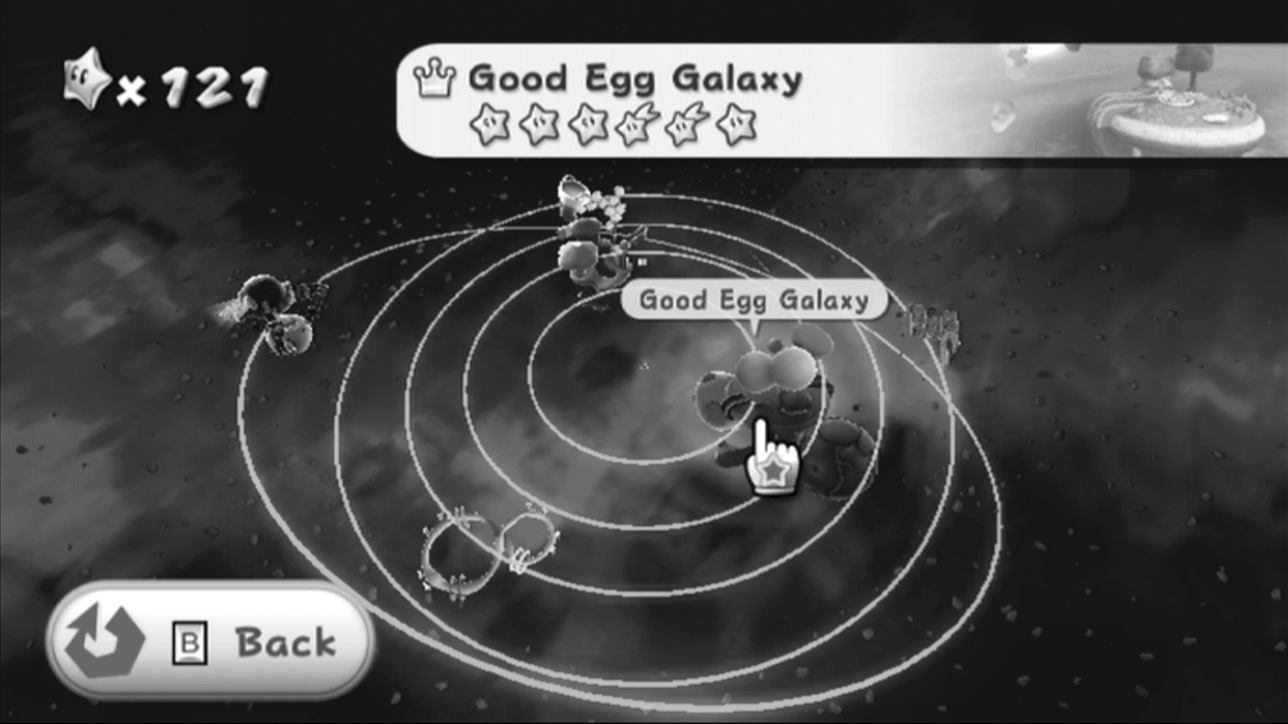
The central conceit of Super Mario Galaxy is that the perennial villain Bowser has once again kidnapped Mario’s beloved Princess Peach and is travelling through the universe with her as his prisoner. After some introductory levels, Mario finds himself on a space observatory, which, due to its low power levels, is only able to observe a small set of galaxies, the game’s basic platforming stages. Each galaxy is associated with one or more missions; through completing them, Mario accumulates ‘power stars’, which re-energize the Observatory so that it is able to reach further out into space, allowing Mario access to more galaxies with more power stars, and ultimately Bowser’s hideout.
Methodology 1: Formal Analysis – Theme and Variation
Elaine Sisman, in her article on variation in The New Grove Dictionary of Music and Musicians, defines it as ‘A form founded on repetition, and as such an outgrowth of a fundamental musical and rhetorical principle, in which a discrete theme is repeated several or many times with various modifications’, and she shows that one purpose of the form is epideixis, a rhetoric of ceremony and demonstration, where the purpose of the repetitions is to amplify, ‘revealing in ever stronger terms the importance of the subject’.Footnote 10 In a classical set, the listener is often presented with variations of greater and greater complexity with the final variation serving as a climactic whirlwind of virtuosity that Roger Moseley has described as a musical ilinx, a ‘dizzying, unruly play of motion’.Footnote 11 Musical variations appear in the score to Super Mario Galaxy, which features compositions that are readily understood as variations of others. I will consider two examples here: the developing orchestration to the Observatory Waltz, and the fragmenting of the Battlerock music in subsequent galaxies.
The waltz accompanies Mario’s exploration of the Observatory, during which it becomes evident that because the Observatory is not fully powered, there are many dark, inaccessible sections in it (see Figure 12.1). The waltz is sparsely orchestrated: after an introductory standing-on-the-dominant, a vibraphone carries the melody with a simple bass accompaniment played by a cello; the harmonic progression of the passage is thus implied by a two-voice contrapuntal framework (see Example 12.1). As Mario explores the galaxy and accumulates power stars, the Observatory is re-energized, and more areas become illuminated and accessible (see Figure 12.2). As this happens, the waltz becomes more lushly orchestrated and new countermelodies are added. Example 12.2 presents an excerpt from the final stage of musical development: the bassline, still articulated by the cello, is joined by horns that fill out the chords in an oom-pah-pah rhythm. Violins now carry the basic melody, adding an expressivity not present in the vibraphone, and the flute, which in the earlier iteration simply doubled the vibraphone upon repetition, now sounds a new melody in counterpoint with the violins. The rich variations of the basic waltz theme thus become an aural metaphor for the enlivened Observatory and the wide array of areas that are now open for play and exploration. Moreover, the variations do not appear simply as an exercise in progressive musical elaborations that we, the players, passively hear. Rather, the player, through Mario, is afforded a degree of agency in causing the variations’ development: it is through our actions that the Observatory is re-energized, and so, within the fiction of the gameworld, it is we who bring about the subsequent variations.

Example 12.1 Comet Observatory waltz, early (excerpt). All transcriptions by the author

Example 12.2 Comet Observatory waltz, late (excerpt)

Figure 12.1 Comet Observatory, early; note darkened, inaccessible area in background*

Figure 12.2 Comet Observatory, late; background now illuminated and accessible
In a case opposite to the first example, a theme is varied by stripping its elements down – reduction, rather than elaboration: in an early stage, the Battlerock Galaxy, Mario leaps between platforms and dodges bullets and force fields beside and through an enormous battle station built into an asteroid. The level’s music, a brief reduction of which is excerpted in Example 12.3, features a martial and memorably tuneful scoring that alternates between two primary melodies with a march-like accompaniment, resembling countless science-fiction space epics, like Star Wars (1977), or the original Battlestar Galactica television series (1978–1979).
Example 12.3 Reduction of Battlerock Galaxy music, first theme (excerpt)
The music appears in an unaltered form in the later ‘Dreadnought Galaxy’, and the repetition of the theme connects the military qualities of the battleship with the earlier battle station. However, the initial introduction to this galaxy takes place in a sequence entitled ‘Infiltrating the Dreadnought’, in which Mario sneaks onto the ship by way of a pipe hidden on its side. During this portion of the level, the music that plays is a nearly unrecognizable, minimalistic version of the Battlerock tune: entitled ‘Space Fantasy’ on the official soundtrack release,Footnote 12 the string melody has disappeared, and the basic chord progression is implied only by the frantic, unpredictably leaping arpeggios that appear deep in the mix of the Battlerock music (see Example 12.4). If we imagine the process of variation to be one of further elaboration of a basic structure, then the ‘Space Fantasy’ music serves as a kind of anti-variation, having stripped the Battlerock music of its elaborations to provide only its basic structure. There is a clever thematic parallel to the story taking place on screen: Mario’s ‘infiltration’ of the Dreadnought implies that he stealthily evades detection during his entry – how fitting, then, that the musical accompaniment is a furtive echo of the bombastic battle tune, whose presence is so subtle that it may even elude detection by the player.

Example 12.4 Reduction of ‘Space Fantasy’ (excerpt), same passage as that associated with Example 12.3. Although the surface chords change in the sixth bar of Example 12.3, the arpeggios that play beneath them at that point are the same as they appear here
‘Space Fantasy’ underscores several other galaxies as well, including the ‘Matter Splatter Galaxy’. Though this level mostly consists of a nebulous void, surfaces appear when droplets of matter fall in the manner of raindrops splattering on pavement, and as these ‘dry up’, the platforms that they comprise vanish until new ones fall in their place (see Figure 12.3). Once again, the appearance of the Battlerock tune invites the observant listener to conceptually connect these ostensibly disparate levels and to imagine a narrative thread that connects them. Perhaps the matter-splatter phenomenon is the result of a devastating battle that once took place, and just as the ‘Space Fantasy’ presents a disjointed, nearly unrecognizable anti-variation of the Battlerock theme, so too has all of the matter of the galaxy been fragmented, with only the sparsest bits being recognizable as traversable ground.

Figure 12.3 Matter Splatter Galaxy
Elsewhere, I have examined the interaction of theme and variations with gameplay in Portal 2 (Valve Corporation, 2011).Footnote 13 There, I showed that there was a distinct correlation of the game’s procedures for training the player in its mechanics with a development in the musical accompaniments: that the gameplay itself is organized according to the musical principle of theme and variations. Portal 2 is not unique in this regard; video games are often designed around iterative storytelling and gameplay mechanics: video game stories are often told and retold.Footnote 14 In the world of Super Mario Bros. this could mean an iterative story in which Mario explores three stages plus a fortress, only to find that ‘OUR PRINCESS IS IN ANOTHER CASTLE’, meaning that he must repeat the exercise seven more times in increasingly difficult challenges. It could also mean the iterative process by which almost all entries in the franchise involve Bowser kidnapping Peach and Mario exploring grander and grander spaces (Land … World … Galaxy) to rescue her, with each title introducing and requiring of the player more and more complex gameplay techniques to do so.Footnote 15 Given this narratological structure, which is fundamental to the series, the similarly iterative musical principle of theme and variations offers a particularly well suited means of accompanying Mario’s adventures.
Methodology 2: Reductive Analysis
Twentieth-century tonal music theory in North America was dominated by Schenkerian analysis, a methodology developed in the first half of the twentieth century by pianist, composer and editor Heinrich Schenker (1868–1935). Schenkerian analysis is a form of reductive analysis with two essential features: first, it examines a piece with the goal of determining which of its pitches are structural and which are ornamental. A structural pitch is emblematic of a governing harmony at a particular moment, and may be decorated, or prolonged, by ornamental ones. The process occurs on several levels of resolution, referred to as the foreground, middleground and background. A foreground analysis accounts for nearly every note of a work’s outer voices (bass and soprano). Notes determined to be structural at the foreground level are then reproduced at a middleground level, and are once again examined to determine their relative structural or ornamental significance in that higher-order context. The process can continue through several layers of middleground, but eventually the analysis will identify a specific set of tones that cannot be reduced further: these pitches constitute the background. One of the greatest insights of Schenker’s theory is the idea that tonal processes are self-similar – that is, those that govern the musical surface also govern the deepest structure of a work, up to and including the background.
The background level also highlights the second essential feature of the methodology: for Schenker, tonal music is organized around a teleological principle whereby the pitch representing either scale degree 3 or scale degree 5 undertakes a descent to arrive at scale degree 1, accompanied by a bass arpeggiation outlining a I–V–I progression – the combination of the melodic descent and the bass arpeggiation is called the work’s Ursatz, or fundamental structure (see Figure 12.4).Footnote 16 Tonal processes being self-similar, as noted above, a Schenkerian analysis is likely to identify many analogous teleological descents taking place in short form over the course of an entire work.

Figure 12.4 The two archetypal Schenkerian backgrounds (Ursätze). Schenker also allows for the theoretical possibility of a background that descends by octave, but these are rare in practice
To some degree, Schenkerian methodologies have fallen out of favour, in part due to criticism from musicology for their ideological privileging of the Austro-Germanic musical tradition and assumptions about the relationship between organicism and genius, amongst others.Footnote 17 Indeed, a principal criticism of the theory is its circularity, in that it prioritizes a certain kind of musical organization, and then deems as ‘good’ works that conform to its desired criteria, such works having been carefully selected from the common-practice canon.Footnote 18 But perhaps even more importantly, the late twentieth century saw a general disciplinary widening of American music theory, from the purviews of both methodology and repertoire. On the one hand, this meant that music theorists began analysing works from outside the canon of Western art music, the tonal compositions in which Schenkerian elucidation finds its richest rewards. On the other hand, new analytical methodologies arose that, if not entirely supplanted, then at least displaced Schenkerian analysis from its position as the dominant toolset for studying triadic music – one of these, neo-Riemannian analysis, we will consider below.Footnote 19
But while many criticisms of the theory as a whole are legitimate, that does not mean that it needs to be rejected wholesale: the techniques of reductive analysis that Schenker pioneered are powerful and can be employed without being oriented towards its problematic ends.Footnote 20 It is, for example, perfectly reasonable to assign structural significance to certain musical tones without needing to implicate them as part of a controversial Ursatz, and when I teach Schenkerian analysis to my own students, I emphasize how identifying the relative structural weight of specific notes in a melody can contribute to their vision for an artful performance regardless of how well those tones group on the background level in the abstract. Certainly, other productive ends are possible, too, and this section will focus on one sequence in Super Mario Galaxy – the battle with the boss character King Kaliente – to show how the musical logic of the encounter proposes a hearing that is captured particularly well through a reductive reading that departs from many of the central tenets of conventional Schenkerian theory.Footnote 21
King Kaliente is encountered as part of a mission in the early Good Egg Galaxy. After navigating through the level, the player arrives on a planetoid on which is a pool of lava surrounded by a small ring of land. King Kaliente spits out two kinds of projectiles at Mario: fireballs, which must be dodged, and coconuts, which Mario must volley back at him (see Figure 12.5). The pattern of the battle is typical for Mario games: the first volley strikes the boss; on the second volley, the boss returns the coconut, which Mario must strike a second time before it connects; and on the third volley, the boss returns the coconut a second time, so Mario must strike it three consecutive times before it hits. Once it does, the encounter ends. In sum, on the first volley there are two hits – the first when Mario returns the coconut, and the second when it strikes King Kaliente; on the second volley there are four hits, and on the third volley six. Each hit is accompanied by a different tone, so on each successive volley two new tones are heard. The music that accompanies the battle alternates between two principal themes, and the pitches that sound with each hit change depending on which theme is playing. Table 12.1 presents the pitches that sound during the first theme only, but it is worth noting that both versions end on the same B♭.

Figure 12.5 Mario volleys a coconut at King Kaliente
Table 12.1 Number of hits and pitches sounded during each volley of the King Kaliente battle
| Volley # | Number of hits | Pitches sounded |
|---|---|---|
| 1 | 2 | C, G |
| 2 | 4 | C, E♭, F, G |
| 3 | 6 | C, E♭, F, F♯, G, B♭ |
Figure 12.6 presents each of the three volleys in a rudimentary Schenkerian notation. In so doing, it suggests a reading wherein each of the successive volleys ‘composes out’ the preceding. Hence, the E♭ in the second volley is seen as a consonant skip from the opening C, and the F as an incomplete lower neighbour to the closing G: these additional tones thus ornament the structural perfect fifth. In the third volley, the notes from the second are given stems to indicate their relative structural weight as compared to the newly added tones: the F♯, a chromatic passing tone between the incomplete neighbour F and the structural G, and the B♭, a consonant skip from the structural G.

Figure 12.6 Reductive analysis of the King Kaliente hits
Although the techniques used to create Figure 12.6 are heavily drawn from Schenkerian practices, its interpretive implications are quite different. First, a conventional Schenkerian reading presupposes that the various levels examine the same passage of music at different degrees of resolution: the background level presents only its most structurally significant tones, the middleground level presents all tones above a certain threshold of structural significance and the foreground level replicates most tones, if not every tone of the outer voices. In typical practice, Schenkerian backgrounds and middlegrounds are not intended to reflect passages that are literally heard in performance, let alone in serial presentation,Footnote 22 yet here, the three successive volleys present, in order, background, middleground and foreground readings of a singular musical idea.
Figure 12.6 thus suggests that each successive volley is a more musically detailed version of the preceding one – that the tones accompanying the initial volley present only the background structure of the attack’s musical logic, and that the successive attacks come closer and closer to its musical surface. That musical observation may cause us to recast our experience of the gameplay challenge presented to us. In principle, the structure of the encounter will be familiar to most gamers: once players master a simple gameplay mechanic, they are then asked to contend with more difficult and complicated variations of it. In this view, the first volley may be understood as a prototype that is developed and varied in the successive volleys. Instead, rather than seeing later iterations of the attack as complications of a basic process, the Schenkerian reading allows us to read the final volley as the fundamental process. Rather than the encounter representing the growth and development of a simple technique, it can be understood as an enacted actualization of a complex task through an iterative presentation of versions that begin simply and become progressively more complex. This way of thinking is not only native to gameplay design;Footnote 23 Jeffrey Swinkin has also shown that such a ‘thematic actualization’ is a productive lens for understanding Romantic variation sets, where ‘variations retroactively define what the theme is’ and ‘themes often do not reside at a determinate point in musical space [i.e., at the beginning] but rather come into being gradually as the piece unfolds’.Footnote 24
Second, Schenkerian logic takes the position that the move from foreground to background reveals the basic tonal structure of a composition through the revelation that each tone of the foreground in some way participates in the prolongation of the tones of the Ursatz, which features a descending scale in either the major or minor mode – a suitable enough distinction for the common-practice tonal works for which Schenkerian analysis is most effectively deployed.Footnote 25 Notably, the background presented in Figure 12.6 does not resemble the conventional backgrounds of Figure 12.4. Furthermore, the King Kaliente battle music is composed in a modal idiom that is not well captured by a major/minor binary: specifically, the C-minor blues scale, the complete collection of which not only appears in the third volley, but also constitutes the basic piano vamp accompanying the encounter (see Example 12.5). Thus, it is the foreground, rather than the background level, that clarifies the tune’s basic tonal language.

Example 12.5 King Kaliente battle music (A theme only) (excerpt)
Crucially, notwithstanding the ways in which the present reductive reading diverges from conventional Schenkerian practice, it is still able to engage with the first of the central Schenkerian insights: that being the relationship between background structures and foreground gestures. Specifically, as already noted, the foreground version of the hits exactly replicate the piano vamp; moreover, as shown in Figure 12.7, the background of Figure 12.6 is identical to the background of the synth melody, which also features structural motion from C up to G – also note the resemblance of the foreground of Figure 12.6 to that of Figure 12.7: each features an initial consonant skip from C to E♭, an F# approach to G and registral and melodic prominence of a high B♭.

Figure 12.7 Reductive analysis of first half of synth melody
The nuances elucidated by a reductive analysis of the King Kaliente theme further provide an explanation for something that long ago caught my attention, and this relates to the second feature of Schenkerian methodology. Video games and Schenkerian analysis are similarly goal-oriented: in this example, the player’s goal is to defeat the enemy, while in the Ursätze of Figure 12.4, the music’s goal is to descend to C. When first encountering this boss fight and experiencing the musical coordination of pitch hits with Mario’s attacks, I had expected that the final note would be the high C, thereby allowing the six-note figure of the third volley to cadence, thus co-ordinating musical closure with the end of the battle. Such a resolution would align well with other teleological theories, like Eugene Narmour’s implication-realization model,Footnote 26 but a high C here would not serve a reductive reading well. First, as a cadential pitch, it would be tempting to grant it structural significance, but since it would only appear in the foreground version of the motive, there would be no compelling way to add it to the background version. Second, the presence of the B♭ is not only necessary to flesh out the complete blues scale, but it also ensures complete pitch variety for the third volley attack: a high C would replicate the pitch class of the first note. Finally, a high C does not participate at all in the musical surface of Example 12.5, except for a brief appearance as an incomplete upper neighbour to the B♭ in the second half of the melody – and so again, it would be a mistake to afford the high C the structural significance it would need to be a goal tone for the passage.
All told, then, the reductive reading presents a more compelling explanation for the pitch selection of the third volley than might a competing theory based on realized implications. In my modified Schenkerian view, the structural pitches of the encounter are C and G – a motive established in the first volley and confirmed in the second. But, and I thank Scott Murphy for phrasing it thusly, ‘permanently vanquishing is categorically different than temporarily stunning’,Footnote 27 and the third volley makes the distinction audibly clear. While the hits for each volley feature the same musical structure, it is only the final, successful volley that transcends the structural G to land on the vanquishing upper B♭.
The criticisms of the late twentieth century certainly impacted Schenkerian analysis’s dominance within the field of North American music theory, but a thoughtful analysis can still carefully tailor the undeniably powerful and unique insights that the methodology is capable of elucidating while avoiding the larger ideological and contextual problems that hazard its practice. In my view, this is to be embraced: on the one hand, the jazzy King Kaliente music, like much music of the post-common-practice era, is not composed according to the assumptions that Schenkerian practice is designed to accommodate, and any attempt to ‘Schenkerize’ it according to them would be doomed to fail. On the other hand, the Observatory waltz of Examples 12.1 and 12.2 could, with relative ease, submit to a conventional Schenkerian reading with a normative Ursatz, but it is hard to imagine what the purpose of such an exercise would be, beyond making a claim that the Observatory waltz fulfils the tonal expectations of the common-practice idiom after which it is modelled, a fact that should already be obvious to anyone with enough background in music theory to ‘Schenkerize’ it. By contrast, reading the King Kaliente hits through a more flexible reductive instrument can certainly amplify and enhance our understanding of their specific idiomatic construction.
Methodology 3: Transformational Analysis
Current trends in transformational music theories began with the publication of David Lewin’s Generalized Musical Intervals and Transformations (GMIT), and although Lewin’s adaptation of mathematical group theory is designed to be applicable to any kind of musical structure, its most common current application is known as neo-Riemannian theory, which explores relationships between major and minor triads not from the standpoint of function (as did Hugo Riemann, the fin-de-siècle music theorist for whom it is named), but rather from the standpoint of voice-leading. As a theory that does not require that the tonal organizations it analyses orient chords with respect to a central tonic, neo-Riemannian theory is well equipped to handle triadic music of the late Romantic period and neo-Romantic music, where the latter enjoys a particular prominence in film scores.Footnote 28
A central technique of neo-Riemannian analysis – as early as its inception in GMIT – is the creation of visual networks that describe transformational relationships amongst chords. Figure 12.8 provides a sample neo-Riemannian network for a hypothetical musical passage with the chords A major, A minor and F♯ minor.
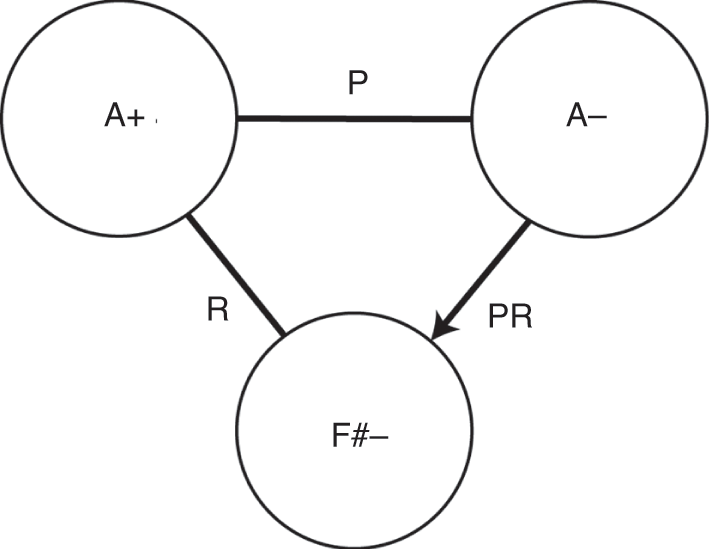
Figure 12.8 A neo-Riemannian network
The diagram indicates that the closest relationship between A major and A minor is a P (Parallel) transformation, which holds the perfect fifth of a triad fixed and moves the remaining note by a half step. It also indicates that the closest relationship between A major and F♯ minor is an R (Relative) transformation, which holds the major third of a triad fixed and moves the remaining note by whole step. Finally, it indicates that the closest relationship between A minor and F♯ minor is a composite move where P is followed by R. The arrow between these latter two nodes indicates that the composite transformation PR will only transform A minor to F♯ minor; reversing the move requires reversing the transformations, so getting from F♯ minor to A minor requires the composite transformation RP.
There are three atomic transformations in neo-Riemannian theory: in addition to P and R, there is an L (Leading-tone exchange) transformation, which holds the minor third of a triad fixed and moves the remaining note by a half step. Any triad may be transformed into any other triad using some combination of these three basic moves. These basic transformations can be combined to form compound transformations, where, for example, S (Slide) = LPR or RPL, H (Hexatonic pole) = PLP or LPL, and N (Neighbour) = PLR or RLP. Some accounts of neo-Riemannian theory treat these compound transformations as unary in their own right.Footnote 29 For the purposes of this chapter, I will be counting individual P, L and R moves when considering tonal distance, so that the compound transformations will be treated as three individual moves.
By itself, Figure 12.8 is of limited usefulness: ideally, networks will be deployed in the interest of a larger analytical point; say, drawing a hermeneutic meaning from its arrangement, like Frank Lehman’s discussion of the Argonath sequence in The Fellowship of the Ring (Peter Jackson, 2001),Footnote 30 or showing that two disparate passages operate under the same transformational logic, such as David Lewin’s comparison of the Tarnhelm and Valhalla motives in Das Rheingold.Footnote 31 Often such networks are treated according to the presumptions of mathematical graph theory – in such cases, all that matters is the specific relationship amongst the network’s nodes and edges (here, chords and transformations) and its actual geometrical arrangement on the page is ancillary. Other times, theorists use a graph’s visual appearance to suggest a specific analytical interpretation – for example, as is often the case in Lewin’s diagrams, there could be a presumed temporal dimension that reads from left to right;Footnote 32 in Figure 12.8, perhaps the triads are heard in the order A major, F♯ minor, A minor.
In addition to analytic networks, another common way of visualizing harmonic motion is through a Tonnetz (see Figure 12.9). In such diagrams, pitch-classes are arranged along three axes – the horizontals represent perfect fifths; the ascending diagonals major thirds; and the descending diagonals minor thirds. Triads are then represented by the triangles established by the axes: upward-pointing triangles represent major triads while downward-pointing triangles represent minor triads. Neo-Riemannian thinking presumes enharmonic equivalence; so, resembling the logic of Pac-Man (Namco, 1980), the diagram wraps around itself, establishing the doughnut-shaped geometric figure called a torus. To clarify: continuing along the lower horizontal past G leads to the D on the middle left; continuing down along the descending diagonal past the G leads to the B♭ on the lower left; and continuing down along the ascending diagonal from the G leads to the D♯ in the upper right, which is enharmonically equivalent to E♭. The Tonnetz makes visually clear how combinations of the atomic transformations create greater tonal distances – how, for example, the PR transformation is more tonally remote than any of the atomic transformations alone.Footnote 33
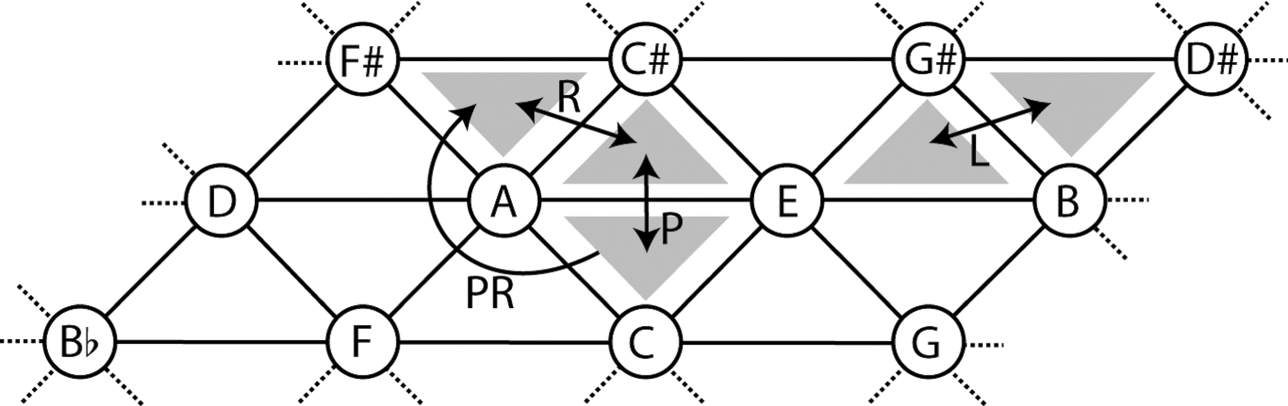
Figure 12.9 Tonnetz representation of the network in Figure 12.8 (left), and of the third atomic transformation, L (right)
A potentially puzzling aspect of neo-Riemannian networks is that we often understand music to be a linear art form, by which I mean that its events are usually performed and experienced through time in one specific order, and yet its diagrams present music on a plane, suggesting that its nodes can be explored in any number of ways. According to this logic, the chords in Figures 12.8 and 12.9 could appear in any order, with any number of internal repetitions. How can we reconcile the planar, non-linear aspect of neo-Riemannian theory’s geometric representations with the conventionally temporal, linear manner in which music is experienced?
The problem is compounded when we consider that Lewin would prefer not to understand analytical networks from a bird’s-eye perspective (what he calls the ‘Cartesian view’), but rather wants to imagine a listener inhabiting the networks, experiencing them from a first-person perspective, which he calls the ‘transformational attitude’: ‘“If I am at [a point] s and wish to get to [a point] t”’, Lewin asks, ‘“what characteristic gesture … should I perform in order to arrive there?” … This attitude’, he continues, ‘is by and large the attitude of someone inside the music, as idealized dancer and/or singer. No external observer (analyst, listener) is needed’.Footnote 34 Considering again Figure 12.8, if we imagine ourselves inside the network, hearing these three chords from a first-person perspective, then what exactly would it mean for our musical experience to move ‘clockwise’ or ‘counterclockwise’? And is there a conceptual difference between these two experiences that should dictate the placement of the network’s nodes?
In contrast to instrumental music, and even music that accompanies opera, film, musical theatre or television – perhaps game music’s closest relatives – video games are inherently spatial: when we play, we are very frequently tasked with directing a character – our in-game avatar – through a digital world.Footnote 35 Given that distinction, it is comparatively quite easy to imagine moving through a musical space, if that musical space is somehow co-ordinated with the virtual space the player moves through.
In Super Mario Galaxy, the principle way that the game space is organized is that the Comet Observatory serves as a central hub for a handful of domes; in each dome is a portal to a galaxy cluster, allowing Mario to select a specific galaxy to travel to. Some of these galaxies feature boss battles or other one-off tasks, and in such cases, the musical material is usually borrowed from similar levels elsewhere in the game. Table 12.2, then, lists each primary galaxy for each dome and the key centre for its principle musical accompaniment; I here define ‘primary’ galaxy to be one for which the game offers more than one mission. Observing that the Engine Room and Garden employ a lot of reused music (and one atonal tune without a clear key centre), the following discussion restricts its purview to the first four domes, which also happen to be the four domes that are accessible from the first floor of the Observatory.
Table 12.2 Primary galaxies with their key centres in Super Mario Galaxy
| Dome | Galaxy | Key Centre | Notes |
|---|---|---|---|
| Terrace | Good Egg | C major | |
| Honeyhive | C major | ||
| Fountain | Space Junk | A♭ major | |
| Battlerock | E major | ||
| Kitchen | Beach Bowl | A major | |
| Ghostly | D minor | ||
| Bedroom | Gusty Garden | D♭ major | |
| Freezeflame | D minor | ||
| Dusty Dune | E major | ||
| Engine Room | Gold Leaf | C major | Reuses ‘Honeyhive’ music |
| Sea Slide | A major | Reuses ‘Beach Bowl’ music | |
| Toy Time | C major | Uses theme from very first Super Mario Bros. game (Nintendo, 1985) | |
| Garden | Deep Dark | N/A | Atonal – no clear key centre |
| Dreadnought | E major | Reuses ‘Battlerock’ music | |
| Melty Molten | D minor |
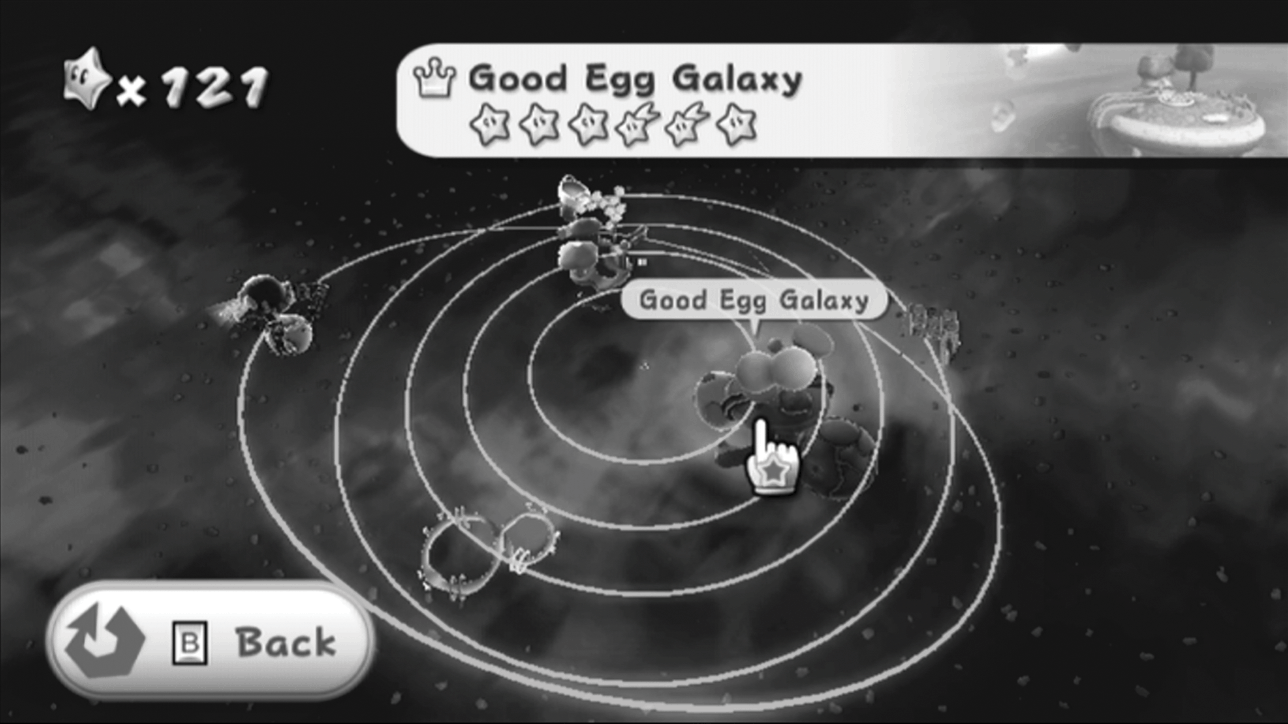
Figure 12.10 reimagines the first four domes, along with the Comet Observatory as a central hub, as part of a transformational network. In so doing, it extends the logic of the neo-Riemannian transformations beyond labelling voice-leadings between adjacent chords in a local progression to encompass modulations between key areas, and describes them by the transformations that would be required to move from one tonic triad to the next.Footnote 36 The diagram analyses the transformations needed to get from the key centre of the Observatory to any of the included galaxies, and also analyses transformations amongst galaxies that appear in a single dome. The length of each segment in the diagram is relative to the number of transformational moves it takes to get from key to key. Consider first the transformational connections within each dome: for domes 1, 2 and 3, there are only two primary galaxies, and therefore there is only one transformation: in the first dome, the Identity transformation maps C major onto C major; in the second dome, a composite PL transforms A♭ major into E major, for a total of two moves; and in the third dome, a composite transformation N, which requires three moves as shown in the figure, turns A major to D minor. The growth in transformational complexity is indicated by the relative lengths of the edges between the nodes, and as a result, the space of the tonal galaxy clusters gets progressively larger. The largest tonal galaxy cluster of the four, of course, is the Bedroom, owing to the multiplicity of transformational edges required to connect all of the nodes. Significantly, the player’s access to each dome is unlocked in precisely the order from smallest to largest: Terrace, Fountain, Kitchen and Bedroom. Thus, progress through the available galaxy clusters is correlated with their internal tonal complexity.
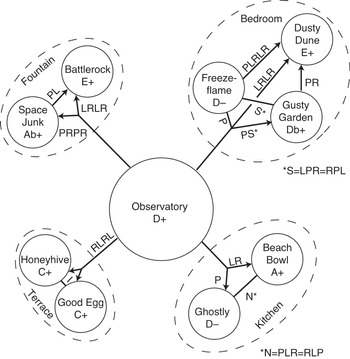
Figure 12.10 Transformational analysis of the first four domes of Super Mario Galaxy
Note too, that in almost every case, the tonal distance between galaxies within a dome is smaller than the tonal distance between the Observatory and the galaxy cluster, where this distance is measured as the combined number of transformational moves to get from the Observatory to the galaxies in one cluster. Thus, it takes a total of four transformations to get from the Observatory to the galaxies in the Terrace, eight to get to the Fountain, three to the Kitchen and nine to the Bedroom. These distances nicely capture the implied vast astronomical space between the Observatory and each cluster, relative to the smaller astronomical distance between galaxies in any one cluster. Moreover, ordering the domes about the hub from shortest distance to longest replicates the order of the physical locations of each dome around the central hub of the Observatory. This implies a ready metaphor between the locations of each dome on the tonal map and their physical locations in the gameworld.
Whereas the planar logic of transformational networks often chafes against a typically linear listening experience, in the case of Figure 12.10, the spatial, exploratory nature of Super Mario Galaxy’s design readily lends itself to thinking about its musical score in a similarly spatial way. It is not difficult to imagine ourselves as listeners moving through Figure 12.10 in a first-person perspective, going from key area to key area in a manner isomorphic to the way that Mario travels between the Observatory and the various galaxies, because there is a ready metaphor that connects tonal distances with segment length and another that correlates size with tonal complexity; these metaphors are at the heart of a powerful interpretative resonance between the geography of the game and the geometry of the diagram. The composite tonal distances between the Observatory waltz and the galaxies of each cluster are correlated with the physical layout of the Comet Observatory. Tonal complexity within a cluster is correlated with the order in which Mario gains access to these four domes, which further suggests a reading that tonal complexity is also correlated with the game’s power stars. This means that greater power to the Comet Observatory implies a capacity for listener-Mario to negotiate greater tonal complexity, just as character-Mario is being asked to negotiate more and more difficult platforming tasks. When transformational moves are correlated with astronomical distance, the organization of Figure 12.10 can imply how remote each cluster is from the Comet Observatory relative to how close they are to each other. And finally, there is a happy coincidence that Figure 12.10 itself resembles the star maps in the various domes that Mario uses to travel to the game’s galaxies (see Figure 12.11). In these ways, Figure 12.10 presents a particularly apt representation of the musical – but also physical – adventures of Mario.
Conclusions
I began my research for this chapter by taking seriously two existential problems with modern music theory: first, the notion that a musical work can exist as a singular entity frozen in time through musical notation treats the act of musical performance as a supplement to the ‘real’ musical work that takes place between composer and listener. The second is that the techniques and methodologies that underpin modern music theory are well suited to music frozen in time, but strain when asked to account for music that cannot be fixed in such a way. As a result, modern music theory is incentivized to privilege notated music and to downplay non-notated and improvised musics, even if these are vastly more characteristic of the grand scope of human music-making than the former.
As a practising music theorist, though, my experience has been that most analysts are sensitive musicians in their own right, who use theoretical tools to advance deeply musical insights that can inform performance. At the same time, it is certainly true that most analytical methodologies rely on treating some kind of fixed musical notation as an input and begin to break down when such notation can be neither acquired nor self-produced through transcription. But since there continues to exist vast amounts of music that can be fixed into notation, there has not generally been felt a widespread, urgent need to rework or revise existing methodologies to accommodate those that cannot. This has been true despite the experiments in the 1960s with chance-based, or aleatoric, music; or the rise of the cultural importance of jazz, rock, jam-band or dee-jayed electronic music, genres that may all rely on moment-by-moment indeterminacy. Furthermore, this is true despite the historical reality that the vast majority of human music-making has been improvised and non-notated: as Philip V. Bohlman has observed, ‘The fundamentally oral nature of music notwithstanding, musicology’s canons arise from the field’s penchant for working with texts.’Footnote 37 In the end, the problem is a specific case of a general one, identified by literary theorists, that overlooks the reality that a present-day conception of artworks as unified, static entities is both recent and anomalous, stemming from a nineteenth-century European shift in patterns of cultural consumption.Footnote 38
Each of the three methodologies in this chapter was intentionally selected to apply an analytical technique in current practice in the field – and, equivalently, a technique designed with fixed, notated music in mind – to a genre of music that is often dynamic and indeterminate. What excites me as a music theorist is that the theories did not break, but were instead refracted by the logic of the game’s design. To adopt a video-gaming metaphor, the theories ‘levelled-up’: more than just proven in battle, they are enhanced and ready to take on new, challenging analytical encounters.
But of even greater significance than our ability to apply music-theoretical approaches to a new, underrepresented musical medium, is the realization that the indeterminate nature of video game play perhaps aligns the medium more closely with other improvised artistic practices than do its more static relatives in film, television or opera. Video game musical analysis requires that music theories grapple with uncertainty, and the toolsets used to analyse video game music can be adapted to shed light on other kinds of improvised musics. We can and should invert the obvious question – ‘what can music theory tell us about game audio?’ – and instead ask how video game music can transform music theory, and in so doing, create for it opportunities to study musics that at first glance seem wholly unrelated to those that accompany Mario’s journeys through the universe.