Hostname: page-component-6dbcb7884d-4vmf6 Total loading time: 0 Render date: 2025-02-14T08:16:29.086Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON SUBNORMAL SUBGROUPS IN DIVISION RINGS CONTAINING SOLVABLE SUBGROUPS

Part of: Division rings and semisimple Artin rings Rings and algebras arising under various constructions Structure and classification of infinite or finite groups

Published online by Cambridge University Press:  11 January 2023

LE QUI DANH Open the ORCID record for LE QUI DANH [Opens in a new window]  and
TRINH THANH DEO Open the ORCID record for TRINH THANH DEO [Opens in a new window]
LE QUI DANH*
Affiliation:
Faculty of Mathematics and Computer Science, University of Science, Ho Chi Minh City, Vietnam; Vietnam National University, Ho Chi Minh City, Vietnam and University of Architecture Ho Chi Minh City, 196 Pasteur Street, District 3, Ho Chi Minh City, Vietnam
TRINH THANH DEO
Affiliation:
Faculty of Mathematics and Computer Science, University of Science, Ho Chi Minh City, Vietnam and Vietnam National University, Ho Chi Minh City, Vietnam e-mail: ttdeo@hcmus.edu.vn
*
e-mail: danh.lequi@uah.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let D be a division ring and N be a subnormal subgroup of the multiplicative group 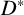$D^*$. We show that if N contains a nonabelian solvable subgroup, then N contains a nonabelian free subgroup.

Keywords

division ringfree subgroupsolvable subgroupsubnormal subgroup

MSC classification

Primary: 16K20: Finite-dimensional
Secondary: 16S85: Rings of fractions and localizations 16S36: Ordinary and skew polynomial rings and semigroup rings 20E05: Free nonabelian groups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 3 , December 2023 , pp. 422 - 427
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first author is funded by Vietnam National University Ho Chi Minh City (VNUHCM) under grant number T2022-18-03.

References

Bell, J. P. and Gonçalves, J., ‘On free subgroups in division rings’, Proc. Amer. Math. Soc. 148 (2020), 1953–1962.10.1090/proc/14888CrossRefGoogle Scholar
Bien, M. H. and Hai, B. X., ‘On subnormal subgroups in division rings containing a non-abelian solvable subgroup’, Bull. Math. Soc. Sci. Math. Roumanie (N.S.) 63(111)(2) (2020), 151–162.Google Scholar
Danh, L. Q. and Khanh, H. V., ‘Locally solvable subnormal and quasinormal subgroups in division rings’, Hiroshima Math. J. 51 (2021), 267–274.Google Scholar
Gonçalves, J. Z., ‘Free groups in subnormal subgroups and the residual nilpotence of the group of units of group rings’, Canad. Math. Bull. 27 (1984), 365–370.10.4153/CMB-1984-055-6CrossRefGoogle Scholar
Gonçalves, J. Z. and Mandel, A., ‘Are there free groups in division rings?’, Israel J. Math. 53 (1986), 69–80.10.1007/BF02772670CrossRefGoogle Scholar
Goodearl, K. R. and Warfield, R. B. Jr, An Introduction to Noncommutative Noetherian Rings, London Mathematical Society Student Texts, 61 (Cambridge University Press, Cambridge, 2004).10.1017/CBO9780511841699CrossRefGoogle Scholar
Hai, B. X. and Thin, N. V., ‘On locally nilpotent subgroups of ${\mathrm{GL}}_1(D)$ ’, Comm. Algebra 37(2) (2009), 712–718.10.1080/00927870802255287CrossRefGoogle Scholar
Hai, B. X. and Thin, N. V., ‘On subnormal subgroups in general skew linear groups’, Vestnik St. Petersburg Univ. Math. 46 (2013), 43–48.10.3103/S1063454113010020CrossRefGoogle Scholar
Lam, T. Y., A First Course in Noncommutative Rings, Graduate Texts in Mathematics, 131 (Springer, Berlin, 2001).10.1007/978-1-4419-8616-0CrossRefGoogle Scholar
Lichtman, A. I., ‘On subgroups of the multiplicative group of skew fields’, Proc. Amer. Math. Soc. 63(1) (1977), 15–16.10.1090/S0002-9939-1977-0447432-0CrossRefGoogle Scholar
Lichtman, A. I., ‘Free subgroups of normal subgroups of the multiplicative group of skew fields’, Proc. Amer. Math. Soc. 7 (1978), 174–178.10.1090/S0002-9939-1978-0480623-2CrossRefGoogle Scholar
Ore, O., ‘Theory of non-commutative polynomials’, Ann. of Math. (2) 34(3) (1933), 480–508.10.2307/1968173CrossRefGoogle Scholar
Tits, J., ‘Free subgroups in linear groups’, J. Algebra 20 (1972), 250–270.10.1016/0021-8693(72)90058-0CrossRefGoogle Scholar