No CrossRef data available.
Article contents
Multi-linear forms, graphs, and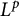 
$L^p$-improving measures in 
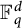${\Bbb F}_q^d$
Published online by Cambridge University Press: 27 December 2023
Abstract
The purpose of this paper is to introduce and study the following graph-theoretic paradigm. Let 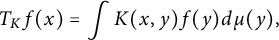where 
$$ \begin{align*}T_Kf(x)=\int K(x,y) f(y) d\mu(y),\end{align*} $$
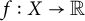$f: X \to {\Bbb R}$, X a set, finite or infinite, and K and 
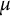$\mu $ denote a suitable kernel and a measure, respectively. Given a connected ordered graph G on n vertices, consider the multi-linear form where 
$$ \begin{align*}\Lambda_G(f_1,f_2, \dots, f_n)=\int_{x^1, \dots, x^n \in X} \ \prod_{(i,j) \in {\mathcal E}(G)} K(x^i,x^j) \prod_{l=1}^n f_l(x^l) d\mu(x^l),\end{align*} $$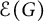
${\mathcal E}(G)$ is the edge set of G. Define 
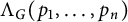$\Lambda _G(p_1, \ldots , p_n)$ as the smallest constant 
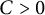$C>0$ such that the inequality (0.1)holds for all nonnegative real-valued functions 
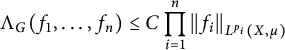$$ \begin{align} \Lambda_G(f_1, \dots, f_n) \leq C \prod_{i=1}^n {||f_i||}_{L^{p_i}(X, \mu)} \end{align} $$
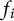$f_i$, 
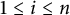$1\le i\le n$, on X. The basic question is, how does the structure of G and the mapping properties of the operator 
$T_K$ influence the sharp exponents in (0.1). In this paper, this question is investigated mainly in the case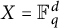 
$X={\Bbb F}_q^d$, the d-dimensional vector space over the field with q elements, 
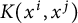$K(x^i,x^j)$ is the indicator function of the sphere evaluated at 
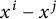$x^i-x^j$, and connected graphs G with at most four vertices.
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
A. Iosevich and P. Bhowmik were supported in part by the National Science Foundation (Grant No. HDR TRIPODS-1934962) and the National Science Foundation (Grant No. DMS-2154232). D. Koh was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (Grant No. RS-2023-00249597). T. Pham was supported by the research project QG.23.03 of Vietnam National University, Hanoi.
References
Assarf, B., Gawrilow, E., Herr, K., Joswig, M., Lorenz, B., Paffenholz, A., and Rehn, T.,
Computing convex hulls and counting integer points with polymake
. Math. Program. Comput. 9(2017), no. 1, 1–38.CrossRefGoogle Scholar
Bennett, M., Chapman, J., Covert, D., Hart, D., Iosevich, A., and Pakianathan, J.,
Long paths in the distance graph over large subsets of vector spaces over finite fields
. J. Korean Math. 53(2016), 115–126.CrossRefGoogle Scholar
Bennett, M., Hart, D., Iosevich, A., Pakianathan, J., and Rudnev, M.,
Group actions and geometric combinatorics in
${F}_q^d$
. Forum Math. 29(2017), no. 1, 91–110.CrossRefGoogle Scholar
${F}_q^d$
. Forum Math. 29(2017), no. 1, 91–110.CrossRefGoogle ScholarCarbery, A., Stones, B., and Wright, J.,
Averages in vector spaces over finite fields
. Math. Proc. Camb. Philos. Soc. 144(2008), no. 1, 13–27.CrossRefGoogle Scholar
Chapman, J., Erdog̃an, M., Hart, D., Iosevich, A., and Koh, D.,
Pinned distance sets, Wolff’s exponent in finite fields and sum-product estimates
, Math. Z. 271(2012), no. 1–2, 63–93.CrossRefGoogle Scholar
Gawrilow, E. and Joswig, M.,
Polymake: a framework for analyzing convex polytopes
. In: Polytopes – combinatorics and computation (Oberwolfach, 1997), Birkhäuser, Basel, pp. 43–73.Google Scholar
Greenleaf, A., Iosevich, A., Krause, B., and Liu, A.,
Lp estimates for bilinear generalized radon transforms in the plane
. In: Combinatorial and additive number theory, Springer, Cham, 2022, pp. 179–198.CrossRefGoogle Scholar
Hanson, B., Lund, B., and Roche-Newton, O.,
On distinct perpendicular bisectors and pinned distances in finite fields
. Finite Fields Appl. 37(2016), 240–264.CrossRefGoogle Scholar
Iosevich, A., Jardine, G., and McDonald, B.,
Cycles of arbitrary length in distance graphs on
${F}_q^d$
. Proc. Steklov Inst. Math. 314(2021), no. 1, 27–43.CrossRefGoogle Scholar
${F}_q^d$
. Proc. Steklov Inst. Math. 314(2021), no. 1, 27–43.CrossRefGoogle ScholarIosevich, A. and Rudnev, M.,
Erdős distance problem in vector spaces over finite fields
. Trans. Amer. Math. Soc. 359(2007), no. 12, 6127–6142.CrossRefGoogle Scholar
Koh, D. and Lee, S.,
Averages and maximal averages over product
$j$
-varieties in finite fields
. Finite Fields Appl. 79(2022), 101984.CrossRefGoogle Scholar
$j$
-varieties in finite fields
. Finite Fields Appl. 79(2022), 101984.CrossRefGoogle ScholarKoh, D. and Shen, C. Y.,
Extension and averaging operators for finite fields
. Proc. Edinb. Math. Soc. 56(2013), no. 2, 599–614.CrossRefGoogle Scholar
Koh, D., Shen, C. Y., and Shparlinski, I.,
Averaging operators over homogeneous varieties over finite fields
. J. Geom. Anal. 26(2016), no. 2, 1415–1441.CrossRefGoogle Scholar
Lidl, R. and Niederreiter, H., Finite fields, Cambridge University Press, Cambridge, 1997.Google Scholar
Murphy, B., Petridis, G., Pham, T., Rudnev, M., and Stevenson, S.,
On the pinned distances problem in positive characteristic
. J. Lond. Math. Soc. 105(2022), no. 1, 469–499.CrossRefGoogle Scholar
Stein, E. M.,
Harmonic analysis: real-variable methods, orthogonality, and oscillatory integrals
. In: With the assistance of Timothy S. Murphy, Princeton Mathematical Series, 43, Monographs in Harmonic Analysis, III, Princeton University Press, Princeton, NJ, 1993, xiv + 695 pp.Google Scholar