Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-14T10:59:46.553Z Has data issue: false hasContentIssue false
  • English
  • Français

A partial converse to the Andreotti–Grauert theorem

Part of: Holomorphic fiber spaces Global differential geometry (Co)homology theory

Published online by Cambridge University Press:  19 November 2018

Xiaokui Yang
Xiaokui Yang*
Affiliation:
Morningside Center of Mathematics, HCMS, CEMS, NCNIS, HLM, UCAS, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing, 100190, China email xkyang@amss.ac.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 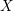$X$ be a smooth projective manifold with 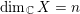$\dim _{\mathbb{C}}X=n$. We show that if a line bundle 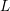$L$ is 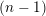$(n-1)$-ample, then it is 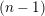$(n-1)$-positive. This is a partial converse to the Andreotti–Grauert theorem. As an application, we show that a projective manifold 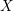$X$ is uniruled if and only if there exists a Hermitian metric 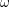$\unicode[STIX]{x1D714}$ on 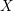$X$ such that its Ricci curvature 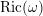$\text{Ric}(\unicode[STIX]{x1D714})$ has at least one positive eigenvalue everywhere.

Keywords

vanishing theorem(n - 1)-ample(n - 1)-positivepseudoeffectiveuniruled manifolds

MSC classification

Primary: 14F17: Vanishing theorems 32L20: Vanishing theorems 53C55: Hermitian and Kählerian manifolds
Type
Research Article
Information
Compositio Mathematica , Volume 155 , Issue 1 , January 2019 , pp. 89 - 99
Copyright
© The Author 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andreotti, A. and Grauert, H., Théorème de finitude pour la cohomologie des espaces complexes , Bull. Soc. Math. France 90 (1962), 193–259.Google Scholar
Andreotti, A. and Vesentini, E., Carleman estimates for the Laplace–Beltrami equation on complex manifolds , Publ. Math. Inst. Hautes Études Sci. 25 (1965), 81–130.Google Scholar
Boucksom, S., Demailly, J.-P., Paun, M. and Peternell, P., The pseudoeffective cone of a compact Kähler manifold and varieties of negative Kodaira dimension , J. Algebraic Geom. 22 (2013), 201–248.Google Scholar
Brown, M.-V., Big q-ample line bundles , Compos. Math. 148 (2012), 790–798.Google Scholar
Chu, J.-C., Tosatti, V. and Weinkove, B., The Monge-Ampère equation for non-integrable almost complex structures, J. Eur. Math. Soc. (JEMS), to appear. Preprint (2016), arXiv:1603.00706.Google Scholar
Demailly, J.-P., Singular Hermitian metrics on positive line bundles , in Complex algebraic varieties, Lecture Notes in Mathematics, vol. 1507, eds Hulek, K., Peternell, T., Schneider, M. and Schreyer, F. (Springer, Berlin, 1992), 87–104.Google Scholar
Demailly, J.-P., A converse to the Andreotti–Grauert theorem , Ann. Fac. Sci. Toulouse Math. (6) 20 (2011), 123–135; Fascicule Special.Google Scholar
Demailly, J.-P., Peternell, T. and Schneider, M., Holomorphic line bundles with partially vanishing cohomology , in Proceedings of the Hirzebruch 65 conference on algebraic geometry, Israel Mathematical Conference Proceedings, vol. 9 (Bar-Ilan University, Ramat Gan, 1996), 165–198.Google Scholar
Gauduchon, P., Le théorème de l’excentricitè nulle , C. R. Acad. Sci. Paris Sér. A-B 285 (1977), A387–A390.Google Scholar
Gauduchon, P., Fibrés hermitiens à endomorphisme de Ricci non-négatif , Bull. Soc. Math. France 105 (1977), 113–140.Google Scholar
Gauduchon, P., La 1-forme de torsion d’une varietè ehermitienne compacte , Math. Ann. 267 (1984), 495–518.Google Scholar
Greb, D. and Küronya, A., Partial positivity: geometry and cohomology of q-ample line bundles , in Recent advances in algebraic geometry, London Mathematical Society of Lecture Note Series, vol. 417 (Cambridge University Press, Cambridge, 2015), 207–239.Google Scholar
Küronya, A., Positivity on subvarieties and vanishing of higher cohomology , Ann. Inst. Fourier (Grenoble) 63 (2013), 1717–1737.Google Scholar
Lamari, A., Courants kähleriens et surfaces compactes , Ann. Inst. Fourier (Grenoble) 49 (1999), 263–285.Google Scholar
Matsumura, S., Asymptotic cohomology vanishing and a converse to the Andreotti–Grauert theorem on surfaces , Ann. Inst. Fourier (Grenoble) 63 (2013), 2199–2221.Google Scholar
Michelsohn, M. L., On the existence of special metrics in complex geometry , Acta Math. 149 (1982), 261–295.Google Scholar
Ottem, J.-C., Ample subvarieties and q-ample divisors , Adv. Math. 229 (2012), 2868–2887.Google Scholar
Totaro, B., Line bundles with partially vanishing cohomology , J. Eur. Math. Soc. (JEMS) 15 (2013), 731–754.Google Scholar
Yang, X.-K., Hermitian manifolds with semi-positive holomorphic sectional curvature , Math. Res. Lett. 23 (2016), 939–952.Google Scholar
Yang, X.-K., Scalar curvature on compact complex manifolds. Trans. Amer. Math. Soc., to appear. Preprint (2017), arXiv:1705.02672.Google Scholar
Yang, X.-K., RC-positivity, rational connectedness and Yau’s conjecture , Cam. J. Math. 6 (2018), 183–212.Google Scholar