Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-14T10:02:15.461Z Has data issue: false hasContentIssue false
  • English
  • Français

ON ${\omega _1}$-STRONGLY COMPACT CARDINALS

Published online by Cambridge University Press:  17 April 2014

JOAN BAGARIA  and
MENACHEM MAGIDOR
JOAN BAGARIA
Affiliation:
ICREA (INSTITUCIÓ CATALANA DE RECERCA I ESTUDIS AVANÇATS) AND DEPARTAMENT DE LÒGICA, HISTÒRIA I FILOSOFIA DE LA CIÈNCIA UNIVERSITAT DE BARCELONA, MONTALEGRE 6 8001 BARCELONA, CATALONIA, SPAIN E-mail: joan.bagaria@icrea.cat
MENACHEM MAGIDOR
Affiliation:
EINSTEIN INSTITUTE OF MATHEMATICS, THE HEBREW UNIVERSITY OF JERUSALEM EDMOND J. SAFRA CAMPUS, GIVAT RAM JERUSALEM 91904, ISRAEL E-mail: menachem.magidor@huji.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

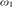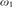An uncountable cardinal κ is called ${\omega _1}$-strongly compact if every κ-complete ultrafilter on any set I can be extended to an ${\omega _1}$-complete ultrafilter on I. We show that the first ${\omega _1}$-strongly compact cardinal, 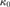${\kappa _0}$, cannot be a successor cardinal, and that its cofinality is at least the first measurable cardinal. We prove that the Singular Cardinal Hypothesis holds above 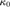${\kappa _0}$. We show that the product of Lindelöf spaces is κ-Lindelöf if and only if 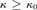$\kappa \ge {\kappa _0}$. Finally, we characterize 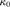${\kappa _0}$ in terms of second order reflection for relational structures and we give some applications. For instance, we show that every first-countable nonmetrizable space has a nonmetrizable subspace of size less than ${\kappa _0}$.

Keywords

Primary: 03E5503E75. Secondary: 54D1554D2054E35ω1-strongly compact cardinalSingular Cardinal HypothesisLindelöf spacesecond-order reflectioncountably chromatic graphmetrizable spacecompletely regular space
Type
Articles
Information
The Journal of Symbolic Logic , Volume 79 , Issue 1 , March 2014 , pp. 266 - 278
Copyright
Copyright © Association for Symbolic Logic 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bagaria, J. and Magidor, M., Group radicals and strongly compact cardinals. Transactions of the American Mathematical Society, vol. 366 (2014), pp. 1857–1877.Google Scholar
Dugas, M. and Göbel, R., On radicals and products. Pacific Journal of Mathematics, vol. 118 (1985), pp. 79–104.Google Scholar
Eda, K. and Abe, Y., Compact cardinals and abelian groups. Tsukuba Journal of Mathematics, vol. 11 (1987), no. 2, pp. 353–360.Google Scholar
Eisworth, T., Successors of singular cardinals, Handbook of set theory (Foreman, M. and Kanamori, A., editors), vol. 2, Springer, Dordrecht, 2010.Google Scholar
Eklof, P. C. and Mekler, A., Almost free modules: Set-theoretic methods. Revised Edition, vol. 65, North-Holland Mathematical Library, North-Holland, Amsterdam, 2002.Google Scholar
Jech, T., Set theory. The third millenium edition, Revised and Expanded. Springer Monographs in Mathematics. Springer-Verlag, Berlin, Heidelberg, 2003.Google Scholar
Kanamori, A., The higher infinite: Large cardinals in set theory from their beginnings. Perspectives in Mathematical Logic. Springer-Verlag, Berlin, Heidelberg, 1994.Google Scholar
Magidor, M., How large is the first strongly compact cardinal? or: A study on identity crises. Annals of Mathematical Logic, vol. 10 (1976), pp. 33–57.Google Scholar
Magidor, M., On the role of supercompact and extendible cardinals in logic. Israel Journal of Mathematics, vol. 10 (1971), pp. 147–157.Google Scholar
Shelah, S., Cardinal arithmetic. Oxford Logic Guides 29, The Clarendon Press, Oxford University Press, New York, 1994.CrossRefGoogle Scholar
Solovay, R. M., Strongly compact cardinals and the GCH. Proceedings of the Tarski symposium (Leon Henkin, editor). Proceedings of Symposia in Pure Mathematics, vol. 25, American Mathematical Society, Providence, Rhode Island, pp. 365–372, 1974.CrossRefGoogle Scholar
Solovay, R. M., Reinhardt, W. N., and Kanamori, A., Strong axioms of infinity and elementary embeddings. Annals of Mathematical Logic, vol. 13 (1978), pp. 73–116.Google Scholar