Hostname: page-component-6bf8c574d5-26wn4 Total loading time: 0 Render date: 2025-02-14T10:57:44.972Z Has data issue: false hasContentIssue false
  • English
  • Français

Coniveau filtrations and Milnor operatio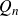n $Q_n$

Part of: Fiber spaces and bundles Cycles and subschemes Homology and homotopy of topological groups and related structures Linear algebraic groups and related topics

Published online by Cambridge University Press:  08 May 2023

NOBUAKI YAGITA
NOBUAKI YAGITA*
Affiliation:
Department of Mathematics, Faculty of Education, Ibaraki University, Zip 310-8512, Bunkyo 2-1-1, Mitoshi, Ibaraki, Japan. e-mail: nobuaki.yagita.math@vc.ibaraki.ac.jp
Get access Rights & Permissions [Opens in a new window]

Abstract

Let BG be the classifying space of an algebraic group G over the field 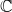${\mathbb C}$ of complex numbers. There are smooth projective approximations X of 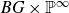$BG\times {\mathbb P}^{\infty}$, by Ekedahl. We compute a new stable birational invariant of X defined by the difference of two coniveau filtrations of X, by Benoist and Ottem. Hence we give many examples such that two coniveau filtrations are different.

MSC classification

Primary: 20G10: Cohomology theory 55R35: Classifying spaces of groups and $H$-spaces 14C15: (Equivariant) Chow groups and rings; motives
Secondary: 57T25: Homology and cohomology of $H$-spaces
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 175 , Issue 3 , November 2023 , pp. 521 - 538
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benoist, O. and Ottem, J.. Two coniveau filtrations. Duke Math J. 170 (2021), 2719–2753.CrossRefGoogle Scholar
Bloch, S. and Ogus, A.. Gersten’s conjecture and the homology of schemes. Ann. Sci. Ecole Norm. Sup. 7 (1974), 181–202.CrossRefGoogle Scholar
Colliot Thérène, J. L. and Voisin, C.. Cohomologie non ramifieet conjecture de Hodge entíere. Duke Math. J. 161 (2012), 735–801.Google Scholar
Ekedahl, T.. Approximating classifying spaces by smooth projective varieties. Preprint 44 (2009), arXiv:0905.1538.Google Scholar
Kameko, M. and Yagita, N.. The Brown–Peterson cohomology of the classifying cohomologies of projective unitary group PU(n) and exceptional Lie groups. Trans. Amer. Math. Soc. 360 (2008), 2265–2284.CrossRefGoogle Scholar
Kordonskii, E.. Stable rationality of the group $Spin_{10}$ . Russian Math. Soc. 360 (2000), 178–179.CrossRefGoogle Scholar
Merkurjev, A.. Rationality problem for classifying spaces of Spinor groups. Proc. Skeklov Inst. Math. 307 (2019), 115–124.Google Scholar
Milnor, J.. The Steenrod algebra and its dual. Ann. Math. 67 (1958), 150–171.CrossRefGoogle Scholar
Paranjape, K.. Some spectral sequences for filtered complexes and applications. J. Algebra 186 (1996), 793–806.CrossRefGoogle Scholar
Pirutka, A. and Yagita, N.. Note on the counterexamples for the integral Tate conjecture over finite fields. Doc. Math. (2015), 501–511. Extra vol. Alexander S. Merkurjev’s sixtieth birthday.CrossRefGoogle Scholar
Quillen, D.. Elementary proofs of some results of the cobordism theory using Steenrod operations. Adv. Math. 7 (1971), 29–56.CrossRefGoogle Scholar
Quillen, D.. The mod 2 cohomology rings of extra-special 2-groups and the spinor groups. Math. Ann. 194 (1971), 197–212.CrossRefGoogle Scholar
Ravenel, D., Wilson, S. and Yagita, N.. Brown–Peterson cohomology from Morava K-theory. K-theory. 15 (1998), 147–199.CrossRefGoogle Scholar
Reichstein, Z. and Scavia, F.. The Noether problem for spinor groups of small rank. J. Algebra 48 (2020), 134–152.CrossRefGoogle Scholar
Tamanoi, M.. The image of the BP-Thom map for Eilenberg–MacLane spaces. Trans. Amer. Math. Soc. 249 (1997), 1209–1237.CrossRefGoogle Scholar
Tezuka, M. and Yagita, N.. The image of the map from group cohomology to Galois cohomology. Trans. Amer. Math. Soc. 363 (2011), 4475–4503.CrossRefGoogle Scholar
Totaro, B.. The Chow ring of classifying spaces. Proc.of Symposia in Pure Math. “Algebraic K-theory” (University of Washington, Seattle, 1997) 67 (1999), 248-281.Google Scholar
Voevodsky, V.. The Milnor conjecture. www.math.uiuc.edu/K-theory/0170 (1996).Google Scholar
Voevodsky, V.. Reduced power operations in motivic cohomology. Publ. Math. Inst. Hautes Études Sci. 98 (2003), 1–57.CrossRefGoogle Scholar
Voevodsky, V.. Motivic cohomology with ${\mathbb Z}/2$ coefficient. Publ. Math. Inst. Hautes Études Sci. 98 (2003), 59–104.CrossRefGoogle Scholar
Voevodsky, V.. On motivic cohomology with ${\mathbb Z}/l$ -coefficients. Ann. Math. bf 174 (2011), 401–438.Google Scholar
Yagita, N.. Coniveau filtration of cohomology of groups. Proc. London Math. Soc. 101 (2010), 179–206.CrossRefGoogle Scholar
Yagita, N.. Algebraic BP-theory and norm varieties. Hokkaido Math. J. 41 (2012), 275–316.Google Scholar
Yagita, N.. Chow rings of nonabelian p-groups of order $p^3$ . J. Math. Soc. Japan 64 (2012), 507–531.CrossRefGoogle Scholar
Yagita, N.. Chern classes and the Rost cohomological invariant. Kodai Math. J. 36 (2013), 174–178.CrossRefGoogle Scholar