Hostname: page-component-6bf8c574d5-fppsw Total loading time: 0 Render date: 2025-02-14T09:55:19.751Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry and topology of the space of Kähler metrics on singular varieties

Part of: Global differential geometry Differential operators in several variables

Published online by Cambridge University Press:  19 July 2018

Eleonora Di Nezza  and
Vincent Guedj
Eleonora Di Nezza
Affiliation:
Department of Mathematics, Imperial College London, London SW7 2AZ, UK
Vincent Guedj
Affiliation:
Institut de Mathématiques de Toulouse, Université de Toulouse, CNRS UPS, F-31062 Toulouse Cedex 9, France email vincent.guedj@math.univ-toulouse.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 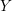$Y$ be a compact Kähler normal space and let 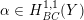$\unicode[STIX]{x1D6FC}\in H_{\mathit{BC}}^{1,1}(Y)$ be a Kähler class. We study metric properties of the space 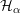${\mathcal{H}}_{\unicode[STIX]{x1D6FC}}$ of Kähler metrics in 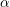$\unicode[STIX]{x1D6FC}$ using Mabuchi geodesics. We extend several results of Calabi, Chen, and Darvas, previously established when the underlying space is smooth. As an application, we analytically characterize the existence of Kähler–Einstein metrics on 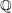$\mathbb{Q}$-Fano varieties, generalizing a result of Tian, and illustrate these concepts in the case of toric varieties.

Keywords

Kähler metricsMonge–Ampère equationMabuchi distance

MSC classification

Primary: 53C55: Hermitian and Kählerian manifolds
Secondary: 32W20: Complex Monge-Ampère operators 53C25: Special Riemannian manifolds (Einstein, Sasakian, etc.)
Type
Research Article
Information
Compositio Mathematica , Volume 154 , Issue 8 , August 2018 , pp. 1593 - 1632
Copyright
© The Authors 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

1

Current address: IHES, Université Paris Saclay, 91400 Bures sur Yvette, France email dinezza@ihes.fr

References

Arezzo, C. and Spotti, C., On cscK resolutions of conically singular cscK varieties , J. Funct. Anal. 271 (2016), 474–494.Google Scholar
Aubin, T., Equation de type Monge–Ampère sur les variétés kählériennes compactes , Bull. Sci. Math. 102 (1978), 63–95.Google Scholar
Bedford, E. and Taylor, B. A., A new capacity for plurisubharmonic functions , Acta Math. 149 (1982), 1–40.Google Scholar
Berman, R., From Monge–Ampère equations to envelopes and geodesic rays in the zero temperature limit, Preprint (2013), arXiv:1307.3008v3.Google Scholar
Berman, R., Boucksom, S., Eyssidieux, P., Guedj, V. and Zeriahi, A., Kähler–Ricci flow and Ricci iteration on log-Fano varieties, J. Reine Angew. Math., to appear.Google Scholar
Berman, R., Boucksom, S., Guedj, V. and Zeriahi, A., A variational approach to complex Monge–Ampère equations , Publ. Math. Inst. Hautes Études Sci. 117 (2013), 179–245.Google Scholar
Berman, R., Boucksom, S. and Jonsson, M., A variational approach to the Yau–Tian–Donaldson conjecture, Preprint (2015), arXiv:1509.04561.Google Scholar
Berman, R., Darvas, T. and Lu, H. C., Regularity of weak minimizers of the K-energy and applications to properness and K-stability, Preprint (2016), arXiv:1602.03114.Google Scholar
Berman, R. and Demailly, J.-P., Regularity of plurisubharmonic upper envelopes in big cohomology classes , in Perspectives in analysis, geometry, and topology, Progress in Mathematics, vol. 296 (Birkhäuser, Boston, MA, 2012), 39–66.Google Scholar
Berndtsson, B., Probability measures related to geodesics in the space of Kähler metrics, Preprint (2009), arXiv:0907.1806.Google Scholar
Berndtsson, B., A Brunn–Minkowski type inequality for Fano manifolds and some uniqueness theorems in Kähler geometry , Invent. Math. 200 (2015), 149–200.Google Scholar
Boucksom, S., Eyssidieux, P. and Guedj, V., An introduction to the Kähler–Ricci flow, Lecture Notes in Mathematics, vol. 2086 (Springer, Cham, 2013).Google Scholar
Boucksom, S., Eyssidieux, P., Guedj, V. and Zeriahi, A., Monge–Ampère equations in big cohomology classes , Acta Math. 205 (2010), 199–262.Google Scholar
Bourbaki, N., Eléments de mathématiques , in Topologie générale (Springer, Berlin, Heidelberg, 2007), Fsc VIII, livre III, Ch. 9; edition originale publiée par Herrman, Paris, 1974.Google Scholar
Bridson, M. and Haefliger, A., Metric spaces of non-positive curvature, Grundlehren der Mathematischen Wissenschaften, vol. 319 (Springer, Berlin, 1999).Google Scholar
Bruhat, F. and Tits, J., Groupes réductifs sur un corps local , Publ. Math. Inst. Hautes Études Sci. 41 (1972), 5–251.Google Scholar
Calabi, E. and Chen, X. X., The space of Kähler metrics. II , J. Differential Geom. 61 (2002), 173–193.Google Scholar
Chen, X. X., The space of Kähler metrics , J. Differential Geom. 56 (2000), 189–234.Google Scholar
Chen, X. X., Space of Kähler metrics III. On the lower bound of the Calabi energy and geodesic distance , Invent. Math. 175 (2009), 453–503.Google Scholar
Chen, X. X., Donaldson, S. and Sun, S., Kähler–Einstein metrics on Fano manifolds. III , J. Amer. Math. Soc. 28 (2015), 235–278.Google Scholar
Chen, X. X. and Sun, S., Space of Kähler metrics V. Kähler quantization , in Metric and differential geometry, Progress in Mathematics, vol. 297 (Birkhäuser, Basel, 2012), 19–41.Google Scholar
Chen, X. X. and Tian, G., Geometry of Kähler metrics and foliations by holomorphic discs , Publ. Math. Inst. Hautes Études Sci. 107 (2008), 1–107.Google Scholar
Chu, J., Tosatti, V. and Weinkove, B., C 1, 1 regularity of degenerate complex Monge–Ampère equations and geodesic rays , Comm. Partial Differential Equations 43 (2018), 292–312.Google Scholar
Coman, D., Guedj, V. and Zeriahi, A., Extension of plurisubharmonic functions with growth control , J. Reine Angew. Math. 676 (2013), 33–49.Google Scholar
Darvas, T., The Mabuchi geometry of finite energy classes , Adv. Math. 285 (2015), 182–219.Google Scholar
Darvas, T., Metric geometry of normal Kähler spaces, energy properness, and existence of canonical metrics , Int. Math. Res. Not. (IMRN) 2017 (2017), 6752–6777.Google Scholar
Darvas, T., Weak geodesic rays in the space of Kähler metrics and the class E(X, 𝜔) , J. Inst. Math. Jussieu 16 (2017), 837–858.Google Scholar
Darvas, T., The Mabuchi completion of the space of Kähler potentials , Amer. J. Math. 139 (2017), 1275–1313; arXiv:1401.7318.Google Scholar
Darvas, T., Di Nezza, E. and Lu, C., On the singularity type of full mass currents on big cohomology classes , Compositio Math. 154 (2018), 380–409.Google Scholar
Darvas, T. and Lempert, L., Weak geodesics in the space of Kähler metrics , Math. Res. Lett. 19 (2012), 1127–1135.Google Scholar
Darvas, T. and Rubinstein, Y., Kiselman’s principle, the Dirichlet problem for the Monge–Ampère equation, rooftop obstacle problems , J. Math. Soc. Japan 68 (2016), 773–796.Google Scholar
Darvas, T. and Rubinstein, Y., Tian’s properness conjectures and Finsler geometry of the space of Kahler metrics , J. Amer. Math. Soc. 30 (2017), 347–387.Google Scholar
Di Nezza, E., Stability of Monge–Ampère energy classes , J. Geom. Anal. 25 (2015), 2565–2589.Google Scholar
Donaldson, S. K., Symmetric spaces, Kähler geometry and Hamiltonian dynamics, American Mathematical Society Translations, Series 2, vol. 196 (American Mathematical Society, Providence, RI, 1999), 13–33.Google Scholar
Eyssidieux, P., Guedj, V. and Zeriahi, A., Singular Kähler–Einstein metrics , J. Amer. Math. Soc. 22 (2009), 607–639.Google Scholar
Eyssidieux, P., Guedj, V. and Zeriahi, A., Corrigendum: Viscosity solutions to complex Monge–Ampère equations , Comm. Pure Appl. Math. 70 (2017), 815–821.Google Scholar
Gilbarg, D. and Trudinger, N., Elliptic partial differential equations of second order, second edition (Springer, Berlin, 1983).Google Scholar
Guedj, V., The metric completion of the Riemannian space of Kähler metrics, Preprint (2014), arXiv:1401.7857.Google Scholar
Guedj, V. and Zeriahi, A., Intrinsic capacities on compact Kähler manifolds , J. Geom. Anal. 15 (2005), 607–639.Google Scholar
Guedj, V. and Zeriahi, A., The weighted Monge–Ampère energy of quasiplurisubharmonic functions , J. Funct. Anal. 250 (2007), 442–482.Google Scholar
Guedj, V. and Zeriahi, A., Degenerate complex Monge–Ampère equations, EMS Tracts in Mathematics, vol. 26 (European Mathematical Society, 2017).Google Scholar
Kiselman, C. O., Partial Legendre transformation for plurisubharmonic functions , Invent. Math. 49 (1978), 137–148.Google Scholar
Kolodziej, S., The complex Monge–Ampère equation and pluripotential theory, Memoirs of the American Mathematical Society, vol. 178 (American Mathematical Society, Providence, RI, 2005).Google Scholar
Lempert, L. and Vivas, L., Geodesics in the space of Kähler metrics , Duke Math. J. 162 (2013), 1369–1381.Google Scholar
Mabuchi, T., Some symplectic geometry on compact Kähler manifolds , Osaka J. Math. 24 (1987), 227–252.Google Scholar
Michor, P. W. and Mumford, D., Vanishing geodesic distance on spaces of submanifolds and diffeomorphisms , Doc. Math. 10 (2005), 217–245.Google Scholar
Phong, D. H., Song, J., Sturm, J. and Weinkove, B., The Moser–Trudinger inequality on Kähler–Einstein manifolds , Amer. J. Math. 130 (2008), 1067–1085.Google Scholar
Ross, J. and Witt-Nyström, D., Harmonic discs of solutions to the complex homogeneous Monge–Ampère equation , Publ. Math. Inst. Hautes Études Sci. 122 (2015), 315–335.Google Scholar
Semmes, S., Complex Monge–Ampère and symplectic manifolds , Amer. J. Math. 114 (1992), 495–550.Google Scholar
Streets, J., The consistency and convergence of K-energy minimizing movements , Trans. Amer. Math. Soc. 368 (2016), 5075–5091.Google Scholar
Tian, G., Kähler–Einstein metrics with positive scalar curvature , Invent. Math. 130 (1997), 239–265.Google Scholar
Yau, S. T., On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation. I , Comm. Pure Appl. Math. 31 (1978), 339–411.Google Scholar