Hostname: page-component-6bf8c574d5-gr6zb Total loading time: 0 Render date: 2025-02-14T11:59:03.778Z Has data issue: false hasContentIssue false
  • English
  • Français

BIFURCATION PROPERTIES FOR A CLASS OF CHOQUARD EQUATION IN WHOLE ℝ3

Part of: Difference and functional equations Difference equations Partial differential equations

Published online by Cambridge University Press:  11 July 2019

CLAUDIANOR O. ALVES ,
ROMILDO N. DE LIMA  and
ALÂNNIO B. NÓBREGA
CLAUDIANOR O. ALVES
Affiliation:
Unidade Acadêmica de Matemática, Universidade Federal de Campina Grande, Campina Grande, PB, CEP: 58429-900, Brazil e-mails: coalves@mat.ufcg.edu.br, romildo@mat.ufcg.edu.br, alannio@mat.ufcg.edu.br
ROMILDO N. DE LIMA
Affiliation:
Unidade Acadêmica de Matemática, Universidade Federal de Campina Grande, Campina Grande, PB, CEP: 58429-900, Brazil e-mails: coalves@mat.ufcg.edu.br, romildo@mat.ufcg.edu.br, alannio@mat.ufcg.edu.br
ALÂNNIO B. NÓBREGA
Affiliation:
Unidade Acadêmica de Matemática, Universidade Federal de Campina Grande, Campina Grande, PB, CEP: 58429-900, Brazil e-mails: coalves@mat.ufcg.edu.br, romildo@mat.ufcg.edu.br, alannio@mat.ufcg.edu.br
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper concerns the study of some bifurcation properties for the following class of Choquard-type equations: (P)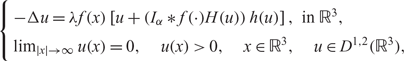

$$\left\{ {\begin{array}{*{20}{l}} { - \Delta u = \lambda f(x)\left[ {u + \left( {{I_\alpha }*f( \cdot )H(u)} \right)h(u)} \right],{\rm{ in }} \ {{\mathbb{R}}^3},}\\ {{{\lim }_{|x| \to \infty }}u(x) = 0,\quad u(x) > 0,\quad x \in {{\mathbb{R}}^3},\quad u \in {D^{1,2}}({{\mathbb{R}}^3}),} \end{array}} \right.$$
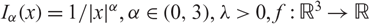where ${I_\alpha }(x) = 1/|x{|^\alpha },\,\alpha \in (0,3),\,\lambda > 0,\,f:{{\mathbb{R}}^3} \to {\mathbb{R}}$ is a positive continuous function and h : 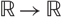${\mathbb{R}} \to {\mathbb{R}}$ is a bounded Hölder continuous function. The main tools used are Leray–Schauder degree theory and a global bifurcation result due to Rabinowitz.

MSC classification

Primary: 39A28: Bifurcation theory
Secondary: 35A16: Topological and monotonicity methods
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 62 , Issue 3 , September 2020 , pp. 531 - 543
Copyright
© Glasgow Mathematical Journal Trust 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Alves, C. O., Figueiredo, G. M. and Yang, M., Multiple semiclassical solutions for a nonlinear Choquard equation with magnetic field, Asymptot. Anal. 96(2), 135–159 (2016).CrossRefGoogle Scholar
Alves, C. O., Nóbrega, A. B. and Yang, M., Multi-bump solutions for Choquard equation with deepening potential well, Calc. Var. Partial Differ. Eq. 55(3), 48 (2016).10.1007/s00526-016-0984-9CrossRefGoogle Scholar
Alves, C. O., de Lima, R. N. and Souto, M. A. S., Existence of a solution for a non-local problem in ℝN via bifurcation theory, Proc. Edin. Math. Soc. 61, 825–845 (2018).CrossRefGoogle Scholar
Alves, C. O. and Souto, M. A. S., Existence of solutions for a class of elliptic equations in ℝN with vanishing potentials, J. Differ. Equ. 252, 5555–5568 (2012).CrossRefGoogle Scholar
Alves, C. O. and Yang, J., Existence and regularity of solutions for a Choquard equation with zero mass, To appear in Milan J. Math.Google Scholar
Efinger, H. J., On the theory of certain nonlinear Schrödinger equations with nonlocal interaction, Nuovo Cimento B 80(2), 260–278 (1984).CrossRefGoogle Scholar
Fröhlich, H., Theory of electrical breakdown in ionic crystal, Proc. R. Soc. Ser. A 160, 230–241 (1937).Google Scholar
Fröhlich, H., Electrons in lattice fields, Adv. Phys. 3(11) (1954).CrossRefGoogle Scholar
Genev, H. and Venkov, G., Soliton and blow-up solutions to the time-dependent, Discrete Contin. Dyn. Syst. Ser. S 5(5), 903–923 (2012).Google Scholar
Ghergu, M. and Taliaferro, S. D., Pointwise bounds and blow-up for Choquard–Pekar inequalities at an isolated singularity, J. Differ. Equ. 261(1), 189–217 (2016).CrossRefGoogle Scholar
Küpper, T., Zhang, Z. and Xia, H., Multiple positive solutions and bifurcation for an equation related to Choquard’s equation, Proc. Edin. Math. Soc. 46, 597–607 (2003).CrossRefGoogle Scholar
Lieb, E. H., Existence and uniqueness of the minimizing solution of Choquard nonlinear equation, Stud. Appl. Math. 57(2), 93–105 (1976/77).CrossRefGoogle Scholar
Lieb, E. and Loss, M., Analysis, Gradute Studies in Mathematics (AMS, Providence, Rhode Island, 2001).CrossRefGoogle Scholar
Ma, L. and Zhao, L., Classification of positive solitary solutions of the nonlinear Choquard equation, Arch. Ration. Mech. Anal. 195(2), 455–467 (2010).CrossRefGoogle Scholar
Mercuri, C., Moroz, V. and Van Schaftingen, J., Groundstates and radial solutions to nonlinear Schrodinger–Poisson–Slater equations at the critical frequency, Calc. Var. Partial Differ. Equ. 55, 146 (2016). https://doi.org/10.1007/s00526-016-1079-3CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J., Groundstates of nonlinear Choquard equations:existence, qualitative properties and decay asymptotics, J. Funct. Anal. 265, 153–184 (2013).CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J., Existence of groundstates for a class of nonlinear Choquard equations. Trans. Amer. Math. Soc. 367, 6557–6579 (2015).CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J., A guide to the Choquard equation, J. Fixed Point Theory Appl. 19, 773–813 (2017).CrossRefGoogle Scholar
Moroz, V. and Van Schaftingen, J., Groundstates of nonlinear Choquard equation: Hardy–Littlewood–Sobolev critical exponent, To appear in Commun. Contemp. Math. arXiv:1403.7414v1Google Scholar
Moroz, I. M., Penrose, R. and Tod, P., Spherically-symmetric solution of the Schrödinger-Newton equation, Classical Quantum Gravity 15, 2733–2742 (1998).10.1088/0264-9381/15/9/019CrossRefGoogle Scholar
Pekar, S., Untersuchung über die Elektronentheorie der Kristalle (Akademie Verlag, Berlin, 1954), p. 2.Google Scholar
Rabinowitz, P., Some global results for nonlinear eigenvalue problems, J. Funct. Anal. 7, 487–513 (1971).10.1016/0022-1236(71)90030-9CrossRefGoogle Scholar
Struwe, M., Variational methods: applications to nonlinear partial differential equations and Hamiltonian systems (Springer, Berlin, 1990).CrossRefGoogle Scholar
Stuart, C. A., Bifurcation for variational problems when the linearisation has no eigenvalues, J. Funct. Anal. 38(2), 169–187 (1980).CrossRefGoogle Scholar
Sun, X. and Zhang, Y., Multi-peak solution for nonlinear magnetic Choquard type equation, J. Math. Phys. 55(3), 031508 (2014).CrossRefGoogle Scholar
Yang, M. and Wei, Y., Existence and multiplicity of solutions for nonlinear Schrödinger equations with magnetic field and Hartree type nonlinearities, J. Math. Anal. Appl. 403(2), 680–694 (2013).CrossRefGoogle Scholar