Hostname: page-component-6bf8c574d5-26wn4 Total loading time: 0 Render date: 2025-02-14T12:03:14.772Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear global and asymptotic stability analysis of the flow past rectangular cylinders moving along a wall

Published online by Cambridge University Press:  29 June 2023

Alessandro Chiarini Open the ORCID record for Alessandro Chiarini [Opens in a new window]  and
Franco Auteri Open the ORCID record for Franco Auteri [Opens in a new window]
Alessandro Chiarini*
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156 Milano, Italy
Franco Auteri
Affiliation:
Dipartimento di Scienze e Tecnologie Aerospaziali, Politecnico di Milano, via La Masa 34, 20156 Milano, Italy
*
Email address for correspondence: alessandro.chiarini@polimi.it
Get access Rights & Permissions [Opens in a new window]

Abstract

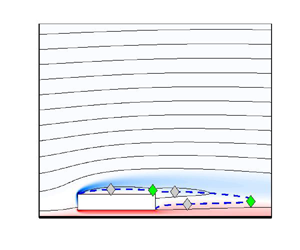
The primary instability of the steady two-dimensional flow past rectangular cylinders moving parallel to a solid wall is studied, as a function of the cylinder length-to-thickness aspect ratio ${A{\kern-4pt}R} =L/D$ and the dimensionless distance from the wall $g=G/D$. For all ${A{\kern-4pt}R}$, two kinds of primary instability are found: a Hopf bifurcation leading to an unsteady two-dimensional flow for $g \ge 0.5$, and a regular bifurcation leading to a steady three-dimensional flow for $g < 0.5$. The critical Reynolds number $Re_{c,2\text{-}D}$ of the Hopf bifurcation ($Re=U_\infty D/\nu$, where $U_\infty$ is the free stream velocity, $D$ the cylinder thickness and $\nu$ the kinematic viscosity) changes with the gap height and the aspect ratio. For ${A{\kern-4pt}R} \le 1$, $Re_{c,2\text{-}D}$ increases monotonically when the gap height is reduced. For ${A{\kern-4pt}R} >1$, $Re_{c,2\text{-}D}$ decreases when the gap is reduced until $g \approx 1.5$, and then it increases. The critical Reynolds number $Re_{c,3\text{-}D}$ of the three-dimensional regular bifurcation decreases monotonically for all ${A{\kern-4pt}R}$, when the gap height is reduced below $g < 0.5$. For small gaps, $g < 0.5$, the hyperbolic/elliptic/centrifugal character of the regular instability is investigated by means of a short-wavelength approximation considering pressureless inviscid modes. For elongated cylinders, ${A{\kern-4pt}R} > 3$, the closed streamline related to the maximum growth rate is located within the top recirculating region of the wake, and includes the flow region with maximum structural sensitivity; the asymptotic analysis is in very good agreement with the global stability analysis, assessing the inviscid character of the instability. For cylinders with $AR \leq 3$, however, the local analysis fails to predict the three-dimensional regular bifurcation.

JFM classification

Instability: Absolute/convective instability Wakes/Jets: Vortex streets
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 966 , 10 July 2023 , A22
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Present address: Complex Fluids and Flows Unit, Okinawa Institute of Science and Technology Graduate University, 1919-1 Tancha, Onna-son, Okinawa 904-0495, Japan.

References

Barkley, D., Gomes, M.G.M. & Henderson, R.D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.CrossRefGoogle Scholar
Barkley, D. & Henderson, R.D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.CrossRefGoogle Scholar
Bayly, B.J. 1988 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31 (1), 56–64.CrossRefGoogle Scholar
Bayly, B.J., Orszag, S.A. & Herbert, T. 1988 Instability mechanisms in shear-flow transition. Annu. Rev. Fluid Mech. 20 (1), 359–391.CrossRefGoogle Scholar
Bearman, P.W. & Zdravkovich, M.M. 1978 Flow around a circular cylinder near a plane boundary. J. Fluid Mech. 89 (1), 33–47.CrossRefGoogle Scholar
Bosch, G. & Rodi, W. 1996 Simulation of vortex shedding past a square cylinder near a wall. Intl J. Heat Fluid Flow 17 (3), 267–275.CrossRefGoogle Scholar
Chiarini, A., Quadrio, M. & Auteri, F. 2021 Linear stability of the steady flow past rectangular cylinders. J. Fluid Mech. 929, A36.CrossRefGoogle Scholar
Chiarini, A., Quadrio, M. & Auteri, F. 2022 a An almost subharmonic instability in the flow past rectangular cylinders. J. Fluid Mech. 950, A20.CrossRefGoogle Scholar
Chiarini, A., Quadrio, M. & Auteri, F. 2022 b A new scaling for the steady flow past two-dimensional bluff bodies. J. Fluid Mech. 936, R2.CrossRefGoogle Scholar
Chiarini, A., Quadrio, M. & Auteri, F. 2022 c On the frequency selection mechanism of the low-Re flow around rectangular cylinders. J. Fluid Mech. 933, A44.CrossRefGoogle Scholar
Chomaz, J.-M. 2005 Global instabilities in spatially developing flows: non-normality and nonlinearity. Annu. Rev. Fluid Mech. 37 (1), 357–392.CrossRefGoogle Scholar
Citro, V., Giannetti, F., Brandt, L. & Luchini, P. 2015 Linear three-dimensional global and asymptotic stability analysis of incompressible open cavity flow. J. Fluid Mech. 768, 113–140.CrossRefGoogle Scholar
Crow, S.C. 1970 Stability theory for a pair of trailing vortices. AIAA J. 8 (12), 2172–2179.CrossRefGoogle Scholar
Durão, D.F.G., Gouveia, P.S.T. & Pereira, J.C.F. 1991 Velocity characteristics of the flow around a square cross section cylinder placed near a channel wall. Exp. Fluids 11 (6), 341–350.CrossRefGoogle Scholar
Gallaire, F., Marquillie, M. & Ehrenstein, U. 2007 Three-dimensional transverse instabilities in detached boundary layers. J. Fluid Mech. 571, 221–233.CrossRefGoogle Scholar
Ghia, K.N., Osswald, G.A. & Ghia, U. 1989 Analysis of incompressible massively separated viscous flows using unsteady Navier–Stokes equations. Intl J. Numer. Meth. Fluids 9 (8), 1025–1050.CrossRefGoogle Scholar
Giannetti, F. 2015 WKBJ analysis in the periodic wake of a cylinder. Theor. Appl. Mech. Lett. 5 (3), 107–110.CrossRefGoogle Scholar
Giannetti, F. & Luchini, P. 2007 Structural sensitivity of the first instability of the cylinder wake. J. Fluid Mech. 581, 167–197.CrossRefGoogle Scholar
Godeferd, F.S., Cambon, C. & Leblanc, S. 2001 Zonal approach to centrifugal, elliptic and hyperbolic instabilities in Stuart vortices with external rotation. J. Fluid Mech. 449, 1–37.CrossRefGoogle Scholar
Görtler, H. 1954 On the three-dimensional instability of laminar boundary layers on concave walls.Google Scholar
Griffith, M.D., Thompson, M.C., Leweke, T., Hourigan, K. & Anderson, W.P. 2007 Wake behaviour and instability of flow through a partially blocked channel. J. Fluid Mech. 582, 319–340.CrossRefGoogle Scholar
Hammond, D.A. & Redekopp, L.G. 1997 Global dynamics of symmetric and asymmetric wakes. J. Fluid Mech. 331, 231–260.CrossRefGoogle Scholar
Hecht, F. 2012 New development in FreeFem++. J. Numer. Maths 20 (3-4), 251–266.Google Scholar
Houdroge, F.Y., Leweke, T., Hourigan, K. & Thompson, M.C. 2017 Two- and three-dimensional wake transitions of an impulsively started uniformly rolling circular cylinder. J. Fluid Mech. 826, 32–59.CrossRefGoogle Scholar
Hourigan, K., Thompson, M.C. & Tan, B.T. 2001 Self-sustained oscillations in flows around long blunt plates. J. Fluids Struct. 15 (3), 387–398.CrossRefGoogle Scholar
Huang, W.-X. & Sung, H.J. 2007 Vortex shedding from a circular cylinder near a moving wall. J. Fluids Struct. 23 (7), 1064–1076.CrossRefGoogle Scholar
Jackson, C.P. 1987 A finite-element study of the onset of vortex shedding in flow past variously shaped bodies. J. Fluid Mech. 182, 23–45.CrossRefGoogle Scholar
Jiang, H. & Cheng, L. 2018 Hydrodynamic characteristics of flow past a square cylinder at moderate Reynolds numbers. Phys. Fluids 30 (10), 104107.CrossRefGoogle Scholar
Kerswell, R.R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34 (1), 83–113.CrossRefGoogle Scholar
Landman, M.J. & Saffman, P.G. 1987 The three-dimensional instability of strained vortices in a viscous fluid. Phys. Fluids 30 (8), 2339–2342.CrossRefGoogle Scholar
Lehoucq, R.B., Sorensen, D.C. & Yang, C. 1998 ARPACK Users’ Guide: Solution of Large-scale Eigenvalue Problems with Implicitly Restarted Arnoldi Methods. SIAM.CrossRefGoogle Scholar
Lifschitz, A. & Hameiri, E. 1991 Local stability conditions in fluid dynamics. Phys. Fluids Fluid Dyn. 3 (11), 2644–2651.CrossRefGoogle Scholar
Luchini, P. & Bottaro, A. 2014 Adjoint equations in stability analysis. Annu. Rev. Fluid Mech. 46 (1), 493–517.CrossRefGoogle Scholar
Mahir, N. 2009 Three-dimensional flow around a square cylinder near a wall. Ocean Engng 36 (5), 357–367.CrossRefGoogle Scholar
Marquet, O., Sipp, D. & Jacquin, L. 2008 Sensitivity analysis and passive control of cylinder flow. J. Fluid Mech. 615, 221–252.CrossRefGoogle Scholar
Monkewitz, P.A. 1988 The absolute and convective nature of instability in two-dimensional wakes at low Reynolds numbers. Phys. Fluids 31 (5), 999–1006.CrossRefGoogle Scholar
Monkewitz, P.A., Huerre, P. & Chomaz, J.-M. 1993 Global linear stability analysis of weakly non-parallel shear flows. J. Fluid Mech. 251, 1–20.CrossRefGoogle Scholar
Monkewitz, P.A. & Nguyen, L.N. 1987 Absolute instability in the near-wake of two-dimensional bluff bodies. J. Fluids Struct. 1 (2), 165–184.CrossRefGoogle Scholar
Nakamura, Y. & Nakashima, M. 1986 Vortex excitation of prisms with elongated rectangular, H and $_vdash$ cross-sections. J. Fluid Mech. 163, 149–169.CrossRefGoogle Scholar
Nishino, T., Roberts, G.T. & Zhang, X. 2007 Vortex shedding from a circular cylinder near a moving ground. Phys. Fluids 19 (2), 025103.CrossRefGoogle Scholar
Noack, B.R. & Eckelmann, H. 1994 A global stability analysis of the steady and periodic cylinder wake. J. Fluid Mech. 270, 297–330.CrossRefGoogle Scholar
Park, D. & Yang, K.-S. 2016 Flow instabilities in the wake of a rounded square cylinder. J. Fluid Mech. 793, 915–932.CrossRefGoogle Scholar
Pralits, J.O., Giannetti, F. & Brandt, L. 2013 Three-dimensional instability of the flow around a rotating circular cylinder. J. Fluid Mech. 730, 5–18.CrossRefGoogle Scholar
Price, S.J., Sumner, D., Smith, J.G., Leong, K. & Païdoussis, M.P. 2002 Flow visualization around a circular cylinder near to a plane wall. J. Fluids Struct. 16 (2), 175–191.CrossRefGoogle Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard-von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.CrossRefGoogle Scholar
Rao, A., Radi, A., Leontini, J.S., Thompson, M.C., Sheridan, J. & Hourigan, K. 2015 a A review of rotating cylinder wake transitions. J. Fluids Struct. 53, 2–14.CrossRefGoogle Scholar
Rao, A., Thompson, M.C. & Hourigan, K. 2016 A universal three-dimensional instability of the wakes of two-dimensional bluff bodies. J. Fluid Mech. 792, 50–66.CrossRefGoogle Scholar
Rao, A., Thompson, M.C., Leweke, T. & Hourigan, K. 2013 The flow past a circular cylinder translating at different heights above a wall. J. Fluids Struct. 41, 9–21.CrossRefGoogle Scholar
Rao, A., Thompson, M.C., Leweke, T. & Hourigan, K. 2015 b Flow past a rotating cylinder translating at different gap heights along a wall. J. Fluids Struct. 57, 314–330.CrossRefGoogle Scholar
Robichaux, J., Balachandar, S. & Vanka, S.P. 1999 Three-dimensional Floquet instability of the wake of square cylinder. Phys. Fluids 11 (3), 560–578.CrossRefGoogle Scholar
Ryan, K., Thompson, M.C. & Hourigan, K. 2005 Three-dimensional transition in the wake of bluff elongated cylinders. J. Fluid Mech. 538, 1–29.CrossRefGoogle Scholar
Saad, Y 2011 Numerical Methods for Large Eigenvalue Problems. Society for Industrial and Applied Mathematics.CrossRefGoogle Scholar
Sipp, D. & Jacquin, L. 2000 Three-dimensional centrifugal-type instabilities of two-dimensional flows in rotating systems. Phys. Fluids 12 (7), 1740–1748.CrossRefGoogle Scholar
Sipp, D., Lauga, E. & Jacquin, L. 1999 Vortices in rotating systems: centrifugal, elliptic and hyperbolic type instabilities. Phys. Fluids 11 (12), 3716–3728.CrossRefGoogle Scholar
Stewart, B.E., Thompson, M.C., Leweke, T. & Hourigan, K. 2010 a Numerical and experimental studies of the rolling sphere wake. J. Fluid Mech. 643, 137–162.CrossRefGoogle Scholar
Stewart, B.E., Thompson, M.C., Leweke, T. & Hourigan, K. 2010 b The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.CrossRefGoogle Scholar
Theofilis, V. 2011 Global linear instability. Annu. Rev. Fluid Mech. 43 (1), 319–352.CrossRefGoogle Scholar
Thompson, M.C., Leweke, T. & Hourigan, K. 2021 Bluff bodies and wake–wall interactions. Annu. Rev. Fluid Mech. 53 (1), 347–376.CrossRefGoogle Scholar
Waleffe, F. 1990 On the three-dimensional instability of strained vortices. Phys. Fluids A 2 (1), 76–80.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.CrossRefGoogle Scholar
Williamson, C.H.K. 1996 b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28 (1), 477–539.CrossRefGoogle Scholar
Yoon, D.-H., Yang, K.-S. & Choi, C.-B. 2010 Flow past a square cylinder with an angle of incidence. Phys. Fluids 22 (4), 043603.CrossRefGoogle Scholar
Zdravkovich, M.M. 1997 Flow Around Circular Cylinders, Volume 1. Oxford University Press.Google Scholar